EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 615 (July 2018) A&A, 615 (2018) A176 Full HTML
Free Access
Issue
A&A
Volume 615, July 2018
Article Number A176
Number of page(s) 10
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201832741
Published online 07 August 2018

© ESO 2018

1 Introduction

Over the last few years, the formation of astronomical complex organic molecules (COMs) in the interstellar medium (ISM) has received considerable attention due to their potential prebiotic role. Understanding how the building blocks of biological molecules were formed in abiotic environments (being either the primitive Earth or the ISM) is in fact an extremely topical issue. In particular, amines (RNH2) might play a key role as intermediates in the formation of astrobiologically important molecules, such as amino acids (Holtom et al. 2005; Bossa et al. 2008; Lee et al. 2009; Kim & Kaiser 2011). Almost 200 molecules have been detected in space, thus implying that even in the harsh conditions of the ISM, a rich chemistry takes place. Focusing on planetary atmospheres, Titan has the most active one within the Solar System, from a chemical perspective. It has been shown that, starting from the simple parent molecules N2 and CH4, small N-containing species up to large macromolecules (with masses up to 3000 Dalton) are produced in the upper and most rarefied region of the atmosphere (Balucani 2012; Ali et al. 2015, and relevant references therein). Extraterrestrial gaseous species are mainly identified via observations of their rotational signatures, knowledge of which is derived from laboratory experiments that in turn can be effectively supported and extended by theoretical predictions (Barone et al. 2015b; Biczysko et al. 2017).

Propargylamine (HC ≡C–CH2–NH2) is a N-containing derivative of acetylene, which is structurally related to other astrophysically relevant species such as aminoacetonitrile (N ≡C–CH2–NH2; Belloche et al. 2008) and methylacetylene (CH3 C ≡CH; Snyder & Bull 1973) which have been detected in molecular clouds. The formation routes of propargylamine in the ISM have still to be investigated in detail; nonetheless, there are a number of reasons to regard this COM as a spectroscopic target of potential astrochemical interest.

It is nowadays accepted that reactions on dust-grain surface play a major role in building the chemical complexity in the ISM. Hydrogenation, in particular, is a very efficient process on grains due to the high mobility of H atoms on these surfaces at T < 20 K (Tielens & Hagen 1982; Tielens & Charnley 1997; Fuchs et al. 2009). This reaction tends to saturate multiple bonds of the simple molecules that are frozen onto dust-grain mantles during the cold pre-collapse phases of star formation. The resulting products are then released into gas phase at the proto-star stage, when the mantles are evaporated by the heating produced by the central source (Ceccarelli et al. 2001). Surface hydrogenation of iced CO is postulated to be the formation route of CH3 OH and other O-bearing COMs (e.g., Watanabe & Kouchi 2002; Bisschop et al. 2007; Garrod et al. 2007; Ioppolo et al. 2010). Similarly, a related series of H-addition reactions could take place on grain surfaces to generate the simplest member of the amine family, CH3 NH2, starting from the very abundant HCN species (e.g., Theulé et al. 2011), and a natural extension of this reasoning lead to infer that propargyl-imine and propargyl-amine could be obtained through 2H- and 4H- partial saturation of HC3 N, a carbon chain which proved to be ubiquitous in the ISM (Bizzocchi et al. 2017).

Two conformers (trans and gauche forms) can exist for propargylamine, but only the rotational spectrum of the most stable trans form (whose structure is shown in Fig. 1) has been detected by microwave spectroscopy, just as in the case of the isoelectronic aminoacetonitrile molecule.

Rotational lines of trans-propargylamine (Cs symmetry group) were first observed by Bolton et al. (1968). A subsequent study in the 8–40 GHz frequency range (Cervellati et al. 1977) allowed the determination of the rotational constants of nine isotopically substituted species, from which a reliable molecular structure could be calculated. Additionally, the dipole moment of trans-propargylamine was determined by Stark effect measurements (the values μa = 0.586 D and μb = 0.445 D being derived), but the very limited frequency range over which the rotational spectrum was studied prevented from obtaining very accurate values of the centrifugal distortion constants. Although Cervellati et al. (1977) were able to observe rotational lines of the 13C and 15N containing species in natural abundance, the search for transitions of the gauche conformer was unsuccessful. This non-detection, combined with a theoretical evaluation of the dipole moment components of the gauche form, made it possible to estimate a lower limit of approximately 2600 cal mol−1 (corresponding to 910 cm−1) for the energy difference between the gauche and the trans forms.

The low-resolution, gas-phase infrared spectrum of propargylamine (Hamada et al. 1984) led to the assignment of all the 21 fundamental bands of the trans-conformer (A′ symmetry from ν1 to ν13, A″ symmetry from ν14 to ν21). The recorded spectrum did not reveal any prominent absorption band assignable to the gauche form, for which a room temperatureabundance not larger than 3% was guessed, corresponding to an energy difference of at least 810 cm−1. Later, the ν8 and ν9 fundamental bands of propargylamine were studiedin the 900–1100 cm−1 region usinga 2 MHz-resolution electric resonance optothermal molecular beam spectrometer with a microwave sideband CO2 laser (Andrews et al. 1994). In both bands, tunneling doublets with 3:1 relative intensities were observed, indicative of an amine proton interchange (Andrews et al. 1998).

In this work, the pure rotational spectrum of propargylamine in its vibrational ground state has been thoroughly reinvestigated. We have measured 256 new rotational lines in the millimeter-wave (mm-wave) and submillimeter-wave (submm-wave) regions up to 554 GHz and a rotational quantum number J of 65, allowing for a very comprehensive centrifugal distortion analysis. In addition to high-frequency measurements, the centimeter-wave (cm-wave) spectrum of propargylamine in the vibrational ground state has been investigated using a Fabry–Perot-type resonator pulsed-jet Fourier Transform microwave (FTMW) spectrometer. Thirty-four hyperfine structure components belonging to low-J rotational transitions have been recorded in the 7–19 GHz range, and their analysis yielded accurate values of the 14N electric quadrupole coupling constants.

With the increased sensitivity and angular resolution of new observatories, with particular mention to the Atacama Large Millimeter/submillimeter Array (ALMA), the number of unidentified lines in the astronomical spectra has grown, especially in those of hot cores associated with star formation. Among the unidentified lines, a good fraction is thought to be due to rotational transitions in the low-lying excited vibrational states of a relatively small number of molecules. Also for this reason, the rotational spectra of propargylamine in excited vibrational states have been recorded and analyzed for the first time. Over 350 lines belonging to the three lowest excited states have been assigned in the 75−360 GHz frequency range, spanning J values from 7 to 42. From line intensity ratio measurements it was possible to approximately evaluate the vibrational energies of the observed states, which were found in partial disagreement with previous assignments (Hamada et al. 1984).

The spectroscopic characterization of propargylamine has been supported by a well-tested hybrid coupled-cluster/density functional theory (CC/DFT) protocol (Barone et al. 2013, 2014b, 2015a; Puzzarini et al. 2014).

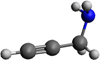thumbnail Fig. 1

Structure of trans-propargylamine. Blue atom is nitrogen, dark-gray are carbon, and light-gray are hydrogen.

2 Experimental and computational details

2.1 Experiment

The rotational spectrum of propargylamine was investigated using a source-modulation mm-/submm-wave spectrometer located in Bologna (Dipartimento di Chimica “Giacomo Ciamician”) and a Fabry–Perot-type resonator pulsed-jet FTMW spectrometer at the Gottfried-Wilhelm-Leibniz Universitätin Hannover (Institut für Physikalische Chemie and Elektrochemie). Commercial samples of propargylamine (Sigma Aldrich) were used for the measurements without further purification. The mm- and submm-wave lines were recorded in selected frequency regions between 75 and 555 GHz using the spectrometer already employed to record the spectra of other stable (Degli Esposti et al. 2017) and short-lived molecules (Degli Esposti et al. 2014; Bizzocchi et al. 2016) of astrophysical interest. Gunn-diode oscillators were used as main radiation sources to cover the fundamental frequency range 75−125 GHz, and higher frequencies were generated using passive harmonic multiplication. The oscillators were phase-locked through a suitable locking chain to a computer-controlled frequency synthesizer, which was referenced to an external rubidium frequency standard. The source was frequency modulated at 6 kHz and phase sensitive detection at 2f was employed, so that the second derivative of the actual spectrum profile was recorded. Schottky-barrier diodes and a liquid-helium-cooled InSb bolometer were used as detectors in the mm- and submm-wave regions, respectively. A 3.5-m-long free-space absorption cell filled with propargylamine vapor at pressures of 1.3−2.7 Pa was employed for the measurements. The spectrometer used for FTMW supersonic expansion measurements has been described in detail previously (Grabow & Stahl 1990; Grabow et al. 1996). The sample was prepared by injecting a few drops of propargylamine into a 5 liter steel cylinder that was then filled with Argon at a total pressure of 500 kPa. Given that propargylamine has a vapor pressure of 10.3 kPa at 300 K, the resulting gaseous mixture has a volume fraction of approximately 2%. The measurements were performed in the 7–19 GHz frequency interval, employing a stagnation pressure of 50–150 kPa with a nozzle repetition rate of 20 Hz.

2.2 Computations

The computational strategy relies on coupled-cluster (CC) calculations (at the CC singles and doubles augmented by a perturbative treatment of triple excitations level, CCSD(T); Raghavachari et al. 1989) of equilibrium geometries, electric properties, and quadratic force constants in a normal-mode representation (i.e., harmonic frequencies), also considering extrapolation to the complete basis set (CBS) limit and core-valence correlation (CV) contributions. These results are then complemented by density functional theory (DFT) evaluations of the anharmonic contributions (Barone et al. 2014a; Bloino et al. 2015, 2016) employing the double hybrid B2PLYP functional (Grimme 2006; Biczysko et al. 2010) including the D3BJ dispersion corrections (Grimme et al. 2010, 2011) in conjunction with the aug-cc-pVTZ basis set.

For the equilibrium structure determination, from which the equilibrium rotational constants are straightforwardly derived, a composite approach was used based on the additivity of relevant contributions at a gradient level (Heckert et al. 2005, 2006), as implemented in the CFOUR package1 Stanton et al. (2011). The three contributions taken into account are: the Hartree–Fock self-consistent-field (HF-SCF) energy extrapolated to the complete basis-set (CBS) limit, the valence correlation energy at the CCSD(T) (Raghavachari et al. 1989), extrapolated to the CBS limit as well, and the core-valence (CV) correlation correction. The correlation-consistent cc-p(C)VnZ (n = T,Q,5) basis sets (Dunning Jr. 1989; Woon & Dunning Jr. 1995) were employed. The overall best-estimated geometry, accounting for the extrapolation to the CBS limit and CV correction, is shortly denoted in the following as CCSD(T)/CBS+CV. A similar composite scheme was also employed for obtaining the best-estimated equilibrium values of the electric dipole moment components. The only difference lies in the inclusion of the contribution of diffuse functions in the basis set.

The best-estimated harmonic force field was evaluated by means of the following composite scheme (Barone et al. 2013): 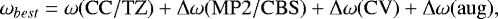ωbest=ω(CC/TZ)+Δω(MP2/CBS)+Δω(CV)+Δω(aug),\begin{equation*}\omega_{best} = \omega(\mathrm{CC/TZ}) &#x002B; {\rm{\Delta}}\omega(\mathrm{MP2/CBS}) &#x002B; {\rm{\Delta}}\omega(\mathrm{CV}) &#x002B; {\rm{\Delta}}\omega(\mathrm{aug}) ,\end{equation*}(1)

where the harmonic frequencies at the CCSD(T)/cc-pVTZ (ω(CC∕TZ)) level are corrected to account for the extrapolation to the CBS limit (Δω(MP2∕CBS)), core-valence correction (Δω(CV)), and contribution of diffuse functions in the basis set (Δω(aug)) using second-order Møller–Plesset perturbation theory (MP2; Møller & Plesset 1934). Harmonic force constants were obtained at the corresponding optimized geometry using analytic second derivatives, as implemented in CFOUR (Stanton et al. 2011; Gauss & Stanton 1997). As a byproduct, best-estimated quartic centrifugal-distortion and nitrogen-quadrupole coupling constants were obtained from the best-estimated harmonic force field and the corresponding geometry optimizations, respectively.

Anharmonic contributions to vibrational energies and spectroscopic constants were calculated at the second order of the vibrational perturbation theory (VPT2; Nielsen 1951; Krohn et al. 1974. This includes vibrational corrections to the rotational and nitrogen-quadrupole coupling constants and to the electric dipole moment, as well as calculation of sextic centrifugal distortion constants. For the vibrational states of interest in the present study, no resonances related to the VPT2 formalism were found, and therefore the standard equations were used.

The cubic and semi-diagonal quartic force field needed for the VPT2 calculations was obtained from numerical differentiation of displaced analytic harmonic force constants along the normal coordinates computed at the B2PLYP-D3BJ/aug-cc-pVTZ level. The hybrid force field was obtained in a normal-coordinate representation by adding the cubic and quartic B2PLYP-D3BJ/aug-cc-pVTZ force constants to the best-estimated harmonic frequencies. When the normal modes computed at different levels of theory are very similar, as in the present case, DFT cubic and quartic force constants can be used without any transformation. The DFT and VPT2 computations were done with the Gaussian 16 suite of quantum chemical programs (Frisch et al. 2016).

Although the aim of this study is to provide accurate rest frequencies for the most stable conformer of propargylamine, that is, the trans form, a computational investigation of the molecular structure and dipole moment for the gauche conformer was also carried out at the B2PLYP-D3BJ/aug-cc-pVTZ level, mainly to check the reliability of the conclusions drawn by Cervellati et al. (1977) about the energy of the undetected gauche form. The following values of the dipole moment components of the two isomers were obtained at the same level of theory: μa = 0.5215 D and μb = 0.4351 D for the trans form, and μa = 0.7334 D, μb = 0.7265 D, and μc = 1.0480 D for the gauche form. Using the newly evaluated theoretical values of the μa components, a lower limit of approximately 3500 cal mol−1 (1220 cm−1) can be estimated for the energy difference between the two conformers.

3 Observed spectra and analysis

3.1 Ground state

Trans-propargylamine is a near-prolate asymmetric-top molecule (κ = −0.966) of Cs symmetry, with non-zero dipole moment components along the a and b principal axes that define the symmetry plane of the molecule (Cervellati et al. 1977). Regarding the vibrational ground state, initial assignments in the mm-wave region were guided by the spectroscopic constants available from the previous cm-wave investigation (Cervellati et al. 1977). aR-branch transitions and additional b-type lines were first recorded in the 100 GHz region. New predictions, based on improved rotational and centrifugal distortion constants, were then used to guide measurements in the submm-wave region, at frequencies up to 554 GHz. In this way our measurements probed rotational energy levels in the J interval from 5 to 65 and the Ka interval from 0 to 26. Small splittings due the 14N nuclear spin were observed for a few aR-type transitions with high Ka values measured around 100 GHz.

To improve the precision of the hyperfine-structure parameters, complementary measurements were performed also in the 7−19 GHz range on low-J lines, which were observed in supersonic expansion and with fully resolved 14N-nuclear quadrupole hyperfine structure. Seven rotational transitions were recorded at sub-Doppler resolution by FTMW spectroscopy: they include the a-type J = 1 ← 0 and J = 2 ← 1 transitions, plus three low-lying b-type transitions with Ka = 0, 1, so that a total number of 34 hyperfine-component frequencies could be measured with high precision.

The complete dataset for the ground state was therefore assembled by combining the mm- and submm-wave transition frequencies from the present work, with previous hyperfine-unresolved cm-wave lines (Cervellati et al. 1977), and with newly measured hyperfine resolved frequencies for low-J transitions. Different weights 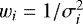wi=1/σi2$w_i = 1/\sigma_i^2$ were used for the various datasets in order to take into account differences in measurement precision: σi values in the range from 10 to 100 kHz were assigned to the newly measured mm- and submm-wave transitions, depending on the signal-to-noise ratio (S/N) and the width of each line, accidental overlaps of lines, as well as the frequency uncertainty produced by unresolved 14N quadrupole components. For the present FTMW measurements, we adopted a conservative value of σi = 5 kHz to take into account the asymmetric line broadening produced by the blending of hyperfine components due to the nuclear spins of the five hydrogen atoms. The previous Stark-modulation measurements (Cervellati et al. 1977) were given with an average uncertainty of σi = 85 kHz.

The resulting dataset was analyzed using Pickett’s SPFIT program (Pickett 1991), adopting Watson’s S-reduced Hamiltonian in its Ir representation (Watson 1977). The standard coupling scheme F = J + I, between the rotational angular momentum J and the 14N-nuclear spin I, was used to analyze the observed hyperfine-structure components.

A large set of centrifugal distortion parameters was fitted for the vibrational ground state; in detail, all quartic and sextic centrifugal-distortion constants could be derived, as well as a few octic distortion terms. Likewise, the diagonal elements of the nuclear electric quadrupole tensor in the principal axis system could be precisely determined. The results are reported in Table 1 together with the corresponding theoretical results. We note that the computed rotational and quartic centrifugal-distortion constants agree well with their experimental counterparts, with deviations below 0.3% and ≃ 5%, respectively. For sextic centrifugal terms, larger discrepancies, that is, on the order of 15%−20%, were expected, but still the accuracy was sufficient for a satisfactory prediction of the experiment. These findings are consistent with the literature on this topic (Puzzarini et al. 2008; Puzzarini 2013). A good agreement can also be noted for nitrogen-quadrupole coupling constants and dipole moment components. In Table 1, the ground-state rotational and centrifugal distortion constants determined for aminoacetonitrile (Motoki et al. 2013) are also reported for comparison. As already stated in the Introduction, propargylamine is structurally very similar to aminoacetonitrile, and similar rotational parameters are therefore expected. This is confirmed by an inspection of Table 1.

thumbnail Fig. 2

Portion of the J = 11 ← 10, a-type band of propargylamine in the v13 = 1 state. Splittings caused by electric quadrupole coupling are observable for Ka = 7, 8, and 9. The asymmetry doublet of the Ka = 4 transition is also visible.

3.2 Excited states

Rotational transitions belonging to three low-lying excited vibrational states were also observed and analyzed. The three lowestvibrational modes were assigned by IR spectroscopy (Hamada et al. 1984) in the following way: ν13 at 230 cm−1 (A′ symmetry, in-plane C ≡C–C linear bending), ν21 at 334 cm−1 (A″ symmetry, –NH2 torsion), and ν20 at 339 cm−1 (A″ symmetry, out-of-plane C ≡C–C linear bending). At room temperature, all these states are sufficiently populated to ensure the detection of the respective rotational spectra. We started the search for the excited-state rotational lines in the 75–110 GHz frequency range. Near each aR branch of the ground state (J from 8 to 11) we were able to identify three different sequences of lines with the same Ka structure, but with reduced intensities, as expected for vibrational satellites produced by low-lying vibrational states. An example is provided in Fig. 2, showing the compact Ka sequence of the central part of the J = 11 ← 10 a-type band of the υ13 = 1 state. Thesecharacteristic sequences of lines, always observed at frequencies higher than those of the ground state, were the fingerprints used to identify the various excited states.

Intensity ratio measurements provided approximate values of the excited-state vibrational energies, which were 185, 233, and 327 cm−1, respectively, not fully consistent with the old IR data. The measurements for the three excited states were then extended up to 360 GHz, including both a- and b-type transitions. The rotational lines belonging to the state of highest energy (v20= 1) could be very well fitted using the standard semi-rigid Hamiltonian, with all sextic centrifugal-distortion constants fixed to the ground-state values. The results are listed in Table 2, together with the rotational constants predicted by quantum-chemical calculations. Conversely, this procedure gave unsatisfactory results for the two states of lower energy. Indeed, large deviations, opposite in sign, were observed for aR lines with Ka > J∕2. Moreover, the fittings produced strongly diverging values of the quartic centrifugal-distortion constants DK and d2. This was a clear indication of the existence of some rovibrational interaction between the two states of lower energy, as it was observed foraminoacetonitrile (Degli Esposti et al. 2017).

Since trans-propargylamine is a non-planar molecule of Cs symmetry (the c axis being perpendicular to the symmetry plane) its vibrations must belong to the A′ or A″ irreducible representations. Two fundamental levels of the same symmetry are connected by the c-axis term included in the H21 Coriolis operator, while two states of different symmetry can be coupled by a- and b-axis Coriolis operators (Papoušek & Aliev 1982).

As a matter of fact, the quality of the fits could be greatly improved by assuming the existence of an a-type Coriolis interaction, which demonstrates that the two lowest vibrational states of trans-propargylamine must be of different symmetry. The two states were considered coupled through the off-diagonal Ga Pz Coriolis operator, and the transition frequencies of the two states were simultaneously analyzed by also fitting the Coriolis coupling coefficient Ga and the vibrational energy difference between the two states. The standard deviation of the fit then decreased from 2 MHz to 50 kHz, even if small systematic residuals still remained, indicating the need for improvement of the coupling model. No significant effect was obtained by considering either a b-axis Coriolis interaction or higher-orderterms deriving from H22 (Papoušek & Aliev 1982), while a further improvement of the fit was achieved by taking into account small dependencies of Ga on the rotational quantum numbers J and K.

The best results were obtained adopting an off-diagonal Coriolis operator of the form 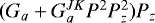(Ga+GaJKP2Pz2)Pz$(G_a &#x002B; G_a^{JK}{P}^2{P}_z^2){P}_z$ and fitting the 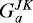GaJK$G_a^{JK}$ parameter: this led to a standard deviation of the fit smaller than 20 kHz. It must be noted that the same improvement could be alternatively obtained by fitting the sextic distortion constants HKJ of both resonant states, but in this case two very unreliable values, differing by more than a factor of six, are derived. 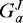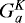On the contrary, no significant improvement was obtained by releasing the GaJ$G_a^J$ and GaK$G_a^K$ coefficients, which were poorly determined and were therefore held fixed. 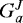GaJ$G_a^J$ was constrained to the fairly accurate value which was determined for aminoacetonitrile (Degli Esposti et al. 2017), while 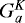GaK$G_a^K$ was simply fixed to zero. The results of the least-squares fits for these two interacting states are presented in Table 2, where the rotational constants obtained by quantum-chemical calculations are also reported. No important anomaly appears in the values of the centrifugal distortion constants determined for the two resonant states, but we note that the fitted DK constants still differ considerably, in a symmetrical way, from the ground-state value (ca. ± 13%). This could indicate an incomplete correction of resonance effects (totally uncorrected values were DK = 434 kHz for ν13 and DK = 1307 kHz for ν21). DK values much closer to that of the ground state can be obtained by fixing the centrifugal coefficient 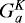GaK$G_a^K$ to − 2.0 MHz, even if a negligible increasing (≈ 1.5 kHz) of the standard deviation of the fit occurs. At the same time, Ga changes from 18734 to 19163 MHz. Unfortunately, it is not convenient to simultaneously fit the two DK constants and the 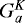GaK$G_a^K$ coefficient, because correlations are very high, so that 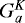GaK$G_a^K$ assumes a small value with a large uncertainty (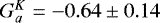GaK=−0.64±0.14$G_a^K = -0.64\pm 0.14$ MHz) and the DK constants converge again to values which are fairly different (± 9.4%) from that of the ground state.

Analysis of the theoretical vibrational wavenumbers obtained from VPT2 computations with the hybrid CC/DFT force field confirms the experimental results. The fundamental bands predicted at 193, 213, and 322 cm−1 agree well with the previously mentioned excited-state vibrational energies derived by intensity ratio measurements, thus allowing the assignment of the lowest energy level to the in-plane C ≡C–C linear bending of A′ symmetry (ν13) and of the next one to the –NH2 torsion of A″ symmetry (ν21). Furthermore, the computed energy difference between the A′ and A″ states (20 cm−1) fully justifies a significant a-type Coriolis resonance between the two lowest vibrational levels. The third, unperturbed band at 327 cm−1 is assigned to the out-of-plane C ≡C–C linear bending of A″ symmetry (ν20).

Inspection of Table 2 shows that the changes in the rotational constants caused by the excitation of the ν20 vibrational mode (i.e., the contribution of the α20 vibration–rotation interaction constants) are well predicted by ab initio calculations. From Table 2, it is apparent that this is also true for the B and C rotational constants of the ν13 and ν21 modes, but not for the A constants of both states. This can be explained by considering that the a-type Coriolis resonance existing between these two states produces very different values of the A α13 and A α21 vibration–rotation interaction constants depending on the way it is treated. In the experimental A rotational constants, the resonant term, which is inversely proportional to the small vibrational energy difference ν21 − ν13, is removed from the Aα13 and Aα21 vibration–rotation interaction constants because the Coriolis coupling is treated variationally. On the contrary, the theoretical calculation makes use of the standard second-order perturbation theory of vibro-rotational interactions (Papoušek & Aliev 1982), so that a large resonant term of approximately 400 MHz is included (with opposite signs) in the computed values of the A rotational constants of the two interacting states.

The fitted value of the main Coriolis coupling coefficient is Ga = 18734 ± 5 MHz, which can be compared with the one derived from computations. The Ga coefficient coupling the v13 = 1 and v21 = 1 fundamental levels has the following theoretical expression (Papoušek & Aliev 1982): 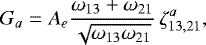Ga=Aeω13+ω21ω13ω21 ζ13,21a,\begin{align*} G_a = A_e\frac{\omega_{13}&#x002B;\omega_{21}}{\sqrt{\omega_{13}\omega_{21}}}\,\zeta^a_{13,21} ,\end{align*}(2)

where Ae is the equilibrium value of the rotational constant A, ω13, and ω21 are the harmonic frequencies of the interacting states, and 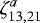ζ13,21a$\zeta^a_{13,21}$ is the corresponding Coriolis coupling constant. Using the best-estimated computed values, namely the CCSD(T)/CBS+CV equilibrium rotational constant (Ae = 29767.78 MHz), the harmonic wavenumbers as obtained from Eq. (1) (ω13 = 192.78 cm−1, ω21 = 226.09 cm−1), and 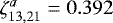ζ13,21a=0.392$\zeta^a_{13,21} = 0.392$ from a composite scheme analogous to Eq. (1), a value of 23412.1 MHz was obtained, which compares qualitatively well to the experimental datum.

The IR spectra of propargylamine (Hamada et al. 1984) and aminoacetonitrile (Bak et al. 1975) are quite similar below 500 cm−1. Three fundamental bands are in that range: two bendings of A′ and A″ symmetries, respectively, and the NH2 torsion. Table 3 shows the comparison between selected spectroscopic constants determined for the three lowest vibrationally excited states of trans-propargylamine (present work) and trans-aminoacetonitrile (Degli Esposti et al. 2017). Vibration–rotation interaction constants (α), quartic centrifugal distortion constants, and parameters related to the Coriolis resonance between the two lowest excited states of each molecule are included in the table. As expected, the vibration–rotation interaction constants and the quartic centrifugal distortion constants exhibit rather parallel trends upon vibrational excitation. The energy separation between the two resonant states is smaller for propargylamine, while the corresponding Ga value is greater, so that the perturbation effects produced by the Coriolis resonance are more marked in the rotational spectra of propargylamine than in those of aminoacetonitrile.

The complete list of the analyzed rotational transitions is provided at the CDS. An excerpt is reported in Table 4 for guidance.

Table 1

Ground-state spectroscopic constants of trans-propargylamine (present work) compared with those of trans-aminoacetonitrile (Motoki et al. 2013).

Table 2

Spectroscopic constants determined for the v13 = 1 and v21 = 1 resonant states and for the v20 = 1 unperturbed state of trans-propargylamine.

Table 3

Comparison between selected spectroscopic constants of the three lowest vibrationally excited states of trans-propargylamine and trans-aminoacetonitrile.

4 Astrophysical implications

The presence of COMs in the harsh conditions of the ISM has been known for decades (see e.g., Herbst & van Dishoeck 2009, and references therein). Earlier detections of organic molecules have been restricted to massive star formation regions (e.g., Rubin et al. 1971) but recently they have also been revealed in smaller objects (low-mass protostars, Cazaux et al. 2003), which are considered to be the progenitors of Solar-like planetary systems. Typically, COMs thrive in warm gases (T > 100 K). The large majority of them has been identified toward the Galactic center, in SgrB2 (e.g., Belloche et al. 2013, 2016), but a number of detections in hot-corinos (e.g., van Dishoeck et al. 1995) and in the shocked regions generated by protostar ouflows (Codella et al. 2015; Lefloch et al. 2017) have also been reported. At these temperatures, COMs typically have large partition functions thus showing highly crowded rotational spectra. As a result, these individual lines might be weak and therefore hidden in the “line forest” due to the so-called “weeds” or even contributing to it.

In many cases, this line forest consists of rotational lines not only belonging to the vibrational ground state, but also to low-lying vibrational states, which might be significantly populated. Furthermore, lines of different species overlap and blend together thus bringing sensitive spectral observations close to the confusion limit. Ideally, a firm analysis of an unbiased survey would require an accurate modeling of all known molecules, in order to point out blended features and to prevent misassignments.

To help assignment of propargylamine features in unbiased spectral surveys, we provide a list of rest frequencies and transition moments for lines up to 230 GHz. Both transitions belonging to the ground state and to the low-lying vibrational states v20 = 1, v13 = 1, and v21 = 1 are included. To this purpose, the spectroscopic constants of Tables 1 and 2 are used, also taking into account the Coriolis coupling between the v13 = 1 and v21 = 1 states.

For each line, the Einstein spontaneous emission A coefficient can be computed using the formula: 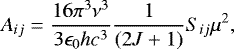Aij=16π3ν33ϵ0hc31(2J+1)Sijμ2,\begin{equation*}A_{ij} = \frac{16\pi^3 \nu^3}{3\epsilon_0 hc^3} \frac{1}{(2J &#x002B; 1)}S_{ij}\mu^2, \end{equation*}(3)

where all quantities are expressed in SI units and the line strengths Sij μ2 are obtained projecting the squared rotation matrix onto the basis set that diagonalizes the rotational Hamiltonian (Gordy & Cook 1984). The spectral calculations were performed in the 25 ≤ ν ≤ 250 GHz frequency interval selecting lines with Eu∕k < 500 K and Einstein’s A > 1 × 10−8 s. A further filter based on the prediction uncertainty was applied in order to select all the lines for which 1σ < 0.050 MHz, corresponding to 0.03 km s−1 at 500 GHz.The procedure yielded a sample of 3833, 769, 732, and 83 lines for the ground, v21 = 1, v13 = 1, and v20 = 1 states, respectively. Generally speaking, the predicted frequency uncertainties are model-dependent, that is, additional Hamiltonianterms, which are indeterminable from a given set of experimental data, can cause their increase. However, the spectroscopic constants used in the calculation described above have been determined from measurements extending up to 555 GHz, wethus expect that the precision of the resulting rest frequencies is reliably estimated.

At the typical temperature of a hot molecular core (e.g., SgrB2, T ~ 200 K, Belloche et al. 2013), propargylamine produces a crowded emission spectrum including many features belonging to some low-lying vibrational excited states. This is illustrated in Fig. 3, where the stick spectra of the ground, v20 = 1, v13 = 1, and v21 = 1 states are plotted in the 66–190 GHz frequency range. This interval matches the frequency span of the EMIR E090 and EMIR150 receivers installed at the IRAM 30m telescope, and the ALMA bands from 2 to 5. The lower panel expands the 84–116 GHz region covered by ALMA band 3, that is the band used in the EMoCA survey of SgrB2(N) performed during ALMA Cycle 0 and Cycle 1 (Belloche et al. 2016). The fact that several lines corresponding to the excited vibrational states show non-negligible intensity indicates that propargylamine might increase the confusion limit.

Table 4

Assignments, measured line positions, and least-squares residuals for the analysed transitions of propargylamine.

thumbnail Fig. 3

Upper panel: stick spectra of ground, v20 = 1, v13 = 1, and v21= 1 states in the 66–190 GHz frequency range. Lower panel: expansion of the 84–116 GHz region. Intensities are computed at 200 K.

5 Conclusions

This paper presents the results of a comprehensive investigation of the rotational spectrum of propargylamine extending well into the submm-wave region. The rotational spectrum of the vibrational ground state has been studied over a large frequency range, leading to greatly improved spectroscopic constants with respect to those available from earlier cm-wave measurements (Cervellati et al. 1977). The complete set of sextic centrifugal-distortion constants has been accurately determined for the first time, together with a few octic terms. Additionally, pulsed-jet FTMW measurements made it possible to perform an accurate analysis of the 14N-quadrupole hyperfine structure.

The rotational spectra of the three lowest vibrational excited states have also been identified for the first time. Their energies have been approximately evaluated by means of intensity ratio measurements, which provided values not completely consistent with the vibrational bands assigned in Hamada et al. (1984). Theoretical calculations of vibrational energies agree much better with the newly estimated values (i.e., a fundamental level exists just below 200 cm−1) but there are not two nearly degenerate fundamental vibrations just above 300 cm−1.

Unlike the findings of Andrews et al. (1994) from the 10 μm infrared spectrum, no tunneling doublets, indicative of amine proton interchange, were observed either in the FTMW ground-state spectrum or in the excited states spectra studied in this work. However, we note that in rotational studies, information about the tunnelling effect must be inferred from minor differences between the effective rotational constants of the doublet states. These differences are typically small even when the tunnelling energy splitting is sizable.

Propargylamine is structurally similar to well-known interstellar species containing the acetylenic group (e.g., CH3C ≡CH, HC ≡C-CN, and HC ≡C–CNH+) or the amino group (CH3NH2 and NC–CH2–NH2). Propargylamine itself can therefore be considered a molecule of potential astrochemical interest. The sets of spectroscopic constants obtained in this study allow for very accurate predictions of the rotational frequencies of propargylamine in its vibrational ground state and even of the weaker rotational features due to the low-lying vibrational states, thus offering a valuable support for a targeted search for this molecule in the ISM.

Acknowledgements

This work was supported by Italian MIUR (PRIN 2012 “STAR: Spectroscopic and computational Techniques for Astrophysical and atmospheric Research”; PRIN 2015 “STARS in the CAOS (Simulation Tools for Astrochemical Reactivity and Spectroscopy in the Cyberinfrastructure for Astrochemical Organic Species)”), by the University of Bologna (RFO funds), the Deutsche Forschungsgemeinschaft (DFG), the Land Niedersachsen, and in Shanghai by the National Natural Science Foundation of China (Grant No. 91641128). The SMART@SNS Laboratory (http://smart.sns.it) is gratefully acknowledged for the use of computer resources. The support of the COST CMTS-Actions CM1405 (MOLIM: MOLecules In Motion) and CM1401 (Our Astro-Chemical History) is acknowledged.

References

  1. Ali, A., Sittler Jr., E. C., Chornay, D., Rowe, B. R., & Puzzarini, C. 2015, Planet Space Sci., 109–110, 46 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrews, A. M., Fraser, G. T., & Pate, B. H. 1994, J. Phys. Chem., 98, 9979 [CrossRef] [Google Scholar]
  3. Andrews, A. M., Fraser, G. T., & Pate, B. H. 1998, J. Chem. Phys., 109, 4290 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bak, B., Hansen, E. L., Nicolaisen, F. M., & Nielsen, O. F. 1975, Can. J. Phys., 53, 2183 [NASA ADS] [CrossRef] [Google Scholar]
  5. Balucani, N. 2012, Chem. Soc. Rev., 41, 5473 [CrossRef] [Google Scholar]
  6. Barone, V., Biczysko, M., Bloino, J., & Puzzarini, C. 2013, Phys. Chem. Chem. Phys., 15, 10094 [CrossRef] [PubMed] [Google Scholar]
  7. Barone, V., Biczysko, M., & Bloino, J. 2014a, Phys. Chem. Chem. Phys., 16, 1759 [CrossRef] [Google Scholar]
  8. Barone, V., Biczysko, M., Bloino, J., & Puzzarini, C. 2014b, J. Chem. Phys., 141, 034107 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barone, V., Biczysko, M., Bloino, J., et al. 2015a, J. Chem. Theory Comput., 11, 4342 [Google Scholar]
  10. Barone, V., Biczysko, M., & Puzzarini, C. 2015b, Acc. Chem. Res., 48, 1413 [CrossRef] [PubMed] [Google Scholar]
  11. Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Belloche, A., Müller, H. S., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Biczysko, M., Panek, P., Scalmani, G., Bloino, J., & Barone, V. 2010, J. Chem. Theory Comput., 6, 2115 [CrossRef] [PubMed] [Google Scholar]
  15. Biczysko, M., Bloino, J., & Puzzarini, C. 2018, WIREs Comput. Mol. Sci., 8, e1349 [Google Scholar]
  16. Bisschop, S. E., Fuchs, G. W., Van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 474, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Bizzocchi, L., Dore, L., Degli Esposti, C., & Tamassia, F. 2016, ApJ, 820, L26 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bizzocchi, L., Tamassia, F., Laas, J., et al. 2017, ApJS, 233, 11 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bloino, J., Biczysko, M., & Barone, V. 2015, J. Phys. Chem. A, 119, 11862 [CrossRef] [PubMed] [Google Scholar]
  20. Bloino, J., Baiardi, A., & Biczysko, M. 2016, Int. J. Quantum Chem., 116, 1543 [CrossRef] [Google Scholar]
  21. Bolton, K., Owen, N. L., & Sheridan, J. 1968, Nature, 217, 164 [NASA ADS] [CrossRef] [Google Scholar]
  22. Bossa, J.-B., Borget, F., Duvernay, F., Theulé, P., & Chiavassa, T. 2008, J. Phys. Chem. A, 112, 5113 [CrossRef] [PubMed] [Google Scholar]
  23. Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ceccarelli, C., Loinard, L., Castets, A., et al. 2001, A&A, 372, 998 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cervellati, R., Caminati, W., Degli Esposti, C., & Mirri, A. M. 1977, J. Mol. Spectr., 66, 389 [NASA ADS] [CrossRef] [Google Scholar]
  26. Codella, C., Fontani, F., Ceccarelli, C., et al. 2015, MNRAS, 449, L11 [NASA ADS] [CrossRef] [Google Scholar]
  27. Degli Esposti, C., Dore, L., & Bizzocchi, L. 2014, A&A, 565, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Degli Esposti, C., Dore, L., Melosso, M., et al. 2017, ApJS, 230, 26 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dunning Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  30. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT [Google Scholar]
  31. Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Gauss, J., & Stanton, J. F. 1997, Chem. Phys. Lett., 276, 70 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gordy, W., & Cook, R. L. 1984, Microwave Molecular Spectra, 3rd edn. (New York: Wiley) [Google Scholar]
  35. Grabow, J.-U., & Stahl, W. 1990, Z. Naturforsch., 45a, 1043 [NASA ADS] [CrossRef] [Google Scholar]
  36. Grabow, J.-U., Stahl, W., & Dreizler, H. 1996, Rev. Sci. Instrum., 67, 4072 [NASA ADS] [CrossRef] [Google Scholar]
  37. Grimme, S. 2006, J. Chem. Phys., 124, 034108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  38. Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  39. Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comput. Chem., 32, 1456 [Google Scholar]
  40. Hamada, Y., Tsuboi, M., Nakata, M., & Tasumi, M. 1984, J. Mol. Spectr., 107, 269 [Google Scholar]
  41. Heckert, M., Kállay, M., & Gauss, J. 2005, Mol. Phys., 103, 2109 [NASA ADS] [CrossRef] [Google Scholar]
  42. Heckert, M., Kállay, M., Tew, D. P., Klopper, W., & Gauss, J. 2006, J. Chem. Phys., 125, 044108 [NASA ADS] [CrossRef] [Google Scholar]
  43. Herbst, E., & van Dishoeck, E. F. 2009, Annu. Rev. Astron. Astrophys., 47, 427 [Google Scholar]
  44. Holtom, P. D., Bennett, C. J., Osamura, Y., Mason, N. J., & Kaiser, R. I. 2005, ApJS, 626, 940 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ioppolo, S., Cuppen, H. M., Van Dishoeck, E. F., & Linnartz, H. 2010, MNRAS, 410, 1089 [Google Scholar]
  46. Kim, Y. S., & Kaiser, R. I. 2011, ApJ, 729, 68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Krohn, B., Ermler, W., & Kern, C. 1974, J. Chem. Phys., 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lee, C.-W., Kim, J.-K., Moon, E.-S., Minh, Y. C., & Kang, H. 2009, ApJ, 697, 428 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lefloch, B., Ceccarelli, C., Codella, C., et al. 2017, MNRAS, 469, L73 [NASA ADS] [CrossRef] [Google Scholar]
  50. Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [NASA ADS] [CrossRef] [Google Scholar]
  51. Motoki, Y., Tsunoda, Y., Ozeki, H., & Kobayashi, K. 2013, ApJS, 209, 23 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nielsen, H. H. 1951, Rev. Mod. Phys., 23, 90 [NASA ADS] [CrossRef] [Google Scholar]
  53. Papoušek, D., & Aliev, M. R. 1982, Molecular Vibrational-Rotational Spectra (Elsevier Science Ltd) [Google Scholar]
  54. Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
  55. Puzzarini, C. 2013, Phys. Chem. Chem. Phys., 15, 6595 [CrossRef] [PubMed] [Google Scholar]
  56. Puzzarini, C., Heckert, J., & Gauss, J. 2008, J. Chem. Phys., 128, 194108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Puzzarini, C., Biczysko, M., Barone, V., et al. 2014, J. Phys. Chem. Lett., 5, 534 [CrossRef] [PubMed] [Google Scholar]
  58. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rubin, R. H., Swenson, Jr. G. W., Benson, R. C., Tigelaar, H. L., & Flygare, W. H. 1971, ApJ, 169, L39 [NASA ADS] [CrossRef] [Google Scholar]
  60. Snyder, L. E.,& Bull, D. 1973, Nature Phys. Sci., 243, 45 [Google Scholar]
  61. Stanton, J. F., Gauss, J., Harding, M. E., & Szalay, P. G. 2011, CFOUR A quantum chemical program package. For the current version, see http://www.cfour.de [Google Scholar]
  62. Theulé, P., Borget, F., Mispelaer, F., et al. 2011, A&A, 534, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
  64. Tielens, A. G. G. M., & Charnley, S. B. 1997, in Planetary and Interstellar Processes Relevant to the Origins of Life (Springer), 23 [CrossRef] [Google Scholar]
  65. van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
  66. Watanabe, N.,& Kouchi, A. 2002, ApJ, 567, 651 [NASA ADS] [CrossRef] [Google Scholar]
  67. Watson, J. K. G. 1977, in Vibrational Spectra and Structure, ed. J. R. Durig (New York: Marcel Dekker), 6, 1 [Google Scholar]
  68. Woon, D. E., & Dunning Jr., T. H. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Ground-state spectroscopic constants of trans-propargylamine (present work) compared with those of trans-aminoacetonitrile (Motoki et al. 2013).

In the text
Table 2

Spectroscopic constants determined for the v13 = 1 and v21 = 1 resonant states and for the v20 = 1 unperturbed state of trans-propargylamine.

In the text
Table 3

Comparison between selected spectroscopic constants of the three lowest vibrationally excited states of trans-propargylamine and trans-aminoacetonitrile.

In the text
Table 4

Assignments, measured line positions, and least-squares residuals for the analysed transitions of propargylamine.

In the text

All Figures

thumbnail Fig. 1

Structure of trans-propargylamine. Blue atom is nitrogen, dark-gray are carbon, and light-gray are hydrogen.
In the text
thumbnail Fig. 2

Portion of the J = 11 ← 10, a-type band of propargylamine in the v13 = 1 state. Splittings caused by electric quadrupole coupling are observable for Ka = 7, 8, and 9. The asymmetry doublet of the Ka = 4 transition is also visible.
In the text
thumbnail Fig. 3

Upper panel: stick spectra of ground, v20 = 1, v13 = 1, and v21= 1 states in the 66–190 GHz frequency range. Lower panel: expansion of the 84–116 GHz region. Intensities are computed at 200 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.