| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201832645 | |
| Published online | 06 July 2018 | |
The Gaia-ESO Survey: a kinematical and dynamical study of four young open clusters
1
Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze,
via G. Sansone 1,
50019
Sesto Fiorentino (Firenze),
Italy
e-mail: bravi@arcetri.astro.it
2
INAF – Osservatorio Astrofisico di Arcetri,
largo E. Fermi 5,
50125
Firenze,
Italy
3
Leiden Observatory,
Niels Bohrweg 2,
2333
CA Leiden,
The Netherlands
4
Astrophysics Group, Keele University,
Keele,
Staffordshire
ST5 5BG,
UK
5
Université Grenoble Alpes, IPAG,
CS 40700,
38085
Grenoble Cedex 9,
France
6
CNRS, IPAG,
38000
Grenoble,
France
7
Department of Signal Theory and Communications, Universidad Carlos III de Madrid
28911
Leganés,
Madrid,
Spain
8
ASI Space Science Data Center,
via del Politecnico snc,
00133
Roma
9
Universidade de São Paulo, IAG, Departamento de Astronomia,
Rua do Matão 1226,
São Paulo,
05509-900
SP,
Brasil
10
Departmento de Astrofísica, Centro de Astrobiología (INTA-CSIC), ESAC Campus,
Camino Bajo del Castillo s/n,
28692
Villanueva de la Cañada,
Madrid,
Spain
11
INAF – Osservatorio Astrofisico di Catania,
via S. Sofia 78,
95123
Catania,
Italy
12
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
13
INAF – Osservatorio di Astrofisica e Scienza dello Spazio,
via Gobetti 93/3,
40129
Bologna,
Italy
14
INAF – Osservatorio Astronomico di Palermo G. S. Vaiana,
Piazza del Parlamento 1,
90134
Palermo,
Italy
15
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot,
5 Place Jules Janssen,
92190
Meudon,
France
16
McWilliams Center for Cosmology, Department of Physics, Carnegie Mellon University,
5000 Forbes avenue, Pittsburgh,
PA
15213,
USA
17
Instituto de Física y Astronomía, Universidad de Valparaíso,
Chile
18
Millennium Nucleus “Núcleo Planet Formation”, Universidad de Valparaíso,
Chile
19
Dipartimento di Fisica e Astronomia, Università di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova,
Italy
20
Departamento de Didáctica, Universidad de Cádiz,
11519
Puerto Real,
Cádiz,
Spain
21
Núcleo de Astronomía, Facultad de Ingeniería, Universidad Diego Portales,
Av. Ejército 441,
Santiago,
Chile
22
Laboratoire d’astrophysique, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny,
1290
Versoix,
Switzerland
23
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto,
CAUP,
Rua das Estrelas,
4150-762
Porto,
Portugal
24
INAF – Padova Observatory,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
Received:
15
January
2018
Accepted:
3
March
2018
Context. The origin and dynamical evolution of star clusters is an important topic in stellar astrophysics. Several models have been proposed in order to understand the formation of bound and unbound clusters and their evolution, and they can be tested by examining the kinematical and dynamical properties of clusters over a wide range of ages and masses.
Aims. We use the Gaia-ESO Survey products to study four open clusters (IC 2602, IC 2391, IC 4665, and NGC 2547) that lie in the age range between 20 and 50 Myr.
Methods. We employ the gravity index γ and the equivalent width of the lithium line at 6708 Å together with effective temperature Teff and the metallicity of the stars in order to discard observed contaminant stars. Then we derive the cluster radial velocity dispersions σc, the total cluster mass Mtot, and the half mass radius rhm. Using the Gaia-DR1 TGAS catalogue, we independently derive the intrinsic velocity dispersion of the clusters from the astrometric parameters of cluster members.
Results. The intrinsic radial velocity dispersions derived by the spectroscopic data are higher than those derived from the TGAS data, possibly due to the different masses of the considered stars. Using Mtot and rhm we derive the virial velocity dispersion σvir and we find that three out of four clusters are supervirial. This result is in agreement with the hypothesis that these clusters are dispersing, as predicted by the “residual gas expulsion” scenario. However, recent simulations show that the virial ratio of young star clustersmay be overestimated if it is determined using the global velocity dispersion, since the clusters are not fully relaxed.
Key words: stars: pre-main sequence / stars: kinematics and dynamics / open clusters and associations: general / stars: formation / techniques: spectroscopic / techniques: radial velocities
© ESO 2018
1 Introduction
The majority of stars form in clusters and associations inside giant molecular clouds. However, most clusters dissipate within 10–100 Myr, leaving more than 90% of the stellar population dispersed in the Galactic field (e.g., Lada & Lada 2003; Piskunov et al. 2006). The scientific debate on the origin of bound and unbound clusters, along with the processes leading to their dissolution, is still open. Several authors have suggested that all stars form in dense clusters (density ≳103–104 stars pc−3), which rapidly dissipate after feedback from massive stars (i.e., supernova explosions, stellar winds, and radiation pressure) sweeps out the gas that was keeping the cluster bound (e.g., Tutukov 1978; Lada et al. 1984; Goodwin 1997; Kroupa et al. 2001; Goodwin & Bastian 2006; Baumgardt & Kroupa 2007; Bastian 2011). These models predict that after this gas dispersion the clusters should be found in a supervirial state. Recent observations and simulations question this scenario, and suggest that clusters have their origin in a hierarchically structured environment covering a wide range of densities and that stellar feedback and gas expulsion are irrelevant for the cluster dispersion, which is instead driven by two-body interactions (e.g., Bressert et al. 2010; Kruijssen et al. 2012; Parker & Dale 2013; Wright et al. 2016; Parker & Wright 2016).
In order to achieve a full understanding of the origin and the fate of star clusters, it is fundamental to study the kinematic properties of their stellar components at different stages of evolution. However, until a few years ago this kind of study had been carried out only for a few clusters (e.g., Cottaar et al. 2012a; Tobin et al. 2015), due to the lack of precise and homogeneous measurements of radial velocities and other stellar parameters for large stellar samples. The observational scenario has radically changed very recently, thanks to large high-resolution spectroscopic surveys like APOGEE (Majewski et al. 2017) and the Gaia-ESO Survey (GES, Gilmore et al. 2012; Randich et al. 2013). The latter is a large public survey of all the Milky Way components performed with the multi-object optical spectrograph FLAMES at the Very Large Telescope (VLT). One of the main goals of the survey is the observations of several clusters in the 1–100 Myr age range to derive radial velocities (RVs) and stellar parameters that can be used to investigate their dynamical evolution.
Several interesting results have already been obtained from the first clusters that have been observed (ρ Oph, Chamaeleon I, Gamma Velorum), namely the discovery of multiple stellar kinematical populations (Jeffries et al. 2014; Sacco et al. 2015; Mapelli et al. 2015) and a significant discrepancy between the kinematic properties of pre-stellar cores and pre-main sequence stars formed in the same environment (Foster et al. 2015; Rigliaco et al. 2016; Sacco et al. 2017).
So far, all these studies have focused on clusters younger than 10–20 Myr. Nevertheless, the complete understanding of the cluster dispersion process requires the study of slightly older (age ~20–50 Myr) systems. Clusters in this age range have already lost their residual gas and have nearly completed the process of “violent relaxation” predicted by models based on stellar feedback (e.g., Goodwin & Bastian 2006; Proszkow & Adams 2009), but have not yet been affected by tidal effects due to external gravitational fields that occur on longer timescales (~100–300 Myr; e.g., Portegies Zwart et al. 1998, 2010; Baumgardt & Makino 2003; Lamers et al. 2005, and references therein).
In this paper we investigate this particular age interval using the GES data to analyze the kinematical and dynamical properties of IC 2602, IC 2391, IC 4665, and NGC 2547. The paper is organized as follows: in Sect. 2 we describe the observations and the GES parameters used in this paper; in Sect. 3 we illustrate the properties of these clusters andthe target selection; in Sect. 4 we explain how we derived the kinematical properties of these clusters; in Sect. 5 we discuss our results; and in Sect. 6 we draw our conclusions.
Cluster properties.
2 Gaia-ESO observations and data
The Gaia-ESO Survey is obtaining medium- and high-resolution optical spectra of ~105 stars selected in the Galactic field and in star clusters in order to provide a homogeneous overview of the distributions of kinematics and chemical element abundances in the Galaxy. Specifically, GES is collecting a large dataset of radial velocities (RVs), stellar parameters (effective temperature, surface gravity, metallicity), and elemental abundances for large numbers of representative stars in clusters, covering a wide range of ages and stellar masses.
Gaia-ESO observations are performed with the FLAMES instrument (Pasquini et al. 2002), using the GIRAFFE and UVES spectrographs, which permit the simultaneous allocation of 132 and 8 fibers, respectively. In the observations of young nearby open clusters, GIRAFFE is used for late-type stars with a V magnitude between 11 and 19 with the HR15N setup, which obtains medium-resolution spectra (R ~ 17000) in the wavelength range 6470 Å < λ < 6790 Å. UVES acquires higher resolution spectra (R ~ 47000) of brighter stars (9 < V < 15) with a spectral range of 2000 Å and with two central wavelengths, 5200 Å (UVES 520) and 5800 Å (UVES 580). The GIRAFFE/HR15N and UVES/580 setups both contain the lithium line at 6708 Å, which is useful for identifying young stars.
Pipeline reduction of GIRAFFE spectra and RV determination are centralized at the Cambridge Astronomy Survey Unit (CASU), while UVES reduction and RV analysis are performed at INAF – Osservatorio Astrofisico di Arcetri. The data reduction is described in Jeffries et al. (2014) and Sacco et al. (2014) for GIRAFFE and UVES data, respectively. The reduced spectra are then analyzed using common methodologies to produce a uniform set of stellar parameters, which along with RVs, is periodically released to all the members of the GES consortium via a science archive1.
Spectrum analysis is distributed among several working groups (WGs) and several nodes. WG12 analyzes the pre-main sequence (PMS) stars and different nodes provide estimates of the stellar parameters and chemical abundances. Specifically, two nodes analyze GIRAFFE targets, INAF – Osservatorio Astrofisico di Catania (OACT) and INAF – Osservatorio Astronomico di Palermo (OAPA), and four nodes focus on the UVES targets, OACT, Centro de Astrofisica de Universidade do Porto (CAUP), Universidad Complutense de Madrid (UCM), and INAF – Osservatorio Astrofisico di Arcetri. The products delivered by the nodes are combined to produce the recommended set of measurements provided by WG12 (Lanzafame et al. 2015), which in turn is homogenized with those from WG10 and WG11 (respectively GIRAFFE and UVES analysis of FGK stars) in order to produce the final recommended values (Pancino et al. 2017, Hourihane et al., in prep.).
During this work, we make use of the RV, the effective temperature of the star (Teff), the surface gravity (log g), the gravity index (γ), the equivalent width of the lithium line at 6708 Å (EW(Li)), and the metallicity ([Fe/H]). The γ index is an efficient gravity indicator for the GIRAFFE targets when it is combined with the effective temperature of the stars. It is an empirical index and it is sensitive to stellar gravity over a wide range of spectral types, allowing a clear separation between the low-gravity giants and the higher gravity main sequence (MS) and PMS stars for spectral types later than G (see Damiani et al. 2014, for details). We use γ as gravity indicator because its measurement is available for a larger number of GIRAFFE spectra than the log g parameter, with the exception of the stars observed only with UVES for which γ is not derived. For these stars we use instead the value of log g, which is available for most of the observed sources.
The RVs for the GIRAFFE targets were obtained as explained in Jackson et al. (2015), while RVs from UVES are described by Sacco et al. (2014). The uncertainties on the RV measurements for GIRAFFE were calculated empirically using the formula described in Jackson et al. (2015), where they compared repeated measurements of the RV for the same star to determine the underlying distribution of measurement uncertainties as a function of signal-to-noise ratio (S/N), Teff, and rotational broadening (v sin i). In this paper, we use the data from the fourth internal data release (GESviDR4). The values of v sin i are not available; therefore, we use the measurements given by WG12. In a number of cases, the recommended values of EW(Li) and Teff from the final homogenization process were not provided. In some of these cases we use the EW(Li) and Teff derived by the nodes of WG12. This choice is justified by the fact that the values measured by different nodes are in agreement, within the errors, with those recommended by WG12, when they are available.
3 Sample clusters
3.1 Cluster properties
The four clusters have similar ages (from ~20 Myr to ~50 Myr) and different distances. IC 2602 and IC 2391 are among the closest clusters to the Sun (distance ~ 150 pc), while the other two clusters are more distant (~365 pc). Given the uniform magnitude limit for the observations of clusters in GES, we reach stars with different mass limits in the different clusters (see next section). The cluster properties are summarized in Table 1, where distances, ages, and reddening values are from Randich et al. (2018). Each cluster has been subject to a variety of studies carried out to identify the stellar population based on combinations of X-ray data (e.g., Prosser 1993; Randich et al. 1995; Patten & Simon 1996; Martin & Montes 1997; Jeffries & Tolley 1998), optical photometry (e.g., Prosser et al. 1996; Jeffries et al. 2004), and optical spectroscopy (e.g., Randich et al. 1997; Stauffer et al. 1997; Barrado y Navascués et al. 1999; Jeffries et al. 2000, 2009; Jeffries & Oliveira 2005; Platais et al. 2007; Manzi et al. 2008); many high- and low-mass cluster members have been identified using the position in the HR diagram, presence of the lithium absorption line at 6708 Å, and RVs. These studies show that the number of previously known spectroscopically confirmed members in the four clusters range from 40 in IC 4665 to 75 in NGC 2547. In the case of NGC 2547, Sacco et al. (2015) found a secondary population that is kinematically distinct from the main cluster population.
3.2 Target selection
One of the main goals of GES is the study of cluster kinematics and dynamics based on large, unbiased samples of members. Known members from the literature do not provide suitable samples because they are often biased by the selection method. For this reason GES adopts an inclusive selection strategy: all candidate members observed with GIRAFFE have been selected in an unbiased way, down to the 19th magnitude (V band) and covering a relatively large area on the sky, from a strip around the cluster sequence. This is defined asthe sequence drawn by the known members reported in the literature in the different color-magnitude diagrams (CMDs). When the optical photometry catalogues are either inhomogeneous or incomplete, the selection is based mainly on the photometry of the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006). We note that this strategy implies that our final candidate samples include a very large number of foreground and background stars. Inside the magnitude range and spatial coverage observed by GES, some of the samples are relatively complete; however, in nearby and extended clusters, like those analyzed in the present paper, the level of completeness is lower. While it is necessary to correct for this incompleteness, our strategy of target selection ensures that the final samples are unbiased (in particular with respect to the kinematics) and are representative of the entire cluster population.
UVES targets are mainly observed to derive the cluster chemical pattern (Spina et al. 2014a,b, 2017) and are therefore selected with a different strategy; namely, when information is available the UVES fibres are assigned to brighter stars that are already known or are likely members.
In the case of IC 2602 ESO archival data have also been retrieved and analyzed. In order to be consistent with the Gaia-ESO selection method, we considered only the archive data for stars that are in the strip of the CMD used for the GES selection.
Table 2 summarizes the number of targets observed in each cluster. We list the number of stars observed with the differentGIRAFFE and UVES setups, as well as the number of targets for which stellar parameters were derived.
Number of targets observed in the four clusters.
3.3 Completeness
As discussed in the previous section, the initial targets were selected in order to be complete within the magnitude range of GES and within the area that contains all the stars selected as initial candidate targets, which is defined by the radius RGES. Therefore, the level of completeness within the observed magnitude range is calculated by dividing the number of the observed stars by the number of stars selected as initial candidate targets in GES and located within these circular regions, which we assume contains the whole cluster. We obtain a ~25% level of completeness for IC 2602 and IC 2391, while for IC 4665 and NGC 2547 we derive a level of completeness of ~ 65% and ~ 75%, respectively.We note that the level of completeness of IC 2602 and IC 2391 is much lower because only a part of the area of the sky including known cluster members from the literature has been observed.
4 Membership analysis
Starting from the initial sample of observed cluster targets, thanks to the spectroscopic parameters derived by the GES consortium, we were able to exclude stars that do not belong to the clusters. Then, using the RV of the spectroscopically selected candidates, we determined the probability that each remaining star is a cluster member, and we used the Hertzsprung–Russell (HR) diagram to estimate a mass for that star.
 |
Fig. 1 Gravity index γ as a function of the stellar effective temperature Teff for the starsobserved with GIRAFFE. The yellow filled dots are the stars identified as giants, while the remaining stars are shown as green filled dots. The black line indicates the threshold used to separate the giants and the non-giants. |
4.1 Spectroscopic candidates
To exclude stars that do not belong to the clusters we used three independent spectroscopic criteria based on the gravity index γ (or log g for UVES spectra), the EW(Li), and the metallicity [Fe/H]. All stars where any of the first two parameters or the effective temperature were not measured have been excluded. We retained stars without the metallicity measurement since very few stars were discarded on the basis of this parameter. More specifically, our method can be divided into three steps.
The main source of contamination in a sample of candidate members of a nearby young cluster are the background giants. These objects have a lower gravity than cluster members and can be identified using the surface gravity index γ (Damiani et al. 2014). Figure 1 shows γ as a function of the effective temperature. We consider as giants all the stars within the region defined by the black line, which has a approximate Teff value that is lower than 5400 K and a γ value higher than 0.98, within a 1σ error bar. For UVES targets the gravity index is not defined and we use the surface gravity: we consider as giants stars with log g lower than 3.75. In order to check the consistency between using γ or log g, we plot in Fig. 2 the comparison between these two parameters for IC 2602: it is clear that the selection of the giants is basically the same whether we consider targets with γ > 0.98 and Teff < 5400 K or targets with log g < 3.75. All the targets identified as giants with γ and Teff are indeed distinctly below the value of log g = 3.75.
We use the EW(Li) to exclude dwarf non-members from the sample of stars remaining from the first selection step. Depending on stellar mass, lithium starts to be depleted during the PMS phase (e.g., Soderblom 2010); therefore, it can be used as an indicator of youth in specific temperature ranges. Specifically, between 20 and 50 Myr the EW(Li) can be used to select candidate members between 4000 K and 6000 K because stars with Teff < 4000 K have already burned all their lithium, and above 6000 K Li is preserved even in much older stars. Also, the Li I 6708 Å line, which is the main diagnostic, becomes very weak and difficult to measure. In Fig. 3 we show the EW(Li) as a function of Teff for the four clusters. We classify as secure non-members all the stars below the threshold indicated with a continuous black line between 4000 K and 6000 K. All the other stars are selected as candidate members. The threshold was defined using previous observations of these four clusters available in the literature (Martin & Montes 1997; Randich et al. 1997, 2001; Jeffries et al. 2003, 2009; Jeffries & Oliveira 2005).
The final selection step is to exclude targets with a measured [Fe/H] < –0.5 dex that would be incompatible with the nearly solar metallicity of these clusters (Spina et al. 2017).
To summarize, we retain from the criteria 101, 53, 121, and 187 stars for IC 2602, IC 2391, IC 4665, and NGC 2547, respectively. We define these stars as “spectroscopic candidates”. Given the different target selection strategy used for UVES targets, we also consider as spectroscopic candidate UVES stars without Teff, γ, and/or EW(Li) that are known members from the literature.
 |
Fig. 2 Gravity index (γ) as a function of the surface gravity (log g) for IC 2602. The blue dots are the targets with an effective temperature greater than 5400 K, while the gray dots are those with a Teff < 5400 K. The solid lines delimit the regions in which a target is considered a giant star based on its γ index (above the horizontal black line) and on its log g value (to the left of the vertical black line). |
4.2 Kinematic analysis
The precision of the RVs (~0.3 km s−1) obtained from GES observations (Jackson et al. 2015) allows us to study the kinematic properties of the cluster samples. We use the RVs to determine the intrinsic RV dispersion of each cluster, σc, and the probability that a spectroscopic candidate belongs to the cluster. For each cluster we use the stars selected as spectroscopic candidates from the analysis in Sect. 4.1.
In Fig. 4 the RV distributions of each cluster are shown. We modeled these distributions using a maximum likelihood technique developed by Cottaar et al. (2012b)2. Briefly, this technique fits the observed distribution with a model that assumes a Gaussian intrinsic RV distribution that is broadened by the orbital motions of unresolved binary systems and by uncertainties in the RV measurements. The broadening due to the binaries is modeled by assuming the same distribution of orbital parameters as found in solar-type field stars, namely a log-normal distribution of the binary periods with a mean of 5.03 and dispersion of 2.28 in log10 days (Raghavan et al. 2010), a power law 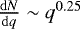 for 0.1 < q < 1 (Reggiani & Meyer 2013) for the secondary-to-primary mass ratio (q), and a flat distribution of eccentricity between 0 and the maximum value emax defined in Parker & Goodwin (2009).
for 0.1 < q < 1 (Reggiani & Meyer 2013) for the secondary-to-primary mass ratio (q), and a flat distribution of eccentricity between 0 and the maximum value emax defined in Parker & Goodwin (2009).
Since the analysis in Sect. 4.1 excludes the obvious non-members, the sample of spectroscopic candidates will not be entirely clean of contaminating field stars. Therefore, we add a second broader Gaussian distribution to the model to account for their presence. In the model the properties of field populations are free parameters without boundaries. In the case of NGC 2547 we perform the fit with three distinct Gaussian populations to take into account the presence of the population B of young stars in the Vela OB2 associations found by Sacco et al. (2015).
Since the uncertainties on the RV measurements have been empirically calculated only for the GIRAFFE targets (Jackson et al. 2015), we exclude the UVES targets from the fits. We perform three fits for each cluster, with the fraction of the binaries (fbin) fixed at three different values: 0.2, 0.5, and 0.8. For all clusters, we model only the stars with RVs within the range –90 ≤RV ≤ 90 km s−1.
Table 3 shows the results of the fits. The central velocity vc and the intrinsic dispersion σc derived for a binary fraction of 0.2 and 0.8 are both within the error bounds of the best values obtained for a fraction of 0.5 (within 1σ for IC 2602 and IC 2391 and 2σ for NGC 2547); therefore, we adopt the results obtained with a binary fraction set to 0.5 as the best values for the rest of the paper. Sincethe intrinsic RV dispersion for IC4665 is too low to be resolved with our data, we can only estimate an upper limit of ~ 0.5 km s−1, which is slightly larger than the typical error of our RV measurements (~0.3 km s−1).
Our mean RV estimates are in agreement with the values found by previous works for IC 2602 and IC 2391 (Marsden et al. 2009), for IC 4665 (Jeffries et al. 2009), and for NGC 2547 (Sacco et al. 2015).
Using the RVs of the spectroscopic candidates, we also estimate the probability that each of them is a true member. In particular, starting from the assumptions of our models, we can calculate the probability that a cluster member (pc (vr)) and a field star (pf(vr)) have RV = vr given the set of best fitparameters. Starting from these functions, the membership probability of a star is pcl (vr) = pc(vr)∕(pc(vr) + pf(vr)).
Best parameters from the fits of the RV distributions.
Assumptions on binary properties and robustness of fits
Our model assumes that the properties of binaries are distributed as for solar mass stars in the solar neighborhood. However, as discussed by Burgasser et al. (2007); Raghavan et al. (2010) and Duchêne & Kraus (2013), binary properties probably change as a function of the stellar mass or may depend on the dynamical evolution of the star-forming region where they have been formed (e.g., Marks et al. 2011). Therefore, we perform tests in order to investigate how the results depend on the assumed binary properties. Specifically, we calculate the best fit values assuming a) a mean binary period a factor of five lower and higher than that found for solar mass stars by Raghavan et al. (2010); b) a distribution of eccentricities in the form f(e) ~ e2 between 0 and emax, instead of a flat distribution; and c) a flat distribution for the mass ratio q rather than the power law defined by Reggiani & Meyer (2013). In the case of mass ratio q, for the test we used the flat distribution since it is strongly supported by observational evidence (e.g., Mermilliod & Mayor 1999; Patience et al. 2002; Bender & Simon 2008; Duchêne & Kraus 2013, for a review). Other distributions have been proposed in the literature, for example the random pairing distribution, where the lowest mass is randomly drawn from the mass distribution (e.g., Kroupa 1995). However, the random pairing distribution has been ruled out both theoretically and observationally (Kouwenhoven et al. 2005, 2007a,b, 2009; Kobulnicky & Fryer 2007; Metchev et al. 2008). The results of our tests, reported in Table 4, show that our assumptions of the binary properties do not strongly affect our final results. Since we estimate an upper limit on the σc of IC 4665, we do not consider this cluster in these tests.
 |
Fig. 3 Equivalent width of the lithium line as a function of Teff. The purple stars are the known members of the four clusters used to trace the lower envelope of the bulk of cluster spectroscopic candidates (solid line), as given in the literature. The open red circles show the members of each cluster that were reported in the literature and observed again by GES. The green symbols mark the stars selected as spectroscopic candidates. The stars excluded by the lithium criterion are shown in black. We also highlight the sources with an estimate of EW(Li) (dots and squares) or only an upper limit (arrows and crosses). |
4.3 Velocity dispersion from TGAS
The clusters studied in this work have been investigated by (Gaia Collaboration 2017; hereafter G17), who used the Tycho-Gaia Astrometric Solution (TGAS) subset of the first Gaia data release (DR1, Gaia Collaboration 2016a; Gaia Collaboration 2016b) to derive cluster memberships, mean parallaxes, and proper motion values. Parallaxes have also been determined by Randich et al. (2018), who found an excellent agreement for these clusters.
There is not much overlap between the TGAS (exclusively brighter stars) and GES samples. On the one hand this can be considered a limitation (e.g., we have RVs for the GES stars, but we lack astrometry, and vice versa); on the other hand it can also be seen as an opportunity to derive certain cluster properties in an independent way. We focus on the velocity dispersion of the four clusters, and on the comparison of the values obtained using the two samples.
To derive the velocity dispersion using the TGAS data, we apply the maximum likelihood procedure described in (Lindegren et al. 2000; hereafter L00), in particular in their Appendix A.4, to the stars selected as members by G173. Assuming that all the stars in a moving group share the same space velocity with a low isotropic internal velocity dispersion, L00 determine the group centroid space motion, the internal velocity dispersion, and the individual parallaxes for all members. The observables used by L00 are parallaxes and proper motions, which are modeled as random variables with a probability density function (PDF) that depends on the model parameters: the cluster centroid space motion v0, the velocity dispersion σv, and the n parallaxes of the n stars ϖ. They also assume that the observations are independent and unbiased.
The likelihood function is the product of the single PDFs of all the stars. The method requires that the model provide a statistically corrected description of the data. In particular, it must be applied to actual members of the cluster or tothe sources whose space motion agrees with the model. Outliers can be detected by computing a suitable goodness of fit statistic for each star in the solution. Lindegren et al. (2000) named this quantity gi for each star with index i (with i = 1, ..., n), and find that gi approximately follows a χ2 distribution. Therefore, for a given significance level, the star should be considered a kinematic outlier if gi > glim. For example, a 1% significance level requires glim ~ 14. The outlier rejection procedure is iterative: at each step the star with the highest gi is rejected from the sample. A new solution is then computed, including new gi values. The process is repeated until all gi < glim.
Unfortunately, the internal velocity dispersion σv is strongly underestimated by this method. The bias in the σv estimate is probably related to the fact that an isotropic velocity dispersion is assumed for the cluster, while in practice only one component of this velocity can be measured astrometrically, i.e., the one perpendicular to the plane containing the line of sight and the centroid velocity vector (called η⊥,i by L00). Lindegren et al. (2000) deal with the problem by using the proper motion residuals to compute the peculiar velocity components (η⊥,i) and their observational uncertainties. They then compute an estimate of σ⊥, and hence of σv, assuming isotropic dispersion. They test the method using Monte Carlo simulations, and conclude that σ⊥ is in practice an unbiased estimate of σv.
We applied the likelihood maximization procedure described above first considering all the stars identified as members by G17, then restricting the samples to the areas defined by the radii (RGES) shown in Table 6. We derived the centroid space velocity for the four clusters, and then we computed σ⊥. The results are listed in Table 5, together with their statistical errors4.
The estimated values for the velocity dispersion of the clusters analyzed in this study depend strongly on the number of stars considered. For example, the velocity dispersion of IC 2602 changes from ~ 0.48 km s−1 to ~ 0.20 km s−1 after the exclusion of only three stars. A similar trend can also be observed for the other clusters. Furthermore, changing the likelihood maximization method (see Table A.1) causes the velocity dispersion estimates to change slightly as well. For these reasons, the results given in Tables 5 and A.1 needs to be interpreted with care. In particular, the errors in Tables 5 and A.1 correspond to the statistical errors, and do not take into account any systematic effect. A tentative estimate of the accuracy of the velocity dispersions obtained can be computed using half the difference between the velocity dispersion values obtained with the two different methods, considering the same number of stars (i.e., Ni and 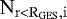 ). In this way, we obtain systematic errors between ~0.01 km s−1 and ~0.1 km s−1, depending on the cluster.
). In this way, we obtain systematic errors between ~0.01 km s−1 and ~0.1 km s−1, depending on the cluster.
 |
Fig. 4 Radial velocity distribution. The blue, black, and red dashed lines represent the fits performed by setting the binary fraction to 0.2, 0.5, and 0.8, respectively. |
Robustness of the fits assuming different conditions of the binary properties.
Velocity dispersion estimates obtained with the maximum likelihood procedure described in the text using the Nelder–Meadmethod, except those indicated by an asterisk (where the Newton Conjugate Gradient method was employed).
4.4 Stellar mass and radii
The analysis of the dynamics of clusters requires an estimation of its total mass and its half mass radius. As the first step, we calculated the mass of each spectroscopic candidate by interpolating the PMS evolutionary tracks developed by Tognelli et al. (2011) at the positions of the stars in the HR diagram. We used effective temperatures measured from the GES spectra and luminosities estimated from the V magnitude, or the J magnitude from the 2MASS catalogue when the former was not available. To estimate luminosities from magnitudes, we corrected for extinction, using the reddening values given in Table 1 and the extinction law from Savage & Mathis (1979); we applied bolometric corrections BCV and BCJ derived by interpolating the relations given in Table A5 of Kenyon & Hartmann (1995) at the stellar effective temperature; we converted relative bolometric magnitudes into luminosities adopting the distances from Table 1 and a solar bolometric magnitude M⊙ = 4.74. Figure 5 shows the HR diagram for each cluster, color-coded by membership probability. We note that high-probability spectroscopic candidates tend to be closer to the cluster sequence than low-probability ones. This validates that our approach works.
Once we evaluated the mass of the spectroscopic candidates, we estimated the total mass of the cluster (Mtot) using a general method. We took into account the stars within a magnitude range and we obtained the observed mass (Mobs) adding up all star masses in the sample. Then, we needed to divide Mobs by the level of completeness of the observations (Sect. 3.3). This factor takes into account the fraction of potential cluster members within the magnitude range and within the area covered by the observations that have not been observed for technical reasons (e.g., the impossibility of allocating the fibers). After this, we multiplied Mobs by a factor of 1.25, which takes into account the presence of binaries, under the assumption of a 50% binary fraction and a mass ratio with a flat distribution. For the last step, in order to estimate Mtot we needed to multiply the observed mass by another factor that takes into account the fraction of the cluster mass in stars outside the magnitude range. This is calculated analytically, using the assumption that the mass function of the clusters follows a multi-power-law behavior described in Kroupa (2001) between 0.01 M⊙ and the mass of the most massive cluster star known in the literature.
We consider two different samples of stars:
the stars that we selected as spectroscopic candidate with GES. Within the GES sample we also use two different approaches: (i) we only consider the spectroscopic candidates with a probability of being a member greater than 0.8, and (ii) we consider all spectroscopic candidates weighted by their corresponding pcl;
the stars identified as members by G17 within the area defined by RGES. For this sample, we assume a level of completeness of 100% since TGAS is assumed to be complete.
Table 6 shows the magnitude range of GES, the RGES, and the derived completeness.
The total masses found with the different samples agree within a factor of ~ 1.8. In particular, the results show a good correspondence between the masses estimated through the spectroscopic candidates weighted by pcl (Mtot,w) and those calculated with the TGAS sample (Mtot,TGAS) within the GES region. This validates our results, since the masses are estimated starting from almost independentstar samples (only a tiny fraction of them are in common). Therefore, we will adopt Mtot,w for the subsequent dynamical analysis.
To study the dynamical properties of each cluster we also need an estimate of the half mass radius (rhm). This radius is critically dependent on the presence of mass segregation in the clusters. Indeed, rhm decreases with an increasing level of mass segregation. Given that the GES magnitude range does not allow the observation of very bright (and massive) stars, it is difficult to take into account the presence of mass segregation with the GES data. Instead, in the TGAS sample there are the brightest stars of each cluster and the observations are spatially complete. Therefore, we use the stars identified as members by G17 within RGES. To correctly take into account the presence of mass segregation, we also consider the cluster members present in the literature outside the Gaia magnitude range (stars with V ≲ 6). We define rhm as the radius that contains half of the mass given by the sum of masses of TGAS and literature stars. The rhm of the four clusters are listed in Table 6.
 |
Fig. 5 Hertzsprung–Russell diagram of the sample of clusters. The colored filled dots represent GES targets retained after the procedure of cleaning from the obvious contaminants. The spectroscopic candidates color-coded depending on the probability of belonging to the cluster (scale at right). The magenta and blue lines are the isochrones at 20 and 50 Myr, respectively, and the black and red lines are the PMS evolutionary tracks (Tognelli et al. 2011). |
5 Discussion
5.1 GES versus TGAS velocity dispersion
In this section we compare the velocity dispersion obtained from the GES (see Sect. 4.2) and TGAS data (see Sect. 4.3). We decided to use the values of σ⊥ estimated from the sample of G17 within the radius RGES (last row of Table 5) with an error given by the sum of statistical error and systematic error (~ 0.1 km s−1). In Fig. 6 we show, for each of the four clusters, the spatial distribution of the members selected by G17 from the TGAS catalogue and the spectroscopic candidates selected by GES. The G17 members of IC 2602 and IC 2391 within RGES are uniformly distributed in the whole area of GES observations. Instead, for IC 4665 and NGC 2547, the TGAS members seem to cover only a section of the cluster area. This may be related to the greater distance of these clusters; the membershipselection in G17 is based on position, parallaxes, and proper motions, so it is strongly affected by distance.
The velocity dispersions derived from the GES data are higher than those derived from the TGAS data but consistent within 2σ. Furthermore, we stress that the typical error uncertainty on proper motions in DR1 (Gaia Collaboration 2016a) is ~ 1 mas yr−1, which corresponds to about 0.7–1.7 km s−1 at the distance of the four clusters studied in this paper. Therefore, we are pushing the Gaia data to their limit of precision, and their systematic errors need to be better investigated.
However, all four clusters analyzed in this work show the same trend, i.e., TGAS dispersions are lower than those of GES. The origin of this discrepancy could have two explanations. The first is the presence of asymmetries in the system (Baumgardt & Kroupa 2007). To derive the velocity dispersions in GES we use the radial velocity of stars, while in TGAS we use the velocity perpendicular to the plane containing the line of sight. In either case, it is unlikely that all clusters show the same trend of asymmetry. The second is the energy equipartition. After the relaxation, a cluster tends to evolve towards the energy equipartition where the more massive stars settle on the center of cluster and cede kinetic energy to the less massive ones. In this case, the velocity dispersion is related to the mass m of stars as σ(m) ∝ m−0.5. So, we expect that the more massive stars are dynamically colder (i.e., have a lower velocity dispersion). The four clusters in this work might already be relaxed (relaxation times 10–30 Myr) and we found that the median mass of GES samples is lower than that of TGAS samples by a factor between ~2.5 and ~4, depending on the cluster. Therefore, we expect differences in velocity dispersions between a factor ~ 1.6 and ~2, which is about what we found. We recall that the presence of energy equipartition in star clusters is still very debated. Spera et al. (2016) and Parker et al. (2016) noted that energy equipartition may not occur even after many two-body relaxation timescales.
These are still preliminary results and more data with better accuracy are needed. The second release of the Gaia data, expected for April 2018, will include parallaxes and proper motions of low-mass population of these clusters. We will therefore be able to investigate this discrepancy more thoroughly. In light of this, in the next section we will discuss only the results obtained with GES data.
Completeness, total mass, and half mass radius of the four clusters calculated with the three different methods.
 |
Fig. 6 Spatial distribution of GES and TGAS stars in the four clusters. The black points are the stars observed with GES and the red filled dots are the spectroscopic candidates selected in Sect. 4.1. The blue diamonds are the stars selected as members by G17 within the radius RGES. The stars identified by red dots and blue diamonds are those used to derive the velocity dispersions in the GES and TGAS sample, respectively. |
5.2 Effect of feedback on the cluster dissipation mechanism
The main goal of this paper is to probe the dynamical state of four 20–50 Myr clusters (IC 2602, IC 2391, IC 4665, and NGC 2547) in order to investigate the mechanism leading to cluster dispersion. In particular, determining if they are “supervirial” or “subvirial” is critically important. Indeed, according to the “residual gas expulsion” scenario (e.g., Kroupa et al. 2001; Goodwin & Bastian 2006), young clusters become supervirial after feedback from massive stars sweeps out the gas that did not form stars. Otherwise, according to other models, the gas dispersion does not affect the virial ratio of the cluster and the dynamical interactions in the denser regions of a cluster drive the dynamical evolution (e.g., Kruijssen et al. 2012; Parker & Wright 2016).
We can understand whether a cluster is supervirial by comparing the measured one-dimensional velocity dispersion σc with the value derived analytically (σvir) from the cluster properties under the assumption of virial equilibrium, which is given by the equation
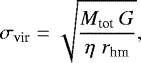 (1)
(1)
where rhm is the half mass radius;G is the gravitational constant; η is a dimensionless factor, which depends on the cluster density profile and is approximately equal to 10 for a Plummer sphere profile (e.g., Spitzer 1987; Portegies Zwart et al. 2010); and Mtot is the cluster mass. In Table 7 we list the velocity dispersions derived from the GES RVs (see Sect. 4.2) and from Eq. (1).
The observed velocity dispersions are higher than the values calculated by assuming virial equilibrium by about a factor two, leading to the conclusion that three out of four clusters (except IC 4665, which has an upper limit on the velocity dispersion) are supervirial. We can rule out that this conclusion is due to errors on the estimates of the velocity dispersion σvir. In particular, uncertainties on the mass are lower than a factor 1.5, as shown in Table 6; the half mass radius rhm could be underestimated in case of mass segregation because it was calculated using the more massive stars in the sample, but a larger rhm implies a smaller σvir, so it supports our conclusion on the virial ratio of the clusters. Finally, Elson et al. (1987) and Fleck et al. (2005) found that deviation of the density profile from a Plummer sphere can lead to a value of η that is lower by a factor 2. However, considering that σvir ∝ η−1∕2 this deviation cannot explain a discrepancy of a factor two.
The presence of clusters in a supervirial state after gas expulsion has been predicted by several N-body simulations (e.g., Bastian & Goodwin 2006; Baumgardt & Kroupa 2007) supporting the residual gas expulsion scenario. In particular, Baumgardt & Kroupa (2007) suggest that after the gas that did not form stars is swept out, clusters expand so the virial dispersion decreases and the virial ratio increases. They then return in a virial state only after the unbound stars are dispersed, which should occurs after about 20–40 crossing times. If we calculate the crossing time as σc ∕rhm, the clusters studied in this paper have a dynamical age of about 20–30 crossing times; therefore, our results are in good agreement with these simulations. However, we note that the crossing time used to track the cluster evolution in the simulations is calculated at cluster formation. We do not know the initial crossing time of these four clusters, but it is likely shorter than the current one, so the evolution of these clusters could be slower than observed in the simulations.
Parker & Wright (2016) performed N-body simulations of the cluster evolution assuming an initial spatial distribution that better resembles the hierarchical structure observed in young star forming region and investigated whether the ratio σc∕σvir can be used to trace the dynamical state of a cluster. They found that clusters that are initially subvirial or are in global virial equilibrium but subvirial on local scale relax to virial equilibrium after 25–50 crossing times. However, the measured ratio σc /σvir would lead to the conclusions that they are supervirial. This apparent inconsistency arises because clusters are never fully relaxed but keep an imprint of early non-equilibrium even after several crossing times.
Finally, we point out that G17 found members up to 15 pc from the cluster center and outside the cluster radius considered in this paper. It is not clear whether these distant stars are actual cluster members, unbound escaping stars, or field stars with kinematic properties consistent with the cluster, but if we calculate the total mass of the cluster and the half mass radius using the full G17 sample, we find similar virial velocity dispersions σvir, and therefore our conclusions would not change.
Properties of the four clusters.
6 Summary
In this paper we analyzed the iDR4 internal products of the Gaia-ESO survey to study the kinematical and dynamical properties of the young (age 20–50 Myr) open clusters IC 2602, IC 2391, IC 4665, and NGC 2547.
Using the gravity index, the lithium equivalent width, and the metallicity we derived a sample of candidate members for each cluster. Then, we used the RVs to derive the cluster intrinsic velocity dispersion and membership probabilities for each candidate member. Photometry from the literature and the effective temperature from GES spectra were used to estimate stellar masses and the total mass of each cluster after correcting for the presence of binaries and completeness.
Furthermore, we independently derived the intrinsic velocity dispersion of the clusters from the astrometric parameters of cluster members in the TGAS catalogue.
On the basis of this analysis we obtained the following main results:
The velocity dispersion measured from the RVs is higher than that measured from TGAS data. Given the masses of the stars in the GES and in the TGAS sample, this discrepancy would suggest that the system is relaxed and in a state of energy equipartition. However, given the limited numbers of cluster members in the TGAS sample and the error on astrometric parameters, we are not able to draw a firm conclusion. Important progress will be possible very soon with the second Gaia data release.
The velocity dispersion measured with GES data is about a factor two higher than that calculated by assuming virial equlibrium given the masses of the clusters and the spatial distribution of their members. This result indicates that clusters are in supervirial state and two explanations are given to interpret it. The first is the residual gas expulsion scenario (e.g., Kroupa et al. 2001; Goodwin & Bastian 2006), which suggests that clusters became unbound after the feedback from massive stars swept out the gas that did not form stars. The second is that the observed velocity dispersion could be higher than the virial dispersion because most stellar systems do not fully relax, even after 20–30 crossing times, as shown in the N-body simulations of Parker & Wright (2016).
In each cluster we found many new high-probability members and confirmed many of those known in the literature. New high-probability members are extended across the whole area covered by GES observations, suggesting that these clusters could be more extended than previously thought.
When the observations of the Gaia-ESO survey are completed and data from the second Gaia data release are available, we will be able to study the kinematics of a larger sample of young clusters in a six-dimensional space and we will be able solve the many open issues in this area of star formation.
Acknowledgements
The authors thank the referee, R. J. Parker, for his review. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the Gaia-ESO Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and the Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012” and from PRIN-INAF 2014. The results presented here benefited from discussions held during the Gaia-ESO workshops and conferences supported by the European Science Foundation (ESF) through the GREAT Research Network Programme. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. L.B. wishes to thank J. G. Fernández-Trincado and B. Tang for the useful comments and G. Conte who worked on the production of Fig. 3. E. Z. wishes to thank A. Brown, T. Marchetti, and C. F. Manara for useful discussions. J.L.-S. acknowledges the Office of Naval Research Global (award no. N62909-15-1-2011) for partial support. F. J. E. acknowledges financial support from the ASTERICS project (ID:653477, H2020-EU.1.4.1.1. – Developing new world-class research infrastructures). A. Bayo is grateful for support from the Millenium Science Initiative, Chilean Ministry of Economy. S. G. S. acknowledges the support from FCT through Investigador FCT contract of reference IF/00028/2014 and the support from FCT through the project PTDC/FIS-AST/7073/2014. E. M. acknowledges financial support from the “StarFormMapper” project funded by the European Union’s Horizon 2020 Research and Innovation Action (RIA) programme under grant agreement number 687528.
Appendix A Velocity dispersion using the Newton Conjugate Gradient maximization method
In this section we show the results of the radial velocity dispersions obtained with the TGAS data using the Newton Conjugate Gradient maximization method.
References
- Barrado y Navascués, D., Stauffer, J. R., & Patten, B. M. 1999, ApJ, 522, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N. 2011, in Stellar Clusters and Associations: A RIA Workshop on Gaia, eds. Alfaro Navarro, E. J., Gallego Calvente, A. T., & Zapatero Osorio, M. R., 85 [Google Scholar]
- Bastian, N., & Goodwin, S. P. 2006, MNRAS, 369, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, C. F., & Simon, M. 2008, ApJ, 689, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Bressert, E., Bastian, N., Gutermuth, R., et al. 2010, MNRAS, 409, L54 [NASA ADS] [Google Scholar]
- Burgasser, A. J., Reid, I. N., Siegler, N., et al. 2007, Protostars and Planets V, eds. V, B. Reipurth, D. Jewitt, & K. Keil (Arizona: University of Arizona Press), 427 [Google Scholar]
- Cottaar, M., Meyer, M. R., Andersen, M., & Espinoza, P. 2012a, A&A, 539, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cottaar, M., Meyer, M. R., & Parker, R. J. 2012b, A&A, 547, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, F., Prisinzano, L., Micela, G., et al. 2014, A&A, 566, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Elson, R. A. W., Fall, S. M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Fleck, J.-J., Boily, C., Lançon, A., Heggie, D., & Deiters, S. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 605 [Google Scholar]
- Foster, J. B., Cottaar, M., Covey, K. R., et al. 2015, ApJ, 799, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (van Leeuwen, F., et al.) 2017, A&A, 601, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Goodwin, S. P. 1997, MNRAS, 284, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, R. J., Jeffries, R. D., Lewis, J., et al. 2015, A&A, 580, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffries, R. D., & Oliveira, J. M. 2005, MNRAS, 358, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., & Tolley, A. J. 1998, MNRAS, 300, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Totten, E. J., & James, D. J. 2000, MNRAS, 316, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Oliveira, J. M., Barrado y Navascués, D., & Stauffer, J. R. 2003, MNRAS, 343, 1271 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jeffries, R. D., Naylor, T., Devey, C. R., & Totten, E. J. 2004, MNRAS, 351, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., James, D. J., & Cargile, P. A. 2009, MNRAS, 400, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Cottaar, M., et al. 2014, A&A, 563, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Zinnecker, H., Kaper, L., & Portegies Zwart S. F. 2005, A&A, 430, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., & Kaper, L. 2007a, A&A, 464, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven,M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007b, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven,M. B. N., Brown, A. G. A., Goodwin, S. P., Portegies Zwart, S. F., & Kaper, L. 2009, A&A, 493, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 1995, MNRAS, 277, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Maschberger, T., Moeckel, N., et al. 2012, MNRAS, 419, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Margulis, M., & Dearborn, D. 1984, ApJ, 285, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzafame, A. C., Frasca, A., Damiani, F., et al. 2015, A&A, 576, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Madsen, S., & Dravins, D. 2000, A&A, 356, 1119 [NASA ADS] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Manzi, S., Randich, S., de Wit, W. J., & Palla, F. 2008, A&A, 479, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mapelli, M., Vallenari, A., Jeffries, R. D., et al. 2015, A&A, 578, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marks, M., Kroupa, P., & Oh, S. 2011, MNRAS, 417, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, S. C., Carter, B. D., & Donati, J.-F. 2009, MNRAS, 399, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, E. L.,& Montes, D. 1997, A&A, 318, 805 [NASA ADS] [Google Scholar]
- Mermilliod, J.-C., & Mayor, M. 1999, A&A, 352, 479 [NASA ADS] [Google Scholar]
- Metchev, S. A., Kirkpatrick, J. D., Berriman, G. B., & Looper, D. 2008, ApJ, 676, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Lardo, C., Altavilla, G., et al. 2017, A&A, 598, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, R. J., & Dale, J. E. 2013, MNRAS, 432, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., & Goodwin, S. P. 2009, MNRAS, 397, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., & Wright, N. J. 2016, MNRAS, 457, 3430 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., Goodwin, S. P., Wright, N. J., Meyer, M. R., & Quanz, S. P. 2016, MNRAS, 459, L119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Patience, J., Ghez, A. M., Reid, I. N., & Matthews, K. 2002, AJ, 123, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Patten, B. M., & Simon, T. 1996, ApJS, 106, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R.-D. 2006, A&A, 445, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Platais, I., Melo, C., Mermilliod, J.-C., et al. 2007, A&A, 461, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., Hut, P., Makino, J., & McMillan, S. L. W. 1998, A&A, 337, 363 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. F. 1993, AJ, 105, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. F., Randich, S., & Stauffer, J. R. 1996, AJ, 112, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Proszkow, E.-M., & Adams, F. C. 2009, ApJS, 185, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Schmitt, J. H. M. M., Prosser, C. F., & Stauffer, J. R. 1995, A&A, 300, 134 [NASA ADS] [Google Scholar]
- Randich, S., Aharpour, N., Pallavicini, R., Prosser, C. F., & Stauffer, J. R. 1997, A&A, 323, 86 [NASA ADS] [Google Scholar]
- Randich, S., Pallavicini, R., Meola, G., Stauffer, J. R., & Balachandran, S. C. 2001, A&A, 372, 862 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Randich, S., Tognelli, E., Jackson, R., et al. 2018, A&A, 612, A99 [Google Scholar]
- Reggiani, M., & Meyer, M. R. 2013, A&A, 553, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Wilking, B., Meyer, M. R., et al. 2016, A&A, 588, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Jeffries, R. D., Randich, S., et al. 2015, A&A, 574, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Spina, L., Randich, S., et al. 2017, A&A, 601, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D.,& Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R. 2010, ARA&A, 48, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Spera, M., Mapelli, M., & Jeffries, R. D. 2016, MNRAS, 460, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014a, A&A, 568, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014b, A&A, 567, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Magrini, L., et al. 2017, A&A, 601, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1987, Dynamical evolution of globular clusters (Princetown: Princetown University Press) [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., Prosser, C. F., et al. 1997, ApJ, 479, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Hartmann, L., Fűrész, G., Hsu, W.-H., & Mateo, M. 2015, AJ, 149, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2011, A&A, 533, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tutukov, A. V., 1978, A&A, 70, 57 [NASA ADS] [Google Scholar]
- Wright, N. J., Bouy, H., Drew, J. E., et al. 2016, MNRAS, 460, 2593 [NASA ADS] [CrossRef] [Google Scholar]
The GES science archive is run by the Royal Observatory of Edinburgh. More information on the archive are available at their website: ges.roe.ac.uk
Available online at https://github.com/MichielCottaar/velbin
The python implementation of the procedure is available at: https://github.com/eleonorazari/KinematicModelling.
All Tables
Velocity dispersion estimates obtained with the maximum likelihood procedure described in the text using the Nelder–Meadmethod, except those indicated by an asterisk (where the Newton Conjugate Gradient method was employed).
Completeness, total mass, and half mass radius of the four clusters calculated with the three different methods.
All Figures
 |
Fig. 1 Gravity index γ as a function of the stellar effective temperature Teff for the starsobserved with GIRAFFE. The yellow filled dots are the stars identified as giants, while the remaining stars are shown as green filled dots. The black line indicates the threshold used to separate the giants and the non-giants. |
| In the text | |
 |
Fig. 2 Gravity index (γ) as a function of the surface gravity (log g) for IC 2602. The blue dots are the targets with an effective temperature greater than 5400 K, while the gray dots are those with a Teff < 5400 K. The solid lines delimit the regions in which a target is considered a giant star based on its γ index (above the horizontal black line) and on its log g value (to the left of the vertical black line). |
| In the text | |
 |
Fig. 3 Equivalent width of the lithium line as a function of Teff. The purple stars are the known members of the four clusters used to trace the lower envelope of the bulk of cluster spectroscopic candidates (solid line), as given in the literature. The open red circles show the members of each cluster that were reported in the literature and observed again by GES. The green symbols mark the stars selected as spectroscopic candidates. The stars excluded by the lithium criterion are shown in black. We also highlight the sources with an estimate of EW(Li) (dots and squares) or only an upper limit (arrows and crosses). |
| In the text | |
 |
Fig. 4 Radial velocity distribution. The blue, black, and red dashed lines represent the fits performed by setting the binary fraction to 0.2, 0.5, and 0.8, respectively. |
| In the text | |
 |
Fig. 5 Hertzsprung–Russell diagram of the sample of clusters. The colored filled dots represent GES targets retained after the procedure of cleaning from the obvious contaminants. The spectroscopic candidates color-coded depending on the probability of belonging to the cluster (scale at right). The magenta and blue lines are the isochrones at 20 and 50 Myr, respectively, and the black and red lines are the PMS evolutionary tracks (Tognelli et al. 2011). |
| In the text | |
 |
Fig. 6 Spatial distribution of GES and TGAS stars in the four clusters. The black points are the stars observed with GES and the red filled dots are the spectroscopic candidates selected in Sect. 4.1. The blue diamonds are the stars selected as members by G17 within the radius RGES. The stars identified by red dots and blue diamonds are those used to derive the velocity dispersions in the GES and TGAS sample, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


