| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832855 | |
| Published online | 20 June 2018 | |
Timescales of major mergers from simulations of isolated binary galaxy collisions
1
Departament de Física Quàntica i Astrofísica and Institut de Ciències del Cosmos (ICCUB) Universitat de Barcelona C. Martí i Franquès, 1, 08028 Barcelona, Spain
e-mail: jm.solanes@ub.edu
2
Instituto de Astrofísica de Andalucía, IAA–CSIC Glorieta de la Astronomía s/n, 18008 Granada, Spain
Received:
19
February
2018
Accepted:
27
April
2018
A six-dimensional parameter space based on high-resolution numerical simulations of isolated binary galaxy collisions has been constructed to investigate the dynamical friction timescales, τmer, for major mergers. Our experiments follow the gravitational encounters between ∼600 pairs of similarly massive late- and early-type galaxies with orbital parameters that meet the predictions of the Λ-cold dark matter (ΛCDM) cosmology. We analyse the performance of different schemes for tracking the secular evolution of mergers, finding that the product of the intergalactic distance and velocity is best suited to identify the time of coalescence. In contrast, a widely used merger-time estimator such as the exhaustion of the orbital spin is shown to systematically underpredict τmer, resulting in relative errors that can reach 60% for nearly radial encounters. We find that the internal spins of the progenitors can lead to total variations in the merger times larger than 30% in highly circular encounters, whereas only the spin of the principal halo is capable of modulating the strength of the interaction prevailing throughout a merger. The comparison of our simulated merger times with predictions from different variants of a well-known fitting formula has revealed an only partially satisfactory agreement, which has led us to recalculate the values of the coefficients of these expressions to obtain relations that fit major mergers perfectly. The observed biases between data and predictions, which do not only apply to the present work, are inconsistent with expectations from differences in the degree of idealisation of the collisions, their metric, spin-related biases, or the simulation set-up. This indicates a certain lack of accuracy of the dynamical friction modelling, arising perhaps from a still incomplete identification of the parameters governing orbital decay.
Key words: galaxies: halos / galaxies: interactions / galaxies: kinematics and dynamics / methods: numerical
© ESO 2018
1. Introduction
A consequence of the hierarchical nature of structure formation in a cold dark matter (CDM) Universe is that dark haloes are built through the merging of earlier generations of less massive haloes. To cause gravitationally bound interactions between extendedlf-gravitating haloes (and their galaxies) typically requires a dissipative process that reduces the initial orbital energies of the colliding objects. Dynamical friction fulfils this role by transferring energy and momentum from their relative motion to internal degrees of freedom. As a result, the orbits of interacting galaxies evolve and may eventually decay and culminate in a merger. The accurate determination of the merging timescales driven by dynamical friction is therefore a centrepiece of studies of the evolution of galaxies. For example, in semi-analytic models of galaxy evolution, the merger times are directly involved in the assessment of many fundamental quantities such as the luminosity/stellar mass function, the amount of gas available to form new stars, the star formation rate, the abundance of first-ranked galaxies, and the distribution of galaxy sizes, metallicities, colours, and morphologies (e.g. Kauffmann et al. 1993; Lacey 2001; Ricciardelli & Franceschini 2010; Hirschmann et al. 2012; Benson 2012; Muñoz-Arancibia et al. 2015). Of all galaxy- galaxy interactions, the class of so-called major mergers, involving pairs of objects with similar mass, are especially relevant as they play a central role, not only in the assembly history of galaxies (e.g. Lidman et al. 2013; Tasca et al. 2014), but also in that of their central supermassive black holes (SMBH) and the subsequent triggering of nuclei activity (e.g. Foreman et al. 2009; Yu et al. 2011; Liu et al. 2011; Koss et al. 2012; Capelo et al. 2017).
Virtually all formulas that are currently used to estimate the merger time, τmer, are based on the idealised Chandraseckhar (1943) description of the deceleration caused by dynamical friction on a point mass (representing the satellite) travelling through an infinite, uniform, and collisionless medium (representing the host). They are mostly prescriptions inferred from the analytic or semi-analytic modelling of mergers (e.g. Lacey & Cole 1993; van den Bosch et al. 1999; Taffoni et al. 2003; Gan et al. 2010; Petts et al. 2015; Silva et al. 2016) or parametric equations tuned by direct comparison with the outcome of numerical simulations of collisions of live galaxy pairs (e.g. Boylan-Kolchin et al. 2008; Jiang et al. 2008; Just et al. 2011; McCavana et al. 2012; Villalobos et al. 2013), or both (e.g. Colpi et al. 1999). However, although several decades of studies of galactic mergers have allowed reaching a general consensus on what probably are the most relevant parameters in any process of this type, the extent of their impact is still a matter of debate. Factors such as continued mass losses due to tidal interactions, the drag force exerted by tidal debris, the re-accretion of some of this material onto the colliding galaxies, or the mutual tidal distortion of their internal structures are elements that introduce nontrivial uncertainties in any attempt to calculate τmer using analytical expressions. To these difficulties, which are caused by physical complexity, one must add the lack of a 100% standard methodology regarding the way mergers are tracked. The starting point of this work is precisely the definition of a new metric for calculating τmer, which is an obligatory first step to compare the outcomes of different experiments under equal conditions and derive universally valid formulas, in a form that is suitable for major mergers. With this aim, we have run a suite of nearly 600 high-resolution N-body simulations of isolated major mergers, with which we further explored the dependence of the merger time on a range of orbital parameters and on the mass-ratios, spins, and morphologies of the progenitors that are representative of such systems.
Several reasons justify the realisation of this type of research with controlled experiments. On one hand, they involve a substantial increase in resolution with respect to what would feasible in an entirely cosmological context, at least for samples of binary collisions as large as ours, allowing both host and satellites to have more realistic internal structures. On the other hand, we aim to extend former studies that focussed on the duration of mergers from the standpoint of isolated systems by correcting their main weaknesses, for instance, the systematic adoption of ad hoc initial conditions, such as strongly radial orbits and small pericentric distances. Although there is some physical basis in this approach, the intention is above all to lead to fast merging that saves CPU time (e.g. Khochfar & Burkert 2006). In addition, the initial equilibrium galaxy models of controlled investigations of dynamical friction, especially the oldest ones, frequently do not conform to the paradigm that is currently accepted for these systems by including haloes with a parameterisation of their internal structure (e.g. isothermal) that is derived from first principles, and sometimes, with the just minimum extension required by the observed flatness of the rotation curves of galactic discs.
While today it is not difficult to find pre-prepared simulations of binary collisions that offer realistic galaxy models that satisfy observational constraints (e.g. Boylan-Kolchin et al. 2008; Van Wassenhove et al. 2012; Villalobos et al. 2013; Barnes 2016; Capelo et al. 2017), the assignment of initial orbital conditions is a problem that is still solved guided more by common wisdom than by specific evidence. Nevertheless, this does not have to be the case. If the results of binary mergers served at the time as a guide for the first fully cosmological experiments, we can now use these experiments as feedback to establish realistic initial conditions for the merger and thus to compare the results of both types of simulations on a roughly equal footing. In this regard, we wish to emphasise that the present work represents the first study of dynamical friction based on gravitational encounters of well-resolved pairs of galaxies resembling local objects whose set-up relies entirely on initial conditions inferred from large-scale-structure simulations carried out in the framework of the standard concordant ΛCDM model, including those that incorporate baryon physics (e.g. Khochfar & Burkert 2006; Jiang et al. 2008; Bryan et al. 2013).
Working with stand-alone systems also enables both isolating the effects of the different parameters that regulate dynamical friction and clarifying and enhancing the accuracy of measurements compared to those that are possible in a large-scale-structure formation context. We therefore compare our measured timescales with predictions arising from different variants of a physically motivated approximating relation that is widely used in both isolated and cosmological runs. Our original goal was to establish whether it holds true that when the initial conditions governing mergers are similar, so is their duration, regardless of the local distribution of matter around the galaxies. We have found a relatively important bias between measured and estimated times, however, that we had not anticipated, whose magnitude and behaviour surpass what would be expected from differences in the degree of idealisation of the merger context (isolated versus cosmological), in the metric, or in the configuration of the simulations. The present investigation is completed by using our simulations to recalculate the coefficients of the most popular versions of the merger-time formula with the aim of providing analytical prescriptions that are suitable for major mergers.
This then is the layout of the paper. In Sect. 2 we present our suite of simulated binary collisions. After discussing different alternatives for tracking major mergers and measuring their length, the new, accurate metric for major mergers is defined in Sect. 3, while in Sect. 4 we explore the dependence of τmer on a series of parameters that are known to regulate the effectiveness of dynamical friction. Finally, in Sect. 5, we first compare the outcome of our simulations with the predictions from a well-known set of parametric models for τmer and conclude by readjusting the coefficients of these models, so that they offer an improvement in the predicted timescales for major mergers. After outlining our conclusions in Sect. 6, we conclude with two appendices that provide details for the provision of rotation to our haloes (Appendix A) and the strategy we followed to relate the initial conditions of our simulated galaxy pairs to their subsequent orbital evolution driven by gravity (Appendix B).
Physical scales are calculated throughout the manuscript assuming a standard flat ΛCDM cosmology with present-epoch values of the Hubble parameter, and total mass and dark energy density parameters equal to H0 = 70 km s−1 Mpc−1, Ωm,0 = 0.3, and ΩΛ,0 = 0.7, respectively.
2. Simulations
In this section we explain the main ideas behind the numerical method we used to create our suite of galaxy mergers. Further details regarding the galactic halo models used here can be found in Darriba & Solanes (2010), Darriba (2013), and Solanes et al. (2016).
2.1. Models of galaxy pairs
Each galaxy pair consists of two non-overlapping extended spherical haloes whose global properties (mass, spin, concentration, and density profile of the dark component) are used to set the scalings of their central baryonic (stellar) cores. Progenitor galaxies of late-type are made of a spherical Navarro et al. (1997, NFW) CDM halo and of a central exponential disc of stars-surrounding a non-rotating spherical Hernquist (1990) stellar bulge. For the largest progenitors, the bulge mass, Mb, is taken equal to 25% of the disc mass, Md, as they are intended to represent a Hubble-type Sb spiral, while Mb = 0.1 Md for the smallest progenitors, which imitate local Sc galaxies (Graham 2001). Early-type galaxy models also consist of a spherical NFW CDM halo and an inner non-rotating stellar component represented by an oblate Hernquist profile with an intrinsic flattening c/a = 0.7, which is the most common value among local elliptical galaxies (Statler 1995). In all cases, the mass of the luminous component is taken equal to 5% of the total galaxy mass. Unlike other galaxy models that find it preferable to smoothly taper off the density profiles using an exponential cut-off (e.g. Springel & White 1999; Barnes 2016), we sharply truncated the stellar distributions at a radius encompassing 95% of the luminous mass and the dark particle distributions at the halo virial radius, and we redistributed the leftover mass within these radii. We expect our calculations to be relatively insensitive to the details of the truncation procedure.
As customary, we employed a numerically convenient dimensionless system of units in our simulations. We adopted G = 1 for Newton’s gravity constant, with the virial mass, velocity, and radius of the primary galaxies set to 1. Since these objects are assumed to have a total mass equal to that commonly associated with a MW-sized galaxy in the local Universe, which is around 1012 h−1 M⊙ (see e.g. Klypin et al. 2002; Boylan-Kolchin et al. 2009, and references therein), according to the adopted cosmology, our models may therefore be compared with real galaxies using the following physical scaling per simulation unit (su) for mass, length, velocity, and time: Msu = 1.42 × 1012 M⊙, Rsu = 297 kpc, Vsu = 144 km s−1, and Tsu = τdyn(z = 0) = 2.02 Gyr (see Eq. (4)). As a general rule, all quantities in this text are given in these units unless otherwise noted.
Parent galaxies of unit mass were modelled using a total of 210 000 particles, while all our experiments adopted a 50–50 split in number between luminous and dark bodies. This can be shown to provide a much better sampling of the former at the cost of a modest increase in the numerical heating that compensates for the relatively moderate resolution of the experiments dictated by the large size of the sample (Sect. 2). A single extra particle representing an SMBH was added at the centre of each galaxy. The SMBH particle masses were calculated assuming a mean ratio 〈MSMBH/Mb〉 ∼ 0.003 that is typical of massive galaxies in the local Universe (see, e.g. Graham 2016, and references therein). We set the Plummer equivalent softening length for the star particles to 30 pc, which in our simulations is comparable to the minimum physical scale at which we can resolve the dynamics of the largest remnants given the number of bodies adopted (see Sect. 3). In the case of the more massive bodies (DM and SMBH), we took a softening length proportional to the square root of their body mass to achieve the same maximum interparticle gravitational force.
Our multi-component galaxy models were generated with the aid of a much-improved version of the computationally efficient MAGALIE open-source code (Boily et al. 2001) that is included in the NEMO Stellar Dynamics Toolbox1. Our upgraded version of the code allows simulated galaxies to begin very close to equilibrium, and they require a negligible additional time to settle. The new approximate solution adopted for the velocity field causes a minor initial structural readjustment when the models are evolved. In practice, this means that with a large enough number of particles (N ≳ 100 000), transients damp out in less than one-half of a revolution at the half-mass radius, settling swiftly to values close to those sought from the initial conditions. When the short transitional period is completed, we have checked that the structural and kinematic properties of all our galaxy models remain statistically unchanged for as long as a Hubble time when they evolve in isolation, even at the lowest resolution (∼70 000 particles per galaxy).
A rotation is imparted to the DM haloes of our galaxies to incorporate the effect of large-scale fluctuations. Appendix A shows that the net fraction of DM halo particles that must spin in the positive direction along the Z axis (we chose this to be the rotation axis) to produce a given dimensionless halo spin parameter, λ, can be inferred from![$$ \begin{array}{l}{f}_{\mathrm{h}}\equiv \frac{{N}_{\bullet,{j}_z^{+}-}{N}_{\bullet,{j}_z^{\thinspace-\thinspace}}}{{N}_{\bullet }}\approx 3\frac{\lambda }{\alpha {g}_{\mathrm{c}}}\frac{[\mathrm{\ln}\left(1+c\right)-c/(1+c){]}^{5/2}}{[1-1/{\left(1+c\right)}^2-2 \mathrm{\thinspace ln}(1+c)/(1+c){]}^{1/2}},\\ \end{array} $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq1.gif) (1) where N• is the total number of particles of the dark halo component, α a is model-dependent factor whose value must be set empirically, and c is the halo concentration inferred from the median concentration-mass relation used in the galaxy halo models of Darriba & Solanes (2010),
(1) where N• is the total number of particles of the dark halo component, α a is model-dependent factor whose value must be set empirically, and c is the halo concentration inferred from the median concentration-mass relation used in the galaxy halo models of Darriba & Solanes (2010),![$$ c\left(M,z\right)=9.35{\left[\frac{M}{1{0}^{12\thinspace}{\mathrm{h}}^{-1}{M}_{\odot }}\right]}^{-0.094}{\left(1+z\right)}^{-1}, $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq2.gif) (2) which provides a reasonable approximation to the results from high-resolution N-body simulations of the standard concordant ΛCDM cosmology measured over the ranges of halo masses, M ∼ 1012 M⊙, and redshifts, z ∼ 0, we are interested in2. For our model galaxies, we found that to obtain the desired amount of angular momentum, we must take α ≃ 1/2, which agrees well with the radial velocity dispersion profile of isotropic NFW haloes with c ∼ 10 (Łokas & Mamon 2001). We refer to Appendix A for the definitions of the parameters λ, c, and α.
(2) which provides a reasonable approximation to the results from high-resolution N-body simulations of the standard concordant ΛCDM cosmology measured over the ranges of halo masses, M ∼ 1012 M⊙, and redshifts, z ∼ 0, we are interested in2. For our model galaxies, we found that to obtain the desired amount of angular momentum, we must take α ≃ 1/2, which agrees well with the radial velocity dispersion profile of isotropic NFW haloes with c ∼ 10 (Łokas & Mamon 2001). We refer to Appendix A for the definitions of the parameters λ, c, and α.
2.2. Initialising the models
Traditionally, idealised binary merger simulations were hampered by the lack of knowledge of the appropriate initial conditions. In recent years, however, several high-resolution, large-scale cosmological simulations have carried out detailed investigations of the orbital parameters of merging pairs of CDM haloes, which provided sufficient information to fill this gap (e.g. Benson 2005; Khochfar & Burkert 2006; McCavana et al. 2012). In the present work, the full set-up of the mergers is based on cosmologically motivated initial conditions. This means that the values of all the parameters that define the initial orbital configurations of the pairs were set taking their corresponding probability distribution functions (PDF) as predicted by currently favoured cosmological models into account.
2.2.1. Parameters that define the orbits
We have set the initial orbital parameters of our merging galaxies by assuming that at t = 0, they behave to a large extent as point-mass objects, which allows applying the solution of the Keplerian two-body problem.
As discussed in Appendix B, under this approximation, three parameters are required to completely define the initial orbit of two interacting galaxies. For our investigation, we chose the initial modulus r0 of the relative position vector connecting the nuclear regions of the galaxies, which in all our experiments was taken equal to the sum of the two virial radii of the galactic halos, the initial orbital energy, which we represent, as usual, by the dimensionless parameter rcir,p expressing the radius of a circular orbit with the same orbital energy of the merger in units of the virial radius of the primary halo, and the initial orbital circularity, ϵ, which is a proxy for the initial orbital angular momentum. We note in passing that our choices for the intercentre separation and the initial orbital energy lead to initial values for the time derivative of r0, that is, for the relative radial velocity of the galaxies, ν0, of about 100–150 km s−1 that are consistent with the observed “cold Hubble flow” (low value for the root-mean-square galaxy velocity) in the Local Volume (see, e.g. Teerikorpi et al. 2005, and references therein).
Various authors (Tormen 1997; Zentner et al. 2005; Khochfar & Burkert 2006; Jiang et al. 2008; McCavana et al. 2012) have used cosmological simulations of merging DM haloes to study the distribution of orbital circularities in merging pairs. There is general consensus that the circularity parameter follows a universal distribution, with a central peak near ϵ ≃ 0.45 (corresponding to an ellipticity ϵ ≃ 0.9) and a strongly platykurtic behaviour characterised by a substantial, log-normal distributed spread with σ ∼ 0.4, which accounts for the stochastic nature of merger processes with equivalent initial conditions, and which points to a relative overabundance of highly circular bound orbits with respect to highly radial ones. Based on these results, and to take into account the effect that different amounts of orbital angular momentum transfer may have on the remnants, we simulated collisions along three different orbital trajectories defined by ϵ ≃ 0.20, 0.45, and 0.70. From now on, we refer to the geometry of these orbits as radial, tangential, and elliptical, respectively.
As shown by McCavana et al. (2012), the initial orbital energy of their bias-free dataset obeys a right-skewed distribution that peaks slightly beyond 1 and has a long tail towards extremely energetic orbits. Following the results from these authors (see their Fig. 3) and in line with our procedures for the other orbital parameters, we adopted three different values for rcir,p that encompass the bulk of the distribution of McCavana et al. (2012): 1.3 ≃ 4/3, intended to approximate the modal value of their PDF, 2, and 2.7 ≃ 8/3.
Table 1 summarises the values of the initial orbital parameters that we adopted for galaxy pairs with a reduced initial orbital energy rcir,p = 4/3 and the three integer mass ratios that commonly define major mergers. The Greek letter η ≡ Mp/Ms is used throughout to express the ratio between the masses of the largest galaxy and its merger partner.
Initial parameters for major mergers with rcir,p = 4/3.
2.2.2. Magnitude and relative orientation of internal spins
Cosmological N-body simulations and observational estimates agree in that the dimensionless spin parameter of galactic haloes (see Eq. A.6) follows a roughly universal positively skewed lognormal PDF, P(λ), of median, λ0, close to 0.04, even when the non-gravitational processes acting on the baryons are considered (see, e.g. Shaw et al. 2006; Hernandez et al. 2007, Bryan et al. 2013 and references therein). In an attempt to take into account the wide range of values shown by this parameter, we decided to construct late-type galaxy models that include up to four different dark halo spin values: λ = 0.02, 0.04, and 0.06, which sample the central region of P(λ) where the probability is highest, and λ = 0.0,, which is used as a reference for calibrating the effect of halo rotation in our results. In the case of early-type galaxies, Eq. (1) with α = 1/2 is regarded as a convenient formula that allows us to provide haloes with the correct spin. Since it is reasonable to expect that the dark haloes associated with early-type galaxies have less angular momentum than those associated with discs, we modelled the former using solely λ = 0.02.
The spin of galactic haloes can have a substantial effect on the encounter rate of their constituent particles, affecting the strength of the dynamical friction force that is mutually exerted by the galaxies and, by extension, the merger time (see Sect. 4) and even the structure of the remnant. For this reason, the outcome of a galaxy collision is expected to depend on both the moduli and the degree of alignment between the orbital and halo spin vectors – according to the numerical studies of merging by Benson (2005) and Khochfar & Burkert (2006), the angles between the two spin planes of the galaxies, between each one of the spin planes and the orbital plane, between the infall direction and the infall velocity, and between the infall velocity of satellites and the angular momentum of their host haloes are all essentially uncorrelated. Therefore, to assess the full scope of these contributions, we adopted the 12 extremal configurations for the initial relative orientations of the galaxies that maximise/minimise the coupling between the internal and orbital spin vectors, in addition to simulating haloes with different rotation speeds (see Appendix A). Given that the orbits of all our mergers lie in the XY plane, we can use the standard versors of the 3D Cartesian coordinate system, î, ĵ, and 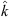 , to identify the different directions that were initially adopted for the internal spins of the primary and secondary galaxies, Jp and Js, respectively. They are listed in Table 2.
, to identify the different directions that were initially adopted for the internal spins of the primary and secondary galaxies, Jp and Js, respectively. They are listed in Table 2.
Initial orientations of the internal spins of the primary (p) and secondary (s) progenitors.
2.3. Library of binary mergers
The evolution of the galaxy mergers was performed using GyrfalcON, a fully developed serial N-body tree-code using Dehnen’s force algorithm of complexity 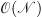 (Dehnen 2000) that is implemented in the NEMO toolbox. We took Ncrit = 6 for the maximum number of bodies that avoid cell splitting when building the tree, a tolerance θ = 0.40, and a longest timestep of ∼0.001 simulation time units. The time integration we adopted uses an adaptive block-step scheme that assigns individual time-steps to the bodies by dividing the longest step into 26 parts as controlled by the parameters fac = 0.03 and fph = 0.0015. For all simulations the merger remnants were allowed to evolve ∼1.5 Tsu (∼ 3 Gyr) after the centres of the two galaxies coalesced. This has enabled us to obtain as a byproduct a massive suite of merger remnants that are suitable, for instance, for studying the effect of initial conditions on the structure of these systems and the manner in which they approach their final state of equilibrium. This and other related questions will be addressed in forthcoming papers.
(Dehnen 2000) that is implemented in the NEMO toolbox. We took Ncrit = 6 for the maximum number of bodies that avoid cell splitting when building the tree, a tolerance θ = 0.40, and a longest timestep of ∼0.001 simulation time units. The time integration we adopted uses an adaptive block-step scheme that assigns individual time-steps to the bodies by dividing the longest step into 26 parts as controlled by the parameters fac = 0.03 and fph = 0.0015. For all simulations the merger remnants were allowed to evolve ∼1.5 Tsu (∼ 3 Gyr) after the centres of the two galaxies coalesced. This has enabled us to obtain as a byproduct a massive suite of merger remnants that are suitable, for instance, for studying the effect of initial conditions on the structure of these systems and the manner in which they approach their final state of equilibrium. This and other related questions will be addressed in forthcoming papers.
We tested numerical convergence in our merging pair simulations by running a specific subset of configurations: DD equal-mass mergers with modal values of the reduced orbital energy and halo spin parameter (4/3 and 0.04, respectively), but with resolution (N) higher by a factor five. Comparison of the intercentre separation evolutions shows negligible differences, except for the final pericentric passage and merger times, which on average are shorter at high resolution by only a small 1.3% or about 60 Myr. We take this value as indicative of the typical uncertainty in the inferred merger times. The primary data output was made every 0.015 simulation time units or ∼30 Myr.
As described in the previous sections, the suite of binary mergers investigated in this paper combines different realisations of six quantities: mass ratio, orbital energy, orbital eccentricity (or circularity), module and orientation of the halo spin, and galaxy morphology. Nevertheless, not all the combinations allowed by the subsets of discrete values we adopted for them were performed. In an effort to optimise memory space and computational time, we avoided certain combinations of parameters that add nothing new to the investigation. Thus, the core of the encounter survey that most of the results of this study are based on is formed by 144 Sb + Sb (η = 1) mergers; this figure arises from multiplying the three values adopted for the circularity of orbits by the four possible values of the spin of galactic halos (in our simulations, the two progenitors share identical values of λ) and by the 12 distinct relative orientations of these spins: 144 Sb + Sc (η = 3) mergers and 36 E3 + E3 (η = 1) mergers, all ran with a reduced orbital energy rcir,p of 4/3. This primary sample was completed with 144 sb + sb (η = 1) mergers, plus 36 E3 + E3 (η = 1) mergers with orbital energy 2.0, as well as by 36 E3 + Sc (η = 3) and 36 Sb + E3 (η = 3) mergers with rcir,p of 4/3. All subsets with an E3 galaxy had λ fixed to 0.02. Finally, a subset of 18 additional S + S encounters with rcir,p of 8/3 and λ = 0.04 were run with the sole purpose of completing a number of combinations of orbital parameters that allow a fitting formula for major mergers to be obtained with a minimum level of accuracy (see Sect. 5.2). This gives a total of 594 major merger simulations, which is the largest science sample of numerical models of isolated galaxy pairs ever built to study these types of phenomena.
3. Merging timescale
Our definition of the merger timescale, τmer, follows the same general lines as have been adopted in previous numerical studies of dynamical friction that considered galaxy mergers that were either isolated or developed within a cosmological context (e.g. Boylan-Kolchin et al. 2008; Jiang et al. 2008; McCavana et al. 2012; Villalobos et al. 2013). The start of a merger is defined as the instant when the centre of mass of the satellite-to-be galaxy first crosses the virial radius of its host halo (Benson 2010), which means that the initial radial distance between a given primary galaxy and its satellites is always the same, while a merger ends at the instant when it is no longer possible to distinguish two separated entities. There are, however, several ways to pinpoint the endpoint that yield similar but not identical results. A popular criterion based on the classically perceived picture of the merger process is to use the time at which the satellite has lost (almost) all of its specific angular momentum relative to the host (e.g. Boylan-Kolchin et al. 2008). Alternatively, one can seek for the minimisation of some other function of the relative separation of galaxies in phase space Δ(t) ≡ f(r(t), ν(t)) or of the number of bound particles of the satellite, Nbound,s(t). This last option is best suited to track mergers in which satellites are fully tidally disrupted before the galaxies coalesce, which is not the case in our major merger simulations. Approaches of this type, based on the nullification of some characteristic time-decreasing property, need to solve a serious difficulty: it is computationally not feasible to achieve such cancellation. To overcome this problem, a frequent recourse that has been used, for example, in the works cited at the beginning of this section, is to adopt a priori a reasonable minimum threshold for this property, which is generally expressed as a small fraction of its initial value (5% is the most frequent choice), below which the merger is considered complete. Nevertheless, there is no guarantee that this procedure works well in all situations. To begin with, the fact that none of the properties suitable for tracking the evolution of a merger follows an entirely monotonic decrement entails the risk that any threshold, however small, is reached occasionally before the end of the merger, which would then lead to an underestimated merger timescale. In addition, the adoption of an extremely low threshold value is not the solution either, since the aim is to define a standard metric that can be applied to any simulation regardless of its resolution. This has led us to propose a new strategy based on the monitoring of the temporary evolution of the behaviour, rather than the quantitative value, of Δ(t). As we show below, the shape of the intercentre separation history provides not only a straightforward, but more importantly, an accurate and resolution-free way of defining the instant at which the galaxies coalesce, especially for the type of simulations we study.
3.1. Tracking scheme
To track the orbital evolution of the galaxies throughout the span of the entire simulation, we reduced in each snapshot the galactic haloes to a system of two point masses. Thus, throughout the entire simulations, the progenitors are represented in phase-space by the six coordinates of the centre of mass of the upper decile of the most closely bound particles of their baryonic cores, which constitute the region of highest matter density for any galaxy. Since the galactic cores have a larger spread in velocity than in position (Barnes 2016), 10% of the stars of each galaxy averages over enough bodies to provide an accurate determination of the galaxy velocity. This is also the reason why all variables that depend on ν(t), such as the orbital angular momentum, present a higher level of noisiness than those depending on r(t). Particle binding energies are computed according to the gravitational potential calculated from all the remaining bodies assigned to the parent galaxy at the start of the merger. We show in Fig. 1 the time evolution of the mean separation in configuration space between the dynamical centres, defined using different fractions of bound particles and by the particle representing the central SMBH, of a pair of Sb + Sc galaxies colliding along a radial orbit with an initial energy rcir,p of 4/3, so in this case Δ(t) = r(t). It is obvious from this plot that galactic cores defined using the average position of subsets of the most bound particles allow tracking the evolution of the merger even along its most advanced stages, when the global structure of the progenitors is heavily disrupted by the violently changing gravitational field and the variation in their overall centre-of-mass positions and velocities is no longer predictable. As this evolution is computed, it is straightforward to identify the instants ti of closest approach (pericentric passages) as those points in which the relative distance between the dynamical centres of host and satellite, r(t), reaches a local minimum (that behaves as a non-differentiable type I discontinuity). In addition, the logarithmic scale used in the Y axis permits appreciating that coalescence is punctuated by a nearly instantaneous, and in most cases, sharper-than-a-pericentric-passage drop in the intercentre distance that resembles a jump or step discontinuity (we show below that this abrupt minimisation is extensive, to a greater or lesser extent, to any function of the six coordinates of phase space). This well-defined step facilitates in practice identifying the time of coalescence, tcoal, by starting the analysis of the time history of Δ(t) beyond the completion of each merger and tracing back its evolution. The galaxies coalesce when the relative variation of the separation reaches its highest value, which is reflected, for example, in the maximisation of the time derivative of the logarithm of Δ(t). To facilitate the identification of such jump, it may sometimes be necessary to apply a low-pass filter to Δ(t).
 |
Fig. 1 Time evolution of the intercentre distance r, in units of the radius Rp of the primary halo, of a pair of Sb + Sc galaxies with mass ratio 3:1 and internal spin parameter λ = 0.04 colliding along a radial orbit. The initial orientation of the internal spin of the haloes is X90Y90 (see Table 2). Different solid curves show merger histories calculated using different definitions of the galactic cores: green shows the 5% fraction of the most closely bound luminous particles, black shows the 10% fraction, blue shows the 25% fraction, and coral the 50% fraction, while the red line shows the merger evolution as determined from the central SMBH. The intersection of these curves with the grey horizontal dotted line marks the onset of the merger. The plot shows that the final coalescence of the galaxies at t/τdyn ∼ 2.4 is better delineated when the galactic cores are defined using a moderate fraction, between 5 and 25%, of the most closely bound particles. |
In addition, Fig. 1 reveals that shortly after coalescence, the intercentre separation, still calculated from the bodies initially assigned to each parent galaxy, begins to oscillate steadily around a constant residual value with an also constant amplitude (the particles defining the galactic cores can vary between consecutive steps, which explains why these fluctuations are not fully harmonic). We note that when the dynamic centres are optimally defined, the mean intercentre distance in the post-coalescence phase provides a direct estimate of the minimum spatial resolution scale of the remnant. In our 3:1 mergers, it is found that this value is ∼5 × 10−4 Rsu (see Fig. 1), while for 1:1 mergers, it decreases until it reaches ∼10−4 Rsu, which just happens to be similar to the force-softening scale adopted for the luminous component. This implies that our choice of softening length provides a good compromise between efficiency and fidelity for our N-body experiments.
3.2. Accurate metric for major mergers
In Figs. 2 and 3 we show four examples of functions that can be used to track the merger history Δ(t) in two extreme encounter configurations. Figure 2 depicts the merger of equal-mass disc galaxies along elliptical orbits, while Fig. 3 shows the evolution of Sb + Sc 3:1 mergers along radial orbits, in both cases with λ = 0.04. The 12 curves shown in each panel correspond to the 12 extremal relative orientations of the galaxies listed in Table 2. A comparison between the two figures shows some common trends as well as noticeable differences. It is a trend that for the two groups of merger histories the different relative orientation of the discs leads to appreciable variations in the coalescence time in the order of 0.3–0.4 Tsu or ∼0.6–0.8 Gyr. On the other hand, the main differences have to do with the fact that collisions along the most circular orbital configurations proceed in a more orderly fashion, which indicates that the strength of the dynamical friction, that is the duration of the mergers, is modulated by the initial relative orientation of the internal spin of the principal halo with respect to the orbital spin (see also next section). However, this is not the case for radial collisions, where we observe that the maximum length of mergers corresponds to the Y90Y90 and Y270Y90 configurations. This indicates that the more eccentric the orbits, the more effective the scrambling of the initial internal spin of the merging haloes through collisions.
 |
Fig. 2 Time evolution of the intercentre separation of Sb + Sb mergers of equal-mass galaxies with internal spin parameter λ = 0.04 colliding along elliptical orbits. Different panels show different choices for Δ(t): panel a) the intercentre distance, panel b) the specific orbital angular momentum, panel c) a weighted non-canonical distance in phase space based on the Euclidean notion of distance, and panel d) the product of the intercentre distance and relative velocity. Normalisation units Rp and Vp refer to the virial radius and velocity of the primary halo, respectively. Galaxy centres are calculated from the 10% fraction of the most closely bound luminous particles. Coloured solid curves in each panel show the merger histories corresponding to the 12 initial orientations adopted for the internal spin of the haloes (see legend in panel a and Table 2). In panel a, the intersection of the curves with the black horizontal dotted line marks the onset of the mergers. In panel b, the black horizontal dotted line marks the value of j05 inferred for the black solid curve (X90Y90). The values of j05 for the other curves are very similar. |
Pericentric, and depending on the function used to estimate Δ(t), apocentric, passages are also more clearly highlighted in head-on collisions. The strongest differences correspond to the merger histories depicted in panels b and d. The specific orbital angular momentum j(t) represented in panel b begins to experience noticeable losses only after the first pericentric passage, but its evolution is essentially monotonic and nearly constant in time for elliptical orbits, while it is impulsive (step-wise) for radial collisions, at least along the first pericentric passages. In contrast, the evolution of the product of the relative distance and velocity of the centres, rν(t), shown in panel d, is always non-monotonic, with the most eccentric collisions showing substantially deeper local minima associated with passages through the extreme points of the orbit.
Figure 2, and especially Fig. 3, also reveal that regardless of the merger tracker function, the centres can continue to sink for quite a long time after Δ(t) has dipped within 5% of the value it had the first time the satellite galaxy crossed the virial radius of the primary (this threshold for j(t), which we refer to as j05, is indicated by the horizontal black dotted line in the b panels). It is therefore apparent that definitions of the merger timescale that are based on this or similar conditions may lead to a systematic underestimation of the merger length. Thus, for the particular case of j05, our Fig. 4 indicates that regardless of the mass ratio of the progenitors, the use of this quantity for calculating merger timescales results in fractional differences with a median value of about 6% for major mergers along elliptical orbits. The differences increase to about 16% at intermediate orbital circularities and are distributed into two narrow and clearly separated peaks at about 20% and 60% for radial collisions (in the bottom panel of Fig. 4, corresponding to the Sb + Sc case, most data points exceed 20% by far). Moreover, a comparison of Figs. 2 and 3 shows that the difficulty in monitoring the final act of the orbital decay increases with increasing mass ratio and orbital eccentricity, which entails that not all possible merger histories Δ(t) are equally suitable for determining tcoal. Of those investigated in Figs. 2 and 3, the best overall behaviour corresponds to the product r(t)ν(t), although the difference with respect to j(t) is very small; this makes sense because the latter is the cross product of r and ν , so that its magnitude carries only an extra sin θ factor. Nevertheless, since the numerical calculation of the former function is not only straightforward but somewhat more stable numerically, we adopted the secular evolution of rν as our preferred merger tracker.
 |
Fig. 4 Comparison between τmer and τj05 measured from all the mergers depicted in Figs. 2 (left) and 3 (right). In all cases, τl05 < τmer, even when j(t) behaves as a purely monotonically decreasing function. |
4. Dependencies of τmer
In this section, we complete what has been said about the parameters that control the length of mergers by validating not only the dependencies expected from the classically perceived picture of this phenomenon, that is, variations with the initial circularity of the orbits, orbital energy, and mass ratio, but also some others that have seldom been discussed in previous works, at least with the level of detail that we provide here, such as dependencies on the magnitude and orientation of the initial internal spins and on the morphology of the progenitor galaxies.
4.1. Orbital parameters
Figures 5 and 6 illustrate the effects of varying the initial orbital energy and mass ratio, respectively, on the merger time, in both cases as a function of the initial circularity of the orbit. All our simulations show a clear trend for the full length of the merger to increase with these three parameters, consistently with earlier studies of dynamical friction. The increase in the value in either of the first two parameters delays the merger more markedly as circularity increases. Within the ranges of values chosen for our simulations, we find that the affectations in the location and scale of the merger time distributions induced by varying rcir,p and η are similar, with the sole difference that in the most radial collisions (є = 0.2), the changes in the orbital energy have barely any effect on τmer (≲ 5%). These two plots also show that the set of extremal initial relative orientations adopted for the internal spins of the parent galactic haloes introduces a significant scatter in τmer, which grows in line with the modulus of λ. In the most favourable configurations of all the mergers investigated (i.e. those with rcir,p = 2.0, η = 3, λ = 0.06), the spread can be up to ± 15%, equivalent to a total time-span of about 3 Gyr. Nevertheless, it can be estimated by assuming that the spin plane of the main halo and the orbital angular momentum plane are uncorrelated (Khochfar & Burkert 2006), that only ≲ 2% of the pairs in a given configuration participate in the most extremal deviations.
 |
Fig. 5 Examples of merger times measured in our simulations, τmer, as a function of the initial circularity of the orbit, є, showing the effect of varying the orbital energy, rcir,p, while keeping all other parameters unchanged. This plot shows results for equal-mass mergers of spiral galaxies with the modal value of the spin parameter (λ = 0.04). Open squares are used for mergers with rcir,p = 2.0, while open circles identify rcir,p = 4/3 mergers. Data points are shown with different offsets around the true values of є for clarity. |
 |
Fig. 6 Same as Fig. 5, but showing the effect of varying the mass ratio,η. Data points show results for mergers of spiral galaxies with the modal value of the orbital energy (rcir,p = 4/3). Open squares are used for mergers with η = 3, while open circles identify η = 1 mergers. |
4.2. Internal spins of host and satellite
The role of the progenitors’ spin in the duration of mergers can be better understood with the aid of Fig. 7. Since under normal circumstances it is reasonable to expect that Jorb >> Jhalo >> Jstars – even the fast-rotating stellar discs contribute modestly to the total spin of galaxies endowed with rotating massive DM haloes; in our primary late-type galaxies with λ = 0.04 for example, the stellar component provides less than 3.5% of the total internal angular momentum – a boost in є, η, or rcir,p, which are all parameters that directly influence Jorb, must easily bring about significant changes in the length of the merger time. In addition, any increase (decrease) in the value of the last two parameters while keeping all the other constant automatically leads to an increase (decrease) on the relative velocity of the collision, that is, on the amount of orbital energy, while the efficiency at which this energy is transformed into internal random motions decreases (increases): the force from dynamical friction behaves as fdyn ∝ Mpρs/v2. The strength of the dynamical friction prevailing on any merger is therefore essentially controlled by є, η, or rcir,p. In contrast, changes in λ only affect Jhalo, so that this parameter is expected to have a weaker influence on the merger time than the previous ones, which is detected as an increase in the spread of τmer. The observed symmetry on the scale of the deviations (see Fig. 7) relates to the symmetry of the adopted spin configurations (we recall that in our simulations both host and satellite are assumed to have the same spin parameter) and to the result, as shown in the previous section, that in mergers involving mass ratios higher than unity only the spin of the main progenitor matters. This characteristic also helps us to comprehend why the merger times of the simulations with η = 3 are not evenly allocated, but show a tendency to aggregate into distinct peaks that become more evident as the orbital circularity increases (see Fig. 6). Thus, although the peculiar trimodal distribution obtained for the most circular encounters is caused in part by the extreme configurations adopted for the initial relative orientations of the internal spins, its root cause is found when one considers which configurations make up the different groupings. In particular, we find that all set-ups in which both internal spins are orthogonal to that of the orbital plane, that is, those identified in our simulations with the labels X90X90, X90X270, Y90Y90, Y90Y270, and X90Y90, behave as collisions of spinless haloes, giving rise to merger times that are grouped around the central part of the time distribution inferred for є = 0.7. In three other configurations, RR, RX90, and RY90, the spin of the host determines that the collisions are basically retrograde, giving rise to the longest merger times, all also with durations similar to each other, while for the remaining four configurations, DD, DR, DX90, and DY90, the direct rotation of the main halo enhances the effectiveness of the encounters, producing the lower peak that is associated with the shortest timescales. These results are consistent with the outcome of the work by Villalobos et al. (2012), who studied the evolution of disc galaxies within the global tidal field of the group environment, finding that discs on retrograde orbits retain their internal structures and kinematics longer than prograde discs.
 |
Fig. 7 Same as Fig. 5, but showing the effect of varying the halo spin parameter, λ. Data points show results for equal-mass mergers of Sb galaxies with the modal value of the reduced orbital energy (rcir,p = 4/3). Open symbols identify different values of the spin parameter: λ = 0.00 (triangles), λ = 0.02 (squares), λ = 0.04 (circles), and λ = 0.06 (diamonds). Data points are shown with different offsets around the true values of є for clarity. |
The role of the satellites’ spin seems to be restricted to establishing the degree of interaction of the stellar cores, which determines the efficiency with which Jstars is drained. Thus, if we compare, for instance, the configurations DY90 and DX90 belonging to the same mode, we see that the small difference in their merger times arises because in the first case, the relative orientations of the galaxies favour a somewhat more intense contact between them, which leads to narrower close approaches near coalescence that slightly increase the speed of the orbital decay. Interestingly, although the segregation of the timescales induced by λ gradually develops from the first moments of the collision, it has no effect on the total number of pericentric passages experienced by the galaxies in the pre-coalescence stage, which is the same (four) in all cases; nor do we observe this number to depend on the mass ratio of the progenitors or the ellipticity of the orbit (compare Figs. 2 and 3).
4.3. Morphology of progenitors
Lastly, we have also tested the effects of changing the internal distributions of the baryonic component (stars) on merging timescales. As shown in Fig. 8, mergers of pure stellar spheroids are somewhat faster than those of identical characteristics, but involving disc galaxies, as expected because in the first case, the density in the innermost region of the galactic haloes is higher. Nevertheless, since this difference only matters at late stages in the merger, we observe a quite modest cropping of the merger times: less than around 5% and 8%, respectively, in highly and moderately radial collisions, which favour the proximity of the centres of host and satellite during the pre-coalescence phase, and virtually zero for collisions along nearly circular orbits. Interestingly, in mergers of elliptical galaxies, the behaviour of the scatter associated with the different internal spin orientations is found to be a mirror image of that of spirals, growing as the circularity diminishes.
 |
Fig. 8 Same as Fig. 5, but showing the effect of varying the morphology of the central object. Data points show results for equal-mass mergers of galaxies with reduced orbital energy rcir,p = 4/3 and halo spin parameter λ = 0.02. Open squares are used for mergers of pairs of E3 galaxies, while open circles identify Sb + Sb mergers. |
5. Major merger timescales
The most robust and accurate fitting formulas for the merger timescale obtained from simulations are revisions of the analytical expressions developed by Lacey & Cole (1993), which were inspired by the idealised description of the phenomenon of dynamical friction given by Chandraseckhar (1943). These equations tie τmer to the orbital parameters that define the trajectory of any closed two-body system and to the mass ratio between host and satellite, for which, according to the dynamical friction theory, the merger time is expected to show a rather strong positive correlation. The general form of the models, which treat each factor contributing to the dynamical friction separately, is given by (cf. Boylan-Kolchin et al. 2008; Jiang et al. 2008; McCavana et al. 2012)![$$ \frac{{\tau }_{\mathrm{mer}}}{{\tau }_{\mathrm{dyn}}}=A\frac{{\eta }^B}{\mathrm{ln}\left(1+\eta \right)}f\left(\mathrm{\epsilon };{C}\right){\left[\frac{{r}_{\mathrm{cir}}}{{R}_{\mathrm{p}}}\right]}^D, $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq16.gif) (3) where constants B and D parameterise the dependence of the merger timescale on the mass ratio η and reduced orbital energy rcir,p, respectively, ln(1 + η), is a widely used approximation to the Coulomb logarithm, ln Λ, that works well for major mergers (e.g. Jiang et al. 2008)3, while f(є; C) is intended to represent the different parametric functions that are used to encapsulate the dependence on the orbital circularity є (see Sects. 5.1 and 5.2).The factorisation also affects the dependence on the cosmology, which is exclusively provided by the halo-independent dynamical timescale:
(3) where constants B and D parameterise the dependence of the merger timescale on the mass ratio η and reduced orbital energy rcir,p, respectively, ln(1 + η), is a widely used approximation to the Coulomb logarithm, ln Λ, that works well for major mergers (e.g. Jiang et al. 2008)3, while f(є; C) is intended to represent the different parametric functions that are used to encapsulate the dependence on the orbital circularity є (see Sects. 5.1 and 5.2).The factorisation also affects the dependence on the cosmology, which is exclusively provided by the halo-independent dynamical timescale:![$$ \begin{array}{l}{\tau }_{\mathrm{dyn}}\equiv \frac{{R}^{3/2}}{{\left({GM}\right)}^{1/2}}=0.978{\left[\frac{{\mathrm{\Omega }}_0{\Delta }_{\mathrm{vir}}(z)}{200}\right]}^{-1/2}{\left(1+z\right)}^{-3/2\thinspace }{\mathrm{h}}^{-1}\thinspace \mathrm{Gyr},\\ \end{array} $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq17.gif) (4)with Δvir the virial overdensity in the spherical collapse model (cf. Bryan & Norman 1998):
(4)with Δvir the virial overdensity in the spherical collapse model (cf. Bryan & Norman 1998):![$$ {\Delta }_{\mathrm{vir}}(z)\simeq \frac{18{\pi }^2\thinspace{+}\thinspace82\left[{\mathrm{\Omega }}_{\mathrm{m}}(z)-1\right]-39{\left[{\mathrm{\Omega }}_{\mathrm{m}}(z)-1\right]}^2}{{\mathrm{\Omega }}_{\mathrm{m}}(z)}, $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq18.gif) (5)and where the cosmological density parameter can be easily inferred from
(5)and where the cosmological density parameter can be easily inferred from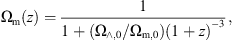 (6)so that for the adopted cosmology Δvir = 368 at the present epoch.
(6)so that for the adopted cosmology Δvir = 368 at the present epoch.
To avoid ambiguities in applying Eq. (3), the masses of host and satellite are defined by convention as the virial masses of both objects immediately before their haloes start to overlap. For the same reason, it is preferable that the values of the remaining orbital parameters are determined at that same instant, before significant interaction has occurred, when the orbital energy is still conserved and galaxies essentially behave as test particles moving along Keplerian orbits. Using the asymptotic Keplerian values of the orbital parameters instead of locally defined quantities renders the equation for the merger timescale independent of the details of the internal structure of the merging haloes.
5.1. Comparison of merger timescales
We now compare the merger times obtained from our simulations to four well-known empirical models of the merger timescale in the literature. These are models that obey Eq. (3) with different best-fit parameters and circularity functions. One is the formula given by Boylan-Kolchin et al. (2008), which we label B08, which has (A, B, D) = (0.216, 1.3, 1.0) and f (є; C) = exp (1.9 є); another is the formula from McCavana et al. (2012), labelled M12, which has (A, B, D) = (0.9, 1.0, 0.1) and f (є; C) = exp (0.6 є); finally, the last two expressions are from Jiang et al. (2008); one, labelled J08, which does not depend on the energy of the satellite and is given by (A, B, D) = (1.163, 1.0, 0.0) and f (є; C) = 0.94 є0.6 + 0.6, and another, labelled J08e, which does depend on these energy, and is characterised by (A, B, D) = (0.163, 1.0, 0.5) and f (є; C) = 0.90 є0.47 + 0.6.
To illustrate this comparison, we show in Fig. 9 the ratios between the merging times measured in our simulations, τsim, and the predictions of the models B08, J08, J08e, and M12, τmod, from a subset of our experiments involving disc mergers with reduced orbital energy rcir,p = 4/3 and mass ratios η = 1 and 3 (top and middle panels, respectively), and with rcir,p = 2.0 and η = 1 (bottom panel). The analysis of the predicted merger timescales as a function of the initial orbit of the galaxies shows quite different results, with a reduced level of agreement between the B08 model and those with a cosmological basis, especially for head-on encounters. The largest differences between the predictions and our experiments are also found with respect to the B08 model, which significantly underpredicts major merger times. For mergers with the most likely orbital energy (rcir,p = 4/3), this model underestimates the timescale of pairwise radial encounters by a factor of ~2.3. The comparison to B08 produces much tighter agreement for 3:1 mergers, where this model exhibits fractional deviations of compar- able strength (≲ 30%), but different sign to the other functional forms. The relatively important disagreement between our measurements and the predictions from the B08 formula is somewhat surprising since the latter was derived from simulations of isolated mergers of the same type as those presented in this work. We note, however, that although the Boylan-Kolchin et al. (2008) experiments and ours cover a similar range of initial circularities, the ranges of both the initial orbital energy and mass ratio of the mergers are quite different (in particular, BKMQ08 Boylan-Kolchin et al. 2008 studied minor mergers with η ≤ 0.3 and reduced energies lower than 1). This suggests that at least part of the discrepancy may be attributable to the fact that our simulations fall beyond the range of validity of their approximation. Another factor that may contribute to the observed mismatch are differences in the definition of the merger endpoint. B08 used a 5% threshold in the specific orbital spin of their dark haloes, while we are able to track the coalescence of the baryonic cores of the galaxies. As discussed in Sect. 3 (see also Fig. 4), the use of the specific angular momentum to monitor the final act of the orbital decay systematically underestimates τmer in an amount that increases with increasing orbital eccentricity. However, any possible bias attributable to the metric appears to fall short of explaining the significant deviation detected.
 |
Fig. 9 Comparison between predictions from the models B08, J08, J08e, and M12 and our measurements for the case of merger simulations with a reduced orbital energy of 4/3 and mass ratios 1:1 and 3:1 (panels a and b, respectively), and for equal-mass mergers with an initial energy of 2.0 (panel c) as a function of the initial orbital circularity of the satellites. All ratios are shown with different offsets around the true values of є for clarity. |
In contrast, the comparison to the two J08 models and the model M12, all derived from mergers simulated in a cosmological context, shows a better agreement. Independently of the initial value of the orbital energy and mass ratio, the J08 and M12 formulas tend to underestimate (overestimate) τmer for galaxies with higher (lower) initial circularity, with both the J08 and M12 models performing in much the same way overall. On the other hand, the J08e functional form appears to be fine-tuned to accurately predict time-scales for mergers in highly circular orbits, but the predictions for moderate and nearly radial encounters are somewhat worse than those from the other two formulas calibrated with cosmological experiments. Although the values of the deviations are apparently not as problematic as those resulting from the comparison with the B08 model, their sign and the positive correlation that the ratio τsim/τmod shows with the circularity are troublesome. Thus, for example, the tendency of the M12 model to overestimate τmer in nearly radial encounters, especially noticeable when rcir,p = 4/3, is inconsistent with the metric used by McCavana et al. (2012) that was based on the minimisation of the orbital angular momentum. This is similar for J08, where shorter merger times may be expected from the overcooling problem that affected their simulations (Jiang et al. 2010). Similarly, an explanation based on the different contexts in which the simulations have been performed, isolated versus cosmological, is unlikely to work either. If this were the case, one would expect the timescales inferred from our simulations to show a progressive tendency to be biased low with respect to the cosmologically founded formulas with increasing є, contrarily to what is observed; arguably, environmental effects should progressively delay mergers with time. The same is true for other factors, such as the possible differences in the internal structure of the halos that would result from the fact that we have ignored the response of DM to the condensation of baryons, since the adiabatic contraction of our dark halos would have increased its central densities and would therefore have decreased τmer, thus further increasing the inconsistency. Nor does it seem likely that the discrepancies can be attributed to large differences in the respective parameter spaces. In contrast to the B08 model, the values of orbital circularities and mass ratios adopted in our simulations fall squarely within the range of validity of the cosmological expressions, whilst the reduced orbital energies show a partial overlap only with respect to the study by Jiang et al. (2008), which examined simulations limited to values of this parameter below 1.5.
Finally, we have also discarded the possibility that the largest discrepancies between our simulations and the different predictions arise from any of the arguments put forward in the former comparison work by Villalobos et al. (2013). These authors have conducted experiments of isolated mergers between a single galaxy and a much larger main halo at different redshifts, finding that prescriptions based on Eq. (3) significantly underestimate long merger timescales. Villalobos et al. (2013) attributed the mismatch to the neglect of the evolution of halo concentration in controlled experiments and to the possible undersampling of long-term mergers in cosmological simulations. In both cases, they were able to partially compensate for the observed offsets by including in Eq. (3) an extra term of the form (1 + z)E, with E ~ 0.45–0.60. We note, however, that this is a correction designed for very long-term mergers (≳ 8τdyn), so it is not applicable to the moderately long mergers investigated in this paper.
5.2. Adapting existing prescriptions to major mergers
Deriving a new, more accurate prescription for estimating major merger timescales is beyond the scope of this work. Instead, we have chosen to recalculate the coefficients of the general formula (3) provided above, using both exponential and power-law functions for the orbital angular momentum factor as proposed in the literature, by fitting it to our results, so we produce expressions suitable for major mergers.
To perform this task, the results from our simulations were reduced to a 3D grid in the space (η, ϵ, r cir,p) by taking the median values over all relative orientations and moduli of the internal galactic spins, resulting in a total of 27 data points. Just like in earlier studies, we gave the same weight to each one of these average values.
We have accounted not just for the different proposals made in the literature for f (ϵ; C ), but also for the different strategies used in the fits. On the one hand, some authors used a maximum likelihood estimate of all variables simultaneously, holding fixed or letting vary the values of some parameters (e.g. Boylan-Kolchin et al. 2008). On the other hand, Jiang et al. (2008) and McCavana et al. (2012) applied a sequential procedure, fitting the free parameters of the prescriptions associated with each one of the variables ordered from more to less impact on the merger time: first η, then ϵ, and finally rcir,p. If, as expected, the magnitudes involved in the calculation of τmer are independent, the two methods should give very similar results, if this is not the case, the order of the fits matters – some testing with our data has shown that initiating the sequence of the fits using either η or ϵ introduces no significant variations in the parameter estimates. The combination of expressions for the circularity and fitting strategies allows a total of ten different fitting variants for the parameters of Eq. (3) that we list in Table 3. To facilitate comparison, this table also provides the values attributed in the original works to these parameters on which our procedure is based.
We now attempt to gain some insight by examining the similarities and differences among the outcomes from our fits. In the first place, Table 3 shows that the mass dependence for τmer adopted in Eq. (3) with B ≈ 1 provides a good match for the whole range of mass ratios, regardless of whether major mergers are performed in either an isolated or a cosmological context. In contrast, both the circularity and (reduced) energy dependencies exhibit disagreements that are hard to dismiss. Thus, when using an exponential form for the circularity, the fits to our numerical results give exponents that are not too different from the 1.9 value found by Boylan-Kolchin et al. (2008), but far from the 0.6 adopted in the M12 model. On the other hand, fits to τmer using a pure power-law expression for the circularity yield exponents identical to or somewhat higher than the value of 0.78 analytically derived by Lacey & Cole (1993), while those based on the linear power-law introduced by Jiang et al. (2008) lead to substantially stronger dependencies, even when the zero offset is forced to be 0.6, as these authors did to ensure that their formula gives τmer ≈ τdyn for equal-mass mergers – our simulations show that this is not the case even for highly radial orbits (see, e.g. our Fig. 4). Regarding the pure power-law form also adopted for the dependence on the orbital energy, we find that the values of the exponent in the range 0.43–0.77 provide the best match to our major merger data. This is in contrast with the canonical value of D = 2 derived analytically (e.g. Binney & Tremaine 1987; Taffoni et al. 2003), but is in line with previous numerical simulations, which find exponents equal to or lower than 1. The agreement is indeed rather good with respect to the J08e model, for which D = 0.5, and somewhat less satisfactory for the B08 model, for which D = 1.0, while the dependence obtained by the M12 model D = 0.1 seems excessively weak according to our results. On the other hand, the J08 model does not include an explicit orbital energy dependence, so D = 0, but this was done to keep their fitting formula simple.
In Fig. 10 we plot the residuals resulting from the comparison between the merger timescales computed according to the different variants of Eq. (3) listed in Table 3 and the average merging times measured from our simulations. As the last column of Table 3 shows, the two fitting procedures produce similarly accurate results, with a slender and insignificant advantage for the sequential fitting regarding the size of the standard deviation of the residuals or RMSE: in relative terms, it ranges from around 11% to 24%. The good performance of the fits does not hide the clear pattern in the point clouds of the figure, however, which indicates that the models are not entirely accurate. This may help to explain, for instance, the substantial variations in the value of the power D of the rcir,p function reported in the literature (see the corresponding column in Table 3). Furthermore, regarding the different alternative forms adopted for f(ϵ; C), Table 3 also shows that the approximating formulas with an exponential, exp(Cϵ), and a full linear power-law dependence, ϵC1 + C2, provide the tightest match to our data, with nearly identical values of the RMSE. Since the former expression has only one free parameter, it can be considered the best choice of all the investigated recipes to describe the circularity dependence of the timescale of major mergers from Eq. (3). On the other hand, the pure power-law fit, ϵC1, shares with the two former expressions a similar but somewhat more extended non-linear distribution of residuals, while the two power-law models with a zero offset of 0.6 offer the worst performance in terms of the RMSE. However, the residuals of these latter models are roughly linearly distributed, so they should be easier to minimise when the prediction of τmer is to be improved.
 |
Fig. 10 Residuals of the comparison between the merger timescales measured in our simulations and the different predictions arising from the best fits of the models listed in Table 3. The plots are organised into two rows, corresponding to the two fitting procedures considered (top: (Seq)uential; bottom: (Sim)ultaneous), and five columns showing the different functionals for f (ϵ; C) adopted in Table 3. The log–log scale adopted facilitates appreciating the magnitudes and the deviation trends. |
6. Discussion and conclusions
We thoroughly examined the orbital decay time for major mergers of galaxies, which are a centrepiece of cosmic evolution. This was accomplished with the aid of nearly 600 high-resolution N-body simulations of collisions of isolated pairs of similarly massive galaxies on bound orbits. Our dissipationless experiments followed the merging of live models of late- and early-type objects, composed of a rotating NFW CDM halo and a central stellar core, with mass ratios ranging from 1:1 to 3:1, and with orbital parameters and global properties broadly consistent with the predictions of the standard ΛCDM cosmology. These simulations were used to perform a detailed analysis of the merger times driven by dynamical friction, which ranges from its definition and the factors that determine its length to the comparison of our inferred values for τmer with predictions drawn from approximating formulas existing in the literature. Although we studied gas-free experiments, we expect our conclusions to apply to both dry and (moderately) wet mergers, as the baryonic physics is known to have only a weak effect on the merger time-scale (e.g. Jiang et al. 2010; Colpi 2014). The main and newest results of the present work are for the first two of these aspects are listed below.
-
We have identified the need of a unified criterion to qualify binary galaxy mergers. This is not a minor issue, as apparently small differences in the definition of the virial radius of host and satellite, in the input values of the orbital parameters, or in the start and end points of the merger, can lead to relatively large divergences in the determination of τmer. In particular, the strategy commonly used in numerical experiments of defining the time of coalescence of the galaxies as the moment at which the specific orbital angular momentum of the system reaches 5% of its initial value, τj05, has been shown to systematically underestimate the merger timescale, resulting in fractional deviations that in major mergers can be as large as 60% for nearly radial collisions. Accordingly, to determine the time of coalescence in this type of mergers, we recommend instead using the instant at which the time derivative of the logarithm of the product of the relative distance, r, and speed, ν, of the progenitors’ cores reaches its absolute maximum. To facilitate identification, it may be necessary to apply a low-pass filter to the function rν(t).
-
In major mergers, the internal spin of the parent galaxies may lead to variations of τmer above 15% in highly circular collisions. In our simulations this corresponds to differences of up to ~3 Gyr in the duration of mergers. This implies that in controlled experiments, the distribution of the initial relative orientations of the internal spins might bias the outcome. In the real Universe, however, the largest deviations in τmer are expected to affect only a small number of pairs (<2%) within a given orbital configuration.
-
Except in nearly radial encounters, the initial orientation of the internal spin of the host regulates the strength of the dynamical friction prevailing on any merger. In contrast, the duration of major mergers, much as with minor collisions, is largely independent of the initial orientation of the internal spin of the satellite. Neither this spin nor that of the main halo, neither the mass ratio of the progenitors nor the circularity of its orbit influence the number of pericentric passages in the pre-coalescence stage, which is determined exclusively by the orbital energy of the merger.
-
In accordance with expectations, binary mergers of pure stellar spheroids are somewhat faster that those of identical characteristics, but involving discs. In our major mergers the differences are quite modest, however, as we measure fractional deviations in τmer that are ≲8% in encounters that take place following very or fairly elongated orbits and that are negligible for those configurations in which the two merger partners spend most of their time at large separations. This is in sharp contrast with the results of the study of tidal stripping efficiency on minor mergers by Chang et al. (2013), who concluded that the morphology of small satellites has a very strong effect on the efficiency of stellar stripping.
On the other hand, the comparison of the merger times obtained from our simulations to the predictions arising from some of the better-known empirically derived formulas existing in the literature has revealed unexpected important discordances. We find that the B08 formula, which like this work relied on isolated mergers, systematically underpredicts τmer, concentrating the strongest variations (of more than a factor of two) on the most radial encounters. This behaviour is qualitatively consistent with the use of τj05 by these authors to measure merger time and the fact that their simulations are biased against major encounters. According to Villalobos et al. (2012), mass losses via tidal stripping and gravitational shocking against merger companions are relatively more important for more massive galaxies. If so, our pairs should merge more slowly than minor-merger-based formulas predict. Quantitatively, however, the poor agreement found between the magnitude of the predictions and our data, especially for the equal-mass case, suggests that other factors beyond differences in the metric or in the ranges of the orbital parameter values used in both simulations might contribute to the observed discrepancy. For the expressions with a cosmological basis, the situation is quite the opposite. In this case, our numerical values are, as a whole, relatively well described by the J08 and M12 approximating formulas (for some parameter combinations, the match is very good), but the signs and trends of the differences stand out. In particular, we have found that many individual predictions overestimate our observed merger times. This is in contrary to expectations since some specific features of cosmological simulations suggest that they should also show a tendency to anticipate the coalescence of the satellite and the central galaxy. Furthermore, and perhaps more importantly, in all the cases we investigated, the differences between our merger timescales and the cosmological predictions show a trend with the orbital circularity that is at odds with what might be expected from possible environmental effects. Again, differences in the metric, the physics, and/or the context of the simulations do not appear sufficient to explain the characteristics of the biases we observe.
Finally, the adaptation to our data of the coefficients of well-known timescale models, generalised through the use of five alternative expressions for the dependence of circularity and two different fitting strategies, has allowed us to demonstrate that the form adopted in Eq. (3) for the relation between τmer and the mass ratio works well for all types of mergers and contexts provided that the exponent B ≈ 1. In contrast, we find a relatively low degree of agreement among the values of the coefficients of the expressions used to model the dependence of the merger time on the circularity and, especially, the initial orbital energy, that is not exclusive of major mergers. Such a lack of consensus that apparently stems from an ill-suited description of the data has prevented us from drawing any firm conclusion about which relationship would be the most adequate. These findings suggest that the analytical prescriptions traditionally adopted to describe the dependence of τmer on the orbital parameters, or at least some parts of them, are open to improvement.
Therefore, we conclude that there is still considerable ground to be covered in the modelling of a problem as complex as that of dynamical friction. To begin with, we have shown the need to reach a general consensus on the quantification of the fiducial start and end points of mergers, as well as on the definitions of the parameters governing the merging time, which have to be clear and unambiguous. In addition, future investigations of dynamical friction (merging) must take steps to perform a complete identification of the physical mechanisms governing the timescales of the orbital decay. Only in this way will we be able to extend the first principles contained in the original Chandraseckhar theory to live objects assembling in cosmologically relevant simulations, to replace its simplifying assumptions by realistic considerations, and ultimately, to derive a single formula for the merger timescale that is accurate and valid across the entire range of mass ratios and orbital parameters of the parent galaxies.
Acknowledgments
The authors acknowledge financial support from the Spanish AEI and European FEDER funds through the research project AYA2016-76682-C3 as well as from the Program for Promotion of High- Level Scientific and Technical Research of Spain under contract AYA2013-40609-P.
References
- Barnes J. E. 2016, MNRAS, 455, 1957 [NASA ADS] [CrossRef] [Google Scholar]
- Benson A. J. 2005, MNRAS, 358, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Benson A. J. 2010, Phys. Rep., 495, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Benson A. J. 2012, New Astron., 17, 175 [Google Scholar]
- Binney J., & Tremaine S. 1987,Galactic Dynamics (Princeton University Press: Princeton) [Google Scholar]
- Boily C. M., Kroupa P., & Peñarrubia-Garrido J. 2001, New Astron., 6, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin M, Ma C-P, & Quataert E 2008, MNRAS, 383, 93 (B08) [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin M., Springel V., White S. D. M., & Jenkins A. 2009, MNRAS, 406, 896 [NASA ADS] [Google Scholar]
- Bryan G., & Norman M. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan S. E., Kay S. T., Duffy A. R., et al. 2013, MNRAS, 429, 3316 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock J. S., Kolatt T. S., Sigad Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Capelo P. R., Dotti M., Volonteri M., et al. 2017, MNRAS, 469, 4437 [NASA ADS] [CrossRef] [Google Scholar]
- Chandraseckhar S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chang J., Macciò A. V., & Kang X. 2013, MNRAS, 431, 3533 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi M. 2014, Space Sci. Rev., 183, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi M., Mayer L., & Governato F. 1999, ApJ, 525, 2 [Google Scholar]
- Comerford J. M., Gerke B. F., Newman J. A., et al. 2009, ApJ, 698, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Darriba L. 2013, Ph.D. Thesis, University of Barcelona, Barcelona [Google Scholar]
- Darriba L., Solanes J. M. 2010, A&A, 516, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehnen W. 2000, ApJ, 536, L39 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Foreman G., Volonteri M., & Dotti M. 2009, ApJ, 693, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Gan J., Kang X., van den Bosch F.-C., & Hou J. 2010, MNRAS, 408, 2201 [NASA ADS] [CrossRef] [Google Scholar]
- Graham A. W. 2001, AJ, 121, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Graham A. W. 2016, in Galactic Bulges, eds. E. Laurikainen, R. Peletier, & D. Gadotti (Switzerland: Springer Int. Publ.), Astrophysics and Space Science Library, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez X., Park C., Cervantes-Sodi B., & Choi Y. Y. 2007, MNRAS, 375, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann M., Naab T., Somerville R. S., Burkert A., & Oser L. 2012, MNRAS, 419, 3200 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang C. Y., Jing Y. P., Faltenbacher A, Lin WP, & Li C 2008, ApJ, 675, 1095 (J08, J08e) [NASA ADS] [CrossRef] [Google Scholar]
- Jiang C. Y., Jing Y. P., & Lin W. P. 2010, A&A, 510, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Just A., Khan F. M., Berczik P., Ernst A., & Spurzem R. 2011, MNRAS, 411, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann G., White S. D. M., & Guiderdoni B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar S., & Burkert A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klypin A., Zhao H., & Somerville R. S. 2002, ApJ, 573, 597 [Google Scholar]
- Koss M., Mushotzky R., Treister E., et al. 2012, ApJ, 746, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey C. 2001, in The Physics of Galaxy Formation, eds. M. Umemura, M. Umemura, & H. Susaeds (San Francisco: ASP), ASP Conf. Ser., 222, 273 [NASA ADS] [Google Scholar]
- Lacey C., & Cole S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Lidman C., Iacobuta G., Bauer A. E., et al. 2013, MNRAS, 433, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Liu X., Greene J. E., Shen Y., & Strauss M. A. 2010, ApJ, 715, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Liu X., Shen Y., Strauss M. A., & Hao L. 2011, ApJ, 737, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas E. L., & Mamon G. A. 2001, MNRAS, 321, 155 [NASA ADS] [CrossRef] [Google Scholar]
- McCavana T, Micic M, Lewis GF, et al 2012, MNRAS, 424, 361 (M12) [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Arancibia A. M., Navarrete F. P., Padilla N. D., et al. 2015, MNRAS, 446, 2291 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro JF, Frenk CS, & White SDM 1997, ApJ, 490, 493 (NFW) [NASA ADS] [CrossRef] [Google Scholar]
- Okoli, C. 2017, ArXiv e-prints [arXiv:1711.05277] [Google Scholar]
- Peebles P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Petts J. A., Gualandris A., & Read J. I. 2015, MNRAS, 454, 3778 [NASA ADS] [CrossRef] [Google Scholar]
- Ricciardelli E., & Franceschini A. 2010, A&A, 518, 14 [CrossRef] [EDP Sciences] [Google Scholar]
- Rosario D. J., McGurk R. C., Max C. E., et al. 2011, ApJ, 739, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw L. D., Weller J., Ostriker J. P., & Bode P. 2006, ApJ, 646, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Shen Y., Liu X., Greene J. E., & Strauss M. A. 2011, ApJ, 735, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Silva J. M., Lima J. A. S., de Souza R. E., et al. 2016, JCAP, 5, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Solanes J. M., Perea J. D., Darriba L., et al. 2016, MNRAS, 461, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Springel V., & White S. D. M. 1999, MNRAS, 307, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S. 1995, in Fresh Views on Elliptical Galaxies, eds. A. Buzzoni, A. Renzini, & A. Serrano, (San Francisco: ASP), ASP Conf. Ser., 86, 27 [NASA ADS] [Google Scholar]
- Taffoni G., Mayer L., Colpi M., Governato F. 2003, MNRAS, 341, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca L. A. M., Le Fèvre O., López-Sanjuan C., et al. 2014, A&A, 565, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teerikorpi P., Chernin A. D., & Baryshev Yu. V. 2005, A&A, 440, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tormen G. 1997, MNRAS, 290, 411 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch F. C., Lewis G. F., Lake G., & Stadel J. 1999, ApJ, 515, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Van Wassenhove S., Volonteri M., Mayer L., et al. 2012, ApJ, 748, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos Á., De Lucia G., Borgani S., & Murante G. 2012, MNRAS, 424, 2401 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos Á., De Lucia G., Weinmann S. M., Borgani S., & Murante G. 2013, MNRAS, 433, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Yu Q, Lu Y, Mohayaee R, & Colin J. 2011, ApJ, 738, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Zentner A. R., Berlind A. A., Bullock J. S., Kravtsov A. V., & Wechsler R. H. 2005, ApJ, 624, 505 [NASA ADS] [CrossRef] [Google Scholar]
Recent investigations of the c(M, z) relation (see, e.g. the review by Okoli 2017, and references therein) have confirmed that the evolution of the halo concentration is more complex than this simple form based on the inside-out growth of structure (Bullock et al. 2001). However, most concentration–mass relations from the literature agree very well with Eq. (2) in the regime relevant for this work.
Λ in the Coulomb logarithm ln Λ is defined as the ratio of the maximum and minimum impact parameters for which encounters between the satellite and the background sea of matter from the host can be considered effective; the ad hoc approximation ln(1 + Mp/Ms) is used in the literature to make the original formula of Lacey & Cole (1993), which is valid for minor mergers, also applicable to major mergers.
Extended interacting galaxies will eventually begin to deviate from this idealised orbit for two reasons: on one hand, the mutual gravitational acceleration of two spatially extended mass distributions is less than that of two equivalent point masses; on the other, dynamical friction induces orbital decay after the outer halo regions start to interpenetrate.
Appendix A
Galactic halo rotation
Inspired by SW99, we modelled the mean streaming velocity of the dark haloes,  , which in a static, axisymmetric system can be freely chosen to set its rotation, as some fixed fraction, fh, of the local value of the radial velocity dispersion used to generate the DM particle speeds,
, which in a static, axisymmetric system can be freely chosen to set its rotation, as some fixed fraction, fh, of the local value of the radial velocity dispersion used to generate the DM particle speeds,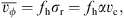 (A.1)where
(A.1)where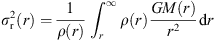 (A.2)for a DM halo with an isotropic velocity tensor, and α ≡ 〈σr/νc〉r≤R is a factor that we introduce to explicitly take into account the expectation value of the ratio between the scale of DM particle speeds, σr, and the local azimuthal circular velocity, νc, inside the halo virial radius. This factor is model dependent and must be determined empirically.
(A.2)for a DM halo with an isotropic velocity tensor, and α ≡ 〈σr/νc〉r≤R is a factor that we introduce to explicitly take into account the expectation value of the ratio between the scale of DM particle speeds, σr, and the local azimuthal circular velocity, νc, inside the halo virial radius. This factor is model dependent and must be determined empirically.
With α fixed, conservation of the specific angular momentum during galaxy formation, which is a reasonable assumption for late-type galaxies but certainly not for merger-made early-type objects, also leads to the conservation of fh, which can therefore be computed from the total angular momentum J of the initial halo. To infer the latter, the angular momenta of infinitesimally thick spherical shells, dJ = (2/3)rνcdM must be integrated up to the virial radius, which from the azimuthal streaming model given by Eq. (A.1), an NFW halo mass density profile, and the fact that for a spherical mass distribution, the maximum azimuthal circular speed is achieved at the equator, so that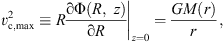 (A.3)gives
(A.3)gives![$$\begin{array}{*{20}{l}} J&{ = \frac{2}{3}4\pi {f_{\rm{h}}}\alpha \int_0^R {{r^2}\rho \left( r \right){v_c}\left( r \right)r{\rm{d}}r} }\\ {}&{ = \frac{2}{3}{f_{\rm{h}}}\alpha {{\left\{ {\frac{{G{M^3}{r_{\rm{s}}}}}{{{{\left[ {\ln \left( {1 + c} \right) - c/(1 + c)} \right]}^3}}}} \right\}}^{1/2}}{g_{\rm{c}}},} \end{array} $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq35.gif) (A.4)where R and M are the total (virial) radius and mass of the galactic halo, rs is the characteristic radius of the NFW density profile and gc is the integral
(A.4)where R and M are the total (virial) radius and mass of the galactic halo, rs is the characteristic radius of the NFW density profile and gc is the integral![$$ {g}_{\mathrm{c}}\equiv {{\int }_0^c\left[\mathrm{ln}\left(1+x\right)-\frac{x}{1+x}\right]}^{1/2}\frac{{x}^{3/2}}{(1+x{)}^2}\mathrm{d}x, $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq36.gif) (A.5)with c ≡ R/rs the usual definition of the concentration parameter. Combining this result with the definition of the dimensionless spin parameter λ (cf. Peebles 1969),
(A.5)with c ≡ R/rs the usual definition of the concentration parameter. Combining this result with the definition of the dimensionless spin parameter λ (cf. Peebles 1969),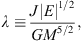 (A.6)and taking into account that the total energy E of a galactic halo can be inferred from the virial theorem by assuming that all DM particles move on circular orbits around the centre, so that
(A.6)and taking into account that the total energy E of a galactic halo can be inferred from the virial theorem by assuming that all DM particles move on circular orbits around the centre, so that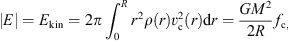 (A.7)with
(A.7)with![$$ {f}_c=\frac{c}{2}\frac{1-1/(1+c{)}^2-2\mathrm{\thinspace ln}(1+c)/(1+c)}{{\left[\mathrm{ln}(1+c)-c/(1+c)\right]}^2} $$](/articles/aa/full_html/2018/06/aa32855-18/aa32855-18-eq39.gif) (A.8)for an NFW halo. We note that this standard procedure is, however, an approximation, as strictly speaking isolated haloes satisfy the scalar virial theorem in the limit r → ∞. At the virial radius, objects with NFW profiles are only near dynamical equilibrium, with those of lower mass and lower velocity anisotropy being closer (Łokas & Mamon 2001).
(A.8)for an NFW halo. We note that this standard procedure is, however, an approximation, as strictly speaking isolated haloes satisfy the scalar virial theorem in the limit r → ∞. At the virial radius, objects with NFW profiles are only near dynamical equilibrium, with those of lower mass and lower velocity anisotropy being closer (Łokas & Mamon 2001).
Appendix B
Solving the two-body problem for extended objects
We summarise here the most important equations involved in the standard approach we followed to solve the motion of two extended objects interacting via a gravitational force. Similar treatments of this classical issue can be found elsewhere (e.g. Khochfar & Burkert 2006). However, given its great utility in establishing the orbital evolution of galaxy mergers from a given set of initial conditions, we have decided to include it in an appendix in order to provide a more complete view of our experiments.
Under the Keplerian approximation, the motion of a pair of gravitationally bound galactic haloes can be solved analytically by transforming it into an equivalent one-body problem of a fictitious particle of mass equal to the reduced mass of the system, defined by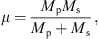 (B.1)with Mp and Ms the virial masses of the host and satellite galactic haloes, respectively, moving under the influence of a central force equal to the gravitational interaction exerted by one onto the other, and with a position vector
r
=
r
p −
r
s whose modulus at t = 0, r0 gives the initial relative distance between the point masses chosen to represent the haloes (see Sect. 3). Throughout this work, quantities that refer to the more massive of the two merging galaxies (primary, host, or central) are identified by the subindex “p’’, while subindex “s’’ identifies those referring to the less massive member of the pair (secondary or satellite). Of course, the assignation of indexes is irrelevant in equal-mass mergers.
(B.1)with Mp and Ms the virial masses of the host and satellite galactic haloes, respectively, moving under the influence of a central force equal to the gravitational interaction exerted by one onto the other, and with a position vector
r
=
r
p −
r
s whose modulus at t = 0, r0 gives the initial relative distance between the point masses chosen to represent the haloes (see Sect. 3). Throughout this work, quantities that refer to the more massive of the two merging galaxies (primary, host, or central) are identified by the subindex “p’’, while subindex “s’’ identifies those referring to the less massive member of the pair (secondary or satellite). Of course, the assignation of indexes is irrelevant in equal-mass mergers.
Under these conditions, all the essential information about the initial motion of the system is contained in the orbit equation of the reduced body4, whose geometry is entirely specified by two constants of the motion, the total orbital energy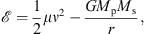 (B.2)and angular momentum, whose magnitude is
(B.2)and angular momentum, whose magnitude is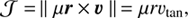 (B.3)where we use the notation
(B.3)where we use the notation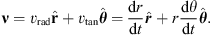 (B.4)
(B.4)
Equation (B.2) can then be solved for the first derivative dr/dt
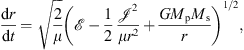 (B.5)which can be integrated directly for r(t). Since there are no external forces, the orbit of the reduced body lies in a plane, with the angular momentum a constant vector pointing perpendicular to this plane. We note, however, that the complete solution of the equation of motion requires providing, in addition to the values of ℰ and ℐ, one extra boundary condition at t0. Since it is a very good idea to take t0 = 0, the natural choices are therefore the modulus r0 of the initial relative separation of the galaxies or of its time detivative v0.
(B.5)which can be integrated directly for r(t). Since there are no external forces, the orbit of the reduced body lies in a plane, with the angular momentum a constant vector pointing perpendicular to this plane. We note, however, that the complete solution of the equation of motion requires providing, in addition to the values of ℰ and ℐ, one extra boundary condition at t0. Since it is a very good idea to take t0 = 0, the natural choices are therefore the modulus r0 of the initial relative separation of the galaxies or of its time detivative v0.
Alternatively, the two constants of the motion can be replaced by two geometrical parameters, one describing the initial orbital eccentricity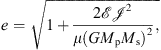 (B.6)and other the initial pericentric distance
(B.6)and other the initial pericentric distance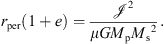 (B.7)
(B.7)
For closed two-body systems (ℰ < 0), it is also possible to replace the eccentricity and pericentric distance by two other fully independent quantities: the circularity of the elliptical orbit, expressing the ratio between the lengths of its semi-major, a, and semi-minor, b, axes, 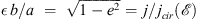 , which is also a measure of the specific angular momentum of the orbit, j ≡ rvtan, relative to the specific angular momentum of a circular orbit with the same energy, and a parameter representing the initial orbital energy in dimensionless form. In merger studies, it is customary to use for the latter the ratio rcir,p ≡ rcir (ℰ)/Rp, with Rp the virial radius of the primary halo, and rcir(ℰ) the radius of a circular orbit with the same orbital energy ℰ. From the virial theorem:
, which is also a measure of the specific angular momentum of the orbit, j ≡ rvtan, relative to the specific angular momentum of a circular orbit with the same energy, and a parameter representing the initial orbital energy in dimensionless form. In merger studies, it is customary to use for the latter the ratio rcir,p ≡ rcir (ℰ)/Rp, with Rp the virial radius of the primary halo, and rcir(ℰ) the radius of a circular orbit with the same orbital energy ℰ. From the virial theorem: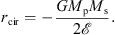 (B.8)
(B.8)
Finally, from Eqs. (B.6) and (B.7), we obtain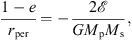 (B.9)which combined with the definition (B.8) of the circular radius leads to
(B.9)which combined with the definition (B.8) of the circular radius leads to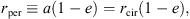 (B.10)a result that could have been anticipated because for circular orbits, the semi-major axis a is equal to rcir. Given that rcir is
(B.10)a result that could have been anticipated because for circular orbits, the semi-major axis a is equal to rcir. Given that rcir is 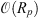 and the modal values of e are close to 1 (see below), this last relationship allows us to understand why small pericentric separations are more frequent than larger ones. Moreover, since not only the PDF of e but also that of rper is independent of the mass ratio of the progenitors, Eq. (B.10) also implies that the initial orbital energy as measured by rcir,p must be equally universal for a given cosmological model. This is consistent with the self-similarity of the galaxy formation process.
and the modal values of e are close to 1 (see below), this last relationship allows us to understand why small pericentric separations are more frequent than larger ones. Moreover, since not only the PDF of e but also that of rper is independent of the mass ratio of the progenitors, Eq. (B.10) also implies that the initial orbital energy as measured by rcir,p must be equally universal for a given cosmological model. This is consistent with the self-similarity of the galaxy formation process.
Another aspect to take into consideration in the initial set-up of idealised binary merger simulations is the fact that it is a fairly widespread procedure to place the galaxies on parabolic orbits with a small pericentric distance (typically a small fraction of Rp) that leads to fast merging. As noted by Khochfar & Burkert 2006, this attempt to save computational time is, however, inconsistent with the outcome of cosmological simulations, which show that most of the mergers are on orbits with ℰ ≲ 0, e ≲ 1 and rper ≳ 0.1Rp, independently of the mass ratio of the progenitors. Because to first order, rper ∝ ℐ2 (Eq. B.7), this means that by underestimating rper, we also underestimate the amount of orbital angular momentum transferred to the remnant. This may have a noticeable effect on its structure.
Finally, it is important to keep in mind that the values of the initial parameters involved in the Keplerian two-body problem cannot be chosen in a completely arbitrary manner since certain combinations of them do not lead to physically plausible results. Thus, for the major mergers of the present study, the initial circularities and separations adopted (see Sect. 2.2.1 and Table 1) imply that rcir,p ≳ 1, as shown in Fig. B.1.
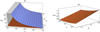 |
Fig. B.1 Panel a: Portion of the domain of definition of the initial orbital parameters є, r0, and rcir,p involved in the Keplerian two-body problem (shaded in grey). The blue and brown surfaces depict limiting cases. Panel b: A closer view of the lower boundary of this domain (brown surface). It allows for a greater appreciation of the values of the initial orbital energy, rcir,p, below which the initial relative velocity, ν0, is not defined. |
All Tables
Initial orientations of the internal spins of the primary (p) and secondary (s) progenitors.
All Figures
 |
Fig. 1 Time evolution of the intercentre distance r, in units of the radius Rp of the primary halo, of a pair of Sb + Sc galaxies with mass ratio 3:1 and internal spin parameter λ = 0.04 colliding along a radial orbit. The initial orientation of the internal spin of the haloes is X90Y90 (see Table 2). Different solid curves show merger histories calculated using different definitions of the galactic cores: green shows the 5% fraction of the most closely bound luminous particles, black shows the 10% fraction, blue shows the 25% fraction, and coral the 50% fraction, while the red line shows the merger evolution as determined from the central SMBH. The intersection of these curves with the grey horizontal dotted line marks the onset of the merger. The plot shows that the final coalescence of the galaxies at t/τdyn ∼ 2.4 is better delineated when the galactic cores are defined using a moderate fraction, between 5 and 25%, of the most closely bound particles. |
| In the text | |
 |
Fig. 2 Time evolution of the intercentre separation of Sb + Sb mergers of equal-mass galaxies with internal spin parameter λ = 0.04 colliding along elliptical orbits. Different panels show different choices for Δ(t): panel a) the intercentre distance, panel b) the specific orbital angular momentum, panel c) a weighted non-canonical distance in phase space based on the Euclidean notion of distance, and panel d) the product of the intercentre distance and relative velocity. Normalisation units Rp and Vp refer to the virial radius and velocity of the primary halo, respectively. Galaxy centres are calculated from the 10% fraction of the most closely bound luminous particles. Coloured solid curves in each panel show the merger histories corresponding to the 12 initial orientations adopted for the internal spin of the haloes (see legend in panel a and Table 2). In panel a, the intersection of the curves with the black horizontal dotted line marks the onset of the mergers. In panel b, the black horizontal dotted line marks the value of j05 inferred for the black solid curve (X90Y90). The values of j05 for the other curves are very similar. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for Sb + Sc mergers with a mass ratio 3:1 colliding along radial orbits. |
| In the text | |
 |
Fig. 4 Comparison between τmer and τj05 measured from all the mergers depicted in Figs. 2 (left) and 3 (right). In all cases, τl05 < τmer, even when j(t) behaves as a purely monotonically decreasing function. |
| In the text | |
 |
Fig. 5 Examples of merger times measured in our simulations, τmer, as a function of the initial circularity of the orbit, є, showing the effect of varying the orbital energy, rcir,p, while keeping all other parameters unchanged. This plot shows results for equal-mass mergers of spiral galaxies with the modal value of the spin parameter (λ = 0.04). Open squares are used for mergers with rcir,p = 2.0, while open circles identify rcir,p = 4/3 mergers. Data points are shown with different offsets around the true values of є for clarity. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but showing the effect of varying the mass ratio,η. Data points show results for mergers of spiral galaxies with the modal value of the orbital energy (rcir,p = 4/3). Open squares are used for mergers with η = 3, while open circles identify η = 1 mergers. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, but showing the effect of varying the halo spin parameter, λ. Data points show results for equal-mass mergers of Sb galaxies with the modal value of the reduced orbital energy (rcir,p = 4/3). Open symbols identify different values of the spin parameter: λ = 0.00 (triangles), λ = 0.02 (squares), λ = 0.04 (circles), and λ = 0.06 (diamonds). Data points are shown with different offsets around the true values of є for clarity. |
| In the text | |
 |
Fig. 8 Same as Fig. 5, but showing the effect of varying the morphology of the central object. Data points show results for equal-mass mergers of galaxies with reduced orbital energy rcir,p = 4/3 and halo spin parameter λ = 0.02. Open squares are used for mergers of pairs of E3 galaxies, while open circles identify Sb + Sb mergers. |
| In the text | |
 |
Fig. 9 Comparison between predictions from the models B08, J08, J08e, and M12 and our measurements for the case of merger simulations with a reduced orbital energy of 4/3 and mass ratios 1:1 and 3:1 (panels a and b, respectively), and for equal-mass mergers with an initial energy of 2.0 (panel c) as a function of the initial orbital circularity of the satellites. All ratios are shown with different offsets around the true values of є for clarity. |
| In the text | |
 |
Fig. 10 Residuals of the comparison between the merger timescales measured in our simulations and the different predictions arising from the best fits of the models listed in Table 3. The plots are organised into two rows, corresponding to the two fitting procedures considered (top: (Seq)uential; bottom: (Sim)ultaneous), and five columns showing the different functionals for f (ϵ; C) adopted in Table 3. The log–log scale adopted facilitates appreciating the magnitudes and the deviation trends. |
| In the text | |
 |
Fig. B.1 Panel a: Portion of the domain of definition of the initial orbital parameters є, r0, and rcir,p involved in the Keplerian two-body problem (shaded in grey). The blue and brown surfaces depict limiting cases. Panel b: A closer view of the lower boundary of this domain (brown surface). It allows for a greater appreciation of the values of the initial orbital energy, rcir,p, below which the initial relative velocity, ν0, is not defined. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


