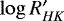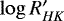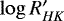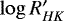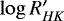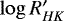| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732529 | |
| Published online | 27 June 2018 | |
The HARPS search for southern extra-solar planets
XLIII. A compact system of four super-Earth planets orbiting HD 215152★
1
Observatoire de l’Université de Genève,
51 chemin des Maillettes, 1290
Sauverny, Switzerland
e-mail: jean-baptiste.delisle@unige.ch
2
ASD, IMCCE, Observatoire de Paris - PSL Research University, UPMC Univ. Paris 6, CNRS,
77 avenue Denfert-Rochereau,
75014
Paris, France
3
Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales,
Buenos Aires, Argentina
4
CONICET - Universidad de Buenos Aires, Instituto de Astronomía y Física del Espacio (IAFE),
Buenos Aires, Argentina
5
Instituto de Astrofísica de Canarias,
38205
La Laguna, Tenerife, Spain
6
Dpto. de Astrofísica, Universidad de La Laguna,
38206 La Laguna,
Tenerife, Spain
7
Physikalisches Institut, Universitat Bern,
Silderstrasse 5,
3012 Bern, Switzerland
8
School of Physics and Astronomy, University of St Andrews,
North Haugh,
St Andrews, Fife KY16 9SS, UK
9
Aix Marseille Université, CNRS,
LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326,
13388
Marseille, France
10
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto, Portugal
11
Institut d’Astrophysique et de Géophysique, Université de Liège,
Allée du 6 Août 17,
Bat. B5C,
4000
Liège, Belgium
12
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching bei München, Germany
13
Canada France Hawaii Telescope Corporation,
Kamuela
96743, USA
14
Department of Physics, University of Warwick,
Coventry
4 7AL, UK
15
Cavendish Laboratory,
J J Thomson Avenue,
Cambridge
3 0HE, UK
16
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre
4169-007,
Porto, Portugal
Received:
22
December
2017
Accepted:
8
February
2018
We report the discovery of four super-Earth planets around HD 215152, with orbital periods of 5.76, 7.28, 10.86, and 25.2 d, and minimum masses of 1.8, 1.7, 2.8, and 2.9 M⊕ respectively. This discovery is based on 373 high-quality radial velocity measurements taken by HARPS over 13 yr. Given the low masses of the planets, the signal-to-noise ratio is not sufficient to constrain the planet eccentricities. However, a preliminary dynamical analysis suggests that eccentricities should be typically lower than about 0.03 for the system to remain stable. With two pairs of planets with a period ratio lower than 1.5, with short orbital periods, low masses, and low eccentricities, HD 215152 is similar to the very compact multi-planet systems found by Kepler, which is very rare in radial-velocity surveys. This discovery proves that these systems can be reached with the radial-velocity technique, but characterizing them requires a huge amount of observations.
Key words: planets and satellites: general / planets and satellites: detection / planets and satellites: dynamical evolution and stability
The HARPS data used in this article are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/614/A133
© ESO 2018
1 Introduction
The properties of extrasolar planetary systems are very diverse and often very different from those in the solar system (e.g., Mayor et al. 2014). Transit surveys, and especially the Kepler telescope, have discovered many systems of super-Earth planets in compact orbital configurations. In particular, Kepler found many systems with period ratios (Pout∕Pin) lower than 1.5 (Lissauer et al. 2011; Fabrycky et al. 2014). These compact planetary systems raise several interesting questions regarding their formation and long-term evolution, such as whether these systems formed in situ or by converging migration of the planets in the proto-planetary disk, and the role played by mean-motion resonances in setting up their architecture and in their long-term stability. These questions are still open, and new observational data would help in better constraining the formation models. While compact systems are favored by observational biases in transit surveys (e.g., Steffen & Hwang 2015), such systems are particularly challenging to separate with the radial velocity (RV) method. To our knowledge, only three pairs of planets with Pout∕Pin < 1.5 have been found using the RV technique:
-
HD 5319b and c, giant planets with Pout∕Pin = 1.38 (see Robinson et al. 2007; Giguere et al. 2015);
-
HD 200964b and c, giant planets with Pout∕Pin = 1.34 (see Johnson et al. 2011); and
-
GJ 180b and c, super-Earth planets with Pout∕Pin = 1.40 (see Tuomi et al. 2014).
Only one of these systems consists of super-Earth planets (GJ 180). Several other systems have been claimed, but were subsequently contested (e.g., Díaz et al. 2016).
In this article we present a system of four super-Earth planets around HD 215152, with periods of 5.76, 7.28, 10.86, and 25.2 d (period ratios of 1.26, 1.49, and 2.32). Such a compact system of super-Earth planets is very similar to the compact systems found by Kepler. Separating these signals required a huge observational effort, in which 373 high-quality HARPS RV measurements were taken over 13 yr.
In Sect. 2 we describe the stellar properties and the data we used. We then describe the method we employed to analyze the data in Sect. 3. In Sect. 4 we assess the orbital stability of the system and deduce additional constraints on the orbital parameters. Finally, we discuss our results in Sect. 5.
2 HARPS data and stellar properties
We present here 373 RV measurements of the K-dwarf HD 215152 that have been obtained with the HARPS high-resolution spectrograph mounted on the 3.6 m ESO telescope at La Silla Observatory (Mayor et al. 2003). The observations span 13 yr, from June 2003 to September 2016. The optical fibers feeding the HARPS spectrograph were changed in May 2015 (Lo Curto et al. 2015), which results in an offset between the 284 measurements taken before and the 89 measurements taken after the upgrade. The RV points have been taken in 330 different nights. Of these 330 nights, 287 have a single point, and 43 have two points.
Dumusque et al. (2015) found that the stitching of the HARPS detector could introduce a spurious RV signal of small amplitude with periods close to one year or an harmonic of it. The stitching of the detector creates pixels of different sizes every 512 pixels in the spectral direction, which perturbs the wavelength solution that is obtained by interpolating the wavelength of the thorium emission lines on an even scale. Owing to the barycentric Earth RV, the spectrum of a star is shifted on the CCD in the spectral direction, and some lines can cross stitches. When this is the case, the mismatch in the wavelength solution at the position of the stitch creates a spurious RV effect, which, coupled with the shift of the spectrum on the CCD over time, creates a signal typically with the period of the rotation of Earth around the Sun or an harmonic of it. To remove this spurious signal from the data, we adopted the method proposed in Dumusque et al. (2015), that is, we removed all the lines that crossed stitches from the computation of the RV.
In addition to the RVs, we also derived the 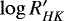 activity index from each of the 373 spectra. As for the RV, this index might also be affected by the fiber upgrade. The RV and
activity index from each of the 373 spectra. As for the RV, this index might also be affected by the fiber upgrade. The RV and 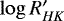 measurements are shown in Fig. 1. We also provide a brief summary of the properties of HD 215152 in Table 1. The mass and the radius of the star as well as their uncertainties were derived using the Geneva stellar evolution models (Mowlavi et al. 2012). The interpolation in the model grid was made through a Bayesian formalism using observational Gaussian priors on Teff, MV, logg, and [Fe/H] (Marmier 2014). The rotation period of the star, estimated using Mamajek & Hillenbrand (2008) and Noyes et al. (1984), is 42 days. HD 215152 is a quiet star similar to the Sun, with a mean
measurements are shown in Fig. 1. We also provide a brief summary of the properties of HD 215152 in Table 1. The mass and the radius of the star as well as their uncertainties were derived using the Geneva stellar evolution models (Mowlavi et al. 2012). The interpolation in the model grid was made through a Bayesian formalism using observational Gaussian priors on Teff, MV, logg, and [Fe/H] (Marmier 2014). The rotation period of the star, estimated using Mamajek & Hillenbrand (2008) and Noyes et al. (1984), is 42 days. HD 215152 is a quiet star similar to the Sun, with a mean 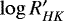 of − 4.86 and values between − 5 and − 4.8 (see Table 1 and Fig. 1). However, we clearly observe a long-term evolution in the
of − 4.86 and values between − 5 and − 4.8 (see Table 1 and Fig. 1). However, we clearly observe a long-term evolution in the 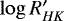 activity index, with a period of about 3000 d (see Fig. 1). This evolution is most likely related to the magnetic cycle of the star. We also observe a long-period signal in the RVs, which is anticorrelated with the signal found in the activity index (see Fig. 1). Using only the data taken before the fiber upgrade (to avoid offset issues), we find a correlation coefficient of − 0.44 ± 0.05 (computed using Figueira et al. 2016) between the RVs and the
activity index, with a period of about 3000 d (see Fig. 1). This evolution is most likely related to the magnetic cycle of the star. We also observe a long-period signal in the RVs, which is anticorrelated with the signal found in the activity index (see Fig. 1). Using only the data taken before the fiber upgrade (to avoid offset issues), we find a correlation coefficient of − 0.44 ± 0.05 (computed using Figueira et al. 2016) between the RVs and the 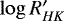 index. This anticorrelation is surprising since a correlation is usually found (and expected) on the timescale of the magnetic cycle (Lovis et al. 2011; Dumusque et al. 2011). However, for late-K and M stars, the correlation might reverse (Lovis et al. 2011, Fig. 18), which might be evidence for convective redshift (Kürster et al. 2003).
index. This anticorrelation is surprising since a correlation is usually found (and expected) on the timescale of the magnetic cycle (Lovis et al. 2011; Dumusque et al. 2011). However, for late-K and M stars, the correlation might reverse (Lovis et al. 2011, Fig. 18), which might be evidence for convective redshift (Kürster et al. 2003).
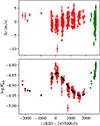 |
Fig. 1 Time series of the RV (top) and the |
Stellar properties of HD 215152.
3 Analysis
We modeled the RVs of HD 215152 as follows: For the kth data point, we have
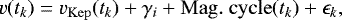 (1)
(1)
where vKep(tk) is the Keplerian motion of the star, γi is the radial proper motion of the system plus instrumental offset (one independent constant for each instrument), Mag. cycle(tk) is the component of the RV generated by the magnetic cycle of the star, and ϵk is the noise. We here only worked with a single instrument (HARPS), but since the fiber upgrade of May 2015 might induce an offset, we considered measurements before and after the fiber upgrade as coming from two independent instruments, and introduced two constants γ1 (before) and γ2 (after). The noise term ϵk in Eq. (1) takes the white and the correlated components of the noise into account (instrumental error, short-term activity of the star, etc.).
3.1 Magnetic cycle correction
In order to account for the effect of the magnetic cycle on the RVs (see Sect. 2), we introduce a proportionality coefficient between the RVs and the activity index in our model. While an (anti)correlation is expected between the two quantities on long timescales because of the magnetic cycles, on shorter timescales, other effectsmight break this correlation (stellar rotation, appearing and disappearing active regions, or different types of active regions). In order to avoid introducing artificial short-term signals in the RVs, we first filtered the 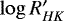 index to keep onlythe long-term trend by averaging it using a Gaussian kernel. We used a six-month width for the Gaussian kernel, which approximately corresponds to one observational season, in order to clean the high-frequency part of the
index to keep onlythe long-term trend by averaging it using a Gaussian kernel. We used a six-month width for the Gaussian kernel, which approximately corresponds to one observational season, in order to clean the high-frequency part of the 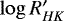 while preserving the 3000 d cycle. Since there might be a small offset in the
while preserving the 3000 d cycle. Since there might be a small offset in the 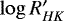 values after the fiber change, we filtered the two data sets independently. The smoothed activity index is shown in Fig. 1, superimposed with the initial
values after the fiber change, we filtered the two data sets independently. The smoothed activity index is shown in Fig. 1, superimposed with the initial 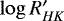 index. In Fig. 2 we also compare the periodogram of the raw
index. In Fig. 2 we also compare the periodogram of the raw 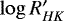 index, the smoothed activity index, and the residuals of the
index, the smoothed activity index, and the residuals of the 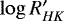 after subtracting this smooth component. For these periodograms, we adjusted for a possible offset between the data taken before and after the fiber upgrade. We observe, as expected, that the smoothed activity index captures the long-term evolution of the
after subtracting this smooth component. For these periodograms, we adjusted for a possible offset between the data taken before and after the fiber upgrade. We observe, as expected, that the smoothed activity index captures the long-term evolution of the 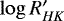 index while cleaning the high-frequency part of the signal (see Fig. 2). We do not observe any significant signal at the rotation period of the star (around 42 d) in the periodogram of the residuals of the
index while cleaning the high-frequency part of the signal (see Fig. 2). We do not observe any significant signal at the rotation period of the star (around 42 d) in the periodogram of the residuals of the 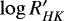 index (see Fig. 2).
index (see Fig. 2).
The magnetic cycle component in Eq. (1) is thus given in this simple model by
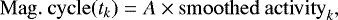 (2)
(2)
where A is the proportionality coefficient that is to be adjusted. In order to have velocity units for A and to minimize correlations between A and γi, we rescaled and centered the smoothed activity indicator to have a zero mean and a semi-amplitude of one.
The magnetic cycle component of Eq. (2) might introduce an offset in our model before and after the fiber change as a result of the possible offset in the 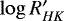 index. This offset adds up to the offset in RV that is already considered in our model (parameters γi in Eq. (1)). In the following results, the fitted offset (γ2 − γ1) is therefore always a combination of the RV offset and the
index. This offset adds up to the offset in RV that is already considered in our model (parameters γi in Eq. (1)). In the following results, the fitted offset (γ2 − γ1) is therefore always a combination of the RV offset and the 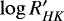 offset.
offset.
Figure 3 shows a periodogram (see Sect. 3.3) of the RV data with and without the magnetic cycle in our model. When the magnetic cycle is ignored, the periodogram is dominated by a peak around 3000 d (see Fig. 3). The period of this signal is compatible with the period found in the 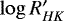 index (see Fig. 2), but the phase is opposite. When the (negative) proportionality coefficient between theRVs and the smoothed activity index is adjusted, the low-frequency part of the periodogram (P ≳100 d) almost disappears (see Fig. 3).
index (see Fig. 2), but the phase is opposite. When the (negative) proportionality coefficient between theRVs and the smoothed activity index is adjusted, the low-frequency part of the periodogram (P ≳100 d) almost disappears (see Fig. 3).
 |
Fig. 2 Periodogram of the raw activity ( |
 |
Fig. 3 Periodogram of the RVs using two different models. The first (black) does not include the corrections for magnetic cycles, while the second (gray) does include them (see Sect. 3.1). The main peak in the black curve is around 3000 d (similar to the period observed in the
|
3.2 Short-term activity and correlated noise
We modeled the short-term part of the activity as well as additional instrumental noise (not included in the measurement uncertainties provided by the pipeline, which only considers the photon noise contribution) using a Gaussian process (e.g., Baluev 2011; Haywood et al. 2014). We assumed the noise (ϵk in Eq. (1)) to follow a multivariate Gaussian random variable with covariance matrix C given by
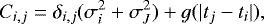 (3)
(3)
where σi is the estimated error bar of the ith measurement, σJ is the stellar jitter, δi,j is the Kronecker symbol, and g is the covariance function which is to be determined. Several shapes for the covariance function have been proposed in the literature: a squared exponential decay (e.g., Baluev 2011) of amplitude σG and correlation timescale (τG)
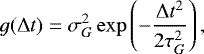 (4)
(4)
or a more complex function (e.g., Haywood et al. 2014) that includes the rotation period of the star (Prot) and a smoothing parameter (η)
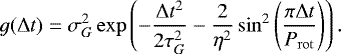 (5)
(5)
In the case of HD 215152, we find that these models give similar results. In particular, in contrast to the case of Corot-7 (Haywood et al. 2014), the activity is weak and does not show significant correlation at the rotation period of the star (i.e., around 42 d). We thus use the simpler squared exponential decay function (Eq. (4)). This function equals 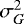 on the diagonal (Δ t = 0) and rapidly decreases for Δt ≫ τG (far from the diagonal). In order to improve the computation efficiency, we neglected all the sub- and super-diagonals for which all terms satisfy
on the diagonal (Δ t = 0) and rapidly decreases for Δt ≫ τG (far from the diagonal). In order to improve the computation efficiency, we neglected all the sub- and super-diagonals for which all terms satisfy 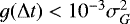 . We thus obtained a band matrix (whose bandwidth depends on τG) that allowedus to use faster dedicated algorithms for the matrix inversion and for computing the determinant.
. We thus obtained a band matrix (whose bandwidth depends on τG) that allowedus to use faster dedicated algorithms for the matrix inversion and for computing the determinant.
For a given noise covariance matrix C and given model parameters, the likelihood function reads (e.g., Baluev 2011)
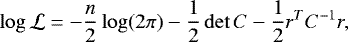 (6)
(6)
where r is the vector of the residuals.
3.3 Periodograms
In order to determine the Keplerian component of our model (Eq. (1)), we started by inspecting the data using periodograms. We sequentially added planets in the model. At each step, we first subtracted the Keplerian part of the last model (previously found planets) from the RVs. For each period P to be tested, we then compared the model with the new planet (sinusoidal signal of period P) with the model without it (reference). For each period P and for the reference, we readjusted all other model parameters (A, γi, σG, and τG), except for the previously found planet parameters, by maximizing the likelihood. We then used the Bayesian information criterion (BIC, see Schwarz 1978)
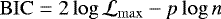 (7)
(7)
(where p is the number of parameters of a given model) to estimate the Bayes factor between the models
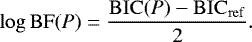 (8)
(8)
Following Feng et al. (2017), we used these logBF values to draw the periodogram, and we used a threshold at log BF = 5 to add a planet candidate in our model. The main difference in our approach is that we modeled the correlated noise using a Gaussian process (see Sect. 3.2), in contrast to Feng et al. (2017), who used a moving-average model. The complete model (including all previous planets) was then readjusted by maximizing the likelihood using a downhill simplex algorithm (Nelder & Mead 1965), and we iterated the process. At this stage, we did not allow eccentric orbits. The successive periodograms thus built are shown in Fig. 4. The evolution of the noise and planetary parameters at each step of the process are detailed in Table 2. We find four planet candidates at periods 10.87, 5.76, 7.28, and 25.2 d.
The aliases at one sidereal day (1.16 and 1.04 d) of the two last candidates (7.28 and 25.2 d, respectively) show slightly higher log BF values than the periods we selected. Given that we find a correlation timescale (τG) of about 1–2 days (see Table 2), we suspect that periods of about one day are significantly affected by the correlated noise, and we considered the candidates at 7.28 and 25.2 d to be more likely than their aliases at one day. However, we cannot rule out any of the possibilities. In order to break the alias at one sidereal day and to better characterize the correlated noise, we would need a dedicated observing strategy with several points per night during several consecutive nights. The signal-to-noise ratio (S/N) and the 43 nights with two points are not sufficient in this case to apply a dealiasing technique such as is described in Dawson & Fabrycky (2010). As in the case of the 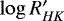 index, there does not seem to be a significant signal at the rotation period of the star (about 42 d) in the periodogram of the RV residuals (see Fig. 4).
index, there does not seem to be a significant signal at the rotation period of the star (about 42 d) in the periodogram of the RV residuals (see Fig. 4).
We notethat the HD 215152 system was listed in the statistical study of Mayor et al. (2011), with a detailed analysis yet to be published. In this previous analysis, only two planets were detected at 7.28 and 10.87 d. We still find these two planets, but we find two other candidates as well (at 5.76 and 25.2 d). However, the number of data points increased greatly since 2011, from 171 to 373 points, the time span increased from 8 to 13 years, and the sampling is better (more nights with two points per night). Since all the candidates have small amplitudes, it is not surprising that some of them were missed in Mayor et al. (2011). As a comparison, we reran our analysis, but using only the first 171 data points. This analysis differs from the analysis used by Mayor et al. (2011) since we here included the stitching correction, magnetic cycle modeling, and a more complex noise model (Gaussian process). As in Mayor et al. (2011), we find the candidates at 10.87 and 7.28 d (with a strong alias at 1.16 d). The 5.76 d signal is just below the detection threshold (log BF < 5), and we do not detect the 25.2 d signal. This confirms that the huge observational effort employed since 2011 was essential to better characterize this system.
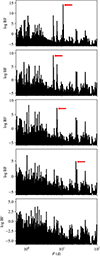 |
Fig. 4 Periodogram of the RVs at each step of constructing our Keplerian model (see Sect. 3.3). We highlight (red arrows) the selected period (highest peak) for each planet: 10.87, 5.76, 7.28, and 25.2 d. We also show (bottom) the periodogram of the residuals. Intermediate values of the planetary and noise parameters are given in Table 2. |
3.4 Full model sampling
In orderto better determine the orbital architecture of the system, we explored the parameter space of our full model (four planets, offsets, magnetic cycle, and Gaussian process) using an adaptive Metropolis approach. The sampling algorithm is described in Appendix A, and the priors are detailed in Table 3. We ran two experiments, one with elliptical orbits and one with circular orbits. In both cases, we ran the algorithm for 2 000 000 steps, but only keep the last 1 500 000 steps to compute statistics. Table 4 shows the results of the elliptical fit, while the results of the circular fit are summarized in Table 5. In both tables, the uncertainty on the mass of the star (see Table 1) is taken into account to derive the minimum masses (m sini) and semi-major axes (a) of the planets. Table 4 clearly shows that the eccentricities cannot be constrained with the current data. This is expected for such low-amplitude signals (K ≲ 1 m s−1 for all four planets). However, all the other parameters remain compatible between the circular and the elliptic fit. Moreover, since the whole system is very compact, we can expect tidal dissipation to have severely damped any initial eccentricity. The circular fit (Table 5) therefore probably represents the system better than the elliptical fit.In the following, we use the set of parameters corresponding to the best circular fit (i.e., maximum likelihood, ML). We show the phase-folded RV curves for each planet in Fig. 5 as obtained with these parameters.
Priors used for the full model sampling.
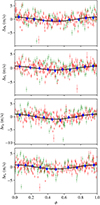 |
Fig. 5 Phase-folded curve for each of the four planets obtained using the parameters of the circular ML. The black line shows the model. Red (green) dots correspond to HARPS data taken before (after) the fiber upgrade. Blue dots show the data binned in phase. For each panel, we subtracted the Keplerian signal associated with all other planets from the data, as well as the magnetic cycle component and instrumental offsets. |
4 System dynamics and stability
The planetary system around HD 215152 is very compact, especially the three inner planets, which exhibit period ratios of Pc ∕Pb = 1.26 (close to 5/4) and Pd∕Pc = 1.49 (close to 3/2). This compact architecture raises several interesting questions regarding the dynamics of the system, such as whether the planets are locked in mean-motion resonances, if the observed system is stable, and how the stability of the system depends on the eccentricities and the inclinations of the planets. In order to partially answer these questions, we ran three sets of N-body integrations of the system. We used the ML solution of the circular model (see Table 5) as a reference and varied the period and eccentricity of Planet c to generate three grids of 161 × 161 (25921) initial conditions. In the first set of simulations (referred to as S90), we assumed the four planets to be coplanar, with inclinations of 90° (m = msini). In the second set of simulations (S30), we assumed the four planets to be coplanar, with inclinations of 30° (m = 2msini). Finally, the third set (S15) corresponds to inclinations of 15° (m ≈ 3.86 msini).
For each initial condition, we integrated the system for 1 kyr using GENGA (Grimm & Stadel 2014), and we assessed the stability of the system using the NAFF stability indicator (Laskar 1990, 1993; Correia et al. 2005). We show the results of these integrations in Fig. 6. In the S90 simulations, where the masses are equal to minimum masses, the system is stable at low eccentricities (ec ≲ 0.03, see Fig. 6 top). If the masses are twice the minimum masses (S30, Fig. 6 center), the system can still be stable, but only at lower eccentricities (ec ≲ 0.02). Finally, for the S15 simulations (Fig. 6 bottom), the system is unstable even at zero eccentricities. We also note in Fig. 6 that stable orbits that are compatible with the data correspond to a system that clearly lies outside both the 5:4 resonance between Planets b and c and the 3:2 resonance between Planets c and d.
These simulations illustrate that constraints on the eccentricities and the inclinations of the planets could be derived from studying the system stability. However, we note that the bounds we obtain on the eccentricity of Planet c should be taken with caution since we only varied a few orbital parameters here (the period and eccentricity of Planet c, and the overall system inclination).In order to obtain more precise constraints, all the orbital parameters of all the planets need to be let free to vary.
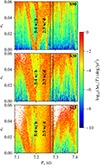 |
Fig. 6 Stability analysis of HD 215152 c around the circular ML solution (see Table 5) and assuming planetary inclinations of 90° (top), 30° (center), and 15° (bottom).Blue points correspond to stable orbits, red points to unstable orbits, and white points correspond to highly unstable solutions (collision or ejection of a planet during the 1 kyr of the simulation). The two vertical black lines highlight the 2σ interval for the period of Planet c. We also highlight the location of the 5:4 resonance with Planet b and the 3:2 resonance with Planet d. |
5 Discussion
We reported the discovery of a compact system of four super-Earth planets around HD 215152. The planets have periods of 5.76, 7.28, 10.86, and 25.2 d, and minimum masses of 1.8, 1.7, 2.8, and 2.9 M⊕ (respectively). Planets b and c are close to but outside of a 5:4 mean motion resonance (period ratio of 1.26), and Planets c and d are close to but outside of a 3:2 mean motion resonance (period ratio of 1.49). Owing to the low masses of the planets (low S/N), it is very difficult to constrain the planets eccentricities. However, using N-body simulations, we showed that interesting constraints on the eccentricities and on the inclinations of the planets could be derived from studying the system stability. Assuming inclinations of 90° for all the planets, we find that the system remains stable for ec ≲ 0.03. If the planets remain coplanar but have inclinations of 30° (masses of twice the minimum masses), the maximum eccentricity is about 0.02. Moreover, for a coplanar system with an inclination of 15°, the system is unstable even at zero eccentricities. Interestingly, these values (ec ≲ 0.03) are on the order of magnitude of eccentricities found in Kepler multi-transiting systems that are close to resonances (eccentricities inferred using transit timing variations, see Wu & Lithwick 2013). This is not surprising as the HD 215152 planetary system shares many properties with Kepler compact multi-planetary systems. In addition, low eccentricities are expected in such a compact system because of the tides exerted by the star on the planets. We note that the bounds we obtain on the eccentricity of Planet c should only be taken as very crude estimates because we did not explore the entire parameter space and only varied a few orbital parameters. A more complete dynamical analysis is thus necessary to obtain precise constraints on the planet eccentricities and inclinations, but this is beyond the scope of this paper.
Acknowledgements
We thank the anonymous referee for his/her useful comments. We acknowledge financial support from the Swiss National Science Foundation (SNSF). This work has in part been carried out within the framework of the National Centre for Competence in Research PlanetS supported by SNSF. XD is grateful to The Branco Weiss Fellowship–Society in Science for its financial support. PF and NCS acknowledge support by Fundação para a Ciência e a Tecnologia (FCT) through Investigador FCT contracts of reference IF/01037/2013/CP1191/CT0001 and IF/00169/2012/CP0150/CT0002, respectively, and POPH/FSE (EC) by FEDER funding through the program “Programa Operacional de Factores de Competitividade – COMPETE”. PF further acknowledges support from Fundação para a Ciência e a Tecnologia (FCT) in the form of an exploratory project of reference IF/01037/2013/CP1191/CT0001. RA acknowledges the Spanish Ministry of Economy and Competitiveness (MINECO) for the financial support under the Ramón y Cajal program RYC-2010-06519, and the program RETOS ESP2014-57495-C2-1-R and ESP2016-80435-C2-2-R.
Appendix A: Adaptive Metropolis algorithm
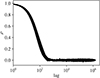 |
Fig. A.1 Autocorrelation functions for the 26 parameters of the elliptical model, the log likelihood, and log posterior, computed on the last 1 500 000 steps of the Metropolis algorithm. The maximum integrated autocorrelation time is 223, which corresponds to an effective sample size of 6721. |
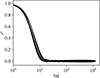 |
Fig. A.2 Autocorrelation functions for the 18 parameters of the circular model, the log likelihood, and log posterior, computed on the last 1 500 000 steps of the Metropolis algorithm. The maximum integrated autocorrelation time is 112, which corresponds to an effective sample size of 13 417. |
In order to explore the parameter space of our model, we used an adaptive Metropolis algorithm inspired by Haario et al. (2001). This algorithm is similar to the classical Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970), except that at each step the proposal is randomly generated around the previous point, using the covariance matrix of all preceding points (see Haario et al. 2001).
We additionally included in the algorithm a possibility to go back around an anterior point (not the previous one). This idea is inspired by the tuned jump proposal described in Farr et al. (2014), and it allowed us to improve the mixing of the chain. We implemented it as follows:
-
At each step, there is a given probability (pgo-back = 0.01 in our case) to make a go-back proposal. Otherwise, a classical proposal around the previous point is made.
-
In case of a go-back proposal, an anterior point is randomly selected, and a proposal is made around this point (still using the covariance matrix of all previous steps).
-
Since the proposal is not symmetrical, and in order to maintain detailed balance, we computed the forward and backward jump probabilities (e.g., Farr et al. 2014) and took them into account in computing the acceptance probability.
-
The computation of forward and backward jump probabilities becomes very expensive in computer time when the number of possible anterior points increases. We thus only considered one point over hundred as a possible go-back point (around which the proposal can be made).
We used this algorithm to explore the parameter space for both the elliptical case and the circular case. The results are detailed in Sect. 3.4 (Tables 4 and 5). In order to illustrate the mixing properties of our chains, we show in Figs. A.1 and A.2 the autocorrelation functions of all parameters in both cases. In the elliptical case, the maximum integrated autocorrelation time is 223 (effective sample size of 6721). This is sufficient to estimate 2σ error bars. In the circular case, the mixing is even better (integrated autocorrelation time of 112, and effective sample size of 13 417). This is not surprising since the problem has fewer dimensions and is much better constrained.
References
- Baluev, R. V. 2011, Celest. Mech. Dyn. Astron., 111, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2005, A&A, 440, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Ségransan, D., Udry, S., et al. 2016, A&A, 585, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Lovis, C., Ségransan, D., et al. 2011, A&A, 535, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., & Latham, D. W. 2015, ApJ, 808, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Farr, B., Kalogera, V., & Luijten, E. 2014, Phys. Rev. D, 90, 024014 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, F., Tuomi, M., & Jones, H. R. A. 2017, MNRAS, 470, 4794 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Faria, J. P., Adibekyan, V. Z., Oshagh, M., & Santos, N. C. 2016, Orig. Life Evol. Biosphere, 46, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giguere, M. J., Fischer, D. A., Payne, M. J., et al. 2015, ApJ, 799, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, et al. 2003, AJ, 126, 2048 [NASA ADS] [CrossRef] [Google Scholar]
- Grimm, S. L.,& Stadel, J. G. 2014, ApJ, 796, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Haario, H., Saksman, E., & Tamminen, J. 2001, Bernoulli, 7, 223 [CrossRef] [MathSciNet] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Johnson, J. A., Payne, M., Howard, A. W., et al. 2011, AJ, 141, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Phys. D Nonlinear Phenom., 67, 257 [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv: 1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Marmier, M. 2014, PhD thesis, Geneva Observatory, University of Geneva, Switzerland [Google Scholar]
- Martínez-Arnáiz, R., Maldonado, J., Montes, D., Eiroa, C., & Montesinos, B. 2010, A&A, 520, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv: 1109.2497] [Google Scholar]
- Mayor, M., Lovis, C., & Santos, N. C. 2014, Nature, 513, 328 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N., Eggenberger, P., Meynet, G., et al. 2012, A&A, 541, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, S. E., Laughlin, G., Vogt, S. S., et al. 2007, ApJ, 670, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Steffen, J. H., & Hwang, J. A. 2015, MNRAS, 448, 1956 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., Jones, H. R. A., Barnes, J. R., Anglada-Escudé, G., & Jenkins, J. S. 2014, MNRAS, 441, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2013, ApJ, 772, 74 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time series of the RV (top) and the |
| In the text | |
 |
Fig. 2 Periodogram of the raw activity ( |
| In the text | |
 |
Fig. 3 Periodogram of the RVs using two different models. The first (black) does not include the corrections for magnetic cycles, while the second (gray) does include them (see Sect. 3.1). The main peak in the black curve is around 3000 d (similar to the period observed in the
|
| In the text | |
 |
Fig. 4 Periodogram of the RVs at each step of constructing our Keplerian model (see Sect. 3.3). We highlight (red arrows) the selected period (highest peak) for each planet: 10.87, 5.76, 7.28, and 25.2 d. We also show (bottom) the periodogram of the residuals. Intermediate values of the planetary and noise parameters are given in Table 2. |
| In the text | |
 |
Fig. 5 Phase-folded curve for each of the four planets obtained using the parameters of the circular ML. The black line shows the model. Red (green) dots correspond to HARPS data taken before (after) the fiber upgrade. Blue dots show the data binned in phase. For each panel, we subtracted the Keplerian signal associated with all other planets from the data, as well as the magnetic cycle component and instrumental offsets. |
| In the text | |
 |
Fig. 6 Stability analysis of HD 215152 c around the circular ML solution (see Table 5) and assuming planetary inclinations of 90° (top), 30° (center), and 15° (bottom).Blue points correspond to stable orbits, red points to unstable orbits, and white points correspond to highly unstable solutions (collision or ejection of a planet during the 1 kyr of the simulation). The two vertical black lines highlight the 2σ interval for the period of Planet c. We also highlight the location of the 5:4 resonance with Planet b and the 3:2 resonance with Planet d. |
| In the text | |
 |
Fig. A.1 Autocorrelation functions for the 26 parameters of the elliptical model, the log likelihood, and log posterior, computed on the last 1 500 000 steps of the Metropolis algorithm. The maximum integrated autocorrelation time is 223, which corresponds to an effective sample size of 6721. |
| In the text | |
 |
Fig. A.2 Autocorrelation functions for the 18 parameters of the circular model, the log likelihood, and log posterior, computed on the last 1 500 000 steps of the Metropolis algorithm. The maximum integrated autocorrelation time is 112, which corresponds to an effective sample size of 13 417. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.