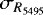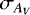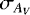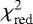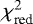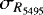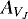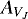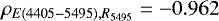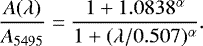| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732050 | |
| Published online | 16 May 2018 | |
Optical-NIR dust extinction towards Galactic O stars★
1
Centro de Astrobiología, CSIC-INTA, campus ESAC,
camino bajo del castillo s/n,
28 692
Villanueva de la Cañada,
Spain
e-mail: jmaiz@cab.inta-csic.es
2
Departamento de Física y Astronomía, Universidad de La Serena,
Av. Cisternas 1200 Norte,
La Serena,
Chile
Received:
5
October
2017
Accepted:
25
December
2017
Context. O stars are excellent tracers of the intervening ISM because of their high luminosity, blue intrinsic SED, and relatively featureless spectra. We are currently conducting the Galactic O-Star Spectroscopic Survey (GOSSS), which is generating a large sample of O stars with accurate spectral types within several kpc of the Sun.
Aims. We aim to obtain a global picture of the properties of dust extinction in the solar neighborhood based on optical-NIR photometry of O stars with accurate spectral types.
Methods. We have processed a carefully selected photometric set with the CHORIZOS code to measure the amount [E(4405 − 5495)] and type [R5495] of extinction towards 562 O-type stellar systems. We have tested three different families of extinction laws and analyzed our results with the help of additional archival data.
Results. The Maíz Apellániz et al. (2014, A&A, 564, A63) family of extinction laws provides a better description of Galactic dust that either the Cardelli et al. (1989, ApJ, 345, 245) or Fitzpatrick (1999, PASP, 111, 63) families, so it should be preferentially used when analysing samples similar to the one in this paper. In many cases O stars and late-type stars experience similar amounts of extinction at similar distances but some O stars are located close to the molecular clouds left over from their births and have larger extinctions than the average for nearby late-type populations. In qualitative terms, O stars experience a more diverse extinction than late-type stars, as some are affected by the small-grain-size, low-R5495 effect of molecular clouds and others by the large-grain-size, high-R5495 effect of H II regions. Late-type stars experience a narrower range of grain sizes or R5495, as their extinction is predominantly caused by the average, diffuse ISM. We propose that the reason for the existence of large-grain-size, high-R5495 regions in the ISM in the form of H II regions and hot-gas bubbles is the selective destruction of small dust grains by EUV photons and possibly by thermal sputtering by atoms or ions.
Key words: dust, extinction / Galaxy: structure / methods: data analysis / methods: observational / stars: early-type
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/613/A9
© ESO 2018
1 Introduction
Soon after the discovery of the existence of an intervening interstellar medium (ISM) that obscures and reddens starlight, Baade & Minkowski (1937) realized that sightlines could differ not only in the amount of obscuration but also in its dependence with wavelength. In current terms, we say that the extinction law is not constant so in order to determine how the ISM changes the light we receive from the stars we need to specify both the amount and the type of extinction. Extinction is a combination of absorption and scattering by the intervening particles and the largest contributor is dust, which produces mostly continuum extinction but also some broad features in the UV and the IR. Atoms and molecules also have an effect in the form of discrete absorption lines and some absorption features (diffuse interstellar bands or DIBs) of unknown origin are also detected, but those will be mostly ignored in this paper, which deals with dust extinction.
Some astronomers are interested in dust extinction because of the information it contains regarding the spatial distribution and properties of the ISM but to most of them it is simply a nuisance, an effect that complicates the calculation of luminosities, and all they want to know is how to eliminate it from their data. Throughout much of the twentieth century astronomers have tried to generate extinction laws but kept hitting a wall: as different sightlines had different types of extinction, an average extinction law could only be an approximation and one that was bound to fail miserably under some circumstances. It was not until the seminal work of Cardelli et al. (1989) (CCM hereafter), that a family (not an average) of extinction laws was produced, with a parameter (R5495, see Appendix A for its relationship with RV) that characterized the type of extinction and that is associated with the average dust grain size (small grains yield a low value of R5495, large grains a high one). CCM became the standard reference in the field for the next quarter of a century, as for the first time it allowed to simultaneously determine the amount and type of dust extinction and eliminate its effect from the observed photometry. CCM had a few problems, though, some of which were treated by the alternative family of extinction laws of Fitzpatrick (1999) (F99 hereafter), and later on by the Maíz Apellániz et al. (2014) family, from now on MA14. MA14 showed that its family of extinction laws provided a better fit to the optical-NIR extinction in 30 Doradus than either CCM or F99, to the point that it was possible for the first time to obtain reasonable estimates of the effective temperatures of O stars from photometry alone, something that was not possible until then due to the problems that exist in the other families. The MA14 family of extinction laws was derived using O stars on 30 Doradus so an obvious follow-up question is: does it also do a better job in characterizing optical-NIR extinction for Galactic O stars? Answering that question is the first objective of this paper.
In the last decade we have been conducting the Galactic O-Star Spectroscopic Survey or GOSSS (Maíz Apellániz et al. 2011), which aims to obtain high S/N, R ~ 2500 blue-violet spectroscopy of all optically accessible Galactic O stars and derive their spectral types. The sample currently available is the largest ever uniform collection of O spectral types ever published. In this paper we use this sample to answer the question in the previous paragraph and a second question: what is the relationship between dust grain size and ISM environment? Previous attempts to answer this question have been hampered by, among other things, limited samples and the methodology employed. Our uses of the GOSSS sample and of the CHORIZOS (Maíz Apellániz 2004) techniques applied in MA14 and in other recent works address both objectives.
This paper is divided as follows. We first present the sample in detail, describing how we have culled the photometry for the sample and eliminated problematic objects, and the CHORIZOS methodology. We then show our results in three parts: a comparison of families of extinction laws, a discussion of quantitative reddening differences between O- and late-type stars, and an analysis of how the properties of dust are a function of the ISM environment. In the final standard section of the paper we present our conclusions and outline future lines of work. There are also five Appendices that discuss extinction terms and techniques in order to better understand the uncertainties and biases involved in this type of analysis. We recommend readers who are unfamiliar with the mathematical aspects of extinction effects to start with Appendices.
2 Data and methods
The sample in this paper is built starting from the 590 O stars in GOSSS-I (Sota et al. 2011), GOSSS-II (Sota et al. 2014), and GOSSS-III (Maíz Apellániz et al. 2016)1. For the initial sample we collected our basic photometric set:
Ground-based Johnson UJ BJ V J photometry using Simbad (Wenger et al. 2000) and the GCPD (Mermilliod et al. 1997).
Near-infrared J H Ks photometry from 2MASS (Skrutskie et al. 2006).
Optical G photometry from the Gaia Data Release 1 or DR1 (van Leeuwen et al. 2017).
The majority of the stars in our sample have photometry in all seven of the basic photometric bands, though our quality control (see below) led us to eliminate some of them. We also compiled the extended photometric set:
Tycho-2 BT V T photometry (Høg et al. 2000).
Strömgren uS vS bS yS photometry from Paunzen (2015).
The reason to differentiate between basic and extended photometric sets is that in the final sample all objects include at least five of the seven basic photometric points but not necessarily the extended photometric ones, whose coverage is more limited (complete or near-complete for bright stars but incomplete for dim ones). This led us to divide the final sample into four subsamples: J2G, J2GT, J2GS, and J2GTS, where the naming convention refers to the photometry included, that is, J(ohnson), 2(MASS), G(aia), S(trömgren), and T(ycho-2), respectively.
After compiling the photometry for the initial sample we carefully analyzed each object to produce a final clean sample in the following way:
For the GOSSS objects with nearby companions (visual binaries and multiples) we analyzed which ones had separate Johnson, 2MASS, and Strömgren magnitudes and for which ones the available basic photometry was a combination of two or more components (because we had been able to obtain spatially resolved spectral types). In the latter case we merged the information on the different GOSSS components (see below for Gaia and Tycho-2). We also eliminated a few cases where no reliable photometry could be found. This process reduced the sample to 571 stars.
The 2MASS photometry for bright stars is of very poor quality (uncertainties larger than 0.2 mag). Whenever possible, we searched for alternative sources such as Ducati (2002) to be used as substitutes. In the majority of cases where we used the2MASS photometry we applied the 2MASS uncertainties directly, with the exception being the stars with poor quality flags, where we increased the uncertainty values.
For objects with NIR excesses we followed two different strategies. Oe stars, whose circumstellar environment can contribute significantly to the NIR photometry, were eliminated, leaving a final sample of 562 stars. For the rest, we applied acorrection to the J H Ks photometry based on the infrared colors that also increased the photometric uncertainties in those cases. The correction was based on the facts that [a] all O stars have very similar photospheric intrinsic J − H and H − Ks colors and that [b] the extinction vector in the color-color plane has a nearly constant direction for the range of E(4405 − 5495) values considered here (neither of those assumptions is true for most optical or optical-NIR colors, see Appendix B). There are numerous literature examples of this effect, one is shown in Fig. 4 of Arias et al. (2006).
For the values of the Johnson and Strömgren uncertainties, see Maíz Apellániz (2006). In those cases where the source was suspected to be of poor quality, we increased the value of the uncertainties. For the zero points, see Maíz Apellániz (2007).
Tycho-2 photometry supposedly has no saturation limit while G saturates around magnitude 6.0 for DR1 (van Leeuwen et al. 2017; Maíz Apellániz 2017). However, when comparing photometry from different sources we discovered a slight saturation effect for the brightest Tycho-2 stars, so we eliminated those magnitudes from our analysis. Regarding saturated G DR1 magnitudes, we used the Maíz Apellániz (2017) correction.
Gaia DR1 does not include variability information and G magnitudes appear to be the average ones. This effect turned out to be especially important for some eclipsing binaries, for which we also eliminated that magnitude. We used the calibration of Maíz Apellániz (2017), who corrected the nominal passband of Jordi et al. (2010).
Another relevant effect when comparing ground-based (Johnson, 2MASS, and Strömgren) and space (Gaia and Tycho-2) photometry is spatial resolution: the published space photometry may include different components of a multiple system that are seen as a single source from the ground. We revised all cases in turn to decide which components were detected. This led in some cases to combining the space photometry from two components (as we did with the ground-based photometry) and in others to discarding the Gaia or Tycho-2 photometric points.
Finally, all the photometry was revised to determine the mutual compatibility in an iterative process that took weeks of work and led to a final culling of the used magnitudes. This is necessary because published photometry contains a significant number of errors2. The reader is invited to look up in online tools, such as Simbad and VizieR any of the stars in the sample with a large number of entries there. A quick perusal easily reveals cases in which, for example, Johnson photometry from different sources is incompatible. When comparing different photometric systems such incompatibility may not be obvious at first, as any two magnitudes generate a colour (even V J − yS, something commonly ignored), but it becomes apparent when no valid single-star SED can be built with the combination independently of the parameters or extinction-law families used. We have recently started a different project called GALANTE (see below) with which we will obtain uniform-quality photometry for a significant fraction of the sources here but its results are still far in the future.
The collected Johnson photometry is available from the web site of the Galactic O-Star Catalog (GOSC; Maíz Apellániz et al. 2004; Sota et al. 2008)3. The final subsamples have 109 (J2G), 152 (J2GT), 38 (J2GS), and 263 (J2GTS) stars. Of the final 562 stars, 28, 6, 13, 13, and 111 have UJ, J, H, Ks, and G missing, respectively.
The photometry was processed using the latest version of the CHORIZOS code (Maíz Apellániz 2004) to determine the amount and type of extinction to each of the star. We have used this method successfully in the past (e.g., Maíz Apellániz et al. 2015b), here we describe the specific details of the CHORIZOS runs used in this paper:
We used the Milky Way grid of Maíz Apellániz (2013b), in which the two grid parameters are effective temperature (Teff) and photometric luminosity class (LC). The latter quantity is defined in an analogous way to the spectroscopic equivalent, but instead of being discrete it is a continuous variable that ranges from 0.0 (highest luminosity for that Teff) to 5.5 (lowest luminosity for that Teff). We note that the range is selected in order to make objects with spectroscopic luminosity class V (dwarfs) have LC ≈ 5 and objects with spectral luminosity class I (supergiants) have LC ≈ 1. In this paper we are only interested in O stars, whose spectral energy distributions (SEDs) are TLUSTY (Lanz & Hubeny 2003).
Each star was processed three times, once each with the CCM, F99, and MA14 families of extinction laws. The type of extinction is parameterized by R5495 and the amount of extinction4 is parameterized by E(4405 − 5495). See Appendix A for a discussion on the use of those parameters.
The Teff-spectral type conversion used is an adapted version of Martins et al. (2005) that includes the spectral subtypes and luminosity classes used in GOSSS I+II+III.
Teff and LC were fixed while R5495, E(4405 − 5495), and logd were left as free parameters. The values of the Teff were established from the used Teff-spectral type conversion (see previous point). For LC we used the spectroscopic luminosity class available from the GOSSS spectral classification. We note that, in any case, optical-NIR colors of O stars are very weakly dependent on luminosity other than wind effects.
The four subsamples were run separately. The number of photometric points for the stars in each sample is 7 (J2G), 9 (J2GT), 11 (J2GS), and 13 (J2GTS). As we are fitting three parameters with CHORIZOS, the degrees of freedom (d.o.f.), are four, six, eight, and ten, respectively5. The reduced χ2 of the best model,
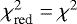 /d.o.f. is used to evaluate the quality of the fit for each star.
/d.o.f. is used to evaluate the quality of the fit for each star.
The results from the CHORIZOS runs are given in Table 1 (online), available at the CDS. The spectroscopic logarithmic distances (log d) are given with only one digit after the decimal point as that is their expected level of precision6. In the next section we discuss the scientific results. Prior to that, we comment on some issues regarding the methodology. The reader is referred to Appendices for explanations of why we have used monochromatic quantities instead of filter-integrated ones to characterize extinction and on some of the numerical consequences of using multifilter photometry to determine extinction properties.
The quantities listed in Table 1 (online) are the direct output of CHORIZOS and the uncertainties should be taken as the random ones. They do not include systematic uncertainties, of which there are three possible origins:
Photometric. Here we have possible zero-point errors and discrepancies between different photometric sources. As previously mentioned, we have minimized those problems by analyzing the zero points in different systems (Maíz Apellániz 2005, 2006, 2007) and by assigning quality flags (and associated uncertainties) to different sources.
SED. Inprinciple, the optical-NIR SEDs of O stars are well known and depend little on metallicity. However, one should be careful not to include or to correct for those cases where the SED is anomalous. We have done this by excluding Oe stars from our sample and by correcting for NIR excesses when present.
Extinction laws. One can obtain results assuming any extinction law. However, that does not mean that the used extinction law is the correct one. If it is not, a systematic error is likely to be introduced in the process. In the next section we discuss how we have checked this.
Regarding systematic uncertainties, we specifically point out the differences in the uncertainties in V J,0 as calculated by two possible methods described in Appendix C. The uncertainties in Table 1 (online) are calculated using the whole CHORIZOS likelihood grid (second method in Appendix C). As a consequence, the uncertainties in V J,0 are smaller than those in  . For logd we only give two significant figures and no random uncertainties, as there are two large sources of systematic uncertainties: the intrinsic width of the luminosity class-luminosity relationship and the non-inclusion of the existence of multiple systems (astrometric or spectroscopic) in the photometric data. The reader is referred to Maíz Apellániz et al. (2015a,b) for an example of how those issues complicate the use of spectroscopic parallaxes for O stars. We will revisit this issue in future papers once accurate Gaia parallaxes are available for a large fraction of the sample.
. For logd we only give two significant figures and no random uncertainties, as there are two large sources of systematic uncertainties: the intrinsic width of the luminosity class-luminosity relationship and the non-inclusion of the existence of multiple systems (astrometric or spectroscopic) in the photometric data. The reader is referred to Maíz Apellániz et al. (2015a,b) for an example of how those issues complicate the use of spectroscopic parallaxes for O stars. We will revisit this issue in future papers once accurate Gaia parallaxes are available for a large fraction of the sample.
Figure 1 shows the dependence of the R5495 uncertainties from the CHORIZOS runs on E(4405 − 5495). For the J2 sample the values agree reasonably well with the predictions of Eq. (D.2). The results for the other subsamples indicate that it is possible to reduce the random uncertainty of R5495 by including additional filters in the analysis, that is, the more (good) data, the better, as expected.
 |
Fig. 1
|
3 Results
3.1 Comparing extinction-law families
We begin our analysis by comparing the results obtained with the CCM, F99, and MA14 families of extinction laws7. In Fig 2 we plot 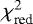 as a function of E(4405 − 5495) for each family. Figure 3 shows two similar plots but with the
as a function of E(4405 − 5495) for each family. Figure 3 shows two similar plots but with the 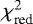 differences between MA14 and CCM (left) / F99 (right) on the vertical axis. Figure 4 shows the
differences between MA14 and CCM (left) / F99 (right) on the vertical axis. Figure 4 shows the 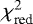 histograms for the three families compared with the expected combined distribution, built from the sum of the distributions for each star, each one with its d.o.f.
histograms for the three families compared with the expected combined distribution, built from the sum of the distributions for each star, each one with its d.o.f.
The most important result of the comparison is that the MA14 family provides much better results than either CCM or F99. For MA14 all stars have 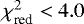 while for theother two families there is a long tail that extends to values above ten. The MA14 results show no strong trends as a function of E(4405 − 5495) or differences between subsamples. Its
while for theother two families there is a long tail that extends to values above ten. The MA14 results show no strong trends as a function of E(4405 − 5495) or differences between subsamples. Its  histogram has a cutoff at the expected location but is more heavily populated in the 1.5–3.0 region than the expected distribution. This could be caused either by systematic errors in the input photometry (for example, due to variability) or by the need to fine-tune the extinction laws. However, that issue appears to be a minor effect for low-intermediate extinction values, so we can conclude that the MA14 family of extinction laws provides the best description of Galactic optical extinction for E(4405 − 5495) < 3.0 available to date. This statement is true even though the MA14 laws were derived using 30 Doradus, not Galactic, data; such validity was already noted in the MA14 paper itself for a very limited sample of Galactic stars. We also note that we had already reached this conclusion when we presented the preliminary results of this paper at two scientific conferences (Maíz Apellániz 2015b; Maíz Apellániz et al. 2017b).
histogram has a cutoff at the expected location but is more heavily populated in the 1.5–3.0 region than the expected distribution. This could be caused either by systematic errors in the input photometry (for example, due to variability) or by the need to fine-tune the extinction laws. However, that issue appears to be a minor effect for low-intermediate extinction values, so we can conclude that the MA14 family of extinction laws provides the best description of Galactic optical extinction for E(4405 − 5495) < 3.0 available to date. This statement is true even though the MA14 laws were derived using 30 Doradus, not Galactic, data; such validity was already noted in the MA14 paper itself for a very limited sample of Galactic stars. We also note that we had already reached this conclusion when we presented the preliminary results of this paper at two scientific conferences (Maíz Apellániz 2015b; Maíz Apellániz et al. 2017b).
Why does the MA14 family work better than either CCM or F99? In the case of CCM there are two culprits. the use of a seventh-degree polynomial in 1∕λ for wavelength interpolation (Maíz Apellániz 2013a) and the behavior for the U band (see MA14). Thefirst effect is clearly seen in the left panels of Figs. 2 and 3: for a given value of E(4405 − 5495) the typical 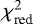 is worse when Strömgren photometry (which has filters intercalated between U and B and between B and V) is present than when is not. The F99 results are significantly worse than for MA14. This is especially true for large values of R5495, which are the worst offenders for E(4405 − 5495) < 1.5 (as explained below, our sample does not contain objects with both large E(4405 − 5495) and R5495).
is worse when Strömgren photometry (which has filters intercalated between U and B and between B and V) is present than when is not. The F99 results are significantly worse than for MA14. This is especially true for large values of R5495, which are the worst offenders for E(4405 − 5495) < 1.5 (as explained below, our sample does not contain objects with both large E(4405 − 5495) and R5495).
It is interesting to compare our results with those of Schlafly et al. (2016). Those authors find that the MA14 family provides a good description of the mean optical extinction curve and of its variation with R5495. However, they find that the quality of the MA14 fit becomes poorer in the NIR. The explanation for the latter effect is that their photometry has a better coverage for wavelengths longer than 6000 Å (our optical photometry only has the redwards portion of Gaia G in that range) and an average reddening larger than the one in our sample: the MA14 derivation assumed the Rieke & Lebofsky (1985) power-law form in the NIR with α = −1.61 because of the impossibility of using the relatively low-extinction 30 Dor stars to measure α. This is an illustration of a chronic problem in extinction studies: a strong extinction effect in the UV becomes a weak one in the optical and an undetectable one in the IR while a star with a strong effect in the IR is hard to observe in the optical and impossible in the UV. As a result, one is forced to build UV-optical-IR extinction laws by stitching together results for stars of different amount of extinction. In the specific case of MA14, that paper specifically mentions this is an expected issue and recommends not using its results for large NIR extinctions: that is also why we indicate above that the results of this paper apply to the optical for E(4405 − 5495) < 3.0. For a more detailed discussion of the different wavelength regimes, see Maíz Apellániz (2015a) and Maíz Apellániz et al. (2017b) and the last subsection below.
 |
Fig. 2
|
 |
Fig. 3
|
 |
Fig. 4
|
3.2 Quantitative reddening differences between O-type and late-type stars
Older studies of the spatial distribution of extinction (e.g., Fitzgerald 1968; Neckel et al. 1980) were based on the analysis of early-type stars. Such studies had systematic uncertainties due to some of the issues discussed in this paper (photometric biases, extinction law errors, spectral type mismatches) and were limited by small samples, as early-type stars are relatively scarce and fewer of them had accurate spectral types at the time of those studies compared to today. More recent studies have taken advantage of larger photometric databases and concentrate on the more numerous late-type stars (Marshall et al. 2006; Lallement et al. 2014; Sale et al. 2014; Green et al. 2015). The use of late-type stars allows for a much better spatial sampling that is allowed with early-type stars but that does not eliminate the need for early-type studies because extinction may not affect different spectral types in the same manner (statistically speaking). Given the young age of O stars, they are expected to be located preferentially close to their natal molecular clouds. Also, their strong UV fluxes ionize the surrounding ISM, in some cases producing H II regions. In either circumstance, either the quantity or the type of extinction they experience should be different from the typical extinction experienced by late-type stars, which should be dominated by the diffuse Galactic ISM. In other words, the light we receive from O stars is expected to have crossed a more local, clumpy, and diverse ISM than the light from late-type stars. This idea is what prompted us to study O-star extinction taking advantage of modern capabilities and data. In this subsection we analyze the quantitativeaspects (amount of extinction) and in the following subsection we analyze the qualitative ones (type of extinction).
To test the differences between the extinction experienced by O-type and cool stars we use the results from Green et al. (2015), G15 from now on. G15 combined a large sample of Pan-STARRS 1 (Kaiser et al. 2010) and 2MASS photometry from mostlycool stars to derive a 3D reddening map of three quarters of the sky with an angular resolution of 3.′4–13.′7 and a maximum distance resolution of 25%. Their database contains the E(B − V) for 262 of the stars in our sample assuming the values oflogd from Table 1 (online). We compared them with our E(4405 − 5495) results in Fig. 5, where we also plot the expected relationship between E(B − V) and E(4405 − 5495) for three different Teff using an MA14 extinction law with R5495 = 3.0 (see Maíz Apellániz 2013a and Appendix A). For most low-extinction stars our results are consistent with those of G15: in those cases there appears to be nothing special regarding the ISM that surrounds the O stars, making their reddenings similar to those of late-type stars in their neighborhood.
On the other hand, for the majority of objects with E(4405 − 5495) > 1.0, G15 systematically and growingly underestimates O-star reddenings by approximately a factor of 2. This indicates that such O stars have an additional reddening component that is not present in the sightline towards the surrounding late-type stars. That additional component is likely to be the dense gas clumps left over from the natal cloud that are known to have sub-pc structures (see e.g., Alves et al. 2001; Scappini et al. 2002; Maíz Apellániz et al. 2015a). Therefore, O stars located at ~1 pc projected distances to the clouds will experience the additional extinction only in a statistical sense, as some sightlines will intercept the dense cores and some will not. Most late-type stars will be located farther away from the clouds and only a few of their sightlines will be affected by them. This interpretation is consistent with the scatter seen in Fig. 5 for E(4405 − 5495) > 1.0.
The differences between the G15 E(B − V) values and E(4405 − 5495) are clearly seen for the Cygnus-X region in Fig. 6, where the most negative values take place at the location of the CO clouds with the highest column depths. However, the beam size is too large to visualize the correlation between the CO gas and the clumpy extinction at sub-pc scales. To do this, it is better to look at the relationship between the foreground dust lanes that obscure H II regions in the optical and the amount of extinction affecting O stars. We have selected four Galactic H II regions that have three or more O stars where the correlation between dust lanes and extinction is clear, and we discuss them with reference to Fig. 7:
The top left panel shows a section of the Carina Nebula, whose optical structure is dominated by a V-shaped dust lane several tens of pc in size (see e.g., Smith et al. 2000). The section shown corresponds to the southern tip of the dust lane (in the top half of the image), where the two segments of the V meet, and where part of the dust lane is seen as a CO cloud (Rebolledo et al. 2016). Two stars, V662 Car (a.k.a. FO 15) and [ARV2008] 206 are located inside the dust lane and those two objects are the ones with the highest reddening [E(4405 − 5495) ~ 1.1]. On the other hand, the two objects located farther away from the dust lane, HDE 305 523 and QZ Car AaAc (a.k.a. HD 93 206 AaAc) have the lowest reddening [E(4405 − 5495) < 0.4]. The rest of the stars, located closer to the dust lane, have intermediate values of E(4405 − 5495). Therefore, in this case it is clear that the dust lane is a large factor in the differential extinction in the Carina Nebula8.
A section of M 16, including the iconic “pillars of creation” (Hester et al. 1996) is shown in the top right panel. The famous pillars themselves (in the bottom left quadrant) are at least partially immersed in the H II region, as indicated by their surface brightness in emission lines, but a bigger dark cloud towards the north that includes a thicker pillar (see Hill et al. 2012) is likely to be in the foreground and is partially responsible for giving the nebula its eagle shape. There are three objects from our sample near the center of the nebula (HD 168 137 AaAb, HD 168 076 AB, and HD 168 075) with E(4405 − 5495) ~ 0.7. The two objects closer to the thick northern pillar have significantly higher reddenings, indicating that the dark cloud is responsible for the additional extinction experienced by them (see Belikov et al. 1999).
NGC 7822 is an H II region ionized by the Berkeley 59 cluster, as shown in the bottom left panel. Three O stars, BD +66 1674, BD +66 1675, and Tyc 4026-00424-1 are located near the center of the image and of the Hα nebulosity. The first two have very similar extinctions but the third one is located at the same position in the sky as a dust lane and that increases its reddening by one magnitude. A fourth star, V747 Cep, is inside the H II region but close to a dust wall (the right third of the image is peppered with red stars visible only in J) at the location of a CO cloud (Yang & Fukui 1992) and has an intermediate extinction between the extremes of the other three.
The bottom right panel shows a section of Sharpless 2–132. The region contains BD +55 2722, a system with three O stars and similar extinction values (AB is unresolved in our photometry and is analyzed as a single source). A fourth O star, ALS 12 320 sits at the location of a dust lane that coincides with a CO cloud (Vásquez et al. 2010) and has a significantly larger E(4405 − 5495).
These examples show that the explanation behind the differential extinction seen within young stellar clusters and associations lies in the presence of parsec-scale clouds containing dust and, in many cases, dense enough to be detected in CO. This is, of course, not a new idea, but clearly showing it in these cases is a required preliminary step for the relationship with R5495 that will be analyzed in the next subsection.
In Fig. 8 we use the values of AV and log d from Table 1 (online) to plot AV ∕d, the extinction per unit distance for our sample. We have also divided the sample by Galactic octant and calculated the median, and lower and upper 1σ equivalents in each one of them. Given our understanding of how GOSSS is proceeding, we expect the sample to be complete to ~1 kpc and mostly complete to ~1.5 kpc, though for some directions incompleteness does not become important until we reach several kpc. A median value of ~1 mag kpc−1 is a reasonable approximation for the extinction experienced by O stars, in line with previous studies of early-type stars (Fitzgerald 1968; Neckel et al. 1980; Forbes 1985), but should be used with care for the following reasons:
There is a considerable dispersion in AV∕d in all of the octants, an indication that some of the extinction is caused by a clumpy medium.
The lower uncertainty, probably a better measurement of the diffuse (non-clumpy) part of extinction, is ~0.5 mag kpc−1.
There are differences among octants – the first, second, and eighth (three of the four inner octants) having significantly higher extinctions than the other five. As expected, there is more dust towards the inner Milky Way than in the opposite direction.
The two regions that contribute the largest number of objects to our sample, Cygnus in the second octant and Carina in the fifth one, have an effect on the histogram. Cygnus is a high-extinction region (e.g., Fig. 6) that produces the largest median and dispersion in any octant and is the direction along which sample incompleteness becomes important at shorter distances. Extinction is lower than average towards Carina, in part because many sightlines cross the interarm space between the Sagittarius and Scutum-Centaurus arms. Hence, the extinction distribution in the fifth octant resembles the four outer octants, not the other three inner ones9.
Stars within 1 kpc of the Sun are concentrated towards the outer octants and show a large scatter than the most distant sample. This is consistent with an ISM where extinction is produced by a slowly varying diffuse component and a clumpy component: scatter in AV∕d is expected to increase at shorter distances, where some stars will be dominated by the clumpy component (Lallement et al. 2014). Indeed, the object with the largest value of AV∕d in our sample is Tyc 4026-00424-1 (see previous discussion about the bottom left panel in Fig. 7).
One important characteristic of the solar neighborhood relevant for our analysis is that we are located inside a cavity filled with hot gas called the Local Bubble (Snowden et al. 1998; Sfeir et al. 1999; Maíz Apellániz 2001; Lallement et al. 2014). Typical reddenings measured to stars located at the edge of the Local Bubble (~ 80 pc) at the Galactic plane are E(bS − yS) = 0.02 (Reis et al. 2011), with maxima around E(bS − yS) = 0.04 (which corresponds to E(4405 − 5495) ~ 0.05). We note that for R5495 = 3.1 the first of those values yields AV∕d of ~ 1.0 mag kpc−1, which is thetypical value measured above for O stars. Therefore, we do not need a dense medium to produce thediffuse component of Galactic extinction: an ISM as thin as that inside the Local Bubble (~0.01 atoms cm−3) appears to be sufficient.
The Local Bubble has a complex shape and, in particular, it has a finger that extends towards the Orion OB1 association (Lallement et al. 2014), which is located at a distance of ~400 pc and is separated from the Galactic plane (a fact that also contributes to the reduction of material in its sightlines). Some of the BA stars in the foreground part of the association have near-zero extinction (Alves & Bouy 2012). We confirm this by measuring very small reddenings towards some of the O stars in Orion, with E(4405 − 5495) values between 0.022 and 0.044 for δ Ori AaAb, ζ Ori AaAbB, σ Ori AaAbB, ι Ori, and υ Ori. μ Col, an O star ejected from Orion OB1, has an even lower reddening. The other O-type objects in Orion, λ Ori A, θ1 Ori CaCb, and θ2 Ori A, have significantly higher extinctions due to their surrounding material, something which will we come back to in the next subsection. The irregularity of the ISM around the Local Bubble is confirmed by the ζ Oph sightline. That object is the closest O star and is located at a high latitude (it is another runaway star like μ Col) in a direction nearly opposite to Orion OB1 but it is the star with the second largest AV ∕d in Fig. 8: a good example of the large scatter in the extinction experienced by nearby objects. We note that the ζ Oph sightline is used as a reference for the study of the elemental composition of dust in the intervening ISM (Draine 2011). Also, ζ Oph is the prototype ζ sightline for DIBs (σ Sco is the prototype σ sightline, see Krełowski et al. 1997; Cox et al. 2005; Maíz Apellániz 2015b), thought to represent an ISM shielded from exposure to UV radiation.
 |
Fig. 5 Comparison between the reddenings measured by G15 and those in this paper. The error bars include the uncertainty in logd (G15 gives E(B − V) as a function of distance), assumed to be 0.1 (corresponding to an uncertainty of 0.5 in the distance modulus). The three colored lines show the expected difference between E(B − V) and E(4405 − 5495) for three different temperatures assuming an MA14 extinction law with R5495 = 3.0. |
 |
Fig. 6 Difference between the G15 E(B − V) values and E(4405 − 5495) for the O stars with E(4405 − 5495) > 1.0 in the Cygnus-X region plotted on top of the CO J = 1 ← 0 map of Leung & Thaddeus (1992). The value is encoded in the color of each symbol (see scale on left panel and compare with the vertical axis of Fig. 5). The left panel shows the whole region while the right panel zooms in the blue rectangular region, which corresponds to Cyg OB2. The beam FWHM is 8.′7 (~4 pc at the distance of Cyg OB2), so the CO clouds are likely to have substructure not seen in the map. The angular resolution ofthe G15 values is similar to the beam size. The axes are in Galactic coordinates and the units are degrees. |
 |
Fig. 7 Extinction measurements for O stars in four H II regions: (top left) the Carina Nebula, (top right) M 16/NGC 6611, (bottom left) Berkeley 59/NGC 7822, and (bottom right) Sharpless 2-132. The top two images are from ESO press releases 1250 (BgrHα) and 0926 (BV R), respectively. The bottom two images are RGB combinations of J2MASS+RDSS2+BDSS2. North is towards the top and east towards the left and the approximate physical scale is indicated in all cases. Only a section of each H II region is shown to better visualize the dust lanes. |
 |
Fig. 8 AV∕d for the sample in this paper divided into stars closer than and beyond 1 kpc. No error bars are plotted but they are estimated at ~20%, with the larger part of the error budget coming from the distance uncertainty. The underlying histograms show the 16th, 50th, and 84th percentiles (median plus lower and upper 1σ equivalents) per Galactic octant. We note that only 19 stars have |b| > 10o, of which seven are in Orion (see Fig. 12). |
3.3 The E(4405 − 5495)-R5495 plane and the properties of dust
3.3.1 What our results show
To study the relationship between amount and type of extinction we present three figures and one table. Figure 9 shows the distribution of objects in the E(4405 − 5495)-R5495 plane. Figure 10 shows the R5495 histograms for five different E(4405 − 5495) ranges, from0.00–0.25 (very low extinction, blue) to 1.50–3.00 (highest extinction in our sample, dark gray). Figure 11 shows R5495 as a function of AV ∕d, a measurement of average dust density along the sightline (E(4405 − 5495) is a measurement of column density). Table 2 gives the ranges of E(4405 − 5495) and R5495 for the more relevant clusters and associations.
The most obvious feature in Figs. 9 and 10 is the existence of a clear relationship between E(4405 − 5495) and R5495. High-reddening stars have low values of R5495 (median ~3 for E(4405 − 5495) > 1.50) and a narrow distribution. At lower reddenings, both the median and the width of the distribution are increased. Part of the increase of the width of the distribution is due to the increase in the individual values of 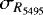 (Fig. 1) but that is a minor effect: at high reddenings there are no examples with large values of R5495 while for low reddenings there are cases with both high and low values of R5495 with low uncertainties. When we reach the E(4405 − 5495) < 0.25 range, the median R5495 value is ~4. Figure 11 is relatively similar to Fig. 9 but five objects are conspicuously placed: the previously discussed Tyc 4026-00424-1 and ζ Oph at low R5495 values and three more at high R5495 values, Herschel 36, θ2 Ori A, and θ1 Ori CaCb. We analyze these later in this paper.
(Fig. 1) but that is a minor effect: at high reddenings there are no examples with large values of R5495 while for low reddenings there are cases with both high and low values of R5495 with low uncertainties. When we reach the E(4405 − 5495) < 0.25 range, the median R5495 value is ~4. Figure 11 is relatively similar to Fig. 9 but five objects are conspicuously placed: the previously discussed Tyc 4026-00424-1 and ζ Oph at low R5495 values and three more at high R5495 values, Herschel 36, θ2 Ori A, and θ1 Ori CaCb. We analyze these later in this paper.
In the next subsubsection we combine these results with those of other authors to build a picture of how R5495 varies with ISM phases. Before doing that, we address a preliminary point: when a sightline has two or more clouds of different R5495 and extinction is described by the MA14 (or CCM) families, the resulting extinction law is also a member of the family with the equivalent R5495 being an average of the individual values weighted by the individul reddenings (see Appendix C of MA14). This can be seen as an advantage or an inconvenience: it is the first from the point of view of correcting for extinction because it provides a universality to extinction laws but it is the second from the point of view of studying dust because it partially erases the information contained in the individual clouds.
Some papers (e.g., Valencic et al. 2003) use the above property to measure extinction decomposing between a foreground and a cluster component. The foreground component has R5495 = 3.1 and the R5495 of the cluster extinction is measured by the paper. We have decided not to do that in this paper for the following three reasons:
-
While R5495 = 3.1 may be close to the average Galactic extinction, it is not necessarily the case for every sightline. For example, some objects with low extinction have large values of R5495, so the foreground (likely the only extinction) cannot have R5495 = 3.1.
The decomposition between two components usually assumes that the foreground extinction is constant in space but that may also be false. See the interesting case of 30 Doradus (van Loon et al. 2013), where the velocity separation between the Galactic (“foreground”) and LMC (“cluster”) ISM lines allows for maps of both components. See also Bellini et al. (2017) for a detailed study of the variations in the foreground extinction to a globular cluster.
The assumption of a constant R5495 for the cluster component is wrong in some cases (see Figure 7 and discussion below).
Number of objects and ranges of E(4405 − 5495) and R5495 for some of the clusters and associations in this paper.
 |
Fig. 9 R5495 as a functionof E(4405 − 5495) for the CHORIZOS runs in this paper using the MA14 family of extinction laws. The color coding is the same as in Fig. 1. See Fig. 10 for the histograms derived from this plot by dividing the horizontal axis in five different ranges. |
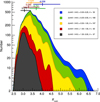 |
Fig. 10 R5495 cumulative histograms for different values of E(4405 − 5495) (see legend for ranges and number of objects in each one) for the CHORIZOS runs in this paper using the MA14 family of extinction laws. Each object is represented by a normalised Gaussian with a width of |
3.3.2 Consistency with other results: R5495 of different ISM phases
There are previous studies of the distribution of R5495 in the Galaxy, but most of them refer to single clusters or associations, not to samples that cover the whole Galactic plane or a significant part of it. We start by looking at the ones that refer to objects listed in Table 2: Belikov et al. (1999) find a variable RV between 2.8 and 3.9 in M 16, Pang et al. (2016) a variable RV between 2.48 and 4.06 in NGC 3603, Lim et al. (2014) a canonical extinction law (R5495 = 3.1) towards NGC 1893, and Vázquez et al. (1996) RV = 4.70 ± 0.65 in the Carina Nebula. Going to older studies, the high value of R5495 in the Orion Nebula has been known for a long time, as it has been the prototype for a non-canonical extinction law since the 1930s (Baade & Minkowski 1937). All of these results are consistent with ours, with some small differences that can be explained by the sample and method differences.
In a second group, we look at modern, large-area studies of extinction type. Schlafly et al. (2016), a paper we already discussed in the previous subsection, obtain RV results different from ours: they find an average value of 3.32, a dispersion of 0.18, and no significant variation with the amount of extinction. There are no tails in their distribution, so few stars have values under 3.0 and even less values over 4.0. Another study is that of Fitzpatrick & Massa (2007), who find a mean value for RV of 2.99 and a dispersion of 0.27, with a long tail that extends to large values beyond 4.0. How can we reconcile the different results from the three papers? We consider the following points in the discusion below:
Fitzpatrick & Massa (2007) do not distinguish between R5495 and RV. They claim to give RV but we suspect it is R5495 they are working with. However, their sample consists of OB stars with typical values of E(B − V) around 0.45, so the differences between the two should be small (see Fig. 3 in Maíz Apellániz 2013a). A similar argument can be made about E(B − V) and E(4405 − 5495). Schlafly et al. (2016) use the approximation of defining monochromatic wavelengths for each filter, therefore ignoring non-linear effects in the reddening trajectories. This could bias their measurements when comparing high and low extinctions.
Fitzpatrick & Massa (2007) use UJBJV JJHKs photometry, so their wavelength coverage is similar to ours. Schlafly et al. (2016), on the other hand, use a filter set weighted towards longer wavelengths.
Most importantly, the three samples are different in terms of targets, amount of extinction, and average distances. Fitzpatrick & Massa (2007) sample is relatively similar to ours but it is biased towards B stars, which tend to be older and to be located farther away from H II regions. The amount of extinction range it covers is also smaller (only low values) and their sample is less concentrated towards the Galactic plane and is located at shorter distances (on average) compared to ours. Schlafly et al. (2016) sample is fundamentally different from the other two, as it is much larger and consists of red giants and red clump stars, with very few of them (if any) located close to H II regions. The distribution of the amount of extinction is similar to ours but they lack a significant fraction of close objects, as their typical distances are between 1 and 5 kpc.
Another example of the second group of studies is He et al. (1995), who analyzed the extinction experienced by a sample of southern OB stars with E(4405 − 5495) < 2. He et al. (1995) is affected by some of the issues discussed in Appendices (in this paper) and it also has the additional problem that most ofits “spectral types” are actually photometric classifications (i.e., not true spectral types), which are known to have frequent large errors. Furthermore, many of their true spectral types are obtained from the Michigan Catalog (whose last volume was published as Houk & Swift 1999), which also contains many errors due to the imprecisions associated with objective-prism spectroscopy (poor spectral resolution, source confusion, and nebular contamination), something that can be checked by comparing the spectrograms published in GOSSS I+II+III with the Michigan spectral types. As an example of the errors, ALS 4923 is listed in He et al. (1995) as having a spectral type of O6 V as derived from photometry and of O9.5 III as derived from spectroscopy (Vijapurkar & Drilling 1993). The GOSSS spectral type shows that it is actually an O8.5 V + O8.5 V SB2 (see GOSSS III for a spectrogram). Therefore, He et al. (1995) is likely to include systematic errors and an analysis of the sample in common with the stars in this paper shows that it tends to underestimate AV. Nevertheless, the paper has an interesting result that is consistent with what we find here: their measured average RV decreases with distance, being 3.31 for stars closer than 1 kpc and 2.98 for stars farther away than 5 kpc (see Fig. 10 – we note that more distant stars are, on average, more extinguished than closer ones).
In a third group, we look at studies of individual clusters and associations not included in this paper. In the case of H II regions, Westerlund 2 (Zeidler et al. 2015; Hur et al. 2015), NGC 1931 (Lim et al. 2015), and 30 Doradus (MA14) have values of R5495 > 4, in the case of 30 Doradus with a large scatter (see below). For objects without an H II region, Straižys et al. (2014) find an RV of 2.87 ± 0.16 for NGC 6913, a cluster in Cygnus with an intermediate extinction, and Marco et al. (2014) find eight stars in VdBH 222 with R5495 between 2.7 and 3.0 and a high reddening (E(4405 − 5495) between 2.5 and 2.9).
The results in this paper and in the previously listed references can be explained if we model the dust in the ISM within several kpc of the Sun as having three different regimes depending on the ambient UV radiation level:
Regions with high levels of UV radiation have large values of R5495 (>4). This includes H II regions but also cavities filled with hot gas such as the Local Bubble where UV radiation can travel relatively unimpeded. H II regions can have significant dust densities but, given their small sizes, only in exceptional situations they provide column densities large enough to produce strong extinctions. Cavities occupy much larger volumes but they have low dust densities so their signature is easily erased when the sightline includes denser clouds.
Regions with low levels of UV radiation have small values of R5495 (<3). These regions are those with significant column densities of CO or, alternatively, those that are easily detected as dust lanes in the optical. They occupy a small fraction of the ISM volume but they have the highest dust densities, so their R5495-reducing signature is harder to erase than that of cavities with high values of R549510.
Regions with intermediate levels of UV radiation have intermediate values of R5495 (between 3 and 4). These regions represent a typical warm to cold ISM (excluding H II regions, cavities, and molecular clouds) that fills the majority of the volume in the Galactic disk.
That model can explain all of the results previously described. OB stars in the Local Bubble (and adjacent bubbles) detected in the samples in this paper and in the Fitzpatrick & Massa (2007) sample will have low values of E(4405 − 5495) and high values of R5495 with a relatively large scatter caused by large uncertainties and the presence of small clouds that provide partial shielding from UV radiation. This is what is observed for the off-plane stars in Fig. 12, which are relatively nearby and for which the Local Bubble contribution to extinction should be generally larger than for objects closer to the Galactic plane. We note that no Schlafly et al. (2016) objects are present in the Local Bubble. Moving to longer distances (and ignoring H II regions for the moment) we see mostly the effect of the typical ISM in the three samples, as the signature of the Local Bubble is easily erased. This region (up to 1–2 kpc) is the classical regime for extinction studies and the origin of the definition of 3.1 as the canonical R5495 value, although some of the objects here (e.g., those in Cyg OB2) already show the effect of molecular-cloud extinction. Once we start moving out, the Fitzpatrick & Massa (2007) sample disappears and we are left only with the other two samples. Cool stars will likely not be associated with molecular clouds, so their R5495 should not change much, especially if they are in one of the outer Galactic quadrants (we note that the Schlafly et al. (2016) does not include objects in the fourth quadrant). O stars in the inner quadrants (excepting those whose sightlines are dominated by an interarm space such as those in NGC 3603) will likely have a molecular cloud in their sightline and will end up having low values of R5495.
As we have seen in the previous subsection, H II regions are complicated in terms of extinction because the sightlines towards different stars cross different environments: the H II region itself (first type), possibly a molecular cloud (thirdtype), and in most cases the diffuse, typical ISM (second type). Therefore, almost every value of R5495 is possible. In three of the panels of Fig. 7 there is a clear anticorrelation between E(4405 − 5495) and R5495: when we approach a dust lane E(4405 − 5495) increases, as we had already discussed, but R5495 decreases. This is consistent with our model, where R5495 is correlatedwith UV flux. The fourth panel, NGC 7822/Berkeley 59, shows a different behavior with the four sightlines having R5495 < 3. The likely explanation is that most of the extinction common to the four sightlines is coming from a molecular cloud that affects all sightlines, which is consistent with the four stars having large values of AV ∕d. To understand H II region extinction better, we should look at three of the extreme cases in Fig. 11: θ1 Ori CaCb and θ2 Ori A, the two O stars in the Orion Nebula, and Herschel 36 in M 8 (Fig. 13):
As we have previously mentioned, the foreground extinction towards the Orion OB1 association (including the Orion Nebula) is very small. The reddenings of the two O stars in the Orion Nebula are significantly higher, indicating that their extinction must be fundamentally local. Evidence for this effect has been found by van der Werf et al. (2013), who estimate that the extinction for Trapezium stars takes place within 1–2 pc, and by O’Dell & Harris (2010), who determine that the nebular extinction at the edges of the nebula essentially goes to zero. θ1 Ori CaCb is closer to the center of the nebula than θ2 Ori A, as it is the main ionization source, and correspondingly has a higher extinction. Those circumstances explain why the Orion Nebula stars are the prototype for high R5495 extinction: they are located in the (nebular) bright part of an H II region with very little intervening material in the sightline (either as nearby molecular clouds or as a typical ISM). That configuration yields R5495 > 6.
The foreground extinction towards M 8 is lower than average for its distance, as evidenced by the low E(4405 − 5495) of HD 164 536 and HD 164 816, and likely caused by the in-between region being an interarm space. Looking at the right panel in Fig. 13 we see that Herschel 36 has both significantly larger E(4405 − 5495) and R5495. Compare this to the opposite relationship between those two quantities in, for example, the Carina Nebula. The explanation is the geometry described by Maíz Apellániz et al. (2015c): Herschel 36 is seen through a tunnel carved in the molecular cloud where the gas is exposed to the strong ionizing radiation of the Herschel 36 multiple O-star system (Arias et al. 2010; Sánchez-Bermúdez et al. 2014)11. The resulting long optical depth yields not only a large R5495 but also a large E(4405 − 5495).
The model presented here implies that the Herschel 36 case (simultaneous high E(4405 − 5495) and high R5495) is difficult to find. Outside of the sample in this paper, only in Damiani et al. (2017) we find some more extreme examples: four stars with E(4405 − 5495) > 1.3 and R5495 > 4.0 and three stars with E(4405 − 5495) > 2.0 and R5495 > 3.5. Those stars would be placed in an empty region in Fig. 9 and they are all in the Carina Nebula. That is a logical place to find such objects, as the foreground extinction is low (the sightline is mostly an interarm region) and the Carina Nebula is the brightest and largest H II region in the solar neighborhood, thus making it possible to have large column densities of material exposed to UV radiation.
A final check on our model can be performed with the MA14 extinction analysis of 30 Doradus, where the foreground extinction is low and a wide range of values of R5495 ca be foundmore easily than for most Galactic H II regions. We have selected the three stars with E(4405 − 5495) > 0.3 and R5495 > 6.0 in the sample, VFTS 451, VFTS 464, and VFTS 579 (Fig. 14), that is, the three stars with more H II-like extinction. Where are they located in 30 Doradus? They are in different positions but in the same type of environment: a compact H II region at the top of a dust pillar created by the radiation and winds from R136. The first two are in relatively small pillars while VFTS 579 is in a large one called knot 1 by Walborn & Blades (1987). Therefore, their environmentis precisely the one predicted by our model, as they are immersed in a dense gas subjected to a strong UV field.
 |
Fig. 11 R5495 as a functionof AV∕d for the CHORIZOS runs in this paper using the MA14 family of extinction laws. The colour coding is the same as in Fig. 1. We note that the horizontal scale is logarithmic. |
 |
Fig. 12 Extinction measurements for Galactic O stars plotted on top of the full-sky Hα image of Finkbeiner (2003). Different colors are used for five ranges of R5495 with the size of the symbol increasing with E(4405 − 5495). The background image is showed in a logarithmic intensity scale and in Galactic coordinates with a Cartesian projection centered on the Galactic anticenter. |
 |
Fig. 13 Extinction measurements for O stars in two H II regions: (left) the Orion Nebula, (right) M 8. The left image is from STScI press release 2006–01 (BV Hαiz) and the rightimage is from ESO press release 1403 (ugrHαi). North is towards the top and east to the left. The approximate physical scale is indicated in both cases. |
 |
Fig. 14 Environment around VFTS 451 (left), VFTS 464 = [P93] 702 (center), and VFTS 579 = [P93] 1201 (right), the three stars from the MA14 sample in 30 Doradus with E(4405 − 5495) > 0.3 and R5495 > 6.0. The three objects are at the top of pillars that point towards R136. The background image is a F814W + F656N (red) + F555W (green) + F336W (blue) WFC3 mosaic built from WFC3-ERS data. Each field is 8′′ × 8′′ (2 pc × 2 pc) with north to the top and east to the left. See Walborn et al. (2002) for an alternative view of knot 1, the environmentaround VFTS 579. |
3.3.3 The physics behind R5495 variations
Cardelli (1988) found anticorrelations between R5495 and either log(H2∕AV) or log(CH/AV), where H2 and CH represent the column densities of those molecules. He also found similar results when substituting AV by the totalhydrogen column density. Cardelli (1988) concluded that the decrease in the abundance of H2 when R5495 increases was a combination of (a) a reduction in the formation rate of H2 due to the smaller total grain surface per unit mass for larger grains and (b) an increase in photodestruction via a decrease in UV dust extinction, as R5495 anticorrelates with AUV∕AV (CCM).
Our results are similar to Cardelli (1988) in the sense that we find that stars behind CO clouds or dust lanes have low values of R5495. However, an important difference is that his sample is biased towards low extinctions (only two stars have AV > 3) and small grain sizes (only seven stars in the 4.0 ≤ R5495 < 4.4 range and none above that). In other words, Cardelli (1988) does not include objects in H II regions or subject to Local-Bubble-only extinction, where the physical conditions are different than the more stable and benign considered by him. H II regions are short-lived dynamic structures where destruction processes dominate formation ones and regions inside bubbles are too thin for dust grains to form. Therefore, we propose that the ISM regions with large values of R5495 are produced by the selective destruction of smaller dust grains with respect to large grains.
What processes could be responsible for such selective destruction? One possibility is thermal sputtering, the erosion of grains by impacting thermal atoms or ions (Draine 2011). The grain lifetime in such a high-temperature is proportional to its size, thus reproducing the observed behavior. Thermal sputtering is insignificant around 104 K but can become important above 105 K. That makes it an unlikely source for grain destruction in H II regions but a possible candidate in regions like the Local Bubble. An alternative destruction mechanism is heating by EUV radiation (Guhathakurta & Draine 1989; Jones 2004), which also acts preferentially on small grains. This is the likely cause in H II regions, where the sources of EUV photons are the O stars.
We point out that dust extinction is not the only ISM observable that is affected by the strength of the UV field. Another observable is the ratio of the equivalent widths of two diffuse interstellar bands (or DIBs), DIB 5797 and DIB 5780 (Cami et al. 1997; Vos et al. 2011; Maíz Apellániz 2015b; Maíz Apellániz et al. 2015a). W(5797)∕W(5780) can be as large as ~0.7 or smaller than 0.1. Sightlines with large ratios are produced by ζ clouds (after the prototype sightline of ζ Oph) while small ratios are produced by σ clouds (after the prototype sightline of σ Sco)12. Even though the carriers themselves are not identified at this point, the observed relationship indicates that DIB 5797 isfound only in regions shielded from UV radiation while DIB 5780 can originate in either shielded or unshielded regions. This led Cami et al. (1997) to hypothesize a skin effect in ISM clouds, where the core (ζ sightlines) includes the carriers of both DIBs and the outer layers (σ sightlines) only the DIB 5780 carrier. The correlation between W(5797)∕W(5780) and R5495 was detected by Cami et al. (1997) and confirmed in a much larger sample by Maíz Apellániz (2015b).
4 Conclusions and future work
The main conclusions of this paper are:
The MA14 family of extinction laws provide a better description than the CCM or F99 ones for the conditions described in this paper: Galactic O stars with optical-NIR photometry up to E(4405 − 5495) = 3 (the response to the question we ask in the introduction). However, there are signs that in other cases such as higher reddenings or IR-only data MA14 fails (as expected), so further work is required to generate an improved new family.
Many O stars have extinctions similar to those of nearby late-type objects but some are located close to obscuring material that increase their extinction and can change the effective value of R5495.
Young stellar clusters and associations can have large variations in the amount and type of extinction from star to star. In those cases the use of average E(4405 − 5495) and R5495 values fails and one needs to determine the amount and type of extinction star by star. Some notorious examples include H II regions such as the Carina Nebula and M 8.
The average dust grain size and, hence, R5495, is determined by the level of UV radiation. On the one extreme, shielded ISM regions such as molecular clouds have small grains (low R5495) and exposed ISM regions such as H II regions have large grains (high R5495), with the average diffuse ISM in an intermediate position in size and R5495. Several mechanisms have been proposed to explain this relationship but we expect that the dominant one for the existence of high R5495 regions is the selective destruction of small grains by heating by EUV radiation.
Our lines of future work include the following:
We plan to analyse the extinction law that affects OB stars in the IR using a combination of 2MASS, Spitzer, WISE, and ISO data for stars for which we also have GOSSS optical spectroscopy. See Maíz Apellániz et al. (2017b) for some examples.
For the extinction-law families described in this paper the optical part was derived from photometric data and later interpolated in wavelength. An alternative method that yields more information and potentially eliminates imprecisions is to use spectrophotometry. To that purpose, we have obtained HST/STIS 1700–10 200 Å data for several tens of stars in 30 Doradus (GO program 14 104) which we are currently analyzing.
There are two opposing views on the correlation between UV and IR extinction. On the one hand, CCM claim that they are tightly correlated in the sense that large-R5495 optical-NIR extinctions correspond to flat UV extinctions while small-R5495 optical-NIR extinctions correspond to steep UV extinctions. On the other hand, Fitzpatrick & Massa (2007) claim that with the exception of some extreme cases, the UV and IR portions of Galactic extinction curves are not correlated with each other. We plan to use the results of this paper in combination with IUE data to analyze those opposing claims.
The largest source of systematic errors in the quantities derived in this paper is the lack of uniformity between the sources used for Johnson and Strömgren photometry. Addressing that issue is one of the objectives of GALANTE, a seven-band photometric survey of the northern Galactic plane we are undertaking using the 80 cm telescope of the Javalambre Astrophysical Observatory in Teruel, Spain. The survey includes a significant fraction of the stars in this paper and is being obtained with narrow and intermediate filters specially designed to measurethe properties of OB stars. GALANTE is using exposure times from 0.1 s to 100 s to obtain S/N > 100 from the brightest stars in our sample to AB magnitudes of 16–17. The large field of view of the camera (1.4° × 1.4°) combined with a pixel size of 0.′′55 allows for alternative internal and external calibration techniques to reduce systematic errors such as zero-point offsets. The survey began in 2016 and, when complete, will be used to revisit the results in this paper.
We will extend this work to larger samples once additional GOSSS spectra are published.
The 2016 (first) Gaia data release included the TGAS parallaxes (Michalik et al. 2015) but those were of little use to estimate distances to O stars (Maíz Apellániz et al. 2017a). The second Gaia data release is planned for 2018 and should include accurate parallaxes for the majority of the stars in this paper, significantly improving the poor-quality spectroscopic parallaxes in Table 1 (online) and facilitating exciting new science.
Acknowledgements
We would like to thank the anonymous referee for a detailed and careful reading of the paper, which led to its significant improvement. We also thank the collaborators who have contributed throughout the last decade and a half to the building of the GOSC database that has made this paper possible. In chronological order, those are H. Á. Galué, L. H. Wei, R. Y. Shida, A.Sota, A. T. Gallego Calvente, M. Penadés Ordaz, Á. Alonso Moragón, L. Ortiz de Zárate Alcarazo, A. Martín Gutiérrez, and M. Oliva Rubio. J. M. A. acknowledges support from the Spanish Government Ministerio de Economía y Competitividad (MINECO) through grants AYA2013-40 611-P and AYA2016-75 931-C2-2-P (plus other long expired grants). R. H. B. acknowledges support from the ESAC Faculty Council Visitor Program, which allowed the two authors to get together for one last time and wrap up the paper. This research has made use of the SIMBAD database and the VizieR catalog access tool, both operated at CDS, Strasbourg, France.
Appendix A On the use of filter-integrated or monochromatic quantities for studying extinction
In previous works (Maíz Apellániz 2013a; MA14) we have briefly discussed the problems associated with the use of filter-integrated quantities for studying extinction, an issue that has been known of for a long time (Blanco 1956, 1957) but frequently ignored. In these appendices we provide a more thorough treatment. Observed photometric magnitudes, such as Johnson UJ BJ V J, Tycho-2 BT V T, Strömgren uS vS bS yS, Gaia G or 2MASS J H Ks are filter-integrated quantities, for example, for Johnson V J :
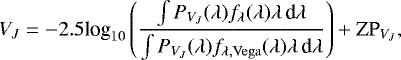 (A.1)
(A.1)
where 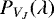 is the total-system dimensionless sensitivity function, fλ(λ) is the spectral energy distribution (SED) of the object, fλ,V ega(λ) is the Vega SED, and ZP
is the total-system dimensionless sensitivity function, fλ(λ) is the spectral energy distribution (SED) of the object, fλ,V ega(λ) is the Vega SED, and ZP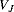 is the photometric zero-point (Maíz Apellániz 2005, 2006, 2007). If the equivalent unextinguished SED, fλ,0 (λ) has a Johnson V J magnitude of V J,0, then the extinction in that filter,
is the photometric zero-point (Maíz Apellániz 2005, 2006, 2007). If the equivalent unextinguished SED, fλ,0 (λ) has a Johnson V J magnitude of V J,0, then the extinction in that filter, 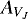 , can be expressed as
, can be expressed as
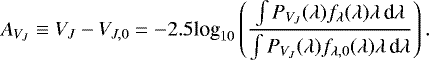 (A.2)
(A.2)
An equivalent expression for other magnitudes can be easily written, for example, for Johnson BJ :
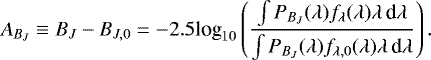 (A.3)
(A.3)
From the previous equations we arrive at the frequently used definition of (filter-integrated) colour excess (or reddening):
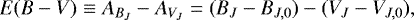 (A.4)
(A.4)
where, for notation convenience13, we have dropped the J subscript in E(B − V). The final filter-integrated quantity of interest is RV, defined as the ratio between total extinction in the Johnson’s V filter and the colour excess:
 (A.5)
(A.5)
where we have also dropped the J subscript in RV for notation convenience.
Extinction by dust alters fλ,0(λ) to yield fλ(λ) and is usually expressed in magnitude form as
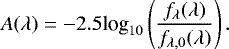 (A.6)
(A.6)
where A(λ) is the total monochromatic extinction and is a function of the dust properties and of the amount of extinction. It is usuallynormalised by the amount of extinction (see below) and in that case it is expressed as a(λ). That quantity is referred to as the extinction law and is a function only of the dust properties14.
We can use Eq. (A.6) to express fλ(λ) as a function of fλ,0(λ) and insert the result in Eqs. (A.1)–(A.3). From there, we can see that Eqs. (A.4) and (A.5) depend not only on a(λ) but also on integrals that include fλ,0(λ) and the amount of extinction. In other words, E(B − V) and RV are quantities that depend in a complex way on the amount and type of dust (or extinction) and also on the type of star we are observing. This is contrary to the commonuse of E(B − V) to linearly characterize the amount of extinction (independent of dust type and SED) and of RV to characterize the type of dust (independent of amount of exinction and SED).
In Maíz Apellániz (2004) we began by using the monochromatic (or single-wavelength) equivalents to Eqs. (A.4) and (A.5):
![\begin{align} &E(4405-5495) \equiv A_{4405} - A_{5495} \nonumber \\ & \qquad\qquad \qquad\ \ = [f_{\lambda}(4405) - f_{\lambda,0}(4405)] \nonumber\\ &\qquad\qquad\ \ \qquad -[f_{\lambda}(5495) - f_{\lambda,0}(5495)],\\ &{}R_{5495} \equiv \frac{A(5495)}{E(4405-5495)},\end{align}](/articles/aa/full_html/2018/05/aa32050-17/aa32050-17-eq19.png)
where wavelengths are expressed in Å. By avoiding the integrals in Eqs. (A.2) and (A.3), Eq. (A.7) is a direct and linear measurement of the amount of extinction (or, more properly, of reddening but for a given extinction law one is a multiple of the other) and Eq. (A.8) depends only on the type of extinction (or the extinction law). Examples of the differences between E(B − V) and E(4405 − 5495) and between RV and R5495 are shown in Fig. 3 of Maíz Apellániz (2013a) for CCM extinction laws (the effect of switching to other families of extinction laws, such as MA14 is small). One can see there that E(B − V) (or, indeed, any other filter-integrated colour excess) has a non-linear dependence on the amount of extinction.
The values of 4405 Å and 5495 Å were chosen by Maíz Apellániz (2004) as representative of the central wavelengths of the BJ and V J filters, respectively, and also to approximately satisfy the limits:

for OB-star SEDs. The choice is reflected in Fig. 3 of Maíz Apellániz (2013a): in the left panel RV ≈ R5495 for Teff = 30 000 K and E(4405 − 5495) = 0 and in the right panel E(B − V) ≈ E(4405 − 5495) for Teff = 30 000 K in the range E(4405 − 5495) = 0–1. We note, however, that outside those values there are significant differences between the monochromatic and filter-integrated quantities.
For the reasons above, the family of extinction laws of MA14 are parameterised in terms of E(4405 − 5495) (amount of extinction) and R5495 (type of extinction) instead of E(B − V) and RV. But what about other families? The authors of the CCM and F99 papers either were unaware of the issue or did not consider it to be important. In any case, we have used their family of extinction laws by substituting the filter-integrated quantities by their monochromatic equivalents, as not doing it is [a] unpractical in terms of calculations (the process would require several iterations until convergence) and [b] unlikely to have been the authors intentions.
We propose that this issue is so often ignored in the literature for two likely reasons. The first is that as long as one is working with low-extinction OB stars, Eqs. (A.9) and (A.10) tell us that substituting the monochromatic quantities by their filter-integrated equivalents can be a good approximation. The second reason is that filter-integrated quantities can be easily computed from the observed photometry and spectral types while monochromatic quantities have to be calculated using additional information and numerical techniques. Indeed, those two reasons may have been valid 40 or 50 years ago, when most targets of extinction studies were low-extinction OB stars and computing facilities were limited. However, today they are not valid excuses as massive photometric and spectroscopic studies provid us with data for stars of all spectral types and for extinctions that probe into much larger Galactic distances. Confusing the two types of quantities can easily lead (as it is too often the case) to biases in photometric measurements of extinction.
Appendix B Limitations of the Q approximation
The Q approximation is a method used to determine extinctions of early-type stars that dates back to Johnson & Morgan (1953). Q is a linear combinationof (U − B) and (B − V) of the form:
 (B.1)
(B.1)
where α is a constant for which Johnson & Morgan (1953) give a value of 0.72 ± 0.03. They claimed that Q is nearly independent of extinction and can be used to determine the spectral type of the target, giving values that start at − 0.93 for most O stars (except the later types), − 0.70 for B2, − 0.44 for B5, and 0.00 for A015. As Q can be used as aproxy for the spectral type, the color excess can be also calculated in a second step. Johnson & Morgan (1953) give:
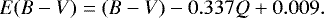 (B.2)
(B.2)
In its original form or in adapted versions, the Q approximation is used even today due to its simplicity. Nevertheless, it has some known limitations:
Unless some additional information is present, it is restricted to OB stars. For A stars and later types, solutions become multiple as, for example, a low-extinction A star can be confused with a higher-extinction late-B star (Maíz Apellániz 2004).
The value of α depends on the extinction law for example, R5495, so it is not a real constant. Johnson & Morgan (1953) did their analysis assuming an average extinction law but for non-canonical values of R5495 one needs to compute the corresponding α (see below for examples). With such an additional parameter, the application of the Q approximation is not straightforward.
For late-B stars (and later types) two stars of the same spectral types but different luminosity classes can have significantly different intrinsic Johnson colours, thus complicating the method.
Emission-line stars need to be excluded beforehand in order to avoid biased results.
The Q approximation can be adapted to similar filter sets (e.g., HST/WFPC2 F336W+F439W+F555W) but the equivalent values of α have to be computed.
Values of α as a function of Teff calculated from synthetic photometry for different values of E(4405 − 5495), luminosity class (main sequence, MS, or supergiant, SG), and R5495.
To those limitations one has to add the non-linearity of colors described in Appendix A: (U − B) and (B − V) do not increase with the amount of extinction at a constant rate, as the rate depends on the amount of extinction and on the spectral type. Therefore, in an (U − B) versus (B − V) color plane, the trajectories created by increasing extinction are not straight lines (as Eq. (B.1) indicates) and are not parallel for the same amount of extinction if the spectral type is different. The reader is referred to Fig. 1 of Maíz Apellániz (2004) for a graphical representation of the effect.
Even though knowledge of those limitations should be widely known, unfortunately one still sees papers where the Q approximation is incorrectly applied and, as a result, the published extinction results are biased. To show the relevance of the effects described above, we have used the SED grid of Maíz Apellániz (2013b) and the MA14 family of extinction laws to compute the real value of α for different amounts and types of extinction as well as input SEDs (Table B.1). In that way we can quantify some of the effects described above:
-
The first column in Table B.1 lists α for low canonical extinction applied to MS stars, in other words, the case that was likely considered by Johnson & Morgan (1953). For Teff ≥ 10 000 K, the classical value of 0.72 is not a poor approximation, but there is considerable scatter (from 0.709 to 0.780) and the average is above 0.72 (see the cases below for possible explanations of the latter effect). For lower values of Teff, α can be significantly higher already in this regime.
-
The next two columns show increasingly larger values of the canonical extinction applied to MS stars. Already for E(4405 − 5495) = 1.0 we see how non-linear effects increase the value of α to the point of making it larger than 0.72 for all MS OB stars (and much larger for cool stars). For E(4405 − 5495) = 3.0 α is considerably higher and the simple Q approximation fails completely.
A comparison between the second and fourth columns in Table B.1 shows the effect of changing R5495 from 3.1 to 5.0. The increase in R5495 reduces the value of α. It is possible that the original Johnson & Morgan (1953) analysis included some objects with R5495 above the canonical value that decreased their average α.
Finally, a comparison between the first and fifth columns shows the effect of luminosity class (or gravity). Differences are negligible for O and early-B stars but become appreciable for late-B stars and very large for cool stars. Late-B supergiants have lower values of α than their MS counterparts, which could also help explain the average 0.72 value of Johnson & Morgan (1953).
We conclude that the Q approximation can only be applied (and with care) to OB stars with low canonical extinction. In other cases it yields biased results both for E(4405 − 5495) and Teff. On the other hand, the use of a code that combines optical and NIR information handling extinction properly (such as CHORIZOS) can accurately determine Teff from photometric data (Maíz Apellániz & Sota 2008), as shown by MA14. It may have been reasonable to use such an approximation decades ago but with the current computing capabilities and extensive availability of well calibrated NIR data it has ceased to be so in most cases. As this paper shows, it is possible to avoid biases and, at the same time, compute E(4405 − 5495) and R5495 simultaneously and detect cases with extreme anomalous SEDs caused by, for example, IR excesses.
Appendix C Anticorrelation between E(4405 − 5495) and R5495
When using optical+NIR photometry to simultaneously fit E(4405 − 5495) and R5495 to a star with a known unextinguished SED, one obtains uncertainties for both quantities, that is, σE(4405−5495) and  . However, the final objective of the process is usually to obtain the extinction in a given band (e.g.,
. However, the final objective of the process is usually to obtain the extinction in a given band (e.g.,  ) or the unextinguished magnitude (e.g., V J,0), so the fitted quantities are intermediate values. One may be tempted to obtain
) or the unextinguished magnitude (e.g., V J,0), so the fitted quantities are intermediate values. One may be tempted to obtain  by multiplying E(4405 − 5495) and R5495 and to obtain its relative uncertainty (
by multiplying E(4405 − 5495) and R5495 and to obtain its relative uncertainty ( , dropping the J to avoid a triple subscript) by summing in quadrature the relative uncertainties for E(4405 − 5495) and R5495. This is wrong for two reasons. The first is that:
, dropping the J to avoid a triple subscript) by summing in quadrature the relative uncertainties for E(4405 − 5495) and R5495. This is wrong for two reasons. The first is that:
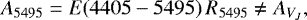 (C.1)
(C.1)
as A5495 is a monochromatic quantity and  a filter-integrated one. The second reason is that the two fitted quantities, E(4405 − 5495) and R5495, can be correlated so the propagation of uncertainties yields:
a filter-integrated one. The second reason is that the two fitted quantities, E(4405 − 5495) and R5495, can be correlated so the propagation of uncertainties yields:
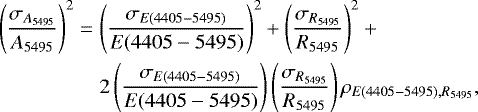 (C.2)
(C.2)
where 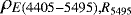 is the Pearson correlation coefficient between the two quantities. In principle,
is the Pearson correlation coefficient between the two quantities. In principle, 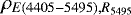 could be of either sign but, as we show in Appendix D, it is always negative and large under reasonable assumptions, in other words, E(4405 − 5495) and R5495 are strongly anti-correlated in most situations.
could be of either sign but, as we show in Appendix D, it is always negative and large under reasonable assumptions, in other words, E(4405 − 5495) and R5495 are strongly anti-correlated in most situations.
Figure C.1 shows the CHORIZOS likelihood output for an example built from input synthetic photometry. As expected,  , though the effect is small in this particular case (it becomes larger for higher extinctions or for later types). On the other hand, the effect in
, though the effect is small in this particular case (it becomes larger for higher extinctions or for later types). On the other hand, the effect in 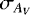 is very large due to the high value of
is very large due to the high value of 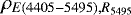 . This example is representative of the sample in this paper, indicating that the anti-correlation between E(4405 − 5495) and R5495 is an important effect that should be taken into account when computing uncertainties for optical extinctions.
. This example is representative of the sample in this paper, indicating that the anti-correlation between E(4405 − 5495) and R5495 is an important effect that should be taken into account when computing uncertainties for optical extinctions.
 |
Fig. C.1 R5495-E(4405 − 5495) plane likelihood for a simulated CHORIZOS run. The input UJ BJ V J J H Ks photometry corresponds to a SED with input Teff = 30 000 K, LC = 5, MW-metallicity, E(4405 − 5495) = 1.0, R5495 = 4.0 at a distance of 10 pc with uncertainties of 0.01 mag for each filter. The output has E(4405 − 5495) = 1.0003 ± 0.0067, R5495 = 3.999 ± 0.039, A5495 = 4.0002 ± 0.0151, and |
We now turn our attention to an explanation behind this anticorrelation. One way to look at it is that if, for a given unextinguished SED, one knows V J and Ks, then 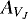 is relatively well determined because the Ks magnitude “anchors” the total extinction reasonably well, as that filter is little affected (in relative terms) by the presence of dust along the light path. How to fit the additional photometric points is a different story, as it becomes possible to vary E(4405 − 5495) and R5495 in synchrony maintaining a fixed total extinction. This is the kind of effect that a numerical code that processes multifilter photometry simultaneously can find that simpler methods, such as the Q approximation cannot.
is relatively well determined because the Ks magnitude “anchors” the total extinction reasonably well, as that filter is little affected (in relative terms) by the presence of dust along the light path. How to fit the additional photometric points is a different story, as it becomes possible to vary E(4405 − 5495) and R5495 in synchrony maintaining a fixed total extinction. This is the kind of effect that a numerical code that processes multifilter photometry simultaneously can find that simpler methods, such as the Q approximation cannot.
An additional related issue is how to obtain V J,0 and its uncertainty. One could simply calculate 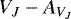 and sum theuncertainties in quadrature. Alternatively, one can use the whole likelihood grid calculated by CHORIZOS (2D if E(4405 − 5495) and R5495 are the only quantities being fitted or of higher dimensions if other quantities, such as log d or Teff are included in the fit) and derive V J,0 directly by summing over the whole grid. The second method (which is the one used in Table 1) has two advantages: [a] it uses information from all the photometric points and [b] it naturally takes into account the possible anti-correlation between V J and
and sum theuncertainties in quadrature. Alternatively, one can use the whole likelihood grid calculated by CHORIZOS (2D if E(4405 − 5495) and R5495 are the only quantities being fitted or of higher dimensions if other quantities, such as log d or Teff are included in the fit) and derive V J,0 directly by summing over the whole grid. The second method (which is the one used in Table 1) has two advantages: [a] it uses information from all the photometric points and [b] it naturally takes into account the possible anti-correlation between V J and 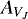 (as a dim V J can be caused by a large
(as a dim V J can be caused by a large 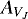 ). Both of those advantages tend to lower the uncertainties. On the other hand, the second method has the disadvantage of being model-dependent and, hence, more prone to be affected by systematic uncertainties (caused by e.g., stars with strong emission lines). It is easy to set up an example where the second method improves the value of V J,0 over the first one thanks to the use of information from all photometric points: for a low-extinction SED where one has both Johnson and Tycho-2 photometry and
). Both of those advantages tend to lower the uncertainties. On the other hand, the second method has the disadvantage of being model-dependent and, hence, more prone to be affected by systematic uncertainties (caused by e.g., stars with strong emission lines). It is easy to set up an example where the second method improves the value of V J,0 over the first one thanks to the use of information from all photometric points: for a low-extinction SED where one has both Johnson and Tycho-2 photometry and 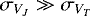 , then the information contained on V T reduces
, then the information contained on V T reduces 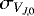 considerably16.
considerably16.
Appendix D Uncertainties in extinction as a function of photometric uncertainties
To test that CHORIZOS yields the correct values for the extinction parameters, we set up the following experiment:
-
For a star with a known unextinguished SED, we computed UJ BJ V J J H Ks for a range of E(4405 − 5495) values between 0.05 and 1.00 and R5495 values between 3.0 and 7.0 using the MA14 familiy of extinction laws.
-
We assigned the same photometric uncertainty to all filters (e.g.,
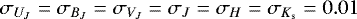 mag) and we randomly changed each magnitude according to a Gaussian distribution with that uncertainty. The process was repeated using different Montecarlo realisations and different photometric uncertainties.
mag) and we randomly changed each magnitude according to a Gaussian distribution with that uncertainty. The process was repeated using different Montecarlo realisations and different photometric uncertainties. -
We processed each of the simulated objects through CHORIZOS fitting E(4405 − 5495), R5495, and logd simultaneously while leaving the rest of the parameters fixed (to their known values).
The fitted E(4405 − 5495) and R5495 and their uncertainties (σE(4405−5495) and  ) were compared with the input values and the results were excellent:
) were compared with the input values and the results were excellent:
-
No significant bias is present. When a large number of Montecarlo realizations with the same input parameters were processed through CHORIZOS, the difference between the mean of the fitted values and the input was always much less than the calculated uncertainties.
-
The calculated uncertainties are consistent with the dispersion observed in the Montecarlo realisations. In other words, combining this point and the previous one, CHORIZOS correctly calculates random uncertainties without introducing systematic errors.
-
The calculated uncertainties follow functional forms that allow approximate analytical results to be derived:

From Eqs. (C.1) and (D.1)–(D.3) we obtain:
 (D.4)
(D.4)
which, for R5495 in the range from 3 to 7, varies between − 0.943 and − 0.983 (i.e., strongly anti-correlated, as anticipated in Appendix C).
One important consequence of Eq. (D.2) is that there is a limit to how well can R5495 be measured that depends strongly on E(4405 − 5495). For example, if 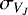 = 0.03, an extinction of E(4405 − 5495) = 0.10 and R5495 = 4.0 allowsone to measure the latter with an uncertainty of 1.2, which is too large to yield much information. We can qualitatively describe what is going on: it is easy to measure the properties of an effect when the effect is large but difficult when the effect is small. It is also important to keep in mind that, unfortunately, when working with real-world photometry from multiple sources there are usually hidden calibration issues (e.g., Maíz Apellániz 2005, 2006, 2007) plus possible disparities between the real and model SEDs (emission lines, IR excesses…) that introduce systematic errors. Therefore, one should avoid low-extinction objects when calculating optical-NIR extinction properties.
= 0.03, an extinction of E(4405 − 5495) = 0.10 and R5495 = 4.0 allowsone to measure the latter with an uncertainty of 1.2, which is too large to yield much information. We can qualitatively describe what is going on: it is easy to measure the properties of an effect when the effect is large but difficult when the effect is small. It is also important to keep in mind that, unfortunately, when working with real-world photometry from multiple sources there are usually hidden calibration issues (e.g., Maíz Apellániz 2005, 2006, 2007) plus possible disparities between the real and model SEDs (emission lines, IR excesses…) that introduce systematic errors. Therefore, one should avoid low-extinction objects when calculating optical-NIR extinction properties.
We would like to end with a cautionary note on the value of Eqs. (D.1)–(D.4). They have been calculated for the specific experiment described here. We would expect that if the experiment conditions are somewhat altered (different filters, known distance, unknown Teff, non-uniformphotometric uncertainties…) the qualitative behavior should be similar but the quantitative one (i.e., coefficients) should change (e.g., see Fig. 1 where increasing the number of filters decreases the value of 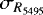 ).
).
Appendix E On the FM09 family of extinction laws
It was not our original intention to comment on the applicability of the Fitzpatrick & Massa (2009) or FM09 family of extinction laws to our data but the referee requested that we explain why it was not included along with CCM and F99 in our list of comparison families and so we discuss it in this Appendix.
In FM09, ACS/HST spectrophotometry was used in the 6000–9500 Å range combined with V J and 2MASS JHKs photometry to derive a new family of extinction laws of the form (Eq. (5) in their paper):
 (E.1)
(E.1)
where λ is in microns and we have adapted their notation to the one in this paper. The FM09 family of extinction laws is different from the CCM. F99, or MA14 ones in that it is a two-parameter family (RV and α) instead of a one-parameter family. The introduction of a second parameter should ease the fitting of a larger number of photometric points but, of course, it should be used only when necessary, as Occam’s razor dictates. FM09 use as an argument for doing so their previous results of Fitzpatrick & Massa (2007), their paper V (FM09 is their paper VI).
We can use Eq. (A.5) to rearrange Eq. (E.1) into a more convenient form:
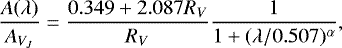 (E.2)
(E.2)
where we have divided the right side of the equation into two different terms to study their effect on the left side. The first term depends only on RV (the first parameter), so it is a constant for a given choice of the extinction law. The second term contains the dependence on λ as well as that on α (the second parameter).
The first issue with Eq. (E.2) we have dealt with in Appendix A: 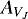 and RV are filter-integrated quantities that cannot be properly used to characterize an extinction law, as they depend in a complex way on the amount and type of extinction and also on the SED we are observing. Therefore, we need to findthe equivalent to Eq. (E.2) using monochromatic quantities. We can simply substitute
and RV are filter-integrated quantities that cannot be properly used to characterize an extinction law, as they depend in a complex way on the amount and type of extinction and also on the SED we are observing. Therefore, we need to findthe equivalent to Eq. (E.2) using monochromatic quantities. We can simply substitute  by A5495 but in the case of RV we make the substitution f = (0.349 + 2.087RV)∕RV for reasons that will become clear later. Therefore, we end up with:
by A5495 but in the case of RV we make the substitution f = (0.349 + 2.087RV)∕RV for reasons that will become clear later. Therefore, we end up with:
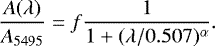 (E.3)
(E.3)
Once we have reached this point, there is one point that is unclear in FM09: what is the range of applicability of Eq. (E.3)? Does it extend to shorter wavelengths than 6000 Å (e.g., to the whole optical-NIR range) or is it constrained to λ > 6000 Å? We consider both of those options below.
Option 1: Equation (E.3) extends to the whole optical-NIR range. If this is the case, we can plug in λ = 5495 Å = 0.5495 μm to Eq. (E.3). As the left hand side has to be equal to one, then:
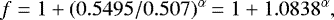 (E.4)
(E.4)
We note that Eq. (E.5) is independent of R5495 (or of RV) that is, it is actually a single-parameter family of extinction laws, as the only parameter left in the equation is α. Furthermore, the definition of f and Eq. (E.4) lead to:
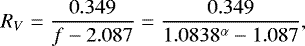 (E.6)
(E.6)
that is, RV is a function of α, not an independent parameter. We can also plug in λ = 4405 Å = 0.4405 μm in Eq. (E.3) and use Eqs. (A.8) and (E.4) to arrive at:
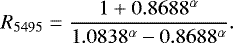 (E.7)
(E.7)
Equations (E.6) and (E.7) are incompatible. For example, for α = 1.6 the first one yields 6.92 and the second one 5.31 while for α = 2.9 the first one yields 1.99 and the second one 2.79. We note that changing the central wavelengths of the BJ V J filters to values other than 4405 Å and 5495 Å changes the coefficients in Eqs. (E.6) and (E.7) but not the functional forms, which are incompatible.
This reasoning leads us to the conclusion that option 1 is not what the authors of FM09 must have intended and therefore we discard it. We note, however, that other authors may be unaware of this17.
Option 2: Equation (E.3) is applicable only to λ >6000 Å. In this case, the authors would have implied that a different extinction law is required blueward of that wavelength. However, that extinction law is not explicitly mentioned anywhere in their paper. Since the majority of the photometric data in our paper is in the 3000–6000 Å range, we are unable to apply the FM09 family of extinction laws for our data. Nevertheless, let us explore the consequences of the FM09 family of extinction laws redwards of 6000 Å.
We start by noting that if a different extinction law has to be used, then Eq. (E.4) is not strictly true, as A(λ)∕A5495 has a different (not specified) form around that wavelength. However, extinction curves are continuous and differentiable and since 5495 Å is close in wavelength to 6000 Å, then Eq. (E.4) has to be approximately valid. We show that is indeed the case in Table E.1, where we extract the results of Table 4 of FM09 and compute the first term of Eq. (E.2) and the inverse of the second term of that same equation evaluated at 5495 Å. As it can be seen, the values are nearly identical (in most cases the differences can be adscribed to round-off issues in the FM09 table). The conclusion from this experiment is that, effectively, FM09 is a single-parameter family of extinction laws, not a two-parameter family as claimed, as RV is completely determined by α. Therefore, Eq. (E.5) is a valid parametrization for FM09 redwards of 6000 Å (we suspect this formula or a similar one is what Schlafly et al. 2016 used, see footnote above). An interesting corollary is that for the blueward extension of FM09 to be consistent in the sense of RV ≈ R5495, its functional form would have to be well constrained by the redwards portion (and different from Eq. (E.5)), so even then it would be a quasi-single-parameter family.
Transformation of the results from Table 4 of FM09 using the functions described in the text.
This does not necessarily mean that the results of FM09 are invalid. What those authors could have derived is a single-parameter family of extinction laws valid for λ > 6000 Å that behaves as apower law in the long-wavelength regime and becomes modified in the optical, an idea that they adopted from a suggestion by Karl Gordon (see their footnote 6). However, before accepting the FM09 results we must end with three additional words of caution.
Firstly, the authors state that “We thus quadratically combine the standard 2MASS uncertainties with values of 0.007, 0.040, and 0.017 mag for J, H, and Ks, respectively, to arrive at the total uncertainty for each magnitude”. In this paper we did not require such additional uncertainties (except for objects with bad quality flags), which leads us to think that 2MASS photometry is correct and that there must be a source of uncertainties unaccounted for in FM09.
Secondly, the FM09 sample consists only of 14 objects. We think that number is too small to properly constraint a family of extinction laws, as it does not provide an adequate sampling of the parameter space. Furthermore, some of the stars in their sample havequite a low extinction, making the IR measurements suspect. For example, for HD 46 106 we derive E(4405 − 5495) = 0.392 ± 0.007 and the spectral type is O9.7 III(n), not B1 V as stated in FM09. Also, only two stars in their Table 1 are listed as having E(B − V) > 1.0.
Finally, the object that FM09 chose as their highest-R5495 representative is Herschel 36 (a.k.a. HD 164 740), a star to which they pay special attention. However, the authors are apparently unaware of the work of Goto et al. (2006), who showed that an obscured companion has a significant contributionin the NIR, or of Arias et al. (2006), whose Fig. 2 clearly showed the NIR excess in comparison with the primary SED, in both cases three years prior to the publication of their paper (see also the discussion regarding Herschel 36 in the main body of this paper). The presence of such anomalous objects in a sample is the reason why any target list used for extinction law calculations has to be carefully culled, as we have done in this paper.
References
- Alves, J., & Bouy, H. 2012, A&A, 547, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arias, J. I., Barbá, R. H., Maíz Apellániz, J., Morrell, N. I., & Rubio, M. 2006, MNRAS, 366, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Arias, J. I., Barbá, R. H., Gamen, R. C., et al. 2010, ApJ, 710, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W., & Minkowski, R. 1937, ApJ, 86, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Belikov, A. N., Kharchenko, N. V., Piskunov, A. E., & Schilbach, E. 1999, A&AS, 134, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellini, A., Anderson, J., van der Marel, R. P., et al. 2017, ApJ, 842, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, V. M. 1956, ApJ, 123, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, V. M. 1957, ApJ, 125, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822 [NASA ADS] [Google Scholar]
- Cardelli, J. A. 1988, ApJ, 335, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Kaper, L., Foing, B. H., & Ehrenfreund, P. 2005, A&A, 438, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, F., Klutsch, A., Jeffries, R. D., et al. 2017, A&A, 603, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog: II/237 [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, M. P. 1968, AJ, 73, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2009, ApJ, 699, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. 1985, AJ, 90, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Gamen, R. C., Arias, J. I., Barbá, R. H., et al. 2012, A&A, 546, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, M., Stecklum, B., Linz, H., et al. 2006, ApJ, 649, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D. P., et al. 2015, ApJ, 810, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P. & Draine, B. T. 1989, ApJ, 345, 230 [NASA ADS] [CrossRef] [Google Scholar]
- He, L., Whittet, D. C. B., Kilkenny, D., & Spencer Jones, J. H. 1995, ApJS, 101, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J., Scowen, P. A., Sankrit, R., et al. 1996, AJ, 111, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2012, A&A, 542, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Houk, N., & Swift, C. 1999, Michigan Catalogue of Two-Dimensional Spectral Types for the HD Stars; 5 (Department of Astronomy, University of Michigan) [Google Scholar]
- Hur, H., Park, B.-G., Sung, H., et al. 2015, MNRAS, 446, 3797 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., & Morgan, W. W. 1953, ApJ, 117, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 347 [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaiser, N., Burgett, W., Chambers, K., et al. 2010, in Ground-based and Airborne Telescopes III, Proc. SPIE, 7733, 77330E [Google Scholar]
- Krełowski, J., Schmidt, M., & Snow, T. P. 1997, PASP, 109, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, H. O., & Thaddeus, P. 1992, ApJS, 81, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, B., Sung,H., Kim, J. S., Bessell, M. S., & Park, B.-G. 2014, MNRAS, 443, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, B., Sung,H., Bessell, M. S., et al. 2015, AJ, 149, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2001, ApJ, 560, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2004, PASP, 116, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2005, PASP, 117, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2006, AJ, 131, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2007, in, The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Series, 364 227 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J. 2013a, in HSA7 (Barcelona: Sociedad Española de Astronomía), 583 [Google Scholar]
- Maíz Apellániz, J. 2013b, in HSA7 (Barcelona: Sociedad Española de Astronomía), 657 [Google Scholar]
- Maíz Apellániz, J. 2015a, in HSA8 (Barcelona: Sociedad Española de Astronomía), 402 [Google Scholar]
- Maíz Apellániz, J. 2015b, Mem. Soc. Astron. It., 86, 553 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J. 2017, A&A, 608, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., & Sota, A. 2008, Rev. Mex. Astron. Astrofis., 33, 44 [Google Scholar]
- Maíz Apellániz, J., Walborn, N. R., Galué, H. Á., & Wei, L. H. 2004, ApJS, 151, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Sota, A., Walborn, N. R., et al. 2011, in HSA6 (Barcelona: Sociedad Española de Astronomía), 467 [Google Scholar]
- Maíz Apellániz, J., Evans, C. J., Barbá, R. H., et al. 2014, A&A, 564, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Sota, A., & Simón-Díaz, S. 2015a, A&A, 583, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Negueruela, I., Barbá, R. H., et al. 2015b, A&A, 579, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Úbeda, L., Barbá, R.-H., et al. 2015c, in HSA8 (Barcelona: Sociedad Española de Astronomía), 604 [Google Scholar]
- Maíz Apellániz, J., Sota, A., Arias, J. I., et al. 2016, ApJS, 224, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Simón-Díaz, S., Negueruela, I., & Trigueros Páez, E. 2017a, in The Lives and Death-Throes of Massive Stars, eds. J. J. Eldridge, J. C. Bray, L. A. S. McClelland, & L. Xiao, IAU Symposium, 329, 136 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J., Trigueros Páez, E., Bostroem, A. K., Barbá, R. H., & Evans, C. J. 2017b, in HSA9 (Barcelona: Sociedad Española de Astronomía), 510 [Google Scholar]
- Marco, A., Negueruela, I., González-Fernández, C., et al. 2014, A&A, 567, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalik, D., Lindegren, L., & Hobbs, D. 2015, A&A, 574, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, T., Klare, G., & Sarcander, M. 1980, A&AS, 42, 251 [NASA ADS] [Google Scholar]
- O’Dell, C. R., & Harris, J. A. 2010, AJ, 140, 985 [CrossRef] [Google Scholar]
- Pang, X., Pasquali, A., & Grebel, E. K. 2016, AJ, 151, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E. 2015, A&A, 580, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebolledo, D., Burton, M., Green, A., et al. 2016, MNRAS, 456, 2406 [NASA ADS] [CrossRef] [Google Scholar]
- Reis, W., Corradi, W., de Avillez, M. A., & Santos, F. P. 2011, ApJ, 734, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Sale, S. E., Drew, J. E., Barentsen, G., et al. 2014, MNRAS, 443, 2907 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Bermúdez, J., Alberdi, A., Schödel, R., et al. 2014, A&A, 572, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scappini, F., Casu, S., Cecchi-Pestellini, C., & Olberg, M. 2002, MNRAS, 337, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Meisner, A. M., Stutz, A. M., et al. 2016, ApJ, 821, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Sfeir, D. M., Lallement, R., Crifo, F., & Welsh, B. Y. 1999, A&A, 346, 785 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Egan, M. P., Carey, S., et al. 2000, ApJ, 532, L145 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Snowden, S. L., Egger, R., Finkbeiner, D. P., Freyberg, M. J., & Plucinsky, P. P. 1998, ApJ, 493, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., & Shida, R. Y. 2008, Rev. Mex. Astron. Astrofis., 33, 56 [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Morrell, N. I., et al. 2014, ApJS, 211, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Milašius, K., Boyle, R. P., et al. 2014, AJ, 148, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Valencic, L. A., Clayton, G. C., Gordon, K. D., & Smith, T. L. 2003, ApJ, 598, 369 [NASA ADS] [CrossRef] [Google Scholar]
- van der Werf, P. P., Goss, W. M., & O’Dell, C. R. 2013, ApJ, 762, 101 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F., Evans, D. W., De Angeli, F., et al. 2017, A&A, 599, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J. T., Bailey, M., Tatton, B. L., et al. 2013, A&A, 550, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vásquez, J., Cappa, C. E., Pineault, S., & Duronea, N. U. 2010, MNRAS, 405, 1976 [NASA ADS] [Google Scholar]
- Vázquez, R. A., Baume, G., Feinstein, A., & Prado, P. 1996, A&AS, 116, 75 [NASA ADS] [Google Scholar]
- Vijapurkar, J.,& Drilling, J. S. 1993, ApJS, 89, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, D. A. I., Cox, N. L. J., Kaper, L., Spaans, M., & Ehrenfreund, P. 2011, A&A, 533, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Maíz Apellániz, J., Martins, F., et al. 2012, MNRAS, 425, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., & Blades, J. C. 1987, ApJL, 323, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Maíz Apellániz, J., & Barbá, R. H. 2002, AJ, 124, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, J., & Fukui, Y. 1992, ApJ, 386, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Zeidler, P., Sabbi, E., Nota, A., et al. 2015, AJ, 150, 78 [NASA ADS] [CrossRef] [Google Scholar]
The GOSSS spectral types were derived from spectra gathered with five facilities: the 1.5 m Telescope at the Observatorio de Sierra Nevada (OSN), the 2.5 m du Pont Telescope at Las Campanas Observatory (LCO), the 3.5 m Telescope at Calar Alto Observatory (CAHA), and the 4.2 m William Herschel Telescope (WHT) and 10.4 m Gran Telescopio Canarias (GTC) at Observatorio del Roque de los Muchachos (ORM).
Variability is also an issue but a minor one. Most sources of variability in O stars such as the rotation of oblique magnetic fields (Wade et al. 2012), wind, or turbulence variability significantly affect emission lines but produce only small changes in the continuum. Eruptive Oe stars such as HD 120 678 (Gamen et al. 2012) have been excluded from the sample, so they should not concern us. The most relevant source of large broad-band flux variability in the sample is eclipsing binaries. Most of them, however, are accounted for in the literature and those that are not can be revealed through comparison of different sources. Nevertheless, it is possible that a few hidden binaries may be lurking in our sample, especially in the J2G subsample, where there are less bands to compare among.
We have recently moved the main URL to https://gosc.cab.inta-csic.es from the old URL at http://gosc.iaa.es, which will be kept as a mirror site for the time being.
We refer the reader to Appendix E for an explanation of why we did not include Fitzpatrick & Massa (2009) in our list of comparison families of extinction laws.
Another consequence of the existence of the interarm space in some fifth-octant sightlines is that we are able to include in our sample stars from NGC 3603, located approximately three times farther away than the Carina Nebula, at a distance similar to that of the Galactic Center but with much lower extinctions.
Herschel 36 has a nearby companion that dominates the flux in the MIR (Goto et al. 2006) and which is already significant in the NIR. The existence of that companion complicates extinction measurements and produces discrepancies between different works depending on the photometry, extinction laws, and techniques used (see Arias et al. 2006 and Maíz Apellániz et al. 2015c). We note, however, that all results consistently yield E(4405 − 5495) values in the 0.78–0.85 range and R5495 values in the 5.4–5.9 range.
Cami et al. (1997) refer to the extreme σ sightlines as of Orion type, since stars in the Orion Nebula have a very weak or non existent DIB 5797.
Here we consider only the “pure” extinction case, where radiation originates in a single point source and the dust cloud is located far away from both the source and the observer. If one relaxes those assumptions the relationship between emitted and observed fluxes depends on radiation transport effects (e.g., scattering back into the beam) and one should talk about dust attenuation, not extinction.
These are the values calculated by Johnson & Morgan (1953) and they can differ from those calculated here for the examples below.
We do not think we are the first to notice this issue with FM09. Schlafly et al. (2016) correctly indicate at one point that “FM09 has a second parameter, RV, that does not change the shape of the extinction curve redwards of V ” and later on mention that “we have excluded the gP1 band, which is outside the region where the FM09 prescription was developed” (note that Schlafly et al. (2016) does include rP1 in their FM09 comparison even though that filter extends redward of 6000 Å). If one adds those two statements together, those authors are saying that FM09 is not applicable to the BJ and V J bands while RV has no effect in its range of applicability. Therefore, their conclusion must be the same as ours: the presence of RV as an independent parameter in FM09 is spurious.
All Tables
Number of objects and ranges of E(4405 − 5495) and R5495 for some of the clusters and associations in this paper.
Values of α as a function of Teff calculated from synthetic photometry for different values of E(4405 − 5495), luminosity class (main sequence, MS, or supergiant, SG), and R5495.
Transformation of the results from Table 4 of FM09 using the functions described in the text.
All Figures
 |
Fig. 1
|
| In the text | |
 |
Fig. 2
|
| In the text | |
 |
Fig. 3
|
| In the text | |
 |
Fig. 4
|
| In the text | |
 |
Fig. 5 Comparison between the reddenings measured by G15 and those in this paper. The error bars include the uncertainty in logd (G15 gives E(B − V) as a function of distance), assumed to be 0.1 (corresponding to an uncertainty of 0.5 in the distance modulus). The three colored lines show the expected difference between E(B − V) and E(4405 − 5495) for three different temperatures assuming an MA14 extinction law with R5495 = 3.0. |
| In the text | |
 |
Fig. 6 Difference between the G15 E(B − V) values and E(4405 − 5495) for the O stars with E(4405 − 5495) > 1.0 in the Cygnus-X region plotted on top of the CO J = 1 ← 0 map of Leung & Thaddeus (1992). The value is encoded in the color of each symbol (see scale on left panel and compare with the vertical axis of Fig. 5). The left panel shows the whole region while the right panel zooms in the blue rectangular region, which corresponds to Cyg OB2. The beam FWHM is 8.′7 (~4 pc at the distance of Cyg OB2), so the CO clouds are likely to have substructure not seen in the map. The angular resolution ofthe G15 values is similar to the beam size. The axes are in Galactic coordinates and the units are degrees. |
| In the text | |
 |
Fig. 7 Extinction measurements for O stars in four H II regions: (top left) the Carina Nebula, (top right) M 16/NGC 6611, (bottom left) Berkeley 59/NGC 7822, and (bottom right) Sharpless 2-132. The top two images are from ESO press releases 1250 (BgrHα) and 0926 (BV R), respectively. The bottom two images are RGB combinations of J2MASS+RDSS2+BDSS2. North is towards the top and east towards the left and the approximate physical scale is indicated in all cases. Only a section of each H II region is shown to better visualize the dust lanes. |
| In the text | |
 |
Fig. 8 AV∕d for the sample in this paper divided into stars closer than and beyond 1 kpc. No error bars are plotted but they are estimated at ~20%, with the larger part of the error budget coming from the distance uncertainty. The underlying histograms show the 16th, 50th, and 84th percentiles (median plus lower and upper 1σ equivalents) per Galactic octant. We note that only 19 stars have |b| > 10o, of which seven are in Orion (see Fig. 12). |
| In the text | |
 |
Fig. 9 R5495 as a functionof E(4405 − 5495) for the CHORIZOS runs in this paper using the MA14 family of extinction laws. The color coding is the same as in Fig. 1. See Fig. 10 for the histograms derived from this plot by dividing the horizontal axis in five different ranges. |
| In the text | |
 |
Fig. 10 R5495 cumulative histograms for different values of E(4405 − 5495) (see legend for ranges and number of objects in each one) for the CHORIZOS runs in this paper using the MA14 family of extinction laws. Each object is represented by a normalised Gaussian with a width of |
| In the text | |
 |
Fig. 11 R5495 as a functionof AV∕d for the CHORIZOS runs in this paper using the MA14 family of extinction laws. The colour coding is the same as in Fig. 1. We note that the horizontal scale is logarithmic. |
| In the text | |
 |
Fig. 12 Extinction measurements for Galactic O stars plotted on top of the full-sky Hα image of Finkbeiner (2003). Different colors are used for five ranges of R5495 with the size of the symbol increasing with E(4405 − 5495). The background image is showed in a logarithmic intensity scale and in Galactic coordinates with a Cartesian projection centered on the Galactic anticenter. |
| In the text | |
 |
Fig. 13 Extinction measurements for O stars in two H II regions: (left) the Orion Nebula, (right) M 8. The left image is from STScI press release 2006–01 (BV Hαiz) and the rightimage is from ESO press release 1403 (ugrHαi). North is towards the top and east to the left. The approximate physical scale is indicated in both cases. |
| In the text | |
 |
Fig. 14 Environment around VFTS 451 (left), VFTS 464 = [P93] 702 (center), and VFTS 579 = [P93] 1201 (right), the three stars from the MA14 sample in 30 Doradus with E(4405 − 5495) > 0.3 and R5495 > 6.0. The three objects are at the top of pillars that point towards R136. The background image is a F814W + F656N (red) + F555W (green) + F336W (blue) WFC3 mosaic built from WFC3-ERS data. Each field is 8′′ × 8′′ (2 pc × 2 pc) with north to the top and east to the left. See Walborn et al. (2002) for an alternative view of knot 1, the environmentaround VFTS 579. |
| In the text | |
 |
Fig. C.1 R5495-E(4405 − 5495) plane likelihood for a simulated CHORIZOS run. The input UJ BJ V J J H Ks photometry corresponds to a SED with input Teff = 30 000 K, LC = 5, MW-metallicity, E(4405 − 5495) = 1.0, R5495 = 4.0 at a distance of 10 pc with uncertainties of 0.01 mag for each filter. The output has E(4405 − 5495) = 1.0003 ± 0.0067, R5495 = 3.999 ± 0.039, A5495 = 4.0002 ± 0.0151, and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.