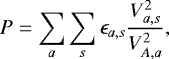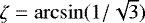EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 613 (May 2018) A&A, 613 (2018) A23 Full HTML
Free Access
Issue
A&A
Volume 613, May 2018
Article Number A23
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201731852
Published online 25 May 2018

© ESO 2018

1 Introduction

The adiabatic expansion of the solar wind predicts important deviations from the isotropy of the temperature, for example, an isotropic plasma parcel from the outer corona will arrive at 1 AU from the Sun with a temperature anisotropy Aa = T⊥,a∕T∥,a ≤ 0.03 (where T⊥,a and T∥,a denote the temperatures in the directions perpendicular and parallel to the ambient magnetic field, respectively, and index a refers to protons a = p, or electrons a = e) (Phillips & Gosling 1990). However, the in-situ observations by the Wind spacecraft have shown (Bale et al. 2009; Hellinger et al. 2006; Štverák et al. 2008; Maruca et al. 2011) that the temperature anisotropy at 1 AU is limited; it is 0.1 ≲ Ap ≲ 10 for protons and 0.5 ≲ Ae ≲ 2 for electrons. In the histograms reporting the observed anisotropy Aa as a function of parallel plasma beta β∥,a = 8πnkBT∥,a∕B2 (B is the strength of the ambient magnetic field, n the number density, and kB the Boltzmann constant), the data distribute into a specific region of rhombic shape centered on the equipartition of the particle kinetic energy density and the magnetic energy density, β∥≃ 1. There are different models that attempt to explain the observed bounds on the temperature anisotropy. Interesting results were obtained from hybrid Vlasov-Maxwell simulations (Servidio et al. 2014). These simulations use an isotropic turbulent Maxwellian plasma (Aa = 1) as an initial condition and the time evolution shows, in particular, that the plasma turbulence self-consistently generates temperature anisotropy similar to the solar wind observations (Bale et al. 2009). In the absence of particle collisions, an alternative explanation of the observed limitations on the temperature anisotropy may result from the instability constraints (Hellinger et al. 2006; Štverák et al. 2008; Bale et al. 2009): plasma driven beyond the stable range of parameters causes fluctuations which determine the plasma to return to a stable regime. These quasistationary plasma states change their (β∥, A)-bounds with the heliocentric distance (Matteini et al. 2007). In the current study, we focus exactly on this possibility.

The velocity distributions of the solar wind protons are usually modeled by a drifting bi-Maxwellian (Kasper et al. 2002, 2006; Maruca et al. 2011; Maruca 2012), while the electrons exhibit a dual (thermal core plus suprathermal halo) composition described either by a sum of two bi-Maxwellians (Feldman et al. 1975; Marsch 1991) or by a combination of a bi-Maxwellian and a bi-kappa distribution (Maksimomic et al. 2005; Štverák et al. 2008; Lazar et al. 2016). For non-streaming bi-Maxwellian plasmas, linear theory predicts instabilities of mirror, firehose, and electromagnetic cyclotron fluctuations (Bale et al. 2009; Hellinger et al. 2006; Štverák et al. 2008; Maruca et al. 2011). Compared with the observations, thresholds of these instabilities can constrain (Hellinger et al. 2006; Lazar et al. 2017) only the temperature anisotropy of high-β∥,a > 1 plasmas, whereas they fail for β∥,a < 1. There is therefore an open question: Which instabilities can operate in the low-β∥,a < 1 regimes that would explain the limits of the temperature anisotropy observed in the solar wind.

An attempt to modify the well-known instability conditions has been made by Schlickeiser et al. (2011) who incorporated the effect of collisional damping, but without a satisfactory agreement with the observations. In the context of the solar wind an additional source of free energy, which can destabilize the plasma, can be provided by the differential streaming (or counterstreaming) of different species and particle components. The observations demonstrate that the velocity distributions of solar wind electrons (Štverák et al. 2008) and protons (Marsch et al. 1982) exhibit quite often a second peak along the magnetic field corresponding to a beam (or strahl) component. These beaming components are a characteristic of the fast winds, which may also lead to counterstreaming (or double-strahls) structures at a co-rotating interaction (CIR) or any closed magnetic field topologies (e.g., in interplanetary shocks, coronal mass ejections).

The temperature anisotropy instabilities in magnetized (counter-)streaming bi-Maxwellian plasmas have been revisited recently showing that differential streaming may change drastically the instability conditions (Ibscher et al. 2013; Ibscher & Schlickeiser 2013, 2014; Schlickeiser & Yoon 2014; Vafin et al. 2014, 2015a,b; Chen et al. 2016). However, a detailed comparison with the solar wind data has not been provided yet. The present paper provides realistic estimations for the new instability conditions (Vafin et al. 2015b) (e.g., mirror, firehose) for conditions typically encounteredin the solar wind, and the instability thresholds are contrasted with the observed limits of temperature anisotropy. It should be stressed that our study considers only the instability conditions and not the maximum growth rates of the instabilities. The latter issue is important, since the nonlinear cascade rate can be fast enough to invalidate the constancy of parameters assumed in the linear processes (Matthaeus et al. 2014). However, this question requires more detailed comparative investigations going beyond the scope of the current manuscript.

2 Instability conditions for counterstreaming bi-Maxwellian plasma

Although the solar wind plasma is extremely complex, here we use a simplified model to identify the main trends. To a good approximation, the counterstreaming distributions of protons (a = p) and electrons (a = e) can be assumed to be bi-Maxwellian: 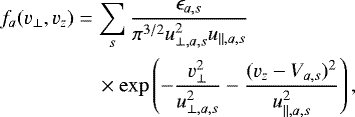fa(v⊥,vz)=∑sϵa,sπ3/2u⊥,a,s2u∥,a,s        ×exp(−v⊥2u⊥,a,s2−(vz−Va,s)2u∥,a,s2),\begin{align*} &f_a(v_{\perp } ,v_z )= \sum _{s} {\epsilon_{a,s}\over \pi^{3/2} u^2_{ \perp, a,s} u_{\parallel ,a,s}}\nonumber \\ &\quad\quad\quad\quad\,\,\,\,\times \exp \left(-{v_{\perp }^2\over u^2_{\perp ,a,s}} -{(v_z -V_{a,s})^2\over u^2_{\parallel ,a,s}} \right) ,\end{align*}(1)

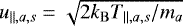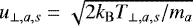where ϵa,s = na,s∕n, na,s is the number density of particles a streaming with velocity V a,s, n is the total plasma number density, and u∥,a,s=2kBT∥,a,s/ma$u_{\parallel ,a,s}=\sqrt{2k_{\mathrm{B}}T_{\parallel ,a,s}/m_a}$ and u⊥,a,s=2kBT⊥,a,s/ma$u_{\perp ,a,s}=\sqrt{2k_{\mathrm{B}}T_{\perp ,a,s}/m_a}$ are, respectively, the parallel and perpendicular thermal velocities. The conditions for charge and current neutrality require ∑ sϵa,s = 1 and ∑ sϵa,sV a,s = 0. In the solar wind, protons and electrons have comparable temperatures (at 1 AU they may differ only by a factor 2–3Breech et al. 2010), and here we assume their temperature components to be equal, that is, T∥,a,s = T∥ and T⊥,a,s = T⊥. We have also adopted the premise that the temperatures are independent of streaming components, which is not always the case (Marsch 2012). Furthermore, the plasma is considered homogeneous enough and in a locally constant and homogeneous magnetic field B. Our previous work (Vafin et al. 2015b) on the linear instability analysis of bi-Maxwellian counter-streaming plasmas provides that, for 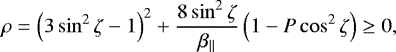ρ=(3sin2ζ−1)2+8sin2ζβ∥(1−Pcos2ζ)≥0,\begin{eqnarray*} \rho= \left(3\sin^2\zeta-1 \right)^2 &#x002B; {8\sin^2\zeta\over\beta _{\parallel }}\left(1-P\cos^2\zeta \right)\geq0,\end{eqnarray*}(2)

where P=∑a∑sϵa,sVa,s2VA,a2,\begin{eqnarray*} P=\sum_a \sum_s \epsilon_{a,s} {V_{a,s}^2 \over V_{A,a}^2},\end{eqnarray*}(3)

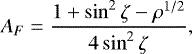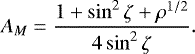the instability conditions of firehose and mirror fluctuations are given, respectively, by 0 < A < AF and A > AM. Here, AF=1+sin2ζ−ρ1/24sin2ζ,\begin{eqnarray*} A_F={1&#x002B;\sin^2\zeta-\rho^{1/2}\over4\sin^2\zeta},\end{eqnarray*}(4) AM=1+sin2ζ+ρ1/24sin2ζ.\begin{eqnarray*} A_M={1&#x002B;\sin^2\zeta&#x002B;\rho^{1/2}\over4\sin^2\zeta}.\end{eqnarray*}(5)

For ρ < 0, these modes become unstable at all temperature anisotropies A = T⊥∕T∥≥ 0. Here, β∥ = 8πnkBT∥∕B2, 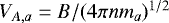VA,a=B/(4πnma)1/2$V_ {A,a}=B/(4\pi n m_a)^{1/2}$, and ζ is the angle between the wave-vector and the ambient magnetic field. We note that based on our assumptions we drop the subscripts p and e for A and β∥. Thus, the curves AF(β∥) and AM (β∥) describe the marginal instability conditions in the plane (β∥, A).

For a non-streaming plasma (V a,s = 0), Eqs. (4) and (5) reduce to the well-known instability conditions (Stix 1962) invoked previously to explain the solar wind temperature anisotropy (Bale et al. 2009; Kasper et al. 2002; Maruca et al. 2011; Hellinger et al. 2006). For the particular cases of parallel (ζ = 0) and perpendicular (ζ = π∕2) propagation, the instability conditions read, respectively, 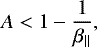A<1−1β∥,\begin{eqnarray*} A<1-{1\over\beta_{\parallel}},\end{eqnarray*}(6) A>12[ 1+(1+2β∥)1/2 ].\begin{eqnarray*} A>{1\over2}\left[ 1&#x002B; \left( 1&#x002B; {2\over\beta_{\parallel}} \right)^{1/2} \right].\end{eqnarray*}(7)

Although the plasma state in a nonstreaming model is defined by the four quantities n, T⊥, T∥, and B, they enter the instability conditions (6) and (7) only via two parameters A and β∥. In this case, Eqs. (6) and (7) can be straightforwardly illustrated in the (β∥, A)-plane. However, for V a,s≠0 the instability conditions (4) and (5) depend additionally on n and B through the parameter 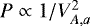P∝1/VA,a2$P\propto 1/V_{A,a}^2$. Thus, in order to compare these instability conditions with the observations (Maruca et al. 2011; Štverák et al. 2008; Bale et al. 2009; Hellinger et al. 2006), we need to specify the counterstreaming parameter P as a function of β∥, which is a non-trivial problem.

Due to their mass, protons make the major contribution to this parameter, and the instability criteria are mainly conditioned by the proton counterstreams. Let us assume that the protons have two components with the number densities nc and nb and the streaming velocities Vc and Vb denoted as “core” (subscript c) and “beam (subscript b), respectively. Due to the quasi-neutrality nc + nb = n = ne, in the proton center of mass that moves with velocity Vp = (ncVc + nbVb)∕n, the velocities of this components become accordingly ΔVc =Vc −Vp and ΔVb =Vb −Vp. In this referential frame they result in counterstreams (since ncΔVc + nbΔVb = 0), and the parameter P becomes 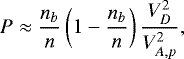P≈nbn(1−nbn)VD2VA,p2,\begin{eqnarray*} P\approx {n_b\over n}\left( 1- {n_b\over n} \right){V_D^2\over V_{A,p}^2},\end{eqnarray*}(8)

where V D = V b − V c.

At the same time, the observations in the fast solar wind indicate (i) 0.1 < β∥ < 1 depending on the heliocentric distance (Hellinger et al. 2006), and (ii) the drifting velocity V D in the fast wind is frequently higher than in the slow wind (Marsch et al. 1982). Thus, it is reasonable to expect for the ratio V D ∕V A,p a maximum value depending on β∥ and, implicitly, on the heliocentric distance. Moreover, Tu et al. (2004) have found the power low dependence 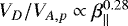VD/VA,p∝β∥0.28$V_D/V_{A,p}\propto \beta_{\parallel}^{0.28}$ for 0.1 < β∥ < 0.6. Therefore, we also use power functions to construct a model dependence for V D ∕V A,p that has a maximum at some β∥. As a result, to study the streaming effect we propose the following model: 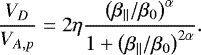VDVA,p=2η(β∥/β0)α1+(β∥/β0)2α.\begin{eqnarray*} {V_D\over V_{A,p}}= 2\eta {\left(\beta_{\parallel}/\beta_0 \right)^{\alpha}\over 1 &#x002B; \left(\beta_{\parallel} /\beta_0 \right)^{2\alpha}}.\end{eqnarray*}(9)

In this case, the ratio V D∕V A,p reaches its maximum value η at β∥= β0. The observed value of η is limited by η ≲ 3 (Marsch et al. 1982). In the current work, we aim to figure out the principal behavior of the instability conditions in the presence of counterstreams for the solar wind conditions. However, Eq. (9) is expected to be more complicated, implying additional effects, for example, interplay with temperature anisotropy (Chen et al. 2016), which need first to be clarified by the observational analysis. Using Eq. (9), the counterstreaming parameter (8) becomes 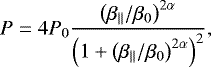P=4P0(β∥/β0)2α(1+(β∥/β0)2α)2,\begin{eqnarray*} P= 4 P_0 {\left(\beta_{\parallel}/\beta_0 \right)^{2\alpha}\over \left( 1 &#x002B; \left( \beta_{\parallel}/\beta_0 \right)^{2\alpha}\right)^2 },\end{eqnarray*}(10)

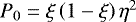where P0=ξ(1−ξ)η2$P_0= \xi \left( 1- \xi \right)\eta^2$ is the maximum value of the counterstreaming parameter and ξ = nb∕n is the relative beam-plasma density. Observations show (Marsch et al. 1982; Tu et al. 2004) that typically ξ < 0.2 (although, higher values of ξ are also observed Goldstein et al. 2000). Now, Eq. (10) can be plugged into Eqs. (4) and (5) to obtain conditions AF(β∥) and AM(β∥).

3 Results

Figure 1 illustrates the instability conditions for β0 = 1 and α = 0.3 (similar to Tu et al. 2004), and different values of the maximum value of the counterstreaming parameter P0. When the value of P0 is increased, the instability conditions AF(β∥) and AM(β∥) approach each other, extending the unstable regions in the lower and upper parts of the (β∥, A)-plane. When P0 approaches 1.5, the two marginal conditions split leading to two distinct stable regions. One is at small β∥ and limited by the left-hand black or blue curves in Fig. 1, and the other region of stability lies within the area bounded by the right-hand black or blue lines. The existence of these two separated stable regions seems to disagree with the observations, which do not exhibit similar contours (Bale et al. 2009; Hellinger et al. 2006). The properties of the solar wind particles at 1 AU correspond in principle to the right-hand side stable region in Fig. 1, while the second stable region is notwell represented. It is, however, interesting to note that from a glance at the data distribution in Fig. 6.10 from Maruca (2012), we can identify a contour with a saddle point similar to that shown by the red curve in Fig. 1.

These results reveal that the instability conditions of firehose and mirror fluctuations are extremely sensitive to the presence of counterstreams. The instability conditions are drastically modified, when ρ approaches 0, because the region of stability in this case becomes considerably smaller because it splits into two separate parts. Our quantitative estimates demonstrate that the minimum value of P0 for this modification to take place is around 1.5. At the same time, the observed limits (Marsch et al. 1982) provide ξ ≲ 0.2 and η ≲ 3 resulting in P0 ≲ 1.44. This number is very close to the value 1.5 found in our model. Thus, we can conclude that the upper limits on ξ and η can be explained by relative streaming ofplasma particles. Once ξ ≫ 0.2 and η ≫ 3, the unstable region in the parameter space (β∥, A) becomes large, but the solar wind plasma reacts to reduce such large deviations in the limits ξ ≲ 0.2 and η ≲ 3 reported (statistically) by the observations.

We have compared our analytical instability criteria Eqs. (4) and (5) with available solar wind data (Hellinger et al. 2006; Matteini et al. 2007). Results are shown in Figs. 2 and 3. For the best agreement we set the values ofξ and η close to 0.2 and 3, respectively. The value of β0 is chosen such that the counterstreaming parameter P achieves its maximum close to the maximum of observational counts (A, β∥). We have determined by visual inspection the value of α such that our analytical predictions approach the observed contours. The cyan region illustrates the maximum of the probability distribution function in (β∥, A). The color lines in Figs. 2 and 3 show the predicted instability conditions for different angles ζ between the wave vector and the ambient magnetic field. For a given value of ζ, the curves AF (β∥) and AM (β∥) have the same color. The upper line (of the same color) always shows AM and the lower one AF. The plasma is stable between the upper and lower curves (area where the plasma is stable at all angles).

The top panel of Fig. 2 compares our results with the fast solar wind data from Helios at 0.3 AU, with most of the data present at β∥≲ 0.3. We have therefore set α = 0.3, which is similar to that found by Tu et al. (2004) for the low beta regime. Other parameters are β0 = 0.1, η = 2.79, and ξ = 0.18. The stability strongly depends on the wave vector angle with respect to the magnetic field. Under the given parameters, there is a stable region (limited by the upper yellow and lower magenta lines) where the plasma is stable at all angles, and which can therefore explain fairly well the observations.

In the middle and bottom panels of Fig. 2 the contrast is made with the fast wind data at 0.9 AU and 1.5–2.5 AU, respectively. To achieve a good agreement, we have increased α, accordingly, to 0.7 and 1.7. Other parameters were specified as β0 = 0.25, η = 2.8, ξ = 0.18 for the middle panel and β0 = 0.7, η = 2.8, ξ = 0.17 for the bottom one. Most of the data in these cases are found at β∥≈ 1, which is not covered in the study by Tu et al. (2004).

Additionally, Fig. 3 provides comparisons with the large data collection from the Wind/solar wind experiment (SWE; Hellinger et al. 2006). In the fast wind conditions (top panel of Fig. 3, β0 = 0.6, η = 2.9, ξ = 0.18), we recovered the value α = 1.4, which is close to the corresponding value for the Helios data. We also found some agreement from an attempt at comparison, for example, in the bottom panel of Fig. 3 (α = 1, β0 = 0.4, η = 2.8, ξ = 0.18), with the slow solar wind data where the (counter-) streams can be present infrequently (Marsch et al. 1982), making the validity of our model rather arguable.

thumbnail Fig. 1

Instability conditions for the firehose and mirror instabilities, ζ=arcsin(1/3)$\zeta=\arcsin(1/\sqrt{3})$, β0 = 1, α = 0.3. Magenta: P0 = 0.001. Green: P0 = 1. Red: P0 = 1.45. Black: P0 = 1.51. Blue: P0 = 1.6. Unstable and stable regions are marked by the letters “u” and “s”, respectively.
thumbnail Fig. 2

Comparison between the analytical instability conditions (Eqs. (4) and (5)) and fast solar wind data (V SW > 600 km s−1; Matteini et al. 2007) from the Helios at 0.3 AU (top panel) and 0.9 AU (middle panel), and from Ulysses at 1.5–2.5 AU (bottom panel). Top panel: magenta: ζ = π∕13, red ζ =π∕10, blue: ζ = π∕7.5, green: ζ = π∕6, yellow: ζ = π∕4. Middle panel: magenta: ζ = π∕10, red ζ =π∕8, blue: ζ = π∕7, green: ζ = π∕6, yellow: ζ = π∕4. Bottom panel: magenta: ζ = π∕10, red ζ =π∕7, blue: ζ = π∕5, green: ζ = π∕4, yellow: ζ = π∕3.5.
thumbnail Fig. 3

Comparison between the analytical instability conditions (Eqs. (4) and (5)) and fast (V SW > 600 km s−1, top panel) and slow (V SW < 600 km s−1, bottom panel) solar wind data (Hellinger et al. 2006) from WIND/SWE (1995–2001). Top panel: magenta: ζ = π∕13, red: ζ = π∕7, blue: ζ = π∕5, green: ζ = π∕4, yellow: ζ = π∕3.5. Bottom panel: magenta: ζ = π∕10, red: ζ = π∕7, blue: ζ = π∕5.5, green ζ = π∕5, yellow: ζ = π∕3.5.

4 Summary and discussion

In summary, we have presented a new stability model for the temperature anisotropy instabilities that takes into account the effects of plasma components (counter-)streaming along the ambient magnetic field. Our predicted limits on nb ∕n and V D ∕V A, as well as the value of α for the fast solar wind at 0.3 AU, agree quite well with the observations (Marsch et al. 1982; Tu et al. 2004). The unstable regimes can be markedly changed in the presence of streams, and we have shown that the instability thresholds can shape the anisotropy limits observed in the low-beta regimes. Furthermore, the new instability thresholds can explain the limits of temperature anisotropy reported by the observations at different heliocentric distances. However, a good agreement with the observations requires the values ξ ≈ 0.18 and η ≈ 2.8 leading to the maximum value of the counterstreaming parameter P0 ≈ 1.15. Such high values of ξ and η are already very close to their observed upper limits (Marsch et al. 1982), but from this point of view, it is not surprising that they determine the upper instability limits. Once the counterstreams become strong enough, they induce plasma fluctuations that react back to reduce them (and the value of P). In the stable state, the counterstreaming parameter ranges from 10−5−10−1 (Chen et al. 2016). The counterstreams are therefore expected to play a crucial role in the relaxation of the solar wind kinetic anisotropies. It must be emphasized that the representation of the drift velocity in Eq. (9) is central to our model. As mentioned above, this dependence should be more involved and include temperature anisotropy. However, this issue must be first clarified by the observational analysis.

Acknowledgements

HF, RS, and ML acknowledge support by the Deutsche Forschungsgemeinschaft (Schl 201/35-1).

References

  1. Bale, S. D., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Breech, B., Cranmer, S. R., Matthaeus, W. H., Kasper, J. C., & Oughton, S. 2010, in 12th International Solar Wind Conference, eds. M. Maksimovic, K. Issautler, N. Meyer-Vernet, M. Moncuquet, & F. Pantellini, AIP Conf. Proc., 1216, 214 [NASA ADS] [CrossRef] [Google Scholar]
  3. Chen, C. H. K., Matteini, L., Schekochihin, A. A., et al. 2016, ApJ, 825, L26 [NASA ADS] [CrossRef] [Google Scholar]
  4. Feldman, W., Asbridge, J. R., Bame, S. J., Montgomery, M. D., & Gary, S. P. 1975, J. Geophys. Res., 80, 4181 [NASA ADS] [CrossRef] [Google Scholar]
  5. Goldstein, B. E., Neugebauer, M., Zhang, L. D., & Gary, S. P. 2000, Geophys. Res. Lett., 27, 53 [NASA ADS] [CrossRef] [Google Scholar]
  6. Hellinger, P., Trávníček, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ibscher, D., & Schlickeiser, R. 2013, Phys. Plasmas, 20, 042121 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ibscher, D., & Schlickeiser, R. 2014, Phys. Plasmas, 21, 022110 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ibscher, D., Lazar, M., Michno, M. J., & Schlikeiser, R. 2013, Phys. Plasmas, 20, 012103 [NASA ADS] [CrossRef] [Google Scholar]
  10. Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 1839 [NASA ADS] [CrossRef] [Google Scholar]
  11. Kasper, J. C., Lazarus, A. J., Steinberg, J. T., Ogilvie, K. W., & Szabo, S. 2006, J. Geophys. Res., 111, A03105 [NASA ADS] [CrossRef] [Google Scholar]
  12. Lazar, M., Fichtner, H., & Yoon, P. H. 2016, A&A, 589, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Lazar, M., Shaaban, S. M., Poedts, S., & Štverák, S.^ 2017, MNRAS, 464, 564 [NASA ADS] [CrossRef] [Google Scholar]
  14. Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., et al. 2005, J. Geophys. Res., 110, A09104 [NASA ADS] [Google Scholar]
  15. Marsch, E. 1991, in Physics of the Inner Heliosphere II, eds. R. Schwenn, & E. Marsch (Berlin: Springer-Verlag) [Google Scholar]
  16. Marsch, E. 2012, Space Sci. Rev., 172, 23 [NASA ADS] [CrossRef] [Google Scholar]
  17. Marsch, E., Mühlhäuser, K.-H., Schwenn, R., et al. 1982, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] [Google Scholar]
  18. Maruca, B. A. 2012, Doctoral dissertation (Harvard University) [Google Scholar]
  19. Maruca, B. A., Kasper, J. C., & Bale, S. D. 2011, Phys. Rev. Lett., 107, 201101 [NASA ADS] [CrossRef] [Google Scholar]
  20. Matteini, L., Landi, S., Hellinger, P., et al. 2007, Geophys. Res. Lett., 34, L20105 [NASA ADS] [CrossRef] [Google Scholar]
  21. Matthaeus, W. H., Oughton, S., Osman, K. T., et al. 2014, ApJ, 790, 155 [Google Scholar]
  22. Phillips, J. L., & Gosling, J. T. 1990, J. Geophys. Res., 95, 4217 [NASA ADS] [CrossRef] [Google Scholar]
  23. Schlickeiser, R., Michno, M. J., Ibscher, D., Lazar, M., & Skoda, T. 2011, Phys. Rev. Lett., 107, 201102 [NASA ADS] [CrossRef] [Google Scholar]
  24. Schlickeiser, R., & Yoon, P. H. 2014, Phys. Plasmas, 21, 072119 [NASA ADS] [CrossRef] [Google Scholar]
  25. Servidio, S., Osman, K. T., Valentini, F., et al. 2014, ApJ, 781, L27 [NASA ADS] [CrossRef] [Google Scholar]
  26. Stix, T. H. 1962, The Theory of Plasma Waves (New York: McGraw-Hill) [Google Scholar]
  27. Štverák S., Trávníček, P., Maksimovic, M., et al. 2008, J. Geophys. Res., 113, A03103 [Google Scholar]
  28. Tu, C.-Y., Marsch, E., & Qin, Z.-R. 2004, J. Geophys. Res., 109, A05101 [Google Scholar]
  29. Vafin, S., Schlickeiser, R., & Yoon, P. H. 2014, Phys. Plasmas, 21, 104504 [NASA ADS] [CrossRef] [Google Scholar]
  30. Vafin, S., Lazar, M., & Schlickeiser, R. 2015a, Phys. Plasmas, 22, 022129 [NASA ADS] [CrossRef] [Google Scholar]
  31. Vafin, S., Schlickeiser, R., & Yoon, P. H. 2015b, Phys. Plasmas, 22, 092131 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Instability conditions for the firehose and mirror instabilities, ζ=arcsin(1/3)$\zeta=\arcsin(1/\sqrt{3})$, β0 = 1, α = 0.3. Magenta: P0 = 0.001. Green: P0 = 1. Red: P0 = 1.45. Black: P0 = 1.51. Blue: P0 = 1.6. Unstable and stable regions are marked by the letters “u” and “s”, respectively.
In the text
thumbnail Fig. 2

Comparison between the analytical instability conditions (Eqs. (4) and (5)) and fast solar wind data (V SW > 600 km s−1; Matteini et al. 2007) from the Helios at 0.3 AU (top panel) and 0.9 AU (middle panel), and from Ulysses at 1.5–2.5 AU (bottom panel). Top panel: magenta: ζ = π∕13, red ζ =π∕10, blue: ζ = π∕7.5, green: ζ = π∕6, yellow: ζ = π∕4. Middle panel: magenta: ζ = π∕10, red ζ =π∕8, blue: ζ = π∕7, green: ζ = π∕6, yellow: ζ = π∕4. Bottom panel: magenta: ζ = π∕10, red ζ =π∕7, blue: ζ = π∕5, green: ζ = π∕4, yellow: ζ = π∕3.5.
In the text
thumbnail Fig. 3

Comparison between the analytical instability conditions (Eqs. (4) and (5)) and fast (V SW > 600 km s−1, top panel) and slow (V SW < 600 km s−1, bottom panel) solar wind data (Hellinger et al. 2006) from WIND/SWE (1995–2001). Top panel: magenta: ζ = π∕13, red: ζ = π∕7, blue: ζ = π∕5, green: ζ = π∕4, yellow: ζ = π∕3.5. Bottom panel: magenta: ζ = π∕10, red: ζ = π∕7, blue: ζ = π∕5.5, green ζ = π∕5, yellow: ζ = π∕3.5.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.