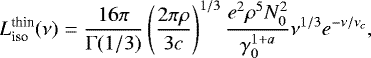| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731820 | |
| Published online | 01 June 2018 | |
Coherent curvature radiation and fast radio bursts
1
INAF - Osservatorio Astronomico di Brera,
Via Bianchi 46,
23807
Merate, Italy
e-mail: gabriele.ghisellini@brera.inaf.it
2
Università di Milano Bicocca, Dip. di Fisica G. Occhialini,
Piazza della Scienza 3,
20126
Milano, Italy
3
Università di Bologna,
Via Zamboni,
33,40126
Bologna, Italy
Received:
23
August
2017
Accepted:
12
February
2018
Fast radio bursts are extragalactic radio transient events lasting a few milliseconds with a ~Jy flux at ~1 GHz. We propose that these properties suggest a neutron star progenitor, and focus on coherent curvature radiation as the radiation mechanism. We study for which sets of parameters the emission can fulfil the observational constraints. Even if the emission is coherent, we find that self-absorption can limit the produced luminosities at low radio frequencies and that an efficient re-acceleration process is needed to balance the dramatic energy losses of the emitting particles. Self-absorption limits the luminosities at low radio frequency, while coherence favours steep optically thin spectra. Furthermore, the magnetic geometry must have a high degree of order to obtain coherent curvature emission. Particles emit photons along their velocity vectors, thereby greatly reducing the inverse Compton mechanism. In this case we predict that fast radio bursts emit most of their luminosities in the radio band and have no strong counterpart in any other frequency bands.
Key words: radiation mechanisms: non-thermal / masers / radio continuum: general
© ESO 2018
1 Introduction
Fast radio bursts (FRB) are ultrafast radio transients that are typically a millisecond in duration with a flux at the Jy level at ~1 GHz. Their extragalactic origin is suggested by the measured dispersion measure (DM) exceeding the Galactic value. Recently, FRB 121102 has been associated with a galaxy at a redshift z = 0.19, roughly confirming the distance estimated with the observed DM (Chatterjee et al. 2017; Tendulkar et al. 2017).
The extragalactic nature of FRBs implies luminosities around 1043 erg s−1 and energetics of the order of 1040 erg. The large flux, short duration, and cosmological distances also imply a huge brightness temperature of the order of TB ~ 1034–1037 K. This in turn requires a coherent radiation process.
Many models have already been proposed to explain the origin of FRBs1. Before the discovery of the host galaxy of FRB 121102 even the Galactic scenarios were believed to be feasible, although by a minority of the scientific community (e.g. Loeb et al. 2014; Maoz et al. 2015). Now this idea is disfavoured, but not completely discarded, since the repeating behaviour of this FRB remains unique. This makes the existence of two classes of FRBs still possible, which is analogous to the early times of gamma ray bursts and soft gamma ray repeaters.
Progenitor theories of extragalactic FRBs include the merging of compact objects (neutron stars: Totani 2013, white dwarfs: Kashiyama et al. 2013), flares from magnetars and soft γ-ray repeaters (Popov & Postnov 2010; Thornton et al. 2013; Lyubarsky 2014; Beloborodov 2017), giant pulses from pulsars (Cordes & Wasserman 2016), the collapse of supramassive neutron stars (Zhang 2014; Falcke & Rezzolla 2014), and dark matter induced collapse of neutron stars (Fuller & Ott 2015). There are even exotic ideas, such as FRBs explained by the propulsion of extragalactic sails by alien civilizations (Lingam & Loeb 2017) or the result of lightning in pulsars (Katz 2017).
A huge brightness temperature is probably the most important property of FRBs. There are two mechanisms that can result in coherence: the first is a maser and the second is bunches of particles contained in a region of a wavelength size, accelerated synchronously in such a way that their electric fields add up in phase. In this second case the produced radiation depends on the square of the number of particles in the bunch times the number of bunches. In the maser case, particles are not required to be contained in a small volume, since the radiation is produced by stimulated emission and is emitted in phase and in the same direction of the incoming photons by construction. There are two kinds of masers. The usual type uses different, discrete energy levels of which one is metastable. Free radiative transition from this level is somewhat inhibited, allowing stimulated emission to be effective. This means that a maser requires a population inversion (high energy levels more populated than low energy levels). The second type of maser is associated with free electrons with no discrete energy levels and there is no need for population inversion. This type of maser occurs when a photon hν can trigger stimulated emission with a greater probability than true absorption. This occurs rarely, but it does occur with some special configuration, such as when electrons of the same pitch angle and energy emit, by synchrotron, some photons outside the beaming cone of angle 1∕γ; that is theseelectrons emit at relatively large angles with respect to their instantaneous velocity (see e.g. Ghisellini & Svensson 1991).
In Ghisellini (2017) we investigated whether a synchrotron maser can be at the origin of observed radiation of FRBs. The result was that it is possible, but as long as the magnetic field is of the order of B ~10–100 G if the emitters are electrons, and B ~ 104–105 G if the emitting particles are protons. These relatively weak values of the magnetic field are required to produce radiation in the GHz radio band. These values of B are appropriate for main sequence stars (if the emitters are electrons) and white dwarf (if protons), which would make it difficult to explain large super-Eddington luminosities on a millisecond timescale. We therefore think that the proposed synchrotron maser would be a valid model if FRBs were Galactic (i.e. with a factor ~ 1012 less energy and luminosity), but it is less likely if all of these are extragalactic.
We (Locatelli & Ghisellini 2017, herafter LG17) then explored the possibility to have maser emission for the curvature radiation process, but we found that it is not possible. The reason is in the different energy dependence of the single particle emitted power P upon the particle energy γ: P ∝ γ2 for synchrotron and P ∝ γ4 for curvature radiation. We are thus back to the particle bunching possibility.
The fact that the phenomenon of FRB is observed in radio wavelengths with such a short duration suggests that the particles emit by a primary (non reprocessed) non-thermal process. The observed power (if extragalactic) suggests a compact object, such as a neutronstar or an accreting stellar black hole, at the origin of the energetics. The large luminosities and energetics imply that the number of emitting particles is very large. This in turn suggests that the FRB emission comes from the vicinity of the powerhouse responsible for the injection and acceleration of the emitting particles. The compactness of the object, the energetics, and the requirement of being close to the powerhouse suggest a strong value of the magnetic field. This in turnexcludes the synchrotron mechanism, which would produce frequencies that are too large. The other remaining possibility is curvature radiation from bunches of particles emitting coherently. In this prospective the roughly millisecond duration gives an even stronger limit on the size of the emitting region, which is required to be R < ct ~300 km. This strengthens the arguments in favour of a compact object as central engine.
The curvature radiation process has already been discussed by several authors, mainly to explain the origin of the pulses in pulsars, which also show huge TB, and shorter duration than in FRBs, but much lower luminosities. The most recent and complete work suggesting coherent curvature radiation to explain FRBs is Kumar et al. (2017, hereafter K17). They found a set of constraints limiting the geometry, density, and energy of the emitting particles in models that can successfully explain FRBs. Perhaps the most severe limitation they found is about the requirement on the magnetic field. It has to be equal or stronger than the critical magnetic field 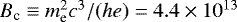 G to be comparable with the Poynting vector of the produced radiation. This suggests strongly magnetized neutron stars as progenitors.
G to be comparable with the Poynting vector of the produced radiation. This suggests strongly magnetized neutron stars as progenitors.
In this paper, following the study of K17, we consider what limits are posed by the process of self-absorption, finding solutions aiming to minimize the required total energy. Furthermore, we consider power law particle distributions as well as mono-energetic particle distributions, illustrating the effects that coherence has on the observable spectrum, both in the thick and thin part. Finally, we study the importance of inverse Compton radiation. We illustrate that in the highly ordered geometries, associated with curvature radiation in highly magnetized neutron stars, inverse Compton emission is severely limited. This agrees with the non-detection, so far, of FRBs in any other frequency band other than the radio (see Scholtz et al. 2017 and Zhang & Zhang 2017 for FRB 121102) This may imply that the FRB is mainly a radio phenomenon with no counterparts at other frequencies.
2 Set up of the model
First let us introduce the notation, that is
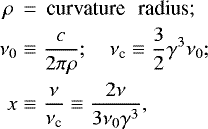 (1)
(1)
where ν0 would correspond to the fundamental frequency if the trajectory of the particle were a real circle of radius ρ. The observer sees radiation from the relativistic particles for a time (ρ∕c)∕γ of the trajectory and the Doppler effect shortens it by another factor ~ 1∕γ2. Thus the typical observed frequency νc is a factor γ3 higher than ν0.
The monochromatic power emitted by the single particle is written as (see e.g. Jackson 1999; LG17)
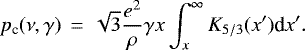 (2)
(2)
Usually, the monochromatic luminosity, which we denote L(ν), is the single electron power multiplied by the particle density at a given γ, integrated over all γ, and then multiplied by the volume. This assumes that particles emit incoherently and that they are distributed isotropically. In these conditions as well the emitted luminosity is isotropic.
For ordered magnetic geometry, we must take into account that the observed times are Doppler contracted for lines of sight along the particle velocity direction. Furthermore, the radiation is collimated.
If an observer located orthogonally to the motion measures a time Δ t⊥, the observer located within an angle 1∕γ along the velocity direction receives photons within a time Δt∥, that is
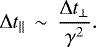 (3)
(3)
As discussed in K17, the volume of a bunch of particles observed to emit coherently may extend in the lateral dimensions (lateral with respectto the velocity direction, which coincides with the line of sight). On the other hand, extending the lateral dimensions too much requires to consider particles moving along magnetic field lines of different curvature radii, therefore emitting at other frequencies, possibly in a incoherent way. We assume that along the line of sight the coherence length is ρ∕γ, the same length for which the produced radiation reaches us. This size is along a single magnetic field line, perpendicular to the radial direction; radial here means with respect to the centre of the neutron star. Along the latter, we assume that the relevant size is the same, ρ∕γ. Perpendicular to this, along the longitudinal direction, the magnetic field lines could have the same curvature radius for an extension of the order of ρ, if there are indeed particles along the corresponding field lines. In general we parametrize this uncertainty defining the volume as
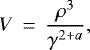 (4)
(4)
where a can be zero or one.
The observed emission is not isotropic, but it is beamed within a solid angle much smaller than 4π. The single particle emits mainly within ΔΩ ~ π∕γ2, but the general case, for an ensemble of particles, depends on the assumed geometry.
As said above for the volume, particles in the longitudinal size may indeed contribute to the coherent luminosity. If so, the corresponding solid angle is πρ2∕(γR2) ~ π∕γ. Here R is the distance from the centre of the neutron star. The other case corresponds to fewer lines occupied by the emitting particles. For simplicity, we assume in this case a solid angle πρ2∕(γ2R2) ~ π∕γ2. Again, we may parametrize the two cases assuming
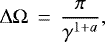 (5)
(5)
where a is the same parameter of Eq. (4), so that
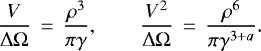 (6)
(6)
Coherent radiation depends on the square of the number of particles contained in the coherence volume2. Taking into account the Doppler contraction of times and the collimation of the radiation we have
![\begin{eqnarray*} L^{\textrm{thin}}_{\textrm{iso}}(\nu)\, &=&\, \int_{\gamma_1}^{\gamma_2} p(\nu,\gamma) \left[N(\gamma) V\right]^2 \frac{\mathrm{\Delta} t_{\mathrm \perp} }{ \mathrm{\Delta} t_{\mathrm \parallel} } \, \frac{4\pi }{ \mathrm{\Delta} \mathrm{\Omega}} \textrm{d}\gamma \nonumber \\ &=& \int_{\gamma_1}^{\gamma_2} 4\, p(\nu,\gamma) \frac{\rho^6}{\gamma^{1+\alpha} } N^2(\gamma) \textrm{d}\gamma.\end{eqnarray*}](/articles/aa/full_html/2018/05/aa31820-17/aa31820-17-eq8.png) (7)
(7)
2.1 Monoenergetic particle distribution
For a monoenergetic particle distribution we have
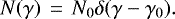 (8)
(8)
where we used the following approximation:
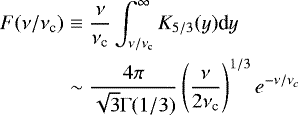 (10)
(10)
as in Ghisellini (2013), applied in that work for the synchrotron process, but also valid here.
2.2 Power law particle distribution
Assume now that the particles are distributed as a power law,
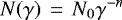 (11)
(11)
between γ1 and γ2. Eq. (7) with this particle distribution gives
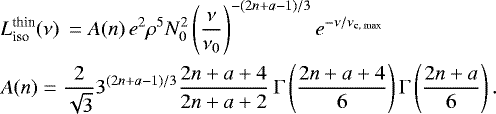 (12)
(12)
3 Absorption
The absorption could be coherent, but there is a very important difference: the absorption cross section and hence the absorption coefficient depends on the mass of the particle. Therefore even if particles absorb as the square of their number, as if they were a single charge Q = N(γ)e, their equivalent mass is M = N(γ)m, such that the absorption coefficient is α(ν) ∝ Q2∕M = (e2∕m)N(γ), as in the incoherent process (see e.g. Cocke & Pacholczyk 1975). Therefore the absorption optical depth is the same as in the incoherent process.
The elementary process of absorption of curvature radiation is appropriately described by the corresponding cross section, derived by Locatelli & Ghisellini (2017), as follows:
![\begin{eqnarray*} \sigma_{\nu} &=&\, \frac{1}{ 2 m \nu^2} \left(\frac{\textrm{d}\,p(\nu, \gamma)}{ \textrm{d}\gamma}\right) \nonumber\\ &=&\, \frac{1}{ 2\sqrt{3}}\, \frac{e^2\rho }{ \gamma^6 mc^2} \left[ K_{5/3}(x) -\frac{2}{ 3} \, \frac{ \int_x^{\infty} K_{5/3}(y) \textrm{d}y }{ x} \right].\end{eqnarray*}](/articles/aa/full_html/2018/05/aa31820-17/aa31820-17-eq14.png) (13)
(13)
For small arguments y of the Bessel function, Ka(y) → 2a−1Γ(a)y−a. Using this approximation up to y = 1 and setting Ka(y) = 0 above, we find that σν(γ) ∝ ν−1 at low frequencies
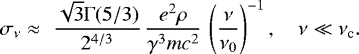 (14)
(14)
This also agrees with numerical results.
3.1 Absorption by a monoenergetic particle distribution
If the particle distribution is monoenergetic, N(γ) = N0δ(γ − γ0), the absorption optical depth for a layer of length ρ∕γ0 is
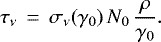 (15)
(15)
The self-absorption frequency νt is defined setting τν = 1. Using the low frequency approximation of Eq. (14) we have
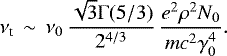 (16)
(16)
3.2 Absorption by a power law particle distribution
Using the N(γ) distribution of Eq. (11) and using a (γ-dependent) layer of length ρ∕γ we have
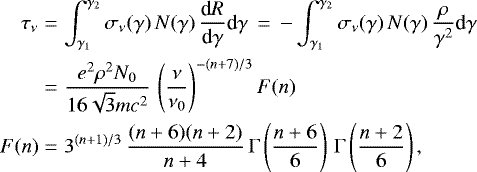 (17)
(17)
where dR∕dγ = −ρ∕γ2. We note that the choice of ρ∕γ as the appropriate length introduces an extra dependence on the observed frequency with respect to the choice of a fixed length. The self absorption frequency is
![\begin{equation*} \nu_{\textrm{t}} = \nu_0 \left[ \frac{e^2 \rho^2 N_0 }{ 16 \sqrt{3} mc^2}F(n) \right]^{\, 3/(n+7)} .\end{equation*}](/articles/aa/full_html/2018/05/aa31820-17/aa31820-17-eq19.png) (18)
(18)
4 SED of coherent curvature radiation
Rather generally, we can account for both the thin and thick part of the spectrum setting, that is
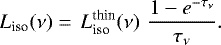 (19)
(19)
With this equation we can calculate the entire spectrum. The model parameters are
-
The curvature radius ρ. Since we are dealing with neutron stars, ρ is likely associated with (be a multiple of) the radius of the neutron star. The K17 work found a lower limit to the magnetic field that is able to guide the emitting particles, and found that the guiding magnetic field must be stronger than B = 1013 G. If true, this implies that the emitting particles are not too far from the surface of the neutron star. For illustration, we use ρ = 106 cm.
-
The particle density ~N0. This is to be found considering two limits: the first is the luminosity produced by the ensemble of the emitting particles in a coherent way; the second is that self-absorption can decrease the observed luminosity in a severe way.
-
The particle distribution, assumed to be a power law of index n or monoenergetic. We investigate both cases and for the slope n of the power law we preferentially use n = 2.5, but we show how the spectral energy distribution (SED) changes for different n. We consider that the coherent nature implies that the observed radiation, in the thin part, is proportional to the square of particle distribution, giving L(ν) ∝ ν−(2n+a−1)∕3 (Eq. (12)). For a given n, the observed spectrum is steeper with respect to the incoherent case.
-
The minimum and maximum particle energy, or equivalently, the corresponding Lorenz factors γmin and γmax. For simplicity, when treating the power law case, we assume γmin = 1. The high energy end of the particle distribution is not energetically important if L(ν) ∝ ν−α, where α > 1.
-
The collimation factor, parametrized by a in Eq. (5), associated with the choice of the emitting volume as in Eq. (4). We do not have arguments in favour or against either possibility, so we consider both cases.
-
The number of emitting leptons with respect to protons. Protons suffer less self-absorption, since τν ∝ m−1. This makes the solutions with emitting protons more economical. On the other hand, the regions close to the surface of a highly magnetized neutron stars are the kingdom of electron–positron pairs, that can greatly outnumber protons. In any case, we consider both cases.
4.1 Mononergetic particle distribution
Figure 1 shows how the SED changes by changing one parameter at a time in the case of a monoenergetic particle distribution. The reference values of the input parameters are indicated as ρ = 106 cm, N0 = 1015 cm−3, a = 1, and γmax = 103. For all the figures shown in this paper, we chose the ν − νLν representation. In this way we see in which band most of the luminosity is produced. The νLν luminosity is a proxy for the bolometric luminosity.
Changing particle density – The top panels shows the SED produced by protons (solid line) and leptons (dashed line) for different densities. We note that the absorption for leptons occurs at greater frequencies.
Changing ρ – The middle panel shows SEDs produced by different curvature radii ρ. The emission is stronger for greater ρ. In this case the emitting volume is larger, which more than compensates for the smaller acceleration.
Changing γmax – The bottom panel shows that for small values of γmax the emission is completely self-absorbed, and remains so for larger values of γmax for leptons than for protons. Once the optically thin regime is achieved, we observe the ν1∕3 slope.
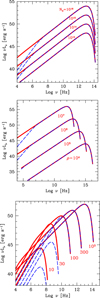 |
Fig. 1 Examples of SED produced by a monoenergetic particle distribution for changing input parameters. The reference values of the parameters are a = 1, ρ = 106 cm, N0 = 1015 cm−3, γmax = 103. The solid lines indicate SED produced by protons; the dashed line indicates SED produced by leptons. Top panel: the changing density N0 of the particles distribution is shown. Middle panel: the changing ρ is indicated. Bottom panel: the changing maximum electron energy γmax is shown. |
 |
Fig. 2 How the SED changes when changing the input parameters. The reference values of the parameters are a = 1, ρ = 106 cm, N0 = 1015 cm−3, n = 2.5, γmax = 103. The solid lines indicate SED produced by protons; the dashed line represents SED produced by leptons. Top left panel: the changing n is shown; contrary to the incoherent case, the self-absorbed spectrum also changes slope when changing n. Top right panel: the changing the density N0 of the particles distribution is shown. Bottom left panel: the changing the maximum electron energy γmax is indicated. Bottom right panel: the changing ρ is represented. |
4.2 Power law particle distribution
We show in Fig. 2 how the SED changes by changing one parameter at a time, keeping the others fixed. The reference values of the input parameters are ρ = 106 cm, N0 = 1015 cm−3, n = 2.5, a = 1, and γmax = 103.
Changing slope – The top left panel of Fig. 2 shows SEDs with different slopes n of the power law distribution of particles. The self-absorbed spectrum 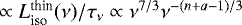 . The slope does depend on n, contrary to the incoherent case, for which the self-absorbed spectrum is ∝ ν2. Since the absorption coefficient is smaller for protons, the corresponding self-absorbed spectrum has a higher luminosity than for leptons, and the self-absorption frequency is smaller.
. The slope does depend on n, contrary to the incoherent case, for which the self-absorbed spectrum is ∝ ν2. Since the absorption coefficient is smaller for protons, the corresponding self-absorbed spectrum has a higher luminosity than for leptons, and the self-absorption frequency is smaller.
Changing particle density – The top right panel of Fig. 2 shows the SEDs for different density N0 of the power law distribution of particles. We note that the thick part of the spectrum ∝ N0, while the thin part 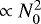 .
.
Changing γmax – The bottom left panel of Fig. 2 shows the SEDs for different γmax. For small γmax, the spectrum is entirely self-absorbed, peaking at the characteristic maximum frequency νc. Larger γmax allows the thin part of the SED to be visible, that is equal for protons and leptons.
Changing ρ – The bottom right panel of Fig. 2 shows the SEDs when changing ρ. We note that the maximum frequency ∝ ν0 ∝ ρ−1.
5 Application to fast radio bursts
We are looking for models that are able to reproduce the typical characteristic observed properties of FRBs, namely νLν~ 1043 erg s−1 at ν~1 GHz, and that are compatible in size with theobserved duration of ~1 ms. If these properties can be reproduced, then the model is automatically consistent with the observed brightness temperatures. Since the information about the slope of the radio spectrum is uncertain, we do not constrain it; this means that, in principle, we allow for both optically thin and optically thick cases. Another criterion we adopt is to look for models requiring the minimum amount of energy.
5.1 Illustrative examples
Table 1 reports the chosen values of the parameters. In general, the cases with a = 0 are more economical, since the optically thin luminosity depends on V 2∕ΔΩ ∝ γ−3−a (Eq. (6)). In these illustrative examples, the SED is always optically thin at 1 GHz and the slope α ≡(2n + a − 1)∕3 of L(ν) ∝ ν−α is α =5∕3 (a = 1) or α =4∕3 (a = 0). In the self-absorbed regime (τν ≫ 1), we have 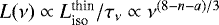 . As mentioned above, the slope of the self-absorbed part of the SED does depend on n. In our case, with n = 2.5, we have L(ν) ∝ ν11∕6 (if a = 0) or L(ν) ∝ ν3∕2 (if a = 1). Figure 3 shows two sets of models with a power law particle distribution with the same slope n =2.5 and different ρ. In Fig. 3 the vertical and horizontal lines correspond ν = 1 GHz and νLν = 1043 erg s−1.
. As mentioned above, the slope of the self-absorbed part of the SED does depend on n. In our case, with n = 2.5, we have L(ν) ∝ ν11∕6 (if a = 0) or L(ν) ∝ ν3∕2 (if a = 1). Figure 3 shows two sets of models with a power law particle distribution with the same slope n =2.5 and different ρ. In Fig. 3 the vertical and horizontal lines correspond ν = 1 GHz and νLν = 1043 erg s−1.
5.2 Suppression of the inverse Compton process
Usually, the importance of the inverse Compton process is measured by the Comptonization parameter y, defined as
 (20)
(20)
Compton up-scattering is important for y > 1. If particles are relativistic and the seed photons are isotropically distributed, we have y ~ τT⟨γ2⟩ when the scattering optical depth τT is smaller than unity. In our case of highly ordered geometry, both the average number of scatterings and the fractional energy gain of the scattered photons are largely reduced. In fact, the curvature radiation process produces photons moving along the same direction of the emitting particle: the typical angle between seed photons and particles is of the order of ψ = 1∕⟨γ⟩. Since the rate of scatterings is ∝ (1 − βcosψ) ~ (1 −⟨β2⟩), we have a reduction of a factor 1∕⟨γ2⟩ with respectto an isotropic case.
The frequency of the scattered photons ν1 depends upon the angles between the electron velocity and the photons before (ψ) and after (ψ1) the scattering. Both are measured in the observer frame. We have (see e.g. Ghisellini 2013)
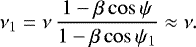 (21)
(21)
In the comoving frame, the pattern of the scattered radiation has a backwards–forwards symmetry, and this implies that in the observed frame, most of the scattered radiation in concentrated along the electron velocity vector, within an angle ψ1 ~ 1∕γ, independent of ψ. As a result, not only the scattering rate is largely reduced, but the scattered photons, on average, do not change their frequency.
Anotherpossible process is inverse Compton scattering with photons produced by the hot surface of the neutron star. For monoenergetic particles with Lorentz factor γ, the observed luminosity, accounting for collimation, is
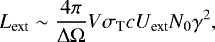 (22)
(22)
where N0 is the approximately the particle density and Uext is the radiation energy density produced externally to the scattering site. If the latter is close to the neutron stars surface of temperature T, Uext ~ aT4 In this case we have
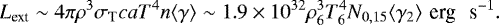 (23)
(23)
This luminosity should last the same time as the FRBs and should be observed at hν ~ 3γ2kT ~ 2 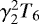 MeV.
MeV.
We conclude that it is very unlikely that the inverse Compton process plays a significant role in the proposed scenario. Therefore we expect that FRBs are weak or very weak emitters of X-rays or γ-rays.
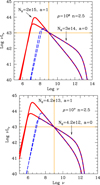 |
Fig. 3 Spectra, in the ν–νLν representation, produced by a power law distribution of particles accounting for a luminosity of 1043 erg s−1 at 1 GHz. The adopted slope is n = 2.5. The solid lines show spectra produced by protons; the dashed lines represent the spectra produced by leptons. The different slopes are due to the different a value, controlling the amount of collimation of the radiation, and not to a differentslope of the electron distribution. The top panel gives examples for ρ = 106 cm. The bottom panel shows examples for ρ = 107 cm. Parameters, listed in Table 1, were found to minimize the required total energy. N0 indicated in units of cm−3 and ρ in cm. |
6 Cooling timescales
In the absence of coherent effects, the frequency integrated power emitted by a single particle is
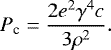 (24)
(24)
Instead, for coherent emission, the power emitted by the single particle depends on the square of the number of other particles emitting in the same volume V of the bunch. The cooling timescale can be calculated dividing the total energy of particles by the total power they emit as follows:
![\begin{eqnarray*} t_{\textrm{cool}} \,& =&\, \frac{ [V N(\gamma)] \gamma mc^2 }{ [V N(\gamma)]^2 P_{\textrm{c}} } =\, \frac{ \gamma mc^2}{ V N(\gamma) P_{\textrm{c}} } \, =\, \frac{ 3 \gamma^{n+a-1} mc^2 }{ 2e^2 N_0 \, \rho\, c } \nonumber \\ \, & =&\, 1.7\times 10^{-17} \, \frac{ \gamma^{n+a-1} }{ N_{0, 13}\, \rho_6 } \,\, \textrm{s} ,\end{eqnarray*}](/articles/aa/full_html/2018/05/aa31820-17/aa31820-17-eq30.png) (25)
(25)
where we have assumed m = me, N0 = 1015N0,15 cm−3 and ρ = 106ρ6 cm. For n > 1, tcool increases for larger γ: the radiative process is more efficient for lower energy particles. This strange behaviour occurs because (for positive n) there are fewer and fewer particles for increasing γ, and thus the power of coherent emission decreases. However, this is true for thin coherent emission. Low energy particles self-absorb the radiation they themselves produce, inhibiting their radiative cooling. In the absence of re-acceleration or injection of new particles, most of the radiation is then emitted at the self-absorption frequency (by electron of corresponding Lorentz factor γt), which must evolve (decrease) very quickly. The cooling time is therefore long for electron energies γ ≪ γt, has a minimum at γ ≳ γt and then increases again for γ ≫ γt.
The typical value of γ required to emit 1 GHz emission is 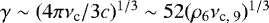 . At 1 GHz, for n = 3, N0 = 1013 cm−3 and a = 1, tcool ~ 2.4 × 10−12 s for any ρ. In this extremely short timescale the particle can travel for a mere 7 × 10−2 cm. This severe problem can be relaxed if fewer particles per bunch are needed to produce the observed luminosity, namely if the observed emission is produced bymany (M) bunches, each containing V N0∕M particles.
. At 1 GHz, for n = 3, N0 = 1013 cm−3 and a = 1, tcool ~ 2.4 × 10−12 s for any ρ. In this extremely short timescale the particle can travel for a mere 7 × 10−2 cm. This severe problem can be relaxed if fewer particles per bunch are needed to produce the observed luminosity, namely if the observed emission is produced bymany (M) bunches, each containing V N0∕M particles.
Alternatively, we should have an efficient acceleration mechanism that is able to balance the radiation losses. One possibility is an electric field parallel to the magnetic field. In this case, particles with γ ≪ γt increase their energy up to the point where radiative losses dominate. Particles would tend to accumulate at the energy where gains and losses balance. In this scenario (acceleration of low energy particles, no re-injection, and cooling) the emitting particle distribution would be quasi-monoenergetic.
Even if we can conceive some solutions, we consider the problem of these extremely short radiative cooling timescales very challenging. We not only require either many bunches or a re-acceleration mechanism, but we have still to explain why the typical duration of the observed pulses is ~1 ms: it cannot be associated with a typical radiative cooling timescale.
7 Discussion and conclusions
We studied the coherent curvature radiation process and its self-absorption process to find if a region of the parameter space exists that is allowed to reproduce the observed properties. To this aim, we were forced to consider a well-defined geometry with a high degree of order, located close to the surface of a neutron star, where it is more likely to find the required large densities of relativistic particles responsible for the coherent emission. Furthermore, we discussed the main properties of the SED predicted in this case, which is qualitatively different from the non-coherent case. Owing to Doppler time contraction (Eq. (3)) the size ρ∕γ visible to the observer corresponds to a time ρ∕(cγ3) and to an observed wavelength λc = c∕(γ3ν0). In other words, the observed wavelength is short, but particles are distributed in a much larger region and can still emit coherently.
We did not investigate the reasons for having such a short and powerful burst of energy in the vicinity of the neutron star. However, the involved energetics are not extreme for a neutron star. The isotropic equivalent observed energetic is Eiso ~ 1040 erg, which can be reduced by a factor 102 –103 if the emission is collimated. Giant flares from magnetars, by comparison, can reach energetics one million times larger (see e.g. Palmer et al. 2005 for SGR 1806–20). This implies that repetition is well possible from the energy point of view.
The findings and conclusions of our work can be summarized as follows:
-
Self-absorption of coherent curvature radiation is an important process towards constraining the allowed choices of the parameters, such as the curvature radius and the particle density. On the other hand, there is indeed a region of the parameter space in which the observed properties of FRBs can be reproduced.
-
The emitted SED is likely to be steep (i.e. α > 1, for F(ν) ∝ ν−α) above the self-absorption frequency. Because of the limited range of the allowed values of the parameters, it is likely that theemission is self-absorbed at frequencies below 1 GHz. This predicts that the observed radio spectrum at ~1 GHz, once scintillation is accounted for, is either close to its peak (i.e. α ~ 0) or steep (α > 1), at least when leptons dominate the emission.
-
Coherent curvature radiation is possible if the geometry of the magnetic field and the emitting region is well ordered. Curvature photons are produced along the same direction of the particle velocities, much depressing the possibility to scatter. Therefore the model predicts an absent or very weak inverse Compton emission at high energies.
-
This makes the ~GHz-millimeter band the preferred band where FRBs can be observed. The weakness of the produced emission at high (X and γ-ray) energies is a strong prediction of the model.
Acknowledgements
We thank the anonymous referee for her/his critical comments that helped improve the paper.
References
- Beloborodov, A. M. 2017, ApJ, 843, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Law, C. J., Wharton, R. S., et al. 2017, Nature, 541, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Cocke, W. J., & Pacholczyk, A. G., 1975, ApJ 195, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Wasserman, I. 2016, MNRAS, 457, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Rezzolla, L. 2014, A&A, 562, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, J., & Ott, C. D. 2015, MNRAS, 450, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G. 2013, Radiative Processes in High Energy Astrophysics, Lecture Notes in Physics, (Switzerland: Springer), 873 [Google Scholar]
- Ghisellini, G. 2017, MNRAS, 465, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Svensson, R. 1991, MNRAS, 252, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. D. 1999, Classical electrodynamics, 3rd edn., (Hoboken, NJ: John Wiley and Sons, Inc.) [Google Scholar]
- Kashiyama K., Ioka, K., & Meszaros, P. 2013, ApJ, 776, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. I. 2017, MNRAS, 469, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Lu, W., & Bhattacharya, M. 2017, MNRAS, 468, 2726 (K17) [NASA ADS] [CrossRef] [Google Scholar]
- Locatelli, N., & Ghisellini, G. 2017, A&A submitted, [arXiv:1708.06352] (LG17) [Google Scholar]
- Loeb, A., Shvartzvald, Y. & Maoz, D. 2014, MNRAS, 439, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Lingam, M., & Loeb, A. 2017, ApJ, 837, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. 2014, MNRAS, 442, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Loeb, A., & Shvartzvald, Y., et al. 2015, MNRAS, 454, 2183 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, D. M., Barthelmy, S., Gehrels, N., et al. 2005, Nature, 434, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, S. B.,& Postnov, K. A. 2010, in Proc. of the Conference held 15–18 Sep 2008 in Yerevan and Byurakan, Armenia, eds. H. A. Harutyunian, A. M. Mickaelian & Y. Terzian, (Yerevan: Publishing House of NAS RA), 129 [Google Scholar]
- Scholtz, P., Bogdanov, S., Hessels, J. W. T., et al. 2017, ApJ, 846, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Tendulkar, S. P., Bassa, C. G. Cordes, J. M., et al. 2017, ApJ, 834, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Totani, T. 2013, PASJ, 65, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2014, ApJ, 780, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. B., & Zhang, B. 2017, ApJ, 843, L13 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Examples of SED produced by a monoenergetic particle distribution for changing input parameters. The reference values of the parameters are a = 1, ρ = 106 cm, N0 = 1015 cm−3, γmax = 103. The solid lines indicate SED produced by protons; the dashed line indicates SED produced by leptons. Top panel: the changing density N0 of the particles distribution is shown. Middle panel: the changing ρ is indicated. Bottom panel: the changing maximum electron energy γmax is shown. |
| In the text | |
 |
Fig. 2 How the SED changes when changing the input parameters. The reference values of the parameters are a = 1, ρ = 106 cm, N0 = 1015 cm−3, n = 2.5, γmax = 103. The solid lines indicate SED produced by protons; the dashed line represents SED produced by leptons. Top left panel: the changing n is shown; contrary to the incoherent case, the self-absorbed spectrum also changes slope when changing n. Top right panel: the changing the density N0 of the particles distribution is shown. Bottom left panel: the changing the maximum electron energy γmax is indicated. Bottom right panel: the changing ρ is represented. |
| In the text | |
 |
Fig. 3 Spectra, in the ν–νLν representation, produced by a power law distribution of particles accounting for a luminosity of 1043 erg s−1 at 1 GHz. The adopted slope is n = 2.5. The solid lines show spectra produced by protons; the dashed lines represent the spectra produced by leptons. The different slopes are due to the different a value, controlling the amount of collimation of the radiation, and not to a differentslope of the electron distribution. The top panel gives examples for ρ = 106 cm. The bottom panel shows examples for ρ = 107 cm. Parameters, listed in Table 1, were found to minimize the required total energy. N0 indicated in units of cm−3 and ρ in cm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.