| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201730513 | |
| Published online | 15 May 2018 | |
Scattering linear polarization of late-type active stars
Kiepenheuer-Institute für Sonnenphysik,
Schöneckstr. 6,
79104
Freiburg, Germany
e-mail: yakobchuk@leibniz-kis.de, sveta@leibniz-kis.de
Received:
27
January
2017
Accepted:
29
December
2017
Context. Many active stars are covered in spots, much more so than the Sun, as indicated by spectroscopic and photometric observations. It has been predicted that star spots induce non-zero intrinsic linear polarization by breaking the visible stellar disk symmetry. Although small, this effect might be useful for star spot studies, and it is particularly significant for a future polarimetric atmosphere characterization of exoplanets orbiting active host stars.
Aims. Using models for a center-to-limb variation of the intensity and polarization in presence of continuum scattering and adopting a simplified two-temperature photosphere model, we aim to estimate the intrinsic linear polarization for late-type stars of different gravity, effective temperature, and spottedness.
Methods. We developed a code that simulates various spot configurations or uses arbitrary surface maps, performs numerical disk integration, and builds Stokes parameter phase curves for a star over a rotation period for a selected wavelength. It allows estimating minimum and maximum polarization values for a given set of stellar parameters and spot coverages.
Results. Based on assumptions about photosphere-to-spot temperature contrasts and spot size distributions, we calculate the linear polarization for late-type stars with Teff = 3500 K–6000 K, log g = 1.0–5.0, using the plane-parallel and spherical atmosphere models. Employing random spot surface distribution, we analyze the relation between spot coverage and polarization and determine the influence of different input parameters on results. Furthermore, we consider spot configurations with polar spots and active latitudes and longitudes.
Key words: starspots / stars: activity / polarization / stars: late-type / stars: individual: XX Tri
© ESO 2018
1 Introduction
Numerous studies on stellar activity have been performed in the past decades using spectroscopic Doppler imaging and photometric light curve inversion techniques (e.g., see reviews by Berdyugina 2005; Strassmeier 2009). Together with the prospects of using polarimetry to characterize exoplanet atmospheres (e.g., Seager et al. 2000; Berdyugina et al. 2008), this raises the interest in stellar polarimetry. The field is also favored by current instrumental progress because detecting stellar polarization often demands high accuracies of up to 10−5–10−6. In particular, two major surveys by Bailey et al. (2010) and Cotton et al. (2016) have been completed in recent years, totaling nearly 100 nearby bright stars measured with polarization sensitivities at the parts-per-million level. Most targets from the sample of Northern bright stars by Bailey et al. (2010) showed measurable linear polarization that was mainly of interstellar origin, however, and only for a few stars was the polarization deduced to be due to intrinsic polarigenic mechanisms. The subsequent study of Cotton et al. (2016) for Southern hemisphere stars found stronger polarizations in general, with an intrinsic mechanism identified for more than 20 stars.
Considering the different spectral types, evolutionary status, environment, rotation, and binarity, the intrinsic stellar polarization can be explained by different mechanisms. However, the main sources of polarization are usually related to either light scattering or magnetic fields. Scattering by free electrons or dust (in cooler environments) results in the polarization of stars or binaries that have circumstellar asymmetric envelopes (e.g., Brown & McLean 1977; Pfeiffer 1979), while the so-called magnetic intensification predicts the net linear polarization from optically thick spectral lines in strong magnetic fields (e.g., Leroy 1962; Mullan & Bell 1976). In addition to circumstellar scattering, Harrington (1969) proposed another mechanism: temperature variations in the photosphere that produce a disk asymmetry might also lead to the observable net scattering polarization.
Early observations by Dyck & Jennings (1971), who performed a UBV broadband polarimetric survey of 55 cool stars of K and M type, showed intrinsic polarization for late-type supergiants and no polarization for class III giants. When the survey was complemented with infrared (IR) photometry (Dyck et al. 1971b) and near-IR polarimetry (Dyck et al. 1971a), the polarization was associated with the optically thin circumstellar clouds of solid particles. Piirola (1977) and Tinbergen (1982) investigated the interstellar polarization in the solar neighborhood and concluded that any intrinsic polarization of the stars in the sample, if present, is close to the error limits, which precluded them from drawing further conclusions. However, they indicated that there is a tendency for higher polarizations to be mostly confined to the stars with spectral type F and later. Huovelin et al. (1985) reported five-color (UBV RI) polarimetric observations of 13 solar-type stars that showed a clear wavelength dependence. This decreased from ultraviolet to red, with time variations. The observed linear polarization was suggested to be at least partly intrinsic and was explained by either magnetic intensification or scattering in the presence of spot-induced disk asymmetry. Huovelin et al. (1989) described the magnetic intensification as the dominant effect in the linear polarization in the most active single late-type dwarfs (F7−K5), while based on the wavelength dependence, it might result from a combination of Rayleigh and Thompson scattering in less active dwarfs.
In the recent study by Cotton et al. (2016), most stars in the sample showed positive detections with polarizations of more than 10−5, with several classical Be stars exceeding 10−3. Significant intrinsic polarization was found in most B stars in the sample, and it was also apparent for a number of late-type giants. It was attributed mainly to circumstellar dust shells. However, in some cases, other explanations were used. For the dust-free M giant δ Oph, for instance, the variable and high-degree polarization was associated with Rayleigh scattering in the photosphere. Another recent studyby Cotton et al. (2017) focused on nearby FGK dwarfs, for which they measured the linear polarization of 32 active, inactive, and debris-disk host stars with the same high precision. It was found that active stars in the sample have a mean polarization of (23.0 ± 2.2) × 10−6 (after subtracting the interstellar polarization), with maximum levels ranging up to ~45 × 10−6. In their discussion of the mechanisms, the authors suggested the magnetic intensification as a most likely mechanism for active late-type dwarfs.
Binary stars reveal polarization that in most cases is produced by the same phenomena as in single stars, but it involves a more complex geometry and new asymmetries (see the review by Manset 2005). One particular class of non-eclipsing active binaries that are frequent in polarimetric studies is RS CVn-type close binaries, where one component is usually an active late-type evolved star and the second component is a faint unresolvable dwarf. Scaltriti et al. (1993) measured UBV RI linear and circular polarization in 15 RS CVn-type binaries, of which 6 systems showed evidence of circumbinary dust envelopes from the IR excess, 6 binaries did not show the excess, and the rest had uncertain detections. Later polarimetric observations of RS CVn systems reached similar conclusions, ascribing detected signals either to circumbinary envelopes or to the interstellar medium (e.g., Yudin & Evans 2002; Berdyugin et al. 2006; Pandey et al. 2009).
In this paper, we simulate the intrinsic linear polarization of late-type active stars that is due to spot-induced disk asymmetry. The simulations are based on the calculated data for the scattering polarization in continuum for plane-parallel and spherical stellar models. In Sect. 2 we describe the method we developed to generate spots of different size and surface distribution, and perform the disk integration to obtain the total Stokes parameters. In Sect. 3 we place constraints on the maximum polarization levels for different stellar models and present results for a random spot surface distribution. We analyze how our results depend on the inclination, wavelength, and photosphere-to-spot temperature contrast. In a few subsections, we consider the polarization signatures expected from polar spots and active latitudes and longitudes. Section 4 concludes the paper.
2 Method
2.1 Generating spots
We developed a code that generates different spot distributions by coordinates, size, and temperature to calculate light curves and Stokes parameter variations over a stellar rotation period. Previously obtained surface maps and Doppler-imaging temperature/filling factor maps can also be used as input. The stellar surface is represented by a uniform spherical grid over longitude and latitude. For our simulations we chose a 1° × 1° grid resolution, which gives optimal accuracy and short computation times. The main model ingredients were chosen as described below.
2.1.1 Temperatures
Different methods indicate a tendency for hotter stars to have more highly contrasting spots than cooler stars, which seemsto hold for active stars independent of their luminosity class (Berdyugina 2005). Based on available published data (which are still scarce and inhomogeneous), Andersen & Korhonen (2015; see the dashed blue line in Fig. 2) used a linear fit to describe the dependence between the effective temperature Teff of a star and the spot temperaturecontrast ΔT. We adopted it in our simulations to determine the temperature of spot umbrae as follows:
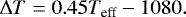 (1)
(1)
By setting the corresponding area and temperature ratios, we also added an option to include the penumbra for each spot. It was selectedin our calculations, with the temperature ratio for penumbrae set to the mid-point between the photosphere and the umbra.
2.1.2 Sizes
With the exception of the Sun, no information is available about the spot size distribution on other stars, not to mention its dependence on the activity and spectral type. Therefore, spot sizes in the program can be set either manually (along with the coordinates), uniformly random within the specified size range, or following normal or lognormal distribution.
In the first statistically significant study by Bogdan et al. (1988), which covered the period from 1917 to 1982, sunspot umbral areas were found to be distributed lognormally. Using parameters of the lognormal fit from this study, obtained for combined solar minimum and maximum, Solanki & Unruh (2004) extrapolated them to higher activity levels of solar-like stars, suggesting several scaling laws. Bogdan et al. (1988) gave the size distribution as
![\begin{equation*} \frac{\mathrm{d}N}{\mathrm{d}A} = \left( \frac{\mathrm{d}N}{\mathrm{d}A} \right)_{\mathrm{max}} \exp \left[ - \frac{(\ln A - \ln \langle A \rangle)^2}{2 \ln \sigma_A} \right],\end{equation*}](/articles/aa/full_html/2018/05/aa30513-17/aa30513-17-eq2.png) (2)
(2)
where ⟨A⟩ is the mean spot umbral area, and σA determines the width of the lognormal distribution. Bogdan et al. (1988) expressed the area and the width of the distribution in units of 10−6A1∕2⊙. Solanki & Unruh (2004) suggested that these parameters change with the total starspot area coverage as
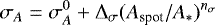 (3)
(3)
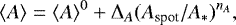 (4)
(4)
where Δσ and ΔA are coefficients determining the increase in the width and mean area of the spot size distribution with increasing activity, expressed as the ratio of the area occupied by spots to the total stellar surface area Aspot∕A*. Next, 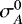 and
and 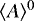 are parameter values in the limit of zero spot coverage. It is assumed that the dependence on the activity is a power law, with exponents nσ and nA. In practice, Δσ and ΔA and the zero-limit parameter values were determined by solving Eqs. (3) and (4) using the known spot coverage and the distribution width of the solar minimum and maximum from Bogdan et al. (1988) for a selected power nσ or nA.
are parameter values in the limit of zero spot coverage. It is assumed that the dependence on the activity is a power law, with exponents nσ and nA. In practice, Δσ and ΔA and the zero-limit parameter values were determined by solving Eqs. (3) and (4) using the known spot coverage and the distribution width of the solar minimum and maximum from Bogdan et al. (1988) for a selected power nσ or nA.
It should be noted that except for the paper by Solanki & Unruh (2004) for solar-like stars, no comprehensive studies have been devoted to spot size distributions in stars of different spectral type and activity (for low-mass stars, also see Jackson & Jeffries 2013). Current Doppler-imaging studies, which potentially approach the topic most directly, offer a resolution no better than several square degrees (e.g., Strassmeier 2009; Kochukhov 2016), which is not sufficient for meaningful size distribution constraints. Although Doppler maps of many stars reveal large active areas, it is therefore not possible to distinguish whether they are homogeneous structures or agglomerates of many smaller spots.
Because Solanki & Unruh (2004) only extrapolated their size distributions for solar-like stars, additional assumptions were needed for other late-type stars. By simply using the scaling laws with solar values for other stars, we obtain overly small spots for giants and too large spots for dwarfs, both of which seems improbable. We finally adopted the scaling relations (3) and (4), but instead of absolute solar spot sizes, we chose relative angular sizes with the same parameter values, but in stellar surface area units of 10−6 A1∕2*.
Using the scaling law in Eq. (3) for σA, we assumed that the other parameter, ⟨A⟩, was fixed at 0.57 × 10−6A1∕2* (i.e., equal to the solar value at R* = 1 R⊙ from Bogdan et al. 1988). Accordingly, when scaling ⟨A⟩ with Eq. (4), the distribution width, σA, remained constant and equal to 4 × 10−6A1∕2*. Owing to the ambiguity of the results from varying two parameters simultaneously, Solanki & Unruh (2004) refrained from considering these extrapolations in detail. Below we present the results we obtained using scalings for σA and ⟨A⟩ for selected nσ and nA exponents in the range between 0.5 (square-root law) to 1.0 (linear), following the prescriptions of Solanki & Unruh (2004).
Finally, the starspots in our study were assumed to have circular shape and to consist of umbral and penumbral regions with areas ratios 1:4. Similarly to Solanki & Unruh (2004), the area in Eq. (2) also corresponded to the umbral area, while for the totalspot coverage in Eqs. (3) and (4), we integrated the stellar surface grid by pixels including both umbral and penumbral parts.
2.1.3 Coordinates
We added several options for how spots could be distributed on the stellar surface. Along with the manually set coordinates, this includes random distribution, active latitudes and longitudes, and polar spot generation. The simulation for a random spot distribution implies that the spots are distributed uniformly randomly in longitude, ϕ, and in sine of latitude, sin(θ), to produce an equal probability across the stellar surface. We avoided overlapping of generated spots: before we placed each spot, we iteratively checked for overlaps with umbral regions of previously added spots on the surface map and then relocated when necessary (1000 iterations at most).
Additionally, we assumed that spots do not evolve in time in size and position, and there is no differential stellar rotation, although this can be readily implemented in the code.
2.2 Integrating the disk
Our calculations are based on the previously developed code for exoplanet transit polarization simulations (Kostogryz et al. 2015), and it employs two-dimensional grid integration. Here we chose a uniform Cartesian grid representing the sky plane, integrating over only those grid pixels whose centers are inside the stellar disk. We tried different binning as well as a more advanced polar grid integration that accounted for partially divided pixels (this includes both spot and photosphere-projected stellar surface elements) to test the reliability of the method. The uniform grid was found to be sufficiently accurate for resolutions after a certain level and did not show any noticeable artifacts related to the pixelation of the limb. Similarly, we found that partially divided pixels do not need special consideration. A grid of 1000 × 1000 pixels size was chosen, which is both fast and accurate enough for the required polarization levels.
During integration, we transformed the coordinates of each grid pixel into the spherical coordinate system of the star, finding the corresponding longitude/latitude and the temperature (or the filling factor), according to a given stellar rotation axis orientation and phase angle. The total Stokes parameters at each rotation phase were calculated by summing all grid pixels of the visible stellar disk as follows:
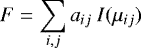 (5)
(5)
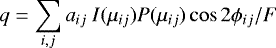 (6)
(6)
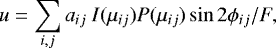 (7)
(7)
where a is the area of the i, j pixel (constant for a regular grid), μ is the anglebetween the surface normal and the line of sight to the observer, ϕ is the polar angle of a system with the origin at the disk center, F is the total stellar flux, and q and u are normalized Stokes parameters. We note that the relative flux is normalized to the total flux of an unspotted photosphere in our analysis. The center-to-limb variations ofintensity I(μij) and polarization P(μij) were found through trilinear interpolation using the look-up tables from Kostogryz & Berdyugina (2015) and Kostogryz et al. (2016), according to the selected wavelength, surface gravity, and temperature of a star. Kostogryz & Berdyugina (2015) calculated the tables for continuum spectra of FGK stars (Teff = 4500 K–6900 K, log g = 2.0–5.0, and wavelength range 4000–7000 Å) for the Phoenix grid of plane-parallel models, and in Kostogryz et al. (2016) similar calculations were made for a wider range of models (Teff = 4000 K–7000 K and log g = 1.0–5.5) assuming a spherical stellar atmosphere. In addition, we used unpublished data on intensity and polarization variations for both plane-parallel and spherical cooler models with temperatures down to 3000 K, obtained with the same code by Kostogryz (2016, priv. comm.). It should be noted that these data for cooler stars do not include atomic and molecular absorption lines, which can lead to overestimated polarization values, especially for blue wavelengths and for dwarfs with higher surface gravities (depending on the selected wavelength). Evidently, a proper spectrum synthesis code is needed to calculate the intrinsic polarization for these cases. However, the depolarizing effect from absorption lines may not be very significant because when the absorption line suppresses the polarization, the intensity is also reduced. In turn, this will affect the normalized polarization parameters that we calculate less strongly. Additionally, coherent scattering processes, especially in molecular bands, as seen on the Sun (e.g., Berdyugina et al. 2002) probably increase polarization further, which counteracts the effect of the absorption lines.
3 Results
3.1 Constraining the upper polarization limits
According to the definition of the Stokes Q and U parameters, for any arbitrarily spotted disk, a direction exists in which Q takes its maximum value and U is zero. Thus, the problem of determining the highest possible polarization degree for a given star can be reduced to the problem of determining the highest normalized Q∕I. Since the Stokes Q is proportional to the cosine of the double angle, the stellar disk is divided into four Q quadrants of opposite sign that cancel each other out. Every point at a distance μ from the disk center has seven counterpart points in the other octants that can take the same Q and I absolute values. In the two-temperature model, the highest total polarization from the combination of these eight points is obtained when 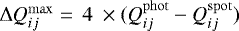 , with the total flux being
, with the total flux being 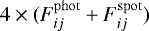 . Searching for the normalized polarization degree, that is, for the ratio of the total polarized flux to the total flux from a star, we began by calculating the minimum total flux
. Searching for the normalized polarization degree, that is, for the ratio of the total polarized flux to the total flux from a star, we began by calculating the minimum total flux 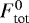 , which corresponds to the fully spotteddisk with zero Qtot. Next, we searched for the sky plane grid pixels in succession that would give the maximum
, which corresponds to the fully spotteddisk with zero Qtot. Next, we searched for the sky plane grid pixels in succession that would give the maximum 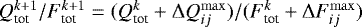 , where
, where 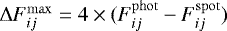 . In parallel, the following condition was checked:
. In parallel, the following condition was checked: 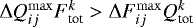 . When the right part exceeded the left, the remaining grid pixels were considered as occupied by spots, meaning that their contribution to the total polarization due to a lower flux exceeded the
. When the right part exceeded the left, the remaining grid pixels were considered as occupied by spots, meaning that their contribution to the total polarization due to a lower flux exceeded the 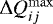 contribution.
contribution.
Figure 1 shows the highest polarization degree that can be reached by different types of stars assuming the spot temperature contrasts from Andersen & Korhonen (2015) for selected wavelengths corresponding to the effective midpoints of B, V, and I broadband filters. The solid lines mark the results obtained with spherical atmosphere models, and the dashed lines show the plane-parallel models. We note that spherical models include lower gravity log g = 1, which is not available for the plane-parallel model data. The two model sets match well for higher gravities and stars in the lower and upper effective temperature ranges. In general, the curves for the plane-parallel models appear to be less sensitive to the temperature, especially for lower log g, while the spherical models show a noticeable depression in between 4500 K and 5500 K that grows at lower wavelengths. This feature is discussed in detail in Kostogryz et al. (2017), who considered the differences between plane-parallel and spherical models of a host star atmosphere for exoplanet transit polarimetry. Similarly, the transit polarization for spherical atmospheres in this temperature range was also found to be lower than for plane-parallel atmospheres. This is explained by the noticeable temperature differences between atmospheric layers in the input plane-parallel and spherical models, which affect the calculated center-to-limb intensity and polarization profiles. Specifically, spherical models are systematically cooler than the plane-parallel models by up to 500 K at Teff = 5000 K (see Fig.4 in Kostogryz et al. 2017), and this temperature difference diminishes rapidly toward higher Teff, similarly to what is observed in Fig. 1.
In Fig. 2 we show several examples of disk asymmetries that result in the highest linear polarization for the selected active stars. They show that the highest polarization is obtained when most of a star is covered by spots, with the quiet photosphereconfined to narrow segments at the top and bottom in Fig. 2. For other stellar models we found similar visible disk appearances with an intermediate ratio of spots and quiet photosphere. Evidently, these asymmetries are not to be observed, and the expected scattering polarization levels due to the spots are probably significantly lower than the derived upper limits.
 |
Fig. 1 Highest polarization degree as a function of effective temperature for different types of stars in selected wavelengths using plane-parallel (dashed) and spherical (solid) model atmospheres. |
 |
Fig. 2 Spotted area distribution on a stellar disk resulting in the highest polarization for two models at λ = 4450 Å: (a) Teff = 3500 K, Tspot = 3000 K, and log g = 2.0, and (b) Teff = 5100 K, Tspot = 3875 K, and log g = 2.0. The spotted area is shown with the darker color. For other stellar models, the highest possible polarizations are obtained at intermediate spot coverage with similar disk appearances, in which photosphere regions at the top and bottom vary between the two cases. |
3.2 Spot coverage dependency
Using the scaling relations (3) and (4) for a lognormal size distribution and a random surface spot configuration, we next checked how the polarization depends on the total spot coverage for different types of stars. As mentioned above, the coverage was calculated as a fraction of the spherical grid elements occupied by umbral and penumbral regions, as in Solanki & Unruh (2004). According to this definition, the polarization will not fully cancel out and become zero for a 100% spotted star because of the remaining umbra-penumbra inhomogeneities. It can be noted that for a given size distribution and total coverage, the random surface distribution statistically gives a lower limit polarization constraint, and any systematic deviations from it will increase the disk asymmetry and the net polarization.
Solanki & Unruh (2004) suggested that reasonable choices of the exponents nA and nσ in the scaling relations of Eqs. (3) and (4) lie within the range of 0.5 to 1.0. Figure 3 illustrates how the choice of the scaling law for the average spot size affects the polarization levels. The difference between linear and square-root laws is significant; it amounts to almost a factor of 3 for the amplitude and the maximum polarization degree per rotation period. Our tests for nσ showed a similar tendency with an even greater discrepancy.
To analyze the connection between the polarization and the total spot coverage, we selected several model stars with different gravities and temperatures. The spot temperature contrast for each model was found from Eq. (1), and the stellar rotation axis was directed parallel to the sky plane, meaning that it had an inclination of 90° (see the next subsection for the effect of inclination). Accounting for the large polarization scatter obtained using different initial random seeds, we ran 100 iterations for each spot coverage and then averaged the results. In Fig. 4 we plot the maximum polarization degree against the total spot coverage for three model stars: 1) a K5V dwarf with Teff = 4300 K, Tspot = 3450 K, and log g = 4.5, 2) a K1IV subdwarf with Teff = 5100 K, Tspot = 3875 K, and log g = 3.0, and 3) an M2III giant with Teff = 3500 K, Tspot = 3000 K, and log g = 1.5. In addition to considerable scatter, there is a large difference between the lower and upper curves that is on the order of one magnitude. We conclude from Figs. 3 and 4 that the greater the width of distribution σA and average size ⟨A⟩, the more inhomogeneous the produced surface maps, and consequently, the greater the disk asymmetries and the higher the total polarization. We also found that the average polarization degree values per rotation period correlate with the maximum values, being in general twice as low, with a small scatter between 1.8 and 2.2. Forselected model stars, the corresponding upper limit constraints from the previous section are ~10–100 times higherthan the maximum polarization degrees per rotation period, depending on the scaling law used.
No data are available on the ratio of umbra-to-penumbra area for other stars, and it is questionable whether the solar value we adopted here is universal and does not vary between different stellar types. To check the influence of this parameter on our results, we therefore ran several tests using the same parameters and scalings, but generating spots without penumbra. As a result, we found very similar correlations for polarization and spot coverage, within the scatter shown in Fig. 4. This implies that the umbra-to-penumbra ratio plays a less important role in defining polarization levels than the other parameters, such as size or surface distributions.
For a total spot coverage of 30%, the maximum polarization degree per rotation period versus effective temperature for the stars with different surface gravity, using spherical atmosphere models, is shown in Fig. 5. For each model, 50 random spot configurations were simulated, and the results were averaged. We used the scaling relation for the average spot area with nA equal to 0.5, which gives a lower polarization (as seen in Fig. 1). We also checked the scaling for the distribution width with nσ = 1, and it gives identical results over the whole temperature range, but higher by a factor of 1.5. While tests with nA = 0.5 showed very small scatter with standard deviations of about 0.5%, for nσ = 1 the scatter was significantly larger, amounting to nearly 25%.
Assuming that the selected two-temperature model, the photosphere-to-spot temperature contrasts, and the spots size distributions are reasonable, the relations shown in Figs. 4 and 5 present lower estimates of the linear scattering polarization for a given set of stellar models. In the following we analyze how the different input parameters influence our simulations.
 |
Fig. 3 Relative flux and polarization degree phase curves for a model M2IV star with Teff = 3500 K, Tspot = 3000 K, and log g = 3.0 at λ = 4450 Å for one total spot coverage of 30%, but different average spot sizes ⟨A⟩ (1.63 and 9.38 [ × 10−6A1∕2*]), calculated using nA = 0.5 (top) and 1.0 (bottom). |
 |
Fig. 4 Maximum polarization degree per rotation period for three stellar models versus total spot coverage for λ = 4450 Å. We show results for two scaling laws for distribution width σA (in blue) andaverage spot size ⟨A⟩ (in red). The solid lines correspond to the linear scaling law, and the dash-dotted lines show the square-root law. |
 |
Fig. 5 Maximum polarization degree per rotation period for model stars with a spherical atmosphere, simulated for 30% spot coverage and a lognormal spot size distribution with a square-root scaling of the average spot area. |
 |
Fig. 6 Polarization degree amplitude (top) and average (bottom) values per rotation period for different axis inclination angles at λ = 4450, (normalized to 90°). Models are the same as in Fig. 4. For each model, different spot coverages were tested, using two scalings for σA with nσ, equal to 0.5 (dash-dotted line) and 1.0 (dashed line). The average curve from all simulations is shown as the black solid line. |
3.3 Inclination effect
Since our present model does not include spot evolution, the Stokes parameters Q and U for a star that is seen pole-on will vary harmonically during the rotation period, producing a constant polarization degree. Obviously, changing the inclination angle of the rotation axis from 0° (pole-on) to 90° will result in an increase of the polarization degree amplitude. We selected the same stellar models as in the previous section and generated 100 random spot configurations per spot coverage for each model, which ranged from10% to 90% with a step of 10%, scaling the width parameter of the spot size distribution using nσ = 0.5 and 1.0. Each simulated spot configuration was used to calculate the polarization at all inclination angles, the results were normalized to i = 90° and then averaged over 100 iterations. Analyzing the data, we did not find any dependency on the total spot coverage and averaged results over this parameter. Figure 6 shows the normalized polarization degree amplitude and its average overthe rotation period versus the inclination of the rotation axis for the selected stellar models, using two scaling laws. The gradual increase in average polarization toward lower inclination angles is likely to result from the insufficient statistics and is not a real feature, because the same curves as obtained using the median average showed the decrease. When we analyzed the other dependencies, the K1IV model showed a noticeable deviation from M2III and K5V, also for different scalings. In general, the average polarization degree amplitude increases with the inclination of the rotation axis, rising more rapidly at smaller inclinations and not changing significantly after i > 40°.
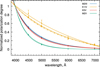 |
Fig. 7 Average polarization degree per rotation period at different wavelengths, normalized to λ = 4000. For each stellar model the overlying curves are the power-law best fit obtained for 10% total spot coverage, while the underlying curves are for 50% coverage. For K1IV, the results for two different size distributions are shown (see text). |
3.4 Wavelength dependence
To determine the wavelength dependence of the polarization, we used two spot size distributions that resulted in lower and upper polarization estimates for the stellar models in Fig. 4, scaling the average spot size using nA = 0.5 and the width of the distribution with nσ = 1.0. Theywere used to generate surface maps with total spot coverages of 10% and 50%. Similarly to the inclination above, each simulated spot configuration was run through all selected wavelengths. We performed 50 iterations per parameter set and stellar model. The results were averaged and normalized to the wavelength of 4000. In Fig. 7 we show the dependencies for four different stellar models. Although Rayleigh scattering is the dominating process for the intrinsic polarization in most late-type stars, it is evident that the wavelength dependencies show significant deviations from the λ−4 law, even though the input intrinsic polarizations for the quiet photosphere and spots separately generally follow it. This is explained by the complex interplay of both limb-darkening and polarization wavelength dependence for a given temperature of spots and photosphere, when the total normalized Stokes parameters are calculated. Fits using the power-law function for our entire model set resulted in a wide range of exponents nλ between −2 and −10. We found that steeper curves are more characteristic for cooler stars with a higher surface gravity. Tests also showed a minor dependence on the selected size distribution and total spot coverage. Figure 7 shows that curves for 10% and 50% spot coverage nearly coincide for the K5V, M2III, and M2V models. On the other hand, tests for the hotter K1IV model showed a higher degree of scattering for the different iterations and a stronger dependency on spot sizes and total coverage. To understand this, the following approximated ratio of polarization degrees p at different wavelengths and distance μ from the disk center can be considered:
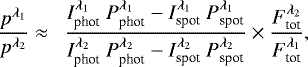 (8)
(8)
where P and I are functions of μ, as in Eqs. (5)–(7), and Ftot is the total stellar flux, assuming no spots. We found that the ratio is almost independent of μ for the K5V, M2III, and M2V models, and it is close to values in Fig. 7. This can explain the convergence of results for these stellar models for different spot sizes and coverage. On the other hand, for the K1IV model, the ratio was found to vary significantly with μ, which is visible in the wider variations in Fig. 7.
 |
Fig. 8 Average polarization degree per rotation period versus spot temperature contrast (normalized to the contrasts in Andersen & Korhonen 2015). For each stellar model, the dash-dotted lines show the 10% total spot coverage, and the solid lines show 50% coverage. |
3.5 Spot temperature contrast
Accounting for a small number of available measurements of spot temperatures for different active stars, the Andersen & Korhonen (2015) linear fit that relates the spot contrast to the effective temperature can be used only as a first approximation because the real dependence is probably more complex and depends on more parameters. We performed additional tests to verify how this parameter affects our simulations. Like in previous subsections, the tests were made for several total spot coverages (scaling the width of the size distribution using nσ = 1.0) with multiple runs averaged and normalized to values from Eq. (1). Figure 8 illustrates the average polarization degree per rotation period versus the relative spot temperature contrast for five different stellar models. All models showed a certain dependency on the total spot coverage and the choice of the spot size distribution. As expected, the polarization grows with the spot temperature contrast, with the average degree higher by 1.2 times to 4 times in Fig. 8 when the contrast is increased by a factor of 1.75. Similar reverse trends are observed when the temperature contrast is decreased by a factor of 4. In general, depending on selected stellar model, knowing the spot temperature is important for linear polarization simulations.
3.6 Active latitudes
As shown previously, there is a large scatter of polarization estimates for random spot configurations. However, it can be shown that introducing any deviation from a random surface distribution for a fixed total spot coverage is expected to systematically increase the polarization degree. Similarly to the Sun, where the sunspot occurrence is confined to certain latitudes, we performed simulations for starspots by selecting a Gaussian surface distribution with different width over latitude in both hemispheres. Figure 9 shows our results of modeling active latitudes at ±40°, with the width equal to ±10° for a K1IV star with 10% total spot coverage. One common feature that is also found below for a polar spot configuration is the upward shift observed in the Stokes Q phase curve, which increases the average polarization degree as well. For a given orientation in the sky plane, this can be explained schematically: breaking the axisymmetry between the left and right parts of the disk results in residual total Stokes U, while changing the axisymmetry between top right and bottom left parts affects Stokes Q, as seen in this case. The Stokes parameters are always defined in the instrumental system, therefore a comparison of our simulations and observations requires knowing the stellar rotation axis orientation, which is rarely known. However, with sufficient sensitivity, polarimetry is also a technique that may allow determining the rotation axis orientation (e.g., from continuous phase curves of recurring spots). That said, the degree of polarization depends on the rotation axis inclination angle alone, being invariant to the orientation of axis projection in the sky plane.
It is worth noting that only varying the width of the Gaussian distribution over latitude for a fixed spot configuration can retain the amplitudes of polarization parameters nearly unchanged. However, depending on the inclination of the rotation axis combined with the location of active latitudes, the phase curves can change significantly, which complicates the analysis.
3.7 Polar spots
Essentially, we found the same peculiarities in simulating polar spots as in active latitudes: a shift in the Stokes parameters and an offset in the degree of the polarization phase curves. Since the inclination angles of the rotation axis of known active stars usually constitute 50–60 degrees or more, high-latitude and polar spots can be seen closer to the limb than the lower active latitude spots, producing higher linear polarization. In addition, reported large high-latitude spots, particularly in RS CVn systems, areoften long-lasting phenomena (e.g., Xiang et al. 2015; Künstler et al. 2015; Kővári et al. 2015, 2016), which makes them suitable targets for limb-polarization effect detection, as discussed on the example of XX Tri below.
XX Triangulum
Polar and high-latitude spots have been reported for many stars, based mainly on Doppler imaging (e.g., Table 2 in Strassmeier 2009), and more recently also from interferometric observations, particularly for λ And (Parks et al. 2015) and ζ And (Roettenbacher et al. 2016). The spot sizes range from 0.1% to more than 10% of the stellar surface. To estimate the linear polarization expected due to the disk asymmetry, we selected the very active close RS CVn binary XX Tri (HD 12545), the bright component of which is a spotted red giant of K0III spectral type. It is one of the record holders in terms of the spot coverage, and is particularly known to have a polar superspot comprising about 10% of the whole stellar surface, as shown by Strassmeier (1999) from Doppler imaging. In the later study by Künstler et al. (2015), conducted in a time span of six years with the same technique, but using a different inversion code, the large high-latitude spots were confirmed and their formation, merging, and decay were analyzed.
Taking the properties of XX Tri as listed in Künstler et al. (2015), we simulated the polar active region of the star with our code to estimate the linear polarization for it. The active region was simulated as consisting of smaller spots using the scaling law with nA = 1.0 and setting a Gaussian surface distribution centered on the latitude of 70° (see Fig. 10). We adopted a total spot coverage from 5% to 15% and varied the Gaussian width from 10° to 20°, and found the resulting average polarization degree to lie between 3 × 10−5 and 6 × 10−5 with an amplitude range of 1.2−1.8 × 10−5 (the lower values were found for larger standard deviation). Identical results are obtained when a single large spot of the same size is added. Apparently, a polarization of this degree can be measured even with modern polarimeters such as DIPOL-2 (Piirola et al. 2014), POLISH2 (Wiktorowicz & Nofi 2015), and HIPPI (Bailey et al. 2015), which makes XX Tri a reasonable target for the limb-polarization effect detection.
 |
Fig. 9 Relative flux, normalized Stokes Q and U parameters, and polarization degree, simulated for a K1IV star with active latitudes at ±40° and a total spot coverage of 10% (solid lines). The same results for a random surface spot distribution are shown with dashed lines. |
 |
Fig. 10 Same as in Fig. 9, simulated for XX Tri with a polar spot configuration and a total spot coverage of 8%. |
3.8 Active longitudes
Active longitudes are a persistent surface feature that was reported for many chromospherically active stars (Jetsu et al. 1993; Berdyugina & Tuominen 1998; Korhonen et al. 2001), including the Sun (Berdyugina & Usoskin 2003). The majority of such stars are components of RS CVn binaries or belong to single rapidly rotating variables of FK Com and BY Dra type (Berdyugina 2005; Korhonen & Järvinen 2007). Two long-lived active longitudes are often observed, separated by ~180°, one showing a higher level of spot activity than the other. The phenomenon of the switching between active longitudes is known as flip-flop. For many stars, the flip-flop cycles of periods in the range of a few years up to a decade have been revealed (Berdyugina 2005; Berdyugina & Henry 2007; Korhonen & Järvinen 2007). While being observationally well grounded, further theoretical studies are needed to explain active longitudes and related flip-flop cycles (e.g., Elstner & Korhonen 2005; Berdyugina et al. 2006).
In the framework of our modeling, we considered active longitudes in a simple manner, for instance, excluding time evolution and differential stellar rotation. To investigate characteristic polarization variation curves, we chose a model K1III giant (Teff = 5100 K, Tspot = 3885 K, log g = 2.5), which is common among the reported objects. The active regions were placed on the opposite hemispheres at 45° latitude and simulated with the same parameters as for the XX Tri polar region above. Simulations were performed using different activity level ratios between the two longitudes: 0.0 (only one active region), 0.05, 0.25, and 1.0 (equal-size regions). The total spot coverage was fixed to 7% for all cases. The calculation results are shown in Fig. 11. Evidently, switching the dominant activity to the second longitude shifts the polarization curves by 0.5 in phase. In general, the curves for equally active longitudes revealed smaller amplitudes with four similar peaks than the double-peaked more varied phase curves for one active longitude. The results can also vary noticeably, depending on the inclination and the latitudes of the active regions. At the same time, substituting the regions generated using a lognormal spot size distribution with single spots of approximately the same size was found to affect the curves not and only resulted in slightly higher and narrower sinusoidal peaks.
4 Conclusions
We have theoretically investigated the scattering linear polarization effect in continuum produced by starspots on active late-type stars. Assuming a simple two-temperature photosphere model with circular non-evolving spots and using spot temperaturecontrasts from Andersen & Korhonen (2015), we developed a code to generate different surface spot configurations and calculate the Stokes parameters and degree of polarization phase curves over the stellar rotation period. As afirst approximation, we used extrapolations from the solar to starspot size distributions by Solanki & Unruh (2004) and selected random spot configurations. We analyzed how different input parameters influence our simulations. Active latitudes and longitudes and polar spots were then considered. The following conclusions were reached.
- (i)
The linear scattering polarization should be much higher in the blue spectral bands than in visual and red bands. It is less dependent on the effective temperature, except in the region between 4500 K and 5500 K, where the polarization drops significantly for the spherical model atmospheres we used. The effect is more varied between luminosity classes, with lower gravity stars showing higher polarization.
- (ii)
When we assumed a lognormal distribution of starspots by size, the polarization levels varied significantly such that wider distributions and those with larger average spot sizes resulted in generally higher polarization levels. When we fixed the total spot coverage, the difference between the selected size distributions was found to be on the order of one magnitude.
- (iii)
The average polarization degrees for different stars increase gradually up to high spot coverages of 70–80%. However, the values obtained from different random runs are spread significantly, such that it is hard to distinguish between selected spot size distributions.
- (iv)
Tests using random spot configurations showed a systematic increase in the amplitudes of the polarization degree phase curves as the stellar rotation axis orientation changed from pole-on to equator-on; it was steeper for axial inclination angles of less than 40°.
- (v)
Despite a power-law wavelength dependence of the polarization, it was found to vary significantly between different stellar models, which was explained by the interplay of wavelength dependencies of the input limb-darkening and polarization for the two-temperature photosphere model we adopted. Fitting the curves resulted in power-law exponents ranging from −2 to −10 for a given model set and spot temperature contrasts. On the other hand, the wavelength dependences for most models we obtained were almost not influenced by the choice of the spot size distribution and total coverage.
- (iv)
For a fixed spot coverage, any deviations from the random surface distribution are expected to increase the average polarization of a star. Simulating reoccurring long-lasting formations, that is, active latitudes and longitudes and polar caps, tended to increase the average polarization degrees by a certain constant background level.
- (v)
Because the axial inclination angles of known active stars are often more than 60°, high-latitude and polar spots, which are closer to the limb, are expected to produce higher and longer lasting polarization. Simulating the high-latitude spot configuration for XX Triangulum using Doppler-imaging data, we estimated polarization degree for it to lie between 3 × 10−5 and 6 × 10−5 with an amplitude range of 1.2–1.8 × 10−5, which may be detected with modern polarimeters (e.g., Cotton et al. 2016).
Overall, our simulations for late-type active stars show that the effect of linear scattering polarization due to starspots is relatively small, with typical values of between 10−6 and 10−4. However, these levels are characteristic for many problems of upcoming astrophysical studies. While interesting on its own, the effect can complement existing photometric and spectroscopic methods used in starspot studies. In addition, the limb polarization effect is important for exoplanetary research for planets orbiting active host stars, particularly for their atmosphere characterization, where high-precision polarimetry will play an important role.
 |
Fig. 11 Relative flux, normalized Stokes Q and U parameters, and polarization degree, simulated for the K1III star (i = 60°) with two active longitudes with different activity levels ratios: 0 (black), 0.05 (blue), 0.25 (yellow), and 1.0 (red). The total spot coverage is 7% for all cases. |
Acknowledgements
This work was supported by the European Research Council Advanced Grant HotMol (ERC-2011-AdG291659).
References
- Andersen, J. M. & Korhonen, H. 2015, MNRAS, 448, 3053 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J., Lucas, P. W., & Hough, J. H. 2010, MNRAS, 405, 2570 [NASA ADS] [Google Scholar]
- Bailey, J., Kedziora-Chudczer, L., Cotton, D. V., et al. 2015, MNRAS, 449, 3064 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugin, A. V., Berdyugina, S. V., Piirola, V., & Butkevich, A. G. 2006, ApJ, 651, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Berdyugina, S. V., & Henry, G. W. 2007, ApJ, 659, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., & Usoskin, I. G. 2003, A&A, 405, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Stenflo, J. O., & Gandorfer, A. 2002, A&A, 388, 1062 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Moss, D., Sokoloff, D., & Usoskin, I. G. 2006, A&A, 445, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2008, ApJ, 673, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bogdan, T. J., Gilman, P. A., Lerche, I., & Howard, R. 1988, ApJ, 327, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & McLean, I. S. 1977, A&A, 57, 141 [NASA ADS] [Google Scholar]
- Cotton, D. V., Bailey, J., Kedziora-Chudczer, L., et al. 2016, MNRAS, 455, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, D. V., Marshall, J. P., Bailey, J., et al. 2017, MNRAS, 467, 873 [NASA ADS] [Google Scholar]
- Dyck, H. M., & Jennings, M. C. 1971, AJ, 76, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Dyck, H. M., Forbes, F. F., & Shawl, S. J. 1971a, AJ, 76, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Dyck, H. M., Forrest, W. J., Gillett, F. C., et al. 1971b, ApJ, 165, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Elstner, D., & Korhonen, H. 2005, Astron. Nachr., 326, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, J. P. 1969, Astrophys. Lett., 3, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Huovelin, J., Linnaluoto, S., Piirola, V., Tuominen, I., & Virtanen, H. 1985, A&A, 152, 357 [NASA ADS] [Google Scholar]
- Huovelin, J., Linnaluoto, S., Tuominen, I., & Virtanen, H. 1989, A&AS, 78, 129 [NASA ADS] [Google Scholar]
- Jackson, R. J. & Jeffries, R. D. 2013, MNRAS, 431, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L., Pelt, J., & Tuominen, I. 1993, A&A, 278, 449 [NASA ADS] [Google Scholar]
- Kochukhov, O. 2016, in Lect. Notes Phys., eds. J.-P. Rozelot, & C. Neiner (Berlin: Springer-Verlag), 914, 177 [Google Scholar]
- Korhonen, H. & Järvinen, S. P. 2007, in Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, eds. W. I. Hartkopf, P. Harmanec, & E. F. Guinan, IAU Symp., 240, 453 [NASA ADS] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Strassmeier, K. G., & Tuominen, I. 2001, A&A, 379, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostogryz, N. M., & Berdyugina, S. V. 2015, A&A, 575, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostogryz, N. M., Yakobchuk, T. M., & Berdyugina, S. V. 2015, ApJ, 806, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Kostogryz, N. M., Milic, I., Berdyugina, S. V., & Hauschildt, P. H. 2016, A&A, 586, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostogryz, N. M., Yakobchuk, T. M., Berdyugina, S. V., & Milic, I. 2017, A&A, 601, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Z., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Z., Künstler, A., Strassmeier, K. G., et al. 2016, A&A, 596, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Künstler, A., Carroll, T. A., & Strassmeier, K. G. 2015, A&A, 578, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, J. L. 1962, Ann. Astrophys., 25, 127 [NASA ADS] [Google Scholar]
- Manset, N. 2005, in Astronomical Polarimetry: Current Status and Future Directions, eds. A. Adamson, C. Aspin, C. Davis, & T. Fujiyoshi, ASP Conf. Ser., 343, 389 [NASA ADS] [Google Scholar]
- Mullan, D. J. & Bell, R. A. 1976, ApJ, 204, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, J. C., Medhi, B. J., Sagar, R., & Pandey, A. K. 2009, MNRAS, 396, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Parks, J. R., White, R. J., Baron, F., et al. 2015, ArXiv e-prints [arXiv:1508.04755] [Google Scholar]
- Pfeiffer, R. J. 1979, ApJ, 232, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Piirola, V. 1977, A&AS, 30, 213 [NASA ADS] [Google Scholar]
- Piirola, V., Berdyugin, A., & Berdyugina, S. 2014, in Proc. SPIE, 9147, Ground-based and Airborne Instrumentation for Astronomy V, 91478I [Google Scholar]
- Roettenbacher, R. M., Monnier, J. D., Korhonen, H., et al. 2016, Nature, 533, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., Piirola, V., Coyne, G. V., et al. 1993, A&AS, 102, 343 [NASA ADS] [Google Scholar]
- Seager, S., Whitney, B. A., & Sasselov, D. D. 2000, ApJ, 540, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Unruh, Y. C. 2004, MNRAS, 348, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 1999, A&A, 347, 225 [NASA ADS] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Tinbergen, J. 1982, A&A, 105, 53 [NASA ADS] [Google Scholar]
- Wiktorowicz, S. J., & Nofi, L. A. 2015, ApJ, 800, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, Y., Gu, S., Cameron, A. C., & Barnes, J. R. 2015, MNRAS, 447, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Yudin, R. V., & Evans, A. 2002, A&A, 386, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Highest polarization degree as a function of effective temperature for different types of stars in selected wavelengths using plane-parallel (dashed) and spherical (solid) model atmospheres. |
| In the text | |
 |
Fig. 2 Spotted area distribution on a stellar disk resulting in the highest polarization for two models at λ = 4450 Å: (a) Teff = 3500 K, Tspot = 3000 K, and log g = 2.0, and (b) Teff = 5100 K, Tspot = 3875 K, and log g = 2.0. The spotted area is shown with the darker color. For other stellar models, the highest possible polarizations are obtained at intermediate spot coverage with similar disk appearances, in which photosphere regions at the top and bottom vary between the two cases. |
| In the text | |
 |
Fig. 3 Relative flux and polarization degree phase curves for a model M2IV star with Teff = 3500 K, Tspot = 3000 K, and log g = 3.0 at λ = 4450 Å for one total spot coverage of 30%, but different average spot sizes ⟨A⟩ (1.63 and 9.38 [ × 10−6A1∕2*]), calculated using nA = 0.5 (top) and 1.0 (bottom). |
| In the text | |
 |
Fig. 4 Maximum polarization degree per rotation period for three stellar models versus total spot coverage for λ = 4450 Å. We show results for two scaling laws for distribution width σA (in blue) andaverage spot size ⟨A⟩ (in red). The solid lines correspond to the linear scaling law, and the dash-dotted lines show the square-root law. |
| In the text | |
 |
Fig. 5 Maximum polarization degree per rotation period for model stars with a spherical atmosphere, simulated for 30% spot coverage and a lognormal spot size distribution with a square-root scaling of the average spot area. |
| In the text | |
 |
Fig. 6 Polarization degree amplitude (top) and average (bottom) values per rotation period for different axis inclination angles at λ = 4450, (normalized to 90°). Models are the same as in Fig. 4. For each model, different spot coverages were tested, using two scalings for σA with nσ, equal to 0.5 (dash-dotted line) and 1.0 (dashed line). The average curve from all simulations is shown as the black solid line. |
| In the text | |
 |
Fig. 7 Average polarization degree per rotation period at different wavelengths, normalized to λ = 4000. For each stellar model the overlying curves are the power-law best fit obtained for 10% total spot coverage, while the underlying curves are for 50% coverage. For K1IV, the results for two different size distributions are shown (see text). |
| In the text | |
 |
Fig. 8 Average polarization degree per rotation period versus spot temperature contrast (normalized to the contrasts in Andersen & Korhonen 2015). For each stellar model, the dash-dotted lines show the 10% total spot coverage, and the solid lines show 50% coverage. |
| In the text | |
 |
Fig. 9 Relative flux, normalized Stokes Q and U parameters, and polarization degree, simulated for a K1IV star with active latitudes at ±40° and a total spot coverage of 10% (solid lines). The same results for a random surface spot distribution are shown with dashed lines. |
| In the text | |
 |
Fig. 10 Same as in Fig. 9, simulated for XX Tri with a polar spot configuration and a total spot coverage of 8%. |
| In the text | |
 |
Fig. 11 Relative flux, normalized Stokes Q and U parameters, and polarization degree, simulated for the K1III star (i = 60°) with two active longitudes with different activity levels ratios: 0 (black), 0.05 (blue), 0.25 (yellow), and 1.0 (red). The total spot coverage is 7% for all cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


