EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 612 (April 2018) A&A, 612 (2018) L6 Full HTML
Free Access
Issue
A&A
Volume 612, April 2018
Article Number L6
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/201833091
Published online 04 May 2018

© ESO 2018

1 Introduction

Mass (M) and specific angular momentum (j = J∕M) are two independent and key galaxy properties, subject to physical conservation laws, which are correlated in a fundamental scaling relation, the j*−M* law. This was first introduced by Fall (1983), as a basis for a physically motivated classification of galaxies, and therefore we call it the Fall relation hereafter. Empirically, massive spiral galaxies (log M*∕M⊙≳ 9) are found to lie on a power-law relation close to j∗∝M∗2/3${j_{\ast}}\propto{M_{\ast}}^{2/3}$ (Romanowsky & Fall 2012, hereafter RF12).

In a Λ cold dark matter (ΛCDM) Universe, this fundamental relation highlights the intimate link between galaxies and their host dark matter haloes; in fact, the specific angular momentum of haloes scales precisely as their mass to the power 2∕3 as a result of tidal torques (Peebles 1969; Efstathiou & Jones 1979). As highlighted by early semi-analytic models (Dalcanton et al. 1997; Mo et al. 1998), this connection is mediated by two fundamental physical parameters: fM,*≡ M*∕Mh, the so-called global star-formation efficiency, and fj,*≡ j*∕jh, the so-called retained fraction of angular momentum, which encapsulates several processes relevant to galaxy formation, including angular momentum losses due to interactions and the possibility that the gas which contributes to star formation does not sample the global angular momentum distribution in a uniform manner. In particular, the observed Fall relation is key to constraining fj,* as a function of other galaxy properties (Posti et al. 2018; Shi et al. 2017).

Several galaxy formation models are now able to correctly predict the amount of angular momentum in massive spiral galaxies (e.g. Genel et al. 2015; Teklu et al. 2015; Zavala et al. 2016). However, these predictions become rather discrepant and uncertain for the lower-mass systems (log M*∕M⊙≲ 9), where some models predict a flattening of the relation (Obreja et al. 2016; Stevens et al. 2016; Mitchell et al. 2018), while others do not see any change with respect to the relation for larger spirals (El-Badry et al. 2018). These discrepancies are arising also because observational estimates of the j*−M* relation over a wide galaxy stellar-mass range are lacking.

The aim of the present Letter is to provide the benchmark for the Fall relation from dwarf to massive spirals in the local Universe. We use spirals of all morphological types spanning an unprecedented mass range (7 ≲ log M*∕M⊙≲ 11.5), using accurate near-infrared (NIR) photometry/HI data to trace the stellar mass/galaxy rotation out to several effective radii. Unlike many previous estimates of massive (RF12; Obreschkow & Glazebrook 2014; Cortese et al. 2016) and dwarf (Butler et al. 2017; Chowdhury & Chengalur 2017) galaxies, separately, we homogeneously measure j* profiles for all galaxies and determine the relation using only those with a converged value of the total j*.

The paper is organised as follows. Section 2 introduces the dataset used. Section 3 explains our method and selection criteria and presents our determination of the Fall relation. In Sect. 4 we discuss the implications of our findings for galaxy formation models. We summarize and conclude in Sect. 5.

2 Data

The sample of spiral and irregular galaxies considered in this work comes from the Spitzer Photometry and Accurate Rotation Curves (SPARC) sample (Lelli et al. 2016b, hereafter LMS16). For these 175 nearby galaxies, from S0 to Irr, surface brightness profiles at 3.6 μm, derived from Spitzer Space Telescope photometry, and high-quality neutral hydrogen (HI) rotation curves, derived from interferometric HI data, are available.

Near-infrared profiles best trace the stellar mass distribution (e.g. Verheijen 2001), as the mass-to-light ratio at 3.6 μm is nearly constant over a broad range of galaxy masses and morphologies (e.g. Bell & de Jong 2001; McGaugh & Schombert 2014). For this work, we assume the fiducial values used in Lelli et al. (2017) for stellar population models with a Chabrier (2003) initial mass function: Υb[3.6]=0.5$\mathrm{\Upsilon}^{[3.6]}_{\textrm{b}}=0.5$ and Υd[3.6]=0.7$\mathrm{\Upsilon}^{[3.6]}_{\textrm{d}}=0.7$ for the bulge and disc at 3.6 μm, respectively1. The photometric profiles have also been decomposed in bulge/disc as described in LMS16.

In a disc galaxy, most stars are on almost circular orbits and rotate with velocities close to the local circular speed. We use the available HI rotation curves (from LMS16) to trace the circular velocity; we then apply a correction for the asymmetric drift (Binney & Tremaine 2008, Sect. 4.8.2) to obtain the stellar rotation curve (see Appendix A).

3 The specific angular momentum-mass relation

If a galaxy is axisymmetric and rotates on cylinders about its symmetry axis, then the specific stellar angular momentum j* ≡ |J*|∕M* within the radius R from the galactic centre writes as 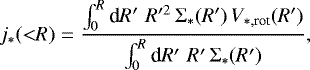j∗(<R)=∫0Rd R′  R′ 2 Σ∗(R′) V∗,rot(R′)∫0Rd R′  R′ Σ∗(R′),\begin{equation*}{j_{\ast}}({<}R) = \frac{\int_0^R \textrm{d} R&#x0027; \,\, R&#x0027;^2\,\mathrm{\Sigma}_{\ast}(R&#x0027;)\,V_{\ast,\textrm{rot}}(R&#x0027;)} {\int_0^R \textrm{d} R&#x0027; \,\, R&#x0027;\,\mathrm{\Sigma}_{\ast}(R&#x0027;)}, \end{equation*}(1)

where Σ∗(R)=Υb[3.6] Ib(R)+Υd[3.6] Id(R)$\mathrm{\Sigma}_{\ast}(R) = \Upsilon^{[3.6]}_{\textrm{b}}\,I_{\textrm{b}}(R) &#x002B; \Upsilon^{[3.6]}_{\textrm{d}}\, I_{\textrm{d}}(R)$ is the surface stellar mass density, with Ib and Id being the surface brightnesses of the bulge/disc at 3.6 μm, and V *,rot the stellar rotation curve. The total specific stellar angular momentum is j* ≡ j*(<Rmax), where Rmax is the outermost radius at which Σ* is measured. We compute the galaxy stellar mass as M∗=2π∫0Rmaxd R′ R′Σ∗(R′)${M_{\ast}}=2\pi\int_0^{R_{\textrm{max}}} \textrm{d} R&#x0027;\,R&#x0027;\mathrm{\Sigma}_{\ast}(R&#x0027;)$.

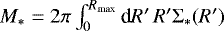3.1 Specific angular momentum profiles and sample selection

We use Eq. (1) to compute the specific angular momentum as a function of radius. We plot the resulting j* (< R) profiles for all the galaxies in the SPARC sample in Fig. 1. We find that for most galaxies, j* (< R) rises steeply in the inner parts and then flattens at about ~5Rd. The profiles typically flatten close to the value of the specific angular momentum of a thin exponential disc (with scale length Rd) with a constant rotation curve V f, i.e. j*,exp = 2RdV f. As expected, most of the specific angular momentum of a spiral galaxy resides further out than its optical half-light radius, and radially extended rotation curves, such as those provided by HI observations, are crucial to properly measure this momentum. In fact, all the galaxies with extended rotation curves have fully converged j* profiles, while only lower limits on j* can be determined for some galaxies for which the rotation curve at large radii is not known.

The value j*,exp = 2RdV f has been used by several authors as an estimate of the specific angular momentum for disc galaxies (Fall 1983; RF12). However, the actual j* (< R) of spirals flattens at about j*,exp with a significant scatter (~0.12 dex at ~5Rd), hence we caution against using simple estimates of the specific angular momentum.

To determine robustly the Fall relation for local spirals, we use only galaxies with an accurate measurement of j*, that is, only those with a converging j*(<R) profile. Thus, being R0, …, RN the radii at which the j* profiles are sampled, we select galaxies satisfying the following criteria: 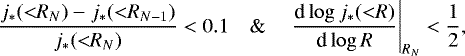j∗(<RN)−j∗(<RN−1)j∗(<RN)<0.1 & dlogj∗(<R)dlogR|RN<12,\begin{equation*}\frac{{j_{\ast}}({<}R_N) - {j_{\ast}}({<}R_{N-1})}{{j_{\ast}}({<}R_N)} < 0.1 \quad \& \quad \left.\frac{\textrm{d}\log{j_{\ast}}({<}R)}{\textrm{d}\log R}\right|_{R_N} < \frac{1}{2}, \end{equation*}(2)

that is, that the last two points of the j* profile differ by less than 10% and that the logarithmic slope of the j* profile in the outermost point is less than one half.

To further illustrate our selection, we highlight in Fig. 1 the individual j* profiles of three galaxies in the SPARC sample, representative of different converging properties. NGC 3198 has a perfectly converged j* profile (blue circles). In our sample, 28 galaxies, covering the entire SPARC mass range, show a similar feature: these are the galaxies for which j* is best measured. NGC 3972 (yellow squares) is the archetype of the galaxies that merely comply to the criteria of Eq. (2); these galaxies have a converging j* profile and the difference between the last two points of the profile is smaller than 10%. NGC 4068 (red triangles) has a steeply rising j* profile that does not meet Eq. (2) criteria; 34 similar galaxies are excluded from the calibration of the local Fall relation since their total j* might be severely underestimated.

We finally excluded galaxies with inclination angles below 30°, as their rotation velocity is very uncertain, and we are left with a sample of 92 galaxies with masses 7 ≲ log M*∕M⊙≲ 11.5. For those, we estimate the uncertainty in the stellar mass following Lelli et al. (2016a, see their Sect. 2.3) and the error on j* as 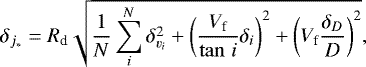δj∗=Rd1N∑iNδvi2+(Vftan iδi)2+(VfδDD)2,\begin{equation*} \delta_{{j_{\ast}}} = {R_{\textrm{d}}}\sqrt{\frac{1}{N}\sum_i^N\delta_{v_i}^2 &#x002B; \left(\frac{{V_{\textrm{f}}}}{\tan\,i}\delta_i\right)^2 &#x002B; \left({V_{\textrm{f}}}\frac{\delta_D}{D}\right)^2 }, \end{equation*}(3)

where V f is the velocity in the flat part of the rotation curve (see Lelli et al. 2016a), i is the inclination and δi its uncertainty, D is the distance and δD its uncertainty and 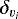δvi$\delta_{v_i}$ is the uncertainty at each point in the rotation curve. The error on distance often dominates the error budget. Of the 92 galaxies selected, 49 (53%) have relatively uncertain distances estimated with the Hubble flow (with relative errors of 10− 30%), while 43 (47%) have distances known within better than 10% (mostly from red giant branch tip).

thumbnail Fig. 1

Stellar specific angular momentum profiles for 175 disc galaxies in the SPARC sample. Grey contours represent the distribution of all the points in the profile of each galaxy. The radius is normalised to the disc scale length (Rd at 3.6 μm) and j* to that of a thin exponential disc with the same Rd and with a constant rotation curve. We also show the full profiles for three representative galaxies in our initial sample: a galaxy with a fully converged j* (< R) profile (blue circles), a galaxy with a converging profile (yellow squares) and a galaxy with a non-converging profile (red triangles). For our determination of the Fall relation, we excluded galaxies with a non-converging profile.
thumbnail Fig. 2

Left panel: specific stellar angular momentum-stellar mass relation (Fall relation) for a sample of 92 nearby disc galaxy. Each galaxy is represented by a circle coloured by Hubble type. The black dashed line is the best-fitting linear model and the grey band is the 1σ orthogonal intrinsic scatter. Bottom panel: orthogonal residuals around the linear model. Right panel: as in the left panel, but for the discs only (i.e. after removing the contribution from the bulges).

3.2 The j*−M* relation for galaxies and their discs

The left-hand panel of Fig. 2 shows our determination of the specific angular momentum-mass relation for nearby disc galaxies over ~5 dex in stellar mass. We fit a linear relation (in logarithm) to the data points allowing for an orthogonal intrinsic2 scatter. We assume uninformative priors for the three parameters (slope, normalisation and scatter) and explore the posterior distribution with a Monte Carlo Markov chain (MCMC) method (using the python implementation by Foreman-Mackey et al. 2013). With a model that follows logj∗=α [log(M∗/M⊙)−11]+β,\begin{equation*} \log{j_{\ast}} = \alpha\,[\log({M_{\ast}}/{M_{\odot}}) - 11] &#x002B; \beta, \end{equation*}(4)

we find a best-fitting slope α = 0.55 ± 0.02, a normalisation β = 3.34 ± 0.03, and an orthogonal intrinsic scatter σ⊥ = 0.17 ± 0.01 dex. We repeated this exercise i) varying the thresholds in Eq. (2) and ii) considering only the 20 galaxies with converged j* profiles that have relative distance uncertainties smaller than 10%, and found no significant difference in the best-fit relation. 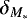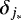In these estimates we have assumed the uncertainties in M* and j* to be uncorrelated; however, this is likely not the case since both δM∗$\delta_{{M_{\ast}}}$ and δj∗$\delta_{{j_{\ast}}}$ are often dominated by distance errors. Therefore, we recomputed the distributions of the model parameters in the extreme case of fully correlated uncertainties (correlation coefficient unity): we find no significant difference ineither the slope or the normalisation, but we find a slightly larger orthogonal intrinsic scatter σ⊥ = 0.179 ± 0.014 dex.

The best-fitting values are consistent, albeit having a smaller intrinsic scatter, with previous estimates of the Fall relation for high-mass spirals. We also confirm that the residuals correlate with galaxy morphology; earlier galaxy types are found systematically below the relation and viceversa for later types (RF12; Cortese et al. 2016). While significantly improving the determination of the relation at high masses3, we have robustly measured that the Fall relation extends to dwarf galaxies as a single, unbroken power-law. This is a crucial observational result that challenges many state-of-the-art galaxy formation models, which predict a flattening of the relation at low masses (Stevens et al. 2016; Obreja et al. 2016; Mitchell et al. 2018).

We note that two previous works looked at the baryonic version of the specific angular momentum-mass law for dwarf irregulars and found them to be offset towards larger jbaryon with respect to the relation for massive spirals (Butler et al. 2017; Chowdhury & Chengalur 2017). Our rotation curves (from the SPARC sample) have been specifically selected to be of the highest possible quality and therefore better trace the axisymmetric gravitational potential. We are planning to use this dataset to investigate the baryonic relation in a forthcoming paper. Butler et al. (2017) also showed a j* − M* relation down to low-mass galaxies which is offset towards larger j* and much more scattered than ours. This is most likely due to i) the different quality of their rotation curves (see e.g. Iorio et al. 2017, their Fig. 24) and ii) their use of fitting functions to extrapolate the total j* as opposed to our check of its convergence on each individual galaxy. Moreover, we have compared our results with a different determination of the circular velocities for a sample of 17 dwarf irregulars by Iorio et al. (2017), who used the state-of-the-art three-dimensional (3D) software 3D-BAROLO (Di Teodoro & Fraternali 2015). We found that the j* profiles of the galaxies in common with SPARC are consistent.

The Fall relation in the left-hand panel of Fig. 2 is amongst the tightest known scaling laws for spiral galaxies4. However, the relation gets even tighter if one considers just the disc component of spiral galaxies, by removing the bulge contribution to the light profile. The right-hand panel of Fig. 2 shows the disc specific angular momentum-mass relation (jd −Md) and Table 1 summarises the results for both the j*−M* and jd−Md relations. We find that the relation for discs has the following important differences with respect to the one for the whole stellar body:

  • S0-Sb galaxies with log M*∕M⊙≳ 9.5 scatter around null residuals in the jd−Md relation. This significantly alleviates the trend of the residuals with galaxy morphology, present in the j*−M* relation.

  • The scatter of the jd−Md relation, σ⊥ = 0.15 ± 0.01 dex, is slightly smaller, and its slope, α = 0.585 ± 0.020, is slightly larger than that of the j*−M* relation.

These two points are particularly important because they suggest that the jd − Md is more fundamental than the j*−M* relation. In particular, the best-fit slope of the relation for discs is closer to that of dark matter haloes, 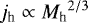jh∝Mh2/3${j_{\textrm{h}}}\propto {M_{\textrm{h}}}^{2/3}$, possibly indicating a simpler link to dark haloes of discs compared to bulges (e.g. Mo et al. 1998). In the following section we discuss some implications of the jd−Md relation for galaxy formation models.

Table 1

Best-fit parameters, and their 1σ errors, of the function log j = α (log M − 11) + β fitted to the data in Fig. 2 for galaxies and their discs. σ⊥ is the orthogonal intrinsic scatter.

4 Physical models

In a LambdaCDM cosmology, dark matter haloes acquire angular momentum from tidal torques such that their specific angular momentum 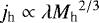jh∝λMh2/3${j_{\textrm{h}}} \propto \lambda{M_{\textrm{h}}}^{2/3}$, Mh being their (virial) massand λ the so-calleddimensionless spin parameter (which is independent from mass, see Peebles 1969). It follows that discs, which form inside these haloes out of gas that has initially the same initial angular momentum as the dark matter, will have specific angular momentum 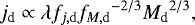jd∝λfj,dfM,d−2/3Md2/3,\begin{equation*}{j_{\textrm{d}}} \propto \lambda {f_{j,\rm d}} {f_{M,\rm d}}^{-2/3} {M_{\textrm{d}}}^{2/3}, \end{equation*}(5)

where we have defined the stellar disc’s “global star-formation efficiency” fM,d ≡ Md∕Mh and the stellar disc’s “retained fraction of angular momentum” fj,d ≡ jd∕jh (e.g. Posti et al. 2018). In what follows, we use the recent estimate of the stellar-to-halo mass relation for late-type galaxies by Rodríguez-Puebla et al. (2015) as our fiducial fM,d (see Posti et al. 2018, for other choices).

We first consider the case in which all spirals retain the same fraction of the halo’s angular momentum (e.g. Mo et al. 1998). This case is of particular interest since several state-of-the-art semi-analytic galaxy formation models are based on the assumption of a constant fj,d for all masses (see e.g. Knebe et al. 2015, for a comparison of many of these). In this case, Eq. (5) reduces to 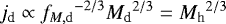jd∝fM,d−2/3Md2/3=Mh2/3${j_{\textrm{d}}} \propto {f_{M,\rm d}}^{-2/3}{M_{\textrm{d}}}^{2/3}={M_{\textrm{h}}}^{2/3}$, which we show in Fig. 3 in comparison with the data (red dot-dashed line). We fitted this model for the value of the constant retained fraction and we found it significantly smaller than unity, fj,d = 0.77 ± 0.7 (similar to previous findings, e.g. Dutton & van den Bosch 2012; RF12). While the model provides a decent fit to the data for high-mass discs ( log M*∕M⊙~ 10.5), indicating that about 70−80% of the halo’s angular momentum is incorporated in these galaxies, the model also clearly over-predicts jd in low-mass galaxies ( log M*∕M⊙≲ 9), which instead require a much smaller fj,d (see also Fig. 1 in Posti et al. 2018).

Some semi-analytic galaxy formation models (Knebe et al. 2015; Stevens et al. 2016), as well as some others based on numerical hydrodynamical simulations (Genel et al. 2015; Obreja et al. 2016; Mitchell et al. 2018), show similar predictions of a flattening of the Fall relation at M* ~ 109 M⊙, which are inconsistent with our accurate determination of the j*−M* law. This is, in fact, related to the retained fraction of angular momentum fj,d which they either assume or find to be relatively constant as a function of galaxy mass. In other models, instead, strong stellar feedback is crucial to make low-mass discs have a lower fj,d, which also decreases to smaller masses. These models are in fact able to qualitatively predict the Fall relation in the full mass range that we probe observationally (El-Badry et al. 2018).

The last physical models that we consider in this discussion are inside-out cooling models in which star formation proceeds from angular-momentum-poor to angular-momentum-rich gas: the so-called biased collapse models (Dutton & van den Bosch 2012; Kassin et al. 2012; RF12). Following Posti et al. (2018), if for the gas, as for the dark matter, the angular momentum is distributed as 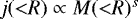j(<R)∝M(<R)s$j({<}R) \propto M({<}R)^s$, with s being a constant slope (see Bullock et al. 2001), then 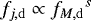fj,d∝fM,ds${f_{j,\rm d}}\propto{f_{M,\rm d}}^s$ (van den Bosch 1998; Navarro & Steinmetz 2000). Plugged into Eq. (5), this yields 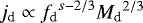jd∝fds−2/3Md2/3${j_{\textrm{d}}}\propto{f_{\textrm{d}}}^{s-2/3}{M_{\textrm{d}}}^{2/3}$. We fit this prediction for the best value of s, which we find to be s = 0.4 ± 0.1, and we show how that compares to the observed Fall relation in Fig. 3 (blue dashed line). This model provides a remarkable fit to the observations over the entire mass range and it is preferred to the constant-fj,d one (according to the Bayesian information criterion). The slope s in this model is related to the canonical angular momentum distribution d M∕dj ∝ jq where s = 1∕(1 + q) and, perhaps unsurprisingly, its best-fitting value is compatible with that expected for pure discs (q ≃ 1 in the low-j regime, van den Bosch et al. 2001).

Finally we note that the scatter that we measure for the Fall relation (σ⊥= 0.15 dex) is significantly smaller than what one might expect from Eq. (5), given that the scatters in the λ distribution and the stellar-to-halo mass relation are ~0.25 dex and ~ 0.15 dex, respectively. This suggests that i) the scatters of the λ−Mh, fj,d −Mh and Md −Mh relations arecorrelated such that when combined in Eq. (5) they yield the observed scatter and/or ii) the λ distribution of haloes hosting spiral galaxies is intrinsically narrower than that of the full halo population (even if the latter is not sufficient to explain the measured specific angular momenta of massive spirals and ellipticals; see Posti et al. 2018).

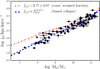thumbnail Fig. 3

Predicted distribution in the jd−Md plane of a model with a constant retained fraction of angular momentum fj (red dot-dashed line) and for a biased collapse model (blue dashed line) compared to the data as in Fig. 2. To compute the two models we have used the stellar-to-halo mass relation from Rodríguez-Puebla et al. (2015).

5 Summary & conclusions

In this Letter we study the relation between specific angular momentum and mass (Fall relation) of nearby disc galaxies spanning an unprecedented range in stellar mass (7 ≲ log M*∕M⊙≲ 11.5). We use Spitzer 3.6 μm photometry and HI rotation curves, compiled in the SPARC sample, to trace the stellar mass surface density and rotation velocity profiles, respectively. We determine specific angular momentum profiles for all galaxies and use only those with converging profiles in the determination of the scaling law, since they guarantee accurate measurement of the total galactic angular momentum. We find that:

  • (i)

    the Fall relation j*−M* is remarkably well represented by a single power-law, with slope α = 0.55 ± 0.02 and scatter σ⊥ = 0.17 ± 0.01 dex, from massive to dwarf spiral galaxies;

  • (ii)

    the disc-only relation jd−Md has a slightly steeper slope α = 0.585 ± 0.020 and a slightly smaller scatter σ⊥ = 0.15 ± 0.01 dex;

  • (iii)

    the observed Fall relation is a powerful benchmark for galaxy formation scenarios and poses a challenge to some of the current models, which predict a change of slope at low masses.

Being a scaling law that tightly relates two fundamental and independent quantities subject to physical conservation laws, the Fall relation stands out as one of the most (if not the most) fundamental scaling relations for disc galaxies. From dwarf irregulars to massive spirals, from early-type (S0) to late-type spirals (Sd-Sm), all disc galaxies in the local Universe appear to lie on a single power-law relation, which may already be in place in the early Universe (Burkert et al. 2016; Harrison et al. 2017).

We also discussed how these remarkable observations can be used to constrain galaxy formation models. In particular, the Fall relation uniquely constrains how much of the angular momentum initially present in the baryons ends up being encapsulated in the stellar body of a galaxy. Models assuming this to be a constant with galaxy mass will inevitably fail at reproducing the observations.

Among those considered, an inside-out cooling model (biased collapse) works better in reproducing the observed law. This scenario also points to some angular momentum redistribution taking place during star formation, possibly due to feedback, or to significant differences between the angular momenta of dark matter and baryons in the beginning stages of formation. Understanding the precise nature of these processes and, in general, giving account of the observed straight and tight j* − M* relation across almost five orders of magnitude in stellar mass is a key challenge of modern theoretical astrophysics.

Appendix A: Asymmetric drift correction

The circular velocity V c is equal to the sum in quadrature of the stellar rotation velocity V *,rot and the asymmetric drift velocity V AD, that is, 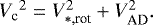Vc2=V∗,rot2+VAD2.${V_{\textrm{c}}}^2 = V_{\ast,\textrm{rot}}^2&#x002B;V_{\textrm{AD}}^2.$ We use the (inclination-corrected) HI observed rotation curve to trace V c at each radius. Then, following the findings of the DiskMass Survey on a sample of 30 well-studied face-on nearby spirals (Martinsson et al. 2013), we assume the vertical stellar velocity dispersion to vary exponentially with radius σz = σ0,z exp(−R∕2Rd), where Rd is the disc scale length measured at 3.6 μm. The normalisation σ0,z is found to be a function of the galaxy’s central surface brightness μ0 at 3.6 μm: σz,0≃ 20 km s−1 for μ0 ≲ 20 mag arcsec−2 and σz,0 ≃ 70 km s−1 for μ0 ~ 16 mag arcsec−2 (see Martinsson et al. 2013).

By further assuming that the disc scale height is constant with radius and that the system is isotropic, that is, σR = σz, we can write the asymmetric drift velocity as (e.g. Binney & Tremaine 2008, Sect. 4.8.2) 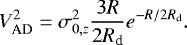VAD2=σ0,z23R2Rde−R/2Rd.\begin{equation*}V_{\textrm{AD}}^2 = \sigma_{0,z}^2 \frac{3R}{2{R_{\textrm{d}}}} e^{-R/2{R_{\textrm{d}}}}. \end{equation*}(A.1)

In this Letter we use Eq. (A.1) to correct for asymmetric drift. In general, this introduces only a small correction, of less than 5%, to the estimate of the specific angular momentum. We have also considered i) the anisotropic case 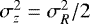σz2=σR2/2$\sigma_z^2=\sigma_R^2/2$ and ii) the extreme case of a uniform vertical dispersion σz = σ0,z throughout the galaxy and found in both cases small differences (less than 10%) in the derived specific angular momenta.

References

  1. Binney, J., Tremaine, S. 2008, Galactic Dynamics: 2nd edn. (New Jersey: Princeton University Press) [Google Scholar]
  2. Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012, MNRAS, 419, 771 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bullock J. S., Dekel, A., Kolatt, T. S., Kravtsov, A. V., et al. 2001, ApJ, 555, 240 [NASA ADS] [CrossRef] [Google Scholar]
  5. Burkert, A., Förster Schreiber, N. M., Genzel, R., et al. 2016, ApJ, 826, 214 [NASA ADS] [CrossRef] [Google Scholar]
  6. Butler, K. M., Obreschkow, D., & Oh, S.-H. 2017, ApJ, 834, L4 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chowdhury, A., & Chengalur, J. N. 2017, MNRAS, 467, 3856 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cortese, L., Fogarty, L. M. R., Bekki, K., et al. 2016, MNRAS, 463, 170 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dalcanton, J. J., Spergel, D. N., & Summers, F. J. 1997, ApJ, 482, 659 [NASA ADS] [CrossRef] [Google Scholar]
  11. Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dutton, A. A., & van den Bosch, F. C. 2012, MNRAS, 421, 608 [NASA ADS] [Google Scholar]
  13. Efstathiou G., & Jones B. J. T. 1979, MNRAS, 186, 133 [NASA ADS] [CrossRef] [Google Scholar]
  14. El-Badry, K., Quataert, E., Wetzel, A., et al. 2018, MNRAS, 473, 1930 [Google Scholar]
  15. Fall, S. M. 1983, IAU Symp., 100, 391 [Google Scholar]
  16. Fall, S. M., & Romanowsky, A. J. 2013, ApJ, 769, L26 [NASA ADS] [CrossRef] [Google Scholar]
  17. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  18. Genel, S., Fall, S. M., Hernquist, L., et al. 2015, ApJ, 804, L40 [NASA ADS] [CrossRef] [Google Scholar]
  19. Harrison, C. M., Johnson, H. L., Swinbankn, A. M., et al. 2017, MNRAS, 467, 1965 [NASA ADS] [CrossRef] [Google Scholar]
  20. Iorio, G., Fraternali, F., Nipoti, C., et al. 2017, MNRAS, 466, 4159 [NASA ADS] [Google Scholar]
  21. Kassin S. A., Devriendt, J., Fall, S. M., de Jong, R. S., Allgood, B., & Primack, J. R. 2012, MNRAS, 424, 502 [NASA ADS] [CrossRef] [Google Scholar]
  22. Knebe, A., Pearce, F. R., Thomas, P. A., et al. 2015, MNRAS, 451, 4029 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, ApJ, 816, L14 [Google Scholar]
  24. Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016b, AJ, 152, 157 [Google Scholar]
  25. Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
  26. Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mitchell, P. D., Lacey, C. G., Lagos, C. D. P., et al. 2018, MNRAS, 474, 492 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
  30. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
  31. Navarro, J. F., & Steinmetz, M. 2000, ApJ, 538, 477 [NASA ADS] [CrossRef] [Google Scholar]
  32. Obreja, A., Stinson, G. S., Dutton, A. A., et al. 2016, MNRAS, 459, 467 [NASA ADS] [CrossRef] [Google Scholar]
  33. Obreschkow, D., & Glazebrook, K. 2014, ApJ, 784, 26 [NASA ADS] [CrossRef] [Google Scholar]
  34. Peebles, P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ponomareva, A. A., Verheijen, M. A. W., Papastergis, E., Bosma, A., & Peletier, R. F. 2018, MNRAS, 474, 4366 [NASA ADS] [CrossRef] [Google Scholar]
  36. Posti, L., Pezzulli, G., Fraternali, F., & Di Teodoro, E. M. 2018, MNRAS, 475, 232 [NASA ADS] [CrossRef] [Google Scholar]
  37. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Rodríguez-Puebla, A., Avila-Reese, V., Yang, X., et al. 2015, ApJ, 799, 130 [NASA ADS] [CrossRef] [Google Scholar]
  39. Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [NASA ADS] [CrossRef] [Google Scholar]
  40. Shi, J., Lapi, A., Mancuso, C., Wang, H., & Danese, L. 2017, ApJ, 843, 105 [Google Scholar]
  41. Stevens, A. R. H., Croton, D. J., & Mutch, S. J. 2016, MNRAS, 461, 859 [NASA ADS] [CrossRef] [Google Scholar]
  42. Teklu, A. F., Remus, R.-S., Dolag, K., et al. 2015, ApJ, 812, 29 [Google Scholar]
  43. van den Bosch, F. C. 1998, ApJ, 507, 601 [NASA ADS] [CrossRef] [Google Scholar]
  44. van den Bosch, F. C., Burkert, A., & Swaters, R. A. 2001, MNRAS, 326, 1205 [Google Scholar]
  45. Verheijen, M. A. W. 2001, ApJ, 563, 694 [NASA ADS] [CrossRef] [Google Scholar]
  46. Zavala, J., Frenk, C. S., Bower, R., et al. 2016, MNRAS, 460, 4466 [NASA ADS] [CrossRef] [Google Scholar]
1

These values are comparable with those used by Fall & Romanowsky (2013) in their updated calibration of the Fall relation with respect to RF12, who used ϒK = 1 (in K-band) for both bulge and disc.

2

We subtract the contribution to the total scatter from measurement uncertainties.

3

RF12 used the simple j*,exp estimator, Cortese et al. (2016) computed j* only within the optical effective radius and Obreschkow & Glazebrook (2014) had only 16 objects.

4

For comparison the baryonic Tully–Fisher relation has an intrinsic orthogonal scatter of about ~ 0.07 − 0.05 dex (Ponomareva et al. 2018).

All Tables

Table 1

Best-fit parameters, and their 1σ errors, of the function log j = α (log M − 11) + β fitted to the data in Fig. 2 for galaxies and their discs. σ⊥ is the orthogonal intrinsic scatter.

In the text

All Figures

thumbnail Fig. 1

Stellar specific angular momentum profiles for 175 disc galaxies in the SPARC sample. Grey contours represent the distribution of all the points in the profile of each galaxy. The radius is normalised to the disc scale length (Rd at 3.6 μm) and j* to that of a thin exponential disc with the same Rd and with a constant rotation curve. We also show the full profiles for three representative galaxies in our initial sample: a galaxy with a fully converged j* (< R) profile (blue circles), a galaxy with a converging profile (yellow squares) and a galaxy with a non-converging profile (red triangles). For our determination of the Fall relation, we excluded galaxies with a non-converging profile.
In the text
thumbnail Fig. 2

Left panel: specific stellar angular momentum-stellar mass relation (Fall relation) for a sample of 92 nearby disc galaxy. Each galaxy is represented by a circle coloured by Hubble type. The black dashed line is the best-fitting linear model and the grey band is the 1σ orthogonal intrinsic scatter. Bottom panel: orthogonal residuals around the linear model. Right panel: as in the left panel, but for the discs only (i.e. after removing the contribution from the bulges).
In the text
thumbnail Fig. 3

Predicted distribution in the jd−Md plane of a model with a constant retained fraction of angular momentum fj (red dot-dashed line) and for a biased collapse model (blue dashed line) compared to the data as in Fig. 2. To compute the two models we have used the stellar-to-halo mass relation from Rodríguez-Puebla et al. (2015).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.