| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201732200 | |
| Published online | 13 February 2018 | |
Letter to the Editor
Effect of core cooling on the radius of sub-Neptune planets
Astronomical Institute Anton Pannekoek, University of Amsterdam, The Netherlands
e-mail: a.vazan@uva.nl
Received:
30
October
2017
Accepted:
17
December
2017
Sub-Neptune planets are very common in our Galaxy and show a large diversity in their mass-radius relation. In sub-Neptunes most of the planet mass is in the rocky part (hereafter, core), which is surrounded by a modest hydrogen-helium envelope. As a result, the total initial heat content of such a planet is dominated by that of the core. Nonetheless, most studies contend that the core cooling only has a minor effect on the radius evolution of the gaseous envelope because the cooling of the core is in sync with the envelope; that is most of the initial heat is released early on timescales of ~10–100 Myr. In this Letter we examined the importance of the core cooling rate for the thermal evolution of the envelope. Thus, we relaxed the early core cooling assumption and present a model in which the core is characterized by two parameters: the initial temperature and the cooling time. We find that core cooling can significantly enhance the radius of the planet when it operates on a timescale similar to the observed age, i.e. ~Gyr. Consequently, the interpretation of the mass-radius observations of sub-Neptunes depends on the assumed core thermal properties and the uncertainty therein. The degeneracy of composition and core thermal properties can be reduced by obtaining better estimates of the planet ages (in addition to their radii and masses) as envisioned by future observations.
Key words: methods: numerical / planetary systems / planets and satellites: composition / planets and satellites: interiors / planets and satellites: physical evolution
© ESO, 2018
1 Introduction
Super-Earths and mini-Neptunes (hereafter, sub-Neptunes) – planets with masses between terrestrial planets and ice giant planets – are a very common type of planet of our Galaxy (e.g. Howard et al. 2012; Batalha et al. 2013; Coughlin et al. 2016). Many of these planets are inferred to contain some amount of hydrogen and helium, typically several percent by mass (Lopez et al. 2012; Jontof-Hutter et al. 2016; Wolfgang & Lopez 2015; Fulton et al. 2017), and show a large scatter in their observed mass-radius (MR) relation. Usually the MR-scatter is interpreted in terms of a compositional diversity, where planets of a larger radius (for the same mass) are assigned a larger portion of hydrogen and helium (e.g. Lopez & Fortney 2014).
However, the planet radius is time-dependent and is affected by the thermal evolution of the planet. The radius evolution of the rocky part of the planet (hereafter, core1) is only weakly dependent on its composition owing to the degeneracy in heavy elements properties (Rogers & Seager 2010). A much larger indirect effect of the core on the radius of the planet occurs when the core is covered by a hydrogen-helium (HHe) envelope of only a few percent in mass, as is the case for many sub-Neptune planets. Hence, for sub-Neptune planets, most of the mass is in the core, while the radius of the planet is determined by the entropy of the HHe-dominated envelope.
The energy content of the core is usually expected to be smaller than the envelopes for planets with a large fraction of HHe due to the lower heat capacity of rocks in comparison to hydrogen and helium, as derived from equations of state. But for planets with an envelope mass of a few percent most of the energy is in the core (Ginzburg et al. 2016). Moreover, the initial core energy content – a property determined by the planet formation process – can be much higher than that of the envelope, and raise the importance of the core as an energy reservoir for the envelope. As a result, of any planet type we can expect the radius evolution of gas-rich sub-Neptune planets to be most affected by the underlying thermal evolution of its rocky core.
In most works (e.g. Lopez et al. 2012; Nettelmann et al. 2011; Chen & Rogers 2016) the thermal evolution of the core is not followed explicitly; instead, the core cooling rate, dTcore∕dt is simply taken to be identical to the cooling at the base of the envelope (Tenv), such that the luminosity generated by core cooling is
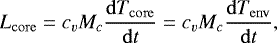 (1)
where cv is the core specific heat capacity, Mc the core mass. Implicitly, the assumption entering Eq. (1) is that core cooling is as fast as the cooling of the adiabatic envelope, that is determined by the radiative cooling rate at the outer atmosphere. Under this assumption (hereafter, standard approximation) the long-term thermal evolution is not affected by core properties (Chen & Rogers 2016). But the core cooling timescale may be different than that of the envelope. If the envelope cools faster than the core, the core contribution becomes dominant after the envelope has cooled. Thus, the role of the core in the thermal evolution depends on its cooling timescale.
(1)
where cv is the core specific heat capacity, Mc the core mass. Implicitly, the assumption entering Eq. (1) is that core cooling is as fast as the cooling of the adiabatic envelope, that is determined by the radiative cooling rate at the outer atmosphere. Under this assumption (hereafter, standard approximation) the long-term thermal evolution is not affected by core properties (Chen & Rogers 2016). But the core cooling timescale may be different than that of the envelope. If the envelope cools faster than the core, the core contribution becomes dominant after the envelope has cooled. Thus, the role of the core in the thermal evolution depends on its cooling timescale.
Since most of the detected planets orbit main-sequence field stars (i.e. ages of 1–10 Gyr), the core cooling timescale is a key parameter for the interpretation of observed radii by structure evolution models of sub-Neptunes. In this Letter we examine the importance of the core cooling rate for the thermal evolution of the envelope; that is we relax the assumption that the core heat transport is as rapid as that of the envelope. We introduce a parameter tcool for the timescale of core cooling and investigate the consequences of short and long core cooling timescales on the radius evolution of the planet.
2 Model
When the core cooling operates on a timescale longer than that ofthe envelope, the standard assumption no longer applies. To account for these effects, we consider the following alternative expression for the core luminosity:
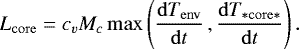 (2)
(2)
In Eq. (2) the core luminosity is taken to be the maximum between the natural core cooling rate, dT*core*∕dt, and the envelope cooling rate, dTenv∕dt, set by the radiative cooling through the atmosphere2.
In this exploratory work, the natural core contribution by dT*core*∕dt is highly simplified because it is determined by only two parameters: the core initial temperature, Tc,0, which reflects the initial core energy content, and the timescale for core cooling, tcool, which regulates how fast heat is transported between core and the envelope. Hence, we have
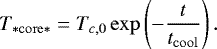 (3)
(3)
All uncertainties regarding initial core heat contents and core heat transport are encapsulated in these two parameters. We insert Eq. (3) in Eq. (2) and solve for the core luminosity as function of time, yielding
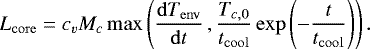 (4)
(4)
The envelope cooling timescale of dTenv∕dt term in Eq. (4) is of the order of several 107 yr for solar metallicity opacity (e.g. Lopez & Fortney 2014; Chen & Rogers 2016). Thus, the contribution of the initial energy content of dTenv∕dt is negligible in comparison to dT*core*∕dt for timescales longer than 107 yr. Concerning the timescale tcool, we identify the following three regimes:
-
tcool ≪ t: the timescale for heat release from the core is much shorter than the current age; the core has already cooled to the temperature of the atmosphere by the time t, and thus the contribution of the core luminosity dT*core*∕dt → 0. As a result, the evolution is determined entirely by the cooling of the envelope (dTenv∕dt), which is the standard approximation.
-
tcool ~ t: the age of the system is about equal to the timescale of core cooling; in this case the significant heat flux from the core cooling keeps the envelope extended. Hence, we get the maximal effect of the core luminosity on the envelope thermal evolution.
-
tcool ≫ t: the core cooling timescale is much longer than the planet age. Most of the heat is still locked up in the core, but the core luminosity is reduced by Tc,0∕tcool → 0. Therefore, the dT*core*∕dt → 0 and the evolution is determined again by the envelope.
We apply our models for planets in the sub-Neptune mass regime. The envelope mass fraction increases with mass (Mordasini et al. 2012); here we take 3, 5, 10 M⊕ planets with envelope masses of 1%, 10%, 15%, respectively. We consider different core cooling timescales tcool, while the envelope cooling time is not constrained.
The initial core temperature Tc,0 is estimated from the gravitational binding energy of the core. For a core of mass Mc and radius Rc,
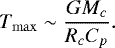 (5)
(5)
This assumes no radiative or advective losses. The fraction of the gravitational binding energy that remains in the core in the form of thermal energy is determined by the solid accretion rate during core formation. Since we do not specify a model for the core formation, we consider an arbitrary value of ~20% of the binding energy to remain in the core after formation. We calculate the core radii using our rock (SiO2) equation of state (Vazan et al. 2013). The resulting initial core temperatures for the planets in our model are 2.5 ×104 K, 3.1 ×104 K, and 5.6 ×104 K, respectively.
We calculate the evolution with a 1D hydrostatic planetary evolution code (Vazan et al. 2013) that solves the structure and evolution equations for the rocky (SiO2) core and hydrogen-helium envelope. We consider the core luminosity, as in Eq. (4), to be embedded in a gaseous envelope of hydrogen and helium in a solar ratio. The initial envelopes are adiabatic and have entropy of s = 9 kB∕baryon. In order to isolate the effect of core cooling on the radius evolution, we minimize other thermal effects of opacity, irradiation, and photo-evaporation: (1) Radiative opacity determines the atmosphere heat transport and therefore the cooling of the planet. High metallicity opacity slows the planet cooling and keeps the planet radius larger for longer. We use radiative opacities of Sharp & Burrows (2007) for solar metallicity (non-enhanced) planetary atmospheres. (2) Irradiation by the parent star is not included in the model. Stellar irradiation is expected to slow the planet cooling, and therefore enhance core thermal evolution effects (Baraffe et al. 2008). (3) The planet mass is constant during the evolution, that is no photo-evaporation (Owen & Wu 2013) or accretion are included in the model.
3 Results
To validate our model, we calculated the thermal evolution of sub-Neptune planets under the standard approximation, (dT*core*∕dt = 0) and compared our results to Baraffe et al. (2008) and Lopez & Fortney (2014). We find convergence in the radii of the planets between the models with differences at the 2% level3.
Then, we added the core luminosity dT*core*∕dt as described in Eq. (4), for five (order of magnitude) core cooling timescales tcool between 1 × 108 and 1 × 1011 yr. In Fig. 1 we present the radius evolution of a 5 M⊕ planet with a rocky core and a 10% HHe envelope. The different colours correspond to the different core cooling timescales and the dotted curve corresponds to the standard approximation of core cooling on envelope cooling ratio (dT*core*∕dt = 0). As is shown in Fig. 1, the radius evolution is clearly affected by the core cooling timescale. When we focus on the radius evolution in the typical observation timescale (grey rectangle zoom in), we find significantly different radii for the different models. In general, the radius evolution is similar to the standard case whenever the energy flux from the core is minor. On the core cooling timescale the envelope remains extended as long as the core energy is being released. When the heat flux from the core diminishes the planet contracts to the radius of the standard case. Thus, the greater change in radius occurs right after the core cooling time.
Therefore, if the core cools on a timescale similar to the observed age (e.g. purple and magenta curves in Fig. 1), the core cooling effect on the radius is maximal. If the core cools on 1 Gyr time (purple curve), the change in radius from 1 Gyr to 10 Gyr is about 30%. This is much larger than the change in the adiabatic evolution case (dotted curve) within the same time period. For a core cooling timescale of 10 Gyr (magenta curve) the planet radius is ~15% larger than the radius of the standard case through most of the evolution between 1–10 Gyr. On the other hand, planets with core cooling timescales much shorter than 1–10 Gyr (cyan and light blue curves) have already released most of their core heat contents by ~1 Gyr, rendering its radius evolution similar to the standard case. Finally, when the core cooling time is much longer than the typical observation age (red curve) the core stays hot but its thermal effect on the radius is small by ~10 Gyr.
This calculation has been conducted for a particular choice (20%) of the initial energy content as derived from Eq. (5). Higher (lower) initial core temperatures increase (decrease) the core thermal effect on the radius.
In Fig. 2 we illustrate planet and core radii after 5 Gyr for various planetary masses and values of core cooling times. We find the differences in radius between core cooling timescale of 10 Gyr and the standard models to be 11%, 15%, and 9%, respectively, for this age (5 Gyr). As the planet mass increases or decreases from the sub-Neptune mass range, the effect of the core cooling becomes weaker. More massive planets feature a stronger gravity, which diminishes the importance of thermal effects on the envelope. In addition, higher HHe mass fractions in more massive planets lower the core-to-envelope mass ratio and therefore reduce the core contribution. On the other hand, the small amounts of HHe that lower mass planets contain imply that their total radius is dominated by that of the core, rendering core and envelope thermal effects insignificant. Hence, we find the maximal effect for the 5 M⊕ planet in our model.
In Table 1 we provide radii for the different masses in this work for planet ages of 1, 5, and 10 Gyr. In the bottom part of the table we present radii for 5 M⊕ and 10 M⊕ planets with different envelope mass fractions than above. As was shown for 5 M⊕ in Fig. 1, a short cooling time of 0.01 Gyr and a long coolingtime of 100 Gyr result in radii that are very similar to the standard core cooling between 1–10 Gyr. Therefore we do not include them in the table, but add the standard case instead. The radius trend we find for 5 M⊕ planets is also apparent for the 3 M⊕ and 10 M⊕ planets, but are more moderate.
The maximum we find for core thermal effects in 5 M⊕ planet is valid when the mass of the envelope is increasing with the mass of the core. For independent envelope mass (e.g. same envelope fraction for different core mass), the effect of the core on the radius evolution increases as the planet mass decreases owing to lower gravity. As shown in the bottom part of Table 1, a 5 M⊕ planet with 1% HHe envelope exhibits smaller change in radius in comparison to the 3 M⊕ planet with the same 1% HHe (upper table) for the same cooling properties. Similar trend operates for a 10% HHe envelope of a 5 M⊕ planet (upper table) in comparison to a 10 M⊕ planet (lower table).
 |
Fig. 1 Radius evolution of a 5 M⊕ planet with 10% HHe envelope for different core cooling times. The dashed curve is for standard core cooling rate approximation. The initial conditions are the same for all cases. In the rectangular box, the radius evolution is represented between 1–10 Gyr. |
 |
Fig. 2 Core and envelope radii at age of 5 Gyr for different planet types and values of tcool . The radii are to scale. Once the core cooling time is similar to the planet age (i.e. middle column), the liberated heat causes the radius to expand. |
Planet radii for various planetary masses and cooling timescales.
4 Discussion
In this Letter we have demonstrated that protracted core cooling can, under certain conditions, significantly increase the radii of sub-Neptune planets on timescales of ~Gyr. Therefore, the conversion of observed radius-mass relation into envelope mass fraction actually gives an upper bound to the HHe mass fraction when the standard core cooling approximation is adopted, as is common. The diversity in mean density of sub-Neptunes is not determined solely by composition (i.e. hydrogen and helium fraction), but can also be driven by a different formation history and by a diversity in the cooling timescale(s) of planet cores.
What, then, are realistic value for Tc,0 and tcool? Broadly, energy transport in the core is either convective or conductive, and the former is able to support much larger heat fluxes than the latter. Convective heat transport is determined by the Rayleigh number, which depends on structure properties (gravity, density, layer length, and temperature profile), but also on material properties such as thermal expansion coefficient, thermal diffusivity, and kinematic viscosity. For modellers, the problem is the large uncertainty of these properties as a function of temperature and pressure (e.g. Valencia et al. 2006; Tachinami et al. 2011; van den Berg et al. 2010; Stamenković et al. 2012). Within the uncertainly limits, Stamenković et al. (2012) for example showed that different dependencies of viscosity on pressure provide various core cooling timescales. In van den Berg et al. (2010), the authors suggested that conductivity in high pressure conditions can make conduction favourable over convection in the long term. Thus, mechanisms that operated for Earth-like conditions may not be equally applicable to sub-Neptune pressure-temperature conditions. Conductive heat transport, on the other hand, can be estimated by 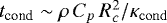 . For conductive opacities kcond from Potekhin et al. (1999), the conductive timescale is of the order of 1010 –1012 yr. Given their implications on the radius evolution of sub-Neptunes, as outlined by this Letter, a closer understanding of the core cooling properties is clearly an important subject for further investigation.
. For conductive opacities kcond from Potekhin et al. (1999), the conductive timescale is of the order of 1010 –1012 yr. Given their implications on the radius evolution of sub-Neptunes, as outlined by this Letter, a closer understanding of the core cooling properties is clearly an important subject for further investigation.
In our calculations in Sect. 3 we considered that the thermal energy content of the core was solely due to its gravitational binding energy, where we adopted an efficiency of 20%. This amounts to a specific energy of ~1011 erg/g. However, additional heat generation mechanisms can operate in the core and increase the core energy content. Release of latent heat in phase transitions depends on the evolution of the core pressure-temperature profile. Latent heat for SiO2, for example, in liquid-solid transition is ~6 × 109 erg/g (Richet et al. 1982). Radiogenic heating also contributes the core energy during the evolution. The dominant radioactive elements U238, U235, Th232, and K40 have half lives in the Gyr regime and provide ~3 × 1010 erg/g for meteorite-like composition (Grevesse & Noels 1993; Nettelmann et al. 2011). Similarly, core contraction (Baraffe et al. 2008) is an additional contributor to the energy balance of the core. Given these additional heat-generating mechanisms, core thermal effects on the radius evolution can be enhanced.
The model presented in this Letter is a first step towards a more complete model of the simultaneous evolution of core and envelope. In order to identify the core thermal contribution and to constrain the structure and composition of these planets, the core should be modelled in more detail. Indeed, a proper model for Lcore entails that we include the core in a centre-to-surface model together with the envelope. In a future study (Vazan et al., in prep.) we will investigate the effect of various thermal parameters on the radius evolution by such multi-zone model for the core.
Our results reveal a significant degeneracy in the mass-radius relation between composition (mainly core to envelope mass ratio) and core cooling behaviour. This degeneracy takes place when the core cooling timescale is similar to the age at which we observe the planet. Future observations can, however, help to break this degeneracy with a better estimation of the planet (or stellar) ages and more precise mass-radius observations. Our results indicate that the planet radius evolution can exhibit a characteristic trend over ~Gyr timescales, which is a direct consequence of the core cooling behaviour (tcool). Hence, if the temporal dimension is added, a statistical analysis of observed mass-radius-age data for sub-Neptune planets can constrain core cooling models and the core properties. For example, several planets in the sub-Neptune mass range with extended radii (super-puffs), such as Kepler-51b,c (Steffen et al. 2013; Masuda 2014) or Kepler-79d (Jontof-Hutter et al. 2014) are planets in systems younger than 3.5 Gyr. Therefore, if the typical core cooling timescale is of the order of 1 Gyr, a much more modest HHe fraction would be required to explain their radii than what is currently suggested.
Acknowledgments
We thank the anonymous referee for constructive comments that improved this manuscript. A.V. acknowledges support by the Amsterdam Academic Alliance (AAA) Fellowship. C.W.O. is supported by the Netherlands Organization for Scientific Research (NWO; VIDI project 639.042.422).
References
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H., & Rogers, L. A. 2016, ApJ, 831, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, J. L., Mullally, F., Thompson, S. E., et al. 2016, ApJS, 224, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2016, ApJ, 825, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jontof-Hutter, D., Lissauer, J. J., Rowe, J. F., & Fabrycky, D. C. 2014, ApJ, 785, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jontof-Hutter, D., Ford, E. B., Rowe, J. F., et al. 2016, ApJ, 820, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., Fortney, J. J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, K. 2014, ApJ, 783, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Georgy, C., et al. 2012, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nettelmann, N., Fortney, J. J., Kramm, U., & Redmer, R. 2011, ApJ, 733, 2 [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345 [NASA ADS] [Google Scholar]
- Richet, P., Bottinga, Y., Denielou, L., Petitet, J. P., & Tequi, C. 1982, Geochim. Cosmochim. Acta, 46, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., & Seager, S. 2010, ApJ, 712, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, C. M., & Burrows, A. 2007, ApJS, 168, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Stamenković, V., Noack, L., Breuer, D., & Spohn, T. 2012, ApJ, 748, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Fabrycky, D. C., Agol, E., et al. 2013, MNRAS, 428, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Tachinami, C., Senshu, H., & Ida, S. 2011, ApJ, 726, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., O’Connell, R. J., & Sasselov, D. 2006, Icarus, 181, 545 [NASA ADS] [CrossRef] [Google Scholar]
- van den Berg, A. P., Yuen, D. A., Beebe, G. L., & Christiansen, M. D. 2010, Phys. Earth Planet. Inter., 178, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 434, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfgang, A., & Lopez, E. 2015, ApJ, 806, 183 [NASA ADS] [CrossRef] [Google Scholar]
To conduct a proper comparison, we adjusted our model to match the set-up of the Baraffe et al. (2008), in which the core is made of H2O, and Lopez & Fortney (2014), in which stellar irradiation is included.
All Tables
All Figures
 |
Fig. 1 Radius evolution of a 5 M⊕ planet with 10% HHe envelope for different core cooling times. The dashed curve is for standard core cooling rate approximation. The initial conditions are the same for all cases. In the rectangular box, the radius evolution is represented between 1–10 Gyr. |
| In the text | |
 |
Fig. 2 Core and envelope radii at age of 5 Gyr for different planet types and values of tcool . The radii are to scale. Once the core cooling time is similar to the planet age (i.e. middle column), the liberated heat causes the radius to expand. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


