| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731875 | |
| Published online | 28 February 2018 | |
Comparing the birth rate of stellar black holes in binary black hole mergers and long gamma-ray bursts
1
IRAP, Université de Toulouse, CNRS, UPS, CNES,
Toulouse,
France
e-mail: jean-luc.atteia@irap.omp.eu
2
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, CNRS/IN2P3,
Montpellier,
France
3
INAF-Osservatorio Astronomico di Brera,
via E. Bianchi 46,
23807
Merate,
Italy
Received:
1
September
2017
Accepted:
1
December
2017
Context. Gravitational wave interferometers have proven the existence of a new class of binary black hole (BBH) weighing tens of solar masses, and have provided the first reliable measurement of the rate of coalescing black holes (BHs) in the local Universe. Furthermore, long gamma-ray bursts (GRBs) detected with gamma-ray satellites are believed to be associated with the birth of stellar-mass BHs, providing a measure of the rate of these events across the history of the Universe, thanks to the measure of their cosmological redshift. These two types of sources, which are subject to different detection biases and involve BHs born in different environments with potentially different characteristics, provide complementary information on the birth rate of stellar BHs.
Aims. We compare the birth rates of BHs found in BBH mergers and in long GRBs.
Methods. We construct a simple model that makes reasonable assumptions on the history of GRB formation, and takes into account some major uncertainties, like the beaming angle of GRBs or the delay between the formation of BBHs and their coalescence. We use this model to evaluate the ratio of the number of stellar mass BHs formed in BBH mergers to those formed in GRBs.
Results. We find that in our reference model the birth rate of stellar BHs in BBH mergers represents a significant fraction of the rate of long GRBs and that comparable birth rates are favored by models with moderate beaming angles. These numbers, however, do not consider subluminous GRBs, which may represent another population of sources associated with the birth of stellar mass BHs. We briefly discuss this result in view of our understanding of the progenitors of GRBs and BBH mergers, and we emphasize that this ratio, which will be better constrained in the coming years, can be directly compared with the prediction of stellar evolution models if a single model is used to produce GRBs and BBH mergers with the same assumptions.
Key words: stars: black holes / gravitational waves / gamma-ray burst: general
© ESO 2018
1 Introduction
The LIGO and VIRGO interferometers have opened a new window on the Universe with the detection of gravitational waves (GWs) from the coalescence of massive stellar black holes (BHs) in binary systems (Abbott et al. 2016b,c, 2017). Beyond the performance of detecting gravitational waves on Earth, these observations had a strong astronomical impact with the detection of previously unknown binary systems of two massive stellar BHs. Additionally, the gravitational wave interferometers have provided the first reliable measurement of the rate of coalescing BHs in the local Universe, which occur at a rate ranging from 12 to 213 yr−1 Gpc−3 for BHs with masses larger than 5 M⊙ (Abbott et al. 2016b, 2017).
After the discovery of such systems, various authors have studied their possible origin (e.g., Dominik et al. 2015; Eldridge & Stanway 2016; Marchant et al. 2016; Belczynski et al. 2016, 2017; Kushnir et al. 2016; van den Heuvel et al. 2017; Hotokezaka & Piran 2017; Mapelli et al. 2017; Bogomazov et al. 2018), concluding that the majority of them result from the evolution of isolated massive star binaries born in low-metallicity environments. In such systems, the stellar evolution quickly leads to the formation of a system of two BHs that will merge after a long time. Since the orbital decay time is expected to be much longer than the lifetime of the parent stars, the GW signals point to pairs of BHs which were eventually born several Gyr in the past, and the local rate of binary mergers is the convolution of the history of binary black hole (BBH) formation with their coalescence time. It is also possible to form BBH mergers dynamically in dense stellar clusters, however at smaller rates (e.g., Rodriguez et al. 2016).
Gamma-ray bursts (GRBs) offer another view at the birth of stellar BHs, especially long GRBs, which are believed to be associated with the core collapse of massive stars (Hjorth et al. 2003; Mészáros 2003; Price et al. 2003; Vedrenne & Atteia 2009). The measurement of hundreds of GRB redshifts, thanks to their fast localization with Swift (Gehrels et al. 2004) and rapid ground-based spectroscopic follow-up observations, have led to a good understanding of the history of GRB formation over the ages (e.g. Daigne et al. 2006; Wanderman & Piran 2010; Salvaterra & Chincarini 2007; Salvaterra et al. 2012; Shahmoradi 2013; Howell et al. 2014; Lien et al. 2014; Petrosian et al. 2015; Tan & Wang 2015; Deng et al. 2016; Pescalli et al. 2016).
GRBs and BBH mergers thus offer two complementary views on the history of stellar BH formation, based on two a priori different BH sub-populations. This paper aims at comparing the rates of BH formation measured in these two types of event. Unlike several recent papers, which discuss the emission of GRBs during the merger itself (e.g., Connaughton et al. 2016; Savchenko et al. 2016), we compare the formation rates of BHs in the past, at the time of their birth. Our analysis is based on a simple analytical model which takes into account the current rate of BBH mergers, the time between the formation of BBHs and their coalescence, the history of GRB formation, the GRB beaming factor, and the possibility of different formation histories of GRBs and BH mergers parametrized with a density evolution index. This model is described in the following section. The comparison of the BH birth rate from BBH mergers and from long GRBs is discussed in Sect. 3, while Sect. 4 addresses some astrophysical consequences of our analysis. Cosmological calculations are performed with the astropy.cosmology package with a flat Λ CDM model with H0 = 70 km s−1 Mpc−1 and ΩM = 0.3.
2 Comparing the rates of BBH mergers and long GRBs
After the formation of an isolated binary of two BHs, the evolution of the system is entirely determined by general relativity. One crucial parameter of the binary is its coalescence time, which is very sensitive to the initial configuration of the system. As shown by Peters (1964), the coalescence time of a system of two BHs depends on the fourth power of their separation and on the third power of their mass. The observation of GW 150914, with a coalescence time smaller than the age of the Universe constrains the initial separation between the two BHs to be smaller than ~45 R⊙ (Abbott et al. 2016a; Hotokezaka & Piran 2017), and even smaller separations are required if the coalescence time is shorter.
Integrating over the full distribution of coalescence times, the rate of present-day mergers can be written as:
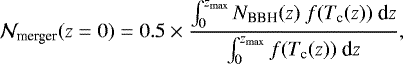 (1)
(1)
where NBBH(z) is the birth rate of BHs in BBH mergers at redshift z and Tc (z) is the coalescence time of a BBH system born at redshift z and merging at z = 0 (Tc (z) is equivalent to the look-back time at redshift z). Here, f(Tc(z)) represents the distribution of the coalescence times of BBH mergers born at redshift z, which is assumed to be redshift independent, and zmax is the highest redshift at which a BBH contributes to present-day mergers. The factor 0.5 is justified by the fact that the mergers detected by Advanced LIGO involve two BHs.
If we assume a power law distribution of coalescence times (with Tc ≥ 100 Myr), Eq. (1) becomes:
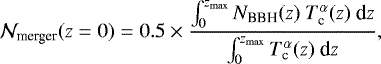 (2)
(2)
where α < 0 is the index of the power law distribution of coalescence times, which depends on the unknown distribution of the initial parameters of the BBH system.
Writing NBBH(z) = R(z) × NGRB(z) = R0 × ξ(z) × NGRB(z), where R(z) is the ratio of the number of BHs born in BBHs at redshift z divided by the number of BHs in GRBs at the same redshift, we can now express Eq. (2) as a function of NGRB(z);
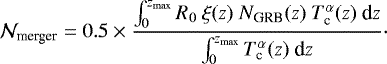 (3)
(3)
NGRB(z) can be expressed as a function of the local observed GRB rate η0, the beaming factor fb and the GRB formation history, with the following equation:
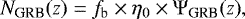 (4)
(4)
where ΨGRB(z) follows the history of the comoving GRB formation rate, 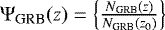 .
.
By replacing NGRB(z) in Eq. (3), we obtain:
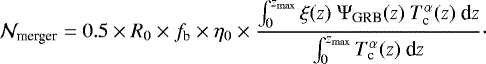 (5)
(5)
Finally, calling A(α) the ratio of the two integrals, we compute R0 as:
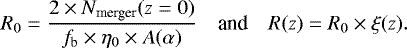 (6)
(6)
Equation (6) underlines the main sources of uncertainty in the evaluation of R0. One of them is Nmerger(z = 0), the local rate of BBH mergers. After the detection of four GWs, Abbott et al. (2017) estimate this rate to be in the range from 12 to 213 yr−1 Gpc−3, for BHs with masses larger than 5 M⊙. The main reason for this large uncertainty is the small number of detected GW events. It is nevertheless expected that this uncertainty will decrease quickly in the future after the detection of more BBH mergers. In the following, we compute R0 for the two extreme values of Nmerger(z = 0).
The beaming factor 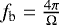 (where Ω is the solid angle of GRB emission) is another important source of uncertainty. However, since R0 is inversely proportional to fb, it is straightforward to derive R0 for other values of fb. We adopt fb = 250 in this paper, corresponding to a beaming angle of ~5° (Frail et al. 2001; Racusin et al. 2009; Ryan et al. 2015). For comparison, using fb = 75 proposed by Guetta et al. (2005) leads to values of R0 which are more than three times larger.
(where Ω is the solid angle of GRB emission) is another important source of uncertainty. However, since R0 is inversely proportional to fb, it is straightforward to derive R0 for other values of fb. We adopt fb = 250 in this paper, corresponding to a beaming angle of ~5° (Frail et al. 2001; Racusin et al. 2009; Ryan et al. 2015). For comparison, using fb = 75 proposed by Guetta et al. (2005) leads to values of R0 which are more than three times larger.
The distribution of the coalescence times between the formation of the BHs and their coalescence is also uncertain, and we compute R0 for various values of α. We have also checked that R0 is independent of zmax for zmax ≥ 4, and we use this value.
The other factors have better measurements; this is the case for the local GRB rate η0 and for the GRB formation history ΨGRB(z). Various authors have studied the GRB formation history (e.g., Daigne et al. 2006; Wanderman & Piran 2010; Salvaterra & Chincarini 2007; Salvaterra et al. 2012; Shahmoradi 2013; Howell et al. 2014; Lien et al. 2014; Petrosian et al. 2015; Tan & Wang 2015; Deng et al. 2016; Pescalli et al. 2016). Here we have chosen two recent models, which have been validated with Swift data and are representative of current estimates of the GRB formation rate. The first model, proposed by Lien et al. (2014) (see also Wanderman & Piran 2010), uses a broken power law cosmic GRB rate and a broken power law luminosity function whose parameters are adjusted to reproduce the GRB population detected by Swift/BAT (see their Table 2). In this model, the cosmic GRB formation rate is proportional to the cosmic star formation rate. The second model, proposed bySalvaterra et al. (2012), uses a cosmic GRB rate that presents a density evolution proportional to 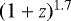 with respect to the star formation rate, and a broken power law luminosity function (see their Table 2).
with respect to the star formation rate, and a broken power law luminosity function (see their Table 2).
The prevalent models of BBH mergers favor their origin as massive stars born in low-metallicity regions (e.g., Eldridge & Stanway 2016; Marchant et al. 2016; Belczynski et al. 2017; Hotokezaka & Piran 2017) raising the possibility of a difference in evolution between massive BBHs and GRBs. We take this possibility into account with a redshift evolution function ξ(z) that favors the creation of massive BBHs at high redshift. Considering that the formation of GRBs is also favored in low-metallicity environments (see Sect. 4.1), we have chosen evolution parameters that add only moderate extra evolution for BBHs. We study two functional forms: 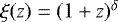 and ξ(z) = 1∕10βz. The first option involves a simple parametrization of the density evolution (e.g., Schmidt 1999; Salvaterra et al. 2012); for the purpose of this study we have chosen δ = 0.6, which provides a slightly stronger density evolution of BBHs with respect to GRBs, by a factor two at redshift z = 2. The second option considers that the formation of BBHs is favored (with respect to the formation of GRBs), in a manner which is inversely proportional to the metallicity. For the purpose of this study, we parametrize the evolution of metallicity with β = −0.15, following the work of Li (2008). This function also gives a density evolution which is stronger for BBHs than for GRBs, by a factor two at redshift z = 2.
and ξ(z) = 1∕10βz. The first option involves a simple parametrization of the density evolution (e.g., Schmidt 1999; Salvaterra et al. 2012); for the purpose of this study we have chosen δ = 0.6, which provides a slightly stronger density evolution of BBHs with respect to GRBs, by a factor two at redshift z = 2. The second option considers that the formation of BBHs is favored (with respect to the formation of GRBs), in a manner which is inversely proportional to the metallicity. For the purpose of this study, we parametrize the evolution of metallicity with β = −0.15, following the work of Li (2008). This function also gives a density evolution which is stronger for BBHs than for GRBs, by a factor two at redshift z = 2.
Finally, Eq. (6) is based on median values, excluding the possibility of correlations between the different parameters. However, considering the other uncertainties involved in the calculation of R0, this limitation isnot decisive in the context of our simplified model.
3 Results
Figure 1 shows the ratio R as a function of α for different values of the parameters appearing in Eq. (5). In the top panels, R is calculated assuming that the rates of GRBs and BBH mergers are proportional: R(z) = R0. The beaming factor is fb = 250 in the left panel and fb = 70 in the right panel. In the bottom panels, R is calculated assuming that BBH mergers are formed more efficiently than GRBs in the past: R(z) = R0 × ξ(z), where 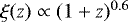 in the left panel and ξ(z) ∝ 100.15z in the right panel. The plots show R at redshift z = 2.5, which is close to the median redshift of GRBs detected by Swift (Jakobsson et al. 2006; Gehrels et al. 2009).
in the left panel and ξ(z) ∝ 100.15z in the right panel. The plots show R at redshift z = 2.5, which is close to the median redshift of GRBs detected by Swift (Jakobsson et al. 2006; Gehrels et al. 2009).
This figure illustrates the main result of our calculation, which is that, for the fiducial value α = −1 (e.g., Belczynski et al. 2016), the birth rate of stellar BHs in BBH mergers is a few times smaller than the birth rate of stellar BHs in GRBs.
In our reference model, with a beaming factor fb = 250 and identical redshift evolution of BH birth in GRBs and BBH mergers (top left panel of Fig. 1), this ratio varies from 0.02 to 1 for α = 0 and from 0.2 to 6 for α = −2.5, depending on the assumptions on the history of the GRB formation rate and on the local rate of BBH mergers. In this model, values of R0 in the range [0.1–1.0] are compatible with most values of α. The interpretation of this result and some of its astrophysical consequences are briefly addressed in the following section.
From Fig. 1, we can derive the main features of R0; first of all it decreases for larger values of α, which correspond to an increased contribution of mergers with long coalescence times. Since BH births were more numerous in the past, the larger contribution of mergers with long coalescence times can produce the present-day merger rate with a smaller fraction of BHs in BBH mergers. R0 is also sensitive to the GRB population model, whose impact is larger for α ≥ −1.5. Finally, R0 is larger for smaller beaming factors, as shown in the top right panel of Fig. 1 with fb =70. The uncertainty on R0 is expected to decrease quickly in the coming years, with additional detections of BBH mergers, allowing to reduce the size of the shaded areas in Fig. 1.
Hotokezaka & Piran (2017) find that BHs in BBHs and GRBs are produced at roughly similar rates. We verified that, with the beaming factor fb = 70 adopted by these authors, our analysis finds R0 in the range [0.1–7], allowing the formation of BBH mergers and GRBs at about the same rate, similar to Hotokezaka & Piran (2017). This result is illustrated in the top right panel of Fig. 1.
We have not included subluminous GRBs in our calculation of R0, since very few have been detected and their link with long classical GRBs is debated. These events could however change the ratio R0 under two conditions: if subluminous GRBs trace the birth of stellar BHs and if their local density is comparable to or higher than the local space density of classical GRBs. Both conditions are probably met. On one hand, the similarity of the supernovae of type Ibc associated with normal and subluminous GRBs (Galama et al. 1998; Iwamoto et al. 1998; Hjorth et al. 2003; Stanek et al. 2003) justifies the hypothesis that their end products are the same. On the other hand, various studies have shown that the local rate of subluminous GRBs equals or exceeds the local rate of classical GRBs (e.g., Soderberg et al. 2004; Daigne & Mochkovitch 2007). It is thus quite probable that subluminous GRBs represent another population of events associated with the birth of new BHs; this population is however much less known than GRBs or BBHs.
 |
Fig. 1 Ratio of the stellar BH birth rate measured in BBH mergers and in GRBs, as a function of α the index of the power law distribution of the coalescence times of BBH mergers. The solid and dashed lines show the fraction calculated for the median value of the local rate of BBH mergers measured by Advanced LIGO (Abbott et al. 2017), while the shaded areas indicate the full range of allowed values considering the errors on the local rate of BBHs mergers. The four panels correspond to different values (given in the inset) of the parameters appearing in Eq. (5). |
4 Discussion
In this section, we discuss the possible connections between BBH mergers and GRBs, in the context of the formation of stellar BHs.
4.1 The progenitors of GRBs
The connection between GRBs and stellar BH formation encompasses major uncertainties. While several nearby long GRBs have been associated with exploding massive stars, thanks to their connection with luminous supernovae (Galama et al. 1998; Iwamoto et al. 1998; Hjorth et al. 2003; Stanek et al. 2003), the simulations show that specific conditions are required to produce a GRB (see e.g., the reviews of Woosley & Bloom 2006; Levan et al. 2016). First, the core of the exploding star has to keep a large angular momentum, allowing the formation of an accretion disk around the newly formed BH, a situation that may be facilitated in binary systems (e.g., Podsiadlowski et al. 2004; Cantiello et al. 2007). Second, the relativistic jet must be able to pass through the atmosphere of the progenitor without being slowed down and losing its energy within the star. This second condition may explain why GRBs have been observed to be associated with supernovae of type Ibc, which have ejected their hydrogen and helium external layers. Various authors have shown that these conditions, and hence the production of GRBs, are more easily met in low-metallicity environments. The progenitors of GRBs thus appear to be massive Wolf–Rayet stars born in low-metallicity environments, possibly in binary systems. Considering these stringent requirements, it is probable that the majority of stellar BHs form silently without a GRB (e.g., MacFadyen & Woosley 1999; Heger et al. 2003). This vision is however mitigated by Levan et al. (2016) who note that for a typical beaming factor fb = 260, the long GRB rate is only a factor of three below the formation rate of low-metallicity massive stars.
On the other hand, long GRBs may not always be associated with the birth of a BH. Indeed, the collapse of a massive star accommodates both the direct collapse to a BH and the formation of a proto-magnetar in those cases where fast-rotating cores produce a magneto-rotational explosion (Dessart et al. 2012). The newly born magnetar may be long-lived, or it may eventually collapse to a BH when it spins down. From a phenomenological point of view, it has been proposed that the plateau phase observed in 50% of long GRBs detected by Swift is evidence for the presence of a long-lived magnetar central engine (Dai & Lu 1998; Zhang & Mészáros 2001; Corsi & Mészáros 2009; Metzger et al. 2011; Dall’Osso et al. 2011; Bernardini et al. 2012, 2013). In this context, the sharp drop observed at the end of the plateau in a few cases, which is inconsistent with any afterglow model, has been interpreted as the collapse of an unstable magnetar to a BH (Lyons et al. 2010; Rowlinson et al. 2013; Chen et al. 2017). The fraction of long GRBs that may be powered by a long-lived magnetar could be higher than 50% (see e.g., Bernardini 2015).
Given these uncertainties, we conclude that the GRB rate cannot be straightforwardly connected with the formation rate of stellar BHs.
4.2 The progenitors of BBH mergers
Interestingly, the progenitors of BBH mergers appear quite similar to those of GRBs. The large BH masses and their coalescence time, which is shorter than the age of the Universe, require massive progenitors born in low-metallicity environments, as shown by various authors (e.g., Eldridge & Stanway 2016; Marchant et al. 2016; Belczynski et al. 2017). Moreover, the low aligned spin of the coalescing BHs constrains the radius of their progenitors since large progenitors in close binaries synchronize quickly, leading to a large aligned spin. This practically reduce the candidates to Wolf–Rayet stars or population III stars (e.g., Kushnir et al. 2016; Hotokezaka & Piran 2017).
While gravitational wave observations clarify the nature of the progenitors of BBH mergers, at present they are too few to significantly constrain the fraction of stellar BHs that end up in these systems. In addition, despite abundant literature on the relative rates of various systems of double compact objects, we have found few estimates of the absolute fraction of BHs that end their life in BBH mergers. Such an estimate is provided by Elbert et al. (2017) who show that the detection rate of BBH mergers with advanced LIGO can be explained if ~1% of the total BH population is found in BBH mergers. With the detection of an increasing number of BH mergers and the progress of stellar evolution models for massive stars in various environments, it is reasonable to expect better constraints on the fraction of stellar BHs in BBH mergers in the near future.
4.3 Discussion
GRBs and BBH mergers open two windows on the birth of stellar mass BHs. It is striking to consider that the formation of their progenitors invoke the same ingredients: a massive star born in a low-metallicity environment which has lost its external layers. Binarity, which is mandatory in BBH mergers, may also play an important role in GRB models. At this stage however, we have no observational clues on the possible links between BBH mergers and GRBs, and we briefly speculate on the connection between these two populations with two extreme hypotheses: BHs in BBH mergers are born with a GRB, or BHs in BBH mergers are born “silently”, without a GRB.
With R0 ≤ 1 for α ≥−1.5, our simple analysis shows that the birth rate of BHs in long GRBs is most probably larger than the birth rate of BHs in BBH mergers. In principle this allows all BHs born in BBH mergers to emit a GRB at birth. Furthermore, BHs in BBH mergers have more chance than other BHs of emitting a GRB at birth since they have similar progenitors. Considering that Swift has already detected more than 1100 GRBs, several of them could be associated with the birth of BHs in BBH systems. If we could recognize the GRBs associated with the birth of these BHs, we would be in the situation of observing the beginning and the end of the life of binary systems of massive stellar BHs and we could obtain precious information on the demography and mass spectrum of stellar BHs, on the fraction of BHs born in binary systems, or on the coalescence time. Unfortunately, for the moment we have no indication of characteristic features that could help to distinguish GRBs associated with the birth of massive BHs in binary systems.
Alternatively, it is possible that BHs born in BBH mergers were born silently (in gamma-rays), making them a distinct population from long GRBs. Since GRBs require stellar cores with a large angular momentum (MacFadyen & Woosley 1999; Heger et al. 2003), this situation could happen if the progenitors of BBHs are massive stellar cores with low angular momentum, collapsing silently without making a GRB. If they constitute an entirely distinct population, the BBH mergers may significantly change our vision of the BH demography based on the GRB formation history.
While BH are in principle simple objects uniquely characterized by their mass, charge and their spin, their environment and history play a major role in their observability and in the true distribution of their properties. It is thus essential to measure the parameters of existing BHs and to understand the biases that affect these measurements if we want to check the validity of theoretical predictions concerning the population of stellar BHs (e.g., Fryer & Kalogera 2001; Heger et al. 2003; Spera et al. 2015). In this context, BBH mergers offer new insight into BH formation with accurate mass measurements and information on the BH spins. This should help deciphering the formation channel of BBHs and clarify their connection with GRBs and possibly the impact of the BH spin on the formation of GRB jets. This could eventually lead to some improvements in our understanding of accretion/ejection processes at work around BHs of all masses and on the formation of relativistic jets. In this context, the measurement of the ratio of BH formation in these two subpopulations provides an interesting constraint on future models aiming to simulate the diversity of BH formation channels. This ratio can be directly compared with the output of stellar evolution models, as long as they are designed to produce both BBH mergers and GRBs.
In the coming years, the expected increase of BBH and BHNS merger detections (Abbott et al. 2016a) and the refinement of merger models will permit a much more precise evaluation of the stellar BH birth rate across the ages and a much better understanding of the BH population sampled with this technique. The increased reach of gravitational wave detectors will also permit the measurement of the past history of BBH merger formation offering a powerful tool to compare the BH subpopulations explored with BBH mergers and GRBs. The new understanding coming from GW detections may also lead to a new interpretation of previously known sources. Inoue et al. (2016) for instance, propose that Ultra Luminous X-ray sources could be due to a massive star orbiting a young BH, a system that will evolve into a pair of BHs after the explosion of the massive star, and finally into a BBH merger. A list of several sources that are potential BBH progenitors is also presented in Bogomazov et al. (2018). Finally, additional probes of young stellar BH populations, such as subluminous GRBs and off-axis GRBs, will soon come into play. In a few years, the ECLAIRs gamma-ray imager onboard SVOM will explore the realm of soft subluminous GRBs with its energy threshold at4 keV (Godet et al. 2014; Cordier et al. 2015; Wei et al. 2016), while the LSST will detect dozens of optical afterglows from off-axis GRBs in the local Universe (see the LSST Science book by the LSST Science Collaboration 2009).
5 Conclusion
We have compared the birth rate of stellar BHs measured with two completely different observing channels: BBH mergers detected with GW interferometers and GRBs detected with gamma-ray satellites. We have taken into account the coalescence time of BBH mergers to perform the comparison at the time of the BH formation. The main result of our study is that the birth rate of stellar BHs in BBH mergers is a few times smaller than the rate of long GRBs. However, considering the numerous uncertainties involved in the calculation, especially on the present rate of BBH mergers and on the beaming factor of GRBs, we cannot exclude that BHs are formed at the same rate in GRBs and in BBH mergers. This observation raises two questions: what is the fraction of the total BH population in GRBs and in BBH mergers? And what are the possible connections between these two BH subpopulations? The second question is particularly relevant since GRBs and BBH mergers require similar progenitors: massive stars born in a low-metallicity environment. We suggest that this question could be primarily addressed with stellar evolution models, which should be designed to produce both BBH mergers and GRBs. In this context, the measured ratio of the rate of BBH mergers over GRBs provides a constraint that is directly comparable with the predictions of the models.
Finally, the availability of two windows on the population of stellar BHs is only the beginning of the story. Significant observational progress is expected in the near future, with the increased sensitivity of gravitational wave interferometers, and with the opening of new windows on the birth of stellar BHs in the local Universe, such as the detection of off-axis GRBs with the LSST and of soft subluminous GRBs with SVOM.
Acknowledgements
MGB acknowledges the support of the OCEVU LabEx (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government program managed by the ANR. The authors thank the referee for pointing out the constraints imposed by the observation of small aligned spins in binary BH mergers detected with LIGO. JLA thanks R. Mochkovitch for fruitful discussions that improved the content of the paper.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, ApJ, 818, L22 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016c, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 118, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Klencki, J., Meynet, G., et al. 2017 ArXiv e-prints [arXiv:1706.07053] [Google Scholar]
- Bernardini, M. G. 2015, J. High Energy Astrophys., 7, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardini, M. G., Margutti, R., Mao, J., Zaninoni, E., & Chincarini, G. 2012, A&A, 539, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardini, M. G., Campana, S., Ghisellini, G., et al. 2013, ApJ, 775, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Bogomazov, A. I., Cherepashchuk, A. M., Lipunov, V. M., & Tutukov, A. V. 2018, New Astron., 58, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Yoon, S.-C., Langer, N., & Livio, M. 2007, A&A, 465, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W., Xie, W., Lei, W.-H., et al. 2017, ApJ, 849, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Connaughton, V., Burns, E., Goldstein, A., et al. 2016, ApJ, 826, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Cordier, B., Wei, J., Atteia, J.-L., et al. 2015, ArXiv e-prints [arXiv:1512.03323] [Google Scholar]
- Corsi, A., & Mészáros, P. 2009, ApJ, 702, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1998, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 2007, A&A, 465, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daigne, F., Rossi, E. M., & Mochkovitch, R. 2006, MNRAS, 372, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Osso, S., Stratta, G., Guetta, D., et al. 2011, A&A, 526, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deng, C.-M., Wang, X.-G., Guo, B.-B., et al. 2016, ApJ, 820, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., O’Connor, E., & Ott, C. D. 2012, ApJ, 754, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Berti, E., O’Shaughnessy, R., et al. 2015, ApJ, 806, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Elbert, O. D., Bullock, J. S., & Kaplinghat, M. 2017, MNRAS, 473, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Kalogera, V. 2001, ApJ, 554, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Ramirez-Ruiz, E., & Fox, D. B. 2009, ARA&A, 47, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Godet, O., Nasser, G., Atteia, J.-L., et al. 2014, Proc. SPIE, 9144, 914424 [CrossRef] [Google Scholar]
- Guetta, D., Piran, T., & Waxman, E. 2005, ApJ, 619, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hotokezaka, K., & Piran, T. 2017, ApJ, 842, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, E. J., Coward, D. M., Stratta, G., Gendre, B., & Zhou, H. 2014, MNRAS, 444, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, Y., Tanaka, Y. T., & Isobe, N. 2016, MNRAS, 461, 4329 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Mazzali, P. A., Nomoto, K., et al. 1998, Nature, 395, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsson, P., Levan, A., Fynbo, J. P. U., et al. 2006, A&A, 447, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A., Crowther, P., de Grijs, R., et al. 2016, Space Sci. Rev., 202, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X. 2008, MNRAS, 388, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Lien, A., Sakamoto, T., Gehrels, N., et al. 2014, ApJ, 783, 24 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Lyons, N., O’Brien, P. T., Zhang, B., et al. 2010, MNRAS, 402, 705 [NASA ADS] [CrossRef] [Google Scholar]
- MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Giacobbo, N., Ripamonti, E., & Spera, M. 2017, MNRAS, 472, 2422 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mészáros, P. 2003, Nature, 423, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Giannios, D., Thompson, T. A., Bucciantini, N., & Quataert, E. 2011, MNRAS, 413, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Pescalli, A., Ghirlanda, G., Salvaterra, R., et al. 2016, A&A, 587, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Petrosian, V., Kitanidis, E., & Kocevski, D. 2015, ApJ, 806, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Mazzali, P. A., Nomoto, K., Lazzati, D., & Cappellaro, E. 2004, ApJ, 607, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Price, P. A., Fox, D. W., Kulkarni, S. R., et al. 2003, Nature, 423, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Chatterjee, S., & Rasio, F. A. 2016, Phys. Rev. D, 93, 084029 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Metzger, B. D., Tanvir, N. R., & Levan, A. J. 2013, MNRAS, 430, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, G., van Eerten, H., MacFadyen, A., & Zhang, B.-B. 2015, ApJ, 799, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., & Chincarini, G. 2007, ApJ, 656, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Campana, S., Vergani, S. D., et al. 2012, ApJ, 749, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Mereghetti, S., et al. 2016, ApJ, 820, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1999, ApJ, 523, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Shahmoradi, A. 2013, ApJ, 766, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Kulkarni, S. R., Berger, E., et al. 2004, Nature, 430, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Spera, M., Mapelli, M., & Bressan, A. 2015, MNRAS, 451, 4086 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Matheson, T., Garnavich, P. M., et al. 2003, ApJ, 591, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, W.-W., & Wang, F. Y. 2015, MNRAS, 454, 1785 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [NASA ADS] [CrossRef] [Google Scholar]
- Vedrenne, G., & Atteia, J. 2009, Gamma-Ray Bursts: The Brightest Explosions in the Universe (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
- Wanderman, D., & Piran, T. 2010, MNRAS, 406, 1944 [NASA ADS] [Google Scholar]
- Wei, J., Cordier, B., Antier, S., et al. 2016, ArXiv e-prints [arXiv:1610.06892] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Ratio of the stellar BH birth rate measured in BBH mergers and in GRBs, as a function of α the index of the power law distribution of the coalescence times of BBH mergers. The solid and dashed lines show the fraction calculated for the median value of the local rate of BBH mergers measured by Advanced LIGO (Abbott et al. 2017), while the shaded areas indicate the full range of allowed values considering the errors on the local rate of BBHs mergers. The four panels correspond to different values (given in the inset) of the parameters appearing in Eq. (5). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


