| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 33 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201730694 | |
| Published online | 13 February 2018 | |
Multi-technique investigation of the binary fraction of A-F type candidate hybrid variable stars discovered by Kepler⋆,⋆⋆
1 Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussel, Belgium
e-mail: patricia.lampens@oma.be
2 Konkoly Observatory, MTA CSFK, Konkoly Thege M. u. 15-17, 1121 Budapest, Hungary
3 Instituut voor Sterrenkunde (IvS), Katholieke Universiteit Leuven, 3000 Leuven, Belgium
4 Institut d’Astronomie & Astrophysique, Université Libre de Bruxelles, 1050 Brussels, Belgium
5 Thüringer Landessternwarte, 07778 Tautenburg, Germany
6 Department of Theoretical Physics and Astrophysics, Physics Faculty, University of Tabriz, 51664 Tabriz, Iran
Received: 24 February 2017
Accepted: 1 September 2017
Context. Hundreds of candidate hybrid pulsators of intermediate type A–F were revealed by recent space missions. Hybrid pulsators allow us to study the full stellar interiors, where both low-order p- and high-order g-modes are simultaneously excited. The true hybrid stars must be identified since other processes, related to stellar multiplicity or rotation, might explain the presence of (some) low frequencies observed in their periodograms.
Aims. We measured the radial velocities of 50 candidate δ Scuti −γ Doradus hybrid stars from the Kepler mission with the Hermes and ace spectrographs over a time span of months to years. We aim to derive the fraction of binary and multiple systems and to provide an independent and homogeneous determination of the atmospheric properties and v sin i for all targets. The long(er)-term objective is to identify the (probable) physical cause of the low frequencies.
Methods. We computed one-dimensional cross-correlation functions (CCFs) in order to find the best set of parameters in terms of the number of components, spectral type(s), and v sin i for each target. Radial velocities were measured using spectrum synthesis and a two-dimensional cross-correlation technique in the case of double- and triple-lined systems. Fundamental parameters were determined by fitting (composite) synthetic spectra to the normalised median spectra corrected for the appropriate Doppler shifts.
Results. We report on the analysis of 478 high-resolution Hermes and 41 ace spectra of A/F-type candidate hybrid pulsators from the Kepler field. We determined their radial velocities, projected rotational velocities, and atmospheric properties and classified our targets based on the shape of the CCFs and the temporal behaviour of the radial velocities. We derived orbital solutions for seven new systems. Three preliminary long-period orbital solutions are confirmed by a photometric time-delay analysis. Finally, we determined a global multiplicity fraction of 27% in our sample of candidate hybrid stars.
Key words: techniques: spectroscopic / techniques: photometric / binaries: spectroscopic / stars: oscillations / stars: variables: δScuti / stars: rotation
Based on observations obtained with the Hermes spectrograph, which is supported by the Research Foundation − Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland, and the Thüringer Landessternwarte Tautenburg, Germany.
Tables 2 and 3 are only, and Tables C.1–C.3 are also, available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/610/A17
© ESO, 2018
1. Introduction
Many different physical processes compete in the outer atmospheres of A- and F-type main-sequence (MS) stars and their slightly more evolved cousins. In the corresponding region of the H-R diagram, we find the following important transitions:
− 1. The transition from average “slow” to average “fast” rotation. The distribution of v sin i as a function of spectral type shows that stars cooler than F5 have small v sin i (typically <10 km s-1), whereas v sin i can reach several hundreds of km s-1 for hotter stars (Royer 2009; cf. Fig. 2 from Royer et al. 2014). − 2. The transitionfrom deep to shallow convection, that is, from convective to radiative envelopes. Theoretical models indicate a dramatic change in the structure of the outer envelopes near the red edge (RE) of the δ Sct instability strip, that is, near Teff = 7000 K (Christensen-Dalsgaard 2000). This transition (where the sudden onset of convection in the stellar envelope starts, see D’Antona et al. 2002) has also been described as a second “Böhm-Vitense gap”. − 3. The transition from mode driving by convective blocking near the base of the convective envelope (exciting gravity modes of type γ Dor) (Dupret et al. 2004, 2005) to mode driving by the opacity mechanism (exciting acoustic modes of type δ Sct). The two instability strips are largely overlapping, which suggests that two regimes of modes could be simultaneously excited in some stars (i.e. the so-called “hybrid” stars). A recent study of a large sample of candidate γ Dor stars suggests that the latter are confined to the Teff-range from 6900 to 7400 K on the MS, which corresponds to the region in the Hertzsprung-Russell (H-R) diagram where γ Dor pulsations are theoretically predicted (Tkachenko et al. 2013).
− 4. The transition from significant chromospheric activity and (coronal) X-ray emission to (almost) null emission. Such X-ray emission is expected for cool stars (type A7 and later) as a result of magnetic activity and for hot stars (type B2 and earlier) as a result of wind shocks. Intermediate spectral types are virtually X-ray dark (Schröder & Schmitt 2007; Robrade & Schmitt 2009). Theformer transition occurs abruptly, over a temperature interval no larger than 100 K in width, that is, at approximately Teff = 8250 ± 50 K (Simon et al. 2002). Within this narrow temperature range, chromospheric emission abruptly drops from solar brightness levels to more than one order of magnitude lower. These phenomena are linked to surface convection zones and stellar magnetic fields, which are ultimately held responsible for the observed activity (Schröder & Schmitt 2007). Exceptions are the young Herbig Ae/Be stars and the peculiar Ap/Bp stars, where fossil magnetic fields are thought to play a role in the production of X-rays.
The origin of the stellar magnetic fields should also be considered. Dynamo processes generate fields in most of the low-mass stars of the MS, whereas the origin of the large-scale magnetic fields in massive stars is not yet understood (Fossati et al. 2015; Morel et al. 2015). On the other hand, magnetic fields are rare among the intermediate-mass stars. There is indeed no normal A star known with a fossil magnetic field of average strength (Aurière et al. 2007; Lignières et al. 2014): either the fields are (very) strong (Blong> 100 G), as in Ap stars (e.g. Mathys 2001), or ultra weak (Blong< 1 G), as in Am stars (Blazère et al. 2014). Most chemically peculiar stars, however, appear to possess a magnetic field that brakes the rotation and stabilizes the atmosphere, enabling processes of atomic diffusion (Michaud et al. 2015).
In this complex region (see also Antoci 2014), a new group of pulsators has been revealed on the basis of the analysis of the Kepler light curves: they are called the δ Sct – γ Dor or γ Dor – δ Sct candidate hybrid stars (Grigahcène et al. 2010; Uytterhoeven et al. 2011). These candidate hybrid stars are A/F-type pulsating stars located across the instability strips of the δ Sct and the γ Dor pulsators. Their light curves exhibit frequencies in both regimes. A first suspicion of the coexistence of both p- and g- modes already arose from a search for multiperiodicity in early A-type stars based on the Hipparcos epoch photometry (e.g. Koen 2001). Because the hotter ones are unexplained by theoretical models (Grigahcène et al. 2010; Balona et al. 2015), it is important to unravel the physical origin of their low frequencies and to confirm the cases of genuine hybrid pulsation. In the case of KIC 9533489, an object with Teff of 7500 K, the authors concluded in favour of a true hybrid character of the oscillations (Bognár et al. 2015). It is furthermore critical to search for binarity in such stars. One reason is that some of the low frequencies should not be attributed to pulsation but perhaps to ellipsoidality and reflection or even something more exotic (like shallow eclipses or a heartbeat phenomenon). Another reason is that tidal forces in close companions may excite a number of g-modes (as harmonics of the orbital frequency) that would not be excited if the star were single.This could be the case of a pulsating star in an eccentric close binary, where the dynamical tidal forces excite g-mode pulsations (Willems & Aerts 2002). Moreover, a normal γ Dor star coupled to a normal δ Sct star will also mimic a γ Dor – δ Sct hybrid.
The confirmation of genuine cases of hybrid pulsation thus represents an unavoidable step in the study of the A/F-type hybrid phenomenon. In this work, we aim to estimate the fraction of short-period (i.e. with orbital periods between about 1 and 50 d) spectroscopic systems in a sample of brighter A/F-type candidate hybrid stars discovered by the Kepler satellite. Some preliminary results have been reported by Lampens et al. (2015). This survey is based on the 171 candidate hybrid Kepler stars first studied by Uytterhoeven et al. (2011). The following definition of a hybrid star was used in their study:
-
frequencies detected in the γ Dor (i.e. <5 d-1) and δ Sct (i.e. >5 d-1) domains;
-
the amplitudes in both domains are either comparable, or they do not differ by more than a factor of 5–7;
-
at least two independent frequencies detected in both regimes with amplitudes higher than 100 ppm.
Section 2 describes the target selection, the observational strategy, the campaigns, and the observations. Section 3 reports the data processing. In Sect. 4 we explain the method and the data analysis. In Sects. 5 and 7 we present the results of the classification and the orbital solutions of the newly discovered systems, respectively. The extraction of the physical parameters is discussed in Sect. 6. In Sect. 8 we study the periodograms based on the Kepler data and present an observational H-R diagram in Sect. 9. A discussion and conclusions from this work are provided in Sect. 10.
2. Sample and observational strategy
We selected 50 of the brightest objects of the A/F-type candidate hybrid stars classified by Uytterhoeven et al. (2011, cf. Table 3). The observations were performed in the observing seasons from Aug. 2013 until Dec. 2016 with the high-resolution fibre-fed échelle spectrograph Hermes (High Efficiency and Resolution Mercator Echelle Spectrograph, Raskin et al. 2011) mounted at the focus of the 1.2 m Mercator telescope located at the international observatory Roque de los Muchachos (ORM, La Palma, Spain). The instrument is operated by the University of Leuven under the supervision of the Hermes Consortium. It records the optical spectrum in the range λ = 377−900 nm across 55 spectral orders in a single exposure. The resolving power in the high-resolution mode is R = 85 000. Advantages of the instrument are its broad spectral coverage, high stability (the velocity stability of a radial velocity standard star is about 50 m s-1, priv. comm., IvS, Leuven) and excellent throughput (Raskin et al. 2011). Table 1 lists the journal of the spectroscopic campaigns.
More spectra were obtained with the new Ace fibre-fed échelle spectrograph attached to the 1m RCC telescope of the Konkoly Observatory at Piszkés-tető, Hungary. The Ace spectrograph covers the 415−915 nm wavelength range with a resolution R = 20 000. A total of 41 Ace spectra was acquired for 11 targets between October 2014 and March 2015 (Table 1).
Log of spectroscopic observations.
The KIC magnitudes of our targets are brighter than or equal to 10.3 mag. For a target brightness of 9.5 mag, an exposure time of 10 min was usually sufficient to reach a signal-to-noise ratio (S/N) of at least 50 per bin (at λ = 650 nm). The exposure times ranged between 5 and 30 min mostly, leading to a S/N of about 200 in the cross-correlation function (CCF; with over 100 useful lines in the spectrum). We expected to achieve a precision of 1 km s-1 in the measurement of the radial velocities in most cases. We acquired a minimum of four high-resolution spectra for all our targets. Sampling was made irregularly over a total time base of four years. We planned at observing each target during two successive nights in the first week, once after at least a full week, and once more after a time lapse of at least one month. This intended scheme could, however, not always be maintained due to practical circumstances. On average, we dispose of 5−10 Hermes spectra per target. Our spectra cover timescales of a few days, weeks, and months up to a few years per target. The objective is to be able to (spectroscopically) detect binarity for orbital periods ranging from a day up to a few months. The actual temporal distribution of most spectra is illustrated in Fig. 1.
An additional goal is to determine improved atmospheric stellar parameters and v sin i for our targets, in particular for the single-lined cases, in order to pinpoint their position in the H-R diagram. The combination of (at least) four spectra per target allows us to reach a reasonable precision on the effective temperature (Teff) and the surface gravity (log g).
 |
Fig. 1 Distribution of time intervals between successive Hermes spectra for the sample stars showing peaks of 1 and 6 days as well as ~1 and ~3 months. Note the rapidly increasing bin size along the X-axis. |
3. Data reduction and processing
The spectra were reduced with the dedicated reduction pipeline elaborated for Hermes spectra, which includes the subtraction of the bias and stray light, order-by-order extraction, correction for the flat-field, and the scaling in wavelength using calibration frames (obtained with thorium–argon lamps) followed by cosmic-ray removal and order merging (Raskin et al. 2011). The procedure also provides the S/N, which in our case is in the range of 60−70 (at λ = 650 nm) on average. All the spectra were normalised to the local continuum by fitting a low-order polynomial through the continuum parts in wavelength bins of about 50 nm long using the IRAF1 task “continuum”. The average S/N of the median spectra is of the order of 150−200.
The ace spectra were reduced using IRAF standard tasks including bias, aperture extraction, dark and flat-field corrections, and wavelength calibration using thorium–argon exposures. The normalisation, cosmic-ray filtering, order merging (and cross-correlation, see below) was performed by in-house programmes (developed by Á.S.). The systematic errors introduced by the data processing and the stability of the wavelength calibration system of the ace instrument was found to be better than 0.36 km s-1, based on observations of radial velocity standards (Derekas et al. 2017). All the spectra were systematically corrected for barycentric motion.
 |
Fig. 2 Cross-correlation functions in the case of an unresolved double-lined spectroscopic binary system showing obvious asymmetric profiles as well as velocity shifts, e.g. KIC 7756853. |
4. Data analysis
As a first-look analysis, we computed a series of one-dimensional CCFs in the wavelength intervals 415−445, 445−510, and 510−570 nm using different preselected masks. The correlation masks were built from line lists computed with the code synspec (Hubeny & Lanz 1995). In the case of a double- or multiple-lined system, these one-dimensional CCFs may show striking features such as (strong) asymmetric broadening (Fig. 2) or multiple minima (Fig. 3). Occasionally, a composite profile consisting of a narrow profile embedded in a broader one was also detected (e.g. KIC 11572666, Fig. 16). In the complex situations, using various masks, we were able to estimate the number of components in the system as well as derive preliminary values for the component’s spectral types and projected rotational velocities.
4.1. Radial velocities
4.1.1. Single stars and single-lined systems
In the following step, we searched for the most adequate set of fundamental parameters by fitting synthetic models (templates) to the spectrum on the basis of a “minimum distance” method (i.e. by determining the smallest χ2). Thus, we explored the parameter space in terms of spectral type and v sin i and compared each observed spectrum to a variety of synthetic spectra in four distinct spectral bins chosen in the wavelength interval 415−570 nm. The synthetic spectra, suitably broadened to the estimated projected rotational velocity, were computed using the code synspec (Hubeny & Lanz 1995) together with the atlas9 atmosphere models for Teff < 15 000 K and log g = 4 (Castelli & Kurucz 2003). Except for Sect. 4.2.1, the same method was used for all synthetic spectra discussed from hereon. Upon finding the closest match in parameter space, we adopted this best-fit model and computed the radial velocity by Doppler shifting the synthetic spectrum until it matched the observed spectrum. This procedure was repeated for (typically ten) smaller wavelength bins, and the mean and scatter of the radial velocity measurement (RV) were derived from the values for the different bins, after the outliers were omitted.
4.1.2. Double- or multiple-lined systems
In the case of non-single or composite objects, we applied an in-house programme (developed by Y.F.) that uses the algorithm of todcor (Mazeh & Zucker 1994). This code also makes use of synspec (Hubeny & Lanz 1995) and the atlas9 models (Castelli & Kurucz 2003) with the estimated input parameters and log g = 4 to build a suitably broadened synthetic spectrum for each component, and computes the two-dimensional cross correlation and the corresponding radial velocities. It allows us to extract the velocities even when the components are not fully resolved (i.e. the case of blended profiles). We tested different values of spectral type and v sin i and adopted the best-fitting parameters based on the same criterion of “minimum distance” between the observed and the synthetic composite spectrum. Since the ratio of the light contributions is another free parameter obtained during the fitting, we also derived its most probable value. For illustrations of a triple- and a double-lined system, we refer to Figs. 4 and 5, respectively. Finally, we computed two-dimensional CCFs using this best-fit model for a large number of wavelength bins (usually ten bins of 6−20 nm length) and derived the mean and scatter of the RVs from the individual values after the outliers were omitted.
In the case of a triple-lined system, we repeated this procedure in a two-step sequence: first, with components A and B to search for the best-fitting two-component model and the light ratio lA,B = lB/lA, and secondly, adding another component (C) to search for the best-fitting three-component model and the additional light ratio lAB,C = lC/lA + B.
 |
Fig. 3 Cross-correlation functions in the case of a well-resolved double-lined spectroscopic binary showing two distinct minima and velocity shifts in its profile, e.g. KIC 5219533. |
 |
Fig. 4 Case of a triple system: part of the spectrum (in black) and composite model (in red) for KIC 4480321 using the synthetic spectra for three components of type (F0, v sin i =10), (F0, v sin i =10), and (A5, v sin i =160). The thin line (in grey) represents the scaled contribution of the two (F0, v sin i =10) components. |
 |
Fig. 5 Case of a binary system: part of the spectrum (in black) and composite model (in red) for KIC 8975515 using the synthetic spectra (A7, v sin i = 170) and (A7, v sin i = 30). The thin line (in grey) represents the scaled contribution of the (A7, v sin i = 30) component. |
4.2. Atmospheric properties
An additional purpose of the newly acquired spectra is the determination of atmospheric stellar properties. For a reliable characterization and unambiguous location in the H-R diagram, the effective temperature and the surface gravity of the selected targets should be known as reliably and accurately as possible. This requires a comparison between observed and synthetic spectra. For single stars and single-lined systems, we fitted several regions of the normalised median spectrum. For non-single objects, we fitted several regions of the normalised individual spectra.
4.2.1. Single stars and single-lined systems
From each spectrum, three regions of width of 45−70 nm centred on the Hα, Hβ, and Hγ lines were extracted. Continuum normalisation was performed in two steps: first, by dividing each region of interest by the best-fitting model as defined in Sect. 4.1.1, and secondly, by dividing by a polynomial representation of the local continuum. This low-degree polynomial was computed independently also using sigma clipping. We next combined all the normalised spectra of each region into a normalised single median spectrum of higher quality. These median spectra were subsequently compared to synthetic spectra using grids computed in slightly different ways.
Multi-region fits.
Firstly, we performed fits of the three regions of interest containing the lines Hα, Hβ, and Hγ, respectively. An extended grid of high-resolution synthetic spectra computed with plane-parallel model atmospheres was retrieved from the Pollux database (Palacios et al. 2010). We selected the models with a microturbulence of 2 km s-1 (a typical value for A/F-type MS stars, Gebran et al. 2014) and a solar metallicity, for which Teff ranged from 7000 to 9000 K (with a step of 200 K) and log g ranged from 3.5 to 4.9 dex (with a step of 0.2 dex). Only Teff and log g were varied since the extracted regions include the Balmer lines to a large extent, even though they may contain a few shallow metal lines. With this method, the synthetic spectra were selected at the nearest node of the atmospheric values. In general, we adopted the previous estimate for the parameter v sin i since it was found to be precisely determined (cf. Sect. 4.1.1). This procedure provided an averaged value of Teff and a range of probable values for log g, which are listed in Table C.1 (Cols. 11, 12).
Single-region fit.
As an independent final step, we simultaneously (re)derived the three parameters Teff, log g, and v sin i by fitting the range [415−450] nm (including Hγ, cf. Fig. 6) using the code girfit (Frémat et al. 2006). With this method, the model spectra (cf. description above) are interpolated in a grid of (Teff, log g)-values instead of being selected at the nearest node of the atmospheric values. These model spectra were next convolved with the rotational profile and a Gaussian instrument profile to account for the spectrograph resolution.
The results of this spectrum synthesis method are displayed in Table C.1 (Cols. 13−15). At this point, the probable errors are assumed to be of the order of the grid steps (i.e. ϵTeff = 250 K for Teff and ϵlog g = 0.5 dex for log g), since the procedure uses interpolation. In Sect. 6 we confirm that these assumptions are also realistic. An example of the adjustment using girfit for a single object is presented in Fig. 6. We also note the excellent agreement between both determinations (Cols. 11−15 in Table C.1). A direct comparison between the results of the two methods furthermore provides a reliable way to estimate the uncertainties involved.
 |
Fig. 6 Part of the observed spectrum (in black) for KIC 6432054 and model (in red) using the best-fitting set of atmospheric stellar properties Teff = 7542 K, log g = 4.44, and v sin i = 184 km s-1 derived with girfit. |
4.2.2. Double- or multiple-lined systems
The programme girfit was next modified in order to extend the same analysis to spectra with n components (in practice, the spectra of double- and triple-lined systems). The modified programme interpolates the component spectra in the usual grid and combines them into a composite spectrum to find the solution that minimizes the residuals. The minimisation is performed using the Simplex algorithm. In this extended form of girfit (developed by Y.F.), the radial velocities and the light ratios can either be kept fixed or be considered as additional free parameters (our choice). The radial velocities served as a consistency check of the solutions, while the light ratios were considered as added value. For each system, we fitted all the individual normalised spectra using various sets of atmospheric input parameters and up to three spectral regions in order to verify the reliability of our results.
5. Classification
Based on the shape of the one-dimensional CCFs and the evolution of the RV measurements with time, we classified each target according to the following categories: S (for stable), VAR (for currently unexplained possible long-term RV variations), SB (for a spectroscopic binary or triple system), P (for a pulsating star with line-profile variability and/or rotating with the presence of structures on the surface such as chemical spots or temperature gradients), and CMP (i.e. composite, for stars with a narrow, shallow, and almost central absorption feature in their – usually – broad profiles). The P-class may contain A/F-type pulsators of the δ Scuti type where chemical peculiarities appear on the stellar surface as a result of a (weak) magnetic field (e.g. KIC 5988140 = HD 188774, Neiner & Lampens 2015) or where stellar rotation is so fast that it deforms the stellar surface and perturbs the homogeneity of the surface intensity distribution (e.g. Böhm et al. 2015). Our determination of v sin i alone does not suffice to distinguish between the two scenarios. We provide a class for each target of the sample based on the currently available spectroscopic information in Table C.1 (Col. 9). To justify the adopted classification, we provide illustrations for all objects, except for those presented in the text, in the form of one-dimensional CCFs (computed with a mask of type F0 in the wavelength range [510−570] nm for all but for KIC 9775454, where we used a K0-mask) as well as radial velocity plots in Appendices A and B, respectively. We present the list of all RV measurements in Tables 22 and 32.
We briefly comment below on the classification of various particular targets, including the double- and triple-lined systems. For a detailed description of the orbital solutions, however, we refer to Sect. 7. Further results concerning the classification of the selected targets come from our analysis of the photometric data of the Kepler mission and their periodograms (cf. Sect. 8).
 |
Fig. 7 Comparison of the various determinations of Teff. A linear fit using the literature values lower than 7600 K (open symbols) shows an obvious discrepancy in the slope, illustrating the fact that our values for Teff lower than 7700 K are systematically slightly higher than the literature values. The outlier (red symbol) is KIC 7119530, for which two very different literature values were found. |
6. Characterization of stellar atmospheres
Table C.13 summarises the physical information derived from the study of the CCFs and the spectral analyses. This includes the atmospheric stellar properties (cf. Sect. 4.2), as well as the classification of the target into one of the subsequent categories: S (stable), VAR (RV variable), SB (1/2/3) (single-, double-, or triple-lined spectroscopic system, respectively), P (pulsating or possibly rotating), or CMP (composite spectrum). We list the following information: the identifier (Col. 1), period (Col. 2), spectral type (Col. 3), Teff (Col. 4), log g (Col. 5), and magnitude (Col. 6) all from the Kepler Input Catalogue (KIC), except for the spectral type, which comes from Uytterhoeven et al. (2011, Table 1 and references therein), the number of Hermes and ace spectra collected (Col. 7), a comment (Col. 8), the classification (Col. 9), and the model parameters adopted for reconstructing the (in casu composite) spectrum (Col. 10), the mean Teff (Col. 11), the mean log g (Col. 12) based on three regions of interest ([620−686] nm including Hα, [450−520] nm including Hβ, [415−460] nm including Hγ), which allows checking for consistency, and, lastly, the Teff (Col. 13), log g (Col. 14), and v sin i (Col. 15) as derived with girfit in the wavelength range [415−450] nm.
We have 28 targets in common with other studies. This allowed us to perform a useful comparison. Table C.23 summarises the atmospheric stellar properties derived from this work, together with some recently published values. The referred studies are mentioned in the footnotes (Col. 16 from Table C.2). In Figs. 7−9 we illustrate the overall agreement between the various determinations. In particular, the agreement is excellent in Teff and v sin i. The scatter in Teff matches the estimated uncertainty of ±250 K well (Fig. 7). While there is clearly no systematic trend in v sin i, there seems to exist a small systematic offset in Teff in the temperature range [7300−7700] K. Our temperature values appear to be slightly overestimated in this range with respect to the published values (or vice versa). This effect reminds us of the (known) fact that the KIC-values for Teff lower than 7700 K are believed to be systematically underestimated. The scatter in v sin i reflects the estimated uncertainty of ±5−10 km s-1 well, but this depends to some extent on the absolute value (Fig. 9). Two extremely fast-rotating stars deviate from the 1:1 ratio line. The determination of log g, on the other hand, shows a huge spread, which reflects its large uncertainty. It appears from Fig. 8 that some of the literature values were arbitrarily set (or limited) to 4. This is often the case for targets cooler than 7700 K (open symbols). We should also mention that a comparison between previously published values (when possible) shows a similar degree of inconsistency, meaning that the errors are larger than thought. In five cases (e.g. KIC 3429637 (Am), 5965837, 9509296, 9764965 (Am), and KIC 10537907), our determination of log g is very different from that of Catanzaro et al. (2011) or Niemczura et al. (2015). Two such cases (KIC 3429637 and KIC 5965837) are treated in detail in the discussion of the 22 individual targets hereafter. The remaining lack of agreement might also be due to the choice of the spectral intervals, which may not be very sensitive to log g for stars in the temperature range below 8000 K. Still, we conclude that there is no sign of any systematic trend in this plot and that other data points tend to follow the 1:1 ratio line, illustrating the existence of a rough agreement.
 |
Fig. 8 Comparison of the various determinations of log g. Same symbols as in Fig. 7. The largest differences (red symbols) are found for KIC 3429637 (A9m), 5965837 (F2p), 9509296, 9764965 (Am), and KIC 10537907. |
 |
Fig. 9 Comparison of the various determinations of v sin i. Same symbols as in Fig. 7. The largest differences (red symbols) are found for KIC 7119530 and 7827131. |
Searching for common targets also based on lower resolution spectra, we identified 22 targets (26 measurements) in common with the lamost project (De Cat et al. 2015). In Table C.33, we compare the atmospheric stellar properties derived from this work to those derived by the lamost teams using the procedure rotfit (Frasca et al. 2003, 2016). In four cases, different values were derived from the lamost spectra (with a resolution of R ~ 1800). Large differences, in log g mostly, occur for the two fast rotators KIC 3453494 and KIC 9650390, and also in the case of KIC 7748238 (because of our high value of log g). In two cases (KIC 7668791 and KIC 9650390), our value of Teff differs from that of the lamost team, although our determinations of both Teff and log g agree very well with the KIC values. This comparison illustrates the fact that the largest differences occur more often in the fast-rotating A/F-type stars (for which the estimated errors are also large).
6.1. KIC 3429637 = HD 178875
HD 178875 is not a candidate A/F-type hybrid star from Uytterhoeven et al. (2011). This object was classified as a normal δ Scuti star while being suspected of binarity (Catanzaro et al. 2011). For this reason, we included it in our programme. The RV data show variability with an amplitude smaller than ~5 km s-1 on a timescale of several months, but no day-to-day variations (cf. Appendix B). We found no direct trace of spectroscopic duplicity. Since we also detected line profile variations in the CCFs, we classified it as a pulsator accompanied by a long-term RV variability (“P+VAR”). We obtained the following stellar properties: Teff = 7266 K, log g = 2.66, and v sin i = 49 km s-1. While there is a good agreement in Teff and v sin i with Catanzaro et al. (2011), we do not confirm their value of log g = 4, however. In Fig. 8 we note a corresponding large discrepancy. We confirm its status of evolved Am star (cf. Murphy et al. 2012). Since this star is known to have a peculiar spectral type (kF2hA9mF3), its non-standard surface composition may interfere with the gravity determination.
6.2. KIC 3453494
The CCF profiles of this fast-rotating star (estimated v sin i of 220 km s-1) are extremely broad and noisy, which makes it difficult to detect any kind of variability. Notwithstanding the noise and given the limited accuracy, we conclude that the radial velocity and the profiles are stable (“S”). We encountered several other cases of extreme stellar rotation, namely KIC 6756481, 7119530, 7827131, 9650390, and KIC 11602449, as well as KIC 4989900 and KIC 6670742 (the latter two classified as “S/P?”, with some ambiguity in their classification; cf. Sect. 10).
6.3. KIC 4480321
This object is a new spectroscopic triple system (SB3). The spectrum shows a twin-like inner binary orbiting a slightly more luminous and fast-rotating third component (cf. Fig. 4 and the CCF profiles in Appendix A). We have excellent RV coverage for the close binary system and estimate the uncertainty of the component RV measurements to be significantly smaller than 1 km s-1. From two campaigns of 11 nights each, we derived an initial value near 9 days for the orbital period of the close binary. An orbital solution for the inner binary is presented in Sect. 7. A tentative orbital solution for the outer system is also provided, although the period is probably longer than the available time span.
Using a composite model consisting of three synthetic spectra (A5, v sin i = 160), (F0, v sin i = 10), and (F0, v sin i = 10), we were able to reconstruct parts of the observed spectra very well (see Fig. 4). We next applied the extended three-dimensional version of girfit in three different regions of the normalised spectra using a composite model to find the solution that minimizes the residuals between the model and the observations. We fixed the log g values to 4 (for MS phase) and the projected rotational velocities to our previous estimations (of 160 km s-1, 10 km s-1, and 10 km s-1, respectively), and varied the initial values for the effective temperatures and the two luminosity ratios (the only free parameters left). We found component effective temperatures of Teff1 = 7900 ± 100 K with both Teff2 and Teff3 in the range between 6300 and 6900 K (probably of similar temperature), in accordance with some of the observed spectra. However, no unique solution was found that would fit all our spectra in any of the inspected wavelength regions [415−450], [500−520], or [630−680] nm. The component properties are thus not well known. We conclude that high-S/N spectra are crucial for a more precise component characterization of this triple system.
6.4. KIC 5219533
This target forms a visual double system with HD 189178 (5.5 mag, component A) at an angular separation of 65′′. It is a well-resolved double-lined spectroscopic system (cf. Fig. 3), with a primary component of type Am (A2−A8, Renson & Manfroid 2009). We furthermore deduce the presence of a more rapidly rotating component of a slightly cooler spectral type based on two arguments: (a) from the unusual aspect of the (component and systemic) radial velocities (cf. Appendix B); and (b) from a comparison of the observed spectra with models. For example, we found that a two-component synthetic spectrum is unable to reproduce the broad features found in various parts of the spectrum (cf. Fig. 10). We therefore conclude that this object is a new triple-lined spectroscopic system (SB3). An orbital solution for the inner binary is presented in Sect. 7.
In order to compute reliable values for the component’s atmospheric parameters and because the third component is very diluted, we applied the two-dimensional version of girfit to different regions of the normalised observed spectra in search of the two-component model that best minimizes the residuals. Because of the complexity of this spectrum, we fixed the log g values to 4 and kept the projected rotational velocities constant by adopting our previous estimations of v sin i (i.e. 10 km s-1 for both components). The component effective temperatures and the luminosity ratio were the only free parameters. Allowing for more free parameters did not allow us to find any reliable solution. We chose various initial values and spectral regions, which gave us estimates for the uncertainties on the free parameters. Although both components are usually well resolved, we were unable to find a unique solution for all our spectra. The most promising results were obtained in the interval [500−520] nm, where a consistent solution was found for most spectra (7 out of 12). In this case, the mean effective temperatures of Teff1 = 8300 ± 100 K and Teff2 = 8200 ± 100 K coupled to a light factor l1 equal to 0.53 ± 0.02 were obtained. This indicates that the pair might consist of nearly identical “twin” stars of spectral type A5. In the ranges [415−450] nm and [640−670] nm, however, a more pronounced temperature difference between the components was derived, but the solutions from the individual spectra showed less consistency. Since our models assume a standard solar composition, possible explanations for this behaviour might be the non-standard metallicity of the component(s) or the influence of the diluted third companion. A few spectra of high(er) S/N are needed to improve the characterization of this new triple system.
 |
Fig. 10 Observed spectrum of KIC 5219533 (in black) vs. model spectra consisting of two narrow-lined components (in red). An extra broad-lined component of a similar spectral type could explain the additional wings and parts with missing continuum. |
6.5. KIC 5724440
The CCF presents an extremely broad profile together with some additional features that seem to be variable. The broad profile appears to be stable in RV. We classified this target as “P?”. The fast rotation could be the reason why previous determinations of Teff showed a large scatter (Catanzaro et al. 2011), but our value matches both the spectroscopic determination by Niemczura et al. (2015) and the photometric one by Masana et al. (2006) perfectly. This object closely resembles KIC 6432054, which was also classified as a pulsator.
6.6. KIC 5965837
The CCF presents a narrow profile that is reflected by the extremely low v sin i. The changes in the profile core are obviously due the presence of non-radial pulsations (classified as “P”, cf. Appendix A). The radial velocities show a distinct variable pattern with a very low amplitude, a possible indication of radial pulsation. It is the coolest candidate hybrid star in our sample. We derived the following stellar properties: Teff = 6800 K, log g = 3.3, and v sin i = 15 km s-1. While there is an excellent agreement in Teff and v sin i, we cannot confirm the value of log g = 4 (Catanzaro et al. 2011). Instead, we derived log g = 3.3 based on the Mg ii triplet using the spectral range [510−520] nm. Furthermore, we discovered that its chemical composition is non-standard and heavily enhanced in metals. In fact, this star’s spectrum almost perfectly matches that of 20 CVn, a well-known ρ Puppis star (Fig. 11). In conclusion, KIC 5965837 is a newly discovered ρ Puppis star, that is, an evolved and cool giant star with a metal-rich surface composition also showing pulsations. This is an interesting Kepler star for a detailed study in view of the coexistence of pulsation and metallicism (Kurtz et al. 1995).
 |
Fig. 11 Part of the observed spectrum for KIC 5965837 (in black) and the corresponding part of the elodie spectrum of 20 CVn artificially broadened to the same rotation velocity (v sin i = 15 km s-1) (in red). |
6.7. KIC 6381306
This object is another new spectroscopic triple system (SB3). It consists of a “twin”-like binary and a slightly more luminous, more rapidly rotating primary component. For the inner binary system, we estimated an orbital period of ~4 days. For the outer system, a periodicity of between about 100 and 200 days is expected. Both orbital solutions are presented in Sect. 7.
We applied the extended three-dimensional version of girfit in different regions of each spectrum to find the solution that best minimizes the residuals. The model spectrum is a composite of three components. We fixed the log g values to 4 and the projected rotational velocities were set close to our previous estimates (90−100 km s-1, 5−10 km s-1, and 5−10 km s-1, respectively). The component effective temperatures and two luminosity ratios were the only free parameters left. We chose various initial values for these input parameters. Very similar results were found across both intervals [415−450] and [500−520] nm, although a consistent solution for only half of 13 spectra was obtained at best. From these computations, we obtained mean effective temperatures of Teff1 = 9000 ± 100 K, Teff2 = 7400 ± 100 K, and Teff3 = 7200 ± 50 K coupled to light factors of 0.79, 0.11, and 0.10 (for l1,l2, and l3, respectively). It is moreover evident that such a complex model requires spectra of high(er) S/N ratio for a better characterization of this system.
6.8. KIC 6756386 and KIC 6951642
Both objects have been classified as“P+VAR”. Their CCF profiles show clear line-profile variations that are due to stellar pulsations (cf. Appendix A). In addition, the temporal evolution of both RV data sets indicates a long-term variability with a low amplitude, whose origin cannot yet be determined (cf. Appendix B).
6.9. KIC 6756481 and KIC 7119530
The CCFs present an extremely broad profile but with an additional sharp-peaked feature (cf. Appendix A). Unlike the case of the very fast rotator KIC 5724440, we verified that the narrow central feature of KIC 6756481 remains constant on the velocity scale, suggesting the possible presence of a circumstellar shell. In this case, the broad lines would correspond to the stellar photosphere and the narrow central lines to a circumstellar shell (e.g. Mantegazza & Poretti 1996). In the case of KIC 7119530, this feature is nearly central and appears to be stronger in the red part of the spectrum. The RVs of the broad absorption profiles are constant (cf. Appendix B). In Fig. 12 we compare the Hα profile of KIC 6756481 with that of KIC 6670742 of the same Teff and v sin i to search for a sharp absorption core (e.g. Henry & Fekel 2003). We see that the two profiles are almost identical except in the small core region, where the profile of KIC 6756481 is sharper and slightly deeper. In the case of KIC 7119530, we found a perfect match with the Hα profile of KIC 4989900 (of the same Teff and v sin i). We classified both stars as “CMP” (which stands for composite spectrum). Their atmospheric parameters are similar, although not exactly identical, see the high projected rotational velocity of KIC 6756481, for instance. Owing to its fast rotation, the uncertainties on the RVs are larger than usual, which makes it very difficult to detect any trace of variability. Similar cases among the late A/early F-type stars known in the literature are seven objects that were reported as possible shell stars by Fekel et al. (2003). An alternative explanation is that these objects consist of (at least) two components of similar type and without any detectable RV variation on the short-term scale. Such a physical cause was eventually confirmed (Henry & Fekel 2003), also more recently by Fekel (2015) for the triple system HD 207561.
 |
Fig. 12 Comparison of two Hα-profiles: KIC 6756481 (plotted in black) versus KIC 6670742 (in grey). |
6.10. KIC 7756853
The CCF shows a highly variable and sometimes asymmetric profile that is due to the presence of a companion (cf. Fig. 2). The variations in RVs with time confirm the detection as a new double-lined spectroscopic binary (SB2). Both components present a v sin i difference of about 20 km s-1 (Table C.1). We applied the two-dimensional version of girfit in different regions of each spectrum to find the solution that best minimizes the residuals. We explored the parameter space by varying the number and the initial values of the input parameters. To restrict the number of free parameters, we used our previous estimates of log g and projected rotational velocity. The latter appeared to be reliable and very consistent, in such a way that we kept their values fixed in most fits. The log g values of the models were fixed to the value 4 (MS phase). This also provided estimates of the uncertainties on the adopted input parameters.
While a good match was found with a model consisting of an A1-type primary with v sin i1 = 50 km s-1 and an A5-type secondary with v sin i2 = 30 km s-1 during the initial analysis, the actual process converged towards a pair of solutions signalling the existence of (at least) two minima. Imposing log g = 4 and v sin i, a first stable solution was found in the region [415−450] nm with Teff1 = 9600 ± 100 K and Teff2 = 8260 ± 60 K and a light factor l1 equal to 0.61 ± 0.03, but another stable solution was also found with a light factor l1 equal to 0.54 after reversing the assignment of v sin i to the components. This smaller light factor indicates compensation for the fact that the v sin i value corresponding to the component with the lower Teff is higher.
In the region [500−520] nm, where the residuals were smallest, a first stable solution with larger temperature differences was found with Teff1 = 9880 ± 100 K and Teff2 = 7480 ± 170 K and a light factor l1 equal to 0.73 ± 0.04 (model A). However, exchanging the values of v sin i, we found a second stable solution with Teff1 = 9980 ± 120 K and Teff2 = 7300 ± 140 K and a light factor l1 equal to 0.66 ± 0.04 that fitted all our spectra equally well (model B). When we included v sin i as additional free parameters, similar values of Teff were retrieved. Model B thus consists of an A1-type primary with v sin i1 = 27 ± 5 km s-1 and an A5/F0-type secondary with v sin i2 = 57 ± 5 km s-1. The distinction between the different solutions is hard to make as the computed composite spectra look very similar except for a few blended absorption lines. We compared the two possible models with a single observed spectrum in the range [415−450] nm and observed that the noise level in the spectrum does not allow us to distinguish between them. To allow for better distinction, we simulated the composite CCF for each model using a mask of spectral type A4 (Fig. 13). This comparison shows that model B represents the observed composite CCF more adequately than model A. This is also confirmed by the residual values. In addition, we compared two spectra with the solutions of model B in the spectral range [386−404] nm. In this range, the solution with the higher temperature (Teff2 = 8400 K) reproduces the Ca ii line (λ = 393 nm) very well. This binary is clearly a difficult study case because of the large blends between the components. We tentatively adopted the solution named “model B” found in the region [500−520] nm.
 |
Fig. 13 Observed versus modelled CCF in the case of KIC 7756853. The spectral range used is [415−450] nm. Model A is shown in green/lilac, while model B is shown in (light/dark) blue. |
6.11. KIC 7770282
The CCF profiles show clear asymmetric variations that were first attributed to the presence of a companion. Upon closer inspection, however, we found that the CCF shape is maximally distorted in the core and the red wing only, while the blue wing remains apparently unaffected (cf. Fig. 14). The RV data indicate a scatter higher than normal and thus possible variability of amplitude smaller than a few km s-1, but we attribute this RV scatter to the line profile variations (cf. Appendix B). The distortions seen in the CCFs are probably caused by features that are located at the stellar surface. They could be the signature of pulsations (“bumps”) or rotational modulation (“spots”). It should also be remarked that the dominant period found in the Kepler photometry is almost equal to one day. We conclude that this object is (most) probably not a spectroscopic binary, but should rather be considered as “P”. It deserves to be re-examined in the light of several high(er) quality spectra.
 |
Fig. 14 CCF profiles of four different spectra of KIC 7770282. They illustrate the largest observed distortions. |
6.12. KIC 8975515
This object is another new double-lined spectroscopic system (SB2) with an orbital period of at least 1000 days. The RV curve presents a well-defined modulation of the slowly rotating component with an amplitude smaller than 10 km s-1. An orbital solution for this long-period binary system is presented in Sect. 7.
Unlike the case of KIC 5219533, the two components have dissimilar projected rotational velocities (cf. Fig. 5 and CCF profiles in Appendix A). Therefore, we let the component effective temperatures, the v sin is, and the luminosity ratio be free parameters, but fixed the log g values to 4. As for KIC 5219533, a wide variety of initial values and spectral regions was explored in search for a consistent solution. In this case also, we observed that the resulting values depend on the chosen spectral region. In the interval [415−450] nm, the mean effective temperatures of Teff1 = 6800 ± 20 K and Teff2 = 8250 ± 4 K coupled to v sin is of 161 ± 1 and 32 ± 1 km s-1, respectively, with a light ratio l1 equal to 0.49 ± 0.02 were obtained. In the interval [500−520] nm, the mean effective temperatures of Teff1 = 7440 ± 20 K and Teff2 = 7380 ± 21 K coupled to v sin is of 164 ± 0.5 and 31 ± 1 km s-1, respectively, with a light ratio l1 equal to 0.65 ± 0.03 were obtained. In the interval [640−670] nm, the mean effective temperatures of Teff1 = 6960 ± 150 K and Teff2 = 7850 ± 150 K coupled to v sin is of 154 ± 2 and 32 ± 1 km s-1, respectively, with a light ratio l1 equal to 0.51 ± 0.04 were obtained. Since the residual sum of squares (RSS) of all our spectra is much lower in the [500−520] nm interval, we decided to adopt the atmospheric parameters derived from this region. This indicates that the pair might consist of two nearly identical stars of type A8. The projected rotational velocities, v sin i1 and v sin i2, are safely determined to be 162 ± 2 and 32 ± 1 km s-1. In the ranges [415−450] nm and [640−670] nm, however, a more pronounced temperature difference (~1000 K) between the components was found, as in some other cases. Follow-up as well as high(er) S/N spectra are required to obtain more accurate component properties of this system.
6.13. KIC 9700679
The few Hermes spectra that were acquired indicate an obvious shift in the radial velocity (cf. Appendix B). This object is another single-lined spectroscopic system (SB1). Since it has a KIC temperature of about 5070 K, it is (much) too cool to be considered as a potential A/F-type hybrid star.
6.14. KIC 9775454
The CCF (computed with a mask of type K0 instead of F0) presents clear distortions in shape, accompanied by a narrow feature that moves but remains close to the central position. Furthermore, we detected a change of small amplitude in RV (cf. Appendix A). This is most certainly another long-term spectroscopic binary system. We classified this object as “SB1”, although some lines due to the secondary component obviously affect the observed spectrum (the companion is difficult to detect; until we obtain RVs for the secondary, we will not use the “SB2” classification). Based on the appearance of the RV curve (cf. Appendix B), we suggest a simple estimate of the order of 1700 days for the period. We plan to continue the RV monitoring of this system and to search for an orbital solution of type SB2. Since the time-delay analysis supports the existence of a similar periodicity (cf. Sect. 8), we intend to combine both data types into a joint analysis in the future. This is one of the coolest objects of the sample.
6.15. KIC 9790479
The CCF presents a probable stable profile accompanied by long-term variations in RV. We classified it as a single-lined spectroscopic binary (SB1). A possible orbital period is of the order of 230 days (see Fig. 22 in Sect. 7). This system needs follow-up observations during the next two years.
6.16. KIC 10537907
The CCF profiles clearly show the signature of pulsations (cf. Appendix A), also accompanied by a small shift in RV on a timescale of ~1500 days (cf. Appendix B). We classified it as a probable single-lined spectroscopic binary with pulsations (“P+SB1”). The system also needs additional follow-up observations.
6.17. KIC 10664975
Some CCF profiles of higher quality display features in the form of “moving bumps” probably caused by pulsations (cf. Appendix A), while the RV data are stable (cf. Appendix B). We thus classified it as a pulsator (“P”).
6.18. KIC 11180361
The CCF shows an extremely broad and noisy profile that also appears to be stable in RV (cf. Appendix B). This target (KOI-971) is a new Kepler eclipsing binary system (Slawson et al. 2011) with an orbital period of 0.5331 days. It has been classified as stable (“S”) based on our adopted criteria. This means that the secondary component does not visibly affect the observed spectrum.
6.19. KIC 11445913
The CCFs show a superposition of two components (cf. Appendix A). This is a new double-lined spectroscopic system (SB2) consisting of an early F-type star with a K-type companion, both with a low v sin i (Fig. 15). The primary component is probably of type Am. The variations in RV indicate a long-term change, mostly due to one older measurement and another measurement apparently in anti-phase with respect to the remainder of the data (cf. Appendix B). The orbital period is not yet known.
A variety of initial values and spectral regions was explored in the search for a consistent match between the observed spectra and the models. We let the component effective temperatures, the v sin is and the luminosity ratio be free parameters while fixing the log g values to 4. Here again, the best fits were obtained in the [500−520] nm interval. Thus, we decided to adopt the atmospheric parameters derived from this region. The mean effective temperatures of Teff1 = 7180 ± 20 K and Teff2 = 5750±21 K coupled to v sin is of 55 ± 1 and 8 ± 4 km s-1, respectively, with a light ratio l1 equal to 0.95 ± 0.01 were obtained. This solution was found to be consistent with all our spectra. In the [630−680] nm interval, the temperature difference between the components appeared to be about 500 K larger, although the quality (in terms of RSS) is poorer. This system definitely deserves more follow-up observations in the next years.
 |
Fig. 15 Observed versus modelled spectrum for KIC 11445913 showing the two distinct contributions in red and blue. The plotted range includes the Paschen series and a line of Ca triplet. |
6.20. KIC 11572666
KIC 11572666 is another double-lined spectroscopic binary whose lines are strongly blended, with one extremely broad and one narrow component (SB2). It is very similar to the systems analysed by Fekel et al. (2003). We used the extended version of Girfit to derive the component’s spectral characteristics. For each observed spectrum, we chose several models and used different initial values based on our previous estimations of the spectral types and the projected rotational velocities. Here, we also let the projected rotational velocities and the log g values be free parameters. For consistency, we repeated the fitting process with the two log gs fixed to 4 (MS phase). In this case, a unique model appeared to be compatible with all our spectra. In the spectral range [415−450] nm, we found the mean parameters Teff1 = 7950 ± 40 K, (log g1 = 3.9 ± 0.2 or 4 (fixed)), v sin i1 = 267 ± 5 km s-1 in combination with Teff2 = 6000 ± 150 K, log g2 = 4 (fixed) and v sin i2 = 22 ± 3 km s-1. In the spectral interval [500−520] nm, we derived Teff1 = 7900 ± 80 K, v sin i1 = 253 ± 2 km s-1 in combination with Teff2 = 6150 ± 200 K and v sin i2 = 20 ± 2 km s-1. Both solutions agree with each other, the model consists of a rapidly rotating F0-type primary with v sin i1 = 250 km s-1 and a F/G-type secondary with v sin i2 = 20 km s-1. We also simulated the composite CCF using a mask of spectral type A4 (Fig. 16). This plot shows that the adopted model represents the observed composite CCF extremely well. The RVs were previously determined using the model of an A5-type primary with v sin i1 = 250 km s-1 and an F3-type secondary with v sin i2 = 20 km s-1. The RVs of the secondary component are very well defined, whereas those of the primary component are only poorly determined because of its fast rotation (cf. Fig. 23). This system contains a primary component of type Am and requires further RV monitoring.
 |
Fig. 16 Observed versus modelled CCF in the case of KIC 11572666. The combinations used for the models are F0-G2, F0-F3, A7-G2, A7-F3, A5-G2, and A5-F3. The closest match is found for the model with two early F-type components of very different v sin i (in light blue). The next best match is for the A7-G2 model (in pink). |
7. Multiplicity rate and orbital solutions
We repeatedly observed 50 targets and KIC 3429637 (previously classified as a δ Scuti star) with Hermes and ace, and we found direct evidence for spectroscopic duplicity in ten cases. This concerns the single-lined (SB1) systems KIC 9700679, 9775454, and KIC 9790479, the double-lined (SB2) systems KIC 7756853, 8975515, 11445913, and KIC 11572666, and the triple-lined (SB3) systems KIC 4480321, 5219533, and KIC 6381306. The well-detected new spectroscopic systems represent 20% of the total sample. Furthermore, we also identified two extremely fast rotators where a narrow and almost central feature is superposed onto a very broad stellar profile, which we classified as “C(o)MP(osite)” (i.e. KIC 6756481 and KIC 7110530). In both cases, the central feature might be linked to a shell-like contribution or to an unknown stellar companion (Fekel 2015).
With respect to the sample of A/F-type candidate hybrid stars, we did not consider KIC 9700679, which is too cool for an A/F-type star in the following discussion. Thus, we detected nine spectroscopic systems among 49 targets. In addition, we should consider the targets with a long-term and low-amplitude variability of their radial velocities classified as “VAR”, as these may turn out to be (mostly single-lined) long-period systems. There are three such detections, which gives a total number of 12 (out of 49), corresponding to a spectroscopic multiplicity fraction of 24%. When we add to this the known eclipsing binary KIC 11180361, we derive a global multiplicity fraction of 27%. This number indicates that at least one-fourth of our sample of candidate hybrid stars belongs to a binary or a multiple system of stars.
For four systems (with periods shorter than 100 days), our RV measurements have sufficient phase coverage to allow a reliable determination of the orbital period and a search for an orbital solution. In six more cases (of which three refer to different systems), we propose a preliminary or plausible orbital solution only. In all the remaining cases, the RVs plotted as a function of time are provided in Appendix B.
7.1. KIC 4480321
We computed a best-fitting orbital period of 9.2 days using period04 (Lenz & Breger 2014). This result was subsequently refined using an updated version of the Fortran code vcurve_SB for double-lined systems (priv. comm., IvS, Leuven). The presence of the third component influences the systemic velocity of the inner binary, thus we allowed for systematic offsets of its value with time. The two component RV curves are illustrated in Fig. 17. The residuals are small and homogeneously distributed around null. The final orbital parameters are listed in the upper panel of Table 4.
We found that orbital periods of the order of the time span (e.g. a period of 1500 days) or longer provided convincing solutions for the wide system (AB-C). Based on the currently available RVs, the best possible outer orbital solution (in terms of rms) has a period of about 2280 days. The RV curves of the centre of mass of the close pair AB, together with that of component C, illustrate the solution and are displayed in Fig. B.2. The parameters of this tentative orbital solution are listed in the bottom panel of Table 4. We can derive a limitation on both inclinations when we consider that each component of the SB3 system should have a mass in the range [1−3.5] M⊙ (following the conclusion in Sect. 6.3). We thus obtain the following conditions on i and iout: 36 < i < 63° and 42 < iout < 57°. In Sect. 8 we show that the outer orbital solution can be confirmed and improved. However, to further constrain the parameters of the wide orbit, we will continue the long-term RV monitoring of this interesting system.
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 4480321.
 |
Fig. 17 Radial velocities for components A and B of the new triple-lined system KIC 4480321 plotted together with the orbital solution of the inner binary (AB) system and adjusted systemic velocity offsets. The residuals are shown in the bottom part. |
7.2. KIC 5219533
From the RV plot, we estimated an orbital period of the order of 32 days and derived a corresponding plausible orbital solution for the inner binary (AB) of this new SB3 system. Our solution confirms the twin character of the inner pair. The orbital parameters are listed in the upper panel of Table 5. Because of the (diluted) third component, which influences the systemic velocity of the inner binary, we allowed for variability of this parameter. The two component RV curves are illustrated in Fig. 18. We find a limitation on the inclination i when we consider that each component of the inner binary should have a mass in the range [1.5−3.5] M⊙ (following the conclusion in Sect. 6.4). We then obtain the condition 46.5 <i< 72°. A preliminary solution for the systemic radial velocity of the close pair indicates that a period of the order of 1600 days accommodates the current RV data well (see Fig. B.3). The parameters of this tentative orbital solution are listed in the bottom panel of Table 5. One data point is an obvious outlier caused by a blend. Additional RVs are planned to determine a more accurate orbital solution for the AB pair and to better constrain the wide orbit of this system. In Sect. 8 we present new evidence for the outer orbital solution.
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 5219533.
 |
Fig. 18 Radial velocities for components A and B of the new triple-lined system KIC 5219533 plotted with a plausible orbital solution for the inner binary (AB) system. The residuals are shown in the bottom part. |
7.3. KIC 6381306
We computed the best-fitting orbital period using period04 and obtained the value of 3.9 days. This value was subsequently refined using the code vcurve_SB for double-lined systems. The presence of the third component influences the systemic velocity of the inner binary, thus we allowed for systematic offsets of its value with time. The two component RV curves are represented in Fig. 19. The residuals are very small and show no systematic trend. The orbital parameters of the close (AB) and the wide (AB-C) system are listed in Table 6. We remark that since the eccentricity of the AB pair is consistent with null, the orbit is circular, therefore neither ω nor T0 are very meaningful. The RV curves of the centre of mass of the close pair AB, together with that of of component C, based on an orbital period of 212 days, are displayed in Fig. B.4. We can furthermore derive strict limitations on both inclinations from the condition that each component of this system should have a mass in the range [1−3.5] M⊙ (following the conclusion in Sect. 6.7). We thus obtain the conditions 8.5 <i< 13°and 8.4 <iouter < 10°. We note that there is a high probability of coplanarity.
 |
Fig. 19 Radial velocities for components A and B of the new triple-lined system KIC 6381306 plotted together with the orbital solution of the inner (AB) binary system and adjusted systemic velocity offsets. The residuals are shown in the bottom part. |
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 6381306.
7.4. KIC 7756853
KIC 7756853 is an SB2 whose spectral lines are mostly blended. We recomputed its RVs using synthetic spectra with the parameters of model B (cf. Sect. 6.10) and compared them to the original data set. An orbital solution was derived for both cases. We estimated an orbital period of the order of ~100 days based on the RV plot of 14 spectra. A slightly better agreement in terms of root mean squared residuals was found using model B: the mean residuals stay below 1 km s-1 and are systematically smaller than with model A. We therefore consider that the best choice consists of an A1-type primary with v sin i1 = 30 km s-1 and an A5-type secondary with v sin i2 = 60 km s-1 (model B). The adopted orbital solution is illustrated in Fig. 20. Table 7 lists the corresponding orbital parameters with their uncertainties.
 |
Fig. 20 Radial velocities for components A and B of the new double-lined system KIC 7756853 plotted with the proposed orbital solution of the binary. The residuals are shown in the bottom part. |
Values and standard deviations of the constrained parameters of the orbital solution for KIC 7756853.
7.5. KIC 8975515
The RV plot of the slowly rotating (named secondary) component presents a clearly defined modulation with an amplitude well below 10 km s-1. From this, we estimated an orbital period of the order of 1000 days (possibly longer) for this new SB2 system with dissimilar components. Owing to the extreme scatter on the RVs of the fast-rotating (named primary) component, we applied the code vcurve_SB for single-lined systems to the data of the secondary (only), and found possible orbital solutions with a period close to either 800 days or twice as long. Since the time-delay analysis supports the existence of a 1600-day long variation (cf. Sect. 8), we chose the second possibility. A tentative set of orbital parameters is listed in Table 8. The preliminary orbital solution is illustrated in Fig. 21. It is obvious that this solution accommodates the currently available RVs of component B very well since the residuals are really small. In Sect. 8 we present new evidence to confirm this solution. We will also extend the RV monitoring for another season, in order to further improve the orbital parameters, whilst offering the benefit of a solution of type SB2.
 |
Fig. 21 Radial velocities for the companion of KIC 8975515 plotted with the preliminary orbital solution of the binary (type SB1). The residuals are shown in the bottom part. |
Values and standard deviations of the constrained parameters of the orbital solution for KIC 8975515.
7.6. KIC 9790479
The RV plot of this single-lined system and a preliminary orbital solution based on an approximated period of 231 days are illustrated by Fig. 22. A tentative set of orbital parameters is listed in Table 9.
 |
Fig. 22 Radial velocities for the single-lined system KIC 9790479 showing a preliminary orbital solution. The residuals are plotted in the bottom part. |
7.7. KIC 11572666
The RV plot for the cooler secondary component of this new SB2 system enabled us to derive an estimated orbital period of 611 days, as well as a tentative set of orbital parameters that is listed in Table 10. This preliminary orbital solution is illustrated in Fig. 23. Owing to the huge scatter of the RVs of the primary component, a modelling of type SB2 based on the (weighted) velocities of both components did not allow us to improve upon this preliminary solution.
Values and standard deviations of the constrained parameters of the orbital solution proposed for KIC 9790479.
Values and standard deviations of the constrained parameters of the orbital solution proposed for KIC 11572666.
 |
Fig. 23 Radial velocities for the companion of KIC 11572666 showing a preliminary orbital solution (type SB1). The residuals are plotted in the bottom part. |
8. Time-delay analysis
The orbital motion of a system with a pulsating component introduces a periodic shift of the pulsation frequencies (or their phases) that is caused by variations of the light travel-time along the orbit. This is known as the “light travel-time effect” (hereafter LiTE). In the case of a multi-mode pulsator, we expect that all the pulsation frequencies show the same cyclical variability pattern. This approach was successfully applied by Murphy et al. (2014) to a sample of δ Sct stars observed by the Kepler satellite. We applied the same method to the Kepler light curves of all the targets in our sample.
First, we determined all the frequencies with a significance level S/N > 4 (see, e.g. Breger et al. 1993) on the basis of each full data set. Next, we selected the 20 frequencies with the highest S/N. Then, each data set was divided into segments of random length between 9 and 11 days in order to prevent undesired aliasing. Subsequently, the data of each segment were fitted using a non-linear least-squares fitting routine lcfit (Sódor 2012) with fixed frequencies and starting epoch. In this way, we derived the time-dependent amplitudes and phases for all 20 frequencies. The time delay Δtij for a given frequency νj and time segment i is then easily computed using 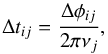 (1)where Δφij is the difference between φij and the mean phase calculated from all the segments.
(1)where Δφij is the difference between φij and the mean phase calculated from all the segments.
 |
Fig. 24 Time delays suggesting orbital motion in nine Kepler candidate hybrid stars. The frequencies are not explicitly listed − their values are listed in Table 12. The symbols and colours in all panels are the same as in the top left panel. The black circles show the weighted (50 days) averages. |
The analysis of the time delays (TDs) is complicated by several factors. Firstly, the phases of the low frequencies (those that might correspond to γ Dor frequencies) are often highly scattered, since the corresponding periods are only slightly shorter than the length of the segments and since the frequency spectra often show close peaks that cannot be resolved in the subsets. This is the main reason why we detected correlated phase variations almost exclusively among the higher δ Sct frequencies. Secondly, some frequencies show significant changes in amplitude and/or phase (usually both) and are thus unstable (Bowman et al. 2016). Such changes will often conceal the overall phase variations caused by LiTE. The analysis can furthermore be affected by the frequency content and distribution. For example, KIC 5965837 shows two most dominant modes with amplitudes of a few mmag in the γ Dor regime, while the rest of the frequencies has amplitudes about 30 times lower. In order to reduce the problems with the close frequencies, we also constructed and analysed subsets with a length of 20, 50, and 100 days. Although generally less scattered, these results still remained very close to those of the 10-day long subsets. We adopted the LiTE interpretation as the cause for the detected phase variations when at least three independent frequencies showed the same time-delay pattern.
We discovered correlated variations of comparable amplitude in the TDs of nine objects. In Fig. 24 we illustrate the detection of this LiTE. For the sake of clarity, we show only a few frequencies with the lowest scatter. To highlight the general patterns, we plotted the means of five points based on a weighted average computed for 10-day long segments4. Whenever the low (γ-Dor like) frequencies showed some apparent trend, these always followed the trend of the higher (δ-Sct like) frequencies, suggesting that both frequency regimes arise in the same star (e.g. f2 in KIC 9775454). This is also confirmed by the detection of combination peaks of low and high frequencies in the periodograms.
Figure 24 furthermore shows that the timescales of the detected variations are comparable to the length of the full data sets (i.e. of the order of 4 yr or longer). In six cases (cf. the upper two rows), RV variability due to orbital motion was also detected (cf. Sect. 7). In three cases (cf. the bottom row), the time delays provide evidence for (undetermined) orbital motions with a long period. However, these targets were classified by us as spectroscopically stable (class “S” or “S?”). It is relevant to note that two of these show extremely broad profiles indicative of very fast rotation, which could hamper the detection of spectroscopic multiplicity (KIC 3453494 and KIC 9650390).
In four cases, the LiTE amplitude is large (≥0.01 days, i.e. KIC 4480321, 5219533, 9775454, and KIC 9650390). In five other cases (three are SB2 systems, e.g. KIC 8975515), the LiTE amplitude is of the order of some thousandths of a day at most. The shortest orbital periods, including 3.9 (KIC 6381306), 9.2 (KIC 4480321), 32 (KIC 5219533), 99 (KIC 7756853), and 212 days (KIC 6381306), were not detected. To increase the chances of detecting the tiny time delays produced by the shortest-period orbits (with an expected total LiTE amplitude of the order of a few 10-4 days, such as in KIC 6381306 and KIC 4480321), we divided each data set into bins of width 0.10 in orbital phase. We thus obtained ten data sets containing several thousands of points with a time span almost equal to that of the full set for each target. However, even with this modification, the phase variations remained undetected in these two cases. This is not due to the method itself, since the smallest LiTE amplitude thus far found in Kepler data equals 8 × 10-5 days (Murphy et al. 2016a), while the shortest LiTE period yet detected in such light curves is 9.15 days (Murphy et al. 2016b). We conclude that the non-detections may be the consequence of the true LiTE amplitude in combination with the pulsation characteristics of a particular star or system. An alternative and physical explanation is that the detected pulsations might not arise in the close binary itself but in the outer, third component.
In order to show that the detected LiTE has the same physical cause as the long-term RV variations, we performed a simple modelling based on both data types for the systems KIC 4480321, 5219533, and KIC 8975515. We have different orbital solutions for each: KIC 4480321 is an SB3 system with two SB2 solutions, KIC 5219533 is an SB3 system with one SB2 and one SB1 solution (for the outer system), while KIC 8975515 is an SB2 system with one SB1 solution (for the slower rotating component). KIC 4480321 AB-C shows the longest detected orbital period (Porb ~ 2300 d). The inclusion of the TDs allows us to confirm and improve the previous orbital solution. To this purpose, we modelled the TDs adopting the orbital parameters of the RV solution except for the parameter (aC. sin iout), which was fitted to match the TDs only (cf. Table 11). Figure 25 shows the excellent agreement between the two data types. The TD residuals in the sense observed minus modelled are small and homogeneously distributed around zero. The gain is a more accurate determination of the mass ratio 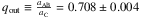 . KIC 5219533 AB-C has Porb ~ 1600 d. We modelled the TD variations adopting all orbital parameters of the RV solution, but fitted an additional parameter (aC. sin iout) (Table 11). Figure 26 shows the excellent agreement between the two data types. The TD residuals are small and homogeneously distributed around zero. The gain is the determination of the mass ratio qout
. KIC 5219533 AB-C has Porb ~ 1600 d. We modelled the TD variations adopting all orbital parameters of the RV solution, but fitted an additional parameter (aC. sin iout) (Table 11). Figure 26 shows the excellent agreement between the two data types. The TD residuals are small and homogeneously distributed around zero. The gain is the determination of the mass ratio qout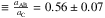 . KIC 8975515 AB also has Porb ~ 1600 d. We modelled the TD variations adopting all orbital parameters of the RV solution, but fitted an additional parameter (aA. sin i) (Table 11). Figure 27 shows the good agreement between the two data types. The TD residuals are small, but somewhat inhomogeneously distributed around zero, as they show a small discrepancy in eccentricity. The gain here as well is the determination of the mass ratio
. KIC 8975515 AB also has Porb ~ 1600 d. We modelled the TD variations adopting all orbital parameters of the RV solution, but fitted an additional parameter (aA. sin i) (Table 11). Figure 27 shows the good agreement between the two data types. The TD residuals are small, but somewhat inhomogeneously distributed around zero, as they show a small discrepancy in eccentricity. The gain here as well is the determination of the mass ratio 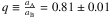 . In all three cases, we confirm that the observed TDs are consistent with the previously derived RV orbital solutions.
. In all three cases, we confirm that the observed TDs are consistent with the previously derived RV orbital solutions.
 |
Fig. 25 LiTE versus RV orbital solution for KIC 4480321. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The blue and red solid lines refer to the RV solution (see Fig. B.2). The dashed line shows the computed model. |
 |
Fig. 26 LiTE versus RV orbital motion for KIC 5219533. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The solid line refers to the RV solution (see Fig. B.3). The dashed line shows the computed model. |
 |
Fig. 27 LiTE versus RV orbital motion for KIC 8975515. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The solid line refers to the RV solution (see Fig. 21). The dashed line shows the computed model. |
Results of a fit of the LiTE adopting the previously derived RV orbital solutions.
These examples illustrate that the TD method can identify long-term changes that nicely complement the results of the spectroscopic analyses. Although the argument for long-term variations caused by orbital motion is quite strong, we should not exclude the possibility that the parabola-shaped variations of the TDs such as observed in KIC 7756853 might also be caused by some intrinsic evolutionary effect. Indeed, such a behaviour was reported in the δ Sct star 4 CVn. Although 4 CVn is also a short-period spectroscopic binary system (Schmid et al. 2014), the secular variations detected in (only) some pulsation modes follow different patterns that are related to a change of the rotational splitting (Breger 2016). In the case of the above discussed Kepler stars, however, the reported patterns of the secular variations are common to all investigated frequencies.
9. Observational H-R diagram
 |
Fig. 28 (Teff, log g)-representation for the 50 candidate hybrid stars and 1 evolved δ Scuti star. We show the location of the objects belonging to the classes S, P(+VAR), CMP, and SB, as well as the rapidly rotating stars (FAST). The empirical borders of the classical δ Scuti (in black) and γ Dor (in colour) instability strips are represented by solid lines. |
In Fig. 28 we plotted the distribution of the updated atmospheric parameters for our sample of A/F-type candidate hybrid stars. In this observational (Teff, log g)-diagram, we represented the five categories of our classification using different symbols. Based on the new v sin i measurements, we furthermore indicate the objects that are subject to (very) fast rotation (i.e. with v sin i > 200 km s-1). Of course, both CMP-targets are fast rotators. The borders of the classical δ Scuti and the γ Doradus instability strips reproduced by Uytterhoeven et al. (2011) are also shown. It is remarkable that all the P-targets are located within these limits. The SB objects located (far) outside the instability strips are KIC 6381306 (Teff = 9000 K) and KIC 7756853 (Teff = 9980 K).
10. Discussion and conclusions
We classified a sample of 50 regularly observed bright A/F-type candidate hybrid stars and one δ Scuti star of the Kepler mission into different classes according to the shape (in some cases, the model) of their cross-correlation profiles and the evolution of their radial velocities with time. Classes were defined as S (for stable), SB (for spectroscopic binary or triple system), VAR (for long-term RV variable star), P (for pulsating and/or rotating), and CMP (for composite spectrum). According to these spectroscopic criteria, we find the following distribution (without considering the cool object KIC 9700679, which is also SB1): 49% (S-stars), 22% (P-stars), 18% (SB-objects), 6% (VAR-stars), and 4% (CMP-objects) (Fig. 29). In addition, the VAR stars are (most) probably long-period SB1 systems. Including the known eclipsing binary KIC 11180361 (KOI-971), we find a global multiplicity fraction of 27%. This indicates that at least 25% of our sample of potential hybrid stars belongs to a binary or a multiple system.
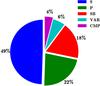 |
Fig. 29 Classification results of the A/F-type candidate hybrid stars. |
We (re)determined the fundamental atmospheric properties such as Teff, log g, and v sin i based on the high-resolution Hermes spectra, which are important physical parameters, for all of our targets including − where feasible − for the components of the newly detected systems. A comparison with the published data showed that our values agree in most cases, although some evident discrepancies were also reported. Evidently, in the case of the multiple systems where the ambiguity is higher, several possible models were found. In these cases, we usually adopted the solution from the [500−520] nm interval. Consequently, we presented an updated observational H-R diagram.
At this point, we can start to address our longer term goal by taking a closer look at the frequency content of the newly reported systems in the region of interest, that is, in the γ Dor regime. In Fig. 30 we present the periodograms in the low-frequency range, that is, [0−4] d-1, based on the Kepler data sets for the seven spectroscopic (binary and multiple) systems of Sect. 7. The aim is to search for orbital frequencies in the original periodograms. We see that in most cases, the amplitudes in the vicinity of the orbital frequency are either much lower than the amplitudes of the obvious peaks or fully embedded in the noise. There are two exceptions, however: KIC 4480321 and KIC 6381306. In the case of KIC 4480321 (SB3), which shows the highest power in the explored range, there is a well-detected peak (with an amplitude of 0.04 parts per thousand (ppt)), which is similar, but not identical, to the orbital frequency. In the case of KIC 6381306 (SB3), the dominant peak (with an amplitude of 0.1 ppt) agrees perfectly with the spectroscopically derived orbital frequency. In all other cases, we can find no clear sign of the orbital frequency in the periodograms. The figure furthermore demonstrates that all the systems are rather strongly multi-periodic in the low-frequency regime.
 |
Fig. 30 Periodograms of the Kepler light curves for the seven SB systems discussed in Sect. 7. For each object, the position corresponding to the newly revealed orbital frequency is plotted as a dashed line indicated by an arrow, and the frequency value and its amplitude (expressed in relative intensity units) are given. |
We also searched for regular frequency spacings in the full-scale periodograms of these objects, which might be linked to the orbital frequency. In an eccentric binary system, the tidal potential can indeed be represented by a Fourier series with many forcing frequencies. When one of the forcing frequencies happens to be close to an eigenfrequency, the oscillation mode is resonantly excited (tidally induced) (Willems 2003). A well-known example of detected tidal excitation is the Kepler main-sequence binary KOI-54, where the strongest oscillations occur at 90 and 91 times the orbital frequency (Fuller & Lai 2012). Table 13 lists the relevant spacings for each target. In Fig. 31 we plot the frequency spacings in the range [0−4] d-1 on a logarithmic scale for the SB systems discussed in Sect. 7. We see that KIC 4480321 has the most dominant and most densely distributed spacing pattern. In comparison, the spacing density of the other systems is very poor. In the case of KIC 4480321, the most frequent spacing (S1 = 0.0085 d -1) corresponds to the exact difference of the next two most frequent ones, that is, 0.0928 and 0.1013 d-1, which are both very similar, but not equal, to the orbital frequency (0.1091 d-1). We conclude that this signals the influence of the orbital frequency of the close (AB) pair on the other frequencies of KIC 4480321. In the case of KIC 6381306, we highlight the single significant spacing in this range (S1 = 1.3355 d-1).
 |
Fig. 31 Frequency spacings for the SB systems discussed in Sect. 7. The weights (plotted on the y-axis) were computed as the product of the amplitudes of both frequencies. For each object, a different colour is used. KIC 4480321 presents by far the richest spacing pattern. Its dominant spacings are located in the vicinity of the orbital frequency. The arrows indicate two of the most frequent spacings and their difference. |
This study represents an unavoidable step in the investigation of the new A/F-type hybrid phenomenon. We find a significant rate of both short- and long-period binary/multiple systems in our targets. The multiplicity comes with different flavours. When we add the positive detections from the photometric time-delay analysis, we may include the targets KIC 3453494, 4044353, and KIC 9650390 as (most probably) belonging to the class of single-lined long-period binary systems. The multi-year monitoring of the RVs enabled the detection of several long-period systems with orbital periods of the order of 4-6 years: KIC 4480321, 5219533, 8975515, and KIC 9775454. It is our intention to continue the monitoring for these interesting systems. Moreover, since the photometric time-delay analysis − which is based on the four-year time span of the Kepler mission − shows the existence of periodicities of the same order, we intend to combine both data types into a simultaneous modelling in the near future. We have shown that the orbital solutions currently based on the RVs alone are confirmed by a simple modelling of the LiTE in three cases. Overall, we may safely conclude that about one-third of our sample of candidate hybrid stars belongs to a binary or a multiple system. This number is very close to the fraction of binary and multiple systems suggested from a spectroscopic-photometric analysis for a sample of 32 candidate SX Phe stars in the Kepler field (Nemec et al. 2017).
This result implies that the physical cause of the low frequencies that are detected in the Kepler periodograms could be related to the orbital motions, and that these so-called hybrid stars may not be genuine hybrid pulsators. They may have forced oscillations coupled to the orbital frequency (its harmonics), or show ellipsoidal modulations in their light curves. In two of the seven SB systems, we found straightforward evidence for the orbital frequency in the periodograms (KIC 4480321 and KIC 6381306). In KIC 6381306, the orbital frequency is the most dominant peak. It is worth noting that this interaction was detected in the short-period systems with an orbital period smaller than 10 d. In the remaining cases (those with orbital periods beyond 30 d), there is no influence at first sight, the more dominant peaks are situated in the range [0.5−3] d-1, as is usual for the g-mode pulsators of γ Dor type. The multiperiodicity and apparent complexity of the frequency content in this region still need an explanation in most of the (long-period) systems.
We are not yet able to distinguish between the true hybrid pulsators and stars where spots or fast rotation introduce inhomogeneities on the stellar surface. On the one hand, an extended analysis of the Kepler data including a precise identification of the g-mode period spacing patterns may help out, provided there are enough visible g-modes to reliably detect such patterns (e.g. Van Reeth et al. 2015). On the other hand, detailed spectropolarimetric investigations (e.g. Neiner & Lampens 2015) can provide true physical insight regarding the origin of the low frequencies in some cases. In conclusion, the resulting orbital periods and elements of the newly identified systems, projected rotational velocities, and homogeneous atmospheric properties provide relevant and essential information for a more reliable and deeper physical understanding of the Kepler periodograms.
Acknowledgments
This research is based on high-resolution spectra obtained with the Hermes échelle spectrograph (2013−2016) installed at the Mercator telescope, operated by the IvS, KULeuven, funded by the Flemish Community, and located at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias, and with the ace échelle spectrograph (2014−2015) attached to the 1m RCC telescope of the Konkoly Observatory at Piszkés-tető, Hungary. The observations performed at Piszkés-tető were supported by the Lendület grant LP2012-31 of the Hungarian Academy of Sciences. We furthermore made usage of the very high-quality data collected by the Kepler satellite. Funding for the Kepler mission is provided by the NASA Science Mission directorate. The authors gratefully acknowledge the financial support from the Royal Observatory of Belgium to the Hermes Consortium, as well as the help of the Hermes observers J. Boulangier, W. Homan, R. Karjalainen, R. Lombaert, R. Manick, C. Paladini, A. Tkachenko, M. Van de Sande, and H. Van Winckel. We thank the referee for most useful comments and suggestions for improvements. M.S. acknowledges the support of the postdoctoral fellowship programme of the Hungarian Academy of Sciences and the Konkoly Observatory as a host institution. Á.S., M.S., and Zs.B. acknowledge the support of the Hungarian NKFIH Grants K-113117, K-115709 and K-119517. Á.S. received a János Bolyai Research Scholarship (Hungarian Academy of Sciences). Zs.B. acknowledges the support of the Hungarian NKFIH Grant PD-123910. H.L. acknowledges the support of the DFG grant LE 1102/3-1. This work was performed using the POLLUX database (http://pollux.graal.univ-montp2.fr) operated by LUPM, Université Montpellier − CNRS, France with the support of the PNPS and INSU, as well as the SAO/NASA Astrophysics Data System (ADS) and the SIMBAD database operated at the CDS, Strasbourg, France (http://simbad.u-strasbg.fr/Simbad).
References
- Antoci, V. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 333 [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balona, L. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2015, MNRAS, 452, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Blazère, A., Petit, P., Lignières, F., et al. 2014, in SF2A-2014: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 463 [Google Scholar]
- Bognár, Z., Lampens, P., Frémat, Y., et al. 2015, A&A, 581, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm, T., Holschneider, M., Lignières, F., et al. 2015, A&A, 577, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 2016, A&A, 592, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993,A&A, 271, 482 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A20 [Google Scholar]
- Catanzaro, G., Ripepi, V., Bernabei, S., et al. 2011, MNRAS, 411, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 187 [Google Scholar]
- D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cat, P., Fu, J. N., Ren, A. B., et al. 2015, ApJS, 220, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Derekas, A., Plachy, E., Molnár, L., et al. 2017, MNRAS, 464, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2004, A&A, 414, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fekel, F. C. 2015, AJ, 149, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., Warner, P. B., & Kaye, A. B. 2003, AJ, 125, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Castro, N., Morel, T., et al. 2015, A&A, 574, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Alcalá, J. M., Covino, E., et al. 2003, A&A, 405, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Molenda-Żakowicz, J., De Cat, P., et al. 2016, A&A, 594, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Neiner, C., Hubert, A.-M., et al. 2006, A&A, 451, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, J., & Lai, D. 2012, MNRAS, 420, 3126 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gebran, M., Monier, R., Royer, F., Lobel, A., & Blomme, R. 2014, in Putting A Stars into Context: Evolution, Environment, and Related Stars, eds. G. Mathys, E. R. Griffin, O. Kochukhov, R. Monier, & G. M. Wahlgren, 193 [Google Scholar]
- Grigahcène, A., Antoci, V., Balona, L., et al. 2010, ApJ, 713, L192 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, G. W., & Fekel, F. C. 2003, AJ, 126, 3058 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Koen, C. 2001, MNRAS, 321, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Garrison, R. F., Koen, C., Hofmann, G. F., & Viranna, N. B. 1995, MNRAS, 276, 199 [NASA ADS] [Google Scholar]
- Lampens, P., Bognár, Z., Frémat, Y., et al. 2015, in EPJ Web Conf., 101, 06043 [Google Scholar]
- Lenz, P., & Breger, M. 2014, Astrophysics Source Code Library [record ascl:1407.009] [Google Scholar]
- Lignières, F., Petit, P., Aurière, M., Wade, G. A., & Böhm, T. 2014, in Magnetic Fields throughout Stellar Evolution, eds. P. Petit, M. Jardine, & H. C. Spruit, IAU Symp., 302, 338 [Google Scholar]
- Mantegazza, L., & Poretti, E. 1996, A&A, 312, 855 [NASA ADS] [Google Scholar]
- Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G. 2001, in Magnetic Fields Across the Hertzsprung-Russell Diagram, eds. G. Mathys, S. K. Solanki, & D. T. Wickramasinghe, ASP Conf. Ser., 248, 267 [Google Scholar]
- Mazeh, T., & Zucker, S. 1994, Ap&SS, 212, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Alecian, G., & Richer, J. 2015, Atomic Diffusion in Stars (Switzerland: Springer International Publishing) [Google Scholar]
- Morel, T., Castro, N., Fossati, L., et al. 2015, in New Windows on Massive Stars, eds. G. Meynet, C. Georgy, J. Groh, & P. Stee, IAU Symp., 307, 342 [Google Scholar]
- Murphy, S. J., Grigahcène, A., Niemczura, E., Kurtz, D. W., & Uytterhoeven, K. 2012, MNRAS, 427, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Bedding, T. R., Shibahashi, H., Kurtz, D. W., & Kjeldsen, H. 2014, MNRAS, 441, 2515 [Google Scholar]
- Murphy, S. J., Bedding, T. R., & Shibahashi, H. 2016a, ApJ, 827, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Shibahashi, H., & Bedding, T. R. 2016b, MNRAS, 461, 4215 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., & Lampens, P. 2015, MNRAS, 454, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Balona, L. A., Murphy, S. J., Kinemuchi, K., & Jeon, Y.-B. 2017, MNRAS, 466, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Niemczura, E., Murphy, S. J., Smalley, B., et al. 2015,MNRAS, 450, 2764 [Google Scholar]
- Palacios, A., Gebran, M., Josselin, E., et al. 2010, A&A, 516, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renson, P., & Manfroid, J. 2009, A&A, 498, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robrade, J., & Schmitt, J. H. M. M. 2009, A&A, 497, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Royer, F. 2009, in The Rotation of Sun and Stars (Berlin: Springer Verlag), Lecture Notes in Physics, 765, 207 [CrossRef] [Google Scholar]
- Royer, F., Gebran, M., Monier, R., et al. 2014, in Putting A Stars into Context: Evolution, Environment, and Related Stars, eds. G. Mathys, E. R. Griffin, O. Kochukhov, R. Monier, & G. M. Wahlgren, 265 [Google Scholar]
- Schmid, V. S., Themeßl, N., Breger, M., et al. 2014, A&A, 570, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, C., & Schmitt, J. H. M. M. 2007, A&A, 475, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2002,ApJ, 579, 800 [Google Scholar]
- Slawson, R. W., Prša, A., Welsh, W. F., et al. 2011, AJ, 142, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Sódor, A. 2012, Konkoly Observatory Occasional Technical Notes, 15 [Google Scholar]
- Tkachenko, A., Aerts, C., Yakushechkin, A., et al. 2013, A&A, 556, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 218, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B. 2003, MNRAS, 346, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., & Aerts, C. 2002, A&A, 384, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Cross-correlation functions of A/F-type candidate hybrid stars
 |
Fig. A.1 Cross-correlation functions for 48 Kepler objects. The epochs were chosen so as to show as much contrast as possible between two CCFs. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
Appendix B: Radial velocity curves
 |
Fig. B.1 Radial velocity plots for 44 Kepler objects. The symbols indicate data collected with the Hermes (°, •) or ace spectrographs (△). |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.2 Radial velocities for the mass centre of the inner binary (AB) and for component C of KIC 4480321, plotted over a possible orbital solution with a period of 2280 days. The residuals are shown in the bottom part. |
 |
Fig. B.3 Radial velocities for the mass centre of the inner binary (AB) in the triple system KIC 5219533 plotted over a tentative orbital solution with a period of about 1600 days. The residuals are shown in the bottom part. |
 |
Fig. B.4 Radial velocities for the mass centre of the inner binary (AB) and for component C of KIC 6381306, plotted over the outer orbital solution with a period of 212 days. The residuals are shown in the bottom part. |
Appendix C: Tables which are also available at the CDS
Classification, model parameters, and atmospheric stellar parameters obtained from the Hermes spectra.
Comparison of atmospheric stellar parameters obtained in this work with published values (assuming other parameters are equivalent).
Comparison of atmospheric stellar parameters obtained in this work with the lamost results based on the rotfit procedure (22 targets in common).
All Tables
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 4480321.
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 5219533.
Values and standard deviations of the constrained parameters of the orbital solutions for KIC 6381306.
Values and standard deviations of the constrained parameters of the orbital solution for KIC 7756853.
Values and standard deviations of the constrained parameters of the orbital solution for KIC 8975515.
Values and standard deviations of the constrained parameters of the orbital solution proposed for KIC 9790479.
Values and standard deviations of the constrained parameters of the orbital solution proposed for KIC 11572666.
Results of a fit of the LiTE adopting the previously derived RV orbital solutions.
Classification, model parameters, and atmospheric stellar parameters obtained from the Hermes spectra.
Comparison of atmospheric stellar parameters obtained in this work with published values (assuming other parameters are equivalent).
Comparison of atmospheric stellar parameters obtained in this work with the lamost results based on the rotfit procedure (22 targets in common).
All Figures
 |
Fig. 1 Distribution of time intervals between successive Hermes spectra for the sample stars showing peaks of 1 and 6 days as well as ~1 and ~3 months. Note the rapidly increasing bin size along the X-axis. |
| In the text | |
 |
Fig. 2 Cross-correlation functions in the case of an unresolved double-lined spectroscopic binary system showing obvious asymmetric profiles as well as velocity shifts, e.g. KIC 7756853. |
| In the text | |
 |
Fig. 3 Cross-correlation functions in the case of a well-resolved double-lined spectroscopic binary showing two distinct minima and velocity shifts in its profile, e.g. KIC 5219533. |
| In the text | |
 |
Fig. 4 Case of a triple system: part of the spectrum (in black) and composite model (in red) for KIC 4480321 using the synthetic spectra for three components of type (F0, v sin i =10), (F0, v sin i =10), and (A5, v sin i =160). The thin line (in grey) represents the scaled contribution of the two (F0, v sin i =10) components. |
| In the text | |
 |
Fig. 5 Case of a binary system: part of the spectrum (in black) and composite model (in red) for KIC 8975515 using the synthetic spectra (A7, v sin i = 170) and (A7, v sin i = 30). The thin line (in grey) represents the scaled contribution of the (A7, v sin i = 30) component. |
| In the text | |
 |
Fig. 6 Part of the observed spectrum (in black) for KIC 6432054 and model (in red) using the best-fitting set of atmospheric stellar properties Teff = 7542 K, log g = 4.44, and v sin i = 184 km s-1 derived with girfit. |
| In the text | |
 |
Fig. 7 Comparison of the various determinations of Teff. A linear fit using the literature values lower than 7600 K (open symbols) shows an obvious discrepancy in the slope, illustrating the fact that our values for Teff lower than 7700 K are systematically slightly higher than the literature values. The outlier (red symbol) is KIC 7119530, for which two very different literature values were found. |
| In the text | |
 |
Fig. 8 Comparison of the various determinations of log g. Same symbols as in Fig. 7. The largest differences (red symbols) are found for KIC 3429637 (A9m), 5965837 (F2p), 9509296, 9764965 (Am), and KIC 10537907. |
| In the text | |
 |
Fig. 9 Comparison of the various determinations of v sin i. Same symbols as in Fig. 7. The largest differences (red symbols) are found for KIC 7119530 and 7827131. |
| In the text | |
 |
Fig. 10 Observed spectrum of KIC 5219533 (in black) vs. model spectra consisting of two narrow-lined components (in red). An extra broad-lined component of a similar spectral type could explain the additional wings and parts with missing continuum. |
| In the text | |
 |
Fig. 11 Part of the observed spectrum for KIC 5965837 (in black) and the corresponding part of the elodie spectrum of 20 CVn artificially broadened to the same rotation velocity (v sin i = 15 km s-1) (in red). |
| In the text | |
 |
Fig. 12 Comparison of two Hα-profiles: KIC 6756481 (plotted in black) versus KIC 6670742 (in grey). |
| In the text | |
 |
Fig. 13 Observed versus modelled CCF in the case of KIC 7756853. The spectral range used is [415−450] nm. Model A is shown in green/lilac, while model B is shown in (light/dark) blue. |
| In the text | |
 |
Fig. 14 CCF profiles of four different spectra of KIC 7770282. They illustrate the largest observed distortions. |
| In the text | |
 |
Fig. 15 Observed versus modelled spectrum for KIC 11445913 showing the two distinct contributions in red and blue. The plotted range includes the Paschen series and a line of Ca triplet. |
| In the text | |
 |
Fig. 16 Observed versus modelled CCF in the case of KIC 11572666. The combinations used for the models are F0-G2, F0-F3, A7-G2, A7-F3, A5-G2, and A5-F3. The closest match is found for the model with two early F-type components of very different v sin i (in light blue). The next best match is for the A7-G2 model (in pink). |
| In the text | |
 |
Fig. 17 Radial velocities for components A and B of the new triple-lined system KIC 4480321 plotted together with the orbital solution of the inner binary (AB) system and adjusted systemic velocity offsets. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. 18 Radial velocities for components A and B of the new triple-lined system KIC 5219533 plotted with a plausible orbital solution for the inner binary (AB) system. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. 19 Radial velocities for components A and B of the new triple-lined system KIC 6381306 plotted together with the orbital solution of the inner (AB) binary system and adjusted systemic velocity offsets. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. 20 Radial velocities for components A and B of the new double-lined system KIC 7756853 plotted with the proposed orbital solution of the binary. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. 21 Radial velocities for the companion of KIC 8975515 plotted with the preliminary orbital solution of the binary (type SB1). The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. 22 Radial velocities for the single-lined system KIC 9790479 showing a preliminary orbital solution. The residuals are plotted in the bottom part. |
| In the text | |
 |
Fig. 23 Radial velocities for the companion of KIC 11572666 showing a preliminary orbital solution (type SB1). The residuals are plotted in the bottom part. |
| In the text | |
 |
Fig. 24 Time delays suggesting orbital motion in nine Kepler candidate hybrid stars. The frequencies are not explicitly listed − their values are listed in Table 12. The symbols and colours in all panels are the same as in the top left panel. The black circles show the weighted (50 days) averages. |
| In the text | |
 |
Fig. 25 LiTE versus RV orbital solution for KIC 4480321. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The blue and red solid lines refer to the RV solution (see Fig. B.2). The dashed line shows the computed model. |
| In the text | |
 |
Fig. 26 LiTE versus RV orbital motion for KIC 5219533. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The solid line refers to the RV solution (see Fig. B.3). The dashed line shows the computed model. |
| In the text | |
 |
Fig. 27 LiTE versus RV orbital motion for KIC 8975515. Note that the TDs (pink symbols) were corrected by removing a linear trend from the original data. The solid line refers to the RV solution (see Fig. 21). The dashed line shows the computed model. |
| In the text | |
 |
Fig. 28 (Teff, log g)-representation for the 50 candidate hybrid stars and 1 evolved δ Scuti star. We show the location of the objects belonging to the classes S, P(+VAR), CMP, and SB, as well as the rapidly rotating stars (FAST). The empirical borders of the classical δ Scuti (in black) and γ Dor (in colour) instability strips are represented by solid lines. |
| In the text | |
 |
Fig. 29 Classification results of the A/F-type candidate hybrid stars. |
| In the text | |
 |
Fig. 30 Periodograms of the Kepler light curves for the seven SB systems discussed in Sect. 7. For each object, the position corresponding to the newly revealed orbital frequency is plotted as a dashed line indicated by an arrow, and the frequency value and its amplitude (expressed in relative intensity units) are given. |
| In the text | |
 |
Fig. 31 Frequency spacings for the SB systems discussed in Sect. 7. The weights (plotted on the y-axis) were computed as the product of the amplitudes of both frequencies. For each object, a different colour is used. KIC 4480321 presents by far the richest spacing pattern. Its dominant spacings are located in the vicinity of the orbital frequency. The arrows indicate two of the most frequent spacings and their difference. |
| In the text | |
 |
Fig. A.1 Cross-correlation functions for 48 Kepler objects. The epochs were chosen so as to show as much contrast as possible between two CCFs. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. B.1 Radial velocity plots for 44 Kepler objects. The symbols indicate data collected with the Hermes (°, •) or ace spectrographs (△). |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.2 Radial velocities for the mass centre of the inner binary (AB) and for component C of KIC 4480321, plotted over a possible orbital solution with a period of 2280 days. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. B.3 Radial velocities for the mass centre of the inner binary (AB) in the triple system KIC 5219533 plotted over a tentative orbital solution with a period of about 1600 days. The residuals are shown in the bottom part. |
| In the text | |
 |
Fig. B.4 Radial velocities for the mass centre of the inner binary (AB) and for component C of KIC 6381306, plotted over the outer orbital solution with a period of 212 days. The residuals are shown in the bottom part. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


