| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201732203 | |
| Published online | 09 February 2018 | |
Letter to the Editor
The magnetic environment of the Orion-Eridanus superbubble as revealed by Planck
1
Max-Planck-Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg, Germany
e-mail: soler@mpia.de
2
Nordita, KTH Royal Institute of Technology and Stockholm University,
Roslagstullsbacken 23,
10691
Stockholm, Sweden
e-mail: andrea.bracco@su.se
3
Laboratoire AIM, Paris-Saclay, CEA/IRFU/SAp – CNRS – Université Paris Diderot,
91191
Gif-sur-Yvette Cedex, France
4
Department of Physics and Astronomy, University of Western Ontario,
1151 Richmond Street,
London,
ON
N6A 3K7, Canada
Received:
30
October
2017
Accepted:
8
December
2017
Using the 353-GHz polarization observations by the Planck satellite we characterize the magnetic field in the Orion-Eridanus superbubble, a nearby expanding structure that spans more than 1600 square degrees in the sky. We identify a region of both low dispersion of polarization orientations and high polarization fraction associated with the outer wall of the superbubble identified in the most recent models of the large-scale shape of the region. We use the Davis-Chandrasekhar-Fermi method to derive plane-of-the-sky magnetic field strengths of tens of μG toward the southern edge of the bubble. The comparison of these values with existing Zeeman splitting observations of HI in emission suggests that the large-scale magnetic field in the region was primarily shaped by the expanding superbubble.
Key words: magnetic fields / stars: formation / ISM: bubbles / ISM: individual objects: Orion-Eridanus Superbubble / polarization / Galaxy: disk
© ESO, 2018
1 Introduction
The Orion-Eridanus superbubble is a large circular structure with a diameter close to 45 deg (Heiles 1976; Reynolds & Ogden 1979; Heiles et al. 1999). It is most likely the result of the combined effects of ionizing UV radiation, stellar winds, and a sequence of supernova (SN) explosions from the Orion OB association (Burrows et al. 1993; Brown et al. 1995; Guo et al. 1995; Bally 2008). Due to its proximity (d <500 pc) and its association with the Orion molecular cloud, it has been studied in multiple wavelengths, serving as a benchmark to the study of superbubbles and of feedback in the process of star formation (Ochsendorf et al. 2015; Pon et al. 2016, and references therein).
The magnetic field of the Orion-Eridanus bubble has previously been characterized using observations of Zeeman splitting of atomic hydrogen (HI) emission at 21-cm, which provide the strength and direction of the line-of-sight component of the magnetic field (B∥ ), and with optical polarization measurements, which indicate the orientation of the plane-of-the-sky component of the magnetic field (B⊥; Heiles 1989, 1997). Around the Orion molecular cloud, these observations show a sharp reversal of B∥, which is thought to be related to a large-scale shock sweeping over the dense clouds. However, a large-scale characterization of the magnetic field of the region is still missing because of the paucity of HI Zeeman-splitting and stellar polarization observations at Galactic latitudes b ≲−22 deg. In this Letter we examine the multiphase structure of the Orion-Eridanus superbubble and its global magnetic-field properties using, for the first time, the Planck all-sky polarization observations at 353 GHz (850 μm) (Planck Collaboration Int. XIX 2015).
2 Superbubble morphology
Figure 1 shows the orientation of B⊥, inferred from the Planck 353-GHz polarization observations (Planck Collaboration I 2016), overlaid on the Hα integrated emission from the Southern H-Alpha Sky Survey Atlas (SHASSA; Gaustad et al. 2001; Finkbeiner 2003), and the 21-cm emission, integrated between − 20 and 20 km s−1 (vLSR), from the all-sky HI survey based on the EBHIS and GASS surveys (HI4PI; HI4PI Collaboration et al. 2016). The most prominent Hα features of the superbubble, Arc A, B, and C (Johnson 1978), the λ Orionis HII region (Mathieu 2008), and Barnard’s Loop (Barnard 1894), are also labeled in the right-hand-side panel of the image.
We consider the Planck 353-GHz polarization observations, originally taken at 4′.8 resolution, smoothed with a 1 deg FWHM Gaussian beam to reach a signal-to-noise ratio of at least 3 over the whole region (see Appendix A). These observations reveal three separate regions with different orientations of B⊥: (i) Toward the north of the superbubble, for b >−15 deg, B⊥ appears to be relatively uniform and oriented parallel to the Galactic plane, apparently unaffected by Barnard’s loop or λ Orionis. This is potentially the product of both the angular resolution of the polarization observations and the line-of-sight confusion toward the Galactic plane. (ii) In the center of the superbubble, B⊥ appears much more tangled. (iii) Along the eastern and southern edges of the superbubble, for b <−15 deg, B⊥ clearly follows the rim of the superbubble across tens of degrees.
We quantify the dispersion of the orientation of B⊥ using the polarization angle dispersion function (Hildebrand et al. 2009; Planck Collaboration Int. XIX 2015),
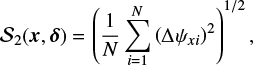 (1)
(1)
where Δψxi = ψ(x) − ψ(x + δi) is the difference in polarization angle (ψ, see Eq. (A.1)) between a given position x and a position offset by a displacement δ. The top panel of Fig. 2 presents 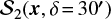 , the same δ value used in Planck Collaboration Int. XIX (2015); although our conclusions do not depend on this particular selection (see Appendix A). This quantity shows a clear decrease in the polarization angle dispersion along the edge of the superbubble, particularly in the eastern and southern edges, relative to the surroundings. These low
, the same δ value used in Planck Collaboration Int. XIX (2015); although our conclusions do not depend on this particular selection (see Appendix A). This quantity shows a clear decrease in the polarization angle dispersion along the edge of the superbubble, particularly in the eastern and southern edges, relative to the surroundings. These low 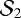 values are further accompanied by relatively high polarization fractions (p, Eq. (A.1)), as illustrated in the bottom panel of Fig. 2. Both these observations are expected from the large-scale organization of the magnetic field along the wall of the superbubble, following its expansion (Ferriere et al. 1991; Planck Collaboration Int. XXXIV 2016; Soler & Hennebelle 2017).
values are further accompanied by relatively high polarization fractions (p, Eq. (A.1)), as illustrated in the bottom panel of Fig. 2. Both these observations are expected from the large-scale organization of the magnetic field along the wall of the superbubble, following its expansion (Ferriere et al. 1991; Planck Collaboration Int. XXXIV 2016; Soler & Hennebelle 2017).
Figures 1 and 2 show that both Arc B and Arc C are inside and run parallel to the low-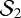 and high-p outline. This observation decisively rules out the skinny-bubble shape proposed by Pon et al. (2014), who suggested that Arc C is a filament outside of the bubble that is merely ionized by photons penetrating the bubble wall. The superbubble wall also seems to extend beyond Barnard’s Loop, as suggested by the
and high-p outline. This observation decisively rules out the skinny-bubble shape proposed by Pon et al. (2014), who suggested that Arc C is a filament outside of the bubble that is merely ionized by photons penetrating the bubble wall. The superbubble wall also seems to extend beyond Barnard’s Loop, as suggested by the 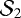 map, confirming the suggestion of Ochsendorf et al. (2015) that Barnard’s Loop is a separate shell nested within the larger Orion-Eridanus superbubble. Moreover, since Barnard’s Loop is expanding within the cavity evacuated by the superbubble, there was not a lot of neutral matter nor magnetic field lines for it to sweep up, therefore it is unsurprising that it does not show up prominently in Fig. 2. Unfortunately, due to confusion along the Galactic plane, the northern end of the superbubble cannot be definitively located using the polarization data, meaning that it is unclear whether or not the bubble extends up to a latitude of 5 deg (Robitaille et al. 2017), instead of only going to − 5 deg (Pon et al. 2016).
map, confirming the suggestion of Ochsendorf et al. (2015) that Barnard’s Loop is a separate shell nested within the larger Orion-Eridanus superbubble. Moreover, since Barnard’s Loop is expanding within the cavity evacuated by the superbubble, there was not a lot of neutral matter nor magnetic field lines for it to sweep up, therefore it is unsurprising that it does not show up prominently in Fig. 2. Unfortunately, due to confusion along the Galactic plane, the northern end of the superbubble cannot be definitively located using the polarization data, meaning that it is unclear whether or not the bubble extends up to a latitude of 5 deg (Robitaille et al. 2017), instead of only going to − 5 deg (Pon et al. 2016).
The B⊥ orientation shown in Fig. 1 seems to follow the orientation of Arc A, although this structure does not appear prominently in Fig. 2. Distance estimates determined using optical photometry of stars from PanSTARRS-1 (Schlafly et al. 2014) conclusively place Arc A within 200 pc of the Sun and they find no evidence of significant reddening beyond 500 pc toward this position (18 in their Table 2). As such, we consider the non-detection of Arc A in 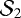 to be due to its projection and confusion, rather than it being a background feature behind the superbubble (Boumis et al. 2001; Welsh et al. 2005).
to be due to its projection and confusion, rather than it being a background feature behind the superbubble (Boumis et al. 2001; Welsh et al. 2005).
In the 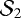 map, the superbubble appears relatively circular. Such a round superbubble is more consistent with the evolution of a superbubble in an exponential-density-profile atmosphere than the highly elongated models of Pon et al. (2014). Therefore, additional processes, such as turbulent shaping and shear from Galactic differential rotation, are not required to explain the observed morphology, although we do not rule out the possibility that such processes have affected the Orion-Eridanus superbubble. One inescapable fact that strikes the eye from these polarization measurements is that the Galactic magnetic field and the expanding Orion-Eridanus superbubble have clearly interacted and influenced one another.
map, the superbubble appears relatively circular. Such a round superbubble is more consistent with the evolution of a superbubble in an exponential-density-profile atmosphere than the highly elongated models of Pon et al. (2014). Therefore, additional processes, such as turbulent shaping and shear from Galactic differential rotation, are not required to explain the observed morphology, although we do not rule out the possibility that such processes have affected the Orion-Eridanus superbubble. One inescapable fact that strikes the eye from these polarization measurements is that the Galactic magnetic field and the expanding Orion-Eridanus superbubble have clearly interacted and influenced one another.
 |
Fig. 1 Stereographic projections of observations toward the Orion-Eridanus superbubble. The drapery pattern, produced using the line integral convolution technique (LIC; Cabral & Leedom 1993), corresponds to plane-of-the-sky magnetic field orientation inferred from the Planck 353-GHz polarization observations. Left: total integrated Hα emission map. The dashed line indicates the approximate location of the edge of the superbubble. The yellow symbols correspond to the main stars in the Orion constellation. Right: total integrated Hα emission (Gaustad et al. 2001) and HI 21-cm emission (HI4PI Collaboration et al. 2016) integrated between − 20 and 20 km s−1 shown in red and teal colors, respectively. The yellow symbols correspond to the line-of-sight magnetic field directions derived fromthe HI emission-line Zeeman splitting observations (Heiles 1989, 1997). The circles and triangles correspond to magnetic fields pointing toward and away from the observer, respectively. The three white circles in the bottom are the regions analyzed in this Letter. |
3 Magnetic field strengths
Quantifying the magnetic properties of the whole Orion-Eridanus superbubble is beyond the scope of this Letter. We present an estimate of the magnetic field strength in the region where polarization observations were previously not available and the line-of-sight confusion is less severe, that is, b < − 30 deg. In particular, we focus on three positions located at the interface of the Hα and HI shells in the southern edge of the superbubble, where prior measurements of B∥, based upon the HI Zeeman effect in the 21-cm emission line (Heiles 1989), are available. Toward these three positions, illustrated in Fig. 1, we complement the observations of B∥ with the estimates of B⊥ obtained with the Davis-Chandrasekhar-Fermi method (hereafter the DCF, Davis 1951; Chandrasekhar & Fermi 1953).
The DCF method provides an estimate of B⊥ in the interstellar medium. Under the assumptions that the magnetic field is frozen into the gas and that the dispersion of the local magnetic-field orientation angle is due to transverse and incompressible Alfvén waves,
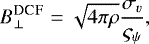 (2)
(2)
where σv is the velocity dispersion of the gas, ρ is the gas-mass density, and ςψ 1 is the angular dispersion of the local magnetic-field orientations. Recent studies of the DCF method based on simulations of magnetohydrodynamical (MHD) turbulence in molecular clouds (Ostriker et al. 2001) provide a correction factor of 0.5 to Eq. (2). We choose to omit this factor due to the dissimilar physical conditions in the considered regions and the MHD simulations employed to estimate this correction factor.
We estimate 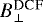 in circles of 3 deg in diameter centered at the positions listed in Table 1. The angular resolution of the polarization observations (1 deg) is slightly lower than that of the Zeeman observations (0°.6). As such, we do not probe exactly the same regions in
in circles of 3 deg in diameter centered at the positions listed in Table 1. The angular resolution of the polarization observations (1 deg) is slightly lower than that of the Zeeman observations (0°.6). As such, we do not probe exactly the same regions in 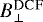 as in B∥. Nevertheless, the three Zeeman splitting values are consistent, that is, they reflect B∥ pointing towards the observer without a reversal. Therefore, to first order, we assume that the B∥ values are representative of the larger region sampled by our analysis.
as in B∥. Nevertheless, the three Zeeman splitting values are consistent, that is, they reflect B∥ pointing towards the observer without a reversal. Therefore, to first order, we assume that the B∥ values are representative of the larger region sampled by our analysis.
We estimate σv using the HI spectra averaged in the three-degree circles mentioned above and the spectral decomposition procedure described in Appendix B. For all three cases, the spectra present narrow components and wide wings associated with an additional underlying, broad spectral line. We assume that the HI emission comes from a mixture of two stable gas phases (Wolfire et al. 2003), the cold neutral medium (CNM) and the warm neutral medium (WNM), which produce the narrow and broad components, respectively. Recent studies of dust polarized emission and HI data show a strong correlation between magnetic-field and CNM structures, in contrast with the poor correlation with the WNM (Clark et al. 2014; Planck Collaboration Int. XXXII 2016). Motivated by these results, we choose to only use the CNM component to estimate the gas properties involved in the calculation of 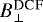 , which we present in Table 1. If instead of using the CNM component we considered the WNM component, the magnetic-field strengths in Table 1 would be larger given its larger HI velocity dispersion. Thus, our estimates of B⊥ constitute lower limits to the true values.
, which we present in Table 1. If instead of using the CNM component we considered the WNM component, the magnetic-field strengths in Table 1 would be larger given its larger HI velocity dispersion. Thus, our estimates of B⊥ constitute lower limits to the true values.
The volume density, nH, is derived from the HI column density assuming that the line-of-sight depth, Δ, of the CNM component is of a few parsec. A lower limit for Δ (roughly 1 pc) is set by the negligible molecular gas fraction toward the three positions (Planck Collaboration XIII 2014). An upper limit for Δ is set by the typical densities of CNM gas, nH ≈ 30 cm−3. For the sake of simplicity, we use Δ ≈ 5 ±1 pc in the three regions.
The angular dispersion of the local magnetic field orientation, ςψ, is estimatedusing two methods. First, directly computing the angular dispersion from the Stokes Q and U using Eqs. (D.5) and (D.11) in Planck Collaboration Int. XXXV (2016), and second, using the structure function of polarization angles as describedin Appendix C. Central coordinates, velocity dispersions, volume densities, angular dispersions of B⊥, strengths of B⊥, and Alfvénvelocities of the three positions are given in Table 1.
Estimates of the magnetic field strength.
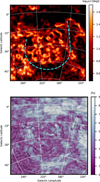 |
Fig. 2 Polarization angular dispersion function, S2(δ =30′) (top) and polarization fraction (bottom), toward the Orion-Eridanus superbubble. |
4 Discussion and conclusions
The magnetic field strengths within the shell, reported in Table 1, tend to be a factor of a few larger than the average field strength of CNM clouds in the solar neighborhood ( ~6 μG, Heiles & Crutcher 2005), as expected for magnetic fields compressed by expanding bubbles. The plane-of-the-sky magnetic field, B⊥, shows obvious signs of interaction with the superbubble. The maps of the polarization angular dispersion and polarization fraction clearly highlight the location of the outer wall of the superbubble. This outer wall traces out a relatively spherical superbubble, consistent with the expansion of the superbubble in the exponential density profile of the Galactic disk. These data rule out the skinny bubble models of Pon et al. (2014) and are more consistent with the models put forth by Ochsendorf et al. (2015) and Pon et al. (2016).
The values of B⊥ and B∥ indicate that the magnetic field vector has a large component in the plane of the sky, as expected from the relatively large polarization fractions observed toward these regions. The Alfvén velocities in the shell, inferred from the combination of B⊥ and B∥, and listed in Table 1, are below the shell expansion velocity reported in Reynolds & Ogden (1979), approximately 23 km s−1, further suggesting that the magnetic field was swept up and organized by the expanding bubble. This is also illustrated by Figs. 1 and 2, where B⊥ lies parallel to the shell surface over a large portion of its projected extent. Although it is expected that the initial magnetic field in the region hinders the expansion of the superbubble perpendicular to its mean direction (Tomisaka 1998), the circular shape of the superbubble and the data in hand indicate that the magnetic field is not dynamically important for the expansion of the superbubble itself. This is in agreement with results of recent numerical MHD simulations that show that moderate initial magnetic fields do not modify the total amount of momentum injected by SNe explosions into the ISM (Kim & Ostriker 2015; Iffrig & Hennebelle 2017).
However, the now-compressed magnetic field may play a significant role in the continuing evolution of the shell structure, both generating surfaces more stable to dynamical instabilities and suppressing the formation of dense gas. The enhanced magnetic field provides additional support, reducing the dense gas fraction (Walch et al. 2015; Ntormousi et al. 2017) and potentially shaping the photoionization region produced by the generation of stars that follow the SN explosion (Basu et al. 1999; Pellegrini et al. 2007). The investigation of these effects motivates the pursuit of additional observations of Zeeman splitting and dust polarized emission at higher angular resolution toward the Orion-Eridanus and other superbubbles.
Acknowledgements
JDS acknowledges the support from the European Research Council (ERC) under the Horizon 2020 Framework Program via the Consolidator Grant CSF-648505. AB acknowledges the support from the ERC Advanced Grant ORISTARS under the European Union’s Seventh Framework Programme (Grant 291294). AP was partly funded by a Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship. We thank the referee M. Alves for her constructive comments that have led to improvements in this presentation of our results. Thanks to M. Houde and S. Basu for their comments on the early versions of this work. We also thank the following people who helped with their encouragement and conversation: P. G. Martin, H. Beuther, C. Heiles, T. Robishaw, M.-A. Miville-Deschênes, and A. Roy. Special thanks go to Thomas Müller at the Haus der Astronomie for his assistance in the magnetic field visualization.
Appendix A Planck polarization maps
A.1 Stokes I, Q and U maps
We use the publicly available 353-GHz Stokes, I, Q and U maps and the associated noise maps made with the five independent consecutive sky surveys of the Planck cryogenic mission. We refer to publications by the Planck Collaboration for details on the data processing, including mapmaking, photometriccalibration, and photometric uncertainties (Planck Collaboration I 2016, and references therein). The Q and U maps are initially constructed with an effective beamsize of 4′.8. The three maps are in HEALPix format (Górski et al. 2005) with a pixelization at Nside =2048, which corresponds to an effective pixel size of 1′.7. To guarantee a signal-to-noise ratio greater than 3 in the extended polarized emission observations over the whole region, we smooth the Planck 353-GHz maps to 1 deg resolution using a Gaussian approximation to the Planck beam. The smoothing is produced with the ismoothing routine of HEALPix, which decomposes the Q and U maps into E and B maps, applies Gaussian smoothing in harmonic space, and transforms the smoothed E and B back into Q and U maps.
 |
Fig. A.1 Planck 353-GHz Stokes Q (top) and U (bottom) maps toward the Orion-Eridanus superbubble at 1 deg FWHM resolution. |
We compute the polarization angles and fractions used for the analysis using
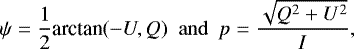 (A.1)
(A.1)
respectively. The minus symbol is needed to change the HEALPix format maps into the International Astronomical Union (IAU) convention for ψ, measured from the local direction to the north Galactic pole with increasing positive values toward the east.
A.2 Dispersion function maps
In the main body of this Letter, we considered the particular case 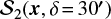 . Here, for the sake of comparison, we present in Fig. A.2 the maps of
. Here, for the sake of comparison, we present in Fig. A.2 the maps of 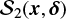 computed at displacements δ = 60 ′ and 90′. Both panels show that the low-
computed at displacements δ = 60 ′ and 90′. Both panels show that the low-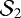 region identified in Fig. 2 and associated with the wall of the expanding superbubble is also visible in the maps obtained with larger values of δ, thus confirming that it is not the product of the correlation introduced by the resolution of the observations.
region identified in Fig. 2 and associated with the wall of the expanding superbubble is also visible in the maps obtained with larger values of δ, thus confirming that it is not the product of the correlation introduced by the resolution of the observations.
 |
Fig. A.2 Polarization angular dispersion function, S2(x, δ), Eq. (1), toward the Orion-Eridanus superbubble. The top and bottom panels correspond to S2 (δ =60′) and S2 (δ =90′), respectively. |
A.3 Gradient of polarization maps
The computation of extended 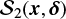 maps is costly and time consuming. An alternative approach is computing the quantity
maps is costly and time consuming. An alternative approach is computing the quantity
![\begin{equation*}\frac{|\nabla P|}{P}=\frac{1}{{\sqrt{Q^2 + U^2}}}\left[\left(\frac{\partial Q}{\partial x}\right)^{2}+\left(\frac{\partial Q}{\partial y}\right)^{2}+\left(\frac{\partial U}{\partial x}\right)^{2}+\left(\frac{\partial U}{\partial y}\right)^{2}\right]^{1/2}, \end{equation*}](/articles/aa/full_html/2018/01/aa32203-17/aa32203-17-eq17.png) (A.2)
(A.2)
which was introduced in Gaensler et al. (2011) and traces the changes in the orientation of B⊥.
Figure A.3 shows maps of |∇P|∕P where the spatial derivatives of Stokes Q and U are calculated using derivative kernels with diameters 60′, 120′, and 180′, as introduced in Soler et al. (2013). In practice, this means that we smooth the data with a two-dimensional Gaussian with FWHM equal to the corresponding diameter and then calculate the gradient using next-neighbour differences. This operation is equivalent to calculating the derivative using differences of points inside a vicinity with the same diameter. The diameter of the derivative kernel is roughly comparable to the displacement δ in 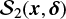 . The |∇P|∕P maps show that the low-polarization-angle-dispersion region identified in Fig. 2 is also visible in |∇P|∕P at scales around and above the angular resolution of the observations.
. The |∇P|∕P maps show that the low-polarization-angle-dispersion region identified in Fig. 2 is also visible in |∇P|∕P at scales around and above the angular resolution of the observations.
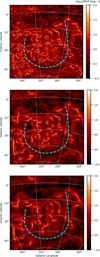 |
Fig. A.3 Maps of |∇P|∕P, Eq. (A.2), toward the Orion-Eridanus superbubble. The spatial gradients are calculated using derivative kernels of diameters 60′ (top), 120′ (middle), and 180′ (bottom). |
Appendix B Gaussian decomposition of HI spectra
In order to account for the multiphase nature of the HI emission (Wolfire et al. 2003) in our implementation of the DCF method, we apply a simple Gaussian decomposition of the spectra. Assuming a bistable atomic gas, we separate the emission from the CNM and the WNM. For the three spectra in Fig. B.2, we show the decomposed Gaussians with the key parameters in the corresponding tables. In all cases, we find narrow spectral lines with σG ~ 2 km s−1, typical of CNM emission, on top of a broad WNM line with σG > 9 km s−1. In this Letter, we focus on the narrow CNM component (line a in Fig. B.2) at positive velocities for which Heiles (1989) estimated the strengths of B∥ from Zeeman measurements.
 |
Fig. B.1 Average spectra in vicinities of 3 deg in diameter centered on the 21-cm emission-line Zeeman splitting observationspresented in Heiles (1989). |
 |
Fig. B.2 Gaussian decomposition of the HI spectra presented in Fig. B.1 with colors representing the three central positions. The solid lines correspond to full average spectra while dashed lines to the decomposed Gaussians. The parameters of each Gaussian component: intensity, centroid velocity (vG ), and standard deviation (σG), are listed in each panel. |
We estimate the CNM column density for the three different regions using the relation
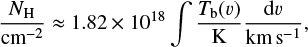 (B.1)
(B.1)
where Tb is the observed 21-cm line brightness temperature (line intensity in the figures) at radial velocity v with respect to the local standard of rest (Kulkarni & Heiles 1987).
Appendix C Dispersion function of polarization angles
The structure function, S2(ℓ), which is simply the dispersion function of the polarization angles (Eq. (1)) averaged over all the positions x, such that S2 (ℓ) ≡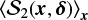 , is useful for the evaluation of the dispersion of polarization angles, ςψ, while avoiding the effect of large-scale non-turbulent perturbations (Hildebrand et al. 2009). The evaluation of ςψ is made by fitting
, is useful for the evaluation of the dispersion of polarization angles, ςψ, while avoiding the effect of large-scale non-turbulent perturbations (Hildebrand et al. 2009). The evaluation of ςψ is made by fitting 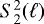 with a second-order polynomial,
with a second-order polynomial, 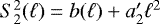 , and evaluating the intercept, b(0). The values of S2(ℓ) and the aforementioned fits are presented in the top panel of Fig. C.1.
, and evaluating the intercept, b(0). The values of S2(ℓ) and the aforementioned fits are presented in the top panel of Fig. C.1.
In principle, the DCF magnetic field estimates can be corrected for the effect of line-of-sight integration if one can reliably estimate the number of independent turbulent cells along the line of sight, N (Houde et al. 2009). Unfortunately, the correlation introduced by the effective Planck beam dominates the values of b(ℓ), as illustrated in the bottom panel of Fig. C.1, and it is not possible to determine the characteristic scale of turbulence (see Miville-Deschênes et al. 2016, for a detailed discussion) necessary to estimate N from these data alone.
 |
Fig. C.1 Structure function of the polarization angles, S2(ℓ), and normalized autocorrelation function of the plane-of-the-sky component of the magnetic field, b2 (ℓ) (Houde et al. 2009), in the vicinities of 3 deg in diameter centered on the 21-cm emission-line Zeeman splitting observations presented in Heiles (1989). In the top panel, the dashed lines correspond to the fit to the values of S2 (ℓ) in the range ℓ > 1 deg, which is theeffective resolution of the Planck observations, represented by the vertical solid line. In the bottom panel, the solid black lines correspond to the expected correlation produced by the effective resolution of the observations. |
References
- Bally, J. 2008, in Handbook of Star Forming Regions, Vol. I, ed. B. Reipurth (San Francisco, CA: ASP Monograph Publications), 459 [NASA ADS] [Google Scholar]
- Barnard, E. E. 1894, Popular Astronomy, 2, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., Johnstone, D., & Martin, P. G. 1999, ApJ, 516, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Boumis, P., Dickinson, C., Meaburn, J., et al. 2001, MNRAS, 320, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., Hartmann, D., & Burton, W. B. 1995, A&A, 300, 903 [NASA ADS] [Google Scholar]
- Burrows, D. N., Singh, K. P., Nousek, J. A., Garmire, G. P., & Good, J. 1993, ApJ, 406, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Cabral, B., & Leedom, L. C. 1993, in Special Interest Group on GRAPHics and Interactive Techniques Proc. (New York: ACM), 263 [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, L. 1951, Phys. Rev., 81, 890 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ferriere, K. M., Mac Low, M.-M., & Zweibel, E. G. 1991, ApJ, 375, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Burkhart, B., et al. 2011, Nature, 478, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gaustad, J. E., McCullough, P. R., Rosing, W., & Van Buren D. 2001, PASP, 113, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Z., Burrows, D. N., Sanders, W. T., Snowden, S. L., & Penprase, B. E. 1995, ApJ, 453, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1976, ApJ, 208, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1989, ApJ, 336, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1997, ApJS, 111, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, in Cosmic Magnetic Fields, eds. R. Wielebinski & R. Beck (Berlin: Springer Verlag), Lect. Notes Phys., 664, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., Haffner, L. M., & Reynolds, R. J. 1999, in New Perspectives on the Interstellar Medium, eds. A. R. Taylor, T. L. Landecker, & G. Joncas, ASP Conf. Ser., 168, 211 [NASA ADS] [Google Scholar]
- HI4PI Collaboration, Ben Bekhti, N., Flöer, L., et al. 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H., Kirby, L., Dotson, J. L., Houde, M., & Vaillancourt, J. E. 2009, ApJ, 696, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., & Kirby, L. 2009, ApJ, 706, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Iffrig, O., & Hennebelle, P. 2017, A&A, 604, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, P. G. 1978, MNRAS, 184, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2015, ApJ, 802, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R., & Heiles, C. 1987, in Interstellar Processes, eds. D. J. Hollenbach & H. A. Thronson, Jr., Astrophys. Space Sci. Lib., 134, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D. 2008, in The λ Orionis Star Forming Region, ed. B. Reipurth, 757 [Google Scholar]
- Miville-Deschênes, M.-A., Duc, P.-A., Marleau, F., et al. 2016, A&A, 593, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ntormousi, E., Dawson, J. R., Hennebelle, P., & Fierlinger, K. 2017, A&A, 599, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ochsendorf, B. B., Brown, A. G. A., Bally, J., & Tielens, A. G. G. M. 2015, ApJ, 808, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., Stone, J. M., & Gammie, C. F. 2001, ApJ, 546, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Brogan, C. L., et al. 2007, ApJ, 658, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, 571, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int XXXIV. 2016, A&A, 586, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int XXXV. 2016, A&A, 586, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pon, A., Johnstone, D., Bally, J., & Heiles, C. 2014, MNRAS, 444, 3657 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Ochsendorf, B. B., Alves, J., et al. 2016, ApJ, 827, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R. J., & Ogden, P. M. 1979, ApJ, 229, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, J.-F., Scaife, A. M. M., Carretti, E., et al. 2017, MNRAS, 468, 2957 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Green, G., Finkbeiner, D. P., et al. 2014, ApJ, 786, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, J. D., & Hennebelle, P. 2017, A&A, 607, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, J. D., Hennebelle, P., Martin, P. G., et al. 2013, ApJ, 774, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 1998, MNRAS, 298, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S., Girichidis, P., Naab, T., et al. 2015, MNRAS, 454, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., Sallmen, S., & Jelinsky, S. 2005, A&A, 440, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stereographic projections of observations toward the Orion-Eridanus superbubble. The drapery pattern, produced using the line integral convolution technique (LIC; Cabral & Leedom 1993), corresponds to plane-of-the-sky magnetic field orientation inferred from the Planck 353-GHz polarization observations. Left: total integrated Hα emission map. The dashed line indicates the approximate location of the edge of the superbubble. The yellow symbols correspond to the main stars in the Orion constellation. Right: total integrated Hα emission (Gaustad et al. 2001) and HI 21-cm emission (HI4PI Collaboration et al. 2016) integrated between − 20 and 20 km s−1 shown in red and teal colors, respectively. The yellow symbols correspond to the line-of-sight magnetic field directions derived fromthe HI emission-line Zeeman splitting observations (Heiles 1989, 1997). The circles and triangles correspond to magnetic fields pointing toward and away from the observer, respectively. The three white circles in the bottom are the regions analyzed in this Letter. |
| In the text | |
 |
Fig. 2 Polarization angular dispersion function, S2(δ =30′) (top) and polarization fraction (bottom), toward the Orion-Eridanus superbubble. |
| In the text | |
 |
Fig. A.1 Planck 353-GHz Stokes Q (top) and U (bottom) maps toward the Orion-Eridanus superbubble at 1 deg FWHM resolution. |
| In the text | |
 |
Fig. A.2 Polarization angular dispersion function, S2(x, δ), Eq. (1), toward the Orion-Eridanus superbubble. The top and bottom panels correspond to S2 (δ =60′) and S2 (δ =90′), respectively. |
| In the text | |
 |
Fig. A.3 Maps of |∇P|∕P, Eq. (A.2), toward the Orion-Eridanus superbubble. The spatial gradients are calculated using derivative kernels of diameters 60′ (top), 120′ (middle), and 180′ (bottom). |
| In the text | |
 |
Fig. B.1 Average spectra in vicinities of 3 deg in diameter centered on the 21-cm emission-line Zeeman splitting observationspresented in Heiles (1989). |
| In the text | |
 |
Fig. B.2 Gaussian decomposition of the HI spectra presented in Fig. B.1 with colors representing the three central positions. The solid lines correspond to full average spectra while dashed lines to the decomposed Gaussians. The parameters of each Gaussian component: intensity, centroid velocity (vG ), and standard deviation (σG), are listed in each panel. |
| In the text | |
 |
Fig. C.1 Structure function of the polarization angles, S2(ℓ), and normalized autocorrelation function of the plane-of-the-sky component of the magnetic field, b2 (ℓ) (Houde et al. 2009), in the vicinities of 3 deg in diameter centered on the 21-cm emission-line Zeeman splitting observations presented in Heiles (1989). In the top panel, the dashed lines correspond to the fit to the values of S2 (ℓ) in the range ℓ > 1 deg, which is theeffective resolution of the Planck observations, represented by the vertical solid line. In the bottom panel, the solid black lines correspond to the expected correlation produced by the effective resolution of the observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


