| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731819 | |
| Published online | 23 January 2018 | |
Transient events in bright debris discs: Collisional avalanches revisited
1 LESIA-Observatoire de Paris, UPMC Univ. Paris 06, Univ. Paris-Diderot, France
e-mail: philippe.thebault@obspm.fr
2 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
Received: 23 August 2017
Accepted: 16 November 2017
Context. A collisional avalanche is set off by the breakup of a large planetesimal, releasing vast amounts of small unbound grains that enter a debris disc located further away from the star, triggering there a collisional chain reaction that could potentially create detectable transient structures.
Aims. We investigate this mechanism, using for the first time a fully self-consistent code coupling dynamical and collisional evolutions. We also quantify for the first time the photometric evolution of the system and investigate whether or not avalanches could explain the short-term luminosity variations recently observed in some extremely bright debris discs.
Methods. We use the state-of-the-art LIDT-DD code. We consider an avalanche-favoring A6V star, and two set-ups: a “cold disc” case, with a dust release at 10 au and an outer disc extending from 50 to 120 au, and a “warm disc” case with the release at 1 au and a 5−12 au outer disc. We explore, in addition, two key parameters: the density (parameterized by its optical depth τ) of the main outer disc and the amount of dust released by the initial breakup.
Results. We find that avalanches could leave detectable structures on resolved images, for both “cold” and “warm” disc cases, in discs with τ of a few 10-3, provided that large dust masses (≳1020−5 × 1022 g) are initially released. The integrated photometric excess due to an avalanche is relatively limited, less than 10% for these released dust masses, peaking in the λ ~ 10−20 μm domain and becoming insignificant beyond ~40–50 μm. Contrary to earlier studies, we do not obtain stronger avalanches when increasing τ to higher values. Likewise, we do not observe a significant luminosity deficit, as compared to the pre-avalanche level, after the passage of the avalanche. These two results concur to make avalanches an unlikely explanation for the sharp luminosity drops observed in some extremely bright debris discs. The ideal configuration for observing an avalanche would be a two-belt structure, with an inner belt (at ~1 or ~10 au for the “warm” and “cold” disc cases, respectively) of fractional luminosity f ≳ 10-4 where breakups of massive planetesimals occur, and a more massive outer belt, with τ of a few 10-3, into which the avalanche chain reaction develops and propagates.
Key words: circumstellar matter
© ESO, 2018
1. Introduction
Debris discs are detected around main sequence stars through the luminosity excess due to circumstellar dust particles. They are believed to be made of the leftover material that has not been used in planetary formation. The standard picture of these systems’ evolution is that this material is progressively eroding through a steady-state collisional cascade, starting at the largest bodies in the disc and ending at dust grains small enough to be blown away by radiation pressure (Krivov 2010).
In addition to being detected in photometry, more than 130 discs have now also been imaged at wavelengths ranging from the optical to the millimetre1. A large fraction of these resolved systems display pronounced spatial structures, such as rings, arcs, spirals, clumps, two-side asymmetries, or warps, which bear witness to complex processes shaping these systems (e.g. Matthews et al. 2014). Most proposed explanations for these observed structures imply that they are relatively long-lived, being either due to the perturbing effect of (observed or unseen) planets (e.g. Mouillet et al. 1997; Wyatt 2006; Reche et al. 2009; Thebault et al. 2012; Nesvold & Kuchner 2015; Pearce & Wyatt 2015) or stellar companions (Thebault et al. 2010; Thebault 2012; Nesvold et al. 2016), or to interactions with gas (Takeuchi & Artymowicz 2001; Lyra & Kuchner 2013).
The collisional avalanche scenario.
Alternatively, some models consider that the observed features are transient and created in the aftermath of the destruction of a large planetesimal or planetary object (Jackson et al. 2014; Kral et al. 2015). One of the main issues with these scenarios is that they require giant impacts that might be uncommon past the first 10–20 Myr of the planet-formation phase (Wyatt & Jackson 2016). To alleviate this possible shortcoming, an alternative version of the breakup-aftermath scenario has been proposed, the so-called collisional avalanche mechanism. In this model, first mentioned by Artymowicz (1997), the breakup of a planetesimal releases small dust grains below the radiation pressure cutoff size sblow, which are placed on outbound trajectories and then impact at very high velocities a debris disc located further out. If this outer disc is dense enough, a chain reaction can be triggered, because these high-Δv impacts will produce a new generation of small, s<sblow grains which will again impact particles in the disc, on their way out, producing new small outbound debris and so on (see Fig. 1). This chain reaction might considerably amplify the level of dustiness produced by the initial breakup, thus requiring a less massive object to reach observability than for an isolated planetesimal breakup.
This scenario was first quantitatively investigated by Grigorieva et al. (2007, hereafter GAT07), using a then unique numerical code coupling the dynamical and collisional evolution of a disc. This study showed that collisional avalanches can indeed strongly amplify the geometrical cross section of the initially breakup-released dust, and produce spiral shaped patterns in the disc that can last for a few orbital periods. GAT07 quantified an avalanche’s amplitude by a cross section “amplification factor” F and found that this parameter increases exponentially with the outer disc’s density (quantified by its radial optical depth τr). However, for the nominal case they considered, that is, a breakup releasing 1020 g of dust and a β Pictoris-like disc, GAT07 found that collisional avalanches induce luminosity increases much too small to be observed. They extrapolated that a system at least five times denser than β Pic, a disc already at the upper end of bright debris discs, should be required in order for an avalanche to be observable in a resolved debris disc. At the time, only one such very bright disc was known, BD+20307 Song et al. (2005), an unresolved system, thus not allowing a straightforward application of the avalanche hypothesis.
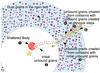 |
Fig. 1 Schematic description of the avalanche process. First, a large body is shattered in the inner region of the planetary system, releasing very small unbound grains that are blown out by radiation pressure. Then these small grains penetrate an outer disc located further away from the star. There they will collide, at very high velocities, with “native” target grains, producing a new generation of small unbound grains, which will also be blown out and collide with other target grains in the disc, creating new fragments that will again collide with targets further out in the disc, etc. If the main disc is dense enough, this chain reaction can produce an excess of small grains largely exceeding the amount initially produced by the breakup. |
Avalanches in “extreme” debris discs?
However, in the past decade, several other very luminous discs (with IR fractional luminosities f ≳ 10-2) have been discovered (e.g. Meng et al. 2015; Genda et al. 2015; Melis 2016). For these “extreme” debris discs, the amount of dust required to explain their current luminosities, especially at wavelengths shortward of 24 μm, cannot be sustained by a steady-state collisional cascade over these system’s estimated ages (e.g. Wyatt et al. 2007b; Gáspár et al. 2013; Kennedy & Wyatt 2013; Wyatt & Jackson 2016)2. The observed dust could be transient, possibly produced in the aftermath of the breakup of a massive body (Meng et al. 2014; Wyatt & Jackson 2016), or be sustained by comet or asteroid scattering in closely packed multiple-planet systems (Bonsor et al. 2013).
The discovery of this new class of extreme discs has spawned a renewed interest in the collisional avalanche scenario, which could indeed be greatly facilitated by these system’s high level of dustiness. This interest has been compounded by the fact that a handful of these discs exhibit brightness variations on very short timescales, of the order of a year, for which avalanches have been suggested as a possible explanation (Meng et al. 2015). It is worth noting that avalanches have been mostly invoked as being able to explain the rapid luminosity decrease in some of these systems, in particular the ~50% decay over ~370 days following the initial brightening of ID8 (Meng et al. 2014, 2015), and the abrupt luminosity drop (by a factor 30) observed for the TYC 8241 2652 1 system over the course of less than two years (Melis et al. 2012). The argument is that the passage of the avalanche would leave the main disc depleted in ≲100 μm particles, as they have been “sandblasted” by the high-velocity impacts with the outbound avalanche grains, making the post-avalanche system (after the transient luminosity excess due to unbound grains) less luminous than it was prior to the avalanche. Interestingly, this luminosity drop consequence of an avalanche had not been mentioned by GAT07, who insisted only on the luminosity increase that it might trigger. It is true that the temporal evolution of the amplification factor F showed a progressive decay after a strong initial increase, but this parameter only measures the avalanche geometrical cross section with respect to that of the initially released grains, but not that of the total avalanche+disc system. As a matter of fact, the photometric evolution of the total system was not investigated in GAT07, the focus being essentially on spatial signatures and localised luminosity contrasts.
Revisiting the avalanche mechanism.
In light of this new context, it appears important to reinvestigate the collisional avalanche mechanism and reassess its relevance with respect to observed systems. Such a reinvestigation was in any case necessary and long overdue, firstly because the pioneering study of GAT07 left many issues unexplored (photometric evolution, wavelength dependence, etc.), which maybe opened the door to some misconceptions about the avalanche phenomenon, but also because new debris disc modelling codes have been developed in the past decade, which allow a more accurate study of this complex mechanism. The most advanced of this new generation of codes is probably the LIDT-DD model developed by Kral et al. (2013), which is to date the only one that allows for a coupled study of collisions and dynamics taking into account the crucial size-dependent effect of radiation pressure. LIDT-DD allows to relax some of the simplifications done in GAT07; mainly the fact that “avalanche” (i.e. the initially released debris and all new debris they will collisionally generate) and “field” (i.e. grains in the outer disc not affected by collisions with avalanche grains) particles were treated separately, but also that the possible presence of “native” unbound grains in the field disc itself was not taken into account.
We thus here revisit the collisional avalanche scenario using the state-of-the-art LIDT-DD code. Furthermore, we now consider two different configurations: a “cold disc” case similar to that of GAT07, with the breakup event at 10 au and the outer disc at 50−120 au, and also a “warm disc” case, closer to the new class of observed “extreme” discs, with the breakup at 1 au and the outer disc at 5−12 au. We also explore different values of the main disc density. We present the main characteristics of our model and set-up in Sect. 2. Results for all explored cases are presented in Sect. 3. In Sect. 4, we discuss the main implications of these results, in particular the dependence of avalanche strength on disc density and the likelihood of avalanche-triggering events in real systems. A detailed summary and our conclusions are given in the last section.
2. Model
2.1. The LIDT-DD code
The LIDT-DD code has been described in detail in Kral et al. (2013, 2015), but we recall here some of its main characteristics. It is in essence a hybrid code, taking some of its structure from a protoplanetary-disc model developed by Charnoz & Taillifet (2012), coupling an N-body scheme to compute the dynamics and a statistical particle-in-a-box approach to follow the collisional evolution. The base elements of this model are “super particles” (SPs), each representing a cloud of grains of a given size (or, more exactly, a size bin) at a given location, whose dynamical evolution is computed with a standard Burlish-Stoer algorithm. The collisional evolution is then performed by dividing the system into three-dimensional (3D) spatial cells, and estimating all mutual collisions between the SPs contained in each cell. Each of these mutual SP collisions is treated in a statistical way, as being between two clouds of grains having the physical sizes represented by each SP and sharing their local dynamical characteristics. The physical outcomes of the grain-grain collisions can be fragmentation, cratering, or accretion, depending on the grain sizes and relative velocities. The collisional fragments produced by cratering or fragmenting collisions will either be reattributed to existing SPs in the same cell, or assigned to newly created SPs in cases where SPs representing similar sizes and dynamical characteristics do not already exist in the cell.
One crucial aspect of LIDT-DD, which sets it apart from other similar hybrid codes (e.g. Levison et al. 2012; Nesvold et al. 2013), is that it takes into account the size-dependent effect of stellar radiation pressure. Because dynamical evolution then strongly varies with the grains’ physical sizes, each SP only stands for one given size bin, instead of representing a whole size distribution as in other codes. Given the wide radial excursion of small grains affected by radiation pressure, this does also mean that, in any given region of the system, SPs representing the same grain size can have very different dynamical characteristics depending on where the grain population they stand for was originally produced. Accordingly, the code is equipped with a procedure that sorts out, for any given size bin in a given spatial cell, all SPs into distinct dynamical families that collisionally interact with each other.
2.2. Setup
In accordance with the standard avalanche scenario, we consider here the breakup of a planetesimal, producing a cloud of fragments, of which a fraction are placed on unbound orbits and will impact grains located in an extended main debris disc located further out (Fig. 1).
We consider two basic configurations. One of them is the same as in GAT07, with an initial breakup occurring at 10 au from the central star, and the outer disc located between 50 and 120 au. This “cold” debris disc case is considered mainly in order to investigate the spatial signature of an avalanche, because this ~50–100 au range is the one where most spatial structures have been observed in imaged debris discs (Schneider et al. 2014). The other configuration is scaled down by a factor of 10, with a breakup occurring at 1 au and the outer disc between 5 and 12 au. This “warm disc” case is motivated by the study of the potential photometric signature of an avalanche, in particular in the ≲24 μm wavelength domain where most of the short term luminosity variations of “extreme” discs have been observed.
In order to avoid multiplying the number of free parameters to an unmanageable level, some of them are fixed in our set-up. For the grain composition, we consider a standard astrosilicate case (Draine 2003) with zero porosity. Classically, the grain’s resistance to impacts is parameterized by the critical specific energy Q∗ required to disperse 50% of an impacted target, for which we assume the empirical expression derived by Benz & Asphaug (1999). Collision outcomes (cratering, fragmentation) are then treated following the procedure described in Kral et al. (2013). For the central star, we assume an A6V spectral type, similar to the β-Pic case considered in GAT07, as such a luminous early-type star is more favourable to avalanche development. Indeed, for such stars, there is a much larger fraction of dust grains with β> 0.5 (β being the ratio between stellar radiation and gravity, and β = 0.5 being the limit for unbound orbits for grains produced from circular orbits) than for solar-type stars (see for instance Fig. 2 in Beust et al. 2001). The initial eccentricities of particles in the main disc are uniformly distributed between 0 and emax = 0.1 and their inclinations between 0 and emax/ 2, which is a standard assumption for “classical” debris discs (e.g. Thebault 2009). We follow the evolution of all particles with sizes comprised between smin = 20 nm (2 × 10-8 m) and smax = 1 m, distributed onto 48 logarithmically spaced size bins. We note that smin is well below the blowout size for an A6V star, which is sblow ~ 1.6 μm for compact astrosilicates, so that we cover a large size range of bodies with unbound orbits (β ≥ 0.5, see Fig. 2). The initial size distribution follows a standard power law in dN ∝ s-3.5ds down to the cutoff size sblow, but this initial profile is quickly relaxed as we let the system evolve towards a collisional steady-state before launching the avalanche.
 |
Fig. 2 Value of β, the ratio between radiation pressure and gravitational forces, as a function of particle size, computed for non-porous astrosilicates. The β(s) curve is shown for the luminous A6V star considered as a reference case in our runs, as well as for the TYC 8241 2652 1 K star discussed in Sect. 4.4. The dotted horizontal line marks the β = 0.5 limit, above which grains are no longer on bound orbits around the star (if produced from progenitors on circular orbits). |
This leaves us with two main free parameters, both crucial to avalanche development. The first one is of course the mass minit of dust released by the initial planetesimal breakup. GAT07 considered a case with minit = 1020 g of grains of size s< 1 cm, corresponding to the mass of an object of radius ~20 km, and we explore different values of minit around this reference value. Of course, not all of the fragments produced by this hypothetical shattered planetesimal of mass Mbreakup are in the s< 1 cm range, but we defer a discussion about the link between minit and Mbreakup to the discussion. The size distribution of the released fragments follows a slightly steeper law in dN ∝ s-3.8ds, corresponding to the crushing law expected for the outcome of violent massive collisions (e.g. Takasawa et al. 2011; Leinhardt & Stewart 2012), all the way down to smin = 2 × 10-8 m (see Sect. 4.5 for a discussion on this point).
The second free parameter, which GAT07 considered to be the most important one, is the dust density in the main outer disc. GAT07 parameterized this density by the radial optical depth τr, which scales the amount of material an outward moving grain will cross on its way through the disc. However, we choose here to take the more commonly used normal optical depth parameter τ⊥. This parameter then allows comparison to one easily observable quantity that is the fractional infrared luminosity f = LIR/Lbol (Wyatt et al. 2007a), at least as long as the grains dominating the geometrical cross section excess also dominate the excess in IR flux (which might not always be the case, see discussion in Sect. 3.1.1). For a disc of radial width Δr located at an average distance r from its star with an average normal optical depth τ⊥, we have (Zuckerman & Song 2012): 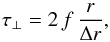 (1)the relation between τ⊥ and τr is
(1)the relation between τ⊥ and τr is  (2)where h is the vertical thickness of the disc. For the considered case of an extended disc with Δr/r ~ 0.8, τ⊥ and f only differ by a factor 1.5 3, whereas the ratio between τr and τ⊥ is ~5−10 if we consider a typical disc thickness of 0.05–0.1 (Thebault 2009). We consider as a reference the ⟨τ⊥⟩ ~ 2 × 10-3 value (and thus τr ~ 0.02) taken by GAT07 for their β-Pictoris-like case, and explore values around this nominal case. As for the radial distribution of the particle volumic number density within the main disc, we assume that it follows an initial profile in 1 /r, corresponding to a flat radial distribution for τ⊥. The setup is summarised in Table 1.
(2)where h is the vertical thickness of the disc. For the considered case of an extended disc with Δr/r ~ 0.8, τ⊥ and f only differ by a factor 1.5 3, whereas the ratio between τr and τ⊥ is ~5−10 if we consider a typical disc thickness of 0.05–0.1 (Thebault 2009). We consider as a reference the ⟨τ⊥⟩ ~ 2 × 10-3 value (and thus τr ~ 0.02) taken by GAT07 for their β-Pictoris-like case, and explore values around this nominal case. As for the radial distribution of the particle volumic number density within the main disc, we assume that it follows an initial profile in 1 /r, corresponding to a flat radial distribution for τ⊥. The setup is summarised in Table 1.
The procedure for the simulations is then the following. We first consider the main outer debris disc, which we allow to evolve until a collisional steady state is reached, that is, until the shape of the size distribution no longer evolves and only its absolute level decreases. We then release the avalanche dust grains and follow the evolution of the combined avalanche+main-disc system. Contrary to GAT07, we do not measure the amplitude of an avalanche by the cross section amplification factor F, because this parameter, while allowing a good description of how an avalanche unfolds, does not give any indication about the real signature it leaves in a disc and its observability. We instead adopt a more classical approach where we evaluate an avalanche’s strength by two criteria: firstly by estimating, on 2D synthetic images, the luminosity contrast of avalanche-related structures with respect to the background disc, and secondly by measuring the system-integrated photometric variations it induces. For deriving both these synthetic images and the integrated fluxes, we use the GRaTer radiative transfer package (Augereau et al. 1999).
Set-up for the “cold” and “warm” disc configurations.
3. Results
 |
Fig. 3 Normalized synthetic images, in scattered light, showing the evolution of an avalanche in a cold debris disc (extending from 50 to 120 au) of average optical depth τ⊥ ~ 2 × 10-3, for an initial breakup, at t = 0, releasing 5 × 1022 g of dust at 10 au from the star. |
 |
Fig. 4 Radial cuts of the vertical optical depth, passing by the avalanche’s peak luminosity location, at four different epochs of the avalanche’s evolution. The profile at t = 0 serves as a reference profile to which the avalanche-induced dust-excess can be compared. |
3.1. “Cold outer disc” case
3.1.1. Reference GAT07 configuration
We first consider the same set-up as GAT07, that is, a “cold disc” case with an average vertical optical depth τ⊥ ~ 2 × 10-3 (i.e. τr ~ 2 × 10-2) and minit = 1020 g of dust released by the breakup. We confirm that, in this case, the effect of an avalanche is negligible. In fact, at all considered wavelengths, the pattern that it potentially leaves in the outer disc is below the natural noisiness of the disc as simulated by LIDT-DD. If we follow GAT07 and take as a simplified threshold for avalanche observability that a local contrast of ~100% with the background disc can be measured at some location in scattered light images, we find that, to meet this criteria, the released amount of dust has to be very large, minit ~ 5 × 1022 g, which is equivalent to the mass of a ~150 km object.
Figure 3 shows synthetic head-on images of the system in scattered light, for an unfolding avalanche in this massive minit ~ 5 × 1022 g breakup case. It is qualitatively similar to what was obtained by GAT07, with a tail of high-β grains escaping on a spiral-like trajectory from the breakup location, and then penetrating the outer disc where they produce a collisional chain-reaction (the avalanche) that leaves a bright outward propagating trail. The main difference between this and GAT07 is that, while this earlier study, by artificially separating avalanche grains from field particles, was able to visualise the unfolding avalanche regardless of its actual strength, we have a more realistic estimate of an avalanche’s actual magnitude, for which it only becomes detectable, on synthetic images, for the much larger amount of released dust considered here. Our more realistic approach also explains why the avalanche appears to fade in the outer parts of the disc (Figs. 3d−f). This is not because the avalanche stops propagating or becomes weaker in terms of the relative excess of small grains it can locally create, but because these outer regions are fainter, in scattered light, due to the geometrical flux dilution. To illustrate this point, we plot in Fig. 4 the evolution of the radial profile of the disc’s vertical optical depth at the approximate longitude of the avalanche4. The outward propagation of the avalanche is here much more apparent, even in the outer regions. As a matter of fact, the τ⊥contrast between the outward-moving peak of the avalanche-induced excess and the background disc is relatively constant with time (of the order of a factor 2), and does not decrease as the avalanche propagates. What decreases is the luminosity of the regions reached by the outward propagating avalanche. We note also that the regions reached by the avalanche continue to display an excess τ⊥ after the passage of the avalanche front “wave”. Another important result is that, even if the outward propagation of the avalanche is relatively fast, it is, however, much slower than the purely dynamical outward movement of the initial grains through the disc (Fig. 5). This means that the avalanche does not only consist of first generation fragments created by collisions with the initial “trigger” grains sweeping through the disc, because in this case its outward propagation would simply follow that of these trigger grains. Its much slower propagation confirms that it is in fact a chain reaction involving several successive generations of fragments.
 |
Fig. 5 Same as Fig. 4, but for a test simulation with no outer disc, that is, showing only the dynamical outward motion of the grains released by the initial breakup event at 10 au. It can be clearly seen that the front of this outward propagation is, after only 40 yr, already well beyond 200 au (we show the radial profiles up to t = 40 yr instead of the 70 yr of Fig. 4, because there are no high-β initial grains left in the <200 au region after 70 yr). |
 |
Fig. 6 Cold disc case: scattered light synthetic image, at the time of the maximum brightness of the avalanche (t = 11 yr), for the same case as in Fig. 3 but for a system viewed edge-on. |
 |
Fig. 7 Cold disc case: disc-integrated luminosity as a function of time, at three different wavelengths, as well as for the total geometrical cross section. All fluxes are normalized to their value before the onset of the avalanche. The inset figure is a zoom-in on the first 100 yr of the simulation. The brief initial spike corresponds to the luminosity of the dust that is released at the moment of the breakup. |
 |
Fig. 8 Cold disc case: system-integrated SED (using the GRaTer package for a system at a distance of 30 pc), at the peak of the avalanche luminosity, for the reference GAT07 τ⊥ ~ 2 × 10-3 disc and for a denser τ⊥ ~ 10-2 disc. The dashed lines give the luminosity excess due to the avalanche (computed by subtracting the SED of a reference avalanche-free case). The cutoff of the dashed-blue line beyond 50 μm reflects the fact that, for this dense disc case, the avalanche-system is slightly less luminous, at these long wavelengths, than an avalanche-free counterpart. This is because, beyond 50 μm, the flux is mostly dominated by large grains, which are slightly eroded by the passage of the avalanche (see discussion in Sect. 4.4.1). |
If the system was to be seen edge-on (Fig. 6), the maximum avalanche-induced luminosity contrast drops to ~30%, about one third of its value in the head-on images.
If we now consider the disc-integrated photometry (Fig. 7), we see that, even for this very massive breakup event, the peak avalanche-induced luminosity excess is relatively limited, comprised between 0.2% (at λ = 70 μm) and 8% (at λ = 24 μm) in thermal emission, and is ~5% in scattered light (λ = 0.6 μm). This also means that the luminosity excess is at its weakest at the wavelength where this cold disc is the brightest, that is, around 70 μm, as appears clearly when plotting the system’s spectral energy distribution (SED; red curve in Fig. 8), where we see that the avalanche-induced luminosity rapidly drops beyond λ ~ 40 μm. This is due to the fact that the dust particles produced by the avalanche are very small grains, mostly ≤1 μm, which, even if they contribute to most of the avalanche-induced excess in terms of geometrical cross section, are very poor emitters at long wavelengths. At 24 μm, however, this decreased emissivity is compensated by the fact that these tiny grains are warmer than the larger grains of the main disc and that we are here in the Wien domain of the Planck function, for which a temperature increase results in an exponential increase of the Bλ(λ,T) parameter.
In addition, it is important to note that, for this reference τ⊥ ~ 2 × 10-3 case, the breakup event itself creates a luminosity excess which exceeds, at all wavelengths, that of the subsequent avalanche (see inset in Fig. 7). In other words, from a photometric point of view, the avalanche is not able to amplify the signal produced in the immediate aftermath of the breakup. This seems to be in disagreement with GAT07, who obtained an “amplification” factor F ~ 200 for a similar set-up. This difference is mostly due to the fact that F measures geometrical cross sections and not actual luminosities. As such it does not account for the fact that the initial breakup occurs closer to the star, where both the scattered light (because of the stellar flux dilution in 1 /r2) and thermal emission (because dust closer to the star is warmer and thus more luminous, at least in the 24−70 μm range) of a given dust grain are higher than further out in the disc. When considering the disc-integrated total geometrical cross section, we retrieve GAT07’s results, which is that the avalanche does indeed have an amplification effect when compared to the initially released dust population (full line in Fig. 7).
What the avalanche does, however, is to extend the duration of the luminosity excess period. Indeed, while the luminosity excess created by the breakup itself quickly drops to a much lower level, the subsequent avalanche-induced excess lasts for a much longer time, of the order of ~100 yr, roughly a third of the dynamical timescale at the innermost part of the main disc. This duration is, however, shorter than what was found by GAT07 (see Fig. 3 of that paper), a difference that is once again due to the fact that GAT07 were considering the system’s cross section and not its photometry. Indeed, the cross section amplification happening in the outer parts of the disc, which strongly contributes to the extended period of excess when plotting this parameter (see also Fig. 4), concerns grains whose contribution to the system’s IR-photometry (be it in thermal emission or scattered light) is much less important.
3.1.2. Denser outer disc
 |
Fig. 9 As in Fig. 7, but for a denser main disc with τ⊥ ~ 10-2; all other parameters (released dust mass, disc location and width) being the same. The initial luminosity flash due to the breakup event itself appears less pronounced here because all luminosities are rescaled to the main disc’s brightness, which is here higher than for our previous reference case. |
We now increase the density in the outer disc by a factor ~5, that is, to values comparable to those measured for “extreme” debris discs, with τ⊥ of the order of 10-2 (i.e. τr ~ 10-1). To allow easy comparison, we consider the same massive initial dust release (minit ~ 5 × 1022 g) that was the threshold for the avalanche to become visible in the previous reference case. We see that, this time, the disc-integrated luminosity of the avalanche exceeds that of the initial breakup at λ = 24 μm (Fig. 9). However, this luminosity amplification over the initial breakup remains relatively limited, barely reaching a factor ~1.1, and being still below 1 at all other wavelengths (see inset in Fig. 9). In fact, if we consider the relative luminosity ratio between the avalanche and the main disc, we see that this ratio is actually slightly lower, for the same amount of post-breakup released dust, than in the previous case of a more tenuous disc (Fig. 9). Likewise, on synthetic 2D images (not shown here), the maximum local contrast in scattered light with the main disc is now only ~60% instead of the ~100% obtained for the τ⊥ = 2 × 10-3 disc.
This seems to sharply contradict the results of GAT07, who estimated that an avalanche’s amplitude should exponentially vary with the main disc’s density, and should increase by almost 2 orders of magnitude when increasing τr by a factor 4 (see Fig. 14 of that paper). This fundamental difference with GAT07 is due to one simplification that was made in that paper, which is that their main disc was devoid of unbound grains. While this approximation might be justified for systems with low τ⊥, it becomes much more questionable for denser discs. As an illustration, we see that, for the present τ⊥ ~ 10-2 case, unbound grains are not at all negligible in the main outer disc, and even marginally dominate its total geometrical cross section (Fig. 10). As a consequence, the additional influx of unbound grains coming from the planetesimal breakup is much less “felt” by the main disc. Granted, these avalanche unbound grains have a much higher destructive power because of their higher outward velocities, but they are not numerous enough, even for a massive dust release of minit ~ 5 × 1022 g, to create an important difference. An additional effect that weakens the avalanche’s amplitude is that, because of the presence of these unbound grains in the main disc at steady-state, this disc is depleted of small bound grains in the ~1–10 μm range (Fig. 12), which correspond to the grains that are mostly eroded by the unbound grains of the avalanche and thus make up the reservoir to fuel the avalanche’s evolution.
 |
Fig. 10 Cold disc case: disc-integrated geometrical cross section per logarithmic size bin, for the disc at collisional steady-state immediately before the onset of the avalanche. The vertical dashed line marks the β = 0.5 limit for unbound particles (if produced from progenitors on circular orbits) |
3.2. “Warm disc” case
As explained in Sect. 2, this case is scaled down in stellar distance by a factor 10 as compared to the previous case. In order to have discs with fractional luminosities equivalent to those in the cold disc case, we scale down the main disc’s mass by a factor of 100. This means that, in terms of optical depths, we consider the same two cases as before, that is, a reference main disc with τ⊥ ~ 2 × 10-3 and a bright disc case with τ⊥ of the order of 0.01.
3.2.1. Reference τ⊥ ~ 2 × 10-3 disc
 |
Fig. 11 Same as Fig. 7, but for the “warm disc” case (outer main disc between 5 and 12au with an optical depth τ⊥ ~ 2 × 10-3), and a mass minit ~ 1020 g of dust released at 1 ua. |
Not surprisingly, applying the same criteria of a local surface scattered-light luminosity contrast of ~100% with the background disc, we find that the avalanche becomes significant for a smaller released dust mass than in the cold disc case. We find, however, that this 100% contrast threshold is reached for minit ~ 1020 g, which is a factor ~5 less than what would have been found by scaling down minit by the same factor 100 as the disc’s total mass. This can be explained by the fact that impact velocities are much higher than for the cold disc case, because here we are ten times closer to the star, meaning that the destructive power of avalanche grains, and the number of debris they produce, are much higher as they sweep through the disc. For an equivalent set-up, avalanches are thus more powerful in warm discs. They would in fact be even more powerful if their strength was not reduced by the large population of unbound grains already present in the outer disc before the avalanche’s passage (Fig. 12). The avalanche-dampening effect due to these “native” unbound grains (in particular the depletion of avalanche-fueling target grains in the 1−10 μm range) had also been observed for the cold disc case, but only for a dense disc with τ⊥ ~ 10-2 (see Sect. 3.1.2), whereas here it is already noticeable for τ⊥ ~ 2 × 10-3. This important population of unbound grains at lower τ⊥ is the direct consequence of more violent collisions (because of higher vcol) in the main disc itself.
We note, however, that the avalanche’s “amplification” power, in terms of its peak luminosity as compared to that of the initially released dust, is of the same order as for the τ⊥ ~ 2 × 10-3 cold disc case, with the initial post-breakup “flash” also being brighter here, at all considered wavelengths, than the subsequent avalanche (see inset in Fig. 11). The main effect of the avalanche is again to produce a luminosity excess that lasts longer than the very transient initial peak. Its duration is of the order of 3−4 yr, which is, logically, roughly the ~100 yr timescale of the cold disc scaled down by a factor (100 au/10 au)1.5. The maximum relative photometric excess due to the avalanche is of the order of 7–8% and peaks in the ~10−15 μm wavelength domain (Fig. 13). Interestingly, and contrary to the cold disc case, this wavelength domain is also roughly that where the disc itself is the brightest.
In any case, the onset of an observable avalanche still requires the initial release of a very large amount of dust mass, minit ~ 1020 g being equivalent to the mass of a ~20 km sized object, which, combined with the fact that the avalanche is more short-lived than in the cold disc case, might not render this 5−12 au case as avalanche-friendly as it appears (see Sect. 4).
 |
Fig. 12 Warm disc case: disc-integrated geometrical cross section per logarithmic size bin, for the disc at collisional steady-state just before the onset of the avalanche. |
 |
Fig. 13 Warm disc case: system-integrated SEDs, for two different outer disc densities, at the time the avalanche reaches its peak luminosity. |
3.2.2. Denser disc
As for the cold disc case, increasing the main disc optical depth to τ⊥ ~ 10-2 does not lead to the much stronger avalanches expected from using the GAT07 empirical relations. Granted, the avalanche does get somehow stronger in absolute magnitude than for a τ⊥ ~ 2 × 10-3 disc, with its peak luminosity now slightly exceeding that of the initial post-breakup flash (Fig. 14). However, its relative luminosity with respect to the main disc is lower. As for the cold disc case, this unexpected result is due to the crucial role played by native unbound grains already present in the main disc. As Fig. 12 indeed clearly shows, in a 5−12 au disc with τ⊥ ~ 10-2 at steady state, the geometrical section is dominated by β> 0.5 grains, even more so than in our cold disc case (Fig. 10). As a consequence, both effects due to these native unbound grains (denser backdrop onto which avalanche unbound grains are added and depletion of avalanche-fueling targets in the 1−10 μm range) are more pronounced here and concur to weaken the avalanche.
4. Discussion
4.1. Dependence on disc density
One crucial difference with Grigorieva et al. (2007) is that we do not get significantly stronger avalanches when increasing the density of the disc within which they propagate, whereas GAT07 found that avalanche strength exponentially increases with τr (and thus with τ⊥ for most non- “exotic” disc configurations; see Eq. (2)). As explained in Sect. 3.1.2, this is mostly because dense discs (τ⊥ ~ 10-2) already contain large amounts of unbound grains before the passage of the avalanche, a fact that was not accounted for in GAT07. These native unbound grains weaken the avalanche in two ways, firstly by creating a dense background that reduces the relative excess density due to avalanche-induced unbound grains, and secondly by preemptively eroding the population of small bound grains from the main disc (in the ~1−10 μm range) which makes up most of the mass reservoir for fueling the avalanche propagation. This means that the empirical relation derived by GAT07 for estimating the strength of an avalanche (or more exactly its cross section “amplification factor” F) as a function of disc density cannot be used in realistic systems (even when overlooking the fact that F is a very imperfect and ambiguous measure of an avalanche’s amplitude).
As a consequence, avalanches do not get easier to observe in discs denser than τ⊥ ~ 2 × 10-3. This means that, contrary to what could have been expected, very bright “extreme” discs are probably not such a favourable ground for avalanche propagation (see Sect. 4.4). Conversely, additional test simulations show that avalanche amplitude quickly drops for discs more “tenuous” than our τ⊥ ~ 2 × 10-3 reference case. This is an expected result, as the breakup-released unbound grains will then basically cross a faint outer disc without encountering any resistance, making this case very similar in essence to that of a large breakup in a dust-free system (see, for instance Kral et al. 2015).
This makes discs with optical depths of a few 10-3 probably the optimum cases for maximising the contrast between an avalanche and the disc it propagates through.
4.2. Photometric signature and wavelength dependence
A new result from the present study is that we show that, for all considered cases, avalanches have a relatively limited effect on disc-integrated photometry. For a cold disc, even the avalanche triggered by the massive release of 5 × 1022 g of dust does not create a luminosity excess of more than ~10%. Moreover, at λ> 50 μm wavelengths where the disc is the brightest, the avalanche-induced excess drops to almost zero because of the poor emissivity of the tiny avalanche grains in the far IR. For warm discs at ~10 au, the situation becomes more favourable, with the photometric avalanche-induced excess peaking in the λ ~ 10−20 μm domain where the system is the brightest (Fig. 13). However, this luminosity increase is, here again, limited to less than ~10%.
Such 5–10% photometric variations in the 10–20 μm wavelength domain could, however, be within the reach of mid-IR observing facilities such as the Wide-field Infrared Survey Explorer (WISE), which has a relative photometric accuracy of less than 10% at these wavelengths (Melis et al. 2012), or the Spitzer MIPS instrument, having an accuracy of ~2% at 24 μm (Rieke et al. 2008).
Of course, these luminosity excesses could become more prominent when considering even larger masses of initially released dust minit, because avalanche amplitudes scale linearly with minit (GAT07). There is, however, a trade-off, as increasing the mass of the initial breakup object strongly decreases the likelihood for such a breakup to occur (see following section). Moreover, above a given size, the breakup object becomes large enough to trigger, in addition to the initial short-lived luminosity flash mainly due to the unbound grains it releases, a collisional cascade amongst its own debris that is brighter and much more long lived than the avalanche. Such a post-breakup collisional cascade might thus be much easier to detect (see, for instance, the simulations of Kral et al. 2015, investigating the aftermath of the destruction of a Ceres-like planetesimal) than the avalanche.
4.3. Duration and likelihood
For a large enough initial dust release, an avalanche is able to leave an observable signature (both in photometry and on resolved images) on a timescale taval that is typically a fraction of an orbital period in the main outer disc. We find taval−cold ≃ 100 yr for the cold disc and taval−warm ~ 3 yr for the warm disc cases, respectively. Not surprisingly, the ratio between these two timescales is close to the one between dynamical timescales for these two configurations, that is, 101.5. As a consequence, we estimate that the typical duration for an avalanche follows the empirical law taval ~ 100 (rdisc−in/ 50 au)1.5, or taval ~ 0.3 torb−in, where rdisc−in is the location of the inner edge of the main outer disc and torb−in is the orbital period at this location.
We note that taval exceeds the time it takes for small unbound grains with high β, produced at the breakup’s location, to directly cross the main disc. Using the asymptotic limit for the radial velocity of such a grain (vlim = vkep(2β−1)0.5; see Sezestre et al. 2017), we find that, for the cold disc case, a grain produced at 10 au with β = 5 crosses the 50 to 120 au radial extension of the disc in less than 10 yr, ten times less than the photometric duration of an avalanche (see Figs. 7 and 9)5. This point is clearly illustrated by the comparison of Figs. 4 and 5.
However, taval remains extremely short when compared to the typical age tage of even the youngest debris discs. This means that, in order to be observed, an avalanche-producing breakup event needs to occur on a typical timescale tbreak that does not greatly exceed taval. The probability of witnessing an avalanche is then, for a given system, of the order of taval/tbreak. The problem is that tbreak is expected to sharply decrease with object sizes and that our simulations have shown that the threshold for avalanche detectability is only reached for the breakup of very large bodies. If we follow GAT07 and make the relatively optimistic hypothesis that 10% of the shattered object is converted into s ≤ 1 cm dust, then we need to shatter a ~300 km object around 10 au to trigger an observable avalanche in a cold disc, and a ~40 km object around 1 au for a warm disc. Estimating the shattering frequency of such objects is a complex task, as it might depend on several poorly constrained parameters (or strongly varying from system to system), such as the size distribution of large objects in the system, their average dynamical excitation, and so on. For the sake of simplicity, we consider the asteroid belt as a proxy for a typical disc of kilometre-sized bodies in the 1−10 au region6. If we take the estimates for the interval between disruptions in the main belt as a function of asteroid sizes derived by Bottke et al. (2005), we get tbreak(s > 300 km) ~ 3 × 109 yr and tbreak(s > 40 km) ~ 3 × 107 yr, respectively. These values exceed by several orders of magnitude our taval estimates (100 yr and 3 yr, respectively), making avalanche-inducing breakups very unlikely events in asteroid-like belts.
However, the asteroid belt is a relatively tenuous and mass-depleted disc, and breakup rates could be higher in denser systems. All other parameters (distance to the central star, profile of the size distribution, impact speeds) being equal, the rate of catastrophic breakups should scale as (Mdisc/Mast)2, where Mast is the total mass of the asteroid belt, implying that a disc ~ 3 × 103 more massive than the asteroid belt is needed to reach tbreak(s > 40 km) = taval−warm, with (Mdisc/Mast) ~ 5 × 103 being necessary to get tbreak(s > 300 km) = taval−cold.
We note that the cold and warm disc estimates for (Mdisc/Mast) are relatively close, because the smaller size of the object that has to be broken in the warm disc case is compensated by the fact that an avalanche is then more short lived and has to occur more frequently than for the cold disc case. Considering that the current asteroid belt has a fractional luminosity of f ~ 10-7 (Dermott et al. 2002), it would imply that such an “enhanced” belt would have a fractional luminosity of a few 10-4, which is within the range of observed fractional luminosities of warm discs (Chen et al. 2014; Kral et al. 2017b, and references therein).
In this case, an ideal configuration for an “avalanche-friendly” system could be a two-belt structure with a relatively bright (f ≳ 10-4) asteroid belt around 1 au (warm disc case) or 10 au (cold disc case), and an extended disc further away from the star. Such a configuration would be very similar to the ones investigated by Geiler & Krivov (2017), who identified several double-belt systems fitting this description (see Fig. 2 of that paper).
4.4. Avalanches in “extreme” debris discs?
4.4.1. Negligible post-avalanche luminosity drop
As discussed in Sect. 1, avalanches have been recently invoked as a possible mechanism for explaining the rapid luminosity drops observed in some bright debris discs, under the assumption that, after the passage of the avalanche, the remaining main disc would be left depleted from a fraction of its s ≤ 1 mm grains, which have been “sandblasted” by the avalanche’s passage, and would thus become less luminous than it was before the avalanche. Our simulations do indeed show a slight luminosity drop (as compared to the pre-avalanche level) in the wake of an avalanche, but this post-avalanche decrease remains limited to less than 1% in the best case (dense “warm” disc case, see Fig. 14), that is, much less than the luminosity increase during the avalanche. Moreover this luminosity drop is also limited in time, never lasting much longer than the avalanche itself. We thus conclude that this “sandblasting” eroding effect leaves a very limited imprint on the disc’s luminosity, and that the brightness of a post-avalanche disc is very close to the one it had prior to the passing of the avalanche. The only way to observe a luminosity drop in the context of an avalanche would be to start observing the system exactly right after the avalanche-induced luminosity peak. In this case, the system would indeed appear to become fainter with time. This scenario seems, however, very unlikely, as it would require that the initial detection of the system almost coïncides with the short-lived luminosity maximum of an avalanche.
Collisional avalanches could of course explain short-term luminosity increases in some extreme discs, provided that a big enough object has been shattered. However, even for the very large minit considered in our simulations, we do not obtain photometric variations that exceed 10%. Of course, higher excesses could be reached for even larger initially broken-up objects, but, as underlined in the previous section, the break-up of such larger objects are even less likely to occur.
4.4.2. Vaporised matter
Another problem is that, for the warm discs that make up most of these extreme systems, avalanches should imply grain-grain collisions at speeds high enough to at least partially vaporise dust grains in the outer main disc. For silicates and carbon dust grains, Czechowski & Mann (2007) estimate that the threshold impact velocity for vaporising some fraction of a target grain is around ~20 km s-1. However, quantifying the fraction of the target’s mass that is vaporised relative to the fraction that is fragmented is a difficult task that requires addressing complex issues about the micro-physics and chemistry of collisions that exceed the scope of the present paper. If we take as a reference the simplified prescription of Czechowski & Mann (2007), and consider, in addition, that a typical avalanche-fueling collision involves an unbound grain hitting a target five times bigger, we find that the target mass that is vaporised becomes comparable to the one converted into solid fragments for velocities approaching ~70 km s-1 (see Figs. 2 and 3 and Appendix A of Czechowski & Mann 2007). Such very high velocities are in fact reached, for our warm disc case, by β ≥ 3 grains, produced at 1 au by the initial breakup, when they impact bodies in the main disc at 5−12 au. Even if such β ≥ 3 grains do not make up the majority of the initially released unbound population (which peaks around β = 5; see Fig. 2) they do, however, represent a non-negligible fraction of it.
As a consequence, a sizable proportion of the collisions needed to fuel the avalanche will likely produce clouds or plumes of vapour instead of new debris that can further the chain reaction. Eventually, such vapour plumes are expected to recondense into solid matter through a nucleation-growth-quenching process (Johnson & Melosh 2012), but this condensation process might be much more inefficient in the present case, where the gas density and pressure are likely to be much lower than in the case of large impacts on rocky planets considered by Johnson & Melosh (2012). In addition, even if successful, this recondensation process is likely to form a relatively homogenously sized population of spherules in the 100–500 μm range (Johnson & Melosh 2012), much larger than the submicrometric unbound grains the avalanche’s propagation relies upon. As a consequence, even though quantifying the impact of this vaporisation/recondensation process on the avalanche mechanism is a very complex task, it is safe to conclude that our simulations are very likely to overestimate avalanche strength for warm discs.
4.4.3. TYC 8241 2652 1
The individual system for which the avalanche scenario has been set forth with most insistence is TYC 8241 2652 1, arguably the most extreme “extreme” disc, which had a very high fractional luminosity (f ~ 0.11) until the end of 2008 but suddenly (in ~1 yr) became more than one order of magnitude fainter at 10 and 20 μm (Melis et al. 2012), and has remained at this level since then.
In light of the present simulations, we believe that the avalanche scenario can probably be ruled out as a potential explanation for this system’s unusual behaviour. First and foremost, we find that the “sandblasting” luminosity drop in the wake of an avalanche is extremely limited, orders of magnitude lower than the factor 30 decrease observed for TYC 8241 2652 1. And even if we consider the unlikely assumption of a “giant” avalanche produced by the breakup of an extremely large object that could have a much stronger sandblasting effect, we would still be unable to explain the photometric evolution of the TYC 8241 2652 1 system before the 2009/2010 luminosity drop, that is, a seemingly constant photometric level for more than 30 yr (Melis et al. 2012) which is impossible to reconcile with the short-lived luminosity peak triggered by an avalanche (see Fig. 11).
Another, perhaps even more fundamental argument against the avalanche scenario is that TYC 8241 2652 1 is a low-mass K star (L = 0.7 L⊙) for which only a very limited range of grain sizes, around s ~ 0.2 μm, can reach β ≥ 0.5 and have unbound orbits (Fig. 2). This leaves much too little “fuel” for creating and propagating an avalanche. This problem is compounded by the fact that this disc’s brightness before the luminosity drop, that is, f ~ 0.11, combined with its estimated radial distance, ~0.4 au, makes it optically thick (Melis et al. 2012), meaning that stellar radiation is reduced inside the disc, thus further lowering the β values of small grains.
4.5. Possible limitations
Even if our main results and conclusions are probably relatively robust, we are aware that because of the time-consuming character of the LIDT-DD runs, we could not explore the full parameter space linked to the complex avalanche mechanism. One of these parameters is the location rinit of the dust-releasing breakup event, which was fixed for both cold (at 10 au) and warm (at 1 au) disc cases. However, because high-β grains quickly reach their asymptotic radial velocity (see Fig. 8 of GAT07), the effect of changing rinit is relatively straightforward to predict: lower values of rinit will change the avalanche grain velocity according to 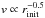 while larger values of rinit will prevent the released grains from reaching high-enough velocities. Likewise, we have not explored the spatial structure of the outer disc, which, apart from being scaled by a factor 10 between the cold and warm cases, remains fixed in terms of its radial slope and relative width Δr/r. Taking wider discs could for instance increase the value of the radial optical depth τr for the same value of τ⊥, which could in principle lead to stronger avalanches by increasing the impact probability of disc-crossing outbound grains without increasing too much the fraction of “native” unbound grains that could weaken the avalanche (see Sect. 4.1). However, the disc we have considered is already very wide, with a width of Δr/r = 0.8, which is relatively large compared to the more narrow belt-like configurations that seem to be inferred for a large fraction of debris discs (Wyatt et al. 2007b, 2015; Kral et al. 2017a). As a consequence, our results should probably be considered as a best-case scenario from the point of view of the system’s spatial structure (release location and outer-disc width). Another parameter is the dynamical excitation of the main outer disc. One would possibly expect dynamically “colder” discs to be more favourable to avalanche propagation for the dense τ⊥ ~ 10-2 cases, because the lower collisional activity should lead to a lower level of avalanche-hindering native unbound grains in the main disc. However, test simulations with lower ⟨ e ⟩ values did not lead to significant differences in terms of avalanche amplitude. This is mainly because the avalanche-favouring depletion of native unbound grains is compensated by the avalanche-hindering depletion of small bound grains (which are the main mass reservoir for fueling the avalanche) that comes with a lower dynamical excitation. This depletion of small bound grains in dynamically cold discs is a classical result that has been identified by Thebault & Wu (2008).
while larger values of rinit will prevent the released grains from reaching high-enough velocities. Likewise, we have not explored the spatial structure of the outer disc, which, apart from being scaled by a factor 10 between the cold and warm cases, remains fixed in terms of its radial slope and relative width Δr/r. Taking wider discs could for instance increase the value of the radial optical depth τr for the same value of τ⊥, which could in principle lead to stronger avalanches by increasing the impact probability of disc-crossing outbound grains without increasing too much the fraction of “native” unbound grains that could weaken the avalanche (see Sect. 4.1). However, the disc we have considered is already very wide, with a width of Δr/r = 0.8, which is relatively large compared to the more narrow belt-like configurations that seem to be inferred for a large fraction of debris discs (Wyatt et al. 2007b, 2015; Kral et al. 2017a). As a consequence, our results should probably be considered as a best-case scenario from the point of view of the system’s spatial structure (release location and outer-disc width). Another parameter is the dynamical excitation of the main outer disc. One would possibly expect dynamically “colder” discs to be more favourable to avalanche propagation for the dense τ⊥ ~ 10-2 cases, because the lower collisional activity should lead to a lower level of avalanche-hindering native unbound grains in the main disc. However, test simulations with lower ⟨ e ⟩ values did not lead to significant differences in terms of avalanche amplitude. This is mainly because the avalanche-favouring depletion of native unbound grains is compensated by the avalanche-hindering depletion of small bound grains (which are the main mass reservoir for fueling the avalanche) that comes with a lower dynamical excitation. This depletion of small bound grains in dynamically cold discs is a classical result that has been identified by Thebault & Wu (2008).
Other potential issues are related to the LIDT-DD code itself, in particular the unavoidably finite resolution of the spatial grid it uses to compute collisions. Ideally, the size of each collision “cell”, within which all tracers are considered to mutually collide, should not be much larger than the spatial extension of the propagating avalanche, in order to avoid an artificial dilution effect. In all runs, the azimuthal width of the collision cell is 36 degrees, which is in fact slightly more than the azimuthal extension of the avalanche “arm” as it enters the main disc, which is of the order of ~20–25 degrees. We thus expect the presence of a some numerical dilution effect, but it should remain relatively moderate and should not drastically change the measured avalanche amplitude or duration
Perhaps the most critical issue is that of the amount of small dust released by the initial breakup event. How realistic is it to assume that the shattering of a 40−300 km-sized planetesimal will release this large amount of sub-micrometre dust and that the post-breakup fragment size distribution can be extended in a self-similar way down to 0.02 μm grains (see Table 1)? To our knowledge, there is no reliable experimental or theoretical information regarding the size distribution of the smallest fragments produced after large fragmenting impacts, especially for sizes more then 8 orders of magnitude smaller than the shattered object. One of the few attempts at addressing this problem in the context of debris discs is that of Krijt & Kama (2014) and Thebault (2016), who looked at it from the perspective of surface energy conservation and found that there should indeed be a minimum physical fragment size, which could in some cases be ≥1 μm. However, for the case of impacts on large 40−300 km-sized bodies, this theoretical minimum size should be much lower than the 0.02 μm smallest grains considered in the present runs. The fact, however, that there is no energy-conservation impossibility for the presence of sub-micron fragments does not mean that such fragments will necessarily be produced. This is a very difficult issue that clearly exceeds the scope of the present study, but, here again, our prescription is probably a best-case scenario.
5. Summary and conclusion
A collisional avalanche is a complex mechanism, set off by the sudden release of a large amount of small grains on unbound orbits (following, for instance, the breakup of a large planetesimal), which then enter, at high velocity, a debris disc further away from the star, triggering there a collisional chain-reaction producing amounts of dust potentially greatly exceeding the initially released population.
We investigate this mechanism using, for the first time, a fully self-consistent code, LIDT-DD, coupling the dynamical and collisional evolution of the system. We quantify, also for the first time, the photometric signature of avalanches, and investigate whether or not they could be responsible for the short-term luminosity variations recently observed in some very bright debris discs. We consider an avalanche-favouring luminous A6V star, and two set-ups: a “cold disc” case with a dust release at 10 au and an outer disc extending from 50 to 120 au, and a “warm disc” case scaled down by a factor of 10 (release at 1 au and 5−12 au outer disc), taking the outer disc’s density (parameterized by its vertical optical depth τ⊥) as a free parameter.
Our main results can be summarised as follows:
-
We confirm the results of Grigorievaet al. (2007), and find thatavalanches can be set off in outer discs withτ⊥ ≳ 10-3. We show, in addition, that this result holds for both “cold” and “warm” discs.
-
To reach a local 100% contrast on resolved scattered light images, the dust mass released by the initial breakup event has to be very large, that is, minit−c ~ 5 × 1022 g (the mass of a ~150 km body) for the cold disc case, and minit−w ~ 1020 g (the mass of a ~20 km body) for a warm disc.
-
The integrated photometric excess of avalanches is more limited, not exceeding 10% at any wavelength, even for the high minit−c and minit−w considered here. Furthermore, for the cold disc case, this excess becomes negligible at the long wavelengths where the 50−120 au disc is the brightest, probably making avalanches very difficult to observe in unresolved Kuiper belt-like cold discs. The situation is more favourable for warm discs, where the avalanche excess peaks at the 10−20 μm wavelengths where the main disc itself is at its brightest. In this mid-IR domain, photometric variations of ~5−10% should be within the reach of current instruments.
-
The duration taval of an avalanche is of the order of 0.3 torb−in, where torb−in is the orbital period at the inner edge of the main outer disc. This is relatively short but still roughly one order of magnitude larger than the time it would take for breakup-released unbound grains to simply cross the outer disc without colliding.
-
Contrary to what could be expected from earlier simplified prescriptions, the avalanche strength does not significantly increase when increasing the outer disc’s density beyond τ⊥ ~ 2 × 10-3. In terms of the relative contrast between the avalanche and the main disc, τ⊥ values of a few 10-3 are probably the optimum case. This is mainly because, for higher τ⊥ values, the outer disc already has a significant population of unbound grains before the avalanche’s passage. These native unbound grains weaken the avalanche by creating a dense background that reduces the relative excess density due to avalanche grains, but also by preemptively eroding the main disc from its population of small bound grains (s ~ 1−10 μm) that makes up most of the target reservoir for fueling the avalanche propagation.
-
We observe a slight luminosity deficit, as compared to the pre-avalanche level, after the passage of the avalanche, due to the erosion of ~1–100 μm targets in the disc, but this “sandblasting” effect remains very limited, less than 1%, and short-lived, its duration never greatly exceeding that of the avalanche itself.
-
This very weak post-avalanche luminosity deficit makes avalanches an unlikely explanation for the much larger photometric drops observed in some very bright “extreme” debris discs, like the ~50% decrease for ID 8 or, even more problematic, the factor 30 luminosity fall of TYC 8241 2652 1. For the latter system, an additional argument against avalanches is that the central star is not luminous enough to place a significant fraction of grains on unbound orbits (a prerequisite for setting off and fueling an avalanche).
-
The likelihood for witnessing an avalanche in a given system crucially depends on two parameters: 1) the outer disc density, which has to be such that τ⊥ is of the order of a few 10-3, and 2) the average time tbreak between two avalanche-triggering planetesimal breakups, the probability of witnessing an avalanche being ~ taval/tbreak.
-
We estimate that the “ideal” case would thus be a system with a double-disc structure, with an inner belt (located at ~1 au or ~10 au depending on the “cold” or “warm” disc case) of fractional luminosity f ≳ 10-4, which produces a high-enough rate of avalanche-triggering breakups, and an outer disc with τ⊥ ~ 2 × 10-3, located at ~5−10 times the location of the inner belt, into which the avalanche propagates. Cold disc systems would then be the most favourable to the detection of features on resolved images in scattered light, because of their larger scale, while warm discs would be more suited to the detection of photometric variations in the mid-IR, because the avalanche-induced excess peaks at wavelengths where the disc itself is at its brightest. Such double-belt configurations seem to have been identified for several observed discs (Geiler & Krivov 2017), and will be investigated in future studies.
We note that a debris disc does not necessarily have to be “extremely” luminous in order to exceed the maximum possible luminosity Lmax expected from a collisional cascade. L ≥ Lmax situations could for example be obtained for lower fractional luminosity f ~ 10-3 values if the system is very old. So these extreme discs do not represent all “anomalously bright” systems as defined by Wyatt et al. (2007b).
The fractional infrared luminosity f would be equal to the radial optical depth if the dust was distributed onto a spherically symmetric shell (Zuckerman & Song 2012).
We are aware that it is an oversimplification to consider the asteroid belt as a proxy for belts hosting avalanche-triggering events for both our “cold” and “warm” disc cases. We are hereby overlooking the fact that the avalanche-releasing breakup occurs at ~10 au in the former and at ~1 au in the latter, and that the conditions for large planetesimal breakups might be different at these two locations. However, we will not enter into this complex issue here and keep the asteroid belt as a satisfying first-order middle ground between these two locations.
Acknowledgments
The authors thank Rik Van Lieshout for fruitful discussions and an anonymous referee for an insightful review. Q.K. acknowledges funding from STFC via the Institute of Astronomy, Cambridge, consolidated grant. P.T. dedicates this paper to the memory of André Brahic.
References
- Artymowicz, P. 1997, Ann. Rev. Earth Planet. Sci., 25, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Augereau, J. C., Lagrange, A. M., Mouillet, D., Papaloizou, J. C. B., & Grorod 1999, A&A, 358, 557 [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., Karmann, C., & Lagrange, A.-M. 2001, A&A, 366, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonsor, A., Augereau, J. C., & Thebault, P. 2013, A&A, 548, A104 [Google Scholar]
- Bottke, W., Durda, D., Nesvorny, D., et al. 2005, Icarus, 179, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Charnoz, S., & Taillifet, E. 2012, ApJ, 753, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, ApJS, 211, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Czechowski, A., & Mann, I. 2007, ApJ, 660, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, S., Kehoe, T., Durda, D., et al. 2002, in Proc., Asteroids, Comets, Meteors, ed. B. Warmbein, 319 [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Gáspár, A., Rieke, G. H., & Balog, Z. 2013, ApJ, 768, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Geiler, F., & Krivov, A. V. 2017, MNRAS, 468, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Genda, H., Kobatashi, H., & Kokubo, E. 2015, ApJ, 810, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorieva, A., Artymowicz, P., & Thebault, P. 2007, A&A, 461, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, A. P., Wyatt, M. C., Bonsor, A., & Veras, D. 2014, MNRAS, 440, 375 [Google Scholar]
- Johnson, B. C., & Melosh, H. J. 2012, Icarus, 217, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Wyatt, M. C. 2013, MNRAS, 433, 2334 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., & Kama, M. 2014, A&A, 566, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kral, Q., Thebault, P., & Charnoz, S. 2013, A&A, 558, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kral, Q., Thebault, P., Augereau, J.-C., Boccaletti, A., & Charnoz, S. 2015, A&A, 573, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kral, Q., Clarke, C., & Wyatt, M. 2017a, ArXiv e-prints [arXiv:1703.08560] [Google Scholar]
- Kral, Q., Krivov, A. V., Defrere, D., et al. 2017b, Astron. Rev., 13, 69 [Google Scholar]
- Krivov, A. V. 2010, Res. Astron. Astrophys., 10, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Leinhardt, Z. M., & Stewart, S. T. 2012, ApJ, 745, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Duncan, M. J., & Thommes, E. 2012, AJ, 144, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Kuchner, M. 2013, Nature, 449, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. C., Krivov, A. V., Wyatt, M. C., Bryden, G., & Eiroa, C. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 521 [Google Scholar]
- Melis, C., 2016 [Google Scholar]
- Melis, C., Zuckerman, B., Rhee, J., et al. 2012, Nature, 487, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, H., Su, K., Rieke, G., et al. 2014, Science, 345, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, H., Su, K., Rieke, G., et al. 2015, ApJ, 805, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A. M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nesvold, E. R., & Kuchner, M. J. 2015, ApJ, 777, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvold, E. R., Kuchner, M. J., Rein, H., & Pan, M. 2013, ApJ, 798, 83 [Google Scholar]
- Nesvold, E. R., Naoz, S., Vican, L., & Farr, W. M. 2016, ApJ, 826, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Pearce, T. D., & Wyatt, M. C. 2015, MNRAS, 453, 3329 [NASA ADS] [CrossRef] [Google Scholar]
- Reche, R., Beust, H., & Augereau, J.-C. 2009, A&A, 463, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., Blaylock, M., Decin, L., et al. 2008, AJ, 135, 2245 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Grady, C. A., Hines, D. C., et al. 2014, AJ, 148, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Sezestre, E., Augereau, J.-C., Boccaletti, A., & Thebault, P. 2017, A&A, 607, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, I., Zuckerman, B., Weinberger, A., & Becklin, E. 2005, Nature, 436, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Takasawa, S., Nakamura, A. M., Kadono, T., et al. 2011, ApJ, 733, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Artymowicz, P. 2001, ApJ, 557, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Thebault, P. 2009, A&A, 505, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P. 2012, A&A, 537, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P. 2016, A&A, 587, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., Marzari, F., & Augereau, J.-C. 2010, A&A, 524, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., Kral, Q., & Ertel, S. 2012, A&A, 547, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C. 2006, ApJ, 639, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., & Jackson, A. P. 2016, Space Sci. Rev., 205, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Smith, R., Greaves, J. S., et al. 2007a, ApJ, 658, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Smith, R., Su, K. Y. L., et al. 2007b, ApJ, 663, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Panić, O., Kennedy, G. M., & Matrà, L. 2015, Ap&SS, 357, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., & Song, I. 2012, ApJ, 758, 77 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic description of the avalanche process. First, a large body is shattered in the inner region of the planetary system, releasing very small unbound grains that are blown out by radiation pressure. Then these small grains penetrate an outer disc located further away from the star. There they will collide, at very high velocities, with “native” target grains, producing a new generation of small unbound grains, which will also be blown out and collide with other target grains in the disc, creating new fragments that will again collide with targets further out in the disc, etc. If the main disc is dense enough, this chain reaction can produce an excess of small grains largely exceeding the amount initially produced by the breakup. |
| In the text | |
 |
Fig. 2 Value of β, the ratio between radiation pressure and gravitational forces, as a function of particle size, computed for non-porous astrosilicates. The β(s) curve is shown for the luminous A6V star considered as a reference case in our runs, as well as for the TYC 8241 2652 1 K star discussed in Sect. 4.4. The dotted horizontal line marks the β = 0.5 limit, above which grains are no longer on bound orbits around the star (if produced from progenitors on circular orbits). |
| In the text | |
 |
Fig. 3 Normalized synthetic images, in scattered light, showing the evolution of an avalanche in a cold debris disc (extending from 50 to 120 au) of average optical depth τ⊥ ~ 2 × 10-3, for an initial breakup, at t = 0, releasing 5 × 1022 g of dust at 10 au from the star. |
| In the text | |
 |
Fig. 4 Radial cuts of the vertical optical depth, passing by the avalanche’s peak luminosity location, at four different epochs of the avalanche’s evolution. The profile at t = 0 serves as a reference profile to which the avalanche-induced dust-excess can be compared. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for a test simulation with no outer disc, that is, showing only the dynamical outward motion of the grains released by the initial breakup event at 10 au. It can be clearly seen that the front of this outward propagation is, after only 40 yr, already well beyond 200 au (we show the radial profiles up to t = 40 yr instead of the 70 yr of Fig. 4, because there are no high-β initial grains left in the <200 au region after 70 yr). |
| In the text | |
 |
Fig. 6 Cold disc case: scattered light synthetic image, at the time of the maximum brightness of the avalanche (t = 11 yr), for the same case as in Fig. 3 but for a system viewed edge-on. |
| In the text | |
 |
Fig. 7 Cold disc case: disc-integrated luminosity as a function of time, at three different wavelengths, as well as for the total geometrical cross section. All fluxes are normalized to their value before the onset of the avalanche. The inset figure is a zoom-in on the first 100 yr of the simulation. The brief initial spike corresponds to the luminosity of the dust that is released at the moment of the breakup. |
| In the text | |
 |
Fig. 8 Cold disc case: system-integrated SED (using the GRaTer package for a system at a distance of 30 pc), at the peak of the avalanche luminosity, for the reference GAT07 τ⊥ ~ 2 × 10-3 disc and for a denser τ⊥ ~ 10-2 disc. The dashed lines give the luminosity excess due to the avalanche (computed by subtracting the SED of a reference avalanche-free case). The cutoff of the dashed-blue line beyond 50 μm reflects the fact that, for this dense disc case, the avalanche-system is slightly less luminous, at these long wavelengths, than an avalanche-free counterpart. This is because, beyond 50 μm, the flux is mostly dominated by large grains, which are slightly eroded by the passage of the avalanche (see discussion in Sect. 4.4.1). |
| In the text | |
 |
Fig. 9 As in Fig. 7, but for a denser main disc with τ⊥ ~ 10-2; all other parameters (released dust mass, disc location and width) being the same. The initial luminosity flash due to the breakup event itself appears less pronounced here because all luminosities are rescaled to the main disc’s brightness, which is here higher than for our previous reference case. |
| In the text | |
 |
Fig. 10 Cold disc case: disc-integrated geometrical cross section per logarithmic size bin, for the disc at collisional steady-state immediately before the onset of the avalanche. The vertical dashed line marks the β = 0.5 limit for unbound particles (if produced from progenitors on circular orbits) |
| In the text | |
 |
Fig. 11 Same as Fig. 7, but for the “warm disc” case (outer main disc between 5 and 12au with an optical depth τ⊥ ~ 2 × 10-3), and a mass minit ~ 1020 g of dust released at 1 ua. |
| In the text | |
 |
Fig. 12 Warm disc case: disc-integrated geometrical cross section per logarithmic size bin, for the disc at collisional steady-state just before the onset of the avalanche. |
| In the text | |
 |
Fig. 13 Warm disc case: system-integrated SEDs, for two different outer disc densities, at the time the avalanche reaches its peak luminosity. |
| In the text | |
 |
Fig. 14 Same as Fig. 11, but for a denser disc with optical depth τ⊥ ~ 10-2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


