| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731729 | |
| Published online | 09 February 2018 | |
Gravity darkening in late-type stars
I. The Coriolis effect
1
School of Astronomy, Institute for Research in Fundamental Sciences (IPM),
PO Box 19395-5531,
Tehran,
Iran
e-mail: raphael.raynaud@ipm.ir
2
Université de Toulouse, UPS-OMP, IRAP,
Toulouse,
France
e-mail: Michel.Rieutord@irap.omp.eu
3
CNRS, IRAP,
14 avenue Édouard Belin,
31400
Toulouse,
France
4
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, École normale supérieure,
75005
Paris,
France
e-mail: ludovic@lra.ens.fr
5
Institut de Physique du Globe de Paris, Sorbonne Paris Cité, Université Paris-Diderot, UMR 7154 CNRS,
1 rue Jussieu,
75005
Paris,
France
Received:
7
August
2017
Accepted:
4
December
2017
Context. Recent interferometric data have been used to constrain the brightness distribution at the surface of nearby stars, in particular the so-called gravity darkening that makes fast rotating stars brighter at their poles than at their equator. However, good models of gravity darkening are missing for stars that posses a convective envelope.
Aim. In order to better understand how rotation affects the heat transfer in stellar convective envelopes, we focus on the heat flux distribution in latitude at the outer surface of numerical models.
Methods. We carry out a systematic parameter study of three-dimensional, direct numerical simulations of anelastic convection in rotating spherical shells. As a first step, we neglect the centrifugal acceleration and retain only the Coriolis force. The fluid instability is driven by a fixed entropy drop between the inner and outer boundaries where stress-free boundary conditions are applied for the velocity field. Restricting our investigations to hydrodynamical models with a thermal Prandtl number fixed to unity, we consider both thick and thin (solar-like) shells, and vary the stratification over three orders of magnitude. We measure the heat transfer efficiency in terms of the Nusselt number, defined as the output luminosity normalised by the conductive state luminosity.
Results. We report diverse Nusselt number profiles in latitude, ranging from brighter (usually at the onset of convection) to darker equator and uniform profiles. We find that the variations of the surface brightness are mainly controlled by the surface value of the local Rossby number: when the Coriolis force dominates the dynamics, the heat flux is weakened in the equatorial region by the zonal wind and enhanced at the poles by convective motions inside the tangent cylinder. In the presence of a strong background density stratification however, as expected in real stars, the increase of the local Rossby number in the outer layers leads to uniformisation of the surface heat flux distribution.
Key words: convection / hydrodynamics / methods: numerical / stars: interiors
© ESO, 2018
1 Introduction
Fifty years ago, Lucy (1967) published a work on “Gravity darkening for stars with a convective envelope”. At the time, the motivation was the interpretation of the light curves of the W Ursa Majoris stars. Gravity darkening is indeed one of the phenomena that can modify the surface brightness of a star and thus be important in the interpretation of stellar light curves. Usually this phenomenon is associated with fast rotating early-type stars. We recall that for such stars, endowed with a radiative envelope, the flux varies with latitude basically because their centrifugal flattening makes the equatorial radius larger than the polar one. The temperature drop between the centre and the pole or the equator of the star being roughly the same, the temperature gradient is slightly weaker in the equatorial plane. Hence, the local surface flux is slightly less at the equator than at the poles; the equator appears darker (e.g. Monnier et al. 2007). For many decades this phenomenon was approximated by the von Zeipel (1924) law:  . Sometimes, fitting data requires a more general relation and von Zeipel’s law was changed to
. Sometimes, fitting data requires a more general relation and von Zeipel’s law was changed to  , and β adjusted.
, and β adjusted.
Observational works that have put constraints on the gravity-darkening exponent β come essentially from the photometry of eclipsing binaries (Djurašević et al. 2006) and interferometric observations of fast rotating stars (e.g. Domiciano de Souza et al. 2014). On the theoretical side, much progress has been made recently with the construction of the first self-consistent (dynamically) two-dimensional (2D) models of fast rotating stars (e.g. Espinosa Lara & Rieutord 2007, 2013; Rieutord et al. 2016). With these models it has been possible to make more precise predictions of the gravity-darkening effect, in particular for rapidly rotating early-type stars (Espinosa Lara & Rieutord 2011; Rieutord 2016). Currently, interferometric data and the most recent ESTER models agree very well on the gravity-darkening exponents (Domiciano de Souza et al. 2014). However, this is only valid for early-type stars.
For late-type stars the situation is less clear. As pointed out above, Lucy (1967) was the first to propose a theoretical estimate of gravity darkening for late-type stars. He actually suggested that β ≈ 0.08 for main sequence stars with masses approximately equal to the solar mass. However, as shown in Espinosa Lara & Rieutord (2012), Lucy’s approach leads to a gravity-darkening exponent that is essentially controlled by the opacity law in the surface layers and does not reflect the effects of the expected anisotropies of the underlying rotating convection. Interferometric data from the star β Cas, which is beyond the main sequence and most likely owns a convective envelope, point to β ≈ 0.14 (Che et al. 2011), thus also requiring a new modelling.
However, modelling the latitude dependence of the heat flux in a fast rotating late-type star is a thorny problem. Basically, three effectscombine and potentially modulate the heat flux (Rieutord 2016). The first, which is expected to be the mostimportant one, is the effect of the Coriolis acceleration. It tends to make the flows in a columnar shape, with columns parallel to the rotation axis, inhibiting convection near the pole and favouring it near the equator, thus pointing to a negative gravity-darkening exponent. The second effect is the centrifugal effect that diminishes the buoyancy in the equatorial regions and thus contributes to a positive gravity-darkening exponent. Finally, fluid flows generate magnetic fields that can also inhibit heat transfer, both in the bulk or at the surface via spots.
The above arguments show that modelling gravity darkening for stars possessing a convective envelope is far from easy. To make a step forward in this modelling, we investigate here the latitudinal variations of the flux at the surface of a fluid contained in a rotating spherical shell and heated from below. To that end, we perform direct numerical simulations using the anelastic approximation (sound waves are filtered out but background density variations are taken into account). As a first step, we concentrate solely on the Coriolis effect. Thus centrifugal and dynamo effects are neglected. They will be implemented and investigated in the subsequent studies.
The paper is organised as follows: Sect. 2 introduces the anelastic models and the numerical solvers used for this study. Results are presented in Sect. 3 and discussed in Sect. 4. Finally, a set of critical Rayleigh numbers for the linear onset of convection and the overview of the numerical simulations carried out are given in Appendices A and B, respectively.
2 Modelling
We consider a spherical shell in rotation at angular velocity Ω ez, bounded by two concentric spheres of radius ri and ro, and filled with a perfect gas with kinematic viscosity ν, turbulent entropy diffusivity κ, and specific heat cp (all taken as constants). Independently of the shell aspect ratio χ = ri∕ro, we assume that the mass bulk is concentrated inside the inner surface ri and we further neglect the centrifugal acceleration, which results in the radial gravity profile g = −GMer∕r2, where G is the gravitational constant and M the central mass. The fluid flow is modelled using the LBR anelastic equations, named after Braginsky & Roberts (1995) and Lantz & Fan (1999). Our set-up is actually equivalent to the one used in the anelastic dynamo benchmark (Jones et al. 2011), in which the closure relation for the heat flux is expressed in terms of the entropy gradient. Convection is then driven by an imposed entropy difference ΔS between the inner and outer boundaries. In the following, we recall the equations for completeness and refer the reader to Wood & Bushby (2016) for a discussion of the definition of consistent thermodynamic variables in sound-proof approximations of the Navier-Stokes equation (see also Calkins et al. 2015).
In our models, the reference state is the polytropic solution of the hydrostatic equations for an adiabatically stratified atmosphere, which reads
 (1)
(1)
The constants Pc, ϱc and Tc in Eq. (1) are the reference-state pressure, density, and temperature midway between the inner and outer boundaries. These reference values serve as units for these variables, whilst length is scaled by the shell width d = ro − ri, time by the viscous time d2∕ν, and entropy by the entropy drop ΔS. Then, the coupled Navier-Stokes and heat transfer equations take the form

The control parameters of the above system are:

together with the shell aspect ratio χ and the polytropic index n. In Eq. (4), P′ denotes the pressure perturbation and the viscous force Fν is given by Fν = ζ−n∇S, where the rate of strain tensor S is defined by
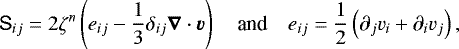 (11)
(11)
since the kinematic viscosity is assumed to be constant. The viscous heating Qν is then given by
![\begin{equation*} Q_{\nu}=2\left[e_{ij}e_{ji}-\frac{1}{3}(\boldsymbol{\nabla}\cdot\vec{v})^2\right] . \end{equation*}](/articles/aa/full_html/2018/01/aa31729-17/aa31729-17-eq8.png) (12)
(12)
Finally, the expression of the dissipation parameter  in Eq. (5) reduces to
in Eq. (5) reduces to
 (13)
(13)
where the last equality follows from the hydrostatic balance  and the equation of state of an ideal gas close to adiabatic,
and the equation of state of an ideal gas close to adiabatic,  .
.
Since we are primarily interested in modelling stellar convection zones, we impose impenetrable and stress-free boundary conditions for the velocity field,
 (14)
(14)
whereas the entropy is fixed at the inner and outer boundaries. Stress-free conditions are justified even at the bottom of the convection zone since the (turbulent) viscosity of the convection zone is much larger than the viscosity of the radiative region (Rüdiger 1989; Rieutord 2008).
The time integration of the anelastic system (Eqs. (4)–(6)) has been performed with two different pseudo-spectral codes, PARODY (Dormy et al. 1998; Schrinner et al. 2014) and MAGIC1 (Gastine & Wicht 2012; Schaeffer 2013). These codes both use a poloidal-toroidal decomposition to ensure the solenoidal constraint (Eq. (6)), the major difference lying in the radial discretization: PARODY is based on a finite difference scheme, while MAGIC uses Chebyshev polynomials. Both numerical solvers reproduce the anelastic dynamo benchmark (Jones et al. 2011) and we checked on a test case that the results we obtain do not differ from one solver to another. In practice, one must be careful that the default definition of the Rayleigh number in MAGIC slightly differs from the one given in Eq. (7) and obeys the relation  .
.
The reader will find a set of critical Rayleigh number values for the linear onset of convection in Table A.1. These have been calculated solving the eigenvalue problem of the linearized equations of perturbations as in Jones et al. (2009), using a spectral decomposition on the spherical harmonics and Chebyshev polynomials together with an Arnoldi-Chebyshev solver (Rieutord & Valdettaro 1997; Valdettaro et al. 2007). Other critical Rayleigh numbers may be found in Schrinner et al. (2014). Table B.1 contains the summary of the numerical models and specifies their integration time Δ t (expressed in turnover time units  computed with the non-zonal velocity field) and their spatial resolution. Numerical convergence has been empirically checked on the basis of a decrease of at least two orders of magnitude in the kinetic energy spectra; although this criterion is not always sufficient to prevent spurious fluctuations of the Nusselt number at the poles. This latter is defined as the output luminosity normalised by the conductive state luminosity and its expression at the outer surface reduces to
computed with the non-zonal velocity field) and their spatial resolution. Numerical convergence has been empirically checked on the basis of a decrease of at least two orders of magnitude in the kinetic energy spectra; although this criterion is not always sufficient to prevent spurious fluctuations of the Nusselt number at the poles. This latter is defined as the output luminosity normalised by the conductive state luminosity and its expression at the outer surface reduces to  , with the conductive entropy profile Sc
, with the conductive entropy profile Sc
 (15)
(15)
where ζo is given by Eq. (3) and ζi = (1 + χ − ζo)∕χ. The above equations result in the distribution of the surface heat flux as a function of colatitude θ given by
 (16)
(16)
In the bulk, we must account for the heat advected by the flow, which gives
 (17)
(17)
with the entropy perturbation S′ = S − Sc.
3 Results
For a Boussinesq fluid characterised by a Prandtl number of approximately unity, it is well known that the onset of convection driven by differential heating in a rotating spherical shell takes the form of columns aligned with the rotation axis, sometimes described in terms of quasi-geostrophic, eastward travelling thermal Rossby waves (Busse 1970; Jones et al. 2000; Dormy et al. 2004). In this regime, the axially aligned convective rolls do not break the equatorial symmetry and transfer heat preferentially in the direction perpendicular to the rotation axis, whereas regions inside the tangent cylinder are nearly stagnant. The heat flux is then maximum at the equator and symmetric with respect to the equatorial plane (Tilgner & Busse 1997; Busse & Simitev 2006; Yadav et al. 2016). For fluids with a radially decreasing mean density submitted to differential heating, it has been shown that compressibility tends to push the convection cells outward, away from the tangent cylinder (Glatzmaier & Gilman 1981; Jones et al. 2009; Gastine & Wicht 2012). We find that this directly affects the latitudinal heat flux profile and that these changes are more or less pronounced depending on the shell thickness. For a thick convective zone (χ = 0.35), we see in Fig. 1a that the concavity of the heat flux rapidly changes with the background density contrast. As expected, the heat flux is maximum at the equator for a quasi-Boussinesq set-up with Nϱ = 0.1 (solid blue line). As Nϱ increases, it tends to flatten (Nϱ = 0.5, dotted black line) and eventually peaks at two different latitudes (Nϱ = 2, red dashed line) which are located closer to the colatitudes  where the tangent cylinder crosses the outer surface, determined by
where the tangent cylinder crosses the outer surface, determined by  and
and 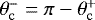 . For a solar-like convective zone (χ = 0.7), the surface of the polar caps that lie inside the tangent cylinder increases, representing 29% of the total outer surface, whereas it is only 6% when χ = 0.35. Consequently, the impact of the density stratification on the heat flux profile at the onset of convection gets more confined on either side of the equator, as we can see in Fig. 1b.
. For a solar-like convective zone (χ = 0.7), the surface of the polar caps that lie inside the tangent cylinder increases, representing 29% of the total outer surface, whereas it is only 6% when χ = 0.35. Consequently, the impact of the density stratification on the heat flux profile at the onset of convection gets more confined on either side of the equator, as we can see in Fig. 1b.
When we depart further from the onset, convective motions progressively develop in the tangent cylinder and we observe the emergence of heat flux maxima located inside the tangent cylinder. This is a general tendency, independent of other parameters like the shell aspect ratio, the density stratification or the Ekman number. An example of this transition is given in Fig. 2a, which shows the averaged Nusselt profile (solid black line) for a thin shell with moderate stratification. For Ra∕Rac = 8, the heat flux profile displays three distinct maxima as a function of latitude. The local one that is centred on the equator corresponds to the equatorial maximum we observe at the onset of convection in thin shells. Its average value is about  and has increased by 25% when compared to its value for Ra∕Rac = 4. The pair of absolute maxima located at the boundary of the tangent cylinder does not exist for Ra ∕Rac = 4. When we double again the Rayleigh number to reach Ra∕Rac = 16, we switch from this intermediate state to a situation where the surface heat flux is predominantly concentrated inside the tangent cylinder, as we can see in Fig. 2b. The contrast between the equatorial heat flux and the heat flux at the tangent cylinder has more than doubled. However, we still distinguish a local maximum at the equator with almost the same value, surrounded by two dips at θ∕π ≈ 0.4 and θ∕π ≈ 0.6. When comparing Figs. 2a and b, we note that the latitudes of the extrema are identical in both cases. A similar situation prevails in thick shells, except that we do not observe any extrema in the equatorial belt where the heat flux profile tends to be flat for
and has increased by 25% when compared to its value for Ra∕Rac = 4. The pair of absolute maxima located at the boundary of the tangent cylinder does not exist for Ra ∕Rac = 4. When we double again the Rayleigh number to reach Ra∕Rac = 16, we switch from this intermediate state to a situation where the surface heat flux is predominantly concentrated inside the tangent cylinder, as we can see in Fig. 2b. The contrast between the equatorial heat flux and the heat flux at the tangent cylinder has more than doubled. However, we still distinguish a local maximum at the equator with almost the same value, surrounded by two dips at θ∕π ≈ 0.4 and θ∕π ≈ 0.6. When comparing Figs. 2a and b, we note that the latitudes of the extrema are identical in both cases. A similar situation prevails in thick shells, except that we do not observe any extrema in the equatorial belt where the heat flux profile tends to be flat for ![$\theta/\pi \in \left[0.4, 0.6\right]$](/articles/aa/full_html/2018/01/aa31729-17/aa31729-17-eq24.png) . In this regime, the signature of the tangent cylinder is then the characteristic feature of the latitudinal variations of the Nusselt number.
. In this regime, the signature of the tangent cylinder is then the characteristic feature of the latitudinal variations of the Nusselt number.
For higher density stratification, we observe a similar regime where the heat flux is stronger inside the tangent cylinder, with the difference that the Nusselt number tends to be maximum at the poles but not anymore at the tangent cylinder boundaries, as illustrated in Fig. 2c. Moreover, increasing both the density stratification and the Rayleigh number leads us to the discovery of a third type of Nusselt profile almost constant in latitude. This regime strongly differs from previous observations and seems typical of turbulent, large Nϱ models. The limit of highRa and high Nϱ is, of course, very difficult to achieve numerically, but our set of simulations indicates that the heat flux has a tendency to flatten for high enough Rayleigh numbers and ultimately become independent of the latitude, as shown in the example displayed in Fig. 2d. In both thin and thick shells, the flattening of the heat flux profile results from the decrease of the contrast between the equatorial and polar heat fluxes. It is relatively smooth and for this reason, it is sometimes difficult to arbitrarily distinguish this regime from the previous one. Nevertheless, we notice that the evolution toward a homogeneous surface heat flux is favoured by high density contrasts, since we did not observe such flat profiles for Nϱ ≤ 2 for Ra ∕Rac ≤ 40. The larger Nϱ, the faster we reach this regime when increasing the Rayleigh number.
 |
Fig. 1 Nusselt number as a function of colatitude close to the onset of convection with increasing density stratification, for thick (a) and thin (b) shells. The positions of the equator and the tangent cylinder are indicated by vertical dotted lines. |
 |
Fig. 2 Nusselt (black) and zonal velocity (blue) profiles as a function of colatitude for different thin shell models. The colour insets represent snapshots of S(r = 0.98ro) and vφ (r = ro). The positions of the equator and the tangent cylinder are indicated by vertical dotted lines. |
4 Discussion
Our systematic parameter study reveals that the variations in latitude of the heat flux transported by convection at the surface of a rotating spherical shell strongly vary in the parameter space. Various profiles have indeed been identified, ranging from brighter to darker equator or uniform profiles. These different regimes can be identified in Fig. 3, which displays the ratio  as a function of the ratio
as a function of the ratio  . The maximum and minimum values have been computed after performing a running average in latitude of the Nusselt profile in order to remove small-scale fluctuations, and the equator and the polar values have been averaged on an angular sector of 10°. One can see that the weakly supercritical models mainly stand on the dashed curve y = 1∕x, since the equator is usually brighter at the onset of convection. For Ra∕Rac ≳ 10, the points tend to fall on the dashed line y = x, which indicates that we switch from a brighter to a darker equator. We also note that the contrast tends to be stronger. Finally, the third regime is indicated by the group of points that tends to accumulate close to the intersection of the dashed lines, where models with Nϱ ≥ 6 are predominant (see the inset). Of course, we stress that this representation is too simple to render with precision all the variations of the Nusselt number that have been observed, especially when the heat flux is maximum at the tangent cylinder (see Fig. 2, top panels). This peculiar configuration has been preferentially found for low stratification, which explains why a few points do not fall on the dashed lines.
. The maximum and minimum values have been computed after performing a running average in latitude of the Nusselt profile in order to remove small-scale fluctuations, and the equator and the polar values have been averaged on an angular sector of 10°. One can see that the weakly supercritical models mainly stand on the dashed curve y = 1∕x, since the equator is usually brighter at the onset of convection. For Ra∕Rac ≳ 10, the points tend to fall on the dashed line y = x, which indicates that we switch from a brighter to a darker equator. We also note that the contrast tends to be stronger. Finally, the third regime is indicated by the group of points that tends to accumulate close to the intersection of the dashed lines, where models with Nϱ ≥ 6 are predominant (see the inset). Of course, we stress that this representation is too simple to render with precision all the variations of the Nusselt number that have been observed, especially when the heat flux is maximum at the tangent cylinder (see Fig. 2, top panels). This peculiar configuration has been preferentially found for low stratification, which explains why a few points do not fall on the dashed lines.
At the onset of convection, one can gain some intuition about the variations reported in Fig. 1a by examining the Nϱ dependence of the radial conductive profile Sc defined by Eq. (15). In order to estimate the latitude at which the heat transfer will be more efficient at the onset of the convective instability, one can compute the radial entropy drop δSc between two cylindrical radii s1 and s2 that roughly correspond to the position of the convective columns (sketched out in Fig. 4). It turns out that this quantity displays latitude variations similar to the Nusselt number profile: when comparing Figs. 1a and 4, we see that the maximum location switches from the equator to mid-latitudes as the stratification increases from Nϱ = 0.1 to Nϱ = 2. Thus, the latitude dependence of the heat flux profile at the onset of convection is intrinsically linked to the conductive entropy profile Sc, which explains why it mainly depends on the shell aspect ratio and density stratification.
To better understand the regimes shown in Fig. 2, it is interesting to compare the variations in latitude of the Nusselt number (black lines) to those of the zonal velocity field  (blue lines). In Figs. 2b and c, the intensity of the zonal wind is stronger at the equator, which coincides with the position of the Nusselt minimum. This observation is consistent with the behaviour reported for Boussinesq models (Aurnou et al. 2008; Yadav et al. 2016) and clearly illustrates the phenomenon of zonal flows impeding the heat transfer at low latitudes (Goluskin et al. 2014). Then, the observation of a darker equator results both from the development of a prograde equatorial jet sustained by Reynolds stresses and from the growth of convective motions inside the tangent cylinder, where they are less affected by the zonal flows. Besides, one may notice that the Nusselt maxima in Fig. 2b coincides with the retrograde jets anchored to the tangent cylinder. These jets, that ensure the conservation of angular momentum, are typical of stress-free boundary conditions in Boussinesq simulations (Christensen 2002; Aurnou & Heimpel 2004). We do not observe a similar differential rotation profile in Fig. 2c which only displays a single equatorial prograde jet and a global heat flux minimum at the equator.
(blue lines). In Figs. 2b and c, the intensity of the zonal wind is stronger at the equator, which coincides with the position of the Nusselt minimum. This observation is consistent with the behaviour reported for Boussinesq models (Aurnou et al. 2008; Yadav et al. 2016) and clearly illustrates the phenomenon of zonal flows impeding the heat transfer at low latitudes (Goluskin et al. 2014). Then, the observation of a darker equator results both from the development of a prograde equatorial jet sustained by Reynolds stresses and from the growth of convective motions inside the tangent cylinder, where they are less affected by the zonal flows. Besides, one may notice that the Nusselt maxima in Fig. 2b coincides with the retrograde jets anchored to the tangent cylinder. These jets, that ensure the conservation of angular momentum, are typical of stress-free boundary conditions in Boussinesq simulations (Christensen 2002; Aurnou & Heimpel 2004). We do not observe a similar differential rotation profile in Fig. 2c which only displays a single equatorial prograde jet and a global heat flux minimum at the equator.
However, it is important to note that this correlation between zonal wind and heat flux profiles weakens for models withhigher density contrasts, as we can see in the example given in Fig. 2d: the zonal wind is nowretrograde at the equator while the heat flux profile has become almost constant in latitude. As we mention above, this flattening of the heat flux profile is characteristic of strongly stratified models, but it appears independentof the specific nature of the differential rotation profile (solar-like or antisolar). Since in the limit Ω → 0 the system is expected to recover a central symmetry and a Nusselt number invariant in latitude, we believe that the homogenisation of the heat flux results from the relative diminution of the Coriolis force in the outer layers of the fluid shell. Indeed, only strongly stratified anelastic models can exhibit different dynamical regimes that coexist inside the convective zone, due to the important variation of the force balance as a function of depth. In a first approximation, Gastine et al. (2013) showed that the radius rmix at which the transition from rotation-dominated to buoyancy-dominated regimes occurs can be estimated by solving the equation Roc (rmix) = 1, where the convective Rossby number is defined by
 (18)
(18)
In what they call the transitional regime, the region above rmix tends to exhibit three-dimensional, radially oriented convective structures. This hydrodynamic transition naturally impacts the advective component of the Nusselt number which is always dominant over the conductive one in the bulk. In practice, we see in Fig. 5a the flattening of the Nusselt profile induced by the increase of the density stratification, while Fig. 5b displays the corresponding increase of convective Rossby number close to the outer surface. Since the radial dependence of Roc is only determined by the conductive entropy profile shown in Fig. 5c, this explains why uniform heat fluxes prevail at high Nϱ. Indeed, when the stratification increases, Sc tends to keep values close to Sc(ri) in the bulk and sharply drops in the outer layers in order to match the surface boundary conditions.
However, we stress that a prognostic quantity like Roc simply intends to deliver a rough description of the evolution of the force balance as a function of depth. A finer estimate of the balance between inertial and Coriolis forces can be achieved by computing a local Rossby number Roℓ = vrms∕(Ωl) (Christensen & Aubert 2006), where l = π∕ℓ is a typical length scale based on the mean harmonic degree ℓ of the velocity field. We recall that previous studies highlighted the importance of the mean value of local Rossby numbers in understanding the field topology of convective dynamos (Christensen & Aubert 2006; Schrinner et al. 2012) or the direction of the surface differential rotation (Gastine et al. 2014). Figure 5d displays the radial profiles of our local Rossby number for different density stratification. We see that it exceeds unity only in the outer layers of the model with the highest stratification (blue curve); but deeper in the bulk, the flow always remains rotationally constrained. Figure 6 also shows that the pole/equator luminosity contrast increases with depth, and that the heat flux tends to be maximum at the equator deep inside the bulk. As already pointed out by Durney (1981), this confirms that large pole/equator heat flux differences in the lower part of the convection zone may coexist with a negligible luminosity contrast at the surface.
Finally, Fig. 7 shows that the surface value of the local Rossby number seems to control the heat flux distribution at the top of the convective zone. If we do not focus on the models close to the onset of convection, we see that this contrast rapidly decreases when Roℓ (ro) > 1, whereas it tends to reach its maximum for Roℓ(ro) ∈ [0.1, 1] when the poles are brighter than the equator (shaded area). We stress that the collapse of the different models we see in Fig. 7 would not be obtained using the average value of the local Rossby number, which tends to be lower than the surface value for Nϱ > 1 (the higher the stratification, the lower the ratio Roℓ∕Roℓ(ro)). This is consistent with the fact that, in our models, the uniformisation of the heat flux occurs locally, close to the outer boundary. Although it is theoretically possible to reach a similar regime with an incompressible model, in practice, the radial dependence of the conductive entropy profile Sc at large Nϱ is the main cause of the rapid increase of the local Rossby number in the outer layers of the fluid shell (see Figs. 5c and d). This impact of the density stratification is illustrated in Fig. 8 which displays snapshot slices of the entropy, velocity amplitude, and Nusselt number. For the highest density contrasts (Figs. 8a and b), the velocity amplitude highlights the transition from rotation-dominated to buoyancy-dominated flows close to the radius rmix. Moreover, the outer Nusselt slice in Fig. 8a has been performed just above the transition Roℓ (r) > 1 when the heat flux uniformisation becomes effective. In contrast, this limit is not achieved in the other panels with lower stratification.
 |
Fig. 3 Ratio |
 |
Fig. 4 Left: δSc = Sc(s = s1) − Sc(s = s2) as a function of colatitude for increasing density stratification. Right: sketch illustrating the definition of δSc. |
 |
Fig. 5 Left: normalised Nusselt profiles (a) averaged in time for a subset of thick shell models with decreasing density stratification. Right: radial profiles of the convective Rossby number (b), conductive entropy (c) and local Rossby number (d) for the same subset of models. |
 |
Fig. 6 Nusselt profiles as a function of colatitude at different depths, for different density stratification. A running average in latitude has been applied to the mean profiles (solid lines) and the shaded areas highlight the fluctuation envelopes. |
 |
Fig. 7 Relative pole/equator contrast as a function of Roℓ(ro) for our sample of models. Solid (dashed) lines indicate E = 3 × 10−4 (E = 10−4) models. Themeaning of the symbols is defined in the caption of Fig. 3. |
 |
Fig. 8 Entropy, velocity magnitude and Nusselt number snapshots for decreasing density stratification in thick shell models. Nusselt spherical slices have been performed at 0.96ro (a)–(c) and midway between the inner and outer boundaries (a), (b). Wireframe surfaces (a), (b) materialize the radius rmix. |
5 Conclusion
As a first numerical approach toward modelling the gravity darkening in late-type stars endowed with a convective envelope, we carried out a systematic parameter study to investigate the heat flux distribution at the surface of a rotating spherical shell filled by a convective ideal gas. In the majority of cases, our results are consistent with the tendencies that have been reported in Boussinesq simulations: at the onset of convection, the equator is usually brighter, but it becomes darker than the polar regions when the ratio Ra ∕Rac increases and convective motions fill the tangent cylinder. Favoured by our choice of stress-free boundary conditions, the equatorial zonal flow is then efficient at impeding the radial heat transfer at low latitudes (Goluskin et al. 2014).
Besides, thanks to the use of the anelastic approximation, we show that, among all the system control parameters, the background density stratification has the strongest impact on the Nusselt number profile. Indeed, as the stratification increases, the Nusselt number tends to fluctuate around a constant value in latitude. We show that this uniformisation of the heat flux distribution turns out to be primarily controlled by the surface value of the local Rossby number Roℓ (ro), which indicates that it becomes effective in the outer fluid layers where the Coriolis force is no longer dominating the dynamics. In our numerical models, the background density drop and the shape of the conductive entropy profile Sc at high Nϱ strongly favour the sharp increase of the local Rossby number close to the outer boundary. This is the reason why we found uniform profiles only in highly stratified simulations (Nϱ ≥ 6). In this regime, the anti-correlation between zonal flows and heat flux which usually characterises the strongest pole/equator luminosity contrasts vanishes. Interestingly, we note that the observation of a uniform energy flux density coexisting with the non-uniform rotation of the solar surface was at the heart of the so-called heat-flux problem in theories aimed at explaining the Sun’s differential rotation (Rüdiger 1982). Rast et al. (2008) indeed report a weak ≈ 0.1% enhancement of the solar intensity at polar latitudes. The absence of stronger latitudinal variations of the mean solar photospheric intensity could then be explained by the fact that convective flows are probably not rotationally constrained anymore in the near-surface shear layer that spans the outermost 35 Mm of the Sun (Greer et al. 2016a,b). Greer et al. (2016a) suggest weak rotational constraint in the outer layers above r ≈ 0.96ro, while we find for the thin shell model displayed in Fig. 2d that the transition Roℓ = 1 occurs at r ≈ 0.9ro – a value which is slightly lower than the one predicted from observations, but we may have deeper transitions in numerical models given the much lower density stratification of the convective zone. Moreover, we stress that for this numerical model the radial profile of the local Rossby number is in very good agreement with the profile we expect according to the mixing length theory.
In orderto connect our results to previous theoretical studies on the gravity darkening, it would have been interesting to infer gravity-darkening exponents from our set of direct numerical simulations. However, by construction, we cannot have access to any effective gravity geff relying on our numerical models only. Assuming a Roche model for the surface effective gravity geff, the generalized von Zeipel’s law should read  , but one has to find a way to estimate the RHS. For thin shell models, we attempted to do so using the velocity profile given by a one-dimensional model of the Sun to derive a rotation rate, but this approach did not provide a valuable result.
, but one has to find a way to estimate the RHS. For thin shell models, we attempted to do so using the velocity profile given by a one-dimensional model of the Sun to derive a rotation rate, but this approach did not provide a valuable result.
Nevertheless, our study has shown that despite its strength, the Coriolis force does not seem to be able to break the spherical symmetry of the exiting heat flux in a rotating star if the local Rossby number exceeds unity in the surface layers. The short time scale associated with a short length scale of surface convection seems to be able to screen the anisotropy of the deep motions of rotating convection. The natural step forward is now to investigate the effects of the centrifugal acceleration, which can loosen the vigour of convection in equatorial regions thanks to reduced gravity. However, the whole picture might also be strongly perturbed by magnetic fields. Indeed, Yadav et al. (2016) showed with Boussinesq models that the Nusselt number is enhanced in presence of a magnetic field which affects the convective motions and tends to quench the zonal flow at low latitudes. Both effects of magnetic fields and centrifugal acceleration will be investigated in forthcoming studies.
Acknowledgements
This study was granted access to the HPC resources of MesoPSL financed by the Région Île-de-France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. Numerical simulations were also carried out at the TGCC Curie and CINES Occigen computing centers (GENCI project A001046698) as well as at CALMIP – computing center of Toulouse University (Grant 2016-P1518). R. R. thanks C. A. Jones for comments.
Appendix A Critical Rayleigh numbers for the onset of convection
Critical values.
Appendix B Numerical models
References
- Aurnou, J. M., & Heimpel, M. H. 2004, Icarus, 169, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Aurnou, J., Heimpel, M., Allen, L., King, E., & Wicht, J. 2008, Geophys. J. Int., 173, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Braginsky, S. I., & Roberts, P. H. 1995, Geophys. Astrophys. Fluid Dyn., 79, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H. 1970, J. Fluid Mech., 44, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H., & Simitev, R. D. 2006, Geophys. Astrophys. Fluid Dyn., 100, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Calkins, M. A., Julien, K., & Marti, P. 2015, Geophys. Astrophys. Fluid Dyn., 109, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U. R. 2002, J. Fluid Mech., 470, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U. R., & Aubert, J. 2006, Geophy. J. Int., 166, 97 [Google Scholar]
- Djurašević, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2006, A&A, 445, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Moser Faes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dormy, E., Cardin, P., & Jault, D. 1998, Earth Planet. Sci. Lett., 160, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dormy, E., Soward, A. M., Jones, C. A., Jault, D., & Cardin, P. 2004, J. Fluid Mech., 501, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 1981, ApJ, 244, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2007, A&A, 470, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2012, A&A, 547, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gastine, T., & Wicht, J. 2012, Icarus, 219, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Wicht, J., & Aurnou, J. M. 2013, Icarus, 225, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Yadav, R. K., Morin, J., Reiners, A., & Wicht, J. 2014, MNRAS, 438, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzmaier, G. A., & Gilman, P. A. 1981, ApJS, 45, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Goluskin, D., Johnston, H., Flierl, G. R., & Spiegel, E. A. 2014, J. Fluid Mech., 759, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Greer, B. J., Hindman, B. W., & Toomre, J. 2016a, ApJ, 824, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Greer, B. J., Hindman, B. W., & Toomre, J. 2016b, ApJ, 824, 4 [Google Scholar]
- Jones, C. A., Soward, A. M., & Mussa, A. I. 2000, J. Fluid Mech., 405, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C. A., Kuzanyan, K. M., & Mitchell, R. H. 2009, J. Fluid Mech., 634, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C. A., Boronski, P., Brun, A. S., et al. 2011, Icarus, 216, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Lantz, S. R., & Fan, Y. 1999, ApJS, 121, 2470 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rast, M. P., Ortiz, A., & Meisner, R. W. 2008, ApJ, 673, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 2008, Comptes Rendus Physique, 9, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 2016, in Cartography of the Sun and the Stars, Lect. Notes Phys., eds. J.-P. Rozelot, & C. Neiner, 914, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Valdettaro, L. 1997, J. Fluid Mech., 341, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comp. Phys., 318, 277 [Google Scholar]
- Rüdiger,G. 1982, Astron. Nachr., 303, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G. 1989, Differential Rotation and Stellar Convection: Sun and Solar-type Stars, The Fluid Mechanics of Astrophysics and Geophysics (Gordon and Breach Science Publishers) [Google Scholar]
- Schaeffer, N. 2013, Geochem. Geophys. Geosyst., 14, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Petitdemange, L., & Dormy, E. 2012, ApJ, 752, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Petitdemange, L., Raynaud, R., & Dormy, E. 2014, A&A, 564, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tilgner, A., & Busse, F. H. 1997, J. Fluid Mech., 332, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Valdettaro, L., Rieutord, M., Braconnier, T., & Fraysse, V. 2007, J. Comput. Appl. Math., 205, 382 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, T. S., & Bushby, P. J. 2016, J. Fluid Mech., 803, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Gastine, T., Christensen, U. R., Duarte, L. D. V., & Reiners, A. 2016, Geophys. J. Int., 204, 1120 [NASA ADS] [CrossRef] [Google Scholar]
MAGIC is available online at https://github.com/magic-sph/magic. It uses the SHTns library available at https://bitbucket.org/nschaeff/shtns.
All Tables
All Figures
 |
Fig. 1 Nusselt number as a function of colatitude close to the onset of convection with increasing density stratification, for thick (a) and thin (b) shells. The positions of the equator and the tangent cylinder are indicated by vertical dotted lines. |
| In the text | |
 |
Fig. 2 Nusselt (black) and zonal velocity (blue) profiles as a function of colatitude for different thin shell models. The colour insets represent snapshots of S(r = 0.98ro) and vφ (r = ro). The positions of the equator and the tangent cylinder are indicated by vertical dotted lines. |
| In the text | |
 |
Fig. 3 Ratio |
| In the text | |
 |
Fig. 4 Left: δSc = Sc(s = s1) − Sc(s = s2) as a function of colatitude for increasing density stratification. Right: sketch illustrating the definition of δSc. |
| In the text | |
 |
Fig. 5 Left: normalised Nusselt profiles (a) averaged in time for a subset of thick shell models with decreasing density stratification. Right: radial profiles of the convective Rossby number (b), conductive entropy (c) and local Rossby number (d) for the same subset of models. |
| In the text | |
 |
Fig. 6 Nusselt profiles as a function of colatitude at different depths, for different density stratification. A running average in latitude has been applied to the mean profiles (solid lines) and the shaded areas highlight the fluctuation envelopes. |
| In the text | |
 |
Fig. 7 Relative pole/equator contrast as a function of Roℓ(ro) for our sample of models. Solid (dashed) lines indicate E = 3 × 10−4 (E = 10−4) models. Themeaning of the symbols is defined in the caption of Fig. 3. |
| In the text | |
 |
Fig. 8 Entropy, velocity magnitude and Nusselt number snapshots for decreasing density stratification in thick shell models. Nusselt spherical slices have been performed at 0.96ro (a)–(c) and midway between the inner and outer boundaries (a), (b). Wireframe surfaces (a), (b) materialize the radius rmix. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





