| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731113 | |
| Published online | 05 January 2018 | |
The GTC exoplanet transit spectroscopy survey
VIII. Flat transmission spectrum for the warm gas giant WASP-80b⋆
1 Instituto de Astrofísica de Canarias (IAC), 38200 La Laguna, Tenerife, Spain
e-mail: hannu@iac.es
2 Dept. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
3 Sub-department of Astrophysics, Department of Physics, University of Oxford, Oxford, OX1 3RH, UK
4 Key Laboratory of Planetary Sciences, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008, PR China
5 School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK
6 Theoretical Meteorology group, Klimacampus, University of Hamburg, Grindelberg 5, 20144 Hamburg, Germany
Received: 5 May 2017
Accepted: 6 September 2017
Aims. We set out to study the atmosphere of WASP-80b, a warm inflated gas giant with an equilibrium temperature of ~800 K, using ground-based transmission spectroscopy covering the spectral range from 520 to 910 nm. The observations allow us to probe the existence and abundance of K and Na in WASP-80b’s atmosphere, existence of high-altitude clouds, and Rayleigh-scattering in the blue end of the spectrum.
Methods. We observed two spectroscopic time series of WASP-80b transits with the OSIRIS spectrograph installed in the Gran Telescopio Canarias (GTC), and use the observations to estimate the planet’s transmission spectrum between 520 nm and 910 nm in 20 nm-wide passbands, and around the K I and Na I resonance doublets in 6 nm-wide passbands. We jointly model three previously published broadband datasets consisting of 27 light curves, prior to a transmission spectroscopy analysis in order to obtain improved estimates of the planet’s orbital parameters, average radius ratio, and stellar density. The parameter posteriors from the broadband analysis are used to set informative priors on the transmission spectroscopy analysis. The final transmission spectroscopy analyses are carried out jointly for the two nights using a divide-by-white approach to remove the common-mode systematics, and Gaussian processes to model the residual wavelength-dependent systematics.
Results. We recover a flat transmission spectrum with no evidence of Rayleigh scattering or K I or Na I absorption, and obtain an improved system characterisation as a by-product of the broadband- and GTC-dataset modelling. The transmission spectra estimated separately from the two observing runs are consistent with each other, as are the transmission spectra estimated using either a parametric or nonparametric systematics model. The flat transmission spectrum favours an atmosphere model with high-altitude clouds over cloud-free models with stellar or sub-stellar metallicities.
Conclusions. Our results disagree with the recently published discovery of strong K I absorption in WASP-80b’s atmosphere based on ground-based transmission spectroscopy with FORS2 at VLT.
Key words: planets and satellites: individual: WASP-80b / planets and satellites: atmospheres / stars: individual: WASP-80 / techniques: photometric / techniques: spectroscopic / methods: statistical
The analysis code with the raw and processed data are publicly available through GitHub from https://github.com/hpparvi/Parviainen-2017-WASP-80b
© ESO, 2017
1. Introduction
Transmission spectroscopy allows us to probe the existence and abundance of atmospheric species in the atmospheres of transiting extrasolar planets (Seager & Sasselov 2000; Brown 2001). The method requires a high observing precision, which has made the space-based studies most successful in finding significant features in the transmission spectra (Charbonneau et al. 2002; Sing et al. 2011; Gibson et al. 2012a), but the developments in instrumentation, observing techniques, and data analysis methods have also enabled transmission spectroscopy studies to be carried out successfully using ground-based telescopes.
The signal of interest – variations in the effective planetary radius as a function of wavelength – is minute, corresponding to changes of ~ 0.01% in the observed transit depth and ~ 0.1% in the effective planet-star radius ratio. Further complications arise from possible high-altitude clouds, which can mask any atmospheric extinction features, leading to a flat transmission spectrum (Kreidberg et al. 2014; Berta et al. 2012), and from the fact that atmospheric extinction is not the only source of wavelength-dependent features in transmission spectra. Both instrumental and astrophysical sources, such as host star’s spots (Ballerini et al. 2012) and plages (Oshagh et al. 2014), flux contamination from a possible unresolved source, and incorrectly accounted-for stellar limb darkening, can all imprint features that can be difficult to disentangle from the atmospheric signal.
Notwithstanding the complications, ground-based transmission spectroscopy has been used successfully to identify features attributed to absorption in planetary atmospheres. Simultaneous measurements of the target star and several comparison stars – a process similar to relative photometry (Bean et al. 2010; Gibson et al. 2013) – and the use of Gaussian processes have facilitated the robust modelling of systematics (Gibson et al. 2012b; Roberts et al. 2013; Rasmussen & Williams 2006), and the use of Bayesian inference methods has allowed for realistic uncertainty estimation that is crucial when assessing the true significance of the identified transmission spectrum features.
We report a ground-based transmission spectroscopy study of WASP-80b (Triaud et al. 2013). We have observed spectroscopic time series of two WASP-80b transits with the Optical System for Imaging and low-Intermediate-Resolution Integrated Spectroscopy (OSIRIS spectrograph; Sánchez et al. 2012) installed in the 10.4 m Gran Telescopio Canarias (GTC) on La Palma, Spain. The observations cover the spectral range from 520 to 910 nm, probing the planet atmosphere for a possible Rayleigh scattering signal in the blue end of the spectrum, and the visible-light extinction features of the K I and Na I resonance doublets at 767 nm and 589.4 nm, respectively.
WASP-80b (Triaud et al. 2013; Mancini et al. 2014; Fukui et al. 2014; Triaud et al. 2015, see also Table 1), a warm gas giant orbiting a bright (V = 11.87) late-K/early-M dwarf on a 3.07 d orbit, was identified as a promising target for transmission spectroscopy from its discovery. The planet has a low surface gravity (Mp = 0.56 MJup, Rp = 0.99 RJup, g = 14.34 m s-2, Mancini et al. 2014), and its large radius ratio leads to ~3% deep transits, which, combined with the brightness of its host star, enhance our abilities to detect any possible transmission spectrum features. WASP-80b is a warm gas giant with an equilibrium temperature of ~800 K (Triaud et al. 2013; Mancini et al. 2014). This very likely places the planet into the pL class (no temperature inversion) in the classification by Fortney et al. (2008). The main spectroscopic features in the visible passband for pL class planets are expected to be from Rayleigh scattering and K I and Na I resonance doublet absorption, of which K I absorption detection was recently claimed by Sedaghati et al. (2017) based on transmission spectroscopy analysis carried out with the FORS2 spectrograph installed in the VLT.
Identifiers for WASP-80 with its coordinates and magnitudes (SIMBAD, retrieved 2017-07-04).
Our study consists of two main analyses: a joint analysis of 27 previously published broadband transit light curves observed in seven passbands (broadband dataset), and a joint analysis of the two GTC-observed spectroscopic transit time series (transmission spectroscopy dataset). Both consist of a set of analyses with different prior assumptions and modelling approaches carried out to ensure the robustness of the final results.
The broadband dataset analysis is carried out to obtain improved estimates for the planet’s broadband radius ratios, orbital parameters, and stellar density (system parameters). The marginal parameter posteriors from the broadband dataset analysis are then used as priors in the GTC-data analysis. The GTC transmission spectroscopy starts with a direct-modelling analysis with a flexible Gaussian-process-based systematics model to further constrain the system parameters, and the final transmission spectroscopy uses a divide-by-white approach with either a parametric or nonparametric residual systematics model.
This paper is roughly divided into three sections. We outline the numerical methods and the generic equations for the calculation of posterior probability densities in Sect. 2. We continue in Sect. 3 by carrying out a detailed joint modelling of three previously observed broadband datasets described in Triaud et al. (2013), Mancini et al. (2014), and Fukui et al. (2014). The datasets cover 27 transit light curves observed in g′, r′, i′, I, z′, J, H, and K. We describe the GTC observations and data reduction in Sect. 4 , detail the analysis in Sect. 5, present the transmission spectroscopy results in Sect. 6, and discuss the results in Sect. 7. Finally, we conclude the paper in Sect. 8.
The raw data are publicly available from Zenodo and the GTC data archive, and the whole analysis with reduced data is available from GitHub1 as an easy-to-follow set of IPython notebooks and Python codes to help with the reproducibility of the study.
2. Numerical methods and theory
2.1. Overview
We use a fully Bayesian approach to transmission spectroscopy: our parameter estimates are based on the marginal posterior densities derived from a joint posterior density estimated with Markov chain Monte Carlo (MCMC) sampling, and the marginal parameter posteriors from the broadband dataset analysis are used as priors in the GTC transmission spectroscopy analysis.
Our datasets consist of light curves observed either photometrically, or constructed from spectroscopic observations. A light curve is modelled as a product of a baseline and transit model, where the combined model is parametrised with a parameter vector θ. When modelling multiple light curves jointly, the parameter vector is divided into parameters shared between all the light curves, passband-specific parameters shared between light curves observed in the same passband, observing-run-specific parameters, and light-curve-specific parameters. Especially, the parameters defining the planetary orbit (zero epoch, orbital period, impact parameter, and stellar density) are shared between all the light curves included in the analysis, and thus the likelihoods from all the light curves contribute to the parameter posteriors. The planet-star radius ratios and stellar limb-darkening coefficients are considered as passband-dependent, but observing-run-independent parameters (although this is not strictly true, since spots and plages, whether occulted or not, have an effect on the transit depths). That is, the light curves observed in a given passband all contribute to the radius ratio and limb-darkening posteriors for the passband. Finally, the parameters defining the baseline and noise properties are considered either observing-run-specific or light-curve-specific, that is, they depend both on the passband and observing run (this depends on the specific modelling approach, as detailed later).
Joint modelling leads to relatively high-dimensional models. The number of free parameters in the analyses presented here varies from 10 to ~250. However, the approach allows us to utilise the data fully. Simultaneous modelling of different observing runs reduces our sensitivity on systematics, and simultaneous multiband analysis reduces the degeneracies between the estimated radius ratios, orbital impact parameter, and stellar-limb darkening.
The parameter posteriors are estimated using a two-step process. First, a population-based global optimisation method (differential evolution implemented in PyDE) is used to obtain a parameter vector population that is clumped close to the global posterior maximum. The parameter vector population is then used to initialise the emcee MCMC sampler (Foreman-Mackey et al. 2013; Goodman & Weare 2010), which is used to create a sample of parameter vectors drawn from the model posterior (see the analysis-specific Sections for practical details).
The transit model uses the quadratic limb-darkening formalism by Mandel & Agol (2002), and is calculated using PyTransit (Parviainen & Aigrain 2015). PyTransit contains optimisations to compute a transit in multiple passbands with only a minor additional computational cost to the computation of a single passband transit, which reduces the computational burden due to the joint modelling approach.
The analyses have been carried out both with and without LDTk-based constraints on the stellar limb darkening. Quadratic limb darkening is parametrised using the parametrisation presented in Kipping (2013), which is aimed for efficient sampling of the physically allowed limb-darkening-coefficient space. When the limb darkening is not constrained, we marginalise over the whole limb-darkening-parameter space allowed by the data. When the limb darkening is constrained, it is done by fitting the observational data jointly with the limb-darkening profiles created using the LDTk-package (Parviainen et al. 2016), and by marginalising over the limb-darkening coefficients allowed by the stellar density profiles. LDTk uses phoenix-calculated stellar atmosphere library by Husser et al. (2013) to construct limb-darkening profiles with the uncertainties in the stellar properties propagated into the uncertainties in the limb-darkening profiles.
We also repeat the analyses for different systematics-modelling approaches, for separate subsets of data, and with synthetic mock data, and using the target star alone without dividing by the comparison star, to test the reliability of our approach.
Unless otherwise specified, the parameter point estimates correspond to posterior medians, and the uncertainties correspond to the central 68% posterior intervals. We do not plot point parameter estimates (these are listed in tables), but prefer to show either the posterior distributions or limits based on central posterior intervals.
The analyses rely on Python- and Fortran-based code utilising SciPy, NumPy (van der Walt et al. 2011), IPython (Perez & Granger 2007), Pandas (Mckinney 2010), matplotlib (Hunter 2007), seaborn2, PyFITS3, and F2PY (Peterson 2009). The transits were modelled with PyTransit4 (Parviainen & Aigrain 2015); the limb-darkening computations were carried out with LDTk5 (Parviainen et al. 2016); global optimisation was carried out with PyDE6; the MCMC sampling was carried out with emcee (Foreman-Mackey et al. 2013; Goodman & Weare 2010); and the Gaussian processes were computed using George7 (Ambikasaran et al. 2014).
2.2. Posteriors and likelihoods
The unnormalised log posterior density for a dataset consisting of nlc light curves observed in npb passbands is 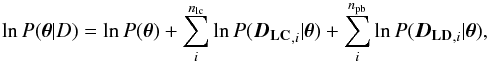 (1)where θ is the parameter vector encapsulating all the model parameters, lnP(θ) is the log prior, DLC are the light curves, lnP(DLC | θ) is the log likelihood for the photometry, DLD are the theoretical limb-darkening profiles calculated by LDTk, and lnP(DLD | θ) is the log likelihood for the limb-darkening profile.
(1)where θ is the parameter vector encapsulating all the model parameters, lnP(θ) is the log prior, DLC are the light curves, lnP(DLC | θ) is the log likelihood for the photometry, DLD are the theoretical limb-darkening profiles calculated by LDTk, and lnP(DLD | θ) is the log likelihood for the limb-darkening profile.
Assuming that the uncertainties (noise) in the observations are normally distributed, we can write the log likelihood for the data D in vector form as 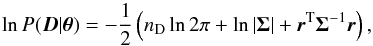 (2)where nD is the number of datapoints, r is the residual vector, and Σ is the covariance matrix. If the noise is white (uncorrelated), the covariance matrix is diagonal, and the likelihood can be written out explicitly in scalar form as
(2)where nD is the number of datapoints, r is the residual vector, and Σ is the covariance matrix. If the noise is white (uncorrelated), the covariance matrix is diagonal, and the likelihood can be written out explicitly in scalar form as 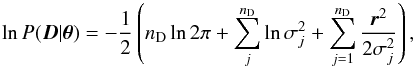 (3)where σj is the uncertainty of the jth datapoint. If the per-point uncertainty does not vary significantly, this equation can be simplified further into
(3)where σj is the uncertainty of the jth datapoint. If the per-point uncertainty does not vary significantly, this equation can be simplified further into 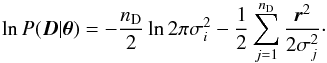 (4)If the noise (here used to describe the leftover variation not explained by the parametric transit and baseline models) is not white, the covariance matrix will have off-diagonal elements, and the matrix needs to be inverted for the likelihood evaluation. This is the case when the noise is presented as a Gaussian process (Rasmussen & Williams 2006; Gibson et al. 2012b; Roberts et al. 2013). The covariance matrix Σ in Eq. (2)is now
(4)If the noise (here used to describe the leftover variation not explained by the parametric transit and baseline models) is not white, the covariance matrix will have off-diagonal elements, and the matrix needs to be inverted for the likelihood evaluation. This is the case when the noise is presented as a Gaussian process (Rasmussen & Williams 2006; Gibson et al. 2012b; Roberts et al. 2013). The covariance matrix Σ in Eq. (2)is now 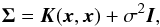 (5)where K(x,x) is defined by a covariance function (also known as a covariance kernel).
(5)where K(x,x) is defined by a covariance function (also known as a covariance kernel).
We describe the likelihood and covariance functions separately for the broadband dataset analysis and GTC transmission spectroscopy in Sects. 3 and 5, respectively, since the two analyses use slightly different modelling approaches.
3. Broadband dataset analysis
3.1. Overview
We estimate the posterior densities for the WASP-80b orbital parameters based on the three datasets observed by Mancini et al. (2014), Triaud et al. (2013), and Fukui et al. (2014), henceforth abbreviated to M14, T13, and F14, respectively.
The datasets contain 27 light curves (Fig. 4) observed in g′, r′, i′, I, z′, J, H, and K. We model all the light curves jointly, and, in contrast to Mancini et al. (2014), include the M14 GROND J, H, and K light curves. We also simplify the analysis slightly by merging the I and i′ passbands.
The analysis is carried out assuming either a parametric or nonparametric systematics model (white or red noise), constant or wavelength-dependent radius ratio, and with and without LDTk to constrain the stellar limb darkening, which leads to eight separate analysis sets defined in Table 2. The T13 and M14 datasets, as obtained from VizieR, were detrended by their original authors, and do not include information other than the observation time, flux, and error estimates. The F14 dataset was kindly provided by the author without detrending, and included all the auxiliary information (such as the airmass, and x- and y-centroid shifts for each exposure) used in the original analysis presented in Fukui et al. (2014).
Broadband analysis runs for the external datasets.
We used the T13 and M14 datasets for an initial modelling with a parametric systematics model and white additive noise, and include the F14 dataset in the final runs using a nonparametric systematics model. The nonparametric systematics model represents the systematics (and white noise) as a Gaussian process (GP) with time as the only covariate for the T13 and M14 datasets, and with time, airmass, x-shift, and y-shift as covariates for the F14 dataset. We do not marginalise over the GP hyperparameters in the broadband data analysis, but fix them to the values fitted from the white-noise run residuals.
As described in Sect. 2.1, the parameter estimation starts with a parameter vector population that fills the prior space uniformly. A differential evolution (DE) optimisation is used to clump the population close to the global posterior maximum (the number of DE iterations depending slightly on the run, but is usually close to 1000), after which MCMC sampling is carried out using emcee. The sampler is run for 10 000 iterations, which yields 12 000 independent posterior samples when using a population size of 150, thinning factor of 100, and burn-in period of 2000 iterations, where the thinning factor and burn-in period were chosen by studying the parameter chain populations and the average parameter autocorrelation lengths.
3.2. Log posterior and likelihoods
The log posterior for the combined broadband dataset given a parameter vector θ is 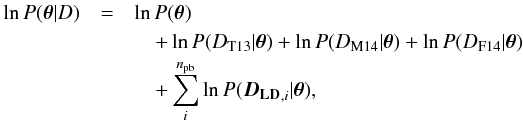 (6)where the first term is the log prior, followed by the per-dataset log likelihoods, and the last term is the sum of the LDTk-calculated log likelihoods for the limb-darkening coefficients for each passband.
(6)where the first term is the log prior, followed by the per-dataset log likelihoods, and the last term is the sum of the LDTk-calculated log likelihoods for the limb-darkening coefficients for each passband.
The exact form of the three likelihoods follows either Eqs. (2)or (4), depending on the chosen systematics model. The parametric (white noise) model assumes a constant average per-light-curve uncertainty (that is, the observation noise is the same for all the datapoints in a single light curve), and the kernels for the GP model are detailed below.
The light curve model consists of a product of a baseline function and a transit model with quadratic limb darkening calculated using PyTransit. The residual vector for a single light curve in Eq. (2)is 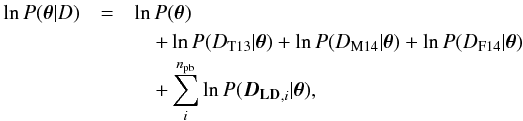 (7)where fo is the observed flux, fm the modelled flux, ℬ the baseline model,
(7)where fo is the observed flux, fm the modelled flux, ℬ the baseline model, 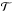 the transit model, X is a matrix containing the input parameters (covariates), t are the mid-exposure times, and θ is the model parameter vector.
the transit model, X is a matrix containing the input parameters (covariates), t are the mid-exposure times, and θ is the model parameter vector.
3.3. Gaussian process kernels
The T13 and M14 datasets do not include auxiliary information other than the mid-exposure times. Thus, we model the noise as a Gaussian process with time as the only covariate, the kernel being a sum of an exponential kernel and a white noise term ![\begin{equation} k = A_t \exp\left[ - \eta_t (t_i-t_j) \right] + \sigma^2 \delta_{ij}, \end{equation}](/articles/aa/full_html/2018/01/aa31113-17/aa31113-17-eq48.png) (8)where t are the time values, At is the GP output amplitude, ηt the inverse time scale, σ the average white noise standard deviation, and δ the Kronecker delta.
(8)where t are the time values, At is the GP output amplitude, ηt the inverse time scale, σ the average white noise standard deviation, and δ the Kronecker delta.
The F14 dataset also includes airmass, and per-observation x- and y-centroid estimates. This allows us to use a slightly more complex kernel, where we have an exponential time component, squared exponential airmass component, squared exponential PSF-centroid component, and a white noise term. The kernel becomes ![\begin{eqnarray} k &=& A_t \exp\left[-\eta_t (t_i-t_j) \right] \nonumber \\ &&\quad + A_a \exp\left[-\eta_a (a_i-a_j)^2 \right] \nonumber \\ &&\quad + A_{xy} \exp\left[-\eta_x (x_i-x_j)^2 -\eta_y (y_i-y_j)^2 \right] \nonumber\\ &&\quad + \sigma^2\delta_{ij}, \end{eqnarray}](/articles/aa/full_html/2018/01/aa31113-17/aa31113-17-eq54.png) (9)where t, a, x, and y are the time, airmass, x, and y estimates, respectively; At, Aa, Axy are the GP time, airmass and xy output amplitudes; and ηt, ηa, ηx, and ηy the time, airmass, x and y inverse time scales.
(9)where t, a, x, and y are the time, airmass, x, and y estimates, respectively; At, Aa, Axy are the GP time, airmass and xy output amplitudes; and ηt, ηa, ηx, and ηy the time, airmass, x and y inverse time scales.
3.4. Results
We adopt the ckrn_ldtk (passband-independent radius ratio, GP systematics, and limb darkening constrained using the LDTk) run as our final analysis, and report the stellar, orbital, and planetary parameter estimates in Tables 3 and 4. The posterior distributions are all close-to normal, as shown in Figs. 1 and 2. The parameter estimates agree with the previous WASP-80b studies.
The broadband transmission spectrum from the vkrn_ldtk run, shown in Fig. 2 is consistent with a flat line. The result agrees with a previous broadband transmission spectrum analysis by Triaud et al. (2015). We used the ExoTransmit transmission spectrum modelling package to test different atmosphere scenarios, but the precision in radius ratios is not sufficient to meaningfully distinguish between any of the physically plausible scenarios.
Marginal posterior medians from the external data broadband analysis (run ckrn_ldtk with systematics modelled using GPs, wavelength-independent radius ratio, and limb darkening constrained with LDTk).
Broadband radius ratio estimates and their uncertainties from the vkrn_ldtk run.
 |
Fig. 1 Marginal- and joint-posteriors for the radius ratio, stellar density, and impact parameter corresponding to the final ckrn_ldtk run. The 68% central interval is marked with a darker shade. |
 |
Fig. 2 Broadband radius ratio posteriors estimated by jointly modelling the three prior datasets. The results correspond to the final vkrn_ldtk run with red noise modelled using GPs and limb darkening constrained using LDTk. |
 |
Fig. 3 Broadband quadratic limb-darkening coefficient posteriors. The results correspond to the final ckrn runs with red noise modelled with GPs and limb darkening either unconstrained (left) or constrained using LDTk (right). |
The limb-darkening coefficient posteriors are plotted in Fig. 3, both with and without constraints from LDTk. The two versions agree with each other within uncertainties. The observed light curve, conditional model distribution (for the red noise model), and the residuals are shown in Fig. 4.
4. GTC observations and data reduction
4.1. Observations
We observed two WASP-80b transits simultaneously with one comparison star using the OSIRIS spectrograph installed in the GTC on the nights starting 16 July 2014 and 25 August 2014 (observing runs R1 and R2, respectively). The R1 observations carried from 23:30 UT until 3:41 UT and the R2 observations from 20:35 UT until 1:00 UT. The observing conditions were good, with a seeing of ~0.8′′ at the beginning of each night, and all the observations were carried out with an airmass smaller than 1.4.
OSIRIS (Cepa 1998) contains two Marconi CCD42-82 2048×4096 pixel CCDs, which were used in the standard 2×2 binning mode yielding a plate scale of 0.254′′. The observations were carried out using grism R1000R with a 40′′-wide custom-designed slit that aims to minimise the systematics related to variations in flux loss.
We chose TYC 5165-00235-1 as the comparison star, located at a distance of 6.9′ from WASP-80. The star has a similar V magnitude (V = 11.62), but is slightly redder (J = 8.376). The two stars were positioned equidistantly from the optical axis close to the centre of each CCD. The slit does not include other stars bright enough to be useful in the analysis.
The exposure time was 6 s for R1 and 5 s for R2. While the exposure time was short, it was long enough for the comparison star to saturate during the final parts of the WASP-80b ingress during R1. This was fixed by defocusing the instrument, but meant that the comparison star cannot be used in the reduction during this saturated period.
For R1, 81 flat fields were taken before the transit, and 66 bias frames after the transit. For R2, 100 flat fields were taken after the transit, and 15 bias frames before the transit. Three arc frames (Xe, HgAr, and Ne) for R1 were observed on 14 July and for R2 on the same night as the observations, after the transit.
 |
Fig. 4 The 27 broadband light curves observed by Triaud et al. (2013, T), Mancini et al. (2014, M), and Fukui et al. (2014, F) after the removal of the mean GP trend, the posterior model medians, and the residuals. |
4.2. Data reduction and passband sets
The passband-integrated light curves are produced from the raw data using the pipeline described in Chen et al. (2016, 2017). The pipeline carries out the basic CCD data-reduction steps, calculates a 2D wavelength solution, removes the sky, and generates a reduced 1D spectrum for WASP-80 and the comparison star (Fig. 5). The light curves are then generated by integrating the spectra multiplied by a transmission function defining the passband. We created four sets of passbands (datasets) listed in Table 5. The w dataset consists of a single light curve covering the whole usable spectrum (white light curve), the NB (narrow-band dataset) covers the whole usable spectrum in 20 nm-wide bins, and the na i and k i datasets cover the Na and K lines, respectively, in 6 nm-wide bins. The final white-light WASP-80 and reference star light curves with the relative light curve are shown in Fig. 6.
The white-light white noise estimates for R1 and R2 are 400 and 520 ppm, respectively. For the NB narrow-band dataset, the white noise level varies from 600 to 2100 ppm, with a median level of 720 and 870 ppm for R1 and R2, respectively. The difference in the white noise levels is expected due to the different exposure times used in R1 and R2 (6 and 5 s, respectively).
Passband sets extracted from the GTC spectroscopy.
4.3. Systematics
The relative light curves in Fig. 6 feature systematics not corrected by division by the comparison star. Further, the baseline is affected by a smooth trend that cannot be modelled by a simple parametric model as a function of time (or any of the simultaneously measured auxiliary variables). The trend causes a pre- and post-transit baseline difference of ~ 2% during run 1, and a ~ 1% difference during run 2. A similar, smooth, nearly linear variation as a function of the rotator angle accompanied by relatively smooth “bumps”, has been observed in previous OSIRIS transmission spectroscopy studies, and is likely caused by vignetting in the telescope pupil space (Nortmann et al. 2016).
Fortunately, the systematics are mainly common-mode, without significant variation across the spectrum. Common-mode systematics can be removed by either fitting the white-light light curves with a flexible GP, which can be used to create a common-mode systematics model, or by using a divide-by-white approach. After the common-mode correction, the residual wavelength-dependent systematics can be accounted for either with parametric or non-parametric approaches, both of which were used in our analyses.
5. GTC analysis
5.1. Overview
The GTC transmission spectroscopy covers the modelling of the white light curves and the three narrowband datasets described in Sect. 4.2. We used three modelling approaches:
-
dir: direct modelling with flexible GP-based systematics;
-
dww: divide-by-white with parametric systematics;
-
dwr: divide-by-white with GP-based systematics.
The first approach, direct modelling of the light curves with a flexible GP-based systematics model, was used to obtain a model for the common-mode systematics (from the white light curves), and to improve the system characterisation (from the full-spectrum 20 nm-wide dataset). The divide-by-white (DW) approaches were then used for transmission spectroscopy, with the direct-modelling posteriors used as priors on the wavelength-independent system parameters (the motivation for this is discussed later). The analyses were repeated with and without LDTk to assess how sensitive the results are to assumptions about limb darkening, and modelling the two nights separately and jointly, to test whether or not the results were consistent from night to night.
The parameter posteriors are estimated in a similar fashion to the prior data analysis in Sect. 3.1. Differential evolution is used to create a parameter vector population clumped around the global posterior maximum, which is used to initialise the emcee sampler. The sampler is run over 10 × 15000 iterations (that is, ten sets of 15000 iterations where each set is initialised from the final state of the previous set) with 600 chains and a thinning factor of 100, which gives us a final set of 75 000 independent posterior samples. The number of iterations, chains, and the thinning factor were chosen after studying the chain populations and per-parameter autocorrelation lengths.
Unlike in the broadband dataset analysis, we keep the GP hyperparameters free and marginalise over them. This slows down the sampling process, but yields more reliable posteriors, and allows us to study how well the GP kernels represent the systematics.
5.2. Modelling approaches
Direct model with GP systematics
The direct-modelling approach dir reproduces the light curves as a product of a baseline and a transit model directly. We model all the passbands jointly for both nights in a dataset, which leads to a slightly involved parameterisation, but aims to fully utilise the data. As mentioned earlier, the model parameters can be divided into four categories: a) passband- and baseline-independent parameters, b) achromatic per-night baseline parameters, c) chromatic per-light-curve parameters, and d) chromatic parameters that should remain constant between observation runs.
The direct model parametrisation and the parameter priors are listed in Table 6. Priors for the zero epoch, orbital period, impact parameter, and stellar density are based on the broadband dataset analysis posteriors (run ckrn_ldtk). The u and v limb-darkening coefficients correspond to the Kipping (2013) quadratic limb-darkening model parametrisation, where uniform priors from 0 to 1 lead to uninformative priors covering the physically viable values for the quadratic limb-darkening priors.
 |
Fig. 5 Normalised, sky-subtracted, and wavelength-calibrated spectra for WASP-80b (dark blue line) and the comparison star (orange line). |
 |
Fig. 6 White-light light curves for the comparison star (top), WASP-80 (middle), and the relative light curve (bottom) for both observing runs. A small number of clear outliers have been omitted for clarity. |
The GP hyperparameters can be chosen to be night- or light-curve-dependent, but we choose to keep them independent for practical reasons. Our approach adds three GP hyperparameters to the analysis, and requires two covariance matrix inversions per posterior evaluation (one per night). Making the GP hyperparameters light-curve-dependent would add three free parameters to the model for each light curve, and require a covariance matrix inversion for each light curve, which would make marginalisation over the GP hyperparameters costly. Making the GP hyperparameters night-dependent would be feasible, since the approach would add only three more parameters to the model, and would not require additional covariance matrix inversions. However, our analyses for separate nights result in compatible GP hyperparameter posteriors, and we choose the simplest approach.
Model parametrisations and priors.
The direct model represents each light curve as a Gaussian process 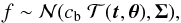 (10)where cb is a baseline constant,
(10)where cb is a baseline constant, 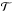 is the transit model, and Σ is the covariance matrix. We use airmass x, and telescope rotator angle, α, as GP input parameters (covariates), with a covariance matrix defined as the sum of a linear kernel and squared-exponential kernel,
is the transit model, and Σ is the covariance matrix. We use airmass x, and telescope rotator angle, α, as GP input parameters (covariates), with a covariance matrix defined as the sum of a linear kernel and squared-exponential kernel, 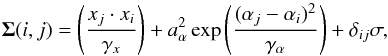 (11)where aα is an output scale parameter, γx and γα are the input scale parameters, and σ is the average white noise. Any residual airmass-dependent systematics should be approximately linear, and can be modelled with a linear kernel, while the possible chromatic rotator-angle dependencies are expected to be smooth, and well-modelled by a squared-exponential kernel.
(11)where aα is an output scale parameter, γx and γα are the input scale parameters, and σ is the average white noise. Any residual airmass-dependent systematics should be approximately linear, and can be modelled with a linear kernel, while the possible chromatic rotator-angle dependencies are expected to be smooth, and well-modelled by a squared-exponential kernel.
 |
Fig. 7 NB light curves for both observing runs and the dir approach posterior median model (black line) as a function of the phase. Passband centres are marked in nanometres. |
We also tested a GP with time as a covariate (with a Matern kernel), but it did not affect the posteriors significantly. Also, the power spectral density (PSD) of the residuals with the transit and the two-covariate GP mean removed is approximately constant, which suggests that the noise is white after the residual airmass and rotator-angle dependencies are accounted for.
The white noise level does not vary significantly from passband to passband in our datasets, and we choose to use a single average white noise estimate for an observing run (again, so that we do not need to invert the covariance matrix separately for each light curve). The white noise estimate is an average of the estimates calculated separately for each light curve, which are calculated as 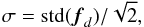 (12)wherefd = fi−fi−1. That is, we estimate the white noise from the standard deviation of the light curve differentials.
(12)wherefd = fi−fi−1. That is, we estimate the white noise from the standard deviation of the light curve differentials.
The radius ratios and limb-darkening coefficients yield three free parameters per passband, and the baseline constant yields a further free parameter per light curve. In total, the number of free parameters for a direct model reaches 108 for the 20-nm run with 20 passbands. The computations can still be carried out with a modern laptop in a matter of hours8 for a single analysis9, but tests must be carried out to ensure that the final posterior sample gives a reliable representation of the true posterior distribution.
Divide-by-white model with and without GP systematics
The divide-by-white (DW) approach10 allows us to remove any common-mode systematics from the dataset with the cost of increased per-passband white noise. The residual vector r in Eq. (2)for the DW approach is 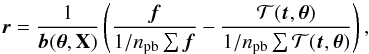 (13)where f is the observed flux vector, 𝒯 is the transit model, and b is the residual baseline model. That is, we divide both the observed and modelled fluxes by the values averaged over all the passbands in the dataset.
(13)where f is the observed flux vector, 𝒯 is the transit model, and b is the residual baseline model. That is, we divide both the observed and modelled fluxes by the values averaged over all the passbands in the dataset.
The DW approach does not only remove the common-mode systematics, but all colour-independent signals. Effectively, the signals left in the data are due to colour-dependent systematics, changes in the radius ratio, and changes in stellar-limb darkening. The system parameters, such as the orbital period and impact parameter, are poorly constrained, so we set informative priors based on the nb_ldtk direct-model analysis on them. The average radius ratio is not well constrained either, so we set a prior on the median radius ratio based on the broadband dataset analysis. We use median instead of mean to ensure that the prior does not affect the scaling of the transmission spectrum, as using mean would.
We repeat the DW analysis using first a parametric baseline model (dww approach), and then a more flexible Gaussian process-based baseline model (dwr approach). The parametric model represents the baseline for each light curve as a linear function of time and airmass 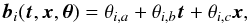 (14)where θi,a, θi,b, and θi,b are the light curve specific baseline constant, linear time coefficient and linear airmass coefficient, respectively. The residual noise is considered white, which makes the approach significantly faster than using GPs, but yields three free parameters per light curve to the model.
(14)where θi,a, θi,b, and θi,b are the light curve specific baseline constant, linear time coefficient and linear airmass coefficient, respectively. The residual noise is considered white, which makes the approach significantly faster than using GPs, but yields three free parameters per light curve to the model.
The dwr analysis uses the same GP kernel as the dir approach, changing only the GP mean function to the one in Eq. (13).
6. Results
6.1. System characterisation
The direct-modelling dir runs were used to improve the system characterisation from the broadband dataset analysis, and yield the final WASP-80b parameter estimates listed in Table 7. The estimates correspond to the full-spectrum narrow-band dataset (NB) with LDTk. The narrow-band run was preferred over the white-light run since the colour information allows us to mitigate the degeneracy between the average impact parameter, radius ratio, and limb darkening, leading to improved posterior estimates.
Results from the final GTC characterisation run (nb_12_ldtk with systematics modelled using GPs, wavelength-dependent radius ratio, and limb darkening constrained with LDTk).
6.2. Transmission spectroscopy
We show the transmission spectra for the NB, k i, and na i datasets in Fig. 8. These results correspond to the joint dwr run with a GP systematics model and limb-darkening coefficients constrainted by LDTk. The figures show the central 68% and 99% radius ratio posterior intervals, and the point estimates are listed in Table 8.
Passband centres, ranges, and radius-ratio estimates for the three narrow-band datasets from the final dwr approach.
Comparison of the results from the two different divide-by-white approaches can be found below in Sect. 7.3, and a comparison of the results obtained using only the light curves from one of the two can be found in Sect. 7.4. We do not show the results for the analysis without LDTk. Unconstrained limb darkening does not have a significant effect on the radius ratio posterior medians, but does increase the posterior width significantly due to the strong degeneracy caused by the DW approach.
 |
Fig. 8 Transmission spectra for the NB dataset with 20 passbands spanning from 520 nm to 920 nm (top), the na i set covering the Na I doublet (bottom left), and the k i dataset covering the K I double (bottom right). The inner boxes correspond to the central 68% posterior intervals, the outer boxes to the central 99% posterior intervals, and Na I and K I lines are marked as black lines. The light grey line shows an Exo-Transmit spectrum with Na and K described in Sect. 7.2, the black dots show the Exo-Transmit spectrum binned to the dataset binning, and the slashed horizontal line shows the transmission spectrum mean. |
7. Discussion
7.1. Flat transmission spectrum
We adopt the results from the more conservative approach, dwr, as the final results of the analysis. All the spectra in Fig. 8 are flat within uncertainties, in agreement with the broadband analysis, and the broadband transmission spectroscopy carried out by Triaud et al. (2015).The NB features a single strongly deviating passband centred at 807 nm, with a significantly smaller radius ratio than the average. The passband is likely affected by instrumental observation-geometry-dependent systematics (the deviation is evident in both observing runs, albeit slightly different), and we discuss it in more detail in Sect. 7.5.
The flat transmission spectrum allows us to rule out strong Rayleigh scattering or Na I or K I absorption in WASP-80b’s atmosphere, but does not justify detailed atmospheric modelling. However, basic modelling with Exo-Transmit (Kempton et al. 2017) strongly favours a flat spectrum over a spectrum from an atmosphere with 0.1 or 1 solar metallicity and K and Na: a likelihood ratio test between the Exo-Transmit spectra and a flat spectrum favours the flat model with likelihood ratios around 1000–5000. (We fit the model spectra to the estimated spectrum with a free scaling factor, and the flat spectrum is the mean of the estimated spectrum.) Figure 8 includes an Exo-Transmit spectrum with K and Na calculated assuming Solar metallicity, gas-phase chemistry, Teq = 800 K, log g = 3.18, R⋆ = 0.57 R⊙, and k = 0.17 as an example.
The dwr approach was chosen over dww because the dww results show greater discrepancies in the spectra estimated from R1 and R2 separately, as discussed below. It is likely that the parametric systematics model is not flexible enough, and the unaccounted-for systematics lead to biases in the radius ratio values. The GP kernel in the dwr approach is flexible enough to marginalise over the systematics, and still allows for a reliable radius ratio estimation (tested with two mock datasets discussed in Sect. 7.6).
7.2. Comparison with the previous K I detection
Sedaghati et al. (2017) reported of a detection of strong K I absorption in WASP-80b’s atmosphere based on transmission spectroscopy with the FORS2 spectrograph. Our results disagree with the reported K I detection, as shown in Fig. 9, but agree with the redmost part of their spectrum.
Both of our divide-by-white approaches are consistent with each other, as are the transmission spectra estimated separately from the two observing runs (as discussed below in Sects. 7.3 and 7.4), which leads us to believe that the strong K I signal reported by Sedaghati et al. (2017) is due to systematics, even though the analysis described in their paper seems rigorous in all standards.
 |
Fig. 9 Comparison between the results from the GTC analysis and the results presented by Sedaghati et al. (2017). |
 |
Fig. 10 Radius ratio posterior distributions approximated as normal distributions for the NB DWW (left) and DWR (right) runs. |
 |
Fig. 11 Radius ratio posterior distributions approximated as normal distributions for the Na DWW (left) and DWR (right) runs. |
7.3. Comparison of modelling approaches
The two divide-by-white approaches differ in their way of modelling the systematics. The dww approach models the systematics with parametric model as a combination of linear functions of time and airmass, and assumes that everything else is white normally distributed noise, while the dwr approach models the systematics as a Gaussian process. In the dww case all systematics not corrected by the division by the dataset average light curve or modelled by the parametric model may cause biases in the radius ratio estimates. The GP kernel in the dwr case is relatively flexible, even when we impose a linear relation on airmass, and should yield less bias-prone radius ratio estimates. This is true especially since we’re integrating over the GP hyperparameters, and do not significantly constrain them with priors11.
We compare the transmission spectra obtained with dww and dwr approaches in Figs. 10–12. The differences are small for the Na and K analyses, which can be expected due to the small wavelength range covered by the datasets. However, the NB set analysed with dww approach features a Rayleigh-like signal in the bluemost passbands that is not visible in the dwr results. When analysing the two nights separately (Sect. 7.4), we can see that the Rayleigh-like signal arises from the second night, and is not significant in the first night. However, the first night shows an increasing trend towards the red end of the spectrum, not visible in the second night spectrum.
In theory, the varying Rayleigh-like slope could be interpreted as variations in stellar activity. However, a more likely explanation is residual wavelength-dependent systematics not accounted for properly by the parametric model.
 |
Fig. 12 Radius ratio posterior distributions approximated as normal distributions for the K DWW (left) and DWR (right) runs. |
7.4. Comparison of individual nights
We show the transmission spectra estimated separately from run 1 or run 2 either with the dww or dwr approach in Figs. 13−15. The results from the different nights agree with some exceptions. Both the blue and red ends of the dww NB spectrum differ systematically, as mentioned earlier. The Rayleigh-like signal visible in the dww model originates clearly only from R2, while the corresponding passbands are close or below the mean level for R1. However the three redmost passbands are well above the mean level for R1, while R2 shows a flat spectrum in the red. These differences disappear in the dwr analysis, where both runs give compatible flat-within-uncertainties spectra.
 |
Fig. 13 Radius ratio posterior distributions approximated as normal distributions for the NB dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
 |
Fig. 14 Radius ratio posterior distributions approximated as normal distributions for the na i dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
 |
Fig. 15 Radius ratio posterior distributions approximated as normal distributions for the k i dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
7.5. Outlier passband at 807 nm
A single passband centred at 807 nm in the NB dataset transmission spectrum deviates from the mean. This signal is visible on both nights, and a detailed analysis shows that the feature is smooth, but somewhat different from one night to the next. We could not trace the source of the feature, but can only speculate.
First, the feature is very unlikely of astrophysical origin. Certain astrophysical phenomena, such as non-transited star spots and flares, can affect the radius ratio estimates, but the feature would require a bright narrow-band source.
Second, the feature is not caused by the comparison star. We repeated the DW NB analyses using absolute photometry without dividing with the comparison star (practical since the divide-by-white approach removes the common-mode systematics), but this did not affect the feature.
7.6. Mock dataset analysis
We also carry out sensitivity (reality) checks by using two mock datasets based on the NB dataset. We calculate synthethic light curves using the observed time stamps and the system parameter posterior medians from the direct modelling. The radius ratios follow a saw-tooth-like pattern for the mock dataset 1, and a transmission spectrum calculated by Exo-Transmit for the mock dataset 2, and the limb-darkening coefficients are based on the theoretical values calculated using LDTk. The baselines are modelled as sums of a linear time trend and a linear airmass trend with normally distributed random coefficients, and we add normally distributed white noise with standard deviation corresponding to the true light curve standard deviation estimates.
The radius ratio posterior densities from the mock dataset analyses agree with the true radius ratios for both DW approaches.
8. Conclusions
We have carried out a transmission spectroscopy analysis for WASP-80b using two OSIRIS-observed spectroscopic time series, and a joint analysis of 27 previously observed broadband light curves to provide reliable parameter priors for the transmission spectroscopy analysis.
The OSIRIS data feature strong common-mode systematics, but these can be removed using either a divide-by-white (DW) approach or initial white-light GP modelling. We chose the divide-by-white approach, (or, more accurately, divide-by-dataset-average) which increases the per-passband white noise levels, but removes any systematics-model dependencies from the common-mode systematics removal.
The transmission spectroscopy analyses were repeated modelling both datasets jointly and separately, with or without LDTk-constructed stellar limb-darkening priors, and using either a parametric or nonparametric (GP-based) systematics model. We chose the most conservative approach as the final analysis detailed in this paper: a DW approach accompanied with a flexible Gaussian process systematics model where the GP hyperparameters are marginalised over in the posterior sampling process. This was motivated by significant nightly variations in the transmission spectrum obtained using the parametric systematics model.
Despite the nightly variations in the dww analysis, the joint analyses are consistent with each other: the transmission spectrum is flat within uncertainties. Furthermore, we do not detect significant Na or K absorption, and, our results do not agree with the detection of K by Sedaghati et al. (2017).
The absence of significant features does not justify detailed atmospheric modelling. However, basic Exo-Transmit modelling favours a truly flat spectrum over atmosphere models with stellar or sub-stellar metallicity and K and Na.
Ground-based observations are prone to complex systematics, and transmission spectroscopy is carried out at the limits of what the instruments are capable of, or were designed for. The most robust approach for ground-based transmission spectroscopy should try to account for this by repeating the observations several times, preferably with different instruments covering the same wavelength range. Repeated observations improve not only the final precision that can be reached, but also our
capability to decouple the systematics from the minute transit depth variations.
Freely available from https://github.com/hpparvi/PyTransit
Available from https://github.com/hpparvi/ldtk
Available from https://github.com/hpparvi/PyDE
Available from https://dan.iel.fm/george
Acknowledgments
We thank the anonymous referee for their constructive and useful comments. H.P. has received support from the Leverhulme Research Project grant RPG-2012-661. F.M. acknowledges the support of the French Agence Nationale de la Recherche (ANR), under the program ANR-12-BS05-0012 Exo-atmos. The work has been supported by the Spanish MINECO grants ESP2013-48391-C4-2-R and ESP2014-57495-C2-1-R. G.C. acknowledges the support by the National Natural Science Foundation of China (Grant No. 11503088) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20151051). Based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. The authors wish to acknowledge the contribution of Teide High-Performance Computing facilities to the results of this research. TeideHPC facilities are provided by the Instituto Tecnológico y de Energías Renovables (ITER, SA). The authors wish to acknowledge the contribution of Glamdring computing cluster in the Subdepartment of Astrophysics, Department of Physics, University of Oxford, to the results of this research.
References
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2014, [Google Scholar]
- Ballerini, P., Micela, G., Lanza, A. F., & Pagano, I. 2012, A&A, 539, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bean, J. L., Kempton, E. M.-R., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Cepa, J. 1998, Ap&SS, 263, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., Palle, E., Murgas, F., et al. 2016, A&A, submitted [Google Scholar]
- Chen, G., Guenther, E. W., Palle, E., et al. 2017, A&A, 600, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, A., Kawashima, Y., Ikoma, M., et al. 2014, ApJ, 790, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N., Aigrain, S., Pont, F., et al. 2012a, MNRAS, 422, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Roberts, S., et al. 2012b, MNRAS, 419, 2683 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Barstow, J. K., et al. 2013, MNRAS, 428, 3680 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Engin., 9, 90 [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kempton, E. M.-R., Lupu, R., Owusu-Asare, A., Slough, P., & Cale, B. 2017, PASP, 129, 044402 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2014, A&A, 562, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mckinney, W. 2010, in Proceedings of the 9th Python in Science, 51 [Google Scholar]
- Nortmann, L., Palle, E., Murgas, F., et al. 2016, A&A, 594, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oshagh, M., Santos, N. C., Ehrenreich, D., et al. 2014, A&A, 568, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
- Parviainen, H., Pallé, E., Nortmann, L., et al. 2016, A&A, 585, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perez, F., & Granger, B. 2007, Comput. Sci. Engin., 9, 21 [Google Scholar]
- Peterson, P. 2009, Int. J. Comput. Sci. Engin., 4, 296 [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. 2006, Gaussian Processes for Machine Learning (The MIT Press) [Google Scholar]
- Roberts, S., Osborne, M., Ebden, M., et al. 2013, Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 371, 20110550 [Google Scholar]
- Sánchez, B., Aguiar-González, M., Barreto, R., et al. 2012, in Proc. SPIE, 8446, 84464T [Google Scholar]
- Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Sedaghati, E., Boffin, H. M. J., Delrez, L., et al. 2017, MNRAS, 468, 3123 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Désert, J.-M., Fortney, J. J., et al. 2011, A&A, 527, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Anderson, D. R., Collier Cameron, A., et al. 2013, A&A, 551, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Gillon, M., Ehrenreich, D., et al. 2015, MNRAS, 450, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Engin., 13, 22 [Google Scholar]
Appendix A: DW model fit and residuals
Figures A.1 and A.2 show the dwr analysis model fit and residuals, respectively.
 |
Fig. A.1 NB light curves for both observing runs and the dwr approach posterior median model (black line) as a function of the phase. Passband centres are marked in nanometres. |
 |
Fig. A.2 NB residuals from the dwr analysis. Passband centres are marked in nanometres. |
All Tables
Identifiers for WASP-80 with its coordinates and magnitudes (SIMBAD, retrieved 2017-07-04).
Marginal posterior medians from the external data broadband analysis (run ckrn_ldtk with systematics modelled using GPs, wavelength-independent radius ratio, and limb darkening constrained with LDTk).
Results from the final GTC characterisation run (nb_12_ldtk with systematics modelled using GPs, wavelength-dependent radius ratio, and limb darkening constrained with LDTk).
Passband centres, ranges, and radius-ratio estimates for the three narrow-band datasets from the final dwr approach.
All Figures
 |
Fig. 1 Marginal- and joint-posteriors for the radius ratio, stellar density, and impact parameter corresponding to the final ckrn_ldtk run. The 68% central interval is marked with a darker shade. |
| In the text | |
 |
Fig. 2 Broadband radius ratio posteriors estimated by jointly modelling the three prior datasets. The results correspond to the final vkrn_ldtk run with red noise modelled using GPs and limb darkening constrained using LDTk. |
| In the text | |
 |
Fig. 3 Broadband quadratic limb-darkening coefficient posteriors. The results correspond to the final ckrn runs with red noise modelled with GPs and limb darkening either unconstrained (left) or constrained using LDTk (right). |
| In the text | |
 |
Fig. 4 The 27 broadband light curves observed by Triaud et al. (2013, T), Mancini et al. (2014, M), and Fukui et al. (2014, F) after the removal of the mean GP trend, the posterior model medians, and the residuals. |
| In the text | |
 |
Fig. 5 Normalised, sky-subtracted, and wavelength-calibrated spectra for WASP-80b (dark blue line) and the comparison star (orange line). |
| In the text | |
 |
Fig. 6 White-light light curves for the comparison star (top), WASP-80 (middle), and the relative light curve (bottom) for both observing runs. A small number of clear outliers have been omitted for clarity. |
| In the text | |
 |
Fig. 7 NB light curves for both observing runs and the dir approach posterior median model (black line) as a function of the phase. Passband centres are marked in nanometres. |
| In the text | |
 |
Fig. 8 Transmission spectra for the NB dataset with 20 passbands spanning from 520 nm to 920 nm (top), the na i set covering the Na I doublet (bottom left), and the k i dataset covering the K I double (bottom right). The inner boxes correspond to the central 68% posterior intervals, the outer boxes to the central 99% posterior intervals, and Na I and K I lines are marked as black lines. The light grey line shows an Exo-Transmit spectrum with Na and K described in Sect. 7.2, the black dots show the Exo-Transmit spectrum binned to the dataset binning, and the slashed horizontal line shows the transmission spectrum mean. |
| In the text | |
 |
Fig. 9 Comparison between the results from the GTC analysis and the results presented by Sedaghati et al. (2017). |
| In the text | |
 |
Fig. 10 Radius ratio posterior distributions approximated as normal distributions for the NB DWW (left) and DWR (right) runs. |
| In the text | |
 |
Fig. 11 Radius ratio posterior distributions approximated as normal distributions for the Na DWW (left) and DWR (right) runs. |
| In the text | |
 |
Fig. 12 Radius ratio posterior distributions approximated as normal distributions for the K DWW (left) and DWR (right) runs. |
| In the text | |
 |
Fig. 13 Radius ratio posterior distributions approximated as normal distributions for the NB dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
| In the text | |
 |
Fig. 14 Radius ratio posterior distributions approximated as normal distributions for the na i dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
| In the text | |
 |
Fig. 15 Radius ratio posterior distributions approximated as normal distributions for the k i dww (up) and dwr (below) runs using only the data from night 1 (left) or night 2 (right). |
| In the text | |
 |
Fig. A.1 NB light curves for both observing runs and the dwr approach posterior median model (black line) as a function of the phase. Passband centres are marked in nanometres. |
| In the text | |
 |
Fig. A.2 NB residuals from the dwr analysis. Passband centres are marked in nanometres. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


