| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | C2 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526463e | |
| Published online | 05 February 2018 | |
The growth of planets by pebble accretion in evolving protoplanetary discs (Corrigendum)
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University, 22100 Lund, Sweden
e-mail: bert@astro.lu.se
Key words: accretion, accretion disks / planets and satellites: formation / protoplanetary disks / planet-disk interactions / errata, addenda
1. Introduction
In the planet formation simulations presented in Bitsch et al. (2015b) a programming error led to an overestimate of the column density of pebbles. Correcting this error results in pebble column densities <0.1 g cm-2 at 10 AU after 1 Myr of protoplanetary disc evolution – significantly lower than observed pebble column densities in protoplanetary discs. As a consequence, the pebble accretion rates of growing protoplanets are lowered significantly. We demonstrate here how a revised model for the formation of pebbles in protoplanetary discs produces pebble surface densities more consistent with observations. The revised model assumes that the outer regions of protoplanetary discs are not depleted by mass accretion onto the star, which results in a significant increase in the pebble flux through the inner disc. Using this model, the conclusions of Bitsch et al. (2015b) remain unchanged: pebble accretion accelerates the growth of cores in the outer disc to out-compete planetary migration, yielding final orbits that are consistent with cold gas giants in the solar system as well as in exoplanetary systems.
2. Pebble accretion and drift-limited pebble growth
The growth of planetary embryos can be greatly accelerated through the process of pebble accretion (Johansen & Lacerda 2010; Ormel & Klahr 2010; Lambrechts & Johansen 2012; Morbidelli & Nesvorny 2012; Johansen & Lambrechts 2017). The growth rate of protoplanets that accrete in the 2D Hill regime depends on the pebble surface density Σp at the planet’s location of the protoplanetary disc, 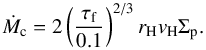 (1)Here rH denotes the planetary Hill radius, vH the Hill speed at which the particles enter (given by vH = rHΩK) and τf is the Stokes number of the pebbles. In the drift-limited approach to pebble growth (Birnstiel et al. 2012), the pebble surface density depends on the pebble flux Ṁpeb (Lambrechts & Johansen 2014) in the following way
(1)Here rH denotes the planetary Hill radius, vH the Hill speed at which the particles enter (given by vH = rHΩK) and τf is the Stokes number of the pebbles. In the drift-limited approach to pebble growth (Birnstiel et al. 2012), the pebble surface density depends on the pebble flux Ṁpeb (Lambrechts & Johansen 2014) in the following way 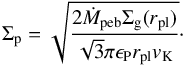 (2)The pebble sticking efficiency can be taken as ϵP = 0.5 under the assumption of near-perfect sticking (Lambrechts & Johansen 2014). The parameter Σg(rpl) denotes the gas surface density at the planet’s location rpl and vK is the Keplerian speed at the planet’s location. The pebble flux can be calculated through the expression
(2)The pebble sticking efficiency can be taken as ϵP = 0.5 under the assumption of near-perfect sticking (Lambrechts & Johansen 2014). The parameter Σg(rpl) denotes the gas surface density at the planet’s location rpl and vK is the Keplerian speed at the planet’s location. The pebble flux can be calculated through the expression 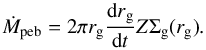 (3)Here, rg marks the orbital distance at which dust particles have just grown to pebble size and start drifting inwards and Σg(rg) denotes the gas surface density at the location of the pebble production line. The quantity Z denotes the fraction of solids (metallicity) in the disc that can be transformed into pebbles at the pebble production line rg at time t. Lambrechts & Johansen (2014) derived the time-dependent radial location of the pebble production line as
(3)Here, rg marks the orbital distance at which dust particles have just grown to pebble size and start drifting inwards and Σg(rg) denotes the gas surface density at the location of the pebble production line. The quantity Z denotes the fraction of solids (metallicity) in the disc that can be transformed into pebbles at the pebble production line rg at time t. Lambrechts & Johansen (2014) derived the time-dependent radial location of the pebble production line as 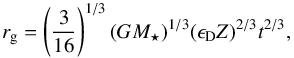 (4)and thus
(4)and thus 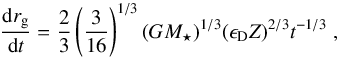 (5)where M⋆ is the stellar mass, which we set to 1 M⊙, G is the gravitational constant and ϵD = 0.05 is related to the logarithmic growth range from dust to pebble sizes.
(5)where M⋆ is the stellar mass, which we set to 1 M⊙, G is the gravitational constant and ϵD = 0.05 is related to the logarithmic growth range from dust to pebble sizes.
In Fig. 1 we show the pebble flux Ṁpeb as a function of time for the protoplanetary disc evolution model used in Bitsch et al. (2015b) and Bitsch & Johansen (2016).
 |
Fig. 1 Pebble flux Ṁpeb as a function of time using the time-dependent protoplanetary disc evolution model (solid red line) and for a protoplanetary disc evolution model where the outer gas disc does not evolve in time (dotted red line). In blue we show constant pebble fluxes of 45 ME/Myr (solid line) and 270 ME/Myr (dotted line). In principle, a pebble flux of 45 ME/Myr is large enough to grow a planet from 5 to 10 ME in 1 Myr, but the migration timescale is a factor of a few shorter than that, indicating that planet would be lost to the central star. Higher pebble fluxes of ≈270 ME/Myr allow growth fast enough to reach the pebble isolation mass and thus allow gas accretion and the transition to type-II migration before type-I migration drives the planet all the way to the central star. Our revised disc evolution model is able to reproduce these high pebble fluxes (dotted red line). |
In Bitsch et al. (2015b), we mistakenly overestimated the pebble flux in Eq. (3), due to a programming error (Brügger and Alibert (Uni Bern), priv. comm.). Correcting this error, we obtain very low pebble growth rates through Eq. (1). Planetary embryos are therefore no longer able to grow fast enough to compete with planetary migration.
Using a simple power law disc with the following parameters 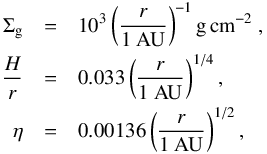 (6)where η denotes the pressure gradient parameter of the disc given by
(6)where η denotes the pressure gradient parameter of the disc given by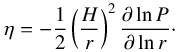 (7)In this expression, P is the pressure in the protoplanetary disc and H/r the local aspect ratio in the disc. We used a surface density power law of − 1, because this roughly corresponds to the surface density profile in the outer parts of accreting protoplanetary discs dominated by stellar irradition (Bitsch et al. 2015a). Using these parameters, we can define the filtering factor f, which relates the mass flux of pebbles directly to the growth rate due to pebble accretion (Lambrechts & Johansen 2014) as
(7)In this expression, P is the pressure in the protoplanetary disc and H/r the local aspect ratio in the disc. We used a surface density power law of − 1, because this roughly corresponds to the surface density profile in the outer parts of accreting protoplanetary discs dominated by stellar irradition (Bitsch et al. 2015a). Using these parameters, we can define the filtering factor f, which relates the mass flux of pebbles directly to the growth rate due to pebble accretion (Lambrechts & Johansen 2014) as 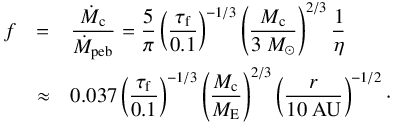 (8)With the filtering factor we can define the growth timescale
(8)With the filtering factor we can define the growth timescale 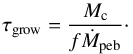 (9)A planetary core of five Earth masses at 10 AU accreting pebbles with Stokes number τf = 0.1 has a filtering efficiency of ≈11%, implying that a pebble mass flux of Ṁpeb = 45ME/Myr is sufficient for the planet to grow to ten Earth masses within 1 Myr. However, in our disc evolution model, the pebble flux drops beneath this threshold after 1.5 Myr (Fig. 1), prolonging the growth timescale (Eq. (9)).
(9)A planetary core of five Earth masses at 10 AU accreting pebbles with Stokes number τf = 0.1 has a filtering efficiency of ≈11%, implying that a pebble mass flux of Ṁpeb = 45ME/Myr is sufficient for the planet to grow to ten Earth masses within 1 Myr. However, in our disc evolution model, the pebble flux drops beneath this threshold after 1.5 Myr (Fig. 1), prolonging the growth timescale (Eq. (9)).
More crucially, the planet migrates inwards in type-I migration. We find for migration timescale τmig (Tanaka et al. 2002) with the scalings of our disc model (Eq. (6)) 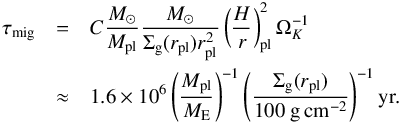 (10)Here, C is a constant depending on the disc profile, which is ≈0.308 for our disc profile and (H/r)pl denotes the aspect ratio of the disc at the planet’s location. For the same five Earth mass planet at 10 AU in our disc, the migration timescale is ≈315 kyr, a factor of three shorter than the time for this planet to double its mass with a pebble flux of 45 ME/Myr. This indicates that planets forming in discs with such low pebble fluxes will migrate to the central star before they can reach the pebble isolation mass. At pebble isolation mass, the planet generates a pressure bump outside of it is orbit, accelerating the azimuthal gas velocity to super-Keplerian speeds which prevent the inward drift of pebbles due to a reversed gas drag force (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014). The planetary atmosphere is then not heated by in-falling pebbles any more and the planet can start to accrete gas and eventually become a gas giant.
(10)Here, C is a constant depending on the disc profile, which is ≈0.308 for our disc profile and (H/r)pl denotes the aspect ratio of the disc at the planet’s location. For the same five Earth mass planet at 10 AU in our disc, the migration timescale is ≈315 kyr, a factor of three shorter than the time for this planet to double its mass with a pebble flux of 45 ME/Myr. This indicates that planets forming in discs with such low pebble fluxes will migrate to the central star before they can reach the pebble isolation mass. At pebble isolation mass, the planet generates a pressure bump outside of it is orbit, accelerating the azimuthal gas velocity to super-Keplerian speeds which prevent the inward drift of pebbles due to a reversed gas drag force (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014). The planetary atmosphere is then not heated by in-falling pebbles any more and the planet can start to accrete gas and eventually become a gas giant.
Increasing the pebble flux to ≈150 ME/Myr allows an equal growth and migration timescale, but the planet would still migrate significantly inwards before growing to the pebble isolation mass, where it can then grow to become a gas giant and transition into the slower type-II migration. Only for larger pebble fluxes does the growth timescale become shorter than the migration timescale, allowing efficient growth to reach the pebble isolation mass before isothermal inward type-I migration moves the planet all the way to the central star. Additionally, this scenario requires a formation far away from the central star in order to compensate for the loss of semi-major axis before gap opening. However, in order for planets to grow to the pebble isolation mass in the outer parts of the protoplanetary disc (r> 30 AU), the pebble flux has to be larger by a factor of a few (e.g. 270 ME/Myr).
2.1. Confronting drift-limited pebble growth with observations
We show the gas surface density Σg, the dust surface density Σd and the pebble surface density Σp as a function of orbital distance and time in the disc model of Bitsch et al. (2015a), which was used in the planet growth simulations of Bitsch et al. (2015b), in Fig. 2. Here we assume a dust-to-gas ratio of 0.01.
Integrating the total mass of pebbles in our disc models with drift-limited pebble growth (using the nominal values of Eq. 2) results in 13 ME of pebbles in discs that are 1 Myr old, and in 10 ME in discs that are 2 Myr old. The mass of the pebbles does not decrease as significantly as one could have expected, which is related to the outward movement of the pebble formation front rg (Lambrechts & Johansen 2014), which moves from 120 AU (1 Myr) to 180 AU (2 Myr) and releases new pebbles formed from the dust in that region into the disc which drift inwards.
 |
Fig. 2 Gas surface density Σg, the dust surface density Σd and the pebble surface density Σp as a function of orbital distance and time in the disc evolution model of Bitsch et al. (2015a), which is used in the planet formation model of Bitsch et al. (2015b). The times are (top to bottom) 104, 105, 106 and 107 yr. The large bump that connects the pebble surface density with the dust surface density indicates the pebble production line rg. The blue lines correspond to the pebble surface density calculated with a frozen dust distribution outside of 50 AU (Sect. 2.2). The blue arrow indicates the typical pebble surface densities inferred at 10 AU from observations of protoplanetary discs (Williams & Cieza 2011). |
Protoplanetary disc column densities can be measured through resolved observations of optically thin emission of solid particles at mm and cm wavelengths. Williams & Cieza (2011) summarise measurements of a high number of protoplanetary discs and report pebble column densities in the range 0.2–2 g/cm2 at 10 AU (or, correspondingly, gas column densities in the range 20–200 g/cm2). This range is indicated in Fig. 2 with a blue arrow as well. The protoplanetary disc survey of Ansdell et al. (2017) measured the masses of mm-sized pebbles in young star forming regions (with estimated ages in the interval of 1−2 Myr) to be between 5−100ME, whose lower range is in rough agreement with our values. However, most of the discs analysed in Ansdell et al. (2017) are only ≈50−100 AU in size, which indicates that the surface density of pebbles is higher by a factor of a few compared to the drift limited solution we use here.
Observations by Wilner et al. (2005) of TW Hya estimate a total pebble mass of 300 ME, which is about a factor of 30 higher than in the drift limited pebble solution (Eq. (2)). Carrasco-González et al. (2016) measured the pebble surface density in HL Tau with VLA and inferred Σp ≈ 1 g/cm2 at 10 AU. With a nominal dust-to-gas ratio this results in Σg ≈ 100 g/cm2. At those distance and for those gas surface densities the drift limited solution again under-predicts the pebble surface density by at least a factor 10 (Fig. 2).
2.2. An improved pebble growth model
The observations of pebble column densities discussed above imply that our model of drift-limited pebble growth strongly underestimates the actual column density in protoplanetary discs.
We first considered whether the discrepancy could be fixed by assuming a lower value of ϵP in Eq. (2). With ϵP = 0.05 the resulting pebble Stokes numbers would be a factor of ten lower than shown in our models with ϵP = 0.5 (see Fig. 3), that is, τf ~ 0.01, and the column density a factor 10 higher, in better agreement with observations. However, the low Stokes number becomes problematic because most protoplanetary discs are dominated in opacity by cm-sized particles in their 10 AU regions (Wilner et al. 2005; Testi et al. 2014; Carrasco-González et al. 2016), a size that has an approximate Stokes number τf ~ 0.1 for Σg = 100 g/cm2. Assuming porous dust aggregate pebbles, with filling factor of f = 0.1, does not yield more consistent results, because the dominant pebble size a in protoplanetary discs, inferred from the measured opacity index, in fact yields a·f due to the voids within porous particles (Kataoka et al. 2014). Therefore the assumption f = 0.1 (instead of f = 1.0) implies that observed pebbles are 10 cm in radius (instead of a = 1 cm) and hence have Stokes number τf ~ 0.1, in conflict with the results of the model of drift-limited pebble growth for ϵP = 0.05.
Instead we consider the discrepancy between the modelled pebble column densities and the observed column densities to be an artefact of our application of the model of drift-limited pebble growth to an evolving protoplanetary disc. We have assumed that the pebble formation front moves over remote regions that have instantaneously adapted to the current gas accretion rate measured on the star. However, simulations of viscously evolving discs that include infall from the natal envelope onto the outer regions of the disc show only small variations of the gas surface density outside of 50 AU as the inner disc is accreted in time (Hueso & Guillot 2005), while viscous disc evolution simulations starting from a power law disc model, show no evolution of the gas disc outside of 50 AU at all during the accretion of the inner disc (Baillié et al. 2015).
 |
Fig. 3 Pebble sizes in terms of their Stokes number and their physical size in the disc model of Bitsch et al. (2015a) as a function of time. The times are (top to bottom) 104, 105, 106 and 107 yr. The pebbles start their inward drift from the outermost point of the curves, indicating that they will grow as they drift inwards. The jump in the pebble sizes at ≈7 AU at t = 104 and t = 105 yr as well as at 1.5 AU at t = 106 yr is caused by the transition at the water ice line, where we assume that the pebble flux reduces by 50% due to the evaporation of water ice. The sizes and Stokes numbers of the pebbles correspond to the nominal pebble flux marked by the solid red line in Fig. 1 and to the pebble surface densities marked by the black dotted lines in Fig. 2. |
This means that the pebble production line still moves outwards in time, but that we can assume that pebbles are formed from a dust surface density that corresponds to a disc evolution state when the pebble production line reached 50 AU. This results in a pebble surface density at later times that is larger compared to the model used in Bitsch et al. (2015b) and shown as the blue lines in Fig. 2. The resulting pebble surface density then matches the lower limit of the observations presented in Williams & Cieza (2011). The corresponding pebble flux is shown as the dotted red line in Fig. 1 and corresponds roughly to 300ME/Myr, large enough to outgrow type-I migration.
We note that a similar approach is taken in Lambrechts & Johansen (2014), where the flux of pebbles is assumed to depend on the exponential decaying surface density, which is effectively close to the initial surface density until disc dissipation. Therefore, Lambrechts & Johansen (2014) also find a dependence of the pebble flux in time that scales with t− 1/3, as shown in the dotted red line in Fig. 1. With their simpler power-law disc model, they also conclude that giant planets are able to form fast enough to survive type-I migration.
 |
Fig. 4 Final masses of planets (total mass MP = Mc + Menv) as a function of formation distance r0 and formation time t0 in the disc. Planets that are below the dark blue line have reached pebble isolation mass and can accrete gas. All planets that are below the white line have Mc<Menv, indicating that they have undergone runaway gas accretion. The black lines indicate the final orbital distance rf of the planet. The black bottom right corner of the plot corresponds to orbital distances which the pebble production line did not reach at the time t0. This figure corresponds to Fig. 4 in Bitsch et al. (2015b). |
2.3. Planetary growth
Planetary growth tracks by pebble accretion were mapped in Bitsch et al. (2015b) through probing the parameter space in orbital distance and in starting time. In Fig. 4 we show the final mass of the planets as a function of their formation distance r0 and formation time t0 when applying our revised pebble formation front scheme present in Sect. 2.2. The general results of Bitsch et al. (2015b) are very well reproduced. Namely, the formation of gas giants at large orbital distance within the lifetime of the protoplanetary disc is possible. In the very inner regions of the protoplanetary disc, the planetary growth at late stages is reduced compared to the original simulations of Bitsch et al. (2015b), while it becomes easier to form giant planet at large orbital distances at late times.
3. Conclusion
In this erratum we analyse the effect of a programming error in the drift-limited pebble growth model used in Bitsch et al. (2015b) and also in Bitsch & Johansen (2016). We find that the correction of this error yields pebble column densities that are lower than the typical range of column densities inferred from protoplanetary disc observations. We propose that the discrepancy is an artefact arising from the application of drift-limited pebble growth to an evolving protoplanetary disc, since the outer regions of the disc that form pebbles may not yet be influenced by the ongoing gas accretion onto the star. Fixing the column density of gas and dust outside of 50 AU yields pebble column densities in better agreement with observations and pebble accretion growth rates similar to those in Bitsch et al. (2015b) and Bitsch & Johansen (2016). The drift-limited pebble growth model is nevertheless still a crude approximation of dust growth in protoplanetary discs, since the model ignores the potentially important effects of bouncing, fragmentation and vapour condensation. We are therefore currently developing more realistic pebble growth models and will present those and their effect on planetary growth by pebble accretion in future publications.
Acknowledgments
We thank Natacha Brügger and Yann Alibert (Uni Bern) for identifying the calculation error in Bitsch et al. (2015b) and bringing it to our attention. We thank the referee John Chambers for his comments that helped to improve this manuscript.
References
- Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baillié, K., Charnoz, S., & Pantin, É. 2015, in Proc. of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 271 [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Johansen, A. 2016, A&A, 590, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015a, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015b, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco-González, C., Henning, T., Chandler, C. J., et al. 2016, ApJ, 821, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Johansen, A., & Lambrechts, M. 2017, Annu. Rev. Earth Planet. Sci, 45, 359 [Google Scholar]
- Kataoka, A., Okuzumi, S., Tanaka, H., & Nomura, H. 2014, A&A, 568, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI, 339 [Google Scholar]
- Williams, J. P., & Cieza, L. 2011, ARA&A, 490, 67 [CrossRef] [Google Scholar]
- Wilner, D. J., D’Alessio, P., Calvet, N., Claussen, M. J., & Hartmann, L. 2005, ApJ, 626, L109 [NASA ADS] [CrossRef] [Google Scholar]
© ESO, 2018
All Figures
 |
Fig. 1 Pebble flux Ṁpeb as a function of time using the time-dependent protoplanetary disc evolution model (solid red line) and for a protoplanetary disc evolution model where the outer gas disc does not evolve in time (dotted red line). In blue we show constant pebble fluxes of 45 ME/Myr (solid line) and 270 ME/Myr (dotted line). In principle, a pebble flux of 45 ME/Myr is large enough to grow a planet from 5 to 10 ME in 1 Myr, but the migration timescale is a factor of a few shorter than that, indicating that planet would be lost to the central star. Higher pebble fluxes of ≈270 ME/Myr allow growth fast enough to reach the pebble isolation mass and thus allow gas accretion and the transition to type-II migration before type-I migration drives the planet all the way to the central star. Our revised disc evolution model is able to reproduce these high pebble fluxes (dotted red line). |
| In the text | |
 |
Fig. 2 Gas surface density Σg, the dust surface density Σd and the pebble surface density Σp as a function of orbital distance and time in the disc evolution model of Bitsch et al. (2015a), which is used in the planet formation model of Bitsch et al. (2015b). The times are (top to bottom) 104, 105, 106 and 107 yr. The large bump that connects the pebble surface density with the dust surface density indicates the pebble production line rg. The blue lines correspond to the pebble surface density calculated with a frozen dust distribution outside of 50 AU (Sect. 2.2). The blue arrow indicates the typical pebble surface densities inferred at 10 AU from observations of protoplanetary discs (Williams & Cieza 2011). |
| In the text | |
 |
Fig. 3 Pebble sizes in terms of their Stokes number and their physical size in the disc model of Bitsch et al. (2015a) as a function of time. The times are (top to bottom) 104, 105, 106 and 107 yr. The pebbles start their inward drift from the outermost point of the curves, indicating that they will grow as they drift inwards. The jump in the pebble sizes at ≈7 AU at t = 104 and t = 105 yr as well as at 1.5 AU at t = 106 yr is caused by the transition at the water ice line, where we assume that the pebble flux reduces by 50% due to the evaporation of water ice. The sizes and Stokes numbers of the pebbles correspond to the nominal pebble flux marked by the solid red line in Fig. 1 and to the pebble surface densities marked by the black dotted lines in Fig. 2. |
| In the text | |
 |
Fig. 4 Final masses of planets (total mass MP = Mc + Menv) as a function of formation distance r0 and formation time t0 in the disc. Planets that are below the dark blue line have reached pebble isolation mass and can accrete gas. All planets that are below the white line have Mc<Menv, indicating that they have undergone runaway gas accretion. The black lines indicate the final orbital distance rf of the planet. The black bottom right corner of the plot corresponds to orbital distances which the pebble production line did not reach at the time t0. This figure corresponds to Fig. 4 in Bitsch et al. (2015b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


