EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 608 (December 2017) A&A, 608 (2017) A123 Full HTML
Free Access
Issue
A&A
Volume 608, December 2017
Article Number A123
Number of page(s) 13
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201731476
Published online 15 December 2017

© ESO, 2017

1. Introduction

Cosmic reionization was a major phase transition in the early history of the Universe, and great efforts have been made in the past decade to place constraints on when and how it occurred, as well as to identify the main sources of ionizing photons. Planck provided the most accurate measurement to date of the Thomson optical depth (τ = 0.066 ± 0.013), which allowed deriving an instantaneous reionization redshift of z = 8.8 ± 0.9 (Planck Collaboration XIII 2016). The candidate sources that are currently thought to be responsible for cosmic reionization are star-forming galaxies, with a main contribution coming from the faintest galaxies (e.g., Bouwens et al. 2015a, 2016b; Finkelstein et al. 2015; Robertson et al. 2015; Livermore et al. 2017), while the contribution from faint active galactic nuclei (AGN) could be more important than previously thought (Madau & Haardt 2015; Giallongo et al. 2015).

In recent years, a growing number of galaxies with unambiguous ionizing photon leakage have been identified both in the nearby Universe and at high redshift (Leitet et al. 2011, 2013; Borthakur et al. 2014; De Barros et al. 2016; Vanzella et al. 2016b; Shapley et al. 2016; Izotov et al. 2016; Bian et al. 2017), but the total number of confirmed Lyman continuum (LyC) emitters remains small (≲ 10), and this could be a consequence of viewing-angle effects with LyC photons escaping through a minority of solid angles (e.g., Kimm & Cen 2014; Cen & Kimm 2015). This lack of statistically significant samples of star-forming LyC emitters precludes a firm identification of ionizing photon leakage signatures that is necessary to identify LyC emitters in the reionization era, although some proposed diagnostics seem promising, such as the [O iii]/[O ii] line ratio, the strength of interstellar absorption lines, a deficit of Balmer emission lines, or the structure of the Lyα line (e.g., Heckman et al. 2011; Jones et al. 2012; Jaskot & Oey 2013; Zackrisson et al. 2013; Nakajima & Ouchi 2014; Verhamme et al. 2015, but see also Rutkowski et al. 2017).

It is impossible to directly observe the escape of ionizing photons from high-redshift galaxies because the intergalactic medium (IGM) is opaque to LyC photons (e.g., Vanzella et al. 2015). Several spectroscopic surveys have therefore attempted to detect the Lyα emission from star-forming galaxies at z ≥ 6 because resonant scattering in a partially neutral IGM will affect the detectability of Lyα emission (Dayal et al. 2011). Therefore the Lyα photon visibility evolution can be used to place some constraints on cosmic reionization. The overall conclusion of these surveys is that a drop in the Lyman-α emitter (LAE) fraction among the Lyman break galaxy (LBG) population is observed from z ~ 6 to z ~ 7 (e.g., Fontana et al. 2010; Ouchi et al. 2010; Stark et al. 2011; Pentericci et al. 2011; Ono et al. 2012; Ota et al. 2012; Caruana et al. 2014; Schenker et al. 2014), leading to the conclusion that cosmic reionization ended between z ~ 6 and z ~ 7. However, the amplitude of the median LAE fraction drop is such that it is difficult to explain by invoking plausible reionization models because it would require an extremely fast evolution of the neutral hydrogen fraction (Dijkstra et al. 2011; Jensen et al. 2013). Dijkstra et al. (2014) suggested that this drop can be explained with a moderate increase of the neutral hydrogen fraction and an increasing LyC escape fraction with increasing redshift, reaching a LyC escape fraction fesc(LyC) ~ 0.65 at z ~ 6, strongly contrasting with current constraints on fesc(LyC) for z ~ 3 galaxies (fesc(LyC) < 0.02−0.2; e.g., Vanzella et al. 2012; Guaita et al. 2016; Grazian et al. 2016). However, alternative explanations have been proposed, such as an increase in incidence of optically thick systems that would require a lower neutral fraction (Bolton & Haehnelt 2013), or a contribution from evolving galaxy properties (Mesinger et al. 2015).

It has been pointed out in several studies that the IGM might also strongly affect Lyα visibility even in a fully ionized Universe. Dijkstra et al. (2007) and Zheng et al. (2010) derived at z ~ 6 a mean IGM transmission to Lyα photons (TIGM ≤ 0.3) and Laursen et al. (2011) found TIGM=0.26-0.18+0.13\hbox{$\tigm=0.26^{+0.13}_{-0.18}$}. This low Lyα transmission in a fully ionized Universe is due to the low transmission through the IGM of the Lyα photons, which are blueshifted because they interact with the interstellar medium (ISM) within galaxies (e.g., Verhamme et al. 2008). At z ~ 3, while some high-redshift LAEs exhibit double-peaked Lyα emission (e.g., Vanzella et al. 2008), the majority of them exhibit either weak Lyα blue bumps, or they are entirely absent (Shapley et al. 2003; Kulas et al. 2012). Expanding shell models have been successful in reproducing observed Lyα profiles (Verhamme et al. 2008), and the study of interstellar absorption line velocities also supports a picture where outflows are ubiquitous in z ~ 3 star-forming galaxies (Steidel et al. 2010), while the IGM transmission to Lyα photons is expected to be high.

The Lyα line can be used as a tool to constrain the IGM neutral fraction as long as the evolution of the galaxy physical properties influencing the escape of Lyα photons is known. At low and intermediate redshift (z ≤ 3), fesc(Lyα), and EW(Lyα) have been found to be related to the stellar mass (M⋆), star-formation rate (SFR), the age of the stellar population, ISM physical properties, and the dust extinction (e.g., Hayes et al. 2014; Hathi et al. 2016; Trainor et al. 2016). Physical properties of z ~ 6 galaxies can be derived directly from photometry, such as the UVβ slope (fλ ∝ λβ; e.g., Bouwens et al. 2009, 2012, 2014; McLure et al. 2011; Castellano et al. 2012, 2014; Finkelstein et al. 2012; Dunlop et al. 2013), and through spectral energy distribution (SED) fitting (e.g., Eyles et al. 2005, 2007; Schaerer & De Barros 2009, 2010; McLure et al. 2011; Curtis-Lake et al. 2013; Jiang et al. 2016). Early analysis of z ~ 6 photometry (combining optical, near-infrared, and mid-infrared data) provided a picture where galaxies were already massive (M⋆ ≥ 1010M⊙) and relatively old (> 100 Myr), with a substantial Balmer break (Eyles et al. 2005, 2007; Yan et al. 2005, 2006). Zackrisson et al. (2008) showed that nebular emission and notably emission lines could have a strong effect on photometry at high redshift and this possibility has been explored in Schaerer & De Barros (2009, 2010). Accounting for the impact of nebular emission on high-redshift galaxy physical properties is now a widespread approach (e.g., Chary et al. 2005; Robertson et al. 2010, 2013; Vanzella et al. 2010, 2014b; Labbé et al. 2010, 2013; Ono et al. 2012; Oesch et al. 2013a,b, 2014; Stark et al. 2013; De Barros et al. 2014; Duncan et al. 2014; Smit et al. 2014; Salmon et al. 2015). Taking nebular emission into account generally leads to lower stellar masses and younger ages, particularly for z ~ 6 galaxies, for which the two first Spitzer/IRAC bands are contaminated by strong emission lines, namely [O iii]+Hβ and Hα respectively, while these two bands provide the strongest constraints on both stellar mass and the Balmer break. Unfortunately, the contamination of the two bands IRAC1 and IRAC2 prevents any empirical estimation of line contributions in these bands at z ~ 6, which is different from the situation at z ~ 4 (e.g., Shim et al. 2011; Stark et al. 2013) and some other redshifts (Shivaei et al. 2015; Labbé et al. 2013; Smit et al. 2014; Faisst et al. 2016; Mármol-Queraltó et al. 2016; Rasappu et al. 2016). Furthermore, the lack of constraints on galaxy redshifts also introduces uncertainties about which bands are affected by emission lines.

thumbnail Fig. 1

2D signal-to-noise ratio spectra and sky spectra of two faint Lyα emitters. The two insets show the corresponding one-dimensional FORS2 spectra, with red arrows highlighting positions of the Lyα-break, which are also visible in 2D spectra. For the galaxy at the top, EW(Lyα) ≤ 1.3 Å, and for the galaxy at the bottom, EW(Lyα) = 10.0 ± 1.3 Å.

In this paper, we present the analysis of a large sample of spectroscopically confirmed galaxies at z ~ 6 from VLT/FORS2 observations in five different fields (Castellano et al. 2017; Pentericci et al., in prep.). Our analysis aims to derive the LAE fraction at z ~ 6 and compare it with previous results to highlight which processes dominate the observed LAE fraction drop. We also derive physical parameters of this sample with SED fitting to determine whether the LAE fraction evolution is related to an evolution of the physical parameters instead of the evolution of the IGM neutral state. While we minimize the number of assumptions in our analysis, we verified that the models reproduce the observed properties, but also reproduce the predicted properties for which we do not have empirical constraints at z ~ 6, namely the [O iii]+Hβ emission line equivalent widths. This increases the confidence in the derived physical parameters. We then study the physical properties, focusing on the relations between Lyα emission and other physical parameters.

The paper is structured as follows. The selection procedure and the spectroscopic and photometric data are described in Sect. 2. The results regarding the LAE fraction at z ~ 6 are shown in Sect. 3, while we describe the SED fitting method and the derived physical properties in Sect. 4. In Sect. 5 we discuss the implications of our results regarding the IGM transmission to Lyα photons at z ~ 6. We summarize our conclusions in Sect. 6.

We adopt a Λ-CDM cosmological model with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. We assume a Salpeter interstellar mass function (IMF; Salpeter 1955). All magnitudes are expressed in the AB system (Oke & Gunn 1983).

2. Data

2.1. Spectroscopic data

We used data obtained in the context of the CANDELSz7 ESO large program (ID: 190.A-0685, PI: L. Pentericci) that acquired deep observations of three of the CANDELS fields: the Great Observatories Origins Deep Survey (GOODS; Giavalisco et al. 2004) Southern field, the Cosmological Evolution Survey (COSMOS; Scoville et al. 2007; Koekemoer et al. 2007) field, and the UKIDSS Ultra-Deep Survey (UDS; Lawrence et al. 2007; Cirasuolo et al. 2007; Mortlock et al. 2015) field. One hundred and forty hours of observations have been allocated to this program. We also added the results from another VLT/FORS2 program (ID: 085.A-0844, 084.A-0951, 088.A-0192, PI: A. Fontana, Fontana et al. 2010; Castellano et al. 2010a,b) with a total of 63 h of observations, distributed among the New Technology Telescope Deep Field (NTTDF; Arnouts et al. 1999; Fontana et al. 2000, 2003), the Bremer Deep Field (BDF; Lehnert & Bremer 2003), the GOODS-S, and the UDS fields. Finally, we also used the results from an archival VLT/FORS2 program (ID: 088.A-1013, PI: A. Bunker; Caruana et al. 2014) that targeted the Hubble Ultra Deep Field (HUDF) with 27 h allocated. All the data combined typically provide 15–30 h of integration time for each target. The FORS2 600z grism configuration provides a useful area of 7′ × 4.33′. Eight masks were used in the CANDELSz7 program, with five additional masks in total from the other programs.

For the GOODS-S, COSMOS, and UDS fields, we used the publicly available CANDELS (Grogin et al. 2011; Koekemoer et al. 2011) catalogs for each of these fields (Guo et al. 2013; Nayyeri et al. 2017; Galametz et al. 2013, respectively) with a wavelength coverage from ~ 0.3 μm to 8.0 μm. For the BDF and NTTDF fields, we used the available photometry in the V, R, I, Z, Y, J, and KS bands (Castellano et al. 2010b). Details of the observation and data reduction are comprehensively described in the different papers cited previously, we refer to these references as well as to Pentericci et al. (in prep.) for the CANDELSz7 survey description.

The targets from CANDELS fields have been homogeneously selected using a similar selection as was used in Bouwens et al. (2015b), with the i-dropout criteria being: i775−z850>1.0;Y105−H160<0.5;\begin{eqnarray} &&i_{775}-z_{850}>1.0; \nonumber\\ &&Y_{105}-H_{160}<0.5; \nonumber\\ &&(S\!/\!N(B_{435})<2)\land (V_{606}-z_{850}>2.7\lor S\!/\!N(V_{606})<2), \label{eq:dropout} \end{eqnarray}(1)to which we added an additional criterion with H160< 27.5. For the BDF and NTTDF, given that no HST data are available, the detection band was the HAWK-I Y-band. Although this is bluer than the CANDELS H-band, it is still free of contamination from the emission line at z ~ 6. For BDF and NTTDF, selection criteria were: I−Z>1.3;\begin{eqnarray} &&I-Z>1.3; \nonumber\\ &&S\!/\!N<2\ \textrm{in all bands blueward of the }I\textrm{ band}, \label{eq:dropout2} \end{eqnarray}(2)with Y< 26.5 for the two fields. While the criteria are slightly different for BDF and NTTDF compared to the other fields, the color criteria are equivalent. Galaxies from these two fields make up only a small fraction of our entire sample (9%). The only two spectroscopically confirmed low-redshift contaminants have been observed in the NTT and BDF fields (z = 1.3 and z = 0.5, respectively).

The VLT/FORS2 wavelength coverage ranges from 5700 Å to 10 000 Å (depending on the slit position), allowing the detection of Lyα emission at z ~ 4−7.2 if present, and even in some cases directly detect the continuum emission and the Lyman break. Furthermore, the wavelength coverage allows us to identify low-redshift interlopers by detecting multiple emission lines, such as [O iii]λλ4959,5007, Hα, or [O ii]λ3727 emissions at z ≤ 1, z ≤ 0.5, and 0.5 ≤ z ≤ 1.7, respectively (e.g. Vanzella et al. 2011). In case of single emission detection, for a signal-to-noise ratio S/N> 6, the resolution R = 1390 allows us to identify the typical asymmetric profile of Lyα, which can be used to distinguish between low- and high-redshift galaxies. We also checked for any inconsistency between the measured spectroscopic redshift and the redshift probability distribution function. Data reduction was performed as described in Vanzella et al. (2011, 2014a) following the “A-B” dithering scheme method. The high quality of the deep spectra allowed us to identify faint z ~ 6 Lyα emission, as shown in Fig. 1.

The final sample consists of 127 galaxies, with 74 galaxies in GOODS-S (58% of the sample), 23 in UDS (18%), 19 in COSMOS (15%), 7 in BDF (6%), and 4 in NTT (3%). For 81 of these galaxies, we can derive a spectroscopic redshift, mainly from the presence of the Lyα emission line or in few bright cases (N = 10), from the presence of continuum emission with a drop consistent with the Lyman break (Fig. 1). The properties of all objects with a spectroscopic confirmation will be published in a table in Pentericci et al. (in prep.). For 46 objects, it was not possible to derive a spectroscopic redshift given that no features were detected in the deep spectra. In this paper, we assume that all the undetected objects are also at z ≃ 6, consistently with their photometric redshifts (Fig. 2). Assuming that all undetected objects are low-z interlopers and accounting for the two spectroscopically confirmed low-z galaxies in NTT and BDF, we can set a robust upper limit for the interloper fraction with 38 interlopers from a sample of 129 observed objects. The upper limit for the interloper fraction is then ≤ 29%.

thumbnail Fig. 2

Redshift distributions for the spectroscopically confirmed and photometric samples in white and black, respectively.

2.2. EW(Lyα) measurement

Lyα equivalent widths were derived by using the nearest redward HST bands from the Lyα emission (excluding bands affected by Lyα) and deriving the UVβ slope directly from the photometry (Castellano et al. 2012; Pentericci et al., in prep.). To derive the UVβ slopes, we derived fluxes using apertures of 1.75 FWHM instead of isophotal, as in the CANDELS published catalogs. We found that for small galaxies as in our sample, colors measured in small apertures are more stable than the original isophotal ones. To estimate the continuum at 1216 Å (rest-frame), we used the Y- or J-band magnitudes from the CANDELS catalogs that are corrected to total flux via aperture correction. For a non-detection of the Lyα line, 3σ upper limits on the equivalent width were derived from the S/N of Lyα lines as described in Vanzella et al. (2014a). We did not apply any aperture correction to the Lyα flux measurements. Even if there is extended Lyα emission due to the scattering of Lyα photons in the circum-galactic medium (CGM; Wisotzki et al. 2016), the relatively small intrinsic sizes of the observed galaxies (Curtis-Lake et al. 2016) should prevent flux losses. Furthermore, no correction is usually applied at z ~ 6 (e.g., Stark et al. 2011). The error on the β slope is not propagated to the EW(Lyα) estimation, but we estimate that the total error on EW(Lyα) is not larger than 35%. We show in Fig. 3 the comparison between EW(Lyα) derived from spectra only for the ten galaxies for which the continuum is spectroscopically detected, and using the aforementioned method. While this small subsample is strongly biased toward bright galaxies and so toward galaxies with faint Lyα emission (Sect. 4.2), EW(Lyα) measurements from the two methods are consistent.

For all the programs the slit width was always 1″. For Bunker’s program, some slits had a slit length as small as 6″, the minimum slit length was 8″ for the CANDELSz7 program, and the slit length was always above 10″ for Fontana’s program. Simulations were performed to estimate the minimum line flux that is measurable for this sample. These simulations are similar to those performed in Vanzella et al. (2011, 2014b) and Pentericci et al. (2014). Artificial 2D asymmetric Lyα lines were added in the raw science frame, exploring a range of typically observed fluxes and FWHM (by varying emerging values from 280 to 520 km s-1), with a fiducial FWHM of 300 km s-1. We then applied the reduction pipeline and response curve. At fixed flux, the larger the FWHM, the lower the S/N. From 280 to 520 km s-1 (emerging FWHM), the S/N decreases by a factor of ~ 1.5. We derive that our observations detect Lyα flux as low as 2.2 × 10-18 erg s-1 cm-2 at 3σ over the entire wavelength range probed in this work (which means that we can recover even fainter Lyα lines in wavelength ranges free of sky lines). Assuming that the nearest band redward of Lyα (and not contaminated by this line) provides a measurement of the continuum at the Lyα wavelength, we estimate that our sample is complete at > 95% for a Lyα equivalent width of EW(Lyα) ≥ 25 Å.

thumbnail Fig. 3

Comparison of EW(Lyα) derived from spectra alone and from spectra and photometry (see Sect. 2.2). We show the results for the ten galaxies with a spectroscopically detected continuum. The dashed line shows the one-to-one relation, and the dotted lines show ± 25% from the one-to-one relation.

thumbnail Fig. 4

Distribution of the sample as a function of the number of measured fluxes in Spitzer/IRAC bands (black histogram). We show in blue and red the distribution of the flux measurement with S ! N ≥ 2 and S ! N ≥ 3, respectively.

Owing to the importance of the Spitzer/IRAC detections in constraining the stellar mass, age (Balmer break), and emission line contribution (e.g., Jiang et al. 2016), we show in Fig. 4 the number of flux measurements in Spitzer/IRAC bands.

3. Lower Lyα emitter fraction at z ~ 6

Based on our large spectroscopic sample, we can derive the LAE fraction (defined as the fraction of LAE with a rest-frame equivalent width EW(Lyα) > 25 Å) at z ~ 6, which allows us to place constraints on the ionization state of the IGM. This fraction has previously been described as rising from z ~ 4 to z ~ 6 (Stark et al. 2011, S11 hereafter) and rapidly declining at z> 6 (e.g., Pentericci et al. 2011). This evolution of the LAE fraction between z ~ 6 and z> 6 has been interpreted as the effect of partially neutral IGM on the Lyα photons emitted from high-z galaxies (e.g., Schenker et al. 2012) and so as our witnessing of the cosmic reionization end.

We show in Fig. 5 the LAE fractions for our bright (MUV< −20.25) and faint (MUV> −20.25) subsamples. The absolute UV magnitude MUV refers to the absolute magnitude at 1500 Å. To determine it for each galaxy, we used the integrated SED flux in an artificial filter of 200 Å width centered on 1500 Å. Our data cover five fields which should mitigate the cosmic variance effect on our results (e.g., Ouchi et al. 2008). Comparing our results with previous studies (e.g., Stark et al. 2011; Pentericci et al. 2011), the LAE fractions that we derived at z ~ 6 are consistent with a trend of increasing and then decreasing LAE fraction with redshift, the main uncertainty being at which redshift the peak of the LAE fraction lies. However, the LAE fraction found by Curtis-Lake et al. (2012, hereafter CL12) at z ~ 6 is significantly higher than our result or those of S11. We verified that the color selection criterion i−z is not the cause of this discrepancy by applying the same criterion as S11 to our sample (i−z> 1.3), as well as the criterion (i−z> 1.7) used in CL12, in both cases to the bright sample (MUV< −20.25). While the fraction of LAE (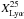XLyα25\hbox{$X_\mathrm{\lya}^{25}$}) increases (up to 0.16 using the CL12 criterion), the fraction of unconfirmed sources (defined as sources for which we cannot assign a spectroscopic redshift) remains constant ~ 0.35 for all i−z cut, showing that interlopers are unlikely to be the cause of the difference between the results of CL12 and our own (and those of S11). Lyα equivalent widths are derived using a narrow-band filter in CL12, instead of a broad-band filter in S11/this work, but it is also unlikely that this difference can introduce such a large discrepancy because the maximum 3σ EW(Lyα) upper limit for unconfirmed object is < 16 Å and there is only one object with a measured EW(Lyα) near the EW threshold we used (25 Å). Therefore, it would require a difference in the UV continuum flux estimation by a large factor (> 2) to explain the difference between our work and CL12. Alternative explanations can be the small statistics of the CL12 sample or the fact that particularly bright Lyman break galaxies (LBGs) can exhibit unusually strong Lyα emission (e.g., Bagley et al. 2017; Matthee et al. 2017).

thumbnail Fig. 5

Fraction of LAEs (with EW(Lyα) > 25 Å, XLyα25\hbox{$X_\mathrm{\lya}^{25}$}) at 4 ≤ z ≤ 8 for the brightest (MUV< −20.25, left panel) and faintest (MUV> −20.25, right panel) galaxies. We show the results from Stark et al. (2011), Schenker et al. (2014), Ono et al. (2012), Pentericci et al. (2011), Tilvi et al. (2014), Cassata et al. (2015), and Curtis-Lake et al. (2012). We introduce slight offsets in redshift to increase clarity when necessary.

Comparing our results with S11, we find a lower median LAE fraction in both the bright and faint samples, and while results are consistent within 1σ uncertainties between the two studies, we still discuss the differences between the medians as these values have been used to study galaxy evolution and cosmic reionization (e.g., Dijkstra et al. 2014).

Our sample size is ~ 60% larger than the S11 sample. Furthermore, at z ~ 6, the Lyα line can affect the dropout selection (Stanway et al. 2008): for a sample relying only on the z850 band as the detection band, strong emitters are scattered in this band because of the emission line strength, and not because of the continuum. The main difference in terms of color criteria comes from our IR criterion, that is, H< 27.5. Without this IR criterion, a color selection of z ~ 6 is biased toward faint galaxies with strong Lyα emission: we show in Fig. 6 two examples of galaxy with large EW(Lyα) (> 100 Å) and with z850 = 27.50 (top) and z850 = 26.30 (bottom). These two galaxies would have been selected using the S11 color criterion but not in our sample because they are not detected in H160. When they are corrected for the Lyα contribution, their z850 magnitudes are > 28.28 and > 27.40, respectively, which implies that non-Lyα emitters as faint as these two LAEs are likely absent from the S11 sample. Our selection criteria should prevent this bias, and at a given luminosity, we should select both LAE and non-LAE. We conclude that the most likely reason for the differences between our results on the LAE fraction and the fraction reported in S11/CL12 arises because our sample is H-band detected, while other samples are z-band detected, with the z-band being contaminated by the Lyα emission.

Considering our upper limit on interlopers (≤ 29%), our measured LAE fractions can be considered as lower limits, and the true value should be between 1 and the values given in Fig. 5. However, our upper limit was derived assuming that all undetected objects are interlopers, which we consider as unlikely given the typical exposure time (Sect. 2.1). Soon, the James Webb Space Telescope (JWST) will permit spectroscopic redshift confirmation even for galaxies with weak or absent Lyα.

Dijkstra et al. (2014) explored different models of cosmic reionization to derive the EW(Lyα) cumulative distribution at z ~ 7 from the cumulative distribution at z ~ 6, assuming a fully ionized Universe at z ~ 6 (see their Fig. 3). Matching the z ~ 7 distribution required an extremely rapid evolution of the neutral fraction ΔxH i ~ 0.5, and they explore a scenario where the LyC escape fraction increased with redshift, alleviating the requirement for a rapid evolution of the IGM state. Using our sample with MUV> −20.25 and EW(Lyα) measurements led to a EW(Lyα) cumulative distribution with a steeper slope than in Dijkstra et al. (2014), with values P(EW> 25 Å) ~ 0.5, P(EW> 50 Å) ~ 0.2, and P(EW> 75 Å) ~ 0.1. This latter value is consistent with the upper limit on P(EW> 75 Å) at z ~ 7 used in Dijkstra et al. (2014). A detailed analysis, including a comparison between the z ~ 6 and z ~ 7 Lyα equivalent distribution derived from our new survey will be presented in a forthcoming paper.

Based on our results on the EW(Lyα) distribution and on the evolution of the LAE fraction (Fig. 5), we conclude that the IGM evolution from z ~ 6 to z ~ 7 is slower than previously thought, assuming that the LAE visibility mostly depends on the IGM state. The median LAE fraction plus 1σ uncertainties that we derive at z ~ 6 is also consistent with a flattening of the relation between LAE fraction and redshift at 5 <z< 6, which can imply that the IGM neutral fraction starts to increase between z ~ 5 and z ~ 6, more likely at 5.5 <z< 6.0 (Becker et al. 2015). We study the physical properties of the galaxies in our below in detail to determine whether they differ from the properties of other samples, and if these properties can affect the derived LAE fraction.

4. Physical properties of the galaxies

While the LAE fraction evolution is used to constrain the IGM neutral fraction, it is known that the Lyα properties are related to other physical properties such as luminosity and UV slopes, and the increase in LAE fraction up to z ~ 5−6 is likely related to the decreasing galaxy dust obscuration with increasing redshift (e.g., Stark et al. 2010). In the following, we compare the Lyα properties of our sample with other physical properties to assess which parameters affect the LAE fraction.

thumbnail Fig. 6

2D S/N and sky spectra for two faint LAEs at z = 5.92 (top) and z = 6.09 (bottom) with EW(Lyα) = 101 Å and EW(Lyα) = 330 Å, respectively (see text).

thumbnail Fig. 7

Top: EW([O iii]+Hβ) evolution with age for Z = 0.2 Z⊙ and the range of star formation used in this work: exponentially rising (blue), and exponentially declining (red). Bottom: same for EW(Lyα).

4.1. SED modeling

To derive the physical properties of the galaxies such as stellar mass or the age of the stellar population, we used a modified version of Hyperz (Bolzonella et al. 2000), accounting for nebular emission (lines and continuum, Schaerer & De Barros 2009, 2010). We generated a set of spectral templates with the GALAXEV code of Bruzual & Charlot (2003) for three different metallicities (Z = 0.004, 0.04, 0.02) and using a unique star formation history (SFH) defined with a star formation rate as SFR ∝ exp(t/τ) with τ = [ −10, − 30, − 50, − 70, − 100, − 300, − 500, − 700, − 1000, − 3000, ∞, 3000, 1000, 700, 500, 300, 100, 70, 50, 30, 10] Myr. This choice of SFH also allowed us to explore a wide range of possible emission line equivalent widths (Fig. 7). The stellar age was defined as the age since the onset of star-formation. We did not consider a minimum age because the dynamical timescale at z ~ 6 is likely to be short (td ~ 10 Myr, e.g., De Barros et al. 2014).

We considered three different dust attenuation curves: the Small Magellanic Cloud (SMC) curve (Prevot et al. 1984), the Calzetti curve (Calzetti et al. 2000), and the Reddy curve (Reddy et al. 2015). The Calzetti and Reddy curves were derived using Balmer decrement on local and z ~ 2 samples of star-forming galaxies, respectively, while there is mounting evidence that at z ~ 6, the most appropriate curve is an SMC-like curve (Capak et al. 2015; Bouwens et al. 2016a), and this could be also the case at z ~ 2 (Reddy et al. 2017). For simplicity, we used the same dust attenuation curve for the stellar continuum and the nebular emission, and a Calzetti curve with this assumption yields SFR(SED) consistent with SFR(UV+IR) (Shivaei et al. 2015). A typical ratio has been generally assumed between nebular and stellar color excesses (Calzetti et al. 2000), but recent observations have shown that at z ~ 2, there is no simple linear relation between nebular and color excesses, while the average ratio is ~ 1 (Reddy et al. 2015). For simplicity, we assumed that E(B−V)stellar = E(B−V)nebular. We excluded bands that might be affected by the Lyα emission from the SED fitting.

Minimization of χ2 over the entire parameter space yields the best-fit SED. Best-fit parameters are assumed to be the median of the marginalized likelihood, and uncertainties are determined through the likelihood marginalization for each parameter of interest with ℒ ∝ exp(− χ2/ 2).

While we cannot compare SFRSED with usual SFR tracers such as SFRHα or SFRUV + IR, we can derive SFRLyα (Atek et al. 2014), keeping in mind that the SFRLyα always provides a firm lower limit of the true SFR because of the loss of Lyα photons due to the radiative transfer effect of the ISM and dust attenuation (ISM, Schaerer & Verhamme 2008; Verhamme et al. 2008), the possible effect of the IGM (Zheng et al. 2010; Dijkstra et al. 2011; Laursen et al. 2011), and also slit loss. By comparing SFRLyα and SFRSED (Fig. 9), we show that assuming a declining SFH leads to an underestimate of the true SFR for ~ 50% of the sample for which we are able to measure a Lyα flux. The SFR underestimation under the assumption of a declining SFH is similar to results obtained at z ~ 2 (Wuyts et al. 2011; Reddy et al. 2012; Price et al. 2014). Assuming a constant or rising SFH leads to SFRSED consistent with SFRLyα, therefore we exclude in the following declining SFHs from the range of possible SFH. We note that in the range of stellar mass explored with our z ~ 6 sample, effects of stochastic SFH are expected (e.g., Hopkins et al. 2014). These can lead to difference in SFR estimation because different timescales are probed by different tracers (e.g., UV and nebular emission lines; Domínguez et al. 2015). While we explore a wide range of SFH and ages younger than 100 Myr (the UV to SFR conversion assumes a constant SFH for 100 Myr; Kennicutt 1998), which make possible large differences between SFRUV and SFRSED, we find that on average, SFRSED and SFRUV do not differ by more than a factor of 2.

thumbnail Fig. 8

Observed (black and white squares) and best-fit SEDs (solid lines) of a z = 5.786 galaxy. White squares show bands not used in the SED fitting because of possible impact of the Lyα line. The error bars of the observed wavelength indicate the surface of the normalized filter transmission curve. SED fits in blue and red are based on Bruzual & Charlot (2003) models with (red) and without (yellow) nebular emission, and a fit using BPASSv2.0 (Eldridge & Stanway 2016; Stanway et al. 2016) is shown in blue (Sect. 4.4). Color crosses show the synthesized flux in the filters. Without nebular emission, age and stellar mass are ~ 109 yr and ~ 1010.5M⊙ respectively, while accounting for nebular emission gives ~ 106 yr and ~ 109M⊙.

thumbnail Fig. 9

Relation between log (SFRSED) and log (SFRLyα/SFRSED) for galaxies with detected Lyα emission, assuming a declining (red dots) and a constant SFH (blue dots). Lyα luminosities have not been corrected for dust. The dashed line shows log (SFRLyα) = log (SFRSED). We recall that SFRLyα is a lower limit to the true SFR (see text).

thumbnail Fig. 10

EW([O iii]+Hβ) vs. redshift for different studies that empirically derived EW from the photometry (Shim et al. 2011; Labbé et al. 2013; Stark et al. 2013; Smit et al. 2014; Faisst et al. 2016; Mármol-Queraltó et al. 2016; Rasappu et al. 2016; Castellano et al. 2017) and the results obtained for the three SFHs used in the present work (rising, constant, and declining) assuming an SMC attenuation curve (alternative curves do not affect the results) and BC03 templates. We also show the result using BPASS templates (Sect. 4.4). For the studies deriving EW(Hα), we assume the typical ratio between this line and [O iii]+Hβ from Anders & Fritze-v. Alvensleben (2003) for a metallicity Z = 0.2 Z⊙. We show the relation between EW and redshift derived in Fumagalli et al. (2012), extrapolated to high redshift and for two different stellar masses (Smit et al. 2014).

Finally, we compared the predicted EW([O iii]λλ4959,5007+ Hβ), based on our SED fitting, with an EW derived empirically at lower and higher redshift: at z ~ 3.8−5.0 and z ~ 5.1−5.4, Hα+[N ii]λ6583 can be constrained by the IRAC1−IRAC2 color (e.g; Shim et al. 2011) and [O iii]λλ4959,5007+Hβ can be constrained with the same color at z ~ 6.6−7.0 (e.g., Smit et al. 2014; Castellano et al. 2017). We note again that such an empirical constraint at z ~ 6 is not possible because the IRAC1 and IRAC2 bands are both contaminated by [O iii]λλ4959,5007+Hβ and Hα, respectively (Fig. 8). In Fig. 10 we show the results for the three different SFHs. Most of the recent studies claim that EW([O iii]+Hβ) (or EW(Hα)) increases with increasing redshift (e.g., Smit et al. 2014; De Barros et al. 2014), which would be related to the increase in specific SFR (sSFR = SFR/M⋆) with redshift, but also possibly related to a change of the ISM physical conditions (Faisst et al. 2016), or a change in the IMF. Our comparison shows that the EW([O iii]+Hβ) predicted by our SED fitting code is consistent with the observed trend. We discuss the BPASS results in Sect. 4.4.

We conclude that while little is known about the nature of the stellar populations (e.g., IMF, SFH, metallicity, binary/rotation contribution) or the ISM physical conditions at z ~ 6, our SED fitting procedure is able to provide results consistent with previously observed trends (EW([O iii]+Hβ) vs. redshift) and consistent with available SFR tracers.

4.2. Relation between Lyα and UV properties

Several studies either in the local Universe (e.g., Hayes et al. 2014) or at high redshift (e.g., Shapley et al. 2003; Erb et al. 2006; Reddy et al. 2006; Pentericci et al. 2007, 2010; Kornei et al. 2010; Hathi et al. 2016; Matthee et al. 2016; Trainor et al. 2016) have found physical differences between Lyα emitters and non-Lyα emitters (but see also Hagen et al. 2016). The general trend is that UV-selected LAEs with the largest EW(Lyα) have bluer UVβ slopes (fλ ∝ λβ), fainter absolute UV magnitude, younger stellar populations, lower stellar masses, lower SFRs, and are less dusty than galaxies with lower EW(Lyα).

thumbnail Fig. 11

EW(Lyα) vs. MUV. We show individual Lyα detections with black dots and 3σ upper limits with gray downward triangles. We also show the average EW in magnitude bins (red stars). These average values are derived by setting EW(Lyα) to zero for all undetected objects, which should provide a good approximation of the true relation between EW(Lyα) and MUV (Schenker et al. 2014).

We first compare EW(Lyα) with two quantities that are not dependent on assumptions: the UV absolute magnitudes, and the UVβ slopes. The absolute UV magnitude MUV refers to the absolute magnitude at 1500 Å that we derive by using the integrated SED flux in an artificial filter of 200 Å width centered on 1500 Å. We find that UV-bright galaxies with large Lyα equivalent widths are absent, while fainter galaxies exhibit a large EW(Lyα) range (Fig. 11). This trend is consistent with results from numerous previous high-redshift studies (Ando et al. 2006; Pentericci et al. 2009; Schaerer et al. 2011; Stark et al. 2011; Cassata et al. 2015), and it has been interpreted as the result of the spatial extension of Lyα emission, since the spatial extension scales with galaxy size (Wisotzki et al. 2016). As the UVβ slope is an observed property and a proxy for the dust attenuation (e.g., Bouwens et al. 2014), we show in Fig. 12 the relation between EW(Lyα) and the UVβ slope for our sample. β slopes are derived directly from the photometry (Castellano et al. 2012). The highest EW(Lyα) are found for the bluest β slopes, while EW(Lyα) as high as ~ 80 Å can be found for any observed slope value.

The trend between EW(Lyα) and UV magnitude is stronger than between EW(Lyα) and β, but the relatively large uncertainties affecting the UV slope derivation (Fig. 12) prevent us from concluding about a possible stronger dependence of EW(Lyα) on the UV magnitude. Nevertheless, compared to previous samples (e.g., Stark et al. 2011), we find similar relations between Lyα and UV properties.

4.3. Relation between Lyα and other physical properties

Based one the nebular emission modeling, we can add an additional constraint to our SED fitting procedure: for each galaxy, we compared predicted Lyα fluxes from SED fitting with the observed fluxes, and we excluded solutions predicting “intrinsic” Lyα fluxes (i.e., SED predicted) lower than observed fluxes. With this method, SFRLyα and SFRSED are consistent for any SFH, including declining SFHs.

We show the relations between EW(Lyα) and physical properties (age, stellar mass, color excess, and SFR) in Fig. 13. In all cases, we assume a constant SFH and an SMC attenuation curve (we find qualitatively the same results for any set of assumptions described in Sect. 4.1).

thumbnail Fig. 12

EW(Lyα) vs. UVβ slope. Same symbols as in Fig. 11. For clarity, we show β error bars randomly for half of the sample.

Accounting for nebular emission at z ~ 6 leads to best-fit parameters with lower stellar masses and younger ages (Schaerer & De Barros 2009), but when we account for uncertainties, the result is less clear regarding ages, with a typical error of ± 1 dex. Age estimation depends on the assumed SFH and on the fit of both the UVβ slope and a color constraining the Balmer break, for example, at z ~ 6, the K−IRAC1 color. When we use our models with nebular emission (assuming zero dust attenuation), K−IRAC1 varies between 0.40 and 0.90, and it increases from − 0.85 to 0.70 with no nebular emission. Another difference between the two models is that K−IRAC1 increases from 1 Myr to 1 Gyr in models without nebular emission (because of the increasing Balmer break), while it decreases from 1 Myr to ~ 50 Myr (0.39 <K−IRAC1 < 0.84) and increases from ~ 50 Myr to 1 Gyr (0.39 <K−IRAC1 < 0.77) when nebular emission is accounted for. This is explained by the fact that from 1 Myr to 50 Myr, the K−IRAC1 color is dominated by strong emission lines that affect the IRAC1 channel ([O iii]+Hβ), and between 50 Myr to 1 Gyr, the impact of the Balmer break increases. The median K−IRAC1 color of our sample (0.71-0.49+1.01\hbox{$0.71^{+1.01}_{-0.49}$}) can be explained by relatively old ages for models without nebular emission or by a wide range of ages for models accounting for nebular emission. In an attempt to break this degeneracy between age and emission line equivalent width, we defined the effective escape fraction fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} as the ratio between the observed Lyα flux to the SED-predicted Lyα flux, and this quantity is the result of the combined effect from Lyα radiative transfer in the ISM and the effect of the CGM and intergalactic medium (Nagamine et al. 2010; Dijkstra & Jeeson-Daniel 2013). Assuming fesceff(Lyα)≤1\hbox{$\fefflya\leq1$} in the SED fitting procedure, we break the degeneracy between age and EW([O iii]+Hβ) for galaxies with EW(Lyα) > 80 Å, and the number of acceptable fit is reduced for galaxies with 40 Å <EW(Lyα) < 80 Å, but this does not affect significantly the best-fit parameters. Using this additional constraint (fesceff(Lyα)≤1\hbox{$\fefflya\leq1$}), we find that the relation between EW(Lyα) and age is similar to the relation observed at low-z, with the galaxy exhibiting largest EW(Lyα) being the youngest (e.g., Hayes et al. 2014). For the other physical parameters, we find that the LAEs with the largest EW(Lyα) are less dusty, less massive, and less star forming than non-LAEs or LAEs with lower EW(Lyα). The relations between EW(Lyα) and physical parameters are similar at low and high redshift, and this suggests that the escape of Lyα photons is likely driven by similar physical processes.

thumbnail Fig. 13

Comparison between physical parameters (color excess, age, SFR, and stellar mass) derived with and without accounting for nebular emission, assuming a constant SFH and an SMC curve. Dashed lines show the one-to-one relations. The distribution for each parameter is shown at the top of each figure along the x-axis for parameters derived with nebular emission (blue histograms) and at the right side along the y-axis for parameters derived without nebular emission (red histograms). Typical error bars for each parameter are shown on the lower right side.

We find that z ~ 6 galaxies in our sample have a median stellar mass log(M⋆/M⊙)=8.7-0.7+1.3\hbox{$\log(\mstar/\msun)=8.7^{+1.3}_{-0.7}$}, an age of 25-24+769Myr\hbox{$25^{+769}_{-24}~\mathrm{Myr}$}, an instantaneous SFR log(SFR/M⊙yr-1)=1.4-0.7+0.9\hbox{$\log(\textit{SFR}/\msunyr)=1.4^{+0.9}_{-0.7}$}, and a color excess E(B−V)=0.06-0.06+0.11\hbox{${E(B-V)}=0.06^{+0.11}_{-0.06}$} (assuming an SMC curve, twice this value for a Calzetti or Reddy curve). When we define an LAE as a galaxy with EW(Lyα) ≥ 20 Å, then we find than non-LAE have typical properties similar to the average of the sample (they made up 75% of the sample), while LAEs are slightly less massive, less star forming, and have a higher specific SFR (SFR/M⋆). The main difference between LAEs and non-LAEs is the dust extinction, with LAEs having twice lower color excesses than the typical value for non-LAEs. Again, this relation between dust extinction and the ability for Lyα photons to escape has been found in previous studies at lower redshift (e.g., Pentericci et al. 2007; Verhamme et al. 2008; Atek et al. 2009; Hayes et al. 2011).

We also derived the median fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} for our sample with fesceff(Lyα)=0.23-0.17+0.36\hbox{$\fefflya=0.23^{+0.36}_{-0.17}$}. This result is mostly independent of the model assumed. Our fesceff(Lyα)\hbox{$\fefflya$} is remarkably consistent with values derived at by comparing the Lyα and UV luminosity functions z ~ 6 (Hayes et al. 2011; Blanc et al. 2011; Dijkstra & Jeeson-Daniel 2013). We discuss the implication of this result in Sect. 5.

4.4. Effect of spectral synthesis models accounting for binary stars

Until recently, the effects of binary stars and stellar rotation were neglected in stellar population synthesis models (e.g., Eldridge et al. 2008; Eldridge & Stanway 2009; Levesque et al. 2012). Models that take these effects into account are able to fit young local star clusters (Wofford et al. 2016) and are necessary to reproduce nebular emission lines that are not typically observed in local galaxies (e.g., C ivλ1550, C iii]λ1909, and He iiλ1640) but seem more common at high-z (e.g., Shapley et al. 2003; Stark et al. 2014; Steidel et al. 2016; Vanzella et al. 2016a; Amorín et al. 2017; Smit et al. 2017; Vanzella et al. 2017). These lines require harder ionizing spectra and cannot be reproduced by models that do not take binaries or rotation into account. The main difference between the standard BC03 templates that are used to perform SED fitting in this work and models that account for binaries and/or rotation is an increased ionizing flux and a harder ionizing flux (Stanway et al. 2016). Models with an increased ionizing photon output have also been favored recently because of the current stringent constraints on the typical LyC escape fraction of star-forming galaxies (e.g., Grazian et al. 2016) that are difficult to reconcile with a realistic scenario for the cosmic reionization where star-forming galaxies are thought to be the main contributors to the ionizing background (Bouwens et al. 2016b).

The code called Binary Population and Spectral Synthesis (BPASS; Eldridge & Stanway 2009) was developed specifically to take binary evolution into account in modelling stellar populations. We used the BPASSv21 models with Z = 0.2 Z⊙ for a constant SFH to fit our sample, and we compared the results with those obtained with BC03 templates. An example of a fit is shown in Fig. 8. BPASS models are able to reproduce UV slopes as well as BC03 (Sect. 4.1), and the physical parameters are similar to those derived with BC03, except for the stellar mass. As shown in Fig. 10, because BPASS models have a larger ionizing photon output, emission line fluxes and equivalent widths at a given age and dust extinction are larger than in BC03 results. EW([O iii]+Hβ) are more than twice as large with BPASS than with BC03. While the trend of EW([O iii]+Hβ) with redshift is uncertain, mainly because of the gap between z ~ 5.5 and z = 8.0 with no constraints on EW except for the small samples from Smit et al. (2014) and Castellano et al. (2017), it seems that the values that we derive for our z ~ 6 sample using either BC03 or BPASS templates are consistent with expectations regarding results at z< 6 and result at z ~ 8 from Labbé et al. (2013). While results obtained with BPASS and BC03 are consistent within their uncertainties, the large EWs found with BPASS have an effect on stellar mass estimation: on average, stellar masses are 0.4 dex lower using BPASS templates2. Another effect of using BPASS templates is that the predicted Lyα fluxes are higher and the effective escape fraction in this case is fesceff(Lyα)=0.15-0.10+0.24\hbox{$\fefflya=0.15^{+0.24}_{-0.10}$}. This lower fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} value seem in stronger contrast with values from the literature than the fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} derived in Sect. 4.3, but it is still consistent within the uncertainties with the values from other studies (Dijkstra & Jeeson-Daniel 2013).

Using BPASS templates, our results remain generally unchanged, except for the emission lines strength, because of the increased ionizing output. Accordingly, the stellar masses are decreased because of the line contribution to IRAC1 and IRAC2. We cannot conclude about the accuracy of the binary modeling in BPASS, and this will have to be tested with JWST observations (Stanway 2017). A possible test would be to perform SED fitting of high-z galaxies with BPASS at a redshift where empirical constraints on emission line EWs are available (e.g., z ~ 4; Shim et al. 2011).

5. Discussion

Several studies have tried to derive the effect of the IGM on the Lyα visibility in a fully ionized Universe. Dijkstra et al. (2007), Zheng et al. (2010), and Laursen et al. (2011) found the IGM transmission to Lyα (TIGM) to be low with TIGM ≤ 0.01−0.3 at z ~ 6. Values as low as TIGM = 0.01 cannot be reconciled with the effective escape fraction found in our work fesceff(Lyα)=0.23-0.17+0.36\hbox{$\fefflya=0.23^{+0.36}_{-0.17}$}, but higher values (TIGM ~ 0.3) would be consistent. We have defined the effective Lyα escape fraction as the result of the combined effects of ISM, CGM, and IGM, and the relative Lyα escape fraction is defined as the result of ISM alone, then fesceff(Lyα)=TIGM×fescrel(Lyα).\begin{equation} \fefflya=\tigm\times\flyarel. \label{eq:tigm} \end{equation}(3)To constrain TIGM, we therefore need to have constraints on fescrel(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{rel}\mathrm{(Ly}\alpha)$}. Several relations have been derived between E(B−V) and the effective Lyα escape fraction from z ~ 0 to z ~ 3 (e.g., Verhamme et al. 2008; Atek et al. 2009; Kornei et al. 2010; Hayes et al. 2011; Yang et al. 2017), and while the definition of E(B−V) varies among studies, they all find that fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} decreases with increasing color excess. Interestingly, at these lower redshifts, the effect of the IGM on the Lyα visibility is expected to be much lower (TIGM ~ 0.8 at z ~ 3.5; Laursen et al. 2011) and so fesceff(Lyα)~fescrel(Lyα)\hbox{$\fefflya\sim\flyarel$}. While the large uncertainties on our derived physical parameters like E(B−V) and fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} for individual galaxies preclude any attempt to derive similar relations with our data, we stress that on average we find that the main difference between LAEs and non-LAEs is the dust extinction (Sect. 4.3). This result suggests that the processes governing Lyα escape from galaxies at low redshift are similar to those at high redshift. Thus to place constraints on TIGM, we assumed that there is a relation between E(B−V) and fesc(Lyα) at z ~ 6 similar to those found at low redshift.

The first difficulty arises from the choice of the relation that we wish to use at z ~ 6. For example, Atek et al. (2009) derived E(B−V) assuming the Cardelli et al. (1989) attenuation curve and using the Balmer decrement, while Hayes et al. (2011) used stellar color excesses derived from SED fitting and a Calzetti et al. (2000) curve, finally Yang et al. (2017) added a term based on Lyα velocity red peak on the relation between E(B−V) and fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$}.

We chose to use the relation described by Eq. (4) in Hayes et al. (2011) because the E(B−V) values are derived in the same way as in the present work. This relation is fescrel(Lyα)=CLyα×10−0.4 × E(B−V) × kLyα\begin{equation} \flyarel=C_\mathrm{Ly\alpha}\times10^{-0.4\,\times\, {E(B-V)} \,\times\, k_\mathrm{Ly\alpha}} \label{eq:hayes} \end{equation}(4)Hayes et al. (2011) derived a value of CLyα = 0.445 and kLyα = 12 using a Calzetti curve.

However, because of the numerous uncertainties about z ~ 6 galaxies, such as the ionizing output of the stellar population or the dust attenuation curve (Bouwens et al. 2016a), we tested different sets of assumptions to derive the average color excess E(B−V) of our sample, using both BC03 and BPASS templates with Calzetti and SMC curves. The difference in terms of average color excess between BPASS and BC03 is negligible, but the choice of attenuation curve introduces a difference of a factor 2, with the Calzetti curve leading to higher color excess. Using Eq. (4), we obtain fescrel(Lyα)=0.08-0.03+0.12\hbox{$\flyarel=0.08^{+0.12}_{-0.03}$} (BC03+Calzetti), fescrel(Lyα)=0.06-0.03+0.18\hbox{$\flyarel=0.06^{+0.18}_{-0.03}$} (BPASS+Calzetti), and fescrel(Lyα)=0.22-0.15+0.06\hbox{$\flyarel=0.22^{+0.06}_{-0.15}$} (BC03+SMC and BPASS+SMC). Then we use Eq. (3)with the two values derived for fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$} in Sects. 4.3 and 4.4, using BC03 and BPASS templates, respectively, to place constraints on the IGM transmission to Lyα photons. Accounting for all the models considered, we obtain TIGM ≥ 0.18. This value is relatively high in comparison with most of the theoretical studies that derived TIGM, but when they accounted for outflows, Dijkstra et al. (2011) found high TIGM like this at z ~ 6 (TIGM> 0.50). The lower limit that we find for the IGM transmission would therefore be easily explained if outflows were ubiquitous in z ~ 6 galaxies, which seems consistent with current high-redshift observations (Stark et al. 2017), while possibly with a lower velocity than at z ~ 2 (Pentericci et al. 2016). Dijkstra et al. (2011) stressed than even relatively low outflow velocities can be sufficient to cause a high IGM transparency to Lyα photons.

6. Conclusions

We reported deep observations of an i-dropout sample with VLT/FORS2 to search for Lyα emission. The dropout selection was designed to avoid bias toward faint LAEs with large EW(Lyα). Combining our data with archival data, we constructed a large star-forming galaxy sample spectroscopically confirmed at z ~ 6, with 127 galaxies with redshift confirmed either by detecting Lyα emission/continuum emission (Lyman break) or by excluding a low-redshift solution through the lack of detection of Hα, [O iii]λλ4959,5007, or [O ii]λ3727. All our galaxies are H-band detected. The size of our sample, which covers five fields, allowed us to determine a new z ~ 6 LAE fraction, minimizing cosmic variance. We derived physical properties using SED fitting, while we minimized the number of assumptions in our analysis to compare the properties of LAEs and non-LAEs, derived the effective escape fraction fesceff(Lyα)\hbox{${f}_\mathrm{esc}^\mathrm{eff}\mathrm{(Ly}\alpha)$}, and constrained the IGM transmission to Lyα photons TIGM.

In summary, we find the following.

  • 1.

    The median LAE fractions for bright and faint galaxies in oursample are lower than has been found in previous studies(e.g., Starket al. 2011), while it is stillconsistent with results reported in the literature within theuncertainties.

  • 2.

    Our data are consistent with a drop or a flattening of the relation between the LAE fraction and redshift at 5 <z< 6. This can be a sign of an already increasing IGM neutral fraction at z< 6.

  • 3.

    By comparing SFRSED with SFRLyα, we find that declining SFHs underestimate the SFR for 50% of our spectroscopically detected sample.

  • 4.

    Our sample exhibits the same trends between EW(Lyα) and MUV, and between EW(Lyα) and the UVβ slopes as previously reported at lower redshift (e.g., Pentericci et al. 2009): the largest EW(Lyα) is found for the faintest and bluest galaxies. LAEs are slightly less massive and less strongly star-forming than non-LAEs, but these differences are well within the uncertainties. The main difference is the dust extinction, with an average color excess for non-LAEs twice as high as the average LAE color excess. These results are mostly independent of assumptions.

  • 5.

    We tested stellar templates that incorporate the effect of binaries (BPASSv2). This led to similar physical properties, except for increased nebular emission fluxes due to a higher ionizing photon output, and accordingly an increase in EW([O iii]+Hβ), which led to an average decrease in stellar mass by ~ 0.4 dex.

  • 6.

    By comparing observed Lyα luminosities with SED-predicted Lyα luminosities, we derived an effective escape fraction of fesceff(Lyα)=0.23-0.17+0.36\hbox{$\fefflya=0.23^{+0.36}_{-0.17}$}, consistent with values derived by comparing UV and observed Lyα luminosities (Blanc et al. 2011; Hayes et al. 2011).

  • 7.

    Assuming that physical processes governing the escape of Lyα photons from galaxies are similar at low and high redshift, we derived a lower limit to the IGM transmission to Lyα photons TIGM ≳ 0.20. An IGM transmission this large is expected if outflows are present (Dijkstra et al. 2011) which is also consistent with current constraints (Pentericci et al. 2016; Stark et al. 2017).

2

We computed the mass normalization of BPASSv2 assuming a 30% mass fraction recycled in the ISM, as in Castellano et al. (2017).

Acknowledgments

This paper has been greatly improved by the referee’s comments and suggestions. We thank Anne Verhamme, Pascal Oesch, Mark Dijkstra, Matthew Hayes, and Daniel Schaerer for useful discussions and suggestions. R.M. acknowledges support by the Science and Technology Facilities Council (STFC) and the ERC Advanced Grant 695671. QUENCH.

References

  1. Amorín, R., Fontana, A., Pérez-Montero, E., et al. 2017, Nat. Astron., 1, 0052 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anders, P., & Fritze-v. Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Ando, M., Ohta, K., Iwata, I., et al. 2006, ApJ, 645, L9 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arnouts, S., D’Odorico, S., Cristiani, S., et al. 1999, A&A, 341, 641 [NASA ADS] [Google Scholar]
  5. Atek, H., Kunth, D., Schaerer, D., et al. 2009, A&A, 506, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Atek, H., Kunth, D., Schaerer, D., et al. 2014, A&A, 561, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bagley, M. B., Scarlata, C., Henry, A., et al. 2017, ApJ, 837, 11 [NASA ADS] [CrossRef] [Google Scholar]
  8. Becker, G. D., Bolton, J. S., Madau, P., et al. 2015, MNRAS, 447, 3402 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bian, F., Fan, X., McGreer, I., Cai, Z., & Jiang, L. 2017, ApJ, 837, L12 [NASA ADS] [CrossRef] [Google Scholar]
  10. Blanc, G. A., Adams, J. J., Gebhardt, K., et al. 2011, ApJ, 736, 31 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bolton, J. S., & Haehnelt, M. G. 2013, MNRAS, 429, 1695 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bolzonella, M., Miralles, J., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
  13. Borthakur, S., Heckman, T. M., Leitherer, C., & Overzier, R. A. 2014, Science, 346, 216 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2014, ApJ, 793, 115 [Google Scholar]
  17. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015a, ApJ, 811, 140 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015b, ApJ, 803, 34 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016a, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]
  20. Bouwens, R. J., Smit, R., Labbé, I., et al. 2016b, ApJ, 831, 176 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  22. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  23. Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  25. Caruana, J., Bunker, A. J., Wilkins, S. M., et al. 2014, MNRAS, 443, 2831 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cassata, P., Tasca, L. A. M., Le Fèvre, O., et al. 2015, A&A, 573, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Castellano, M., Fontana, A., Boutsia, K., et al. 2010a, A&A, 511, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Castellano, M., Fontana, A., Paris, D., et al. 2010b, A&A, 524, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Castellano, M., Fontana, A., Grazian, A., et al. 2012, A&A, 540, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Castellano, M., Sommariva, V., Fontana, A., et al. 2014, A&A, 566, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Castellano, M., Pentericci, L., Fontana, A., et al. 2017, ApJ, 839, 73 [NASA ADS] [CrossRef] [Google Scholar]
  32. Cen, R., & Kimm, T. 2015, ApJ, 801, L25 [NASA ADS] [CrossRef] [Google Scholar]
  33. Chary, R.-R., Stern, D., & Eisenhardt, P. 2005, ApJ, 635, L5 [NASA ADS] [CrossRef] [Google Scholar]
  34. Cirasuolo, M., McLure, R. J., Dunlop, J. S., et al. 2007, MNRAS, 380, 585 [NASA ADS] [CrossRef] [Google Scholar]
  35. Curtis-Lake, E., McLure, R. J., Pearce, H. J., et al. 2012, MNRAS, 422, 1425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Curtis-Lake, E., McLure, R. J., Dunlop, J. S., et al. 2013, MNRAS, 429, 302 [NASA ADS] [CrossRef] [Google Scholar]
  37. Curtis-Lake, E., McLure, R. J., Dunlop, J. S., et al. 2016, MNRAS, 457, 440 [NASA ADS] [CrossRef] [Google Scholar]
  38. Dayal, P., Maselli, A., & Ferrara, A. 2011, MNRAS, 410, 830 [NASA ADS] [CrossRef] [Google Scholar]
  39. De Barros, S., Schaerer, D., & Stark, D. P. 2014, A&A, 563, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. De Barros, S., Vanzella, E., Amorín, R., et al. 2016, A&A, 585, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Dijkstra, M., & Jeeson-Daniel, A. 2013, MNRAS, 435, 3333 [NASA ADS] [CrossRef] [Google Scholar]
  42. Dijkstra, M., Lidz, A., & Wyithe, J. S. B. 2007, MNRAS, 377, 1175 [NASA ADS] [CrossRef] [Google Scholar]
  43. Dijkstra, M., Mesinger, A., & Wyithe, J. S. B. 2011, MNRAS, 414, 2139 [NASA ADS] [CrossRef] [Google Scholar]
  44. Dijkstra, M., Wyithe, S., Haiman, Z., Mesinger, A., & Pentericci, L. 2014, MNRAS, 440, 3309 [NASA ADS] [CrossRef] [Google Scholar]
  45. Domínguez, A., Siana, B., Brooks, A. M., et al. 2015, MNRAS, 451, 839 [NASA ADS] [CrossRef] [Google Scholar]
  46. Duncan, K., Conselice, C. J., Mortlock, A., et al. 2014, MNRAS, 444, 2960 [NASA ADS] [CrossRef] [Google Scholar]
  47. Dunlop, J. S., Rogers, A. B., McLure, R. J., et al. 2013, MNRAS, 432, 3520 [NASA ADS] [CrossRef] [Google Scholar]
  48. Eldridge, J. J., & Stanway, E. R. 2009, MNRAS, 400, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  49. Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
  50. Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
  51. Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
  52. Eyles, L. P., Bunker, A. J., Stanway, E. R., et al. 2005, MNRAS, 364, 443 [NASA ADS] [CrossRef] [Google Scholar]
  53. Eyles, L. P., Bunker, A. J., Ellis, R. S., et al. 2007, MNRAS, 374, 910 [NASA ADS] [CrossRef] [Google Scholar]
  54. Faisst, A. L., Capak, P., Hsieh, B. C., et al. 2016, ApJ, 821, 122 [Google Scholar]
  55. Finkelstein, S. L., Papovich, C., Salmon, B., et al. 2012, ApJ, 756, 164 [NASA ADS] [CrossRef] [Google Scholar]
  56. Finkelstein, S. L., Ryan, Jr., R. E., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
  57. Fontana, A., D’Odorico, S., Poli, F., et al. 2000, AJ, 120, 2206 [NASA ADS] [CrossRef] [Google Scholar]
  58. Fontana, A., Poli, F., Menci, N., et al. 2003, ApJ, 587, 544 [NASA ADS] [CrossRef] [Google Scholar]
  59. Fontana, A., Vanzella, E., Pentericci, L., et al. 2010, ApJ, 725, L205 [Google Scholar]
  60. Fumagalli, M., Patel, S. G., Franx, M., et al. 2012, ApJ, 757, L22 [NASA ADS] [CrossRef] [Google Scholar]
  61. Galametz, A., Grazian, A., Fontana, A., et al. 2013, ApJS, 206, 10 [NASA ADS] [CrossRef] [Google Scholar]
  62. Giallongo, E., Grazian, A., Fiore, F., et al. 2015, A&A, 578, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
  64. Grazian, A., Giallongo, E., Gerbasi, R., et al. 2016, A&A, 585, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
  66. Guaita, L., Pentericci, L., Grazian, A., et al. 2016, A&A, 587, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
  68. Hagen, A., Zeimann, G. R., Behrens, C., et al. 2016, ApJ, 817, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Hathi, N. P., LeFèvre, O., Ilbert, O., et al. 2016, A&A, 588, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Hayes, M., Schaerer, D., Östlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
  71. Hayes, M., Östlin, G., Duval, F., et al. 2014, ApJ, 782, 6 [NASA ADS] [CrossRef] [Google Scholar]
  72. Heckman, T. M., Borthakur, S., Overzier, R., et al. 2011, ApJ, 730, 5 [Google Scholar]
  73. Hopkins, P. F., Kereš, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
  74. Izotov, Y. I., Orlitová, I., Schaerer, D., et al. 2016, Nature, 529, 159 [Google Scholar]
  75. Jaskot, A. E., & Oey, M. S. 2013, ApJ, 766, 91 [NASA ADS] [CrossRef] [Google Scholar]
  76. Jensen, H., Laursen, P., Mellema, G., et al. 2013, MNRAS, 428, 1366 [NASA ADS] [CrossRef] [Google Scholar]
  77. Jiang, L., Finlator, K., Cohen, S. H., et al. 2016, ApJ, 816, 16 [NASA ADS] [CrossRef] [Google Scholar]
  78. Jones, T., Stark, D. P., & Ellis, R. S. 2012, ApJ, 751, 51 [NASA ADS] [CrossRef] [Google Scholar]
  79. Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
  80. Kimm, T., & Cen, R. 2014, ApJ, 788, 121 [NASA ADS] [CrossRef] [Google Scholar]
  81. Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
  82. Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
  83. Kornei, K. A., Shapley, A. E., Erb, D. K., et al. 2010, ApJ, 711, 693 [NASA ADS] [CrossRef] [Google Scholar]
  84. Kulas, K. R., Shapley, A. E., Kollmeier, J. A., et al. 2012, ApJ, 745, 33 [NASA ADS] [CrossRef] [Google Scholar]
  85. Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 716, L103 [NASA ADS] [CrossRef] [Google Scholar]
  86. Labbé, I., Oesch, P. A., Bouwens, R. J., et al. 2013, ApJ, 777, L19 [NASA ADS] [CrossRef] [Google Scholar]
  87. Laursen, P., Sommer-Larsen, J., & Razoumov, A. O. 2011, ApJ, 728, 52 [NASA ADS] [CrossRef] [Google Scholar]
  88. Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  89. Lehnert, M. D., & Bremer, M. 2003, ApJ, 593, 630 [NASA ADS] [CrossRef] [Google Scholar]
  90. Leitet, E., Bergvall, N., Piskunov, N., & Andersson, B.-G. 2011, A&A, 532, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Leitet, E., Bergvall, N., Hayes, M., Linné, S., & Zackrisson, E. 2013, A&A, 553, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Levesque, E. M., Leitherer, C., Ekstrom, S., Meynet, G., & Schaerer, D. 2012, ApJ, 751, 67 [NASA ADS] [CrossRef] [Google Scholar]
  93. Livermore, R. C., Finkelstein, S. L., & Lotz, J. M. 2017, ApJ, 835, 113 [NASA ADS] [CrossRef] [Google Scholar]
  94. Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [NASA ADS] [CrossRef] [Google Scholar]
  95. Mármol-Queraltó, E., McLure, R. J., Cullen, F., et al. 2016, MNRAS, 460, 3587 [NASA ADS] [CrossRef] [Google Scholar]
  96. Matthee, J., Sobral, D., Oteo, I., et al. 2016, MNRAS, 458, 449 [NASA ADS] [CrossRef] [Google Scholar]
  97. Matthee, J., Sobral, D., Darvish, B., et al. 2017, MNRAS, 472, 772 [NASA ADS] [CrossRef] [Google Scholar]
  98. McLure, R. J., Dunlop, J. S., de Ravel, L., et al. 2011, MNRAS, 418, 2074 [NASA ADS] [CrossRef] [Google Scholar]
  99. Mesinger, A., Aykutalp, A., Vanzella, E., et al. 2015, MNRAS, 446, 566 [NASA ADS] [CrossRef] [Google Scholar]
  100. Mortlock, A., Conselice, C. J., Hartley, W. G., et al. 2015, MNRAS, 447, 2 [NASA ADS] [CrossRef] [Google Scholar]
  101. Nakajima, K., & Ouchi, M. 2014, MNRAS, 442, 900 [NASA ADS] [CrossRef] [Google Scholar]
  102. Nagamine, K., Ouchi, M., Springel, V., & Hernquist, L. 2010, PASJ, 62, 1455 [NASA ADS] [CrossRef] [Google Scholar]
  103. Nayyeri, H., Cooray, A., Jullo, E., et al. 2017, ApJ, 844, 82 [NASA ADS] [CrossRef] [Google Scholar]
  104. Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2013a, ApJ, 773, 75 [NASA ADS] [CrossRef] [Google Scholar]
  105. Oesch, P. A., Labbé, I., Bouwens, R. J., et al. 2013b, ApJ, 772, 136 [NASA ADS] [CrossRef] [Google Scholar]
  106. Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2014, ApJ, 786, 108 [NASA ADS] [CrossRef] [Google Scholar]
  107. Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
  108. Ono, Y., Ouchi, M., Mobasher, B., et al. 2012, ApJ, 744, 83 [NASA ADS] [CrossRef] [Google Scholar]
  109. Ota, K., Richard, J., Iye, M., et al. 2012, MNRAS, 423, 2829 [NASA ADS] [CrossRef] [Google Scholar]
  110. Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [NASA ADS] [CrossRef] [Google Scholar]
  111. Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2010, ApJ, 723, 869 [NASA ADS] [CrossRef] [Google Scholar]
  112. Pentericci, L., Grazian, A., Fontana, A., et al. 2007, A&A, 471, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Pentericci, L., Grazian, A., Fontana, A., et al. 2009, A&A, 494, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Pentericci, L., Grazian, A., Scarlata, C., et al. 2010, A&A, 514, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Pentericci, L., Fontana, A., Vanzella, E., et al. 2011, ApJ, 743, 132 [NASA ADS] [CrossRef] [Google Scholar]
  116. Pentericci, L., Vanzella, E., Fontana, A., et al. 2014, ApJ, 793, 113 [NASA ADS] [CrossRef] [Google Scholar]
  117. Pentericci, L., Carniani, S., Castellano, M., et al. 2016, ApJ, 829, L11 [NASA ADS] [CrossRef] [Google Scholar]
  118. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
  120. Price, S. H., Kriek, M., Brammer, G. B., et al. 2014, ApJ, 788, 86 [NASA ADS] [CrossRef] [Google Scholar]
  121. Rasappu, N., Smit, R., Labbé, I., et al. 2016, MNRAS, 461, 3886 [NASA ADS] [CrossRef] [Google Scholar]
  122. Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
  123. Reddy, N. A., Pettini, M., Steidel, C. C., et al. 2012, ApJ, 754, 25 [NASA ADS] [CrossRef] [Google Scholar]
  124. Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
  125. Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2017, ApJ, submitted [arXiv:1705.09302] [Google Scholar]
  126. Robertson, B. E., Ellis, R. S., Dunlop, J. S., McLure, R. J., & Stark, D. P. 2010, Nature, 468, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  127. Robertson, B. E., Furlanetto, S. R., Schneider, E., et al. 2013, ApJ, 768, 71 [NASA ADS] [CrossRef] [Google Scholar]
  128. Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [NASA ADS] [CrossRef] [Google Scholar]
  129. Rutkowski, M. J., Scarlata, C., Henry, A., et al. 2017, ApJ, 841, L27 [NASA ADS] [CrossRef] [Google Scholar]
  130. Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
  131. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  132. Schaerer, D., & De Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Schaerer, D., & De Barros, S. 2010, A&A, 515, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Schaerer, D., & Verhamme, A. 2008, A&A, 480, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  135. Schaerer, D., De Barros, S., & Stark, D. P. 2011, A&A, 536, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Schenker, M. A., Stark, D. P., Ellis, R. S., et al. 2012, ApJ, 744, 179 [NASA ADS] [CrossRef] [Google Scholar]
  137. Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2014, ApJ, 795, 20 [NASA ADS] [CrossRef] [Google Scholar]
  138. Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
  139. Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
  140. Shapley, A. E., Steidel, C. C., Strom, A. L., et al. 2016, ApJ, 826, L24 [NASA ADS] [CrossRef] [Google Scholar]
  141. Shim, H., Chary, R.-R., Dickinson, M., et al. 2011, ApJ, 738, 69 [NASA ADS] [CrossRef] [Google Scholar]
  142. Shivaei, I., Reddy, N. A., Steidel, C. C., & Shapley, A. E. 2015, ApJ, 804, 149 [NASA ADS] [CrossRef] [Google Scholar]
  143. Smit, R., Bouwens, R. J., Labbé, I., et al. 2014, ApJ, 784, 58 [NASA ADS] [CrossRef] [Google Scholar]
  144. Smit, R., Swinbank, A. M., Massey, R., et al. 2017, MNRAS, 467, 3306 [NASA ADS] [Google Scholar]
  145. Stanway, E. R. 2017, The Lives and Death-Throes of Massive Stars, Proc. of IAU Symp., 329, 305 [NASA ADS] [Google Scholar]
  146. Stanway, E. R., Bremer, M. N., & Lehnert, M. D. 2008, MNRAS, 385, 493 [NASA ADS] [CrossRef] [Google Scholar]
  147. Stanway, E. R., Eldridge, J. J., & Becker, G. D. 2016, MNRAS, 456, 485 [NASA ADS] [CrossRef] [Google Scholar]
  148. Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [NASA ADS] [CrossRef] [Google Scholar]
  149. Stark, D. P., Ellis, R. S., & Ouchi, M. 2011, ApJ, 728, L2 [NASA ADS] [CrossRef] [Google Scholar]
  150. Stark, D. P., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
  151. Stark, D. P., Richard, J., Siana, B., et al. 2014, MNRAS, 445, 3200 [NASA ADS] [CrossRef] [Google Scholar]
  152. Stark, D. P., Ellis, R. S., Charlot, S., et al. 2017, MNRAS, 464, 469 [NASA ADS] [CrossRef] [Google Scholar]
  153. Steidel, C. C., Erb, D. K., Shapley, A. E., et al. 2010, ApJ, 717, 289 [NASA ADS] [CrossRef] [Google Scholar]
  154. Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
  155. Tilvi, V., Papovich, C., Finkelstein, S. L., et al. 2014, ApJ, 794, 5 [NASA ADS] [CrossRef] [Google Scholar]
  156. Trainor, R. F., Strom, A. L., Steidel, C. C., & Rudie, G. C. 2016, ApJ, 832, 171 [NASA ADS] [CrossRef] [Google Scholar]
  157. Vanzella, E., Cristiani, S., Dickinson, M., et al. 2008, A&A, 478, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  158. Vanzella, E., Grazian, A., Hayes, M., et al. 2010, A&A, 513, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
  160. Vanzella, E., Guo, Y., Giavalisco, M., et al. 2012, ApJ, 751, 70 [NASA ADS] [CrossRef] [Google Scholar]
  161. Vanzella, E., Fontana, A., Pentericci, L., et al. 2014a, A&A, 569, A78 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  162. Vanzella, E., Fontana, A., Zitrin, A., et al. 2014b, ApJ, 783, L12 [NASA ADS] [CrossRef] [Google Scholar]
  163. Vanzella, E., De Barros, S., Castellano, M., et al. 2015, A&A, 576, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  164. Vanzella, E., De Barros, S., Cupani, G., et al. 2016a, ApJ, 821, L27 [NASA ADS] [CrossRef] [Google Scholar]
  165. Vanzella, E., De Barros, S., Vasei, K., et al. 2016b, ApJ, 825, 41 [NASA ADS] [CrossRef] [Google Scholar]
  166. Vanzella, E., Castellano, M., Meneghetti, M., et al. 2017, ApJ, 842, 47 [NASA ADS] [CrossRef] [Google Scholar]
  167. Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  168. Verhamme, A., Orlitová, I., Schaerer, D., & Hayes, M. 2015, A&A, 578, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  169. Wisotzki, L., Bacon, R., Blaizot, J., et al. 2016, A&A, 587, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  170. Wofford, A., Charlot, S., Bruzual, G., et al. 2016, MNRAS, 457, 4296 [NASA ADS] [CrossRef] [Google Scholar]
  171. Wuyts, S., Förster Schreiber, N. M., Lutz, D., et al. 2011, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
  172. Yan, H., Dickinson, M., Stern, D., et al. 2005, ApJ, 634, 109 [NASA ADS] [CrossRef] [Google Scholar]
  173. Yan, H., Dickinson, M., Giavalisco, M., et al. 2006, ApJ, 651, 24 [NASA ADS] [CrossRef] [Google Scholar]
  174. Yang, H., Malhotra, S., Gronke, M., et al. 2017, ApJ, 844, 171 [NASA ADS] [CrossRef] [Google Scholar]
  175. Zackrisson, E., Bergvall, N., & Leitet, E. 2008, ApJ, 676, L9 [NASA ADS] [CrossRef] [Google Scholar]
  176. Zackrisson, E., Inoue, A. K., & Jensen, H. 2013, ApJ, 777, 39 [NASA ADS] [CrossRef] [Google Scholar]
  177. Zheng, Z., Cen, R., Trac, H., & Miralda-Escudé, J. 2010, ApJ, 716, 574 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

2D signal-to-noise ratio spectra and sky spectra of two faint Lyα emitters. The two insets show the corresponding one-dimensional FORS2 spectra, with red arrows highlighting positions of the Lyα-break, which are also visible in 2D spectra. For the galaxy at the top, EW(Lyα) ≤ 1.3 Å, and for the galaxy at the bottom, EW(Lyα) = 10.0 ± 1.3 Å.
In the text
thumbnail Fig. 2

Redshift distributions for the spectroscopically confirmed and photometric samples in white and black, respectively.
In the text
thumbnail Fig. 3

Comparison of EW(Lyα) derived from spectra alone and from spectra and photometry (see Sect. 2.2). We show the results for the ten galaxies with a spectroscopically detected continuum. The dashed line shows the one-to-one relation, and the dotted lines show ± 25% from the one-to-one relation.
In the text
thumbnail Fig. 4

Distribution of the sample as a function of the number of measured fluxes in Spitzer/IRAC bands (black histogram). We show in blue and red the distribution of the flux measurement with S ! N ≥ 2 and S ! N ≥ 3, respectively.
In the text
thumbnail Fig. 5

Fraction of LAEs (with EW(Lyα) > 25 Å, XLyα25\hbox{$X_\mathrm{\lya}^{25}$}) at 4 ≤ z ≤ 8 for the brightest (MUV< −20.25, left panel) and faintest (MUV> −20.25, right panel) galaxies. We show the results from Stark et al. (2011), Schenker et al. (2014), Ono et al. (2012), Pentericci et al. (2011), Tilvi et al. (2014), Cassata et al. (2015), and Curtis-Lake et al. (2012). We introduce slight offsets in redshift to increase clarity when necessary.
In the text
thumbnail Fig. 6

2D S/N and sky spectra for two faint LAEs at z = 5.92 (top) and z = 6.09 (bottom) with EW(Lyα) = 101 Å and EW(Lyα) = 330 Å, respectively (see text).
In the text
thumbnail Fig. 7

Top: EW([O iii]+Hβ) evolution with age for Z = 0.2 Z⊙ and the range of star formation used in this work: exponentially rising (blue), and exponentially declining (red). Bottom: same for EW(Lyα).
In the text
thumbnail Fig. 8

Observed (black and white squares) and best-fit SEDs (solid lines) of a z = 5.786 galaxy. White squares show bands not used in the SED fitting because of possible impact of the Lyα line. The error bars of the observed wavelength indicate the surface of the normalized filter transmission curve. SED fits in blue and red are based on Bruzual & Charlot (2003) models with (red) and without (yellow) nebular emission, and a fit using BPASSv2.0 (Eldridge & Stanway 2016; Stanway et al. 2016) is shown in blue (Sect. 4.4). Color crosses show the synthesized flux in the filters. Without nebular emission, age and stellar mass are ~ 109 yr and ~ 1010.5M⊙ respectively, while accounting for nebular emission gives ~ 106 yr and ~ 109M⊙.
In the text
thumbnail Fig. 9

Relation between log (SFRSED) and log (SFRLyα/SFRSED) for galaxies with detected Lyα emission, assuming a declining (red dots) and a constant SFH (blue dots). Lyα luminosities have not been corrected for dust. The dashed line shows log (SFRLyα) = log (SFRSED). We recall that SFRLyα is a lower limit to the true SFR (see text).
In the text
thumbnail Fig. 10

EW([O iii]+Hβ) vs. redshift for different studies that empirically derived EW from the photometry (Shim et al. 2011; Labbé et al. 2013; Stark et al. 2013; Smit et al. 2014; Faisst et al. 2016; Mármol-Queraltó et al. 2016; Rasappu et al. 2016; Castellano et al. 2017) and the results obtained for the three SFHs used in the present work (rising, constant, and declining) assuming an SMC attenuation curve (alternative curves do not affect the results) and BC03 templates. We also show the result using BPASS templates (Sect. 4.4). For the studies deriving EW(Hα), we assume the typical ratio between this line and [O iii]+Hβ from Anders & Fritze-v. Alvensleben (2003) for a metallicity Z = 0.2 Z⊙. We show the relation between EW and redshift derived in Fumagalli et al. (2012), extrapolated to high redshift and for two different stellar masses (Smit et al. 2014).
In the text
thumbnail Fig. 11

EW(Lyα) vs. MUV. We show individual Lyα detections with black dots and 3σ upper limits with gray downward triangles. We also show the average EW in magnitude bins (red stars). These average values are derived by setting EW(Lyα) to zero for all undetected objects, which should provide a good approximation of the true relation between EW(Lyα) and MUV (Schenker et al. 2014).
In the text
thumbnail Fig. 12

EW(Lyα) vs. UVβ slope. Same symbols as in Fig. 11. For clarity, we show β error bars randomly for half of the sample.
In the text
thumbnail Fig. 13

Comparison between physical parameters (color excess, age, SFR, and stellar mass) derived with and without accounting for nebular emission, assuming a constant SFH and an SMC curve. Dashed lines show the one-to-one relations. The distribution for each parameter is shown at the top of each figure along the x-axis for parameters derived with nebular emission (blue histograms) and at the right side along the y-axis for parameters derived without nebular emission (red histograms). Typical error bars for each parameter are shown on the lower right side.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.