| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731049 | |
| Published online | 30 October 2017 | |
What are we learning from the relative orientation between density structures and the magnetic field in molecular clouds?
1 Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: soler@mpia.de
2 Laboratoire AIM, Paris-Saclay, CEA/IRFU/SAp – CNRS – Université Paris Diderot, 91191 Gif-sur-Yvette Cedex, France
Received: 26 April 2017
Accepted: 4 September 2017
We investigate the conditions of ideal magnetohydrodynamic (MHD) turbulence responsible for the relative orientation between density gradients (∇ρ) and magnetic fields (B) in molecular clouds (MCs). For that purpose, we construct an expression for the time evolution of the angle (φ) between ∇ρ and B based on the transport equations of MHD turbulence. Using this expression, we find that the configuration where ∇ρ and B are mostly parallel, cosφ = ± 1, and where ∇ρ and B are mostly perpendicular, cosφ = 0, constitute equilibrium points, that is, the system tends to evolve towards either of these configurations and they are more represented than others. This would explain the predominant alignment or anti-alignment between column density (NH) structures and the projected magnetic field orientation (⟨B̂⊥⟩) reported in observations. Additionally, we find that departures from the cosφ = 0 configurations are related to convergent flows, quantified by the divergence of the velocity field (∇·v) in the presence of a relatively strong magnetic field. This would explain the observed change in relative orientation between NH structures and ⟨B̂⊥⟩ towards MCs, from mostly parallel at low NH to mostly perpendicular at the highest NH, as the result of the gravitational collapse and/or convergence of flows. Finally, we show that the density threshold that marks the observed change in relative orientation towards MCs, from NH and ⟨B̂⊥⟩ being mostly parallel at low NH to mostly perpendicular at the highest NH, is related to the magnetic field strength and constitutes a crucial piece of information for determining the role of the magnetic field in the dynamics of MCs.
Key words: magnetohydrodynamics (MHD) / turbulence / ISM: general / ISM: structure / ISM: magnetic fields / ISM: clouds
© ESO, 2017
1. Introduction
The advent of novel observations of polarization from dust, in emission at submillimeter wavelengths and in absorption from background stars in the visible and near-infrared, provides an unprecedented amount of information on the magnetic field orientation integrated along the line of sight and projected on the plane of the sky (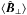 ) at molecular cloud (MC) scales (Crutcher 2012; Planck Collaboration I 2016). However, integrating this information to our understanding of the dynamical processes that produce density structures in the interstellar medium (ISM), from MCs to filaments and eventually stars, remains challenging (Bergin & Tafalla 2007; Hennebelle & Falgarone 2012; Klessen & Glover 2016).
) at molecular cloud (MC) scales (Crutcher 2012; Planck Collaboration I 2016). However, integrating this information to our understanding of the dynamical processes that produce density structures in the interstellar medium (ISM), from MCs to filaments and eventually stars, remains challenging (Bergin & Tafalla 2007; Hennebelle & Falgarone 2012; Klessen & Glover 2016).
One simple approach to obtain insight into the role of the magnetic field is the study of the relative orientation between the observed column density (NH) structures and 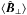 . Multiple studies of
. Multiple studies of 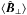 inferred from starlight polarization (e.g., Palmeirim et al. 2013; Li et al. 2013; Sugitani et al. 2011 and more recently Kusune et al. 2016; Santos et al. 2016; Soler et al. 2016; Hoq et al. 2017) use qualitative descriptions of the relative orientation between
inferred from starlight polarization (e.g., Palmeirim et al. 2013; Li et al. 2013; Sugitani et al. 2011 and more recently Kusune et al. 2016; Santos et al. 2016; Soler et al. 2016; Hoq et al. 2017) use qualitative descriptions of the relative orientation between 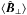 and the NH structures to argue the importance of the magnetic field in structuring the observed regions.
and the NH structures to argue the importance of the magnetic field in structuring the observed regions.
In emission from the diffuse ISM, quantitative analysis of the polarization observations at 353 GHz by the ESA Planck satellite show that over most of the sky, the majority of the elongated NH structures traced by dust thermal emission are predominantly aligned with the magnetic field measured on the structures (Planck Collaboration Int. XXXII 2016). This statistical trend, which becomes less striking with increasing column density, is similar to that found between low column density (NHi ≈ 5 × 1018 cm-2) fibers traced by Hi emission and 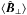 (Clark et al. 2014; Kalberla et al. 2016).
(Clark et al. 2014; Kalberla et al. 2016).
In emission from the denser ISM, quantitative analysis of the Planck polarization observations at 353 GHz towards ten nearby (d< 450 pc) MCs shows that the relative orientation between the column density structures and 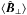 progressively changes with increasing column density from mostly parallel at log (NH/ cm-2) ≲ 21.7 to mostly perpendicular at log (NH/ cm-2) ≳ 21.7 (Planck Collaboration Int. XXXV 2016). Subsequent studies of the relative orientation between NH structures and
progressively changes with increasing column density from mostly parallel at log (NH/ cm-2) ≲ 21.7 to mostly perpendicular at log (NH/ cm-2) ≳ 21.7 (Planck Collaboration Int. XXXV 2016). Subsequent studies of the relative orientation between NH structures and 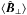 have identified similar trends using NH structures derived from Herschel observations at 20′′ resolution and
have identified similar trends using NH structures derived from Herschel observations at 20′′ resolution and 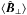 inferred from BLASTPol polarization observation at 250, 350, and 500 μm towards the Vela C molecular complex (Soler et al. 2017) as well as using NH structures derived from Herschel observations together with Planck 353 GHz polarization observations towards the high-latitude cloud L1642 (Malinen et al. 2016).
inferred from BLASTPol polarization observation at 250, 350, and 500 μm towards the Vela C molecular complex (Soler et al. 2017) as well as using NH structures derived from Herschel observations together with Planck 353 GHz polarization observations towards the high-latitude cloud L1642 (Malinen et al. 2016).
From the theoretical point of view, the magnetic field (B), whose observed energy density is in rough equipartition with other energy densities in the local ISM (Heiles & Crutcher 2005), imposes an asymmetry for the formation of condensations from the diffuse ISM. Condensation modes are unaffected when they propagate parallel to the mean direction of the field (B0), but inhibited by the magnetic pressure when they propagate normal to B0 (Field 1965). Consequently, condensations driven by thermal instability arise along B0 and MCs can be formed by shock waves only if the perturbations propagate almost parallel to the mean magnetic field (Hennebelle & Pérault 2000; Hartmann et al. 2001; Inoue et al. 2007; Körtgen & Banerjee 2015).
This theoretical framework suggests that the observed regimes in relative orientation between NH structures and 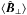 indicate something fundamental about the gathering of gas out of the diffuse ISM, which results in the formation of MCs and their subsequent evolution to form denser structures, such as filaments and cores. In this work, we explore the relation between the observed relative orientation between
indicate something fundamental about the gathering of gas out of the diffuse ISM, which results in the formation of MCs and their subsequent evolution to form denser structures, such as filaments and cores. In this work, we explore the relation between the observed relative orientation between 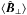 and the NH structures and the conditions imposed by the transport equations of magnetohydrodynamic (MHD) turbulence. For that purpose, we construct an expression for the evolution of the relative orientation between ∇ρ and B and evaluate the physical processes that are potentially responsible for the observed trends.
and the NH structures and the conditions imposed by the transport equations of magnetohydrodynamic (MHD) turbulence. For that purpose, we construct an expression for the evolution of the relative orientation between ∇ρ and B and evaluate the physical processes that are potentially responsible for the observed trends.
This paper is organized as follows. In Sect. 2 we introduce the transport equations of MHD turbulence and derive an expression for the relative orientation between ∇ρ and B. In Sect. 3 we discuss the implications of the derived relation and characterize it using, first, a set of simple cases and, second, the simulations of MHD turbulence in MCs that were used to characterize the analysis method presented in Planck Collaboration Int. XXXV (2016). Section 4 discusses the implications of the studied relation between ∇ρ and B. Finally, Sect. 5 gives our conclusions and anticipates future work. We reserve some additional analyses to Appendix A, where we present an expression for time evolution of the relative orientation between the magnetic fields, B, and the velocity fields, v.
2. Relative orientation between B and iso-density contours
2.1. Transport equations of magnetohydrodynamic turbulence
Using the Lagrangian form of the equations, which corresponds to looking at the fluid motion following an individual parcel as it moves through space and time, the continuity equation, which guarantees the conservation of mass, is 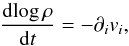 (1)where ρ and vi respectively are the density and velocity; the index i ranges between 0 and 2 and represents the axes of a 3D Cartesian reference frame. Here, and in the rest of the paper, summation over repeated indexes is implied following the Einstein summation convention.
(1)where ρ and vi respectively are the density and velocity; the index i ranges between 0 and 2 and represents the axes of a 3D Cartesian reference frame. Here, and in the rest of the paper, summation over repeated indexes is implied following the Einstein summation convention.
The magnetic field B is described by the Faraday equation 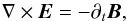 (2)where E is the electric field. Under the assumption of low magnetic diffusivity, Eq. (2)reduces to
(2)where E is the electric field. Under the assumption of low magnetic diffusivity, Eq. (2)reduces to 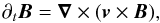 (3)which can be expanded as
(3)which can be expanded as 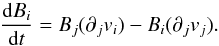 (4)
(4)
2.2. Time evolution of the relative orientation between ∇ρ and B
We construct an expression for the behavior of cosφ, the angle between ∇ρ and B, by combining the equations introduced in Sect. 2.1 as follows. By the definition of the scalar product of vectors, the cosine of the angle between ∇ρ and B corresponds to 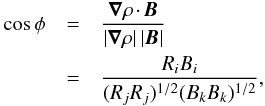 (5)where we introduce the convention Ri ≡ ∂ilog ρ. We note that the distribution of relative orientations between two sets of uniformly distributed random vectors in 3D is flat in the cosine of their separation angle, thus all the discussions of relative orientations in 3D are given in terms of cosφ (see Appendix C of Planck Collaboration Int. XXXV 2016).
(5)where we introduce the convention Ri ≡ ∂ilog ρ. We note that the distribution of relative orientations between two sets of uniformly distributed random vectors in 3D is flat in the cosine of their separation angle, thus all the discussions of relative orientations in 3D are given in terms of cosφ (see Appendix C of Planck Collaboration Int. XXXV 2016).
We apply the time derivative to the square of Eq. (5)and, assuming that the spatial and time derivatives can be commuted, we obtain ![\begin{eqnarray} \label{eq:costheta0} % \frac{{\rm d}(\cos^{2}\phi)}{{\rm d}t} &= &\frac{2}{(R_{k}R_{k})^{2}(B_{k}B_{k})^{2}}\,\bigg[\frac{{\rm d}(R_{i}B_{i})}{{\rm d}t}(R_{i}B_{i})(R_{m}R_{m})(B_{n}B_{n}) \notag \\ &&-\frac{{\rm d}(B_{i})}{{\rm d}t}B_{i}(R_{j}B_{j})^{2}(R_{m}R_{m}) -\frac{{\rm d}(R_{i})}{{\rm d}t}R_{i}(B_{n}B_{n})(R_{j}B_{j})^{2}\bigg]. % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq31.png) (6)Using the definitions
(6)Using the definitions 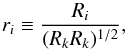 (7)and
(7)and 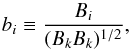 (8)which imply cosφ = ribi, Eq. (6)becomes
(8)which imply cosφ = ribi, Eq. (6)becomes ![\begin{eqnarray} \label{eq:costheta1} % \frac{{\rm d}(\cos\phi)}{{\rm d}t} &=& \frac{1}{(R_{k}R_{k})^{1/2}(B_{k}B_{k})^{1/2}}\,\frac{{\rm d}(R_{i}B_{i})}{{\rm d}t} \nonumber \\ &&-\Bigg[\frac{b_{i}}{(B_{k}B_{k})^{1/2}}\,\frac{{\rm d}(B_{i})}{{\rm d}t}+\frac{r_{i}}{(R_{k}R_{k})^{1/2}}\,\frac{{\rm d}(R_{i})}{{\rm d}t}\Bigg]\cos\phi, \nonumber\\ &=& [r_{i}-b_{i}\cos\phi]\frac{1}{(B_{k}B_{k})^{1/2}}\,\frac{{\rm d}(B_{i})}{{\rm d}t}\nonumber \\ &&+ [b_{i}-r_{i}\cos\phi]\frac{1}{(R_{k}R_{k})^{1/2}}\,\frac{{\rm d}(R_{i})}{{\rm d}t}\cdot % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq35.png) (9)This result is nothing but a generalization of d(cosφ) / dt = − sinφ (dφ/ dt). If dφ/ dt ≠ 0, then dcosφ/ dt = 0 when cosφ = ± 1.
(9)This result is nothing but a generalization of d(cosφ) / dt = − sinφ (dφ/ dt). If dφ/ dt ≠ 0, then dcosφ/ dt = 0 when cosφ = ± 1.
In the particular case where cosφ = ± 1, which corresponds to ri = ± bi, Eq. (9)becomes d(cosφ) / dt = 0, thus implying that this configuration is an equilibrium point, that is, a configuration towards which the system tends to evolve for a wide variety of starting conditions. Potentially, this configuration is also an attractor, meaning that the system can remain in this configuration even if slightly disturbed. This equilibrium point is generic in the sense that it is purely geometrical and does not depend on the details of the physics, as long as the time derivatives in Eq. (9)do not become infinite when cosφ = ± 1.
From Eq. (1)we get ![\begin{eqnarray} \label{eq:continuity2} % \partial_{i}\left[\frac{{\rm d}(\log\rho)}{{\rm d}t}\right] = -\partial_{i}(\partial_{j}v_{j}), % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq41.png) (10)which is equivalent to
(10)which is equivalent to 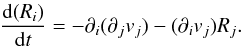 (11)Introducing Eqs. (4)and (11)into Eq. (9)we obtain
(11)Introducing Eqs. (4)and (11)into Eq. (9)we obtain ![\begin{equation} \label{eq:costheta3} \frac{{\rm d}(\cos\phi)}{{\rm d}t} = \frac{\partial_{i}(\partial_{j}v_{j})}{(R_{k}R_{k})^{1/2}}[-b_{i}+r_{i}\cos\phi]+(\partial_{i}v_{j})[r_{i}r_{j}-b_{i}b_{j}]\cos\phi, \end{equation}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq43.png) (12)which corresponds to the time evolution of the cosine of the angle between ∇ρ and B. We note that this expression is entirely based on the transport equations of ideal MHD turbulence. It is composed of the strain tensor ∂ivj (Landau et al. 1986), and the symmetric tensors rirj and bibj, which represent the correlation of the density gradient orientation and the correlation between the components of the magnetic field orientation, respectively.
(12)which corresponds to the time evolution of the cosine of the angle between ∇ρ and B. We note that this expression is entirely based on the transport equations of ideal MHD turbulence. It is composed of the strain tensor ∂ivj (Landau et al. 1986), and the symmetric tensors rirj and bibj, which represent the correlation of the density gradient orientation and the correlation between the components of the magnetic field orientation, respectively.
For the sake of simplicity, in the rest of this document we rewrite Eq. (12)as ![\begin{equation} \label{eq:costhetaCoeff} \frac{{\rm d}(\cos\phi)}{{\rm d}t} = C+ [A_{1}+A_{23}]\cos\phi, \end{equation}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq47.png) (13)where we use the definitions
(13)where we use the definitions 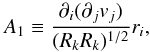 (14)
(14)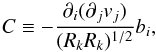 (15)and
(15)and ![\begin{eqnarray} \label{eq:A23} % A_{23} \equiv (\partial_{i}v_{j})[r_{i}r_{j}-b_{i}b_{j}], % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq50.png) (16)which, without any loss in generality, can be expressed as
(16)which, without any loss in generality, can be expressed as ![\begin{eqnarray} \label{eq:A23sym} % A_{23} \equiv \frac{1}{2}(\partial_{i}v_{j}+\partial_{j}v_{i})[r_{i}r_{j}-b_{i}b_{j}]\,. % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq51.png) (17)For the sake of comparison with previous works that studied the relative orientation between B and v (Matthaeus et al. 2008; Banerjee et al. 2009), we obtained a similar expression for the relative orientation between those two quantities and present it in Appendix A.
(17)For the sake of comparison with previous works that studied the relative orientation between B and v (Matthaeus et al. 2008; Banerjee et al. 2009), we obtained a similar expression for the relative orientation between those two quantities and present it in Appendix A.
3. Interpretation
A few points can be readily concluded from Eq. (13). First, given that the coefficient C is on average very small (as will be shown in Sect. 3.2), cosφ = 0 constitutes another equilibrium point. This means that, under the assumptions presented in Sect. 2, we expect either cosφ = ± 1 or cosφ = 0; that is, B tends to be either parallel or perpendicular to the density structures. Second, the relative orientation between ∇ρ and B changes by the effect of the coupling between the motions of the fluid represented by the strain tensor ∂ivj and the symmetric unitary tensors rirj and bibj. To better understand the implications of Eq. (13), we present the study of few simple cases in Sect. 3.1 and of a set of simulations of MHD turbulence in Sect. 3.2.
3.1. Study of simple cases
In order to develop some intuition about the information encompassed in Eq. (13), we study its behavior in a few simple distributions of matter, velocity, and magnetic field. It should be noted that the indexes i and j represent the axes of a 3D Cartesian reference frame, thus i = 0, 1, and 2 correspond to the x-, y-, and z-axis, respectively.
3.1.1. Strong magnetic field
If we consider a very strong magnetic field with respect to the turbulent motions, such that B is oriented almost exclusively along the x-axis, and a converging flow1 along the same direction, Eq. (13)reduces to 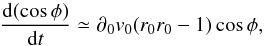 (18)where we ignore the terms depending on ∂i(∂jvj), which are on average much smaller than those related to ∂ivj, as will be shown in Sect. 3.2. Given that
(18)where we ignore the terms depending on ∂i(∂jvj), which are on average much smaller than those related to ∂ivj, as will be shown in Sect. 3.2. Given that 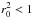 , ∂0v0(r0r0 − 1) > 0 and cosφ → ± 1. That is to say, the contraction along the field lines tends to align the density gradient and the magnetic field.
, ∂0v0(r0r0 − 1) > 0 and cosφ → ± 1. That is to say, the contraction along the field lines tends to align the density gradient and the magnetic field.
If we consider the same configuration of B, but this time consider a convergent flow perpendicular to its mean direction, Eq. (13)reduces to 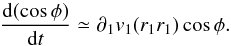 (19)In this case, cosφ → 0 since the term in front of the cosine is negative.
(19)In this case, cosφ → 0 since the term in front of the cosine is negative.
3.1.2. Weak magnetic field
We consider now a magnetic field that is weak with respect to the turbulent motions, a matter initially distributed in a slab perpendicular to the x-axis, and a converging flow along the same direction. Assuming again that the second-order spatial derivatives are negligible, Eq. (13)reduces to 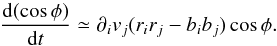 (20)Equation (20)implies that in the case of single compressive flow, the change in relative orientation is the result of two competing terms. The first, rirj, which in this particular configuration is non-zero only for i = 0, indicates the geometrical distribution of ρ and the second, bibj, indicates the distribution of the magnetic field orientation and tends to be larger when the field is stronger. Given that here ∂0v0< 0, which is implied from the converging flow assumption, and in the case of a weak field bibi is on average equal to 1 / 3, Eq. (20)leads to
(20)Equation (20)implies that in the case of single compressive flow, the change in relative orientation is the result of two competing terms. The first, rirj, which in this particular configuration is non-zero only for i = 0, indicates the geometrical distribution of ρ and the second, bibj, indicates the distribution of the magnetic field orientation and tends to be larger when the field is stronger. Given that here ∂0v0< 0, which is implied from the converging flow assumption, and in the case of a weak field bibi is on average equal to 1 / 3, Eq. (20)leads to 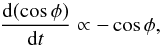 (21)which has solutions that tend towards cosφ = 0.
(21)which has solutions that tend towards cosφ = 0.
Alternatively, if we consider the same ρ and B configurations as in the previous example, but this time a converging flow along the y-axis, Eq. (13)reduces to 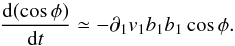 (22)This expression shows that, in this particular example, the relative orientation between ∇ρ and B changes by effect of the y-axis component of the magnetic field. Thus, it implies that even if the magnetic field is weak, motions strictly along the field lines tend to create density structures perpendicular to it.
(22)This expression shows that, in this particular example, the relative orientation between ∇ρ and B changes by effect of the y-axis component of the magnetic field. Thus, it implies that even if the magnetic field is weak, motions strictly along the field lines tend to create density structures perpendicular to it.
3.1.3. Analytical hints on the relative orientation
Since the strain tensor (∂ivj + ∂jvi) / 2 is symmetric, there are at least three mutually perpendicular directions with respect to which the matrix of (∂ivj + ∂jvi) / 2 is diagonal. Geometrically, this means that infinitesimal line elements in these directions remain mutually perpendicular after deformation. These directions are known as principal directions (Lai et al. 2010). If we consider the basis where the strain tensor is diagonal, the principal-directions basis, Eq. (17)can be expressed as 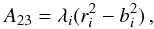 (23)where λi are the eigenvalues of the strain tensor.
(23)where λi are the eigenvalues of the strain tensor.
For the sake of illustration, we can reduce the problem to 2D and consider two eigenvalues, one negative (λc), which is dominant if we consider the case where ∂ivi< 0, and one positive (λs). In general terms, the fluid parcel is compressed in the direction associated with λc and stretched in the other. It can therefore be represented as an ellipsoid whose short axis corresponds to the direction associated with λc and whose major axis to the direction associated with λs. Given that ri is a gradient, it is larger along the short axis, that is, the direction associated with λc.
If the magnetic field is weak, B tends to be parallel to the major axis of the ellipsoid, because the field is compressed by the converging flow. That means that bc is small and A23 is negative, thus taking the system towards the cosφ = 0 configuration. If the field is strong, the compression occurs mainly along the field lines, thus making B parallel to the short axis of the ellipsoid. In this case, 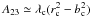 , so the sign depends on the respective values of
, so the sign depends on the respective values of 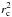 and
and 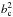 . In the limit where B is very strong, one expects the field lines to be straight and B more organized than ∇ρ, thus
. In the limit where B is very strong, one expects the field lines to be straight and B more organized than ∇ρ, thus 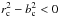 .
.
These simple cases correspond to highly idealized flows and magnetic field configurations. To study configurations where the magnetic field is not infinitely rigid or the flow has more than one single compressive component, we need to consider a realization of a turbulent flow in a molecular cloud, which is accessible through the numerical simulation of MHD turbulence.
3.2. Simulation of magnetohydrodynamic turbulence
 |
Fig. 1 Relative orientation parameter, ξ, as a function of particle density, n ≡ ρ/μ, in the simulations used in Soler et al. (2013). The values of ξ correspond to the relative orientation between ∇ρ and B in n-bins with an equal number of voxels, all with n> 500 cm-3. The values ξ> 0 correspond to ∇ρ mostly perpendicular to B and ξ< 0 correspond to ∇ρ mostly parallel to B. The gray horizontal line is ξ = 0, which corresponds to the case where there is no preferred relative orientation between ∇ρ and B. The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
We consider the simulations of MHD turbulence introduced in Dib et al. (2010) and used in Soler et al. (2013). These simulations correspond to a 4-parsec-side periodic box with mean number density n = 536 cm-3, and include the effect of self-gravity, magnetic field, and decaying turbulence. The medium inside the box is isothermal (T = 11.4 K) and has an initial sonic Mach number ℳS = 10. These simulations were computed in an adaptive mesh refinement (AMR) grid with maximum resolution of 2-9 pc and we analyze them in a regular grid with 2-7 pc resolution. For the sake of simplicity, we consider only two snapshots taken at 1 / 3 and 2 / 3 of the flow crossing time.
This set of simulations includes realizations with three initial degrees of magnetization, quantified in terms of the ratio of the thermal to magnetic pressure, β; quasi-hydrodynamic, β0 = 100; equipartition, β0 = 1.0; and strong magnetic field, β0 = 0.1. Soler et al. (2013) reported that in 3D, the change in the relative orientation between the magnetic field B and the iso-density contours, inferred from ∇ρ, is related to the initial degree of magnetization. In the realizations with β0 = 0.1 and β0 = 1.0, which correspond to sub-Alfvénic or close to equipartition turbulence, cosφ changes from being mostly zero at low densities to being mostly plus or minus one at the highest densities. In the realization with β0 = 100, super-Alfvénic turbulence, cosφ is mostly zero at all densities. Both of these results were expressed in terms of the relative orientation parameter (ξ), which corresponds to the difference between the number of voxels where cosφ ≈ 0 minus the number of voxels where cosφ ≈ ± 1 divided by the total number of voxels where cosφ ≈ 0 or cosφ ≈ ± 1, as explicitly described in equation 4 of Planck Collaboration Int. XXXV (2016). Consequently, ξ is positive if cosφ is mostly equal to zero, i.e., ∇ρ mostly perpendicular to B, and negative if | cosφ | is mostly one, i.e., ∇ρ mostly parallel to B.
In order to illustrate the interpretation of Eq. (13), we reproduce the relative orientation between B and the iso-ρ contours presented in Soler et al. (2013) for the range of densities n> 5 × 102 cm-3. We estimated ∇ρ using a Lagrange 5-points interpolation to express each ρ data point in the simulation cube as a point on a polynomial and then differentiate that polynomial2. The mean values of ξ in different density bins, presented in Fig. 1, illustrate the different trends in relative orientation between ∇ρ and B for different initial magnetizations. Given that n ≡ ρ/μ and μ, the mean particle mass, is constant in the simulations, we choose to report these results in terms of n without any loss of generality.
 |
Fig. 2 Relative orientation parameter, ξ, as a function of the velocity divergence, ∇·v ≡ ∂ivi, in the simulations introduced in Soler et al. (2013). The values of ξ correspond to the relative orientation between ∇ρ and B in ∇·v-bins with an equal number of voxels, all with n> 500 cm-3. The colors and the symbols follow the conventions introduced in Fig. 1. The gray vertical line, drawn for reference, corresponds to ∇·v = 0 Myr-1. |
Figure 2 shows that in the same density range, the negative values of ξ are associated with ∇·v< 0 in the simulations with β0 = 0.1 and β0 = 1.0. However, this is not the case for the β0 = 100 simulations, thus showing that ∇·v< 0 is not the only condition producing the change in the relative orientation between ∇ρ parallel to B. Furthermore, Fig. 2 illustrates that in the simulations with β0 = 0.1 and β0 = 1.0, the transition between ξ> 0 or cosφ = 0, and ξ< 0 or cosφ = ± 1, happens across ∇·v = 0, but ξ is not strictly negative until the second snapshot, when the values of ∇·v are more negative.
 |
Fig. 3 Mean values of 104A1 (top) and 104C (bottom) as a function of particle density, n, in the simulations introduced in Soler et al. (2013). The values of A1 and C correspond to the definitions in Eqs. (14)and (15), respectively. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
 |
Fig. 4 Mean values of the term A23, defined in Eq. (23), as a function of particle density, n, in the simulations introduced in Soler et al. (2013). The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
We further quantify the source of change in relative orientation in the simulations with β0 = 1 and β0 = 0.1 by focusing on the behavior of the coefficients C, A1, and A23 in Eq. (13). Figures 3 and 4 show the values of C, A1, and A23 in bins of n with an equal number of voxels. The values shown in the figures confirm that C and A1 are considerably smaller than the values of A23, which is expected given that the former depends on second-order spatial derivatives of the velocity field, while the latter depend on first-order derivatives. Additionally, the values of both C and A1 fluctuate around zero, thus making their mean values small with respect to A23.
Given that A23/C ≈ A23/A1 ≈ 104, Eq. (13)reduces to 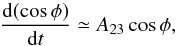 (24)which implies that the change in relative orientation depends mainly on the sign of A23. If A23< 0, cosφ tends to decrease towards 0, which corresponds to B being perpendicular to ∇ρ. If A23> 0, cosφ tends to increase towards ± 1, which corresponds to B being parallel to ∇ρ.
(24)which implies that the change in relative orientation depends mainly on the sign of A23. If A23< 0, cosφ tends to decrease towards 0, which corresponds to B being perpendicular to ∇ρ. If A23> 0, cosφ tends to increase towards ± 1, which corresponds to B being parallel to ∇ρ.
A comparison between Figs. 1 and 4 indicates that the change in relative orientation between ∇ρ and B in the first snapshot of the simulations for β0 = 1 and the β0 = 0.1 happens around the same n values where A23 changes its sign. In contrast, in the β0 = 100 simulation, where there is no change in relative orientation, the values of A23 are always negative. In the second snapshot, Fig. 4 reveals that A23 is negative for the equipartition and high-magnetization simulations and accordingly, the perpendicular relative orientation at the highest densities is less prominent than in the first snapshot.
 |
Fig. 5 Mean values of the principal components of A23, defined in Eq. (26), as a function of density, n, in the simulations introduced in Soler et al. (2013). The component associated with the most negative eigenvalue of the symmetric part of the strain tensor, which corresponds to the dominant compressive mode, is represented by the diamonds. These values are outside of the range in the case of the β0 = 100 simulation, thus they are presented separately in the lower panel. The intermediate and maximum eigenvalues are represented by circles and squares, respectively. |
Given the transformation to the principal-directions basis, 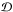 , we write Eq. (17)as
, we write Eq. (17)as ![\begin{equation} \label{eq:A23tranI0} A_{23}=\frac{1}{2}\mathcal{D}[\partial_{i}(v_{j})+\partial_{i}(v_{j})]\mathcal{D}^{-1}\mathcal{D}[r_{i}r_{j}-b_{i}b_{j}]\mathcal{D}^{-1}, \end{equation}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq125.png) (25)which reduces to
(25)which reduces to ![\begin{equation} \label{eq:A23tranI} A_{23}=\lambda_{i}\delta_{ij}\mathcal{D}[r_{i}r_{j}-b_{i}b_{j}]\mathcal{D}^{-1}, \end{equation}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq126.png) (26)where λi are the three eigenvalues of (∂ivj + ∂jvi) / 2 and δij is the Kronecker delta.
(26)where λi are the three eigenvalues of (∂ivj + ∂jvi) / 2 and δij is the Kronecker delta.
The eigenvalues (λi) correspond to the unit strain along each of the principal directions. Thus, the eigenvector associated with the highest eigenvalue describes the axis along which the infinitesimal fluid parcel is mostly elongated. The two other eigenvectors, which are associated with the two other eigenvalues, correspond to the directions along which the shape of the infinitesimal fluid parcel is either stretched or compressed, depending on their signs (Lai et al. 2010).
We diagonalize the strain tensor in each position of the simulation cube and computed the A23 terms associated with each of its eigenvalues, as described in Eq. (26). The mean value of each of these terms in density bins with an equal number of voxels is presented in Fig. 5. In the low-magnetization simulation, all three components of A23 are negative and although one of them is clearly different, which can be associated to some degree with the anisotropy produced by the magnetic field, their sign implies that all of them contribute to keep the cosφ = 0 configuration. In the equipartition and high-magnetization simulations, the component of A23 associated with the most negative eigenvalue, which traces the main compressive mode, increases its mean value with increasing density. This can be interpreted in similar terms to those described in Sect. 3.1.3: ∂ivi is mostly negative, so A23 remains negative as long as the correlation between the orientation of the magnetic field components, represented by bibj is smaller than that of the density gradient represented by rirj. Once bibj becomes larger than rirj by the effect of the compression of the magnetized medium, the sign of A23 changes and the system changes towards the cosφ = ± 1 configuration.
4. Discussion
4.1. What changes when the relative orientation between ∇ρ and B changes?
The clear anisotropy produced by the magnetic field in the velocity and the density distributions is expected, at least in the case of incompressible turbulence (Goldreich & Sridhar 1995). However, the reasons why compressible MHD turbulence produces structures in particular configurations with respect to the magnetic field were less clear.
Hennebelle (2013) shows that non-self-gravitating filaments are a generic consequence of turbulent strains in a magnetized medium and their elongation along the magnetic field lines by effect of the Lorentz force helps to keep them coherent. The fact that the shear modes are mostly responsible for the observed and simulated stretching of matter along the magnetic field, is confirmed by the cosφ = 0 equilibrium point of Eq. (13), which is the dominant in the case that ∂ivi is small. The cosφ = ± 1 equilibrium point of Eq. (13), explains why the change in relative orientation is observed at the highest densities: it is produced by the compressive modes that produce the accumulations of matter. In the light of Eq. (13), the question is not what produces the relative orientation but rather what makes it change and how we can use that information to learn about the magnetic field in MCs.
Chen et al. (2016) describes the transition density, from cosφ = 0 to cosφ = ± 1, as a threshold for the gravity-driven Alfvénic transition from sub- to super-Alfvénic turbulence. This transition in relative orientation is indeed expected; if the turbulence is sub-Alfvénic, slow modes are important and they tend to be anti-correlated with the density field, while it is the contrary for super-Alfvénic turbulence, where fast modes are dominant. This interpretation is not easy to generalize to the ISM, where dense structures are the result of multiple shocks induced by the super-Alfvénic turbulence and the structure of the magnetic field may be inherited from the very large scales. Moreover, it is not clear to what extent one can unambiguously separate regions into sub- and super-Alfvénic turbulence.
For the sake of the discussion, we estimated the relative orientation parameter in bins of Alfvén Mach number, ℳA ≡ σv/vA = ℳSβ2, in the considered set of simulations. If the transition from cosφ = 0 to cosφ = ± 1 were related to the transition from sub-Alfvénic to super-Alfvénic turbulence, one should expect that the regions where ℳA< 1 would be associated with ξ> 0 and the regions where ℳA> 1 would be associated with ξ< 0. Figure 6 shows that this is not necessarily the case in the considered simulations. In the realization with β0 = 100, there is a transition from ℳA< 1 to ℳA> 1, due to the increase in velocity dispersions as a product of the gravitational collapse into denser structures, but there is no change in the sign of ξ. The realization with β0 = 0.1, show that the ξ< 0 values are indeed associated with regions where ℳA> 1, but that ℳA> 1 does not necessarily imply ξ> 0, thus indicating that there must be another quantity that is more directly responsible for the change in relative orientation between ∇ρ and B.
 |
Fig. 6 Relative orientation parameter, ξ, as a function of the Alfvén Mach number, ℳA, in the simulations introduced in Soler et al. (2013). The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The values ξ> 0 correspond to ∇ρ mostly perpendicular to B and ξ< 0 correspond to ∇ρ mostly parallel to B. The gray horizontal line is ξ = 0, which corresponds to the case where there is no preferred relative orientation between ∇ρ and B. The gray vertical line, drawn for reference, corresponds to ℳA = 1, which marks the border between sub-, ℳA< 1, and super-Alfvénic, ℳA> 1, turbulence. |
Equation (13)and the results of the analysis presented in Sect. 3.2 suggest that the change between cosφ = 0 and cosφ = ± 1, or from ∇ρ being predominantly perpendicular to being predominantly parallel to B, are related to the tensors composing the coefficient A23, as stated by Eq. (17). If A23< 0, the flow tends towards the cosφ = 0 configuration; the change in that tendency in the case of a predominantly converging flow, ∂ivi< 0, is related to the change of sign in the tensor (rirj − bibj). Thus, we can infer that the density threshold where cosφ changes is linked to the relation between the rirj and the bibj tensors, which is clearly dependent on the initial magnetization.
Figure 7 presents the distributions of ρ and the B orientation, A23, and ℳA in a slice of the first snapshot of the simulations with weak, β0 = 100, and strong β0 = 0.1 initial magnetization. The upper panel illustrates how B clearly follows the density structure in the simulation with β0 = 100 and how B is more homogeneous in the simulations where β0 = 0.1. For the sake of completeness, we also present the values of ℳA in the middle panel of Fig. 7. The figure shows that the values of ℳA in the lower density regions of the slice correspond to the initial magnetizations, that is, ℳA> 1 in the β0 = 100 and ℳA< 1 in the β0 = 0.1 case. At higher densities, however, these values change and some density structures in the β0 = 100 case present ℳA ≈ 1 and some density structures in the β0 = 0.1 case show ℳA ≳ 1. Both cases, illustrate that the change in relative orientation is not straightforward in some particular structures in the map, but it is rather a statistical trend that is better summarized in the analysis presented in Fig. 6.
Finally, the bottom panel of Fig. 7 shows the distribution of A23, the terms whose sign determines the changes in the relative orientation between ∇ρ and B. In the case with low initial magnetization, A23 is clearly organized in filaments that correspond to many of those seen in the density map. The presence of regions where A23> 0 indicates that there are zones where the relative orientation between ∇ρ and B tends to change, although the average values in particular density ranges shows a general tendency towards the cosφ = 0 configuration. In the case with high initial magnetization, A23 is more inhomogeneous and the density structures do not have clear counterparts in A23. The presence of extended regions with both positive and negative values of A23 shows that the change in relative orientation is a dynamic process that is not localized in a few structures but rather a statistical trend that becomes evident when analyzing particular density ranges, as shown in Fig. 5.
 |
Fig. 7 Distributions of the density and magnetic field (top), the logarithm of the Alfvén Mach number ℳA (middle), and the coefficient A23 of Eq. (13)(bottom) in a slice (z = 256) of the MHD turbulence simulations used in Soler et al. (2013) for initially weak (β = 100, left) and strong (β = 0.1, right) magnetic field in a snapshot taken at one-third of the flow crossing time. The coefficient A23 is the term dominating the change in the relative orientation between ∇ρ and B according to Eq. (13). |
4.2. Relative orientation and scaling of the magnetic field with increasing density
Observations of the Zeeman effect indicate that in the diffuse lines of sight (NH ≲ 1021.5 cm-2), the maximum magnetic field strength Bmax sampled by HI lines does not scale with density. In the denser regions (NH ≳ 1021.5 cm-2) probed by OH and CN spectral lines the same study reports a scaling of the maximum magnetic field strength Bmax ∝ n0.65 (Crutcher et al. 2010; Crutcher 2012, and references therein). The former observation can be interpreted as the effect of diffuse clouds assembled by flows along magnetic field lines, which would increase the density but not the magnetic field strength. The latter observation can be interpreted as the effect of isotropic contraction of weakly magnetized gas. Probably related to these interpretations is the fact that the column density where the magnetic field strength starts scaling with increasing column density is very close to the column densities where Planck Collaboration Int. XXXV (2016) identified the change in relative orientation from 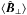 mostly parallel to the iso-NH contours to mostly perpendicular.
mostly parallel to the iso-NH contours to mostly perpendicular.
The column density values around which the Zeeman observations show the scaling of the magnetic field with increasing density are indeed very close to the column densities where the relative orientation between the column density structures and the magnetic field, inferred from the dust polarization observations, changes from mostly parallel to mostly perpendicular. This similarity has been identified in the colliding flow models presented in Chen et al. (2016), where it is assigned to the beginning of gravity-induced acceleration in terms of increasing gas velocity with density. As discussed here, this may not necessarily be the case.
5. Conclusions
We studied the relative orientation between ∇ρ and B using the transport equations of MHD turbulence. Under the assumptions of flux freezing and low magnetic diffusivity, we arrived at Eq. (13), which is an expression that describes the evolution of cosφ, the cosine of the angle between ∇ρ and B.
From the study of Eq. (13)we conclude the following:
-
1.
The configuration where cosφ = ± 1 is a generic equilibrium point, a configuration towards which the system tends to evolve and a potential attractor.
-
2.
The configuration where the cosφ = 0 constitutes another equilibrium point.
-
3.
The changes in the relative orientation are produced by the coupling of the strain tensor ∂ivj and the rirj and bibj tensors, defined in Eqs. (7)and (8), which correspond to the autocorrelations of the density gradient and magnetic field orientations, respectively.
Using the simulations of MHD turbulence used in Soler et al. (2013), we show the following:
-
1.
The configuration cosφ = 0 is dominant at all densities in the quasi-hydrodynamic simulation (β0 = 100) and in all but the highest densities in the initially equipartition (β0 = 1.0) and high-magnetization (β0 = 0.1) simulations, as illustrated in Fig. 1.
-
2.
The cosφ = ± 1 is only present in the regions where ∂ivi< 0 in the β0 = 1.0 and β0 = 0.1 simulations, as shown in Fig. 2.
-
3.
The density over which cosφ changes from 0 to ± 1 in the β0 = 1.0 and β0 = 0.1 simulations corresponds to that where the term A23 changes its sign, as illustrated in Fig. 4
-
4.
In the case of det(∂ivj) < 0, which corresponds to a converging flow, the change of sign in A23 occurs when the bibj tensor dominates over rirj.
-
5.
The density over which A23 changes sign, bringing the system from the cosφ = 0 to the cosφ = ± 1, depends on the strength of the initial magnetic field.
-
6.
The changes in cosφ are mainly related to the compressive modes of the strain tensor ∂ivi and their coupling to a relatively strong magnetic field with respect to the turbulent motions, as illustrated in Fig. 5, and not to a clear transition in the Alfvén Mach number, as shown in Fig. 6.
These results indicate that, once the projection effects are properly accounted for, the observations of the relative orientation between column density structures and the projected magnetic field can be interpreted as follows:
-
1.
The observed low-density structures aligned with the magneticfield are spontaneously produced in regions where shear motionsare dominant over compression.
-
2.
The observed change in relative orientation between the NH structures and
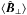 towards molecular clouds is an indication of compressive motions, that is, ∂ivi< 0, which can be the result of either gravitational collapse or converging flows.
towards molecular clouds is an indication of compressive motions, that is, ∂ivi< 0, which can be the result of either gravitational collapse or converging flows. -
3.
The density threshold at which the relative orientation between the NH structures and
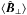 changes from mostly parallel to mostly perpendicular depends on the field strength and not necessarily on the strength of the compressive motions.
changes from mostly parallel to mostly perpendicular depends on the field strength and not necessarily on the strength of the compressive motions.
We have shown that the relative orientation between density structures and the magnetic field are related to the dynamics of MHD turbulence, particularly to the contraction motions and the degree of magnetization. Although the astronomical data are two-dimensional in nature and incorporate signal integrations along the line of sight and across the telescope beam, our calculations suggest that there is a theoretical basis for interpreting the observed changes in the relative orientation between NH structures and 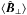 towards molecular clouds as the imprint of the magnetic field playing a significant role in the assembly of the parcels of gas that produce molecular clouds. While a direct estimate of the magnetic field strength using the relative orientation between NH structures and
towards molecular clouds as the imprint of the magnetic field playing a significant role in the assembly of the parcels of gas that produce molecular clouds. While a direct estimate of the magnetic field strength using the relative orientation between NH structures and 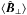 remains elusive, it is clear that the study of this and other statistical correlations is crucial for constraining the range of scales and densities where the magnetic field is shaping the structure of the ISM.
remains elusive, it is clear that the study of this and other statistical correlations is crucial for constraining the range of scales and densities where the magnetic field is shaping the structure of the ISM.
pdiv.pro routine developed by Chris Beaumont (https://github.com/ChrisBeaumont).
Acknowledgments
This work was made possible through the funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement Nos. 306483 and 291294). J.D.S. acknowledges support from the European Research Council under the Horizon 2020 Framework Program via the ERC Consolidator Grant CSF-648505. We thank the referee Martin Houde for his insightful comments that helped to improve this work. Additionally, we thank the following people who helped with their encouragement and conversation: Henrik Beuther, François Boulanger, Jouni Kainulainen, Ralf Klessen, and Alex Lazarian.
References
- Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Boldyrev, S. 2006, Phys. Rev. Lett., 96, 115002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, C.-Y., King, P. K., & Li, Z.-Y. 2016, ApJ, 829, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Hennebelle, P., Pineda, J. E., et al. 2010, ApJ, 723, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] [Google Scholar]
- González-Casanova, D. F., & Lazarian, A. 2017, ApJ, 835, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Bergin, E. A. 2001, ApJ, 562, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, in Cosmic Magnetic Fields, eds. R. Wielebinski, & R. Beck (Berlin: Springer Verlag), Lect. Notes Phys., 664, 137 [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Pérault, M. 2000, A&A, 359, 1124 [NASA ADS] [Google Scholar]
- Heyer, M., Gong, H., Ostriker, E., & Brunt, C. 2008, ApJ, 680, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Goldsmith, P. F., Yıldız, U. A., et al. 2016, MNRAS, 461, 3918 [NASA ADS] [CrossRef] [Google Scholar]
- Hoq, S., Clemens, D. P., Guzmán, A. E., & Cashman, L. R. 2017, ApJ, 836, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., & Kirby, L. 2009, ApJ, 706, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Iffrig, O., & Hennebelle, P. 2017, A&A, 604, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, T., Inutsuka, S.-I., & Koyama, H. 2007, ApJ, 658, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Kerp, J., Haud, U., et al. 2016, ApJ, 821, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course (Berlin Heidelberg: Springer-Verlag), 43, 85 [Google Scholar]
- Körtgen, B., & Banerjee, R. 2015, MNRAS, 451, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Kusune, T., Sugitani, K., Nakamura, F., et al. 2016, ApJ, 830, L23 [CrossRef] [Google Scholar]
- Lai, W. M., Rubin, D., & Krempl, E. 2010, Introduction to Continuum Mechanics, 4th edn. (Butterworth-Heinemann) [Google Scholar]
- Landau, L. D., Pitaevskii, L. P., Kosevich, A. M., & Lifshitz, E. M. 1986, Theory of Elasticity (Course of Theoretical Physics), 3rd edn. (Butterworth-Heinemann), 7 [Google Scholar]
- Li, H.-B., Fang, M., Henning, T., & Kainulainen, J. 2013, MNRAS, 436, 3707 [NASA ADS] [CrossRef] [Google Scholar]
- Malinen, J., Montier, L., Montillaud, J., et al. 2016, MNRAS, 460, 1934 [Google Scholar]
- Matthaeus, W. H., Pouquet, A., Mininni, P. D., Dmitruk, P., & Breech, B. 2008, Phys. Rev. Lett., 100, 085003 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Passot, T., Vazquez-Semadeni, E., & Pouquet, A. 1995, ApJ, 455, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXV. 2016, A&A, 586, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, F. P., Busquet, G., Franco, G. A. P., Girart, J. M., & Zhang, Q. 2016, ApJ, 832, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, J. D., Hennebelle, P., Martin, P. G., et al. 2013, ApJ, 774, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, J. D., Alves, F., Boulanger, F., et al. 2016, A&A, 596, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, J. D., Ade, P. A. R., Angilè, F. E., et al. 2017, A&A, 603, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sugitani, K., Nakamura, F., Watanabe, M., et al. 2011, ApJ, 734, 63 [Google Scholar]
- Yuen, K. H., & Lazarian, A. 2017, ApJ, 837, L24 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Relative orientation between B and v
Following a similar procedure to that described in Sect. 2.1, we obtained an expression for the relative orientation between the magnetic field, B, and the velocity, v, 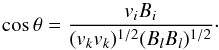 (A.1)Using the definitions,
(A.1)Using the definitions, 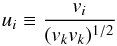 (A.2)and
(A.2)and 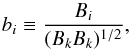 (A.3)we obtain
(A.3)we obtain 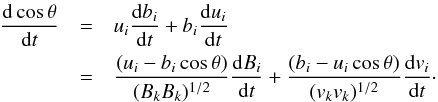 (A.4)We consider the Cauchy momentum equation in a magnetized fluid to obtain
(A.4)We consider the Cauchy momentum equation in a magnetized fluid to obtain ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:momentum} \frac{{\rm d}v_{i}}{{\rm d}t} = -\frac{1}{\rho}\left[\partial_{i}P + B_{j}\partial_{j}B_{i} - B_{j}\partial_{i}B_{j}\right]. \end{equation}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq158.png) (A.5)Combining the continuity and the Faraday equation results in
(A.5)Combining the continuity and the Faraday equation results in 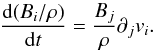 (A.6)Then, inserting Eqs. (A.5)and (A.6)in Eq. (A.4), we obtain
(A.6)Then, inserting Eqs. (A.5)and (A.6)in Eq. (A.4), we obtain ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:Bv2} % \frac{{\rm d}\cos\theta}{{\rm d}t} &=& - {\partial _i P \over \rho (v_k v_k)^{1/2} } (b_i - u_i \cos \theta) \nonumber\\ &&+ b_j \partial_j v_i (u_i - b_i \cos \theta ) - \left[ { B_j \partial_j B_i - B_j \partial_i B_j \over \rho (v_k v_k)^{1/2} }\right] u_i \cos \theta, % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq160.png) (A.7)which can be rearranged as
(A.7)which can be rearranged as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:Bv3} % \frac{{\rm d}\cos\theta}{{\rm d}t} &=& \left[ -\frac{\partial_{i}P}{\rho v} + \left(\frac{B_{j}\partial_{j}B_{i} - B_{j}\partial_{i}B_{j}}{\rho v}\right) + \partial_{i}v \right]\left( b_i - u_i \cos \theta \right) \nonumber \\ &&+ \frac{1}{2}(\partial_{j}v_{i} + \partial_{i}v_{j})[u_{i}u_{j} - b_{i}b_{j}]\cos\theta, % \end{eqnarray}](/articles/aa/full_html/2017/11/aa31049-17/aa31049-17-eq161.png) (A.8)where v ≡ (vkvk)1 / 2.
(A.8)where v ≡ (vkvk)1 / 2.
If cosθ = ± 1, that is to say bi = ± vi, Eq. (A.8)implies that dcosθ/ dt = 0, as its third term vanishes because it corresponds to the Lorenz force times the velocity, which is proportional to B. This implies that alignment between B and v is expected since cosθ = ± 1 constitutes an equilibrium point, as in the case of the relative orientation between ∇ρ and B. However, unlike Eq. (13), the configuration cosθ = 0 is not an equilibrium point due to the first term on the right-hand side of Eq. (A.8), which account for the forces.
 |
Fig. A.1 Relative orientation parameter, ξBV, as a function of particle density, n ≡ ρ/μ, in the simulations used in Soler et al. (2013). The values of ξBV correspond to the relative orientation between B and v in n-bins with an equal number of voxels, all with n> 500 cm-3. The values ξBV> 0 correspond to B mostly perpendicular to v and ξBV< 0 correspond to B mostly parallel to v. The gray horizontal line is ξBV = 0, which corresponds to the case where there is no preferred relative orientation between B and v. The colors and the symbols represent the initial magnetization values quantified by β0. The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
The predominant alignment between B and v was previously reported in Boldyrev (2006), Matthaeus et al. (2008), and Banerjee et al. (2009), and more recently studied in the context of MC formation in Iffrig & Hennebelle (2017). However, Eq. (A.8)constitutes a novel general expression that links the relative orientation between the two vectors. It relates the relative orientation to the underlying physical conditions, which is potentially useful in the interpretation of observations such as those of the magnetically aligned velocity anisotropy reported in Heyer et al. (2008, 2016) and the correlations between the  and the line-of-sight velocity gradients reported in Yuen & Lazarian (2017). Additionally, it provides reference to the assumptions behind methods for the estimation of the magnetic field strength, such as those presented in Houde et al. (2009) and González-Casanova & Lazarian (2017).
and the line-of-sight velocity gradients reported in Yuen & Lazarian (2017). Additionally, it provides reference to the assumptions behind methods for the estimation of the magnetic field strength, such as those presented in Houde et al. (2009) and González-Casanova & Lazarian (2017).
For the sake of illustration, we present the analysis of the relative orientation between B and v in the Soler et al. (2013) simulations in Fig. A.1. There we show that in the range n> 500 cm-3, the alignment between B and v is prevalent under the physical conditions included in those simulations, although the trends for increasing density are not as uniform as in the case of ∇ρ and B. These trends are different in the first and the second snapshot as a consequence of the decay of the turbulence: stronger shocks tend to shift the alignment of B and v, as the transverse component of the magnetic field is amplified and the velocity tends to be perpendicular to it (Passot et al. 1995).
All Figures
 |
Fig. 1 Relative orientation parameter, ξ, as a function of particle density, n ≡ ρ/μ, in the simulations used in Soler et al. (2013). The values of ξ correspond to the relative orientation between ∇ρ and B in n-bins with an equal number of voxels, all with n> 500 cm-3. The values ξ> 0 correspond to ∇ρ mostly perpendicular to B and ξ< 0 correspond to ∇ρ mostly parallel to B. The gray horizontal line is ξ = 0, which corresponds to the case where there is no preferred relative orientation between ∇ρ and B. The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
| In the text | |
 |
Fig. 2 Relative orientation parameter, ξ, as a function of the velocity divergence, ∇·v ≡ ∂ivi, in the simulations introduced in Soler et al. (2013). The values of ξ correspond to the relative orientation between ∇ρ and B in ∇·v-bins with an equal number of voxels, all with n> 500 cm-3. The colors and the symbols follow the conventions introduced in Fig. 1. The gray vertical line, drawn for reference, corresponds to ∇·v = 0 Myr-1. |
| In the text | |
 |
Fig. 3 Mean values of 104A1 (top) and 104C (bottom) as a function of particle density, n, in the simulations introduced in Soler et al. (2013). The values of A1 and C correspond to the definitions in Eqs. (14)and (15), respectively. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
| In the text | |
 |
Fig. 4 Mean values of the term A23, defined in Eq. (23), as a function of particle density, n, in the simulations introduced in Soler et al. (2013). The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
| In the text | |
 |
Fig. 5 Mean values of the principal components of A23, defined in Eq. (26), as a function of density, n, in the simulations introduced in Soler et al. (2013). The component associated with the most negative eigenvalue of the symmetric part of the strain tensor, which corresponds to the dominant compressive mode, is represented by the diamonds. These values are outside of the range in the case of the β0 = 100 simulation, thus they are presented separately in the lower panel. The intermediate and maximum eigenvalues are represented by circles and squares, respectively. |
| In the text | |
 |
Fig. 6 Relative orientation parameter, ξ, as a function of the Alfvén Mach number, ℳA, in the simulations introduced in Soler et al. (2013). The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The values ξ> 0 correspond to ∇ρ mostly perpendicular to B and ξ< 0 correspond to ∇ρ mostly parallel to B. The gray horizontal line is ξ = 0, which corresponds to the case where there is no preferred relative orientation between ∇ρ and B. The gray vertical line, drawn for reference, corresponds to ℳA = 1, which marks the border between sub-, ℳA< 1, and super-Alfvénic, ℳA> 1, turbulence. |
| In the text | |
 |
Fig. 7 Distributions of the density and magnetic field (top), the logarithm of the Alfvén Mach number ℳA (middle), and the coefficient A23 of Eq. (13)(bottom) in a slice (z = 256) of the MHD turbulence simulations used in Soler et al. (2013) for initially weak (β = 100, left) and strong (β = 0.1, right) magnetic field in a snapshot taken at one-third of the flow crossing time. The coefficient A23 is the term dominating the change in the relative orientation between ∇ρ and B according to Eq. (13). |
| In the text | |
 |
Fig. A.1 Relative orientation parameter, ξBV, as a function of particle density, n ≡ ρ/μ, in the simulations used in Soler et al. (2013). The values of ξBV correspond to the relative orientation between B and v in n-bins with an equal number of voxels, all with n> 500 cm-3. The values ξBV> 0 correspond to B mostly perpendicular to v and ξBV< 0 correspond to B mostly parallel to v. The gray horizontal line is ξBV = 0, which corresponds to the case where there is no preferred relative orientation between B and v. The colors and the symbols represent the initial magnetization values quantified by β0. The darker colors represent the early snapshots in the simulation and the lighter colors represent the later snapshots. The gray vertical line, drawn for reference, corresponds to n = 104 cm-3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


