| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 23 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630104 | |
| Published online | 24 November 2017 | |
Shape and spin determination of Barbarian asteroids⋆
1 Université de Liège, Space sciences, Technologies and Astrophysics Research (STAR) Institute, Allée du 6 Août 19c, Sart Tilman, 4000 Liège, Belgium
e-mail: devogele@astro.ulg.ac.be
2 Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, 06300 Nice, France
3 Astronomical Institute, Faculty of Mathematics and Physics, Charles University in Prague, 11636 Staré Město, Czech Republic
4 CdR & CdL Group: Light-curves of Minor Planets and Variable Stars, Switzerland
5 Estación Astrofísica Bosque Alegre, Observatorio Astronómico Córdoba, 5000 BGR Córdoba, Argentina
6 Institute of Geology, Adam Mickiewicz University, Krygowskiego 12, 61-606 Poznań, Poland
7 Observatoire de Chinon, 37500 Chinon, France
8 Geneva Observatory, 1290 Versoix, Switzerland
9 Astronomical Observatory Institute, Faculty of Physics, A. Mickiewicz University, Słoneczna 36, 60-286 Poznań, Poland
10 Unidad de Astronomía, Fac. de Ciencias Básicas, Universidad de Antofagasta, 02800 Avda. U. de Antofagasta, Antofagasta, Chile
11 Korea Astronomy and Space Science Institute, 776 Daedeokdae-ro, Yuseong-gu, 34055 Daejeon, Republic of Korea
12 Osservatorio Astronomico della regione autonoma Valle d’Aosta, 11020 Nus AO, Italy
13 School of Physics, University of Western Australia, M013, Crawley WA 6009, Australia
14 Shed of Science Observatory, 5213 Washburn Ave. S, Minneapolis, MN 55410, USA
15 Akdeniz University, Department of Space Sciences and Technologies, 07058 Antalya, Turkey
16 TUBITAK National Observatory (TUG), Akdeniz University Campus, 07058 Antalya, Turkey
17 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1, Canada
18 Astrophysics Division, Institute of Physics, Jan Kochanowski University, Świ etokrzyska 15, 25-406 Kielce, Poland
19 Laboratory of Space Researches, Uzhhorod National University, Daleka st., 2a, 88000 Uzhhorod, Ukraine
20 Institute of Physics, Faculty of Natural Sciences, University of P. J. Safarik, Park Angelinum 9, 040 01 Kosice, Slovakia
21 Stazione Astronomica di Sozzago, 28060 Sozzago, Italy
22 NaXys, Department of Mathematics, University of Namur, 8 Rempart de la Vierge, 5000 Namur, Belgium
23 Instituto de Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
24 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
25 Mt. Suhora Observatory, Pedagogical University, Podchora¸żych 2, 30-084 Cracow, Poland
26 Instituto de Astrofísica de Andalucía, CSIC, Apt 3004, 18080 Granada, Spain
27 CITEUC – Centre for Earth and Space Science Research of the University of Coimbra, Observatório Astronómico da Universidade de Coimbra, 3030-004 Coimbra, Portugal
28 Agrupación Astronómica Región de Murcia, 30153 Orihuela, Spain
29 Arroyo Observatory, Arroyo Hurtado, Murcia, Spain
30 4438 Organ Mesa Loop, Las Cruces, New Mexico 88011, USA
Received: 21 November 2016
Accepted: 21 June 2017
Context. The so-called Barbarian asteroids share peculiar, but common polarimetric properties, probably related to both their shape and composition. They are named after (234) Barbara, the first on which such properties were identified. As has been suggested, large scale topographic features could play a role in the polarimetric response, if the shapes of Barbarians are particularly irregular and present a variety of scattering/incidence angles. This idea is supported by the shape of (234) Barbara, that appears to be deeply excavated by wide concave areas revealed by photometry and stellar occultations.
Aims. With these motivations, we started an observation campaign to characterise the shape and rotation properties of Small Main-Belt Asteroid Spectroscopic Survey (SMASS) type L and Ld asteroids. As many of them show long rotation periods, we activated a worldwide network of observers to obtain a dense temporal coverage.
Methods. We used light-curve inversion technique in order to determine the sidereal rotation periods of 15 asteroids and the convergence to a stable shape and pole coordinates for 8 of them. By using available data from occultations, we are able to scale some shapes to an absolute size. We also study the rotation periods of our sample looking for confirmation of the suspected abundance of asteroids with long rotation periods.
Results. Our results show that the shape models of our sample do not seem to have peculiar properties with respect to asteroids with similar size, while an excess of slow rotators is most probably confirmed.
Key words: techniques: photometric / minor planets, asteroids: general / methods: observational
The light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/607/A119
© ESO, 2017
1. Introduction
Shape modeling is of primary importance in the study of asteroid properties. In the last decades, ~ 1000 asteroids have had a shape model determined by using inversion techniques1; most of them are represented by convex shape models. This is due to the fact that the most used technique when inverting the observed light-curves of an asteroid – the so-called light-curve inversion – is proven to mathematically converge to a unique solution only if the convex hypothesis is enforced (Kaasalainen & Torppa 2001; Kaasalainen et al. 2001). At the typical phase angles observed for main belt asteroids, the light-curve is almost insensitive to the presence of concavities according to Ďurech & Kaasalainen (2003). Although the classical light-curve inversion process cannot model concavities, Kaasalainen et al. (2001) point out that the convex shape model obtained by the inversion is actually very close to the convex hull of the asteroid shape. Since the convex hull corresponds to the minimal envelope that contains the non-convex shape, the location of concavities corresponds to flat areas. Devogèle et al. (2015) developed the flat surfaces derivation technique (FSDT) which considers flat surfaces on such models to obtain indications about the possible presence of large concavities.
Cellino et al. (2006) reported the discovery of the anomalous polarimetric behaviour of (234) Barbara. Polarisation measurements are commonly used to investigate asteroid surface properties and albedos. Usually, the polarisation rate is defined as the difference of the photometric intensity in the directions parallel and perpendicular to the scattering plane (normalised to their sum): 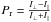 . It is well known that the intensity of polarisation is related to the phase angle, that is, to the angle between the light-source direction and the observer, as seen from the object. The morphology of the phase-polarisation curve has some general properties that are mainly dependent on the albedo of the surface. A feature common to all asteroids is a “negative polarisation branch” for small phase angles, corresponding to a higher polarisation parallel to the scattering plane. For most asteroids, the transition to positive polarisation occurs at an “inversion angle” of ~ 20°. In the case of (234) Barbara, the negative polarisation branch is much stronger and exhibits an uncommonly large value for the inversion angle of approximately 30°. Other Barbarians were found later on (Gil-Hutton et al. 2008; Masiero & Cellino 2009; Cellino et al. 2014; Gil-Hutton et al. 2014; Bagnulo et al. 2015; Devogèle et al. 2017), and very recently, it was discovered that the family of Watsonia is composed of Barbarians (Cellino et al. 2014).
. It is well known that the intensity of polarisation is related to the phase angle, that is, to the angle between the light-source direction and the observer, as seen from the object. The morphology of the phase-polarisation curve has some general properties that are mainly dependent on the albedo of the surface. A feature common to all asteroids is a “negative polarisation branch” for small phase angles, corresponding to a higher polarisation parallel to the scattering plane. For most asteroids, the transition to positive polarisation occurs at an “inversion angle” of ~ 20°. In the case of (234) Barbara, the negative polarisation branch is much stronger and exhibits an uncommonly large value for the inversion angle of approximately 30°. Other Barbarians were found later on (Gil-Hutton et al. 2008; Masiero & Cellino 2009; Cellino et al. 2014; Gil-Hutton et al. 2014; Bagnulo et al. 2015; Devogèle et al. 2017), and very recently, it was discovered that the family of Watsonia is composed of Barbarians (Cellino et al. 2014).
Several hypotheses have been formulated in the past to explain this anomaly. Strong backscattering and single-particle scattering on high-albedo inclusions were invoked. Near-infrared (NIR) spectra exhibit an absorption feature that has been related to the presence of spinel absorption from fluffy-type calcium-aluminium rich inclusions (CAIs; Sunshine et al. 2007, 2008). The meteorite analogue of these asteroids would be similar to CO3/CV3 meteorites, but with a surprisingly high CAI abundance (~ 30%), never found in Earth samples. If this interpretation is confirmed, the Barbarians should have formed in an environment very rich in refractory materials, and would contain the most ancient mineral assemblages of the Solar System. This fact link, the explanation of the polarisation to the presence of high-albedo CAIs, is the main motivation for the study of Barbarians, whose composition challenges our knowledge on meteorites and on the mechanisms of the formation of the early Solar System.
The compositional link is confirmed by the evidence that all Barbarians belong to the L and Ld classes of the Small Main-Belt Asteroid Spectroscopic Survey (SMASS) taxonomy (Bus & Binzel 2002), with a few exceptions of the K class. While not all of them have a near-infrared spectrum, all Barbarians are found to be L-type in the DeMeo et al. (2009) NIR-inclusive classification (Devogèle et al. 2017).
However, the variety of polarimetric and spectroscopic properties among the known Barbarians, also suggests that composition cannot be the only reason for the anomalous scattering properties. In particular, Cellino et al. (2006) suggested the possible presence of large concavities on the asteroid surfaces, resulting in a variety of (large) scattering and incidence angles. This could have a non-negligible influence on the detected polarisation, but such a possibility has remained without an observational verification up to now.
Recent results concerning the prototype of the class, (234) Barbara, show the presence of large-scale concavities spanning a significant fraction of the object size. In particular, interferometric measurements (Delbo et al. 2009) and well-sampled profiles of the asteroid obtained during two stellar occultations indicate the presence of large-scale concave features (Tanga et al. 2015). Testing the shape of other Barbarians for the presence of concavities is one of the main goals of the present study, summarising the results of several years of observation. To achieve this goal, we mainly exploit photometry to determine the shape, to be analysed by the FSDT. We compare our results with the available occultation data (Dunham et al. 2016) in order to check the reliability of the inverted shape model, scale in size, and constrain the spin axis orientation. We also introduce a method capable of indicating if the number of available light-curves is sufficient to adequately constrain the shape model solution.
As we derive rotation periods in the process, we also test another evidence, rather weak up to now: the possibility that Barbarians contain an abnormally large fraction of “slow” rotators, with respect to a population of similar size. This peculiarity – if confirmed – could suggest a peculiar past history of the rotation properties of the Barbarians.
The article is organised as follows. In Sect. 2, we describe the observation campaign and the obtained data. Section 3 presents the approach that was followed to derive the shape models. A new method for analysing the shape model of asteroids is presented and tested on well-known asteroids. In Sect. 4, the characteristics of some individual asteroids are presented as well as a general discussion about the main results of the present work. The incidence of concavities and the distribution of the rotation periods and pole orientations of L-type asteroids are presented. Finally Sect. 5 contains the conclusions of this work.
2. The observation campaigns
2.1. Instruments and sites
Our photometric campaigns involve 15 different telescopes and sites distributed on a wide range in Earth longitudes in order to optimise the time coverage of slowly rotating asteroids, with minimum gaps. This is the only strategy to complete light-curves when the rotation periods are close to 1 day, or longer, for ground-based observers.
The participating observatories (Minor Planet Center (MPC) code in parentheses) and instruments, ordered according to their geographic longitudes (also Table 1), are:
-
the 0.8 m telescope of Observatori Astronòmic delMontsec (OAdM), Spain (C65);
the 1.04 m “Omicron” telescope at the Centre Pédagogique Planète et Univers (C2PU) facility, Calern observatory (Observatoire de la Côte d’Azur), France (010);
the 0.81 m telescope from the Astronomical Observatory of the Autonomous Region of the Aosta Valley (OAVdA), Italy (B04);
the 0.4 m telescope of the Borowiec Observatory, Poland (187);
the 0.6 m telescope from the Mt. Suhora Observatory, Cracow, Poland;
the 0.35 m telescope from Jan Kochanowski University in Kielce, Poland (B02);
the 1 m Zadko telescope near Perth, Australia (D20);
the 0.61 m telescope of the Sobaeksan Optical Astronomy Observatory (SOAO), South Korea (345);
the 0.7 m telescope of Winer Observatory (RBT), Arizona, USA (648);
the 0.35 m telescope from the Organ Mesa Observaory (OMO), NM, USA (G50);
the 0.6 m telescope of the Southern Association for Research in Astrophysics (SARA), La Serena Observatory, Chile (807);
the 0.35 m telescope from the UBC Southern Observatory, La Serena Observatory, Chile (807);
the 1.54 m telescope of the Estaciòn Astrofìsica de Bosque Alegre (EABA), Argentina (821);
the 1.5 m telescope of the Instituto Astrofìsica de Andalucìa (IAA) in Sierra Nevada, Spain (J86);
the 0.77 m telescope from the Complejo Astronømico de La Hita, Spain (I95).
The whole campaign is composed of 244 individual light-curves resulting from approximatively 1400 h of observation and 25 000 individual photometric measurements of asteroids. All the new data presented in this work are listed in Table A.1.
In addition to these observations, we exploited light-curves published in the literature. For the most ancient light-curves, the APC (Asteroid Photometric Catalogue; Lagerkvist et al. 2001) was used. The most recent ones are publicly available in the DAMIT database (Ďurech et al. 2010).
As explained in the following section, we also used sparse photometry following the approach of Hanuš et al. (2011, 2013). The selected datasets come from observations from the United States Naval Observatory (USNO)-Flagstaff station (International Astronomical Union (IAU) code 689), Catalina Sky Survey Observatory (CSS, IAU code 703 Larson et al. 2003), and Lowell survey (Bowell et al. 2014).
The already published data used in this work are listed in Table B.1.
List of the observatories participating in the observation campaigns, with telescope aperture (D), position, and number of light-curves.
2.2. The target sample
We coordinated the observation of 15 asteroids, selected on the basis of the following criteria:
-
Known Barbarians, with a measured polarimetric anomaly;
-
SMASS L or Ld type asteroids, exhibiting the 2 μm spinel absorption band;
-
members of dynamical families containing known Barbarians and/or L-type asteroids: Watsonia (Cellino et al. 2014), the dispersed Henan (Nesvorný et al. 2015), Tirela (Mothé-Diniz & Nesvorný 2008), renamed Klumpkea in Milani et al. (2014).
Figure 1 shows the location (red dots) in semi-major axis and inclination of the asteroids studied in this work. In general, Barbarians are distributed all over the main belt. The concentration in certain regions is a direct consequence of the identification of the Watsonia, Henan, and Tirela families. Future spectroscopic surveys including objects with a smaller diameter could better portray the global distribution.
 |
Fig. 1 Inclination versus semi-major axis plot of main-belt asteroids. The asteroids studied in this work are plotted as red circular dots, while the thinner blue dots represent the asteroid population as a whole. |
For each of the 15 asteroids that have been targeted in this work, our observations have led to the determination of a new rotation period, or increase the accuracy of the previously known one. For eight of them, the light-curves dataset was sufficiently large to determine the orientation of the spin axis and a reliable convex shape model.
Table 2 lists the class in the Tholen (Tholen 1984), SMASS (Bus & Binzel 2002; Mothé-Diniz & Nesvorný 2008) and Bus-Demeo (DeMeo et al. 2009; Bus 2009) taxonomies of the 15 asteroids observed by our network. Each known Barbarian from polarimetry is labelled as “Y” in the corresponding column. The number of the family parent member is given in the corresponding column. The bottom part of Table 2 gives the same information for asteroids not observed by our network, but included in this work to increase the sample.
List of the targets observed by our network (upper part).
3. Modelling method and validation of the results
The sidereal rotation period was searched for by the light-curve inversion code described in Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001) over a wide range. The final period is the one that best fits the observations. It is considered as unique if the chi-square of all the other tested periods is >10% higher. In order to obtain a more precise solution, sparse data are also included in the procedure, as described by Hanuš et al. (2013). When the determination of a unique rotation period is possible, the pole solution(s) can be obtained. As is well known, paired solutions with opposite pole longitudes (i.e. differing by 180°) can fit the data equally well. If four or less pole solutions (usually two sets of two mirror solutions) are found, the shape model is computed using the best fitting pole solution.
The accuracy of the sidereal rotation period is usually of the order of 0.1 to 0.01 times the temporal resolution interval P2/ (2T) (where P is the rotation period and T is the length of the total observation time span). For the typical amount of optical photometry we have for our targets the spin axis orientation accuracy for the light-curve inversion method is, in general, ~ 5°/ cosβ for λ and ~ 10° for β (Hanuš et al. 2011).
All possible shapes were compared with the results derived from stellar occultations whenever they were available. The projected shape model on the sky plane is computed at the occultation epoch using the Ďurech et al. (2011) approach. Its profile is then adjusted, using a Monte-Carlo-Markov-Chain algorithm, to the extremes of the occultation chords.
With this procedure, the best absolute scale of the model is found, thus allowing us to determine the size of the target. For ease of interpretation, the absolute dimensions of the ellipsoid best fitting – the scaled shape model and the volume-equivalent sphere Req are computed.
In some cases, the result of stellar occultations also allows one to discriminate different spin axis solutions.
Eventually, the FSDT is used to analyse all the derived convex shape models. As this procedure depends on the presence of flat surfaces, we must ensure that the shape models are reliable. In fact, portions of the asteroid surface not sufficiently sampled by photometry, can also produce flat surfaces. We thus established the approach explained in the following section, allowing us to estimate the reliability of a shape derived by the light-curve inversion.
3.1. Shape validation by the bootstrap method
Our goal is to evaluate the reliability of shape model details, and to check if a set of light-curves provides a good determination of the spin parameters.
As mentioned above, the light-curve inversion process often provides several sets of spin parameters (rotation period and spin axis orientation) that fit the optical data equally well. In other cases, when only a few light-curves are available, the parameter set may converge with a single, but incorrect solution, often associated with an incorrect rotation period. We see below that the bootstrapping method detects such cases.
Our approach consists in computing the shape model that best fits a subset of light-curves, randomly selected among all those that are available for a given asteroid. By studying how the fraction of flat surfaces ηs evolves with the number of selected light-curves, we obtain a solid indication on the completeness of the data, that is, the need for new observations or not.
In more detail, we proceed as follows:
-
First, a large number of light-curve samples is extracted from thewhole data set. Each of these subsets may contain a number oflight-curves nl ranging from nl = 1 to all those available (nl = Ndl). Sets of sparse data are also included in the process and equal for all samples. In fact, the availability of a sparse data set is a necessary condition to apply the bootstrapping technique. Since shape models can sometimes be derived using sparse data only, they allow the inversion process to converge to a solution even for low values of nl.
-
The second step consists in deriving the shape model corresponding to all the light-curve samples generated in the previous step. The spin axis parameters found by using all the light-curves are exploited as initial conditions for each inversion computation. If different sets of spin parameters are found with equal probability, the whole procedure is executed for each of them.
-
Once all the shape models are determined, we apply the FSDT in order to find the best value of ηs for each shape model.
-
The last step consists in determining the mean value and the dispersion of ηs corresponding to each subset group characterised by nl = 1, 2, 3,...,Ndl light-curves.
An excess of flat surfaces is often interpreted as the qualitative indication that the available photometry does not constrain the shape model adequately. The addition of supplementary light-curves is then a necessary condition to improve the shape. In our procedure, we make the hypothesis that, as the number of light-curves increases, the ηs parameter decreases. In the process, the model converges to the convex hull of the real shape. Ideally, the only flat surfaces remaining should then correspond to concave (or really flat) topological features. Such a convergence should ideally show up as a monotonic decrease of ηs towards an asymptotic value for a large nl. Here, we apply our procedure and show that our quantitative analysis is consistent with this assumption.
We stress here that the number of possible subsets that can be extracted is potentially large, as it is given by the binomial coefficient 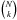 .
.
If the number of light-curves is below 14, all subsets are exploited. If there are additional light-curves, the number of possible combinations increases, but we do not generate more than 10 000 random subsets to limit the computation time. Our results show that this is not a limitation when the light-curve sample is very rich.
3.1.1. Test on (433) Eros
The bootstrap method was first tested on (433) Eros for which the shape is well known thanks to the images taken by the NEAR mission (Gaskell 2008). A large number of dense photometric light-curves (N = 134) is also available for this asteroid which allows us to derive an accurate shape model using light-curve inversion.
The data set of (433) Eros contains 134 dense light-curves and 2 sets of sparse data. Figure 2 shows the average of the flat surface fraction (ηs) as a function of the number of dense light-curves (Ndl) used for the shape modelling.
As expected (Fig. 2), the ηs versus Ndl curve (hereafter called the bootstrap curve) is monotonically decreasing. It is straightforward to verify that an exponential function y = aexp(−bx) + c is well suited to fit the bootstrap curve. In this expression the c parameter corresponds to the asymptotic value ηa, that is, the ηs that would be detected if a very large number of light-curves was used. In the case of (433) Eros we find ηa = 0.134.
 |
Fig. 2 Bootstrap curves for the asteroid (433) Eros. |
 |
Fig. 3 Bootstrap curves for the asteroid (2) Pallas. The panels illustrate the curve obtained for different coordinates of the spin axis. |
For a comparison to the “real” shape, we can take advantage of the detailed shape model of (433) Eros obtained by the analysis of the NEAR space probe images, obtained during the close encounter. For our goal, a low-resolution version (Gaskell 2008) is sufficient, and was used to check the result described above.
By taking the convex-hull (i.e. the smallest convex volume that encloses a non-convex shape), we obtain the shape model that, in an ideal case, the light-curve inversion should provide. In that specific case, the FSDT yields ηa = 0.12. This value is within 6% of the value obtained by the bootstrapping method. This is a first indication that our approach provides a good approximation and can be used to evaluate the “completeness” of a light-curve set.
We may compare our result to the value corresponding to the complete set of Ndl available light-curves. In this case, ηs = 0.18, a much larger discrepancy (20%) with respect to the correct value. This result means that the convex shape model of (433) Eros (derived by photometry only) could probably be somewhat improved by adding new dense light-curves.
In the following sections, we apply this analysis to other objects for the evaluation of their shape as derived from the photometric inversion.
3.1.2. Sensitivity of the bootstrap method to the spin axis coordinates
The behaviour of the bootstrap curve (exponentially decreasing) is related to the choice of the correct spin axis parameters.
This property is illustrated on the asteroid (2) Pallas. Even though Pallas has not been visited by a space probe, its spin axis orientation and shape are well known thanks to stellar occultations and adaptive optics observations (Carry et al. 2010).
The other difference with the case of (433) Eros is that there are less observed dense light-curves. As a matter of fact, the light-curve inversion provides two ambiguous solutions for the spin axis coordinates, at (37.9°, −15.1°) and (199.6°, 39.4°). Both poles yield the same RMS residuals for the fit to the light-curves.
A priori, there is no way to know which solution is the best, without additional constraint such as disk-resolved observations, since both solutions reproduce equally well the observed photometry. However, there is a clear difference between the two when analysing the bootstrap curve (Fig. 3). The first solution follows the well-defined exponential convergence providing ηa = 0.045, which seems to be consistent with the shape model as it is known so far. For the second spin axis orientation solution, we see that the bootstrap curve does not seem to follow the exponential trend. The corresponding ηa ~ 0.15 is in contradiction with the fact that the shape of (2) Pallas does not show any sign of large concave topological features. The rejection of the second pole solution is consistent with the result of stellar occultations and adaptive optics (Carry et al. 2010).
 |
Fig. 4 Composite light-curves of two asteroids in our sample. Each light-curve is folded with respect to the synodic period of the object, indicated below the plot. |
 |
Fig. 5 Example of two asteroid shape models derived in this work. For both shape models, the reference system in which the shape is described by the inversion procedure, is also displayed. The z axis corresponds to the rotation axis. The y axis is oriented to correspond to the longest direction of the shape model on the plane perpendicular to z. Each shape is projected along three different viewing geometries to provide an overall view. The first one (left-most part of the figures) corresponds to a viewing geometry of 0° and 0° for the longitude and latitude respectively (the x axis is facing the observer). The second orientation corresponds to (120°, 30°) and the third one to (240°, −30°). The inset plot shows the result of the bootstrap method. The x axis corresponds to the number of light-curves used and the y axis is ηa. |
Summary of the results pertaining to our survey.
 |
Fig. 6 Fit of the derived shape models for (172) Baucis on the observed occultation chords from the 18 December 2015 event. The left panel represents the shape model corresponding to the first pole solution (λ1, β1). The right panel represents the shape model obtained using the second pole solution. |
 |
Fig. 7 Fit of the derived shape models for (236) Honoria on the observed occultation chords from the 11 October 2011 and the 7 September 2012 events. The left panel represents the 2008 event with the top and bottom panels corresponding to the first and second pole solutions, respectively. The right panel is the same as the left one, but for the 2012 event. |
3.1.3. Distribution of flat surfaces across the available shape-model population
The bootstrap method gives us information on the possible presence of concave topological features. Here, a large number of asteroid shape models are analysed. These shape models are used as a reference population with which the derived shape models of Barbarians can be compared.
This reference was constructed using the shape models available on the DAMIT database (Ďurech et al. 2010). More than 200 asteroid shape models were analysed. For many of them, the result of the bootstrap method clearly shows that more data would be needed to obtain a stable shape. In a minority of cases, we find a behaviour suggesting incorrect pole coordinates. We selected a sample of 130 shape models, for which the bootstrap curve had the expected, regular behaviour towards a convergence, and for them we computed ηa.
4. Results and interpretation
In Fig. 4, one example of a composite light-curve for two asteroids observed by our network is shown. For each target, the synodic period (Psyn) associated to the composite light-curve is provided. Additional light-curves are displayed in Appendix C. For the cases where too few light-curves have been obtained by our survey to derive a reliable synodic period, the sidereal period (Psid) determined based on multi-opposition observations and obtained by the light-curve inversion method is used as an initial guess. In the case of (824) Anastasia, no error bars are provided since our observations were obtained during only one (very long) revolution. In Fig. 5 is displayed two examples of shape model derived in this work. Additional shape models are displayed in Appendix D. The bootstrap curves (see Sect. 3.1.1) are also shown for the different solutions of the pole orientation (except for (387) Aquitania for which no sparse data were used). Table 3 summarises the information about these asteroids, whose physical properties have been improved by our observations. Table 4 is the same as Table 3, except that it lists asteroids that we did not directly observe ourselves, but that are relevant to our discussion.
4.1. Individual asteroids
In the following we compare our results for each asteroid to some data available in the literature; asteroid occultation results (Dunham et al. 2016) in particular.
In Figs. 6 to 9, the occultations data are represented in the so-called fundamental plane (i.e. the plane passing through the centre of the Earth and perpendicular to the observer-occulted star vector) (Ďurech et al. 2011). In that plane, the disappearance and reappearance of the occulted star are represented respectively by blue and red squares and the occultation chords represented by coloured continuous segments. Error bars on the disappearance and reappearance absolute timing are represented by discontinuous red lines. Negative observations (no occultation observed) are represented by a continuous coloured line. Discontinuous segments represent observations for which no absolute timing is available. For each asteroid, the corresponding volume-equivalent radius is computed (corresponding to the radius of a sphere having the same volume as the asteroid shape model). The dimensions of the ellipsoid best fitting the shape model are also given. The uncertainties on the absolute dimensions of the shape models adjusted to stellar occultations are derived by varying various parameters according to their own uncertainties. First, the different shape models obtained during the bootstrap method are used. The spin axis parameters are randomly chosen according to a normal distribution around their nominal values with standard deviation equal to the error bars given in Table 3. Finally the extremes of each occultation chord are randomly shifted according to their timing uncertainties. The observed dispersion in the result of the scaling of the shape model on the occultations chords is then taken as the formal uncertainty on those parameters.
The list of all the observers of asteroid occultations which are used in this work can be found in Appendix D (Dunham et al. 2016). In the following we discuss some individual cases.
(172) Baucis – There are two reported occultations. The first event is a single-chord, while the other (18 December 2015) has two positive chords and two negative ones, and was used to scale the shape model (Fig. 6). According to the fit of the shape model to the occultation chords, both pole solutions seemed equally likely. The two solutions give similar absolute dimensions of (41.1 ± 2,36.3 ± 1.8,31.8 ± 1.6) and (40.8 ± 2.4,36.1 ± 1.7,33.5 ± 1.6) km, respectively. The corresponding volume-equivalent radii are Req = 36.2 ± 1.8 km and Req = 36.7 ± 1.8 km, to be compared to the NEOWISE (Mainzer et al. 2016), AKARI (Usui et al. 2012) and IRAS (Tedesco 1989) radii: 35.3 ± 0.4, 33.5 ± 0.4 and 31.2 ± 0.6 km, respectively. Even though the occultation observations cannot provide information about the best spin axis solution, the bootstrap curve indicates a clear preference for the one with retrograde rotation.
(236) Honoria – There are eight observed occultations. However, over these eight events, only two have ≥two positive chords (in 2008 with two positive chords and 2012 with three positive chords). These were used to constrain the pole orientation and scale the shape model. The result shows that the first pole solution (λ1 and β1 from Table 3) is the most plausible. By simultaneously fitting the two occultations, the obtained dimensions are (48.8 ± 1.4,48.3 ± 1.3,33.7 ± 1.0) km, and the volume-equivalent radius Req = 43.0 ± 2.1 km. In the case of the second pole solution, the dimensions of the semi-axes are (52.3 ± 2.7,52.1 ± 2.6,37.1 ± 1.9) km and the equivalent radius is Req = 45.6 ± 2.3 km. These solutions are compatible with the NEOWISE, AKARI, and IRAS measurements which are respectively 38.9 ± 0.6, 40.6 ± 0.5 and 43.1 ± 1.8 km. The fit of the shape model for the two pole solutions is shown in Fig. 7.
(387) Aquitania – For this asteroid, the result of the light-curve inversion process gives different solutions for the rotation period when sparse data are included. However, the noise on the sparse data is higher than the amplitude of the light-curves themselves. For this reason we decided to discard them. As a consequence, we did not apply the bootstrap method to this asteroid.
There is one well sampled occultation of (387) Aquitania providing four positive and four negative chords. The adjustment of the unique solution of the shape model on the occultation chords shows a good agreement. The scaling leads to an equivalent radius Req = 50.4 ± 2.5 km. The absolute dimensions are (54.2 ± 2.7,50.6 ± 2.5,46.6 ± 2.3) km. This is consistent with the WISE (Masiero et al. 2011), AKARI, and IRAS radii, which are respectively 48.7 ± 1.7, 52.5 ± 0.7, and 50.3 ± 1.5 km. The fit of the shape model on the occultation chords is shown in Fig. 8.
Hanuš et al. (2017) found a relatively similar model, spin axis solution (Psid = 24.14012 h, λ = 123° ± 5°, and β = 46° ± 5°), and size (48.5 ± 2 km) using an independent approach.
(402) Chloe – There are six reported occultations, but only two can be used to adjust the shape models on the occultation chords. These two occultations occurred on the 15 and 23 December 2004. The result clearly shows that the first pole solution is the best one. The other one would require a deformation of the shape that would not be compatible with the constraints imposed by the negative chords. The derived dimensions of (402) Chloe, for the first spin axis solution, are (38.3 ± 1.9,33.7 ± 1.7,24.7 ± 1.2) km and the equivalent radius is Req = 31.3 ± 1.6 km. The second spin solution leads to the dimensions (46.9 ± 2.4,41.3 ± 2.1,29.0 ± 1.5) km and Req = 38.3 ± 1.9 km. The NEOWISE radius is 27.7 ± 0.8 km while the AKARI and IRAS radii are 30.2 ± 1.5 and 27.1 ± 1.4 km, respectively, which agree with the first pole solution, but not with the second one. The fit of the shape model on the occultation chords is shown in Fig. 9.
 |
Fig. 8 Fit of the derived shape model for (387) Aquitania on the observed occultation chords from the 26 July 2013 event. |
 |
Fig. 9 Fit of the derived shape models for (402) Chloe on the observed occultation chords from 15 and 23 December 2014 events. The leftmost part of the figure represents the 23 event with the upper and lower parts corresponding to the first and second pole solutions, respectively. The rightmost part of the figure is the same as the leftmost part, but for the 15 December event. |
(824) Anastasia – The light-curve inversion technique provided three possible pole solutions. However, two of them present a rotation axis which strongly deviates from the principal axis of inertia. This is probably related to the extreme elongation of the shape model. The light-curve inversion technique is known to have difficulty in constraining the relative length along the axis of rotation, in particular. In the case of highly elongated bodies, the principal axis of inertia is poorly constrained.
Two occultations were reported for this asteroid. The models cannot fit the two occultations simultaneously using a single scale factor. We decided therefore not to present the shape model and spin solutions in this paper as new observations are required to better constrain the pole solution. Because of the very large rotation period of this asteroid, the presence of a possible tumbling state should also be tested.
(2085) Henan – This asteroid possesses a relatively large rotation period. Based on our photometric observation, two synodic periods can be considered (110 ± 1 h and 94.3 ± 1 h). However, the light-curve inversion technique seems to support the first one based on our observations and sparse data.
4.2. Presence of concavities
We have applied the flat detection method (FSDT) described in Devogèle et al. (2015) to all the shape models presented in this paper, thus (Sect. 3.1) providing a quantitative estimate for the presence of concavities and for the departure of an asteroid shape from a smooth surface with only gentle changes of curvature.
Figure 10 presents the result of the FSDT for the shape models presented in this work (blue diamonds, see Tables 3 and 4). These results can be compared to the average value of ηa computed by bins of 15 asteroids (red squares) using the asteroid population described in Sect. 3.1.3 (black dots).
 |
Fig. 10 Values of ηa as a function of the asteroids diameters. The black dots correspond to individual asteroids. The red squares correspond to the mean values of ηa and diameter for bins of 15 asteroids. The blue diamonds correspond to Barbarian asteroids. |
From this distribution, a correlation between diameter and fraction of flat surfaces seems to be apparent. Such correlation is expected since small asteroids are more likely to possess irregular shapes than larger ones. However, the quality of asteroid light-curves is directly correlated to the asteroids diameter. For small asteroids (<50 km), this effect might also increase the mean value of ηa. Figure 10 does not show clear differences between Barbarians and other asteroids, as Barbarians seem to populate the same interval of values. As expected, some asteroids like Barbara show a large amount of flat surfaces, but this is not a general rule for Barbarians. Of course the statistics are still not so high, but our initial hypothesis that large concave topological features could be more abundant on objects having a peculiar polarisation does not appear to be valid in view of this first attempt of verification.
4.3. Are Barbarian asteroids slow rotators?
In this section, we compare the rotation periods of Barbarians and Barbarian candidates with those of non-Barbarian type. At first sight the rotation period of confirmed Barbarian asteroids seems to indicate a tendency to have long rotation periods, as the number of objects exceeding 12 h is rather large. For our analysis we use the sample of objects as in Tables 3 and 4. By considering only asteroids with a diameter above 40 km, we are relatively sure that our sample of L-type asteroids is both almost complete, and not affected by the Yarkovsky-O’Keefe-Radzievskii-Paddack effect (Bottke et al. 2006). However, as only 13 asteroids remain in the sample, we also consider a second cut at 30 km, increasing it to 18. As shown below, our findings do not change as a function of this choice.
We proceed by comparing the rotation period of the Barbarians with that of a population of asteroids that possess a similar size distribution. Since the distribution of rotation periods is dependent on the size of the asteroids, we select a sample of asteroids with the same sizes, using the following procedure. For each Barbarian, one asteroid is picked out randomly in a population for which the rotation period is known, and having a similar radiometric diameter within a ± 5 km range. This way we construct a population of asteroids with the same size distribution as the Barbarians. We now have two distinct populations that we can compare. By repeating this process several times, we build a large number of populations of “regular” asteroids. We can then check the probability that the distribution of rotation periods of such a reconstructed population matches the one of the Barbarians.
Considering the sample of asteroids with a diameter larger than 40 km, the sample is too small to derive reliable statistics. However, we notice that the median of the rotation period of the Barbarians is 20.1 h while the median of the population regular asteroid is only 12.0 h.
In order to improve the statistic, we can also take into account asteroids with a diameter between 30 and 40 km. The median of the Barbarian asteroids is now 20.6 h while the regular asteroids population has a median of 11.4 h.
Figure 11 represents the histograms of the rotation periods of Barbarian asteroids (with diameter >30 km) compared to the population of regular asteroids constructed as described in the beginning of this section. The histogram of the Barbarian asteroids shows a clear excess of long rotation periods and a lack of fast-spinning asteroids.
 |
Fig. 11 Normalised histograms of the Barbarian compared to the histogram asteroids having a diameter between 110 and 30 km. |
We adopt the two-sample Kolmogorov-Smirnov (KS) test to compare the distributions of Barbarians and regular asteroids. This is a hypothesis test used to determine whether two populations follow the same distribution. The two-sample KS test returns the so-called asymptotic p-value. This value is an indication of the probability that two samples come from the same population.
In our case, we found p = 0.6%, clearly hinting at two distinct populations of rotation period.
In conclusion our results show that there is clear evidence that the rotations of Barbarian asteroids are distinct from those of the whole population of asteroids. The abnormal dispersion of the rotation periods observed for the Barbarian asteroids is more probably the result of a true difference than a statistical bias.
5. Conclusions
We have presented new observations here for 15 Barbarian or candidate Barbarian asteroids. For some of these asteroids, the observations were secured by us during several oppositions. These observations allow us to improve the value of the rotation period. For eight of them, we were able to determine or improve the pole orientation and compute a shape model.
The shape models were analysed using a new approach based on the technique introduced by Devogèle et al. (2015). We show that this technique is capable of providing an indication about the completeness of a light-curve data set indicating whether or not further observations are required to better define a shape solution of the photometric inversion method. The extrapolation of the trend towards a large number of light-curves gives a more precise determination of ηs. This new method was applied to a large variety of shape models in the DAMIT database. This allowed us to construct a reference to which the shape models determined in this work were compared. Our results show that there is no evidence that our targets have more concavities or are more irregular than a typical asteroid. This tends to infirm the hypothesis that large-scale concavities may be the cause of the unusual polarimetric response of the Barbarians.
The improvement and new determination of rotation periods have increased the number of asteroids for which a reliable rotation period is known. This allows us to have an improved statistic over the distribution of rotation periods of the Barbarian asteroids. We show in this work possible evidence that the Barbarian asteroids belong to a population of rotation periods that contains an excess of slow rotators, and lacks fast spinning asteroids. The relation between the polarimetric response and the unusual distribution of rotation periods is still unknown.
See the Database of Asteroid Models from Inversion Techniques (DAMIT) database for an up-to-date list of asteroid shape models: http://astro.troja.mff.cuni.cz/projects/asteroids3D/
Acknowledgments
The authors thank the referee for his/her comments, which improved the manuscript. M.D. and J.S. acknowledge the support of the Université de Liège. M.D. and P.T. acknowledge the support of the French “Programme Nationale de Planétologie”. Part of the photometric data in this work were obtained at the C2PU facility (Calern Observatory, O.C.A.). N.P. acknowledges funding from the Portuguese FCT – Foundation for Science and Technology. CITEUC is funded by National Funds through FCT – Foundation for Science and Technology (project: UID/ Multi/00611/2013) and FEDER – European Regional Development Fund through COMPETE 2020 – Operational Programme Competitiveness and Internationalisation (project: POCI-01-0145-FEDER-006922). SARA observations were obtained under the Chilean Telescope Allocation Committee program CNTAC 2015B-4. P.H. acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada, and thanks the staff of Cerro Tololo Inter-American Observatory for technical support. The work of A.M. was supported by grant no. 2014/13/D/ST9/01818 from the National Science Centre, Poland. The research of V.K. is supported by the APVV-15-0458 grant and the VVGS-2016-72608 internal grant of the Faculty of Science, P. J. Safarik University in Kosice. M.K. and O.E. acknowledge TUBITAK National Observatory for a partial support in using T100 telescope with project number 14BT100-648.
References
- Bagnulo, S., Cellino, A., & Sterzik, M. F. 2015, MNRAS, 446, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M., Fulchignoni, M., Burchi, R., & D’Ambrosio, V. 1985, Icarus, 61, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Binzel, R. 1987, Icarus, 72, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlick, D., Rubincam, D. P., & Nesvorn, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [Google Scholar]
- Bowell, E., Oszkiewicz, D. A., Wasserman, L. H., et al. 2014, Meteor. Planet. Sci., 49, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Buchheim, R., Roy, R., & Behrend, R. 2007, The Minor Planet Bulletin, 34, 13 [NASA ADS] [Google Scholar]
- Bus, S., & Binzel, R. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J. 2009, IRTF Near-IR Spectroscopy of Asteroids V1.0. EAR-A-I0046-4-IRTFSPEC-V1.0. NASA Planetary Data System [Google Scholar]
- Carreõ-Carcerán, A., Aznar, A., Mansego, E. A., et al. 2016, Minor Planet Bulletin, 43, 92 [NASA ADS] [Google Scholar]
- Carry, B., Dumas, C., Kaasalainen, M., et al., 2010, Icarus, 205, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Belskaya, I. N., Bendjoya, Ph., et al. 2006, Icarus, 180, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Bagnulo, S., Tanga, P., Novakivoc, B., & Delbo, M. 2014, MNRAS, 439, 75 [Google Scholar]
- Debehogne, H., Surdej, A., & Surdej, J. 1977, A&AS, 30, 375 [NASA ADS] [Google Scholar]
- Delbo, M., Ligori, S., Matter, A., Cellino, A., & Berthier, J. 2009, AJ, 694, 1228 [CrossRef] [Google Scholar]
- DeMeo, F., Binzel, R., Slivan, S., & Bus, S. 2009, Icarus, 160, 180 [Google Scholar]
- Denchev, P., Shkodrovb, V., & Ivanovab, V. 2000, Planet. Space Sci., 48, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Devogèle, M., Rivet, J. P., Tanga, P., et al. 2015, MNRAS, 453, 2232 [NASA ADS] [Google Scholar]
- Devogèle, M., Cellino, A., Bagnulo, S., et al. 2017a, MNRAS, 465, 4335 [NASA ADS] [CrossRef] [Google Scholar]
- Devogèle, M., et al. 2017b, Icarus, submitted [Google Scholar]
- di Martino, M., Blanco, D., Riccioli, D., & de Sanctis, G. 1994, Icarus, 107, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, D. W., Herald, D., Frappa, E., et al. 2016, Asteroid Occultations V14.0. EAR-A-3-RDR-OCCULTATIONS-V14.0, NASA Planetary Data System [Google Scholar]
- Ďurech, J., & Kaasalainen, M. 2003, A&A, 709, 404 [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, R. W. 2008, Gaskell Eros Shape Model V1.0. NEAR-A-MSI-5-EROSSHAPE-V1.0, NASA Planetary Data System [Google Scholar]
- Gil-Hutton, R. 1993, Rev. Mex. Astron. Astrofis., 25, 75 [NASA ADS] [EDP Sciences] [Google Scholar]
- Gil-Hutton, R., Mesa, V., Cellino, A., et al. 2008, A&A, 482, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil-Hutton, R., Cellino, A., & Bendjoya, Ph. 2014, A&A, 569, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2013, A&A, 551, A16 [Google Scholar]
- Hanuš, J., Viikinkoski, M., Marchis, F., et al. 2017, A&A, 601, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A., & Young, J. 1989, Icarus, 81, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A., Young, J., Dockweiler, T., et al. 1992, Icarus, 92, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I., Piironen, J., & Erikson, A. 2001, Asteroid photometric catalogue, fifth update (Uppsala Astronomical Observatory) [Google Scholar]
- Larson, S., Beshore, E., Hill, R., et al. 2003, AAS/Division for Planetary Sciences Meeting Abstracts, BAAS, 35, 982 [NASA ADS] [Google Scholar]
- LeCrone, C., Mills, G., & Ditteon, R. 2005, Minor Planet Bulletin, 32, 65 [NASA ADS] [EDP Sciences] [Google Scholar]
- Mainzer, A. K., Bauer, J. M., Cutri, R. M., et al. 2016, NEOWISE Diameters and Albedos V1.0. EAR-A-COMPIL-5-NEOWISEDIAM-V1.0, NASA Planetary Data System [Google Scholar]
- Marciniak, A., Michałowski, T., Polińska, M., et al. 2011, A&A, 529, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Pilcher, F., Oszkiewicz, D., et al. 2016, Proc. Polish Astron. Soc., 3, 84 [Google Scholar]
- Masiero, J., & Cellino, A. 2009, Icarus, 199, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Mothé-Diniz, T., & Nesvorný, D. 2008, A&A, 492, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milani, A., Cellino, A., Knežević, Z., et al. 2014, Icarus, 46, 239 [Google Scholar]
- Nesvorný, D., Broz, M., & Carruba, V. 2015, Asteroids IV (Tucson, AZ: Univ. Arizona Press) [Google Scholar]
- Oey, J. 2012, Minor Planet Bulletin, 39, 145 [NASA ADS] [Google Scholar]
- Piclher, F. 2009, The Minor Planet Bulletin, 36, 133 [NASA ADS] [EDP Sciences] [Google Scholar]
- Schober, H. J. 1979, A&AS, 8, 91 [NASA ADS] [Google Scholar]
- Sunshine, J. M., Connolly, H. C., McCoy, T. J., Bus, S. J., & La Croix, L. 2007, Lun. Planet. Inst. Sci. Conf. Abstact, 1613 [Google Scholar]
- Sunshine, J. M., Connolly, H. C., McCoy, T. J., et al. 2008, Science, 320, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, V., Tungalag, N., Chiorny, V., et al. 2009, Icarus, 1514 [Google Scholar]
- Stephens, R. D. 2013a, Minor Planet Bulletin, 40, 34 [Google Scholar]
- Stephens, R. D. 2013b, Minor Planet Bulletin, 40, 178 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2014, Minor Planet Bulletin, 41, 226 [NASA ADS] [Google Scholar]
- Strabla, L., Quadri, U., & Girelli, R. 2013, Minor Planet Bulletin, 40, 232 [NASA ADS] [Google Scholar]
- Tanga, P., Carry, B., Colas, F., et al. 2015, MNRAS, 448, 3382 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F. 1989, in Asteroid II, 1090 [Google Scholar]
- Tholen, D. J. 1984, Ph.D. Thesis, University of Arizona [Google Scholar]
- Usui, F., et al. 2012, ApJ, 762, 1 [Google Scholar]
- Warner, B. D. 2009, Minor Planet Bulletin, 36, 109 [NASA ADS] [Google Scholar]
- Weidenschilling, S. J., Chapman, C. R., Davis, D. R., et al. 1990, Icarus, 86, 402 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Summary of the new observations used in this work
New observations used for period and shape model determination which were presented in this work and observations that are not included in the UAPC.
Appendix B: Summary of previously published observations used in this work
All observations used for period and shape modelling which have already been published.
Appendix C: Light-curves obtained for this work
 |
Fig. C.1 Composite light-curves of asteroids studied in this works. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
Appendix D: Shape models derived in this work
 |
Fig. D.1 Asteroid shape models derived in this work. For each shape model, the reference system in which the shape is described by the inversion procedure, is also displayed. The z axis corresponds to the rotation axis. The y axis is oriented to correspond to the longest direction of the shape model on the plane perpendicular to z. Each shape is projected along three different viewing geometries to provide an overall view. The first one (left-most part of the figures) corresponds to a viewing geometry of 0° and 0° for the longitude and latitude respectively (the x axis is facing the observer). The second orientation corresponds to (120°, 30°) and the third one to (240°, −30°). The inset plot shows the result of the bootstrap method. The x axis corresponds to the number of light-curves used and the y axis is ηa. Since the shape model of (387) Aquitania was derived without sparse data, the bootstrap method was not applied. |
 |
Fig. D.1 continued. |
Appendix E: List of observers for the occultation data used in this work
 |
Fig. E.1 List of observers of stellar occultation by an asteroid. |
All Tables
List of the observatories participating in the observation campaigns, with telescope aperture (D), position, and number of light-curves.
New observations used for period and shape model determination which were presented in this work and observations that are not included in the UAPC.
All observations used for period and shape modelling which have already been published.
All Figures
 |
Fig. 1 Inclination versus semi-major axis plot of main-belt asteroids. The asteroids studied in this work are plotted as red circular dots, while the thinner blue dots represent the asteroid population as a whole. |
| In the text | |
 |
Fig. 2 Bootstrap curves for the asteroid (433) Eros. |
| In the text | |
 |
Fig. 3 Bootstrap curves for the asteroid (2) Pallas. The panels illustrate the curve obtained for different coordinates of the spin axis. |
| In the text | |
 |
Fig. 4 Composite light-curves of two asteroids in our sample. Each light-curve is folded with respect to the synodic period of the object, indicated below the plot. |
| In the text | |
 |
Fig. 5 Example of two asteroid shape models derived in this work. For both shape models, the reference system in which the shape is described by the inversion procedure, is also displayed. The z axis corresponds to the rotation axis. The y axis is oriented to correspond to the longest direction of the shape model on the plane perpendicular to z. Each shape is projected along three different viewing geometries to provide an overall view. The first one (left-most part of the figures) corresponds to a viewing geometry of 0° and 0° for the longitude and latitude respectively (the x axis is facing the observer). The second orientation corresponds to (120°, 30°) and the third one to (240°, −30°). The inset plot shows the result of the bootstrap method. The x axis corresponds to the number of light-curves used and the y axis is ηa. |
| In the text | |
 |
Fig. 6 Fit of the derived shape models for (172) Baucis on the observed occultation chords from the 18 December 2015 event. The left panel represents the shape model corresponding to the first pole solution (λ1, β1). The right panel represents the shape model obtained using the second pole solution. |
| In the text | |
 |
Fig. 7 Fit of the derived shape models for (236) Honoria on the observed occultation chords from the 11 October 2011 and the 7 September 2012 events. The left panel represents the 2008 event with the top and bottom panels corresponding to the first and second pole solutions, respectively. The right panel is the same as the left one, but for the 2012 event. |
| In the text | |
 |
Fig. 8 Fit of the derived shape model for (387) Aquitania on the observed occultation chords from the 26 July 2013 event. |
| In the text | |
 |
Fig. 9 Fit of the derived shape models for (402) Chloe on the observed occultation chords from 15 and 23 December 2014 events. The leftmost part of the figure represents the 23 event with the upper and lower parts corresponding to the first and second pole solutions, respectively. The rightmost part of the figure is the same as the leftmost part, but for the 15 December event. |
| In the text | |
 |
Fig. 10 Values of ηa as a function of the asteroids diameters. The black dots correspond to individual asteroids. The red squares correspond to the mean values of ηa and diameter for bins of 15 asteroids. The blue diamonds correspond to Barbarian asteroids. |
| In the text | |
 |
Fig. 11 Normalised histograms of the Barbarian compared to the histogram asteroids having a diameter between 110 and 30 km. |
| In the text | |
 |
Fig. C.1 Composite light-curves of asteroids studied in this works. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. D.1 Asteroid shape models derived in this work. For each shape model, the reference system in which the shape is described by the inversion procedure, is also displayed. The z axis corresponds to the rotation axis. The y axis is oriented to correspond to the longest direction of the shape model on the plane perpendicular to z. Each shape is projected along three different viewing geometries to provide an overall view. The first one (left-most part of the figures) corresponds to a viewing geometry of 0° and 0° for the longitude and latitude respectively (the x axis is facing the observer). The second orientation corresponds to (120°, 30°) and the third one to (240°, −30°). The inset plot shows the result of the bootstrap method. The x axis corresponds to the number of light-curves used and the y axis is ηa. Since the shape model of (387) Aquitania was derived without sparse data, the bootstrap method was not applied. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. E.1 List of observers of stellar occultation by an asteroid. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


