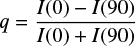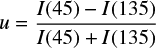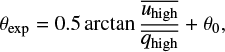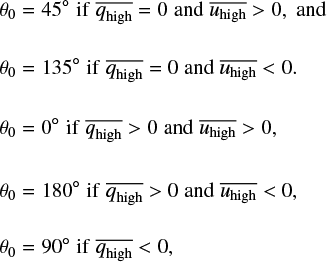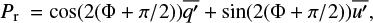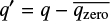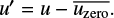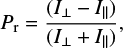| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 17 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202142960 | |
| Published online | 13 September 2022 | |
The Calern Asteroid Polarisation Survey
An updated catalogue of asteroid polarimetric data★
1
Côte d’Azur University, Côte d’Azur Observatory, CNRS, Lagrange Laboratory,
Valsros Campus,
06108
Nice Cedex 02, France
e-mail: philippe.bendjoya@unice.fr
2
INAF, Osservatorio Astrofisico di Torino,
via Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: alberto.cellino@inaf.it
3
Lowell Observatory,
1400 W. Mars Hill Road,
Flagstaff, AZ
86001, USA
4
Armagh Observatory and Planetarium,
College Hill,
Armagh
BT61 9DG, UK
5
Grupo de Ciencias Planetarias, Departamento de Geofísica y Astronomía, Facultad de Ciencias Exactas, Físicas y Naturales, Universidad Nacional de San Juan – CONICET,
Av. J. I. de La Roza 590 Oeste,
J5402DCS
Rivadavia, San Juan, Argentina
6
Physics department, Torino University,
via Pietro Giuria 1,
10025
Torino, Italy
Received:
20
December
2021
Accepted:
13
June
2022
Context. The Calern Asteroid Polarimetric Survey (CAPS), a collaboration between the INAF Astrophysical Observatory of Torino (Italy) and the Observatoire de la Côte d’Azur (Nice, France), has produced new asteroid polarimetric data for a number of years, and is one of the most important, currently active projects of asteroid polarimetry.
Aims. The purpose of this paper is to make public the CAPS data collected thus far, to explain the adopted techniques of data reduction and computation of phase-polarisation curves for the measured objects, and explain, by means of some examples, the importance of the CAPS database.
Methods. The pipeline of data reduction has been recently updated and made as automatic as possible, using numerical algorithms developed specifically for the purposes of CAPS. The derivation of phase-polarisation curves for the observed asteroids is done using established criteria and algorithms that have recently been slightly improved, and are also summarised in this paper.
Results. The CAPS catalogue is a steadily growing source of information which can be exploited for different purposes, including, but not limited to, an updated calibration of the relations existing between different polarimetric parameters and the geometric albedo of the objects, and a study of classes of objects that can be most easily identified by means of their polarimetric properties. These subjects will be more specifically discussed in separate papers.
Conclusions. Asteroid polarimetry data nicely complement the results of other more commonly used techniques, including visible and IR photometry and spectroscopy. CAPS contains a lot of much-desired information about physical properties, which can hardly be inferred by means of other techniques.
Key words: minor planets / asteroids: general / catalogs
Full Tables A.1 and A.2 are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/665/A66
© Ph. Bendjoya, et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Polarimetry is an important tool to derive information about physical properties of the asteroids and other small bodies in our Solar System. The state of partial linear polarisation of sunlight, scattered by asteroid surfaces, changes in different illumination conditions described by the so-called phase angle1. The fraction of linear polarisation and the orientation of the polarisation plane depend on the properties of the surface regolith, including the geometric albedo, refractive index, packing density and size distribution of surface regolith particles (see, for instance, Cellino et al. 2015a; Belskaya et al. 2015). The polarimetric behaviour is determined by the interplay of different physical mechanisms, including the so-called coherent backscattering, which is thought to be important to also explain some photometric properties of atmosphereless Solar System bodies (Muinonen et al. 2002). The observed variety of polarimetric behaviour characterising objects that exhibit different reflectance spectra makes polarimetry a very useful complement to asteroid spectroscopy, and in some cases it makes it possible to more easily identify classes of objects that are more difficult to discover using data obtained through other techniques. Examples are given by the so-called Barbarians (Cellino et al. 2006; Devogèle et al. 2018a) and by some partially active asteroids, such as (3200) Phaethon and (101955) Bennu (Devogèle et al. 2018b; Cellino et al. 2018). An analysis of the polarimetric properties of the asteroid (4) Vesta, visited by the DAWN space probe, has recently made it possible to more directly link the polarimetric behaviour to well-characterised properties of the surface, at least in this particular case (Cellino et al. 2016b).
The Calern Asteroid Polarimetric Survey (hereinafter CAPS) is a project of collaboration between the INAF Astrophysical Observatory of Torino (Italy) and the Observatory of the Côte d’Azur (OCA) in Nice, (France). It aims to obtain asteroid Polarimetrie data using a Polarimeter built at the Torino Observatory, mounted on the Cassegrain focus of the 1.04 m Omicron (West) telescope of the Centre Pédagogique Planète et Univers (C2PU) facility, located on the Calern plateau (southern France, MPC code 010), and managed by the OCA.
The objectives of CAPS, as well as a description of the instrument and a preliminary assessment of its performances, have been described by Devogèle (2017). From 2017 until December 2021, CAPS produced more than 2100 single measurements for about 600 asteroids (a recent observing run carried out in 2022 has produced new data that are still under reduction). This is an important contribution to the field of asteroid polarimetry. As a comparison, the largest database currently available, namely the Asteroid Polarimetric Database (APD), maintained by D.F. Lupishko and available at the NASA Planetary Data System (PDS, Lupishko 2014) at the URL address http://pds.jpl.nasa.gov/, includes a little more than 5100 single measurements obtained by many authors over a much longer time span, starting since the early 1970s. One of the main purposes of the present paper is to make the current CAPS database publicly available. Recently, the whole CAPS data reduction pipeline has been extensively re-designed to speed up and automate most of the required procedures, and improve the overall measurement accuracy, by devoting particular attention to the determination of instrumental polarisation. Moreover, some minor improvements of the criteria used to compute asteroid phase-polarisation curves using the so-called exponential-linear representation, as previously described by Cellino et al. (2015b, 2016a), have also been made.
New best-fit phase-polarisation curves have been obtained for a large sample of objects, combining the CAPS data together with data available in the literature. The latter primarily include data listed in the previously mentioned APD, as well as in the Belskaya Asteroid Polarimetry V1.0 database (Lupishko 2014; Belskaya et al. 2010). In addition, several measurements have been taken from a number of articles published by different authors. Among them, several papers were based on data obtained at the Complejo Astronómico El Leoncito (CASLEO), managed by the Universities of La Plata, Córdoba and San Juan (Argentina), and the Argentinian Scientific and Technical Research Council (CONICET; Gil-Hutton & Cañada-Assandri 2011, 2012; Cañada-Assandri et al. 2012). Several data were obtained in the framework of a long-lasting collaboration between the Torino Astrophysical Observatory and CASLEO that started in the late 1990s. Most obtained measurements were published in several papers, including Gil-Hutton et al. (2008, 2014); Cellino et al. (2005a,b, 1999, 2006); Belskaya et al. (2017). However, some of the CASLEO measurements, in UBVRI colours, have never been published before. In our computations of phase-polarisation curves described in the next sections, we use at least some of our old CASLEO measurements, taking them when needed from a private data file that includes all of them. After an overall check of the situation made by two of us (AC and RGH), we decided to list CASLEO unpublished data in Appendix B.
In this paper we present the current CAPS database and the techniques adopted for data analysis. We will devote separate papers to analysing specific issues based on the data presented here, including, but not limited to, the problem of a better determination of the geometric albedo of many objects. We present in Appendix A the whole CAPS database, but in the text we only discuss some selected subsets of obtained data, in order to show the importance of CAPS, and give an idea of the advancements we can expect from a proper exploitation of this data set. We also briefly discuss the existence of measurement errors affecting both the CAPS database and the data available in the literature, and we list some explanations for the presence of such errors.
In this respect, it is important to note that, as described in Sect. 2, a new assessment of the variability of the instrumental polarisation affecting CAPS measurements led us to revise upwards our estimates of CAPS measurement errors. In the cases of measurements published in previous papers, including those currently included in the APD, the published values of linear polarisation do not change, but the updated values of the associated errors given in Appendix A of this paper should supersede previous versions.
This paper is organised as follows. In Sect. 2 we present the reduction pipeline developed for the CAPS data. In Sect. 3 we mention some recent improvements of the criteria adopted to select the objects for which a reliable phase-polarisation curve can be obtained, and we summarise the algorithms developed to fit the obtained phase-polarisation curves using the so-called exponential-linear data representation. In Sect. 4 we show the good agreement between CAPS data and those present in the literature, and we stress the importance of adding such a large amount of CAPS data to improve the state of the art in asteroid polarimetry. In Sect. 5 we discuss some possible explanations for the existence of measurements that clearly seem to be affected by large errors, both among those available in the literature and in a limited number of CAPS data. In Sect. 6 we show some preliminary examples of applications of the CAPS database to different problems encountered in asteroid polarimetry. A few final conclusions are summarised in Sect. 7.
2 Data reduction
The Torino polarimeter (ToPol) makes use of a wedged double Wollaston configuration to split the incoming light into different polarisation components. It produces four separate replicas of the target field of view, corresponding to four orientations of linear polarisation (0°, 45°, 90°, and 135°). Therefore, the I, Q, and U Stokes parameters can be computed in one single shot (Pernechele et al. 2012; Oliva 1997).
Details of the general CAPS observation and data analysis procedures have been published by Devogèle et al. (2017). The detector is a QSI632 CCD camera. Each night of CAPS operations includes measurements of a set of scientific targets (in nearly all cases asteroids), and a set of both zero-polarisation and highly polarised polarimetric standard stars, for the purposes of instrument calibration. In addition, CCD calibration measurements (bias, darks) are also carried out. However, no flat-field images are taken. In principle, these would be important for calibration purposes, but some problems have been evidenced after the publication of the Devogèle et al. (2017) paper. In particular, it has been found that there are non-negligible internal reflections inside ToPol that results in ‘leakages’ between the four replicas of the field of view (the bottom part of an upper replica is leaking to the upper part of a bottom replica, and vice versa). In the case of a fully illuminated field of view (needed to measure a flat field), these leakages are important and the normalised flat-field images are noticeably affected. On the other hand, for a field of view mostly consisting of low level sky background, these leakages are negligible (see Sect. 4.1 of Devogèle 2017 for a detailed analysis of the flat fielding and internal reflections of ToPol). To compensate for the lack of flat fielding, the observing procedure imposes that the targets are always kept centred into the same pixels, to avoid field-dependent variation of the recorded flux. This is always done with the maximum possible accuracy according to the observing circumstances (the pointing and tracking accuracy of the telescope). Of course, the centring of the target cannot always be considered perfect, in spite of the fact that the moving targets (asteroids) are always observed using telescope differential tracking. However, this effect, which certainly contributes to the overall budget error, does not seem to be the main cause of the amount of variable instrumental polarisation described at the end of this section.
All standard stars used for CAPS were obtained from Hsu & Breger (1982) and Gehrels (1974). They are bright (generally in an interval of V magnitudes between four and seven) and require very short exposure times (rarely above a couple of seconds). Each measurement typically consists of 30 individual acquisitions to account for scintillation noise and other type of noise associated with short exposure acquisitions of bright objects.
Asteroid targets are generally much fainter and require longer exposure times (up to half an hour or more in the most challenging cases) to achieve a reasonable S/R. Each measurement consists of at least ten individual acquisitions (more for relatively bright targets). We recall here that, contrary to the case for most polarimeters used for asteroid investigations, each acquisition provides the full set of Stokes parameters. Thus, the ten individual acquisitions provide ten independent measurements of the target polarisation.
Another change in the data reduction procedure with respect to the situation described by Devogèle et al. (2017), is that the field mask has been reduced from a field of view of 5.31 × 0.95″ to a field of view of 2.65 × 0.95″. This change has been implemented to avoid or minimise internal reflections inside the instrument. Such reflections have been found to be symmetric with respect to the x-axis of the field of view. By covering one half of the field of view, internal reflections of the flux from bright targets are minimised, down to mostly negligible levels (more detail can be found in Devogèle 2017).
Up to around mid-2018, data reduction was carried out manually using the AstroImageJ image processing software (Collins et al. 2017) and a suite of Matlab codes developed for ToPol. These tasks were highly time consuming and needed to be upgraded to be able to process large amounts of data in a timely manner. More recently, a partially automated reduction pipeline has been developed in Python, making use of the publicly available modules: matplotlib, argparse, numpy, operator, astroquery, os, photutil, sys, glob, astropy, scipy, and tkinter.
The general procedure for any observed target (in the case of CAPS, this means Solar System objects and polarisation standard stars) consists of three main steps. The first step is the creation of the master dark for each exposure time and CCD temperature, and correction of the science frames from the master dark. All the observations are performed at the same fixed CCD temperature. This is checked by the data reduction pipeline, which automatically checks the CCD temperature keyword in each dark and science frame. Each science frame is then corrected for the dark by looking for the closest in time master dark frame (of the same CCD temperature).
As a second step we take into account that, due to the small field of view (0.95′ × 2.65′), no automatic, astrometric-based identification of the sources present in the CCD frame can be performed as, most of the time, only the target and no more than one or two extra stars are detected in the field of view. This prevents the user from having an automatic selection of the target based on its sky position. As a consequence, one has to manually identify the target in the uppermost replica of the first acquisition. Since the offsets between the replicas are fixed, the three other replicas are automatically selected. Then, the pipeline will automatically detect the target in all the acquisition series (typically, ten frames per target). The user can then verify that the correct target has been selected in all individual frames and manually modify the selection for each individual frame whenever necessary. One should note that, in the case of asteroids, the danger of mistakenly selecting a wrong target (such as a star) is extremely unlikely, if not impossible. This is because the asteroid is the only object that remains stationary in the field of view from frame to frame as a consequence of the telescope tracking the desired target at a non-sidereal rate matching its motion. The target location on the CCD frame is accurately estimated by fitting a MOFFAT function to each individual replica of the asteroid. Once the target has been correctly identified in each frame, a photometric analysis using a curve-of-growth technique (increasing aperture photometry) is performed.
The third step consists of an analysis of the photometric curve of growth obtained for each individual observation. The aperture photometry provides the counts in analogue digital units (ADU) for each of the four images: I(d), where d = 0°, 45°, 90°, and 135°. From these, the reduced Stokes parameters,
and
can be derived. A plot of the mean value of the q = Q/I and u = U/I reduced Stokes parameters (taking into account all the frames) as a function of aperture size is presented to the users for selection of the optimal aperture size. The latter is the smallest aperture for which the curve of growth reaches a plateau and minimises the deviation of the individual curves of growth of each of the four separate images produced on the focal plane. This approach is discussed in detail by Bagnulo et al. (2016) and has been systematically adopted for CAPS data (Devogèle et al. 2017).
The three steps described above produce preliminary polarimetric measurements of the target.
The next step is the determination of the orientation in sky of the optical axis of the polarimeter. If 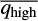 (and
(and 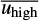 , are the mean values of
, are the mean values of 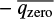 (and
(and 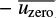 , where the index ‘high’ stands for an observed high-polarisation standard star, the instrumental polarisation angle is computed as:
, where the index ‘high’ stands for an observed high-polarisation standard star, the instrumental polarisation angle is computed as:
where (see Banulo et al. 2006)
From the known value of the polarisation angle of the standard star θstand, the correction angle Δθ = θstand − θexp is determined.
The ToPol instrument is attached to the telescope in a fixed position, and is not subject to any rotation. This means that, once the abovementioned correction angle has been determined with high accuracy, it is supposed to remain constant from night to night. We therefore use, for each observing run (lasting generally between one and two weeks), a fixed Δθ resulting from the measurements of all high-polarisation standard stars obtained in all the nights of the same observing run.
The final step is the computation of the so-called Pr parameter, which is generally used to describe the state of linear polarisation of planetary objects (see also Sect. 3). This is done by applying a rotation to the reference frame such that I(90) is equal to the intensity measured in the scattering plane2. In this reference system, qaster = Pr gives the total fraction of linear polarisation, whereas the uaster Stokes parameter is expected to be zero. The rotation angle ϕ between the object-north pole direction and the position angle of the scattering plane is taken from the JPL Horizons service, where it is available for any object and epoch, using the astroquery.jplhorizons python package for each individual frame. Pr can be finally computed as
where Φ = ϕ + Δθ represents the value of ϕ, after a further correction of Δθ to take into account the orientation of the optical axis of the polarimeter with respect to the position angle of the object-north pole direction.
The necessary information about the Sun coordinates and asteroid phase angle for any epoch of observation is also obtained automatically through a request to the Horizon JPL data server. Finally, the uncertainty on Pr is computed by error propagation, assuming that the errors of q and u are uncorrelated.
As mentioned above, a typical asteroid measurement consists of at least N = 10 individual exposures. During the various exposures, the target polarisation is supposed to remain constant, so that the scattering of the measurements about their average provides an external error estimate, which is practically dominated by photon-noise error.
The results, however, are affected by instrumental polarisation produced by the optical components of the system. To correct for instrumental polarisation, two or more unpolarised standard stars are observed every night. For these stars, it can be assumed that any measured values of q and u ≠ 0 are spurious, being produced by instrumental polarisation. Assuming that q and u are the raw Stokes parameter, while 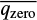 and
and 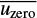 are the mean polarisation measured from several unpolarised standard stars observed during the same night, a preliminary correction of the measured polarisation is computed as:
are the mean polarisation measured from several unpolarised standard stars observed during the same night, a preliminary correction of the measured polarisation is computed as:
and
Measurements of unpolarised stars allow us to estimate and monitor the instrumental polarisation at different epochs. This has been found to be slightly variable over time. In particular, an extensive inspection of the scattering of measurements of unpolarised stars around nightly average values over a time span covering several years led us to conclude that, in any given night, the instrumental polarisation may be determined with an uncertainty of the order of 0.08%, which has to be quadratically added to the photon-noise error.
3 Mathematical representation of obtained phase-polarisation curves
The scattered sunlight we receive from atmosphereless Solar System bodies is in a state of partial linear polarisation. The plane of linear polarisation is always found to be either parallel or perpendicular to the scattering plane. As mentioned in Sect. 2, the degree of linear polarisation is usually expressed by the Pr parameter, defined as
where I⊥ is the intensity of the light beam component having the electric vector aligned along the plane perpendicular to the scattering plane, and I∥ is the intensity of the light beam having the electric vector aligned parallel to that plane.
We will always use the Pr parameter to indicate the measured linear polarisation of asteroids throughout this paper. Its value will always be expressed (and plotted in our figures) in percent (%). According to the above definition of Pr, its sign determines which one of the two possible orientations of the polarisation plane is being observed.
The fundamental property of Pr, as already mentioned in Sect. 1, is that it changes as a function of the phase angle at the epoch of observation. By observing the same object at different epochs and correspondingly different phase angles, one derives its so-called phase-polarisation curve. These curves are characterised by the fact that Pr is found to always be negative in a range of phase angles between 0° and a so-called inversion angle αinv, generally close to 20°. The interval of phase angles in which Pr is negative is generally called the ‘negative polarisation branch’ (see, for instance, Cellino et al. 2015a, and references therein).
Here, we follow the same approach adopted in some previous papers (Cellino et al. 2015b, 2016a, 2018), and we use the following exponential-linear function to represent the observed trend of the relation between Pr and the phase angle a:
where A, B, and C are free parameters to be determined by means of best-fit techniques. According to its mathematical representation, when the parameters A, B, C are all positive, the exponential-linear relation describes a curve which starts at zero for zero phase angle, then reaches increasingly negative values in the negative polarisation branch, up to a value generally named Pmin. As the phase angle increases, the derivative of the curve changes its sign, and Pr starts to have decreasingly negative values and reaches zero at the so-called inversion angle αinv. At larger phase angles, Pr tends to increase linearly, as the exponential term tends quickly to zero. It should be noted that this exponential-linear representation is very satisfactory only up to moderate values of the phase angle, corresponding to the extreme values achievable by main-belt asteroids, which are rarely visible at phase angles larger than about 30°. Much larger values of the phase angle can be attained by near-Earth objects, which may be visible up to phase angles around 100°, depending on their distance from the Earth. In those cases, different representations of the phase-polarisation curve are used, as mentioned in Sect. 5.
The computation of the best-fit representation of phasepolarisation curves using Eq. (1) can be done in many ways. As explained in previous papers (Cellino et al. 2015b, 2016a), we use a genetic algorithm (see, for instance, Banzhaf et al. 1998, and references therein). Starting from a random set of A, B, C values, the algorithm explores the space of possible solution parameters and finds the set of A, B, C values producing the smallest possible residuals with a given set of phase-polarisation data.
The adopted genetic algorithm takes its name from the particular way it explores the space of unknown parameters. It considers any given set of A, B, C values as the ‘DNA’ characterising a particular solution. The ‘fitness’ of any given individual solution is assumed to be the value of its residuals with respect to the set of real data characterising the observed phase-polarisation curve under scrutiny. Starting from an initial population of individual solutions, each one characterised by a fully random set of A, B, C, the algorithm simulates an ‘evolution’ of the population, in which the rule is survival of the fittest. In other words, at each step, a number of solutions coming from the previous generation are taken, and each one is modified either by ‘mating’ with another solution, randomly exchanging their A, B, C values, or by having one single random variation of the DNA of a single solution. Each newly considered ‘baby’ solution is evaluated in terms of residuals with respect to the real data, and is kept in the population (i.e. ‘it survives’) only if it is found to give residuals better than those of some member of the previous generation. In this case, the worst member of the previous generation is removed. As increasingly better solutions are retained in the solution population, the worst members of the previous generations are removed. This process is repeated until some solution is found to give very low residuals, and this solution cannot be further improved.
Due to the intrinsic properties of a genetic approach, the algorithm is executed several times, in order to have a correspondingly high number of solutions, in order to ensure that the best possible solution is not missed. What generally happens is that the same solution is obtained several times, with very small differences in the resulting values of the A, B, C solution parameters. These differences are used to estimate the uncertainty in the determination of each parameter.
We limit the computation of best-fit curves only to cases when available data are of sufficiently good quality and sample satisfactorily the interval of possible phase angles. This means that we impose some strict constraints on the selection of the objects for which we make a best-fit computation. In this respect, we have recently made some mild improvements to our adopted selection criteria, with respect to those described in Cellino et al. (2015b). In particular, our current criteria are the following: we exclude a priori from our analysis all measurements having a nominal accuracy of Pr worse than 0.20%. Moreover, we require at least four accepted measurements taken at phase angles >2°; at least one accepted measurement taken at phase angles ≥17°; at least one accepted measurement taken at phase angles < 14° ; at least three accepted measurements taken at phase angles < 30°; at least one accepted measurements taken at phase angles < 10°; and at least one accepted measurement taken at a phase angle between 6° and 20°.
The above criteria are similar to those adopted by Cellino et al. (2015b), but they include some refinements chosen in such a way to have a better automatic rejection of inadequately sampled phase-polarisation curves.
In the following sections we will show a number of figures displaying asteroid phase-polarisation data, and we will use different colours to distinguish CAPS measurements from available literature data. Whenever possible, best-fit curves computed according to the exponential-linear representation will be displayed together with available data.
Finally, as in the case of previous papers, we limit our analysis to available data obtained in the standard V filter, only. Polarimetric data obtained in other colours are not so abundant. In previous papers, we merged V and R measurements only in very few cases (Cellino et al. 2014, 2019), in which only a few observations of faint objects were available. It is known, in fact, that polarimetric data of asteroids are wavelength-dependent (Bagnulo et al. 2015), and in some cases the detected gradient can be sufficiently steep so as to suggest avoiding the mixing together of data obtained using different filters.
4 Exploring the CAPS database
Our purpose is to present in this paper the current CAPS catalogue of asteroid polarimetric measurements. This includes some data that were already published in the past (Devogèle et al. 2017, 2018b) as well as a large amount of unpublished data obtained in several observing runs, up to December 2021 (the observational work having experienced some interruptions in 2020 due to the COVID-19 pandemic). The whole catalogue is given in Appendix A. For each measurement, the table lists the object identification number, the epoch of observation (year, month, day and the time of the measurement expressed as a fraction of day, the phase angle, the measured value of Pr with its nominal error determined by data reduction, and the filter used in the measurement (B, V, R or I in the Johnson-Cousin photometric system). Every line in this table corresponds to an average of all the single measurements of a given object in the same filter obtained on the indicated night. The indicated epoch of observation corresponds to the mean of the instants of the beginning of different measurements of the same target.
The first obvious test we did aimed to check that CAPS measurements are in agreement with those obtained for objects observed many times in the past by other authors using different instruments. Figure 1 shows the cases of the dwarf-planet (1) Ceres and of the asteroids (2) Pallas, (4) Vesta, (6) Hebe, (16) Psyche, and (44) Nysa. These are objects for which several CAPS data are added to many polarimetric data already available in the literature (the sources of these data are summarised in Sect. 1). We find that for these asteroids, CAPS measurements very nicely fit and complement the data available in the literature. We note that all the best-fit curves, in this and all the other figures shown below, have been obtained using all the available data (from the literature and from CAPS), without any a priori removal of discrepant measurements.
Figure 2 shows the phase polarisation curves of asteroids (17) Thetis, (62) Erato, (89) Julia, and (139) Juewa. These are examples of cases in which CAPS data, due to scarcity of measurements coming from other sources, are essential to compute new phase-polarisation curves. In these cases, even a small number of additional CAPS measurements produce a decisive improvement in the interval of phase angle covered by the observations.
CAPS allows us, in many cases, to derive for the first time new, satisfactory phase-polarisation curves of asteroids for which no data coming from other sources were previously available. A few examples are given in Fig. 3, showing the cases of (28) Bellona, (57) Mnemosyne, (60) Echo, and (510) Mabella.
CAPS data have been obtained for asteroids belonging to a large variety of taxonomic classes, as defined on the basis of their reflectance spectra. Although asteroid phase-polarisation curves can be represented using one single mathematical representation (as the one given by Eq. (1)), it is known that different taxonomic classes exhibit differences in the details of the morphology of their phase-polarisation curves. These differences include the position and depth of the extreme value of negative polarisation (the latter usually being indicated as Pmin), the value of the polarisation inversion angle αinv, the slope of the curve around αinv, and the so-called Ψ parameter, corresponding to the difference in Pr measured at the phase angles of 30° and 10° (Cellino et al. 2015b).
The variety in polarimetric behaviour of different classes of asteroids is generally thought to be a consequence of differences in surface properties, including primarily, but not limited to, the geometric albedo (see, for instance, Cellino et al. 2015b, 2016a). This subject will not be specifically analysed in this paper, since it deserves more specific and detailed investigations, which will be looked at in forthcoming studies.
In choosing the targets of CAPS observing runs, particular attention is devoted to the members of dynamical families (Milani et al. 2014). These are groups of asteroids issued from energetic collisional events. It is therefore interesting to study the surface properties of these objects that were previously parts of the internal layers of their parent bodies. We present a few preliminary results for some particular cases in Sect. 6.4.
 |
Fig. 1 Phase-polarisation curves for the dwarf-planet (1) Ceres and the asteroids (2) Pallas, (4) Vesta, (6) Hebe, (16) Psyche, and (44) Nysa. CAPS measurements are plotted using red symbols, while literature data are plotted in black. The nominal error bars of all the measurements are shown, but are often not larger than the size of the symbols used to display the data. |
 |
Fig. 3 As for Fig. 1, but for the asteroids (28) Bellona, (57) Mnemosyne, (194) Prokne, and (510) Mabella. |
5 Noisy phase-polarisation curves
In the absence of robust predictions based on theoretical considerations, we are forced to fit asteroid phase-polarisation curves using empirical relations such as the one expressed by Eq. (1). Other empirical functions have also been used in the past, including the following trigonometric representation originally proposed by Lumme & Muinonen (1993):
where α is the phase angle, αinvis the value of the inversion angle of polarisation, and K, L, and M are coefficients to be computed by means of least-squares fits. This mathematical representation has been found to provide reasonable fits of the measured phasepolarisation curves of near-Earth objects, which are observable over a much wider range of phase angles than in the case of main-belt asteroids. A recent application of this relation can be found in Devogèle et al. (2018b).
We emphasise the empirical nature of Eqs. (1) and (2) because it turns out that the best-fit solutions based on the above representations usually do not pass a X2 test. This means that the adopted empirical relations may be wrong, and/or that there are problems affecting several measurements of asteroid linear polarisation and the corresponding errors affecting these measurements. If we examine some figures shown in the previous section, we in fact see that there are objects for which some single polarimetric measurements turn out to be well above or below the expected value, according to the best-fit phasepolarisation curve. Such discrepancies can be much larger than the nominal error bars of the measurements. It is therefore reasonable to explain the sporadic presence of evident outlier values in asteroid phase-polarisation curves as due to important observation errors and strong underestimates of their associated errors.
In general terms, because bad data appear to be unusual, they can be easily identified when the phase-polarisation of a given asteroid is computed on the basis of several available measurements. In these cases, the behaviour of the phase-polarisation curve is dominated by good-quality data points, and the presence of one or a few bad measurements does not have a strong effect on the computation of the best-fit curve. The situation is much worse when only a small number of observations are available, since in these cases one or two bad measurements can lead to computing wrong phase-polarisation curves. This is the reason why we put a number of constraints on the number and distribution of polarimetric measurements required for the computation of a phase-polarisation curve, as explained in Sect. 3.
As an alternative point of view, it could be tempting in some cases to interpret a noisy phase-polarisation curve as diagnostic of large-scale surface heterogeneity of the observed asteroid. In fact, in computing best-fit curves, we are merging together data obtained in different observing circumstances, not only in terms of illumination conditions, but also of the illuminated area facing the observers. A major fact in asteroid polarimetry, however, is that very similar values of linear polarisation are usually measured at very different epochs, when the object is observed in different viewing conditions, but at the same phase angle. This suggests that, although the detailed morphology of the phasepolarisation curve of any given asteroid is certainly determined by its individual surface properties, these properties tend to be very homogeneous across its surface.
Moreover, it seems very unlikely that the phase-polarisation curves of some asteroids might be characterised by such abrupt variations that they are hardly represented using a continuous function. We should also not forget that ground-based asteroid polarimetric measurements are disk-integrated, and this tends to smooth out any abrupt variation that, in principle, might be due to local surface features.
In fact, there is only one asteroid for which large-scale surface heterogeneity has been definitely proven to exist and produce easily measurable effects on the resulting linear polarisation. This is the large asteroid (4) Vesta, which has been extensively investigated by different authors (see Cellino et al. 2016b, and references therein). Sets of measurement sequences covering intervals of time comparable to the known 5.342 h spin period of Vesta have been analysed. This led to the confirmation of the expected dependence of linear polarisation on the average composition and regolith properties of Vesta, which is characterised by large-scale surface heterogeneity, as accurately determined by the DAWN space probe (Cellino et al. 2016b).
Apart from (4) Vesta, another exception may be the small (around 5 km in size) near-Earth asteroid (3200) Phaethon. This object was extensively observed by different teams during its last apparition in 2017, when it was visible at high phase angles, mostly larger than 40°. Due to its fast motion on the celestial sphere, the phase angle was rapidly changing from day to day and even during each single night. A modulation of linear polarisation roughly corresponding to the known rotation period of 3.604 h was found by Borisov et al. (2018, see also references therein). The same authors noted that no colour variation was measured during the observations, suggesting that the measured polarimetric variation could be due to regolith texture heterogeneity rather than to surface composition variegation. We can hope that more solid conclusions will be obtained during the next apparition of (3200) Phaethon in 2026.
A few other interesting cases have been found by Wictorowicz & Masiero (2017) for (1) Ceres and (7) Iris. In these two cases, however, the measured modulation of linear polarisation turned out to be extremely weak, and was found by an investigation that specifically aimed to detect such an effect, using a 3 m telescope and a polarimeter producing ultra-precise measurements (Wictorowicz & Masiero 2017). Another possible, but more uncertain case, might be that of (6) Hebe, according to some old findings by Migliorini et al. (1997) that have not yet been confirmed.
It seems, therefore, that in the vast majority of cases, surface heterogeneity is not sufficient to significantly alter the nightly average of polarisation in such a way as to produce relevant noise or discontinuities in the phase-polarisation curve. We are led to conclude that no evidence of surface albedo heterogeneity can be reliably inferred by purely looking at the properties of phasepolarisation curves obtained using nightly averaged values of polarisation measured at different epochs.
The bottom line of this discussion is that bad measurements do occur, and this enhances the importance of deriving asteroid phase-polarisation curves from suitable data, not limited to just a few measurements that poorly sample the interval of possible phase angles. In this respect, the purpose of CAPS is to strongly increase the number of available asteroid polarisation measurements. This is perfectly apposite, given that a lack of data is one of the major challenges for modern asteroid polarimetric studies.
 |
Fig. 4 Shallow phase-polarisation curves for the asteroids (64) Angelina, (71) Niobe, (214) Aschera, and (434) Hungaria. The meanings of the symbols are the same as in Fig. 1. |
6 Some interesting cases
In this section we focus on a number of cases in which the availability of CAPS data is important in order to provide new useful data. These data allow light to be shed on a variety of topics for which the polarimetric behaviour of the objects plays an important role in our understanding of their physical properties.
6.1 Shallow phase-polarisation curves
Figure 4 shows the phase-polarisation curves of asteroids (64) Angelina, (71) Niobe, (214) Aschera, and (434) Hungaria. We note that (434) Hungaria is the lowest-numbered member of an asteroid dynamical family located in the so-called Hungaria region, which is found at heliocentric distances between 1.8 and 2.0 AU, smaller than the inner edge of the classical asteroid main belt (Milani et al. 2014). With the only exception of (214) Aschera, classified as Xc, the asteroids plotted in
Fig. 4 are classified as members of the Xe class, defined in the SMASS taxonomic classification (Bus & Binzel 2002). This class, which replaces the older E class of the Tholen taxonomy developed in the 1980s (Tholen 1984, 1989), is known to consist of very high-albedo objects, according to polarimetric evidence. In fact, the so-called Umov ‘law’, an inverse relation between the degree of polarisation and the albedo (see, for instance, Cellino et al. 2015b, and references therein), predicts shallow phase-polarisation curves for bright asteroids. NEOWISE thermal IR data (Masiero et al. 2014) for the asteroids shown in Fig. 4 suggest high albedo values generally above 0.4, with the only exception of (71) Niobe, for which a more moderate value slightly above 0.3 has been derived.
Interestingly, the abovementioned SMASS classification of (214) Aschera (Xc), based on its spectral reflectance properties, would suggest that this asteroid is a low-albedo object, in agreement also with its Cgh classification in the DeMeo (DeMeo et al. 2009) taxonomy (an extension of SMASS, based on additional data obtained at near-IR wavelengths). This is in disagreement with the Tholen classification of Aschera, Angelina, and Hungaria, as members of the E class. As for Niobe, its Tholen classification was S, implying a moderate albedo.
Looking at Fig. 4, we find that new CAPS measurements of the abovementioned asteroids confirm their very shallow phasepolarisation curves, typical of high-albedo objects. We are then led to conclude that polarimetric data do not support the SMASS and DeMeo classifications of (214) Aschera as low-albedo asteroid, whereas they are in agreement with the older Tholen classification as E type, and with thermal IR albedo estimates. On the other hand, the polarimetric data for (71) Niobe tend to confirm the modern Xe classification and a moderate-to-high albedo.
Figure 5 shows the phase-polarisation data for the asteroids (246) Asporina, (289) Nenetta, (354) Eleonora, and (863) Benkoela. These asteroids belong to the rare A taxonomic class, defined on the basis of spectral reflectance properties that suggest a high abundance of the olivine silicate (Tholen 1989, and references therein). While (246) Asporina, (289) Nenetta, and (863) Benkoela are classified as A-type in the Tholen, SMASS and DeMeo taxonomies, in the case of (354) Eleonora there are classification differences: it is classified as A class in the DeMeo taxonomy, but as S in the Tholen taxonomy, and Sl (one of the different sub-classes of the S complex), in the SMASS taxonomy. Figure 5 shows a first example of a noisy phasepolarisation curve, that of (246) Asporina, in which a general disagreement between CAPS and other literature data is apparent. In particular, CAPS data seem to be more compatible with a quite shallow curve, whereas literature data seem to suggest a slightly deeper negative polarisation branch. It is clear that more observations of this object are needed. Apart from the uncertain case of Asporina, the other three asteroids in Fig. 5 exhibit very shallow curves and look quite similar to each other, in spite of some noisy data for (863) Benkoela, which make the determination of the phase angle corresponding to the extreme value of negative polarisation Pmin more uncertain.
There are NEOWISE albedo estimates of 0.31 ± 0.05, 0.20 ± 0.05, and 0.29 ± 0.03 for (246) Asporina, (354) Eleonora, and (863) Benkoela, respectively, according to the most recent online version of the catalogue, originally published by Masiero et al. (2014). The agreement of the fairly high values for Asporina and Benkoela is very good, whereas the lower albedo found for (354) Eleonora is more common among asteroids belonging to the S class. All these values might look a little underestimated for objects exhibiting such shallow phase-polarisation curves, which look similar to those of high-albedo asteroids shown in Fig. 4. This is a potentially interesting result, but, as already mentioned, we will defer a more specific analysis of the determination of the geometric albedo from polarimetric data, and of the polarimetric properties of different asteroid taxonomic classes, to a forthcoming paper.
 |
Fig. 5 Phase-polarisation data for the asteroids (354) Eleonora, (289) Nenetta, (625) Xenia, and (863) Benkoela. The meanings of the symbols are the same as in Fig. 1. |
6.2 Curves with low inversion angles
The phase-polarisation curves of asteroids are very useful for identifying particular classes of objects that exhibit unusual polarimetric properties. These properties can be diagnostic of a physical behaviour that can be difficult to detect based on data coming from other techniques. A classical example is given by the recovery of the previously known F taxonomic class.
This taxonomic class was first introduced by Gradie & Tedesco (1982). It included asteroids exhibiting a flat (hence F) reflectance spectrum in the wavelength range from 0.3 to 1.1 µm, characterised by an overall lack of absorption features.
F-class asteroids are rare. In the classical asteroid taxonomy classification by Tholen (1984), only 27 asteroids, corresponding to about 3% of all classified objects, were found to belong to this class. Most interestingly, the F class was known to include some objects, including the active asteroid (4015) Wilson-Harrington, showing episodes of surface activity, and therefore suspected to have a cometary origin (see, for instance, Devogèle et al. 2018b, and references therein). This possibility was strengthened by the fact that the typical polarimetric property of F-class asteroids, namely an anomalously low value of the polarisation inversion angle αinv, well below 20° (Belskaya et al. 2005, 2017), was found to be shared also by the nucleus of comet 133P/Elst-Pizarro according to (Bagnulo et al. 2010).
The most modern taxonomic classifications (Bus & Binzel 2002; DeMeo et al. 2009), however, are based on reflectance spectra obtained using CCD detectors, which do not adequately cover the UB spectral region. For this reason, objects previously classified within the F class no longer define a separate taxonomic class, but they are currently merged together with a larger variety of asteroids. The result of this merging is the modern taxonomic B class, defined by Bus & Binzel (2002) and DeMeo et al. (2009). The determination of the polarimetric inversion angle ainv is currently the most effective tool for identifying F-class objects among those included in the current B class.
More recently, the possibility that F-class asteroids can be borderline objects between asteroids and comets has been nicely confirmed by Cellino et al. (2018), who demonstrated that the near-Earth asteroid (101955) Bennu, the target of the space mission OSIRIS-REx, exhibits a low value of the polarimetric inversion angle, typical of the old F class. This is an important discovery, because (101955) Bennu has been found by OSIRIS-REx to display previously unexpected phenomena of surface activity (Hergenrother et al. 2019; Lauretta et al. 2019) and to have an abundance of hydrated minerals (Hamilton et al. 2019).
An extensive analysis of F-class asteroids cannot be presented in this paper. Available polarimetric data are still not sufficient. There are some preliminary indications that not all the asteroids classified within the F class by Tholen (1984) exhibit a sharply low value of the polarimetric inversion angle. This is not unexpected, taking into account possible cases of taxonomic misclassification, and the fact that there were several cases of uncertain, non-univocal classifications (e.g. CF, FC) in the Tholen (1984) taxonomy. Recent polarisation measurements of the near-Earth asteroid (3200) Phaethon, the likely parent body of the Geminid meteor shower, and therefore an excellent candidate to be an active asteroid, have not produced conclusive evidence of a small value of ainv(Devogèle et al. 2018b).
The work of polarimetric analysis of the F taxonomic class is still in progress. One of the goals of current investigations, which will be presented in forthcoming papers, is to check whether the F class is still sharply distinguishable, in terms of polarimetric properties, from asteroids displaying a similar reflectance spectrum at visible wavelengths, or, as it might be possible, whether there is a continuum in the transition from clearly F-class objects to non-F members of the modern B class.
In Fig. 6 we limit ourselves to presenting the cases of four asteroids, (45) Eugenia, (210) Isabella, (419) Aurelia, and (704) Interamnia, which clearly exhibit a low value of αinv, well below 20°, typical of the F class. In all these cases, CAPS observations play a key role in constraining the polarimetric behaviour of these objects.
 |
Fig. 6 Phase-polarisation data for the asteroids (45) Eugenia, (210) Isabella, (419) Aurelia and (704) Interamnia, all of them belonging to the F taxonomic class. The meaning of the symbols is the same as in Fig. 1. The vertical lines at the phase angle of 20° (corresponding to the typical value of the polarisation inversion angle of most asteroid taxonomic classes) are drawn as a reference to illustrate the anomalously low values of the inversion angle characterising this taxonomic class (see text). |
6.3 Barbarians
The so-called Barbarian asteroids are a class of objects exhibiting an anomalous polarimetric behaviour, characterised by an unusually large value of the inversion angle αinv. In this respect, their polarimetric behaviour is opposite to that of F-class asteroids. The prototype of the class is (234) Barbara, whose anomalous phase-polarisation curve was first discovered by Cellino et al. (2006). Since the beginning, Barbarians have been high-priority targets for CAPS observations. The reason is that these objects are rare and very interesting, because some evidence suggests that they could be extremely primitive. In fact, spectroscopic observations have revealed that Barbarians, which are characterised by reddish reflectance spectra, showing strong absorption bands in the near-IR around 2 µm, have surfaces which look extremely enriched in highly refractory compounds, especially the spinel mineral (Sunshine et al. 2008). Spinel is present in calcium-aluminium-rich inclusions (CAIs) found in some meteorites. CAIs are among the oldest samples of solid matter known in the Solar System, and their formation might date back to the early stages of planetesimal growth, or even before (see, for instance Cellino et al. 2015a, and references therein).
Barbarians have been extensively investigated by Devogèle et al. (2018a), who carried out dedicated spectroscopic and polarimetric investigations of these objects. Among their main results, the authors proposed an explanation of the observed polarimetric behaviour as due to the refractive index of the spinel mineral, found to be anomalously abundant on Barbarian surfaces. Moreover, the above authors found evidence that that all the observed Barbarians turn out to be members of the L taxonomic class defined by DeMeo et al. (2009), based on reflectance spectra at visible and near-IR wavelengths. The analysis carried out by Devogèle et al. (2018a) was based on the evidence coming from both spectroscopic and polarimetric data, and included an attempt to interpret the observed visible and near-IR reflectance spectra in terms of surface composition and space weathering effects. In this paper, we instead focus more on details of the polarimetric properties, taking advantage of the much improved database that is now available, including a large number of new CAPS measurements.
Figure 7 shows the available phase-polarisation data in V filter for nearly all the known Barbarians larger than a few/several tens of kilometers. Smaller Barbarians exist, but they have been found to consist only of small members (a few kilometers in size) of a couple of families having a Barbarian largest remnant, as will be mentioned below. The only sizeable object that is not shown in Fig. 7 is (2085) Henan, for which, thus far, we only have a couple of polarimetric measurements, suggesting a deep negative polarisation branch. Only three asteroids shown in Fig. 7 are not included in the DeMeo et al. (2009) taxonomy. They were previously classified as L-type by Bus & Binzel (2002).
These three asteroids are (172) Baucis, (611) Valeria, and (980) Anacostia.
By looking at Fig. 7, one can conclude that there is no evidence of any 1systematic difference between Barbarians that are known members of the DeMeo et al. (2009)L class and those that are not included in the DeMeo et al. (2009) classification. This is not surprising as, in the case of (387) Aquitania and (980) Anacostia, for instance, their close similarity in terms of spectral reflectance data had been known for a longtime (Burbine et al. 1992). It was just the fact that (980) Anacostia had been found to be a Barbarian in terms of polarimetric properties that led Masiero & Cellino (2009) to observe (387) Aquitania, leading to the discovery of the Barbarian polarimetric behaviour of this object.
It should also be noted that (729) Watsonia, whose phasepolarisation curve is shown in Fig. 7, is the largest remnant of the first dynamical family discovered to consist of small Barbarian members (not shown in our figure), according to Cellino et al. (2014). This was an important discovery, because dynamical families are the currently observable outcomes of energetic collisional phenomena, which in the past produced the partial or complete disruption of single parent bodies. As a consequence, current members of the Watsonia family include objects that were buried inside their parent body before the collision. In turn, the fact that the observed Watsonia members display the polarimetric properties typical of Barbarians means that these properties are not simply due to surface processing mechanisms, but to unusual bulk compositions. The Watsonia family is important also for another reason. It is surrounded by three large Barbarians: (387) Aquitania, (599) Luisa, and (980) Anacostia, which are not official members of the Watsonia family, but are so close in the space of orbital proper elements, suggesting that this cannot be due to chance. The most natural explanation (Cellino et al. 2014) seems to be that, in a very remote epoch, one single big Barbarian parent body was completely shattered by a collision, which produced four large fragments: Aquitania, Luisa, Anacostia, and Watsonia. Only at a subsequent epoch did Watsonia experience in turn another collision that produced its currently identified family. If this interpretation is correct, we can expect a close similarity between Aquitania, Luisa, Anacostia, and Watsonia. Figure 7 confirms the close resemblance of the phase-polarisation curves of these four asteroids. Only in the case of (599) Luisa, does it seem that the asteroid displays a slightly deeper negative polarisation branch, but this needs to be confirmed by additional data. We have already mentioned the very close similarity between Aquitania and Anacostia, including also their unusual reflectance spectra.
There are, however, some questions deserving further scrutiny. Looking at Fig. 7, it seems that we can tentatively separate the objects into two different sub-classes. The first and much more populous sub-class, which we call ‘classical Barbarians’, is characterised by very large values of the polarimetric inversion angle αinv, most commonly larger than 28°, and a fairly shallow Pmin, between −1.4 and −1.6%. This combination of a moderate Pmin and a large αinv characterises nearly all of the objects shown in Fig. 7. There are, however, two cases of Barbarians which seem to be characterised by a quite deep value of Pmin, namely (824) Anastasia and (606) Brangäne. Moreover, as mentioned above, a couple of measurements of (2085) Henan, classified as an L-class object in the DeMeo taxonomy, also suggest a fairly deep negative polarisation branch. We note that these three asteroids were considered to be Barbarians by Devogèle et al. (2018a) on the basis of a smaller number of measurements obtained at phase angles between 16° and 20°. At these phase angles, negative values of Pr that are sufficiently deep to suggest a Barbarian polarimetric behaviour, are measured. Interestingly enough, the above authors also found that the reflectance spectrum of (824) Anastasia could hardly be reconciled with the kind of surface composition they found to produce the best fit of the spectra shown by most Barbarians in their adopted sample.
We also note that the Cellino et al. (2019) investigation of the Brangäne family was based on data collected in red light, and no observations were made of Brangäne family members at phase angles smaller than 17°. The transition between the deepest negative values of Pr and the inversion angle was found to be steeper than in the case of (234) Barbara. In the above paper, it was also noted that the αinv value found for the Brangäne family, around 25°, appeared to be unusually low for Barbarians. In Fig. 7 we show four previously unpublished polarisation measurements of Brangäne in the V filter. These measurements were not available at the time of the analyses by Devogèle et al. (2018a) and by Cellino et al. (2019), and their analyses made use of two measurements in the R filter at phase angles around 20°, including one having an error bar larger than 0.2% that should be nominally discarded if we apply the quality selection criteria described in this paper. If one merges all available polarimetric data of Anastasia, Brangäne, and Henan in V light, the resulting best-fit phase-polarisation curve exhibits a deeper Pmin and a slightly smaller value of the inversion angle αinvwith respect to classical Barbarians. This is shown in the left panel of Fig. 8.
These results raise some questions. It seems possible that either there are two different sub-classes of the objects that we collectively call Barbarians, or we must be more careful when we adopt phenomenological criteria to identify Barbarians, based on the values of Pr measured at phase angles between about 18° and 20°. Such a simple criterion could sometimes lead to false positives. Some objects that exhibit deep Pmin and an inversion angle much smaller than 28° could, in unfavourable circumstances, be erroneously classified as Barbarians.
The first interpretation that there are two main classes of Barbarians is supported by the classification as members of the DeMeo L taxonomic class of the three above mentioned asteroids, whose phase-polarisation data look slightly different with respect to those of the majority of other Barbarians. This means that their reflectance spectra are typical of Barbarians, as shown by Devogèle et al. (2018a), except, possibly, in the case of (824) Anastasia, as mentioned above.
The alternative possibility, namely that some objects could be erroneously classified as Barbarians based on insufficient polarimetric data, is supported by the phase-polarisation curve of the asteroid (48) Doris, shown in the right panel of Fig. 8. (48) Doris is a Ch class asteroid, according to both Bus & Binzel (2002) and DeMeo et al. (2009). Its reflectance spectrum is rather flat, as commonly found among members of the C-complex, and has nothing to do with the strongly reddish spectra of Barbarians. However, its phase-polarisation curve, based on currently available data, is characterised by a deep value of Pmin, followed by a steep rise and an inversion angle apparently around 24°, and it looks quite similar to the composite phase-polarisation curve of (824) Anastasia, (606) Brangäne, and (2085) Henan, shown in the left panel of the same figure. Of course, we are aware that we should be careful because there is a lack of data at large phase angles for (48) Doris, and, in any case, the polarimetric inversion angle of this asteroid seems to be considerably lower.
In any case, the existence of asteroids belonging to the C complex, exhibiting a deep Pmin and values of Pr not far from −1.0% at phase angles around 20°, might be not so unusual. Another example is (238) Hypatia, another asteroid belonging to the Ch-class (Bus & Binzel 2002), whose phase-polarisation curve is noisy, but could be similar to that of (48) Doris.
Based on these facts, we conclude that the identification of Barbarians purely based on polarimetric properties, not supported by spectroscopic data, could in some cases lead to false positives. Classification as a Barbarian should not be simply based on the measured value of Pr at phase angles around 20°, as is usually the case these days, but it should include measurements taken at higher phase angles as well. An estimation of Pmin would be also important, because classical Barbarians do not reach Pr values more negative than about −1.6. The presence of a deep negative polarisation branch might be diagnostic of non-Barbarian asteroids belonging to the C-taxonomic complex, in some cases displaying Pr values not very different from those of real Barbarians at relatively high values of phase angle.
Finally, the fact that two asteroids classified as members of the Ch taxonomic class of Bus & Binzel (2002), (48) Doris and (238) Hypatia, exhibit phase-polarisation curves that could be erroneously interpreted in terms of a Barbarian nature, should not be over-interpreted. These might be just two unlucky cases, and we cannot conclude that Ch asteroids are all ‘false Barbarians’. A few examples are shown in Fig. 9, displaying the cases of (19) Fortuna, (134) Sophrosyne, (145) Adeona, and (345) Tercidina. These Ch asteroids exhibit ‘normal’ polarimetric inversion angles around 20°, and values of Pr of the order of −1% are reached at smaller phase angles, although some care is certainly needed in Barbarian searches. Other examples of unusually steep polarimetric data for asteroids belonging to the Ch class, however, will be shown in Sect. 6.6.
 |
Fig. 7 Phase-polarisation data in V for the asteroids currently named ‘Barbarians’, including the prototype of this class, asteroid (234) Barbara. Small members of the dynamical families of (729) Watsonia and (606) Brangane (see text) are not included in this figure, nor are a couple of measurements of (2085) Henan, another Barbarian candidate for which more data are needed. The meanings of the symbols are the same as in Fig. 1. |
 |
Fig. 8 Comparison of the phase-polarisation curves of some asteroids exhibiting very different reflectance spectra. Left: phase-polarisation curve obtained by merging together all the available V measurements of (824) Anastasia, (606) Brangäne, and (2085) Henan. Both literature and CAPS data of these asteroids are shown using the same symbol for each of them. Right: phase-polarisation curve of the asteroid (48) Doris, a member of the SMASS and DeMeo Ch taxonomic classes. The meanings of the symbols in this panel are the same as in Fig. 1. |
 |
Fig. 9 Phase-polarisation curves of the asteroids (19) Fortuna, (134) Sophrosyne, (145) Adeona, and (345) Tercidina. They all belong to the SMASS Ch taxonomic class, but they exhibit quite different phasepolarisation curves with respect to (48) Doris shown in Fig. 8. The meanings of the symbols are the same as in Fig. 1. |
6.4 Families
Asteroid dynamical families are sets of objects sharing very similar values of their orbital proper elements (see, for instance, Bendjoya & Zappalà 2002, and references therein). They are interpreted as the outcomes of energetic collisions having produced a complete shattering and fragmentation of single parent bodies. Since they consist of collisional fragments, most family members are usually fairly small and faint, apart from the largest remnants. Families have been found to be quite homogeneous in terms of spectral reflectance properties (Cellino et al. 2002), apart from the presence of random interlopers, which are nearly always present in family member lists (Migliorini et al. 1995). As mentioned above, Cellino et al. (2014) found the first case of a family, that of (729) Watsonia, consisting of Barbarian asteroid members. More recently, the existence of a second Barbarian family has been proposed by Cellino et al. (2019), as discussed in Sect. 6.3.
The Calern telescope is generally too small to allow us to undertake extensive polarimetric studies of large numbers of members of any given family. We are making an effort, however, to observe as many family members as possible, because polarimetric data are important in order to obtain a better physical characterisation of the objects, and to identify possible interlopers that exhibit properties that are clearly distinct from those of most members of a given family.
An example is the asteroid (194) Prokne. This object is the lowest numbered and brightest member of the Prokne family identified by Milani et al. (2014). Usually, this should be the largest remnant of the family’s parent body, but in this particular case the deep negative polarisation branch and overall morphology of the phase-polarisation curve is typical of a low-albedo asteroid, as also confirmed by NEOWISE thermal IR data (Masiero et al. 2014). Most members of the Prokne family, however, turn out to be moderate-albedo objects, according to Masiero et al. (2014) and a few available taxonomic classifications. Polarisation data of (194) Prokne, in agreement with thermal IR data, therefore suggest that it is an interloper in its family, because it is very unlikely that the parent body could have a composition producing a swarm of fragments that have mutually inconsistent compositions. The actual largest member of the family is most likely the asteroid (686) Gersuind, and the family itself should be accordingly named the Gersuind family.
Apart from the identification of likely family interlopers, there are other ways to exploit the general similarity in the composition of members of the same family. It is possible to derive a common phase-polarisation curve of any given family by merging the available polarimetric data of its members. This can be then compared with those of non-family objects sharing the same taxonomic classification, based on spectral reflectance data. We plan to develop this aspect as much as possible in forthcoming papers.
Here, we present the particularly favourable case of the Koronis family in Fig. 10. This is a family characterised by a fairly shallow size distribution, suggesting that the family-forming collision was quite energetic, leading to an extensive disruption into many small fragments that have similar sizes (Tanga et al. 1999). Some polarimetric data are available for two of the largest members of the family, namely (158) Koronis (ten measurements) and (208) Lacrimosa (nine measurements). As shown in the two top panels of Fig. 10, however, the data are not sufficient to derive an individual phase-polarisation curve for either object, due to insufficient coverage of the phase angle. However, it is fairly evident that these two objects exhibit, as could be expected, a quite similar behaviour, in agreement with their common collisional origin and identical age.
We can in fact merge together their polarimetric data, as well as those available for a few additional family members, including (243) Ida (four measurements) and five other objects, each having up to a couple of measurements. In this way, we obtain a set of data that allows us to compute a phase-polarisation curve, shown in the bottom-left panel of Fig. 10. This curve is based on data taken at phase angles not exceeding 17°, and shows an extreme value of negative polarisation at a phase angle significantly smaller than 10°.
The Koronis family, however, is really special from the point of view of asteroid polarimetry. Little more than ten years ago, Cellino et al. (2010) carried out a polarimetric project with the aim of detecting possible differences in the properties of a sample of very small members of the Koronis family, compared to a similar sample of equal-sized members of the very young Karin family. The latter family is believed to be the outcome of a second-generation family-forming event that caused the disruption of an original member of the Koronis family. The Karin family is supposed to be extremely young, with an estimated age of less than 10 Myr (see Cellino et al. 2010, and references within). The goal of the project was to look for systematic differences in the polarimetric properties of the members of the two families, that could be interpreted as indications of different exposures to space weathering mechanisms. The above study did not detect any statistically significant differences between the members of the two families, but what is important for our present purposes is that that project produced a set of a little less than 40 VLT (FORS 1) polarimetric measurements in V light for small members of the Koronis and Karin families, with associated nominal errors below 0.2% (more uncertain data were obtained by Cellino et al. (2010) for some of the observed objects, but we did not make use of them in the current study). If we merge these measurements to those used to produce the phase-polarisation curve shown in the bottom-left panel of Fig. 10, we obtain a new phase-polarisation curve, shown in the bottom-right panel of the same figure. It is clear that the availability of the additional VLT measurements is extremely important. The range of phase angle covered by the observations increases significantly, and the phase angle corresponding to the extreme value of negative polarisation shifts toward higher values. The resulting curve becomes more similar to the curves of most asteroids belonging to the S taxonomic complex.
Of course, this is just a favourable example of the application of polarimetric data to the study of asteroid families. We plan to cover this subject of investigation in future papers, as soon as we have a sufficient number of measurements at our disposal. Currently, we have data for members of several families, including those of Eos, Themis, Maria, and others. This work is in progress.
 |
Fig. 10 Phase-polarisation data for increasingly larger samples of members of the Koronis dynamical family. Top panels: phasepolarisation data for the two asteroids (158) Koronis and (208) Lacrimosa. In both cases, the data do not allow us to compute a phase-polarisation curve according to our criteria explained in Sect. 3. Bottom-left panel: plotted phase-polarisation curve, obtained by merging the polarimetric data for (158) Koronis and (208) Lacrimosa, as well as some data for a small number of additional Koronis family members. Bottom-right panel: slightly different phase-polarisation curve obtained by adding a fairly large number of Very Large Telescope (VLT) data, obtained by Cellino et al. (2010) for a sample of small members of the Koronis and Karin families (the latter being a sub-family of that of Koronis, see text), to the measurements used to produce the curve shown in the previous panel. |
 |
Fig. 11 Phase-polarisation data for the asteroids (105) Artemis, and (914) Palisana. The meaning of the symbols is the same as in Fig. 1. |
6.5 Near-Earth objects
Near-Earth objects (NEO) are generally faint and most of them are beyond the capabilities of CAPS. Due to their importance, however, we are making a special effort to observe as many NEOs as possible, since they are targets of particular importance. The list of CAPS measurements presented in Appendix A includes several NEO observations, including those of the asteroids (433) Eros, (1036) Ganymede, (1620) Geographos, (1627) Ivar, (1862) Apollo, (3200) Phaethon, and several others. Some NEOs that have been observed most recently are not yet included in Appendix A, because we want to defer their analysis to future papers, after having analysed them in greated detail.
6.6 Other cases
Figure 11 shows the available polarisation data for the asteroids (105) Artemis and (914) Palisana. In both cases, the interval of covered phase angles, which does not include measurements at phase angles smaller than 10°, is not sufficient to derive a reliable best-fit curve according to our criteria. However, these two asteroids are interesting and will certainly deserve new measurements in the future.
The cases of (105) Artemis and (914) Palisana are similar, being characterised by a very steep increase in linear polarisation in the positive polarisation branch. It is important to note the different scale for the vertical axis, with respect to the ‘normal’ scale adopted in the other figures in this paper. In the negative branch, available data can only provide a lower limit, but they are already sufficient to indicate a deep Pmin.
(105) Artemis is another Ch class asteroid, exhibiting an inversion phase angle of about 20°. (914) Palisana is not classified by either the SMASS or the DeMeo taxonomies, whereas Tholen classified this asteroid as CU, meaning there is a large uncertainty. It also exhibits a value of ainv around 20°. Both objects are remarkable because they show a quite spectacular transition from very negative to very positive values of Pr in a limited interval of phase angle.
7 Conclusions and future developments
In this paper we have presented the results of a large effort to increase the database of asteroid polarimetric data. We have given a general description of the quality and quantity of the CAPS database without entering into very specific applications, which are deferred to forthcoming papers.
We think that the interplay between polarimetry and spectroscopy is a major tool in order to significantly improve our knowledge and understanding of asteroids. Thus far, the polarimetric side has been under-exploited, as a consequence of a general lack of data. CAPS has been designed and managed in order to represent a real change in this field. For this reason, we are still continuing our observing project, and we plan to present periodic updates of the CAPS database in the future.
Acknowledgements
The authors thank the staff of the Calern observing station for their wonderful support to the work of observation, both locally and in remote mode. R.G.H. gratefully acknowledges financial support by CONICET through PIP 112-202001-01227 and San Juan National University by a CICITCA grant for the period 2020-2022.
Appendix A The CAPS catalogue
List of CAPS polarimetric measurements
Appendix B Unpublished CASLEO data used in this paper
List of unpublished polarimetric measurements obtained at CASLEO
References
- Bagnulo, S., Boehnhardt, H. Muinonen, et al. 2006, A&A, 450, 1239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Tozzi, G. P., Boehnhardt, H., et al. 2010, A&A, 514, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Cellino, A., & Sterzik, M. F. 2015, MNRAS, 446, L11 [Google Scholar]
- Bagnulo, S., Belskaya, I., Stinson, A., Christou, A. A., & Borisov, G. 2016, A&A 575, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banzhaf, W., Nordin, P., Keller, R., & Francone, F. 1998, Genetic Programming - An Introduction (San Francisco, CA: Morgan Kaufmann) [CrossRef] [Google Scholar]
- Belskaya, I. N., Shkuratov, Yu. S., Efimov, N. M., et al. 2005, Icarus, 178, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I. N., Levasseur-Regourd, A.-C., Cellino, A., et al. 2010, Belskaya Asteroid Polarimetry V1.0. NASA Planetary Data System EAR-A-I0942/I0943-3-BELSKAYAPOL-V1.0. [Google Scholar]
- Belskaya, I. N., Cellino, A., Gil-Hutton, R., et al. 2015, in Asteroids IV, eds. P. Michel, F. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 151 [Google Scholar]
- Belskaya, I. N., Fornasier, S., Tozzi, G. P., et al. 2017, Icarus, 284, 30 [Google Scholar]
- Benjoya, Ph., & Zappala, V. 2002, in Asteroids III, eds. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 613 [CrossRef] [Google Scholar]
- Borisov, G., Devogéle, M., Cellino, A., et al. 2018, MNRAS, 480, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Burbine, T., Gaffey, M., & Bell, J. 1992, Meteorit. Planet. Sci., 27, 424 [Google Scholar]
- Bus, S. J., & Binzel R. P. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Cañada-Assandri, M., Gil-Hutton, R., & Benavidez, P. 2012, A&A, 542, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cellino, A., Gil-Hutton, R., Tedesco, E. F., et al. 1999, Icarus, 138, 129 [CrossRef] [Google Scholar]
- Cellino, A., Bus, S. J., Doressoundiram, A., et al. 2002, in Asteroids III, eds. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel, (Tucson: University of Arizona Press), 633 [CrossRef] [Google Scholar]
- Cellino, A., Yoshida, F., Anderlucci, E., et al. 2005a, Icarus, 179, 297 [CrossRef] [Google Scholar]
- Cellino, A., Gil-Hutton, R., Di Martino, M., et al. 2005b, Icarus, 179, 304 [CrossRef] [Google Scholar]
- Cellino, A., Belskaya, I. N., Bendjoya, Ph., et al. 2006, Icarus, 180, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Delbo, M., Bendjoya, Ph., et al. 2010, Icarus, 209, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Gil-Hutton, R., Dell’Oro, A., et al. 2012, J. Quant. Spectr. Rad. Transf., 18, 2552 [CrossRef] [Google Scholar]
- Cellino, A., Bagnulo, S., Tanga, P., et al. 2014, MNRAS, 439, 75 [Google Scholar]
- Cellino, A., Gil-Hutton, R., & Belskaya, I.N. 2015a, in Polarimetry of Stars and Planetary Systems, eds. L. Kolokolova, J. Hough, & A. Levasseur-Regourd, (Cambridge: Cambridge University Press), 360 [Google Scholar]
- Cellino, A., Bagnulo, S., Gil-Hutton, R., et al. 2015b, MNRAS, 451, 3473 [CrossRef] [Google Scholar]
- Cellino, A., Bagnulo, S., Gil-Hutton, R., et al. 2016a, MNRAS, 455, 2091Cellino, A., Ammannito, E., Magni, G., et al. 2016b, MNRAS, 456, 248 [Google Scholar]
- Cellino, A., Bagnulo, S., Belskaya, I. N., et al. 2018, MNRAS, 481, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Bagnulo, S., Tanga, P., et al. 2019, MNRAS, 485, 570 [Google Scholar]
- Collins, K. A., Kielkopf, J. F., Stassun, K. G., & Hessman, F. V. 2017, ApJ, 153, 77 [Google Scholar]
- DeMeo, F., Binzel, R. P., Slivan, S. M., et al. 2009, Icarus, 202, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Devogèle, M. 2017, Ph.D. Thesis, Université Côte d’Azur, France [Google Scholar]
- Devogèle, M., Cellino, A., Bagnulo, S., et al. 2017, MNRAS, 465, 4335 [CrossRef] [Google Scholar]
- Devogèle, M., Tanga, P., Cellino, A., et al. 2018a, Icarus, 304, 31 [CrossRef] [Google Scholar]
- Devogéle, M., Cellino, A., Borisov, G., et al. 2018b, MNRAS, 479, 3498 [CrossRef] [Google Scholar]
- Gehrels, T. 1974, Planets, stars and nebulae studied with photopolarimetry, University of Arizona Press, Tuscon, 168 [Google Scholar]
- Gil-Hutton, R., & Cañada-Assandri, M. 2011, A&A, 529, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil-Hutton, R., & Cañada-Assandri, M. 2012, A&A, 539, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil Hutton, R., Mesa, V., Cellino, A., et al. 2008, A&A, 482, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil-Hutton, R., Cellino, A., & Bendjoya, Ph., 2014, A&A, 569, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gradie, J., & Tedesco, E.F. 1982, Science, 216, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, V. E., Simon, A. A., Christensen, P. R., et al. 2019, Nat. Astron., 3, 332 [Google Scholar]
- Hergenrother, C. W., Maleszewski, C. K., Nolan, M. C., et al. 2019, Nat. Comm., 10, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, J.-C., & Breger, M. 1982, ApJ, 262, 732 [Google Scholar]
- Lauretta, D., DellaGiustina, D., Bennett, C., et al. 2019, Nature, 568, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, K., & Muinonen, K. 1993, IAU Symp., 160, 194 [Google Scholar]
- Lupishko, D. F. 2014, Asteroid Polarimetric Data Base (APD) V8.0, NASA Planetary Data System EAR-A-3-RDR-APD-POLARIMETRY-V8.0 [Google Scholar]
- Masiero, J. R., & Cellino, A. 2009, Icarus, 199, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Grav, T., Mainzer, A. K., et al. 2014, ApJ, 791, 121 [Google Scholar]
- Migliorini, F., Zappalà, V., Vo, R., et al. 1995, Icarus, 118, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Migliorini, F., Manara, A., Scaltriti, F., et al. 1997, Icarus, 128, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Migliorini, F., Zappalà, V., Vo, R., et al. 2002, in Asteroids III, eds. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 123 [Google Scholar]
- Milani, A., Cellino, A., Kneževic, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Oliva, E. 1997, A&AS, 123, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pernechele, C., Abe, L., Bendjoya, Ph., et al. 2012, Proc. SPIE, 8446, 84462H [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Kiselev, N. N., Shevchenko, V. G., et al. 2005, Icarus, 178, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Shevchenko, V. G., Kiselev, N. N., et al. 2009, Icarus, 201, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Sunshine, J. M., Connolly, H. C., Mc Coy, T. J., et al. 2008, Science, 320, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Cellino, A., Michel, P., et al. 1999, Icarus 141, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J. 1984, Ph.D. thesis, University of Arizona, USA [Google Scholar]
- Tholen, D. J. 1989, in Asteroids II, Asteroid taxonomic classifications, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: University of Arizona Press), 1139 [Google Scholar]
- Wiktorowicz, S., & Masiero, J. R. 2017, AAS DPS Meeting, 49, 110.32 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Phase-polarisation curves for the dwarf-planet (1) Ceres and the asteroids (2) Pallas, (4) Vesta, (6) Hebe, (16) Psyche, and (44) Nysa. CAPS measurements are plotted using red symbols, while literature data are plotted in black. The nominal error bars of all the measurements are shown, but are often not larger than the size of the symbols used to display the data. |
| In the text | |
 |
Fig. 2 As for Fig. 1, but for the asteroids (17) Thetis, (62) Erato, (89) Julia, and (139) Juewa. |
| In the text | |
 |
Fig. 3 As for Fig. 1, but for the asteroids (28) Bellona, (57) Mnemosyne, (194) Prokne, and (510) Mabella. |
| In the text | |
 |
Fig. 4 Shallow phase-polarisation curves for the asteroids (64) Angelina, (71) Niobe, (214) Aschera, and (434) Hungaria. The meanings of the symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 5 Phase-polarisation data for the asteroids (354) Eleonora, (289) Nenetta, (625) Xenia, and (863) Benkoela. The meanings of the symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 6 Phase-polarisation data for the asteroids (45) Eugenia, (210) Isabella, (419) Aurelia and (704) Interamnia, all of them belonging to the F taxonomic class. The meaning of the symbols is the same as in Fig. 1. The vertical lines at the phase angle of 20° (corresponding to the typical value of the polarisation inversion angle of most asteroid taxonomic classes) are drawn as a reference to illustrate the anomalously low values of the inversion angle characterising this taxonomic class (see text). |
| In the text | |
 |
Fig. 7 Phase-polarisation data in V for the asteroids currently named ‘Barbarians’, including the prototype of this class, asteroid (234) Barbara. Small members of the dynamical families of (729) Watsonia and (606) Brangane (see text) are not included in this figure, nor are a couple of measurements of (2085) Henan, another Barbarian candidate for which more data are needed. The meanings of the symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 8 Comparison of the phase-polarisation curves of some asteroids exhibiting very different reflectance spectra. Left: phase-polarisation curve obtained by merging together all the available V measurements of (824) Anastasia, (606) Brangäne, and (2085) Henan. Both literature and CAPS data of these asteroids are shown using the same symbol for each of them. Right: phase-polarisation curve of the asteroid (48) Doris, a member of the SMASS and DeMeo Ch taxonomic classes. The meanings of the symbols in this panel are the same as in Fig. 1. |
| In the text | |
 |
Fig. 9 Phase-polarisation curves of the asteroids (19) Fortuna, (134) Sophrosyne, (145) Adeona, and (345) Tercidina. They all belong to the SMASS Ch taxonomic class, but they exhibit quite different phasepolarisation curves with respect to (48) Doris shown in Fig. 8. The meanings of the symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 10 Phase-polarisation data for increasingly larger samples of members of the Koronis dynamical family. Top panels: phasepolarisation data for the two asteroids (158) Koronis and (208) Lacrimosa. In both cases, the data do not allow us to compute a phase-polarisation curve according to our criteria explained in Sect. 3. Bottom-left panel: plotted phase-polarisation curve, obtained by merging the polarimetric data for (158) Koronis and (208) Lacrimosa, as well as some data for a small number of additional Koronis family members. Bottom-right panel: slightly different phase-polarisation curve obtained by adding a fairly large number of Very Large Telescope (VLT) data, obtained by Cellino et al. (2010) for a sample of small members of the Koronis and Karin families (the latter being a sub-family of that of Koronis, see text), to the measurements used to produce the curve shown in the previous panel. |
| In the text | |
 |
Fig. 11 Phase-polarisation data for the asteroids (105) Artemis, and (914) Palisana. The meaning of the symbols is the same as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.