| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629623 | |
| Published online | 01 November 2017 | |
RefleX: X-ray absorption and reflection in active galactic nuclei for arbitrary geometries⋆
1 Department of Astronomy, University of Geneva, 1205 Versoix, Switzerland
e-mail: stephane.paltani@unige.ch
2 Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, 306, Santiago 22, Chile
e-mail: cricci@astro.puc.cl
3 Kavli Institute for Astronomy and Astrophysics, Peking University, 100871 Beijing, PR China
4 Chinese Academy of Sciences South America Center for Astronomy and China-Chile Joint Center for Astronomy, Camino El Observatorio, 1515 Las Condes, Santiago, Chile
Received: 31 August 2016
Accepted: 19 May 2017
Reprocessed X-ray radiation carries important information about the structure and physical characteristics of the material surrounding the supermassive black hole (SMBH) in active galactic nuclei (AGN). We report here on a newly developed simulation platform, RefleX, which allows to reproduce absorption and reflection by quasi-arbitrary geometries. We show here the reliability of our approach by comparing the results of our simulations with existing spectral models such as pexrav, MYTorus and BNTorus. RefleX implements both Compton scattering on free electrons and Rayleigh scattering and Compton scattering on bound electrons. We show the effect of bound-electron corrections on a torus geometry simulated like in MYTorus. We release with this paper the RefleX executable, as well as RXTorus, a model that assumes absorption and reflection from a torus with a varying ratio of the minor to major axis of the torus. To allow major flexibility RXTorus is also distributed in three components: absorbed primary emission, scattered radiation and fluorescent lines. RXTorus is provided for different values of the abundance, and with (atomic configuration) or without (free-electron configuration) taking into account Rayleigh scattering and bound electrons. We apply the RXTorus model in both configurations on the XMM-Newton and NuSTAR spectrum of the Compton-thick AGN NGC 424 and find that the models are able to reproduce very well the observations, but that the assumption on the bound or free state of the electrons has significant consequences on the fit parameters.
Key words: X-rays: general / galaxies: nuclei / galaxies: Seyfert / methods: numerical
RefleX executable, user manual and example models are available at http://www.astro.unige.ch/reflex. A copy of the RefleX executable is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/607/A31
© ESO, 2017
1. Introduction
X-ray emission is one of the key characteristics of active galactic nuclei (AGN). Its existence is most probably the signature of the release of gravitational energy in a hot plasma in the vicinity of the supermassive black hole (SMBH) through Comptonization of soft photons, presumably from the accretion disk (e.g., Haardt & Maraschi 1993). The study of direct X-ray emission is very interesting in itself, because of the complex physical processes at play. However, X-rays also provide a direct probe of the geometry of AGN through the study of their propagation through the surrounding matter which is irradiated by the central source. A fluorescence iron line at 6.4 keV, corresponding to the Kα transition, was discovered in early X-ray studies of AGN (e.g., Mushotzky et al. 1978) and successively confirmed for a significant number of objects by EXOSAT (e.g., Nandra et al. 1989; Pounds et al. 1989). Studying the composite Ginga spectra of 12 AGN, Pounds et al. (1990) found evidence of a bump at ~30 keV, the reflection hump. Both spectral features can be explained by the reprocessing of primary X-ray photons in the surrounding medium, and are therefore closely linked. While the Fe Kα line can originate in Compton-thin material, the reflection hump implies the presence of material with significant optical depth to Compton scattering, i.e. close to being Compton-thick (CT; i.e. 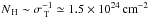 ).
).
Different structures around the supermassive black holes may contribute to the reprocessed X-ray radiation. An optically thick geometrically-thin accretion disk is supposed to channel matter onto the supermassive black hole. Moderately dense clouds (N H ~ 1023−24 cm-2; e.g. Netzer 2015) in the broad-line region (BLR), with an emissivity-weighted radius spanning from a few to hundreds of light days (depending on the AGN luminosity, e.g., Kaspi et al. 2005) are thought to be responsible for the emission of broad lines in the infrared to ultraviolet. More distant and rarefied matter (the narrow-line region or NLR), with densities of n e ~ 103−107 cm-3 (e.g., Baskin & Laor 2005) is responsible for the emission of narrow lines in the optical and infrared. At larger distances, the accretion disk is thought to become thick and form a torus, with the BLR marking possibly the transition between the two; absorbed AGN (N H ≥ 1022 cm-2) are generally thought to be observed through the torus, although a contribution might come also from the BLR or from material located on galactic scales (e.g., Goulding et al. 2012). Finally, evidence for a fully ionized plasma has been found in extremely obscured objects in the form of a scattered component accounting for a few percent of the primary emission (Turner et al. 1997).
The physics of the interaction of X-ray photons with the surrounding material includes several processes. The most important processes are photoionization and elastic or inelastic scattering. Photoionization is furthermore followed by the emission of either an electron (the Auger effect), a fluorescence photon or both (the Coster-Kronig process). The physics of these processes is well understood, and several reflection models are currently available in the standard xspec spectral analysis package (Arnaud 1996). For instance, pexrav and pexmon assume the existence of optically thick, cold material (although it is assumed that H and He are fully ionized), distributed in a slab and covering a given fraction of the X-ray source. The pexrav model (Magdziarz & Zdziarski 1995) ignores fluorescence, while pexmon (Nandra et al. 2007), adds a number of important spectral features, such as the fluorescence lines Fe Kα, Fe Kβ, and Ni Kα, following the Monte Carlo calculations of George & Fabian (1991) and the Compton shoulder (in the form of a Gaussian line of width σ = 35 eV centered at 6.315 keV). While these models are still very popular, they have strong limitations. One of these limitations is that the reflective medium is completely optically thick, so transmission through the medium is totally suppressed. The geometry is limited to a planar geometry, so they are not applicable to realistic geometries beyond the accretion disk. They also assume that the source is very close to the reflecting medium, so that the incident angle of the primary radiation is isotropically averaged.
To overcome these limitations, new models have been developed. MYTorus1 (Murphy & Yaqoob 2009) implements a toroidal geometry with arbitrary column density. Ikeda et al. (2009) and Brightman & Nandra (2011) have developed models that consider a spherical toroidal structure with varying covering factors and constant NH in all directions across the torus. All these torus models are based on Monte Carlo simulations, where primary X-ray photons are propagated through the simulated torus structure, undergoing physical processes along the way, until they are either destroyed through photoionization or they escape the system.
While these models represent a major advance over the traditional slab models, they still do not allow very flexible geometries, or even the self-consistent combination of simple geometries. For instance, in a model of a disk and a torus represented with pexrav+mytorus, photons reflected by the disk are unaware of the presence of the torus. We introduce here a new tool, RefleX, which is able to simulate theoretical X-ray spectra of AGN using quasi-arbitrary geometries. We present in this first paper the implementation of our simulation tool. We demonstrate the validity of our approach by comparing with standard and more recent transmission/reflection models. With this paper, we release publicly the RefleX executable. We provide in addition a series of xspec models, RXTorus (see Sect. 4), generated with RefleX, which are extensions of the MYTorus with varying covering factors and metallicities. The goal is to compute and distribute regularly new X-ray spectral models to the community, adapting the geometry of the reprocessing material to different physical scenarios. In spite of the loss of the Soft X-ray Spectrometer (SXS; Mitsuda et al. 2014) on board Hitomi (Takahashi et al. 2014), the spectacular results of the SXS (Hitomi Collaboration et al. 2016) have demonstrated the need for similar instruments in the future. Therefore, a particular emphasis of our models is to be applicable to future-generation high-resolution X-ray instruments, such as the X-ray Integral Field Unit (X-IFU; Barret et al. 2016) on board the future large X-ray observatory of the European Space Agency Athena (Nandra et al. 2013).
2. Ray-tracing simulations of X-ray transmission and reflection
We developed a ray-tracing code, RefleX, with the aim of being able to simulate realistically the physical processes of propagation of X-rays, which we define as photons with energies from about 0.1 keV to about 1 MeV through matter around the central engine of AGN. The RefleX code uses Monte Carlo simulations to track individual photons. The simulated photons interact with the matter through all the physical processes selected by the user (with sensible defaults), until the photon dies, is downscattered to an energy below a chosen termination energy or exits the system.
The ray-tracing simulation consists of four separate engines that are closely connected: photon creation, geometrical description, photon propagation, and physical processes. The details of these engines are presented below.
The code records the full list of events that are experienced by each photon, although the level of detail is configurable to allow the user to manage the quantity of information produced. This allows us, for instance, to select photons that crossed a particular object or experienced a particular physical process. The time of flight of the photon is also recorded, allowing the user to perform timing studies.
The simulation is geometrically bounded by the World, which is a sphere with a user-defined radius centered on the origin. All processes occurring outside of World are ignored and ray tracing stops when a photon reaches World.
2.1. X-ray generator
The first step of the RefleX Monte Carlo simulation is the creation of photons. A photon is determined by a time, position, direction, and energy. All photons are created at time t = 0. The source can be placed anywhere within the boundary of the simulation (World). The position and directions are drawn at random from some predetermined distributions and geometries selected by the user. The source can currently be a point, sphere, or disk. For each geometry, the photon direction can be either fully isotropic, or restricted to a sector.
The photon energy is drawn from several possible distributions. These distributions are currently: monoenergetic, Gaussian, blackbody, power law, or power law with a high-energy exponential cutoff. New distributions can be easily implemented into RefleX.
2.2. Objects
The main novelty of RefleX is the possibility to define complex geometries for the surrounding material by assembling independent building blocks. An arbitrary number of objects can be set up by the user. Each object is characterized by a position, geometrical shape, composition, and hydrogen density. Four different geometries are currently included: sphere, disk or cylinder, annulus, shell, and torus. Annuli and shells can be used to simulate disks and spheres with density profiles. The objects can be placed anywhere within World, with a few exceptions: the axis of symmetry of disks, annuli and, tori must be parallel to the z-axis. These limitations could be removed in principle, at the price of more complex analytic treatment of the interactions (see Sect. 2.3), if deemed useful. The objects can also be named, so that they can be identified in the tracking of the events.
Once a geometrical object has been defined, its composition needs to be set. A composition is defined by the number density ratios of all elements from Z = 2 (helium) to Z = 30 (zinc) compared to hydrogen. Each object can have a different composition and hydrogen number density. Several compositions have been predefined similarly to those available in xspec. These are angr (Anders & Grevesse 1989), aspl (Asplund et al. 2009), feld (Feldman 1992, except for elements not listed that are given grsa abundances), aneb (Anders & Ebihara 1982), grsa (Grevesse & Sauval 1998), wilm (Wilms et al. 2000, except for elements not listed that are given zero abundance) and lodd (Lodders 2003). The metallicity (abundance of elements with Z> 2) can be modified and the number density ratio of each element can be tuned individually to simulate arbitrary chemical compositions.
2.3. Propagator
Once a photon is created by the X-ray generator, the propagator tracks the photon, propagates it through the objects and determines the occurrence of physical interaction between the photon and the material contained in the objects. For this reason, the propagator always knows in which object the photon resides, and is aware of all interaction cross-sections between the photon and the object in which it resides.
The propagator analytically finds all intersections between the photon trajectory and the objects in order to determine which object is next. Each physical process is then tested sequentially (see Sect. 2.4) to determine if any of these processes takes place inside the object, or if the photon exits the object. In all cases, the photon is first propagated to the location where the interaction takes place, or at the surface of the object if it exits. When an interaction takes place, the trajectory, intersections and cross-sections are recomputed, and the propagator is called again.
By geometrical construction, the propagator always finds one intersection in the future with World. Once the photon hits World, the propagation is terminated and the interaction parameters (location, direction, energy, and time) are recorded. The propagation also terminates if the photon is destroyed or if the photon energy drops below a minimum energy set by the user.
2.4. Main physical processes
The RefleX code implements several physical processes that take place when an X-ray photon crosses matter. We do not attempt to simulate all physical processes, but restrict ourselves to the few that are the most significant, similar to what has been the case in other models such as pexrav (Magdziarz & Zdziarski 1995), pexmon (Nandra et al. 2007) and MYTorus (Murphy & Yaqoob 2009). The modular nature of the code allows us to add new physical processes if needed. In order to provide insight into the physical mechanisms, each process can be turned on and off and the processes that have taken place are recorded or each simulated photon.
2.4.1. Compton and Rayleigh scattering
Compton scattering is the inelastic (incoherent) interaction between a photon and a free electron. In the low-energy limit, the scattering becomes quasi-elastic, and is approximated by the Thomson scattering. The Compton scattering cross-section is given by the Klein-Nishina relativistic differential cross-section. The RefleX code implements the full Klein-Nishina cross-section for free electrons, although the user can disable both the Klein-Nishina correction and inelastic scattering, for educational purposes. Several models, such as pexrav (Magdziarz & Zdziarski 1995), assume that all H and He atoms are fully ionized, and scattering occurs only on these free electrons, neglecting the electrons bound on metallic atoms. The same physical configuration can be selected by the user in RefleX; in the following, we refer to this configuration as the free-electron configuration.
However, electrons bound to atoms have a different behavior with respect to scattering of photons. The RefleX code can therefore adopt a different physical configuration, that we refer to as the atomic configuration, which takes into account the bound state of electrons. We include in RefleX binding correction terms for Compton scattering, called incoherent scattering functions, computed by Hubbell et al. (1975) as an energy- and Z-dependent multiplicative term on the Klein-Nishina cross-section. These corrections are also available in the EPDL97 library2, and strongly decrease the cross-section for Compton scattering at low energy, which is essentially replaced by coherent (Rayleigh) scattering.
Rayleigh scattering is a coherent scattering on atoms due to their polarizability. Contrarily to Compton scattering, the atom is neither ionized nor excited. Rayleigh scattering cross-sections are significantly larger than the Compton scattering cross-sections at low energy, up to several tens of keV for heavy atoms. The angular distribution is identical to that of Compton scattering in the low-energy limit. In the atomic configuration, RefleX implements Rayleigh scattering, unless disabled by the user. The Rayleigh cross-sections have been taken from Hubbell et al. (1975).
Coherent and incoherent scattering on molecular hydrogen, H2, is also included in RefleX in the atomic configuration using the cross-sections of Hubbell et al. (1975). The fraction of hydrogen in molecular form can be set in RefleX.
Several recent models already include these corrections for scattering on bound electrons (Liu & Li 2014; Furui et al. 2016, see Sect. 3.4). Applying these corrections has been shown to make a difference of up to 25% in the reflected spectrum at 1 keV, the effect becoming negligible around and above 10 keV (Liu & Li 2014).
2.4.2. Photoelectric absorption
Photoelectric absorption by bound electrons is another important process affecting transmission and reprocessing of X-rays. We use here the cross-sections determined from the analytic fits for each shell of the 30 elements provided by Verner & Yakovlev (1995) and Verner et al. (1996)3; the cross-sections are computed using the Hartree-Dirac-Slater formalism and are thoroughly checked with existing laboratory measurements. In the current implementation, only neutral atoms are considered, although the analytic representations cover all ionization stages.
The use of analytic functions allows us to avoid performing any interpolation in functions that have sharp edges. The cross-sections are calculated on the fly when the photon is created or when its energy changes, for instance after Compton scattering, at the precise photon energy. The cross-sections are calculated separately for each shell, which allows us to keep track of the shell responsible for the photoelectric absorption.
2.4.3. Recombination
When photoionization occurs, an electron is kicked out of the atom. The vacancy is filled by another electron from an outer electronic shell. Usually, the excess energy is transmitted to an outer-shell electron, which is then ejected. No further photon is emitted, and the simulation simply terminates. This process is known as the Auger effect.
In other cases, a fluorescence photon is emitted at an energy equal to the difference between the outer-shell energy level of the electron having filled the gap and the energy level of the vacancy. It is emitted in a random direction at the location of the interaction. The probabilities of such transitions, the fluorescence yields, which depend strongly on the atomic number of the element, have been taken from LBNL X-ray Data Booklet (Thompson et al. 2009); in particular, the Fe Kα/Fe Kβ ratio is 8.147. The energy levels of a number of X-ray fluorescence lines have been measured in the laboratory by Bearden (1967) and are therefore more accurate than the LBNL ones; we use these measured energies when available. Only fluorescence from K and L shells has been implemented. The L-shell fluorescence lines are considerably weaker and have energies below 1.2 keV, but some lines are astrophysically relevant, as iron L-shell fluorescence has already been detected in an AGN (Fabian et al. 2009). The full list of K-shell fluorescence lines with the adopted fluorescence yields and energy levels is presented in Appendix A.
2.5. Polarization
In the context of reflection of X-rays on cold matter, photon polarization essentially impacts the direction in which incoming photons are scattered in Compton scattering. The formalism is presented in Matt et al. (1996). While there are not many observational constraints on polarization in the X-rays, this could change in the future with the advent of X-ray polarimeters (e.g., Soffitta et al. 2013). Polarization-dependent Compton scattering in the Klein-Nishina regime is implemented as an option in RefleX. The study of polarized reflection with RefleX will be deferred to another paper.
2.6. Normalization of spectra
Since RefleX generates a fixed, user-selected number of photons N, the production of spectra in physical units of flux, either in counts s-1 cm-2 keV-1 or in keV s-1 cm-2 keV-1, requires a normalization factor. This is calculated by setting the luminosity of the unabsorbed source in a given energy range and its redshift; the redshift is in addition applied to all photons escaping to World.
We point out however that the parameter is the unabsorbed luminosity of the primary source of X-ray photons. In addition to the obvious effect of the absorber, two effects impact the observed luminosity. First, some part of the primary emission is reflected, thereby enhancing the observed luminosity; second, in the case of non-isotropic geometry, the flux and luminosity depend on the direction of the observer. The first effect should not be very important, since the reflected flux is generally a small fraction of the unabsorbed primary emission. The second effect may however be important in situations where the primary source is strongly anisotropic.
2.7. Domain of validity
The physical processes implemented in RefleX are exact, i.e. no simplifying assumption is made on the calculation of any of the physical processes described in this section. However, the accuracy of RefleX simulations is limited by a number of factors. Implemented physical processes depend on parameters which are usually only known with some limited precision and accuracy. As an example, the photoelectric cross-sections used in RefleX, while commonly used in astronomy, are not unique; in addition to the cross-sections used in RefleX (vern), xspec can also use the cross-sections from Balucinska-Church & McCammon (1992) with either the new H and He cross-sections from Yan et al. (1998) (bcmc) or the original cross-sections (obcm).
Similarly, while the Klein-Nishina cross-section is computed using the exact formula, corrections for bound electrons and Rayleigh scattering cross-sections are computed using approximations, Compton and Rayleigh cross-sections in RefleX are interpolated using the tables from Hubbell et al. (1975), which are valid from 100 eV to 100 MeV.
Many of the fluorescence lines (and all the most prominent ones) have been measured in the laboratory by Bearden (1967); however, the energy levels of many minor lines have been calculated. More importantly, all probability transitions are also calculated.
The main limitations of RefleX come however from the physical processes that are not implemented, in particular the following:
-
Pair production contributes to opacity at energies above1 MeV, and even starts to dominate around10 MeV. Likewise, photon-photon opacity isnot included.
-
Matter velocities, thermal broadening and turbulence are not included, although we plan to include these processes at a later stage; this may induce unrealistically sharp features in the RefleX spectra. This is mitigated by the limited spectral resolution of X-ray telescopes.
-
Coster-Kronig process is a special case of an Auger effect where the vacancy is filled by an electron from the same shell. In this case, a secondary recombination may occur, which could be in the form of a fluorescence line. Since Coster-Kronig process cannot affect the K shell, only L-shell fluorescence and above can occur. Because L-shell fluorescence is already weak and because Coster-Kronig process is a second-order effect, it has not been implemented in RefleX. Likewise, M-shell (and above) fluorescence is neglected.
-
Raman scattering, which is an inelastic scattering of a photon with an atom or a molecule, is not included, since it has much lower probability than Rayleigh scattering.
3. Comparison with existing models
Before applying our code to simulate the reprocessed emission of AGN, it needs to be validated. We therefore computed detailed simulations that mimic models available in xspec or in the literature.
 |
Fig. 1 Geometry of the pexrav/pexmon model. The reflector is the blue plane. The source of X-ray photons is the magenta plane, parallel to the reflector. The inclination angle i is defined as the angle between the normal to the planes and the observer. The stars illustrate that primary photons are emitted isotropically anywhere in the source plane. Half of the primary photons leave the system without hitting the reflector. |
 |
Fig. 2 Comparison between pexmon and our RefleX simulations assuming the geometry of Fig. 1 for three viewing angles. Top: i = 10 deg; middle: i = 30 deg; and bottom: i = 60 deg. In each panel, the top subplot shows the pexmon model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. In all cases, the primary continuum is defined as a cutoff power law starting at 1 keV with an index Γ = 1.5 and a cutoff energy at 100 keV. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
 |
Fig. 3 Comparison between pexmon and our RefleX simulations assuming the geometry of Fig. 1 for i = 30 deg, limited to the 6–7.6 keV region. The top subplot shows the pexmon model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. The primary continuum is the same as in Fig. 2. |
3.1. pexrav and pexmon
pexrav (Magdziarz & Zdziarski 1995) is the standard reflection model in xspec. This model, which has been computed using analytic approximations of Green’s functions derived from Monte Carlo simulations, assumes that the reflector is an optically thick medium in an infinite plane geometry and that the source is located immediately on top of the reflector; the extension of the source is irrelevant as long as it is significantly smaller than extension of the reflector. The distribution of incident angles follows μ = cosϑ, where ϑ is 0 for an incident photon perpendicular to the plane. Figure 1 illustrates the geometry adopted in pexrav. The primary X-ray emission follows a power law with an exponential cut off, although the reflect convolution model can be used to simulate the same physical processes using an arbitrary primary X-ray emission spectrum. pexrav implements photoelectric absorption and Compton scattering, including Klein-Nishina cross-section. pexrav assumes that all electrons from hydrogen and helium atoms are free, and disregards the other electrons. pexmon (Nandra et al. 2007) is based on the pexrav model and implements the same geometry, but adds the Fe Kα fluorescence line based on the Monte Carlo simulations by George & Fabian (1991). Fe Kβ and Ni Kα fluorescence lines have also been added and their fluxes are fixed at a fraction of the Fe Kα flux. In addition, a Compton shoulder caused by Fe Kα fluorescence line that is scattered and shifted to lower energies has been added in the form of a Gaussian, following the prescription of Matt (2002) regarding its intensity (but not its shape). These models depend on composition, metallicity, inclination angle i of the disk with respect to the observer and on a normalization factor R, with R = 1 indicating that the reflector covers half of the solid angle as seen from the source, i.e. it is quasi-infinite.
Figure 2 shows the comparison between pexmon and our simulations for different inclination angles (i = 10, 30 and 60 deg) and R = 1. The primary continuum is defined as a cutoff power law with an index Γ = 1.5 and a cutoff energy at 100 keV. The termination energy was set to 300 eV. We selected the element abundances from Lodders (2003) in both models and used the same photoionization cross-sections. We find that the shapes of the two spectra match generally well, although there are some significant differences. We observe that the reflected spectrum is slightly harder, in particular below ~3–4 keV, which introduces a ~20% difference in flux at 1 keV. Another difference, which was expected, is the presence of several other fluorescence emission lines in our simulations, which are not implemented in pexmon. These lines have been detected in the Compton-thick AGN in M51 (Xu et al. 2015). Finally, we point out the presence of an excess in the pexmon spectrum below ~0.5 keV. While this energy corresponds to that of the 1s edge of oxygen, such a feature is not really expected. We believe it is due to an imperfect modeling in pexrav/pexmon. With the exception of these differences, we find that the overall normalizations of the two spectra are in excellent agreement. The observed discrepancies are probably related to the approximations adopted in pexrav.
Figure 3 shows a zoom on the 6–7.6 keV region for i = 30 deg. The Gaussian shape of the Compton shoulder implemented in pexmon does not match the results of our simulation at all. The latter is however perfectly similar to the Compton shoulder simulations of Matt (2002), which uses a similar Monte Carlo approach. In addition, the simulation includes separate fluorescence lines for the L2–K1 and L3–K1 transitions Fe Kα2 and Fe Kα1, respectively, whose energies differ by 13 eV (6390.84 vs. 6403.84 eV respectively). These spectral features could be easily resolved by X-ray telescopes equipped with micro-calorimeters, such as Athena. The Fe Kβ and Ni Kα lines also appear different. This is due to the assumptions on the energy of these lines (7050 eV and 7470 eV, respectively) and on the width of these lines (35 eV) in pexmon, while RefleX uses the values of Bearden (1967), i.e., Fe Kβ at 7057.98 eV and two separate Ni Kα2 and Ni Kα1 at 7460.89 eV and 7478.15 eV, respectively, and a 0 eV line width.
3.2. MYTorus
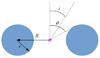 |
Fig. 4 Geometry of the MYTorus model. The reflector is a torus, whose section is shown in blue. The source of X-ray photons is the magenta star in the center, which is isotropic. The inclination angle i is defined as the angle between the normal to the plane of the torus and the observer. In the MYTorus model, the ratio between the major and minor radii of the torus, R/r, is 2, leading to a half opening angle φ = 60 deg. |
 |
Fig. 5 Comparison between MYTorus and our simulations assuming the geometry of Fig. 4 for two viewing angles and two equatorial column densities. For both models we show only reprocessed radiation. Top: i = 30 deg; bottom: i = 75 deg. Left: NH,eq = 1022 cm-2; right: NH,eq = 1024 cm-2. In each panel, the top subplot shows the MYTorus model (black line) and our simulations (crosses); the bottom subplot shows the ratio between our simulations and the MYTorus model. In all cases, the primary continuum is defined as a power law between 1 and 500 keV with a photon index Γ = 1.9. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
MYTorus (Murphy & Yaqoob 2009) is a model for the reflection and transmission of X-rays based on Monte Carlo simulations, which is available in xspec in the form of model tables. MYTorus implements a toroidal geometry as shown in Fig. 4 with a half-opening angle φ = 60 deg, which corresponds to a torus minor radius r (the radius of the tube) half the major radius R (the distance from the center of the tube to the center of the torus). The central source is isotropic and the primary X-ray emission distribution follows a power law with a maximum energy. Because of the circular shape of the section of the torus, primary photons crossing the torus do not see the same hydrogen column densities, but rather 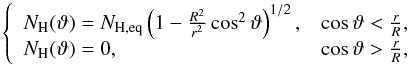 (1)where NH,eq is the equatorial column density, i.e. the column density seen by a photon that crosses the torus radially in the central plane of the torus, and ϑ is the angle between the direction of the primary photon and the perpendicular to the torus.
(1)where NH,eq is the equatorial column density, i.e. the column density seen by a photon that crosses the torus radially in the central plane of the torus, and ϑ is the angle between the direction of the primary photon and the perpendicular to the torus.
Different equatorial column densities can be modeled, from an optically thin torus with NH,eq = 1022 cm-2 to an optically thick torus with NH,eq = 1025 cm-2. The medium has an equivalent temperature of 104 K, meaning that H and He can be considered ionized and Fe ions up to Fe xvii are present, i.e. there is no significant shift in the iron fluorescence line energy. Only Fe Kα (single line representing Fe Kα1+Fe Kα2) and Fe Kβ fluorescence lines are included. Apart from the geometry, the main difference between the pexrav/pexmon and MYTorus models is the fact that, in the latter case, the reflector is not necessarily optically thick, and therefore a transmitted component exists.
The physics included in MYTorus is practically identical to that included in the free-electron configuration of RefleX, and therefore constitutes an important benchmark for the validation of our code. Figure 5 shows the comparison between MYTorus and our simulations for different inclination angles (i = 30 deg, i.e. with a direct view of the central source and i = 75 deg, i.e. through the torus) and different equatorial column densities. For visual clarity, only the reprocessed X-ray radiation is shown. The primary continuum is defined as a power law with a photon index Γ = 1.9. The termination energy was set to 500 eV, similar to the minimum energy in MYTorus. The maximum energy was set to 500 keV. MYTorus implements only the solar element abundances from Anders & Grevesse (1989). The MYTorus and RefleX simulations match perfectly, and the only differences are attributed to the fluorescence lines of low-Z elements which are not included in MYTorus.
 |
Fig. 6 Comparison between MYTorus and our simulations for i = 75 deg and NH,eq = 1024 cm-2, limited to the 6–7.5 keV region. The MYTorus model is shown with a black line and our simulation is shown with a red line. The primary continuum is the same as in Fig. 5. |
Figure 6 shows a zoom on the 6–7.5 keV region for i = 30 deg. Again, the match is excellent. In particular, the shape of the Compton shoulder and the line intensities are perfectly reproduced. The only significant difference is the presence of fluorescence lines, such as Ni Kα at E = 7.470 keV, which are not included in MYTorus.
The remarkable agreement at all column densities between the two simulations, which were developed completely independently, validates the implementation of the physical processes in RefleX.
 |
Fig. 7 Comparison between MYTorus and our simulations assuming the geometry of Fig. 4 for two viewing angles and two equatorial column densities taking into account the cross-sections for bound electrons. For both models we show only reprocessed radiation. Top: i = 30 deg; bottom: i = 75 deg. Left: NH,eq = 1022 cm-2; right: NH,eq = 1024 cm-2. In each panel, the top subplot shows the MYTorus model (black line) and our simulations (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. In all cases, the primary continuum is defined as a power law starting at 1 keV with a photon index Γ = 1.9. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
Figure 7 shows the comparison between MYTorus and RefleX for the same geometry, but using the atomic configuration. The source parameters are identical to those used in Fig. 5. We observe an excess of scattered emission below ~5 keV, which can exceed 50% at 1 keV in the NH,eq = 1024 cm-2 case. This effect is due to the dominance of Rayleigh scattering at low energy. Such an effect has already been pointed out by Liu & Li (2014, see Sect. 3.4. Another difference is that the peak of the reflection hump is located at slightly higher energy than in the free-electron configuration, which results in a bump in the ratio of the two models around 20 keV. Finally, the shape of the Compton shoulder of the Fe Kα fluorescence line is modified, which creates strong residuals below 6.4 keV. Such behavior has also been observed by Furui et al. (2016) using the MONACO model (see Sect. 3.5).
3.3. Spherical-toroidal geometry
Brightman & Nandra (2011) further developed the BNTorus model from an original Monte Carlo code from Nandra & George (1994) to simulate an approximately toroidal geometry based on a sphere with polar conical holes. The geometry is illustrated in Fig. 8 left. A similar geometry was used by (Ikeda et al. 2009), but their model was not publicly released, and therefore it cannot be used for comparison. In RefleX, we can approximate this geometry by superimposing annuli with outer radii approximating a sphere and inner radii approximating a cone of given aperture (Fig. 8 right). We also use this geometry to validate the propagation of photons in multiple objects in RefleX. For these simulations, the original geometry has been simulated using 51 annuli and the free-electron configuration has been used to match the assumptions of Brightman & Nandra (2011).
 |
Fig. 8 Spherical-toroidal geometry of the BNTorus model of Brightman & Nandra (2011; left). The reflector is a sphere with a conical opening of angle φ, whose section is shown in blue. The source of X-ray photons is the magenta star in the center, which is isotropic. The inclination angle i is defined as the angle between the normal to the plane of the torus and the observer. In RefleX, we model this shape by superimposing a number of annuli (right) that approximate the spherical-toroidal geometry. |
 |
Fig. 9 Comparison between the spherical-toroidal geometry and our RefleX simulations assuming the BNTorus geometry (Fig. 8) for two viewing angles and an half-opening angle of θ OA = 30 deg. Top: i = 20 deg; bottom: i = 87 deg. In each panel, the top subplot shows the spherical-toroidal model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the spherical-toroidal model. In all cases, the primary continuum is defined as a power law starting at 1 keV with an index Γ = 1.9 up to 500 keV. The equatorial column density is NH,eq = 1024 cm-2. The BNTorus model has been approximated using 51 annuli in RefleX. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
Figure 9 shows the comparison between the spherical-toroidal model of Brightman & Nandra (2011) and our RefleX simulations for two viewing angles. The primary continuum is defined as a power law with an index Γ = 1.9 up to 500 keV. The termination energy has been set to 300 eV. As for MYTorus, BNTorus uses the solar element abundances from Anders & Grevesse (1989) and a physics similar to the free-electron configuration. The agreement is very good in the case of low inclination at all column densities. In the high-inclination case, while agreement is excellent above 10 keV, there is a strong difference at low energy with the BNTorus model presenting a strong tail that is not present in RefleX. This difference becomes more and more important with increasing column densities. We thus confirm the results of Liu & Li (2015) based on Geant4 simulations (see Sect. 3.4), which identified a problem in the Brightman & Nandra (2011) code. Liu & Li (2015) interpret this behavior by postulating that the BNTorus code fails to treat correctly photons that are backscattered by the torus. Our simulations support this interpretation.
3.4. Geant4-based models
Geant44 (Agostinelli et al. 2003; Allison et al. 2006) is a C++ framework to simulate interactions of particles through matter. Geant4 has originally been developed in the context of high-energy physics to simulate the interactions of particles accelerated in particle accelerators inside detectors. As such, it implements a huge array of physical processes, for example, hadron physics, and very complex geometrical shapes to be able to construct any kind of detector. Although it is not the primary purpose of Geant4, electromagnetic processes are included. It is therefore straightforward to build a simulation tool similar to that presented in this work. Such an approach has been developed by Liu & Li (2014) and Liu & Li (2015).
While extremely powerful, the Geant4 framework has a number of intrinsic limitations. For instance, the photoelectric cross-sections used by Geant4 have been derived from the EPDL89 library (Cullen et al. 1990), instead of the cross-sections from Verner & Yakovlev (1995) and Verner et al. (1996), which are commonly used in astronomy; this leads to differences in the resulting spectrum which can be very significant in high-resolution spectra. Figure 10 shows the example of an absorbed power law, where the absorption edges are found at clearly different energies with differences of 20 eV or more. It is in principle possible to replace the cross-sections, since they are defined in the low-energy electromagnetic process data pack (G4EMLOW), but it is very difficult to do in practice.
 |
Fig. 10 Spectrum of an absorbed power law simulated with the Geant4-based model of Liu & Li (2014) compared with the xspec model phabs; NH was set to 5 × 1022 cm-2. The figure shows that the absorption edges are clearly at different energies. |
Likewise, fluorescence energies in G4EMLOW originate from the EPDL89 library, and do not match the energies measured in the laboratory by Bearden (1967). As an example, the Fe Kα1 6400 eV fluorescence line appears at 6362.71 eV, instead of 6403.84 eV; this is a difference of more than 40 eV. This can fortunately be more easily fixed, and one of us (SP) has actually implemented in Geant4 the energies measured by Bearden (1967), which can be selected by the user, starting with Version 10.1 (G4EMLOW version 6.41).
Geant4 implements the correction for bound electrons, so the model of Liu & Li (2014) should be compared with RefleX simulations using the atomic configuration. However, the only model made available by Liu & Li (2014) and Liu & Li (2015) is a clumpy-torus model, CTorus5; we defer the analysis of clumpiness of the torus with RefleX to another paper.
3.5. MONACO
MONACO is a hybrid simulation tool developed by Odaka et al. (2011). The computation of interactions is performed with Geant4, while the physical processes have been implemented by the authors. MONACO also uses EPDL97 for the atomic cross-sections, and therefore includes the bound-electron corrections.
Furui et al. (2016) have recently applied the MONACO simulation tool to the AGN torus in a MYTorus-like configuration. Comparing with the MYTorus simulations, they found that the shape Compton shoulder is strongly affected by the correction for bound electrons. As in the model of Liu & Li (2014), Furui et al. (2016) have found that the location of the edges differ in MONACO and in MYTorus, because of the different origin of the cross-sections (see Fig. 2 in Furui et al. 2016).
Since no model based on MONACO has been released, a proper comparison cannot be performed.
Results obtained by fitting the XMM-Newton and NuSTAR spectra of NGC 424 with the non-atomic and atomic version of RXTorus.
 |
Fig. 11 NuSTAR and XMM-Newton spectrum of NGC 424 fitted with the non-atomic (left panel) and atomic (right panel) version of RXTorus. The spectral parameters obtained are reported in Table 1. |
4. The RXTorus xspec models
4.1. The model
As a first application of RefleX, we developed a new model, RXTorus, which extends the simulations in MYTorus adopting the same source and absorber geometries, but allowing different values of the r/R opening ratios (see Fig. 4). This model is publicly released in the form of xspec tables6.
We generated the RXTorus models on a grid with the different parameters. For each simulation, 5 × 108 photons were generated. The planar symmetry of the problem was used to double the statistics. RXTorus considers a primary X-ray spectrum in the form of a power law with a photon index Γ between 1.0 and 3.0; the maximum photon energy is set to 300 keV. As in MYTorus, it is the maximum energy of the power law, and not a cutoff energy. The RXTorus torus equatorial column density NH,eq covers the range from 1022 cm-2 up to 1025 cm-2. The ratio r/R varies from 1 (i.e. a horn torus, a torus without central hole, or φ = 0 in Fig. 4) to 0.01. As a function of this ratio, several quantities can be readily obtained as follow:
-
The line-of-sight column density for a given inclination i is given by Eq. (1), with ϑ = i.
-
The opening angle φ, i.e., the angle above which the line of sight crosses the torus is given by
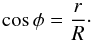 (2)
(2) -
The torus covering fraction, i.e. the fraction of the primary photons that enters the torus is
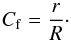 (3)
(3)
Spectra were binned in inclination angle with a 3-degree step. In order to allow the inclination parameter to cover the full 0–90 deg range, the first and last bins are assumed to be centered on 0 and 90 deg, respectively. For compatibility with MYTorus, the composition is taken from Anders & Grevesse (1989), but we provide tables with different metallicities from 0.3 to 2.0 solar. Both free-electron and atomic configurations are available.
The RXTorus model is subdivided into several table components to allow a greater flexibility, i.e.
-
The transmitted continuum contains only photons that did notundergo any physical process.
-
The scattered continuum contains all photons that underwent one or more Compton scatterings, but no photoionization and no fluorescence.
-
The fluorescence emission contains all photons that underwent at least one photoionization and subsequent fluorescence re-emission, plus any number of Compton scatterings.
In addition, a table with the full emission, i.e., the sum of the transmitted continuum, the scattered continuum, and the fluorescence emission, is also provided.
While the SXS micro-calorimeter on board Hitomi has unfortunately been lost with the mission itself, such instruments will certainly play a huge role in the future of X-ray astronomy. Therefore, we provide the RXTorus model with a energy resolution of ΔE = 2 eV in the 0.3–10 keV energy band. Above 10 keV, given the lack of narrow spectral features, we use a logarithmic step of ΔE/E = 0.001.
4.2. Applications – the case of NGC 424
We applied RXTorus to the broadband X-ray spectrum of NGC 424. This source was selected because, at a luminosity distance of d L = 45.6 Mpc, it is one of the closest CT AGN detected by Swift/BAT (Ricci et al. 2015) and observed by NuSTAR. We analyzed the XMM-Newton EPIC spectrum of the source using an 8.2 ks observation (ID 0002942301, PI M. Guainazzi). The source was observed by NuSTAR for 15.5 ks (ID 60061007002) as a part of the campaign aimed at following up AGN detected by Swift/BAT. We reduced XMM-Newton (EPIC/PN, MOS1 and MOS2, Jansen et al. 2001) and NuSTAR FPMA/FPMB (Harrison et al. 2013) data following the standard guidelines7.
The spectral model we used consists in the RXTorus model, which takes into account absorbed continuum, scattered radiation, and fluorescent lines; two collisionally ionized plasmas (apec); and three Gaussian lines (zgauss). We took into account absorption by Galactic material using the tabs model (Wilms et al. 2000), fixing 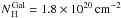 (Kalberla et al. 2005). To the models we also added a cross-calibration constant to take into account possible variability between the non-simultaneous XMM-Newton and NuSTAR observations. The addition of two apec components and three Gaussian lines significantly improved the fit.
(Kalberla et al. 2005). To the models we also added a cross-calibration constant to take into account possible variability between the non-simultaneous XMM-Newton and NuSTAR observations. The addition of two apec components and three Gaussian lines significantly improved the fit.
We first applied the non-atomic version of RXTorus, i.e.,
tabs Gal ×(atable{RXTorus.mod} + 3 × zgauss + 2 × apec).
This results in a good fit: χ2 = 203.3 for 205 degrees of freedom (D.O.F.). The two thermal plasmas have temperatures of 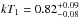 and
and 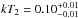 , while the lines have energies of
, while the lines have energies of 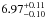 ,
, 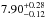 and
and 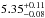 . The equivalent widths of the lines are
. The equivalent widths of the lines are 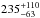 eV,
eV, 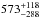 eV, and
eV, and 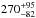 eV, respectively. In Fig. 12 we illustrate the contour plot of the inclination angle versus the ratio of the major to minor radius of the torus.
eV, respectively. In Fig. 12 we illustrate the contour plot of the inclination angle versus the ratio of the major to minor radius of the torus.
We then applied the atomic version of RXTorus, which also takes into account Rayleigh scattering, i.e.,
tabs Gal ×(atable{RXTorus_atom.mod} + 3 × zgauss + 2 × apec).
We find that this model can reproduce equally well the data (χ2/D.O.F. = 204.6/205). The temperatures of the apec components obtained are consistent with those we found using the non-atomic version of RXTorus: 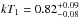 and
and 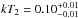 . Similarly, the three emission lines also yield consistent energies and equivalent widths:
. Similarly, the three emission lines also yield consistent energies and equivalent widths: 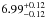 (
(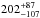 eV),
eV), 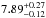 (
(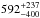 eV) and
eV) and 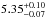 (
(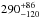 eV).
eV).
 |
Fig. 12 Contour plot of the inclination angle versus the ratio of the major to minor radius of the torus for the fit to the XMM-Newton and NuSTAR spectrum of NGC 424 carried out with the non-atomic RXTorus model. The cross indicates the best fit. The black, red and green lines show the Δχ2 = 2, 3, 4.61 and 9.21 contours respectively (corresponding to 68, 90 and 99% respectively) |
The results of the fits obtained with these two models are reported in Table 1. Both models find that the X-ray source of NGC 424 is heavily obscured and has a very soft primary X-ray emission, which is in agreement with previous studies carried out using NuSTAR data (Baloković et al. 2014; and Brightman et al. 2015). The values of the inclination angle and of log R/r obtained with the two models are significantly different. The fit carried out with the atomic model results in a lower value of the inclination angle and of the ratio of the minor to major axis of the torus (i.e. a larger covering factor). The hydrogen column density along the line of sight is also different in the two cases, with values of 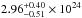 cm-2 and
cm-2 and 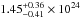 cm-2 in the non-atomic and atomic configurations respectively. The column densities found using RXTorus are lower than the values inferred using MYTorus (3 ± 1 × 1024 cm-2 for the reflecting material and >5 × 1024 cm-2 for the primary X-ray emission; Baloković et al. 2014) and BNTorus (
cm-2 in the non-atomic and atomic configurations respectively. The column densities found using RXTorus are lower than the values inferred using MYTorus (3 ± 1 × 1024 cm-2 for the reflecting material and >5 × 1024 cm-2 for the primary X-ray emission; Baloković et al. 2014) and BNTorus (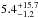 ; Brightman et al. 2015). The covering factors of the torus obtained, calculated using Eq. (3) are
; Brightman et al. 2015). The covering factors of the torus obtained, calculated using Eq. (3) are 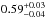 and
and 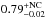 for the non-atomic and atomic model, respectively. These values are larger than those obtained using BNTorus by Brightman et al. (2015), who found a covering factor in the range 0.20−0.45.
for the non-atomic and atomic model, respectively. These values are larger than those obtained using BNTorus by Brightman et al. (2015), who found a covering factor in the range 0.20−0.45.
5. Conclusions
We have presented here RefleX, a new framework to self-consistently simulate absorption and reprocessed X-ray radiation in AGN for complex geometries, which we make publicly available. We showed the reliability of our approach by comparing the results of our simulations to existing X-ray spectral models. Contrarily to what has been commonly carried out in other models, RefleX implements two physical situations, namely the free-electron configuration where hydrogen and helium are completely ionized and all other electrons are ignored, and the atomic configuration where all atoms are neutral and Rayleigh scattering dominates over Compton scattering at low energies. The former configuration is used in pexmon (Nandra et al. 2007), MYTorus (Murphy & Yaqoob 2009), and BNTorus (Brightman & Nandra 2011), while the latter is consistent with Geant4-based models Liu & Li (2014) and MONACO (Odaka et al. 2011). Slight differences are observed with pexmon, which are probably due to the simplified treatment in this model. On the other hand, the MYTorus and BNTorus can be perfectly reproduced, with the exception that all fluorescent lines are included in RefleX, and that BNTorus is affected by a bug that overpredicts the transmission at low energy, which is an effect already noted by Liu & Li (2015). Unfortunately, we cannot make a detailed comparison with either the Liu & Li (2014) model or MONACO, but we point out that the cross-sections used in these models differ from those used in the other models, which are taken from Verner & Yakovlev (1995) and Verner et al. (1996); in particular edge energies are found to differ by more than 20 eV in some cases, which will be easily observed by X-ray micro-calorimeters such as the one on a possible successor to Hitomi or the Athena X-IFU (Barret et al. 2016).
The issue of the choice of the physical configuration is not straightforward, since we expect that hydrogen and helium will be ionized in an accretion disk, but that the distant molecular torus is essentially neutral. RefleX offers the possibility to select the most suitable configuration for each object, allowing for instance the simulation of reflection on a warm accretion disk with free electrons surrounded by a cold molecular torus with bound electrons.
We introduce here the RXTorus model, which we release publicly. RXTorus is similar to the MYTorus (Murphy & Yaqoob 2009) geometry, except that it allows a varying covering factor of the torus. In addition, both the free-electron and the atomic configurations can be selected. The model is distributed in three tables, i.e., absorbed continuum, scattered emission, and fluorescent lines, to allow greater flexibility. This is the first torus model with a varying covering factor that can be decomposed in several components. Our calculations are performed with a spectral resolution of 2 eV below 10 keV and allow us to use different abundances of the circumnuclear material. We applied this new model to reproduce the XMM-Newton and NuSTAR spectra of the CT AGN NGC 424, and discussed the results obtained with or without considering Rayleigh scattering.
In the future, we will release new models corresponding to different geometrical situations, such as, for example, a clumpy torus model.
Available at http://www.mytorus.com/
The RefleX models are available at http://www.astro.unige.ch/reflex
See Ricci et al. (2016) for details on the data reduction procedure adopted.
Acknowledgments
C.R. acknowledges financial support from FONDECYT 1141218, Basal-CATA PFB–06/2007 and from the China-CONICYT fund.
References
- Agostinelli, S., Allison, J., Amako, K., et al. 2003, Nucl. Instr.. Meth., 506, 250 [Google Scholar]
- Allison, J., Amako, K., Apostolakis, J., et al. 2006, IEEE Trans. Nucl. Sci., 53, 270 [Google Scholar]
- Anders, E., & Ebihara, M. 1982, Geochim. Cosmochim. Acta, 46, 2363 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, Astron. Data Anal. Softw. Syst. V, ASP Conf. Ser., 101, 17 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baloković, M., Comastri, A., Harrison, F. A., et al. 2014, ApJ, 794, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Balucinska-Church, M., & McCammon, D. 1992, ApJ, 400, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Lam Trong, T., den Herder, J.-W., et al. 2016, in Sp. Telesc. Instrum. 2016 Ultrav. to Gamma Ray, eds. J.-W. A. den Herder, T. Takahashi, & M. Bautz (International Society for Optics and Photonics), 99052F [Google Scholar]
- Baskin, A., & Laor, A. 2005, MNRAS, 358, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Bearden, J. A. 1967, Rev. Mod. Phys., 39, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Brightman, M., & Nandra, K. 2011, MNRAS, 413, 1206 [CrossRef] [Google Scholar]
- Brightman, M., Balokovic, M., Stern, D., et al. 2015, ApJ, 805, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Cullen, D., Perkins, S., & Rathkopf, J. 1990, The 1989 Livermore Evaluated Photon Data Library (EPDL), Technical Report No. UCRL-ID-103424 (University of California Radiation Laboratory) [Google Scholar]
- Fabian, A. C., Zoghbi, A., Ross, R. R., et al. 2009, Nature, 459, 540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feldman, U. 1992, Phys. Scr., 46, 202 [CrossRef] [Google Scholar]
- Furui, S., Fukazawa, Y., Odaka, H., et al. 2016, ApJ, 818, 164 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Goulding, A. D., Alexander, D. M., Bauer, F. E., et al. 2012, ApJ, 755, 5 [Google Scholar]
- Grevesse, N., & Sauval, A. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hitomi Collaboration, H., Aharonian, F., Akamatsu, H., et al. 2016, Nature, 535, 117 [Google Scholar]
- Hubbell, J. H., Veigele, W. J., Briggs, E. A., et al. 1975, J. Phys. Chem. Ref. Data, 4, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, S., Awaki, H., & Terashima, Y. 2009, ApJ, 692, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., & Li, X. 2014, ApJ, 787, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., & Li, X. 2015, MNRAS, 57, 53 [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G. 2002, MNRAS, 337, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Feroci, M., Rapisarda, M., & Costa, E. 1996, Radiat. Phys. Chem., 48, 403 [Google Scholar]
- Mitsuda, K., Kelley, R. L., Akamatsu, H., et al. 2014, Proc. SPIE 9144, eds. T. Takahashi, J.-W. A. den Herder, & M. Bautz, 91442A [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Mushotzky, R. F., Serlemitsos, P., Boldt, E. A., Holt, S. S., & Becker, R. H. 1978, ApJ, 220, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., & George, I. M. 1994, MNRAS, 267, 974 [NASA ADS] [Google Scholar]
- Nandra, K., Pounds, K. A., Stewart, G. C., Fabian, A. C., & Rees, M. J. 1989, MNRAS, 236, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., O’Neill, P., George, I., & Reeves, J. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Odaka, H., Aharonian, F., Watanabe, S., et al. 2011, ApJ, 740, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Nandra, K., Stewart, G. C., & Leighly, K. 1989, MNRAS, 240, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K., Nandra, K., Stewart, G., George, I., & Fabian, A. 1990, Nature, 344, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Ueda, Y., Koss, M. J., et al. 2015, ApJ, 815, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Bauer, F. E., Treister, E., et al. 2016, ApJ, 819, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Soffitta, P., Barcons, X., Bellazzini, R., et al. 2013, Exp. Astron., 36, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2014, in Proc. SPIE 9144, eds. T. Takahashi, J.-W. A. den Herder, & M. Bautz, 914425 [Google Scholar]
- Thompson, A., Attwood, D., Gullikson, E., et al. 2009, X-ray Data Booklet, LBNL-PUB49 (Lawrence Berkeley National Laboratory) [Google Scholar]
- Turner, T. J., George, I. M., Nandra, K., & Mushotzky, R. F. 1997, ApJS, 113, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, W., Liu, Z., Gou, L., & Liu, J. 2015, MNRAS, 455, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, M., Sadeghpour, H. R., & Dalgarno, A. 1998, ApJ, 496, 1044 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: K-shell (1s1/2) Fluorescence lines implemented in RefleX
List of K-shell (1s1/2) fluorescence lines implemented in RefleX.
All Tables
Results obtained by fitting the XMM-Newton and NuSTAR spectra of NGC 424 with the non-atomic and atomic version of RXTorus.
All Figures
 |
Fig. 1 Geometry of the pexrav/pexmon model. The reflector is the blue plane. The source of X-ray photons is the magenta plane, parallel to the reflector. The inclination angle i is defined as the angle between the normal to the planes and the observer. The stars illustrate that primary photons are emitted isotropically anywhere in the source plane. Half of the primary photons leave the system without hitting the reflector. |
| In the text | |
 |
Fig. 2 Comparison between pexmon and our RefleX simulations assuming the geometry of Fig. 1 for three viewing angles. Top: i = 10 deg; middle: i = 30 deg; and bottom: i = 60 deg. In each panel, the top subplot shows the pexmon model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. In all cases, the primary continuum is defined as a cutoff power law starting at 1 keV with an index Γ = 1.5 and a cutoff energy at 100 keV. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
| In the text | |
 |
Fig. 3 Comparison between pexmon and our RefleX simulations assuming the geometry of Fig. 1 for i = 30 deg, limited to the 6–7.6 keV region. The top subplot shows the pexmon model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. The primary continuum is the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Geometry of the MYTorus model. The reflector is a torus, whose section is shown in blue. The source of X-ray photons is the magenta star in the center, which is isotropic. The inclination angle i is defined as the angle between the normal to the plane of the torus and the observer. In the MYTorus model, the ratio between the major and minor radii of the torus, R/r, is 2, leading to a half opening angle φ = 60 deg. |
| In the text | |
 |
Fig. 5 Comparison between MYTorus and our simulations assuming the geometry of Fig. 4 for two viewing angles and two equatorial column densities. For both models we show only reprocessed radiation. Top: i = 30 deg; bottom: i = 75 deg. Left: NH,eq = 1022 cm-2; right: NH,eq = 1024 cm-2. In each panel, the top subplot shows the MYTorus model (black line) and our simulations (crosses); the bottom subplot shows the ratio between our simulations and the MYTorus model. In all cases, the primary continuum is defined as a power law between 1 and 500 keV with a photon index Γ = 1.9. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
| In the text | |
 |
Fig. 6 Comparison between MYTorus and our simulations for i = 75 deg and NH,eq = 1024 cm-2, limited to the 6–7.5 keV region. The MYTorus model is shown with a black line and our simulation is shown with a red line. The primary continuum is the same as in Fig. 5. |
| In the text | |
 |
Fig. 7 Comparison between MYTorus and our simulations assuming the geometry of Fig. 4 for two viewing angles and two equatorial column densities taking into account the cross-sections for bound electrons. For both models we show only reprocessed radiation. Top: i = 30 deg; bottom: i = 75 deg. Left: NH,eq = 1022 cm-2; right: NH,eq = 1024 cm-2. In each panel, the top subplot shows the MYTorus model (black line) and our simulations (crosses); the bottom subplot shows the ratio between our simulations and the pexmon model. In all cases, the primary continuum is defined as a power law starting at 1 keV with a photon index Γ = 1.9. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
| In the text | |
 |
Fig. 8 Spherical-toroidal geometry of the BNTorus model of Brightman & Nandra (2011; left). The reflector is a sphere with a conical opening of angle φ, whose section is shown in blue. The source of X-ray photons is the magenta star in the center, which is isotropic. The inclination angle i is defined as the angle between the normal to the plane of the torus and the observer. In RefleX, we model this shape by superimposing a number of annuli (right) that approximate the spherical-toroidal geometry. |
| In the text | |
 |
Fig. 9 Comparison between the spherical-toroidal geometry and our RefleX simulations assuming the BNTorus geometry (Fig. 8) for two viewing angles and an half-opening angle of θ OA = 30 deg. Top: i = 20 deg; bottom: i = 87 deg. In each panel, the top subplot shows the spherical-toroidal model (solid line) and the RefleX simulation (crosses); the bottom subplot shows the ratio between our simulations and the spherical-toroidal model. In all cases, the primary continuum is defined as a power law starting at 1 keV with an index Γ = 1.9 up to 500 keV. The equatorial column density is NH,eq = 1024 cm-2. The BNTorus model has been approximated using 51 annuli in RefleX. Spectra are averaged over 2 deg in inclination. 1010 photons were generated. |
| In the text | |
 |
Fig. 10 Spectrum of an absorbed power law simulated with the Geant4-based model of Liu & Li (2014) compared with the xspec model phabs; NH was set to 5 × 1022 cm-2. The figure shows that the absorption edges are clearly at different energies. |
| In the text | |
 |
Fig. 11 NuSTAR and XMM-Newton spectrum of NGC 424 fitted with the non-atomic (left panel) and atomic (right panel) version of RXTorus. The spectral parameters obtained are reported in Table 1. |
| In the text | |
 |
Fig. 12 Contour plot of the inclination angle versus the ratio of the major to minor radius of the torus for the fit to the XMM-Newton and NuSTAR spectrum of NGC 424 carried out with the non-atomic RXTorus model. The cross indicates the best fit. The black, red and green lines show the Δχ2 = 2, 3, 4.61 and 9.21 contours respectively (corresponding to 68, 90 and 99% respectively) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


