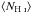| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731666 | |
| Published online | 09 October 2017 | |
The potential of tracing the star formation history with H I 21-cm in intervening absorption systems
School of Chemical and Physical Sciences, Victoria University of Wellington, PO Box 600, Wellington 6140, New Zealand
e-mail: Stephen.Curran@vuw.ac.nz
Received: 28 July 2017
Accepted: 9 August 2017
Unlike the neutral gas density, which remains largely constant over redshifts of 0 ≲ z ≲ 5, the star formation density, ψ∗, exhibits a strong redshift dependence, increasing from the present day before peaking at a redshift of z ≈ 2.5. Thus, there is a stark contrast between the star formation rate and the abundance of raw material available to fuel it. However, using the ratio of the strength of the H i 21-cm absorption to the total neutral gas column density to quantify the spin temperature, Tspin, of the gas, it has recently been shown that 1 /Tspin may trace ψ∗. This would be expected on the grounds that the cloud of gas must be sufficiently cool to collapse under its own gravity. This, however, relies on very limited data and so here we explore the potential of applying the above method to absorbers for which individual column densities are not available (primarily Mg ii absorption systems). By using the mean value as a proxy to the column density of the gas at a given redshift, we do, again, find that 1 /Tspin (degenerate with the absorber-emitter size ratio) traces ψ∗. If confirmed by higher redshift data, this could offer a powerful tool for future surveys for cool gas throughout the Universe with the Square Kilometre Array.
Key words: galaxies: high-redshift / galaxies: star formation / Galaxy: evolution / galaxies: ISM / quasars: absorption lines / radio lines: galaxies
© ESO, 2017
1. Introduction
Neutral hydrogen (H i), the reservoir for star formation, is traced in the distant Universe through 21-cm and Lyman-α absorption by galaxies intervening the sight-line to more distant radio and optical/UV continuum sources (e.g. Wolfe et al. 2005). The majority of this neutral gas (constituting up to 80% of the total in the Universe, Prochaska et al. 2005) arises in the so-called damped Lyman-α absorption systems (DLAs), defined to have neutral hydrogen column densities of NH i ≥ 2 × 1020cm-2.
Since the Lyman-α transition occurs in the ultra-violet band (λ = 1216 Å), the majority of DLAs are detected at redshifts of zabs ≳ 1.7 (e.g. Noterdaeme et al. 2012), where the transition is shifted into the optical band. In addition to space-based observations of the Lyman-α transition (e.g. Rao et al. 2017), the presence of neutral hydrogen at lower redshifts is evident through 21-cm emission studies (currently limited to z ≲ 0.4, Fernández et al. 2016) and may be inferred from the absorption of Mg ii (e.g. Rao et al. 2006), or other low ionised metal species (e.g. Dutta et al. 2017b) which can be observed from the ground. Other intervening absorption systems not detected in the optical band have been identified through 21-cm and millimetre band molecular absorption (Carilli et al. 1993; Lovell et al. 1996; Chengalur et al. 1999; Kanekar & Briggs 2003; Curran et al. 2007a; Allison et al. 2017). In these cases, the redshifts are generally too low (currently limited to zabs ≤ 0.96, Curran et al. 2007a) and the background continuum sources too optically faint/reddened to yield a Lyman-α detection (Curran et al. 2004, 2006).
From observations of H i 21-cm emission and Lyman-α absorption, both of which give the total neutral hydrogen column density, the neutral gas mass density of the Universe has been mapped from the present day to redshifts of z ~ 5 (look-back times of 12.5 Gyr). This has a value relative to the critical density of ΩHI ≈ 0.5 × 10-3 at z ≲ 0.5 (Zwaan et al. 2005; Lah et al. 2007; Braun 2012; Delhaize et al. 2013; Rhee et al. 2013; Hoppmann et al. 2015; Neeleman et al. 2016), rising to ΩHI ≈ 1 × 10-3 at z ~ 0.5, where it remains nearly constant over the observed 0.5 ≲ z ≲ 5 (Rao & Turnshe 2000; Prochaska & Herbert-Fort 2004; Rao et al. 2006; Curran 2010; Prochaska & Wolfe 2009; Noterdaeme et al. 2012; Crighton et al. 2015). Furthermore, the inflow of neutral gas, from within the galaxy or from the intergalactic medium, which may feed fuel to the star formation sites (Michałowski et al. 2015), also exhibits a near constancy with redshift (Spring & Michałowski 2017). This unchanging abundance of neutral gas is in stark contrast to the steep evolution of the star formation density, which exhibits a climb, before peaking at z ~ 3, followed by a decrease at higher redshift (Hopkins & Beacom 2006; Burgarella et al. 2013; Sobral et al. 2013; Lagos et al. 2014; Madau & Dickinson 2014; Zwart et al. 2014).
Thus, there is a clear discrepancy between the star formation history and the reservoir of star forming material (e.g. Lagos et al. 2014). Recently, however, by normalising the strength of the H i 21-cm absorption (which traces the cold component of the gas) by the column density (which traces all of the neutral gas), Curran (2017) found evidence for a similarity between the fraction of cool gas and the star formation density. Although this is physically motivated, as star formation requires cold, dense, neutral gas (e.g. Michałowski et al. 2015), the presence of which is evident from large molecular abundances (e.g. Carilli & Walter 2013), the sample contains only 74 confirmed DLAs and sub-DLAs which have been searched in 21-cm absorption. The connection between the cold gas fraction and the star formation density is based primarily on both peaks occuring at a similar redshift with a common factor of ~10 over the z = 0 value. Given the difficulties in obtaining a large sample of DLAs which exhibit 21-cm absorption1, a significantly larger sample may not be available until the science operations of the Square Kilometre Array, or at least its pathfinders (which are generally limited to zabs ≲ 1, e.g. Allison et al. 2016a; Maccagni et al. 2017). In the meantime, there are a further 176 intervening absorption systems which have been searched in H i 21-cm absorption. Adding these to the sample increases its size by a factor of 3.5. In this paper, we explore the potential of using these systems to provide a measure of the cold gas fraction and how this compares to the star formation history, with the view to future surveys with the next generation of large radio telescopes.
2. Analysis
2.1. Line strengths of the intervening H I 21-cm absorbers
The total neutral atomic hydrogen column density, NHI [cm-2], is related to the velocity integrated optical depth of the H i 21-cm absorption via 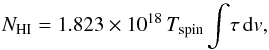 (1)where the harmonic mean spin temperature, Tspin, is a measure of the population of the lower hyperfine level (F = 1), where the gas can absorb 21-cm photons (Purcell & Field 1956), relative to the upper hyperfine level (F = 2). Comparison of the 21-cm line strength with the total column density, from Lyman-α absorption along the same sight-line, therefore provides a thermometer, where Tspin ∝ NH i/∫τ dv.
(1)where the harmonic mean spin temperature, Tspin, is a measure of the population of the lower hyperfine level (F = 1), where the gas can absorb 21-cm photons (Purcell & Field 1956), relative to the upper hyperfine level (F = 2). Comparison of the 21-cm line strength with the total column density, from Lyman-α absorption along the same sight-line, therefore provides a thermometer, where Tspin ∝ NH i/∫τ dv.
However, we cannot measure ∫τ dv directly, since the observed optical depth, which is ratio of the line depth, ΔS, to the observed background flux, Sobs, is related to the intrinsic optical depth via 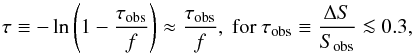 (2)where the covering factor, f, is the fraction of Sobs intercepted by the absorber. Therefore, in the optically thin regime (where τobs ≲ 0.3), Eq. (1) can be approximated as
(2)where the covering factor, f, is the fraction of Sobs intercepted by the absorber. Therefore, in the optically thin regime (where τobs ≲ 0.3), Eq. (1) can be approximated as 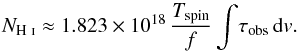 (3)So in order to measure the temperature, we require the velocity integrated optical depth of the 21-cm absorption profile (as well as the total neutral hydrogen column density, discussed in Sect. 3.1).
(3)So in order to measure the temperature, we require the velocity integrated optical depth of the 21-cm absorption profile (as well as the total neutral hydrogen column density, discussed in Sect. 3.1).
For this study we compiled all of the published searches for redshifted intervening H i 21-cm absorption towards Quasi-Stellar Objects (QSOs)2. This comprised 250 absorption systems, 74 of which have measured neutral hydrogen column densities (i.e. DLAs or sub-DLAs), with the remaining 176 consisting of 167 Mg ii absorbers and nine detected through other methods (such as 21-cm spectral scans, Brown & Roberts 1973). For each of these the observed parameters; velocity integrated optical depth, rms noise limit, flux density at the redshifted 21-cm frequency3, full-width half maximum (FWHM) of the profile and the observed spectral resolution were obtained from the compiled literature.
 |
Fig. 1 Distribution of spectral resolution (for the non-detections, unfilled histogram) and the line-widths (for the detections, filled histogram). The non-detections span a range of 0.29−30 km s-1, which are too disparate to show clearly on a linear scale. |
As discussed in Curran (2017), in order to compare the 21-cm absorption results consistently, it is necessary to normalise the sensitives. Since the spectral resolutions span a large range of values (Fig. 1), we re-sample the rms noise levels to a common channel width, which is then used as FWHM of the putative absorption profile. The detections have a mean profile width of ⟨FWHM⟩ = 45 km s-1, which we use to recalculate the 3σ upper limit to the integrated optical depth for each non-detection, i.e. 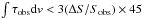 km s-1 (cf. Eq. (2))4. Since there is no evolution in the FWHM of the intervening absorbers detected in 21-cm (Curran et al. 2016a), we do not consider any redshift dependence.
km s-1 (cf. Eq. (2))4. Since there is no evolution in the FWHM of the intervening absorbers detected in 21-cm (Curran et al. 2016a), we do not consider any redshift dependence.
 |
Fig. 2 Velocity integrated optical depth versus the redshift for the intervening absorbers searched in H i 21-cm. The filled symbols show the detections and the unfilled circles the 3σ upper limits, with the shape representing the transition in which the absorption was initially detected: circles – Mg ii, stars – Lyman-α, squares – other (e.g. 21-cm scan). The bottom panel shows the binned values in equally sized bins (10 bins of 25), including the limits, where the horizontal error bars show the range of points in the bin and the vertical error bars the 1σ uncertainty in the mean value. |
Using these and the values quoted in the literature for the detections, in Fig. 2 we show the distribution of the velocity integrated optical depth of the absorption versus the redshift. In the bottom panel, the upper limits are included in the binning as censored data points, via the Astronomy SURVival Analysis (asurv) package (Isobe et al. 1986). The points are binned via the Kaplan-Meier estimator, giving the maximum-likelihood estimate based upon the parent population (Feigelson & Nelson 1985), from which we see no overwhelming bias in the survey sensitivity between the Mg ii absorbers and DLAs.
2.2. The spin temperature/covering factor degeneracy
Since only two of the detections exhibit optically thick (τobs> 0.3) absorption, we can, in principle, use Eq. (3) to determine the spin temperature of the gas. These two absorbers have peak optical depths of τobs ≈ 0.40 (zabs = 1.3265 towards J0850+5159) and τobs ≈ 0.55 (zabs = 1.3603 towards FBQS J2340–0053, Gupta et al. 2009b), Fig. 3, and so the range of possible intrinsic optical depths are τ = 0.40−0.51 and τ = 0.55−0.80, respectively (since τobs < f ≤ 1, O’Dea et al. 1994).
 |
Fig. 3 Variation of the observed optical depth with the intrinsic optical depth. The dotted lines show the maximum effect (where f = 1) on the two optically thick cases. |
Since 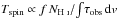 , we also require the covering factor to determine the spin temperature. However, without knowledge of the relative extents of the absorber-frame 1420 MHz absorption and emission cross-sections, nor the alignment between the absorber and the emitter, this is unknown. It will, however, exhibit a strong redshift dependence (Curran & Webb 2006): in the small angle approximation, this is given by
, we also require the covering factor to determine the spin temperature. However, without knowledge of the relative extents of the absorber-frame 1420 MHz absorption and emission cross-sections, nor the alignment between the absorber and the emitter, this is unknown. It will, however, exhibit a strong redshift dependence (Curran & Webb 2006): in the small angle approximation, this is given by 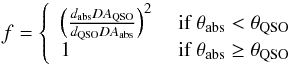 (4)(see Curran 2012; Allison et al. 2016b), where the angular diameter distance to a source is
(4)(see Curran 2012; Allison et al. 2016b), where the angular diameter distance to a source is 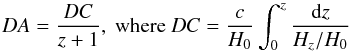 (5)is the line-of-sight co-moving distance (e.g. Peacock 1999), in which c is the speed of light, H0 the Hubble constant and Hz the Hubble parameter at redshift z, given by
(5)is the line-of-sight co-moving distance (e.g. Peacock 1999), in which c is the speed of light, H0 the Hubble constant and Hz the Hubble parameter at redshift z, given by 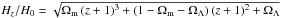 . For a standard Λ cosmology with H0 = 71 km s-1 Mpc-1, Ωmatter = 0.27 and ΩΛ = 0.73, this gives a peak in the angular diameter distance at z ≈ 1.6, which has the consequence that below this redshift DADLA ≪ DAQSO, as well as DADLA ~ DAQSO, is possible (when zabs ≪ zQSO), whereas above zabs ~ 1.6, only DADLA ~ DAQSO is possible. This leads a mix of angular diameter distance ratios (DAabs/DAQSO) at low redshift, but exclusively high values (DAabs/DAQSO ~ 1) at high redshift.
. For a standard Λ cosmology with H0 = 71 km s-1 Mpc-1, Ωmatter = 0.27 and ΩΛ = 0.73, this gives a peak in the angular diameter distance at z ≈ 1.6, which has the consequence that below this redshift DADLA ≪ DAQSO, as well as DADLA ~ DAQSO, is possible (when zabs ≪ zQSO), whereas above zabs ~ 1.6, only DADLA ~ DAQSO is possible. This leads a mix of angular diameter distance ratios (DAabs/DAQSO) at low redshift, but exclusively high values (DAabs/DAQSO ~ 1) at high redshift.
Although we have no information on the absorber/emitter extents nor the DLA–QSO alignment, we can at least account for this angular diameter bias, via (Eqs. (3) and (4), where θabs<θQSO) 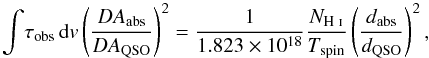 (6)the effect of which we show in Fig. 4. From the binned data there may be a peak in
(6)the effect of which we show in Fig. 4. From the binned data there may be a peak in 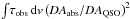 at zabs ~ 2, which is close to where the star formation density, ψ∗, peaks (z = 2.48, e.g. Hopkins & Beacom 2006). Since the ordinate is proportional to (NH i/Tspin)(dabs/dQSO)2, this could indicate a physical connection, with the abundance of cool gas peaking close to the maximum ψ∗, providing that there is no dominant evolution in dabs/dQSO. Without accounting for the column density, however, this only demonstrates a peak in the abundance of cold gas, rather than in its fraction.
at zabs ~ 2, which is close to where the star formation density, ψ∗, peaks (z = 2.48, e.g. Hopkins & Beacom 2006). Since the ordinate is proportional to (NH i/Tspin)(dabs/dQSO)2, this could indicate a physical connection, with the abundance of cool gas peaking close to the maximum ψ∗, providing that there is no dominant evolution in dabs/dQSO. Without accounting for the column density, however, this only demonstrates a peak in the abundance of cold gas, rather than in its fraction.
3. Evolution of the neutral gas
3.1. Neutral gas and star formation
Although for the Mg ii absorbers we do not know the individual NH i values, from the current 21-cm emission and Lyman-α absorption data we do know how the mean column density, 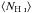 , evolves with redshift. We can obtain this from the evolution of the cosmological mass density (Fig. 5, top) via
, evolves with redshift. We can obtain this from the evolution of the cosmological mass density (Fig. 5, top) via 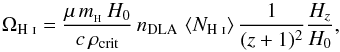 (7)where μ = 1.3 is a correction for the 75% hydrogen composition,
(7)where μ = 1.3 is a correction for the 75% hydrogen composition, 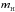 is the mass of the hydrogen atom,
is the mass of the hydrogen atom, 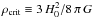 is the critical mass density of the Universe, where G is the gravitational constant, and nDLA = 0.027(zabs + 1)1.682 (Rao et al. 2017) is the redshift number density of DLAs.
is the critical mass density of the Universe, where G is the gravitational constant, and nDLA = 0.027(zabs + 1)1.682 (Rao et al. 2017) is the redshift number density of DLAs.
 |
Fig. 5 Best fit to the cosmological H i mass density of Crighton et al. (2017) [ΩH i = 4.0 × 10-4(zabs + 1)0.60 – dotted line, top panel] and the mean column density obtained from this (bottom panel). The abscissa is mapped to log 10(zabs + 1), in order to demonstrate the contrast between the evolution of NH i and the star formation density (Hopkins & Beacom 2006) [solid curve], where ψ∗ is arbitrarily shifted on the ordinate but retains the relative scaling (right hand scale). |
 |
Fig. 6 Reciprocal of the spin temperature degenerate with the ratio of the absorber/emitter extents (Eq. (6)). As per Fig. 5, the curve shows the best fit to the SFR density (Hopkins & Beacom 2006) arbitrarily shifted for comparison with the binned values of the top panel. |
We show the derived distribution of 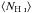 in Fig. 5 (bottom) and applying this to Eq. (6), we can obtain the mean evolution in (1 /Tspin)(dabs/dQSO)2. As per the DLAs, these appear to trace ψ∗, at least as far as the upper redshift limit of the absorbers (Fig. 6). Since actual column densities are available for the confirmed DLAs, which occupy the higher redshifts (Fig. 2), in Fig. 7 we also show the distribution using the measured column densities for the DLAs, as well as applying
in Fig. 5 (bottom) and applying this to Eq. (6), we can obtain the mean evolution in (1 /Tspin)(dabs/dQSO)2. As per the DLAs, these appear to trace ψ∗, at least as far as the upper redshift limit of the absorbers (Fig. 6). Since actual column densities are available for the confirmed DLAs, which occupy the higher redshifts (Fig. 2), in Fig. 7 we also show the distribution using the measured column densities for the DLAs, as well as applying 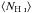 to the Mg ii absorbers alone. From this, we see that actual column densities are consistent with the mean values, although the uncertainties are larger because of the smaller numbers. From the bottom panel, we see that (1 /Tspin)(dabs/dQSO)2 for the Mg ii absorbers only also traces ψ∗, although the redshift range is more truncated (due to the zabs ≲ 2.2 limitation of ground-based Mg ii spectroscopy).
to the Mg ii absorbers alone. From this, we see that actual column densities are consistent with the mean values, although the uncertainties are larger because of the smaller numbers. From the bottom panel, we see that (1 /Tspin)(dabs/dQSO)2 for the Mg ii absorbers only also traces ψ∗, although the redshift range is more truncated (due to the zabs ≲ 2.2 limitation of ground-based Mg ii spectroscopy).
 |
Fig. 7 As Fig. 6, using the mean column density for all of the absorbers (top panel), only the Mgii absorbers normalised by |
 |
Fig. 8 SFR density normalised by (1 /Tspin)(dabs/dQSO)2. The hatching shows the region over which the error bars overlap, 439−457M⊙ yr-1 Mpc-3 K. |
In order to test the similarity between (1 /Tspin)(dabs/dQSO)2 and ψ∗, in Fig. 8 we show the SFR density normalised by the fraction of cool gas ![\begin{equation} \psi_{*}\left[\frac{1.823\times10^{18}}{\left<N_{\text{\HI}}\right>}\!\!\int\!\tau_{\rm obs}\,{\rm d}v \left(\frac{DA_{\rm abs}}{DA_{\rm QSO}}\right)^2\right]^{-1}\! \!=\! \psi_{*}T_{\rm spin}\left(\frac{d_{\rm QSO}}{d_{\rm abs}}\right)^2, \end{equation}](/articles/aa/full_html/2017/10/aa31666-17/aa31666-17-eq95.png) (8)from which the residuals are consistent with zero redshift evolution, within the ± 1σ uncertainties. This implies a direct correlation between these two quantities and the normalisation gives ψ∗Tspin ≈ 450(dabs/dQSO)2M⊙ yr-1 Mpc-3 K, for the dependence of the star formation density upon the spin temperature (see Sect. 3.2).
(8)from which the residuals are consistent with zero redshift evolution, within the ± 1σ uncertainties. This implies a direct correlation between these two quantities and the normalisation gives ψ∗Tspin ≈ 450(dabs/dQSO)2M⊙ yr-1 Mpc-3 K, for the dependence of the star formation density upon the spin temperature (see Sect. 3.2).
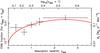 |
Fig. 9 Redshift evolution CNM fraction and the relative star formation density. |
3.2. Star formation and the fraction of cold neutral medium
Neutral gas in the interstellar medium is hypothesised to comprise two components (Field et al. 1969; Wolfire et al. 1995) – the cold neutral medium (CNM, where T ~ 150 K and n ~ 10cm-3) and the warm neutral medium (WNM, where T ~ 10 000 K and n ~ 0.2cm-3). The CNM fraction is derived from the CNM, WNM and spin temperatures, via ![\begin{equation} {\cal F}_{\rm CNM} \equiv{\left[{\frac{1}{T_{\rm spin}} - \frac{1}{T_{\rm WNM}}}\right]} \Bigg/ {\left[{\frac{1}{T_{\rm CNM}} - \frac{1}{T_{\rm WNM}}}\right]}, \end{equation}](/articles/aa/full_html/2017/10/aa31666-17/aa31666-17-eq103.png) (9)giving the distribution in Fig. 9. Again, there is a reasonable trace of the star formation density, although the values are low compared to those observed, specifically ℱCNM ≈ 0.3 in the Milky Way (Heiles & Troland 2003), zabs = 0.09 (Lane et al. 2000) and zabs = 0.22 (Kanekar et al. 2001b), getting as high as ℱCNM ≈ 0.8 at zabs ≈ 2 (Kanekar et al. 2014). The spin temperature we derive is, however, degenerate with the ratio of the absorber/emitter extents and gives CNM fractions similar to those observed if we apply ⟨dQSO⟩ = 4⟨dabs⟩ (Fig. 10). This ratio gives ψ∗Tspin ≈ 30M⊙ yr-1 Mpc -3 K (cf. Fig. 8) and so for a temperature of Tspin ≈ 300 K, we may expect a star formation density of ψ∗ ≈ 0.1M⊙ yr-1 Mpc -3. This is, of course, dependent on any evolution in dabs/dQSO, in addition to the assumption that the covering factor is generally less than unity (Eq. (4)).
(9)giving the distribution in Fig. 9. Again, there is a reasonable trace of the star formation density, although the values are low compared to those observed, specifically ℱCNM ≈ 0.3 in the Milky Way (Heiles & Troland 2003), zabs = 0.09 (Lane et al. 2000) and zabs = 0.22 (Kanekar et al. 2001b), getting as high as ℱCNM ≈ 0.8 at zabs ≈ 2 (Kanekar et al. 2014). The spin temperature we derive is, however, degenerate with the ratio of the absorber/emitter extents and gives CNM fractions similar to those observed if we apply ⟨dQSO⟩ = 4⟨dabs⟩ (Fig. 10). This ratio gives ψ∗Tspin ≈ 30M⊙ yr-1 Mpc -3 K (cf. Fig. 8) and so for a temperature of Tspin ≈ 300 K, we may expect a star formation density of ψ∗ ≈ 0.1M⊙ yr-1 Mpc -3. This is, of course, dependent on any evolution in dabs/dQSO, in addition to the assumption that the covering factor is generally less than unity (Eq. (4)).
With this assumption, dQSO/dabs is the only unknown in Eq. (4) and so we can use the estimate of the mean dQSO/dabs ratio to determine the evolution of the mean covering factor from DAabs < DAQSO/ 4, which applies to all of sample5. The mean covering factors derived are similar to those obtained from the Monte-Carlo simulation of Curran (2017) and the range of mean spin temperatures are consistent with those found in the Milky Way (Dickey et al. 2009) and other near-by galaxies (Curran et al. 2016b), Tspin ≈ 200−2000 K (Fig. 11). We reiterate, however, that this assumes a mean dQSO = 4dabs over all redshifts and a general covering factor of less than unity.
 |
Fig. 11 Estimated covering factor and spin temperature evolution, assuming f < 1 and dQSO = 4dabs. The curve shows 1 /ψ∗ (Hopkins & Beacom 2006), scaled according to ψ∗Tspin ≈ 450(dabs/dQSO)2M⊙ yr-1 Mpc-3 (Sect. 3.1). |
4. Possible caveats
4.1. Column density estimates
One motivation for this work is to investigate the potential of using the evolution of the mean column density to obtain Tspin/f from the 21-cm absorption strength, where individual column density measurements will not be practical. For example, the 150 000 sight-lines to be probed in the First Large Absorption Survey in H i (FLASH) on the Australian SKA Pathfinder (ASKAP, Allison et al. 2016a)6. Since no UV spectrometer is planned for the James Webb Space Telescope, this will be a particular problem for the zH i ≲ 1 limitation of the SKA pathfinders (e.g. Maccagni et al. 2017) upon the demise of the Hubble Space Telescope.
 |
Fig. 12 Estimated covering factor/spin temperature degeneracy (uncorrected for geometry), f/Tspin, obtained using |
From the similarities between the distributions in Fig. 7, it does appear that the estimated column densities are statistically consistent with the measured values. To test this, in Fig. 12 we show the distribution of the 21-cm line strength normalised by the mean column density, 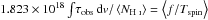 (Eq. (3)). This bears a close resemblance to the f/Tspin distribution for DLAs (Curran 2017), where there is also a flattening of the distribution at low redshift. In Fig. 13, we show the effect that the estimated column density has on the confirmed DLAs and sub-DLAs searched in 21-cm absorption. Although there is considerable spread, this small sample exhibits a strong correlation. This, and the similarity of Fig. 12 to the DLA distribution, gives us confidence in the application of this method to obtain a statistical estimate of the column density at a given redshift.
(Eq. (3)). This bears a close resemblance to the f/Tspin distribution for DLAs (Curran 2017), where there is also a flattening of the distribution at low redshift. In Fig. 13, we show the effect that the estimated column density has on the confirmed DLAs and sub-DLAs searched in 21-cm absorption. Although there is considerable spread, this small sample exhibits a strong correlation. This, and the similarity of Fig. 12 to the DLA distribution, gives us confidence in the application of this method to obtain a statistical estimate of the column density at a given redshift.
 |
Fig. 13 Actual covering factor/spin temperature degeneracy (see Curran 2017) in comparison to the estimated values (Fig. 12). The line has a gradient of unity and zero intercept. A Kendall-tau test, including the limits, gives a probability P(τ) = 2.27 × 10-10 of the observed distribution occuring by chance, which is significant at S(τ) = 6.34σ, assuming Gaussian statistics. |
 |
Fig. 14 Evolution of the angular diameter distance ratio with redshift. Again, the solid curve in the bottom panel shows the star formation density – redshift distribution from Hopkins & Beacom (2006). |
4.2. The correction for geometry effects
As previously stated, the above analysis assumes that there is no evolution in dabs/dQSO, in addition to any absorber-emitter misalignment and emitter structure being averaged out. As well as this, the covering factors are assumed to be generally less than unity. For f < 1, f ∝ (DAQSO/DAabs)2 (Eq. (4)), which we see, by the comparison of Figs. 2 and 4, is the dominant effect in giving the similarity in the redshift evolution (Fig. 12 cf. 14). Regarding this:
-
1.
This implies that ψ∗ ∝ (DAabs/DAQSO)2. Since the latter is purely due to geometry, there must be some more fundamental underlying parameter to which both parameters are related. This is most likely the redshift evolution which peaks at z = 2.5, compared to zabs = 1.6 for DAabs/DAQSO.
-
2.
Correcting the observed optical depth by the covering factor is necessary if f< 1 (Sect. 2.2). Although we have no information on the relative sizes nor the alignment, we do know that the geometry of the expanding Universe introduces a systematic difference in the possible values of DAabs/DAQSO between the low and high redshift regimes. Thus, this must be taken into account before before making any comparison between the low and high redshift optical depths.
-
3.
If unjustified, adding the “noise” of the 21-cm absorption strength (Fig. 12), should not improve the trace of the star formation density, otherwise this would be another coincidence on top of DAabs/DAQSO exhibiting a similar evolution as ψ∗. In fact, although larger uncertainties are introduced, the product
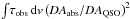 appears to “reign in” the outliers. Specifically, the systematic offset at zabs ≲ 2 and the absence of a zabs ≳ 3 downturn (Fig. 14 cf. 6), also present in the uncorrected data (Fig. 12). Note that an increase in the spin temperature at these redshifts is also advocated by Roy et al. (2013) and Kanekar et al. (2014).
appears to “reign in” the outliers. Specifically, the systematic offset at zabs ≲ 2 and the absence of a zabs ≳ 3 downturn (Fig. 14 cf. 6), also present in the uncorrected data (Fig. 12). Note that an increase in the spin temperature at these redshifts is also advocated by Roy et al. (2013) and Kanekar et al. (2014).
Provided that the assumptions are reasonable, the spin temperature shows a very similar evolution to the star formation density, which is diluted out by a similar evolution in the covering factor (Fig. 11), resulting in a flat distribution of 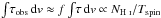 (Fig. 12). While further 21-cm observations of absorbers at low redshift will reduce the uncertainties introduced by
(Fig. 12). While further 21-cm observations of absorbers at low redshift will reduce the uncertainties introduced by 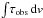 , observations at high redshift could be conclusive in determining whether
, observations at high redshift could be conclusive in determining whether 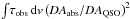 follows the downturn traced by ψ∗ (Fig. 15). As it stands, the top bin is consistent with the ratio of angular diameter distances for zQSO ≈ 3−4 and zabs ≳ 2.5, although we reiterate that a correction for the angular diameter distances is required in order to combine the low and high redshift populations. From the figure it is clear that further high redshift data, particularly at zabs ≳ 4, would be conclusive.
follows the downturn traced by ψ∗ (Fig. 15). As it stands, the top bin is consistent with the ratio of angular diameter distances for zQSO ≈ 3−4 and zabs ≳ 2.5, although we reiterate that a correction for the angular diameter distances is required in order to combine the low and high redshift populations. From the figure it is clear that further high redshift data, particularly at zabs ≳ 4, would be conclusive.
 |
Fig. 15 Star formation evolution (solid curve) and (1 /Tspin)(dabs/dQSO)2 (error bars, scaled by a factor of 450, Sect. 3.2) superimposed upon the ratio of angular diameter distances for various QSO redshifts (broken curves). These are shown for zQSO = 1,2,...,8 where the QSO redshift is given by the terminating value of the curve showing the absorption redshift distribution of (DAabs/DAQSO)2. |
5. Summary
It is an outstanding problem that the total neutral gas content of intervening absorbers does not trace the star formation density, ψ∗, which shows strong evolution with redshift. Recently, however, by using the ratio of the strength of the 21-cm absorption to the total column density as a thermometer, Curran (2017) showed that the cool component of the gas could trace ψ∗. This is physically motivated, since the star formation requires that the gas be sufficiently cool for the cloud to collapse under its own gravity, this cool gas usually being evident through large molecular abundances in the “giant molecular clouds” which host the cool gas. Indeed there may be similar correlation between the H2 density and ψ∗, at least up to z ~ 2 (Lagos et al. 2014, and references therein).
The H i data are, however, limited to a sample of 74 absorbers where both 21-cm absorption has been searched and the column density is known. By binning these in order to overcome individual line-of-sight effects, such as the absorber-QSO alignment, structure in the radio emission and situations where the covering factor may be unity, gives just three bins, which exhibit the same approximate peak at a similar relative magnitude as the star formation density (Curran 2017). Since 21-cm absorption searches of a significantly larger sample of DLAs will most likely have to wait for the Square kilometre Array, we examine the potential of using other intervening absorption systems, where the neutral hydrogen column density is not readily available (e.g. Mg ii absorbers), to trace the star formation history. In order to do this, we:
-
1.
Normalise the upper limits in the integrated optical depth to thesame spectral resolution and include these via a survival analysis,giving a sample total of 250 absorbers.
-
2.
Remove the bias introduced to the covering factor between the low and high redshift absorbers by the geometry effects of an expanding Universe. That is, correcting for the fact that absorbers at zabs ≳ 1.6 are always at a similar angular diameter distance as the background continuum source, whereas at lower redshift there is a mix of angular diameter distances.
-
3.
Assign a column density derived from the evolution of the cosmological H i density.
-
4.
Bin the data in order to average out differences in the individual line-of-sight effects.
This yields (1 /Tspin)(dabs/dQSO)2, which, as for the DLAs, appears to trace the star formation density. For no evolution in the ratio of the absorber–QSO sizes, this would imply that ψ∗ ∝ 1 /Tspin.
As is the case for the DLA-only sample, however, data is lacking at higher redshifts (zabs ≳ 3), meaning that we cannot be certain that (1 /Tspin)(dabs/dQSO)2 follows the same downturn as ψ∗ at look-back times beyond 11 Gyr. However, given that 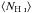 up to z ~ 5 is known, we may need only search for intervening 21-cm absorption. A non-reliance upon an optical spectrum would be advantageous to the next generation of radio band surveys, since optically selected surveys may miss the most dust reddened objects (Webster et al. 1995; Carilli et al. 1998; Curran et al. 2017). This does, however, depend upon the evolution in
up to z ~ 5 is known, we may need only search for intervening 21-cm absorption. A non-reliance upon an optical spectrum would be advantageous to the next generation of radio band surveys, since optically selected surveys may miss the most dust reddened objects (Webster et al. 1995; Carilli et al. 1998; Curran et al. 2017). This does, however, depend upon the evolution in 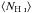 being applicable to the optically faint objects. In any case, follow-up observations of the many newly discovered 21-cm absorbers expected with the Square Kilometre Array (Morganti et al. 2015), with either 21-cm emission (limited to zabs ≲ 1, Staveley-Smith & Oosterloo 2015) or Lyman-α absorption (limited to zabs ≳ 1.7), will be very observationally expensive. Upon confirmation with further data, it is hoped that the methods presented here may offer a solution in determining the evolution of the cold gas fraction over large look-back times.
being applicable to the optically faint objects. In any case, follow-up observations of the many newly discovered 21-cm absorbers expected with the Square Kilometre Array (Morganti et al. 2015), with either 21-cm emission (limited to zabs ≲ 1, Staveley-Smith & Oosterloo 2015) or Lyman-α absorption (limited to zabs ≳ 1.7), will be very observationally expensive. Upon confirmation with further data, it is hoped that the methods presented here may offer a solution in determining the evolution of the cold gas fraction over large look-back times.
Given that the majority (≳80%, Curran et al. 2002) of background sources are “radio-quiet” (≲0.1 Jy for our purposes), the chances of finding a sufficiently strong source, where the absorption would occur in an available radio band, is low.
Davis & May (1978), Brown & Spencer (1979), Briggs & Wolfe (1983), Carilli et al. (1993), Lovell et al. (1996), Chengalur et al. (1999), Chengalur & Kanekar (2000), Lane (2000), Lane & Briggs (2001), Kanekar et al. (2001a,b, 2009, 2013, 2014), Briggs et al. (2001), Kanekar & Chengalur (2001, 2003), Kanekar & Briggs (2003), Darling et al. (2004), Curran et al. (2005, 2007a,b,c, 2010), York et al. (2007), Gupta et al. (2009a,b, 2012, 2013), Ellison et al. (2012), Srianand et al. (2012), Roy et al. (2013), Kanekar (2014), Zwaan et al. (2015), Dutta et al. (2017a,b).
For Lane (2000) the flux densities are not given and so we interpolated these from the neighbouring frequencies.
This resampling results in a scaling of 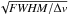 to the r.m.s. noise level, where Δv is the original resolution (Curran 2012).
to the r.m.s. noise level, where Δv is the original resolution (Curran 2012).
The largest ratio is from the zabs = 0.091 absorber towards the zQSO = 0.635 FBQS J074110.6+311200 (Lane et al. 2000), which has DAabs = 346 Mpc and DAQSO = 1413 Mpc, giving DAabs = 0.245DAQSO.
Given the absence of an optical spectrum from which to determine the nature of the absorber, other techniques, such as machine learning, may be able to distinguish whether the absorption is intervening or associated with the background continuum source (Curran et al. 2016a).
Acknowledgments
I would like to thank the anonymous referee for their helpful comments, as well as James Allison for useful comments on a draft of the manuscript. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration and NASA’s Astrophysics Data System Bibliographic Service. This research has also made use of NASA’s Astrophysics Data System Bibliographic Service and asurv Rev 1.2 (Lavalley et al. 1992), which implements the methods presented in Isobe et al. (1986).
References
- Allison, J. R., Sadler, E. M., Moss, V. A., et al. 2016a, Astron. Nachr., 337, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Allison, J. R., Zwaan, M. A., Duchesne, S. W., & Curran, S. J. 2016b, MNRAS, 462, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Allison, J. R., Moss, V. A., Macquart, J.-P., et al. 2017, MNRAS, 465, 4450 [Google Scholar]
- Braun, R. 2012, ApJ, 87, 749 [Google Scholar]
- Briggs, F. H., & Wolfe, A. M. 1983, ApJ, 268, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Briggs, F. H., de Bruyn, A. G., & Vermeulen, R. C. 2001, A&A, 373, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, R. L., & Roberts, M. S. 1973, ApJ, 184, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. L., & Spencer, R. E. 1979, ApJ, 230, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C. L., Rupen, M. P., & Yanny, B. 1993, ApJ, 412, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Menten, K. M., Reid, M. J., Rupen, M. P., & Yun, M. S. 1998, ApJ, 494, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Chengalur, J. N., & Kanekar, N. 2000, MNRAS, 318, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Chengalur, J. N., de Bruyn, A. G., & Narasimha, D. 1999, A&A, 343, L79 [NASA ADS] [Google Scholar]
- Crighton, N. H. M., Murphy, M. T., Prochaska, J. X., et al. 2015, MNRAS, 452, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Crighton, N. H. M., Murphy, M. T., Prochaska, J. X., et al. 2017, in Formation and Evolution of Galaxy Outskirts, eds. A. Gil de Paz, J. H. Knapen, & J. C. Lee, IAU Symp., 321, 309 [Google Scholar]
- Curran, S. J. 2010, MNRAS, 402, 2657 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J. 2012, ApJ, 748, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J. 2017, MNRAS, 470, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., & Webb, J. K. 2006, MNRAS, 371, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Webb, J. K., Murphy, M. T., et al. 2002, PASA, 19, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Murphy, M. T., Pihlström, Y. M., et al. 2004, MNRAS, 352, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Murphy, M. T., Pihlström, Y. M., Webb, J. K., & Purcell, C. R. 2005, MNRAS, 356, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Whiting, M. T., Murphy, M. T., et al. 2006, MNRAS, 371, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Darling, J. K., Bolatto, A. D., et al. 2007a, MNRAS, 382, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Tzanavaris, P., Murphy, M. T., Webb, J. K., & Pihlström, Y. M. 2007b, MNRAS, 381, L6 [NASA ADS] [Google Scholar]
- Curran, S. J., Tzanavaris, P., Pihlström, Y. M., & Webb, J. K. 2007c, MNRAS, 382, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Tzanavaris, P., Darling, J. K., et al. 2010, MNRAS, 402, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Duchesne, S. W., Divoli, A., & Allison, J. R. 2016a, MNRAS, 462, 4197 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Reeves, S. N., Allison, J. R., & Sadler, E. M. 2016b, MNRAS, 459, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. J., Whiting, M. T., Allison, J. R., et al. 2017, MNRAS, 467, 4514 [NASA ADS] [CrossRef] [Google Scholar]
- Darling, J., Giovanelli, R., Haynes, M. P., Bower, G. C., & Bolatto, A. D. 2004, ApJ, 613, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M. M., & May, L. S. 1978, ApJ, 219, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaize, J., Meyer, M. J., Staveley-Smith, L., & Boyle, B. J. 2013, MNRAS, 433, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., Strasser, S., Gaensler, B. M., et al. 2009, ApJ, 693, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, R., Srianand, R., Gupta, N., & Joshi, R. 2017a, MNRAS, 468, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, R., Srianand, R., Gupta, N., et al. 2017b, MNRAS, 465, 4249 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S., Kanekar, N., Prochaska, J. X., Momjian, E., & Worseck, G. 2012, MNRAS, 424, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, X., Gim, H. B., van Gorkom, J. H., et al. 2016, ApJ, 824, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., Srianand, R., Petitjean, P., Noterdaeme, P., & Saikia, D. J. 2009a, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 67 [Google Scholar]
- Gupta, N., Srianand, R., Petitjean, P., Noterdaeme, P., & Saikia, D. J. 2009b, MNRAS, 398, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., Srianand, R., Petitjean, P., et al. 2012, A&A, 544, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, N., Srianand, R., Noterdaeme, P., Petitjean, P., & Muzahid, S. 2013, A&A, 558, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hoppmann, L., Staveley-Smith, L., Freudling, W., et al. 2015, MNRAS, 452, 3726 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E., & Nelson, P. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N. 2014, ApJ, 797, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., & Briggs, F. H. 2003, A&A, 412, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., & Chengalur, J. N. 2001, A&A, 369, 42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., & Chengalur, J. N. 2003, A&A, 399, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., Chengalur, J. N., Subrahmanyan, R., & Petitjean, P. 2001a, A&A, 367, 46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., Ghosh, T., & Chengalur, J. N. 2001b, A&A, 373, 394 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., Prochaska, J. X., Ellison, S. L., & Chengalur, J. N. 2009, MNRAS, 396, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., Ellison, S. L., Momjian, E., York, B. A., & Pettini, M. 2013, MNRAS, 532 [Google Scholar]
- Kanekar, N., Prochaska, J. X., Smette, A., et al. 2014, MNRAS, 438, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Baugh, C. M., Zwaan, M. A., et al. 2014, MNRAS, 440, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Lah, P., Chengalur, J. N., Briggs, F. H., et al. 2007, MNRAS, 376, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, W. M. 2000, Ph.D. Thesis, University of Groningen [Google Scholar]
- Lane, W. M., & Briggs, F. H. 2001, ApJ, 561, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, W. M., Briggs, F. H., & Smette, A. 2000, ApJ, 532, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley, M. P., Isobe, T., & Feigelson, E. D. 1992, in BAAS, 24, 839 [Google Scholar]
- Lovell, J. E. J., Reynolds, J. E., Jauncey, D. L., et al. 1996, ApJ, 472, L5 [Google Scholar]
- Maccagni, F. M., Morganti, R., Oosterloo, T. A., Geréb, K., & Maddox, N. 2017, A&A, 604, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M. J., Gentile, G., Hjorth, J., et al. 2015, A&A, 582, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Sadler, E. M., & Curran, S. 2015, Adv. Astrophys. Square Kilometre Array (AASKA14), 134 [Google Scholar]
- Neeleman, M., Prochaska, J. X., Ribaudo, J., et al. 2016, ApJ, 818, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Carithers, W. C., et al. 2012, A&A, 547, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dea, C. P., Baum, S. A., & Gallimore, J. F. 1994, ApJ, 436, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1999, Cosmological Physics (Cambridge: Cambridge University Press) [Google Scholar]
- Prochaska, J. X., & Herbert-Fort, S. 2004, PASP, 116, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., & Wolfe, A. M. 2009, ApJ, 696, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Herbert-Fort, S., & Wolfe, A. M. 2005, ApJ, 635, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, E. M., & Field, G. B. 1956, ApJ, 124, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S. M., & Turnshek, D. A. 2000, ApJS, 130, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S., Turnshek, D., & Nestor, D. B. 2006, ApJ, 636, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S. M., Turnshek, D. A., Sardane, G. M., & Monier, E. M. 2017, MNRAS, 471, 3428 [NASA ADS] [CrossRef] [Google Scholar]
- Rhee, J., Zwaan, M. A., Briggs, F. H., et al. 2013, MNRAS, 435, 2693 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, N., Mathur, S., Gajjar, V., & Nath Patra, N. 2013, MNRAS, 436, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Spring, E. F., & Michałowski, M. J. 2017, MNRAS, 471, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Srianand, R., Gupta, N., Petitjean, P., et al. 2012, MNRAS, 421, 651 [NASA ADS] [Google Scholar]
- Staveley-Smith, L., & Oosterloo, T. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 167 [Google Scholar]
- Webster, R. L., Francis, P. J., Peterson, B. A., Drinkwater, M. J., & Masci, F. J. 1995, Nature, 375, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- York, B. A., Kanekar, N., Ellison, S. L., & Pettini, M. 2007, MNRAS, 382, L53 [NASA ADS] [Google Scholar]
- Zwaan, M. A., van der Hulst, J. M., Briggs, F. H., Verheijen, M. A. W., & Ryan-Weber, E. V. 2005, MNRAS, 364, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, M. A., Liske, J., Péroux, C., et al. 2015, MNRAS, 453, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Zwart, J. T. L., Jarvis, M. J., Deane, R. P., et al. 2014, MNRAS, 439, 1459 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Distribution of spectral resolution (for the non-detections, unfilled histogram) and the line-widths (for the detections, filled histogram). The non-detections span a range of 0.29−30 km s-1, which are too disparate to show clearly on a linear scale. |
| In the text | |
 |
Fig. 2 Velocity integrated optical depth versus the redshift for the intervening absorbers searched in H i 21-cm. The filled symbols show the detections and the unfilled circles the 3σ upper limits, with the shape representing the transition in which the absorption was initially detected: circles – Mg ii, stars – Lyman-α, squares – other (e.g. 21-cm scan). The bottom panel shows the binned values in equally sized bins (10 bins of 25), including the limits, where the horizontal error bars show the range of points in the bin and the vertical error bars the 1σ uncertainty in the mean value. |
| In the text | |
 |
Fig. 3 Variation of the observed optical depth with the intrinsic optical depth. The dotted lines show the maximum effect (where f = 1) on the two optically thick cases. |
| In the text | |
 |
Fig. 4 As Fig. 2, but corrected for the angular diameter distances (Eq. (6)). |
| In the text | |
 |
Fig. 5 Best fit to the cosmological H i mass density of Crighton et al. (2017) [ΩH i = 4.0 × 10-4(zabs + 1)0.60 – dotted line, top panel] and the mean column density obtained from this (bottom panel). The abscissa is mapped to log 10(zabs + 1), in order to demonstrate the contrast between the evolution of NH i and the star formation density (Hopkins & Beacom 2006) [solid curve], where ψ∗ is arbitrarily shifted on the ordinate but retains the relative scaling (right hand scale). |
| In the text | |
 |
Fig. 6 Reciprocal of the spin temperature degenerate with the ratio of the absorber/emitter extents (Eq. (6)). As per Fig. 5, the curve shows the best fit to the SFR density (Hopkins & Beacom 2006) arbitrarily shifted for comparison with the binned values of the top panel. |
| In the text | |
 |
Fig. 7 As Fig. 6, using the mean column density for all of the absorbers (top panel), only the Mgii absorbers normalised by |
| In the text | |
 |
Fig. 8 SFR density normalised by (1 /Tspin)(dabs/dQSO)2. The hatching shows the region over which the error bars overlap, 439−457M⊙ yr-1 Mpc-3 K. |
| In the text | |
 |
Fig. 9 Redshift evolution CNM fraction and the relative star formation density. |
| In the text | |
 |
Fig. 10 As per Fig. 9 but for dQSO = 4dabs. |
| In the text | |
 |
Fig. 11 Estimated covering factor and spin temperature evolution, assuming f < 1 and dQSO = 4dabs. The curve shows 1 /ψ∗ (Hopkins & Beacom 2006), scaled according to ψ∗Tspin ≈ 450(dabs/dQSO)2M⊙ yr-1 Mpc-3 (Sect. 3.1). |
| In the text | |
 |
Fig. 12 Estimated covering factor/spin temperature degeneracy (uncorrected for geometry), f/Tspin, obtained using |
| In the text | |
 |
Fig. 13 Actual covering factor/spin temperature degeneracy (see Curran 2017) in comparison to the estimated values (Fig. 12). The line has a gradient of unity and zero intercept. A Kendall-tau test, including the limits, gives a probability P(τ) = 2.27 × 10-10 of the observed distribution occuring by chance, which is significant at S(τ) = 6.34σ, assuming Gaussian statistics. |
| In the text | |
 |
Fig. 14 Evolution of the angular diameter distance ratio with redshift. Again, the solid curve in the bottom panel shows the star formation density – redshift distribution from Hopkins & Beacom (2006). |
| In the text | |
 |
Fig. 15 Star formation evolution (solid curve) and (1 /Tspin)(dabs/dQSO)2 (error bars, scaled by a factor of 450, Sect. 3.2) superimposed upon the ratio of angular diameter distances for various QSO redshifts (broken curves). These are shown for zQSO = 1,2,...,8 where the QSO redshift is given by the terminating value of the curve showing the absorption redshift distribution of (DAabs/DAQSO)2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.