EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A73 Full HTML
Free Access

This article has an erratum: [https://doi.org/10.1051/0004-6361/201731282e]

Issue
A&A
Volume 606, October 2017
Article Number A73
Number of page(s) 8
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201731282
Published online 13 October 2017

© ESO, 2017

1. Introduction

Since the discovery of the first exoplanet by Mayor & Queloz (1995) the number of new planets detected has been growing exponentially. First from ground-based radial velocity (Vogt et al. 2000; Valenti & Fischer 2005; Jenkins et al. 2009) and transit surveys (Bakos et al. 2004; Pollacco et al. 2006) and in recent years from the CoRoT and Kepler satellites (Barge et al. 2008; Borucki et al. 2010). Today, several thousand exoplanets are known and our understanding of the population has grown immensely. In particular, we now know that on average a late-type main-sequence star is orbited by at least one planet (Batalha 2014).

Despite these advances, observational biases mean we still know only a few planets transiting both bright and early-type stars. The Multi-site All-Sky CAmeRA (MASCARA; Talens et al. 2017) transit survey aims to fill this gap in parameter space by monitoring all stars with magnitudes 4 <mV< 8.4. MASCARA consists of a northern and a southern station, each equipped with five cameras to cover the entire local sky down to airmass 2 and partially down to airmass 3. In this way MASCARA is expected to find several new transiting hot Jupiters around bright stars, some of which will be of early spectral types (Snellen et al. 2012).

MASCARA was designed to find Jupiter-like planets transiting bright stars because these allow detailed atmospheric characterization. Observations of the planet transmission spectra during transit and thermal emission at secondary eclipse, coupled with detailed atmospheric models, can be used to constrain atmospheric properties such as temperature structure, composition, and the presence of clouds and hazes (Madhusudhan & Seager 2009; Sing et al. 2011, 2016; Deming et al. 2013; Kreidberg et al. 2014). Such observations, however, are expensive if not impossible on fainter stars. In particular, the use of high-resolution transmission spectroscopy has been limited to a few bright targets such as HD 209458 and HD 189733 (Snellen et al. 2010; Brogi et al. 2016), which were first discovered through radial velocity observations.

In addition to finding planets around bright stars, the all-sky, magnitude-limited sample targeted by MASCARA is biased towards early-type stars, which are particularly challenging to follow up at fainter magnitudes. Studying the hot Jupiter population around hot stars is interesting for several reasons. First, these hot Jupiters have the highest equilibrium temperatures, which is expected to have a significant impact on their atmospheric structure and composition, such as the occurrence of inversion layers due to the presence of specific molecular compounds (e.g. TiO/VO Hubeny et al. 2003; Fortney et al. 2008) high up in the atmospheres (e.g. Burrows et al. 2007; O’Donovan et al. 2010; but see also Schwarz et al. 2015). Second, hot Jupiters around early-type stars receive more UV radiation than similar planets around late-type stars. This UV radiation may drive unique chemical processes in the atmospheres of these planets (Casewell et al. 2015). Finally, comparing their orbital properties with those of hot Jupiters orbiting solar-type stars may shed light on their formation. For example, the large incidence of misaligned orbits for hot Jupiters orbiting early-type stars (Winn et al. 2010; Schlaufman 2010; Albrecht et al. 2012) may be linked to orbital migration processes (e.g. Fabrycky & Tremaine 2007; Nagasawa et al. 2008).

In this paper we present the discovery of MASCARA-1 b, which is the first exoplanet discovered by MASCARA. MASCARA-1 b orbits the mV = 8.3 A8 star HD 201585 with a period of 2.15 days. We present our observations in Sect. 2. Stellar and system parameters are described in Sects. 3 and 4, and we conclude with a discussion in Sect. 5.

2. Observations

The northern station of MASCARA, located on La Palma, started science operations in early 2015 and produces photometry for all stars with 4 <mV< 8.4 at a cadence of 6.4 s down to airmass ~3 (Talens et al. 2017). The raw MASCARA photometry is processed using a heavily modified version of the coarse decorrelation algorithm described in Collier Cameron et al. (2006) to remove instrumental systematics and Earth-atmospheric effects. Subsequently, the data are binned to a cadence of 320 s and further detrended by means of an empirical fit to remove both residual variations linked to the target positions on the CCDs and long-term trends in the data. Finally, a box least-squares (BLS; Kovács et al. 2002) transit search algorithm is used to find potential transit signals. The details of the data reduction and transit search algorithms will be discussed in an upcoming paper (Talens et al., in prep.).

After running the BLS algorithm on data taken between February and December 2015, MASCARA-1 (HD 201585, HIP 104513) was among the most promising stars to be listed as a potential exoplanet host. We obtained high-dispersion spectra at R = 85 000 from the HERMES spectograph (Raskin et al. 2011) at the 1.2 m Mercator telescope on La Palma taken between June and September 2016 (see Table 1). A total of 13 spectra were taken and reduced using the HERMES pipeline1, allowing us to characterize the host star and constrain the companion mass from radial velocity (RV) measurements.

In addition to the MASCARA photometry, two transits were observed with the 0.4 m NITES telescope (McCormac et al. 2014) on La Palma. 1092 images with 10 s exposure times were obtained with a Johnson-Bessel R-band filter on 23 July 2016 and 887 images with 15 s exposure times were obtained in the V-band on 17 September 2016. The telescope was defocused slightly on both nights to avoid saturation. The data were reduced in Python with CCDPROC (Craig et al. 2015) using a master bias, dark and flat. Master calibrations were made using a minimum of 21 of each frame. Non-variable comparison stars were selected by hand and aperture photometry was extracted using SEP (Barbary 2016; Bertin & Arnouts 1996). The shift between each defocused image was measured using the DONUTS (McCormac et al. 2013) algorithm and the photometry apertures were recentred between frames. The final aperture size is chosen to minimize the rms of the data points out of transit. The 0.66″ pixel scale of NITES versus 1′ for MASCARA allowed us to check against a faint eclipsing binary system within the MASCARA photometric aperture that could have explained the apparent transit signal.

Additional confirmation about the nature of the system, as well as a measurement of its spin-orbit angle, can come from a detection of the Rossiter-McLaughlin effect using in-transit spectroscopy (e.g. Zhou et al. 2016). We therefore obtained 28 high-dispersion echelle spectra at R ~ 90 000 using the automated 1 m Hertzsprung SONG telescope (Andersen et al. 2014) at Observatorio del Teide on 30 September 2016 (see Table 1). The observations were taken with 10 min exposure times and a slit width of 1.2 arcsec and spanned ~ 5 h in total, covering the transit and post-egress. Ingress occurred during evening twilight. Spectra were extracted from the observations following the procedure outlined in Grundahl et al. (2017), subsequently bad pixels were removed and the spectra were normalized.

Table 1

Observations used in the discovery of MASCARA-1 b.

3. Stellar parameters

At mV = 8.3, most basic properties of MASCARA-1 are available in the literature. The parallax was already measured by Hipparcos (van Leeuwen 2007) to be 5.0 ± 0.7 mas, implying a distance of 201.6 ± 28.9 pc. Recently, the Gaia DR1 (Gaia Collaboration 2016) lists a parallax of 5.3 ± 0.3 mas (188.7 ± 10.7 pc) within 1σ of the Hipparcos value. For our analysis we adopted the Gaia parallax.

Table 2

Transit model parameters and their best-fit values obtained from fits to the MASCARA data, NITES data, and the combined photometric data set.

McDonald et al. (2012) combined the Hipparcos parallaxes with photometry from a number of surveys, including SDSS and 2MASS, to determine the effective temperature and luminosity of over 100 000 stars, including MASCARA-1 for which they derive an effective temperature of 7554 K and a bolometric luminosity of 14.98 L⊙. We verified the effective temperature by fitting the wings of the hydrogen lines in the combined HERMES spectra with PHOENIX spectral models (Husser et al. 2013) and find Teff = 7600 ± 150 K, which is consistent with the work by McDonald et al. (2012). For our further analysis, we used the values as derived by McDonald et al. (2012), assuming uncertainties of 150 K and 5 L⊙ on Teff and L∗, respectively2; these uncertainties are not reported by the authors. We updated the luminosity for the new Gaia distance to be 13.1 ± 3.0 L⊙. From the bolometric luminosity and effective temperature, we derived a stellar radius of R∗ = 2.1 ± 0.2 R⊙. We used bagemass (Maxted et al. 2015), a stellar evolution MCMC code, to determine the stellar mass and age from the effective temperature, metallicity, and stellar density3, finding 1.72 ± 0.07 M⊙ and 1.0 ± 0.2 Gyr, respectively. As an extra check we also computed the stellar radius from the bagemass output and found a value of 1.97 ± 0.07 R⊙, which is consistent with the radius derived from the Gaia parallax.

From the HERMES radial velocity pipeline4 we also obtained the stellar equatorial rotation speed vsini⋆ = 106.7 ± 0.4 km s-1.

4. System parameters

The system parameters were derived from modelling the available photometric and spectroscopic observations. The transit shape was fitted via the available MASCARA and NITES photometric data. The mass of the planet was constrained with the HERMES radial velocity measurements and the projected spin-orbit angle was obtained from the SONG transit data.

4.1. Photometric transit fit

A Mandel & Agol (2002) model was fitted to the photometric data taken by MASCARA with a Markov-chain Monte Carlo (MCMC) approach with the Python packages batman and emcee (Kreidberg 2015; Foreman-Mackey et al. 2013). We fit a circular transit model, optimizing for the normalization F0, transit epoch Tp, orbital period P, transit duration T14, planet-to-star radius ratio p, and impact parameter b using uniform priors on all parameters. We employed a quadratic limb darkening law with fixed coefficients from Claret (2000), using values of u1 = 0.2609, u2 = 0.3405, appropriate for the host star. Subsequently, the NITES photometry was also fitted with the same model, except with the orbital period fixed to the best-fit value obtained from the MASCARA photometry and separate normalization factors F1 and F2 for each transit. In the modelling presented here we do not include the possible effects of non-spherical geometry, which can influence T14 and b, or gravity darkening, which can modify p. Both of these effects might play a role for a rapid rotator such as MASCARA-1. The best-fit parameter values and uncertainties, obtained from the median and the 16th and 84th percentiles of the output MCMC chains, are listed in Table 2.

thumbnail Fig. 1

Photometry and best-fit models used in the characterization of MASCARA-1 b. Panel a: MASCARA photometry obtained between February 2015 and September 2016. Shown are the 320 s cadence data (grey points), the data binned by 0.01 in phase (red points), and the best-fit transit model (black line). Panels b and c: NITES transit observations taken on 23 July 2016 and 17 September 2016, respectively. Shown are the data (grey points), the data binned by 0.01 in phase (red points), and the best-fit transit model (black line).

thumbnail Fig. 2

HERMES RV measurements of MASCARA-1 obtained from June to September 2016. Shown are the data (red points) and the best-fit model (black line). The high projected rotation speed of the star, vsini⋆ = 106.7 km s-1, results in relatively large uncertainties on the RV measurements of order 300 m s-1.

We found that all orbital parameters are consistent between the MASCARA and NITES data with exception of the planet-to-star ratio p, which takes the value of 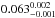0.063-0.0010.002\hbox{$0.063^{0.002}_{-0.001}$} for the MASCARA data and 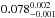0.078-0.0010.002\hbox{$0.078^{0.002}_{-0.001}$} for the NITES data. We considered the possibility that this difference in the value of p is a result of blended light in the MASCARA photometry, caused by the 1′ pixel scale of MASCARA, which would decrease the transit depth and thus the value of p. However, a simple calculation shows that we would need ~ 35% blended light in the MASCARA aperture, which is more than can be explained by the background sources present; we conservatively estimate these sources to contribute a maximum of ~ 20% of the total light. Another possibility comes from the algorithm used to process the MASCARA data, as we are still in the process of investigating possible systematic changes introduced by our methods.

To further investigate this discrepancy we performed a joint fit to the MASCARA and NITES photometry. The reduced chi-square value for the NITES fit indicates that we overestimated the uncertainties on the photometry; this is plausible since we assumed a conservative model for the scintillation noise, i.e. the dominant source of noise in the observations, when calculating the uncertainties. To ensure that we place a similar weight on both the MASCARA and NITES observations, we reduced the NITES uncertainties by a factor 2 for the joint fit. The results of the joint fit are shown in Fig. 1 and the parameters are listed in Table 2. From the joint fit we obtain p = 0.0735 ± 0.0007, which is significantly different from both the NITES and MASCARA values. Also, the lack of baseline in the NITES observations results in a lower normalization in the joint fit, helping to reduce any dicrepancy in the depths. We are unable at this time to explain this discrepancy and adopt a value of p = 0.07 ± 0.01, i.e. midway between and consistent with both the MASCARA and NITES values, for the derivation of the planet radius listed in Table 4.

4.2. Radial velocities and planet mass

We determined stellar radial velocities and their uncertainties from the HERMES spectra via the standard pipeline5, in which a mask of individual lines is cross-correlated with the data to obtain an average line profile. For the observations of MASCARA-1, the HermesF0Mask was used as it is closest to the spectral type of the star of the available masks. The average line profile was subsequently fitted with a rotationally broadened line profile, the dominant source of broadening, to obtain the radial velocities and their uncertainties. The obtained uncertainties are relatively large (~ 300 m s-1) because of the high equatorial rotation speed of the star. The epochs of the RV-data points are phase folded using the best-fit orbital solution derived from the photometry. A circular orbital solution was fitted to the data keeping the period and epoch fixed to the values derived above. The RV data and best-fit solution are shown in Fig. 2, and the best-fit parameters are listed in Table 3. The amplitude of the stellar radial velocity variation is not well constrained to K = 400 ± 100 m s-1, corresponding to a planet mass of Mp = 3.7 ± 0.9 Mjup.

4.3. Rossiter-McLaughlin effect and projected spin-orbit angle

To consolidate the confirmation of the planetary nature of the companion and determine the projection of the spin-orbit angle (obliquity), we observed the systems during a transit with the SONG telescope (see Sect. 2). Simple cross-correlation functions (CCFs) are created from the obtained spectra using a stellar template appropriate for MASCARA-16. The CCFs are shown in Fig. 3 panel A (top left).

To analyse the distortions of the stellar absorption lines and measure the projected obliquity (λ), we used the code presented in Albrecht et al. (2007), including updates presented in Albrecht et al. (2013). In short, we created a pixelated stellar disk in which each pixel is assigned a radial velocity based on stellar rotation, and micro- and macro-turbulence (see e.g. Gray 1984). Here the point spread function (PSF) of the spectrograph is included in the width of the Gaussian function representing the micro-turbulence. We did not include convective blueshift as the CCFs do not have a high enough S/N to constrain this parameter and in turn the influence on λ is small. The light contribution of each pixel in our model is governed by a quadratic limb darkening model. For each observation, a model stellar absorption line is created. During transit, the integration is carried out only over the surface not blocked by the companion. These model CCFs are then compared to the observed CCFs, taking into account shifts due to the orbital velocity.

Table 3

Model parameters used in fitting the RV and RM measurements and their best-fit values.

We ran an MCMC to obtain confidence intervals for λ and vsini⋆, the parameters of interest. For this we allowed the following parameters to vary: λ, vsini⋆, macro-turbulence (ζ), micro-turbulence (ν), transit epoch Tp, planet-to-star radius ratio p, scaled semi-major axis a/R∗, cosine of the orbital inclination cosi, stellar systemic velocity γSONG, stellar RV amplitude K, and limb darkening parameters u1 + u2. We used prior information from the photometric and RV observations for the parameters Tp, a/R∗, p, and K. We further used the prior information for the impact parameter b, and the transit duration T14 also derived from photometry (Table 2), 0.6 ± 0.1 for u1 + u2 (Claret et al. 2013), and uniform priors on all other parameters. Finally for each calculation of the likelihood we allowed each of the observed CCFs to be offset and scaled in intensity (see also Albrecht et al. 2013). This way we included the influence of the non-perfect normalization of the spectra into the uncertainty interval of the final parameters. A mismatch in the continuum normalization of the observed spectrum and the template spectrum causes an offset in the baseline of the obtained CCF. In addition, the size of the CCFs depends on the S/N of the spectra, which did vary throughout the observations. In Table 3 we report the results for the above parameters, including the 68% confidence intervals from the analysis of the CCFs.

Table 4

Parameters describing the MASCARA-1 system, derived from the best-fit models to the photometric and spectroscopic data.

thumbnail Fig. 3

Observations of MASCARA-1 during and after the transit of MASCARA-1 b. In each panel, the solid horizontal line indicates the end of transit and the dashed lines indicate the end of ingress and beginning of egress. The solid black vertical lines show the best-fit value for vsini⋆. The dashed-dotted red lines indicate the mid-transit time and rest-frame velocity of the star. Panel A: the observed CCFs are shown in greyscale. Panel B: the same as in panel A, but with the best-fit model for the undisturbed stellar CCF subtracted, isolating the distortions due to the planetary transit over the rotating stellar photosphere. Panel C: residuals after our best-fitting model, including the planetary transit, is subtracted. Panel D: the corresponding model to the data represented in Panel B is shown.

With a projected obliquity of 69.5 ± 0.3°, we find that the rotation axis of MASCARA-1 is misaligned with respect to the orbit of the planet. This can also be seen in Fig. 3 panel B, where the planet shadow is isolated. Despite a low impact parameter, the trail of the planet does not reach from −vsini⋆ to + vsini⋆, as would be the case if the planet travelled near the stellar equator. For central transits and large misalignments the amplitude of the RM effect is reduced, as the planet travels from pole to pole, and not over the equator. If the impact parameter were larger, MASCARA-1 b would have travelled largely over the receding stellar surface area. We also find that the SONG data prefer a small impact parameter (b = 0.012 ± 0.012), which is consistent with the photometry (b = 0.2 ± 0.1). The transit mid-point is found 7 min later than expected from the photometric ephemeris. We argue that the formal uncertainty in the projected rotation speed (vsini⋆ = 109.0 ± 0.1 km s-1) underestimates the true uncertainty in this parameter. MASCARA-1 is a fast rotator and we expect a departure from the perfect spherical shape assumed in our analysis. In addition, we also expect a significant gravity darkening. This would result in a dark band along the equator for large i⋆ and an apparent increase in the stellar limb darkening for low i⋆. We therefore argue that an uncertainty of 3 km s-1 is more appropriate for the projected rotation speed. We find that our data favour a larger than expected limb darkening u1 + u2 = 0.9 ± 0.1, which we attribute to the simplified physics in our model rather than to a true disagreement with the model limb darkening parameters. Indeed if our data had a high S/N, we might be able to determine i⋆ and therefore the actual obliquity (Ψ) in this system from the RM data alone. However given the S/N in our SONG data we postponed such an analysis until such a data set is available. We also expect the uncertainty in λ to be about 4°, i.e. larger then the formal value quoted above, for the same reasons that we expect the vsini⋆ uncertainty to be underestimated.

5. Discussion and conclusions

Table 4 lists the final physical parameters describing the MASCARA-1 system. We find a planetary mass and radius of 3.7 ± 0.9 MJup and 1.5 ± 0.3 RJup, albeit with a large uncertainty on the mass caused by the high spin-rotation velocity of the star. The uncertainty on Mp can be reduced by obtaining more RV measurements and we have started a monitoring campaign for this purpose. MASCARA-1 b orbits a bright A star in 2.148780 ± 8 × 10-6 days at a distance of 0.043 ± 0.005 AU. The high temperature of the host star means that MASCARA-1 b has a high equilibrium temperature of 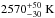2570-30+50K\hbox{$2570^{+50}_{-30}~\rm{K}$} (AB = 0), making it one of the hottest gas giants known.

Figure 4 shows the location of MASCARA-1 b in the planetary mass-radius diagram. From this we can see that while the radius is large it is not the most extreme case found to date, although it is the most irradiated of the more massive (Mp> 3 MJup) hot Jupiters. MASCARA-1 b also follows the empirical relationship between mass, radius, equilibrium temperature, host star metallicity, and tidal heating from Enoch et al. (2012). Figure 5 shows the location of MASCARA-1 compared to other stars hosting transiting exoplanets as a function of visual magnitude and effective temperature. It is clear that MASCARA-1 lies in a part of host star parameter space that has been largely unexplored to date, as it is a bright early-type star.

Currently there are only a few host stars with effective temperatures larger than 7000 K for which the stellar obliquity is known (e.g. WASP-33 Collier Cameron et al. 2010; KELT-17 Zhou et al. 2016; Kepler-13 Mazeh et al. 2012, see also Fig. 5)7 while some constraints exists for other similar systems such as HAT-P-57 (Hartman et al. 2015). This small group of systems displays a large spread in spin orbit alignments and MASCARA-1 confirms this trend. So far it is not clear what causes the large obliquities. They might be caused by dynamical interactions (e.g. Fabrycky & Tremaine 2007; Nagasawa et al. 2008), however they might also be a general feature of star formation. The proposed mechanisms include chaotic star formation (Bate et al. 2010; Thies et al. 2011), magnetic star-disk interaction (Lai et al. 2011; Foucart & Lai 2011; Spalding & Batygin 2015), torques due to neighbouring stars (Batygin 2012; Lai 2014), tidal dissipation (Rogers & Lin 2013), and internal gravity waves (Rogers et al. 2013). We can differentiate between the different theories by measuring obliquities in systems with varying multiplicity, planet mass, orbital separation, and stellar mass and structure (e.g. Albrecht et al. 2013). Detecting and characterizing exoplanets orbiting early-type main-sequence stars should lead to a better understanding of the environment in which planets form.

Since it orbits a bright host star MASCARA-1 b is a particularly interesting target for atmospheric characterization via transmission spectroscopy. This exoplanet is reminiscent of the WASP-33 system (Collier Cameron et al. 2010), in which a 2.1 MJup hot Jupiter transits a Teff = 7400 K A-star. However, while follow-up observations of WASP-33 are significantly hampered by the delta-scuti variations of its host star, no such variability is detected in MASCARA-1. Assuming a temperature of 2550 K and a hydrogen/helium atmosphere, MASCARA-1 b has an atmospheric scale height of H = 215 km, implying that an absorption feature that extends out to 5 × H results in a transmission signal of 0.01%. Interestingly, the sodium feature of the host star is significantly weaker than for a solar type star, in addition to being velocity broadened to 106 km s-1. This will make it significantly more straightforward to isolate the planet atmospheric sodium absorption from stellar effects , for example due to the Rossiter-McLaughlin effect (e.g. Snellen et al. 2008; Di Gloria et al. 2015).

The detection of MASCARA-1 b shows that the Multi-site All-Sky CAmeRA has the potential to increase the number of transiting exoplanets suitable for high-resolution atmospheric studies (e.g. Snellen et al. 2010; Brogi et al. 2012) and to expand our knowledge of planets orbiting early-type stars. The northern MASCARA station on La Palma has now gathered over two years of data and the southern station in La Silla starts observations in June 2017. We expect to find several more planets around both early- and late-type stars in the coming years.

thumbnail Fig. 4

Mass-radius relationship for transiting exoplanets. MASCARA-1 b is indicated by the star marker and the points are coloured by the theoretical equilibrium temperature.

thumbnail Fig. 5

Effective temperature vs. visual magnitude for stars hosting transiting exoplanets. MASCARA-1 is indicated by the red star and systems for which the obliquity has been measured are indicated by open circles. MASCARA targets stars to the left of the dashed black line (4 <mV< 8.4).

2

For Teff we assumed an uncertainty comparable to our own analysis. For L∗ the error on the distance alone implies an uncertainty of 4.3 L⊙, which we round up to account for uncertainties in the total flux.

3

The stellar density was obtained from the fit to the transit light curve as described in Sect. 4.1 using the relations of Seager & Mallén-Ornelas (2003).

4

See footnote 1.

5

See footnote 1.

6

The template was created using the interactive data language (IDL) interface SYNPLOT (I. Hubeny, priv. comm.) to the spectrum synthesis program SYNSPEC (Hubeny et al. 1995), utilizing a Kurucz model atmosphere (see http://kurucz.harvard.edu/grids.html).

7

Visit www.astro.keele.ac.uk/jkt/tepcat/rossiter.html for an up-to-date list of obliquity measurements.

Acknowledgments

I.S. acknowledges support from a NWO VICI grant (639.043.107). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694513). Based on observations made with the Mercator telescope, operated on the island of La Palma by the Flemmish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations obtained with the HERMES spectrograph, which is supported by the Research Foundation – Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany. Based on observations made with the Hertzsprung SONG telescope operated on the island of Tenerife by the Aarhus and Copenhagen Universities in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. The Hertzsprung SONG telescope is funded by the Danish National Research Foundation, Villum Foundation, and Carlsberg Foundation. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. We have benefited greatly from the publicly available programming language Python, including the numpy, matplotlib, pyfits, scipy and h5py packages.

References

  1. Albrecht, S., Reffert, S., Snellen, I., Quirrenbach, A., & Mitchell, D. S. 2007, A&A, 474, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
  3. Albrecht, S., Winn, J. N., Marcy, G. W., et al. 2013, ApJ, 771, 11 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andersen, M. F., Grundahl, F., Christensen-Dalsgaard, J., et al. 2014, in Rev. Mex. Astron. Astrofis. Conf. Ser., 45, 83 [Google Scholar]
  5. Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barbary, K. 2016, The Journal of Open Source Software, 1 [Google Scholar]
  7. Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Batalha, N. M. 2014, Proceedings of the National Academy of Science, 111, 12647 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bate, M. R., Lodato, G., & Pringle, J. E. 2010, MNRAS, 401, 1505 [NASA ADS] [CrossRef] [Google Scholar]
  10. Batygin, K. 2012, Nature, 491, 418 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2012, Nature, 486, 502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Brogi, M., de Kok, R. J., Albrecht, S., et al. 2016, ApJ, 817, 106 [NASA ADS] [CrossRef] [Google Scholar]
  15. Burrows, A., Hubeny, I., Budaj, J., Knutson, H. A., & Charbonneau, D. 2007, ApJ, 668, L171 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  16. Casewell, S. L., Lawrie, K. A., Maxted, P. F. L., et al. 2015, MNRAS, 447, 3218 [NASA ADS] [CrossRef] [Google Scholar]
  17. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  18. Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
  20. Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
  21. Craig, M. W., Crawford, S. M., Deil, C., et al. 2015, Astrophysics Source Code Library [record ascl: 1510.007] [Google Scholar]
  22. Deming, D., Wilkins, A., McCullough, P., et al. 2013, ApJ, 774, 95 [NASA ADS] [CrossRef] [Google Scholar]
  23. Di Gloria, E., Snellen, I. A. G., & Albrecht, S. 2015, A&A, 580, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  26. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  27. Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
  28. Foucart, F., & Lai, D. 2011, MNRAS, 412, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gray, D. F. 1984, ApJ, 281, 719 [NASA ADS] [CrossRef] [Google Scholar]
  31. Grundahl, F., Fredslund Andersen, M., Christensen-Dalsgaard, J., et al. 2017, ApJ, 836, 142 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hartman, J. D., Bakos, G. Á., Buchhave, L. A., et al. 2015, AJ, 150, 197 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hubeny, I., Lanz, T., & Jeffrey, C. 1995, in Newsletter on Analysis of Astronomical Spectra, 20 (University of St. Andrews), 30 [Google Scholar]
  34. Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  35. Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Jenkins, J. S., Jones, H. R. A., Goździewski, K., et al. 2009, MNRAS, 398, 911 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lai, D. 2014, MNRAS, 440, 3532 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lai, D., Foucart, F., & Lin, D. N. C. 2011, MNRAS, 412, 2790 [NASA ADS] [CrossRef] [Google Scholar]
  42. Madhusudhan, N., & Seager, S. 2009, ApJ, 707, 24 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maxted, P. F. L., Serenelli, A. M., & Southworth, J. 2015, A&A, 575, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mazeh, T., Nachmani, G., Sokol, G., Faigler, S., & Zucker, S. 2012, A&A, 541, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. McCormac, J., Pollacco, D., Skillen, I., et al. 2013, PASP, 125, 548 [NASA ADS] [CrossRef] [Google Scholar]
  48. McCormac, J., Skillen, I., Pollacco, D., et al. 2014, MNRAS, 438, 3383 [NASA ADS] [CrossRef] [Google Scholar]
  49. McDonald, I., Zijlstra, A. A., & Boyer, M. L. 2012, MNRAS, 427, 343 [NASA ADS] [CrossRef] [Google Scholar]
  50. Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
  51. O’Donovan, F. T., Charbonneau, D., Harrington, J., et al. 2010, ApJ, 710, 1551 [NASA ADS] [CrossRef] [Google Scholar]
  52. Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  53. Raskin, G., Van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Rogers, T. M., & Lin, D. N. C. 2013, ApJ, 769, L10 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rogers, T. M., Lin, D. N. C., McElwaine, J. N., & Lau, H. H. B. 2013, ApJ, 772, 21 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schlaufman, K. C. 2010, ApJ, 719, 602 [NASA ADS] [CrossRef] [Google Scholar]
  57. Schwarz, H., Brogi, M., de Kok, R., Birkby, J., & Snellen, I. 2015, A&A, 576, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  59. Sing, D. K., Pont, F., Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sing, D. K., Fortney, J. J., Nikolov, N., et al. 2016, Nature, 529, 59 [NASA ADS] [CrossRef] [Google Scholar]
  61. Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  63. Snellen, I. A. G., Stuik, R., Navarro, R., et al. 2012, in Ground-based and Airborne Telescopes IV, 84440I, Proc. SPIE, 8444 [Google Scholar]
  64. Spalding, C., & Batygin, K. 2015, ApJ, 811, 82 [NASA ADS] [CrossRef] [Google Scholar]
  65. Talens, G. J. J., Spronck, J. F. P., Lesage, A.-L., et al. 2017, A&A, 601, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Thies, I., Kroupa, P., Goodwin, S. P., Stamatellos, D., & Whitworth, A. P. 2011, MNRAS, 417, 1817 [NASA ADS] [CrossRef] [Google Scholar]
  67. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  68. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Vogt, S. S., Marcy, G. W., Butler, R. P., & Apps, K. 2000, ApJ, 536, 902 [NASA ADS] [CrossRef] [Google Scholar]
  70. Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
  71. Zhou, G., Rodriguez, J. E., Collins, K. A., et al. 2016, AJ, 152, 136 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observations used in the discovery of MASCARA-1 b.

In the text
Table 2

Transit model parameters and their best-fit values obtained from fits to the MASCARA data, NITES data, and the combined photometric data set.

In the text
Table 3

Model parameters used in fitting the RV and RM measurements and their best-fit values.

In the text
Table 4

Parameters describing the MASCARA-1 system, derived from the best-fit models to the photometric and spectroscopic data.

In the text

All Figures

thumbnail Fig. 1

Photometry and best-fit models used in the characterization of MASCARA-1 b. Panel a: MASCARA photometry obtained between February 2015 and September 2016. Shown are the 320 s cadence data (grey points), the data binned by 0.01 in phase (red points), and the best-fit transit model (black line). Panels b and c: NITES transit observations taken on 23 July 2016 and 17 September 2016, respectively. Shown are the data (grey points), the data binned by 0.01 in phase (red points), and the best-fit transit model (black line).
In the text
thumbnail Fig. 2

HERMES RV measurements of MASCARA-1 obtained from June to September 2016. Shown are the data (red points) and the best-fit model (black line). The high projected rotation speed of the star, vsini⋆ = 106.7 km s-1, results in relatively large uncertainties on the RV measurements of order 300 m s-1.
In the text
thumbnail Fig. 3

Observations of MASCARA-1 during and after the transit of MASCARA-1 b. In each panel, the solid horizontal line indicates the end of transit and the dashed lines indicate the end of ingress and beginning of egress. The solid black vertical lines show the best-fit value for vsini⋆. The dashed-dotted red lines indicate the mid-transit time and rest-frame velocity of the star. Panel A: the observed CCFs are shown in greyscale. Panel B: the same as in panel A, but with the best-fit model for the undisturbed stellar CCF subtracted, isolating the distortions due to the planetary transit over the rotating stellar photosphere. Panel C: residuals after our best-fitting model, including the planetary transit, is subtracted. Panel D: the corresponding model to the data represented in Panel B is shown.
In the text
thumbnail Fig. 4

Mass-radius relationship for transiting exoplanets. MASCARA-1 b is indicated by the star marker and the points are coloured by the theoretical equilibrium temperature.
In the text
thumbnail Fig. 5

Effective temperature vs. visual magnitude for stars hosting transiting exoplanets. MASCARA-1 is indicated by the red star and systems for which the obliquity has been measured are indicated by open circles. MASCARA targets stars to the left of the dashed black line (4 <mV< 8.4).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.