EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A68 Full HTML
Free Access
Issue
A&A
Volume 606, October 2017
Article Number A68
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201730799
Published online 11 October 2017

© ESO, 2017

1. Introduction

Imaging atmospheric Cherenkov telescopes (IACTs) are capable of detecting astrophysical sources at energies above 100 GeV (very-high-energy γ-rays, or VHE), and have effectively opened a new window in the electromagnetic spectrum. Since the discovery of the first VHE extragalactic emitter (Markarian 421, Punch et al. 1992), the number of VHE-detected extragalactic sources has continuously increased, and nowadays 67 of them are known1. The great majority of VHE extragalactic sources are active galactic nuclei (AGN) of the blazar type, similar to what is observed at lower energies (0.1–100 GeV, or high-energy γ-rays, HE) by Fermi-LAT (see Acero et al. 2015, for the most recent catalog of HE γ-ray sources).

A difficult aspect of extragalactic VHE astronomy is its inherent redshift limitation: the γ-ray photons emitted from the blazar can pair-produce on a low-energy (infrared and optical) photon from the diffuse extragalactic background light (EBL). This absorption effect increases with the distance and with the energy of the VHE photon: the result is a softening of blazar spectra for increasing redshifts, and, finally, a limit on the detection of distant blazars above 100 GeV (Salamon & Stecker 1998). On the other hand, this absorption can be used to put constraints on the EBL itself and indeed, the VHE detection of the first blazars at redshifts z ≥ 0.15 imposed strong constraints on early EBL models (Aharonian et al. 2006). Nowadays, among the VHE blazars with a spectroscopic redshift, the most distant ones are the quasars S3 0218+35 (z = 0.944, Ahnen et al. 2016) and PKS 1441+25 (z = 0.939, Ahnen et al. 2015; Abeysekara et al. 2015). Both of these quasars have been detected at VHE only during flaring activity. The most distant persistent source of VHE photons, again among the VHE blazars with a spectroscopic redshift, is PKS 1424+240, observed by both VERITAS (Acciari et al. 2010; Archambault et al. 2014) and MAGIC (Aleksić et al. 2014a). A first firm lower limit on its distance has been established by Furniss et al. (2013) as z ≥ 0.6035. Rovero et al. (2016) associated this blazar with a galaxy cluster at z = 0.601 ± 0.003, in agreement with the lower limit. More recently, Paiano et al. (2017) estimated the redshift of PKS 1424+240 as z = 0.604 from the detection of faint emission lines in its optical spectrum. In the following we have adopted z = 0.6 as the redshift of the object, and we use the EBL model by Franceschini et al. (2008).

thumbnail Fig. 1

Archival SEDs (νLν in erg/s as a function of the rest-frame frequency in Hz) of four iconic VHE blazars: 3C 279 in green, PKS 1424+240 in red, PG 1551+113 in yellow and Mrk 421 in blue. The SEDs have been compiled using the ASDC SED builder tool (http://tools.asdc.asi.it/SED). Among these four sources, 3C 279 is the only one that has been detected at VHE only during flaring activity.

Blazars are radio-loud AGN characterized by a broad non-thermal continuum from radio to γ-rays, rapid variability and a high degree of polarization (see e.g., Angel & Stockman 1980). These observational properties are explained as the non-thermal emission from a relativistic jet pointed in the direction of the observer (Blandford & Rees 1978). The blazar class is further divided into the two-subclasses of BL Lacertae objects and flat-spectrum-radio-quasars (FSRQs) according to the absence (in the former) or presence (in the latter) of emission lines in their optical spectrum (see e.g., Stickel et al. 1991). These two sub-classes are also characterized by different luminosity and redshift distributions (see Padovani 1992; Massaro et al. 2009) and are considered as the blazar version of the two radio-galaxy subclasses defined by Fanaroff & Riley (1974).

The spectral-energy-distribution (SED) of blazars is always comprised of two bumps, peaking in mm-to-X-rays and MeV-to-TeV, respectively. While FSRQs are in general characterized by the first peak at lower frequencies (in infrared), BL Lac objects have different first peak frequencies, and are thus further classified into low/intermediate/high-frequency-peaked BL Lac objects (LBLs, IBLs, HBLs, with a first peak frequency below 1014 Hz, at 1014−15 Hz, or above 1015 Hz, respectively). The majority of VHE blazars are indeed HBLs (for a recent review on VHE results, see de Naurois 2015).

The different blazar subclasses (FSRQs, LBLs, IBLs, HBLs) are characterized not only by different frequencies of the synchrotron peak, but also by different luminosities. Fossati et al. (1998) proposed the existence of a “blazar sequence” characterized by an anticorrelation between luminosity and peak frequency. The most powerful blazars, but with the lowest peak frequencies, would thus be the FSRQs, while the least luminous blazars would be the HBLs. Several authors (see e.g. Ghisellini & Tavecchio 2008; Nieppola et al. 2008; Giommi et al. 2012) have investigated whether this sequence is real or due to selection effects. Padovani et al. (2003); Caccianiga & Marchã (2004); Padovani et al. (2012) have shown that there exist sources which break the blazar sequence (i.e., powerful HBLs or low-luminosity FSRQs). In Fig. 1 we reproduce the average SEDs of PKS 1424+240 together with three well known VHE blazars: the FSRQ 3C 279 (z = 0.5362), the HBL PG 1553+113 (assuming z ≃ 0.5), and the HBL Mrk 421 (z = 0.031). It is clear that the peak luminosity of PKS 1424+240 is at the same level as 3C 279, but with a peak frequency two orders of magnitude higher. Compared to Mrk 421, PKS 1424+240 has a peak frequency a factor of 10 lower, but it is two orders of magnitude more luminous. The SED of PKS 1424+240 is indeed very similar to the SED of PG 1553+113, and both sources can be seen as examples of luminous and high-frequency peaked blazars. However, it is important to remind the reader that the exact redshift of PG 1553+113 is still uncertain, and the current best estimates constrain it to be between 0.395 and 0.58 (Danforth et al. 2010). The value of z = 0.5 adopted here is compatible with the observational constraints, but the source may be closer, and thus less luminous than what is shown in Fig. 1.

Meyer et al. (2011) have extended the blazar sequence into a “blazar envelope”, in which the different blazar subclasses are due to the progressive misalignment of two intrinsically different populations of blazars (which then correspond to the Fanaroff & Riley dichotomy in radio-galaxies). In Fig. 2 we reproduce the Lpeak−νpeak plot from Meyer et al. (2011), including the values for PKS 1424+240, assuming the redshift z = 0.60. It is clear that PKS 1424+240 is an outlier compared to the other known blazars, and its high distance implies that it is indeed a powerful HBL, breaking the Fossati blazar sequence, and representing an intermediate blazar between the “fast-jet” and “slow-jet” blazars proposed by Meyer et al. (2011).

Among the two components of the blazar SED, the low-energy one is clearly associated with synchrotron emission by electrons and positrons moving relativistically along the jet. The origin of the high-energy component is more disputed: in leptonic models it is associated with inverse-Compton scattering between the same e± population and a soft photon field, like their own synchrotron emission (synchrotron-self-Compton model, SSC, see Konigl 1981) or an external photon field, such as the accretion disk, the broad-line-region (BLR), or the dust torus (external-inverse-Compton model, EIC, see Sikora et al. 1994); in hadronic models the high-energy component of the SED is instead associated with synchrotron emission by protons, and/or by secondary particles produced in p–γ interactions (see e.g., Mücke & Protheroe 2001). Blazar emission models are not fully understood and, in general, different kinds of models are used for HBLs or LBLs/FSRQs. In the case of HBLs, the absence of emission lines and of the blue-bump associated with the accretion disk, suggests that the dominant soft photon field is the lepton synchrotron emission, and the models under study are usually limited to the SSC and the hadronic scenario. On the other hand, for LBLs and FSRQs the γ-ray emission is usually explained by EIC models (see e.g., Meyer et al. 2012). In addition, while hadronic models are in general disfavored for FSRQs (Sikora et al. 2009; Petropoulou & Dimitrakoudis 2015; Zdziarski & Böttcher 2015), they can correctly reproduce the SED of HBLs (with the exception of rapid flaring activity). An intermediate object as PKS 1424+240 can thus be very useful to provide insights on the transition between the different blazar subclasses, and ultimately cast light on the physics of relativistic jets from super-massive black holes.

thumbnail Fig. 2

Adapted from Meyer et al. (2011). Distribution of blazars in the Lpeak−νpeak, showing the different blazar subclasses, as well as the two theoretical paths associated with a fast (A) and a slow (B) jet, observed at different angles. We overplot the position of the four VHE blazar shown in Fig. 1: 3C 279 in green, PKS 1424+240 in red, PG 1553+113 in yellow, and Mrk 421 in blue (for the low state). For PG 1553+113, the yellow band represents the uncertainty in its redshift.

Before presenting in details the modeling of PKS 1424+240, it is interesting to discuss the case of PG 1553+113 which, as presented above, shows a SED similar to the one from PKS 1424+240. Different authors have successfully modeled its emission using a simple one-zone SSC model (Albert et al. 2007; Abdo et al. 2010; Aleksić et al. 2010; Tavecchio et al. 2010; Zhang et al. 2012). However, the uncertainty in the distance of this object complicates the modeling task and indeed most solutions adopted redshift values which have later been proven to be incorrect. Albert et al. (2007) successfully modeled the SED assuming z = 0.3, and found that for z> 0.56 the emission from PG 1553+113 is not compatible with a simple one-zone SSC model. Aleksić et al. (2010) and Zhang et al. (2012) also presented a successful one-zone SSC model assuming z = 0.3, while Tavecchio et al. (2010) assumed z = 0.36. Abdo et al. (2010) successfully modeled the SED of PG 1553+113 assuming z = 0.75, but they needed unusual values for the emitting region size (R ≃ 1018 cm, that is a factor of at least ten larger than usual SSC modeling) and an ad-hoc double-broken power-law distribution for the electrons. Another VHE blazar potentially similar to PKS 1424+240 is KUV 00311-1938 (Becherini et al. 2012), but in this case as well the redshift is not well determined and only a firm lower limit of z> 0.51 exists (Pita et al. 2014).

An alternative to standard blazar emission models is represented by radiative processes in the path from the source to the observer. If the blazar is capable of accelerating ultra-high-energy cosmic rays (UHECRs), their interaction with low-energy photon fields while travelling to the Earth may be detected as an additional γ-ray component which suffers a significantly lower EBL attenuation. This UHECR origin of VHE photons has been proposed by several authors such as Essey & Kusenko (2010; Murase et al. (2012). For a specific application of this scenario to PKS 1424+240 see Essey & Kusenko (2014) and Yan et al. (2015).

The most recent γ-ray observations of PKS 1424+240 have been presented by Archambault et al. (2014) and Aleksić et al. (2014a), including multi-wavelength observations in optical and X-rays. In this paper we model the SED of PKS 1424+240 from Archambault et al. (2014) in the framework of the standard stationary blazar leptonic and hadronic models, trying to constrain the particle content of the emitting region and its physical properties.

2. Leptonic models

2.1. Synchrotron-self-Compton model

thumbnail Fig. 3

One-zone SSC modeling of PKS 1424+240. The blue band represents all of the SSC models corresponding to the parameters given in Table 1. The black model represents the SSC solution provided by Kang et al. (2016). The black dashed line in the VHE regime represents the solution provided by Kang et al. (2016) computed at the source, before absorption on the EBL.

The simplest blazar emission model is the one-zone synchrotron self-Compton one (Konigl 1981), that correctly describes the SED of HBLs in their stationary state. The model assumes that the emission is dominated by one plasmoid propagating relativistically in the AGN jet. It is parametrized by its radius R (assuming a spherical geometry), its Doppler factor δ (relative to the observer) and it is assumed to be filled by a homogeneous, tangled, magnetic field B. The stationary particle population energy distribution is non-thermal and parametrized by a broken-power-law function (to take into account the break associated with synchrotron losses). The particle energy distributions adds six additional parameters: the two indices α1,2, the Lorentz factors γmin,br,max and the normalization factor K. The number of free parameters is thus nine, and the model can be constrained only if both SED peaks are well measured. The standard approach to constrain the SSC model parameter space is the one developed by Tavecchio et al. (1998): the peak frequencies and luminosities can be analytically expressed as functions of the model parameters, and thus can be used to constrain them. The current generation of γ-ray telescopes has however greatly improved the measurement of the γ-ray SED peak, and recently, more advanced fitting and constraining algorithms have been developed by several authors (Finke et al. 2008; Mankuzhiyil et al. 2011; Zhang et al. 2012; Cerruti et al. 2013a).

In this work we make use of the constraining algorithm described in Cerruti et al. (2013a), which is a numerical extension of the analytical work by Tavecchio et al. (1998), taking into account the GeV and TeV measurements. We simulated 105 theoretical SEDs, spanning the following parameter space: δ ∈ [30,500]; B ∈ [0.001,0.05] G; R ∈ [1015,2 × 1017]; K ∈ [5 × 10-8,3 × 10-5]; γbr ∈ [104,105]. We assumed α1 = 1.8, α2 = 5.0, γmin = 100, γmax = 5 × 106 (the minimum and maximum Lorentz factors of the electron distribution do not affect the SED as long as they are low and high enough). For each theoretical SED we estimated the flux and frequency of the synchrotron peak, the flux and spectral index in the Fermi-LAT energy band, and the flux and spectral index in the IACT energy band. For the IACT observables, we used the results obtained by Archambault et al. (2014) during the 2013 campaign, that is a detection between 100 and 750 GeV, and a decorrelation energy of 200 GeV. The next-step in the constraining algorithm would be to parametrize every observable as a function of the model parameters, and solve the system for the observable values measured for PKS 1424+240. However we realized that none of the simulated SEDs has a TeV index compatible with the VERITAS one (4.5 ± 0.2): all of them are systematically softer, and range between 5.0 and 7.5. To investigate further the SSC modeling, we then run the constraining algorithm assuming a maximum arbitrary index in the VHE regime of 6.0. In this case the algorithm converges and the results are given in Table 1.

Table 1

Parameters used for the one-zone SSC modeling of PKS 1424+240.

For every SSC solution we recompute the corresponding model which is shown in Fig. 3. Looking at the parameters, it is clear that the critical one is the Doppler factor. A minimum value of δ = 250 is extremely high (by one order of magnitude) compared to the solutions achieved for other blazars (Tavecchio et al. 2010; Zhang et al. 2012). This result, together with the fact that these solutions are all systematically softer than the VHE measurement, implies that the simple one-zone SSC model is highly disfavored to explain the γ-ray emission from PKS 1424+240.

Only two other SSC modeling attempts of PKS 1424+240 are available in the literature, after its redshift of 0.6 has been determined. Kang et al. (2016) has modeled the same 2013 VERITAS campaign using a χ2 minimization algorithm, finding a solution with δ = 51 and B = 0.02, which is not included in our set of solutions. To understand this issue, and compare the results from different fitting algorithms, in Fig. 3 we plot their solution as well, reproduced with our numerical code using their model parameters. By fitting its corresponding spectral index in the VHE regime, we find that the solution is excluded by our algorithm because it has a ΓVHE = 6.4, slightly softer than the limit we adopted. Kang et al. (2016) also disfavor the SSC model, because it has a reduced χ2 value of 2.2. For comparison, our best reduced χ2 is 1.6, but again, achieved only for extreme values of δ. Probably, our solutions with δ> 250 are not reported by Kang et al. (2016) due to a reduction of their parameter space to reasonable parameter values.

Aleksić et al. (2014a) also presented a one-zone SSC modeling of PKS 1424+240 after the new constraint on its redshift: they described the blazar SED assuming an extreme Doppler factor of 70. However, it should be noted that the MAGIC spectrum has a lower exposure compared to the VERITAS one, and that their last significant bin is at an energy of 400 GeV only. We thus re-run our constraining algorithm considering a smaller energy-range (150–400 GeV): the distribution of simulated VHE indices, as expected, becomes harder, and there exist indeed models compatible with the MAGIC spectral index (ΓVHE = 5.0 ± 1.7). Anyhow, the modeling by Aleksić et al. (2014a) also disfavors an SSC origin of the γ-ray photons from PKS 1424+240, due to the high value of δ. The VERITAS detection up to 750 GeV is even more constraining: there are no SSC models which can reproduce the emission from PKS 1424+240, and even when allowing models with ΓVHE = 6.0, only solutions with unrealistic Doppler factors are found.

thumbnail Fig. 4

Two-zone SSC modeling of PKS 1424+240, using the model described in Chen et al. (2015). The green line represents the emission from the accelerating region, and the red one the emission from the diffusion region. The black line represents the combined emission from both zones.

A possible solution to this problem is that the dominant emission process is SSC, but that the acceleration and radiation mechanisms are more complex with, for example, several emitting regions contributing to the γ-ray component. We investigated this option by using the numerical code described in Chen et al. (2015), which simulates the emission from particles both in an acceleration zone and a diffusion zone. The diffusion zone is a much larger spherical zone surrounding the acceleration zone. Particles are only injected and accelerated in the acceleration zone, but they are subject to spatial diffusion and radiative cooling in both zones. The mechanism of acceleration and injection of the particles are conjectured to be magnetic reconnection or second-order Fermi acceleration, whereas the particles in the diffusion zone are the particles escaped from the acceleration zone through spatial diffusion.

In Fig. 4 we present the modeling of the PKS 1424+240 SED during the 2013 campaign in a two-zone scenario. In this case, a good description of the γ-ray emission can be achieved assuming δ = 35, B = 0.033 G, Racc = 5 × 1016 cm and Rdiff = 4 × 1017 cm, where Racc and Rdiff are the radii of the acceleration and diffusion regions, respectively. Contrary to the one-zone SSC modeling, the information from the VHE spectral index is not explicitly used in the two-zone SSC modeling. To ease the comparison between the results achieved with the one-zone and the multi-zone models, we thus performed a fit of the two-zone SSC model within the VERITAS detection range. The result is a spectral index ΓVHE = 5.2. This index is much closer to the measured VERITAS index (4.5 ± 0.2) than in the one-zone SSC scenario. In addition, the value of δ = 35 is much lower than the values obtained in the one-zone SSC modeling, and in line with typical blazar values.

Table 2

Parameters used for the EIC modeling of PKS 1424+240.

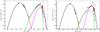thumbnail Fig. 5

Modeling of PKS 1424+240 in an EIC scenario, for the 2009 (left) and 2013 (right) campaigns. The black solid line represents the total emission; the red line represents the synchrotron emission by leptons; the green line the SSC component; the pink line the EIC component assuming that the external photon field is produced by the dusty torus. The model parameters are provided in Table 2. The models do not include absorption over the EBL. The VERITAS data (Archambault et al. 2014) deabsorbed using the EBL model by Franceschini et al. (2008) are plotted in red.

2.2. External-inverse-Compton model

The second scenario we investigated is an EIC model in which the leptons in the emitting region also scatter external photons from the BLR, the dust torus, and/or the accretion disk. The main reason for testing this scenario is that the EIC model correctly describes the SED of powerful FSRQs, and we expect that, if PKS 1424+240 represents indeed an intermediate blazar, it can have an external photon field bright enough to contribute to the overall photon emission. The EIC model has many more free parameters than the SSC one, and a detailed study of the parameter space cannot be performed without the addition of explicit assumptions in order to reduce the number of degrees of freedom. In particular, the energy densities of the external photon fields are free parameters that depend on the exact location of the γ-ray emitting region in the jet. To alleviate this problem, and reduce the number of free parameters, we adopted the approach described in Cerruti et al. (2013b) and Dermer et al. (2014): under the assumption that the emitting region is close to equipartition between magnetic field, particle, synchrotron photon and external photon energy densities (uB, ue, us, and uext, respectively), and that the particle population can be parametrized by a log-parabolic function, we determine the values for the Doppler factor δ, the magnetic field B, the emitting region size R, the peak Lorentz factor of the particle energy distribution γp, and the energy density of the external photon field that correctly model the SED. The equipartition factors are defined as ζe = ue/uB; ζs = us/uB; and ζext = uext/uB.

An important aspect of EIC scenarios is the absorption of γ-rays via pair-production on the external photon field (similarly to the absorption on the EBL discussed above). In particular, Lyα photons (with E = 10.2 eV) from the BLR can efficiently absorb VHE photons (Ghisellini & Tavecchio 2009). The very detection of VHE FSRQs implies that the γ-ray emission is located outside the BLR during the VHE detection, or at the most at its very edge, in order to escape the low-energy photon field and ultimately reach the observer (MAGIC Collaboration et al. 2008; Aleksić et al. 2011; H.E.S.S. Collaboration et al. 2013; Aleksić et al. 2014b; Abeysekara et al. 2015; Ahnen et al. 2015). For PKS 1424+240 the scenario is similar to VHE FSRQs: the detection of γ-ray photons up to 750 GeV means that the γ-ray emitting region is located outside the BLR, or that the BLR itself is extremely underluminous. In the modeling we thus consider as the external photon field only the thermal emission from the dusty torus surrounding the super-massive black hole.

We modeled the two SED compiled by the VERITAS collaboration in 2009 and 2013. We assume a peak frequency of the synchrotron component νpeak = 12 (4) × 1015 Hz, and a luminosity of νpeakLpeak,synch = 5.5 (3.8) × 1047 erg s-1 for the 2009 (2013) season (see Table 2). The Swift/XRT observations constrain the shape of the particle population, and we considered a curvature index b = 0.6 and 0.9 for the 2009 and 2013 seasons, respectively. We assumed a variability time-scale of 105 s (27.8 h), which matches the doubling time-scale of about one-day observed in soft X-rays during the 2009 multi-wavelength campaign (Aleksić et al. 2014a). We impose perfect equipartition between the magnetic field and the lepton energy density (ζe = 1). The values of the density of synchrotron photons and external photons are adjusted to reproduce the γ-ray emission. The SED high-energy bump is associated with SSC scattering and EIC scattering over the dusty torus thermal emission. The output parameters are reported in Table 2: in our scenario the 2013 activity is associated with a higher δ, a lower B and a larger but less dense emitting region; the jet power increases by 20%. The external photon energy density is reduced by a factor of four, but we explain this variability not in terms of variability of the dust torus, but rather by a change in the location of the emitting region. If the emission is produced at a distance r<rIR (where rIR is the radius of the torus), the photon energy density should be several order of magnitudes higher than the 10-7 erg cm-3 inferred from our modeling (Ghisellini & Tavecchio 2009). This means that in our scenario the emission is produced at r>rIR, where the energy density of the infrared photon field is rapidly decaying. Assuming 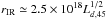cm (where Ld,45 is the luminosity of the accretion disk, in units of 1045 erg s-1) we can thus infer the location of the emitting region at the parsec scale from the super-massive black-hole. This study has been performed using as observables the energies and luminosities of the SED peaks, and by imposing equipartition criteria, but not using as a constraint the index in the VHE range. Following what we did for the two-zone SSC model, in this case as well we performed a fit of the EIC models in the VHE regime. The resulting spectral indices are ΓVHE = 6.1 and ΓVHE = 6.3 for the 2009 and 2013 campaigns, respectively. These indices are softer than the observed one, and similar to the results obtained with the SSC code. However, the value of δ = 30−46 is significantly lower than in the one-zone SSC scenario.

Kang et al. (2016) also attempted an EIC modeling of PKS 1424+240. They presented a solution in which the VHE emission is dominated by EIC scattering over infrared photons from the dust torus, similar to ours. The model parameters are also similar, even though they adopted a minimization algorithm, and did not explicitly force equipartition between the energy densities of the leptons and the magnetic field energy.

3. Hadronic model

thumbnail Fig. 6

Modeling of PKS 1424+240 in a hadronic scenario, for the 2009 (left) and 2013 (right) campaigns, for a value of the Doppler factor δ = 30. Only the overall emission is plotted. The colors, from blue to red, represent a decrease in the size of the emitting region R, and an increase in the strength of the magnetic field B. The model parameters are provided in Table 3. The VERITAS data (Archambault et al. 2014) deabsorbed using the EBL model by Franceschini et al. (2008) are plotted in red.

3.1. Emission at the source

In an alternative scenario, the high-energy component of the SED is associated with protons which either directly radiate synchrotron photons, or produce secondary mesons and leptons via proton-photon interactions. The hadronic modeling is performed using the code described in Cerruti et al. (2015): p–γ interactions are computed using the Monte-Carlo code SOPHIA (Mücke et al. 2000), and the code correctly computes synchrotron emission by μ± (before decaying back into e±) and by synchrotron-supported pair-cascades triggered by the secondary e± and the photons from π0 decay. The Bethe-Heitler pair-production (not included in SOPHIA) is calculated analytically following Kelner & Aharonian (2008). The code does not take into account external photon fields; it assumes that the dominant low-energy photons are the synchrotron ones, and not the ones from the BLR, the torus or the accretion disk. It thus has to be compared directly to the leptonic SSC scenario, and not the EIC.

Blazar hadronic modeling has a much higher number of free parameters, compared to the standard SSC model, due to the additional parameters associated with the proton energy distribution. The particle energy distributions for electrons (subscript e) and protons (subscript p) are parametrized as broken power-laws with indices α1,2. The relevant energies (minimum, break, and maximum) are provided as Lorentz factors γmin,break,max. The normalizations of the particle energy distributions (Ke, and η = Kp/Ke) are provided at γ = 1. Following Cerruti et al. (2015), we can reduce the number of parameters by making two assumptions on the acceleration mechanism: the first one is that the electrons and protons are co-accelerated, and they thus share the same injection index (αe;1 = αe;2); the second one is that the maximum proton energy is constrained by the equality of the acceleration and cooling time-scales. However, even under these hypotheses, the number of free parameters is higher than the number of independent observables: we thus search for solutions only for a given set of Doppler factor values δ = 15, 30, 60. We first search for pure proton-synchrotron solutions, but we fail in modeling the SED. The reason is that the emission from secondary particles from p–γ interactions is important, and significantly modify the γ-ray component. On the other hand we find good hadronic solutions dominated by proton-synchrotron emission in the MeV–GeV part of the spectrum, and by synchrotron emission from secondary leptons in the VHE regime. This type of hadronic solution is very similar to the one obtained for the HBLs Mrk 421 and PKS 2155-304 by Zech et al. (2017). The injection indices for electrons and protons are fixed to 1.8. The parameter space is studied fixing the peak frequency of the proton-synchrotron component, and moving along a line in the R–B plane (see Cerruti et al. 2015,for details). When varying δ, the parameter which compensates for the varying photon emission is the particle density: for the same values of R and B, solutions with lower δ have thus a higher value of particle density, which means a higher contribution from secondary particles produced in p–γ interactions. To better study the effect of the Doppler factor on the model parameters, we relaxed the constraint on the variability timescale: for δ = 15, no solutions are found for τvar< 6.5 days for the 2013 campaign, the reason being that emission from secondary pairs in a small and dense emitting region overshoot the very soft X-ray emission observed with Swift/XRT; for δ = 30,60, we imposed τvar< 3 days. We found good solutions for both the 2009 and 2013 SEDs assuming R = (3.2−32.4) × 1016 cm, and B = 0.4−2.3 G. For lower (respectively, higher) values of R, the emission in the VHE regime becomes too hard (respectively, soft) compared to the observations. The differences in the emission between the 2009 and the 2013 campaign are explained by a lower maximum particle energy (for both electrons and protons) in 2013. The value of δ affects the equipartition of the emitting region: for δ = 30 the emitting region is remarkably close to equipartition (up/uB ≃ 1), while the emitting region is particle dominated for δ = 15, and magnetic-field dominated for δ = 60. The required luminosity is (4−19) × 1046 erg s-1, of the order of the Eddington luminosity of the super-massive black hole powering the blazar (which is 1047 erg s-1 for a super-massive black hole mass of 109M⊙). Given that the observed variability time-scale in X-rays during the 2009 multi-wavelength campaign was about one day, we disfavor the solutions for δ = 15. Solutions for δ = 30 are preferred over the ones for δ = 60 for both a lower luminosity and an equiparition factor close to unity. The hadronic modeling of PKS 1424+240 for the 2009 and 2013 campaigns is presented in Fig. 6 (for δ = 30), and the detailed values assumed in the modeling are listed in Table 3.

A hadronic modeling of PKS 1424+240 has been also presented by Yan & Zhang (2015). The authors found a model similar to ours, in which the γ-ray component is dominated by proton-synchrotron emission and synchrotron emission by secondary leptons from p–γ interactions. On the other hand, the parameter values differ: Yan & Zhang (2015) presented a solution with the same value of δ = 30, but a higher B = 15 G and a smaller R = 5 × 1015 cm. Using these parameters, we cannot fit the SED of PKS 1424+240. The reason is that in their numerical simulation the synchrotron emission by muons is not computed, while this component is important in the VHE regime, and increases the hardening of the γ-ray emission (Zech et al. 2017).

Table 3

Parameters used for the hadronic modeling of PKS 1424+240.

3.2. Cascades in the line of sight

In order to model the potential contribution from line-of-sight cascades from UHECR interactions, we use the CRPropa3 software2. This publicly available tool includes the ability to simulate the propagation of UHECRs and calculate their interactions along the way, including pair production, photo-pion production, photodisintegration, and nuclear decay. In addition, it can track the production and propagation of the byproducts of these interactions (secondary photons, neutrinos, and electron-positron pairs) and output spectra for the primary and the secondary particles (for full details see Alves Batista et al. 2016). For consistency with the modeling in this paper, a small modification is made to the CRPropa3 code to include the Franceschini et al. (2008) EBL model in the photon propagation chain.

Using CRPropa3, cosmic rays are propagated from the PKS 1424+240 distance of z = 0.6. A pure-proton composition is assumed, as in the hadronic model described in Sect. 3.1. For the secondary γ-ray emission to be viable, the strength of the intergalactic magnetic fields (BIGMF) cannot exceed ~1.4 × 10-14 G; otherwise, deflections of the primary cosmic rays away from the line of sight are large enough for the emission from the secondary γ-rays to extend beyond the angular resolution of IACTs and become lost in the background. Following Essey & Kusenko (2014), Yan et al. (2015), we adopt magnetic fields with a strength B = 10-15 G and a correlation length of 1 Mpc. To be consistent with the treatment of the primary emission, the EBL model from Franceschini et al. (2008) is used. The values of parameters used for both scenarios are listed in Table 4.

Table 4

Parameters used in modeling the γ-ray data with UHECR-induced cascade emission.

thumbnail Fig. 7

Gamma-ray emission described by the hadronic scenario together with the predicted secondary γ-ray spectra from UHECR-initiated cascades along the line of sight for the 2009 (left) and 2013 (right) campaigns.

The spectrum of the secondary γ-rays is calculated for two scenarios with line-of-sight UHECR cascade emission as (1) an extension of the hadronic model and (2) as an additional component to the SSC model. Under the first scenario, the aim is to produce a self-consistent model of the primary and the secondary emission from PKS 1424+240. The UHECR-borne secondary γ-rays are considered within the context of the hadronic model presented in Sect. 3.1, with parameters for the secondary emission derived from the primary model. Following the discussion in the previous section, we favor the hadronic solutions for δ = 30, and use the respective model parameters in the following. Specifically, the bulk Lorentz factor (Γ), the spectral properties (γmin, γmax, αp), and the total power of the protons (Lp) are taken from the hadronic model and are used to constrain the range of possible normalizations of the secondary γ-ray spectra. Lp is calculated using the total luminosity of the emitting region (L) and the equipartition parameter (up/uB). It represents the isotropic power from a stationary spectrum of hadrons in the emitting region and accounts for energy losses at the source, including energy required for the production of the primary γ-rays. While during the simulation, the UHECR spectrum is cut off at 0.07 EeV at the lower energy end (due to memory concerns), below which the contribution to the secondary γ-ray emission is negligible, the full spectrum of the UHECR extending down to 1 GeV is used for calculating the power of the UHECRs required for the production of the secondary γ-rays. The Lorentz factor, Γ = 15 determines the opening angle of the UHECRs following θp = 1/Γ = 3.8°, which translates to a factor of 900 amplification of the secondary γ-ray emission over the case where UHECR are emitted isotropically.

We first studied the scenario in which the entire Lp used in Sect. 3.1 goes into the line-of-sight cascade. In this case the emission from UHECR cascades significantly overshoots VERITAS observations, and we can conclude that such a self-consistent model is excluded. A first alternative is that only a fraction of the proton power goes into UHECR cascades, and we thus define an escape fraction ξ = Lp,esc/Lp. VHE observations can thus be used to put a constraint on Lp,esc, under the assumption that the broadband SED is associated with hadronic emission. It is important to underline that this result depends on the choice of BIGMF = 10-15 G, and higher values of BIGMF would appreciably scatter the UHECRs and lower the observed cascade emission.

Figure 7 presents the full range of possible secondary γ-ray spectra calculated for Γ and γmax values from the hadronic model applied to data from 2009 (left) and 2013 (right) campaigns. For both observing campaigns, we found that a self-consistent hadronic model can be achieved assuming a proton escape fraction of one third.

The second scenario treats the secondary γ-rays as an additional component to the best-fit SSC model from Sect. 2.1 for describing the VHE emission. The normalization of the secondary γ-ray spectrum is far less constrained under this scenario, as the parameters of the UHECR spectrum are not predetermined. The choices for αp, Emax, and Γ can vary the normalization of the secondaries by orders of magnitude while keeping the requirement on the power of the UHECRs within an acceptable range (less than the Eddington luminosity). Hence, in this scenario, we focus on the shape of the secondary γ-ray spectrum, which for a given redshift is primarily affected by the choice of the EBL model (Essey et al. 2011). For a selection of three EBL models that span the range of secondary spectrum shapes, the secondary γ-ray spectra are calculated and fit to the VERITAS spectral points with the requirement that the secondaries do not overshoot the VERITAS spectral points. The result for the 2013 campaign shown in Fig. 8 implies that the secondary γ-rays at best can only be responsible for the two highest energy VERITAS spectral points.

thumbnail Fig. 8

Predictions for secondary γ-ray spectra using different EBL models within the SSC scenario for the 2013 campaign. The required UHECR power for producing the secondary γ-rays is included in the legend for each EBL model.

4. Conclusions

PKS 1424+240 is a luminous high-frequency blazar, with a peak luminosity similar to the one from 3C 279, but with a peak frequency similar to Markarian 421 (in its low state); it is currently the most distant VHE blazar detected in a non-flaring state, and thus a unique source of VHE photons. This work presents a systematic modeling attempt of the emission from this source, comparing the results from different blazar emission scenarios in order to investigate the emission mechanism(s) at work in this peculiar blazar.

We first investigated Synchrotron Self Compton (SSC) models including both the standard one-zone and multi-zone SSC models as well as a single-zone SSC model with contributions from external photons from the dusty torus in an External Inverse-Compton (EIC) model. We find that the standard one-zone SSC model (which usually satisfactorily describes the SED of HBLs) cannot describe the SED of PKS 1424+240, unless we adopt values of δ> 250 and we consider a systematic bias in the γ-ray spectrum observed with Cherenkov telescopes. However, a multi-zone SSC model alleviates the issues of the one-zone SSC scenario, and can describe the SED assuming a more reasonable value of δ = 30. The EIC scenario, in which infrared photons from the dust torus are upscattered by leptons in the relativistic jet, is also a viable alternative, requiring similar values of δ.

We next investigated hadronic emission scenarios, including both γ-ray emission from hadrons at the source as well as secondary emission from UHECR line-of-sight interactions. For the source emission models, no reasonable solution was found for a pure proton-synchrotron model; however good solutions were found for proton-synchrotron emission at lower energies with synchrotron emission from secondary leptons producing the VHE emission. Thus we show a hadronic scenario can provide a good description of the data, and naturally predicts a hardening at TeV energies. In this case, the total power of the emitting region remains of the order of the Eddington luminosity and cannot be disfavored on this basis as is regularly done for bright FSRQs.

For γ-ray emission as secondaries from UHECR line-of-sight interactions, we produced a self-consistent hadronic model as well as studied the contribution from UHECR for the one-zone SSC scenario. We find that the γ-ray emission from UHECR in the line of sight can be dominant in the TeV regime for this source, potentially accounting for hardening at these energies.

To further investigate the origin of γ-ray emission from PKS 1424+240, it is fundamental to extend the spectrum in the TeV regime. This will allow us to discriminate between models favoring hadronic emission (both in the source and in the line-of-sight) and leptonic emission. Variability, and thus the detection of any flare, will also be a useful tool to access blazar physics. In this sense, PKS 1424+240 should be a high-priority target for the future Cherenkov Telescope Array (CTA, Acharya et al. 2013; Sol et al. 2013). We also encourage regular monitoring by HESS, MAGIC and VERITAS, and any γ-ray activity should trigger heavy VHE campaigns to try to extend the VHE spectrum to the highest energies.

1

See http://tevcat.uchicago.edu for an up-to-date VHE catalog.

Acknowledgments

This work has been made possible thanks to the computing centers of the Harvard-Smithsonian Center of Astrophysics, Cambridge, USA, and the Laboratoire de Physique Nucléaire et Hautes Energies, Paris, France. The informatics and support teams of both laboratories are greatly acknowledged. Part of this work is based on archival data, software or online services provided by the ASI SCIENCE DATA CENTER (ASDC). The authors wish to thank the anonymous referee for his/her comments and suggestions which improved the quality of the paper. L.F.F. and K.S. acknowledge partial support from the National Science Foundation award PHY-1407326.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 708, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abeysekara, A. U., Archambault, S., Archer, A., et al. 2015, ApJ, 815, L22 [NASA ADS] [CrossRef] [Google Scholar]
  3. Acciari, V. A., Aliu, E., Arlen, T., et al. 2010, ApJ, 708, L100 [NASA ADS] [CrossRef] [Google Scholar]
  4. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
  5. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Nature, 440, 1018 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2015, ApJ, 815, L23 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2016, A&A, 595, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 654, L119 [NASA ADS] [CrossRef] [Google Scholar]
  9. Aleksić, J., Anderhub, H., Antonelli, L. A., et al. 2010, A&A, 515, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
  11. Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2014a, A&A, 567, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2014b, A&A, 569, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Alves Batista, R., Dundovic, A., Erdmann, M., et al. 2016, J. Cosmol. Astropart. Phys., 5, 038 [NASA ADS] [CrossRef] [Google Scholar]
  14. Angel, J. R. P., & Stockman, H. S. 1980, ARA&A, 18, 321 [NASA ADS] [CrossRef] [Google Scholar]
  15. Archambault, S., Aune, T., Behera, B., et al. 2014, ApJ, 785, L16 [NASA ADS] [CrossRef] [Google Scholar]
  16. Becherini, Y., Boisson, C., Cerruti, M., & H. E. S. S. Collaboration 2012, in AIP Conf. Ser., 1505, eds. F. A. Aharonian, W. Hofmann, & F. M. Rieger, 490 [Google Scholar]
  17. Blandford, R. D., & Rees, M. J. 1978, Phys. Scr., 17, 265 [NASA ADS] [CrossRef] [Google Scholar]
  18. Caccianiga, A., & Marchã, M. J. M. 2004, MNRAS, 348, 937 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cerruti, M., Boisson, C., & Zech, A. 2013a, A&A, 558, A47 [EDP Sciences] [Google Scholar]
  20. Cerruti, M., Dermer, C. D., Lott, B., Boisson, C., & Zech, A. 2013b, ApJ, 771, L4 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cerruti, M., Zech, A., Boisson, C., & Inoue, S. 2015, MNRAS, 448, 910 [Google Scholar]
  22. Chen, X., Pohl, M., & Böttcher, M. 2015, MNRAS, 447, 530 [NASA ADS] [CrossRef] [Google Scholar]
  23. Danforth, C. W., Keeney, B. A., Stocke, J. T., Shull, J. M., & Yao, Y. 2010, ApJ, 720, 976 [NASA ADS] [CrossRef] [Google Scholar]
  24. de Naurois, M. 2015, Proc. 34th International Cosmic Ray Conference (ICRC2015), id.21 [Google Scholar]
  25. Dermer, C. D., Cerruti, M., Lott, B., Boisson, C., & Zech, A. 2014, ApJ, 782, 82 [Google Scholar]
  26. Essey, W., & Kusenko, A. 2010, Astropart. Phys., 33, 81 [Google Scholar]
  27. Essey, W., & Kusenko, A. 2014, Astropart. Phys., 57, 30 [NASA ADS] [CrossRef] [Google Scholar]
  28. Essey, W., Kalashev, O., Kusenko, A., & Beacom, J. F. 2011, ApJ, 731, 51 [Google Scholar]
  29. Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
  30. Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [Google Scholar]
  32. Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Furniss, A., Williams, D. A., Danforth, C., et al. 2013, ApJ, 768, L31 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ghisellini, G., & Tavecchio, F. 2008, MNRAS, 387, 1669 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [NASA ADS] [CrossRef] [Google Scholar]
  36. Giommi, P., Padovani, P., Polenta, G., et al. 2012, MNRAS, 420, 2899 [NASA ADS] [CrossRef] [Google Scholar]
  37. H.E.S.S. Collaboration, Abramowski, A., Acero, F., et al. 2013, A&A, 554, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kang, S.-J., Zheng, Y.-G., Wu, Q., & Chen, L. 2016, MNRAS, 461, 1862 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [NASA ADS] [CrossRef] [Google Scholar]
  40. Konigl, A. 1981, ApJ, 243, 700 [NASA ADS] [CrossRef] [Google Scholar]
  41. MAGIC Collaboration, Albert, J., Aliu, E., et al. 2008, Science, 320, 1752 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  42. Mankuzhiyil, N., Ansoldi, S., Persic, M., & Tavecchio, F. 2011, ApJ, 733, 14 [NASA ADS] [CrossRef] [Google Scholar]
  43. Massaro, E., Giommi, P., Leto, C., et al. 2009, A&A, 495, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Meyer, E. T., Fossati, G., Georganopoulos, M., & Lister, M. L. 2011, ApJ, 740, 98 [NASA ADS] [CrossRef] [Google Scholar]
  45. Meyer, E. T., Fossati, G., Georganopoulos, M., & Lister, M. L. 2012, ApJ, 752, L4 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mücke, A., & Protheroe, R. J. 2001, Astropart. Phys., 15, 121 [Google Scholar]
  47. Mücke, A., Engel, R., Rachen, J. P., Protheroe, R. J., & Stanev, T. 2000, Comput. Phys. Comm., 124, 290 [NASA ADS] [CrossRef] [Google Scholar]
  48. Murase, K., Dermer, C. D., Takami, H., & Migliori, G. 2012, ApJ, 749, 63 [Google Scholar]
  49. Nieppola, E., Valtaoja, E., Tornikoski, M., Hovatta, T., & Kotiranta, M. 2008, A&A, 488, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Padovani, P. 1992, MNRAS, 257, 404 [NASA ADS] [CrossRef] [Google Scholar]
  51. Padovani, P., Perlman, E. S., Landt, H., Giommi, P., & Perri, M. 2003, ApJ, 588, 128 [NASA ADS] [CrossRef] [Google Scholar]
  52. Padovani, P., Giommi, P., & Rau, A. 2012, MNRAS, 422, 48 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paiano, S., Landoni, M., Falomo, R., et al. 2017, ApJ, 837, 144 [Google Scholar]
  54. Petropoulou, M., & Dimitrakoudis, S. 2015, MNRAS, 452, 1303 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pita, S., Goldoni, P., Boisson, C., et al. 2014, A&A, 565, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Punch, M., Akerlof, C. W., Cawley, M. F., et al. 1992, Nature, 358, 477 [NASA ADS] [CrossRef] [Google Scholar]
  57. Rovero, A. C., Muriel, H., Donzelli, C., & Pichel, A. 2016, A&A, 589, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Salamon, M. H., & Stecker, F. W. 1998, ApJ, 493, 547 [NASA ADS] [CrossRef] [Google Scholar]
  59. Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [Google Scholar]
  60. Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
  61. Stickel, M., Padovani, P., Urry, C. M., Fried, J. W., & Kuehr, H. 1991, ApJ, 374, 431 [Google Scholar]
  62. Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [Google Scholar]
  63. Tavecchio, F., Ghisellini, G., Ghirlanda, G., Foschini, L., & Maraschi, L. 2010, MNRAS, 401, 1570 [Google Scholar]
  64. Yan, D., & Zhang, L. 2015, MNRAS, 447, 2810 [NASA ADS] [CrossRef] [Google Scholar]
  65. Yan, D., Kalashev, O., Zhang, L., & Zhang, S.-N. 2015, MNRAS, 449, 1018 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zdziarski, A. A., & Böttcher, M. 2015, MNRAS, 450, L21 [Google Scholar]
  67. Zech, A., Cerruti, M., & Mazin, D. 2017, A&A, 602, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Zhang, J., Liang, E.-W., Zhang, S.-N., & Bai, J. M. 2012, ApJ, 752, 157 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Parameters used for the one-zone SSC modeling of PKS 1424+240.

In the text
Table 2

Parameters used for the EIC modeling of PKS 1424+240.

In the text
Table 3

Parameters used for the hadronic modeling of PKS 1424+240.

In the text
Table 4

Parameters used in modeling the γ-ray data with UHECR-induced cascade emission.

In the text

All Figures

thumbnail Fig. 1

Archival SEDs (νLν in erg/s as a function of the rest-frame frequency in Hz) of four iconic VHE blazars: 3C 279 in green, PKS 1424+240 in red, PG 1551+113 in yellow and Mrk 421 in blue. The SEDs have been compiled using the ASDC SED builder tool (http://tools.asdc.asi.it/SED). Among these four sources, 3C 279 is the only one that has been detected at VHE only during flaring activity.

In the text
thumbnail Fig. 2

Adapted from Meyer et al. (2011). Distribution of blazars in the Lpeak−νpeak, showing the different blazar subclasses, as well as the two theoretical paths associated with a fast (A) and a slow (B) jet, observed at different angles. We overplot the position of the four VHE blazar shown in Fig. 1: 3C 279 in green, PKS 1424+240 in red, PG 1553+113 in yellow, and Mrk 421 in blue (for the low state). For PG 1553+113, the yellow band represents the uncertainty in its redshift.

In the text
thumbnail Fig. 3

One-zone SSC modeling of PKS 1424+240. The blue band represents all of the SSC models corresponding to the parameters given in Table 1. The black model represents the SSC solution provided by Kang et al. (2016). The black dashed line in the VHE regime represents the solution provided by Kang et al. (2016) computed at the source, before absorption on the EBL.

In the text
thumbnail Fig. 4

Two-zone SSC modeling of PKS 1424+240, using the model described in Chen et al. (2015). The green line represents the emission from the accelerating region, and the red one the emission from the diffusion region. The black line represents the combined emission from both zones.
In the text
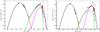thumbnail Fig. 5

Modeling of PKS 1424+240 in an EIC scenario, for the 2009 (left) and 2013 (right) campaigns. The black solid line represents the total emission; the red line represents the synchrotron emission by leptons; the green line the SSC component; the pink line the EIC component assuming that the external photon field is produced by the dusty torus. The model parameters are provided in Table 2. The models do not include absorption over the EBL. The VERITAS data (Archambault et al. 2014) deabsorbed using the EBL model by Franceschini et al. (2008) are plotted in red.

In the text
thumbnail Fig. 6

Modeling of PKS 1424+240 in a hadronic scenario, for the 2009 (left) and 2013 (right) campaigns, for a value of the Doppler factor δ = 30. Only the overall emission is plotted. The colors, from blue to red, represent a decrease in the size of the emitting region R, and an increase in the strength of the magnetic field B. The model parameters are provided in Table 3. The VERITAS data (Archambault et al. 2014) deabsorbed using the EBL model by Franceschini et al. (2008) are plotted in red.
In the text
thumbnail Fig. 7

Gamma-ray emission described by the hadronic scenario together with the predicted secondary γ-ray spectra from UHECR-initiated cascades along the line of sight for the 2009 (left) and 2013 (right) campaigns.
In the text
thumbnail Fig. 8

Predictions for secondary γ-ray spectra using different EBL models within the SSC scenario for the 2013 campaign. The required UHECR power for producing the secondary γ-rays is included in the legend for each EBL model.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.