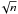| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630140 | |
| Published online | 07 September 2017 | |
Isotopic composition of CO2 in the coma of 67P/Churyumov-Gerasimenko measured with ROSINA/DFMS
1 Physikalisches Institut, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
e-mail: myrtha.haessig@space.unibe.ch
2 Space Science Division, Southwest Research Institute, 6220 Culebra Road, San Antonio, Texas, 78228, USA
3 Center for Space and Habitability, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
4 LATMOS/IPSL, UPMC, 4 place Jussieu, 75252 Paris Cedex 05, France
5 Climate and Space Sciences and Engineering, University of Michigan, Ann Arbor, MI 48109, USA
6 Royal Belgian Institute for Space Aeronomy (BIRA-IASB), Ringlaan 3, 1180 Brussels, Belgium
7 Institute of Computer and Network Engineering (IDA), TU Braunschweig, Hans-Sommer-Strasse 66, 38106 Braunschweig, Germany
8 University of Texas at San Antonio, 1 UTSA Circle, San Antonio, TX 78249, USA
Received: 23 November 2016
Accepted: 8 July 2017
Context. Measurements of isotopic abundances in cometary ices are key to understanding and reconstructing the history and origin of material in the solar system. Comets are considered the most pristine material in the solar system. Isotopic fractionation (enrichment of an isotope in a molecule compared to the initial abundance) is sensitive to environmental conditions at the time of comet formation. Therefore, measurements of cometary isotope ratios can provide information on the composition, density, temperature, and radiation during formation of the molecules, during the chemical evolution from the presolar cloud to the protosolar nebula, and the protoplanetary disk before accretion in solid bodies. Most isotopic abundances of 12C/13C and 16O/18O in comets to date are in agreement with terrestrial abundances. Prior to the Rosetta mission, measurements of 12C/13C in comets were only available for HCN, CN, and C2 and for 16O/18O in H2O. Measurements of 12C/13C in comets were only available from ground based observations and remote sensing, while 16O/18O in H2O had also been measured in-situ. To date, no measurements of the CO2 isotopologues in comets were available.
Aims. This paper presents the first measurements of the CO2 isotopologues in the coma of 67P/Churyumov-Gerasimenko (67P).
Methods. We analyzed measurements taken by the Double Focusing Mass Spectrometer (DFMS) of the ROSINA experiment on board the ESA spacecraft Rosetta in the coma of 67P.
Results. The CO2 isotopologues results for 67P are: 12C/13C = 84 ± 4, 16O/18O = 494 ± 8, and 13C16O2/12C18O16O = 5.87 ± 0.07. The oxygen isotopic ratio is within error bars compatible with terrestrial abundances but not with solar wind measurements.
Conclusions. The carbon isotopic ratio and the combined carbon and oxygen isotopic ratio are slightly (14%) enriched in 13C, within 1σ uncertainty, compared to solar wind abundances and solar abundances. The small fractionation of 12C/13C in CO2 is probably compatible with an origin of the material in comets from the native cloud.
Key words: comets: individual: 67P / astrochemistry / methods: data analysis / Kuiper belt objects: individual: 67P / comets: general
© ESO, 2017
1. Introduction
To understand and reconstruct the history and origin of material in the solar system, measurements of isotopic abundances are key. Since comets are considered to contain some of the most pristine material in the solar system, measurements of isotopic abundance ratios of different atoms in different molecules are important. Isotopic fractionation describes the processes which affect the relative abundances of the isotopes. Isotopic fractionation is sensitive to environmental conditions at the time of comet formation. Therefore, measurements of isotope ratios provide information on the composition, density, temperature, and radiation during formation of the molecules and during the chemical evolution from the presolar cloud to the protosolar nebula and the protoplanetary disk before accretion in solid bodies. This paper focuses on the isotopic abundance of 13C and 18O in CO2 for 67P/Churyumov-Gerasimenko (hereafter: 67P). It is the first time that these isotopologues have been measured in a comet.
The local interstellar medium (ISM) has an isotopic abundance ratio of 12C/13C (CN, CO and H2CO) of 68±15 and this ratio changes over galactic timescales as a function of galactocentric distance and time (Milam et al. 2005). The modeling results of Roueff et al. (2015) for the prestellar core and a moderately dense cloud show that the 12C/13C ratios for various molecules in the ISM are highly sensitive to the chemical evolution time of the prestellar core or moderate dense cloud. Various chemical reactions are responsible for incorporating 13C in molecules and the transition from gas-phase atomic carbon towards CO controls the 13C enrichment. As long as there is still a relatively high carbon-atom concentration in the gas phase, there is enough free 13C to allow strong enrichment of CN through the 13C + CN reaction (Roueff et al. 2015). Because eventually most of the carbon is locked into CO and the 12C/13C ratio is very close to the atomic 12C/13C ratio after 106 yr, this ratio will change very little. Similar ratios are incorporated in CO2 through the reaction of CO with OH (Woods & Willacy 2009).
The present-day terrestrial isotopic abundance ratio of 12C/13C is 89 (Meija et al. 2016). Meija et al. (2016) list the isotopic composition of the elements, while the best measurement of isotopic abundances from a single terrestrial source (NBS 19) is cited as a measurement by Zhang et al. (1990). The terrestrial abundances by Lodders (2003) are based on Rosman & Taylor (1998) and use the same reference as standard for terrestrial 12C/13C abundances. However, there exists a lower ratio of 80±1 for the solar photosphere (Ayres et al. 2006). The 12C/13C ratio of 68 for the local interstellar medium is considerably lower than terrestrial. An even higher ratio than the terrestrial ratio was found in the solar wind by Hashizume et al. (2004). This may be attributed to 12C enrichment caused by the proximity of the Sun to one or more massive stars, which produce 12C in their interiors (Timmes et al. 1995). These stars may have contaminated the solar protoplanetary nebula with 12C-rich material during its formation (Woods & Willacy 2009). The solar wind measurements by Hashizume et al. (2004) are much older than the measurements of the oxygen isotopes in the solar wind by NASA’s Genesis mission (McKeegan et al. 2011). According to the findings by McKeegan et al. (2011) the solar wind measurements do not directly represent the solar abundance. As the most plausible composition of the Sun, the intersection of the calcium-aluminium-rich inclusions of chondritic meteorites and the solar wind measurements was used. However, there are no measurements available from the Genesis mission for carbon isotopes and in Hashizume et al. (2004) no such calculations are provided. Therefore the measurements by Hashizume et al. (2004) are used as the 12C/13C solar abundance, although based on the findings by McKeegan et al. (2011) the real solar abundance might be somewhere between the solar wind measurements of 98 ± 2 and the value of 89 by Anders & Grevesse (1989).
It is important to note, however, that the carbon isotopic ratio is not constant within the solar system. While meteorites in general have isotopic ratios close to 89, interplanetary dust particles (e.g., Zinner et al. 1995: 12C/13C 7 to 4500) and cometary dust (e.g., Jessberger 1999: 12C/13C ~ 5000) show deviations from this mean value. These solar system components conserved part of the original traces of nucleosynthesis in the star from which they obtained their carbon. Carbon trapped within the 50 nm thick surface layer of the lunar regolith exhibits a depletion of 13C in solar wind of at least 10% relative to terrestrial and meteoritic carbon (Hashizume et al. 2004). Hashizume et al. (2004) provide a solar wind value for the 12C/13C ratio of 98 ± 2. In primitive ice, by far the most abundant carbon-bearing molecule is CO, and CO2 is chemically derived from CO. In the native molecular cloud, little 13C enrichment or depletion is expected for these molecules. According to Woods & Willacy (2009), there might be carbon fractionation in the protoplanetary disk depending on the chemical reactions, species, and temperature along the direction perpendicular to the disk, and depending on the distance from the Sun in the case of a solar nebula-like disk. According to their model, C2 would be depleted in 13C compared to CN and HCN. Their model also predicts that CO2 and CO would be enriched in 13C compared to the solar value depending on the location in the disk. Among the molecules remotely observed in several comets are C2, CN, and HCN. Remote sensing measurements of a variety of comets show that there are no large differences in the carbon isotopic abundance depending on the molecule (see Table 3 and Fig. 1). Most measurements are compatible with solar or terrestrial abundances within error bars. Small variations between the different molecules are observed between different comets, but no significant variations are seen for a single species. The error bars of all the remote sensing measurements are more than 10% with the exception of the 12CN/13CN ratio of Manfroid et al. (2009), which represents an average over 21 comets. While on average C2 and CN agree well within terrestrial abundances of 89, HCN appears to be somewhat depleted in 13C although the deviation is less than 2σ. No remote sensing measurements for the isotopic abundance of 12C/13C in CO or CO2 exist because, to this date, no pure rotation spectra in the infrared or microwave regions for CO2 are available. Therefore there is a lack of detections of CO and CO2 detections of rare isotopologues. The terrestrial 16O/18O ratio derived from measurements of Vienna Mean Standard Ocean Water is known to be 499 (Meija et al. 2016; Lodders 2003; and Anders & Grevesse 1989), while the ratio in solar wind samples captured by the Genesis mission provides a solar abundance of 530 (McKeegan et al. 2011). By mass balance the latter could be considered the abundance of the protoplanetary nebula. The measurements presented here are discussed in the context of both of these ratios. Remote sensing and in situ measurements for comets of oxygen isotopes are only available for H2O and these measurements have rather large uncertainties. Most measurements are within error bars compatible with both known values. Solar and terrestrial isotopic abundances for 12C/13C and 16O/18O from the literature are given in Table 1. The purpose of this paper is to report the first in situ measurement of the isotopic abundance of carbon and oxygen in CO2 for 13C and 18O. CO2 is originally derived from CO (due to chemical reactions) and together they represent the largest carbon reservoir in the solar system (Lewis & Prinn 1980). Even if isotopic fractionation plays a role for minor carbon bearing species, it would be difficult to significantly change the 12C/13C ratio in CO and CO2 (see Woods & Willacy 2009). The 12C/13C ratio in CO and CO2 in comets may therefore provide an additional clue as to the initial isotopic ratio for C in the protoplanetary nebula. The Rosetta mission spent months exploring the coma of comet 67P/Churyumov-Gerasimenko, measuring this coma with a wide variety of instruments. One of the instruments on board is ROSINA (Rosetta Orbiter Spectrometer for Ion and Neutral Analysis Balsiger et al. 2007). ROSINA consists of three sensors, out of which the instrument of choice for isotopologues is the Double Focusing Mass Spectrometer (DFMS).
 |
Fig. 1 Measurements of 12C/13C in different molecules for several comets (for references see Table 3). Several measurements of 12C/13C in the coma of 67P were taken by ROSINA/DFMS. The coma of 67P shows an enrichment of 13C in CO2 (black circle, this work) compared to solar abundance. For discussion on uncertainties see Sects. 4 and 5. The dotted horizontal line represents the terrestrial 12C/13C ratio. The solid horizontal line (dashed lines represent uncertainties) represents the solar wind 12C/13C ratio. |
Solar abundances for carbon and oxygen isotopes.
1.1. ROSINA DFMS Sensor on Rosetta
ROSINA/DFMS is a high-resolution mass spectrometer designed to resolve molecules of nearly identical mass and measure isotopic abundances. A detailed description of the instrument and its capabilities can be found in Balsiger et al. (2007), while data analysis methods are extensively described in several ROSINA/DFMS papers (e.g., Le Roy et al. 2015; and Calmonte et al. 2016). DFMS is a double focusing mass spectrometer with a high mass resolution and very high dynamic range, which separates species according to their mass to charge ratio (m/z). The high mass resolution of 3000 at 1% peak level allows the separation of, for example, 12CH from 13C, while the very high dynamic range of ~1010 was very important for the encounter with 67P because the difference in densities from CO2 (and H2O) to the rarest of volatiles was expected to be four orders of magnitude, while the variations in H2O and CO2 outgassing were expected to present an additional three orders of magnitude difference from initial encounter to perihelion. The principles by which DFMS operates are as follows: cometary neutrals (both atoms and molecules) enter ROSINA/DFMS and are ionized by electron ionization. The formed ions are guided through the electrostatic analyzer and the magnet where they are separated according to their mass to charge ratio (m/z). Only ions with a specific m/z value have a stable trajectory through the instrument and DFMS sequentially measures masses between 13 to more than 100 u/e. One m/z scan takes approximately 20 s so that the entire mass range is typically covered in about 45 min. Particles with the selected m/z then hit the micro channel plate (MCP), where they release an avalanche of electrons. A linear detector array (LEDA) consisting of two individual rows with 512 pixels each then detects these electrons. The avalanche of electrons released, thus the gain of the detector, is controlled by the voltage applied over the MCP. The 16 separate voltage settings over the MCP are also called gain steps. The LEDA detects the electron charge of each individual pixel. The collimated ion beam typically hits the center of the MCP. This causes a preferential degradation of the center pixels of the MCP compared to the edge pixels of the MCP as a function of time. To account for this MCP ageing over the mission duration, the ion beam is regularly swept across all MCP/LEDA pixels and the results allow a correction factor for each individual pixel to be established.
 |
Fig. 2 Measured signal averaged over 87 co-added 20s spectra and detected species on m/z 44 u/e, 45 u/e, and 46 u/e. The circles show the measured points on the detector, while the dashed lines are the fit of the according peak fits. The solid line represents the sum of all fits. Error bars represent the uncertainty due to counting statistics ( |
DFMS measurements have already contributed significantly to cometary science by confirming and discovering cometary species (e.g., N2 by Rubin et al. 2015; O2 by Bieler et al. 2015), by providing a link between remote sensing and in situ coma measurements (Le Roy et al. 2015), by discovering high variations in local compositional densities (Hässig et al. 2015; and Luspay-Kuti et al. 2015), and by obtaining measurements of isotopic species with very low abundances (D/H by Altwegg et al. 2015).
1.2. Methodology for determining isotopic abundances with ROSINA/DFMS
Measurements on different gain steps, pixel gain across the MCP, and the time required to measure two individual isotopologue provide the largest uncertainties in measuring isotopic ratios with DFMS. Ideally, these uncertainties are minimized by comparing two mass peaks taken with the same gain step at the same location on the MCP and within as short amount of time as possible. These conditions are not always met and minimizing the uncertainties drives the data analysis. Three possibilities exist to measure isotopic ratios with DFMS: the first and second using two different masses, and the third using nearly the same mass (e.g., HD16O and H217O):
-
1.
The species for an isotopic ratio measurement are on differentmasses. If the isotopic abundance ratio is within dynamic range ofthe LEDA and no other high abundance species is determining thegain of the detector, then the measurements are taken on the samegain step and only corrections for the pixel gain have to be takeninto account. For measurements of species with the peak center onthe same location of the detector, (which is normally the case forisotopologues) the correction due to the individual pixel gain isvery small and measurements are therefore considered veryprecise.
-
2.
The species for an isotopic ratio measurement are on different masses. If the species do not have a similar abundance and the peak center is shifted by several pixels, corrections for the different gain steps and the individual pixel gain have to be taken into account.
-
3.
The isotopic ratio is measured on the same mass but a combination of several isotopes. Therefore, no gain step uncertainties have to be taken into account. However, due to the shift in position between the two peaks, a pixel gain correction is applied to account for the ageing of the multi channel plate (MCP) due to impinging ions on the same location of the MCP. This method is precise, but possible only for a few species, for example, 18OH, HD16O and H
 O, all on mass 19.
O, all on mass 19.
The first method is applied for the measurement of the CO2 isotopes. On m/z 44, 45, 46 u/e the following CO2 isotopologues are found:
-
44 u/e: 12C16O2;
-
45 u/e: 13C16O2 and 12C17O16O;
-
46 u/e: 12C18O16O and 13C17O16O and 12C17O2.
The abundance of molecules containing 17O is one magnitude smaller than that for 13C or 18O and was therefore negligible.
A second source of uncertainty is the subtraction of neighboring peaks that overlap with isotopologues of interest.
In addition to the above-mentioned molecules, the following additional molecules are found on m/z 44, 45, 46 u/e, overlapping with the signal peak of CO2 isotopes (see Fig. 2):
-
44 u/e: CS, C2H4O;
-
45 u/e: CHS, CHO2;
-
46 u/e: CH2S, NO2, CH2O2.
The contribution of C2H4O to the signal for CO2 is clearly negligible, as it is at least three orders of magnitude lower. The difference in mass per charge between NO2 and 12C18O16O is only 0.002 u/e and cannot be resolved with DFMS. The abundance of NO2 was therefore assumed to be negligible (see Sect. 4.), resulting in a possible overestimation of the signal abundance of 12C18O16O. As shown later, there is good observational data to substantiate this assumption.
The peak shape of DFMS is well known and signals of overlapping peaks are resolved by fitting a double Gaussian to the measured points. The peak location is known and the width of the peak is the same for all species on an integer mass spectrum, which then leaves the amplitudes for the different peaks and the common FWHM (Full Width Half Maximum) as fit parameters. This peak-fitting method was already successfully used to separate H217O and HD16O (Altwegg et al. 2015) and to separate N2 from CO (Rubin et al. 2015).
Results of the three different analysis methods to determine the isotopologues of CO2 in the coma of 67P/Churyumov-Gerasimenko measured with ROSINA/DFMS.
2. DFMS measurements in the coma of 67P/Churyumov-Gerasimenko
Two different periods were chosen, 19–24 October 2014 at a distance of ~10 km from the center of the comet during almost circular orbits (3.15 au from the Sun) and 21–25 December 2015 (1.95 au from the Sun). The first period contains measurements covering both cometary hemispheres (−47° to 50° sub-spacecraft latitude, Jorda et al. 2015) and several cometary rotations, while the latter consists of measurement of positive latitudes (34°–70°) covering several cometary rotations at a distance of 75–92 km from the center of the nucleus. The first measurement period was chosen because of the close distance to the comet and therefore high abundances of the species in the coma (especially 13C16O2 and 12C18O16O). The second period was specifically chosen because of its relatively low abundance in CO2, resulting in measurements for m/z 44–46 u/e on the same gain step.
 |
Fig. 3 Signal for 13C16O2 versus 12C18O16O in the coma of 67P. The top panel black squares show the correlation of the signal for 21–25 December 2015. The bottom panel shows the data set of October 2014 (circles) and the measurements of December 2015 (the black squares in the left corner). Error bars show uncertainties of the single measurements. The red line is the least square linear fit. |
3. Data treatment
To deduce the isotopic ratios of 16O/18O and 12C/13C in CO2, measurement of mass per charge 44 u/e, 45 u/e, and 46 u/e are recorded. These masses are measured one after the other during normal measurement scans. The time difference in recording time between the first and the last mass is less than two minutes; therefore the compositional changes in the coma (cf. rotation period ~12 h by Mottola et al. 2014) between measurements of these three masses are assumed to be negligible. Each individual spectrum was corrected for the individual pixel gain of the MCP for the period in question.
The peak of mass per charge 44 u/e is dominated by the signal of CO2. The signal for CS is two orders of magnitude smaller than the signal for CO2 (see Fig. 2) but still taken into account when calculating the signal for CO2. A separation of several peaks is therefore not needed and the signal for CO2 is taken as the sum of the signal under the whole peak. The signal on m/z 45 u/e and 46 u/e were fitted using the above-mentioned method. For the signal for 13C16O2, 12C18O16O and CO2, the sum over the fitted peak is used.
Background contamination of the signal due to spacecraft outgassing (Schläppi et al. 2010) was subtracted from the measured peak signals. For the October 2014 data set, the spacecraft background was determined from the signal of 1 August 2014, when the spacecraft was still far away from the comet and the coma signal was not yet detected. The subtracted spacecraft background for the December 2015 period was determined as the lowest signal for CO2 during this time period (2× smaller than the signal for background determined in 2014) and terrestrial abundances for the signal of the other isotopes were determined. The signal for CO2 is two orders of magnitude higher than the signal for the other (rarer) isotopologues, resulting mostly in measurements on different gain steps and therefore an additional correction has to be taken into account, which adds to the total uncertainty.
 |
Fig. 4 Measured signal on the detector for 13C16O2 and 12C18O16O versus 12C16O2. The red line represents the resulting linear fit. |
To reduce the influence of the gain step, the ratio for m/z 46/45 is used. The signals for 12C18O16O and13C16O2 are similar in abundance (within a factor of ~3) and therefore always measured on the same gain step. The remaining correction is then only due to the individual pixel gain, and since the difference in pixel is never more than three pixels this choice of isotopologues results in a very accurate measurement of the combined isotopic ratio of 13C16O2/12C18O16O.
4. Results
We divide the measured isotopic ratios for CO2 into three sections: 13C16O2/12C18O16O, 16O/18O, and 12C/13C. For the data from the time period in December 2015 (the time where the gain step was similar for each consecutive mass spectrum at m/z 44, 45, 46), three different analysis methods were chosen to calculate the isotopic ratios and therefore provide comparison: a) each individual spectrum was fitted to separate the signals of the different isotopologues in overlapping peaks. Then the total signal for the individual isotopologue was derived by adding up the contribution from all spectra and then divided by the total signal of the other isotopologue to determine the ratio; b) all spectra were co-added based on the mass scale, resulting in a single spectrum for each mass. The signal for the individual isotopologue is determined by fitting the overlapping peaks resulting in signals for each isotopologue; c) each individual spectrum was fitted to separate the isotopologue signal from overlapping peaks. From each triplet of back-to-back measurements of mass per charge 44 u/e, 45 u/e, and 46 u/e isotopic ratios were derived to investigate possible correlations. The slope of the linear fitted curve corresponds then to the measured isotopic ratio. The linear fit takes into account the individual uncertainties of the measurements resulting in a least squares fit.
The total uncertainty of the sum of the signal is composed of the ion statistical counting uncertainty and the pixel gain uncertainty of 5%. The total uncertainty of the co-added spectra takes into account the peak fitting uncertainty (7%) and the ion statistical uncertainty. The uncertainty of the linear fit of the correlation is the standard error of the fit.
Due to stochastic effects, the oxygen isotope has a two times higher probability of being found in the signal for 12C18O16O, therefore a factor of 2 has to be taken into account (compare results for linear fit in Figs. 4 to 5). Table 2 shows an overview of the measured ratios in CO2 for the sum of the signal, the co-added spectra, and the linear fit. The results of the individual analysis methods are all overlapping within uncertainties and show that the results are independent of the analysis method.
13C16O2/12C18O16O in CO2: in addition to the December 2015 data, the measurements for 12C18O16O/13C16O2 in CO2 for the time period of October 2014 are all measured on the same gain step, therefore a total of five measurements (two sum of the signal, two linear fit, and one co-added spectra) are provided. The least square linear fit for the time period of October 2014 and December 2015 is shown in Fig. 3. The measurements of the two time periods show a good correlation (R2 > 0.97). If there were contamination of the 12C18O16O signal by NO2, the correlation is expected to show this due to the compositional changes in the coma between the northern and southern hemisphere (Le Roy et al. 2015). The good correlation therefore shows that either there is no or negligible contamination of the signal with NO2 or the signal would be perfectly correlated with CO2. The results of the different analysis methods for the two time periods are overlapping within uncertainties. The uncertainty of the average takes into account the individual uncertainties as well as the standard uncertainty of the average. The average of these three methods for two time periods and resulting uncertainty for 13C16O2/12C18O16O in the coma of 67P is 2.93 ± 0.04.
16O/18O: the results of the three different analysis methods (least square linear fit in Fig. 4) are overlapping within uncertainties. The uncertainty of the average takes into account the individual uncertainties as well as the standard uncertainty of the average. The average of these three methods and resulting uncertainty for 18O/16O in CO2 in 67P’s coma is 494 ± 8 ((2.03 ± 0.03)×10-3). The average itself shows slight enrichment in 18O, but is within uncertainties still consistent with the terrestrial value by Meija et al. (2016) (499) and also in agreement with earlier measurements in H2O by ROSINA/DFMS 556 ± 62Altwegg et al. (2015).
Isotopic abundances in comets adopted from Jehin et al. (2009), Woods (2009), and Bockelée-Morvan et al. (2015).
 |
Fig. 5 Measurements of 16O/18O in water and carbon dioxide for several comets (for references see Table 3). The measurement of 16O/18O in CO2 shows a significantly smaller error bar than earlier measurements (black circle) and is within uncertainties compatible with a terrestrial abundance by Meija et al. (2016) (dotted line 16O/18O) but not with a solar abundance by McKeegan et al. (2011) of 530 (solid line). |
12C/13C: the ratios of the three different analysis methods (least squares linear fit in Fig. 4) are overlapping within uncertainties. The uncertainty of the average takes into account the individual uncertainties as well as the standard uncertainty of the average. The average of these three methods and resulting uncertainty for 12C/13C in CO2 in 67P’s coma is 84±4 ((1.19±0.05)×10-2). This ratio is not in agreement with the solar wind abundance by Hashizume et al. (2004) nor with the terrestrial standard provided by Zhang et al. (1990), although the latter is almost compatible. The 12C/13C for CO2 in 67P’s coma by ROSINA/DFMS shows an enrichment in 13C of 6% compared to terrestrial abundances by Meija et al. (2016) and a 14% enrichment compared to solar abundances, which is not compatible even within uncertainties (1σ). Other measurements with ROSINA/DFMS in different molecules, namely C2H4, C2H5, and CO show a similar behavior for 12C/13C (including fragments of CO2) (Rubin et al. 2017). However, these measurements provide a substantially larger error bar than presented for the 12C/13C in CO2 in 67P’s coma as their investigated period was specifically chosen to analyze silicon isotopes and shows large interferences between 13CO and HCO, resulting in larger uncertainties.
5. Discussion
The measurements presented show a slight enrichment in 13C in the 12C/13C ratio which is not in agreement with measurements by remote sensing of carbon isotopes in other molecules (see Table 3 and Fig. 1). Contrary to the DFMS results at 67P, two measurements of HCN show even a depletion of 13C compared to the solar system abundance. Measurements of the carbon isotope in HCN are not feasible for DFMS due to overlapping peaks with DCN and CH2N. An overview on feasible isotopic measurements by ROSINA/DFMS is given by Bockelée-Morvan et al. (2015). However, in most cases error limits are too large to make these differences significant. Our ratio is, on the other hand, compatible with measurements in CO (including 1/3 fragments of CO2) and C2H4 and C2H5 (which both are most probably fragments of ethane) in 67P’s coma by ROSINA/DFMS (Rubin et al. 2015).
For the 16O/18O ratio, the DFMS value is compatible with a terrestrial value within the error limit of 2%, the most precise value so far for the 16O/18O ratio in comets. If there is a depletion or enrichment of the heavy oxygen isotope in CO2 it has to be small. The measurements of the combined carbon and oxygen isotopes (13C16O2 and 12C18O16O) are, for the two time ranges, compatible within uncertainties. However, the focus for the selection of those data sets was based on minimizing instrumental uncertainties to detect time dependent variations or heterogeneity in the coma of the comet and would require a careful analysis of the total data available, which is not the scope of this paper.
6. Conclusion
The isotopic measurements for CO2 are the first ever presented in situ measurements of 12C/13C and 16O/18O in CO2 for a cometary coma. The derived 16O/18O ratio of 494±8 is compatible with a terrestrial abundance of 499 by Meija et al. (2016) but not with a solar abundance of 530 by McKeegan et al. (2011). The 12C/13C ratio of 84±4 (1.19±0.05)% is 6% (1σ) lower than the terrestrial value of 1.12% and 14% higher than solar wind abundance, although given the slight difference between the upper limit of the measured value and the terrestrial standard it could be considered compatible with a terrestrial origin. It is in very good agreement with the value derived in 67P for 12C/13C in CO that contains the signal of the CO2 fragment and the parent (Rubin et al. 2017). The model by Woods & Willacy (2009) predicts a slight carbon fractionation in the midplane at distances inside of 25AU as well as for material vertically offset for CO and CO2. The model prediction of the 12C/13C ratio in HCN for comets is not compatible with most measurements in comets provided in Table 3. Several possible explanations are provided by Woods & Willacy (2009). One explanation is that the protosolar disk was heated to a temperature high enough so that carbon isotopic ratios are mixed to the extent that carbon isotopic abundances in all molecules is similar. This explanation can probably be ruled out because measurements of D/H in water taken at the same time show a very high ratio for 67P (Altwegg et al. 2015) compared to other measurements in comets or terrestrial values. With the same argument, the possibility of relying on mixing material up to the surface layers of the disk (dissociating the molecules), which then leads to a reset of the carbon isotope ratio, can also be ruled out. That is, unless there is a difference of volatility between CO and CO2 relative to water because water is frozen out on grains. Then it can be argued that grains did not mix, whereas gas did. In addition, the third explanation of a passing shock affecting the protosolar disk proposed by Woods & Willacy (2009) does not seem plausible for the solar system as again all material would have passed through this shock and no fractionation of isotopes would be seen in cometary volatiles. The small fractionation of 12C/13C in CO and CO2, together with some possible fractionation in HCN (reference in Table 3), is probably compatible with the 12C/13C ratio inherited from the original protosolar cloud. That means that according to the model by Woods & Willacy (2009), 67P formed at distances further away from the Sun than 25 AU. This formation location is then in agreement with D/H in water, D2O, and HDS (Altwegg et al. 2017) which all point to a heritage from the native cloud in the protosolar nebula.
Acknowledgments
ROSINA would not give such outstanding results without the work of the many engineers, technicians, and scientists involved in the mission, in the Rosetta spacecraft, and in the ROSINA instrument team over the last 20 yr, whose contributions are gratefully acknowledged. Rosetta is a European Space Agency (ESA) mission with contributions from its member states and NASA. We acknowledge herewith the work of the whole ESA Rosetta team. Funding: work at University of Bern was funded by the State of Bern, the Swiss National Science Foundation, and the ESA PRODEX (PROgramme de Développement d’Expériences scientifiques) program. Work at Southwest Research Institute was supported by subcontract #1496541 and #1345493 from the Jet Propulsion Laboratory (JPL). Work at the Royal Belgian Institute for Space Aeronomy (BIRA-IASB) was supported by the Belgian Science Policy Office via PRODEX/ROSINA PRODEX Experiment Arrangement 90020. This work was supported by CNES (Centre National d’Études Spatiales). Work at the University of Michigan was funded by NASA under contract JPL-1266313.
Data and materials availability: all ROSINA data have been and will be released to the Planetary Science Archive of ESA (http://www.cosmos.esa.int/web/psa/rosetta) and to the Planetary Data System archive of NASA (https://pds.nasa.gov/). All data needed to evaluate the conclusions in the paper are present in the paper. Additional data related to this paper may be requested from the authors.
The authors would like to thank the referees for constructive criticism, comments, and input, which helped to improve the clarity and quality of the paper.
References
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2015, Science, 347, 1261952 [Google Scholar]
- Altwegg, K., Balsiger, H., Berthelier, J.-J., et al. 2017, Phil. Trans. R. Soc. A, 375, 20160253 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochimica et Cosmochimica acta, 53, 197 [Google Scholar]
- Arpigny, C., Jehin, E., Manfroid, J., et al. 2003, Science, 301, 1522 [CrossRef] [PubMed] [Google Scholar]
- Ayres, T. R., Plymate, C., & Keller, C. U. 2006, ApJS, 165, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Balsiger, H., Altwegg, K., & Geiss, J. 1995, J. Geophys. Res.: Space Phys., 100, 5827 [Google Scholar]
- Balsiger, H., Altwegg, K., Bochsler, P., et al. 2007, Space Sci. Rev., 128, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, Nature, 526, 678 [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Crovisier, J., et al. 2007, Planet. Space Sci., 55, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Biver, N., Moreno, R., Bockelée-Morvan, D., et al. 2016, A&A, 589, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Biver, N., Jehin, E., et al. 2008, ApJ, 679, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Biver, N., Swinyard, B., et al. 2012, A&A, 544, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Calmonte, U., Charnley, S., et al. 2015, Space Sci. Rev., 197, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Calmonte, U., Balsiger, K. A. H., Berthelier, J., et al. 2016, MNRAS, 462, 253 [Google Scholar]
- Decock, A., Jehin, E., Rousselot, P., et al. 2014, in International Comet Workshop (April 1–3), Toulouse, France [Google Scholar]
- Eberhardt, P., Reber, M., Krankowsky, D., & Hodges, R. 1995, A&A, 302, 301 [NASA ADS] [Google Scholar]
- Hashizume, K., Chaussidon, M., Marty, B., & Terada, K. 2004, ApJ, 600, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Hutsemékers, D., Manfroid, J., Jehin, E., et al. 2005, A&A, 440, L21 [CrossRef] [EDP Sciences] [Google Scholar]
- Hutsemekers, D., Manfroid, J., Jehin, E., Zucconi, J.-M., & Arpigny, C. 2008, A&A, 490, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hässig, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 347, 0276 [CrossRef] [Google Scholar]
- Jaworski, W. A., & Tatum, J. B. 1991, ApJ, 377, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Manfroid, J., Cochran, A., et al. 2004, ApJ, 613, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Manfroid, J., Hutsemékers, D., et al. 2006, ApJ, 641, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Manfroid, J., Hutsemekers, D., Arpigny, C., & Zucconi, J.-M. 2009, Earth Moon Planets, 105, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Hutsemekers, D., Manfroid, J., et al. 2011, EPSC Abstracts 2011, 1463 [Google Scholar]
- Jessberger, E. K. 1999, in Composition and Origin of Cometary Materials (Springer), 91 [Google Scholar]
- Jewitt, D. C., Matthews, H. E., Owen, T., & Meier, R. 1997, Science, 278, 90 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jorda, L., Gaskell, R., Hviid, S., et al. 2015, Shape models of 67P/Churyumov-Gerasimenko, Tech. Rep., RO-C-OSINAC/OSIWAC-5-67P-SHAPE-V1. 0., NASA Planetary Data System and ESA Planetary Science Archive [Google Scholar]
- Kleine, M., Wyckoff, S., Wehinger, P. A., & Peterson, B. A. 1995, ApJ, 439, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D., & Danks, A. 1983, ApJ, 268, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Le Roy, L., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, J., & Prinn, R. 1980, ApJ, 238, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D., Keene, J., Young, K., et al. 1997, Icarus, 130, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Luspay-Kuti, A., Hässig, M., Fuselier, S., et al. 2015, A&A, 583, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manfroid, J., Jehin, E., Hutsemékers, D., et al. 2009, A&A, 503, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKeegan, K., Kallio, A., Heber, V., et al. 2011, Science, 332, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Meija, J., Coplen, T. B., Berglund, M., et al. 2016, Pure Appl. Chem., 88, 293 [Google Scholar]
- Milam, S., Savage, C., Brewster, M., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Mottola, S., Lowry, S., Snodgrass, C., et al. 2014, A&A, 569, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosman, K., & Taylor, P. 1998, Pure Appl. Chem., 70, 217 [CrossRef] [Google Scholar]
- Roueff, E., Loison, J., & Hickson, K. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousselot, P., Jehin, E., Manfroid, J., & Hutsemekers, D. 2012, A&A, 545, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubin, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 348, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, M., Altwegg, K., Balsiger, H., et al. 2017, A&A, 601, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schläppi, B., Altwegg, K., Balsiger, H., et al. 2010, J. Geophys. Res.: Space Phys., 115, A12313 [Google Scholar]
- Shinnaka, Y., Kawakita, H., Nagashima, M., et al. 2014, in AAS/Division for Planetary Sciences Meeting Abstracts, 46 [Google Scholar]
- Timmes, F., Woosley, S., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, P. M. 2009, arXiv e-print [arXiv:0901.4513] [Google Scholar]
- Woods, P. M., & Willacy, K. 2009, ApJ, 693, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Wyckoff, S., Lindholm, E., Wehinger, P. A., et al. 1989, ApJ, 339, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Wyckoff, S., Kleine, M., Peterson, B. A., Wehinger, P. A., & Ziurys, L. M. 2000, ApJ, 535, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Chang, T., & Li, W. 1990, Chinese Science Bulletin, 35, 290 [Google Scholar]
- Zinner, E., Amari, S., Wopenka, B., & Lewis, R. S. 1995, Meteoritics, 30, 209 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Results of the three different analysis methods to determine the isotopologues of CO2 in the coma of 67P/Churyumov-Gerasimenko measured with ROSINA/DFMS.
Isotopic abundances in comets adopted from Jehin et al. (2009), Woods (2009), and Bockelée-Morvan et al. (2015).
All Figures
 |
Fig. 1 Measurements of 12C/13C in different molecules for several comets (for references see Table 3). Several measurements of 12C/13C in the coma of 67P were taken by ROSINA/DFMS. The coma of 67P shows an enrichment of 13C in CO2 (black circle, this work) compared to solar abundance. For discussion on uncertainties see Sects. 4 and 5. The dotted horizontal line represents the terrestrial 12C/13C ratio. The solid horizontal line (dashed lines represent uncertainties) represents the solar wind 12C/13C ratio. |
| In the text | |
 |
Fig. 2 Measured signal averaged over 87 co-added 20s spectra and detected species on m/z 44 u/e, 45 u/e, and 46 u/e. The circles show the measured points on the detector, while the dashed lines are the fit of the according peak fits. The solid line represents the sum of all fits. Error bars represent the uncertainty due to counting statistics ( |
| In the text | |
 |
Fig. 3 Signal for 13C16O2 versus 12C18O16O in the coma of 67P. The top panel black squares show the correlation of the signal for 21–25 December 2015. The bottom panel shows the data set of October 2014 (circles) and the measurements of December 2015 (the black squares in the left corner). Error bars show uncertainties of the single measurements. The red line is the least square linear fit. |
| In the text | |
 |
Fig. 4 Measured signal on the detector for 13C16O2 and 12C18O16O versus 12C16O2. The red line represents the resulting linear fit. |
| In the text | |
 |
Fig. 5 Measurements of 16O/18O in water and carbon dioxide for several comets (for references see Table 3). The measurement of 16O/18O in CO2 shows a significantly smaller error bar than earlier measurements (black circle) and is within uncertainties compatible with a terrestrial abundance by Meija et al. (2016) (dotted line 16O/18O) but not with a solar abundance by McKeegan et al. (2011) of 530 (solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.