| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629342 | |
| Published online | 01 September 2017 | |
Increased H2CO production in the outer disk around HD 163296⋆
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA, The Netherlands
e-mail: masoncarney@strw.leidenuniv.nl
2 Department of Astronomy, Harvard University, Cambridge, MA 02138, USA
Received: 19 July 2016
Accepted: 25 May 2017
Context. The gas and dust in circumstellar disks provide the raw materials to form planets. The study of organic molecules and their building blocks in such disks offers insight into the origin of the prebiotic environment of terrestrial planets.
Aims. We aim to determine the distribution of formaldehyde, H2CO, in the disk around HD 163296 to assess the contribution of gas- and solid-phase formation routes of this simple organic.
Methods. Three formaldehyde lines were observed (H2CO 303–202, H2CO 322–221, and H2CO 321–220) in the protoplanetary disk around the Herbig Ae star HD 163296 with ALMA at ~0.5″ (60 AU) spatial resolution. Different parameterizations of the H2CO abundance were compared to the observed visibilities, using either a characteristic temperature, a characteristic radius or a radial power law index to describe the H2CO chemistry. Similar models were applied to ALMA Science Verification data of C18O. In each scenario, χ2 minimization on the visibilities was used to determine the best-fit model in each scenario.
Results. H2CO 303–202 was readily detected via imaging, while the weaker H2CO 322–221 and H2CO 321–220 lines required matched filter analysis to detect. H2CO is present throughout most of the gaseous disk, extending out to ~550 AU. An apparent 50 AU inner radius of the H2CO emission is likely caused by an optically thick dust continuum. The H2CO radial intensity profile shows a peak at ~100 AU and a secondary bump at ~300 AU, suggesting increased production in the outer disk. In all modeling scenarios, fits to the H2CO data show an increased abundance in the outer disk. The overall best-fit H2CO model shows a factor of two enhancement beyond a radius of 270 ± 20 AU, with an inner abundance (relative to H2) of 2 − 5 × 10-12. The H2CO emitting region has a lower limit on the kinetic temperature of T> 20 K. The C18O modeling suggests an order of magnitude depletion of C18O in the outer disk and an abundance of 4 − 12 × 10-8 in the inner disk.
Conclusions. There is a desorption front seen in the H2CO emission that roughly coincides with the outer edge of the 1.3 millimeter continuum. The increase in H2CO outer disk emission could be a result of hydrogenation of CO ices on dust grains that are then sublimated via thermal desorption or UV photodesorption. Alternatively, there could be more efficient gas-phase production of H2CO beyond ~300 AU if CO is photodisocciated in this region.
Key words: astrochemistry / protoplanetary disks / submillimeter: stars
The reduced datacube is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/605/A21
© ESO, 2017
1. Introduction
Protoplanetary disks have a layered temperature and density structure that results in a cold, dense midplane where gaseous molecules freeze out onto icy mantles around small dust grains. Chemical reactions and radiative processing of atoms and molecules locked up in ices can create organic molecules of increasing complexity (Watanabe et al. 2003; Öberg et al. 2009, 2010a; Herbst & van Dishoeck 2009). The high densities and vertical settling of larger grains make the disk midplane an ideal site for grain growth and the formation of comets and planetesimals (Dullemond & Dominik 2005; Andrews & Williams 2005; D’Alessio et al. 2006). The cold, complex molecular reservoir may be incorporated into small icy bodies in the midplane and remain relatively unprocessed, thus comets may preserve the chemical composition of the disk at the time of their formation (van Dishoeck & Blake 1998; Mumma & Charnley 2011). Comets and other planetesimals are possible delivery mechanisms of organics to terrestrial bodies during the early stages of the solar system, thus it is important to understand the chemistry and composition of their natal environments. Observations of molecular emission lines can determine the distribution and abundance of a molecular species and constrain its location in a protoplanetary disk. Characterizing simple organic molecules that may be produced in the disk midplane, such as H2CO, can constrain available formation scenarios for complex organic molecules (COMs). H2CO acts as a precursor to CH3OH, which is an important building block for other COMs (Öberg et al. 2009; Walsh et al. 2014). Thus, determining the dominant formation mechanism for H2CO and its distribution in disks can help to constrain abundances for CH3OH and the complex organic reservoir.
A major formation pathway of H2CO is expected to be the hydrogenation of CO ices in the cold midplane of the disk (Watanabe et al. 2003; Cuppen et al. 2009). H2CO also has a gas-phase formation route via neutral-neutral reactions of CH3 and O that is more efficient at higher temperatures e.g. in the inner disk or surface layers (Fockenberg & Preses 2002; Atkinson et al. 2006). Formaldehyde has already been detected toward several protoplanetary disks (Aikawa et al. 2003; Öberg et al. 2010b, 2017; Qi et al. 2013; van der Marel et al. 2014; Loomis et al. 2015), but it is difficult to determine the contribution of H2CO formed in the gas phase versus that formed via surface reactions. It is important to consider the distribution of H2CO in relation to the freeze-out of CO, i.e., the CO snow line. H2CO that exists well beyond the CO snow line is likely formed on the icy mantles of dust grains while H2CO located within the CO snow line forms via gas-phase pathways at higher temperatures.
HD 163296 observational parameters.
Qi et al. (2013) attempted to reproduce Submillimeter Array (SMA) observations of H2CO around TW Hya and HD 163296 with two simple parameterized models: a power-law H2CO column density with an inner radius and a ring-like H2CO distribution with an upper boundary set by the CO freeze-out temperature. They found that both models indicated H2CO is produced mostly at larger radii beyond the CO snow line in the disk around HD 163296, which is consistent with a scenario in which formaldehyde forms in CO ice and is subsequently released back into the gas phase. Loomis et al. (2015) modeled H2CO in DM Tau observed with the Atacama Large Millimeter/submillimeter Array (ALMA) using a small chemical network with and without grain-surface formation. They found that both gas- and solid-phase production of H2CO were needed to reproduce the centrally peaked emission and the emission exterior to the CO snow line in DM Tau.
HD 163296 (MWC 275) is an ideal testbed for chemical processing in protoplanetary disks, in particular for organics. It is an isolated Herbig Ae protostar with spectral type A2Ve, an age of approximately 5 Myr, and is located at 122 pc (de Gregorio-Monsalvo et al. 2013). The protostar is surrounded by a large gas-rich protoplanetary disk that extends to ~550 AU (Isella et al. 2007) with stellar mass M∗ = 2.3 M⊙, disk mass Mdisk = 0.089 M⊙, and an inclination of 44° based on the Qi et al. (2011) physical model. At such an inclination, vertical structure as well as radial structure can be inferred from molecular line emission. The proximity and size of the disk combined with the strong UV field of the Herbig Ae protostar provides a unique opportunity to fully resolve the location of the CO snow line around HD 163296. Several attempts have already been made to constrain the location of the CO snow line in this disk (Qi et al. 2011; Mathews et al. 2013; Qi et al. 2015). Current estimates by Qi et al. (2015) place CO freeze-out at 90 AU, corresponding to ~24 K in this disk. HD 163296 is one of the best candidates to probe the formation of organics with respect to the freeze-out of abundant volatiles such as CO. Observations of H2CO in combination with tracers of the CO snow line, such as the optically thin C18O isotopologue, DCO+, or N2H+, provide insight into the formation of organic molecules in Herbig Ae/Be disks.
This paper presents ALMA observations of H2CO toward HD 163296 and characterizes its distribution throughout the disk. Our analysis also makes use of C18O Science Verification data, which has been previously reported (Rosenfeld et al. 2013; Qi et al. 2015). Section 2 describes the observations and data reduction. The detection of H2CO, the modeling of H2CO and C18O distributions and abundances, and the calculation of excitation temperatures for H2CO are discussed in Sect. 3. In Sect. 4 we discuss the relationship between H2CO, C18O, and the millimeter continuum, and the implications for H2CO formation.
2. Observations and reduction
HD 163296 (J2000: RA = 17h56m21.280s, Dec = − 21°57′22.441″) was observed on 2014 July 27, 28, and 29 with ALMA in band 6 as part of Cycle 2. In total 33 antennas were used in the C34 configuration to achieve a resolution of ~0.4″. Band 6 operates in the 211–275 GHz range as a 2SB receiver. The upper sideband contained continuum observations in the time domain mode (TDM) correlator setting with 128 channels over a 2 GHz bandwidth centered at 233 GHz, presented in Zhang et al. (2016). Three transitions of H2CO were observed in the lower sideband with the frequency domain mode (FDM) correlator setting: H2CO 303–202 at 218.22219 GHz, H2CO 322–221 at 218.475632 GHz, and H2CO 321–220 at 218.760066 GHz. Each line had a bandwidth of 56.6 MHz with 960 channels, providing a frequency (velocity) resolution of 0.061 MHz (0.084 km s-1). Table 1 summarizes the observational parameters of each line. Three additional lines, DCO+ 3–2 at 216.11258 GHz, DCN 3–2 at 217.23853 GHz, and N2D+ 3–2 231.321828 GHz were also observed with the same spectral parameters and will be presented in Salinas et al. (in prep.).
Visibility data were obtained over four execution blocks of ~30 min (×1) and ~90 min (×3) at 6.05 s per integration for 155 min total time on source. System temperatures varied from 50–150 K. The average precipitable water vapor across all observations was 1.0 mm. The Common Astronomy Software Applications (casa) package was used to calibrate the data with an automated script provided by the ALMA staff. Calibration of each execution block was carried out with J1700-2610 as the delay calibrator, J1733-1304 as the bandpass and gain calibrator, J1733-1304 as the flux calibrator for three out of four blocks, and Titan as the flux calibrator for the final block. After initial calibration of individual execution blocks, gain calibration solutions obtained from models of Titan were used to derive fluxes for J1733-1304, which was then used as the flux calibrator in all spectral windows and all execution blocks for consistency. Amplitudes for HD 163296 were rescaled across all blocks using J1733-1304 as the flux calibrator. The average flux values for J1733-1304 were 1.329 Jy in the lower sideband and 1.255 Jy in the upper sideband. The total flux for HD 163296 was found to be within 5% across all execution blocks. All measurement sets were subsequently concatenated and time binned to 30 s integration time per visibility for imaging and analysis.
Self-calibration for HD 163296 was performed with the continuum TDM spectral window and all line-free channels of the FDM spectral windows. DV11 was chosen as the reference antenna. A minimum of four baselines per antenna and a minimum signal-to-noise ratio (S/N) of two were required. Calibration solutions were calculated twice for phase and once for amplitude. The first phase solution interval (solint) was 500 s, the second phase and amplitude solutions had solint equal to the binned integration time (30 s). Continuum subtraction of the line data was carried out in the uv plane using a single-order polynomial fit to the line-free channels. The CLEAN imaging was performed with natural weighting for each continuum-subtracted H2CO line down to a threshold of 4 mJy.
 |
Fig. 1 Disk-integrated H2CO spectra using a 5.6″ circular aperture. H2CO 303–202, H2CO 322–221, and H2CO 321–220 are at y-offsets of 0, 0.25, and 0.5 Jy, respectively, shown in dashed gray lines. The vertical dashed red line shows the systemic velocity. The spectra are Hanning smoothed to 0.336 km s-1 channels. |
This work also uses C18O 2–1 calibrated data of HD 163296 from the ALMA project 2011.0.00010.SV obtained from the publicly available ALMA Science Verification Data website1. See Rosenfeld et al. (2013) for details on the calibration of the data set. The flux for the C18O 2–1 line (Table 1) is consistent with previously reported values (Rosenfeld et al. 2013; Qi et al. 2015).
The following software and coding languages were used for data analysis in this paper: the casa package (McMullin et al. 2007), the miriad package (Sault et al. 1995), and python.
3. Results
The following sections present results of H2CO observations in the disk around HD 163296. Physical parameters of the lines and their distribution throughout the disk are discussed in Sect. 3.1. Models of H2CO and C18O emission and their abundances are presented in Sect. 3.2. Constraints on the excitation temperature of H2CO are discussed in Sect. 3.3.
3.1. Detection and distribution of H2CO
The spatially integrated spectrum for each H2CO line can be found in Fig. 1. The 303–202 transition is readily detected in the spectrum extracted from CLEAN imaging. The two weaker lines are not detected in the extracted spectra, but when applying a matched-filter technique (see Sect. 3.1.1), the lines are clearly detected and can be used to provide constraints on the H2CO excitation temperature. Physical parameters of the three lines and the continuum can be found in Table 1.
HD 163296 has a VLSR systemic velocity of +5.8 km s-1 (Qi et al. 2011), which corresponds well to the central velocity of the H2CO 303–202 line. The H2CO 303–202 line flux was derived after masking pixels with <3σ emission in the image cube. The cube was then integrated spatially over a 7″ radius and over velocity channels 0.76–10.84 km s-1. Lower limits on H2CO 322–221 and H2CO 321–220 line fluxes are from estimates via the matched-filter method. Upper limits on the lines are based on spectra from the CLEAN images of H2CO 322–221 and H2CO 321–220 and are given at the 3σI level, where 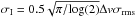 estimates the area of a Gaussian curve, Δv is the FWHM of the detected H2CO 303–202, and σrms is the rms noise in Jy from the disk-integrated spectra.
estimates the area of a Gaussian curve, Δv is the FWHM of the detected H2CO 303–202, and σrms is the rms noise in Jy from the disk-integrated spectra.
The H2CO 303–202 image has a 0.54″ × 0.42″ [66 × 51 AU] synthesized beam (PA = 86.5°). Figure 2 shows a velocity-weighted (first-order moment) map of H2CO 303–202 from 0.76–10.84 km s-1 that is clipped at the 3σ level, which reveals the full extent of the H2CO emission in Keplerian rotation, while Fig. 3 shows the channel maps of H2CO 303–202 around HD 163296 Hanning smoothed to a resolution of 0.336 km s-1 over velocities where molecular emission is present. The inner and outer projected radii (i = 44.0°, PA = 133° east of north) of H2CO 303–202 emission at the 3σ level along the major axis are 0.4″ and 4.5″, respectively, corresponding to projected physical distances Rin ≃ 50 AU and Rout ≃ 550 AU at a distance of 122 pc (van den Ancker et al. 1998).
The extent of H2CO 303–202 was found to be greater than that of the 1.3 mm continuum (shown in black contours in Fig. 2), suggesting that millimeter-sized grains have decoupled from the gas and drifted radially inward. de Gregorio-Monsalvo et al. (2013) observed the same phenomenon in 12CO and the 850 μm continuum. The 1.3 mm continuum has a projected outer radius at 3σ of 2.2″ or 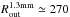 AU. The 1.3 mm emission extends beyond the 850 μm continuum reported by de Gregorio-Monsalvo et al. (2013) due to the increased sensitivity of our observations. Zhang et al. (2016) reported that analysis of the 1.3 mm continuum visibilities in this data set suggests a ring-like structure not seen in imaging at this resolution. The ring-like nature of the millimeter dust was confirmed by high-resolution observations after the original submission of our paper (Isella et al. 2016). They explained the dust morphology as three distinct dust gaps centered at 60, 100, and 160 AU.
AU. The 1.3 mm emission extends beyond the 850 μm continuum reported by de Gregorio-Monsalvo et al. (2013) due to the increased sensitivity of our observations. Zhang et al. (2016) reported that analysis of the 1.3 mm continuum visibilities in this data set suggests a ring-like structure not seen in imaging at this resolution. The ring-like nature of the millimeter dust was confirmed by high-resolution observations after the original submission of our paper (Isella et al. 2016). They explained the dust morphology as three distinct dust gaps centered at 60, 100, and 160 AU.
To calculate the H2CO 303–202 radial intensity profile, an integrated intensity (zero-order moment) map was first created by applying a mask in right ascension, declination, and velocity to the image cube to enhance the S/N. The mask is based on the disk rotational velocity profile, which is assumed to be Keplerian with a mass of M = 2.3 M⊙, corresponding to the mass of the central star. In each velocity channel of the image cube, a subset of pixels were chosen where the calculated Keplerian velocity of the pixels matches the Doppler-shifted velocity of the line. All pixels that did not match these criteria were masked. Yen et al. (2016) use a similar method to extract their integrated intensity maps. The radial intensity profile and integrated intensity map for H2CO 303–202 emission are shown in Fig. 2. Azimuthally-averaged elliptical annuli projected to an inclination of 44° and position angle of 133° were used to calculate the average flux in each radial step. This method provides more S/N per annulus, but results in a decrease in resolution by a factor of two due to the foreshortening along the inclined disk’s minor axis in our radial intensity profiles. Radial step sizes of 0.24″ for H2CO 303–202 and 0.4″ for C18O 2–1 were used for each annulus to provide a sampling of approximately two data points per original beam width.
 |
Fig. 2 Moment maps and radial profile of H2CO 303–202. Left: moment 1 map from 0.76–10.84 km s-1, clipped at 3σ. Solid black contours show the 225 GHz/1.3 mm emission at 5.0 × 10-5 (1σ) × [5, 10, 25, 50, 100, 300, 500, 1000, 1500, 2000] Jy beam-1. Synthesized beam and AU scale are shown in the lower corners. Center: moment 0 map integrated over 0.76–10.84 km s-1 after applying a Keplerian mask. Synthesized beam and AU scale are shown in the lower corners. Right: radial intensity curve from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. Shaded gray area represents 1σ errors. |
 |
Fig. 3 Channel maps of H2CO 303–202 from 2.44–8.82 km s-1, Hanning smoothed to 0.336 km s-1 channels. Channel velocity is shown in the upper right corner. Synthesized beam and AU scale are shown in the lower left panel. |
The radial profile reveals an absence of emission at the center of the disk, a peak in intensity at ~100 AU with emission then decreasing until a turnover in the profile at ~200 AU and a bump at ~300 AU, signifying an enhancement in emission in the outer regions of the disk. The same curve for C18O has centrally peaked emission and intensity decreasing with radius. Already the shape of the radial profiles of the two molecules indicates a difference in abundance gradients throughout the disk. The C18O profile suggests that it follows more or less the smoothly decreasing H2 gas density. On the other hand, H2CO shows a peak at the approximate location of the CO snow line at 90 AU (Qi et al. 2015), and another enhancement is located roughly at the edge of the dust continuum. Such a radial profile highlights the need for two H2CO formation mechanisms to account for the observed emission: one warm route that produces emission at temperatures above that of CO freeze-out in the inner disk within 100 AU and one cold route that produces emission outside of the CO snow line. Further explanations for these features are given in Sects. 3.2 and 4.
3.1.1. Matched filter detections
After subtracting the continuum from the line data, we employed a matched filter technique to the visibilities to detect the weaker H2CO 322–221 and H2CO 321–220 lines. In this technique, an image cube containing a template emission profile is sampled in uv space to obtain a set of template visibilities that act as the filter. The template is then cross-correlated with a set of visibilities with a low S/N ratio (S/N) in an attempt to detect the presence of the template emission within the low S/N data set. The cross-correlation is done by sliding the template visibilities channel-by-channel across the velocity axis of the low S/N visibilities. When the template reaches the source velocity in the low S/N data, there will be a sharp peak in the filter response spectrum of the correlation if the template signal is detected within the low S/N visibilities. This is analogous to image-based stacking approaches (e.g. Yen et al. 2016), but retains the advantages of working in the uv plane. In this work, to obtain a data-based template for the matched filter method, the H2CO 303–202 line was reimaged with CLEAN in 0.084 km s-1 velocity channels using a uv taper to achieve a 1″ synthesized beam. Image channels showing H2CO emission (1.6–10 km s-1) were sampled in the uv plane using the python vis_sample2 routine, and the resulting visibilities were then used as the template signal.
Figure 4 shows the filter impulse responses of the three H2CO visibility data sets to the H2CO 303–202 template. The black curve is the response of the H2CO 303–202 visibility data to the template, highlighting the effectiveness of the filter to recover the line detection. The inset reveals the 4.5σ and 5σ detections of H2CO 322–221 and H2CO 321–220, respectively, where σ is calculated as the standard deviation of the response of emission-free visibility channels to the template. To constrain the total flux of the weaker lines, we compare the ratio of their peak filter responses and the peak response of the H2CO 303–202 visibilities (90σ, Fig. 4). Under the assumption that all three observed H2CO lines are co-spatial, the σ-ratio can be used to estimate the weaker line fluxes reported in Table 1. The response of the template is limited by how well it spatially matches the emission, thus making the derived line fluxes lower limits.
 |
Fig. 4 Matched filter responses of the observed H2CO lines to the H2CO 303–202 data-based template. Self-response (black) shows template recovery of the 303–202 detection. Inset: H2CO 322–221 (red) and H2CO 321–220 (blue) are detected at the 4.5σ and 5σ level, respectively. |
3.2. Modeling H2CO and C18O emission
Previous studies (Qi et al. 2011, 2015; Rosenfeld et al. 2013) have attempted to use CO isotopologues to determine the radial location of CO freeze-out in HD 163296. Qi et al. (2011) modeled the 13CO isotope and found a distinct drop in abundance at ~155 AU, which they attributed to CO freeze-out. However, in Qi et al. (2015) they claim 13CO is a less robust tracer as it is difficult to separate CO freeze-out from opacity effects. 13CO may remain optically thick out to radii beyond 100 AU. Thus, the apparent depletion may be due to a decrease in optical depth rather than an actual drop in abundance. These authors use C18O as a more robust, optically thin tracer of the column density of CO throughout the disk. Following this reasoning, we model only the C18O isotopologue to reveal structure in the CO gas. Although the C18O Science Verification data has been previously reported (Rosenfeld et al. 2013; Qi et al. 2015), we reanalyze the data in an effort to provide a ground truth for the CO surface density – particularly for the outer disk – within the same modeling approach as used for H2CO and within the limits of the data resolution and our disk model.
The aims of modeling H2CO and C18O are to determine likely formation scenarios for H2CO and any relation to the CO snow line. If H2CO is abundant in regions close to or below the CO freeze-out temperature, grain surface formation of H2CO on CO ices will contribute significantly to the overall H2CO abundance. If H2CO is abundant only at high temperatures zones of the disk, then gas-phase production of H2CO dominates. By varying the relative molecular abundances in different regions of the models and comparing the model distribution to the data, we can determine which parts of the disk are harboring reservoirs of H2CO.
 |
Fig. 5 Toy model abundance scenarios for H2CO (left) and C18O (right). X is the molecular abundance with respect to molecular hydrogen (grayscale). Red solid contours show the temperature structure of the gas in the disk. Black dashed contours show the density structure of the gas in the disk as the log of the molecular hydrogen number density. The X distribution in each panel follows the best-fit normalized model (Table 2). |
This section describes the models used to reproduce the observed H2CO 303–202 and C18O 2–1 emission based on the HD 163296 disk model created by Qi et al. (2011). In their paper they constrain the radial and vertical density and temperature structure of a steady viscous accretion disk with an exponentially tapered edge. Fitting the model continuum at multiple wavelengths to the observed spectral energy distribution (SED) constrained the radial structure. Observations of multiple optically thick 12CO transitions were used to constrain the vertical structure. A modified version of this physical model was used by Mathews et al. (2013) to determine the distribution of DCO+ in HD 163296. To constrain the vertical structure of the dust in our physical model, Mathews et al. (2013) refit the SED by varying independently the dust scale heights of Gaussian distributions of small (amax = 25 μm) and large (amax = 1 mm) populations of dust grains. Similarly, the vertical gas density distribution is treated as a two-component model with independent scale heights to simulate a Gaussian distribution at low heights with an extended tail higher in the disk. The gas scale heights are varied to recover the CO fluxes reported in Qi et al. (2011). Given these dust and gas distributions and assuming the dust continuum to be optically thin, the gas surface density of both H2CO and C18O should be robustly measured in our models.
In this work, the Mathews et al. (2013) model was used as the physical disk structure for simulating molecular emission using the LIne Modeling Engine (LIME, Brinch & Hogerheijde 2010) 3D radiative transfer code. Synthesized data cubes were created with LIME for H2CO 303–202 and C18O 2–1 in non-LTE with H2 as the primary collision partner. Both ortho- and para-H2 species were included in collisional excitation, with a temperature-dependent ortho- to para-ratio (OPR) such that OPR = 3 at temperatures ≥200 K and decreases exponentially at lower temperatures. Molecular collision rates were taken from the Leiden Atomic and Molecular Database (LAMDA, Schoeier et al. 2005). The disk inclination, position angle, and distance are set to i = 44.0°, PA = 133.0°, and d = 122 pc.
Four types of models are used to test the distribution of observed H2CO 303–202 with different fractional abundance profiles relative to H2. Figure 5 depicts examples of each of these scenarios with the relevant disk regions. Three of these models are used for C18O 2–1. The first model assumes a constant abundance constrained to low temperatures at which H2CO formation on the surface of icy grains is favorable (Sect. 3.2.1). The low-temperature model is not used for C18O 2–1. In the second model, H2CO 303–202 and C18O 2–1 have a power-law abundance profile (Sect. 3.2.2). The third model has a temperature-based step-abundance profile with a constant inner (high-temp) and outer (low-temp) abundance and a change-over temperature Tc as the boundary (Sect. 3.2.3). The final model has a radial step-abundance profile with a constant inner abundance, constant outer abundance, and change-over radius Rc (Sect. 3.2.4). Analyses of the models make use of the vis_sample routine to read the uv coordinates directly from an observed ALMA measurement set and create synthetic visibilities based on an input sky model.
A central hole is observed in the H2CO data, as seen in Fig. 2, with a size approximately equal to the width of the beam. This hole is likely a result of strong absorption by an optically thick dust continuum (see also Sect. 4.2). Beyond 50 AU, the optical depth radial profile for the LIME model continuum is found to be optically thin with τ< 0.6, which ensures that features in the gas radial profile outside of 50 AU are not caused by dust opacity effects. The inner region (<50 AU) cannot be properly modeled here due to the low resolution of the observations, which do not allow for proper description of any dust substructure. The modeling of Zhang et al. (2016) and new high-resolution observations by Isella et al. (2016) show significant substructure in the dust and a large increase in optical depth in the inner 50 AU. Such substructure is unlikely to be accurately described in our models, thus we ignore radii <50 AU. The central hole is therefore treated as an H2CO abundance inner radius in the modeling.
All H2CO 303–202 models have an inner radius set to Rin = 50 AU. The value Rin was constrained for H2CO by varying the inner radius of a constant abundance model to determine the best fit to the inner 150 AU of the radial intensity curve. Thereafter, Rin remains a fixed parameter in the models. C18O 2–1 models have no such inner radius as the emission is centrally peaked.
Best-fit normalized models.
Each LIME model was continuum-subtracted before running vis_sample. We first tested H2CO 303–202 and C18O 2–1 models normalized to the total flux of the data in order to find the best-fit to the spatial distribution of each line, then we varied the abundance of the best-fit normalized model to match the absolute flux of the data. To determine the total flux, we took a vector average of visibilities with baselines <30 m and integrated over all channels containing emission. The model was then scaled to match the total flux of the data. Goodness of fit for each model was determined by χ2 minimization between the normalized visibilities of the model and the visibilities of the data. Initial reference abundances were chosen for the normalized models to ensure optically thin line emission. The H2CO reference abundance was set to X = 1.0 × 10-12. C18O models used a reference abundance of X = 1.0 × 10-7. All normalized models remained optically thin with τ< 1; there was no significant increase in the optical depth profile of the models for the parameter space explored here. The best-fit normalized model for each line was then used to vary the molecular abundances to find the best agreement between the absolute flux of the model and of the data using χ2 minimization on the visibilities.
 |
Fig. 6 H2CO 303–202 and C18O 2–1 data are compared with best-fit normalized models for each scenario mentioned in Sect. 3.2. The low-temperature model (dot-dashed cyan), power-law model (dotted blue), temperature step-abundance model (dashed red), and radial step abundance model (solid gold) show the radial distribution and spectra. Left: radial intensity curves of the best-fit normalized models obtained from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. The shaded grey region represents 1σ error bars. H2CO profiles are taken from integrated intensity maps after applying a Keplerian mask. Right: disk-integrated spectra of the best-fit normalized models obtained from a 5.6″ circular aperture. H2CO spectra are Hanning smoothed to 0.336 km s-1 channels. Parameters for each model can be found in Table 2. |
3.2.1. Low-temperature abundance model
The low-temperature model simulated H2CO emission that is present due to grain-surface chemistry in regions below the expected CO freeze-out temperature and subsequent non-thermal desorption from icy grains. The models used a constant fractional abundance relative to H2, constrained by a threshold temperature. Above the threshold temperature the H2CO abundance was set to zero everywhere. Based on estimates of CO freeze-out temperatures from Qi et al. (2015), model threshold temperatures range from 14–50 K in steps of 2 K. Below the threshold temperature, gas-phase H2CO is present. It is assumed that there is a mechanism to stimulate sufficient desorption of H2CO from the icy grains, such as UV or X-ray photodesorption, or cosmic rays penetrating the disk midplane.
The best fit for the normalized low-temperature model for H2CO has a threshold temperature of 24±2 K, corresponding to a midplane radius of 65±15 AU. Seen in Fig. 6, the model radial intensity curve fails to recover the sharp decrease in emission between 100–200 AU and the turnover and secondary bump beyond ~200 AU. It is clear that a scenario in which H2CO originates entirely beyond the CO freeze-out temperature is not a good representation of the distribution seen in the observations. H2CO must be present in other parts of the disk.
3.2.2. Power-law abundance model
In these models a varying abundance profile was considered for both H2CO and C18O, following a power-law distribution, 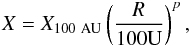 where X100 AU is the abundance at 100 AU, R is the disk radius, and p is the power-law index. C18O is present throughout the disk. H2CO has an inner radius Rin = 50 AU, which was used in all subsequent H2CO modeling.
where X100 AU is the abundance at 100 AU, R is the disk radius, and p is the power-law index. C18O is present throughout the disk. H2CO has an inner radius Rin = 50 AU, which was used in all subsequent H2CO modeling.
The best-fit power-law H2CO model has p = 0.5, with the abundance increasing with radii. The best-fit value found here is more gradual than the p = 2 positive power-law slope found by Qi et al. (2013), but both suggest that there is increased H2CO production occurring in the outer disk. However, the p = 0.5 model does not provide the overall normalized best fit to the H2CO 303–202 data presented here, as seen in Fig. 6. The best-fit C18O model had p = − 2, suggesting C18O is centrally peaked, but with a decreasing abundance in the outer regions of the disk. The model radial intensity curve underproduces emission beyond 200 AU and overproduces emission inside of 200 AU.
The simple power-law model does not capture the distribution seen in either H2CO or C18O. The failure of the H2CO model to recover the shape of the radial intensity profile suggests that there are changes in the distribution of emission not captured in this model; we underestimate the contribution from grain surface formation. The failure of the C18O power-law model indicates that the effect of CO depletion is not properly taken into account. To reproduce the data at our resolution, the C18O abundance profile needs an abrupt change rather than the gradual change provided by the power-law model.
3.2.3. Temperature step-abundance model
Two-phase abundance models with a change-over temperature that distinguishes between the warm and cold regions of the disk were created to test H2CO formed in the gas phase and H2CO originating from icy grains, respectively. We assume that the change-over temperature represents the boundary below which H2CO should form via hydrogenation of CO ice. The temperature step-abundance model for C18O reflects the freeze out of CO, both radially and vertically, since there also is a vertical temperature gradient. While in these models we parameterize the C18O abundance with a change-over temperature, it is important to remember that this results in a radial column density profile that decreases gradually and extends well beyond the midplane CO snow line. Given our limited angular resolution, our data primarily samples the radial extent of the disk surface layer where C18O is present in the gas phase. Although we parameterize this with a temperature, we caution against the simplistic interpretation as an evaporation temperature, since its value depends on how well we know the vertical temperature structure and because our data do not resolve the location of the midplane CO snow line.
The change-over temperature Tc was tested in the range 12–36 K in steps of 2 K. The abundance ratio between the inner and outer regions varies to cover the range X1/X2 from 0.001–10 (0.1–1000 for C18O). The best-fit H2CO model has a change-over temperature Tc = 16 ± 2 K and an abundance ratio X1/X2 = 0.5, indicating a factor of 2 enhancement of H2CO in the outer regions, but the model does not reproduce emission beyond 200 AU well (Fig. 6). C18O is best fit by a change-over temperature Tc = 32 ± 2 K with an order of magnitude reduction (X1/X2 = 10) in the outer regions. The temperature step-abundance model provides an improved normalized fit to the C18O observational data over models 1 and 2 and is consistent with CO depletion in the cold, outer disk.
As explained above, we do not claim that Tc is the evaporation temperature of CO, but rather that the value of Tc results in a reasonable match of the radial column density distribution of C18O given our adopted temperature structure and the limited angular resolution of the data. Even then, the radial profile of this model underproduces C18O within ~400 AU and overproduces C18O outside of ~400 AU.
While this model provides a better fit to the H2CO emission than models 1 and 2, it fails to recover the shape of the turnover in the radial profile seen at ~200 AU. Instead, the temperature-based boundary causes a gradual change in the radial intensity due to the vertical temperature structure in the disk. To better fit the turnover seen in the radial profile, the H2CO abundance profile must have an even more abrupt radial change. The improvement of the C18O normalized model fit over models 1 and 2 suggests CO freeze-out in the cold, outer parts of the disk.
3.2.4. Radial step-abundance model
In these models, molecular gas abundance is constant throughout the vertical extent of the disk with different abundance values in the inner and outer regions across the change-over radius. The outer abundance was varied such that X1/X2 spanned 0.1–10 for H2CO and 0.1–1000 for C18O. The change-over radius Rc ranged from 210–410 AU for H2CO and 70–350 for C18O in steps of 20 AU.
The radial step-abundance model reproduces the turnover seen in the radial intensity of the H2CO emission better than the first three models. Best-fit parameters are a change-over radius Rc = 270 ± 20 AU and an abundance ratio X1/X2 = 0.5. The radial step-abundance model gives a radial intensity profile that has a steep drop between ~100–200 AU and a sharp turnover and plateau beyond ~200 AU. Best-fit C18O models have Rc = 290 ± 20 AU and X1/X2 = 10, indicating a factor of 10 depletion of CO in the outer disk beyond the edge of the millimeter grains. This abundance scenario also provides a better normalized fit than models 1 and 2, and reproduces the distribution of C18O as well as model 3.
In this model the H2CO bump in the radial intensity curve is well-captured due to the sharp change in abundance across the change-over radius. The radial step-abundance model provides the right amount of H2CO production in the inner and outer regions, that is likely a combination of gas-phase and grain-surface formation. Penetrating UV photons could photodesorb H2CO that has formed via hydrogenation of CO ices beyond ~300 AU. There may also be more gas-phase H2CO formation beyond the edge of the millimeter continuum at ~ 270 ± 20 AU if UV photons can photodissociate CO in the upper layers and activate hydrocarbon chemistry for a more efficient CH3 + O pathway. The C18O radial step-abundance model provides an alternative scenario for outer disk CO depletion compared to model 3. If the micron-sized grains are depleted in the outer disk similar to the millimeter-sized grains, UV photons could photodissociate CO beyond ~300 AU.
The fact that both a radial step at 290±20 AU and a temperature step at 32±2 K (32±5 AU near the midplane) equally well fit the C18O data underlines our caution against interpreting the value of Tc as the evaporation temperature. The consequences of each model scenario are further discussed in Sect. 4. The radial step-abundance case is chosen as the C18O normalized model for estimating abundances in Sect. 3.2.5.
3.2.5. H2CO and C18O abundance
To estimate the absolute fractional abundances relative to H2 in the inner and outer regions for H2CO and C18O, LIME was used to vary the abundances for the best-fit normalized scenarios. Abundance ratios across the change-over boundaries, Rc, were kept the same as the normalized models: X1/X2 = 0.5 for the H2CO radial step-abundance model and X1/X2 = 10 for the C18O radial step-abundance model.
 |
Fig. 7 Radial intensity and spectra of observed H2CO 303–202 and C18O 2–1 versus the best-fit models. Left: radial intensity curves from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. HD 163296 data is show in black, best-fits for H2CO and C18O are in gold. The vertical dashed lines indicate the CO snow line (blue dash) from Qi et al. (2015), the 5σ outer radius of the 1.3 mm grains (black dash), and the change-over radii, Rc, for the best-fit radial step-abundance models (gold dash). H2CO profiles are taken from integrated intensity maps after applying a Keplerian mask. Right: disk-integrated spectra. HD 163296 data is shown in filled gray. H2CO spectra are Hanning smoothed to 0.336 km s-1 channels. |
H2CO models had Rc = 270 AU and X1 = [ 1.0,2.0,3.0,4.0,5.0 ] × 10-12. The best-fit fractional abundances were X1 = 4.0 × 10-12 and X2 = 8.0 × 10-12. C18O was found to have best-fit fractional abundances of X1 = 5.0 × 10-8 and X2 = 5.0 × 10-9 with Rc = 290 AU. Radial intensity profiles for these best-fit models are shown in Fig. 7. Error estimates based 3σ error bars of the radial intensity profiles put these abundances in the range X1 = 2 − 5 × 10-12, X2 = 5 − 10 × 10-12 for H2CO and X1 = 4 − 12 × 10-8 and X2 = 4 − 12 × 10-9 for C18O.
Integrated intensity maps of the best-fit models were compared to integrated intensity maps of observed H2CO 303–202 and C18O 2–1 data. Figure 8 shows the images and the residuals. The model and the data are in good agreement for both lines, though the best-fit C18O has residual emission above the 3σ in the central part of the disk. The inner 50 AU are likely not well-described by our models, as noted in Sect. 3.2.
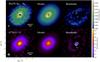 |
Fig. 8 Data, model, and residual integrated intensity maps. H2CO 303–202 data and model maps are created after applying a Keplerian mask to the image cube (see Sect. 3.1). Left: H2CO 303–202 data integrated intensity map from 0.76–10.84 km s-1 and C18O 2–1 data integrated intensity map from –0.88–12.48 km s-1. Synthesized beam and AU scale are shown in the lower corners. Center: integrated intensity map of best-fit model taken over the same velocity channels as the left figure. Right: residual image with contours at 3σ intervals. Dashed contours are negative, solid contours are positive. |
The modeling efforts presented here show that the H2CO abundance is not uniform throughout the disk. Beyond ~300 AU there is an increase in the H2CO abundance by a factor of two, as seen in the radial step-abundance scenario. The H2CO abundance of X1 = 2 − 5 × 10-12, X2 = 4 − 10 × 10-12 is consistent to within a factor of a few with the global abundance value of 1 × 10-11 found in Qi et al. (2013). The increased sensitivity and resolution of our data allow us to better constrain the H2CO abundance in HD 163296 than previous studies. C18O is well described by a model with a depletion of CO at 290±20 AU and a depletion factor of 10. The C18O inner abundance of 4 − 12 × 10-8 corresponds to a 12CO abundance of 2.2 − 6.6 × 10-5, assuming 12CO/C18O = 550. Qi et al. (2015) report similar numbers for the CO abundance, but their depletion factor is lower by half and occurs at a radius of 90 AU. We found that a radius of 90 AU and depletion factor of 5 for our radial step-abundance models significantly overproduces the amount of C18O beyond 300 AU due to our different treatment of the vertical structure.
3.3. H2CO excitation temperature
Line flux ratios H2CO 303–202/H2CO 322–221 and H2CO 303–202/H2CO 321–220 were used to constrain H2CO excitation temperatures. Table 1 provides the line fluxes. We calculated the rotational temperature of the lines, assuming a single rotational temperature, following Qi et al. (2013)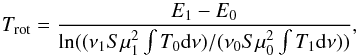 (1)with the following definitions: E0 and E1 are the upper energy levels for the low and high H2CO transitions, respectively; ν is the line frequency; Sμ2 is the temperature-independent transition strength and dipole moment; and ∫Tdν is the integrated line intensity. Line intensity in the Rayleigh-Jeans limit was calculated from the line flux with the following expression:
(1)with the following definitions: E0 and E1 are the upper energy levels for the low and high H2CO transitions, respectively; ν is the line frequency; Sμ2 is the temperature-independent transition strength and dipole moment; and ∫Tdν is the integrated line intensity. Line intensity in the Rayleigh-Jeans limit was calculated from the line flux with the following expression: 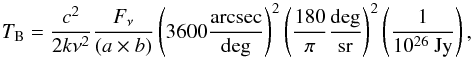 (2)where Fν is the line flux in Jy, TB is the line intensity in Kelvins, ν is the line frequency in Hz, k is the Boltzmann constant, c is the speed of light, and a and b are the semi-major and semi-minor axes of the beam in arcsec.
(2)where Fν is the line flux in Jy, TB is the line intensity in Kelvins, ν is the line frequency in Hz, k is the Boltzmann constant, c is the speed of light, and a and b are the semi-major and semi-minor axes of the beam in arcsec.
The emitting regions of all three lines are expected to be similar, especially if the H2CO reservoir is primarily locked up in icy grains. Local thermodynamic equilibrium (LTE) is a fair assumption for calculating rotational temperatures, as the gas density near the midplane is high in disks (~109 cm-3; Walsh et al. 2014) and the critical densities of the observed transitions at 20 K are 1–3 × 106 (Wiesenfeld & Faure 2013). In the case of LTE, the derived rotational temperature is equal to the kinetic temperature of the gas. The values E and Sμ2 are taken from the CDMS (Müller et al. 2005), as reported on the Splatelogue3 database.
The rotational temperatures of the H2CO transitions are calculated based on the line flux ratios of H2CO 322–221/303–202 and H2CO 321–220/303–202. The matched-filter technique only gives lower limits to the H2CO 322–221 and H2CO 321–220 line flux, thus lower limits on the rotational temperature are >20.5 K and >19.5 K, respectively, while upper limits for the weak lines are <169 K and <326 K based on the integrated flux upper limits listed in Table 1. These lower limits indicate that these transitions can be excited in regions of the disk near the CO freeze-out temperature, supporting the hypothesis that some of the H2CO emission may originate from the cold molecular reservoir. There could also be H2CO emitting at a higher temperature that is not well described by our template filter.
4. Discussion
In this work, the radial step-abundance model suggests an enhancement in H2CO abundance by a factor of a few beyond 270 AU. It is difficult to distinguish which formation route is responsible for this modest increase in abundance.
Aikawa & Herbst (1999) estimated the radial column density and abundance profile of H2CO formed in the gas phase in a T Tauri minimum mass solar nebula (MMSN) disk model extrapolated out to Rout = 700 AU, with an order of magnitude lower mass. They did not consider other mechanisms for producing gas-phase H2CO, such as desorption from icy grains. The initial abundance of atomic oxygen may affect the inferred H2CO abundances. Their model has a mostly flat radial distribution, but is consistent with an enhancement of H2CO abundance by a factor of a few up to one order of magnitude in the outer regions beyond ~300 AU.
Walsh et al. (2014) created a series of increasingly complex T Tauri disk chemical evolution models that include grain-surface formation to estimate abundances of complex organic molecules (COMs) throughout the disk. Beginning with freeze-out and thermal desorption only, they also include nonthermal desorption, grain-surface chemistry, radiative reprocessing of ices, and reactive desorption in their full disk model. The vertical distribution of H2CO included a large gas-phase reservoir above the midplane reaching peak fractional abundances relative to H2 of ~10-8 and an ice reservoir beyond 10 AU with peak fractional abundances of ~10-4. Beyond 50 AU, the radial column density of H2CO in the Walsh et al. (2014) comprehensive disk model shows an increase by a factor of a few.
From these two examples it is clear that a modest outer disk enhancement of H2CO cannot immediately reveal whether gas-phase or grain-surface production is the dominant formation route. Full chemical modeling of H2CO production is required. In this section we discuss possible explanations for the H2CO enhancement in the outer disk around HD 163296, its relation to the CO snow line and the millimeter continuum, and the implications for H2CO formation.
4.1. H2CO and the CO snow line
Previous SMA observations of H2CO in the disk around HD 163296 showed ring-like formaldehyde emission outside the expected CO snow line (Qi et al. 2013). These authors suggested that a scenario with only grain-surface formation could be responsible for the observed distribution and the apparent lack of centrally peaked emission. The lower spatial resolution and S/N per channel of the SMA observations would preferentially place the H2CO emitting region farther away from the central star since the emission at smaller radii is spread out over more velocity channels due to the shear in the Keplerian disk, thus resulting in a false ring-like structure. The ALMA results presented here show that H2CO is not present in a ring, but rather emission is seen throughout most of the gaseous extent of the disk with a central depletion in the inner ~50 AU.
Qi et al. (2015) presented new constraints on the CO snow line in HD 163296 based on observations of C18O and N2H+. N2H+ is readily destroyed by gas-phase CO, thus it is expected to be a reliable tracer of CO depletion. By refitting the location and degree of CO depletion, they found that a factor of 5 depletion in column density at 85–90 AU improved their best-fit models to the visibility data. They interpret this radius as the location of the CO snow line, corresponding to a CO freeze-out temperature of 25 K. The coincident of CO depletion and N2H+ emission inner radius supports the claim that N2H+ traces regions of CO freeze-out. Recent results by van’t Hoff et al. (2017) show that the N2H+ emission can peak from ~5–50 AU beyond the location of the CO snow line and that careful chemical modeling is necessary to properly interpret the location of CO freeze-out from N2H+ observations.
The data presented here show that H2CO extends beyond the Qi et al. (2015) CO freeze-out radius, but with a peak at ~90 AU that coincides with the CO snow line. Öberg et al. (2017) presented H2CO observations in the disk around TW Hya and find that grain-surface formation of H2CO begins at temperatures where CO starts to spend even a short time on the grains, meaning that H2CO can be produced – and the emission can peak – just inside of the CO snow line. Considering our ~50 AU resolution, the peak seen at ~90 AU may be the beginning of grain surface formation of H2CO, likely with some contribution from the warmer, gas-phase formation pathway at the innermost radii.
Recent analysis of ALMA Cycle 0 data for H2CO in DM Tau explored the relative contributions of gas-phase and grain-surface formation pathways (Loomis et al. 2015). Their chemical models required both formation via gas-phase reactions and hydrogenation of CO ice in the outer regions of the disk to reproduce the centrally peaked and outer disk emission. Our simple parameterized models do not include chemical processing, but the presence of H2CO at radii beyond the expected CO snow line at 90 AU and where millimeter grains are present indicates that grain-surface formation is a partial contributor to the H2CO reservoir in the disk around HD 163296. Unlike the DM Tau results, our data also suggests that there is an intrinsic link between the edge of the millimeter continuum and the production of H2CO in HD 163296.
4.2. H2CO inner hole
A sharp drop in H2CO emission within 50 AU is evident in the integrated intensity map (see Fig. 8) and by the best-fit Rin of the H2CO models. Optically thick dust may be responsible for the observed depletion, rather than a drop in H2CO abundance. Photons emitted by H2CO in the midplane of the disk can be absorbed by optically thick dust in the upper layers, causing the inner hole – after continuum subtraction – that is seen in the H2CO integrated intensity map.
Zhang et al. (2016) model the HD 163296 continuum visibilities with a parameterized radial intensity distribution modulated by multiple sine waves. Their best-fit model shows that there is an increase in millimeter-wavelength intensity of ~60% in the innermost 50 AU of the disk, causing the millimeter continuum to become optically thick in this region. Zhang et al. (2016) produced simulated model images with a 0.035″ beam, which clearly shows the strong central continuum emission. At the spatial resolution presented in this work, 0.5″, the millimeter continuum appears smooth. Isella et al. (2016) presented 0.2″ observations of the 1.3 mm continuum and three CO isotopologues. They show central depressions in the 13CO and C18O maps, and concluded that both the CO and the dust become optically thick within 50 AU, leading to large uncertainties in their surface densities.
Öberg et al. (2017) observe a similar central H2CO depression well within the CO snow line in the disk around TW Hya. While they do not rule out dust opacity effects completely, they prefer to explain it as a real drop in abundance, as the central depression is not seen in higher frequency lines of H2CO or CO isotopologues. Observations of additional, high frequency H2CO lines in the HD 163296 disk would be needed to test this scenario. The 13CO and C18O central holes seen by Isella et al. (2016) at high resolution already suggest dust opacity as an explanation for the central H2CO depression in this disk.
4.3. H2CO and the millimeter continuum edge
The millimeter grains in HD 163296 have decoupled from the gas and drifted radially inward. Millimeter emission in the outer disk is truncated at 270 AU while the bulk of the gas, based on 12CO observations, extends to ~550 AU (de Gregorio-Monsalvo et al. 2013). The outer edge of millimeter emission corresponds to the 270±20 AU change-over radius for H2CO enhancement found by the best-fit radial step-abundance model. Grain growth and radial drift in the outer regions of the disk can result in a decrease of small, micron-sized grains beyond ~270 AU. With less shielding from external and protostellar radiation, penetrating UV photons in the outer regions may cause an increase in the H2CO photodesorption directly off icy grain surfaces (Öberg et al. 2009; Huang et al. 2016). Increased UV radiation in a dust-depleted outer disk could also lead to CO photodissociation in the upper layers, opening a more efficient gas-phase route for H2CO where hydrocarbon radicals and atomic oxygen are readily available.
Dust evolution models for HD 163296 by Facchini et al. (2017) show that for a low-turbulence environment, a temperature inversion can occur around 300 AU, causing a second CO desorption front in the outer disk (also suggested qualitatively by Cleeves 2016). In that case, an increase of both C18O and H2CO abundance in the outer disk would be expected, but our models found a CO depletion. It may be that there are competing effects occurring in the outer disk for CO. A temperature inversion and/or UV photodesorption beyond 300 AU can cause the release of grain-surface H2CO and a fraction of CO ice back into the gas phase near the midplane, but CO photodissociation in the upper layers may dominate the C18O surface density profile so that we ultimately see an outer disk depletion in C18O, and an increase in H2CO production.
5. Conclusions
In this work, multiple detections with ALMA of H2CO 3–2 in the protoplanetary disk around HD 163296 were presented: one robust detection via imaging, H2CO 303–202, and two weaker detections via matched filter analysis, H2CO 322–221 and H2CO 321–220. The distribution of H2CO relative to C18O and the millimeter continuum was analyzed using various model abundance profiles to test possible H2CO formation scenarios. The conclusions of this work are as follows:
-
H2CO in HD 163296 is observed out to ~550 AU, equal to the full radial extent of the gas disk as observed with CO. It does not have a ring-like morphology.
-
The kinetic temperature of the observed H2CO gas has a lower limit of >20 K, thus emission from these lines can originate from the cold molecular reservoir near the disk midplane.
-
The best-fit radial step-abundance model to the H2CO 303 − 202 data suggests that H2CO has an inner radius Rin = 50 AU, an outer disk abundance a factor of two higher than the inner disk (X1/X2 = 0.5), and a change-over radius of Rc = 270 ± 20 AU. There is a mechanism causing increased H2CO production in the outer disk beyond the millimeter grains. One explanation is desorption of H2CO from icy grains by thermal desorption due to a temperature inversion or by UV photodesorption where CO is frozen out. Alternatively, photodissociation of CO in the outer disk may increase the efficiency of the CH3 + O gas-phase route to form H2CO.
-
Based on the C18O 2–1 models presented in this work, two scenarios reproduce the data well: step-abundance models with abundance boundaries based on temperature and radius, respectively. The best-fit models both indicate depleted CO in the outer disk based on the recovery of the C18O 2−1 surface density profile. Both models have a CO depletion factor of 10 in the outer disk. The depletion is likely a combination of CO freeze-out in the disk midplane and photodissociation of CO in the disk upper layers due to penetrating UV radiation.
-
The best-fit abundance for the C18O radial step-abundance model was X1 = 4 − 12 × 10-8, X2 = 4 − 12 × 10-9. The best-fit abundance for the H2CO radial step-abundance model was X1 = 2 − 5 × 10-12, X2 = 4 − 10 × 10-12.
Further observations of HD 163296 can unambiguously determine the dominant formation pathway of H2CO in the disk. Constraining the ortho- to para-ratio of the two H2CO isomers can distinguish between grain surface formation and gas-phase formation (Guzmán et al. 2011). The H2CO o/p ratio is expected to be less than three for grain-surface formation (Dulieu 2011; Fillion et al. 2012). Observations of co-spatial H2CO and CH3OH would also constrain the contributions of gas- and solid-phase H2CO, as CH3OH forms similarly via hydrogenation of CO ices and has no known gas-phase formation route.
vis_sample is publicly available at https://github.com/AstroChem/vis_sample or in the Anaconda Cloud at https://anaconda.org/rloomis/vis_sample
Acknowledgments
The authors thank the referee for insightful comments and constructive suggestions. M.T.C. thanks S. Facchini and G. S. Mathews for useful discussion on dust evolution and CO chemistry in HD 163296. The authors acknowledge support by Allegro, the European ALMA Regional Center node in The Netherlands, and expert advice from Luke Maud in particular. This paper makes use of the following ALMA data: ADS/JAO.ALMA# 2013.1.01268.S and 2011.1.00010.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Aikawa, Y., & Herbst, E. 1999, A&A, 351, 233 [NASA ADS] [Google Scholar]
- Aikawa, Y., Momose, M., Thi, W.-F., et al. 2003, PASJ, 55, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Atkinson, R., Baulch, D. L., Cox, R. A., et al. 2006, Atmos. Chem. Phys., 6, 3625 [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cleeves, L. I. 2016, ApJ, 816, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., van Dishoeck, E. F., Herbst, E., & Tielens, A. G. G. M. 2009, A&A, 508, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [NASA ADS] [CrossRef] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dulieu, F. 2011, in The Molecular Universe, eds. J. Cernicharo & R. Bachiller, IAU Symp., 280, 405 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Facchini, S., Birnstiel, T., Bruderer, S., & van Dishoeck, E. F. 2017, ArXiv e-prints [arXiv:1705.06235] [Google Scholar]
- Fillion, J.-H., Bertin, M., Lekic, A., et al. 2012, in EAS Pub. Ser., eds. C. Stehlé, C. Joblin, & L. d’Hendecourt, 58, 307 [Google Scholar]
- Fockenberg, C., & Preses, J. M. 2002, J. Phys. Chem. A, 106, 2924 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, V., Pety, J., Goicoechea, J. R., Gerin, M., & Roueff, E. 2011, A&A, 534, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., Öberg, K. I., & Andrews, S. M. 2016, ApJ, 823, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Testi, L., Natta, A., et al. 2007, A&A, 469, 213 [CrossRef] [EDP Sciences] [Google Scholar]
- Isella, A., Guidi, G., Testi, L., et al. 2016, Phys. Rev. Lett., 117, 251101 [NASA ADS] [CrossRef] [Google Scholar]
- Loomis, R. A., Cleeves, L. I., Öberg, K. I., Guzman, V. V., & Andrews, S. M. 2015, ApJ, 809, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, G. S., Klaassen, P. D., Juhász, A., et al. 2013, A&A, 557, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Bottinelli, S., Jørgensen, J. K., & van Dishoeck, E. F. 2010a, ApJ, 716, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010b, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Guzmán, V. V., Merchantz, C. J., et al. 2017, ApJ, 839, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., D’Alessio, P., Öberg, K. I., et al. 2011, ApJ, 740, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., & Wilner, D. J. 2013, ApJ, 765, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Andrews, S. M., et al. 2015, ApJ, 813, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfeld, K. A., Andrews, S. M., Hughes, A. M., Wilner, D. J., & Qi, C. 2013, ApJ, 774, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schoeier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, VizieR Online Data Catalog: III/43 [Google Scholar]
- van den Ancker, M. E., de Winter, D., & Tjin ADjie, H. R. E. 1998, A&A, 330, 145 [NASA ADS] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., & van Kempen, T. A. 2014, A&A, 563, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., & Blake, G. A. 1998, ARA&A, 36, 317 [NASA ADS] [CrossRef] [Google Scholar]
- van’tHoff, M. L. R., Walsh, C., Kama, M., Facchini, S., & van Dishoeck, E. F. 2017, A&A, 599, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Millar, T. J., Nomura, H., et al. 2014, A&A, 563, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, N., Shiraki, T., & Kouchi, A. 2003, ApJ, 588, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesenfeld, L., & Faure, A. 2013, MNRAS, 432, 2573 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Koch, P. M., Liu, H. B., et al. 2016, ApJ, 832, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Bergin, E. A., Blake, G. A., et al. 2016, ApJ, 818, L16 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Channel Maps
 |
Fig. A.1 H2CO 303–202 data channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
 |
Fig. A.2 H2CO 303–202 best-fit model channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
 |
Fig. A.3 H2CO 303–202 residual (data-model) channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Dashed contours are negative at the same intervals. Synthesized beam and AU scale are shown in the lower left panel. |
 |
Fig. A.4 C18O 2–1 data channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,25,45 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
 |
Fig. A.5 C18O 2–1 best-fit model channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,25,45 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
 |
Fig. A.6 C18O 2–1 residual (data-model) channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,10,20 ] Jy beam-1. Dashed contours are negative at the same intervals. Synthesized beam and AU scale are shown in the lower left panel. |
All Tables
All Figures
 |
Fig. 1 Disk-integrated H2CO spectra using a 5.6″ circular aperture. H2CO 303–202, H2CO 322–221, and H2CO 321–220 are at y-offsets of 0, 0.25, and 0.5 Jy, respectively, shown in dashed gray lines. The vertical dashed red line shows the systemic velocity. The spectra are Hanning smoothed to 0.336 km s-1 channels. |
| In the text | |
 |
Fig. 2 Moment maps and radial profile of H2CO 303–202. Left: moment 1 map from 0.76–10.84 km s-1, clipped at 3σ. Solid black contours show the 225 GHz/1.3 mm emission at 5.0 × 10-5 (1σ) × [5, 10, 25, 50, 100, 300, 500, 1000, 1500, 2000] Jy beam-1. Synthesized beam and AU scale are shown in the lower corners. Center: moment 0 map integrated over 0.76–10.84 km s-1 after applying a Keplerian mask. Synthesized beam and AU scale are shown in the lower corners. Right: radial intensity curve from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. Shaded gray area represents 1σ errors. |
| In the text | |
 |
Fig. 3 Channel maps of H2CO 303–202 from 2.44–8.82 km s-1, Hanning smoothed to 0.336 km s-1 channels. Channel velocity is shown in the upper right corner. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. 4 Matched filter responses of the observed H2CO lines to the H2CO 303–202 data-based template. Self-response (black) shows template recovery of the 303–202 detection. Inset: H2CO 322–221 (red) and H2CO 321–220 (blue) are detected at the 4.5σ and 5σ level, respectively. |
| In the text | |
 |
Fig. 5 Toy model abundance scenarios for H2CO (left) and C18O (right). X is the molecular abundance with respect to molecular hydrogen (grayscale). Red solid contours show the temperature structure of the gas in the disk. Black dashed contours show the density structure of the gas in the disk as the log of the molecular hydrogen number density. The X distribution in each panel follows the best-fit normalized model (Table 2). |
| In the text | |
 |
Fig. 6 H2CO 303–202 and C18O 2–1 data are compared with best-fit normalized models for each scenario mentioned in Sect. 3.2. The low-temperature model (dot-dashed cyan), power-law model (dotted blue), temperature step-abundance model (dashed red), and radial step abundance model (solid gold) show the radial distribution and spectra. Left: radial intensity curves of the best-fit normalized models obtained from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. The shaded grey region represents 1σ error bars. H2CO profiles are taken from integrated intensity maps after applying a Keplerian mask. Right: disk-integrated spectra of the best-fit normalized models obtained from a 5.6″ circular aperture. H2CO spectra are Hanning smoothed to 0.336 km s-1 channels. Parameters for each model can be found in Table 2. |
| In the text | |
 |
Fig. 7 Radial intensity and spectra of observed H2CO 303–202 and C18O 2–1 versus the best-fit models. Left: radial intensity curves from azimuthally-averaged elliptical annuli projected to i = 44°, PA = 133°. HD 163296 data is show in black, best-fits for H2CO and C18O are in gold. The vertical dashed lines indicate the CO snow line (blue dash) from Qi et al. (2015), the 5σ outer radius of the 1.3 mm grains (black dash), and the change-over radii, Rc, for the best-fit radial step-abundance models (gold dash). H2CO profiles are taken from integrated intensity maps after applying a Keplerian mask. Right: disk-integrated spectra. HD 163296 data is shown in filled gray. H2CO spectra are Hanning smoothed to 0.336 km s-1 channels. |
| In the text | |
 |
Fig. 8 Data, model, and residual integrated intensity maps. H2CO 303–202 data and model maps are created after applying a Keplerian mask to the image cube (see Sect. 3.1). Left: H2CO 303–202 data integrated intensity map from 0.76–10.84 km s-1 and C18O 2–1 data integrated intensity map from –0.88–12.48 km s-1. Synthesized beam and AU scale are shown in the lower corners. Center: integrated intensity map of best-fit model taken over the same velocity channels as the left figure. Right: residual image with contours at 3σ intervals. Dashed contours are negative, solid contours are positive. |
| In the text | |
 |
Fig. A.1 H2CO 303–202 data channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. A.2 H2CO 303–202 best-fit model channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. A.3 H2CO 303–202 residual (data-model) channel maps, Hanning smoothed to 0.336 km s-1 channels. Black contours mark 1.5 × 10-3 (1σ) × [ 3,6,9 ] Jy beam-1. Dashed contours are negative at the same intervals. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. A.4 C18O 2–1 data channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,25,45 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. A.5 C18O 2–1 best-fit model channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,25,45 ] Jy beam-1. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
 |
Fig. A.6 C18O 2–1 residual (data-model) channel maps. Black contours mark 4.2 × 10-3 (1σ) × [ 5,10,20 ] Jy beam-1. Dashed contours are negative at the same intervals. Synthesized beam and AU scale are shown in the lower left panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


