| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 18 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201630326 | |
| Published online | 10 July 2017 | |
Can we observe neutrino flares in coincidence with explosive transients?
1 Sorbonne Universités, UPMC Univ. Paris 6 et CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98bis bd Arago, 75014 Paris, France
e-mail: claire.guepin@iap.fr; kotera@iap.fr
2 Laboratoire AIM-Paris-Saclay, CEA/DSM/IRFU, CNRS, Université Paris Diderot, 91191 Gif-sur-Yvette, France
Received: 22 December 2016
Accepted: 1 March 2017
The new generation of powerful instruments is reaching sensitivities and temporal resolutions that will allow multi-messenger astronomy of explosive transient phenomena, with high-energy neutrinos as a central figure. We derive general criteria for the detectability of neutrinos from powerful transient sources for given instrument sensitivities. In practice, we provide the minimum photon flux necessary for neutrino detection based on two main observables: the bolometric luminosity and the time variability of the emission. This limit can be compared to the observations in specified wavelengths in order to target the most promising sources for follow-ups. Our criteria can also help distinguishing false associations of neutrino events with a flaring source. We find that relativistic transient sources such as high- and low-luminosity gamma-ray bursts (GRBs), blazar flares, tidal disruption events, and magnetar flares could be observed with IceCube, as they have a good chance to occur within a detectable distance. Of the nonrelativistic transient sources, only luminous supernovae appear as promising candidates. We caution that our criterion should not be directly applied to low-luminosity GRBs and type Ibc supernovae, as these objects could have hosted a choked GRB, leading to neutrino emission without a relevant counterpart radiation. We treat a set of concrete examples and show that several transients, some of which are being monitored by IceCube, are far from meeting the criterion for detectability (e.g., Crab flares or Swift J1644+57).
Key words: astroparticle physics / neutrinos / gamma-ray burst: general / BL Lacertae objects: general / pulsars: general / supernovae: general
© ESO, 2017
1. Introduction
With their improved sensitivity and time resolution together with the possibility of fast follow-up, current instruments allow the observation of Galactic and extragalactic transient phenomena (blazar flares, gamma-ray bursts, magnetars, superluminous supernovae, to cite but a few) over a wide energy range. Combined radio, optical, X-ray, or gamma-ray observations are a valuable source of information on their emission mechanisms. Moreover, the recent advances in neutrino and gravitational-wave detection open promising perspectives for transient multi-messenger studies. High-energy neutrinos are expected to play a key role in this picture as undeflected signatures of hadronic acceleration.
Among the existing neutrino detectors, the Antares and IceCube experiments focus on high-energy neutrinos (above 100 TeV for IceCube) and have been operating since 2008 and 2010, respectively (Ageron et al. 2011; Halzen & Klein 2010). Recently, IceCube has opened exciting perspectives in neutrino astronomy by detecting very high energy astrophysical neutrinos (Aartsen et al. 2013a). A second-generation detector is being envisioned by the IceCube collaboration to enhance the sensitivity (The IceCube-Gen2 Collaboration et al. 2015). Several detector projects are also being developed to increase the sensitivity at higher energies (> 1017eV), for example, ARA (Allison et al. 2012), ARIANNA (Barwick 2011), GRAND (Martineau-Huynh et al. 2016), or CHANT (Neronov et al. 2017).
Over the past years, the IceCube collaboration has developed and enhanced methods for time-variable searches (e.g., Abbasi et al. 2012b,a; Aartsen et al. 2013b, 2015). Several bright sources are being constantly monitored for flaring activities (see Aartsen et al. 2015 for the latest public list), and real-time analysis using multi-messenger networks such as AMON (Smith et al. 2013) are being conducted. So far, no neutrino detection has been confirmed in association with a transient source.
In this context, it appears timely to derive general criteria for the detectability of neutrinos from powerful transient sources. Such a study giving concrete detectability conditions of neutrino flares is currently lacking in the literature. It could be successfully applied by current and upcoming instruments to target the most promising sources for follow-ups. Conversely, our criteria can also be used to easily distinguish false associations of neutrino events with a flaring source – if the source does not pass the necessary conditions for detectability.
We focus in this work on powerful bursts and flaring sources that are characterized by short (up to months), violent, and irregular emissions, sometimes in addition to a quiescent emission. Such emissions are related to the acceleration of leptonic and/or hadronic particles within the source. The observed photon spectra is often modeled by synchrotron radiation of leptons; hadrons are less frequently invoked, although they also lead to consistent pictures in specific cases, for example, for some blazars where leptons alone fail to provide a satisfactory explanation to the data (e.g., Oikonomou et al. 2014; Petropoulou et al. 2016b, 2017c). In the latter situation, the detection of neutrinos would be an unquestionable indicator of the acceleration of hadrons and of their interaction within the source environment.
From a theoretical perspective, many studies concentrate on one specific type of source (e.g., on gamma-ray bursts – GRBs – or active galactic nucleus – AGN – flares), for which they give detailed estimates of the neutrino flux (see Sect. 5). Rachen & Mészáros (1998) more broadly discussed the maximum energy of neutrinos and the spectrum for transient sources, but focused in particular on GRBs and AGN. Here, in a more general approach, we aim at constraining the parameter space of bursts and flares detectable in neutrinos by providing necessary conditions on the background fields of the source. We note that predicting neutrino flux levels is not the scope of this paper; we focus here on estimating lower limits on the photon flux of the flare, which is required for efficient neutrino production.
For the purpose of deriving these necessary conditions, we demonstrate that we can describe the large variety of existing sources with a handful of variables: the distance from the source Ds, the isotropic bolometric luminosity of the source measured during the flare Lbol and its peak emission energy ϵpeak, the variability timescale of the emission tvar, and the bulk Lorentz factor of the outflow Γ (and the corresponding velocity β for nonrelativistic cases). Using these quantities, we calculate in the Lbol−tvar parameter-space the maximum accessible neutrino energy in these sources and the minimum flux of photons in a flare required at a specific given wavelength, in order to allow detectability with IceCube.
The layout of this paper is as follows. In Sect. 2 we recall the high-energy neutrino production mechanisms and discuss the specificities related to explosive transients. In Sect. 3 we derive the maximum accessible neutrino energies in the luminosity-time variability parameter space. We calculate the photon flux requirements for detectability in Sect. 4 and discuss the case of general categories of transients and of particular sources in Sect. 5 in light of these results. Our results are summarized in Tables 1 and 2.
2. Specificities of neutrino production in transients
Bursts or flares of astronomical sources can be associated with the acceleration of leptonic and hadronic particles. In presence of hadrons, neutrinos can be produced through photo-hadronic and hadronic interactions. In this study, we aim at identifying the conditions under which a detectable neutrino flare can be produced by a photon flare.
Time-dependent neutrino signal searches follow distinctive procedures compared to time-integrated point-source searches. For example, in IceCube, atmospheric neutrinos and muons being the main limiting factor for detection, time-dependent analyses tend to reduce the background (Aartsen et al. 2015). Real-time analysis and follow-ups on alerts can also drastically increase the significance of results. For these observational reasons, we concentrate here on the production of non-steady neutrino signals from flaring sources with typical durations of less than a few months (tvar ≲ 107s).
Focussing on flares has some important theoretical consequences. The observed variability timescale tvar is related to the size of the emitting region R by a condition of causality: 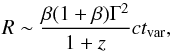 (1)where Γ is the bulk Lorentz factor of the outflow, βc its velocity, and z the redshift of the source. In the following, we neglect the prefactor 1 + β of order unity. For relativistic outflows, it yields
(1)where Γ is the bulk Lorentz factor of the outflow, βc its velocity, and z the redshift of the source. In the following, we neglect the prefactor 1 + β of order unity. For relativistic outflows, it yields 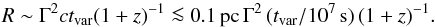 (2)Rachen & Mészáros (1998) discussed that finite injection or radiation timescales can introduce emission delays and affect this causality relation. The orientation and the geometry of the region could also influence variability timescales (Protheroe 2002). In the following we assume a homogeneous and instantaneous emission. Equation (1) implies that the particle escape timescale is limited by the dynamical time of the system tdyn = R/βc = Γ2tvar(1 + z)-1, which corresponds to the adiabatic energy loss time. In particular, magnetic diffusion of particles only intervenes in the acceleration timescale.
(2)Rachen & Mészáros (1998) discussed that finite injection or radiation timescales can introduce emission delays and affect this causality relation. The orientation and the geometry of the region could also influence variability timescales (Protheroe 2002). In the following we assume a homogeneous and instantaneous emission. Equation (1) implies that the particle escape timescale is limited by the dynamical time of the system tdyn = R/βc = Γ2tvar(1 + z)-1, which corresponds to the adiabatic energy loss time. In particular, magnetic diffusion of particles only intervenes in the acceleration timescale.
In the same way, we consider only photo-hadronic interactions of accelerated hadrons on the flaring radiation (the flaring material being usually optically thinner to neutrino production through hadronic interactions, as is demonstrated in Sect. 6). Although accelerated nuclei can also interact with the steady baryon and photon fields in the source or in the cosmic medium, this occurs over a timescale t ≫ tvar because the source is larger than the flaring region and because of the magnetic diffusion of particles. In this configuration, the neutrino emission will be diluted over time and can be viewed as a steady emission stemming from the quiescent source.
Relativistically boosted acceleration regions emit radiation and particles within a narrow cone. Although charged particles could be significantly isotropized by intervening magnetic fields, neutrinos produced through interaction with the beamed photon fields cannot be emitted significantly off-axis. Hence neutrino flares from beamed sources cannot be observed off-axis.
In order to set our detectability requirements on a source, we calculate its maximum achievable neutrino flux, 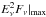 , for a given luminosity Lbol, time variability tvar, and assumed bulk Lorentz factor Γ (and the corresponding velocity β for nonrelativistic cases), without further refined knowledge of the acceleration environment. For each set of (Lbol,tvar,Γ), we work under the most optimistic and/or reliable assumptions to maximize all our variables, except for the flare photon flux level, which is left as a free parameter. By setting the calculated neutrino maximal flux to instrument sensitivities, we then derive the minimum level of background photon flux in the flare that is required at a specified wavelength for a successful detection.
, for a given luminosity Lbol, time variability tvar, and assumed bulk Lorentz factor Γ (and the corresponding velocity β for nonrelativistic cases), without further refined knowledge of the acceleration environment. For each set of (Lbol,tvar,Γ), we work under the most optimistic and/or reliable assumptions to maximize all our variables, except for the flare photon flux level, which is left as a free parameter. By setting the calculated neutrino maximal flux to instrument sensitivities, we then derive the minimum level of background photon flux in the flare that is required at a specified wavelength for a successful detection.
3. Maximum accessible proton energy and indicative maximum neutrino energy
In the following, all primed quantities are in the comoving frame of the emitting region. Quantities are labeled Qx ≡ Q/ 10x in cgs units unless specified otherwise, and except for particle energies, which are in Ex ≡ E/ 10xeV. Numerical applications are given as an illustration for benchmark parameters of GRBs. We consider a proton of energy Ep = γpmpc2, accelerated in a one-zone region of size R = βc Γ2tvar(1 + z)-1, bulk Lorentz factor Γ = (1−β2)− 1 / 2 (with βc the bulk velocity), and of magnetic field strength B, in a source located at redshift z.
The magnetic field strength can be derived by setting LB = ηBLbol, where Lbol is the isotropic bolometric luminosity of the flare and LB is the magnetic luminosity, defined as LB ~ (1 / 2)βc Γ2R2B′2 (e.g., Lemoine & Waxman 2009) ![\begin{eqnarray} B' \!\!\!&=&\!\!\! \left[ \frac{2\eta_{\rm B} L_{\rm bol} (1+z)^{2} }{ \beta^3 c^3 \Gamma^6\,t_{\rm var}^{2} } \right]^{1/2} \nonumber\\ & \sim&\!\!\! 2.7\times 10^5\,{\rm G}\,\eta_{\rm B}^{1/2}L_{\rm bol,52}^{1/2}\Gamma_2^{-3}t_{\rm var,-1}^{-1} (1+z). \label{eq:B} \end{eqnarray}](/articles/aa/full_html/2017/07/aa30326-16/aa30326-16-eq29.png) (3)For maximization reasons, we concentrate on the proton case, which should lead to the highest rates of neutrino production compared to heavier nuclei. The case of heavier nuclei can be derived at the cost of scaling down the expected fluxes in the proton case by a factor of 5−10 (Murase & Beacom 2010).
(3)For maximization reasons, we concentrate on the proton case, which should lead to the highest rates of neutrino production compared to heavier nuclei. The case of heavier nuclei can be derived at the cost of scaling down the expected fluxes in the proton case by a factor of 5−10 (Murase & Beacom 2010).
3.1. Acceleration process
The acceleration timescale of a particle of charge e and energy E experiencing an electric field ℰ reads tacc = E/ (eℰc). Astrophysical plasmas are almost perfectly conducting, implying ℰ + v × B/c = 0 for a plasma moving at velocity v, hence ℰ ≤ B. Therefore, regardless of the acceleration mechanism (unless one invokes peculiar non-conducting plasmas), the acceleration timescale can be related to the particle Larmor time tL ≡ E/ (eBc): tacc = ηtL. As argued in detail in the Lemoine & Waxman (2009), for instance, it is impossible to have η< 1, and in most cases η ≫ 1. η ~ 1 might be achieved in high-voltage drops that can occasionally be found in some regions of the magnetosphere or the wind of neutron stars, or near black holes and their accretion disks. Even in such extreme regions, however, the efficiency of acceleration depends on the (often highly speculative) mechanism of dissipation of energy.
A large variety of particle acceleration processes have been invoked in transient sources, such as nonrelativistic or mildly relativistic shock acceleration (e.g., Bednarek & Idec 2011; Metzger et al. 2015 and Bykov et al. 2012; Marcowith et al. 2016 for reviews), wake-field acceleration (Tajima & Dawson 1979; Chen et al. 2002), or reacceleration in sheared jets (de Gouveia dal Pino & Lazarian 2005; Giannios 2010). Magnetic reconnection is the great favorite, however, for the modeling of explosive phenomena, that exhibit very rapid time variability and impulsive character (e.g., Lyutikov 2006; Baty et al. 2013; Cerutti et al. 2014 and Zweibel & Yamada 2009; Uzdensky 2011, 2016 for reviews). Given the complexity of these models and the wide range of parameters that have to be accounted for, we stick to our maximization strategy and consider in the following the maximally efficient acceleration timescale, with η ~ 1. The acceleration timescale can thus be expressed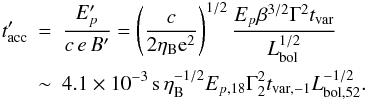 (4)As already described, this timescale is usually overly optimistic in terms of efficiency, but could be adequate for magnetic reconnection. This timescale is conservative to derive the necessary condition for detectability. The nonrelativistic case is delicate, however, as shock acceleration processes becomes significantly less efficient for low shock velocities βsh, as
(4)As already described, this timescale is usually overly optimistic in terms of efficiency, but could be adequate for magnetic reconnection. This timescale is conservative to derive the necessary condition for detectability. The nonrelativistic case is delicate, however, as shock acceleration processes becomes significantly less efficient for low shock velocities βsh, as 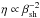 . As described in the next section, this could directly affect the maximum accessible energy and the neutrino flux.
. As described in the next section, this could directly affect the maximum accessible energy and the neutrino flux.
3.2. Energy losses
The maximum energy of accelerated particles is obtained by comparing the acceleration and energy loss timescales. In presence of strong magnetic fields (and thus for a high source luminosity) synchrotron cooling competes with the adiabatic energy losses.
In the comoving frame, the adiabatic loss timescale, corresponding to the dynamical timescale, can be expressed as 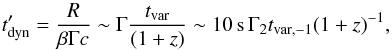 (5)and the proton synchrotron cooling timescale reads
(5)and the proton synchrotron cooling timescale reads 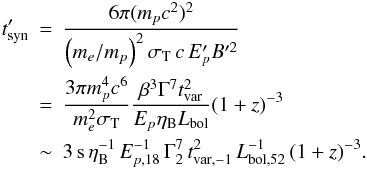 (6)The condition tacc< min(tdyn,tsyn) leads to an estimate of the maximum proton energy. Two regimes can be distinguished. If tdyn<tsyn
(6)The condition tacc< min(tdyn,tsyn) leads to an estimate of the maximum proton energy. Two regimes can be distinguished. If tdyn<tsyn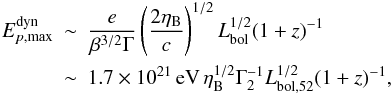 (7)and if tdyn>tsyn
(7)and if tdyn>tsyn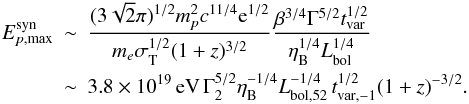 (8)We note that
(8)We note that 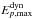 is independent of tvar. In the following, we set ηB = 1: we assume that the magnetic luminosity of the considered region is fully radiated during the flare. This hypothesis is valid if the dominant emission process is synchrotron radiation. Values of ηB< 1 are possible and could lead to higher Ep,max if tdyn>tsyn (Eq. (8)). We note the mild dependency on ηB in Eq. (8), however. Hence no significant enhancement of the maximum accessible energy is expected from this prefactor.
is independent of tvar. In the following, we set ηB = 1: we assume that the magnetic luminosity of the considered region is fully radiated during the flare. This hypothesis is valid if the dominant emission process is synchrotron radiation. Values of ηB< 1 are possible and could lead to higher Ep,max if tdyn>tsyn (Eq. (8)). We note the mild dependency on ηB in Eq. (8), however. Hence no significant enhancement of the maximum accessible energy is expected from this prefactor.
Other energy-loss processes can influence the maximum energy of particles. We choose to neglect them here, out of generality (some processes require a more refined knowledge of the background fields and structure) or for simplicity when they have limited impact. In all cases, neglecting energy losses preserves the maximum achievable nature of Ep,max. We also show in the next section that this is consistent with our derivations of our necessary conditions for neutrino flare detectability. We briefly discuss some of the neglected cooling processes below.
Inverse-Compton (IC) scattering off the flare photon field can also participate in proton cooling at the level of synchrotron radiations in the Thomson regime. However, in the Klein-Nishina regime, IC losses become quickly negligible with respect to synchrotron losses. As the IC regime depends on the photon energy in the proton rest frame, the relative importance of IC and synchrotron losses can only be estimated on a case-by-case basis. In order to keep this study as general as possible, we choose to neglect IC losses. We discuss this process applied to specific source categories in Appendix A.
Bethe-Heitler electron-positron pair production (BH) from interactions of protons on photon fields, for instance, those produced during the flare, is usually a subdominant cooling process compared to photopion production (e.g., Sikora et al. 1987 for AGN), because of its low inelasticity (ξBH ~ 10-3 at the threshold 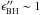 MeV) and mild cross-section (σBH ~ 1.2 mb at threshold). It can become significant over some high-energy range windows for very specific photon spectra (Murase et al. 2014; Petropoulou & Mastichiadis 2015), however – see also the detailed analytical discussion by Rachen & Mészáros (1998). We note that the cooling effect itself is limited even in these situations, although the production of secondary pairs can have an important influence on the resulting gamma-ray spectra. For simplicity, we therefore neglect BH losses in this study.
MeV) and mild cross-section (σBH ~ 1.2 mb at threshold). It can become significant over some high-energy range windows for very specific photon spectra (Murase et al. 2014; Petropoulou & Mastichiadis 2015), however – see also the detailed analytical discussion by Rachen & Mészáros (1998). We note that the cooling effect itself is limited even in these situations, although the production of secondary pairs can have an important influence on the resulting gamma-ray spectra. For simplicity, we therefore neglect BH losses in this study.
We also note that in most cases, πγ processes occur on longer timescales than the dynamical timescale (the optical depth for interaction being usually ≲ 1). Therefore, in general, their effect in terms of energy losses and on the proton flux suppression is negligible. If this were not the case (for highly opaque sources that would produce neutrinos abundantly), our calculations would still correspond to the proton maximum achievable energy.
We caution that in the nonrelativistic case, the production of high-energy neutrinos in the dynamical regime seems favored as 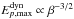 . However, as described before, in the nonrelativistic case η ≫ 1, and a more realistic picture gives
. However, as described before, in the nonrelativistic case η ≫ 1, and a more realistic picture gives 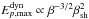 . Therefore, the energy of protons is limited by the loss of efficiency of the acceleration process.
. Therefore, the energy of protons is limited by the loss of efficiency of the acceleration process.
3.3. Decay of secondaries and neutrino maximum energy
Photohadronic interactions can generate neutrinos through the production of charged pions and their subsequent decay: p + γ → n + π+ and π+ → μ+ + νμ followed by 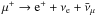 . The decay of secondary neutrons can also generate neutrinos, although their photodisintegration has a higher occurrence rate. This description is simplified as other photohadronic interaction channels contribute to the production of neutrinos, for instance, multi-pion productions (see, e.g., the SOPHIA code, Mücke et al. 1999), but it suffices in our framework. The resulting flavor composition is νe:νμ:ντ = 1:2:0, as we neglect the effect of energy losses or acceleration of pions and muons (e.g., Kashti & Waxman 2005). The expected flavor composition at Earth is 1:1:1 when long-baseline neutrino oscillations are accounted for. In the following the fluxes account for all neutrino flavors.
. The decay of secondary neutrons can also generate neutrinos, although their photodisintegration has a higher occurrence rate. This description is simplified as other photohadronic interaction channels contribute to the production of neutrinos, for instance, multi-pion productions (see, e.g., the SOPHIA code, Mücke et al. 1999), but it suffices in our framework. The resulting flavor composition is νe:νμ:ντ = 1:2:0, as we neglect the effect of energy losses or acceleration of pions and muons (e.g., Kashti & Waxman 2005). The expected flavor composition at Earth is 1:1:1 when long-baseline neutrino oscillations are accounted for. In the following the fluxes account for all neutrino flavors.
As charged pions carry 20% of the proton energy and neutrinos carry 25% of the pion energy, neutrinos produced by photohadronic interactions typically carry 5% of the initial energy of hadrons: Eν = 0.05Ep. The maximum accessible energy of neutrinos therefore depends on the maximally accessible energy of accelerated protons, which is determined by a competition between acceleration and energy losses. Moreover, neutrinos are produced if the charged pions and muons have time to decay before experiencing energy losses by adiabatic or synchrotron cooling.
The pion and muon decay times depend on their energies Eπ and Eμ. In the comoving frame, their decay times read 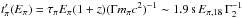 and
and 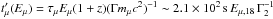 , where the pion and muon lifetimes and masses are τπ = 2.6 × 10-8s, τμ = 2.2 × 10-6s, mπ = 140 MeV c-2 and mμ = 106 MeV c-2, respectively. As τμ>τπ, the muon decay time is usually the main limiting factor for neutrino production. Muons satisfying
, where the pion and muon lifetimes and masses are τπ = 2.6 × 10-8s, τμ = 2.2 × 10-6s, mπ = 140 MeV c-2 and mμ = 106 MeV c-2, respectively. As τμ>τπ, the muon decay time is usually the main limiting factor for neutrino production. Muons satisfying 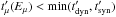 have time to decay and produce neutrinos. If
have time to decay and produce neutrinos. If 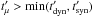 , we derive the maximum energy of muons that can produce neutrinos during the flare by equating
, we derive the maximum energy of muons that can produce neutrinos during the flare by equating 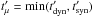 . If tdyn<tsyn
. If tdyn<tsyn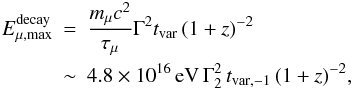 (9)and if tdyn>tsyn
(9)and if tdyn>tsyn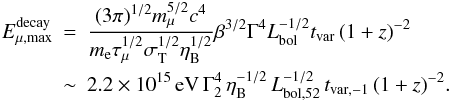 (10)The maximum neutrino energy can then be deduced as ~ 5% of the muon energy.
(10)The maximum neutrino energy can then be deduced as ~ 5% of the muon energy.
For dense photon backgrounds, pions and muons could undergo further μγ or πγ interactions, creating more pions and muons, that would lead to a cascade and thus to a suppression in neutrino flux (see, e.g., Fang et al. 2016). Such cascades are expected to have an effect only if photo-pion production is already highly efficient, that is to say, for dense fields, as the cross-sections of pγ and πγ processes can be considered as similar. We neglect these cascades for simplicity.
Before decaying, secondary pions and muons could undergo reacceleration processes in the same region as for the parent proton, as was discussed, for example, in Koers & Wijers (2007), Murase et al. (2012), Winter et al. (2014). These effects could have an impact if the acceleration process is very efficient. They should be taken into account to maximize the achievable neutrino energy and calculate the pion, muon, and neutrino energies self-consistently. We leave these calculations for further studies; in this sense, the neutrino energies calculated here are indicative and do not represent the maximum achievable neutrino energies. We aim here at giving a range of observable neutrino energies, and further refinements are not required for the purpose of calculating the minimum detectability flux (for this, we show that the maximum achievable proton energy is the crucial parameter).
 |
Fig. 1 Maximum accessible proton energy Ep,max(left column) and corresponding maximum accessible neutrino energy Eν,max (right column) as a function of the variability timescale tvar and the bolometric luminosity Lbol of a flaring source, with bulk Lorentz factor Γ = 1,10,100 (from top to bottom). Overlaid are examples of the location of benchmark explosive transients in the Lbol−tvar parameter space (see Sect. 5). The beige region indicates the domain where no source is expected to be found because of the excessive energy budget. The dots locate recently discovered categories of transients (Kasliwal 2011), superluminous supernovae (SLSNe), peculiar supernovae, and luminous red novae. The small square box (labeled SNe) and the short diagonal line on its upper left indicate core-collapse and thermonuclear supernovae, respectively. Low-luminosity GRBs and type Ibc supernovae should be treated with care (see Sect. 6.2). |
3.4. Results
The maximum accessible energy of protons (left panels) and an indicative (i.e., neglecting possible reacceleration) maximum energy of neutrinos (right panels) as a function of the variability timescale and the total luminosity are displayed in Fig. 1 for three bulk Lorentz factors Γ = 1,10,100 from top to bottom. The beige region is excluded in all figures as it corresponds to an energetic budget tvarLbol> 1054erg: this exceeds the energetic budget of GRBs, which are the most energetic transient events observed with photons in our Universe. White and gray patches locate typical transient sources discussed in Sect. 5.1 in the parameter space.
We can distinguish two regimes in the Lbol−tvar parameter space: adiabatic (synchrotron) cooling is dominant at low (high) luminosity. The transition between the two regimes depends on the bulk Lorentz factor: it is shifted toward higher luminosities when Γ increases. The limits set by disintegration timescales appear as vertical lines in the righthand column of Fig. 1. As expected, they play an important role for low-variability timescales.
For nonrelativistic outflows (Γ ~ 1), mild luminosities Lbol > 1036 erg s-1 and variability timescales longer than tvar ~ 10 s are required to reach Eν > 100 TeV, which is the lower limit of the IceCube detection range. This limit is related to the high fluxes of atmospheric neutrinos at Eν ≲ 100 TeV, although the experiment endeavors to lower this limit (Aartsen et al. 2016a). Sensitivities of future experiments such as ARA, ARIANNA, or GRAND, aiming at energies Eν > 1 EeV, would be reached for higher luminosities Lbol > 1042 erg s-1 and longer variability timescales tvar > 106s.
Our results are consistent with the dedicated studies that can be found in the literature for particular sources with mildly and ultrarelativistic outflows (Γ = 10 and 300 in our examples). We find that high-luminosity (HL) GRBs can accelerate protons up to 1020eV, which corresponds to classical estimates (e.g., Waxman & Bahcall 2000; Murase et al. 2008; Bustamante et al. 2017). They could in principle produce very high energy neutrinos, with Eν≲1018 eV. In this case, muon decay constitutes a very strong limiting factor and hence the maximum energy strongly depends on the variability timescale. Blazars, low-luminosity (LL) GRBs, and tidal disruption events (TDE) are also powerful accelerators with Ep,max ~ 1019eV and associated maximum neutrino energy Eν ~ 1018 eV. We note that muon decay is not a limiting factor for blazars.
We caution again that these estimates are indicative and constitute maximum achievable neutrino energies, neglecting possible secondary reacceleration. In the next section, we evaluate the neutrino fluxes associated with these various flaring events in order to assess their detectability.
4. Neutrino flux and detectability limit
4.1. Maximum neutrino flux
As a first approximation, we consider that the flare photon spectrum follows a broken power-law over the energy range [ ϵmin,ϵmax ], with an observed break energy ϵb, corresponding observed (isotropic equivalent) luminosity set as Lb, and spectral indices a<b, with b> 2: 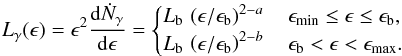 (11)This type of spectrum is adequate to model nonthermal processes such as synchrotron emission. It is quite appropriate in many cases, for instance, for most GRBs or for the Crab flares. However, the spectral energy distribution (SED) of explosive transients shows great diversity, and our approach should be refined by using more realistic SED, adapted to several typical sources such as blazars or magnetars. We leave this issue for further studies.
(11)This type of spectrum is adequate to model nonthermal processes such as synchrotron emission. It is quite appropriate in many cases, for instance, for most GRBs or for the Crab flares. However, the spectral energy distribution (SED) of explosive transients shows great diversity, and our approach should be refined by using more realistic SED, adapted to several typical sources such as blazars or magnetars. We leave this issue for further studies.
The neutrino flux can be estimated from the proton energy spectrum 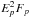 (Waxman & Bahcall 1999):
(Waxman & Bahcall 1999): 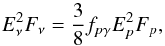 (12)where the photo-pion production efficiency
(12)where the photo-pion production efficiency 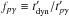 is the key parameter to determine. The photo-pion production timescale in the comoving frame
is the key parameter to determine. The photo-pion production timescale in the comoving frame 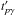 can be written
can be written 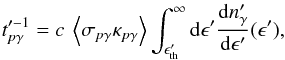 (13)with
(13)with 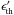 the interaction threshold energy in the comoving frame. We have approximated the cross-section σpγ and inelasticity κpγ profiles by the sum of two step functions, as in Atoyan & Dermer (2003):
the interaction threshold energy in the comoving frame. We have approximated the cross-section σpγ and inelasticity κpγ profiles by the sum of two step functions, as in Atoyan & Dermer (2003):
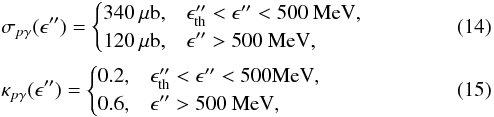 with
with 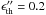 GeV the interaction threshold energy in the proton rest frame. The photon energy density in the comoving frame,
GeV the interaction threshold energy in the proton rest frame. The photon energy density in the comoving frame, 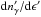 , associated with the flaring event, is estimated from the observations, using Eq. (11)
, associated with the flaring event, is estimated from the observations, using Eq. (11) 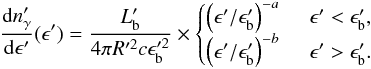 (16)We can obtain an equivalent expression regardless of the geometry of the emitting region, for a spherical blob or wind-type spherical shell geometries (Dermer & Menon 2009).
(16)We can obtain an equivalent expression regardless of the geometry of the emitting region, for a spherical blob or wind-type spherical shell geometries (Dermer & Menon 2009).
The above equations yield the photo-pion production timescale ![\begin{equation} t_{p\gamma}'^{-1} \simeq \frac{\left\langle \sigma_{p\gamma} \kappa_{p\gamma} \right\rangle L_{\rm b} }{ 4 \pi R^2 \Gamma \epsilon_{\rm b}}\frac{1}{1-a} \left[\frac{a-b}{1-b}-\left(\frac{\epsilon_{\rm th}}{{\epsilon}_{\rm b}} \right)^{1-a}\right]\cdot \label{eq:tpgamma1} \end{equation}](/articles/aa/full_html/2017/07/aa30326-16/aa30326-16-eq134.png) (17)The term (a−b) / (1−b) being of order unity, we can readily see that
(17)The term (a−b) / (1−b) being of order unity, we can readily see that 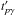 will simplify depending on whether the flare photon spectrum before the break energy is soft (a> 1) or hard (a< 1):
will simplify depending on whether the flare photon spectrum before the break energy is soft (a> 1) or hard (a< 1):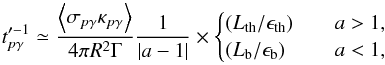 (18)where we have defined the observed photon luminosity at threshold energy Lth ≡ Lγ(ϵth) = Lb(ϵth/ϵb)2−a. The photon energy threshold for photo-pion production reads
(18)where we have defined the observed photon luminosity at threshold energy Lth ≡ Lγ(ϵth) = Lb(ϵth/ϵb)2−a. The photon energy threshold for photo-pion production reads 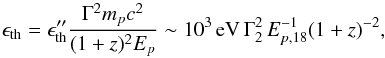 (19)hence
(19)hence 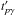 depends on Ep through ϵth.
depends on Ep through ϵth.
We note that Eq. (17) was obtained by assuming ϵth<ϵb. However, this is not always the case as ϵth depends on the proton energy and the bulk Lorentz factor (Eq. (19)). The condition ϵth<ϵb implies Ep>Ep,min with 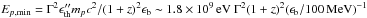 . For ϵth>ϵb,
. For ϵth>ϵb, 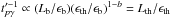 . As we have assumed b> 1, we recover the soft spectrum case (a> 1) of Eq. (18) when ϵth>ϵb.
. As we have assumed b> 1, we recover the soft spectrum case (a> 1) of Eq. (18) when ϵth>ϵb.
We assume that a fraction ηp of the bolometric source luminosity is channeled into a population of accelerated protons, with a peak luminosity xpηpLbol, where xp ≤ 1 is a bolometric correction prefactor that depends on the proton spectral index, peak, and maximum energies. For a transient source located at luminosity distance DL (redshift z), a maximum achievable time-integrated neutrino flux can then be derived from Eq. (12) 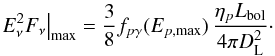 (20)If a> 1, the higher the proton energy Ep, the lower the corresponding ϵth, and the higher the associated photon luminosity and the efficiency fpγ. If a< 1,
(20)If a> 1, the higher the proton energy Ep, the lower the corresponding ϵth, and the higher the associated photon luminosity and the efficiency fpγ. If a< 1, 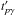 does not depend on Ep. Hence fpγ(Ep,max) = fpγ | max. As we maximize the neutrino flux, we also set xp = 1.
does not depend on Ep. Hence fpγ(Ep,max) = fpγ | max. As we maximize the neutrino flux, we also set xp = 1.
Expressing 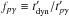 using Eqs. (5) and (18) yields the maximum achievable neutrino flux:
using Eqs. (5) and (18) yields the maximum achievable neutrino flux: 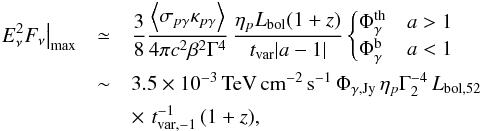 (21)where we have defined
(21)where we have defined 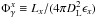 with x = th or b, the observed photon flux of the source at threshold energy ϵth and break energy ϵb, respectively. We note that
with x = th or b, the observed photon flux of the source at threshold energy ϵth and break energy ϵb, respectively. We note that 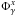 is a directly measurable quantity. For the numerical estimate, Φγ,Jy = Φγ/ (1 Jy), where 1 Jansky ~ 1.5 × 103 ph cm-2 s-1.
is a directly measurable quantity. For the numerical estimate, Φγ,Jy = Φγ/ (1 Jy), where 1 Jansky ~ 1.5 × 103 ph cm-2 s-1.
4.2. Minimum photon flux Φγ,min for neutrino detectability
We consider a neutrino detector of flux sensitivity sexp and corresponding sensitivity in terms of fluence 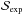 . By equating the maximum achievable neutrino flux to the detector sensitivity in flux,
. By equating the maximum achievable neutrino flux to the detector sensitivity in flux, 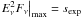 , we calculate the minimum photon flux required to reach the experimental detection limit:
, we calculate the minimum photon flux required to reach the experimental detection limit: 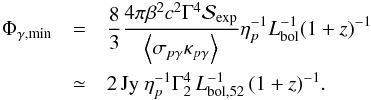 (22)The flux should be estimated 1) for soft photon spectra (a > 1), at the minimum threshold energy (obtained from the maximum energy of accelerated protons):
(22)The flux should be estimated 1) for soft photon spectra (a > 1), at the minimum threshold energy (obtained from the maximum energy of accelerated protons): 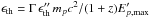 ; 2) for hard photon spectra (a < 1), at the observed spectral break energy ϵb. We have assumed that the detector points toward the source during the entire flaring event, that is, during t ~ tvar. The experimental detection limit then depends on the variability timescale:
; 2) for hard photon spectra (a < 1), at the observed spectral break energy ϵb. We have assumed that the detector points toward the source during the entire flaring event, that is, during t ~ tvar. The experimental detection limit then depends on the variability timescale: 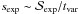 . Here, we have also assumed
. Here, we have also assumed 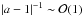 .
.
For IceCube, the sensitivity is characterized by a minimum fluence 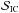 =5×10-4 TeV cm-2 over an energy range 10 TeV−10 PeV, which corresponds to a detection limit sIC~10-11 TeV cm-2 s-1 for a one-year data collection (Aartsen et al.2015). The IceCube-Gen2 project could reach a sensitivity of one order of magnitude better (The IceCube-Gen2 Collaboration et al. 2015). The planned sensitivities for ARA, ARIANNA (Allison et al. 2012; Barwick 2011), CHANT (Neronov et al. 2017), or GRAND (Martineau-Huynh et al. 2016) are 1, 1.5, or 2 orders of magnitude better, respectively, than IceCube, at Eν ~ 1 EeV.
=5×10-4 TeV cm-2 over an energy range 10 TeV−10 PeV, which corresponds to a detection limit sIC~10-11 TeV cm-2 s-1 for a one-year data collection (Aartsen et al.2015). The IceCube-Gen2 project could reach a sensitivity of one order of magnitude better (The IceCube-Gen2 Collaboration et al. 2015). The planned sensitivities for ARA, ARIANNA (Allison et al. 2012; Barwick 2011), CHANT (Neronov et al. 2017), or GRAND (Martineau-Huynh et al. 2016) are 1, 1.5, or 2 orders of magnitude better, respectively, than IceCube, at Eν ~ 1 EeV.
We note that all types of events (tracks or showers) should be considered for detection, and our predictions are given for all flavors. However, energies below 100 TeV are strongly disfavored because of atmospheric background. Furthermore, track events give more information about the arrival direction and therefore allow us to identify coincident photon flares or coincident neutrino events more precisely. If arrival directions are not available (in the case of shower events), temporal coincidence could also help to associate events, with less certainty.
For a fixed ηp and a bulk Lorentz factor Γ of the emitting region chosen following a theoretical model for the source, the minimum photon flux density for neutrino detection is a function of two observed quantities: the bolometric luminosity Lbol, and the variability timescale of the flaring event tvar.
The cosmic-ray loading factor ηp is an unknown parameter that could take values up to ηp ~ 100, which are required for GRBs and blazar populations to reach the flux of observed UHECRs (e.g., Murase et al. 2006). In the following, we set ηp = 1 as a standard estimate, but most conservative limits should be obtained by multiplying Φγ,min by ηp = 100 (Eq. (22)).
We note that because of the factor β in Eq. (22), in the nonrelativistic case the minimum flux should be strongly suppressed and therefore the detectability for nonrelativistic outbursts should be favored. However, the inefficiency of acceleration processes in nonrelativistic cases could compensate for this effect, and values of β ≲ 10-2 are not favored to produce neutrinos above ~ 100 TeV.
 |
Fig. 2 What is the minimum source photon flux required to enable neutrino detection with IceCube? The color map shows the minimum photon flux Φγ,min (in Jy and ph cm-2 s-1) as a function of the bolometric luminosity Lbol and the variability timescale tvar of the flaring event for an outflow bulk Lorentz factor Γ = 1,10,100. A neutrino flare can be detectable if the observed photon flux Φγ,obs ≳ Φγ,min, above the minimum threshold energy ϵth (red lines) for soft photon spectra, and at the observed photon break energy ϵb for hard spectra. Here ηB = ηp = 1, but the most conservative estimate should use ηp = 100. Overlaid objets as in Fig 1. Type Ibc supernovae should be treated with care (see Sect. 6.2). |
4.3. Can we detect a neutrino flare?
We show in Fig. 2 the minimum photon flux required to reach the IceCube detection limit in the Lbol−tvar parameter space for Γ = 1,10,and100 from top to bottom. We set ηp = ηB = 1. Depending on the SED of the emission (soft or hard before the break energy, see Sects. 4.1 and 4.2), this minimum flux Φγ,min should be evaluated at the minimum threshold energy ϵth indicated in red contours (for soft spectra, a> 1) or at the observed spectral break energy ϵb (for hard photon spectra, a< 1).
We locate concrete examples of explosive transients in the parameter space: for Γ ~ 1 Crab flares, supernovae, and novae (list of sources taken from Kasliwal 2011). For Γ ~ 10 and Γ ~ 100 we give the example of blazars, magnetar giant flares, TDEs, LL GRBs, and classical GRBs. These categories and specific source cases are discussed in Sect. 5 and our results are reported in Table 1.
In practice, here we describe how these figures can be used to determine whether an explosive transient could have a chance to be detected in neutrinos with IceCube.
-
1.
Choose a bulk Lorentz factor Γ for the outflow1.
-
2.
Identify a broken power-law shape in the source emission, roughly measure the break energy ϵb and whether the spectrum is soft (a > 1) or hard (a < 1) below the break.
-
3.
Locate the source in the Lbol−tvar parameter space and read the required flux Φγ,min (colored contours).
-
4.
Compare Φγ,min with the observed flux of the source Φγ,obs, around the threshold energy indicated in red contours, ϵth, for soft spectra (a < 1), or at the break energy ϵb for hard spectra (a < 1). We recall that a neutrino flare associated with the photon flare can be detectable if Φγ,obs ≳ Φγ,min.
We note that for many sources, Φγ,obs ≪ Φγ,min over the whole radiation spectrum, thus the knowledge of ϵth or ϵb is not necessary to conclude on the non-detectability. For more refined cases, however, we caution that ϵth is a minimum value because it was derived from Ep,max (a maximum value). When checking detectability, one might wish to extend the comparison between Φγ,obs and Φγ,min for ϵth > ϵth,min, in case the actual maximum proton energy is lower than Ep,max. Extrapolation of spectra should be conducted with care, always trying to maximize the photon flux, in order to avoid missing a detectable case.
For short flares, nonthermal spectra can broadly be approximated by a broken power-law. However, we examine the peculiar case of a double-bump spectrum in Appendix B.
A quiescent photon flux from the source could be dominating the flare radiation in some regions of the spectrum. Taking these photons into account by mistake when evaluating Φγ,obs to compare to Φγ,min does not lead to false negatives (missing detectable sources) as this simply overestimates the observed flux.
The observation of type Ibc SNe with no associated GRB emission (corresponding to completely choked and misaligned GRBs) constitutes a limitation of our model. As discussed in Sect. 6.2, the material surrounding the outburst could prevent the observer from detecting it and from correctly assessing the total amount of energy and the variability of the outburst. Thus our criteria do not apply and these sources should be examined in more detail in order to conclude on their detectability.
5. Implications for categories of transients and specific case studies
The general approach presented up to this point allows us to evaluate the detectability in neutrinos of a large variety of explosive transients. We study the implications for general source categories in Sect. 5.1 and examine several concrete examples in Sect. 5.2.
5.1. Census of existing transients
We summarize the typical ranges of key parameters (bolometric luminosity for equivalent isotropic emission, variability timescale, and bulk Lorentz factor) that intervene in the evaluation of the detectability of neutrino flares for several categories of transients.
For each type of sources, we evaluate the maximum luminosity distance DL,max or maximum redshift zmax at which we can expect to detect an associated neutrino flare with IceCube. In each spectral case, DL,max can be easily derived from the IceCube detection limit and the minimum photon flux by setting 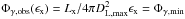 with x = b in the hard case and x = th in the soft case:
with x = b in the hard case and x = th in the soft case: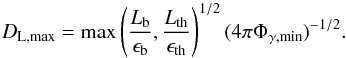 (23)The results are reported in Table 1 and can be compared with the distance of real sources in Table 2.
(23)The results are reported in Table 1 and can be compared with the distance of real sources in Table 2.
As the minimum photon flux Φγ,min is proportional to the detector sensitivity, this threshold will decrease by one or two orders of magnitude for future detectors such as IceCube-Gen2, ARA, ARIANNA, or GRAND.
Typical properties of different flaring source categories.
5.1.1. Novae, supernovae, and luminous supernovae
Thermonuclear SNe, core-collapse SNe, and classical novae have been extensively studied (e.g., Kasliwal 2011 for a review). These events are well characterized by their peak luminosity (Lb ~ 1038−1039 erg s-1 for novae and Lb ~ 1040−1043 erg s-1 for ordinary SNe) and duration (between 1 and 100 days). The classical objects only populate limited regions of the parameter space, but new classes of transients with properties intermediate between novae and SNe are being discovered.
Many studies focus on quiescent neutrino emissions from supernova remnants or from hadronic interactions during the early evolution of classical supernovae (see, e.g., Bednarek et al. 2005, for a more general review of Galactic sources of high-energy neutrinos). The low-energy neutrino emissions throughout the explosion have also been extensively studied. The early production of transient high-energy neutrinos from classical SNe or novae has scarcely been examined so far (but see, e.g., Beall & Bednarek 2002); authors concentrate on superluminous supernovae instead, which seem indeed promising in terms of detectability following our criterion (see Table 1).
The radiation processes related to these explosions are generally considered as thermal emissions; the radiated energy is mainly observed in optical and UV wavelengths. However, nonrelativistic shocks may also occur during these outbursts and lead to nonthermal shock-emissions. In this case, a significant fraction of the optical emission could be shock powered. We emphasize that shocks are mainly expected to occur in dense regions, but gamma-ray emissions have also been detected from novae only a few days after the peak of the optical radiation (Ackermann et al. 2014). Therefore, particle acceleration may be at play in these objects (Metzger et al. 2015). If hadrons are accelerated at high energies, it may lead to neutrino production, but the density of hadronic background could favor purely hadronic over photohadronic neutrino production.
Hypernovae or superluminous supernovae (SLSNe) constitute a rare class of bright transients, with luminosities ten to hundreds of times that of usual core-collapse or thermonuclear SNe (Quimby 2012). Mainly three scenarios have been proposed to explain these exceptionally luminous light curves: they could be powered by the interaction of the supernova (SN) ejecta with the circumstellar medium (e.g., Ofek et al. 2007; Quimby et al. 2011; Chevalier & Irwin 2011; Murase et al. 2011), neutron-star-driven (Kasen & Bildsten 2010; Dessart et al. 2012; Kotera et al. 2013; Metzger et al. 2014; Murase et al. 2015), or pair-instability-driven (Gal-Yam et al. 2009; Gal-Yam & Leonard 2009). In the two former scenarios, associated gamma-ray emission is expected and implies shock regions that would be favorable for cosmic-ray acceleration to very high energies, and subsequent neutrino production. In particular, for neutron-star powered SNe, neutrinos can be produced by pp or pγ interactions on the nonthermal, thermal, or baryonic fields of the ejecta (Murase et al. 2009; Fang et al. 2013, 2016). Only magnetars can lead to reasonably short tvar < 107s transient emissions, however, thanks to their rapid electromagnetic energy losses. For these objects, the dominant process for neutrino production is pγ interactions on background photons that should be mostly directly observed (Kasen & Bildsten 2010; Kotera et al. 2013).
We caution that some stripped core-collapse SNe (types Ibc, superluminous or more ordinary) could be associated with gamma-ray bursts (e.g., Modjaz 2011; Hjorth & Bloom 2012 for reviews). In this case, a different neutrino production mechanism (likely more efficient) might have occurred (see next sections and references therein). As discussed in Sect. 6.2, such scenarios imply that the neutrinos are a precursor of the SN emission, and our minimum flux criterion cannot be applied because the relevant radiation field could be processed in the environment and diluted over the emission timescale.
5.1.2. Gamma-ray bursts
Gamma-ray bursts are the most energetic and violent events observed in our Universe. In the popular fireball model, the observed photons stem from the acceleration of electrons in internal shocks of a relativistic outflow of typical bulk Lorentz factor Γ ~ 102−103. These events last approximately tGRB ~ 10-1−102 s. They show short and puzzling variability timescales tvar ~ 10-3−1 s and very high bolometric luminosities Lbol ~ 1051−1054 erg s-1. Different categories of GRBs can be distinguished depending on their luminosity or duration. Here we focus on high-luminosity GRBs (HL GRBs), and the question of low-luminosity GRBs is discussed in Sect. 5.1.3. Long GRBs, with tGRB > 2 s, are supposedly associated with the death of massive stars, while short GRBs, with tGRB < 2 s, are theoretically associated with compact-object binary mergers. Hence, unlike long GRBs, short GRBs are not associated with supernovae. Ghirlanda et al. (2009) highlighted similarities between the variability, the spectrum, the luminosity, and the Epeak−Liso correlation (corresponding to Eb−Lbol with our notations) of short GRB and the first seconds of long GRB emission. However, the Epeak−Eiso correlation (with Eiso the total isotropic equivalent energy) defined by long GRBs does not seem to be followed by short GRBs. Moreover, except for exceptional detections, short GRBs seem to be located at lower redshift than long GRBs – although the number of precise measurements for short GRBs remains a major limitation.
The prompt HL GRB spectra are well described by broken power-laws with typical low- and high-energy spectral indices a ~ −1−2 and b ~ 2−3 and a break at ϵb ~ 10−1000 keV (Ghirlanda et al. 2005). However, in many cases, the spectrum exhibits a high-energy cut-off. Therefore different spectral models have been suggested to fit the GRBs spectra, such as the “Band” function, exponential cutoff power-laws, or smoothly connected broken power-laws. With these models, systematic spectral analyses of GRBs have been performed to better characterize the distribution of low- and high-energy spectral indices and of peak energies (Goldstein et al. 2013).
Numerous studies have been conducted to precisely evaluate the expected flux of neutrinos from HL GRBs (e.g., Waxman & Bahcall 1997; Murase & Nagataki 2006; Murase et al. 2008 and Mészáros 2015 for a review). Our criteria given in Table 1 are consistent with these works. The production of high-energy neutrinos from GRB early afterglows has also been addressed (e.g., Dermer 2002; Murase 2007). The detection of GeV−TeV neutrinos coincident with the promt emission, guaranteed by recent GRB models (Murase et al. 2013), could also help constrain GRB emission mechanisms.
The IceCube searches for neutrinos produced during the prompt emission of GRBs (Aartsen et al. 2016b) have revealed no excess against the expected atmospheric background. It allows us to constrain the current models for the production of UHECRs and neutrino in GRBs (e.g., He et al. 2012; Baerwald et al. 2015).
For HL GRBs we estimate a neutrino maximal energy Eν,max = 0.1−103 PeV, a threshold energy ϵth = 10−103 eV, a minimum photon flux Φγ,min = 103−106 ph cm-2 s-1 and a maximum redshift zmax ≃ 1.9 for a< 1. However, with a typical photon index a = 1.2, zmax ≃ 3. As the low-energy part of GRB spectra is often soft, ee need to take the value of a into account to estimate the maximum redshift.
5.1.3. Low-luminosity GRBs, trans-relativistic supernovae, and off-axis GRBs
Low-luminosity GRBs (LL GRBs) have been suggested as a separate population from high-luminosity GRBs (HL GRBs; e.g., Virgili et al. 2009; Bromberg et al. 2011). LL GRBs show longer variability timescales, tvar ~ 10−103 s, lower bolometric luminosities Lbol ~ 1046−1048 erg s-1, a softer spectrum, and a lower break energy. They may also be characterized by lower Lorentz factors Γ ~ 10. However, other authors invoke a unified picture by interpreting LL GRBs as GRBs that are observed off-axis (Salafia et al. 2016) or as semi-choked GRBs (Nakar 2015).
In the latter case, the singular characteristics of LL GRBs associated with SNe could be explained by the trans-relativistic shock breakout model (Soderberg et al. 2006; Nakar & Sari 2012). When a stellar explosion occurs, the breakout of the shock going through the object generates the first observable light. In the case of a compact object or a very energetic explosion, the breakout could become mildly or ultra relativistic. Several studies focus on the cosmic rays and high-energy neutrinos from trans-relativistic supernovae shock breakouts (e.g., Budnik et al. 2008; Kashiyama et al. 2013).
The value of Φγ,min given in Table 1 assumes that neutrinos are produced in the region emitting the LL GRB radiation. However, as discussed in Sect. 6.2, the actual bolometric luminosity and the target radiation for neutrino production could be difficult to evaluate. This criterion should therefore be viewed with care.
5.1.4. Blazar flares
Blazars are a subset of AGN whose jet is pointed toward the observer. Unification models (Urry & Padovani 1995) allow to set their mean bulk Lorentz factor to Γj ~ 10. A blazar flare is a very fast and short increase in blazar luminosity that occurs in addition to its “quiescent” emission. In simple models, the bulk Lorentz factor Γ of the region associated with a flare is assumed to be the same as the mean bulk Lorentz factor. However, the rapid variability of blazar flares has led to more realistic scenarii where Γ > Γj (e.g., Ghisellini et al. 2005; Giannios et al. 2009) with Γ ≳ 100. These models predict orphan TeV flares and TeV flares with simultaneous far-UV/soft X-ray flares, respectively.
Blazar SEDs exhibit two nonthermal peaks, at low and high energies. The low-energy part extends from radio to X-rays (in the most extreme cases), while the high-energy part extends from X-rays to gamma-rays. Blazars show strongly variable emissions correlated over frequencies, with a typical variation timescale of months. They also experience flaring events with shorter timescales (e.g., Aharonian et al. 2007); thus we set tvar~102−106 s. In some cases, Blazar flaring emissions can be described by a soft power-law from submillimeter to X-rays, with typically Lb~1045 erg s-1 at ϵb~1 keV (Rachen & Mészáros 1998). Hadronic and leptonic models still coexist to explain the emissions from these objects, although IceCube is expected to soon start constraining the contribution of hadrons (e.g., Petropoulou et al. 2016a).
Our estimates show that ultrarelativistic cases (Γ = 100) are less favorable, as flares can only be detected up to zmax ≃ 3×10-4 (DL,max ~ 1.2 Mpc), against z ≃ 0.7 for Γ = 10. Furthermore, for Γ = 100 the threshold energy falls in the low-flux region of the blazar emission.
5.1.5. Magnetars
Magnetars are strongly magnetized pulsars (B ≳ 1014 G) with high spin-down rates. They are historically divided into two classes: soft gamma-ray repeaters (SGRs) and anomalous X-ray pulsars (AXPs). SGRs are of significant importance in this study as they exhibit several types of flaring events: short bursts (SB), intermediate bursts (IB), and giant flares (GF). Short bursts are characterized by tvar ~ 10-1−1 s, Lb = 1039−1041 erg s-1 with soft spectra at ~ 10 keV. Intermediate bursts are characterized by tvar ~ 1−40 s, Lb = 1041−1043 erg s-1 with similar spectra. Giant flares are rarer, with a first violent emission (the initial spike) followed by a longer pulsating tail lasting t ~ 100 s (Woods & Thompson 2006; Mereghetti 2008; Turolla et al. 2015). The initial spike is characterized by tvar ~ 10-1 s, Lb = 1044−1047 erg s-1 and a very hard spectrum, detected up to 2 MeV, with a peak around 105 eV. It is not clear whether a cooling blackbody or an exponentially cutoff power-law fits the observed spectra best. Moreover, the value of Γ is uncertain and strongly depends on the model adopted to describe the flares. A bulk Lorentz factor Γ = 10 is sometimes assumed for giant flares, see, for example, Lyutikov (2006).
Ioka et al. (2005) estimated neutrino fluxes from magnetar giant flares by considering proton-proton interactions and photohadronic interactions with photospheric thermal radiation. Photohadronic interactions with nonthermal photon fields are considered to be negligible. The case of SGR 1806-20 is also studied by using a fireball model, and promising estimates are calculated, see Sect. 5.2.5 for more detail.
As we consider flaring emissions of neutrinos and not steady emissions (the variability timescale of the neutrino flare should be in the order of the variability timescale of the giant flares), and as we do not consider a specific model for magnetar giant flares, we focus here on photohadronic interactions with the main radiation field, assumed to be nonthermal. We obtain a maximum neutrino energy Eν,max = 10-3−0.1 PeV, a threshold energy ϵth = 10−102 eV, and a minimum photon flux Φγ,min = 104−106 ph cm-2 s-1, which implies DL,max ~ 0.39 Mpc for magnetar giant flares.
5.1.6. Tidal disruption events
Tidal disruption events are assumed to result from the disruption of a star approaching a supermassive black hole. Numerous TDE candidates are known today (Komossa 2015), but several events, referred to as jetted TDEs, show very interesting properties, for example, Swift J1644+57 (Cummings et al. 2011) and Swift J1112-8238 (Brown et al. 2015). Compared to the GRBs, these transients have extremely long durations: the flare rise time is approximately ~ 100 s and its duration ~ 103−104 s. Typical peak luminosities are Lb ~ 1043−1048 erg s-1 (e.g., Donley et al. 2002; Burrows et al. 2011) with a peak in hard X-rays or soft gamma-rays. The lack of spectral information about jetted TDEs does not allow us to characterize the TDE spectra precisely. However, from the observation of Swift J1644+57, we assume that jetted TDEs are characterized by nonthermal and hard spectra (a < 1). The emission is most likely relativistic, with a bulk Lorentz factor Γ ~ 10. Several studies predict a possible acceleration of UHECRs in TDE, for isntance, Farrar & Gruzinov (2009), Farrar & Piran (2014), Pfeffer et al. (2017). Others directly address the question of neutrino production (Dai & Fang 2016; Lunardini & Winter 2017; Senno et al. 2017).
5.1.7. Black hole, neutron star, and white dwarf mergers
The recent detection of gravitational waves by the LIGO collaboration (Abbott et al. 2016b,a) has generated considerable interest in mergers of compact objects. Black hole (BH) mergers are most probably at the origin of these emissions. Mergers of other compact objects, such as neutron star (NS) or white dwarf (WD) mergers, could also produce gravitational waves. Given the huge amount of energy released during the merger of two compact objects, electromagnetic counterparts are often contemplated.
The existence of an electromagnetic counterpart to BH mergers as well as a counterpart in ultrahigh-energy cosmic rays and neutrinos have been proposed by Kotera & Silk (2016), Murase et al. (2016). In this scenario, a powerful electromagnetic outflow is generated through the Blandford-Znajek process (Blandford & Znajek 1977), and an associated luminosity can be roughly estimated (Lyutikov 2011): 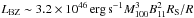 , where M is the mass of the final black hole, B is the external magnetic field strength, and the orbital radius is approximated by the Schwarzschild radius RS. Therefore, we set Lbol ~ 1043−1046 erg s-1 for BH mergers. A variability timescale for electromagnetic emissions tvar ~ 104−5 × 106 can be postulated, as it allows us to reproduce the observed ultrahigh-energy cosmic-ray flux with a population of BH mergers. This represents a comfortable fraction of the maximum duration of the BZ process:
, where M is the mass of the final black hole, B is the external magnetic field strength, and the orbital radius is approximated by the Schwarzschild radius RS. Therefore, we set Lbol ~ 1043−1046 erg s-1 for BH mergers. A variability timescale for electromagnetic emissions tvar ~ 104−5 × 106 can be postulated, as it allows us to reproduce the observed ultrahigh-energy cosmic-ray flux with a population of BH mergers. This represents a comfortable fraction of the maximum duration of the BZ process: 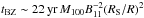 , which can be sustained as long as accretion is sustained – through disruption of planetary or asteroidal debris, for example.
, which can be sustained as long as accretion is sustained – through disruption of planetary or asteroidal debris, for example.
Neutron star mergers are also studied in a multi-messenger perspective. They have been proposed as possible candidates for the production of short GRBs or for the production of UHECR and neutrinos if the merger produces a magnetar (Piro & Kollmeier 2016). The typical spin-down time and spin-down luminosity of magnetars allows us to roughly estimate the variability timescale and maximum bolometric luminosity of the emissions: tvar ~ 103−104 s and Lbol ~ 1046−1048 erg s-1.
Last, WD mergers have been proposed as a source of high-energy neutrinos (Xiao et al. 2016). The variability timescale is obtained from the viscous time, and we take a rough estimate tvar ~ 102−104 s. The maximum bolometric luminosity is obtained from the magnetic luminosity Lbol ~ 1044−1046 erg s-1. In these cases, if the debris disk surrounding the central object is optically thick, the high-energy photons can be hidden from the observer. However, a bright optical counterpart with L ~ 1041−1042 erg s-1 may be observable (Beloborodov 2014).
The Lorentz factors for these mergers being difficult to infer from current data and theory (their acceleration region could equally resemble GRBs or blazar jets, or have Γ ~ 1), we show in Table 1 the estimates for different Γ. Maximum distances are not calculated because we lack of information on the spectral shape of the radiation.
5.2. Case studies
5.2.1. Naked-eye GRB 080319B
An exceptional burst was detected on 2008 March 19 by the Swift and Konus-Wind satellites (Racusin et al. 2008a). This long-duration burst, with t ~ 50 s, was characterized by an extreme isotropic equivalent luminosity at peak: Liso,peak ~ 1053erg s-1 at ϵb ~ 540−740 keV (Racusin et al. 2008b), with a redshift z ~ 0.937 (Vreeswijk et al. 2008). It was the brightest GRB ever detected in optical and reached a magnitude mV,peak ~ 5.3 (Bloom et al. 2009). Observations suggested a very high bulk Lorentz factor Γ = 300−1400. The burst time variability depends on the energy (Margutti et al. 2008; Abbasi et al. 2009), here we consider a broad range: tvar ~ 0.01−1 s. The photon index deduced from high-energy data softens rapidly with time: a = 1.0−2.1 (Racusin et al. 2008b, Fig. 2). The IceCube detector performed searches for muon neutrinos from GRB 080319B, but did not find significant deviation from the background (Abbasi et al. 2009).
From the properties of GRB 080319B, with the assumption Γ ~ 300, we obtain Ep,max ~ 1020−1021eV, Eν,max ~ 1015−1017 eV, ϵth ~ 10−100 eV (soft case), and Φγ,min ~ 10 Jy ~ 104−105 ph cm-2 s-1. The flux of the source at 10 and 100 eV is difficult to estimate because we lack data at these energies. However, we note that the source reached a flux 10 Jy ~ 104 ph cm-2 s-1 at 5 eV and 10-2 Jy ~ 10 ph cm-2 s-1 at 105 eV (Racusin et al. 2008b, Fig. 3). Therefore, despite its extreme brightness, this GRB was still below the IceCube detection limit.
5.2.2. GRB 100316D
The GRB 100316D was detected on 2010 March 16 by the Swift satellite (Starling et al. 2011; Fan et al. 2011). This long-duration (~ 1300 s) and low-luminosity GRB was associated with the energetic SN 2010bh (Wiersema et al. 2010), identified as a type Ic supernova. This LL GRB could therefore be related to a semi-choked jet (see Sect. 6.2).
It was located nearby, at z = 0.059 (Vergani et al. 2010), and was characterized by a low bolometric luminosity Lbol ~ 1047 erg s-1 at peak energy ϵb ~ 20 keV. As the event showed a smooth rise, we set tvar ~ 102−103 s.
As a first estimate, we consider that the emission of GRB 100316D was not choked. We assume Γ ~ 10 (it may be lower, see, e.g., Margutti et al. 2013), and we obtain Ep,max ~ 1019−1020eV, Eν,max ~ 1016−1017 eV, ϵth ~ 0.1 eV and Φγ,min ~ 10 Jy ~ 104−105 ph cm-2 s-1. No counterpart was detected at ~ 0.1 eV, so that we can only give a rough estimate of the source flux: at peak Φγ,obs(ϵb) ~ 10-1 ph cm-2 s-1 and at 1 eV, Φγ,obs(1 eV) ≲ 1 ph cm-2 s-1. In any case, the source flux is far below the IceCube sensitivity limit. For lower values of the bulk Lorentz factor, for example, Γ = 2, Φγ,min ~ 10−102 ph cm-2 s-1, but the observed flux is then still below the IceCube detection requirement.
We note that if GRB 100316D was a semi-choked jet, neutrinos should be searched around 100−1000 s before the onset of photon emission (Senno et al. 2016). The reported absence of precursor neutrinos with IceCube could be used to constrain the thickness of the extended material around the source in the semi-choked model of LL GRBs.
5.2.3. Candidate cosmic neutrino and PS16cgx
After the detection of the candidate cosmic neutrino IceCube-160427A (Blaufuss 2016), Pan-STARRS, the Fermi Gamma-ray Burst Monitor and the Palomar 48-inch Oschin telescope carried out a follow-up in order to identify potential sources (Smartt et al. 2016; Blackburn et al. 2016; Singer et al. 2016). Pan-STARRS identified seven supernova candidates (Smartt et al. 2016). We focus on the most interesting candidate, PS16cgx, consistent with a type Ic supernova, and possibly a choked-jet or an off-axis GRB.
Its apparent magnitude i = 21.84 rose by 0.4 during two days. Therefore we set tvar~105 s. The flux is approximately Fobs~7.5 × 10-14ergcm-2s-1. If the object is indeed a Ic supernova at z~0.1−0.2, its peak luminosity is Lb~1042−1043 ergs-1. If the candidate is indeed a supernova, the outflow is nonrelativistic and the bulk Lorentz factor is Γ~1. We obtain Eν,max~100 PeV, ϵth~0.1 eV, and Φγ,min~105ph cm-2 s-1. These values are rough estimates as the uncertainty on the distance is high. In the most favorable case, assuming that the whole observed luminosity is emitted at the threshold energy ϵth~0.1 eV, we calculate that the flux at this energy is Φγ,obs~0.8 ph cm-2 s-1≪ Φγ,min. We conclude that we should not observe neutrino flares from this source with IceCube (produced through photohadronic interactions). The emission could be mildly relativistic with Γ = 10, but in this case Φγ,min is even higher, therefore the detection is more disfavored.
However, PS16cgx could have hosted a choked GRB jet. In that case, we expect that the neutrino event has been detected before the SN radiation emission, which seems to be compatible with the observations. More details on the light curve of the source and its spectral evolution are necessary to conclude.
We cannot exclude either that the neutrino event was part of a relatively long emission (>months) produced by pp interactions on the SN ejecta. PS16cgx could also be an off-axis GRB that seeded magnetically isotropized accelerated protons in its environment, producing a neutrino flux through interactions on the photon or baryonic backgrounds in the GRB cocoon or the SN ejecta, again on longer timescales. In these cases, more events should be found after integration over several months.
5.2.4. “BigBird” and PKS 1424-418 major outburst
The IceCube Collaboration has detected astrophysical neutrinos up to PeV energies (Aartsen et al. 2014). For the third PeV event (IC 35, Eν ~ 2 PeV), searches for coincidence with AGN flares revealed a possible association with the major outburst of the Blazar PKS 1424-418 (Kadler et al. 2016), located at redshift z = 1.522. A bright gamma-ray emission (Ojha & Dutka 2012) and an increase in X-ray (Ciprini & Cutini 2013), optical (Hasan et al. 2013), and radio (Nemenashi et al. 2013) emissions were observed between 2012 and 2013.
The outburst lasted more than six months; we consider a time variability comparable with the initial rise time: tvar~104−105s. The peak luminosity is Lb~2×1048erg s-1. In the case Γ~10 (as is commonly assumed for blazar flares; for estimates of the bulk Lorentz factors of blazar jets, see, e.g., Lähteenmäki & Valtaoja 1999; Ghisellini et al. 1993; Britzen et al. 2007; Readhead 1994; Hovatta et al. 2009; Jorstad et al. 2005), the threshold energy is ϵth~0.1 eV (for Ep=Ep,max~1020eV), and the corresponding detected flux Φγ,obs(ϵth)~3 × 102 ph cm-2 s-1. The flux necessary for detectability is Φγ,min~1.7 × 103 ph cm-2 s-1, which is very close to the observed flux. Therefore, neutrino flares associated with such outbursts could meet the IceCube detection requirement. Kadler et al. (2016) calculated a maximum number of PeV neutrinos of 4.5 for the three-year IceCube period. As we estimate the number of neutrinos associated with a neutrino flare (with variability timescale in the order of tvar), we obtain a smaller number of ~ 0.6 for an effective area 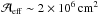 at 1 PeV.
at 1 PeV.
However, in this particular case, as our estimates are very optimistic, the association between the neutrino event and the blazar outburst remains unclear. Moreover, the value of the bulk Lorentz factor can strongly influence the results: if Γ is larger, Φγ,min increases, which disfavors detection.
5.2.5. SGR 1806-20
A magnetar giant flare was detected on 2004 December 27 by INTEGRAL and GRB detectors (Borkowski et al. 2004; Hurley et al. 2004; Boggs et al. 2005; Mazets et al. 2004; Palmer et al. 2005). This is the third of the three magnetar giant flares that have been detected until now. They are usually characterized by a short initial spike and a long pulsating tail. The initial spike lasted approximately 0.2 s, with a rise time ~ 10-3 s and a fall time ~ 0.065 s, therefore we consider tvar ~ 10-3−10-2 s. From Corbel & Eikenberry (2004), DL ~ 15 kpc and therefore Liso,b ~ 2 × 1047erg s-1 with ϵb ~ 105 eV (Hurley et al. 2005; Terasawa et al. 2005).
Assuming Γ~10, as suggested in Lyutikov (2006), we obtain Ep,max~1017−1018eV, Eν,max~1011−1012 eV, ϵth~10−102 eV, and Φγ,min~10 Jy ~104 ph cm-2 s-1. A low-energy power law ϵ-1dN/ dϵ∝ϵ-0.2 has been used to fit observations (Palmer et al. 2005). This is a very hard spectrum, therefore we calculate the observed flux at break Φγ,obs(ϵb)~107 ph cm-2 s-1, which is significantly high and leaves room for a possible detection. However, the maximum neutrino energy is quite low, and at these energies, the IceCube sensitivity is diminished by the atmospheric neutrino background.
If a higher Lorentz factor of the outflow is assumed, for example, Γ~102 (Ioka et al. 2005), we obtain Eν,max~1015−1016 eV, ϵth~102 eV, and Φγ,min~108 ph cm-2 s-1. For very high Lorentz factors (Γ > 10), the detection of neutrinos produced through photohadronic processes is therefore disfavored.
Ioka et al. (2005) calculated the neutrino energies and fluxes for a baryon-poor model (BP) and a baryon-rich model (BR). They obtained for the baryon-poor model 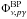 ~7×10-13 GeV-1 cm-2 s-1 with a typical neutrino energy at
~7×10-13 GeV-1 cm-2 s-1 with a typical neutrino energy at 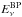 ~8 × 105 GeV. It yields a fluence of 4 × 10-5 GeV cm-2. The BR case is more favorable as the fluence is about three orders of magnitude above the IceCube detection limit (as in our estimates). In this model the neutrino typical energy is lower (around 10 TeV), however, and hadronic emissions dominate.
~8 × 105 GeV. It yields a fluence of 4 × 10-5 GeV cm-2. The BR case is more favorable as the fluence is about three orders of magnitude above the IceCube detection limit (as in our estimates). In this model the neutrino typical energy is lower (around 10 TeV), however, and hadronic emissions dominate.
5.2.6. Swift J1644+57
An interesting flaring event, initially discovered as GRB 110328A, was detected on March 28, 2011 by Swift-BAT (Cummings et al. 2011). The detection of consecutive bursts during the following 48 hours by Swift-BAT (Suzuki et al. 2011) and of a quiescent optical counterpart by the Palomar Transient Factory (Cenko et al. 2011) disfavored the hypothesis of a cosmological long-duration GRB. A precursor of the first flare was also discovered in archival data. The observations suggested a sudden accretion onto a massive black hole with a mildly relativistic outflow Γ ~ 10 (Bloom et al. 2011). Several X-ray flares lasting ~ 103−104 s occurred during ~ 107 s. They were separated by quiescent periods of ~ 5 × 104 s and exhibited very short rise times ~ 100 s, therefore we set tvar ~ 100 s. From optical, near-infrared, and radio observations, the emission came from a source located within 150 pc of the center of a compact galaxy at redshift of z = 0.354 (Levan et al. 2011). The flares were characterized by an isotropic luminosity at break Liso,b ~ 4 × 1048erg s-1 at ϵb ~ 10 keV (Burrows et al. 2011).
With our model we obtain Ep,max~1019eV, Eν,max~1015−1016 eV, ϵth~1 eV, and Φγ,min~103 ph cm-2 s-1. As the spectrum is hard (a< 1) between near-infrared and X-rays, we evaluate the flux of the source at break energy: Φγ,obs(ϵb) ~ 0.6 ph cm-2 s-1, which is far from the IceCube detection requirement.
5.2.7. Crab flares and the April 2011 superflare
Since 2010, violent and brief gamma-ray emissions have been detected in the Crab nebula by AGILE and Fermi/LAT. They led to numerous theoretical models, involving stochastic acceleration processes or magnetic reconnection (Clausen-Brown & Lyutikov 2012; Cerutti et al. 2012, 2013, 2014). The first flares were detected in September 2010 (Tavani et al. 2010; Buehler et al. 2010; Tavani et al. 2011 and Abdo et al. 2011), and indications of optical and X-ray counterparts were detected afterward by HST and Chandra experiments (Tennant et al. 2010; Ferrigno et al. 2010; Horns et al. 2010; Tavani et al. 2011). Other flaring events were identified afterward in the 2007 and 2009 archival data. In April 2011, a particularly intense flare was also observed (Striani et al. 2011; Buehler et al. 2012). Another flare was detected during the next years (e.g., Ojha et al. 2013; Verrecchia et al. 2013), but without exceeding the intensity of the 2011 superflare. These flares last approximately a week, but can also exhibit internal variability or very short rise-time (Balbo et al. 2011; Striani et al. 2011). The shortest variability timescale reported is in the range of 6 to 10 h, thus, tvar ~ 2 × 104−6 × 105s. The peak luminosity during the flaring events are typically Lb ~ 1035−1037 erg s-1 at ϵb ~ 200 MeV. These events can reach more than three times the averaged luminosity of the Crab nebula.
Here we focus on the most extreme 2011 superflare. It is characterized by tvar ~ 6 h and Lbol ~ 2 × 1036 erg s-1. Models propose Γ = 1−5 (e.g., Bednarek & Idec 2011; Komissarov & Lyutikov 2011; Clausen-Brown & Lyutikov 2012). This case is on the border between soft and hard spectra: a = 1.27 ± 0.12 (Weisskopf et al. 2013, Fig. 8).
The maximum energy of neutrinos is slightly above 100 TeV, which is in the IceCube detection range; but atmospheric neutrinos could make the detection difficult. The flux required for detection is about Φγ,min ~ 108 Jy at a threshold energy ϵth ~ 100 eV. The flux associated with the flares at ϵth ~ 100 eV can be estimated to be 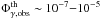 Jy. The difference between the required and observed fluxes exceeds thirteen orders of magnitude; this result does not seem very promising for the detection of neutrinos from Crab flares.
Jy. The difference between the required and observed fluxes exceeds thirteen orders of magnitude; this result does not seem very promising for the detection of neutrinos from Crab flares.
6. Discussion
6.1. Competing processes for neutrino production
Hadronic interactions are invoked as dominant processes over photohadronic interactions in dense source environments (e.g., in some GRB and transrelativistic SN shock-breakout scenarios Murase 2008; Kashiyama et al. 2013). As explained in Sect. 2, we do not consider the steady baryon background as a target for the production of neutrino flares because it is bound to produce a diluted emission over time.
The hadronic energy loss timescale is given by 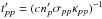 , where σpp is the interaction cross-section, κpp its elasticity, and np is the proton density in the considered region. As
, where σpp is the interaction cross-section, κpp its elasticity, and np is the proton density in the considered region. As 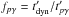 ,
, 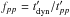 , and
, and 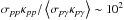 , we can compare the interaction efficiencies by comparing the proton and photon number densities in the comoving frame:
, we can compare the interaction efficiencies by comparing the proton and photon number densities in the comoving frame: 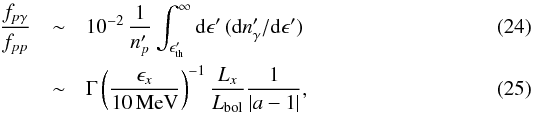 with x = th or b, at threshold energy ϵth and break energy ϵb, respectively. This estimate assumes that
with x = th or b, at threshold energy ϵth and break energy ϵb, respectively. This estimate assumes that 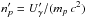 , with the flare bolometric energy density
, with the flare bolometric energy density 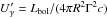 . For hard photon spectra (a< 1), we can see that only emissions that are peaked at an energy ϵb ≫ 10 MeV will be dominated by pp interaction for transient neutrino production. For soft spectra (a> 1), the expression of ϵth (Eq. (19)) indicates that extreme values of Γ ≳ 100 combined with low Ep,max ≲ 100 TeV (that would produce neutrinos below the lower energy threshold for IceCube due to atmospheric backgrounds) could lead to ϵth ≫ 1 and thus to fpγ/fpp ≪ 1. This is illustrated in the alternative photospheric model for GRB prompt emission by Murase (2008) or Kashiyama et al. (2013), for example, who find that neutrinos from the pp interactions can be important at energies around 10 TeV.
. For hard photon spectra (a< 1), we can see that only emissions that are peaked at an energy ϵb ≫ 10 MeV will be dominated by pp interaction for transient neutrino production. For soft spectra (a> 1), the expression of ϵth (Eq. (19)) indicates that extreme values of Γ ≳ 100 combined with low Ep,max ≲ 100 TeV (that would produce neutrinos below the lower energy threshold for IceCube due to atmospheric backgrounds) could lead to ϵth ≫ 1 and thus to fpγ/fpp ≪ 1. This is illustrated in the alternative photospheric model for GRB prompt emission by Murase (2008) or Kashiyama et al. (2013), for example, who find that neutrinos from the pp interactions can be important at energies around 10 TeV.
Although the relative efficiencies of pγ to pp processes depend on each source, it appears in our framework that neutrino production is strongly dominated by pp interactions in only a few marginal cases.
6.2. Optically thick envelopes and choked flares
Many classes of explosive transients are associated with the death of massive stars, with their major source of radiation emitted inside an optically thick stellar envelope. This envelope prevents the emitted photons from escaping until a diffusion timescale td, and/or the electromagnetic outflow to escape from the environment until the break-out time tb. In these cases, it has been discussed that copious neutrino production could occur without a simultaneous radiative smoking gun. Such orphan neutrino scenarios have been developed in particular for LL GRBs and choked GRBs (Murase & Ioka 2013; Senno et al. 2016; Tamborra & Ando 2016), which could appear as ordinary or superluminous type Ibc SNe. As argued in Dai & Fang (2016), TDE are not likely to be choked, however. The orientation of the jet compared to the distribution of the surrounding material makes it unlikely that it collides with high-density media (Senno et al. 2017 also demonstrated that even assuming the presence of a surrounding envelope, only low-luminosity TDEs (L ≲ 2 × 1044erg/s) could be choked). Similar arguments can be applied to blazar flares that could hardly be hidden.
When the GRB jet drives into the stellar envelope, it could emerge or remain choked. In the former case, we witness a successful GRB. If the jet is choked, its energy is deposited in a cocoon, creating a head of thermal photons that usually constitutes the main target to produce neutrino emission (Murase & Ioka 2013; Senno et al. 2016). For powerful jets and not too thick stellar envelopes, a transrelativistic shock can be driven out of the envelope and lead to an observable shock-breakout. It is difficult to relate this emission to the target photon background leading to neutrino production, however, and we have to be careful when applying our detectability criteria. On the other hand, if the jet is choked deep inside the material, neutrino production could still occur on the thermal photons of the jet head, but it is not guaranteed that we can observe this target background. Cocoon signatures should be observed in optical/UV/X (Nakar & Piran 2017), but probably at a lower flux level than the actual target because of dilution over time. A jet-boosted SN should be observed (typically a SN Ibc), but it is difficult to relate this emission to the photons that efficiently produced neutrinos.
We note, however, that for all these objects, neutrinos should be precursors of the radiation. For LL GRBs, for example, a delay of 100−1000 s is expected between the neutrino emission and the escape of the radiation (Senno et al. 2016). More generally, the diffusion timescale for a shell of mass M-2 ≡ M/ (10-2M⊙) expanding adiabatically with velocity v is on the order of td = (Mκ/ 4πvc)1 / 2~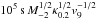 (Arnett 1980), with the opacity-to-electron scattering taken as κ0.2 ≡ κ/ (0.2 g-1 cm2) for optical photons. For the sources considered in this framework, Fig. 2 shows that the relevant background photon energy ranges from 0.1 eV to 100 eV for nonrelativistic to mildly relativistic outflows, and reaches ≳ 103eV for ultrarelativistic cases. An opacity of κ0.2 can then be considered as a lower value, as we can expect that for IR and for UV and energies above, free-free interactions and Compton and pair production processes will cause the medium to be more opaque. Thus the delay between the neutrino and photon emissions should be significant (δt ≫ tvar).
(Arnett 1980), with the opacity-to-electron scattering taken as κ0.2 ≡ κ/ (0.2 g-1 cm2) for optical photons. For the sources considered in this framework, Fig. 2 shows that the relevant background photon energy ranges from 0.1 eV to 100 eV for nonrelativistic to mildly relativistic outflows, and reaches ≳ 103eV for ultrarelativistic cases. An opacity of κ0.2 can then be considered as a lower value, as we can expect that for IR and for UV and energies above, free-free interactions and Compton and pair production processes will cause the medium to be more opaque. Thus the delay between the neutrino and photon emissions should be significant (δt ≫ tvar).
When applying our criteria, sources associated with the onset of type Ibc SNe without an associated GRB therefore need to be considered with caution. If a neutrino has been detected in coincidence with such a source, if the arrival time of the neutrino event is before the supernova peak time, our minimum flux criterion should not be used. A dedicated analysis is required to determine whether the coincidence is true.
7. Conclusion
We have derived the minimum photon flux necessary for neutrino detection from explosive transients, based on two main observables: the bolometric luminosity Lbol, and the time variability tvar of the flaring emission. Our results also depend on the photon spectrum associated with the emission, modeled by a broken power-law and a photon index a below the break energy. The bulk Lorentz factor of the emitting region Γ is also a key parameter to set according to the source model.
We wish to emphasize that the scope of this work is to obtain necessary conditions for neutrinos detection, and we did not calculate a precise neutrino spectrum or present a neutrino flux estimate. Our minimum photon flux requirement can be compared at around the indicated energy to the observed photon flux from various transient sources, in order to assess their detectability in neutrinos.
We find that for nonrelativistic and mildly relativistic outflows, only the photon fields between IR to UV wavelengths (ϵ ~ 0.1−100 eV) are relevant for neutrino production. Sources flaring at very high energy with no optical counterparts will not be observed. Of the NR transient sources, SLSNe appear to be the most promising candidates.
The production of very high energy neutrinos, up to Eν = 1 EeV, requires relativistic outflows. Such neutrinos could be produced by HL GRBs, LL GRBs, blazars, or TDEs. As computed by several authors, very luminous short bursts (GRBs, magnetar flares) have a good chance of being observed. However, cooling processes could prevent detection by strongly reducing the flux at the highest energies. Pions or muons could also leave the flaring region before decaying, and thereby delay the neutrino flare.
Several concrete examples are given as an illustration of our criterion in Sect. 5. Simple order-of-magnitude estimates allow us to conclude on the non-detectability with IceCube of many specific popular bright sources. In particular, no flaring neutrino emission in correlation with neither Swift J1644+57 or the Crab flares can be detected by IceCube or other future experiments. Our results are summarized in Tables 1 and 2.
However, our criterion should not be directly applied to low-luminosity GRBs or type Ibc supernovae because these objects could be off-axis GRBs or have hosted a choked GRB, leading to neutrino emission without a relevant radiation counterpart. We note that if neutrinos are emitted by such sources, they are probably precursors of the radiation.
This study can be applied to a wide range of well-known sources and sensitivities of projected instruments. Our results indicate that with an increase of one to two orders of magnitude in sensitivity, next-generation neutrino detectors could have the potential to discover neutrino flares in PeV or EeV energy ranges.
In general, for a given luminosity, a higher Γ implies a higher Φγ,min (Eq. (22)), and is thus worse in terms of constraints. This can be kept in mind for sources with large uncertainties on Γ.
Acknowledgments
We thank M. Ahlers, P. Beniamini, M. Bustamante, F. Halzen, N. Kurahashi-Neilson, I. Mochol, R. Mochkovitch, and K. Murase for helpful comments and discussions. This work is supported by the APACHE grant (ANR-16-CE31-0001) of the French Agence Nationale de la Recherche. C.G. is supported by a fellowship from the CFM Foundation for Research and by the Labex ILP (reference ANR-10-LABX-63, ANR-11-IDEX-0004-02).
References
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013a, Phys. Rev. Lett., 111, 021103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013b, ApJ, 779, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014, Phys. Rev. Lett., 113, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2015, ApJ, 807, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2016a, ApJ, 824, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2016b, ApJ, 824, 115 [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2009, ApJ, 701, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2012a, ApJ, 745, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2012b, ApJ, 744, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, Science, 331, 739 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2014, Science, 345, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Ageron, M., Aguilar, J. A., Al Samarai, I., et al. 2011, Nuclear Instruments and Methods in Physics Research A, 656, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 664, L71 [Google Scholar]
- Allison, P., Auffenberg, J., Bard, R., et al. 2012, Astropart. Phys., 35, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1980, ApJ, 237, 541 [Google Scholar]
- Atoyan, A. M., & Dermer, C. D. 2003, ApJ, 586, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Baerwald, P., Bustamante, M., & Winter, W. 2015, Astropart. Phys., 62, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Balbo, M., Walter, R., Ferrigno, C., & Bordas, P. 2011, A&A, 527, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barwick, S. 2011, International Cosmic Ray Conference, 4, 238 [NASA ADS] [Google Scholar]
- Baty, H., Petri, J., & Zenitani, S. 2013, MNRAS, 436, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Beall, J. H., & Bednarek, W. 2002, ApJ, 569, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., & Idec, W. 2011, MNRAS, 414, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., Burgio, G. F., & Montaruli, T. 2005, New Astron. Rev., 49, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2014, MNRAS, 438, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Blackburn, L., Briggs, M. S., Burns, E., et al. 2016, GRB Coordinates Network, 19364, 1 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blaufuss, E. 2016, GRB Coordinates Network, 19363, 1 [Google Scholar]
- Bloom, J. S., Perley, D. A., Li, W., et al. 2009, ApJ, 691, 723 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bloom, J. S., Giannios, D., Metzger, B. D., et al. 2011, Science, 333, 203 [CrossRef] [PubMed] [Google Scholar]
- Boggs, S., Hurley, K., Smith, D. M., et al. 2005, GRB Coordinates Network, 2936, 1 [NASA ADS] [Google Scholar]
- Borkowski, J., Gotz, D., Mereghetti, S., et al. 2004, GRB Coordinates Network, 2920, 1 [NASA ADS] [Google Scholar]
- Britzen, S., Brinkmann, W., Campbell, R. M., et al. 2007, A&A, 476, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromberg, O., Nakar, E., & Piran, T. 2011, ApJ, 739, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, G. C., Levan, A. J., Stanway, E. R., et al. 2015, MNRAS, 452, 4297 [NASA ADS] [CrossRef] [Google Scholar]
- Budnik, R., Katz, B., MacFadyen, A., & Waxman, E. 2008, ApJ, 673, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Buehler, R., D’Ammando, F., & Hays, E. 2010, ATel, 2861, 1 [NASA ADS] [Google Scholar]
- Buehler, R., Scargle, J. D., Blandford, R. D., et al. 2012, ApJ, 749, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Kennea, J. A., Ghisellini, G., et al. 2011, Nature, 476, 421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bustamante, M., Heinze, J., Murase, K., & Winter, W. 2017, ApJ, 837, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A., Gehrels, N., Krawczynski, H., et al. 2012, Space Sci. Rev., 173, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Nugent, P. E., Fox, D. B., Ofek, E. O., & Kasliwal, M. M. 2011, GRB Coordinates Network, 11827, 1 [Google Scholar]
- Cerutti, B., Uzdensky, D. A., & Begelman, M. C. 2012, ApJ, 746, 148 [Google Scholar]
- Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2013, ApJ, 770, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2014, Phys. Plasmas, 21, 056501 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P., Tajima, T., & Takahashi, Y. 2002, Phys. Rev. Lett., 89, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chevalier, R. A., & Irwin, C. M. 2011, ApJ, 729, L6 [Google Scholar]
- Ciprini, S., & Cutini, S. 2013, ATel, 4770, 1 [NASA ADS] [Google Scholar]
- Clausen-Brown, E., & Lyutikov, M. 2012, MNRAS, 426, 1374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbel, S., & Eikenberry, S. S. 2004, A&A, 419, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cummings, J. R., Barthelmy, S. D., Beardmore, A. P., et al. 2011, GRB Coordinates Network, 11823, 1 [Google Scholar]
- Dai, L., & Fang, K. 2016, MNRAS, 469, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- de Gouveia dal Pino, E. M., & Lazarian, A. 2005, A&A, 441, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dermer, C. D. 2002, ApJ, 574, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Menon, G. 2009, High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays, and Neutrinos (Princeton University Press) [Google Scholar]
- Dessart, L., Hillier, D. J., Waldman, R., Livne, E., & Blondin, S. 2012, MNRAS, 426, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Donley, J. L., Brandt, W. N., Eracleous, M., & Boller, T. 2002, AJ, 124, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., Zhang, B.-B., Xu, D., Liang, E.-W., & Zhang, B. 2011, ApJ, 726, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, K., Kotera, K., Murase, K., & Olinto, A. V. 2016, J. Cosmol. Astroparticle Phys., 4, 010 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, K., Kotera, K., & Olinto, A. V. 2013, J. Cos. Astro. Phys., 3, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Farrar, G. R., & Gruzinov, A. 2009, ApJ, 693, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Farrar, G. R., & Piran, T. 2014, ArXiv e-prints [arXiv:1411.0704] [Google Scholar]
- Ferrigno, C., Tennant, A., Horns, D., et al. 2010, ATel, 2994, 1 [NASA ADS] [Google Scholar]
- Gal-Yam, A., & Leonard, D. C. 2009, Nature, 458, 865 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gal-Yam, A., Mazzali, P., Ofek, E. O., et al. 2009, Nature, 462, 624 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ghirlanda, G., Ghisellini, G., Firmani, C., Celotti, A., & Bosnjak, Z. 2005, MNRAS, 360, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., Celotti, A., & Firmani, C. 2009, A&A, 496, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannios, D. 2010, MNRAS, 408, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Preece, R. D., Mallozzi, R. S., et al. 2013, ApJS, 208, 21 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Halzen, F., & Klein, S. R. 2010, Rev. Scientific Instruments, 81, 081101 [NASA ADS] [CrossRef] [Google Scholar]
- Hasan, I., MacPherson, E., Buxton, M., et al. 2013, ATel, 4775, 1 [NASA ADS] [Google Scholar]
- He, H.-N., Liu, R.-Y., Wang, X.-Y., et al. 2012, ApJ, 752, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., & Bloom, J. S. 2012, The Gamma-Ray Burst – Supernova Connection (Cambridge: Cambridge University Press), 169 [Google Scholar]
- Horns, D., Tennant, A., Ferrigno, C., et al. 2010, ATel, 3058, 1 [NASA ADS] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, K., Cline, T., Mitrofanov, I., et al. 2004, GRB Coordinates Network, 2921, 1 [NASA ADS] [Google Scholar]
- Hurley, K., Boggs, S. E., Smith, D. M., et al. 2005, Nature, 434, 1098 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ioka, K., Razzaque, S., Kobayashi, S., & Mészáros, P. 2005, ApJ, 633, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Kadler, M., Krauß, F., Mannheim, K., et al. 2016, Nature Physics, 12, 807 [CrossRef] [Google Scholar]
- Kasen, D., & Bildsten, L. 2010, ApJ, 717, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kashiyama, K., Murase, K., Horiuchi, S., Gao, S., & Mészáros, P. 2013, ApJ, 769, L6 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kashti, T., & Waxman, E. 2005, Phys. Rev. Lett., 95, 181101 [NASA ADS] [CrossRef] [Google Scholar]
- Kasliwal, M. M. 2011, Ph.D. Thesis, California Institute of Technology [Google Scholar]
- Koers, H. B. J., & Wijers, R. A. M. J. 2007, ArXiv e-prints [arXiv:0711.4791] [Google Scholar]
- Komissarov, S. S., & Lyutikov, M. 2011, MNRAS, 414, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S. 2015, J. High Energy Astrophys., 7, 148 [Google Scholar]
- Kotera, K., & Silk, J. 2016, ApJ, 823, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Kotera, K., Phinney, E. S., & Olinto, A. V. 2013, MNRAS, 432, 3228 [NASA ADS] [CrossRef] [Google Scholar]
- Lähteenmäki, A., & Valtaoja, E. 1999, ApJ, 521, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine, M., & Waxman, E. 2009, J. Cosmol. Astropart., 11, 009 [CrossRef] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Cenko, S. B., et al. 2011, Science, 333, 199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lunardini, C., & Winter, W. 2017, Phys. Rev. D, 95, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2011, Phys. Rev. D, 83, 124035 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2006, MNRAS, 367, 1594 [CrossRef] [Google Scholar]
- Marcowith, A., Bret, A., Bykov, A., et al. 2016, Rept. Progr. Phys., 79, 046901 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Guidorzi, C., Chincarini, G., et al. 2008, in AIP Conf. Ser. 1065, eds. Y.-F. Huang, Z.-G. Dai, & B. Zhang, 259 [Google Scholar]
- Margutti, R., Soderberg, A. M., Wieringa, M. H., et al. 2013, ApJ, 778, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Martineau-Huynh, O., Kotera, K., Bustamente, M., et al. 2016, EPJ Web Conf., 116, 03005 [CrossRef] [EDP Sciences] [Google Scholar]
- Mazets, E., Golenetskii, S., Aptekar, R., et al. 2004, GRB Coordinates Network, 2922, 1 [NASA ADS] [Google Scholar]
- Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2015, ArXiv e-prints [arXiv:1511.01396] [Google Scholar]
- Metzger, B. D., Finzell, T., Vurm, I., et al. 2015, MNRAS, 450, 2739 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Vurm, I., Hascoët, R., & Beloborodov, A. M. 2014, MNRAS, 437, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M. 2011, Astron. Nachr., 332, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., Rachen, J. P., Engel, R., Protheroe, R. J., & Stanev, T. 1999, PASA, 16, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K. 2007, Phys. Rev. D, 76, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K. 2008, Phys. Rev. D, 78, 101302 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., & Beacom, J. F. 2010, Phys. Rev. D, 81, 123001 [CrossRef] [Google Scholar]
- Murase, K., & Ioka, K. 2013, Phys. Rev. Lett., 111, 121102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Murase, K., & Nagataki, S. 2006, Phys. Rev. Lett., 97, 051101 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Ioka, K., Nagataki, S., & Nakamura, T. 2006, ApJ, 651, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Ioka, K., Nagataki, S., & Nakamura, T. 2008, Phys. Rev. D, 78, 023005 [CrossRef] [Google Scholar]
- Murase, K., Mészáros, P., & Zhang, B. 2009, Phys. Rev. D, 79, 103001 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Thompson, T. A., Lacki, B. C., & Beacom, J. F. 2011, Phys. Rev. D, 84, 043003 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Asano, K., Terasawa, T., & Mészáros, P. 2012, ApJ, 746, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Kashiyama, K., & Mészáros, P. 2013, Phys. Rev. Lett., 111, 131102 [CrossRef] [Google Scholar]
- Murase, K., Inoue, Y., & Dermer, C. D. 2014, Phys. Rev. D, 90, 023007 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Kashiyama, K., Kiuchi, K., & Bartos, I. 2015, ApJ, 805, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Kashiyama, K., Mészáros, P., Shoemaker, I., & Senno, N. 2016, ApJ, 822, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E. 2015, ApJ, 807, 172 [Google Scholar]
- Nakar, E., & Piran, T. 2017, ApJ, 834, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Sari, R. 2012, ApJ, 747, 88 [CrossRef] [Google Scholar]
- Nemenashi, P., Gaylard, M., & Ojha, R. 2013, ATel, 4819, 1 [NASA ADS] [Google Scholar]
- Neronov, A., Semikoz, D. V., Anchordoqui, L. A., Adams, J., & Olinto, A. V. 2017, Phys. Rev. D, 95, 023004 [NASA ADS] [CrossRef] [Google Scholar]
- Ofek, E. O., Cameron, P. B., Kasliwal, M. M., et al. 2007, ApJ, 659, L13 [CrossRef] [Google Scholar]
- Oikonomou, F., Murase, K., & Kotera, K. 2014, A&A, 568, A110 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Ojha, R., & Dutka, M. 2012, ATel, 4494, 1 [NASA ADS] [Google Scholar]
- Ojha, R., Hays, E., Buehler, R., & Dutka, M. 2013, ATel, 4855, 1 [NASA ADS] [Google Scholar]
- Palmer, D. M., Barthelmy, S., Gehrels, N., et al. 2005, Nature, 434, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, M., & Mastichiadis, A. 2015, MNRAS, 447, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, M., Coenders, S., & Dimitrakoudis, S. 2016a, Astropart. Phys., 80, 115 [Google Scholar]
- Petropoulou, M., Dimitrakoudis, S., Padovani, P., et al. 2016b, ArXiv e-prints [arXiv:1601.06010] [Google Scholar]
- Petropoulou, M., Vasilopoulos, G., & Giannios, D. 2017c, MNRAS, 464, 2213 [NASA ADS] [CrossRef] [Google Scholar]
- Pfeffer, D. N., Kovetz, E. D., & Kamionkowski, M. 2017, MNRAS, 466, 2922 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Kollmeier, J. A. 2016, ApJ, 826, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Protheroe, R. J. 2002, PASA, 19, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R. M. 2012, in IAU Symp., 279, 22 [Google Scholar]
- Quimby, R. M., Kulkarni, S. R., Kasliwal, M. M., et al. 2011, Nature, 474, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Rachen, J. P., & Mészáros, P. 1998, Phys. Rev. D, 58, 123005 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Racusin, J. L., Gehrels, N., Holland, S. T., et al. 2008a, GRB Coordinates Network, 7427, 1 [NASA ADS] [Google Scholar]
- Racusin, J. L., Karpov, S. V., Sokolowski, M., et al. 2008b, Nature, 455, 183 [Google Scholar]
- Readhead, A. C. S. 1994, ApJ, 426, 51 [Google Scholar]
- Salafia, O. S., Ghisellini, G., Pescalli, A., Ghirlanda, G., & Nappo, F. 2016, MNRAS, 461, 3607 [NASA ADS] [CrossRef] [Google Scholar]
- Senno, N., Murase, K., & Mészáros, P. 2016, Phys. Rev. D, 93, 083003 [NASA ADS] [CrossRef] [Google Scholar]
- Senno, N., Murase, K., & Meszaros, P. 2017, ApJ, 838, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Kirk, J. G., Begelman, M. C., & Schneider, P. 1987, ApJ, 320, L81 [Google Scholar]
- Singer, L. P., Kasliwal, M. M., Cenko, S. B., et al. 2016, GRB Coordinates Network, 19392, 1 [Google Scholar]
- Smartt, S., Chambers, K. C., Smith, K., et al. 2016, GRB Coordinates Network, 19381, 1 [Google Scholar]
- Smith, M. W. E., Fox, D. B., Cowen, D. F., et al. 2013, Astropart. Phys., 45, 56 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Soderberg, A. M., Kulkarni, S. R., Nakar, E., et al. 2006, Nature, 442, 1014 [CrossRef] [Google Scholar]
- Starling, R. L. C., Wiersema, K., Levan, A. J., et al. 2011, MNRAS, 411, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Striani, E., Tavani, M., Piano, G., et al. 2011, ApJ, 741, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, D., Tristram, P. J., Kobara, S., et al. 2011, GRB Coordinates Network, 11824, 1 [Google Scholar]
- Tajima, T., & Dawson, J. M. 1979, Phys. Rev. Lett., 43, 267 [CrossRef] [Google Scholar]
- Tamborra, I., & Ando, S. 2016, Phys. Rev. D, 93, 053010 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., Striani, E., Bulgarelli, A., et al. 2010, ATel, 2855, 1 [NASA ADS] [Google Scholar]
- Tavani, M., Bulgarelli, A., Vittorini, V., et al. 2011, Science, 331, 736 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tennant, A., Caraveo, P., Costa, E., et al. 2010, ATel, 2882, 1 [NASA ADS] [Google Scholar]
- Terasawa, T., Tanaka, Y. T., Takei, Y., et al. 2005, Nature, 434, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- The IceCube-Gen2 Collaboration, Aartsen, M. G., Abraham, K., et al. 2015, ArXiv e-prints [arXiv:1510.05228] [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rept. Progr. Phys., 78, 116901 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Uzdensky, D. A. 2011, Space Sci. Rev., 160, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Uzdensky, D. A. 2016, in Astrophys. Space Sci. Lib. 427, eds. W. Gonzalez, & E. Parker, 473 [Google Scholar]
- Vergani, S. D., D’Avanzo, P., Levan, A. J., et al. 2010, GRB Coordinates Network, 10512, 1 [Google Scholar]
- Verrecchia, F., Pittori, C., Lucarelli, F., et al. 2013, ATel, 5506, 1 [NASA ADS] [Google Scholar]
- Virgili, F. J., Liang, E.-W., & Zhang, B. 2009, MNRAS, 392, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Vreeswijk, P. M., Milvang-Jensen, B., Smette, A., et al. 2008, GRB Coordinates Network, 7451, 1 [NASA ADS] [Google Scholar]
- Waxman, E., & Bahcall, J. 1997, Phys. Rev. Lett., 78, 2292 [CrossRef] [Google Scholar]
- Waxman, E., & Bahcall, J. 1999, Phys. Rev. D, 59, 023002 [Google Scholar]
- Waxman, E., & Bahcall, J. N. 2000, ApJ, 541, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Tennant, A. F., Arons, J., et al. 2013, ApJ, 765, 56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiersema, K., D’Avanzo, P., Levan, A. J., et al. 2010, GRB Coordinates Network, 10525, 1 [Google Scholar]
- Winter, W., Becker Tjus, J., & Klein, S. R. 2014, A&A, 569, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, P. M., & Thompson, C. 2006, in Compact stellar X-ray sources, eds. W. Lewin, & M. van der Klis (Cambridge, UK: Cambridge University Press), Cambridge Astrophys. Ser., 547 [Google Scholar]
- Xiao, D., Mészáros, P., Murase, K., & Dai, Z.-G. 2016, ApJ, 832, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Zweibel, E. G., & Yamada, M. 2009, ARA&A, 47, 291 [Google Scholar]
Appendix A: Assessing the effect of inverse-Compton losses
Inverse-Compton (IC) losses are difficult to evaluate in the general case because they depend on the SED of the flaring event (and in particular on ϵb). We evaluate the importance of IC losses a posteriori. For this purpose, we need to identify the dominant IC regime (Thomson or Klein-Nishina, KN) for each category of sources. We can consider that for x = ϵ′′/mpc2 ≫ 1, where ϵ′′ is the photon energy in the proton rest frame, IC losses can be neglected (KN regime), and for x ≲ 1, they have a similar effect as synchrotron losses (Thomson regime).
We assume that the maximum proton energy Ep,max is established by the competition between acceleration, synchrotron, and adiabatic losses and evaluate the effect of IC losses on these protons. If IC losses are significant, they can influence the maximum neutrino energy. As x = ϵEp/ Γ2(mpc2)2, IC losses are significant for ϵ ≤ ϵlim = Γ2(mpc2)2/Ep. Typically, IC losses can be neglected when ϵb ≳ ϵlim. In Fig. A.1 we plot ϵlim in the Lbol−tvar parameter space and compare for each category of transients its value with the break energy ϵb quoted in Sect. 5.
 |
Fig. A.1 Limit energy ϵlim in parameter space Lbol,tvar for Γ = 1,10,100 allows approximately assessing the effect of inverse-Compton losses for each category of sources. For a break energy in the photon spectrum ϵb ≥ ϵlim, IC losses can be neglected against synchrotron losses. |
We conclude that blazars are expected to experience large IC losses. As suggested in Murase et al. (2014), these objects are also expected to experience other energy loss processes, for instance, strong Bethe-Heitler losses. For GRBs the IC losses can be neglected as ϵb ~ 103 keV is quite high. The uncertainty on the value of ϵb for magnetar flares is too high to conclude. In the case of the Crab flares, as ϵb ~ 400 MeV, IC losses can be easily neglected. IC losses may also be neglected for TDEs as their emission peaks in hard X-rays or soft gamma-rays. Last, for novae and supernovae, IC losses may not be negligible as the values of ϵb can be borderline, but refined case-by-case studies are required to conclude.
We recall that in any case, neglecting IC losses preserves the maximum achievable nature of Ep,max and thus the validity of the necessary minimum flux Φγ,min.
Appendix B: Treating peculiar spectra with our detectability criterion
In the case of a peculiar spectrum with a double bump (e.g., blazar spectra) at ϵb1 and ϵb2 with photon indices a1, b1, a2, and b2, several cases are to be considered. A schematic double-bump spectrum is illustrated in Fig. B.1. In practice, we need to compare the minimum photon flux Φγ,min with max [ Φobs(ϵth),Φobs(ϵb1),Φobs(ϵb2) ] if ϵth<ϵb1, with max [ Φobs(ϵth),Φobs(ϵb2) ] if ϵb1<ϵth<ϵb2 and with Φobs(ϵth) if ϵth>ϵb2.
We describe these three different cases and give the energy ϵ at which the observed flux Φγ,obs has to be compared with the minimum flux Φγ,min. For ϵth,1, if a1 ≥ 1 we are in the soft case and ϵ = ϵth,1. If a1< 1 we distinguish between two cases: ϵ = ϵb1 if ![\appendix \setcounter{section}{2} \begin{equation} \frac{ \log[ \epsilon_{\rm b2} \Phi_\gamma(\epsilon_{\rm b2})] - \log[ \epsilon_{\rm b1} \Phi_\gamma(\epsilon_{\rm b1})] }{ \log( \epsilon_{\rm b2}) - \log( \epsilon_{\rm b1} ) } \leq 1, \end{equation}](/articles/aa/full_html/2017/07/aa30326-16/aa30326-16-eq547.png) (B.1)and ϵ = ϵb2 otherwise. For ϵth,2, ϵ = ϵth,2 if
(B.1)and ϵ = ϵb2 otherwise. For ϵth,2, ϵ = ϵth,2 if ![\appendix \setcounter{section}{2} \begin{equation} \frac{ \log[ \epsilon_{\rm b2} \Phi_\gamma(\epsilon_{\rm b2})] - \log[ \epsilon_{{\rm th},2} \Phi_\gamma(\epsilon_{{\rm th},2})] }{ \log( \epsilon_{\rm b2}) - \log( \epsilon_{{\rm th},2} ) } \leq 1, \end{equation}](/articles/aa/full_html/2017/07/aa30326-16/aa30326-16-eq551.png) (B.2)and ϵ = ϵb2 otherwise. For ϵth,3, as b2 > 1 by definition, ϵ = ϵth,3.
(B.2)and ϵ = ϵb2 otherwise. For ϵth,3, as b2 > 1 by definition, ϵ = ϵth,3.
 |
Fig. B.1 In this schematic spectrum with a double bump at ϵb1 and ϵb2, we indicate for three different values of threshold energy ϵth,1, ϵth,2 and ϵth,3 the energies ϵ ≥ ϵth at which the observed photon flux can be maximum. These values are marked by circles for ϵth,1, diamonds for ϵth,2, and by squares for ϵth,3. |
All Tables
All Figures
 |
Fig. 1 Maximum accessible proton energy Ep,max(left column) and corresponding maximum accessible neutrino energy Eν,max (right column) as a function of the variability timescale tvar and the bolometric luminosity Lbol of a flaring source, with bulk Lorentz factor Γ = 1,10,100 (from top to bottom). Overlaid are examples of the location of benchmark explosive transients in the Lbol−tvar parameter space (see Sect. 5). The beige region indicates the domain where no source is expected to be found because of the excessive energy budget. The dots locate recently discovered categories of transients (Kasliwal 2011), superluminous supernovae (SLSNe), peculiar supernovae, and luminous red novae. The small square box (labeled SNe) and the short diagonal line on its upper left indicate core-collapse and thermonuclear supernovae, respectively. Low-luminosity GRBs and type Ibc supernovae should be treated with care (see Sect. 6.2). |
| In the text | |
 |
Fig. 2 What is the minimum source photon flux required to enable neutrino detection with IceCube? The color map shows the minimum photon flux Φγ,min (in Jy and ph cm-2 s-1) as a function of the bolometric luminosity Lbol and the variability timescale tvar of the flaring event for an outflow bulk Lorentz factor Γ = 1,10,100. A neutrino flare can be detectable if the observed photon flux Φγ,obs ≳ Φγ,min, above the minimum threshold energy ϵth (red lines) for soft photon spectra, and at the observed photon break energy ϵb for hard spectra. Here ηB = ηp = 1, but the most conservative estimate should use ηp = 100. Overlaid objets as in Fig 1. Type Ibc supernovae should be treated with care (see Sect. 6.2). |
| In the text | |
 |
Fig. A.1 Limit energy ϵlim in parameter space Lbol,tvar for Γ = 1,10,100 allows approximately assessing the effect of inverse-Compton losses for each category of sources. For a break energy in the photon spectrum ϵb ≥ ϵlim, IC losses can be neglected against synchrotron losses. |
| In the text | |
 |
Fig. B.1 In this schematic spectrum with a double bump at ϵb1 and ϵb2, we indicate for three different values of threshold energy ϵth,1, ϵth,2 and ϵth,3 the energies ϵ ≥ ϵth at which the observed photon flux can be maximum. These values are marked by circles for ϵth,1, diamonds for ϵth,2, and by squares for ϵth,3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


