| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201730760 | |
| Published online | 22 June 2017 | |
Dwarf nova outbursts in intermediate polars
1 Observatoire Astronomique de Strasbourg, Université de Strasbourg, CNRS UMR 7550, 67000 Strasbourg, France
e-mail: jean-marie.hameury@astro.unistra.fr
2 Kavli Institute for Theoretical Physics, Kohn Hall, University of California, Santa Barbara, CA 93106, USA
3 Institut d’Astrophysique de Paris, CNRS et Sorbonne Universités, UPMC Paris 06, UMR 7095, 98bis Bd Arago, 75014 Paris, France
4 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
Received: 10 March 2017
Accepted: 23 April 2017
Context. The disc instability model (DIM) has been very successful in explaining the dwarf nova outbursts observed in cataclysmic variables. When, as in intermediate polars, the accreting white dwarf is magnetised, the disc is truncated at the magnetospheric radius, but for mass-transfer rates corresponding to the thermal-viscous instability such systems should still exhibit dwarf-nova outbursts. Yet, the majority of intermediate polars, in which the magnetic field is not large enough to completely disrupt the accretion disc, seem to be stable, and the rare observed outbursts, in particular in systems with long orbital periods, are much shorter than normal dwarf-nova outbursts.
Aims. We investigate the predictions of the disc instability model for intermediate polars in order to determine which of the observed properties of these systems can be explained by the DIM.
Methods. We use our numerical code for the time evolution of accretion discs, modified to include the effects of the magnetic field, with constant or variable mass transfer from the secondary star.
Results. We show that intermediate polars have mass transfer low enough and magnetic fields large enough to keep the accretion disc stable on the cold equilibrium branch. We show that the infrequent and short outbursts observed in long-period systems, such as, for example, TV Col, cannot be attributed to the thermal-viscous instability of the accretion disc, but instead have to be triggered by an enhanced mass-transfer from the secondary, or, more likely, by some instability coupling the white dwarf magnetic field with that generated by the magnetorotational instability operating in the accretion disc. Longer outbursts (a few days) could result from the disc instability.
Key words: accretion, accretion disks / stars: dwarf novae / instabilities
© ESO, 2017
1. Introduction
Dwarf novae (DNe) are cataclysmic variables (CVs), that is, binary systems consisting of a white dwarf accreting from a low-mass companion, that undergo recurrent outbursts. These outbursts usually last for a few days, and their recurrence time is of order of weeks to months (we refer to e.g. Warner 1995, for a review). There is overwhelming evidence that these outbursts are well explained by the thermal-viscous disc instability model (DIM). In this model, the viscosity is parametrised according to the α prescription (Shakura & Sunyaev 1973); the disc becomes thermally and viscously unstable when its temperature is of the order of the ionisation temperature of hydrogen and the opacities are a very sensitive function of temperature (we refer to Lasota 2001, for a review of the DIM). At any given radius, one can determine the surface density Σ of the disc as a function of the local mass transfer rate (or equivalently the effective temperature Teff), and the Σ − Teff curve has an S-shape with the hot upper branch and cool lower branches being stable, and the intermediate one unstable. The DIM accounts well for the observed properties of dwarf novae: recurrence times, outburst durations, and amplitudes, provided that some additional ingredients are included in the model, most notably a change in the viscosity parameter α between the hot and cool branches. Some other effects must be taken into account such as, for example, the truncation of the accretion disc in quiescence as a result of the white dwarf magnetic field or of disc evaporation close to the white dwarf; one must also include the possibility of enhanced mass transfer from the secondary (Hameury et al. 2000), even though it is unclear that irradiation of the secondary can lead to a significant increase of the mass-loss rate because the L1 Lagrangian point is shielded by the accretion disc (Viallet & Hameury 2007, 2008).
According to the DIM, a system is stable if the disc temperature is high enough throughout that hydrogen is fully ionised, which occurs for high mass-transfer rates, or low enough that hydrogen is neutral or in molecular form, which can happen, if the disc extends all the way down the white dwarf surface, for vanishingly small mass transfer rates. Observations are in agreement with this prediction; claims that SS Cyg would be at a distance of 166 pc (Harrison et al. 1999) would have invalidated the DIM (Schreiber & Gänsicke 2002; Lasota & Schreiber 2007), and the conclusion that the distance to SS Cyg must indeed be of the order of 100 pc (Lasota & Schreiber 2007) was later confirmed by radio observations (Miller-Jones et al. 2013) and by the parallax as determined by Gaia (Gaia Collaboration et al. 2016), which set the source distance at 116 pc.
As mentioned earlier, the magnetic field of the white dwarf has a significant influence on the stability properties of the accretion disc, since, for low mass-transfer rates, the outbursts start in the innermost parts of disc that are cut off by magnetic truncation. This is the reason why the presence of a magnetic field has been invoked in some dwarf nova systems; this field is usually assumed to be strong enough to truncate the disc in quiescence, but weak enough that it does not channel the accretion onto the magnetic poles during outbursts, which would cause pulsations at the white dwarf magnetic spin period; such pulsations have not been observed. Such a magnetic field was first suggested to account for the very long recurrence time of systems such as WZ Sge (Lasota et al. 1995; Warner et al. 1996)1 and later used in a more general context.
There are, however, systems in which the white dwarf is observed to be strongly magnetised. In the AM Her stars (or polars), the magnetic field is so strong that the rotation of the white dwarf is synchronous with the orbit, and matter flows directly from the secondary star onto the white dwarf; these systems do not contain accretion discs. In the so-called intermediate polar systems (IPs), the white dwarf is not synchronous with the orbit; depending on the field strength, some of these systems may not possess an accretion disc (Hameury et al. 1986), although it is clear that the vast majority of these systems do. These discs should then be subject to the same thermal-viscous instability as in non-magnetic or weakly magnetic systems, and indeed some of the IPs do show recurrent outbursts. These are, however, different from the standard dwarf nova outbursts; their recurrence time is much longer, and their duration can be as short as a few hours. Surprisingly, little work has been devoted to applying the DIM to IPs; Angelini & Verbunt (1989) suggested that the observed outburst duration and recurrence time of these systems are well explained if the disc is truncated at some large radius. This early work, however, relies on several disputable assumptions; in particular, the inner disc radius is supposed to be the same in quiescence and in outburst, the viscosity is higher (α = 1) than is now deduced from observations (α ≈ 0.2 on the hot branch of the S curve, Smak 1999; Kotko & Lasota 2012) and the disc thermodynamics is treated in a simplified way. Kim et al. (1992) considered the case of GK Per that is a long period (2 days) CV showing long and infrequent outbursts, and concentrated on the shape and duration of these outbursts.
In this paper, we perform a systematic study of the DIM when the white dwarf magnetic field is large. We briefly summarise the observational properties of IP exhibiting outbursts in Sect. 2; in Sect. 3, we apply the DIM to magnetic systems. We conclude that the DIM correctly predicts that many systems should be stable on either the cold or the hot branch, except for systems with short orbital period, which could undergo normal dwarf nova outbursts. The DIM cannot, however, explain the very short outbursts (duration less than 1 day) observed in long period systems. These could be due to a mass transfer instability that we consider in Sect. 4; or, more speculatively, to the interaction of the magnetic field generated by the magnetorotational instability (MRI) with the white dwarf magnetic field.
2. Observational properties of IPs and outbursts
Figure 1 shows the orbital period distribution of outbursting and steady IPs, as compared to that of non-magnetic CVs. Data are taken from Koji Mukai’s on-line catalogue2 for the IPs. From this, we have selected only the confirmed IPs for which the orbital period is well determined. For the non-magnetic CVs, we have used the updated Ritter & Kolb (2003) catalogue3. The list of outbursting IPs is given in Table 1.
It clearly appears from Fig. 1 that there is a strong deficit of outbursting IPs, both below and above the 2−3 h period gap. At short orbital periods, all non-magnetic systems show outbursts, with very few exceptions due to either uncertainties in the orbital period, as for HV And (Rude & Ringwald 2012), uncertainties in the classification (SX LMi and BZ Cir, not classified as DNe in Ritter & Kolb (2003) catalogue have shown outbursts, we refer to Wagner et al. 1998; Kato et al. 2009), or to the fact that the white dwarf underwent a recent nova explosion (T Pyx and BK Lyn, the latter system having transited in 2005 to a dwarf nova, Patterson et al. 2013). CP Pup, classified as a nova-like non-magnetic CV, is probably an IP (Mason at al. 2013). The three out of eight IPs with periods below 2 h that do not exhibit dwarf nova outbursts are therefore a very significant exception.
Observed properties of outbursting intermediate polars.
 |
Fig. 1 Period distribution of outbursting (black) magnetic and non-magnetic CVs, as compared to the total population |
Similarly, there is a very significant excess of stable long period IPs. For non-magnetic CVs, the fraction of outbursting systems is 42%. If this ratio were the same in IPs, one would have expected to have 16 IPs classified as dwarf novae, whereas only 5 are found.
Not only are the outbursts rare in IPs, they are also much shorter than in non-magnetic systems with comparable orbital periods, in particular at long orbital periods; they can in some cases (TV Col, CXOGBS J174954.5-294335) last for less than one orbital period. It is therefore plausible that, as will be discussed below, the very short outbursts are not caused by the thermal/viscous instability of the DIM, but call for a different explanation; this would make the deficit of DNe among IPs even more significant.
3. Disc instabilities
3.1. Stability criteria
According to the DIM, an accretion disc is hot and stable if the accretion rate Ṁ is everywhere in the disc larger than a certain critical value ṀB; as this critical value increases with increasing distance from the white dwarf, this occurs when the mass-transfer rate from the secondary Ṁtr is larger than ṀB(rout), where rout is the outer disc radius. When additional heating terms in the outer disc (heating due to the dissipation of tidal torques and by the stream impact on the disc edge, Buat-Ménard et al. 2001) are included, the disc is stable for mass-transfer rates smaller than ṀB(rout). From our simulations it follows that the disc is stable if 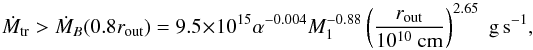 (1)where we have used the fit for ṀB given by Lasota (2001); M1 is the primary mass in solar units and α the Shakura-Sunyaev viscosity parameter.
(1)where we have used the fit for ṀB given by Lasota (2001); M1 is the primary mass in solar units and α the Shakura-Sunyaev viscosity parameter.
The disc is also cold and stable if Ṁtr is smaller than a critical value ṀA throughout; as this critical value also increases with r, this is possible if 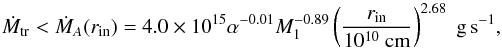 (2)where rin is the inner disc radius. If the disc is not truncated, for hydrogen-dominated discs this is possible only for extremely small, unrealistic mass-transfer rates (cold stable helium-dominated discs are observed in the case of some AM CVn systems, as shown by e.g. Smak 1983; Nelemans 2005; Kotko et al. 2012; this is evidenced by their spectra that show strong emission He lines, in contrast with absorption line spectra characteristic of systems in a high state). In our case, however, the magnetic field truncates the white dwarf at the magnetospheric radius given by (Davidson & Ostriker 1973)
(2)where rin is the inner disc radius. If the disc is not truncated, for hydrogen-dominated discs this is possible only for extremely small, unrealistic mass-transfer rates (cold stable helium-dominated discs are observed in the case of some AM CVn systems, as shown by e.g. Smak 1983; Nelemans 2005; Kotko et al. 2012; this is evidenced by their spectra that show strong emission He lines, in contrast with absorption line spectra characteristic of systems in a high state). In our case, however, the magnetic field truncates the white dwarf at the magnetospheric radius given by (Davidson & Ostriker 1973) 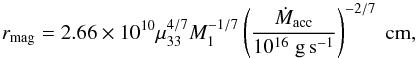 (3)where Ṁacc is the accretion rate onto the white dwarf, which differs from Ṁtr if the system is not steady and μ33 is the white dwarf magnetic moment in units of 1033 G cm3.
(3)where Ṁacc is the accretion rate onto the white dwarf, which differs from Ṁtr if the system is not steady and μ33 is the white dwarf magnetic moment in units of 1033 G cm3.
The usual no-stress inner-boundary condition νΣ = 0, where ν is the kinematic viscosity and Σ is the surface density, has a strong stabilising effect. Because of this condition, the critical, maximum value of Σ on the cold branch cannot be reached at the inner radius, but only at some distance from it. Our simulations have shown that when the disc is not very far from being stable, inside-out outbursts are triggered at approximately 1.5rin. Equation (2) should therefore be evaluated at that position in the disc; combining this with Eq. (3) the stability condition then becomes 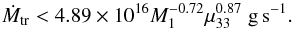 (4)The truncation radius cannot, however, be larger than the circularization radius at which matter would form a circular orbit with the specific angular momentum it had when leaving L1:
(4)The truncation radius cannot, however, be larger than the circularization radius at which matter would form a circular orbit with the specific angular momentum it had when leaving L1: 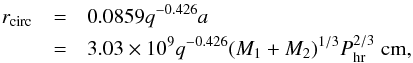 (5)where a is the orbital separation, q = M2/M1 the mass ratio, Phr the orbital period in hours and M2 the secondary mass in solar units. Equation (5) is a fit to Lubow & Shu (1975) Table 2; this fit is accurate to better than 1% for 0.06 <q< 1. This implies that if Ṁtr<ṀA(1.5rcirc), there exists a magnetic moment for which the disc can be stable; otherwise, the system is either unstable or has no disc.
(5)where a is the orbital separation, q = M2/M1 the mass ratio, Phr the orbital period in hours and M2 the secondary mass in solar units. Equation (5) is a fit to Lubow & Shu (1975) Table 2; this fit is accurate to better than 1% for 0.06 <q< 1. This implies that if Ṁtr<ṀA(1.5rcirc), there exists a magnetic moment for which the disc can be stable; otherwise, the system is either unstable or has no disc.
 |
Fig. 2 Critical mass transfer for stability. The upper red curve represents the critical mass transfer rate above which discs are hot and stable. The expected secular mean of the mass transfer is given by the black curve (details can be found in the main text). The green, magenta and blue curves represent the critical mass transfer below which discs are cold and stable (Eq. (4)), for magnetic moments of 4 × 1032, × 1032 and 2.5 × 1031 G cm3 respectively. The disc exists only if its inner radius is smaller than the circularisation radius; the dashed red curve shows the maximum possible mass transfer allowing the disc to be stable and cold at 1.5rcirc. |
Figure 2 shows these critical rates as a function of the orbital period for various values of the magnetic moment, as compared to the expected mass transfer from the secondary as estimated by the revised model of Knigge et al. (2011) for which the primary mass is 0.7 M⊙. Knigge et al. (2011) find that the dispersion of CV properties at a given orbital period is large, which implies that the actual mass transfer rate at a given orbital period may significantly differ from the secular mean, and the dispersion around the black solid line shown in Fig. 2 is large. It clearly appears that IPs below the period gap can be stabilised on the cold branch by a moderate magnetic field, of the order of 5 × 1031 G cm3, insufficient to disrupt a disc. Dwarf nova outbursts at these short orbital periods are possible if the magnetic field is smaller than that, or if the mass transfer rate is higher than the secular mean by a factor of a few. Above the period gap, systems can be stable on the cold branch if their mass-transfer rate is significantly smaller than the secular mean, and if the white dwarf magnetic moment is larger than 1032 G cm3; larger magnetic fields would cause the disruption of the disc, so that the system would appear as either a polar, if it can be synchronised, or as a discless IP if it cannot. Stable discs on the hot branch are possible for large enough mass-transfer rates and long enough orbital periods, as for non-magnetic CVs.
Model parameters and results.
3.2. The case of FO Aqr
FO Aqr is an intermediate polar that has never shown outbursts, and can therefore be considered as steady, but was observed to enter a low state in 2016 (more than 2 mag decrease), from which it gradually recovered between May and July 2016 (Littlefield et al. 2016). The partial eclipse observed during the low state is narrower and shallower than in the high state, indicating that an accretion disc is still present, albeit smaller than during the high state. Because the low state light curve is integrated over a significant duration, it is possible, however, that the disc could have entirely disappeared during a fraction of the low state, and that it reappeared only when the luminosity had significantly increased.
The fact that no outburst has been observed during the rise through the instability strip has two possible explanations: either the accretion disc is present at all times, but is always cold and stable, which implies that the mass transfer is low (few times 1015 g-1) during the high state, close to ṀA(rmag), and that the magnetic moment is of the order of a few times 1032 G cm3, or the disc vanishes during the very low state and reappears only during the rise (Hameury & Lasota 2002). We leave the investigation of these two possibilities for a further paper.
 |
Fig. 3 Time evolution of a system with a 6 h orbital period, for magnetic moments of 0 (black curve), 1031 (red curve) and 1032 (blue curve) G cm3. The top panel shows the V magnitude of the accretion disc (contributions from the secondary, the white dwarf, and the hot spot are not included) and the bottom panel shows the inner disc radius. |
3.3. Time evolution of unstable IPs
In order to follow the time evolution of dwarf nova outbursts in IPs, we have used the version of the DIM described in Hameury et al. (1998) in which we have incorporated heating terms due to the tidal torque and stream impact as described in Buat-Ménard et al. (2001). The disc is truncated at the magnetospheric radius given by Eq. (3). Both the inner and outer disc radii vary with time; time derivatives in our code are calculated in a Lagrangian scheme and we assume that the surface densities for r<rmag or r>rout are zero, and that the temperatures are those at rin and rout, respectively. We considered a system with M1 = 0.8 M⊙, q = 0.6, and Porb = 6 h, appropriate for systems such as TV Col or XY Ari, and Ṁtr = 1017 g s-1, slightly smaller than the expected secular mean, which ensures that the system lies in the unstable regime for dwarf nova outbursts. We further used αc = 0.02, and αh = 0.1. Figure 3 shows the time evolution of this system. The characteristics of the light curve (recurrence time τrec, outburst duration, peak of the mass transfer rate and quiescent level are given in Table 2. As can be seen, for the relatively high mass-transfer rates used here, the impact of disc truncation is limited. On the other hand, for lower mass-transfer rates (Ṁtr = 2 × 1016 g s-1, the effect of disc truncation is large; the recurrence time is very significantly increased, and reaches 254 days between two consecutive outbursts, and 3.5 yr between two major ones for a magnetic moment of 1031 G cm3. For μ ten times larger, we found that the system is marginally stable on the cold branch, although it should have been marginally unstable according to Eq. (4); this is because our code, due to its implicit nature, is able to follow systems on the unstable branch when they are close to the stability limit. It is worth noting, however, that for low values of μ, the magnetospheric radius can be less than the white dwarf radius, which means that the system should not appear as an IP during the high state; this would, for example, happen for the case μ = 1031 G cm3 shown in Fig. 3.
 |
Fig. 4 Time evolution of a system with a 1.5 h orbital period, for magnetic moments of 0 (red curve) and 1031 (black curve) G cm3. The top panel shows the V magnitude of the accretion disc (contributions from the secondary, the white dwarf, and the hot spot are not included) and the bottom panel shows the inner disc radius. |
Figure 4 shows the evolution of a system with a 1.5 hr orbital period, for magnetic moments of 0 and 1031 G cm3. The secondary mass is taken to be 0.16 M⊙, and the mass transfer rate is 5 × 1015 g s-1, typical for this period. Truncation of the inner disc by the white dwarf magnetic field has a major impact on outbursts: the recurrence time is increased by a factor 6, and the outbursts are longer and brighter.
Reducing αc leads to longer recurrence time while reducing αh leads to longer outbursts. Our results are in line with those of Angelini & Verbunt (1989) as far as the recurrence times are concerned, although the value of αc we assume is significantly smaller then theirs (0.02 instead of 0.1), possibly due to the large truncation radius they assume. We never obtain outbursts as short as those of Angelini & Verbunt (1989) because their value for αh is unrealistically high. We can find realistic parameters for the magnetic moment that can fit the observed recurrence times; we cannot, however, reproduce the very short durations observed in some systems, such as V1223 Sgr or TV Col.
3.4. Inner boundary condition
We have used the standard boundary condition νΣ = 0 at the inner disc edge, which corresponds to no torque at the rim of the inner disc. This boundary condition is well adapted to discs around black holes where an innermost stable orbit exists (Paczyński 2000), but might not be suitable when the accretion disc is separated from the stellar surface by a boundary layer (we refer to e.g. Chap. 6 in Frank et al. 2002). A similar situation occurs when the disc is truncated by a magnetic field. Hameury & Lasota (2002) find that the inner boundary condition becomes 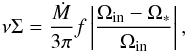 (6)where f ≤ 1 is a numerical factor that accounts for possible matter ejection by the propeller effect, Ω∗ is the rotation frequency of the white dwarf, and Ωin is the Keplerian frequency at the inner edge of the disc. Equation (6) is similar to the condition obtained by Duschl & Tscharnuter (1991) in a slightly different context. The surface density is increased as compared to the standard case, as well as the luminosity because of the work done by the torque, the energy source being the rotation of the white dwarf which is partly redistributed over the whole disc. The stabilising effect of the νΣ = 0 condition may therefore disappear.
(6)where f ≤ 1 is a numerical factor that accounts for possible matter ejection by the propeller effect, Ω∗ is the rotation frequency of the white dwarf, and Ωin is the Keplerian frequency at the inner edge of the disc. Equation (6) is similar to the condition obtained by Duschl & Tscharnuter (1991) in a slightly different context. The surface density is increased as compared to the standard case, as well as the luminosity because of the work done by the torque, the energy source being the rotation of the white dwarf which is partly redistributed over the whole disc. The stabilising effect of the νΣ = 0 condition may therefore disappear.
One should note that the accretion rate entering Eq. (3) is not the mass-transfer rate at the inner edge of the disc, but is instead 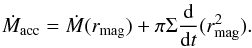 (7)The time derivative term is required for mass conservation and accounts for the fact that a fraction of the mass flow that reaches the inner edge is used to build the disc inner edge when the disc is progressing towards the white dwarf, and conversely that the white dwarf can accrete more than the incoming mass if the disc is recessing.
(7)The time derivative term is required for mass conservation and accounts for the fact that a fraction of the mass flow that reaches the inner edge is used to build the disc inner edge when the disc is progressing towards the white dwarf, and conversely that the white dwarf can accrete more than the incoming mass if the disc is recessing.
The propeller effect plays a role if the Kepler orbital frequency at the inner disc edge ΩK is less than the spin frequency of the white dwarf Ω∗, given in Table 1. Comparing Ω∗ with ΩK(rmag), as given in Table 2 shows that the propeller will be ineffective or only marginally ineffective in most systems, with the possible exceptions of V455 And, XY Ari, and GK Per.
In the following, we have taken f = 1 and ω∗ = 0, which maximises the effect of changing the inner boundary condition; the steady state solution now becomes νΣ = Ṁ/ 3π, in which the [ 1 − (rin/r)1 / 2 ] term that is present in the standard case has disappeared.
As can be seen from Table 2, changing the boundary condition has a significant, but not major, effect. It destabilises the disc, and is somehow equivalent in decreasing the magnetic moment.
4. Enhanced mass-transfer rate
The DIM does not appear to be able to produce very short duration (less than a day) outbursts, in particular in systems that have long orbital periods. It is therefore worth studying the effect that mass transfer variations can have on magnetically truncated discs in IPs. Such variations on various timescales are universally observed in cataclysmic variables, such as AM Her stars, and have been invoked to account for some specific systems such as V513 Cas or IW And; two Z Cam systems that exhibited dwarf nova outbursts during their standstill before entering into a low state (Hameury & Lasota 2014). These outbursts cannot be explained by the DIM since the disc in Z Cam systems during standstills is assumed to be on the hot branch. Hellier & Buckley (1993) suggested that such mass-transfer outbursts were responsible for the short outbursts observed in TV Col, based on the fact that the emission lines, presumably originating from the hot spot region as indicated by the trailed spectrograms, were increased by a factor 30 as compared to quiescence. It is therefore worth exploring the possibility that these short outbursts could be explained by enhanced mass-transfer rate. Even for SS Cyg one has to take into account mass-transfer variations to obtain good agreement of models with observations (Schreiber et al. 2003).
 |
Fig. 5 Visual magnitude of a system undergoing a mass transfer outburst (mass transfer rate multiplied by 20), for initial Ṁtr = 1018 g s-1 (red curve) and 1016 g s-1 (blue curve). The magnitudes have been scaled to be comparable. The outbursts starts at t = − 3 (red curve) and t = 0 (blue curve). |
One requires, however, that the disc either lies on the cold stable branch, or on the hot stable branch, since these systems experiencing short outbursts do not show normal, longer, dwarf nova outbursts. We therefore consider both possibilities. Figure 5 shows the evolution of a system with an orbital period of 6 h in which mass transfer is increased by a factor 20 during 1 day. For the high mass-transfer case, Ṁtr = 1018 g s-1, and the magnetic moment is 2 × 1033 G cm3; for the low mass-transfer case, Ṁtr = 1016 g s-1, and the magnetic moment is 2 × 1032 G cm3. Ṁtr is close to the minimum (resp. maximum) mass transfer possible for a steady state on the hot (resp. cold) branch of the S-curve, and the magnetic moment has been chosen high so as to minimise the disc mass. In both cases, the contribution of the hot spot, whose temperature is 15 000 K, has been included; M1 is taken to be 0.8 M⊙, and q = 0.6. In both cases, the amplitude of the outburst is about 2 mag, compatible with the observations.
In the high Ṁtr case, the disc mass is comparable to the total mass transferred during an outburst, and, because it lies on the hot stable branch, the viscous time is relatively short and the disc response is significant and occurs on a timescale of a few days. As a consequence, the outburst is very asymmetric: A sharp rise is due to the immediate increase of the hot spot luminosity, immediately followed by the disc response, and a slow decline, on the disc viscous timescale after a sharp decline of the hot spot luminosity; the peak of the mass accretion rate onto the white dwarf occurs 1.7 days after the beginning of the mass transfer event, and is 5.5 × 1018 g s-1. In the low Ṁtr case, the disc mass is more than two orders of magnitude larger than the mass transferred during the outburst, because of the much reduced mass-transfer rate and of the lower viscosity; as a consequence, the disc is not greatly affected by the mass transfer fluctuations and responds on a much longer viscous timescale: the mass accretion rate onto the white dwarf reaches its maximum 330 days after the beginning of the outburst, and the relative increase is only of about 4%.
A sudden increase of the mass-transfer rate from the secondary could therefore in principle explain the optical light curve of the short outbursts observed in intermediate polars, provided that the quiescent mass-transfer rate is low enough to allow it to remain cold and stable. This increase is not sufficient to trigger a standard dwarf nova outburst, and the accretion rate onto the white dwarf cannot increase by more than a few percent. This conclusion relies, however, on the assumption that the whole mass-transfer stream is stopped at the outer disc edge, which is probably not correct, since it is very likely that the stream overflowing the disc interacts directly with the magnetosphere, as suggested by Hellier et al. (2000), for example, in the case of EX Hya. This is nonetheless required to account for the X-ray emission accompanying the optical outbursts in systems such as EX Hys (Hellier et al. 2000), YY Dra (Szkody et al. 2002).
5. Conclusions
We have shown that the white dwarf magnetic field can stabilise the accretion disc on the cold branch in intermediate polar systems, explaining the existence of quiescent intermediate polars, in particular below the period gap where all non-magnetic H-rich systems are observed to be dwarf novae with very few exceptions that can be accounted for by some specificity of the system, such as a historical nova explosion. The observational appearance of such systems, permanently stuck in a low state, need not, however, be very different from those in a high state, because X-ray emission is expected in all cases, as X-rays are produced in the accretion column close to the white dwarf surface and because the reprocessing of X-rays on the secondary surface or in the hot spot region will affect the optical spectrum in a similar way in both cases. The white dwarf magnetic field can naturally stabilise the accretion disc in a low state. Stabilising the disc in a high state is certainly not straightforward because the field has little or no influence on the outermost parts of the accretion disc from where the cooling front would start. The DIM can account for the observed outburst properties of systems that undergo (normal) long outbursts, such as XY Ari or YY Dra. The DIM cannot explain, however, the very short, rare outbursts observed in a number of systems. Our results contradict the early ones from Angelini & Verbunt (1989) who assumed high viscosities, which we now know are unrealistic.
These outbursts could, in principle, be due to the mass-transfer rate from the secondary star enhanced by a factor ~20, provided that the quiescent mass-transfer rate is low enough that the disc can sit on the cold stable branch. This hypothesis gains support from the fact that high excitation emission lines are strongly enhanced during an outburst, which, from their time-dependant velocities, seem to originate from the hot spot. In order to account for the concomitant X-ray outburst, the stream from the L1 point must partly overflow the accretion disc and interact directly with the white dwarf magnetosphere. This, however, lowers the efficiency of optical emission, and requires an even larger increase of the mass-transfer rate. It is also uncertain whether or not the hot spot can emit the observed very high excitation lines; we have assumed here a hot spot temperature of 15 000 K, which maximises its optical emission, but is most probably too low, meaning that Ṁtr probably needs to be increased even more.
For all these reasons, an enhanced mass-transfer outburst, although possible, is not necessarily the explanation of short dwarf nova outbursts in IPs. Such large-amplitude, short outbursts should also be present in non-magnetic systems – and they might be present; we refer to, for example, the case of V1316 Cyg (Shears et al. 2006) which, in addition to standard dwarf nova outbursts, exhibits short (less than 1−2 days), faint (average amplitude of 1.4 mag), relatively frequent (6 outbursts recorded over 4 months in 2005) events. The suggestion by Mhlahlo et al. (2007) that EX Hya outbursts could be due to the storage and release of matter outside the magnetosphere, with a similar mechanism to that put forward by Spruit & Taam (1993) to explain the Rapid Burster, is interesting, but it remains to be explained why the recurrence time between short DN outbursts in IPs is so long; longer than the viscous time. Another similar possibility is that the coupling of the magnetic field generated by the MRI with the magnetic field of the white dwarf can, under particular conditions, generate an instability. Exploring this option requires global numerical simulations of the MRI, which are now beginning to be possible (we refer to e.g. Zhu & Stone 2017); the inclusion of the white dwarf magnetic field remains, however, to be implemented.
Warner et al. (1996) could not, however, account for the length of WZ Sge (super)outburst.
Acknowledgments
This work benefited from many discussions with the participants of the KITP 2017 program Confronting MHD Theories of Accretion Disks with Observations, in particular with Paula Szkody and Christian Knigge. This work was supported by a National Science Centre, Poland grant 2015/19/B/ST9/01099 and by the National Science Foundation under Grant No. NSF PHY-1125915. J.P.L. was supported by a grant from the French Space Agency CNES.
References
- Andronov, I. L., Chinarova, L. L., Han, W., Kim, Y., & Yoon, J.-N. 2008, A&A, 486, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angelini, L., & Verbunt, F. 1989, MNRAS, 238, 697 [NASA ADS] [Google Scholar]
- Buat-Ménard, V., Hameury, J. -M., & Lasota, J. -P. 2001, A&A, 366, 612 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crawford, T., Boyd, D., Gualdoni, C., et al. 2008, JAVSO, 36, 60 [NASA ADS] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Duschl, W. J., & Tscharnuter, W. M. 1991, A&A, 241, 153 [NASA ADS] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, 3rd edn (Cambridge: Cambridge University Press) [Google Scholar]
- Gaia Collaboration (Brown, A. G. A.) et al. 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J.-M., & Lasota, J.-P. 2002, A&A, 394, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J.-M., & Lasota, J.-P. 2014, A&A, 569, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J.-M., King, A. R., & Lasota, J.-P. 1986, MNRAS, 218, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Hameury, J-M.., Menou, K., Dubus, G., Lasota, J. -P., & Hure, J.-M. 1998, MNRAS, 298, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Hameury, J.M., Lasota, J.P., & Warner, B. 2000, A&A, 353, 244 [Google Scholar]
- Harrison, T. E., McNamara, B. J., Szkody, P., et al. 1999, ApJ, 515, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., & Buckley, D. A. H. 1993, MNRAS, 265, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Mukai, K., & Beardmore A. P. 1997, MNRAS, 292, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Kemp, J., Naylor, T., et al. 2000, MNRAS, 313, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Hudec, R., Šimon, V., & Skalický, J. 2005, ASP Conf., 330, 405 [NASA ADS] [Google Scholar]
- Ishioka, R., Kato, T., Uemura, M., et al. 2002, PASJ, 54, 581 [NASA ADS] [Google Scholar]
- Johnson, C. B., Torres, M. A. P., Hynes, R. I., et al. 2017, MNRAS, 466, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., Imada, A., Uemura, M., et al. 2009, PASJ, 61, S395 [NASA ADS] [Google Scholar]
- Kato, T., Hambsch, F.-J., Oksanen, A., Starr, P., & Henden, A. 2015, PASJ, 67, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kim S.-W., Wheeler J. C., & Mineshige S. 1992, ApJ, 384, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kotko, I., & Lasota, J. -P. 2012, A&A, 545, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kotko, I., Lasota, J. -P., Dubus, G., & Hameury, J.-M. 2012, A&A, 544, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasota, J. -P. 2001, New Astron. Rev., , 45, 449 [Google Scholar]
- Lasota, J. -P..,Schreiber, M. R. 2007, A&A, 473, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasota J. -P., Hameury J. -M.,& Hure J.-M. 1995, A&A, 302, L29 [NASA ADS] [Google Scholar]
- Littlefield, C., Garnavich, P., Kennedy, M. R., et al. 2016, ApJ, 833, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, E., Orio, M., Mukai, K., et al. 2013, MNRAS, 436, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Mhlahlo, N., Buckley, D. A. H., Dhillon, V. S., et al. 2007, MNRAS, 380, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Sivakoff, G. R., Knigge, C., et al. 2013, Science, 340, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G. 2005, The Astrophysics of Cataclysmic Variables and Related Objects, eds. J.-M. Hameury, & J. -P. Lasota, Proc. ASP Conf., 330, 27 [Google Scholar]
- Nogami, D., Hiroi, K., Suzuki, Y., et al. 2009, ASP Conf., 404, 52 [NASA ADS] [Google Scholar]
- Paczyński, B. 2000, ArXiv e-prints [arXiv:astro-ph/0004129] [Google Scholar]
- Patterson, J., Uthas, H., Kemp, J., et al. 2013, MNRAS, 434, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H., & Kolb U. 2003, A&A, 404, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rude, G. D., & Ringwald, F. A. 2012, New Astron., 17, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I. & Sunyaev, R. A. 1973, A&A, 24, 337 [Google Scholar]
- Schreiber, M. R., & Gänsicke, B. T. 2002, A&A, 382, 124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., Hameury, J. -M., & Lasota, J. -P. 2003, A&A, 410, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shears, J., Boyd, D., & Poyner, G. 2006, Journal of the British Astronomical Association, 116, 244 [NASA ADS] [Google Scholar]
- Šimon, V. 2015, A&A, 575, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smak, J. 1983, Acta Astron., 33, 333 [NASA ADS] [Google Scholar]
- Smak, J. 1999, Acta Astron., 49, 391 [NASA ADS] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 1993, ApJ, 402, 593 [CrossRef] [Google Scholar]
- Szkody, P., & Mateo, M. 1984, ApJ, 280, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P., Nishikida, K., Erb, D., et al. 2002, AJ, 123, 413 [NASA ADS] [CrossRef] [Google Scholar]
- van Amerongen, S., & van Paradijs, J. 1989, A&A, 219, 195 [NASA ADS] [Google Scholar]
- Viallet, M., & Hameury, J.-M. 2007, A&A, 475, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., & Hameury, J.-M. 2008, A&A, 489, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, R. M., Thorstensen, J. R., Honeycutt, R. K., et al. 1998, AJ, 115, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1995, Cataclysmic variable stars, Camb. Astrophys. Ser., 28 [Google Scholar]
- Warner, B., Livio, M., & Tout, C. A. 1996, MNRAS, 282, 735 [NASA ADS] [Google Scholar]
- Zhu, Z., & Stone, J. M. 2017, AAS journals, submitted [arXiv:1701.04627] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Period distribution of outbursting (black) magnetic and non-magnetic CVs, as compared to the total population |
| In the text | |
 |
Fig. 2 Critical mass transfer for stability. The upper red curve represents the critical mass transfer rate above which discs are hot and stable. The expected secular mean of the mass transfer is given by the black curve (details can be found in the main text). The green, magenta and blue curves represent the critical mass transfer below which discs are cold and stable (Eq. (4)), for magnetic moments of 4 × 1032, × 1032 and 2.5 × 1031 G cm3 respectively. The disc exists only if its inner radius is smaller than the circularisation radius; the dashed red curve shows the maximum possible mass transfer allowing the disc to be stable and cold at 1.5rcirc. |
| In the text | |
 |
Fig. 3 Time evolution of a system with a 6 h orbital period, for magnetic moments of 0 (black curve), 1031 (red curve) and 1032 (blue curve) G cm3. The top panel shows the V magnitude of the accretion disc (contributions from the secondary, the white dwarf, and the hot spot are not included) and the bottom panel shows the inner disc radius. |
| In the text | |
 |
Fig. 4 Time evolution of a system with a 1.5 h orbital period, for magnetic moments of 0 (red curve) and 1031 (black curve) G cm3. The top panel shows the V magnitude of the accretion disc (contributions from the secondary, the white dwarf, and the hot spot are not included) and the bottom panel shows the inner disc radius. |
| In the text | |
 |
Fig. 5 Visual magnitude of a system undergoing a mass transfer outburst (mass transfer rate multiplied by 20), for initial Ṁtr = 1018 g s-1 (red curve) and 1016 g s-1 (blue curve). The magnitudes have been scaled to be comparable. The outbursts starts at t = − 3 (red curve) and t = 0 (blue curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


