| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201629756 | |
| Published online | 15 June 2017 | |
Wind asymmetry imprint in the UV light curves of the symbiotic binary SY Mus ⋆
Astronomical Institute, Slovak Academy of Sciences, 059 60 Tatranská Lomnica, Slovakia
e-mail: nshagatova@ta3.sk
Received: 20 September 2016
Accepted: 2 April 2017
Context. Light curves (LCs) of some symbiotic stars show a different slope of the ascending and descending branch of their minimum profile. The origin of this asymmetry is not well understood.
Aims. We explain this effect in the ultraviolet LCs of the symbiotic binary SY Mus.
Methods. We model the continuum fluxes in the spectra obtained by the International Ultraviolet Explorer at ten wavelengths, from 1280 to 3080 Å. We consider that the white dwarf radiation is attenuated by H0 atoms, H− ions, and free electrons in the red giant wind. Variation in the nebular component is approximated by a sine wave along the orbit as suggested by spectral energy distribution models. The model includes asymmetric wind velocity distribution and the corresponding ionization structure of the binary.
Results. We determined distribution of the H0 and H+, as well as upper limits of H− and H0 column densities in the neutral and ionized region at the selected wavelengths as functions of the orbital phase. Corresponding models of the LCs match well the observed continuum fluxes. In this way, we suggested the main UV continuum absorbing (scattering) processes in the circumbinary environment of S-type symbiotic stars.
Conclusions. The asymmetric profile of the ultraviolet LCs of SY Mus is caused by the asymmetric distribution of the circumstellar matter at the near-orbital-plane area.
Key words: scattering / binaries: symbiotic / stars: winds, outflows / stars: individual: SY Mus
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/602/A71
© ESO, 2017
1. Introduction
Asymmetric light curves (LCs) of some interacting binaries along the orbital phase can be caused by a variety of geometrical and physical effects; for example, by the presence of cool or hot spots/areas (e.g., Bopp & Noah 1980; Bell et al. 1984; Pustylnik et al. 2007; Samec et al. 2009; Yuan 2010; Pribulla et al. 2011), an asymmetric wind distribution in symbiotic binaries (e.g., Dumm et al. 1999), a slopping accretion column (Andronov 1986), pulsation of binary components (Kato et al. 2012; Popper 1961,and references therein), a Coriolis effect (e.g., Zhou & Leung 1990), or an eccentric orbit (Elsner et al. 1980). In the X-ray binaries, the asymmetry of the ascending and descending parts of LCs can originate from a relativistic Doppler effect (Watarai et al. 2005).
The asymmetry of ingress and egress branches of the LCs minimum was also indicated for some symbiotic systems (e.g., Dumm et al. 1999; Kolotilov et al. 2002; Skopal et al. 2002, 2012; Więcek et al. 2010). These widest interacting binaries usually comprise a red giant (RG) as the donor star and a white dwarf (WD) as the accretor. The binary components interact via the wind mass transfer from the RG to the WD (e.g., Boyarchuk 1967; Mürset & Schmid 1999).
Using a semi-quantitative analysis, Formiggini & Leibowitz (1990) suggested that a reflection effect can account for the wave-like orbitally related variations in the LCs of three symbiotic systems. Analyzing long-term photometric observations of a group of classical symbiotic stars, Skopal (1998) revealed apparent changes of their orbital period as a consequence of variable, orbitally related nebular emission. In addition, Skopal (2001) found that the observed amplitudes of the LCs are far larger than those calculated within a model of the reflection effect. For a supersoft X-ray symbiotic binary SMC3, the asymmetry of LCs in the V and I filter and the X-rays was modeled by Kato et al. (2013). They assumed a spiral tail of neutral hydrogen at the orbital plane produced by the giant almost filling in its Roche lobe.
Using a Monte Carlo simulation of the Rayleigh scattering effects in symbiotic stars, Schmid (1995) showed that the eclipse width and depth in ultraviolet (UV) LC profiles depend mainly on the extension of the H0 region within the model of Seaquist et al. (1984, hereafter STB), wavelength and contribution of the scattered light.
SY Mus is a quiet eclipsing symbiotic binary, which shows an asymmetry in its UV LCs. Dumm et al. (1999) demonstrated this effect for the continuum fluxes at 1380 Å. They found that the ascending branch of the LC minimum is less steep than the descending one, and shifted more from the position of the spectroscopic conjunction. Further, measuring the neutral hydrogen column densities around the eclipse of the hot component, they revealed the asymmetric wind density distribution around the giant and suggested this effect to be responsible for the asymmetric UV LC around the eclipse. Recently, Shagatova et al. (2016) derived the velocity profiles of the wind in symbiotic systems SY Mus and EG And and they indicated that the wind from the giant is focused at the orbital plane.
In this work we prove that the observed asymmetry in the UV LC profile is primarily caused by the asymmetrical displacement of the circumbinary matter at the orbital-plane-area with respect to the binary axis. In Sect. 2, we present our dataset and in Sect. 3 we introduce our model. Discussion of results and a Conclusion are included in Sects. 4 and 5.
2. Observed continuum fluxes of SY Mus
We used 44 SWP and 39 LWP/LWR International Ultraviolet Explorer (IUE) spectra of SY Mus to measure the continuum fluxes at ten wavelengths from 1280 to 3080 Å (Table 1, available at the CDS). The spectra were dereddened with EB−V = 0.35 mag (Skopal 2005). According to Dumm et al. (1999) we used the ephemeris for the time of the inferior conjunction of the giant as 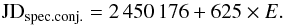 (1)The resulting LCs show an asymmetry of their descending and ascending branches and an offset of the minima position with respect to the time of the inferior conjunction of the giant. These effects weaken towards longer wavelengths (Fig. 6).
(1)The resulting LCs show an asymmetry of their descending and ascending branches and an offset of the minima position with respect to the time of the inferior conjunction of the giant. These effects weaken towards longer wavelengths (Fig. 6).
3. The model
3.1. Components of the continuum radiation
During quiescent phases, the continuum radiation of S-type (stellar) symbiotic binaries consists of three basic components. Radiation from the WD dominates the far-UV range (λ ≲ 1800 Å), whereas the ionized part of the wind, that is, the symbiotic nebula, represents the main contribution within the near-UV and optical (Fig. 7, bottom). The radiation from the RG dominates the spectrum from around VRI passbands to longer wavelengths, depending on its spectral type (e.g., Skopal 2005). Therefore, we assume the WD and nebula as the only sources of radiation in analyzing the UV continuum (120–330 nm) of SY Mus. To model the observed orbitally related flux variation, we use the following assumptions.
-
The hot component radiates as a black-body at the temperatureTh = 105 000 K (Mürset et al. 1991). The radiation is attenuated by the wind material along the line of sight as a function of the orbital phase ϕ, and can be expressed as,
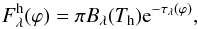 (2)where Bλ(Th) is Planck function and τλ(ϕ) is the total optical depth along the line of sight.
(2)where Bλ(Th) is Planck function and τλ(ϕ) is the total optical depth along the line of sight. -
The radiation from the nebula is for the sake of simplicity approximated by a sine wave as,
![\begin{equation} F^{\rm n}_{\lambda}(\varphi) =\alpha_{\lambda} \sin [2\pi (\varphi-0.25)]+\beta_{\lambda}, \label{Fneb} \end{equation}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq17.png) (3)where αλ and βλ are model parameters. This assumption is based on the fact that the nebular continuum varies with the orbital phase (e.g., Fernández-Castro et al. 1988) and is responsible for the wave-like orbitally-related variation observed in the LCs of symbiotic stars during quiescence (Skopal 2001). Their profile along the orbit can be compared to a sine function (for SY Mus, see Fig. 2 of Pereira et al. 1995; Skopal 2009).
(3)where αλ and βλ are model parameters. This assumption is based on the fact that the nebular continuum varies with the orbital phase (e.g., Fernández-Castro et al. 1988) and is responsible for the wave-like orbitally-related variation observed in the LCs of symbiotic stars during quiescence (Skopal 2001). Their profile along the orbit can be compared to a sine function (for SY Mus, see Fig. 2 of Pereira et al. 1995; Skopal 2009).
The model continuum is then given by their superposition, that is, 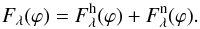 (4)
(4)
3.2. Attenuation in the stellar continuum
In this section, we discuss individual components of the total optical depth, τλ(ϕ), that attenuates the WD continuum radiation on the line of sight. With respect to the ionization structure of the hydrogen in the binary, we consider attenuation processes in the neutral and ionized part of the giant’s wind. Therefore, τλ(ϕ) is a sum of the optical depth of the neutral region, 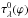 , and that of the ionized region,
, and that of the ionized region, 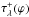 , that is,
, that is, 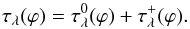 (5)In a dense H0 zone of symbiotic binaries, a strong attenuation of the continuum around the Ly-α line is caused by Rayleigh scattering (Nussbaumer et al. 1989). Further, we consider the scattering on negative hydrogen ion, H−, that attenuates the stellar radiation in cool atmospheres (e.g., Gray 2005). Thus, we can write,
(5)In a dense H0 zone of symbiotic binaries, a strong attenuation of the continuum around the Ly-α line is caused by Rayleigh scattering (Nussbaumer et al. 1989). Further, we consider the scattering on negative hydrogen ion, H−, that attenuates the stellar radiation in cool atmospheres (e.g., Gray 2005). Thus, we can write, 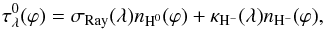 (6)where σRay(λ) is the cross-section of Rayleigh scattering (Eq. (5) and Fig. 2 of Nussbaumer et al. 1989), and nH0(ϕ) and nH−(ϕ) are the functions for the column density of the neutral hydrogen (Sect. 3.3) and negative hydrogen ion, respectively. The H− bound-free absorption coefficients, κH−(λ), are given by Geltman (1962). We used κH−(λ) values from the “ velocity” curve plotted in his Fig. 6. Corresponding κH−(λ) curve reaches its maximum at ≈8500 Å.
(6)where σRay(λ) is the cross-section of Rayleigh scattering (Eq. (5) and Fig. 2 of Nussbaumer et al. 1989), and nH0(ϕ) and nH−(ϕ) are the functions for the column density of the neutral hydrogen (Sect. 3.3) and negative hydrogen ion, respectively. The H− bound-free absorption coefficients, κH−(λ), are given by Geltman (1962). We used κH−(λ) values from the “ velocity” curve plotted in his Fig. 6. Corresponding κH−(λ) curve reaches its maximum at ≈8500 Å.
We assume that the contribution to the H− absorption coefficient due to free-free transitions is negligible, considering the absorption coefficient values given in Geltman (1962), Doughty & Fraser (1966) and Gray (2005). The dependence of the H− column density on the orbital phase, nH−(ϕ), remains a variable in the LC modeling through the neutral region. The values of σRay(λ) and κH−(λ) for selected wavelengths are summarized in Table 2. The Rayleigh scattering is the dominant source of opacity in the neutral region at λ = 1280 Å, however, its effect on the WD radiation is comparable with b-f transitions of H− ion at λ = 1340 Å. At longer wavelengths, these transitions have the dominant attenuating effect in the neutral region (see Fig. 1).
 |
Fig. 1 Comparison of the effect of considered attenuation processes on the WD flux (Sect. 3.2) at shortest (top) and longest (bottom) wavelength of the set. Corresponding column densities of H0 in neutral region and H+ in ionized region are given by the column density model in Fig. 5 and of H− in neutral region and H0 in ionized region by the LC modeling (Sect. 4). Two minima of radiation out of the eclipse for attenuation processes in ionized region (dashed lines) correspond to the orbital phase with line of sight entering/exiting the neutral region. |
In Eq. (6), Rayleigh scattering is treated as an absorption process. However, the Rayleigh scattered photons can contribute to the line-of-sight continuum radiation. Schmid (1995) used Monte Carlo simulations to determine the percentage of these photons in the total flux. In his model SB3, corresponding to a typical symbiotic system, with model parameters closest to that of SY Mus, he obtained values of 7.7% at λ = 1250 Å, 1.9% at λ = 1350 Å and 0.25% at λ = 1700 Å, as seen at the orbital phase ϕ = 0.25. To estimate this effect in our LC modeling, we fitted his values using the function 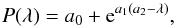 (7)which represents the percentage of flux from Rayleigh scattered photons in the total modeled flux. This function for resulting values of parameters a0 = 0.241, a1 = 0.015 Å-1 and a2 = 1383,66 Å is evaluated in Table 2. The contribution from the Rayleigh scattered photons can vary with orbital phase. However, according to Fig. 8 of Schmid (1995), these variations are not significant for the model SB3 at λ ≥ 1280 Å. Therefore, we neglect them in our modeling. Accordingly, we scale the total flux (4)as
(7)which represents the percentage of flux from Rayleigh scattered photons in the total modeled flux. This function for resulting values of parameters a0 = 0.241, a1 = 0.015 Å-1 and a2 = 1383,66 Å is evaluated in Table 2. The contribution from the Rayleigh scattered photons can vary with orbital phase. However, according to Fig. 8 of Schmid (1995), these variations are not significant for the model SB3 at λ ≥ 1280 Å. Therefore, we neglect them in our modeling. Accordingly, we scale the total flux (4)as 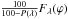 for λ ≤ 1700 Å and set P(λ) ≡ 0 for λ> 1700 Å.
for λ ≤ 1700 Å and set P(λ) ≡ 0 for λ> 1700 Å.
In the predominantly ionized region, the high photon flux from the hot components (LH ≈ 102−104 L⊙, Mürset et al. 1991; Greiner et al. 1997; Skopal 2005) produces free electrons by ionizing the neutral hydrogen in the RG’s wind. Column densities of the free electrons during quiescent phases of symbiotic stars, 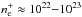 cm-2 were determined by Sekeráš & Skopal (2012) assuming that the Thomson scattering is responsible for the broad wings of the strongest emission lines in the far-UV. Their values of
cm-2 were determined by Sekeráš & Skopal (2012) assuming that the Thomson scattering is responsible for the broad wings of the strongest emission lines in the far-UV. Their values of 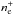 are consistent with our model based on H0 column density modeling (see below Eq. (9)and Fig. 5). Therefore, we suppose that the free electrons can be relevant for the attenuation of the stellar UV continuum by Thomson scattering. Further, the bound-free and free-free transitions on neutral hydrogen can be effective at a high electron temperature of the nebula (Te ≈ 18 500 K, Skopal 2005).
are consistent with our model based on H0 column density modeling (see below Eq. (9)and Fig. 5). Therefore, we suppose that the free electrons can be relevant for the attenuation of the stellar UV continuum by Thomson scattering. Further, the bound-free and free-free transitions on neutral hydrogen can be effective at a high electron temperature of the nebula (Te ≈ 18 500 K, Skopal 2005).
Under these conditions, the optical depth through the ionized part of the wind can be written as,  (8)where σe is the Thomson scattering cross-section, σH0(λ,Te) the total cross-section of neutral hydrogen and
(8)where σe is the Thomson scattering cross-section, σH0(λ,Te) the total cross-section of neutral hydrogen and 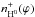 is the column density of H0 in the symbiotic nebula. We set the free electron column density
is the column density of H0 in the symbiotic nebula. We set the free electron column density 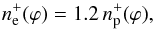 (9)where
(9)where 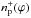 is the column density of protons in the ionized area. The cross-section σH0(λ,Te) accounts for both bound-free and free-free transitions, that is, σH0(λ,Te) = fse(λ,Te)(κbf(H0) + κff(H0)), where κbf(H0) is the absorption coefficient for bound-free transitions and κff(H0) for free-free transitions of neutral hydrogen atom (e.g., Eqs. (8.8) and (8.10) of Gray 2005, for the values used, see Table 2). The factor fse accounts for the stimulated emission and
is the column density of protons in the ionized area. The cross-section σH0(λ,Te) accounts for both bound-free and free-free transitions, that is, σH0(λ,Te) = fse(λ,Te)(κbf(H0) + κff(H0)), where κbf(H0) is the absorption coefficient for bound-free transitions and κff(H0) for free-free transitions of neutral hydrogen atom (e.g., Eqs. (8.8) and (8.10) of Gray 2005, for the values used, see Table 2). The factor fse accounts for the stimulated emission and 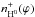 represents the variable in the LC modeling through the ionized wind region. In ionized region, the Thomson scattering and transitions of H0 have comparable attenuation effect on the WD radiation at λ = 1280 Å, while the latter becomes the dominant source of opacity with increasing wavelength (Fig. 1). In Sect. 5, we discuss the effect of other ions to the continuum attenuation.
represents the variable in the LC modeling through the ionized wind region. In ionized region, the Thomson scattering and transitions of H0 have comparable attenuation effect on the WD radiation at λ = 1280 Å, while the latter becomes the dominant source of opacity with increasing wavelength (Fig. 1). In Sect. 5, we discuss the effect of other ions to the continuum attenuation.
Finally, we note that the description of the above-mentioned processes is valid in nebulae under conditions of the local thermodynamic equilibrium (LTE). This assumption is supported by the fact that the free electrons thermalize in nebulae very quickly, because of the extremely short time of their electrostatic encounters with respect to any other inelastic scatterings (see Bohm & Aller 1947). As a result, the energy distribution of free electrons can be characterized by a single Te. Modeling the UV/optical/near-IR spectral energy distribution (SED) during quiescent phases supports this assumption (see figures and Table 3 of Skopal 2005). However, for example, Proga et al. (1998) used a non-LTE photoionization code to calculate the spectrum of a red giant wind illuminated by the hot component of a symbiotic binary. Therefore, the determination of H0 column density in ionized region can suffer from a systematic error in our simplified approach, which can be as high as an order of magnitude or more (compare, e.g., our values in Sect. 4 with results of Schwank et al. 1997).
Values of the Rayleigh scattering cross-section σRay(λ) (in cm2), the percentage of the Rayleigh scattered photons in direction of the line of sight (in %), H− bound-free absorption coefficient κH−(λ) and total cross-section of neutral hydrogen σH0(λ,Te) at Te = 18 500 K (both in cm2) for ten selected wavelengths.
3.3. Column density distribution
To calculate the total optical depth (Eq. (5)) along the line of sight to the WD, we need to determine functions nH0(ϕ) and 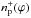 . According to STB, we determine the ionization boundary by solving the parametric equation (see Nussbaumer & Vogel 1987),
. According to STB, we determine the ionization boundary by solving the parametric equation (see Nussbaumer & Vogel 1987), 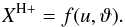 (10)This defines the boundary between neutral and ionized hydrogen at the plane of observations by polar coordinates (u,ϑ) with the origin at the hot star. The ionization parameter XH + is expressed as
(10)This defines the boundary between neutral and ionized hydrogen at the plane of observations by polar coordinates (u,ϑ) with the origin at the hot star. The ionization parameter XH + is expressed as 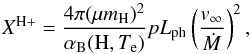 (11)where μ is the mean molecular weight, mH the mass of the hydrogen atom, αB(H,Te) the total hydrogen recombination coefficient for recombinations other than to the ground state (Case B), p the binary separation, Lph the flux of ionizing photons from the WD, v∞ the terminal velocity of the wind from the giant, and Ṁ its mass-loss rate.
(11)where μ is the mean molecular weight, mH the mass of the hydrogen atom, αB(H,Te) the total hydrogen recombination coefficient for recombinations other than to the ground state (Case B), p the binary separation, Lph the flux of ionizing photons from the WD, v∞ the terminal velocity of the wind from the giant, and Ṁ its mass-loss rate.
Then, we can obtain the column density of neutral hydrogen by integrating H0 number density along the line of sight from the observer (− ∞) to the position of the ionization boundary lϕ, 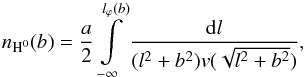 (12)where a = Ṁ/ 2πμmH, l is the coordinate along the line of sight, b is the impact parameter (see Skopal & Shagatova 2012; Shagatova et al. 2016) and
(12)where a = Ṁ/ 2πμmH, l is the coordinate along the line of sight, b is the impact parameter (see Skopal & Shagatova 2012; Shagatova et al. 2016) and 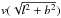 is the wind velocity distribution (Sect. 3.4). The impact parameter represents the position of the binary through the orbital inclination i and phase angle ϕ as b2 = p2(cos2i + sin2ϕsin2i). The value of the integral (12) decreases from the inferior conjunction of the RG and vanishes at the orbital phases, where the line of sight does not cross the H0 zone.
is the wind velocity distribution (Sect. 3.4). The impact parameter represents the position of the binary through the orbital inclination i and phase angle ϕ as b2 = p2(cos2i + sin2ϕsin2i). The value of the integral (12) decreases from the inferior conjunction of the RG and vanishes at the orbital phases, where the line of sight does not cross the H0 zone.
Similarly, we can obtain the column density of protons in the ionized area in the form, 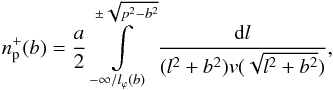 (13)where the lower limit of integration is lϕ(b) for orbital phases, at which the line of sight passes through the neutral area, and − ∞ outside it. The plus sign in the upper limit of integration (i.e., the position of the WD) applies for values of the angle between the line of sight and the line connecting the binary components, ϑ ∈ ⟨ −π/ 2,π/ 2 ⟩, and the minus sign applies for ϑ ∈ ⟨ −π,−π/ 2 ⟩ ∪ ⟨ π/ 2,π ⟩.
(13)where the lower limit of integration is lϕ(b) for orbital phases, at which the line of sight passes through the neutral area, and − ∞ outside it. The plus sign in the upper limit of integration (i.e., the position of the WD) applies for values of the angle between the line of sight and the line connecting the binary components, ϑ ∈ ⟨ −π/ 2,π/ 2 ⟩, and the minus sign applies for ϑ ∈ ⟨ −π,−π/ 2 ⟩ ∪ ⟨ π/ 2,π ⟩.
For the orbital phases during the eclipse, that is, for b ≤ Rg (=the radius of the RG), we integrated nH0(b) up to the giant surface, such that, 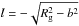 , and put
, and put 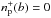 .
.
3.4. Velocity profiles
3.4.1. Components derived from observations
The functions for the column densities of neutral and ionized hydrogen (Eqs. (12)and (13)) are determined by the wind velocity distribution. We adopt the velocity profiles from Shagatova et al. (2016), derived by modeling the H0 column densities, measured from the Rayleigh attenuation around the Ly-α line during ingress and egress orbital phases, using the inversion method of Knill et al. (1993) and the ionization structure model STB. We use their egress model M and ingress model O, denoting them here as ve(r) and vin(r): 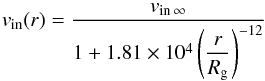 (14)and
(14)and 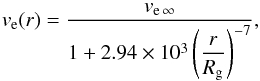 (15)where vin ∞ and ve ∞ are corresponding terminal velocities of the wind. The ingress velocity profile is steeper than the egress profile, thus indicating an asymmetric wind distribution at the plane of observations. For eclipsing binaries, the plane of observations roughly coincides with the orbital plane.
(15)where vin ∞ and ve ∞ are corresponding terminal velocities of the wind. The ingress velocity profile is steeper than the egress profile, thus indicating an asymmetric wind distribution at the plane of observations. For eclipsing binaries, the plane of observations roughly coincides with the orbital plane.
For the egress terminal velocity, we adopted ve∞ = 20 km s-1, which is within a typical range of the terminal velocities of symbiotic stars (e.g., Dumm et al. 1999; Schmid et al. 1999). The selected value of ve∞ yields Ṁ of the model, using Eq. (18) of Shagatova et al. (2016). However, this value represents the spherical equivalent of the mass-loss rate because of the asymmetry in the wind distribution around the RG.
3.4.2. Model of a complete velocity profile
As we aim to model the continuum LCs of SY Mus for the complete range of phases, we need to propose a unified model of the velocity profile by interconnecting vin(r) and ve(r) components around the orbital phase 0, where the observations of column densities are not available; that is for the so-called transition area. We assume that the velocity profile changes gradually in a smooth way from vin(r) to ve(r) at the plane of observations, that is, we are looking for the transition velocity profile, vtrans(r,ψ), where ψ is the azimuth angle at the plane of observations in the coordinate system centered at the RG. Thus, the vtrans(r,ψ) function is defined for ψ ∈ ⟨ ψin,ψe ⟩, where angles ψin and ψe bound the transition area. In determining the vtrans(r,ψ) function, we require the following conditions:
-
the unified function for the velocity profile has to be a smooth(C1) function of ψ;
-
corresponding functions, nH0(ϕ),
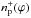 , and the position of the ionization boundary, lϕ, have to be smooth (C1) functions of ϕ;
, and the position of the ionization boundary, lϕ, have to be smooth (C1) functions of ϕ; -
unified model of nH0(ϕ) has to fit the observed H0 column densities.
The transition velocity profile affects the model density distribution of the wind mainly at the area corresponding to the lines of sight during the eclipse.
Since a linear function of ψ cannot meet the conditions for vtrans(r,ψ), we assume the transition velocity profile in the form:  (16)where Cin, Din, Ce and De are parameters. We divided the complete range of ψ, from 0 to 2π, into four areas with different velocity profiles, as depicted in Fig. 2. In front of the RG along the orbital motion, there is an area, where the ve(r) profile applies. At the opposite side, the vin(r) profile is implemented. Finally, there are two more zones in between, where the transitional velocity profile applies.
(16)where Cin, Din, Ce and De are parameters. We divided the complete range of ψ, from 0 to 2π, into four areas with different velocity profiles, as depicted in Fig. 2. In front of the RG along the orbital motion, there is an area, where the ve(r) profile applies. At the opposite side, the vin(r) profile is implemented. Finally, there are two more zones in between, where the transitional velocity profile applies.
 |
Fig. 2 Schematic view of the regions of different velocity profiles as seen perpendicularly to the plane of observations. Denotations are explained in Sect. 3.4. |
From the computational point of view, the vtrans(r,ψ) profile is defined by three functions: v1(r), v23(r) and v4(r). The interconnection of vin(r) and ve(r) from the quadrant II to III of the values of ψ is given by v23(r), the interconnection between the quadrant I and IV is given by two functions, v1(r) and v4(r), because of the discontinuity in values of ψ around ψ = 0 = 2π. The axisymmetric boundaries of ve(r) and vin(r) regions are given by relations between limiting values of ψ (see Fig. 2):  (17)where the subscript “te” denotes the boundary from transitional to egress velocity profile area and “et” the boundary for the transition in the opposite direction, in the direction of increasing values of ψ. Similarly, the subscript “int” denotes the boundary from ingress to transitional zone and “tin” from the transitional to ingress zone. Then, from the conditions of smoothness of the united velocity profile (i.e., the first derivative of the corresponding function has to be continuous for C1 function), we obtain the formulae for velocity profiles defining vtrans(r,ψ):
(17)where the subscript “te” denotes the boundary from transitional to egress velocity profile area and “et” the boundary for the transition in the opposite direction, in the direction of increasing values of ψ. Similarly, the subscript “int” denotes the boundary from ingress to transitional zone and “tin” from the transitional to ingress zone. Then, from the conditions of smoothness of the united velocity profile (i.e., the first derivative of the corresponding function has to be continuous for C1 function), we obtain the formulae for velocity profiles defining vtrans(r,ψ): ![\begin{eqnarray} \label{vtrans1} &&v_{1}(r,\psi)=v_{\rm in}(r)\cos^2[C(\psi-\psi_{\rm int})]+ v_{\rm e}(r)\cos^2[C(\psi-\psi_{\rm te})],~~~~~~~~~~~ \\ \label{vtrans23} &&v_{23}(r,\psi)=v_{\rm in}(r)\cos^2[C(\psi_{\rm tin}-\psi)]+ v_{\rm e}(r)\cos^2[C(\psi-\psi_{\rm et})],~~~~~~~~~~~ \\ \label{vtrans4} &&v_{4}(r,\psi)=v_{\rm in}(r)\cos^2[C(\psi_{\rm int2}-\psi)]+ v_{\rm e}(r)\cos^2[C(\psi-\psi_{\rm te2})],~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq160.png) where
where 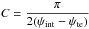 , and corresponding transitional terminal velocities (r → ∞) are:
, and corresponding transitional terminal velocities (r → ∞) are: ![\begin{eqnarray} \label{vnektrans1} &&v_{1\,\infty}(\psi)=v_{\rm in\,\infty}\cos^2[C(\psi-\psi_{\rm int})]+ v_{\rm e\,\infty}\cos^2[C(\psi-\psi_{\rm te})],~~~~~~~~~~~ \\ \label{vnektrans23} &&v_{23\,\infty}(\psi)=v_{\rm in\,\infty}\cos^2[C(\psi_{\rm tin}-\psi)]+ v_{\rm e\,\infty}\cos^2[C(\psi-\psi_{\rm et})],~~~~~~~~~~~ \\ \label{vnektrans4} &&v_{4\,\infty}(\psi)=v_{\rm in\,\infty}\cos^2[C(\psi_{\rm int2}-\psi)]+ v_{\rm e\,\infty}\cos^2[C(\psi-\psi_{\rm te2})].~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq163.png) Equations (18)–(20)and also powers of their right sides to the − 1 and − 2, which are present in formulae for the position of the ionization boundary (Eq. (8) of Nussbaumer & Vogel 1987) and column density (Eqs. (12)and (13)) fulfill the conditions of smoothness. The last condition for vtrans(r,ψ), that is, the correctness of fits to the observed H0 column densities, is linked with the selection of the values of ψte and ψint (see Sects. 3.5 and 4).
Equations (18)–(20)and also powers of their right sides to the − 1 and − 2, which are present in formulae for the position of the ionization boundary (Eq. (8) of Nussbaumer & Vogel 1987) and column density (Eqs. (12)and (13)) fulfill the conditions of smoothness. The last condition for vtrans(r,ψ), that is, the correctness of fits to the observed H0 column densities, is linked with the selection of the values of ψte and ψint (see Sects. 3.5 and 4).
3.5. Ionization parameter
To determine the position of the ionization boundary lϕ, values of the ionization parameter XH + are needed. Similarly as in the previous section, we adopt them from the column density models M and O of Shagatova et al. (2016), that is, we have 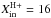 before the eclipse and
before the eclipse and 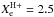 after it. Therefore, using Eqs. (11)and (21)–(23), we obtain the formulae for the transitional ionization parameters:
after it. Therefore, using Eqs. (11)and (21)–(23), we obtain the formulae for the transitional ionization parameters: ![\begin{eqnarray} \label{Xtrans1} X^{\rm H+}_{1}(\psi) & = & X^{\rm H+}_{\rm in}\cos^4[C(\psi-\psi_{\rm int})] \nonumber \\ & & +\ 2\sqrt{X^{\rm H+}_{\rm in}X^{\rm H+}_{\rm e}}\cos^2[C(\psi-\psi_{\rm int})] \cos^2[C(\psi- \psi_{\rm te})] \nonumber \\ & & + \ X^{\rm H+}_{\rm e}\cos^4[C(\psi-\psi_{\rm te})], \end{eqnarray}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq170.png) (24)
(24)![\begin{eqnarray} \label{Xtrans23} X^{\rm H+}_{23}(\psi) & = & X^{\rm H+}_{\rm in}\cos^4[C(\psi_{\rm tin}-\psi)] \nonumber \\ & & +\ 2\sqrt{X^{\rm H+}_{\rm in}X^{\rm H+}_{\rm e}}\cos^2[C(\psi_{\rm tin}-\psi) ]\cos^2[C(\psi-\psi_{\rm et})] \nonumber \\ & & +\ X^{\rm H+}_{\rm e}\cos^4[C(\psi-\psi_{\rm et})], \end{eqnarray}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq171.png) (25)
(25)![\begin{eqnarray} \label{Xtrans4} X^{\rm H+}_{4}(\psi) & = & X^{\rm H+}_{\rm in}\cos^4[C(\psi_{\rm int2}-\psi)] \nonumber \\ & & +\ 2\sqrt{X^{\rm H+}_{\rm in}X^{\rm H+}_{\rm e}}\cos^2[C(\psi_{\rm int2}-\psi)] \cos^2[C(\psi-\psi_{\rm te2})] \nonumber \\ & & + \ X^{\rm H+}_{\rm e}\cos^4[C(\psi-\psi_{\rm te2})], \end{eqnarray}](/articles/aa/full_html/2017/06/aa29756-16/aa29756-16-eq172.png) (26)with the subscript notation equivalent to the previous section.
(26)with the subscript notation equivalent to the previous section.
Further, under the assumption of spherically symmetric mass flux at r → ∞, we can put into equality the expression for Ṁ from Eq. (11)for ingress values of variables with that from the same equation for egress values of variables to obtain a relation, 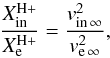 (27)and, then, by evaluating egress and ingress ionization parameters, we obtain a relation between terminal velocities before and after the eclipse,
(27)and, then, by evaluating egress and ingress ionization parameters, we obtain a relation between terminal velocities before and after the eclipse, 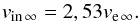 (28)This equation reflects the simple distribution of ionization parameter values (24)–(26)at the orbital plane and the fact that values of
(28)This equation reflects the simple distribution of ionization parameter values (24)–(26)at the orbital plane and the fact that values of 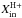 and
and 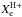 were determined by fitting
were determined by fitting 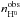 values only at the area close to RG (Fig. 5). Since the derivation of Eq. (28)is based on the equal mass-loss in front and behind the RG with respect to its orbital motion, the difference in corresponding hydrogen densities in radial directions results from the different velocity profiles (14)and (15).
values only at the area close to RG (Fig. 5). Since the derivation of Eq. (28)is based on the equal mass-loss in front and behind the RG with respect to its orbital motion, the difference in corresponding hydrogen densities in radial directions results from the different velocity profiles (14)and (15).
The selection of values of ψint and ψte has to satisfy several conditions. First, it must preserve the correctness of the M and O column density models of Shagatova et al. (2016). At the same time, the range of the angle ψ, where the transitional velocity profile and ionization parameter apply, has to be sufficiently wide to prevent the corresponding interconnection between the ingress and egress ionization boundary from being too sharp.
4. Results
In this section, we use Eqs. (2)–(28)to model the asymmetric UV continuum LCs obtained from low-resolution IUE spectra (Table 1). Main results may be summarized as follows:
-
(i)
We determined the ionization structure by solvingEq. (10)with the united velocity profile (18)–(20)and thecorresponding ionization parameter (24)–(26). The resulting shape ofthe ionization boundary is depicted in Fig. 3.
-
(ii)
Comparing the wind velocity profiles vin(r) and ve(r) (Fig. 4), the ingress wind velocity is lower than the egress velocity at the distance up to ≈1 Rg from the RG surface. It implies a higher hydrogen number density of the wind in front of the RG than behind it, in the direction of the orbital motion. On the other hand, at larger distances, the wind velocity and thus, the wind number density proportion is opposite. The asymmetry of the ionization boundary in Fig. 3 is in agreement with this fact.

Fig. 3 Resulting ionization boundary for the united wind velocity model given by Eqs. (14), (15)and (18)–(28), as seen perpendicularly to the orbital plane (solid line). The corresponding limiting values of ψ are ψint = −0.9 rad and ψte = 0.8 rad. For comparison, the dotted line represents the ionization boundary for
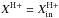 and v(r) = vin(r), whereas the dashed line shows
and v(r) = vin(r), whereas the dashed line shows 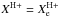 and v(r) = ve(r).
and v(r) = ve(r). 
Fig. 4 Ingress and egress velocity profiles of SY Mus from models M and O of Shagatova et al. (2016) for ve∞ = 20 km s-1 satisfying Eq. (28).
-
(iii)
We determined values of nH0(b) and
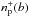 functions within the unified model of the velocity profile and ionization structure according to Eqs. (12)and (13), using Rg as the length unit. Their sum provides the total hydrogen column density nH (see Fig. 5).
functions within the unified model of the velocity profile and ionization structure according to Eqs. (12)and (13), using Rg as the length unit. Their sum provides the total hydrogen column density nH (see Fig. 5). 
Fig. 5 United column density model, nH and its components, nH0 and
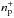 ;
; 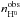 are the measured column densities of the neutral hydrogen from Dumm et al. (1999). During the eclipse, column densities are computed from the observer to the surface of the RG.
are the measured column densities of the neutral hydrogen from Dumm et al. (1999). During the eclipse, column densities are computed from the observer to the surface of the RG. 
Fig. 6 LCs of SY Mus (circles with errorbars) and their models (solid lines). Contribution from the nebula is depicted by dashed lines. Vertical dotted lines represent the position of the inferior conjunction of the giant.
-
(iv)
Finally, we modeled the continuum fluxes of SY Mus (Table 1) using Eq. (4). The resulting models are depicted in Fig. 6. Corresponding contributions from the nebula and a comparison with the values from the model SED at ϕ = 0.62 is shown in Fig. 7. The model SED suggests a slightly more rapid increase of the continuum nebular flux with wavelength than the LC model. However, parameters of the nebular contribution are subject to variation from cycle to cycle (Skopal 2005). The modeling yielded column densities nH−(ϕ) = 5.0 × 10-7nH0(ϕ) and
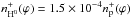 . We estimated their uncertainties by the LC models for λ = 1450 Å and λ = 1950 Å, respectively (see Fig. 8). Corresponding values of nH− and
. We estimated their uncertainties by the LC models for λ = 1450 Å and λ = 1950 Å, respectively (see Fig. 8). Corresponding values of nH− and 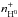 are consistently used in all ten LC models, from λ = 1280 Å to λ = 3080 Å.
are consistently used in all ten LC models, from λ = 1280 Å to λ = 3080 Å.
 |
Fig. 7 Top: model variations of the nebular continuum radiation in SY Mus (Eq. (3)) at ten wavelengths (solid lines). They are compared with the nebular fluxes at ϕ = 0.62 from the model SED (circles with errorbars). Bottom: model SED of SY Mus at ϕ = 0.62. Circles at the nebular component correspond to those plotted at the top panel. |
 |
Fig. 8 Representative LC models for different column densities nH−(ϕ) (top) and |
5. Discussion
Results of our analysis are limited by simplifying assumptions and quality of the data. The basic assumption we made is that the wind from the giant is composed solely of hydrogen in different states/forms and that it flows radially. Further, we neglected an influence of the hot component wind, because it is a factor of ≈10 weaker than that from the RG during quiescent phases (Skopal 2006). As the real composition and the flow of the wind is more complex, these assumptions represent sources of systematic error.
Further simplification is given by the selection of sources attenuating the continuum radiation, that is, H0 atoms, H− ions and free electrons. We tested the sensitivity of our LC model on the value of the product of the column density and the continuum cross-section of atom/ion X, nXσX. We have found no detectable attenuation effect on the LC for 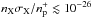 cm2 in the ionized region and for nXσX/nH0 ≲ 10-29 cm2 in the neutral region. Using these relations, we tested H
cm2 in the ionized region and for nXσX/nH0 ≲ 10-29 cm2 in the neutral region. Using these relations, we tested H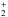 and H− ions as further possible sources of the scattering of continuum that can contribute to the LC attenuation in the ionized region. We found that neither of them has a measurable effect for the column density values from the model for symbiotic stars of Schwank et al. (1997) or even higher values of column density according to the model for planetary nebulae of Aleman & Gruenwald (2004). Also the concentrations of free electrons and protons in the neutral area are too low (Schwank et al. 1997; Crowley 2006) to have a recognizable effect on the continuum UV radiation. However, due to the simplifications in our model, we cannot exclude the effect of species other than those included in our model and, therefore; we consider the resulting functions
and H− ions as further possible sources of the scattering of continuum that can contribute to the LC attenuation in the ionized region. We found that neither of them has a measurable effect for the column density values from the model for symbiotic stars of Schwank et al. (1997) or even higher values of column density according to the model for planetary nebulae of Aleman & Gruenwald (2004). Also the concentrations of free electrons and protons in the neutral area are too low (Schwank et al. 1997; Crowley 2006) to have a recognizable effect on the continuum UV radiation. However, due to the simplifications in our model, we cannot exclude the effect of species other than those included in our model and, therefore; we consider the resulting functions 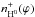 and nH−(ϕ) as the upper limits estimate of the column densities of H0 atoms in the ionized region and H− ions in the neutral region.
and nH−(ϕ) as the upper limits estimate of the column densities of H0 atoms in the ionized region and H− ions in the neutral region.
In determining column densities nH−(ϕ) and 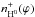 , we preliminary approximated these functions using expressions that qualitatively correspond to the nH−/nH0 and
, we preliminary approximated these functions using expressions that qualitatively correspond to the nH−/nH0 and 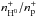 profiles of Aleman & Gruenwald (2004) for planetary nebulae. However, these expressions and their modifications did not represent observed fluxes near to the eclipse. Therefore, H− and H0 densities probably rapidly change at the ionization boundary, as in the models for H0 and H+ populations of Schwank et al. (1997). Thus, we simply used linear functions of the column density of the corresponding prevalent form of hydrogen (Sect. 4, point (iv)). Therefore, functions nH−(ϕ),
profiles of Aleman & Gruenwald (2004) for planetary nebulae. However, these expressions and their modifications did not represent observed fluxes near to the eclipse. Therefore, H− and H0 densities probably rapidly change at the ionization boundary, as in the models for H0 and H+ populations of Schwank et al. (1997). Thus, we simply used linear functions of the column density of the corresponding prevalent form of hydrogen (Sect. 4, point (iv)). Therefore, functions nH−(ϕ), 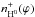 and
and 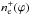 depend on nH0(ϕ) or
depend on nH0(ϕ) or 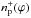 that are given by velocity profiles derived from observations.
that are given by velocity profiles derived from observations.
A large scatter in the observed fluxes (Fig. 6) prevents accurate determination of the nebular continuum variations, 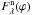 . To put a constraint on the resulting nebular component, we required a monotone increasing of the nebular flux with wavelength for ϕ ≈ 0.5 and its monotone decreasing for ϕ ≈ 1, as in the model SED (Skopal 2009). Figure 7 shows an example of the model SED at the orbital phase ϕ = 0.62 and a comparison of its
. To put a constraint on the resulting nebular component, we required a monotone increasing of the nebular flux with wavelength for ϕ ≈ 0.5 and its monotone decreasing for ϕ ≈ 1, as in the model SED (Skopal 2009). Figure 7 shows an example of the model SED at the orbital phase ϕ = 0.62 and a comparison of its 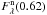 fluxes with those from our LC models. Both models are roughly consistent. However, dependence of our model nebular flux on the wavelength is not monotone for ϕ ≈ 0.1 and 0.9 due to the poorer quality of data.
fluxes with those from our LC models. Both models are roughly consistent. However, dependence of our model nebular flux on the wavelength is not monotone for ϕ ≈ 0.1 and 0.9 due to the poorer quality of data.
Further simplification is given by the approximation that the nebular continuum varies with the orbital phase as a sine function (Eq. (3)). Since during quiescent phases the symbiotic nebula represents the ionized fraction of the wind from the giant, the asymmetric wind distribution will produce a nebula, which is asymmetric with respect to the binary axis and thus its flux. However, with given uncertainties in the data, this effect is not recognizable even for LCs with dominant nebular contribution, for λ> 2000 Å (Fig. 6). Comparing our resulting nebular fluxes with those of Skopal (2005) and Skopal (2009) from model SED at ϕ = 0.02 and ϕ = 0.62, we found different values by a factor 1.04–1.89, which is given by the scatter of the data at a given wavelength (also Fig. 7).
Furthermore, we considered a continuous change of the velocity profile within the transition region (Eq. (16)), which mainly affects the profiles around maxima and minima of the model LCs. Applicability of our transition velocity profile is supported by the resulting LC models that describe the eclipse profiles of the observed LCs. Particularly, a good match was found for the LC at λ = 2700 Å (the reduced χ-squared 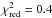 ). Overall, the values of
). Overall, the values of 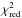 of our models vary from the order of 0.1 to the order of 10.
of our models vary from the order of 0.1 to the order of 10.
To improve the presented modeling, better quality spectra of the symbiotic systems are needed, preferably in such quantity that even single orbital cycles can be covered sufficiently, to avoid physical changes of the particular system with time. With this kind of data, refinement of the model parameters would be possible and also including the asymmetric nebula model would be meaningful.
An independent way of probing the asymmetric distribution of the circumstellar matter in symbiotic binaries from observations, as suggested by our continuum analysis (Shagatova et al. 2016, and this paper), is to investigate dramatic and strictly orbitally-related variation of the Hα line profile observed in the spectra of other quiet symbiotic stars. The main goal is to model the orbital variations of both the absorption and emission component in the Hα line profile as a function of the orbital phase, using our column density model. This means investigating the absorbing/scattering layer of the neutral wind from above the RG photosphere and the line emitting H+ region, with the aim of determining the Hα line profile at each orbital phase (and in the same way, obtaining the corresponding velocity profile of the circumstellar matter, its distribution with respect to the binary axis, and the spherical equivalent of the mass-loss rate). Solving this task should also provide constraints for further theoretical modeling of the RG wind in symbiotic binaries, and its transfer to and accretion onto the compact companion.
6. Conclusion
We modeled the IUE continuum fluxes of the eclipsing symbiotic system SY Mus at ten wavelengths from 1280 to 3080 Å (Table 1). To evaluate attenuation of the WD radiation passing the wind from the RG at different wavelengths and orbital phases, we considered the Rayleigh scattering on neutral hydrogen atoms and the bound-free absorption by negative hydrogen ions in the neutral wind region, the Thomson scattering on free electrons, and the bound-free and free-free transitions on the neutral hydrogen atom in the ionized region (Eqs. (6) and (8)).
To obtain the column densities of relevant forms of hydrogen at all orbital phases, we used the asymmetric wind velocity profile (Sect. 3.4) and the corresponding ionization boundary model (Fig. 3). Accordingly, we obtained the column density distribution of H0 in the neutral region and H+ in the ionized region (Fig. 5). From the shape of the observed LCs, we obtained the distribution of the H− column density nH−(ϕ) /nH0(ϕ) = 5.0 × 10-7 that can be considered as the upper limit due to the simplifications in the model (Sect. 4, Fig. 8). Resulting LC models of SY Mus (Eq. (4), Fig. 6) match well the asymmetric shape of the observed flux profiles. The nebular contribution was approximated by sine waves (Sect. 4, Fig. 7).
This paper presents the first quantitative model of the UV LCs of the S-type symbiotic star. We find that the different shapes of descending and ascending parts of the observed UV continuum LCs of SY Mus are caused by the asymmetric distribution of the wind from the RG at the near-orbital region.
Acknowledgments
The authors thank the referee Hans Martin Schmid for constructive comments. This article was created by the realisation of the project ITMS No. 26220120029, based on the supporting operational Research and development program financed from the European Regional Development Fund. This research was supported by a grant of the Slovak Academy of Sciences, VEGA No. 2/0008/17. This work was supported by the Slovak Research and Development Agency under the contract No. APVV-15-0458.
References
- Aleman, I., & Gruenwald, R. 2004, ApJ, 607, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Andronov, I. L. 1986, AZh, 63, 274 [NASA ADS] [Google Scholar]
- Bell, S. A., Hilditch, R. W., & Hoyle, F. 1984, MNRAS, 208, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Bohm, D., & Aller, L. H. 1947, ApJ, 105, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Bopp, B. W., & Noah, P. W. 1980, Pub. ASP, 92, 717 [Google Scholar]
- Boyarchuk, A. A. 1967, Sov. Astron., 11, 8 [NASA ADS] [Google Scholar]
- Crowley, C. 2006, Red Giant Mass-Loss: Studying Evolved Stellar Winds with FUSE and HST/STIS, Thesis, Trinity College Dublin [Google Scholar]
- Doughty, N. A., & Fraser, P. A. 1966, MNRAS, 132, 267 [NASA ADS] [Google Scholar]
- Dumm, T., Schmutz, W., Schild, H., & Nussbaumer, H. 1999, A&A, 349, 169 [NASA ADS] [Google Scholar]
- Elsner, R. F., Ghosh, P., Darbro, W., & Weisskopf, M. C. 1980, ApJ, 239, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Castro, T., Cassatella, A., Giménez, A., & Viotti, R. 1988, ApJ, 324, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Formiggini, L., & Leibowitz, E. M. 1990, A&A, 227, 121 [NASA ADS] [Google Scholar]
- Geltman, S. 1962, ApJ, 136, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F., 2005, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) [Google Scholar]
- Greiner, J., Bickert, K., Luthardt, R., et al. 1997, A&A, 322, 576 [NASA ADS] [Google Scholar]
- Kato, M., Mikołajewska, J., & Hachisu, I. 2012, Balt. Astron., 21, 157 [NASA ADS] [Google Scholar]
- Kato, M., Hachisu, I., & Mikołajewska, J. 2013, ApJ, 763, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Knill, O., Dgani, R., & Vogel, M. 1993, A&A, 274, 1002 [Google Scholar]
- Kolotilov, E. A., Tatarnikova, A. A., Shugarov, S. Yu., & Yudin, B. F. 2002, Astron. Lett., 28, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Mürset, U., & Schmid, H. M. 1999, A&AS, 137, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mürset, U., Nussbaumer, H., Schmid, H. M., & Vogel, M. 1991, A&A 248, 458 [Google Scholar]
- Nussbaumer, H., & Vogel, M. 1987, A&A, 182, 51 [NASA ADS] [Google Scholar]
- Nussbaumer, H., Schmid, H. M., & Vogel, M. 1989, A&A, 211, L27 [NASA ADS] [Google Scholar]
- Pereira, C. B., Vogel, M., & Nussbaumer, H. 1995, A&A, 293, 783 [NASA ADS] [Google Scholar]
- Popper, D. M. 1961, ApJ 133, 148 [Google Scholar]
- Pribulla, T., Vaňko, M., Chochol, D., Hambálek, L., & Parimucha, Š. 2011, Astron. Nachr., 332, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Kenyon, S. J., & Raymond, J. C. 1998, ApJ, 501, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Pustylnik, I., Kalv, P., Harvig, V., & Aas, T. 2007, Astron. Astrophys. Trans., 26, 4, 339 [Google Scholar]
- Samec, R. G., Figg, E. R., Melton, R., et al. 2009, in Sollar and Stellar Variability: Impact on Earth and Planets, eds. A. G. Kosovichev, A. H. Andrei, & J. P. Rozelot, Proc. IAU Symp., 264, 75 [Google Scholar]
- Schmid, H. M. 1995, MNRAS, 275, 227 [NASA ADS] [Google Scholar]
- Schmid, H. M., Krautter, J., Appenzeller, I., et al. 1999, A&A, 348, 950 [NASA ADS] [Google Scholar]
- Schwank, M., Schmutz, W., & Nussbaumer, H. 1997, A&A, 319, 166 [NASA ADS] [Google Scholar]
- Seaquist, E. R., Taylor, A. R., & Button, S. 1984, ApJ, 284, 202 (STB) [NASA ADS] [CrossRef] [Google Scholar]
- Sekeráš, M., & Skopal, A. 2012, MNRAS, 427, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Shagatova, N., Skopal, A., & Cariková, Z. 2016, A&A, 588, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A. 1998, A&A, 338, 599 [NASA ADS] [Google Scholar]
- Skopal, A. 2001, A&A, 366, 157 [Google Scholar]
- Skopal, A. 2005, A&A, 440, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A. 2006, A&A, 457, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A. 2009, New Astron., 14, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Skopal, A., & Shagatova, N. 2012, A&A, 547, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A., Vaňko, M., Pribulla, T., et al. 2002, CoSka, 32, 62 [NASA ADS] [Google Scholar]
- Skopal, A., Shugarov, S., Vaňko, M., et al. 2012, Astron. Nachr., 333, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Watarai, K., Takahashi, R., & Fukue, J. 2005, PASJ, 57, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Więcek, M., Mikołajewski, M., Tomov, T., et al. 2010, ArXiv e-prints [arXiv:1003.0608] [Google Scholar]
- Yuan, J. 2010, AJ, 139, 1801 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, D.-Q., & Leung, K.-Ch. 1990, ApJ, 355, 271 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Values of the Rayleigh scattering cross-section σRay(λ) (in cm2), the percentage of the Rayleigh scattered photons in direction of the line of sight (in %), H− bound-free absorption coefficient κH−(λ) and total cross-section of neutral hydrogen σH0(λ,Te) at Te = 18 500 K (both in cm2) for ten selected wavelengths.
All Figures
 |
Fig. 1 Comparison of the effect of considered attenuation processes on the WD flux (Sect. 3.2) at shortest (top) and longest (bottom) wavelength of the set. Corresponding column densities of H0 in neutral region and H+ in ionized region are given by the column density model in Fig. 5 and of H− in neutral region and H0 in ionized region by the LC modeling (Sect. 4). Two minima of radiation out of the eclipse for attenuation processes in ionized region (dashed lines) correspond to the orbital phase with line of sight entering/exiting the neutral region. |
| In the text | |
 |
Fig. 2 Schematic view of the regions of different velocity profiles as seen perpendicularly to the plane of observations. Denotations are explained in Sect. 3.4. |
| In the text | |
 |
Fig. 3 Resulting ionization boundary for the united wind velocity model given by Eqs. (14), (15)and (18)–(28), as seen perpendicularly to the orbital plane (solid line). The corresponding limiting values of ψ are ψint = −0.9 rad and ψte = 0.8 rad. For comparison, the dotted line represents the ionization boundary for |
| In the text | |
 |
Fig. 4 Ingress and egress velocity profiles of SY Mus from models M and O of Shagatova et al. (2016) for ve∞ = 20 km s-1 satisfying Eq. (28). |
| In the text | |
 |
Fig. 5 United column density model, nH and its components, nH0 and |
| In the text | |
 |
Fig. 6 LCs of SY Mus (circles with errorbars) and their models (solid lines). Contribution from the nebula is depicted by dashed lines. Vertical dotted lines represent the position of the inferior conjunction of the giant. |
| In the text | |
 |
Fig. 7 Top: model variations of the nebular continuum radiation in SY Mus (Eq. (3)) at ten wavelengths (solid lines). They are compared with the nebular fluxes at ϕ = 0.62 from the model SED (circles with errorbars). Bottom: model SED of SY Mus at ϕ = 0.62. Circles at the nebular component correspond to those plotted at the top panel. |
| In the text | |
 |
Fig. 8 Representative LC models for different column densities nH−(ϕ) (top) and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


