| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629791 | |
| Published online | 05 April 2017 | |
Properties of CO2 clathrate hydrates formed in the presence of MgSO4 solutions with implications for icy moons
1 Astrophysics Group, Lennard-Jones Laboratories, Keele University, Keele, Staffordshire, ST5 5BG, UK
e-mail: e.safi@keele.ac.uk
2 Diamond Light Source, Harwell Science and Innovation Campus, Didcot, Oxfordshire, OX11 0DE, UK
Received: 27 September 2016
Accepted: 25 January 2017
Context. There is evidence to suggest that clathrate hydrates have a significant effect on the surface geology of icy bodies in the solar system. However the aqueous environments believed to be present on these bodies are likely to be saline rather than pure water. Laboratory work to underpin the properties of clathrate hydrates in such environments is generally lacking.
Aims. We aim to fill this gap by carrying out a laboratory investigation of the physical properties of CO2 clathrate hydrates produced in weak aqueous solutions of MgSO4.
Methods. We use in situ synchrotron X-ray powder diffraction to investigate clathrate hydrates formed at high CO2 pressure in ice that has formed from aqueous solutions of MgSO4 with varying concentrations. We measure the thermal expansion, density and dissociation properties of the clathrates under temperature conditions similar to those on icy solar system bodies.
Results. We find that the sulphate solution inhibits the formation of clathrates by lowering their dissociation temperatures. Hysteresis is found in the thermal expansion coefficients as the clathrates are cooled and heated; we attribute this to the presence of the salt in solution. We find the density derived from X-ray powder diffraction measurements is temperature and pressure dependent. When comparing the density of the CO2 clathrates to that of the solution in which they were formed, we conclude that they should sink in the oceans in which they form. We also find that the polymorph of ice present at low temperatures is Ih rather than the expected Ic, which we tentatively attribute to the presence of the MgSO4.
Conclusions. We (1) conclude that the density of the clathrates has implications for their behaviour in satellite oceans as their sinking and floating capabilities are temperature and pressure dependent; (2) conclude that the presence of MgSO4 inhibits the formation of clathrates and in some cases may even affect their structure and (3) report the dominance of Ih throughout the experimental procedure despite Ic being the stable phase at low temperature.
Key words: methods: laboratory: solid state / planets and satellites: surfaces / planets and satellites: individual: Europa / planets and satellites: individual: Enceladus / molecular data
© ESO, 2017
1. Introduction
Clathrate hydrates are formed at high pressures and low temperatures and are cage-like structures in which water molecules bonded via hydrogen bonds can encase guest molecules. The conditions on icy solar system bodies such as Enceladus, Europa, Mars and comets have long been considered as potential for clathrate formation (Max & Clifford 2000; Prieto-Ballesteros et al. 2005; Marboeuf et al. 2010; Bouquet et al. 2015). Clathrates are leading candidates for the storage of gases such as CH4 and CO2 in the solar system (Prieto-Ballesteros et al. 2005; Mousis et al. 2015; Bouquet et al. 2015); therefore understanding the kinetics and thermodynamics of clathrate hydrates under planetary conditions is important.
The type of guest molecule that can be trapped within a clathrate depends on the clathrate structure, of which three are currently known: sI, sII and sH (Sloan & Koh 2007). sI clathrates form a cubic structure with space group Pm-3n. They are composed of two cage types; the smaller 512 (12 pentagonal faces) and the larger 51262 (12 pentagonal faces and 2 hexagonal faces). sI clathrates are constructed of two small cages for every six larger ones, and host relatively large molecules such as CO2 and CH4. sII also form cubic structures and are composed of sixteen small 512 cages and eight large 51264 cages; sII clathrates typically host smaller molecules such as O2 and N2. The least common clathrate hydrate, sH, is composed of one large cage, three smaller cages and two medium 435663 cages. sH clathrates form hexagonal structures and usually require two types of guest species in order to remain stable. Recently a new structure of clathrate has been proposed (Huang et al. 2016); this type of clathrate (“structure III”) is predicted to have a cubic structure and be composed of two large 8668412 and six small 8248 cages.
It has been confirmed that water ice and CO2 are present on the surface of Enceladus (Matson et al. 2013). Among the gases such as CH4 present in the plumes emanating from the satellite’s surface (Waite et al. 2006), CO2 has poor solubility in water. This suggests the trapping of gases in the form of clathrate hydrates, with subsequent release due to their dissociation (Bouquet et al. 2015) could give rise to the plumes. Fortes (2007) used a clathrate xenolith model to account for the origin of Enceladus’ plumes, suggesting that fluids are able to break through the ice shell, metasomatising the mantle by the emplacement of clathrates along fractures and grain boundaries. The clathrates are trapped in the rising cryomagmas as xenoliths, and are carried upwards where they dissociate, releasing their enclosed gas and forming the plumes.
The density of clathrates is a significant factor in determining their fate. If their density is higher than that of the oceans in which they are formed, they sink to the ocean floor; if lower, they rise to the ice/ocean interface. If their destination is the ocean floor then they might be dissociated by heat produced from hydrothermal activity. On the other hand if they ascend, then a clathrate layer would be present at the interface between the ice and ocean surface.
Bouquet et al. (2015) calculated the density of clathrates assuming fully filled cages and a volatile composition based on Enceladus’ plume; they found densities of 1.04 g cm-3 and 0.97 g cm-3 for sI and sII clathrates respectively. When comparing these to their computed ocean densities they deduced that sII clathrates should be buoyant and therefore likely to ascend. However they were unable to arrive at a conclusion regarding the sI clathrates, as there was significant uncertainty regarding the ocean’s salinity and because the clathrate density was too close to that of the ocean itself. Clathrate ascension would, however, enable clathrates to play a part in the formation of the plumes, as their dissociation would increase pressure conditions at the site of the plume’s origin (Bouquet et al. 2015).
The trapping of gases by clathrates could also have a significant impact on Enceladus’ ocean composition and hence the plumes emitted in the south polar region (Bouquet et al. 2015). The enclathration of gases would lower the concentration of volatiles in the ocean to below that observed in the plumes. This would indicate that any clathrates formed would need to dissociate in order to replenish the volatile concentration of the plume. If this is not the case then the gas concentration would need to be restored by an alternative mechanism, such as hydrothermal activity (Bouquet et al. 2015).
Prieto-Ballesteros et al. (2005) evaluated the stability and calculated the density of several types of clathrates thought to be found in the crust and ocean of Europa using thermal models for the crust. They found SO2, CH4, H2S and CO2 clathrates should all be stable in most regions of the crust. They deduced that CH4, H2S and CO2 clathrates should float in an eutectic ocean composition of MgSO4-H2O, but that SO2 clathrates would sink. However the sinking and floating capabilities of various hydrates will also likely depend on the salinity of the ocean since this will affect their buoyancy.
Mousis et al. (2013) investigated clathrates in Lake Vostok (Antarctica) using a statistical thermodynamic model. They assumed temperatures of 276 K and pressures of 35 MPa and found that Xe, Kr, Ar and CH4 should be depleted in the lake, while CO2 should be enriched compared to its atmospheric abundance. They also found that air clathrates should float as they are less dense than liquid water. However, air clathrates have not been observed on the surface of the ice above the lake (Siegert et al. 2000). To account for this McKay et al. (2013) suggested that large amounts of CO2 are also trapped within the clathrates, increasing their relative density.
Clathrates have been found to form in the Sea of Okhotsk (Pacific Ocean), and Takeya et al. (2006) have used X-ray powder diffraction to study their crystal structures and thermal properties. They found that four samples from four different locations each had sI clathrates encaging CH4 and a small amount of CO2. The small amount of encaged CO2 is consistent with McKay et al.’s suggestion that a large amount of trapped CO2 is necessary for clathrates to sink.
It is likely that the type of ice present during the formation of clathrates also has an effect on their dissociation. Using neutron diffraction Falenty et al. (2015) studied the dissociation of CO2 clathrates in pure water ice between 170–190 K, with special attention to the polymorph of ice formed. They found that below 160 K cubic ice (Ic) was the more stable phase, while between 160–190 K Ic transforms to the more thermodynamically stable hexagonal ice (Ih). Falenty et al. (2015) concluded that, due to Ic forming with smaller crystallite sizes compared to Ih, it could provide an additional pathway for the escaped gas molecules originating from clathrate structures, therefore supporting their dissociation.
An important factor when considering clathrate dissociation is ocean salinity. It is well known that saline solutions depress the freezing point of water (e.g. Duan & Sun 2006), suggesting that the temperatures at which clathrates form and dissociate within the oceans on planets and satellites will also be lower. Miller (1961) showed how clathrate dissociation is affected by temperature and pressure conditions in pure water. However, when comparing the results obtained by Miller with the more recent theoretical results obtained by Bouquet et al. (2015) for saline solutions, there is a significant difference, suggesting that increased salinity may indeed lower the temperature at which clathrates are able to form.
 |
Fig. 1 Rietveld refinements of the MS10.5 solution at a 10 bar CO2 pressure experimental data. From top-bottom: 90 K, 180 K, 245 K. The experimental data are shown in black, the calculated fit in red, and the residuals in grey below. All prominent peaks are labelled where C = clathrate peaks and I = hexagonal ice peaks. The larger residuals for some of the ice peaks are due to poor powder averaging due to the way the ice freezes inside the cell (preferred orientation) and the restricted cell rocking angle used to compensate for this during measurement. |
In this paper we use synchrotron X-ray powder diffraction (SXRPD) to investigate the thermal and physical properties of CO2 clathrate hydrates produced from weak aqueous solutions of MgSO4. We replicate possible thermal variations due to seasonal and tidal changes, ocean depth and salt concentration and observe the formation and dissociation conditions of CO2 clathrate hydrates. The SXRPD provides information about the temperature-dependence of clathrate densities and hence their ability to rise or sink in the oceans in which they are formed. We also investigate clathrate dissociation kinetics and the influence of the different polymorphs of ice.
Concentration, temperature range, pressure, density of salt solutions.
2. Experimental work
In this work we use an epsomite (MgSO4·7H2O) salt solution to form the ice and CO2 clathrate system. The concentrations, and the temperature and pressure ranges used are summarised in Table 1, in which the concentration of MgSO4·7H2O has been converted to concentration of MgSO4 per kg H2O, to allow for the contribution that the waters of hydration make to the achieved concentrations. In the following we refer to 20 g MgSO4·7H2O/1 kg H2O as MS10.5 and 5 g MgSO4·7H2O/1 kg H2O as MS3.1. The salt concentrations are similar to those of Enceladus (whose salinity is estimated to lie in the range 2−10 g/kg H2O; Zolotov 2007) and of Europa (MgSO4 concentration estimated to be between 1–100 g/kg H2O; Hand & Chyba 2007).
 |
Fig. 2 CO2 clathrate dissociation curve (red) for CO2 clathrate hydrates in MS10.5 (circles) and MS3.1 (squares) solutions, compared with the CO2 clathrate dissociation curve for CO2 clathrate hyrates in pure water (Miller 1961, blue curve). |
 |
Fig. 3 Temperature dependence of the lattice parameters of CO2 clathrate hydrates formed in solutions of MS10.5 and MS3.1 at various pressures. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. “(1)” and “(2)” indicate that the cooling was performed first, followed by heating. For ease of presentation blue symbols represent values obtained during cooling and red values obtained during heating. |
 |
Fig. 4 Thermal expansion coefficient for CO2 clathrate hydrates formed in solutions of MS10.5 and MS3.1 derived from the polynominal fits to the data in Fig. 3. Black: MS3.1/20 bar; green: MS10.5/5 bar; orange: MS10.5/10 bar. H = Heating and C = Cooling. |
The temperature (T) range we cover is from ~ 90 K to ~ 240 K, and the bulk of our measurements were carried out at pressures (P) of 5, 10 and 20 bar. The range of T is somewhat below that estimated for the sub-surface oceans of (for example) Europa and Enceladus (see e.g. Melosh et al. 2004; Bouquet et al. 2015) and is more representative of these satellites’ surfaces. The pressures we used in this work were necessarily optimised to give a reasonable conversion rate to clathrate with the facility, and within the time, available. In planetary environments the pressures in sub-surface oceans depend on the depth of the overlying ice sheet, but are typically hundreds of bar (see e.g. Melosh et al. 2004), although the pressures in Enceladus’ sub-surface ocean may be as low as a few 10s of bars (Matson et al. 2012; Bouquet et al. 2015).
SXRPD data were collected using beamline I11 at the Diamond Light Source (Thompson et al. 2009) during twelve 8-h shifts. The X-ray wavelength was 0.826220 Å, calibrated against NIST SRM640c standard Si powder; the beam size at the sample was 2.5 mm (horizontal) × 0.8 mm (vertical). The high pressure gas cell and the procedure used to form clathrates are described by Day et al. (2015). A 0.8 mm diameter single-crystal sapphire tube is filled with solution and sealed into the gas cell. This is then mounted onto the central circle of the beamline’s concentric three circle diffractometer, and cooled using a liquid nitrogen Oxford Cryosystems 700+ cryostream. The latter has temperature stability ± 0.1 K and a ramp rate of 360 K/h.
Once frozen at ~240 K, CO2 gas is admitted to the cell at the chosen pressure and a fast position sensitive detector (Thompson et al. 2011) is used to collect in situ powder diffraction data as the temperature is slowly raised. During this time ice and clathrate formation is simultaneously observed. We continue to increase the temperature until both the clathrate and ice are lost, whereupon the temperature ramp is reversed and the cell is cooled once more. Depending on pressure and solution composition, either pure-phase clathrates or an ice-clathrate mix is formed. Using this “second cycle” technique provides increased clathrate formation (see discussion in Day et al. 2015). For the present work we then cycled the temperature between 250 K and 90 K using the Cryostream to replicate diurnal and tidal variations with applied CO2 pressures between 5–20 bar. Dissociation temperatures and pressures were determined by holding the sample at constant pressure and gradually increasing the temperature in 5 K temperature steps until there were no peaks discernible in the X-ray diffraction pattern.
Each SXRPD data-collection cycle, including the time allowed for the sample to come to temperature equilibrium, took approximately 20 min. Once data collection was completed the temperature was changed to the new setting and data collection repeated.
The SXRPD patterns were analysed via Rietveld structure refinement, using TOPAS refinement software (Coelho 2007) and previously published clathrate atom positions and lattice parameters (Udachin et al. 2001) as starting values. Published atom positions and lattice parameters (Fortes 2007) for Ih and Ic were similarly used. From the refinements, the lattice parameter, a, at each temperature step was obtained and hence the thermal expansion and density of the cubic clathrate structures were derived.
3. Results
A typical example of a refinement is shown in Fig. 1, which shows a comparison of the SXRPD patterns for Ih, Ic and CO2 clathrates formed in the MS10.5 solution at a CO2 pressure of 10 bar. The presence of the clathrates at 90 K and 180 K is evident from the formation of multiple features at 14°−19°, 21.4°, 23°−24°, 24.6° and 25.2° 2θ (Day et al. 2015). During fitting the lattice parameters of Ih ice were initially set to 4.497479 Å and 7.322382 Å for the a and c axes respectively (Fortes 2007).
Values for the weighted profile (Rwp) and background-corrected weighted profile (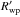 ) fitting agreement parameters between the calculated and experimental diffraction data (see Young 1993; McCusker et al. 1999, for further details) – excluding the ice peaks from the refinement – were Rwp = 6.44% and 1.21% and
) fitting agreement parameters between the calculated and experimental diffraction data (see Young 1993; McCusker et al. 1999, for further details) – excluding the ice peaks from the refinement – were Rwp = 6.44% and 1.21% and 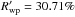 and 27.95%, for the structures formed at 90 K and 180 K respectively. The associated error in the lattice parameter was typically ± 0.001 Å.
and 27.95%, for the structures formed at 90 K and 180 K respectively. The associated error in the lattice parameter was typically ± 0.001 Å.
The bulk densities of the MgSO4 starting solutions were measured using a 1000 μm PhysioCare concept Eppendorf Reference pipette to gather a precise volume of solution and weighed using a Mettler Toledo balance at room temperature. The solution densities are given in Table 1.
3.1. Inhibiting effects on clathrate formation
Figure 2 compares the dissociation temperatures and pressures for the CO2 clathrates formed in the MS10.5 and MS3.1 solutions to those reported by Miller (1961) for pure water. We have fitted the data for the MS10.5 and MS3.1 solutions, for which we have dissociation temperatures at four pressures (5, 10, 15, 20 bar), to a function of the form (cf. Miller 1961) 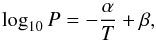 (1)where T is in K, P is in bar and α and β are constants to be determined. While we recognise the limited amount of available data to determine the two parameters α and β, we find α = 1661±292 K and β = 7.74±1.19. These values may be compared with those given by Miller (1961) for the dissociation of CO2 clathrates in pure water: α = 1121.0 K and β = 5.1524; the data in Miller (1961) are based on measurements in the temperature range 175−232 K. Our data confirm the likely inhibiting effect by lowering the temperature at which CO2 clathrates dissociate at a given pressure over the temperature range 235−260 K.
(1)where T is in K, P is in bar and α and β are constants to be determined. While we recognise the limited amount of available data to determine the two parameters α and β, we find α = 1661±292 K and β = 7.74±1.19. These values may be compared with those given by Miller (1961) for the dissociation of CO2 clathrates in pure water: α = 1121.0 K and β = 5.1524; the data in Miller (1961) are based on measurements in the temperature range 175−232 K. Our data confirm the likely inhibiting effect by lowering the temperature at which CO2 clathrates dissociate at a given pressure over the temperature range 235−260 K.
3.2. Thermal expansion
The thermal expansion of clathrate hydrates is an important property that enables us to understand their physical behaviour. For example, it has been suggested that the increase in thermal expansion could be due to greater anharmonicity in the crystal lattice (Tse 1987); the larger thermal expansion of clathrates compared to hexagonal ice could be due to interactions between the guest molecule and host structure (Shpakov et al. 1998).
Figure 3 shows the dependence of the clathrate lattice parameter on temperature at three pressure-composition combinations. We have used a polynomial approach to describe the temperature dependency of the lattice parameter, using the function 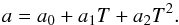 (2)Table 2 gives the values of the coefficients a0, a1, a2, obtained by fitting Eq. (2) to the data. Although the first order term is apparently not significantly different from zero in the bottom two rows of the table, its inclusion was found to significantly improve the fit to our experimental data when inclusion of the second order term is necessary.
(2)Table 2 gives the values of the coefficients a0, a1, a2, obtained by fitting Eq. (2) to the data. Although the first order term is apparently not significantly different from zero in the bottom two rows of the table, its inclusion was found to significantly improve the fit to our experimental data when inclusion of the second order term is necessary.
The MS10.5 solution at a CO2 pressure of 10 bar was cycled once only (cf. Sect. 2) and clathrates appeared at 185 ± 5 K on cooling from 250 K. It seems evident from Fig. 3 that the expansion of the clathrate on heating does not follow the behaviour on cooling: there is hysteresis in that the cooling and heating seem not to be reversible. The MS10.5 solution at a CO2 pressure of 5 bar shows a greater degree of hysteresis compared to the 10 bar solution. It too was thermally cycled and, on cooling, clathrates appeared at 195 ± 5 K. Similarly, the MS3.1 solution at a CO2 pressure of 20 bar was also cycled once, with clathrates appearing at 247.5 ± 2.5 K when cooled from 250 K. This solution shows a significantly lower degree of hysteresis compared to the solutions at 5 and 10 bar CO2 pressure. The difference in behaviour between heating and cooling may be related to differing levels of bonding disorder within the clathrate phase (see discussion in Sect. 4).
The coefficient of thermal expansion at constant pressure is defined in the usual way as [(da/ dT) /a0]P. In the simplest case, the expansion has a linear dependence on temperature and the coefficient of expansion is a1, which is independent of temperature. The coefficients of thermal expansion are plotted as a function of temperature in Fig. 4, and exhibit strong pressure dependency. Those CO2 clathrates formed at the lower pressure of 5 bar display a purely linear expansion, while those formed at higher pressure show more complex behaviour. Since higher pressures result in higher cage occupancy (Hansen et al. 2016), our results imply that the occupancy of the cages may influence the thermal expansion of clathrates. This is discussed further in Sect. 4.
3.3. Density
The density, ρ, of a clathrate depends on the lattice parameter, a, the mass of its water molecules, the mass of the guest molecule and the cage occupancy; it is calculated as follows (Prieto-Ballesteros et al. 2005): 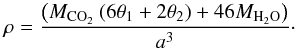 (3)Here MCO2 and MH2O are the masses of the CO2 guest and water molecules respectively, and θ1 and θ2 are the fractional occupancies of the large and small cages respectively. Raman data for CO2 clathrates formed at 20 bar in pure water (Day et al. 2015) indicated that only the large clathrate cages are occupied by CO2 (see also Ratcliffe & Ripmeester 1986). For the time being, we assume in the following that this is also the case for clathrates formed in the presence of MgSO4 and that therefore θ1 = 1 and θ2 = 0. The dependence of the clathrate densities on temperature, calculated using Eq. (3), are shown in Fig. 5. The deduced densities vary with composition and, as would be expected from the hysteresis effect in the lattice parameter (see Fig. 3), on whether the clathrate is being heated or cooled. We discuss this further in Sect. 4.3 below and also consider the effect of fractional occupancy of the cages.
(3)Here MCO2 and MH2O are the masses of the CO2 guest and water molecules respectively, and θ1 and θ2 are the fractional occupancies of the large and small cages respectively. Raman data for CO2 clathrates formed at 20 bar in pure water (Day et al. 2015) indicated that only the large clathrate cages are occupied by CO2 (see also Ratcliffe & Ripmeester 1986). For the time being, we assume in the following that this is also the case for clathrates formed in the presence of MgSO4 and that therefore θ1 = 1 and θ2 = 0. The dependence of the clathrate densities on temperature, calculated using Eq. (3), are shown in Fig. 5. The deduced densities vary with composition and, as would be expected from the hysteresis effect in the lattice parameter (see Fig. 3), on whether the clathrate is being heated or cooled. We discuss this further in Sect. 4.3 below and also consider the effect of fractional occupancy of the cages.
Coefficients of the polynomial expression for describing lattice constants of CO2 clathrate hydrates formed in the MS10.5 and MS3.1 solutions.
 |
Fig. 5 Dependence of density on temperature. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. Symbols/colours, and meaning of “(1)” and “(2)”, as per Fig. 3. |
3.4. Weight percentage of clathrate, Ih, and Ic ice
From the relative contribution of each phase to the overall intensity of features in the powder diffraction pattern we can obtain the relative fraction by weight of each crystalline component present in the sample under study. These are shown in Fig. 6 as a function of temperature for the MS10.5 (at 5 and 10 bar CO2) and MS3.1 (20 bar CO2). It is immediately evident that the proportion of Ic formed in all three samples is small (typically < 5%), even at 90 K.
Figure 6 also shows that the relative composition predominantly depends on pressure and salt concentration. The MS3.1 solution at a CO2 pressure of 20 bar is the lowest concentration and highest pressure sample and contains the highest proportion of clathrates. The other two samples have the same salt concentration but are at lower pressures (5 and 10 bar) and consequently show lower proportions of clathrate. However, in all three samples, the composition of Ic is similar and always less than 5%; this is discussed further in Sect. 4.4.
 |
Fig. 6 Weighted percentage (wt%) curves for solutions. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. Triangles: clathrates; circles: Ih ice; squares Ic ice. Colours are as per Fig. 3. |
4. Discussion
4.1. Inhibiting effect of MgSO4 on clathrate formation
It is well known that electrolytes have an inhibiting effect on the formation of clathrate hydrates (Sabil 2009). This is caused by the ions in the electrolyte solution lowering the solubility of the gas, hence lowering the activity of the water, resulting in the clathrate hydrates forming at lower temperatures relative to their development in pure water (Duan & Sun 2006). Also, the presence of inhibitors impedes the water molecules from forming hydrogen bonds (Sabil 2009), adding a further obstacle to clathrate formation.
Sodium chloride (NaCl) and calcium chloride (CaCl2) electrolyte solutions have been extensively studied as these are some of the major components of terrestrial seawater and rocks and their inhibiting effect is well known. They decrease the dissociation temperature of clathrates by approximately 5 K in concentrations of 10% by weight of solution and by more than 10 K close to the eutectic solution composition (17% by weight; Prieto-Ballesteros et al. 2005). In situ studies of clathrate hydrates formed in chloride solutions will be reported elsewhere (Safi et al., in prep.).
The best electrolyte inhibitors will exhibit maximum charge and minimum radius (Makogon 1981) and, while less is known about magnesium electrolyte solutions (e.g. MgCl2 and MgSO4), they do exhibit an inhibiting effect that is stronger than calcium or sodium electrolyte solutions (Sabil 2009). The smaller ionic size of magnesium increases the surface charge density, and so attracts more water molecules, thus decreasing the activity of water (Sabil 2009).
Prieto-Ballesteros et al. (2005) observed a decrease in the crystallisation temperature of clathrates due to the presence of magnesium. However, the inhibiting effect of the dissolved magnesium in their experiment was small, amounting to about 2 K at 17% MgCl2. Also noted by Prieto-Ballesteros et al. (2005) is that the salt depresses the freezing point of water by approximately 4 K and so a larger temperature difference between ice melting and clathrate dissociation is observed in the eutectic salt system. A similar trend was reported earlier by Kang et al. (1998) who found that, as they increased the concentration of MgCl2, the amount of hydrate formed at a particular pressure becomes less.
Figure 6 shows that there is a larger difference in the wt% of clathrates, during both heating and cooling, for the samples at a CO2 pressure of 10 and 20 bar compared to the samples at 5 and 10 bar. This could be due to the fact that the solutions subjected to 5 and 10 bar CO2 contain 20 g of epsomite per kg water and the solution subjected to a 20 bar CO2 pressure contains 5 g of epsomite per kg water, i.e. the epsomite is acting as a clathrate inhibitor. This is further suggested in Fig. 2 where we compare our clathrate dissociation temperatures with the CO2 clathrate dissociation curve given by Miller (1961). As discussed in Sect. 3.1, this shows that clathrates formed in the salt solution dissociate at lower temperatures.
4.2. Thermal expansion
A surprising feature of the thermal expansion behaviour (Fig. 3) is the apparent hysteresis in the dependence of a on T, depending on whether the sample is being cooled or heated. The variation of a with T for the MS3.1 solution at a CO2 pressure of 20 bar is almost reversible, with little difference between the cooling and heating curves. However for the MS10.5 solution at a CO2 pressure of 10 bar we begin to see a distinct difference between cooling and heating while for the MS10.5 solution at a CO2 pressure of 5 bar the difference is very noticeable. The increase in hysteresis with decreasing pressure may be due to two contributing factors:
-
1.
clathrate stability is greater at higher pressures, so that thermalcycling has a lesser effect;
-
2.
the possibility that during clathrate formation, the ice-phase water molecules that form the clathrate cages shift in position and form hydrogen bonds with liquid-phase water molecules. The latter originate from the fluid inclusions/channels rich in Mg and SO4 ions that result from the eutectic freezing out of the pure-phase water ice. This displacement would cause adjacent water molecules from the surrounding cages to break hydrogen bonds, hence altering neighbouring cages (Shin et al. 2012). Such a process would be expected to affect the elastic properties of the cages, leading to stress hysteresis (Soh et al. 2007) and to the hysteresis we see in the thermal expansion (see Fig. 3). This effect should be strongest in those samples with the highest concentration of epsomite, as is indeed observed. This may also be related to our observation (see Sect. 4.4) that the clathrate structure may play a role in stabilising the Ih ice phase over the Ic phase.
Furthermore, at higher pressures the cage occupancy is higher and could result in an increase of the lattice parameters by several thousandth of an Å (Hansen et al. 2016). Indeed, Hansen et al. found that CO2 molecules situated in the small cages expand the clathrate lattice at higher temperatures. Despite the fact that we have assumed θ1 = 1 and θ2 = 0, it may be that the clathrates formed at higher pressures have a value of θ2> 0. This is what our experimental data suggest as the thermal coefficient of expansion for samples at the higher pressure exhibit a steeper gradient (see Fig. 4). However it is difficult with the data available to draw any firm conclusions about the effects of pressure and salinity on the hysteresis in thermal expansion. Further data, covering a greater area of the pressure and salinity parameter space are needed to address this issue.
4.3. Clathrate density and buoyancy
The variation of clathrate density with temperature (see Fig. 5) has implications for the sinking or rising capabilities of the clathrates in planetary oceans. According to our results the general implication is that the clathrate density is higher at lower temperatures and lower at higher temperatures, implying they have a greater probability of sinking at lower temperatures and of floating at higher temperatures. However, this will also depend on the salinity of the ocean in question.
The MS3.1 and MS10.5 solutions used in this experiment are similar to the salinities of the oceans on Enceladus and Europa (see Table 1). If we compare our clathrate densities at various temperatures with those of the solutions in which they were formed, we see those both the measured solution densities (1.003 g cm-3 and 1.016 g cm-3 for MS3.1 and MS10.5 solutions, respectively) are much lower than the CO2 clathrate density (Fig. 5), irrespective of the temperature and pressure conditions. The higher clathrate densities suggest the clathrates would always sink. Indeed, this is also true if we assume θ2 is between 0.625–0.688 (keeping θ1 = 1) which are the values Hansen et al. (2016) obtained from their experimental investigation. Therefore the sinking of clathrates is the likely scenario for both Enceladus and Europa.
For CO2 clathrates to float in an ocean with salinity close to Enceladus’ and Europa’s they would need lower guest molecule occupancy. From Eq. (3) the clathrates formed in the MS3.1 solution at a CO2 pressure of 20 bar would require the larger cages to be 73% filled, while the MS10.5 solutions at CO2 pressures of 5 and 10 bar would need the larger cages to be 78% and 77% filled respectively (assuming θ2 = 0). As mentioned, pressure directly affects the clathrate cage occupancy in that occupancy (and hence density) is greater at increased pressure. A consequence of this is that clathrates formed deeper in an ocean would have a higher occupancy and would therefore have a greater probability of sinking.
Our results also suggest that if CO2 clathrates were to form at the base of a floating ice shell (cf. Prieto-Ballesteros et al. 2005), they too should sink and transport encased gases to the bottom of the ocean floor. If, on the other hand, the ocean was of eutectic composition of MgSO4 (17 wt%, as suggested for Europa by Prieto-Ballesteros et al. 2005), the ocean density would be 1.19 g cm-3, implying the CO2 clathrates would in fact float; this would cause fracturing and gravitational collapse of the terrain due to rapid release of gas (Prieto-Ballesteros et al. 2005).
The effect of pressure on density can be seen in Fig. 5. If we compare both the MS10.5 solutions at CO2 pressures of 5 and 10 bar, we see that the sample subjected to 5 bar CO2 pressure has a lower density from 95 K to 195 K on heating. From 195 K onwards the sample subjected to a CO2 pressure of 10 bar produces the lowest density clathrates. However, considering the cooling curves in Fig. 5, the MS10.5 solution at a CO2 pressure of 10 bar has the highest density throughout the entire cooling process. For most of the heating curves and all of the cooling curves in Fig. 5 our results are consistent with the conclusion that higher pressure environments produce clathrates with higher densities and which are therefore less buoyant. We should note that our conclusion regarding buoyancy relates to the case of CO2 clathrates. For the case of multiple-guest occupancy (e.g. CO2 + CH4) the sinking/floating capabilities might well be different. However such multiple-guest clathrates would most likely be of the less common sH type (see Sect. 1).
4.4. The nature of the ice
Ic is the most common polymorph of ice at temperatures below 160 K. Therefore investigation into the nature of the ice phase that coexists with clathrates is especially significant in the context of cold extra-terrestrial environments as it would impact on the interpretation of remotely sensed data and our understanding of the physical processing and conditions in these environments (Falenty & Kuhs 2009). Above 240 K water crystallises into the thermodynamically favoured Ih phase, the rate of change of Ih to Ic being highest between 200−190 K, while below ~ 160 K Ic is the stable phase (Falenty et al. 2015). We note that the experimental work of Falenty et al. was undertaken at 6 mbar, typical of Mars’ atmosphere; however the crystallisation temperatures of Ih and Ic do not seem to be sensitive to pressures up to a few 100 bar (see e.g. Zhang et al. 2015).
Despite being thermodynamically favourable at low temperature, our data show that the wt% of Ic is never more than about 5%, even at 90 K (see Fig. 6) and it may be that the clathrate structure preferentially stabilises the Ih phase over the Ic phase. However, it is also possible that, at low temperatures, the rate of transformation is slow and, given sufficient time, all of the Ih would eventually transform to Ic. Furthermore, Ic might be the more favourable phase if the ice were to condense at temperatures lower than those used in this work.
Also, we note that clathrate dissociation does not occur until the temperature reaches approximately 200–240 K, at which point ice would form as Ih after the clathrates have dissociated (Falenty & Kuhs 2009). Therefore, since the CO2 clathrates formed at the pressures and salinities used in this experiment do not seem to dissociate at very low temperatures below 240 K, we would not expect the formation of significant quantities of the Ic phase.
5. Conclusion
By the use of in situ synchrotron X-ray powder diffraction we have studied the formation, dissociation and thermal expansion properties of CO2 clathrate hydrates formed in MgSO4 salt solutions. Specifically, we have:
-
1.
Found the dissociation temperatures and pressures of CO2 clathrate hydrates formed in a salt solution containing epsomite (MgSO4·7H2O) and that the salt solution inhibits clathrate formation.
-
2.
Computed the density of these clathrates at different temperatures and pressures and compared this to the density of the solution in which they were formed. While it was found that the density of the clathrate depends on temperature and pressure (and hence local factors such as seasonal and tidal changes), when compared to the density of the salt solution they formed in they should in general sink, irrespective of the temperature and pressure.
-
3.
Investigated the polymorphs of the associated ice phases. We report the dominance of Ih throughout the experiment despite the expectation of Ic being the thermodynamically stable polymorph at lower temperatures. This may be due to the salt solution inhibiting the Ih to Ic transformation. However further investigation into the thermodynamics and kinetics of ice in relation to clathrates is needed to confirm this.
These experimental observations demonstrate the importance of understanding the role played by salts, clathrates and ice on the surface geology and sub-surface oceans of icy solar system bodies. As a gas transport mechanism the likely sinking of CO2 clathrates formed in saline environments could make a significant contribution to ocean floor geochemistry on such objects.
Acknowledgments
We thank an anonymous referee for their careful and thorough reading of the paper, and for making several comments and suggestions that have helped to clarify and improve the text. This work was supported by the Diamond Light Source through beamtime awards EE-9703 and EE-11174. E.S. is supported by Keele University and Diamond Light Source.
References
- Bouquet, A., Mousis, O., Waite, J. H., & Picaud, S. 2015, Geophys. Res. Lett., 42, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, A. 2007, Topas Academic Version 4.1, Coelho Software, Brisbane [Google Scholar]
- Day, S. J., Thompson, S. P., Evans, A., & Parker, J. E. 2015, A&A, 574, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, Z., & Sun, R. 2006, American Mineralogist, 91, 1346 [NASA ADS] [CrossRef] [Google Scholar]
- Falenty, A., & Kuhs, F. 2009, J. Phys. Chem. B., 113, 15975 [CrossRef] [Google Scholar]
- Falenty, A., Hansen, T. C., & Kuhs, W. F. 2015, ArXiv e-prints [arXiv:1510.08004] [Google Scholar]
- Fortes, A. D. 2007, Icarus, 191, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Hand, K. P., & Chyba, C. F. 2007, Icarus, 189, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, T. C., Falenty, A., & Kuhs, W. F. 2016, J. Chem. Phys., 144, 054301 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y., Zhu, C., Wang, L., et al. 2016, Sci. Adv., 2, e1501010 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, S. P., Chun, M. K., & Lee, H. 1998, Fluid Phase Equilibra, 147, 229 [CrossRef] [Google Scholar]
- Makogon, Y. F. 1981, Hydrates of natural gas (Penwell Books) [Google Scholar]
- Marboeuf, U., Mousis, O., Petit, J.-M., & Schmitt, B. 2010, ApJ, 708, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Matson, D. L., Castillo-Rogez, J. C., Davies, A. G., & Johnson, T. V. 2012, Icarus, 221, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Matson, D. L., Davies, A. G., Johnson, T. V., Castillo-Rogez, J. C., & Lunine, J. I. 2013, AAS, DPS meeting #45, 416.03 [Google Scholar]
- Max, M. D., & Clifford, S. M. 2000, J. Geophys. Res. 105, 4165 [Google Scholar]
- McCusker, L. B., Von Dreele, R. B., Cox, D. E., Louë,R. D., & Scardi, P. 1999, J. Appl. Cryst. 32, 36 [Google Scholar]
- McKay, C. P., Hand, K. P., Doran, P. T., Andersen, D. T., & Priscu, J. C. 2013, Geophys. Res. Lett., 30, 1702 [NASA ADS] [Google Scholar]
- Melosh, H. J., Ekholm, A. G., Showman, A. P., & Lorenz, R. D. 2004, Icarus, 168, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. L. 1961, Proc. Nat. Acad. Sci. USA, 47, 1798 [Google Scholar]
- Mousis, O., Lakhlifi, A., Picaud, S., Pasek, M., & Chassefière, E. 2013, Astrobiology, 13, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Mousis, O., Guilbert-Lepoutre, A., Brugger, B., et al. 2015, ApJ, 814, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto-Ballesteros, O., Kargel, J. S., Fernández-Sampedro, M., et al. 2005, Icarus, 177, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Ratcliffe, C. I., & Ripmeester, J. A. 1986, J. Chem. Phys., 90, 1259 [CrossRef] [Google Scholar]
- Sabil, K. M., 2009, Ph.D. dissertation, Technische Universiteit Delft, Delft, The Netherlands [Google Scholar]
- Shin, K., Kumar, R., Udachin, K. A., Alavi, S., & Ripmeester, J. A. 2012, Proc. Nat. Acad. Sci. USA, 109, 14785 [NASA ADS] [CrossRef] [Google Scholar]
- Shpakov, V. P., Tse, J. S., Tulk, C. A., Kvamme, B., & Belosludov, V. R. 1998, Chem. Phys. Lett., 282, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Siegert, M. J., Kwok, R., Mayer, C., & Hubbard, B. 2000, Nature, 403, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, E. D., & Koh, C. A. 2007, Clathrate hydrates of natural gas, 2nd edn. (Florida: CRC Press) [Google Scholar]
- Soh, T. K. M., Thurn, J., Thomas, J. H., & Talghader, J. J. 2007, J. Phys. D: Appl. Phys., 40, 2176 [NASA ADS] [CrossRef] [Google Scholar]
- Takeya, S., Kida, M., Minami, H., et al. 2006, Chem. Eng. Sci., 61, 2670 [CrossRef] [Google Scholar]
- Thompson, S. P., Parker, J. E., Potter, J., et al. 2009, Rev. Sci. Instrum., 80, 75107 [Google Scholar]
- Thompson, S. P., Parker, J. E., Potter, J., et al. 2011, J. Synchrotron Radiat., 18, 637 [CrossRef] [Google Scholar]
- Tse, J. S. 1987, J. Phys., 48, 543 [Google Scholar]
- Udachin, K. A., Ratcliffe, C. I., & Ripmeester, J. A. 2001, J. Phys. D: Appl. Phys., 40, 2176 [Google Scholar]
- Waite, J. H., Combi, M. R., Ip, W.-H., et al. 2006, Science, 311, 1419 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Young, R. A. 1993, in The Rietveld Method, IUCr Book Series (Oxford University Press), 1 [Google Scholar]
- Zhang, X., et al. 2015, Prog. Solid State Chem., 43, 71 [CrossRef] [Google Scholar]
- Zolotov, M. Y. 2007, Geophys. Res. Lett., 34, L23203 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coefficients of the polynomial expression for describing lattice constants of CO2 clathrate hydrates formed in the MS10.5 and MS3.1 solutions.
All Figures
 |
Fig. 1 Rietveld refinements of the MS10.5 solution at a 10 bar CO2 pressure experimental data. From top-bottom: 90 K, 180 K, 245 K. The experimental data are shown in black, the calculated fit in red, and the residuals in grey below. All prominent peaks are labelled where C = clathrate peaks and I = hexagonal ice peaks. The larger residuals for some of the ice peaks are due to poor powder averaging due to the way the ice freezes inside the cell (preferred orientation) and the restricted cell rocking angle used to compensate for this during measurement. |
| In the text | |
 |
Fig. 2 CO2 clathrate dissociation curve (red) for CO2 clathrate hydrates in MS10.5 (circles) and MS3.1 (squares) solutions, compared with the CO2 clathrate dissociation curve for CO2 clathrate hyrates in pure water (Miller 1961, blue curve). |
| In the text | |
 |
Fig. 3 Temperature dependence of the lattice parameters of CO2 clathrate hydrates formed in solutions of MS10.5 and MS3.1 at various pressures. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. “(1)” and “(2)” indicate that the cooling was performed first, followed by heating. For ease of presentation blue symbols represent values obtained during cooling and red values obtained during heating. |
| In the text | |
 |
Fig. 4 Thermal expansion coefficient for CO2 clathrate hydrates formed in solutions of MS10.5 and MS3.1 derived from the polynominal fits to the data in Fig. 3. Black: MS3.1/20 bar; green: MS10.5/5 bar; orange: MS10.5/10 bar. H = Heating and C = Cooling. |
| In the text | |
 |
Fig. 5 Dependence of density on temperature. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. Symbols/colours, and meaning of “(1)” and “(2)”, as per Fig. 3. |
| In the text | |
 |
Fig. 6 Weighted percentage (wt%) curves for solutions. From top to bottom: MS10.5 at 5 bar, MS10.5 at 10 bar and MS3.1 at 20 bar. Triangles: clathrates; circles: Ih ice; squares Ic ice. Colours are as per Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


