EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 600 (April 2017) A&A, 600 (2017) A42 Full HTML
Free Access
Issue
A&A
Volume 600, April 2017
Article Number A42
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201629784
Published online 28 March 2017

© ESO, 2017

1. Introduction

It is well known that rotation is regarded as a very important factor that needs to be considered to investigate the evolution of the massive star (Heger et al. 2000; Meynet & Maeder 2000; Maeder & Meynet 2012; Langer 2012). The centrifugal force changes the stellar shape from sphere to spheroid. The equatorial radius can be about 1.5 times larger than the polar radius according to Roche approximation when the stars approach the break-up rotation (Georgy et al. 2011). As a result of the deformation of the star, the radiative energy flux and the effective temperature vary with the latitude (von Zeipel 1924). Rotation can drive various mixing processes in the stellar interior and rotational mixing is probably the most important effect in massive stars (Meynet et al. 2006, 2010; Mathis & Zahn 2004; Mathis et al. 2004; Zahn 1992). Meridional circulations and shear turbulence dominate rotationally induced mixing in massive stars, and transfer both angular momentum and chemical species (Maeder & Zahn 1998; Talon & Zahn 1997; Maeder 2003). Fresh nitrogen thus appears at the surface of the star and becomes continuously more enriched as function of time during core-hydrogen burning (Maeder & Meynet 2000b).

In a rotating binary system, the joint effect of rotation and tides modifies the shapes of two components from the perfect sphere to triaxial ellipsoids (Landin et al. 2009; Song et al. 2009, 2011; Huang 2004). Eggleton & Kiseleva (1998) have presented the equations governing the quadrupole tensor of a star distorted both by rotation and by the presence of a companion in a possibly eccentric orbit. During the evolution of massive binaries, mass and angular momentum are transferred from the donor to the recipient during Roche lobe overflow (RLOF). Rapid mass transfer can spin up an accreting star to critical rotation (Packet 1981; Langer et al. 2003; Langer 2012). In the present work, we aim to investigate for the first time how the deformation of stars can be induced by both rotation and tide at critical rotation. In particular, we aim to discover how the critical rotation modifies the structure and evolution of the accreting star.

The paper is organized as follows: the potential function which included the combined effects of rotational and tidal distortions, and the structure equations of rotating binaries are given in Sect. 2. Various torques that affect the accreting star are introduced in Sect. 3. In Sect. 4, the result of numerical calculations are described and discussed in detail. And finally in Sect. 5, conclusions are made.

2. The potential function and the rotating stellar structure equations

2.1. The potential function including the rotational and tidal distortions

We consider a close binary consisting of two stars with masses M1 and M2 in a circular orbit with orbital period Porb, let a be the orbital separation. A coordinate system ℛE rotating with the spin angular velocity of the secondary star M2 is introduced (cf. Fig. 1). The mass center of the secondary star M2 is regarded as the origin. It is presumed that the z-axis is perpendicular to the orbital plane, and the positive x-axis penetrates the mass center of the primary star M1. The two stars rotate with angular velocity Ω1 and Ω2 around an axis perpendicular to the orbital plane.

If the coordinates of the point P are the radius r, the polar angular θ, and the azimuthal angle φ, then the total potential in the stellar interior (to first-order approximation) consists of five parts (Kopal 1960, 1974; Endal & Sofia 1976; Landin et al. 2009): the spherical symmetric part of the gravitational potential, ψgrav, the cylindrically symmetric potential due to rotation, ψrot, the potential due to tides ψtide, and the non-symmetric part of the gravitational potential due to the distortion of the star resulting from rotation, ψdis,rot and tides ψdis,tide. This total potential is written as (1)where r and Ω2 are respectively the radius and the spin angular velocity of the rotating star 2, λ = cosϕsinθ, and Pj(λ) are the jth-order Legendre polynomials. ψr and ψt are, respectively, the potential functions which are induced by rotation (ψr = ψrot + ψdis,rot), and tide (ψt = ψtide + ψdis,tide). In Eq. (1) above, the quantities ηj are of particular importance for our research. They can be derived from the Radau′s differential equation with a 4th-order Runge-Kutta method (Press et al. 1992) 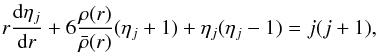(2)where ηj(0) = j−2(j = 2,3,4), ρ(r) is the local density at a distance r from the center, and 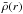is the mean density within inner sphere of radius r.

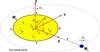thumbnail Fig. 1

Spherical coordinates system associated with the equatorial reference frame ℛE:O,X,Y, Z of an extended body M2; We have rp = (r,θ,ϕ). The spin of M2 is perpendicular to the orbital plane. The dashed line illustrates the orbit of M1.

2.2. The correction factors in the rotating stellar model

Adopting the Kippenhahn and Thomas method, we can define the mean quantities as ⟨ ge ⟩ and 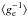. These are the values of effective gravity and its opposite values over the isobar surface (Kippenhahn & Thomas 1970), 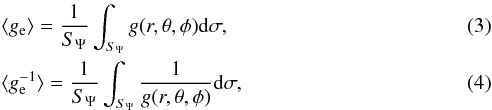where , the mass inside the equipotential surfaces is MΨ and luminosity is LΨ. The equipotential surface has the area of SΨ, and rΨ is the radius of the topological equivalent sphere with the same volume VΨ. We note that the local effective gravity ge has three components which have been derived from Eqs. (A.7)−(A.9). The quantity dσ can be derived from Eq. (A.26).

The correction factors in the rotating stellar model are written as 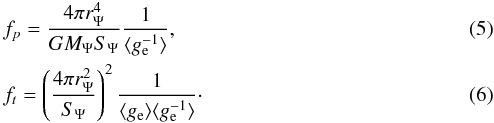In the case of isolated and non-rotating stars, we have used fp = ft = 1. Using the lowest approximation, the correction factors are treated as 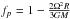and ft = 1 in the traditional rotating model which merely included the hydrodynamical effect of rotation (Kähler 1986).

2.3. The temperature gradients and Solberg-Hoiland criterion for stability

The effect of rotation and tides on the temperature gradient has been included in our computations. They are given by 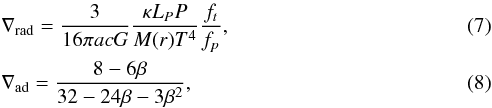where ∇rad and ∇ad are the radiative temperature gradient and the adiabatic gradient, respectively, the quantity 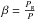is the ratio of gas pressure to the total pressure. A fluid element displaced in a rotating star is also subject to the restoring effect of angular momentum conservation (Kippenhahn & Weigert 1990). This leads to the Solberg-Hoiland criterion for stability, in which 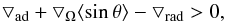(9)with 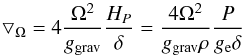(10)for constant angular velocity (Maeder et al. 2008). Here ggrav is the self gravity and Hp designates as the pressure scale height. In one-dimensional stellar model, the quantity ⟨ sinθ ⟩ has a value of ~0.75.

2.4. Expressions of the critical velocity

The high distortion which is induced by rapid rotation and tides has an important impact on the critical velocity. When a rotating star of mass M2, and spin angular velocity Ω2 is in the binary system, the total gravity is the sum of the gravitational, centrifugal, and tidal accelerations: 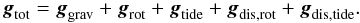(11)The critical angular velocity Ωc,1 corresponds to the angular velocity at equator of the star such that the centrifugal force balances the gravity exactly. The classical critical angular velocity or the Ω − limit (to distinguish it from the ΩΓ limit as defined in Maeder & Meynet 2000) can be given by the equation, 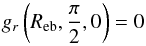(12)where the quantity Reb denotes the equatorial radius at the break-up velocity, the critical velocity is vcrit,1 = RebΩcrit. The quantity Ωcrit is the critical angular velocity.

2.5. The transport equation for angular momentum

The transport of the angular momentum can be treated as a diffusion process (Endal & Sofia 1978; Pinsonneault et al. 1989). The equation can be written as (Heger et al. 2000) (13)where ν is the turbulent viscosity which includes various instabilities (ν = Dconv + Dsem + DDSI + DSHI + DSSI + DES + DGSF), and i is the specific angular momentum of a shell at mass coordinate m. The final term in the above equation (an advection term) accounts for contraction or expansion of the layers at constant mass coordinate.

2.6. The transport of the chemical elements

The diffusion equation of the chemical elements can be given by (Heger et al. 2000) (14)where 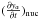is a source term from nuclear reactions, and yα is the relative abundance of αth nuclide. Meridional circulations are the main physical process which can mix the chemical elements in a solid-body rotating star. The diffusion coefficient due to meridional circulations can be used as Ddif ≡ min { dinst,Hv,ES } U2(r). dinst and Hv,ES denote the extent of the instability and the velocity scale height, respectively. We currently use an approximate formula for meridional circulations by Maeder & Zahn (1998), 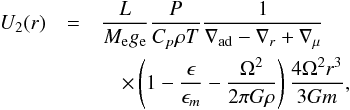(15)where 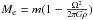, the quantity ϵ = Enuc + Egrav is the total local energy emission, the quantity ϵm is L/m, Cp is the specific heat capacity at constant pressure. The thermodynamic ratio 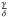used by Maeder & Zahn (1998) is set to unity. This is correct for a perfect gas. We have also approximated the factor 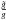of Zahn (1992) by 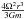. The description of angular momentum transport and rotational mixing in massive stars is given in the references (Maeder & Meynet 2000b; Rieutord 2006; Decressin et al. 2009). The diffusive approach is only a first step for such complex modeling.

3. The spin-up and spin-down mechanisms of the accreting star

The mass-transfer rate from star 1 to star 2 during RLOF is 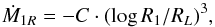(16)where the quantity C is set to 1.0 × 104M⊙/yr. For Roche-lobe radius RL, we use Eggleton’s (1983) analytic expression. During the evolution of massive binaries, mass and angular momentum are transferred from the donor to the recipient during RLOF. Rapid mass transfer can spin up an accreting star to critical rotation (Packet 1981; Langer 2012).

By comparing the radius of the accreting star RA to the minimum distance Rmin of the stream from the centre of the gainer, we determined whether disk accretion, when RA<Rmin or direct impact accretion, when RA>Rmin, occurs. According to Ulrich & Burger (1976), the quantity Rmin can be calculated by Rmin ≈ 0.0425a [q(1 + q)] 1/4. The quantity q is the mass ratio of the companion to the considered star. The variation of spin angular momentum of the accreting star can be expressed as 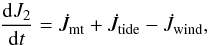(17)where J2 is the spin angular momentum of the accreting star, 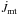is the torque due to mass transfer, 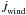is the wind torque, 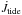is the tide torque. The spinning-up of the gainer due to RLOF is characterized by an enhancement of its rotational angular momentum 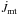, simulating the direct hit scenario which is given by de Mink et al. (2013) as 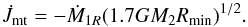(18)The change in the accreting star’s spin angular momentum due to tidal interaction is expressed as (19)where the quantity I2 is the moment of inertia of the star 2, ωorb is the orbital angular velocity and is 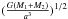, s22 is tidal frequency and is defined as 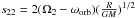, and E2 is a second-order tidal coefficient which depends on the stellar structure (Zahn 1975). It is expressed by 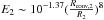(Yoon et al. 2010). The quantity Rconv,2 is the convective-core radius. Tidal interactions spin the star down when Ω2> Ωorb and up Ω2< Ωorb (Song et al. 2013, 2016). The tidal torque in the star with a convective envelop is given by 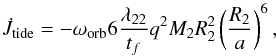(20)where the friction time is 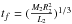, the quantity λ22 is same as that in Zahn (1989). In Eq. (17), the loss of the spin angular momentum through stellar winds is given by 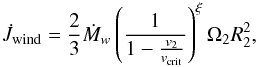(21)where we take ξ = 0.43, Ṁw to be the mass-loss rate by stellar winds and it is given by de Jager et al. (1988). We have adopted the enhanced mass-loss rate of Langer (1998).

thumbnail Fig. 2

Panel a): variation of the force fdis,rot which is derived form the potential function Ψdis,rot versus coordinates θ and ϕ at the surface of accretors in model M1. Panel b): variation of the radial component of tidal forces which is derived from the potential function Ψtide at the surface of accretor versus coordinates θ and ϕ in model M1. Panel c): variation of the gravitational acceleration | geff | at the secondary star’s surface under coordinates θ and ϕ in Roche model. The radius is treated as the constant value. Panel d): variation of the gravitational acceleration | geff | at the secondary star’s surface under coordinates θ and ϕ in model M1. The effective gravitational acceleration can be derived from Eq. (1).

4. Results of numerical calculation

4.1. The depiction of models

We used the most recent stellar evolution code TWIN, originally written by Eggleton (1971, 1972, 1973) and Eggleton et al. (1973). The nuclear reaction rates were from Caughlan & Fowler (1988) and were updated by Pols et al. (1995) and Stancliffe et al. (2005). The procedures used have been more recently updated by Han et al. (1994). The conservative binary-star evolution has been discussed by Nelson & Eggleton (2001). The convection is treated by mixing-length theory (Bohm-Vitense 1958) and a model for convective overshooting is included (Schroder et al. 1997). We have adopted the mass-loss rates of Vink et al. (2001) for massive stars. The two component stars in the binary system were calculated simultaneously. The initial mass of the system components was set at 20 M⊙ and 16 M⊙ with the metallicity of the Sun X = 0.7 and Z = 0.02. We took the mixing length parameter α = l/HP to be 2.0. We note that in this study, we focus on the structure of the accreting star at the critical rotation. We have calculated two different types of model. They are as follows:

  • MKE: the configurations of the two components are assumed tobe spherical. In this case,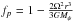, ft = 1, the effect of rotation on stellar structure is only taken into account as a reduction of the effective gravity. This method is referred to as the KE method (Kähler 1986). Moreover, rotational mixing has been included in this model. The initial spin periods Ps,1,2 for two components are taken the values of 1.5 days while the initial orbital period is 2.65 days.

  • M1: the effect of distortions and mixing processes have been included. The accreting star can be spun up during rapid mass transfer. The initial spin periods Ps,1,2 for two components and the initial orbital period are the same as the ones in model MKE.

4.2. Impact of the structure of the rotating star

4.2.1. The distribution of the force derived from the quadrupolar potential Ψdis,rot

In order to investigate the structure of the critically rotating accretor, we have chosen the evolutionary time of t = 6.3323 Myr. The velocity of the secondary star reaches ~0.95vcri,1 due to rapid mass transfer in model M1, and the spin period is 0.729 d. The orbital period is 2.315 d and the mass of the secondary star is 16.153 M⊙. The mass of the primary star is 19.481 M⊙.

Panel a in Fig. 2 shows the variations of the force fdis,rot (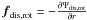) which are derived from the rotational distortion potential Ψdis,rot. The positive value indicates that the force pulls the accretor outward (away from the accretor) whereas the negative value denotes that the force pushes the accretor inward. This force arrives at 1.776 × 102cm/s2 at two polar points E and F (cf. Fig. 1). It goes down to −18.116 cm/s2 and contributes −3.02% to the radial centrifugal force at the point A. The primary minimum has a value of −22.790 cm/s2 at points B and D and dominates a fraction of about −4.14% for the radial centrifugal force. The secondary minimum is −19.438 cm/s2 at the position of point C and contributes −3.39% to the radial centrifugal force. The result implies that the force fdis,rot can lead to a reduction of the self gravity (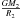) at the two poles, and a increase of the gravity at the equator.

The force fdis,rot can significantly affect the critical velocity and oblateness (cf. Fig. 3) of accretors. The quadrupolar correction due to tides Ψdis,tide is smaller by a factor of ten than the one of rotational distortion Ψdis,rot. Therefore, it may be neglected because of long orbital period of 2.315 d.

thumbnail Fig. 3

Time evolution of the critical velocities for three models. The critical velocity v1,crit is derived from the total potential function Ψ = Ψgrav + Ψrot + Ψtide + Ψdis,rot + Ψdis,tide in model M1(Solid line). The critical velocity v2,crit is derived from potential function Ψ = Ψgrav + Ψrot + Ψtide in model M1 (Dot-dashed line). The critical velocity v3,crit is derived from the potential function Ψr = Ψgrav + Ψrot + Ψdis,rot in model M1 (Dashed line).

4.2.2. The distribution of tidal forces

Panel b shows variations of the radial component of the tidal force which is derived from Ψt = Ψtide + Ψdis,tide at the surface of the secondary star under coordinate θ and ϕ in the model M1. It is shown that the radial component of tidal forces goes up from −2.555 × 103 cm/s2 at two polar points to 5.466 × 102 cm/s2 at the point A. The tidal force can reach 2.59787 × 102 cm/s2 at the point C. The difference in the tidal force between points A and C comes from the term ψtide (j = 3) in Eq. (1) which counteracts the self gravity. Tidal forces greatly shorten the polar radius of accretors, causing the polar radius to become smaller than the equatorial radius. Tides and centrifugal forces pull the accretor outwards at points A and C and cause the equatorial radii to increase. The equatorial radius re1 which confronts the companion star is the biggest one because the tidal force which originates form the term ψtide (j = 3) at point A can strengthen the centrifugal force. The radial component of tidal forces has a value of −2.144 × 102 cm/s2 at the points B and D. For close binaries, the symmetry around the rotation axis is broken by tidal forces and this might produce additional possibilities for internal mixing due to thermal inequalities in the equatorial circle.

These facts show that tidal forces can produce an increase in the effective gravitational acceleration at the two poles. The opposite effect is located at points A and C. At points B and D, tidal forces counteracts with the centrifugal force, leading to a increase in self gravities. Therefore, the shortest equatorial radius is re3.

The critical oblateness (the ratio of the equatorial radius to the polar one) can be increased when the quadrupolar moment is taken into account. The reason is that if ψdis,rot is increased, a test particle at equator will experience a stronger self gravity. The star needs to attain a high spin angular velocity and the new location of test particles is situated closer to the companion star to re-establish a zero-acceleration. At critical rotation, a maximum oblateness can attain a value of 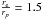according to Roche model. Zahn (2010) shows that the critical flattening can attain 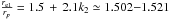in single rotating star when the quadrupolar moment has been included. The quantity k2 is given by 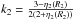and is typically of the order of 10-3−10-2 for main-sequence stars. In our binary model, the critical flattening 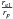can be approximately estimated by the value of 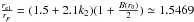at this evolutionary point. Due to tide forces, the critical flattening can exceed the value in the model of single rotating star, produced by Zahn’s model. Furthermore, we find that the critical flattening generally decreases in time due to the star’s nuclear evolution. The reason is that the value of k2 generally decreases in time due to the increasing of the mean molecular weight in the stellar core.

4.2.3. Comparing the effective gravities derived from Roche model and distorted model

The surface gravity | geff | for the accretor M2 which is derived from Roche model in Eq. (A.35) is shown in panel c. The effective gravity | geff |, derived from Eq. (1) is illustrated in panel d. Comparing panel c with d, we find that the effective gravity increases ~48.6% at the two polar points and decreases by ~87.5% at point A for the distorted model. The surface effective gravity can decrease by a factor of ~49.3% at points B and point D. Therefore, the effective gravity has a smaller value at the equator and a higher value at two polar points in distorted models. The main reason for this is that the distribution of the effective gravity depends strongly on the distance between the stellar center and the surface. The deformed model treats the star as the triaxial ellipsoid with different radii, whereas the Roche model treats the stellar surface as a sphere.

4.3. The critical velocity

The time evolution of the critical velocity for three models is displayed in Fig. 3. Comparing v2,crit with v3,crit, we find that tidal forces reduce the critical velocity. The reason for this is that tidal forces can offset the gravity at the points confronting the companion (i.e. at point A). Compared v2,crit with v1,crit, we find that distortions induced by rotation and tide can enhance the critical velocity. This can be understood as the force which is derived from ψdis,rot can help the self gravity to offset the centrifugal force at the point facing towards the companion.

4.4. Two rotational factors fp and ft

Figure 4 shows two correction factors fp and ft as a function of the dimensionless radius R/R⊙ according to the MKE model and to the present method with model M1. We see that fp declines from 1.0 to 0.652 in the MKE model whereas it declines from 1.0 to 0.363 in present method. The factor fp in model M1 is same as that in the MKE model in the central region because stellar core has a high density. We suggest that the MKE model should be applied only to the inner layers where the local density is greater than the mean density.

Compared MKE model with M1, we find that the maximum correction for the factor fp can attain 44.3% at the stellar surface. The result implies that the surface effective gravity ⟨ ge ⟩ in model M1 has a lower value in distorted model than the one in MKE. The main reason is that great distortions can enhance the centrifugal force. The contribution of this effect to the effective gravity can reach the first order effect ~20% (cf. Fig. 4) and can not be neglected. Distortions induced by rotation and tides can contribute a significant fractional importance to the effective gravity in the outer stellar layers.

The small factor fp in model M1 implies that the accreting star will have a bigger radius and that matter may be evaded easily on the surface. Moreover, the lower factor fp can cause the star to shift dramatically towards low temperature and low luminosity due to gravity darkening. The dynamical timescale may be extended because of larger effective radii and cooler surface temperatures. It is more difficult for a rapidly rotating star to attain hydrostatic equilibrium.

Also, we can see that ft keeps a constant value of 1.0 through the whole star in the MKE method whereas it reduces from 1.0 to 0.585 in the present method. It is illustrated that the maximum correction for the factor ft reaches 41.5% at the stellar surface. The ratio of ft to fp in the MKE model is smaller than the one in M1 below stellar surface.

thumbnail Fig. 4

Correction factors fp, ft, and, ft/fp versus the dimensionless radius R/R⊙ according to model MKE (blue curve) and to model M1 (pink curves).

4.5. The expansion of convective zones

It is shown in panel a of Fig. 5 that various temperature gradients are functions of the dimensionless radius R2/R⊙. Without rotation, there is a thin outer convective zone which is close to the stellar surface. It extends from 6.74 R⊙ to 6.80R⊙ – only 0.86% of the radius – and contains a very small fraction of the total stellar mass (~5.0 × 10-7). With a ratio 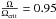in model M1, convective zones of rapid rotating accretors extend according to Solberg-Hoiland criterion. The outer convective zones extend from 6.641 R⊙ to 6.937 R⊙ in model MKE whereas they extend from 6.590 R⊙ to 6.937 R⊙ in the distorted model M1. The outer convective layer is deeper in model M1 than the one in model MKE. The reason is that the quantity 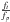in model M1 has a high value in the outer envelope. Therefore, great deformations that are induced by rotation and tides are in favor of convective motion.

thumbnail Fig. 5

Left panel: temperature gradients ∇r, ∇ad, and ∇r−∇Ω as function of the dimensionless radius R/R⊙ according to the MKE model (blue curves) and the M1 model (pink curves) below the stellar surface. The black line denotes the radiative temperature gradient ∇r in the model without rotation. The green line denotes the temperature gradients ∇ad. The red curve indicates the quantity ∇Ω. Right panel: various temperature gradients located at the border of the convective core. The point where black lines cut green lines implies the border of convective core in non-rotating model according to the Schwarzschild criterion. The point where blue lines cut green lines indicates the border of convective core in rotating model according to the Schwarzschild criterion.

thumbnail Fig. 6

Left panel: variations of the energy generation by nuclear reactions as a function of the Lagrangian mass at four different evolution points at critical rotation. The recipient approaches the critical rotation at the time of ~6.33 Myr. Right panel: variation of internal distribution of hydrogen mass fraction as a function of the Lagrangian mass at four different evolution points.

It is shown in panel b that rapidly rotating accretors have a bigger convective core of ~1.338 R⊙ according to the Schwarzschild criterion compared with the non-rotational model with a convective core of 1.331 R⊙. If the Solberg-Hoiland criterion for stability is adopted, rotating accretors will have a small convective core of 1.29 R⊙. Therefore, the Solberg-Hoiland criterion tends to reduce the central convective region and contribute to a low stellar luminosity.

4.6. The energy generation and hydrogen profiles

Variations of the energy generation by nuclear reactions as a function of the Lagrangian mass at four different evolutionary points are shown in left panel of Fig. 6. We find that the region and the intensity of the energy generation through nuclear reactions decrease with the evolution. The reason for this is that centrifugal forces compensate most of the gravity; pressure and temperature in the central parts of accretor are smaller, consequently the energy production rate is also decreasing. (cf. panel b in Fig. 6).

Internal distribution of hydrogen mass fraction of the Lagrangian mass in the model M1 is shown in right panel of Fig. 6. There is a distinct boundary between the convective core and the radiative envelope before mass transfer (at the time of t = 3.5458 Myr). At the time of ~6.320 Myr, the accreting star approaches the critical rotation due to RLOF. From then on, the gradient of internal distribution of hydrogen become smaller and smaller. The reason fo this is that the amplitude of the radial component of the meridional velocity U which scales with Ω is the main driving mechanism for mixing of chemical elements. The result implies that rotationally induced chemical mixing is more efficient and occurs faster than the build-up of chemical gradients at the cutting edge of nuclear fusion (Maeder 1987). Moreover, more massive fuel hydrogen is transported from the outer envelope to the core and these physical processes may prolong the time the accretor spends on the main sequence.

5. Conclusions and summary

The configuration of accretors is one of triaxial ellipsoids which are deformed by tides. The symmetry around the rotation axis is broken by tides and this might produce additional possibilities for internal processes to enhance mixing due to thermal inequalities in the equatorial circle.

The self gravity is balanced by the combined effect of centrifugal forces, rotational distortions, and tidal forces at equator. Therefore, the critical velocity is reduced due to tidal force. The force which is derived from the potential Ψdis,rot can help the self gravity to offset the centrifugal force at the equator. We can derive a higher critical velocity from the distorted model which includes rotational distortion Ψdis,rot.

The mean effective gravity ⟨ ge ⟩ can be reduced dramatically in the distorted model due to a small factor fp. The ratio of ft to fp is bigger in model M1 than that in the MKE model. The star appears a deeper convective zone below stellar surface. The accreting star has a bigger convective core according to the Schwarzschild criterion but it will allow a smaller convective core according to the Solberg-Hoiland criterion.

The critical flattening (defined as the ratio between the equatorial and polar radii) can be increased to 1.5469 and exceed the 1.5 value of Roche model as a result of considering the quadrupolar moment and tidal forces.

The gradient of hydrogen profile becomes smaller and smaller due to rapid meridional circulation and the accretor is mixed efficiently. Both the rate of energy generations and convective core decrease due to the lower temperature produced by the combined effect of rotation and tide. The lifetime of the accreting star during the main sequence can be extended due to efficient mixing and lower rate of energy generations.

Acknowledgments

We thank an anonymous referee. Also, we are very grateful to Professor Peter P. Eggleton for sharing his binary evolution code. This work was sponsored by the National Natural Science Foundation of China (Grant Nos. 11463002 and 11373020), the Open Foundation of key Laboratory for the Structure and evolution of Celestial Objects, Chinese Academy of Science (Grant Nos. OP201405, OP201404(B615015)), the Science Foundation of Jimei University (Grant No. C613030), and Science and Technology Foundation of Guizhou Province (Grant LKK[2013] No. 20).

References

  1. Bohm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  2. Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
  3. Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
  5. de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & Koter, A. D. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
  6. Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
  7. Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
  8. Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
  9. Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
  10. Eggleton, P. P., & Kiseleva, L. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]
  11. Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] [Google Scholar]
  12. Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
  13. Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
  14. Georgy, C., Meynet, G., Maeder, A., et al. 2011, A&A, 527, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
  16. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  17. Huang, R. Q. 2004, A&A, 422, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Huang, R. Q., & Taam, R. E. 1990, A&A, 236, 107 [NASA ADS] [Google Scholar]
  19. Kähler, H. 1986, A&A, 157, 329 [NASA ADS] [Google Scholar]
  20. Kippenhahn, R., & Thomas, H. C. 1970, Stellar Rotation, ed. A. Slettebak (Gordon and Breach Science Publishers), Proc. IAU Colloq., 4, 20 [Google Scholar]
  21. Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin, Heidelberg, New York: Springer-Verlag), Astron. Astrophys. Lib., 468 [Google Scholar]
  22. Kopal, Z. 1959, Close Binary Systems (London, UK: Chapman & Hall) [Google Scholar]
  23. Kopal, Z. 1960, Figures of Equilibrium of celestial bodies (The University of Wisconsin Press) [Google Scholar]
  24. Kopal, Z. 1974, Ap&SS, 27, 389 [NASA ADS] [CrossRef] [Google Scholar]
  25. Landin, N. R., Mendes, L. T. S., & Vaz, L. P. R. 2009, A&A, 494, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
  27. Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
  28. Langer, N., Wellstein, S., & Petrovic, J. 2003, A Massive Star Odyssey: From Main Sequence to Supernova, Proc. IAU Symp., 212, 275 [NASA ADS] [Google Scholar]
  29. Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143M [NASA ADS] [CrossRef] [Google Scholar]
  33. Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
  34. Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
  35. Maeder, A., Georgy, C., & Meynet, G. 2008, A&A, 479, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
  37. Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, A623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
  40. Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
  41. Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarqure, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z., 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  43. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran 77: The art of Scientific Computing (Cambridge University Press) [Google Scholar]
  44. Rieutord, M. 2006, A&A, 451, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Schroder, K. P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 [NASA ADS] [CrossRef] [Google Scholar]
  46. Song, H. F., Zhong, Z., & Lu, Y. 2009, A&A, 504,161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Song, H. F., Lu, Y., & Wang, J. Z. 2011, PASJ, 63, 835 [NASA ADS] [Google Scholar]
  48. Song, H. F., Maeder, A., Meynet, G., et al. 2013, A&A, 556, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Song, H. F., Meynet, G., Maeder, A., Ekström, S., & Eggenberger, P. 2016, A&A, 585, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Stancliffe, R. J. 2005, Ph.D. Thesis, University of Cambridge [Google Scholar]
  51. Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
  52. Ulrich, R. K., & Burger, H. L. 1976, ApJ, 206, 509 [NASA ADS] [CrossRef] [Google Scholar]
  53. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. von Zeipel, H., 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
  55. Yoon, S. C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
  57. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
  58. Zahn, J.-P., & Bouchet, L. 1989, A&A, 223, 112 [Google Scholar]

Appendix A

Appendix A.1 The potential including rotational and tidal distortions and the gravitational acceleration

At the position P(r,θ,ϕ), the total potential for the combined effect of rotation and tide can be expressed in Cartesian spherical coordinate systems. It is given by (Landin et al. 2009; Song et al. 2009) (A.1)The equipotential surface of the distorted star can be described by (Landin et al. 2009) 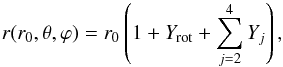(A.2)where Yrot is a measure of the deviation from sphericity caused by rotation and given by 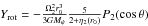. The quantity Yj is a measure of the deviation from sphericity caused by the tide and given by 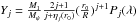. r0 is the radius of the equipotential surface at the angles (θ0,ϕ0), defined such that 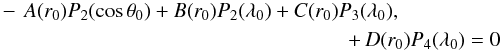(A.3)where the quantities A(r0), B(r0), C(r0), and D(r0) are defined by 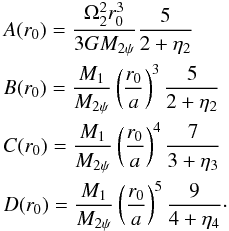(A.4)The equipotential surface of the stars can be described as (A.5)By integrating Eq. (26) from 0 to r(r0,θ,ϕ), we obtain that the volume Vψ of the topologically equivalent sphere with the radius rψ, (A.6)Differenting the potential function, we can derive three components of the effective gravitational acceleration gr, gθ, and, gϕ. They are where where

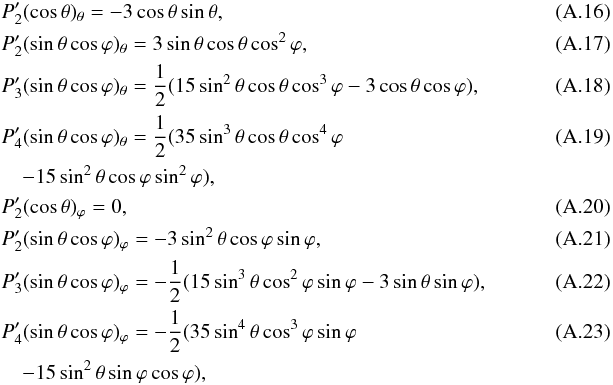The local effective gravity is written as (A.24)

Appendix A.2 The expression of the surface element dσ on an equipotential of a rotating star

On the surface of the distorted star, the normal to the surface does not coincide with the direction of the vector radius. There is an angle ε between the directions of r and of −geff, 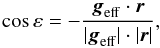(A.25)Therefore, the surface element dσ can be expressed as 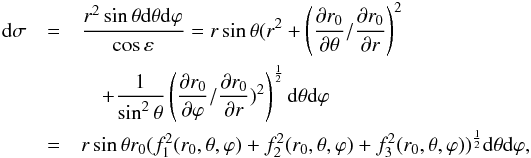(A.26)where

Appendix A.3 Roche potential and the gravitational acceleration

Interactions in a closed binary system are generally treated in the framework of the Roche model (Kopal 1959). We adopt the same coordinate system as the deform model. The gravitational potential which is experienced at the position P(x,y,z) is the sum of the two point mass potential and the rotational potential (Huang & Taam 1990), namely, (A.30)where a be their mutual separation. The coordinates of the position P(x,y,z) can be expressed in Cartesian spherical coordinate systems. Finally, we obtain 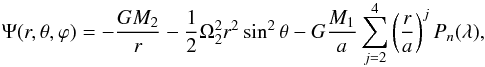(A.31)where χ is the angle between a and r. Three components of the gravitational acceleration gr, gθ, and gϕ take the forms of The local effective gravity is written as (A.35)The potential of the primary star with respect to the center of the primary star can be deduced by substituting M1 for M2. The corresponding effective gravity can be derived with the same method. The stellar radii of two components are treated as the constant value in the Roche model. The radius is not treated as the constant value in the distorted model M1.

All Figures

thumbnail Fig. 1

Spherical coordinates system associated with the equatorial reference frame ℛE:O,X,Y, Z of an extended body M2; We have rp = (r,θ,ϕ). The spin of M2 is perpendicular to the orbital plane. The dashed line illustrates the orbit of M1.
In the text
thumbnail Fig. 2

Panel a): variation of the force fdis,rot which is derived form the potential function Ψdis,rot versus coordinates θ and ϕ at the surface of accretors in model M1. Panel b): variation of the radial component of tidal forces which is derived from the potential function Ψtide at the surface of accretor versus coordinates θ and ϕ in model M1. Panel c): variation of the gravitational acceleration | geff | at the secondary star’s surface under coordinates θ and ϕ in Roche model. The radius is treated as the constant value. Panel d): variation of the gravitational acceleration | geff | at the secondary star’s surface under coordinates θ and ϕ in model M1. The effective gravitational acceleration can be derived from Eq. (1).
In the text
thumbnail Fig. 3

Time evolution of the critical velocities for three models. The critical velocity v1,crit is derived from the total potential function Ψ = Ψgrav + Ψrot + Ψtide + Ψdis,rot + Ψdis,tide in model M1(Solid line). The critical velocity v2,crit is derived from potential function Ψ = Ψgrav + Ψrot + Ψtide in model M1 (Dot-dashed line). The critical velocity v3,crit is derived from the potential function Ψr = Ψgrav + Ψrot + Ψdis,rot in model M1 (Dashed line).

In the text
thumbnail Fig. 4

Correction factors fp, ft, and, ft/fp versus the dimensionless radius R/R⊙ according to model MKE (blue curve) and to model M1 (pink curves).
In the text
thumbnail Fig. 5

Left panel: temperature gradients ∇r, ∇ad, and ∇r−∇Ω as function of the dimensionless radius R/R⊙ according to the MKE model (blue curves) and the M1 model (pink curves) below the stellar surface. The black line denotes the radiative temperature gradient ∇r in the model without rotation. The green line denotes the temperature gradients ∇ad. The red curve indicates the quantity ∇Ω. Right panel: various temperature gradients located at the border of the convective core. The point where black lines cut green lines implies the border of convective core in non-rotating model according to the Schwarzschild criterion. The point where blue lines cut green lines indicates the border of convective core in rotating model according to the Schwarzschild criterion.

In the text
thumbnail Fig. 6

Left panel: variations of the energy generation by nuclear reactions as a function of the Lagrangian mass at four different evolution points at critical rotation. The recipient approaches the critical rotation at the time of ~6.33 Myr. Right panel: variation of internal distribution of hydrogen mass fraction as a function of the Lagrangian mass at four different evolution points.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.