| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201628234 | |
| Published online | 22 March 2017 | |
SOLAR/SOLSPEC mission on ISS: In-flight performance for SSI measurements in the UV⋆
1 Royal Belgian Institute for Space Aeronomy, 3 Ringlaan, 1180 Brussels, Belgium
e-mail: david.bolsee@aeronomie.be
2 LATMOS/IPSL, UVSQ Université Paris-Saclay, UPMC Univ. Paris 06, CNRS, 78280 Guyancourt, France
3 Belgian User Support and Operations Centre (B. USOC), 1180 Brussels, Belgium
4 Space Applications Services, 1932 Zaventem, Belgium
Received: 2 February 2016
Accepted: 24 November 2016
Context. The SOLar SPECtrum (SOLSPEC) experiment is part of the Solar Monitoring Observatory (SOLAR) payload, and has been externally mounted on the Columbus module of the International Space Station (ISS) since 2008. SOLAR/SOLSPEC combines three absolutely calibrated double monochromators with concave gratings for measuring the solar spectral irradiance (SSI) from 166 nm to 3088 nm. This physical quantity is a key input for studies of climatology, planetary atmospheres, and solar physics.
Aims. A general description of the instrument is given, including in-flight operations and performance of the ultraviolet (UV) channel from 175 nm to 340 nm.
Methods. We developed a range of processing and correction methods, which are described in detail. For example, methods for correcting thermal behavior effects, instrument linearity, and especially the accuracy of the wavelength and absolute radiometric scales have been validated by modeling the standard uncertainties.
Results. The deliverable is a quiet Sun UV reference solar spectrum as measured by SOLAR/SOLSPEC during the minimum of solar activity prior to cycle 24. Comparisons with other instruments measuring SSI are also presented.
Key words: Sun: general / Sun: UV radiation / instrumentation: detectors / techniques: spectroscopic / space vehicles: instruments
The quiet Sun UV spectrum (FITS file) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/600/A21
© ESO, 2017
1. Introduction
Solar irradiance, which exhibits a wide spectrum of temporal variability (Ermolli et al. 2013) owing to internal physical processes, is the primary source of energy for planetary atmospheres. As such, the spectral distribution of the solar irradiance is related to the processes taking place within the different layers of the Sun’s atmosphere. The spectral variability in the UV is much higher, at these shorter wavelengths, than the variability of the total solar irradiance (TSI). The solar spectral irradiance (SSI) and its variability are key inputs to models simulating atmospheric photochemical processes and the Earth’s climate system through complex interactions (Haigh et al. 2010; Gray et al. 2010). For instance, the middle atmosphere is very sensitive to the incoming solar UV irradiance, as the absorption by ozone is the primary source of heat and the photochemistry of ozone is highly dependent on solar UV irradiance variability (Shapiro et al. 2013). These solar-driven perturbations of the middle atmosphere can then propagate downwards into the lower atmosphere and affect the climate at the surface (Rozanov et al. 2002). It is therefore important to characterize as accurately as possible the SSI and its variability in the UV domain.
The SSI can be measured using absolutely calibrated spectroradiometers. These measurements must be made from a position at the top of atmosphere (TOA), typically from instruments mounted on rockets or satellites, to avoid extinction by the atmosphere. Accurate SSI measurements from space are challenging owing to the severe environment (cosmic rays, deep UV radiation, outgassing) that affect the operational conditions of the electronics and optical components (BenMoussa et al. 2013) and induce a degradation of the instrument’s absolute response. Consequently, absolute radiometric scales for SSI measurements are difficult to maintain over time in flight, as the degradation of the instrument responsivity must be accurately tracked and corrected for.
One strategy for cross calibration is to make simultaneous measurements from orbit with different instruments which are then referenced back to different laboratory standards. Another strategy is to develop robust instruments containing built-in relative calibration units with redundant optical elements. Ultraviolet SSI measurements from space had important contributions from instruments such as the Solar Backscatter UltraViolet (SBUV) radiometer flown on weather satellites (Markert 1975); the Solar Ultraviolet Spectral Irradiance Monitor (SUSIM; Brueckner et al. 1993); and the SOLar STellar Irradiance Comparison Experiment (SOLSTICE; Rottman et al. 2001) experiments on board the Upper Atmosphere Research Satellite (UARS), which made SSI measurements from Lyman α (Ly-α) to 400 nm during solar cycle 22. Since 2003 measurements have been made by the new SOLSTICE instrument and the Solar Irradiance Monitor (SIM) on board the Solar Radiation and Climate Experiment (SORCE) platform (Rottman 2005), and also by the SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY (SCIAMACHY) instrument (Skupin et al. 2005).
SOLSPEC (SOLar SPECtrum), part of the Solar Monitoring Observatory (SOLAR) payload on board of the International Space Station (ISS), is an important instrument for the continuation of SSI measurements. The main features of SOLSPEC are its three independent channels: ultraviolet (UV), visible (VIS) and infrared (IR), each of which is equipped with internal lamps to maintain the absolute radiometric scale of the spectrometers and to chart variations in response over time. These features have been an integral part of SOLSPEC since the project was initiated in the 1970s by the Centre National de la Recherche Scientifique (CNRS) in France (now the LATMOS-CNRS laboratory) and supervised by the Centre National d’Études Spatiales (CNES), also in France. The Koninklijk Belgisch Instituut voor Ruimte-Aeronomie - Institut royal d’Aéronomie Spatiale de Belgique (BIRA-IASB) in Belgium has contributed significantly to the development of the instrument, particularly the ISS-SOLAR version. The Heidelberg Observatory in Landessternwarte, Germany also made a large contribution to the first version of the instrument.
The SOLSPEC instrument was flown on several space missions in the 1980s and 1990s (Thuillier et al. 1981, 1997, 2003) and provided the well-known composite ATLAS 1 and 3 spectra (Thuillier et al. 2004), where ATLAS is an acronym for ATmospheric Laboratory for Applications and Science on board the Space Shuttle). From (Ly-α) to 200 nm, the data from SUSIM and SOLSTICE on UARS were used for these reference spectra. Between 200 nm and 400 nm, it is a composite of ATLAS-SSBUV (Shuttle Solar Backscatter Ultraviolet Spectrometer), SUSIM (Solar Ultraviolet Spectral Irradiance Monitor) and SOLSPEC data. From 400 nm to 850 nm, data from ATLAS-SOLSPEC were used, and from 800 nm to 2400 nm the spectra were generated from EURECA-SOSP (EUropean REtrieval CArrier – SOlar SPectrum instrument) data. The ATLAS 1 spectrum was released on 29 March 1992, followed by the ATLAS 3 spectrum on 11 November 1994. Both spectra are calibrated to a reference blackbody at the Observatory of Heidelberg, which is itself calibrated to the thermometric reference scale of the Physikalisch-Technische Bundesanstalt (PTB) in Germany, and to the spectral irradiance standard from the National Institute of Standards and Technology (NIST) in the USA.
After flying on the Space Shuttle, SOLSPEC was selected again in December 1997 as part of the SOLAR experiment by the ESA Microgravity and Space Station Utilization Department for a three-year mission intended for SSI measurements on board the International Space Station1. The SOLAR mission began on 7 February 2008 and, after two extensions, is due to finish in February 2017.
The new version of SOLSPEC on board SOLAR is named SOLAR/SOLSPEC. It can measure the SSI with high accuracy over a calibrated spectral range covering 96% of the (TSI) spectrum, from 166 nm to 3088 nm. Two complementary instruments were integrated into the SOLAR payload, the Solar Auto Calibrating EUV/UV Sunphotometer (SolACES) and the SOlar Variable and Irradiance Monitor (SOVIM). SolACES measures the solar Extreme UltraViolet (EUV) irradiance from 16 nm to 150 nm (Schmidtke et al. 2006). Radiometric calibration is maintained using current ionization chambers as primary detector standards. SOVIM, which operated for only 6 months, was a radiometer of high precision and stability for measuring the TSI and SSI at three wavelengths (Mekaoui 2010). The SOLAR payload tracks the position of the Sun using the Coarse Pointing Device (CPD), developed by Alenia Aerospace in Italy (Acquaroli & Onorati 2005).
In Sect. 2 of this manuscript, we present the general design of the SOLAR/SOLSPEC instrument, and focus on the UV channel. In Sect. 3 we describe the most important aspects of the SOLAR mission, including SOLSPEC operations, data handling and storage. In Sect. 4 the SOLAR/SOLSPEC measurement method is described, as are the parameters and variables utilized in the SSI and the corresponding uncertainty calculations. In Sect. 5, the quiet Sun reference SOLAR/SOLSPEC UV spectrum is presented and compared with other instruments and models. In Sect. 6 an overview of the first seven years of the SOLAR/SOLSPEC mission is presented, together with a synthesis of the results and future work prospects.
2. Instrument description
The SOLSPEC that had flown on the ATLAS mission was selected for reflight as part of the SOLAR experiment. While the same key hardware (the spectrometers, scanning mechanism, main shutters and filter wheels) was retained, the instrument was refurbished and several changes were made. For integration onto the CPD, the mechanical interface was modified to attach to either side of a central plate. The software and all the electronics except the photomultiplier tube (PMT) detectors were replaced, as necessitated by the longer duration of the mission. Mechanical shutters and quartz plates were added to shield against short wavelength radiation and contaminants around ISS to limit the degradation of optical components. To accurately monitor and maintain the absolute radiometric and wavelength response during the long-term mission, the internal calibration lamp unit was fully redesigned and improved (Thuillier et al. 2009). The general design of the optics was maintained and the whole instrument based on three independent double spectroradiometers, and we were able to improve the optical alignment of the spectrometers relative to ATLAS 3. Each channel is dedicated to a specific spectral range: UV (155 nm to 371 nm), VIS (285 nm to 908 nm) and IR (646 nm to 3088 nm). This paper is primarily focused on the UV channel of SOLAR/SOLSPEC; it is described in more detail below. A schematic of the spectrometer channels is shown in Fig. 1 and the technical details of the SOLSPEC UV channel opto-mechanical and detection characteristics are given in Table 1.
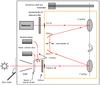 |
Fig. 1 The opto-mechanical configuration of one channel of the SOLAR/SOLSPEC instrument for the SOLAR mission. For the UV channel, only the deuterium and hollow cathode lamps are considered. |
Summary of SOLSPEC UV channel.
The chain of the new SOLAR/SOLSPEC configuration starts with the main shutter located at the top of the instrument. It is only opened for solar irradiance measurements, lasting typically less than 15 min, to avoid contamination. The shutter is followed by a black anodized baffle to limit the field of view (FOV). Below this, there is a four-position wheel. Two of the positions contain quartz plates (Suprasil 311 from Heraeus GmbH, Germany, diameter 25 mm, thickness 1 mm) in addition to the open/close positions (internal shutter). The plates and shutters act as shielding against short wavelength radiation and contaminants from the rest of the ISS. The first active optical surface in front of the spectrometer is designed for spectral irradiance measurements because of its diffusive properties. This is a combination of two frosted Suprasil 311 plates working as a diffuser and covering the whole FOV. The diffuser is illuminated either by sunlight during SSI measurements, or by internal lamps which permit the absolute radiometric and wavelength calibrations to be checked and mantained. Three lamps are coupled to the UV channel: first a hollow cathode (HC) lamp filled with Argon at a 5 mbar pressure and a brass cathode, designed by the LATMOS for providing spectral emission lines for monitoring the spectral response. The illumination of the diffuser by the HC lamp is performed using a fused-silica condenser and an optical fibre. In addition, the two deuterium lamps (Key & Preston 1980) were used as relative spectral irradiance standards to calibrate the radiometric response (Prinz et al. 1996; Floyd et al. 1996). These lamps were originally designed for the SUSIM experiment by Cathodeon Ltd, UK, but instead a new batch of lamps was produced and delivered for SOLAR/SOLSPEC. These lamps (named D1 and D2) have an integrated MgF2 lens for collimation, replacing the front window. Their collimated beam is collected by a concave mirror Al + MgF2 which is coated to ensure the diffuser is well illuminated (Thuillier et al. 2009; Bolsée 2012).
 |
Fig. 2 Schematics of the diffraction grating scanning mechanism. |
A field lens followed by an actuator is inserted between the exit slit and the detector to condense, homogenize and attenuate (when required) the signal reaching the detector. The actuator is mounted on a frosted Suprasil 311 plate. For SOLAR/SOLSPEC, the PMT detector is used in photon counting mode together with a pulse amplifier discriminator (PAD). This detector unit is a heritage from the previously flown SOLSPEC instrument. A pulse associated with an incoming photon is converted to a logical level at the output of the PMT using a CMOS with open collector output. Two acquisition modes are allowed by the software: accumulation of counts during a constant integration time, or a free integration time for reaching a predefined threshold (104 counts, for example) for improved counting statistics.
The diffraction grating scanning mechanism is made up of three parts, as shown in Fig. 2:
-
The stepper motor (with 48 steps per rotation) is connected to areducer gear (factor 33) and turns a high precision screwmechanism on a mechanical shaft.
-
This drives a linear translation stage (where one full rotation of the motor axis corresponds to a translation of 3 mm of the carrier).
-
This stage is then connected to the end of a camshaft, converting the translation to a (sine corrected) rotation of the gratings. These gratings are tangentially mounted on a main mechanical shaft whose axis of rotation is normal to the camshaft. As the mechanical shaft rotates, the gratings in all three channels rotate too, simultaneously scanning the spectral domains.
The relationship between a given motor position and the corresponding wavelength at the detector has been established for SOLAR/SOLSPEC. This relationship requires a zero position reset procedure for the position scale, which is achieved using an optical encoder mounted on the motor and an opto-coupler on the stage. The reproducibility is within one motor step. The spectral wavelength range of the UV channel extends from the Suprasil cut-off at around 155 nm, to 371 nm; however, the absolute calibration starts at 166 nm. There is no second-order filter required for the UV channel. Potential for second-order contamination arises for wavelengths above 310 nm (double the Suprasil cut-off). Ground-based investigations using deuterium lamps during vacuum tests allowed us to make estimations of the relative level of the second order for solar measurements. Results showed that the contribution was limited to 0.027%, 0.15%, and 0.4% respectively at 350 nm, 360 nm and 370 nm. Thus, for solar spectra limited to 340 nm, there is no measurable impact of second order, even without the use of a high pass filter. The SOLAR/SOLSPEC instrument was integrated, tested, and fully radiometrically characterized at BIRA-IASB between 2005 and 2007. This characterization is included in the measurement equation (Eq. (1)) for SSI calculations and uncertainty estimation. In parallel, environmental tests (electromagnetic compatibility, vibration, thermal vacuum) were performed at ESTEC in The Netherlands and Intespace in France. The absolute calibration of SOLAR/SOLSPEC was carried out at PTB in June 2007, before being delivered to ESA in June 2007 and NASA in September 2007 respectively. The last ground based measurements were performed at the NASA Kennedy Space Center (KSC) in September 2007 before SOLSPEC was placed into storage until launch.
3. Solar mission
The European Columbus science laboratory and its SOLAR payload were launched by the Space Shuttle Atlantis (STS-122) on 7 February 2008. The solar payload was installed on the Zenith external platform of Columbus on ISS as shown in Fig. 3.
 |
Fig. 3 SOLSPEC mounted on external COLUMBUS platform (Credit: NASA). |
Successful functional tests for SOLAR/SOLSPEC were followed by a series of internal lamp measurements. The first solar measurements started on 5 April 2008, followed by a commissioning phase on 8 and 9 April. For nominal ISS attitudes, the SOLAR platform is able to track the Sun up to 20 min per ISS orbit, for β−angles (the angle between the Sun vector and the ISS orbital plane) between −24°and +24°. The resulting observation windows, known as Sun visibility windows (SVW), occur on 12 days per month on average.
To manage these observations, the acquisition electronics of SOLAR/SOLSPEC uses a table of 256 parameters, loaded in the PROM2 of the instrument. For the UV spectrometer, this table contains predefined scan acquisition (spectral range, sampling) and automation (filter wheel positions, scanning mechanism, shutters) parameters. Predefined values were set before launch, based on functional tests and radiometric characterization, allowing us to optimize the instrument sensitivity level for solar irradiance measurements. The flight software was developed in such a way that different basic modes of acquisition are loaded into memory, including solar measurements, monitoring of the absolute responsivity using internal lamps, or checking the angular response of the instrument (by raster scanning the FOV through the Sun). Special measurements can be performed for the maintenance of the instrument (to measure filter transmissions for example) or to modify the scanning parameters such as spectral range, sampling, or integration time to improve the signal-to-noise Ratio (S/N). In the latter case, new commands can be sent upon request for temporary modification of the parameter table. For nominal or special operations, the following procedure is implemented: operators at the Belgian User Support and Operations Centre (B. USOC), part of the ground segment of ISS propose a preliminary schedule of activities based on the experiment’s scientific requirements and a set of rules and constraints defined by the SOLAR/SOLSPEC team. A typical measurement day for SOLAR/SOLSPEC consists of one solar observation plus three calibration observations with the three types of lamps. Once discussed and agreed, the science activity plan is inserted into Predictor, the B. USOC planning tool, which verifies that the SOLAR/SOLSPEC rules and constraints are properly followed. The constraints are as follows:
-
no SOLAR/SOLSPEC measurements can be conducted whileflying over the South Atlantic Anomaly (SAA) sincephotomultipliers on UV and VIS channels are perturbed byparticles over this region;
-
no measurements can be executed during ISS thruster events or dockings;
-
there are angular offsets between the optical axis of the sun sensor on the CPD and the two axes of SOLAR/SOLSPEC and SOLACE, so the applied offset must be adapted before and after each measurement.
The activities can be conducted either by direct commands to the instrument, or by command schedules (CSs), stored and executed by the SOLAR Control Unit. This last method is the preferred option, as the satellite coverage is not always sufficient for direct commanding, and therefore one of the constraints is removed from the schedule. The SOLAR/SOLSPEC raw data are stored initially at the Columbus Control Centre (COL-CC) on the Payload Data Centre (PDC). These data are streamed by Yet Another Mission Control System (YAMCS; described in Sela et al. 2012) to B. USOC servers.
4. Data processing
In this section, we describe the general processing of the SOLAR/SOLSPEC data. For each stepper motor position, the raw detector signal in counts (cts) is recorded for a given integration time. The data processing pipeline converts and calibrates this signal into a physical quantity i.e. the spectral irradiance of the Sun as a function of the wavelength. This is described by the measurement equation, which includes all the quantities contributing to the calculation of the SSI. All normalizations performed during this conversion are discussed below.
For the UV channel of SOLAR/SOLSPEC, the spectral irradiance of the Sun Esol(λ,t) as a function of time and wavelength is given by the equation: ![\begin{eqnarray} \label{eq-Measurement equation} E_{\rm sol}\left(\lambda,t\right) &=& \left(\frac{\epsilon(t)\times R(\lambda)}{{\rm Deg}(\lambda,t)\times \left(1-\frac{\Delta T\times \alpha_{\rm T}(\lambda)}{100}\right)}\right) \nonumber \\ && \times \left[\left(S_{\rm net}(\lambda)-\frac{\langle DC\rangle }{\Delta t_{DC}}\right)+C_{\lambda}(\lambda)+C_{\Delta\lambda}(\lambda)\right]. \end{eqnarray}](/articles/aa/full_html/2017/04/aa28234-16/aa28234-16-eq18.png) (1)The variables and parameters are as follows:
(1)The variables and parameters are as follows:
-
Snet(λ) is the linearized signal (cts s-1) obtained after the nonlinearity correction, for which the expression is given by Eq. (2);
-
⟨ DC ⟩ is the average dark current signal, individual values being measured with the main shutter closed for an integration time of ΔtDC (in seconds). Generally, 60 dark current measurements are performed before and after each scan.
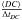 is the mean DC in (cts s-1);
is the mean DC in (cts s-1); -
R(λ) is the absolute response of the UV channel in mW m-2 nm-1 cts-1 s, converting the electronic net signal (DC subtracted, corrected for nonlinearity) into spectral irradiance. The determination of R(λ) is detailed in Sect. 4.4;
-
ϵ(t) is the correction factor due to the eccentricity of the terrestrial orbit. This factor is equal to
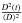 , where ⟨ D ⟩ is one astronomical unit (1 AU = 1.495 × 108 km) and D(t) is the Sun-Earth distance (in km) at a given time t;
, where ⟨ D ⟩ is one astronomical unit (1 AU = 1.495 × 108 km) and D(t) is the Sun-Earth distance (in km) at a given time t; -
Deg(λ,t) is the time and wavelength dependent responsivity change of the UV channel, normalized to unity at the beginning of the mission. Dividing by Deg(λ,t) allows us to remove SOLSPEC instability from the SSI calculation;
-
ΔT(t) is the temperature difference in °C between the measurement of the PMT at PTB and the measurement in space at time t, i.e., ΔT = TPTB−TISS(t);
-
αT(λ) is the thermal and spectral sensitivity coefficient of the PMT describing the change of responsivity in percentage per °C as a function of wavelength;
-
Cλ(λ) and CΔλ(λ) describe, respectively, possible signal changes induced by uncertainties on the instrument wavelength calibration and the effect of the spectrometer’s finite bandpass. These terms average out to zero, and are therefore only of use when discussing measurement uncertainties.
The linearized signal is described as: 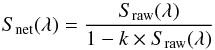 (2)where
(2)where 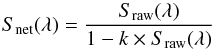 ; N(λ) is the number of counts (raw signal, open scale) collected during integration time ΔtN seconds; Sraw(λ) is the raw signal in counts per second (cts s-1); and k is the nonlinearity coefficient, corresponding to the dead-time of the photon counting electronics (PAD), in seconds, representing the minimum time interval needed to discern two individual pulses (photons).
; N(λ) is the number of counts (raw signal, open scale) collected during integration time ΔtN seconds; Sraw(λ) is the raw signal in counts per second (cts s-1); and k is the nonlinearity coefficient, corresponding to the dead-time of the photon counting electronics (PAD), in seconds, representing the minimum time interval needed to discern two individual pulses (photons).
For simplification, no pointing correction is applied for the UV channel because the stability of the CPD for Sun tracking is within 10 arcmin. Within this range, the angular response of SOLAR/SOLSPEC varies within 0.1% with respect to an optimal alignment on the optical axis. Also, no correction for nonlinearity is applied for signals lower than 500 cts s-1. This applies typically to dark current measurements.
A detailed discussion of the measurement equation and of the in-flight performance of the instrument follows.
4.1. Wavelength scale of SOLAR/SOLSPEC
From grating dispersion theory, given the relationship between the angles of incidence and diffraction of the light, the grating groove properties and the wavelength, and knowing the mechanical connection between motor and grating, the following analytic function was derived by Bolsée (2012): 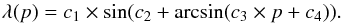 (3)The four parameters (c1,c2,c3,c4) are related to the opto-mechanical design of SOLAR/SOLSPEC and their values can be calculated. The variable p is the motor step. Owing to small adjustments during instrument assembly, instead of using the purely theoretical values, we adjusted them using a nonlinear regression of this function over a sample of spectral line positions {pi,λi} obtained experimentally from the spectra of laboratory spectral lamps measured by SOLAR/SOLSPEC (Thuillier et al. 2009). The best estimate values are shown in Table 2.
(3)The four parameters (c1,c2,c3,c4) are related to the opto-mechanical design of SOLAR/SOLSPEC and their values can be calculated. The variable p is the motor step. Owing to small adjustments during instrument assembly, instead of using the purely theoretical values, we adjusted them using a nonlinear regression of this function over a sample of spectral line positions {pi,λi} obtained experimentally from the spectra of laboratory spectral lamps measured by SOLAR/SOLSPEC (Thuillier et al. 2009). The best estimate values are shown in Table 2.
Experimental parameters of the mechanical grating position and wavelength relation.
The wavelength scale is slightly nonlinear. On average, one motor step corresponds to 0.008 nm in the UV. The spectral resolution and shape of the slit function was analyzed before launch using the same set of spectral lines. We found a very symmetrical Gaussian shape for these functions. For the spectral resolution, we found the wavelength dependent curve shown in Fig. 4. This variation is mainly due to the effect of an optical misalignment of the spectrometer (optimized at 326 nm using a He-Cd laser) and the use of concave gratings (for higher throughput). Despite the reduced astigmatism for holographic and concave gratings designed by the Jobin-Yvon company, the aberrations are still pronounced and are also responsible for the variation of the spectral resolution. This is due to the focus shifts from the tangential to the sagital plane at the intermediate slit when the grating rotates.
 |
Fig. 4 Spectral resolution of the UV channel as a function of the wavelength. |
During the SOLAR mission, the wavelength scale has been carefully monitored using the internal hollow cathode lamp and Fraunhofer solar lines. Since 2008, we have observed wavelength shifts lower than 0.025 nm determined using the methodology described in (Slaper et al. 1995). The method consists in minimizing the function given by: 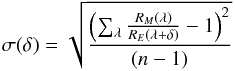 (4)where Ri (with i = M,E) is the ratio between a measurement and its two surrounding measurements. The subscripts E and M stand for the reference and tested spectra, respectively, and n is the number of spectral points analyzed.
(4)where Ri (with i = M,E) is the ratio between a measurement and its two surrounding measurements. The subscripts E and M stand for the reference and tested spectra, respectively, and n is the number of spectral points analyzed.
For this, we selected the well-defined wavelength scale at the beginning of the SOLAR mission as the reference (RE). Then we proceeded to determine the value of δ that minimizes Eq. (4) for each SOLAR/SOLSPEC solar spectrum and then realign them onto the reference within 0.01 nm. For further investigations, we compared the wavelength scale of SOLSTICE3 (level 3, version 13) and SOLAR/SOLSPEC. The first step was to use SOLSTICE as a reference and then convolve it to the variable bandpass of SOLSPEC Then, after systematic comparison of each of our solar spectra using the above methodology, we derived an average difference between the SOLAR/SOLSPEC and SOLSTICE wavelength scales of 0.019 nm. Using this correction, SOLSPEC and SOLSTICE can therefore be placed on the same wavelength scale, which is required before any comparison of SSI in absolute terms.
4.2. Photomultiplier net signal
In photon counting mode, the nonlinearity of the PMT is not negligible. The correction is related to the dead time of the electronics. The parameter N′ is defined as the real number of pulses to be measured on the anode during the ΔtN integration time. Owing to progressive pulse overlapping for increasing flux intensity, the measured number of pulses is lower than the real number. It is shown in Castelletto et al. (2007) that the loss in counts 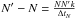 . Knowing that
. Knowing that 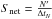 by definition, the counting loss can easily be reformulated and the relation between Snet and Sraw in Eq. (1) is then deduced. This relation is used to retrieve the level of signal that would be produced by a linear detector. The dead time is the key coefficient; it was measured experimentally before flight using a laboratory light source, attenuated by a known amount, and a set of accurately characterized neutral density filters (transmission determined within 0.1%). We simulated the linear signal Snet from the signal obtained with the filter (thus having negligible nonlinearities) by dividing it by the transmission of the filter. By comparing the differences in counts between the raw signal Sraw obtained without the filters and the simulated signal Snet, the best estimate of the dead time k was deduced from the slope of the theoretically linear relationship when plotting Snet/Sraw as a function of Snet. We found a dead time k = (6.06 ± 0.3) × 10-7 s. During the SOLAR mission and under certain thermal conditions, some “jumps” in signal were encountered in the absolute response of SOLAR/SOLSPEC compared to the expected levels observed at the PTB. Analysis is still being performed to understand the physical or electronic nature of this behavior. Here we have selected a sensitivity level in accordance with the level at PTB. Two other levels were also identified but not taken into account, thus being considered as outliers. After normalization to 1 AU (using the ϵ(t) function), three main corrections must still be applied.
by definition, the counting loss can easily be reformulated and the relation between Snet and Sraw in Eq. (1) is then deduced. This relation is used to retrieve the level of signal that would be produced by a linear detector. The dead time is the key coefficient; it was measured experimentally before flight using a laboratory light source, attenuated by a known amount, and a set of accurately characterized neutral density filters (transmission determined within 0.1%). We simulated the linear signal Snet from the signal obtained with the filter (thus having negligible nonlinearities) by dividing it by the transmission of the filter. By comparing the differences in counts between the raw signal Sraw obtained without the filters and the simulated signal Snet, the best estimate of the dead time k was deduced from the slope of the theoretically linear relationship when plotting Snet/Sraw as a function of Snet. We found a dead time k = (6.06 ± 0.3) × 10-7 s. During the SOLAR mission and under certain thermal conditions, some “jumps” in signal were encountered in the absolute response of SOLAR/SOLSPEC compared to the expected levels observed at the PTB. Analysis is still being performed to understand the physical or electronic nature of this behavior. Here we have selected a sensitivity level in accordance with the level at PTB. Two other levels were also identified but not taken into account, thus being considered as outliers. After normalization to 1 AU (using the ϵ(t) function), three main corrections must still be applied.
4.3. Thermal corrections
For thermal regulation, SOLAR/SOLSPEC is equipped with thermostats, heaters, multi-layer insulation (MLI, 12 layers), and white paint on the external plate facing the Sun. A good agreement was found between thermal models before launch, from cold to hot cases, and the in-flight behavior. During the SOLAR mission, the UV solar spectra are measured with a detector at a temperature between 3 °C and 8 °C. Nevertheless, the temperature of the PMT was higher during the absolute calibration at the PTB, around 23.3 ± 1.5°C. Therefore, for each solar spectrum, a normalization must be applied taking into account the responsivity change of the PMT as a function of temperature. This is performed using the factors αT and ΔT in Eq. (1). At this step, we normalize the linearized signal Snet to the level that would have been obtained in the PTB temperature environment. It is performed using a tabulated curve of the temperature sensitivity coefficient αT, relevant for the Cs2Te photocathode and the photon counting mode as discussed in Thuillier et al. (2009) and Bolsée (2012). The solar blind PMT is more sensitive at lower temperatures (αT< 0) for wavelengths shorter than 290 nm. For example, at 220 nm, the amplitude of the thermal correction is about −1.4%.
4.4. Absolute radiometric calibration
This calibration converts the signal in cts s-1 into spectral irradiance in mW m-2 nm-1. The blackbody source BB3200pg at the PTB was used in June 2007 for the absolute calibration of SOLAR/SOLSPEC above 200 nm. The blackbody is a primary standard for the realization and dissemination of spectral irradiance; it is described in detail in Sperfeld et al. (1998), Sperfeld et al. (2000), Sperfeld et al. (2010) and Sapritsky et al. (1997) and summarized in Bolsée et al. (2014) for SOLAR/SOLSPEC applications. The blackbody provides a very stable reference source of known spectral radiance using Planck’s law. The cavity (pressed pyrographite rings) is heated by constant electrical current; the temperature of the cavity is radiometrically determined by the PTB using filter radiometers and is absolutely calibrated against a cryogenic primary detector standard (Friedrich et al. 1995; Werner et al. 2000; Taubert et al. 2003). The diameter of the aperture was 11.909 ± 0.002 mm. The aperture was seen by SOLAR/SOLSPEC under a full angle of 0.493° at a distance of 1384.05 mm, similar to the angular size of the solar disk (≈ 0.5°). The responsivity R(λ) in Eq. (1) was obtained after averaging the signal accumulated during several hours of SOLAR/SOLSPEC exposure in front of the blackbody with spectral irradiance (SI) EBB, where the average signal is defined as SBB. The UV extinction of this signal due to the Rayleigh diffusion and the O2 and O3 molecular absorption has been taken into account by calculating the determination of R(λ). The amplitude of the extinction was about 0.2% and 0.6% respectively at 260 nm and 200 nm and negligible above 300 nm. The absolute calibration below 200 nm was performed at IASB in January 2007, using the vacuum thermal chamber and deuterium lamps (Cathodeon Nos. V0132 and BR066) calibrated under vacuum in radiant intensity μW sr-1 nm-1 at PTB (BESSY II facility, Berlin) (Beckhoff et al. 2009). The conversion of the lamps’ calibration spectra to spectral irradiance and the good consistency between responsivity R(λ) obtained from the blackbody and deuterium lamps has been discussed in Thuillier et al. (2009). We will refer to ED2 and SD2 respectively for the SI of the deuterium lamps and the accumulated signal measured by SOLAR/SOLSPEC.
4.5. Correction of the responsivity degradation during the SOLAR mission
The deuterium lamps described in Sect. 2 were used to provide a link, by comparison of spectra, between the level of responsivity of SOLAR/SOLSPEC during calibration at PTB and the level observed just after the launch at the beginning of the SOLAR mission (8 months later). In this way, we were able to ensure the stability of the UV absolute response despite the vibrations induced by the shuttle launch. After comparing D1 and D2 spectra, we found that the ISS/PTB ratio was oscillating between 0.98 and 1.02 for the spectral range 200 nm to 280 nm. Further investigations over the whole UV spectral range and improvement of the measurement S/N could not be fully achieved owing to issues both pre- and post-launch; however we partially demonstrated the stability of the response during the launch and so a contribution from this factor will be taken into account in the uncertainty calculations. The degradation study during the SOLAR mission must be performed in two steps. First, the loss of transmission of the Suprasil quartz plate (the shielding and the first active surface) has to be monitored. Second, the loss of responsivity of the spectrometer has to be monitored using the deuterium lamps. Through analysis of both of these factors, the reduction in responsivity can be determined. For the quartz plates, the transmission was frequently measured using the Sun and the UV spectrometer, which were considered respectively as a stable light source and instrument during the scan. The loss of transmission is expressed by means of a coefficient in percent for 100 h of Sun exposure. The results are shown in Fig. 5.
 |
Fig. 5 The UV channel front optics: quartz plate Suprasil 311 from Heraeus GmbH (Germany). Degradation of the transmission due to deposits, expressed by means of a coefficient in % of decrease per 100 h of Sun exposure. |
For the loss of responsivity of the spectrometer, the two deuterium lamps were used to determine the relative response. The operating principle was to have one lamp that would be used monthly during the mission, while the second lamp was to be used after each solar spectrum measurement. We used an algorithm developed for the SUSIM experiment, described in detail by Floyd et al. (1996) and Prinz et al. (1996), and adapted for SOLSPEC by Bolsée (2012). The principle is that for lamps proven to have the same aging rate (such lamps were selected during flight model selection in the laboratory), the algorithm is used to monitor and correct the differential aging of the lamps themselves. After this is performed, we can then consider the lamps as stable and thus we are able to monitor the trend of the UV channel response. The deuterium lamp Di (i = 1,2) degrades according to Eq. (5) where its degradation is proportional to its utilization time Ti (i = 1,2) and to a time independent parameter a, which defines the lamps’ aging characteristics, and a1 = a2 = a is a necessary condition for the algorithm to be valid: 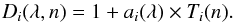 (5)Channel degradation, d can be obtained by Eq. (6), where
(5)Channel degradation, d can be obtained by Eq. (6), where 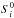 and Si represent lamp Di signal at the first light and at an arbitrary time, respectively. If operational conditions are met and a1 = a2, UV spectrometer degradation d = d1 = d2,
and Si represent lamp Di signal at the first light and at an arbitrary time, respectively. If operational conditions are met and a1 = a2, UV spectrometer degradation d = d1 = d2, 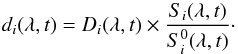 (6)Both conditions were verified in the 200 nm to 220 nm wavelength range. Owing to a unknown event, the voltage source of the deuterium lamps was lost at the end of April 2009 and, consequently, the lamps were lost. This method is thus only applicable to correct the UV spectrometer degradation during the course of the first year of mission. As described before, we combined the contributions from the quartz and the aging of the spectrometer channel to obtain the aging correction to be applied on the solar signal. After responsivity correction, we found a solar signal oscillating around the unity during the first year of the mission. This is the first evidence of the minimum of the solar activity during the studied period. The SSI variations at low frequencies corresponding to the solar SSI UV variability combined to possible errors in aging corrections were obtained after the application of a low pass filter. The fluctuations at higher frequencies removed by the filter involves mainly the precision of the SOLAR/SOLSPEC measurements (repeatability) due to the photon noise and other uncertainties (thermal corrections for example). These measured fluctuations are compared to the uncertainty calculations in the next sections. Figure 6 presents the results for this aging correction study at 210 nm as an example.
(6)Both conditions were verified in the 200 nm to 220 nm wavelength range. Owing to a unknown event, the voltage source of the deuterium lamps was lost at the end of April 2009 and, consequently, the lamps were lost. This method is thus only applicable to correct the UV spectrometer degradation during the course of the first year of mission. As described before, we combined the contributions from the quartz and the aging of the spectrometer channel to obtain the aging correction to be applied on the solar signal. After responsivity correction, we found a solar signal oscillating around the unity during the first year of the mission. This is the first evidence of the minimum of the solar activity during the studied period. The SSI variations at low frequencies corresponding to the solar SSI UV variability combined to possible errors in aging corrections were obtained after the application of a low pass filter. The fluctuations at higher frequencies removed by the filter involves mainly the precision of the SOLAR/SOLSPEC measurements (repeatability) due to the photon noise and other uncertainties (thermal corrections for example). These measured fluctuations are compared to the uncertainty calculations in the next sections. Figure 6 presents the results for this aging correction study at 210 nm as an example.
 |
Fig. 6 Degradation correction of the SOLAR/SOLSPEC UV channel response for the wavelength 210 nm. The diamonds and white dots show the measured solar signal before and after the quartz plate correction respectively. The triangles represent the solar signal corrected by the gray curve, i.e., the result of the deuterium lamps correction method. |
An additional test was performed using a two-component proxy model for the solar activity developed by DeLand & Cebula (DeLand & Cebula 1993). This model uses scaling factors to represent the percent change of solar irradiance for a 1% change in the MgII index (Heath & Schlesinger 1986). We used the time series of NOAA SBUV MgII index4 (Viereck et al. 2004), sampled for the dates of all SOLAR/SOLSPEC measurements, from which we identified the time interval from 6 June 2008 to 26 April 2009 as the most suitable one for a quiet Sun period defining the minimum of solar activity prior to cycle 24. The next step was to define a reference SOLAR/SOLSPEC solar spectrum between 175 nm and 340 nm, using the first five measurements of the SOLAR mission (therefore with no significant aging effects). We modulated this spectrum using the DeLand MgII proxy model for the time interval 6 June 2008 to 29 April 2009. For this spectral range, we found a SSI variation limited to 0.31%, attesting a quiet Sun for this period. We also studied the spectra provided by the SORCE platform and the SATIRE model (Ball et al. 2014) for the dates of all SOLAR/SOLSPEC measurements between the 5 and the 29 April 2009: SATIRE is based on the assumption that the evolution of the magnetic field of the solar surface is directly responsible of the variation of the SSI. For SATIRE, with respect to the mean scan for the given time period and for the 175 nm to 340 nm range, we observed a SSI variation limited to a maximum of −0.22% to + 0.23% . For SORCE, we also observed a stable SSI over one year: the experimental data are more noisier (noise around 3% for wavelengths shorter than 200 nm); therefore we found for SORCE peak to peak measured SSI variation between 1% and 2% in the wavelength region between 200 nm and 310 nm. These studies show that a solar minimum was observed during the selected time period. For the SOLAR/SOLSPEC solar signal, prior to applying the aging correction, we observe a steep trend similar to the one presented at 210 nm, but with a different wavelength dependency. We finally corrected the trend for all wavelengths other than the 200 nm to 220 nm spectral range using a low pass filter through the solar signal. The standard deviations of the signal are presented for comparison with the uncertainty calculations in Fig. 10. The aging correction as a function of time and wavelength, normalized to 1 on 5 April 2008 is shown in Fig. 7.
 |
Fig. 7 Degradation of the UV channel for the sum of both contributions (spectrometer + quartz plate) as a function of time and wavelength. |
As the UV aging of the quartz plate and spectrometer were monitored separately, it was possible to analyze the relative contributions from each could as a function of wavelength. Figure 8 shows the results after one year; we see that the quartz contribution is not negligible.
 |
Fig. 8 Wavelength dependent degradation of the UV channel after the first year of the mission, for both contributions (spectrometer + quartz plate). During this period, the SOLSPEC UV channel was exposed to the Sun for 43.3 h. |
During the first year of the SOLAR mission, the degradation rate of the UV channel of SOLAR/SOLSPEC was shown to be significantly higher than for other space experiments such as SUSIM and SOLSTICE I and II (Floyd et al. 1996; Woods et al. 1998; Snow et al. 2005). Contamination could have accumulated on all internal optical surfaces (quartz plate, diffusor, gratings) or could be due to photochemical processes: the UV radiation causes polymerization of the contaminant deposits present on the optical surfaces (Floyd et al. 1996). The contaminants could come from the mounts of the deuterium lamps, but any provenance is speculative. The interface between the lamp enclosure and mount is constructed of two Invar rings which are fixed on the enclosure using the 3MTM Scotch-Weld paste adhesive 2216 B/A. The temperature of the lamp in use is around 170 °C, so it is possible that outgassing from the adhesive 2216 B/A could have been responsible for the steep change in responsivity during the first year of the mission.
Knowing di(λ,t) is the final part of the data processing model, allowing us to maintain the calibration and to calculate the spectral irradiance of the Sun Esol(λ,t) as a function of time and wavelength.
4.6. Uncertainty calculations
The opto-mechanical design and the accuracy of the absolute calibration of SOLAR/SOLSPEC were improved to fulfill the two scientific objectives for which it was built: the measurement of a reference spectrum and the detection of changes of the SSI during the course of solar cycle 24.
Reference spectrum.
The measurement of a reference spectrum is achieved by accumulating a large number of solar spectra, increasing the effective integration time and therefore reducing the measurement noise, which improves the accuracy of the measured absolute SSI. The dynamic range of the SOLAR/SOLSPEC electronics was adjusted to match the expected level of the measured SSI after absolute calibration had been completed. Non-negligible uncertainties for the response curve remain due to this adjustment, as the primary standards measured during the absolute calibration campaign are considerably less intense than the Sun (e.g. ≈4 × 103 and ≈8 × 102 at 200 nm and 250 nm respectively). The uncertainty on this absolute response acts as a source of systematic error in space and becomes the dominant and irreducible contribution in the uncertainty of the SOLSPEC SSI measurement in space.
UV SSI variability.
The ability to achieve this objective depends on the intrinsic precision of SOLSPEC. It is limited by engineering constraints that aim to preserve the long-term performance of the detectors and to avoid needing to use large nonlinearity corrections. One consequence of this was the limitation of the photon flux to 105 cts s-1, affecting the choice of integration time used, which became the limiting factor for detecting SSI UV changes. This concept is described in more detail in Sect. 5.2. The photon flux limitation was obtained by means of an attenuation filter, activated between 217 nm and 320 nm.
The combined standard uncertainty (CSU) of the SOLSPEC measurements is calculated below, following the mathematical formalism of the law of propagation of uncertainties, according to the recommendations of JCGM (1995). Our study was performed for all measured wavelengths, quantifying the spectral effects of the spectrometer’s finite bandwidth for a solar spectrum measurement using the Fraunhofer lines. Here the uncertainties are only discussed for the range 175 nm to 340 nm; the details are mainly reported in Bolsée (2012). Changes in signal are defined using the variables Cλ(λ) and CΔλ(λ) (1), while their uncertainties are given by u(Cλ(λ)) and u(CΔλ(λ)), respectively. The possible UV signal change due to some wavelength uncertainty ϵλ is represented by Cλ(λ). The amplitude of ϵλ is limited to 0.05 nm for the UV channel and the uncertainty u(Cλ(λ)) includes here the effects of the stability and the repeatability of the wavelength scale for each individual scan. The expected wavelength λref exiting the double monochromator corresponds to the mid spectral interval defined by the slit and linear dispersion. If the light source spectrum exhibits a slope (i.e. a gradient in the exiting photon flux as a function of the wavelength), the effective central wavelength will differ from λref, inducing a change of the measured signal. This is expressed by CΔλ(λ). This variable and Cλ(λ), plus their respective uncertainties, were calculated following the procedure described in Obaton et al. (2007).
4.6.1. Standard uncertainty for the absolute response of the UV channel R(λ)
The absolute response was derived from the SOLAR/SOLSPEC measurements in front of the PTB blackbody and the deuterium lamps V0132 and BR066. The relative standard uncertainty of the calibration curve is shown in Fig. 9. The following uncertainty calculations use the terms derived in Eq. (1) and Sect. 4.4.
Spectral irradiance uncertainty of the standard sources.
For the spectral irradiance of the blackbody, u(EBB), knowing the uncertainties on the cavity temperature, the cavity emissivity, the diameter of the blackbody aperture, and the distance to SOLAR/SOLSPEC, we obtained values ranging from 0.24% to 0.37% for u(EBB) from Planck’s law. For the deuterium lamps, the spectral irradiance uncertainty u(ED2) was certified by PTB to be 2.5%.
 |
Fig. 9 Combined standard uncertainty (CSU) of the response curve of the UV channel after the ground-based calibration campaign. The hatched region between 260 nm and 320 nm is actually caused by the use of a different integration time during calibration. |
Uncertainty of the composite signal.
The blackbody composite signal, SBB (for wavelengths greater than 200 nm) was obtained by averaging, after dark-current subtraction, several SOLAR/SOLSPEC spectra acquired during the two weeks of calibration in June 2007. A wavelength-dependent CSU ranging from 2% to 8% with a local peak at 13% was found. The contributions from the uncertainties on Cλ(λ) and CΔλ(λ) are generally about 0.2% to 0.3%, peaking at around 1%. Other contributions to the total uncertainty such as the PMT nonlinearity correction or UV absorption by air along the optical path were more negligible. For the deuterium composite signal SD2, similar calculations provided a CSU ranging from 0.5% to 1% between 175 nm and 200 nm. Uncertainties on Cλ(λ) and CΔλ(λ) were below 0.3%.
Uncertainty of the response curve.
Knowing that R(λ) is calculated as Ex(λ) /Sx(λ) – where x = BB or D2 for the blackbody or deuterium lamps, respectively – we obtained from the combination of previous studies the CSU for R(λ), which is shown in Fig. 9. The discontinuities are related to the change of standard source at 200 nm and the cut-on of the UV filter at 217 nm. The dominant contribution comes from the composite signal of SOLAR/SOLSPEC, Sx(λ): even after several days of calibration measurements using long integration times. Owing to time limitations during calibration, including the time required for the blackbody to heat up and stabilize, the accumulation of counts on the PMTs was limited, particularly given the very large difference in irradiance between the Sun and the standard sources.
4.6.2. Standard uncertainty for a solar measurement on ISS
From the measurement equation (Sect. 4), we calculated the CSU u(ESol(λ,t)) for a solar measurement with the preset integration time of 0.6 s, and for a large accumulation of spectra that minimizes the random errors, leaving primarily the systematic errors due to the absolute calibration process. First, from the internal deuterium lamp analysis and the observed ratio between measurements made on the ISS and those at PTB, we should reasonably increase the uncertainty on R(λ) by an amount of 1%. For the general CSU study on the solar measurement, we obtained negligible or low contributions for the nonlinearity corrections (uncertainties generally ranging from 0.1% to 0.9% or lower), for thermal corrections, and DC subtraction (uncertainties below 0.1%). The uncertainties on Cλ(λ) and CΔλ(λ) were between 0.1% and 1% but with increases (as expected) for wavelengths corresponding to strong UV Fraunhofer lines (Fig. 10, blue and green curves). The uncertainty on the raw signal Sraw is expressed from the photon noise. For a signal around 105 cts s-1 for a 0.6 s integration time, we typically obtained values for u(Sraw) – away from the wings of the UV spectral range where SOLAR/SOLSPEC is sensitive – of around 7% at 175 nm, decreasing to a value 0.4% to 1.6% for the 195 nm to 340 nm spectral range (black curve in Fig. 10). For the aging contribution u(Deg(λ,t)), the uncertainties are determined between 200 nm and 220 nm from the equations of the SUSIM algorithm for observed photon noise of the deuterium lamps. The uncertainty is generally close to 1%. For wavelengths lower than 200 nm and greater than 220 nm, we calculated the uncertainty of the low pass filter method on the solar signal. We generated a synthetic signal by injecting a given aging trend and a noise with the same amplitude of the solar signal. We compared the retrieved trend after filtering with the injected one. The results range from 0.2% to 0.4%. After combining all the contributions quadratically we obtained an estimation of u(ESol(λ,t)) for a single solar measurement, expressed in percent and shown as the green curve in Fig. 10. As expected for space measurements, the uncertainty on the response curve provided the higher contribution to the final CSU on u(ESol(λ,t)) but locally – owing to the steep slope of the Fraunhofer lines – the contribution u(CΔλ(λ)) becomes dominant. We processed also the uncertainty equations with their partial derivatives (sensitivity coefficients) and individual uncertainties contributions for an integration time increasing to infinity, simulating a large accumulation of spectral measurements. The results are also shown as the blue curve in Fig. 10. In this case, the CSU on ESol(λ,t) is reduced to values close to the u(R(λ)) limit, as expected.
 |
Fig. 10 Combined standard uncertainties for UV SSI measurements: the CSU for the response curve (red); the CSU for the raw, uncalibrated signal – which is mainly the photon noise (black); and the CSU for SSI measured with a 0.6 s integration time (green); and the same for an infinite integration time (blue). Magenta is the baseline of the blue curve subtracted from the contribution of the response curve. |
5. Results
Since its inception, the SOLAR/SOLSPEC instrument has played an important role in the quest to accurately measure the solar spectrum, a role that is continuing with the new design of the instrument as part of the long-term SOLAR mission. Important efforts were made to increase the accuracy of the absolute calibration. In this section we apply the measurement equation in order to calibrate the first year of spectra as measured by the instrument, which corresponds to the minimum of solar activity that occurred prior to cycle 24. It is known that the solar activity evolves in such a way that no two cycles exhibit the same amplitude and duration (Clette et al. 2015): this solar cycle started after an unexpected prolonged minimum. For the SOLAR/SOLSPEC results, we will focus on this period of minimum activity. We present a reference UV quiet Sun spectrum for comparison with other space instruments and a model.
5.1. Deliverables
The levels of products of processed data are defined as follows:
-
Level 0 (L0): raw data coming from the telemetry without anyprocessing in orbit.
-
Level 1a (L1a): first step of data processing, consisting of dark current, detector nonlinearity, thermal effects, Earth’s orbit eccentricity and wavelength scale corrections.
-
Level 1b (L1b): level reserved for the correction of jumps in the instrument sensitivity observed in orbit for some spectra.
-
Level 2 (L2): conversion of L1 data (expressed in engineering units) to a radiometric scale expressed in SI units (W m2 nm-1), achieved by applying the absolute calibration coefficients.
-
Level 3 (L3): application of aging corrections of the channel response providing solar spectra at 1 AU, calibrated in spectral irradiance in a well maintained wavelength and absolute radiometric scale, obtained from a linearized detection chain including the normalization for stable thermal conditions.
5.2. Precision of the measurements
Repeated measurements of the same source (quiet Sun) reduce the random component of the CSU and increase the precision. As the determination of the response curve and its associated uncertainty is the product of ground-based pre-flight operations and cannot be modified on board ISS, we consider this to be one representation of the systematic part of the CSU. We propose to compare the precision with which a solar spectrum was obtained with the estimation from our calculations. For the precision related to the reproducibility of the measurements, as explained at the end of Sect. 4.6.2, we analyzed for every wavelength the observed standard deviation (STD) of our measurements, after applying of the aging correction. It is to be compared to the CSU calculations, after removing the contribution from R(λ) (Eq. (1)).
 |
Fig. 11 Comparison between calculated uncertainties and the standard deviation of real solar measurements: the CSU (%) for a SSI measurement with infinite integration time (blue); the calculated CSU for a SSI uncalibrated measurement with an integration time of 0.6 s and no uncertainty contribution from the response curve (green); and the measured standard deviation of the uncalibrated SOLAR/SOLSPEC as observed from a single solar measurement using a 0.6 s integration time (red). |
The comparison in Fig. 11 shows a similar level of uncertainties, except for the spikes associated with solar lines. For real measurements, the standard deviation was estimated from spectra with shift wavelengths corrected; therefore the contributions of Cλ(λ) and CΔλ(λ) should be negligible here. The curve representing the calculated CSU without any calibration contribution (Fig. 11, blue curve) has to be considered the bottom envelope of the calculations for the discussions. The photon noise is the dominant effect, mainly because the precision of a single solar measurement (Δt = 0.6 s) was not optimized owing to hardware constraints. From this comparison, the CSU without any calibration contribution appears to be correctly estimated by the calculations. The green curve displayed in Fig. 11 shows the CSU with the response curve contribution, for an infinite integration time as shown previously in Fig. 10. The ideal spectral precision of a SOLAR/SOLSPEC measurement is represented by the purple curve in Fig. 10. This curve represents the calculated CSU of Eq. (1), excluding the R(λ) term for an infinite integration time. In this ideal case the detection limit could be as low as 0.2% around 300 nm, which, if implementable from both and operational and an instrumental point of view, would define the maximum ability of SOLAR/SOLSPEC to detect daily UV changes.
5.3. Reference quiet Sun UV solar spectrum from SOLAR/SOLSPEC
In this section we present the L3 SOLAR/SOLSPEC data for the period of minimum solar activity, calculated using the measurement equation from the data processing model developed at BIRA-IASB. The study uses spectra measured between 175 nm and 340 nm with a 0.6 s integration time and a constant sampling in terms of stepper motor movements (thus slightly variable wavelength intervals due to the nonlinear wavelength scale, see Eq. (3)) providing a data point every ~1/3 nm. SOLAR/SOLSPEC does not deliver one solar spectrum per day: owing to the planning of solar measurements on board the ISS, organized in Sun visibility windows, time gaps are present in the datasets, with an approximate rate of measurement of one solar spectrum every three days for the first year. The spectrum is presented in Fig. 12, showing the average of all selected single solar measurements during the first year of the mission after the application of all corrections and calibrations.
 |
Fig. 12 Reference UV solar spectrum for the minimum of solar activity before cycle 24, as measured by SOLAR/SOLSPEC. |
5.4. Comparisons with SORCE, WHI, SATIRE and ATLAS 3
The available SOLAR/SOLSPEC UV spectra for the time interval corresponding to the period of minimum solar activity (6 June 2008 to 29 April 2009) were averaged to give a quiet Sun mean reference spectrum in the UV. The corresponding CSU was also calculated. For purposes of comparison, a selection was done on the SORCE5 spectra in order to produce, by averaging, a similar SORCE quiet Sun reference spectrum. The uncertainty for the radiometric scale of SORCE is calculated to lie between 1.2% and 6% in the UV range6.
The same exercise was performed for the SATIRE model (Yeo et al. 2014) which defined a mean SATIRE quiet Sun UV spectrum, where we selected the WHI 2008 spectrum. ATLAS 3 is associated with a certain level of solar activity, characterized by a SBUV MgII index of 0.26747. First, the spectra were normalized to adjust them to the mean solar activity of our selected time period (Mg II index of 0.26419) using the proxy model described in DeLand & Cebula (1993). For the recalculated ATLAS 3 spectrum, the spectral irradiance was reduced by around 1.5% to 2% between 175 nm and 210 nm and no more than 0.6% after the Al edge. The uncertainty for ATLAS 3 at one-sigma decreases from 2% to 1.1%, from 200 nm to 350 nm as reported in Thuillier et al. (1997). Finally, the spectra were convolved to a spectral resolution of 5 nm to normalize the bandpass and reduce the noise in the ratio of the spectra. In Fig. 13 we present the deviation between the SORCE, SATIRE and the normalized ATLAS 3 spectra with respect to the SOLAR/SOLSPEC reference and its associated standard uncertainty. Deviations are observable between the measured spectra, but when the standard deviation is accounted for the differences are generally acceptable. Except for the region between 230 nm and 270 nm, ATLAS 3 is closer to the new SOLAR/SOLSPEC spectrum than SORCE is.
 |
Fig. 13 Average solar spectra for the time period April 2008−April 2009 for dates of SOLAR/SOLSPEC measurements, compared to SORCE, WHI 2008, ATLAS 3 (normalized to the solar activity of the considered time period) and the SATIRE model. For the presented spectra, the spectral resolution is normalized to 5 nm. |
6. Conclusions
SOLAR/SOLSPEC has been measuring the SSI on board the ISS since February 2008. It is an improved version of the SOLSPEC instrument that participated in various short duration space missions on the space shuttles and spent 6 months on EURECA. It is comprised of three double monochromators with concave gratings (UV, VIS and IR) for SSI measurements covering the range 166−3088 nm. Accurate and continuous SSI measurements from space are essential for studying the photochemistry of planetary atmospheres and climatology, and for solar physics. The aim of SOLAR/SOLSPEC is to determine the reference solar spectra for different levels of solar activity; the instrument is able to detect and quantify, through multiple repeated measurements, the UV changes of the SSI during a solar cycle. Results are calibrated to the highly accurate radiometric scale of the PTB and are provided for the scientific community.
In this engineering paper, we have described in detail the general design of the instrument and the improvements made that have allowed SOLSPEC to perform through the long duration of the SOLAR mission. The measurement equation, as developed in detail for the first time for SOLAR/SOLSPEC in Bolsée (2012), was used to calibrate the observations in order to derive a SSI spectrum. From the extensive pre-flight characterization of the instrument, it was possible to provide an accurate value of each parameter of the measurement equation and to estimate the individual uncertainties and their propagation through to the SSI. Here we have determined the UV reference solar spectrum for the first year of the SOLAR mission, corresponding to the minimum of solar activity before cycle 24, and compared the result to the ATLAS 3 and SORCE spectra which demonstrated an acceptable agreement. Deviations up to 10% between a series of measurements from different instruments can be observed because the uncertainty of SSI measurements from space in the UV are still relatively high. A nonreducible contribution to the uncertainty of SOLAR/SOLSPEC comes from the built-in response curve, determined during ground calibration from deuterium lamps and the blackbody of the PTB, which excels at this type of measurement owing to its low drift and accurate cavity temperature determination. SOLAR/SOLSPEC faced the challenge of bringing this radiometric scale into orbit without alteration, and maintaining it during the mission, which was principally achieved using internal reference lamps. For the first year of the mission, we saw a decrease of 50% around 200 nm. Another contribution to the uncertainties is related to the precision of in-orbit repeated solar measurements. We demonstrated that there is a good correspondence between the observed and calculated uncertainties of this contribution.
Although it was not mainly designed for the detection of daily solar UV variability, SOLAR/SOLSPEC is extremely important in the accurate determination of the absolute SSI spectrum. This is possible thanks to the exhaustive pre-flight calibration work and to the robust performance of the instrument in orbit since 2008. Seven years of solar data are being processed to correct for aging, and special UV measurements with higher S/N ratios are being made to fully utilize the capabilities of the instrument while it is on board the ISS.
Acknowledgments
The participating institutes for the development of the SOLSPEC instrument are the Service d’Aéronomie du CNRS, now LATMOS (France), the Institut royal d’Aéronomie Spatiale de Belgique (Belgium), and the Landessternwarte of Heidelberg (Germany). The SOLSPEC investigation is supported by the Centre National d’Études Spatiales (France), the Centre National de la Recherche Scientifique (France), and the Bundesministerium für Forschung und Technologie (Germany). The authors wish to deeply thank their colleague Ian Thomas for his thorough grammatical review of the manuscript. The authors acknowledge the support from the Belgian Federal Science Policy Office (BELSPO) through the ESA-PRODEX program (contract 4000110593 for 2014-2015) and the funding of the Solar-Terrestrial Centre of Excellence (STCE). The authors wish to thank G. Thuillier, the former PI of SOLSPEC for his expertise and the scientific knowledge that allowed the smooth running of the SOLAR mission.
The SOLAR operations are conducted by the Belgium User Support Operations Center (B-USOC) via the COLUMBUS Control Center of DLR (Oberpfaffenhofen, Germany).
References
- Acquaroli, L., & Onorati, F. 2005, in Spacecraft Structures, Materials and Mechanical Testing, 581, 156 [NASA ADS] [Google Scholar]
- Ball, W. T., Krivova, N. A., Unruh, Y. C., Haigh, J. D., & Solanki, S. K. 2014, J. Atmos. Sci., 71, 4086 [NASA ADS] [CrossRef] [Google Scholar]
- Beckhoff, B., Gottwald, A., Klein, R., et al. 2009, Physica Status Solidi (b), 246, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- BenMoussa, A., Gissot, S., Schühle, U., et al. 2013, Sol. Phys., 288, 389 [Google Scholar]
- Bolsée, D. 2012, Ph.D. Thesis, Free University of Brussels, Belgium [Google Scholar]
- Bolsée, D., Pereira, N., Decuyper, W., et al. 2014, Sol. Phys., 289, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Brueckner, G. E., Edlow, K. L., Floyd, L. E., Lean, J. L., & VanHoosier, M. E. 1993, J. Geophys. Res. Atmos., 98, 10695 [NASA ADS] [CrossRef] [Google Scholar]
- Castelletto, S. A., Degiovanni, I. P., Schettini, V., & Migdall, A. L. 2007, J. Mod. Opt., 54, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Clette, F., Cliver, E. W., Lefévre, L., Svalgaard, L., & Vaquero, J. M. 2015, Space Weather, 13, 529 [NASA ADS] [CrossRef] [Google Scholar]
- DeLand, M. T., & Cebula, R. P. 1993, J. Geophys. Res. A. 98, 12809 [Google Scholar]
- Ermolli, I., Matthes, K., Dudok de Wit, T., et al. 2013, Atmos. Chem. Phys., 13, 3945 [Google Scholar]
- Floyd, L. E., Herring, L. C., Prinz, D. K., & Brueckner, G. E. 1996, SPIE, 23, 36 [Google Scholar]
- Friedrich, R., Fischer, J., & Strock, M. 1995, Metrologia, 32, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, L. J., Beer, J., Geller, M., et al. 2010, Rev. Geophys., 48, 4001 [NASA ADS] [CrossRef] [Google Scholar]
- Haigh, J., Winning, A., Toumi, R., & Harder, J. 2010, Nature, 467, 696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heath, D. F., & Schlesinger, B. M. 1986, J. Geophys. Res. Atmos., 91, 8672 [NASA ADS] [CrossRef] [Google Scholar]
- JCGM 1995, Guide to the Expression of Uncertainty in Measurement (Paris: BIPM) [Google Scholar]
- Key, P. J., & Preston, R. C. 1980, J. Phys. E: Sci. Instr., 13, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Markert, T. H. 1975, Opt. Eng., 14, 323 [Google Scholar]
- Mekaoui, S. 2010, Ph.D. Thesis, Free University of Brussels, Belgium [Google Scholar]
- Obaton, A. F., Ledenberg, J., Fischer, N., Guimier, S., & Dubard, J. 2007, Metrologia, 44, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Prinz, D. K., Floyd, L. E., Herring, L. C., & Brueckner, G. E. 1996, Proc. SPIE 2831, 25 [Google Scholar]
- Rottman, G. 2005, Sol. Phys., 230, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Rottman, G. J., Woods, T. N., Snow, M., & De Toma, G. 2001, Adv. Space Res., 27, 1927 [Google Scholar]
- Rozanov, E., Egorova, T., Fröhlich, C., et al. 2002, in From Solar Min to Max: Half a Solar Cycle with SOHO, ed. A. Wilson, ESA SP, 508, 181 [Google Scholar]
- Sapritsky, V. I., Khlevnoy, B. B., Khromchenko, V. B., et al. 1997, Appl. Opt., 36, 5403 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, G., Brunner, R., Eberhard, D., et al. 2006, Adv. Space Res., 37, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Sela, A., Moreau, D., & Mihalache, N. 2012, in SpaceOps 2012 Conf., American Institute of Aeronautics and Astronautics [Google Scholar]
- Shapiro, A. V., Rozanov, E. V., Shapiro, A. I., et al. 2013, J. Geophys. Res. Atmos., 118, 3781 [NASA ADS] [CrossRef] [Google Scholar]
- Skupin, J., Noël, S., Wuttke, M., et al. 2005, Adv. Space Res., 35, 370 [Google Scholar]
- Slaper, H., Reinen, H. A. J. M., Blumthaler, M., Huber, M., & Kuik, F. 1995, Geophys. Res. Lett., 22, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, M., Mcclintock, W. E., Rottman, G., & Woods, T. N. 2005, Sol. Phys., 230, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Sperfeld, P., Metzdorf, J., Harrison, N. J., et al. 1998, Metrologia, 35, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sperfeld, P., Galal Yousef, S., Metzdorf, J., Nawo, B., & Müller, W. 2000, Metrologia, 37, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Sperfeld, P., Pape, S., & Barton, B. 2010, MAPAN, 25, 11 [CrossRef] [Google Scholar]
- Taubert, D., Friedrich, R., Hartmann, J., & Hollandt, J. 2003, Metrologia, 40, S35 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Simon, P. C., Labs, D., Pastiels, R., & Neckel, H. 1981, Sol. Phys., 74, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Hersé, M., Simon, P., et al. 1997, Sol. Phys., 171, 283 [Google Scholar]
- Thuillier, G., Hersé, M., Labs, D., et al. 2003, Sol. Phys., 214, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Foujols, T., Bolsée, D., et al. 2009, Sol. Phys., 1, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Viereck, R. A., Floyd, L. E., Crane, P. C., et al. 2004, Space Weather, 2, s10005 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, L., Fischer, J., Johannsen, U., & Hartmann, J. 2000, Metrologia, 37, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T., Rottman, G., Russell, C., & Knapp, B. 1998, Metrologia, 35, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Yeo, K. L., Krivova, N. A., Solanki, S. K., & Glassmeier, K. H. 2014, A&A, 570, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Experimental parameters of the mechanical grating position and wavelength relation.
All Figures
 |
Fig. 1 The opto-mechanical configuration of one channel of the SOLAR/SOLSPEC instrument for the SOLAR mission. For the UV channel, only the deuterium and hollow cathode lamps are considered. |
| In the text | |
 |
Fig. 2 Schematics of the diffraction grating scanning mechanism. |
| In the text | |
 |
Fig. 3 SOLSPEC mounted on external COLUMBUS platform (Credit: NASA). |
| In the text | |
 |
Fig. 4 Spectral resolution of the UV channel as a function of the wavelength. |
| In the text | |
 |
Fig. 5 The UV channel front optics: quartz plate Suprasil 311 from Heraeus GmbH (Germany). Degradation of the transmission due to deposits, expressed by means of a coefficient in % of decrease per 100 h of Sun exposure. |
| In the text | |
 |
Fig. 6 Degradation correction of the SOLAR/SOLSPEC UV channel response for the wavelength 210 nm. The diamonds and white dots show the measured solar signal before and after the quartz plate correction respectively. The triangles represent the solar signal corrected by the gray curve, i.e., the result of the deuterium lamps correction method. |
| In the text | |
 |
Fig. 7 Degradation of the UV channel for the sum of both contributions (spectrometer + quartz plate) as a function of time and wavelength. |
| In the text | |
 |
Fig. 8 Wavelength dependent degradation of the UV channel after the first year of the mission, for both contributions (spectrometer + quartz plate). During this period, the SOLSPEC UV channel was exposed to the Sun for 43.3 h. |
| In the text | |
 |
Fig. 9 Combined standard uncertainty (CSU) of the response curve of the UV channel after the ground-based calibration campaign. The hatched region between 260 nm and 320 nm is actually caused by the use of a different integration time during calibration. |
| In the text | |
 |
Fig. 10 Combined standard uncertainties for UV SSI measurements: the CSU for the response curve (red); the CSU for the raw, uncalibrated signal – which is mainly the photon noise (black); and the CSU for SSI measured with a 0.6 s integration time (green); and the same for an infinite integration time (blue). Magenta is the baseline of the blue curve subtracted from the contribution of the response curve. |
| In the text | |
 |
Fig. 11 Comparison between calculated uncertainties and the standard deviation of real solar measurements: the CSU (%) for a SSI measurement with infinite integration time (blue); the calculated CSU for a SSI uncalibrated measurement with an integration time of 0.6 s and no uncertainty contribution from the response curve (green); and the measured standard deviation of the uncalibrated SOLAR/SOLSPEC as observed from a single solar measurement using a 0.6 s integration time (red). |
| In the text | |
 |
Fig. 12 Reference UV solar spectrum for the minimum of solar activity before cycle 24, as measured by SOLAR/SOLSPEC. |
| In the text | |
 |
Fig. 13 Average solar spectra for the time period April 2008−April 2009 for dates of SOLAR/SOLSPEC measurements, compared to SORCE, WHI 2008, ATLAS 3 (normalized to the solar activity of the considered time period) and the SATIRE model. For the presented spectra, the spectral resolution is normalized to 5 nm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


