EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 599 (March 2017) A&A, 599 (2017) A19 Full HTML
Free Access
Issue
A&A
Volume 599, March 2017
Article Number A19
Number of page(s) 6
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201629563
Published online 21 February 2017

© ESO, 2017

1. Introduction

It is now well known that most oscillatory events in the solar atmosphere owe their existence to magnetic fields. The presence of magnetic fields in the solar atmosphere shapes the plasma and creates beautiful events, namely loops, jets, tornadoes, spicules, etc. In the present study the main idea is to study these cylindrical plasma structures, especially the rotating or twisted jets which are named as tornadoes (Harrison 1999; Li et al. 2012; Wedemeyer-Böhm et al. 2012), and to write expressions governing their frequencies and phase speeds due to their twist and rotation.

Today it is crystal clear that magnetohydrodynamic (MHD) waves are present all over the solar atmosphere. It is the MHD waves that are responsible for the density and magnetic field oscillations in solar structures. A firm ground for studying MHD waves in magnetic cylinders was provided in a series of studies carried out in the late 1970s and early 1980s by Roberts & Webb (1978), Webb & Roberts (1978), Roberts (1981), and Edwin & Roberts (1983) where dispersion relations in photospheric and coronal conditions were studied.

A cylindrical plasma structure surrounded by plasma resembles a solar loop, jet, spicule, or a tornado. The density contrast of the structure and the medium external to it may be up to a hundred. These structures act as a wave guide for different MHD waves, namely Alfvén, kink, sausage, longitudinal, ballooning, and torsional (e.g. Edwin & Roberts 1983; Zhugzhda 1996; Nakariakov & Verwichte 2005; Vasheghani Farahani et al. 2010). The kink, sausage, longitudinal, and ballooning waves are compressible, while the Alfvén wave (either torsional or shear) is incompressible (e.g. Van Doorsselaere et al. 2008). As such we have to be careful about the torsional wave, which is azimuthal perturbations of the plasma connected to the azimuthal component of the magnetic field. The torsional Alfvén wave is incompressible, but Zhugzhda & Nakariakov (1999) and Vasheghani Farahani et al. (2010) showed that in the presence of an equilibrium twist, the speed of the torsional wave is higher than the Alfvén speed. They showed that in the presence of an equilibrium twist, in addition to having the torsional Alfvén wave, a torsional wave which is dispersive comes into play. We note that in a plasma cylinder with a straight magnetic field, because a torsional Alfvén wave does not perturb neighbouring magnetic surfaces, a collective phenomenon does not take place, therefore this wave cannot be called a torsional mode (Vasheghani Farahani et al. 2010). It is worth noting that studying the Alfvén wave is very important (e.g. Hood et al. 2009) owing to its role in accelerating the solar (e.g. Cranmer 2009) and stellar (e.g. Charbonneau & MacGregor 1995; Suzuki 2007) winds in addition to its coronal heating aspect (e.g. Ofman 2005). It has also been suggested that a large-scale torsional wave generated by a flare is able to accelerate electrons to high energies (Fletcher & Hudson 2008). The rotation of coronal plasma structures has been reported, for example in macrospicules, by Pike & Mason (1998); these solar tornadoes will be the focus of the present study. A solar tornado (e.g. Wedemeyer & Steiner 2014; Levens et al. 2015) looks quite like a coronal jet (Cirtain et al. 2007; Vasheghani Farahani et al. 2009) accompanied by an equilibrium twist or rotation or both. We note that not all vortex-like motions in the solar atmosphere are an indication of a tornado (Shelyag et al. 2013). It has been already understood that an equilibrium twist and rotation acts as a steady flow in the cylindrical structure which causes an increase in the phase speed of the torsional wave; see Vasheghani Farahani et al. (2010) for details. They showed that when the equilibrium twist and rotation are present, the phase speeds in opposite direction differ. Nonetheless, the effects of the density contrast of the internal and external media in the presence of equilibrium twist and rotation still requires attention.

The observation of Alfvén waves in coronal structures is based on indirect evidence. The observation of magnetic twisted field lines in the solar corona is still not crystal clear. It is interesting to study Jess et al. (e.g. 2009) and Banerjee et al. (2009) in this regard.

The aim here is to derive analytic explicit expressions for the dispersion relation of torsional waves in the presence of equilibrium twist and rotation together with the perturbations of the external medium, and to study the nature of the torsional wave in coronal conditions. The results obtained by explicit expressions are compared with those obtained numerically. The importance of studying the torsional wave in coronal structures is due to their role in coronal seismology.

2. Model and equilibrium conditions

Consider a rotating (0,Vϕ0,0) and twisted magnetic cylinder (0,Bϕ0,Bz0) embedded in a uniform static medium which is magnetised in the direction parallel to the cylinder axis (0,0,Bz0e). This structure resembles a magnetised tornado in the solar atmosphere.

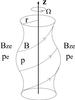thumbnail Fig. 1

Schematic view of a solar tornado.

In order to model such a structure, the MHD theory is used. In this line, for the medium inside the cylinder, the second-order thin flux tube approximation is implemented (Zhugzhda 1996), where the ideal MHD theory is used for the medium external to the cylinder (Edwin & Roberts 1983). The second-order thin flux tube approximation implies the radial dependence of the physical variables to be linearised by performing a Taylor expansion in the r-direction 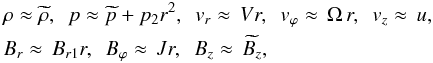(1)where B, v, ρ, and p respectively represent the magnetic field, velocity, density, and pressure of the system. The cylindrical components of each physical parameter is represented by indices. We note that J is the zeroth-order value of the current density, Ω is the zeroth-order value of the vorticity, where V is the radial derivative of the velocity. The superposed tildes represent the zeroth-order terms of the expansions, which will be omitted from this point onward. By substituting the expansions of Eq. (1) in the MHD equations, the closed set of equations regarding axisymmetric (∂/∂ϕ = 0) perturbations of the physical parameters inside the cylinder would be (Zhugzhda 1996) where 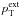is the total pressure of the external medium. The zero index represents equilibrium conditions of the physical parameters. For such a structure the equilibrium pressure balance at the cylinder boundary would be 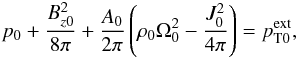(9)where A0 = πa2 is the equilibrium cross-sectional area of the cylinder with radius a. In obtaining Eqs. (2)–(8), the conservation of magnetic flux and angular momentum has been taken into account (see Zhugzhda 1996; Vasheghani Farahani et al. 2010). We note that Vasheghani Farahani et al. (2010) considered the external medium as a vacuum, and therefore neglected the pressure perturbations of the external medium. Now if the external medium is other than a vacuum, the pressure perturbations of the external medium needs to be taken into consideration. As stated by Vasheghani Farahani et al. (2010), when the external medium is vacuum the only force acting against the internal total pressure and the centrifugal forces is the magnetic tension force due to the twist J0. However, in order to understand the interplay of all the effective forces acting on magnetic cylindrical structures, for instance a tornado in the solar atmosphere, the total external pressure needs to be taken into account. This could be taken care of by considering the physical parameters in the external medium proportional to R(r)exp i(ωt + kz), and the internal medium proportional to exp i(ωt + kz).

By solving the ideal MHD equations in the cylindrical geometry for the external medium, the perturbations of the plasma pressure would be 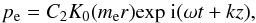(10)where C2 is a constant and K0 is the modified Bessel function of the second kind, with 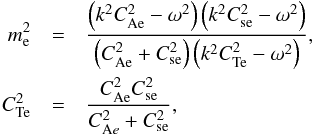(11)where CTe is the external tube speed. The external sound and Alfvén speeds are represented by Cse and CAe, respectively (Edwin & Roberts 1983). We note that for the internal medium the index e is dropped from the speeds. Since for the internal medium the physical parameters are first Taylor expanded and then plugged in the MHD equations, the amplitudes are independent of the radial component. By combining Eqs. (2)–(8) and substituting the perturbations of the internal and external media, the pressure balance on the boundary (r = a) of the tornado (Eq. (8)) gives (12)where we have α = J0/Bz0 and 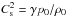. We note that CA is the axial Alfvén speed for the internal medium. In order to fulfil the requirements for tornado collimation, in addition to the pressure balance at the tornado boundary, the continuity of the radial velocity at the boundary also needs to be complied with. Therefore we write 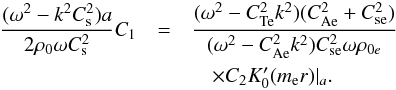(13)The term exp i(ωt + kz) has been eliminated from both sides of Eqs. (12) and (13). In order to eliminate C1 and C2 and write the dispersion relation, Eqs. (12) and (13) must be combined: (14)here the relation has been used (Abramowitz et al. 1988). The dispersion relation presented by Eq. (14), due to the consideration of the perturbations of the medium external to the structure, is a generalisation of the dispersion relation obtained in Zhugzhda (1996). We note that when a tends to zero, Eq. (14) simplifies to the dispersion relation obtained in the primary-order thin flux tube approximation. In the following the possible equilibrium conditions that a magnetic cylinder in the solar atmosphere may experience is studied.

2.1. Initially rotating untwisted tornado

Consider a rotating tornado with a straight magnetic field (Ω0 ≠ 0,J0 = 0). In this case, the dispersion relation (14) reduces to (15)The second term on the left-hand side of Eq. (15) shows the effect of the internal rotation where the third term indicates the confinement of the tube. The term on the right-hand side of Eq. (15) shows the effect of the perturbations of the external medium. If we write the dispersion relation in terms of the fast and slow speeds we would have (16)where (17)and the dimensionless parameter, ℛ, representing the rotation is (18)Equation (17) indicates the modification of the Alfvén speed and the tube speed by the equilibrium rotation to the fast (C+) and slow (C−) magnetosonic speeds, respectively (see also Zhugzhda & Nakariakov 1999; Vasheghani Farahani et al. 2010). As such the torsional wave would propagate with the speed C+, and the longitudinal wave would propagate with the speed C−. If we consider the dispersion to be weak (k2A0 ≪ 1), and take 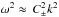, an explicit expression for the dispersion relation could be obtained 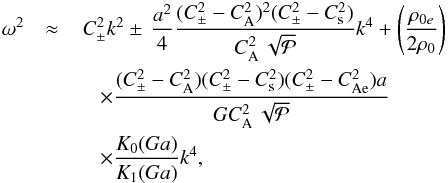(19)where 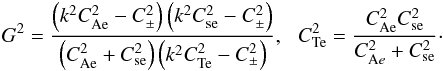(20)The second term on the right-hand side of Eq. (19) is the dispersive correction term, while the third term on the right-hand side represents the effects of the perturbation of the external medium. Equation (19) clearly shows the interplay of the equilibrium rotation and the density contrast of the internal and external media. The modification of the speeds at k = 0 is clearly exhibited by both the rotation and the density contrast. Hence, the modification of the tube and Alfvén speeds to the slow and fast magnetoacoustic speeds is clearly observed, see also Zhugzhda & Nakariakov (1999). In the long wavelength limit where the tube radius is much smaller than the wavelength, the dispersion would be week, therefore the arguments of the modified Bessel function of the second kind K would be small. In such a regime we are able to use the first terms of the expansions of the modified Bessel function of the second kind for small arguments (Abramowitz et al. 1988) which are 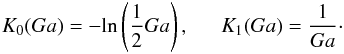(21)By substituting the terms of Eq. (21) in Eq. (19) we obtain an explicit expression that is easier to read: 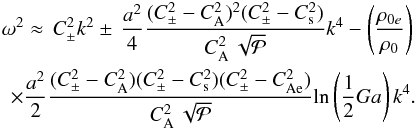(22)Equation (22) represents the dispersion relation for magnetoacoustic waves propagating in a steadily rotating magnetic flux tube (e.g. a solar tornado), which is more convenient for observation purposes and coronal seismology.

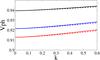thumbnail Fig. 2

Dispersion curves for the torsional wave for various density contrasts. The equilibrium twist is equal to zero and the equilibrium rotation ℛ is equal to 0.1 for all three sets. The black curves are for a density contrast of 4.6, the blue curves for a density contrast of 5.6, and the red curves for a density contrast of 5.9. The solid curves are obtained numerically from Eq. (14), while the dashed curves are plotted from the explicit expression of Eq. (22). The phase speeds are normalised by the internal Alfvén speed.

The effect of the equilibrium rotation on the phase speed of the torsional wave is visualised in Fig. 2. It can be readily seen from Fig. 2 that for an untwisted (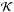) and rotating (ℛ = 0.1) magnetic cylinder, the phase speed of the torsional wave is proportional to the density contrast. This means that in this case the torsional wave is a collective mode (e.g. the fast magnetoacoustic kink mode) in contrast with the torsional waves in a cylinder with a straight field. The red, blue, and black curves are plotted for density contrasts respectively equal to 5.9, 5.6, and 4.6. The solid curves are obtained numerically from Eq. (14), while the dashed curves are plotted from the explicit expression of Eq. (22). The close agreement between the dashed and solid curves is an indication of the robustness of the explicit expression for the phase speed and dispersion of the torsional wave presented in this study.

2.2. Initially rotating and twisted tornado

We consider a magnetic cylinder with a twisted magnetic field which is initially rotating (J0 ≠ 0, Ω0 ≠ 0). The dispersion relation for coronal conditions where the plasma-β can be considered equal to zero would be (23)In the long wavelength limit where the tube radius is much smaller than the wavelength, an explicit version for the phase speed of the torsional wave can be written. We proceed by writing Eq. (23) in the form 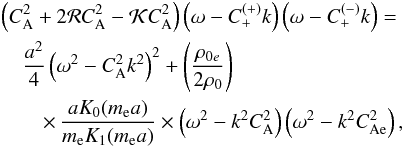(24)where 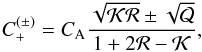(25)with 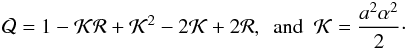(26)We note that the superscript plus-minus sign (±) for C+ represents the right-left propagation of the torsional wave. Hence we write 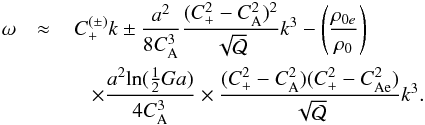(27)Equation (27) provides an explicit form for the phase speed and dispersion of the torsional wave. Equation (27) generalises Eqs. (81) and (27) of Zhugzhda (1996) and Vasheghani Farahani et al. (2010) by considering the perturbations of the pressure external to the coronal structure. It can be noticed from Eq. (25) that if the equilibrium twist and rotation are turned off, the speed of the torsional wave would be equal to the internal Alfvén speed, as it should be. Also, the phase speed of the torsional wave obtained by Eq. (27) would be equal to the speed of the torsional Alfvén wave, which complies with the concept of the torsional Alfvén wave that is incompressible and non-dispersive. Equation (27) clearly shows that the internal twist and rotation are responsible for the increase or decrease in the torsional wave speed (see also Zhugzhda & Nakariakov 1999; Vasheghani Farahani et al. 2010).

We now show how the equilibrium twist and rotation affect the compressibility of the torsional wave. Take the linear perturbation of the twist J equal to jaexp i(ωt + kz), where ja is a constant amplitude, and substitute it in Eqs. (2)–(8). The relation between the amplitude of J and ρ, at k = 0 is obtained as 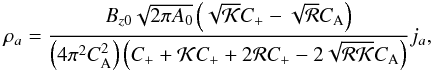(28)where if the equilibrium rotation is zero we have (Vasheghani Farahani et al. 2010) 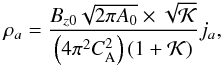(29)and if the equilibrium twist is zero we have 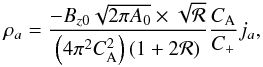(30)and if both the equilibrium twist and rotation are absent, the density perturbation in the linear torsional wave becomes zero. The effects of the equilibrium twist and rotation on the density perturbations are clearly observable in Eqs. (28), (29), and (30) since J represents the twist perturbations.

However, the density contrast of the internal and external media is also effective on the phase speed of the torsional wave. It can be seen from the three terms on the right-hand side of Eq. (27) that the perturbations of the external medium are not only responsible for the dispersion of the torsional wave, as the equilibrium twist and rotation are, but also effect the propagation speed of the wave at k = 0, as the equilibrium twist and rotation do. The interplay of these factors is plotted in Fig. 3, where the blue curve is plotted for the case where the tornado is initially twisted and non-rotating, the red curve is plotted for the case where the tornado is initially rotating and not twisted, and the black line is for an initially twisted and rotating tornado whose effects cancel each other out. It is seen that the dispersion effects cause a decrease in the speed of the wave propagation when the equilibrium rotation is absent, while the dispersion effects cause an increase in the speed of the wave propagation when the equilibrium twist is absent. However, when the normalised equilibrium parameters for twist and rotation (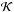 and ℛ) are equal, they cancel each other out leaving no effect on the Alfvén speed. This can be understood by looking at Eqs. (25)–(27); if 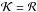then we would have 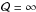, and hence 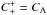. This makes the second and third terms on the right-hand side of Eq. (27) equal to zero, leaving ω = CAk. This justifies the behaviour of the black line in Fig. 3, where the perturbations of the external medium or the density contrast have not caused any shift in the torsional wave speed, leaving it propagating with the Alfvén speed without experiencing dispersion.

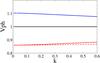thumbnail Fig. 3

Dispersion curves for the torsional wave. The black line is for the torsional wave when the equilibrium twist, , and rotation, ℛ, are both equal to 0.3. The red curves are for the torsional wave when the equilibrium rotation ℛ is equal to 0.3, but the equilibrium twist is equal to zero. The blue curve is for the torsional wave when the equilibrium Twist is equal to 0.3 but the equilibrium rotation is equal to zero. All three solid curves have been obtained numerically from Eq. (14). The red dashed curve is obtained from the explicit expression (Eq. (22)). The speeds are normalised by the internal Alfvén speed.

3. Discussions and conclusions

In the solar atmosphere MHD waves interact with the plasma. When a gradient in the density is present, a wave guide is created which leads to the appearance of collective modes. In this work a magnetised cylindrical structure whose density is higher than its surrounding has been taken into consideration. The collimation (Bisnovatyi-Kogan 2007) of such plasma structures, which could be initially static resembling a coronal jet or initially rotating resembling a solar tornado, has been studied. The interplay of the equilibrium twist and rotation exhibits interesting features of the nature of the torsional wave, which is of interest for coronal seismology. We considered a twisted and rotating magnetic flux tube which resembles a solar tornado and studied the propagation of the torsional wave in the long wavelength limit. The analytic expressions obtained for the dependence of the phase speed of the torsional wave on the equilibrium twist and rotation enabled a quantitative study on the interplay of various actors on its propagation. In all cases, the comparison of the explicit expressions obtained for the phase speed of the torsional wave in the present study with the implicit version proved adequate for the robustness of the explicit expressions. This is reflected in the figures where the numerical results are compared with analytic solutions. We summarise our findings as follows:

  • 1.

    An explicit expression for the dispersion relation and phase speeds of the torsional wave propagating in a solar tornado (Eq. (22)) has been provided in the long wavelength limit. The good agreement between the numerical results and analytic solutions for the phase speed of the torsional wave proves adequate for the robustness of the expressions.

  • 2.

    For an initially rotating magnetic flux tube, the propagation speed of the torsional wave is proportional to the density contrast of the internal and external environments. The density ratio may compensate for some of the phase speed reduction caused by the equilibrium rotation (see Fig. 2). This effect is connected with the collective (magnetoacoustic) nature of the torsional wave, where in this case its phase speed is determined by the Alfvén waves inside and outside the waveguide.

  • 3.

    The interplay of the equilibrium twist and rotation together with the density contrast of the internal and external media shows that whenever the equilibrium twist and rotation cancel out each other’s effects, the density contrast does not affect the propagation speed and allows the wave to propagate with the Alfvén speed being incompressible and non-dispersive. But whenever either the equilibrium twist or the rotation is present, the density contrast has an effect and acts as a speed modifier (see Fig. 2).

Hence, we conclude that the speed of the torsional wave propagating in a magnetic plasma structure highly depends on the equilibrium twist and rotation. In the case where the equilibrium twist and rotation cancel out each other’s effects, the phase speed of the torsional wave would be independent of the perturbations of the external medium and the density contrast. The density contrast between the tornado and its external medium comes into play if either the equilibrium twist or rotation becomes dominant. However, when the equilibrium twist or rotation – or both – is present, the density contrast acts to increase or decrease the phase speed at the long wave length limit (k = 0). In such conditions, by departing from k = 0 the phase speed of the torsional wave descends from its value at k = 0 if the twist is dominant, and ascends from its value at k = 0 if the rotation is dominant. This means that in either case the torsional wave is compressible and dispersive. Whenever the equilibrium twist and rotation cancel out each other’s effects, the density contrast does not affect the torsional polarised wave and leaves the wave incompressible and non-dispersive with propagating speed equal to the Alfvén wave speed. The phase speed of the torsional wave at k = 0 could be either elevated or reduced by the equilibrium configuration of the tornado and therefore proves adequate to have applications in coronal seismology. This means that in order to observe the torsional wave, the propagation and speed readings need careful consideration since they must not be mistaken with torsional Alfvén waves which are non-dispersive and incompressible.

References

  1. Abramowitz, M., Stegun, I. A., & Romer, R. H. 1988, Am. J. Phys., 56, 958 [NASA ADS] [CrossRef] [Google Scholar]
  2. Banerjee, D., Pérez-Suárez, D., & Doyle, J. G. 2009, A&A, 501, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bisnovatyi-Kogan, G. S. 2007, MNRAS, 376, 457 [NASA ADS] [CrossRef] [Google Scholar]
  4. Charbonneau, P., & MacGregor, K. B. 1995, ApJ, 454, 901 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Cranmer, S. R. 2009, Liv. Rev. Sol. Phys., 6, 3 [Google Scholar]
  7. Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
  8. Fletcher, L., & Hudson, H. S. 2008, ApJ, 675, 1645 [NASA ADS] [CrossRef] [Google Scholar]
  9. Harrison, R. A. 1999, J. British Interplanetary Society, 52, 434 [NASA ADS] [Google Scholar]
  10. Hood, A. W., Archontis, V., Galsgaard, K., & Moreno-Insertis, F. 2009, A&A, 503, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Jess, D. B., Mathioudakis, M., Erdélyi, R., et al. 2009, Science, 323, 1582 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Levens, P. J., Labrosse, N., Fletcher, L., & Schmieder, B. 2015, A&A, 582, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Li, X., Morgan, H., Leonard, D., & Jeska, L. 2012, ApJ, 752, L22 [NASA ADS] [CrossRef] [Google Scholar]
  14. Nakariakov, V. M., & Verwichte, E. 2005, Liv. Rev. Sol. Phys., 2, 3 [Google Scholar]
  15. Ofman, L. 2005, Space Sci. Rev., 120, 67 [NASA ADS] [CrossRef] [Google Scholar]
  16. Pike, C. D., & Mason, H. E. 1998, Sol. Phys., 182, 333 [NASA ADS] [CrossRef] [Google Scholar]
  17. Roberts, B. 1981, Sol. Phys., 69, 27 [NASA ADS] [CrossRef] [Google Scholar]
  18. Roberts, B., & Webb, A. R. 1978, Sol. Phys., 56, 5 [NASA ADS] [CrossRef] [Google Scholar]
  19. Shelyag, S., Cally, P. S., Reid, A., & Mathioudakis, M. 2013, ApJ, 776, L4 [NASA ADS] [CrossRef] [Google Scholar]
  20. Suzuki, T. K. 2007, ApJ, 659, 1592 [NASA ADS] [CrossRef] [Google Scholar]
  21. Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2008, ApJ, 676, L73 [NASA ADS] [CrossRef] [Google Scholar]
  22. Vasheghani Farahani, S., Van Doorsselaere, T., Verwichte, E., & Nakariakov, V. M. 2009, A&A, 498, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Vasheghani Farahani, S., Nakariakov, V. M., & Van Doorsselaere, T. 2010, A&A, 517, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Webb, A. R., & Roberts, B. 1978, Sol. Phys., 59, 249 [NASA ADS] [CrossRef] [Google Scholar]
  25. Wedemeyer, S., & Steiner, O. 2014, PASJ, 66, S10 [NASA ADS] [CrossRef] [Google Scholar]
  26. Wedemeyer-Böhm, S., Scullion, E., Steiner, O., et al. 2012, Nature, 486, 505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Zhugzhda, Y. D. 1996, Phys. Plasmas, 3, 10 [NASA ADS] [CrossRef] [Google Scholar]
  28. Zhugzhda, Y. D., & Nakariakov, V. M. 1999, Phys. Lett. A, 252, 222 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Schematic view of a solar tornado.
In the text
thumbnail Fig. 2

Dispersion curves for the torsional wave for various density contrasts. The equilibrium twist is equal to zero and the equilibrium rotation ℛ is equal to 0.1 for all three sets. The black curves are for a density contrast of 4.6, the blue curves for a density contrast of 5.6, and the red curves for a density contrast of 5.9. The solid curves are obtained numerically from Eq. (14), while the dashed curves are plotted from the explicit expression of Eq. (22). The phase speeds are normalised by the internal Alfvén speed.
In the text
thumbnail Fig. 3

Dispersion curves for the torsional wave. The black line is for the torsional wave when the equilibrium twist, , and rotation, ℛ, are both equal to 0.3. The red curves are for the torsional wave when the equilibrium rotation ℛ is equal to 0.3, but the equilibrium twist is equal to zero. The blue curve is for the torsional wave when the equilibrium Twist is equal to 0.3 but the equilibrium rotation is equal to zero. All three solid curves have been obtained numerically from Eq. (14). The red dashed curve is obtained from the explicit expression (Eq. (22)). The speeds are normalised by the internal Alfvén speed.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.