| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201629285 | |
| Published online | 07 February 2017 | |
Magnetorotational dynamo chimeras
The missing link to turbulent accretion disk dynamo models?⋆
1 Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
e-mail: ar764@cam.ac.uk
2 Université de Toulouse, UPS-OMP, IRAP Toulouse, 31400 Toulouse, France
e-mail: francois.rincon@irap.omp.eu
3 CNRS, IRAP, 14 avenue Édouard Belin, 31400 Toulouse, France
4 Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS – Université de Toulouse, Allée du Professeur Camille Soula, 31400 Toulouse, France
5 CNRS, IPAG, 38000 Grenoble, France
6 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
Received: 11 July 2016
Accepted: 21 October 2016
In Keplerian accretion disks, turbulence and magnetic fields may be jointly excited through a subcritical dynamo mechanisminvolving magnetorotational instability (MRI). This dynamo may notably contribute to explaining the time-variability of various accreting systems, as high-resolution simulations of MRI dynamo turbulence exhibit statistical self-organization into large-scale cyclic dynamics. However, understanding the physics underlying these statistical states and assessing their exact astrophysical relevance is theoretically challenging. The study of simple periodic nonlinear MRI dynamo solutions has recently proven useful in this respect, and has highlighted the role of turbulent magnetic diffusion in the seeming impossibility of a dynamo at low magnetic Prandtl number (Pm), a common regime in disks. Arguably though, these simple laminar structures may not be fully representative of the complex, statistically self-organized states expected in astrophysical regimes. Here, we aim at closing this seeming discrepancy by reporting the numerical discovery of exactly periodic, yet semi-statistical “chimeral MRI dynamo states” which are the organized outcome of a succession of MRI-unstable, non-axisymmetric dynamical stages of different forms and amplitudes. Interestingly, these states, while reminiscent of the statistical complexity of turbulent simulations, involve the same physical principles as simpler laminar cycles, and their analysis further confirms the theory that subcritical turbulent magnetic diffusion impedes the sustainment of an MRI dynamo at low Pm. Overall, chimera dynamo cycles therefore offer an unprecedented dual physical and statistical perspective on dynamos in rotating shear flows, which may prove useful in devising more accurate, yet intuitive mean-field models of time-dependent turbulent disk dynamos.
Key words: accretion, accretion disks / dynamo / instabilities / magnetohydrodynamics (MHD) / turbulence
Movies associated to Fig. 1 are available at http://www.aanda.org
© ESO, 2017
1. Introduction
The dynamics and evolution of many accreting astrophysical systems ranging from active galactic nuclei (AGNs) to protoplanetary systems are intrinsically strongly coupled to that of their magnetic fields. This coupling occurs through a variety of complex physical processes whose local and global effects have proven and remain very difficult to describe and model consistently (Balbus & Hawley 1998; Frank et al. 2002; Hartmann 2009; Armitage 2010).
At the heart of this problem lies the magnetorotational instability (MRI; Velikhov 1959; Chandrasekhar 1960; Balbus & Hawley 1991), which provides one of the most important channels by which matter can be accreted from a disk to a central accreting object. In the presence of an externally-imposed net vertical magnetic flux in a disk, the MRI may act as a powerful linear instability which arbitrarily amplifies small perturbations that break down nonlinearly into magnetohydrodynamic (MHD) turbulence (Hawley et al. 1995; Stone et al. 1996). The efficiency of MRI turbulence at driving accretion through the turbulent transport of angular momentum, however, remains a matter of debate, and may depend on the subtle details of dissipative physics. Turbulent-MRI transport may notably be limited in the astrophysically relevant regime of low magnetic Prandtl number (Pm), where Pm denotes the ratio between the kinematic viscosity and magnetic diffusivity of the fluid (Lesur & Longaretti 2007; Balbus & Henri 2008; Meheut et al. 2015, see also Lesur et al. 2014, for other critical microphysical effects).
An important related problem in the context of magnetized accretion is that of the origin and dynamical evolution of the system’s magnetic field itself. In the absence of an external field rooted in the central accreting object, a MRI-supporting magnetic field may nevertheless be generated and sustained inside the disk by a dynamo process. Notably, it has recently been suggested that such a dynamo could drive X-ray binary transitions (Begelman et al. 2015). A plausible dynamo candidate in disks is the so-called subcritical MRI dynamo, by which MHD perturbations excited by the MRI nonlinearly sustain the large-scale field that made the instability possible in the first place (Hawley et al. 1995, 1996; Rincon et al. 2007; Lesur & Ogilvie 2008a; Rincon et al. 2008). Simulations of zero net magnetic flux configurations have shown that this process can be self-sustaining and lead to MHD turbulence that transports significant angular momentum. Interestingly, many simulations of MRI dynamo turbulence also exhibit self-organized large-scale dynamics characterised by chaotic reversals of the large-scale magnetic field, somewhat reminiscent of the “butterfly” diagram of the solar dynamo (Brandenburg et al. 1995; Davis et al. 2010; Simon et al. 2011; Gressel & Pessah 2015).
The viability of a MRI dynamo process in disks remains unclear though, as it also appears to be dependent on dissipative physics. More specifically, numerical studies explicitly taking into account dissipative processes suggest that a MRI dynamo is not possible at Pm ≲ 1 (Fromang et al. 2007). The highest-resolution incompressible simulations to date indicate that no MRI dynamo can be excited at Pm = 1 for magnetic Reynolds numbers (Rm) as large as Rm = 45 000 (Walker et al. 2016), although other studies have found some dependence of this effect on geometry and stratification (Oishi & Mac Low 2011; Shi et al. 2016). This seeming dependence of the dynamo, and more generally of MRI turbulence, on Pm and Rm (at least at moderate Rm) may also have implications for the time-variability of accreting systems such as cataclysmic variables involving a white dwarf, and other accreting compact objects, as it directly connects the magnetic and thermal activity of their accretion disks through the strong thermal dependence of these non-dimensional quantities (Gammie & Menou 1998; Balbus & Henri 2008; Latter & Papaloizou 2012; Potter & Balbus 2014, see also Hirose et al. 2014, for another possible connection).
Overall, a detailed physical understanding of the different processes that cooperate in the subcritical MRI dynamo therefore appears to be required to make better sense of these different numerical results, to assess the exact astrophysical relevance of the MRI dynamo, and to construct effective global models of magnetized accretion disk dynamics. This problem is, however, theoretically very challenging. While direct, high-resolution, numerical simulations factually reveal the process of statistical magnetic self-organization, they are not particularly enlightening as far as formulating a physically-grounded effective statistical dynamo model is concerned. Detailed studies of the three-dimensional dynamics in simplified set-ups and in transitional (mildly turbulent) regimes provide an interesting alternative avenue of research to identify and understand the key physical elements in this problem.
Using this approach, it has notably been shown that simple three-dimensional nonlinear periodic dynamo solutions of the MHD equations (Herault et al. 2011, hereafter H11) computed with a Newton solver provide the first germs of nonlinear MRI dynamo excitation in the Keplerian differential rotation regime in azimuthally elongated shearing box numerical configurations at transitional kinematic (Re) and magnetic Reynolds numbers (Riols et al. 2013, hereafter R13). Further analysis of the energy budget of a few such cycles has also recently proven useful to pinpoint the possible role of a “subcritical” turbulent magnetic diffusion in the seeming decay of the dynamics at low Pm (Riols et al. 2015, hereafter referred to as R15).
One possible caveat with this approach so far, though, has been the lack of demonstrated connection between these spatially-elongated laminar structures and developed, statistically self-organized, turbulent MHD states (“MRI dynamo butterflies”) produced in generic, moderate aspect ratio simulations at larger Re and Rm. In order to bridge part of this gap and establish such a connection, one would have to find periodic solutions with a higher degree of dynamical complexity and statistical organization than the simple cycles already identified, but whose dynamics can still be understood in relatively simple physical terms. Isolating and computing such nonlinear periodic solutions in more turbulent regimes and moderate aspect ratio domains typical of high-resolution simulations is, however, significantly harder, owing to the larger number of degrees of freedom available in such configurations.
The aim of this paper is to present the first three-dimensional nonlinear periodic MRI dynamo solutions of this kind, which we have finally managed to compute thanks to our earlier foundational work on the problem. We call these cycles MRI dynamo chimeras because they are the organized outcome of a succession of MRI-unstable, non-axisymmetric dynamical stages of different forms and amplitudes. Remarkably, while the dynamical complexity of these solutions is reminiscent of the statistical organization observed in generic numerical simulations, their sustainment rests on the exact same few linear and nonlinear processes underlying the dynamics of simpler cycles. As we shall see, this unprecedented, dual physical and statistical perspective on the MRI dynamo problem raises interesting prospects for the statistical modeling of turbulent accretion disk dynamos.
The mathematical and numerical frameworks of our study, as well as a discussion of the dependence of the problem on the aspect ratio, are presented in Sect. 2. Section 3 documents the dynamical properties of two new pairs of dynamically complex chimera MRI dynamo cycles computed in moderate aspect ratio configurations with a Newton-Krylov algorithm, and shows that their existence is limited to Pm larger than a critical value close to 1. Section 4 extends the magnetic energy budget analysis of R15 to these structures, and shows that the enhancement of nonlinear transfers of magnetic energy to small scales at large Re (“subcritical turbulent magnetic diffusion”) prevents the sustainment of these structures at lower Pm, just as in the case of simpler cycles. In Sect. 5, we discuss the semi-statistical nature of these new cycles and the new perspectives that their computation opens for the development of more accurate, yet intuitive statistical models of Keplerian dynamos (and more generally instability-driven dynamos). A summary of the main conclusions and a short discussion of how the results may fit into the wider astrophysical context conclude the paper.
2. Equations and numerical framework
2.1. Model
The equations and numerical frameworks used in the present study have been described extensively in R13. We recall only the essential points here, but provide detailed pointers to the relevant technical literature when necessary. We use the cartesian local shearing sheet description of differentially rotating flows (Goldreich & Lynden-Bell 1965), whereby the axisymmetric differential rotation is approximated locally by a linear shear flow Ux = −Sxey, and a uniform rotation rate Ω = Ω ez, with Ω = (2/3)S for a Keplerian shear flow. Here (x,y,z) are, respectively, the shearwise, streamwise and spanwise directions, corresponding to the radial, azimuthal and vertical directions in accretion disks. We refer to the (x,z) projection of vector fields as their poloidal components and to the y direction as their toroidal (azimuthal) one. We ignore stratification and compressible effects. The evolution of the three-dimensional velocity field perturbations u and magnetic field B is governed by the three-dimensional incompressible, dissipative MHD equations: ![\begin{eqnarray} \label{div}&&\nabla \cdot\vec{u}=0, \quad \nabla\cdot\vec{B}=0.~~~ \\[3mm] \label{velocity_eq}&&\frac{\partial{\vec{u}}}{\partial{t}}\!-\!Sx\frac{\partial{\vec{u}}}{\partial{y}}+\vec{u}\cdot\vec{\nabla u} \!=\! -2\vec{\boldsymbol{\Omega}}\times\vec{u}+Su_x\vec{e}_y-\vec{\nabla}\Pi+\vec{B}\cdot\vec{\nabla B}+\nu\vec{\Delta u}, \\[3mm] \label{magnetic_eq}&&\frac{\partial{\vec{B}}}{\partial{t}}-Sx\frac{\partial{\vec{B}}}{\partial{y}} = -SB_x\vec{e}_y+\nabla\times(\vec{u}\times\vec{B})+\eta\vec{\Delta B}, \end{eqnarray}](/articles/aa/full_html/2017/02/aa29285-16/aa29285-16-eq12.png) where Π is the sum of the gas and magnetic pressure. The density is fixed to ρ = 1. The kinematic and magnetic Reynolds numbers are defined by Re = SL2/ν and Rm = SL2/η, where ν and η are the constant kinematic viscosity and magnetic diffusivity, L is a typical scale of the spatial domain and time is measured with respect to S-1. The magnetic Prandtl number is Pm = ν/η = Rm/Re. B is expressed in terms of an alfvénic velocity. Both u and B are measured in units of SL.
where Π is the sum of the gas and magnetic pressure. The density is fixed to ρ = 1. The kinematic and magnetic Reynolds numbers are defined by Re = SL2/ν and Rm = SL2/η, where ν and η are the constant kinematic viscosity and magnetic diffusivity, L is a typical scale of the spatial domain and time is measured with respect to S-1. The magnetic Prandtl number is Pm = ν/η = Rm/Re. B is expressed in terms of an alfvénic velocity. Both u and B are measured in units of SL.
2.2. Numerical methods
We use the SNOOPY code (Lesur & Longaretti 2007) to perform direct numerical simulations (DNS) of Eqs. (1)–(3). This code provides a spectral implementation of the so-called numerical shearing box model of the shearing sheet, in a finite domain of size (Lx,Ly,Lz), at numerical resolution (Nx,Ny,Nz). The x and y directions are taken as periodic, while shear-periodicity is imposed in x. As the box is shear-periodic, any numerical solution can be decomposed into a set of shearing Fourier modes with wavenumbers 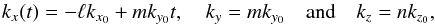 (4)where kx0 = 2π/Lx, ky0 = 2π/Ly, kz0 = 2π/Lz (a detailed description of the spectral decomposition used in the simulations is provided in R13, Appendix A). A shearing wave is a non-axisymmetric wave with m ≠ 0. Because of the shear-periodicity in x, the radial Eulerian wavenumber kx of a given shearing wave increases linearly in time (ℓ is the corresponding integer Lagrangian wavenumber). The wave is “leading” when kxky< 0 and “trailing” when kxky> 0.
(4)where kx0 = 2π/Lx, ky0 = 2π/Ly, kz0 = 2π/Lz (a detailed description of the spectral decomposition used in the simulations is provided in R13, Appendix A). A shearing wave is a non-axisymmetric wave with m ≠ 0. Because of the shear-periodicity in x, the radial Eulerian wavenumber kx of a given shearing wave increases linearly in time (ℓ is the corresponding integer Lagrangian wavenumber). The wave is “leading” when kxky< 0 and “trailing” when kxky> 0.
Nonlinear periodic solutions are computed with the Newton-Krylov solver PEANUTS interfaced to SNOOPY (both described in detail in R13, Appendices A and B), and followed in parameter space using arclength continuation (Keller 1982). We enforce that the dynamics take place in the symmetric subspace defined in R13, Appendix A.4 to facilitate the analysis (this does not compromise the underlying dynamical complexity), and notably monitor the axisymmetric MRI-supporting field 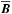 ((x−y) average of B), or, more specifically, its energetically dominant Fourier mode
((x−y) average of B), or, more specifically, its energetically dominant Fourier mode 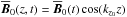 .
.
2.3. Large vs. moderate aspect ratio
In H11, R13 and R15, the nonlinear dynamics was restricted to elongated boxes in the azimuthal direction with typical azimuthal to radial aspect ratio Ly/Lx ~ 30. The main reason for this choice was to simplify the dynamics as much as possible and reduce the number of coexisting cyclic solutions. Indeed, at low Re and Rm (defined on Lx ~ Lz) and Ly/Lx ≫ 1 the dynamics in the (Lx,Lz) plane remains relatively laminar but the dissipation of non-axisymmetric structures is sufficiently small that (just a few) weakly nonlinear three-dimensional structures can be sustained. H11 showed that the sustainment of these large-aspect ratio cycles can be understood in generic physical terms involving shearing effects, the linear physics of non-axisymmetric MRI-unstable perturbations, and nonlinear feedback mechanisms. One may nevertheless argue that large-aspect ratio configurations are somewhat unnatural, and that their connection with turbulent MRI dynamo simulations conducted at moderate aspect ratio is not established.
Here, we therefore attempt to extend this “cycle hunt” to moderate aspect ratios, down to Ly/Lx ~ 4. Because ky0 is larger in this configuration, non-axisymmetric shearing waves are sheared out and dissipated faster for a given set of Re and Rm (once again defined on Lx ~ Lz). Hence, one has to go to larger Re and Rm (typically Rm ~ 3000 for Ly/Lx ~ 4) to recover the first germs of sustained (recurrent) MRI dynamo activity. Doing so, however, also implies that the dynamics in the (Lx,Lz) plane is more complex than in the large aspect ratio case because of the larger available number of poloidal dynamical degrees of freedom. The two main consequences, from the perspective of capturing nonlinear solutions, are that a larger number of them coexist in the phase space of the problem for a given Re and Rm, making it more difficult to converge on any of them, and that resolving them requires a large numerical resolution. The latter is a significant hurdle in this context, as computing a single cyclic solution with a Newton-Krylov algorithm requires many DNS integrations. The resolution used in this study is (48,48,72), ensuring convergence for all parameters considered, but a number of results were also reproduced at the (very computationally demanding) double resolution (96,96,144).
3. Chimera MRI dynamo cycles
3.1. Dynamical structure of the solutions
 |
Fig. 1 Temporal evolution and dynamical decomposition of the lower branch solutions LB1m (left) and LB2m (right). LB1m is shown for Re = 100, Rm = 900 and LB2m for Re = 908, Rm = 3033. From top to bottom, axisymmetric field |
The general method to identify MRI dynamo cycles is to explore the phase space of the system numerically by constructing turbulence lifetime maps using many different simulations initialised with different initial conditions. This technique, described in detail in R13, (Sect. 3 and Figs. 3, 4), makes it possible to isolate islands of recurrent or chaotic dynamics in phase space. Once an initial condition leading to fairly recurrent dynamics is spotted, we use the Newton-Krylov solver to refine the initial condition until a periodic solution is achieved. Using this technique in moderate aspect ratio boxes, we managed to capture two pairs of nonlinear periodic solutions. The first one, labelled SN1m, was found in a box of dimensions (Lx,Ly,Lz) = (0.7,6,2) and has a period TSN1m = 6 S-1Ly/Lx = 51.4 S-1. The second one, labelled SN2m, was found in a (Lx,Ly,Lz) = (0.5,2,1) box, and has a slightly shorter period TSN2m = 5 S-1Ly/Lx = 20 S-1. Each pair of solutions is born out of a saddle node bifurcation and is therefore composed of a lower branch cycle and an upper branch cycle. These solutions are distinct from the different cycle pairs studied by H11 and R13. Crucially, these new solutions, unlike earlier ones, exhibit some statistical organization.
The temporal evolutions of LB1m (LB2m), the lower branch of SN1m (respectively SN2m), are shown in Fig. 1. From a physical point of view, the essential mechanisms and self-sustaining nonlinear process underlying the dynamics of these two cycles are identical to those described by Rincon et al. (2007) and H11. The large-scale axisymmetric component of the field  renders non-axisymmetric velocity and magnetic perturbations unstable to the MRI in the Keplerian flow. For simplicity, we refer to these perturbations as non-axisymmetric MRI-unstable shearing wave packets. Note that we use this nomenclature because the MRI-unstable perturbations taking part in the dynamics documented in both H11 and in the present paper are essentially supported by non-axisymmetric m = 1 shearing Fourier modes. However, these perturbations are not reducible to a single Fourier mode in z, unlike in the uniform toroidal field case (Balbus & Hawley 1992), because the large-scale axisymmetric MRI-supporting “dynamo” field
renders non-axisymmetric velocity and magnetic perturbations unstable to the MRI in the Keplerian flow. For simplicity, we refer to these perturbations as non-axisymmetric MRI-unstable shearing wave packets. Note that we use this nomenclature because the MRI-unstable perturbations taking part in the dynamics documented in both H11 and in the present paper are essentially supported by non-axisymmetric m = 1 shearing Fourier modes. However, these perturbations are not reducible to a single Fourier mode in z, unlike in the uniform toroidal field case (Balbus & Hawley 1992), because the large-scale axisymmetric MRI-supporting “dynamo” field  is non-uniform in z. More specifically, for the class of solutions considered here and in H11, the z-dependence of m = 1 velocity perturbations is decomposed in z as a sum over Fourier modes with odd n, and that of magnetic perturbations as a sum over even n (see Appendix of H11). Magnetic perturbations b with m = 1 and even n are linearly coupled to velocity perturbations v with m = 1 and odd n through inductive and Lorentz force terms
is non-uniform in z. More specifically, for the class of solutions considered here and in H11, the z-dependence of m = 1 velocity perturbations is decomposed in z as a sum over Fourier modes with odd n, and that of magnetic perturbations as a sum over even n (see Appendix of H11). Magnetic perturbations b with m = 1 and even n are linearly coupled to velocity perturbations v with m = 1 and odd n through inductive and Lorentz force terms 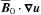 and
and 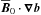 involving the non-uniform MRI-supporting axisymmetric azimuthal field
involving the non-uniform MRI-supporting axisymmetric azimuthal field 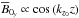 characterized by (m = 0,n = 0). These couplings mediate the MRI. In all cases considered, we found that velocity perturbations are dominated by (m = 1,n = 1), and magnetic perturbations by (m = 1,n = 0) in the linear MRI growth phase.
characterized by (m = 0,n = 0). These couplings mediate the MRI. In all cases considered, we found that velocity perturbations are dominated by (m = 1,n = 1), and magnetic perturbations by (m = 1,n = 0) in the linear MRI growth phase.
As they swing and their amplitude grows, these shearing wave packets transfer energy back to  through nonlinear energy transfers in the form of a quadratic axisymmetric electromotive force (EMF)
through nonlinear energy transfers in the form of a quadratic axisymmetric electromotive force (EMF) 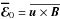 , sustaining it against resistive effects (see Figs. 2 and 4 of H11 for detailed schematics and visualizations of the self-sustained dynamics).
, sustaining it against resistive effects (see Figs. 2 and 4 of H11 for detailed schematics and visualizations of the self-sustained dynamics).
From a statistical dynamics point of view though, we find that the complexity of SN1m and SN2m is significantly larger than that of cycles previously found in longer aspect ratio boxes. Specifically,
-
1.
the successive reversals of
 are asymmetric in time;
are asymmetric in time; -
2.
each large-scale field reversal results from the accumulated nonlinear self-interactions of several successive MRI-unstable shearing wave packets, regularly separated in time by Ly/LxS-1 (the quantized time separation is a consequence of the symmetries of the shearing box model);
-
3.
different shearing wave packets have a different energy content and polarization, and therefore they do not contribute equally to the large-scale field reversals.
These different properties are also illustrated in Fig. 1. In the case of LB1m, the first reversal (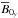 going from positive to negative) is caused by the combined action of three successive non-axisymmetric wave packets with different relative amplitudes (represented by dark blue, blue and cyan curves in the bottom panel). The second reversal also results from the combined action of three distinct wave packets (represented by green to yellow colors) with different relative amplitudes. The amplitudes of the second series of waves are also different from those of the first series, resulting in asymmetric
going from positive to negative) is caused by the combined action of three successive non-axisymmetric wave packets with different relative amplitudes (represented by dark blue, blue and cyan curves in the bottom panel). The second reversal also results from the combined action of three distinct wave packets (represented by green to yellow colors) with different relative amplitudes. The amplitudes of the second series of waves are also different from those of the first series, resulting in asymmetric  reversals. For LB2m, the asymmetry is even more pronounced: the first reversal only involves two wave packets, while the second involves three of them. Note that the period of LB1m and LB2m can be inferred directly from the product Ly/LxS-1 multiplied by the number of waves packets implicated in the cycle, because of the time quantization imposed by the symmetries of the shearing box. Finally, although the dynamics of the MRI-supporting field
reversals. For LB2m, the asymmetry is even more pronounced: the first reversal only involves two wave packets, while the second involves three of them. Note that the period of LB1m and LB2m can be inferred directly from the product Ly/LxS-1 multiplied by the number of waves packets implicated in the cycle, because of the time quantization imposed by the symmetries of the shearing box. Finally, although the dynamics of the MRI-supporting field  is governed by the cumulative action of shearing wave packets, Fig. 1 shows that only a fraction of them are significantly amplified by the MRI and contribute to the EMF. We find that the evolution of these shearing wave packets, from the leading to the trailing phase, is influenced by nonlinear effects on top of their linear MRI amplification.
is governed by the cumulative action of shearing wave packets, Fig. 1 shows that only a fraction of them are significantly amplified by the MRI and contribute to the EMF. We find that the evolution of these shearing wave packets, from the leading to the trailing phase, is influenced by nonlinear effects on top of their linear MRI amplification.
 |
Fig. 2 Left, top panel: selected continuation curves in Rm of SN2m at fixed Re; bottom panel: selected continuation curves in Re at fixed Rm. Right: existence boundary of SN2m in the (Re, Rm) plane (blue/dashed line) obtained by interpolating the different saddle node points Rmc(Re) and Rec(Rm) (blue bullets). The orange area shows the domain of existence of SN2m in parameter space. The red bullet shows a saddle note bifurcation point computed at double resolution (96 × 96 × 144). |
The overall dynamical behaviour of these new “chimera” cycles is therefore remarkable in the sense that it can still be understood in terms of simple building blocks of a nonlinear self-sustanining MRI dynamo process, but is also reminiscent of the fully turbulent butterfly dynamo states observed in generic MRI dynamo simulations (see, for example, the results of the incompressible simulations of Lesur & Ogilvie 2008a, for (Lx,Ly,Lz) = (0.5,2,1)). We exploit this new dual perspective in our discussion of future directions for the statistical modeling of accretion disk dynamos in Sect. 5.
The structure of these solutions finally suggests that self-sustained dynamo cycles with an arbitrarily long period can be constructed from successive MRI-unstable shearing wave packets (each new MRI-unstable shearing wave packet involved in the dynamics of the chimera cycles is generated consistently through a nonlinear physical process of scattering of its predecessor off the radially modulated axisymmetric magnetic field, see H11).
3.2. Cycle continuations and existence boundaries
In order to understand the physical origin of the dependence of the MRI dynamo on dissipative processes, R13 and R15 performed continuations in parameter space of different nonlinear cycles in elongated boxes, and found that their existence is systematically limited to Pm larger than unity. In order to determine if this effect is generic, we performed a similar analysis on the statistically-organized chimera cycle SN2m pair in the (Lx,Ly,Lz) = (0.5,2,1) box. Although the full dynamics in this precise geometry almost certainly involves many other cycles, this is the only nonlinear periodic solution that we managed to compute and follow accurately in parameter space for this box.
Figure 2 (left) shows selected continuation curves for SN2m. Each continuation curve in Fig. 2 (left) represents approximatively 10 000 direct numerical simulations at resolution 48 × 48 × 72. In addition, each branch can encounter many secondary bifurcations, which makes it hard to follow and complete them. We checked the numerical convergence of the results by doubling the resolution in a few cases. At fixed Re, these curves present a turning point at a critical Rmc(Re), confirming that SN2m is born out of a saddle node bifurcation. At fixed Rm, we find that this pair of cycles exists only for a finite range of Re, whose upper bound increases as Rm increases. The domain of existence of SN2m in parameter space, shown in Fig. 2 (right), is obtained by combining all the computed critical Rmc(Re) and Rec(Rm). The cycle existence is restricted to a region of Pm larger than unity for the range of Rm that could be probed. These continuations require a large computational effort. Hence, the results suggest that the conclusion of R13 and R15, that MRI dynamo cycles are only sustained in the region of Pm larger than unity, also holds for statistically-organized chimera cycles in moderate aspect ratio boxes.
4. Energy budgets and turbulent dissipation
Studying the magnetic energy transfers between different modes involved in periodic nonlinear dynamics has previously proven useful in identifying possible physical reasons for the seeming decay of the MRI dynamo at low Pm, and represents an important step towards a rigorous statistical description of this kind of dynamo. R15 showed that the subcritical “turbulent” magnetic diffusion associated with the development of a nonlinear cascade of MRI-unstable fluctuations to smaller scales at increasing Re has a destructive effect on both the large-scale MRI-supporting field and MRI-unstable fluctuations, and may explain the disappearance of dynamo cycles at moderate Rm and low Pm in large aspect ratio boxes. Here, we aim to determine if the same conclusions hold for statistically-organized chimera cycles whose dynamics is arguably more directly representative of high-resolution simulation results.
For this purpose, we examine the energy budget of the saddle node pair SN2m. This analysis is relatively technical, and may be skipped by readers not interested in the details. Its conclusions are summarized in Sect. 6.
4.1. Energetics of the MRI supporting field 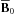
The MRI dynamo intrinsically relies on the sustainment of a large-scale MRI-supporting magnetic field component against dissipative processes, which in shearing box simulations is dominated by the axisymmetric  . It is then of primary importance to analyse the energy budget of
. It is then of primary importance to analyse the energy budget of  over a full cycle period TSN2m = 5 S-1Ly/Lx = 20 S-1,
over a full cycle period TSN2m = 5 S-1Ly/Lx = 20 S-1, 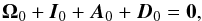 (5)where
(5)where 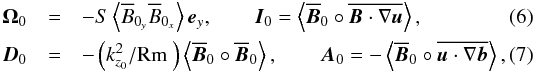 and ⟨⟩ denotes the average volume and cycle period and ° the entrywise product [(X°Y)i = XiYi]. Ω0, I0, A0 and D0 are the energetic contributions to
and ⟨⟩ denotes the average volume and cycle period and ° the entrywise product [(X°Y)i = XiYi]. Ω0, I0, A0 and D0 are the energetic contributions to  associated to the Ω-effect, nonlinear induction, nonlinear advection and ohmic dissipation, respectively. We also define A0;mi, the magnetic energy exchanged through nonlinear advection between
associated to the Ω-effect, nonlinear induction, nonlinear advection and ohmic dissipation, respectively. We also define A0;mi, the magnetic energy exchanged through nonlinear advection between  and a given non-axisymmetric shearing wave packet, labelled mi. Figure 3 shows the x and y projections of Eq. (5) for the lower branch of SN2m as a function of Re, at fixed Rm = 3030 (the upper branch behaves similarly). The MRI-supporting azimuthal field
and a given non-axisymmetric shearing wave packet, labelled mi. Figure 3 shows the x and y projections of Eq. (5) for the lower branch of SN2m as a function of Re, at fixed Rm = 3030 (the upper branch behaves similarly). The MRI-supporting azimuthal field 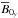 loses most of its energy through the nonlinear advective transfer A0y< 0, which acts as a weakly nonlinear turbulent diffusion. The laminar ohmic dissipation D0y is negligible. The Ω effect is the only net source term for
loses most of its energy through the nonlinear advective transfer A0y< 0, which acts as a weakly nonlinear turbulent diffusion. The laminar ohmic dissipation D0y is negligible. The Ω effect is the only net source term for 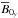 , indicating that the sustainment of the radial
, indicating that the sustainment of the radial 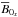 is critical for the dynamo process as a whole. Figure 3 (top) shows that
is critical for the dynamo process as a whole. Figure 3 (top) shows that 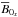 gains energy from both nonlinear induction I0x and advection A0x, and dissipates a large amount of this energy directly through ohmic diffusion. The part of A0x associated with the nonlinear correlations of the dominant MRI-unstable (m = 1,n = 1) velocity perturbation and (m = 1,n = 0) magnetic perturbation (denoted by A0;a1x> 0 in the figure, anticipating the notations introduced in Sect. 4.3.1 below) is positive, and much larger than the total A0x. This implies that some energy is also transferred nonlinearly from
gains energy from both nonlinear induction I0x and advection A0x, and dissipates a large amount of this energy directly through ohmic diffusion. The part of A0x associated with the nonlinear correlations of the dominant MRI-unstable (m = 1,n = 1) velocity perturbation and (m = 1,n = 0) magnetic perturbation (denoted by A0;a1x> 0 in the figure, anticipating the notations introduced in Sect. 4.3.1 below) is positive, and much larger than the total A0x. This implies that some energy is also transferred nonlinearly from 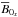 to other smaller-scale modes, which can be interpreted again as a turbulent diffusion acting on
to other smaller-scale modes, which can be interpreted again as a turbulent diffusion acting on 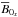 .
.
 |
Fig. 3 x- (top) and y- (bottom) projections of the energy budget (5) of the axisymmetric field component |
This budget is reminiscent of the results of R15 for large aspect ratio cycles. The most notable difference is that I0x is not small here, and is of the same order as A0x. While this term may also be important for the sustainment of the dynamo and for the Pm problem (as Re increases, I0x decreases while A0x increases), in the following we focus on the role of A0x in relation to the results of R15.
4.2. Energetics of shearing wave packets
In the previous analysis, the key quantity A0x included both the (positive) energy exchanged nonlinearly between 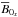 and MRI-unstable perturbations and the (negative) energy exchanged between
and MRI-unstable perturbations and the (negative) energy exchanged between 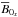 and other smaller-scale perturbations, integrated over a full period of SN2m. To understand the details of these energy transfers in moderate aspect ratio boxes, we now investigate the magnetic energy budget of individual non-axisymmetric wave packets (m ≠ 0). Wave packets with different lagrangian radial wavenumbers ℓ differing by Δℓ = 1 swing in the box one after the other at regular time intervals, and we label each successive packet by its superscript ℓ. For SN2m, ℓ varies from 0 to 4 (the evolution of total energy of each of these waves is shown in Fig. 1). m = 1 wave packets, which dominate the dynamics here, have a typical swinging time S-1Ly/Lx. The magnetic energy budget for a given (m,n), summed over all successive ℓ waves, reads
and other smaller-scale perturbations, integrated over a full period of SN2m. To understand the details of these energy transfers in moderate aspect ratio boxes, we now investigate the magnetic energy budget of individual non-axisymmetric wave packets (m ≠ 0). Wave packets with different lagrangian radial wavenumbers ℓ differing by Δℓ = 1 swing in the box one after the other at regular time intervals, and we label each successive packet by its superscript ℓ. For SN2m, ℓ varies from 0 to 4 (the evolution of total energy of each of these waves is shown in Fig. 1). m = 1 wave packets, which dominate the dynamics here, have a typical swinging time S-1Ly/Lx. The magnetic energy budget for a given (m,n), summed over all successive ℓ waves, reads 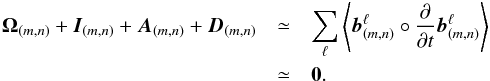 (8)Here, Ω(m,n), I(m,n), A(m,n) and D(m,n) are energetic contributions associated to the Ω-effect, nonlinear induction, nonlinear advection and ohmic dissipation,
(8)Here, Ω(m,n), I(m,n), A(m,n) and D(m,n) are energetic contributions associated to the Ω-effect, nonlinear induction, nonlinear advection and ohmic dissipation, 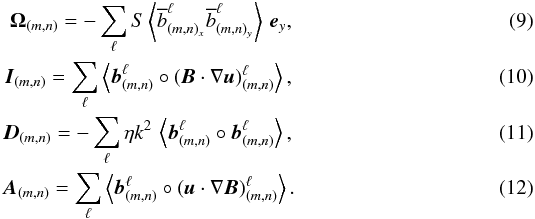 The advective term A(m,n) basically represents the magnetic energy exchanged between (m,n) and all the other modes. The budget is only approximately zero because each ℓ wave carries a very small amount of energy in the strongly leading and trailing phases, and has (very weak) nonlinear couplings to its predecessors and successors (see H11). These couplings can be neglected in the context of this particular energetic analysis. We now analyse the energy budget of two illustrative “active” and “slaved” non-axisymmetric perturbations taking part in the dynamics of LB2m.
The advective term A(m,n) basically represents the magnetic energy exchanged between (m,n) and all the other modes. The budget is only approximately zero because each ℓ wave carries a very small amount of energy in the strongly leading and trailing phases, and has (very weak) nonlinear couplings to its predecessors and successors (see H11). These couplings can be neglected in the context of this particular energetic analysis. We now analyse the energy budget of two illustrative “active” and “slaved” non-axisymmetric perturbations taking part in the dynamics of LB2m.
4.2.1. Active perturbations
We first consider magnetic perturbations with (m = 1, n = 0). As explained in Sect. 3, these perturbations, in conjunction with (m = 1, n = 1) velocity perturbations, dominate the non-axisymmetric MRI-unstable dynamics in the system under consideration. They are subject to energy injection through induction and, through their nonlinear EMF coupling 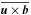 to (m = 1, n = 1) velocity perturbations, act as the main energy provider of
to (m = 1, n = 1) velocity perturbations, act as the main energy provider of  through nonlinear transfers. We therefore label this set of non-axisymmetric perturbations as a1 for “active”.
through nonlinear transfers. We therefore label this set of non-axisymmetric perturbations as a1 for “active”.
The energetics of the radial component of these magnetic perturbations is illustrated in Fig. 4 (top), which shows the radial projection of Eq. (8)for (m = 1,n = 0) a function of Re. As expected of an MRI-unstable situation, energy is gained through the induction term (Ia1x> 0), and redistributed through nonlinear advective transfers (Aa1x< 0) to both  and smaller-scale modes. The azimuthal component (not shown) extracts energy through the Ω-effect. Other m = 1 magnetic modes with n = 2,4 behave in the same way.
and smaller-scale modes. The azimuthal component (not shown) extracts energy through the Ω-effect. Other m = 1 magnetic modes with n = 2,4 behave in the same way.
 |
Fig. 4 x-projection of the cumulative magnetic energy budgets (8) of non-axisymmetric perturbations as a function of Re, for the lower branch LB2m at Rm = 3030. Top: active MRI-unstable perturbation a1 (magnetic perturbation m = 1, n = 0). Bottom: slaved MRI-stable magnetic perturbation (m = 2, n = 1). The sum of all source and dissipative terms remains close to 0. |
A short digression is required at this point. Here and before, we have taken a Eulerian viewpoint, which is easier to analyze numerically but not necessarily very physically transparent. The previous results simply mean that the large-scale lagrangian magnetic field, described in a good first approximation by the sum of  and shearing non-axisymmetric m = 1 waves (and multiple n) at the Re and Rm considered, is basically sustained by MRI induction (Ia1x). The nonlinear advective transfers between
and shearing non-axisymmetric m = 1 waves (and multiple n) at the Re and Rm considered, is basically sustained by MRI induction (Ia1x). The nonlinear advective transfers between  and a1 redistribute energy between these two Eulerian modes but conserve their total energy (see H11, Fig. 4 for a lagrangian picture of MRI dynamo reversals).
and a1 redistribute energy between these two Eulerian modes but conserve their total energy (see H11, Fig. 4 for a lagrangian picture of MRI dynamo reversals).
4.2.2. Slaved perturbations
The previous analysis explains how the large-scale field can be sustained through a dynamo process involving non-axisymmetric MRI-unstable wave packets. However, not all perturbations that take part in the nonlinear dynamics of LB2m are excited by the MRI nor feedback energy into the large-scale dynamo field. As can be seen in Fig. 4 (bottom), magnetic perturbations such as m = 2, n = 1 have I(m,n)x< 0 and A(m,n)x> 0 (a similar budget is obtained for m ≥ 2 and n ≥ 1). Such slaved perturbations represent smaller-scale structures which are not themselves amplified by the MRI. They only gain energy through nonlinear transfers from larger-scale MRI-amplified active perturbations, and dissipate it through laminar dissipation. In other words, they act as a turbulent diffusion for the large-scale field and are therefore destructive for the dynamo. We will use this separation between active and slaved perturbations in the following paragraph to quantify this diffusion in a global way as a function of Re and Rm.
4.3. Characterization of turbulent magnetic dissipation
4.3.1. Formalism
We now use the previous concept of active and slaved perturbations to characterize turbulent magnetic diffusion more quantitatively, and to study its impact on the dynamo at large Re (low Pm). A Fourier mode will be considered as active if 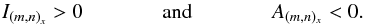 (13)These modes will be labelled ai = 1,...,Na. On the contrary, a magnetic mode will be considered as slaved if I(m,n)x < 0 or A(m,n)x > 0. Slaved modes are stabilized with respect to the MRI by a stronger diffusion and magnetic tension, and will be labelled si = 1,...,Ns. “Small-scale” axisymmetric modes (m = 0, n > 1) will also be considered as slaved because they do not contribute directly to the sustainment of
(13)These modes will be labelled ai = 1,...,Na. On the contrary, a magnetic mode will be considered as slaved if I(m,n)x < 0 or A(m,n)x > 0. Slaved modes are stabilized with respect to the MRI by a stronger diffusion and magnetic tension, and will be labelled si = 1,...,Ns. “Small-scale” axisymmetric modes (m = 0, n > 1) will also be considered as slaved because they do not contribute directly to the sustainment of  .
.
 |
Fig. 5 Left panel: different terms Iax, Dlax and Dtax in the net magnetic energy budget (20) for LB2m as a function of Re, at fixed Rm = 3030. Middle and right panels: ratio Dtax/Dlax for the lower and upper branches of SN2m as a function of Re, for Rm = 3030 and Rm = 3620 respectively (the roughness of the rightmost plot is due to the limited time-sampling of simulation outputs used in the postprocessing analysing stages, not to the numerical resolution of the simulations). |
We can then think of turbulent diffusion as the cumulative nonlinear effect of all slaved modes on all the active ones and on  . The same idea was used in R15 to characterize turbulent diffusion for large aspect ratio cycles. The only difference here is that the physical structure of non-axisymmetric active MRI perturbations taking part in the dynamics of chimera cycles is more complex (it involves a larger number of m and n Fourier modes), and that these cycles involve a succession of such non-axisymmetric structures (different ℓ, see Fig. 1).
. The same idea was used in R15 to characterize turbulent diffusion for large aspect ratio cycles. The only difference here is that the physical structure of non-axisymmetric active MRI perturbations taking part in the dynamics of chimera cycles is more complex (it involves a larger number of m and n Fourier modes), and that these cycles involve a succession of such non-axisymmetric structures (different ℓ, see Fig. 1).
We define the amount of energy exchanged during a cycle period between a mode (m,n) and a mode (m′,n′): 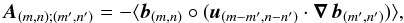 (14)with
(14)with 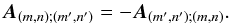 (15)We then have the following relation, using the active/slaved shorthand notation:
(15)We then have the following relation, using the active/slaved shorthand notation: 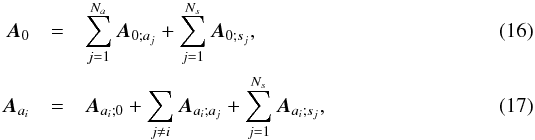 which simply expresses that any active mode exchanges energy with the background field
which simply expresses that any active mode exchanges energy with the background field  , the other active modes and the slaved modes. We define the turbulent dissipation Dta as the total magnetic energy nonlinearly transferred from the system {
, the other active modes and the slaved modes. We define the turbulent dissipation Dta as the total magnetic energy nonlinearly transferred from the system { +active modes} to the slaved modes:
+active modes} to the slaved modes: 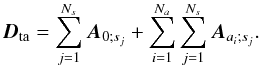 (18)We now focus on the x-component of Eq. (18), as it is the most critical for the sustainment of the dynamo (the y-component of the magnetic field always benefits from the Ω-effect). Summing Eq. (17) over all the active modes, using Eq. (16) and the symmetry condition (15), we obtain
(18)We now focus on the x-component of Eq. (18), as it is the most critical for the sustainment of the dynamo (the y-component of the magnetic field always benefits from the Ω-effect). Summing Eq. (17) over all the active modes, using Eq. (16) and the symmetry condition (15), we obtain 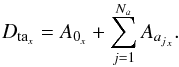 (19)Finally, summing the energy budget (8) over all the active modes, and adding the contribution of the axisymmetric field
(19)Finally, summing the energy budget (8) over all the active modes, and adding the contribution of the axisymmetric field  to the result, we obtain the effective magnetic energy budget of the active radial field component,
to the result, we obtain the effective magnetic energy budget of the active radial field component, 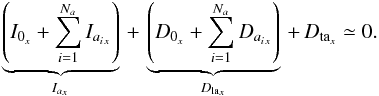 (20)The first curly brace term Iax is the net magnetic energy injected into the system {
(20)The first curly brace term Iax is the net magnetic energy injected into the system { +active modes} over a cycle period. The second curly brace term Dlax, is the magnetic energy directly lost by
+active modes} over a cycle period. The second curly brace term Dlax, is the magnetic energy directly lost by  and active modes through “laminar” ohmic dissipation. Finally, by construction and as desired, Dtax stands for the energy lost by these modes through nonlinear energy transfers to smaller scales. This equation indicates that the magnetic energy injected via the MRI into the active dynamo field balances the sum of laminar and turbulent magnetic dissipations (for a periodic solution).
and active modes through “laminar” ohmic dissipation. Finally, by construction and as desired, Dtax stands for the energy lost by these modes through nonlinear energy transfers to smaller scales. This equation indicates that the magnetic energy injected via the MRI into the active dynamo field balances the sum of laminar and turbulent magnetic dissipations (for a periodic solution).
4.3.2. Turbulent magnetic dissipation for SN2m
Having been through great pains to formalize the analysis of the magnetic energy budgets of the MRI dynamo in the shearing box, we can now apply it to the SN2m chimera cycles. Figure 5 (left) shows the induction term Iax and the two dissipative terms Dlax and Dtax for this pair of cycles as a function of Re, at fixed Rm = 3030. It appears that the turbulent dissipation Dtax for both lower and upper branches increases significantly more rapidly than the laminar dissipation Dlax as Re is increased. As shown in Fig. 5 (middle and right panels), this ratio Dtax/Dlax increases by 7% from Re = 910 to Re = 980. The same result holds at the larger Rm = 3620 at which the cycle is sustained for a wider range of Re. These results therefore suggest that the disappearance of cycles at large Re (low Pm) is caused by the relative enhancement of turbulent magnetic dissipation associated with the development of smaller-scale velocity fluctuations. At larger Re, this additional dissipation can only be compensated for if we can make induction larger relative to laminar dissipation, that is, by going to larger Rm. This seems to efficiently explain the typical existence boundary of MRI dynamo cycles in the (Re, Rm) plane.
4.3.3. Illustration of turbulent magnetic dissipation in aperiodic test simulations
 |
Fig. 6 Magnetic energy change Δℰm of the axisymmetric radial magnetic field component |
To investigate whether the conclusions of the previous analysis pertain to more general circumstances and can explain the seeming disappearance of the MRI dynamo as a whole at low Pm, we finally considered slightly more generic aperiodic test simulations in the phase-space vicinity of SN2m. We performed a series of simulations at different Re and Rm, initialized with the same initial condition, consisting of the initial state of the LB2m cycle computed at Re = 908 and Rm = 3030. Except for these precise values of Re and Rm, the time evolution from this initial condition is not periodic and can result in either a gain or loss of magnetic energy after an integration of the equations over a period of the original cycle TSN2m = 5S-1Ly/Lx. We then computed the magnetic energy change Δℰm in the 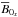 component after this time, as a function of Re and Rm. Figure 6 shows that Δℰm is always negative for Re > 908, and that the energy loss increases with Re at fixed Rm (or equivalently lower Pm). Moreover, the nonlinear term A0x responsible for the sustainment of
component after this time, as a function of Re and Rm. Figure 6 shows that Δℰm is always negative for Re > 908, and that the energy loss increases with Re at fixed Rm (or equivalently lower Pm). Moreover, the nonlinear term A0x responsible for the sustainment of 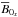 decreases with Re. Although the latter result does not rigorously quantify the turbulent dissipation, it indicates that some magnetic energy injected into MRI-unstable waves is transferred to small scales rather than to
decreases with Re. Although the latter result does not rigorously quantify the turbulent dissipation, it indicates that some magnetic energy injected into MRI-unstable waves is transferred to small scales rather than to 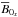 at large Re, resulting in the decay of the MRI-supporting field and therefore of the dynamics as a whole.
at large Re, resulting in the decay of the MRI-supporting field and therefore of the dynamics as a whole.
Figure 7 provides a direct physical illustration of the effects of turbulent magnetic diffusion at large Re. The visualizations show the vertical velocity field and total radial magnetic field Bx in a poloidal (x,z) plane around the time of reversal of  . At Re = 5000, vertical velocity field perturbations clearly have more small-scale structure than at Re = 908, and the non-axisymmetric counter-rotating flow vortices driving the reversal of the large-scale field (see H11) are much less regular. The magnetic field inherits some of this small-scale structure through turbulent advection. The magnetic gradients (electric currents) are clearly larger at Re = 5000 than at Re = 908, leading to enhanced magnetic dissipation.
. At Re = 5000, vertical velocity field perturbations clearly have more small-scale structure than at Re = 908, and the non-axisymmetric counter-rotating flow vortices driving the reversal of the large-scale field (see H11) are much less regular. The magnetic field inherits some of this small-scale structure through turbulent advection. The magnetic gradients (electric currents) are clearly larger at Re = 5000 than at Re = 908, leading to enhanced magnetic dissipation.
 |
Fig. 7 Color snapshots of the vertical velocity field uz (top) and radial magnetic field Bx (bottom) in the poloidal plane (x, z). Left panel: LB2m at Re = 908. Right panel: MHD state integrated from the same initial condition, but at Re = 5000. Rm = 3030 in both cases. The snapshots are taken at the time t = 5 S-1 around which the first |
5. The missing link to turbulent accretion disk dynamo models?
As explained in Sect. 3, the main appeal of chimera dynamo cycles is the dual physical and statistical perspective that they offer on the MRI dynamo process, and their connection to statistical butterfly states observed in simulations.
Although these cycles do not accommodate all the physical elements entering the accretion disk dynamo problem (such as magnetic buoyancy), their discovery raises the prospect that a physically-grounded statistical theoretical MRI dynamo model can be derived from first principles. The aim of this section is to highlight some important dynamical features of the solutions at hand, some but not all of which are already taken into account in existing theoretical statistical models (Lesur & Ogilvie 2008b,a; Gressel 2010; Gressel & Pessah 2015; Squire & Bhattacharjee 2015) in order to provide constructive guidance for future work on statistical theory.
5.1. Statistical linearity vs. dynamical nonlinearity
To introduce matters, in Fig. 8 (top) we reproduce the instantaneous relationship between the large-scale axisymmetric nonlinear EMF 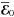 and
and  for the lower branch cycles LB1 and LB2 computed by H11 and R13 in azimuthally elongated shearing boxes. As noted in H11, the standard mean-field theory ansatz of a linear relationship (Steenbeck et al. 1966; Moffatt 1977; Brandenburg & Subramanian 2005; see Gressel 2010; Blackman 2012; Gressel & Pessah 2015, for applications to the accretion disk dynamo context) does not fit these solutions of the full MHD equations (a similar mismatch has been reported for a magnetic-buoyancy driven dynamo, see Cline et al. 2003). A possible explanation for this discrepancy is that such solutions, despite being nonlinear, are not turbulent or statistical in essence, and that the linear mean-field relationship only holds statistically. The question nevertheless arises as to if and how one can rigorously relate the fundamental linear and nonlinear physical processes illustrated by these three-dimensional solutions to a seemingly more abstract statistical two-dimensional effective description. Of particular concern in the mean-field description in the context of instability-driven dynamos (such as the MRI dynamo) is the lack of explicit connection between mean-field effects and fundamental dynamical processes (such as the MRI) in the absence of which there can be no dynamo-generating turbulence at all in the first place in the corresponding systems.
for the lower branch cycles LB1 and LB2 computed by H11 and R13 in azimuthally elongated shearing boxes. As noted in H11, the standard mean-field theory ansatz of a linear relationship (Steenbeck et al. 1966; Moffatt 1977; Brandenburg & Subramanian 2005; see Gressel 2010; Blackman 2012; Gressel & Pessah 2015, for applications to the accretion disk dynamo context) does not fit these solutions of the full MHD equations (a similar mismatch has been reported for a magnetic-buoyancy driven dynamo, see Cline et al. 2003). A possible explanation for this discrepancy is that such solutions, despite being nonlinear, are not turbulent or statistical in essence, and that the linear mean-field relationship only holds statistically. The question nevertheless arises as to if and how one can rigorously relate the fundamental linear and nonlinear physical processes illustrated by these three-dimensional solutions to a seemingly more abstract statistical two-dimensional effective description. Of particular concern in the mean-field description in the context of instability-driven dynamos (such as the MRI dynamo) is the lack of explicit connection between mean-field effects and fundamental dynamical processes (such as the MRI) in the absence of which there can be no dynamo-generating turbulence at all in the first place in the corresponding systems.
This possible limitation of classical mean-field theory has motivated the development of alternative quasi-linear models of the turbulent MRI dynamo describing the cumulative effects of a statistical assembly of shearing waves whose individual physical linear evolution can be computed consistently either analytically or numerically (Lesur & Ogilvie 2008a,b; Squire & Bhattacharjee 2015). The structure of our chimera dynamo cycles qualitatively vindicates this approach (albeit with a few caveats, discussed below). Another encouraging sign that it may be possible to close in on a self-consistent, physically transparent statistical theory is illustrated by Figure 8 (bottom), which shows the instantaneous relationship between the large-scale axisymmetric nonlinear 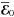 and
and  for the lower branch chimera cycles LB1m and LB2m. While the detailed relationship remains nonlinear, a clear average linear trend emerges in comparison to the LB1 and LB2 cases. This result supports the common intuition that complex three-dimensional nonlinear multiscale dynamics tend to generate statistically simple effective large-scale dynamical states in the turbulent limit.
for the lower branch chimera cycles LB1m and LB2m. While the detailed relationship remains nonlinear, a clear average linear trend emerges in comparison to the LB1 and LB2 cases. This result supports the common intuition that complex three-dimensional nonlinear multiscale dynamics tend to generate statistically simple effective large-scale dynamical states in the turbulent limit.
 |
Fig. 8 Phase portraits of periodic dynamo solutions in the ℰ0y vs. |
5.2. Roles of active and passive perturbations
The most direct explanation for a statistical correlation between the large-scale EMF and large-scale magnetic field in the MRI dynamo problem can be found in the quasi-linear theory of Lesur & Ogilvie (2008a), which predicts a linear dependence between the MRI-supporting field and the nonlinear EMF generated by MRI-amplified shearing wave packets. This is notably expected if the MRI-supporting toroidal field 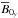 and azimuthal wavenumbers of the shearing waves are such that the MRI is on its weak-field branch, so that the MRI growth rate is proportional to
and azimuthal wavenumbers of the shearing waves are such that the MRI is on its weak-field branch, so that the MRI growth rate is proportional to 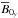 . In a simulation, one would therefore expect that successive shearing waves “see” a slowly time-evolving large-scale field and that their relative growth (and ensuing nonlinear EMF feedback) is modulated according to the amplitude of the MRI-supporting field at the time of their amplification, resulting in the linear trend discussed above. This correlation is not observed for individual ℓ shearing wave packets of our chimera cycles (individual wave amplitudes do not seem to be directly linked to either the sign or amplitude of
. In a simulation, one would therefore expect that successive shearing waves “see” a slowly time-evolving large-scale field and that their relative growth (and ensuing nonlinear EMF feedback) is modulated according to the amplitude of the MRI-supporting field at the time of their amplification, resulting in the linear trend discussed above. This correlation is not observed for individual ℓ shearing wave packets of our chimera cycles (individual wave amplitudes do not seem to be directly linked to either the sign or amplitude of  ) but certainly holds in an average sense (otherwise we would not be able to observe regular field reversals).
) but certainly holds in an average sense (otherwise we would not be able to observe regular field reversals).
Another possible (but as of yet unscrutinized) explanation for the average linear trend described above is that each new MRI-unstable shearing wave packet involved in the chimera dynamics is nonlinearly seeded through a physical process of scattering of its predecessor off the radially modulated large-scale axisymmetric magnetic field (see H11 for a detailed discussion of this effect), resuting in some statistical correlation between the cumulative nonlinear EMF associated with swinging shearing waves and the large-scale field. The early polarization of shearing wave seeds in their strongly leading phase, though, may not be particularly optimal in terms of MRI amplification which, considering their limited lifetime, may explain why they produce seemingly wildly different EMFs (we recall that each shearing wave has only a finite time to grow before it is strongly damped; for LB2m with Ly/Lx = 4 aspect ratio, their “active” lifetime is of the order of few Ω-1 at most). Note that existing quasilinear statistical models randomly drawing shearing wave seeds are currently blind to such scattering effects. Whether this is a limitation remains to be assessed.
Implicit to the discussion above is that the sustainment of the dynamo results from the cumulative effect of MRI-active perturbations as defined in Sect. 4. While it contrasts with the classical view of mean-field effects being related to small-scale, “inertial-range” turbulence, this hypothesis is definitely supported by our numerical simulations and magnetic energy budget analysis1, as well as by other recent numerical results (Bhat et al. 2016). However, another result of the analysis conducted in Sect. 4 is that smaller-scale slaved waves excited mostly through nonlinear interactions (which are also not self-consistently computed in quasi-linear models) are also important in this problem, and notably play an important role in the magnetic Prandtl number dependence of the dynamo through the effect of turbulent magnetic dissipation.
Hence, it is tempting at this stage to sketch a refined physical picture of the full turbulent MRI dynamo process (and more generally of turbulent instability-driven dynamos) in which the EMF associated with non-universal, fairly large-scale active modes feeling the effect of the linear physics constitutes the main engine of the dynamo, while faster, smaller-scale “inertial-range” slaved modes can either impede it (as in our chimera cycles) or reinforce it further (depending on the problem). If this physical picture holds, then the decomposition presented in Sect. 4.3.1 may prove extremely useful in constructing more transparent, physically-grounded, statistical mean-field dynamo models out of the existing ones.
6. Conclusions
Three-dimensional, nonlinear, periodic, magnetorotational dynamo cycles offer an interesting avenue of research to understand the dynamical processes underlying turbulent dynamo action and angular momentum transport in astrophysical accretion disks. Building on our earlier foundational work along these lines, we have been able to compute several new “chimera” dynamo cycles whose principal appeal, compared to previously identified solutions, is to exhibit some form of statistical organization reminiscent of that observed in many fully turbulent simulations of the problem. Yet, we have shown that their sustainment can be understood in terms of the same few linear and nonlinear dynamical processes underlying simpler cycles. These solutions therefore offer an unprecedented dual physical and statistical perspective on dynamo action in Keplerian flow, and, more generally, rotating shear flows. As such, they represent an interesting reference point for improving statistical modeling of turbulent accretion disk dynamos and other astrophysical dynamos.
In order to describe the dynamics of these statistically-organized chimera cycles in a physically transparent way, we have notably found it useful to introduce a formal dynamical decomposition into active and slaved modes. The former include a large-scale axisymmetric MRI-supporting field component, and non-axisymmetric MRI-unstable energy-injecting perturbations. The latter consist of perturbations passively excited through nonlinear interactions that drain energy from larger scales. Using this decomposition, we have been able to understand how the magnetic energy of the system can be sustained via the MRI. In particular, we have found that the turbulent, subcritical magnetic diffusion mediated by passive modes impedes the sustainment of statistically-organized chimera cycles at low Pm. While a similar conclusion was reached in R15 based on the analysis of simpler cycles, the more explicit connection between the dynamics of chimera cycles and high-resolution simulation results now makes it very clear that this form of turbulent diffusion is a key element to consider in the statistical modeling of accretion disk dynamos. With this effect identified and confirmed, it may notably now be possible to determine whether the MRI dynamo can survive in the low Pm, high Re regime (Walker et al. 2016), and its dependence on geometry, size of the vertical domain and stratification (Oishi & Mac Low 2011; Shi et al. 2016; Nauman & Pessah 2016).
The results presented in this paper are obviously not in the astrophysically asymptotic regimes and do not accommodate all the relevant physics in this context, such as magnetic buoyancy and stratification effects. However, we have shown that our physically transparent, fully three-dimensional, nonlinear, magnetorotational dynamo chimeras share some interesting properties with existing effective two-dimensional statistical models of accretion disk dynamo cycles and as such seem to offer an interesting path in parameter space towards statistical asymptotic regimes. This raises the prospect that improved effective statistical models of the MRI dynamo and other instability-driven dynamos (Spruit 2002; Cline et al. 2003; Miesch et al. 2007; Rincon et al. 2008) can be derived from physical first principles, and may in the near future provide trustable insights into magnetic field generation and turbulent transport processes in a variety of stellar and circumstellar environments.
Online material
Movie 1 of Fig. 1 Access here
Movie 2 of Fig. 1 Access here
To complicate the matters further, note that such linear growth effects are in principle captured by test field method calculations (Gressel 2010; Gressel & Pessah 2015), whose original motivations are rooted in the classical mean field theory.
Acknowledgments
We thank Richard Kerswell, Sébastien Fromang, Jonathan Squire and Oliver Gressel for several useful discussions. This research was supported by the University Paul Sabatier of Toulouse under an AO3 grant, by the Midi-Pyrénées region, by the French National Program for Stellar Physics (PNPS), by the Leverhulme Trust Network for Magnetized Plasma Turbulence and by the National Science Foundation under Grant No. PHY05-51164. Numerical calculations were carried out on the CALMIP platform (CICT, University of Toulouse), whose assistance is gratefully acknowledged.
References
- Armitage, P. J. 2010, in Astrophysics of Planet Formation (Cambridge University Press), 294 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1992, ApJ, 400, 610 [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balbus, S. A., & Henri, P. 2008, ApJ, 674, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Armitage, P. J., & Reynolds, C. S. 2015, ApJ, 809, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Bhat, P., Ebrahimi, F., & Blackman, E. G. 2016, MNRAS, 462, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, E. G. 2012, Phys. Scr., 86, 058202 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Proc. Natl. Acad. Sci., 46, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Cline, K. S., Brummell, N. H., & Cattaneo, F. 2003, ApJ, 599, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., Stone, J. M., & Pessah, M. E. 2010, ApJ, 713, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, in Accretion Power in Astrophysics, 3rd edn. (Cambridge University Press), 398 [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F., & Menou, K. 1998, ApJ, 492, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O. 2010, MNRAS, 405, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., & Pessah, M. E. 2015, ApJ, 810, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 2009, in Accretion Processes in Star Formation, 2nd edn. (Cambridge University Press) [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Herault, J., Rincon, F., Cossu, C., et al. 2011, Phys. Rev. E, 84, 036321 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., Blaes, O., Krolik, J. H., Coleman, M. S. B., & Sano, T. 2014, ApJ, 787, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. B. 1982, in Numerical and physical aspects of aerodynamic flows, ed. R. Cebeci (Springer), 3 [Google Scholar]
- Latter, H. N., & Papaloizou, J. C. B. 2012, MNRAS, 426, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008a, MNRAS, 391, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008b, A&A, 488, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Fromang, S., Lesur, G., Joos, M., & Longaretti, P.-Y. 2015, A&A, 579, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miesch, M. S., Gilman, P. A., & Dikpati, M. 2007, ApJS, 168, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K. 1977, in Magnetic field generation in electrically conducting fluids (Cambridge University Press) [Google Scholar]
- Nauman, F., & Pessah, M. E. 2016, ApJ, 833, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Oishi, J. S., & Mac Low, M.-M. 2011, ApJ, 740, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, W. J., & Balbus, S. A. 2014, MNRAS, 441, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F., Ogilvie, G. I., & Proctor, M. R. E. 2007, Phys. Rev. Lett., 98, 254502 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F., Ogilvie, G. I., Proctor, M. R. E., & Cossu, C. 2008, Astron. Nachr., 329, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2013, J. Fluid Mech., 731, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2015, A&A, 575, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, J.-M., Stone, J. M., & Huang, C. X. 2016, MNRAS, 456, 2273 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Hawley, J. F., & Beckwith, K. 2011, ApJ, 730, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Squire, J., & Bhattacharjee, A. 2015, Phys. Rev. Lett., 114, 085002 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforschung Teil A, 21, 369 [Google Scholar]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Velikhov, E. P. 1959, Sov. Phys. JETP, 36, 1398 [Google Scholar]
- Walker, J., Lesur, G., & Boldyrev, S. 2016, MNRAS, 457, L39 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Temporal evolution and dynamical decomposition of the lower branch solutions LB1m (left) and LB2m (right). LB1m is shown for Re = 100, Rm = 900 and LB2m for Re = 908, Rm = 3033. From top to bottom, axisymmetric field |
| In the text | |
 |
Fig. 2 Left, top panel: selected continuation curves in Rm of SN2m at fixed Re; bottom panel: selected continuation curves in Re at fixed Rm. Right: existence boundary of SN2m in the (Re, Rm) plane (blue/dashed line) obtained by interpolating the different saddle node points Rmc(Re) and Rec(Rm) (blue bullets). The orange area shows the domain of existence of SN2m in parameter space. The red bullet shows a saddle note bifurcation point computed at double resolution (96 × 96 × 144). |
| In the text | |
 |
Fig. 3 x- (top) and y- (bottom) projections of the energy budget (5) of the axisymmetric field component |
| In the text | |
 |
Fig. 4 x-projection of the cumulative magnetic energy budgets (8) of non-axisymmetric perturbations as a function of Re, for the lower branch LB2m at Rm = 3030. Top: active MRI-unstable perturbation a1 (magnetic perturbation m = 1, n = 0). Bottom: slaved MRI-stable magnetic perturbation (m = 2, n = 1). The sum of all source and dissipative terms remains close to 0. |
| In the text | |
 |
Fig. 5 Left panel: different terms Iax, Dlax and Dtax in the net magnetic energy budget (20) for LB2m as a function of Re, at fixed Rm = 3030. Middle and right panels: ratio Dtax/Dlax for the lower and upper branches of SN2m as a function of Re, for Rm = 3030 and Rm = 3620 respectively (the roughness of the rightmost plot is due to the limited time-sampling of simulation outputs used in the postprocessing analysing stages, not to the numerical resolution of the simulations). |
| In the text | |
 |
Fig. 6 Magnetic energy change Δℰm of the axisymmetric radial magnetic field component |
| In the text | |
 |
Fig. 7 Color snapshots of the vertical velocity field uz (top) and radial magnetic field Bx (bottom) in the poloidal plane (x, z). Left panel: LB2m at Re = 908. Right panel: MHD state integrated from the same initial condition, but at Re = 5000. Rm = 3030 in both cases. The snapshots are taken at the time t = 5 S-1 around which the first |
| In the text | |
 |
Fig. 8 Phase portraits of periodic dynamo solutions in the ℰ0y vs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


