| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629909 | |
| Published online | 03 January 2017 | |
The evolution of white dwarfs resulting from helium-enhanced, low-metallicity progenitor stars
1 Grupo de Evolución Estelar y Pulsaciones. Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar
2 IALP – CONICET, 1467 La Plata, Argentina
3 Departament de Física, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
4 Institute for Space Studies of Catalonia, c/Gran Capita 2–4, Edif. Nexus 201, 08034 Barcelona, Spain
Received: 15 October 2016
Accepted: 18 November 2016
Context. Some globular clusters host multiple stellar populations with different chemical abundance patterns. This is particularly true for ω Centauri, which shows clear evidence of a helium-enriched subpopulation characterized by a helium abundance as high as Y = 0.4
Aims. We present a whole and consistent set of evolutionary tracks from the ZAMS to the white dwarf stage that is appropriate for the study of the formation and evolution of white dwarfs resulting from the evolution of helium-rich progenitors.
Methods. We derived white dwarf sequences from progenitors with stellar mass ranging from 0.60 to 2.0 M⊙ and for an initial helium abundance of Y = 0.4. We adopted two values of metallicity: Z = 0.001 and Z = 0.0005.
Results. We explored different issues of white dwarf evolution and their helium-rich progenitors. In particular, the final mass of the remnants, the role of overshooting during the thermally pulsing phase, and the cooling of the resulting white dwarfs differ markedly from the evolutionary predictions of progenitor stars with the standard initial helium abundance. Finally, the pulsational properties of the resulting white dwarfs are also explored.
Conclusions. We find that, for the range of initial masses explored in this paper, the final mass of the helium-rich progenitors is markedly higher than the final mass expected from progenitors with the usual helium abundance. We also find that progenitors with initial mass lower than M ≃ 0.65 M⊙ evolve directly into helium-core white dwarfs in less than 14 Gyr, and that, for larger progenitor masses, the evolution of the resulting low-mass carbon-oxygen white dwarfs is dominated by residual nuclear burning. For helium-core white dwarfs, we find that they evolve markedly faster than their counterparts coming from standard progenitors. Also, in contrast with what occurs for white dwarfs resulting from progenitors with the standard helium abundance, the impact of residual burning on the cooling time of white dwarfs is not affected by the occurrence of overshooting during the thermally pulsing phase of progenitor stars.
Key words: stars: evolution / stars: interiors / white dwarfs
© ESO, 2017
1. Introduction
It is now well established that a handful of globular clusters harbour multiple stellar populations characterized by different He enrichments; see, e.g., Bastian et al. (2015). This is the case, for instance, for ω Centauri (Norris 2004; Joo & Lee 2013; Tailo et al. 2016), NGC 2808 (D’Antona et al. 2005; Milone et al. 2012) and NCG 6441 (Caloi & D’Antona 2007; Bellini et al. 2013b) in which subpopulations are clearly visible in their respective color–magnitude diagrams. In particular, He enrichments as high as Y ~ 0.4 have been suggested to explain the observed split main sequences and horizontal branches (HB) of ω Centauri and NGC 2808. Because an increase in He abundance decreases the turnoff mass of a stellar population, the presence of an He-enriched subpopulation has also been invoked to account for the presence of hot and extreme HB stars (D’Antona & Caloi 2008) and the existence of a large fraction of He-core white dwarfs in some globular clusters, such as ω Centauri (Calamida et al. 2008; Bellini et al. 2013a). The origin of these He-rich subpopulations is believed to the result of cluster self-pollution caused by the ejecta of massive-intermediate mass asymptotic giant branch (AGB) stars of the first generation after the occurrence of the second dredge-up and hot bottom burning stage (Ventura et al. 2001) from fast rotating massive stars (Decressin et al. 2007) or from evolved red giant branch (RGB) stars that experienced extra-deep mixing (Denissenkov & Weiss 2004); see also Bastian et al. (2015) for a recent discussion about this issue.
The detection of white dwarf cooling sequences of globular clusters is especially interesting since it allows the study of fundamental properties of these stars and the corresponding stellar populations. Because of their well -understood evolutionary properties (Fontaine & Brassard 2008; Winget & Kepler 2008; Althaus et al. 2010b), white dwarfs can be used as distance indicators and as independent reliable cosmic clocks to date a wide variety of stellar populations, such as our Galaxy (see García-Berro & Oswalt 2016, and references therein, for a recent review on this topic) and open and globular clusters (see Winget et al. 2009; García-Berro et al. 2010; Jeffery et al. 2011; Bono et al. 2013; Hansen et al. 2013, for some examples).
Recently, Althaus et al. (2015) have explored the evolution of white dwarfs formed in metal-poor populations and found that stable hydrogen burning dominates their cooling even at low luminosities. These authors found that the role played by such residual burning is independent of the rate at which stellar mass is lost during the AGB and post-AGB evolution of progenitors, but that it depends on the occurrence of overshooting during the thermally pulsing (TP) AGB phase. In particular, overshooting results in a carbon enrichment of the envelope due to third dredge-up episodes. Carbon enrichment eventually results in final thinner hydrogen envelopes, which are unable to sustain appreciable hydrogen burning during the white dwarf stage. Here, we extend the scope of the study of Althaus et al. (2015) to explore the impact of an initial He enrichment on the formation, evolution, and pulsational properties of the resulting white dwarf stars.
Our main aim is to provide a consistent set of evolutionary tracks from the ZAMS to the cooling phase appropriate for the study of white dwarfs with helium and carbon-oxygen cores formed in He-rich subpopulations. The white dwarf evolutionary sequences are computed from the full evolution of He-rich progenitor stars through all the relevant stellar evolutionary phases, including the ZAMS, the RGB, the core He flash (whenever it occurs), the stable core He burning, the AGB phase, and the entire TP- and post-AGB phases. Specifically, we present full evolutionary sequences for He-rich progenitors with masses ranging from 0.6 to 2.0 M⊙, and for an initial He abundance Y = 0.4. These sequences are provided for two progenitor metallicities Z = 0.001 and Z = 0.0005. To date, no such exploration of the evolution of He-rich stars exists in the literature, and the only exception is that of Chantereau et al. (2015), who presented evolutionary sequences for He-rich progenitors for low-mass stars (up to 1 M⊙) with Z = 0.0005 from the ZAMS to the end of the AGB phase, but did not compute the white dwarf stage. We emphasize that the computation of the entire evolutionary history of progenitor stars allows us to have self-consistent white dwarf initial models. That means that in our sequences the residual masses of the H-rich envelopes and He shells are obtained from evolutionary calculations, instead of using typical values and artificial initial white dwarf models. For the white dwarf regime, we included all the relevant energy sources and physical processes, such as crystallization, carbon-oxygen phase separation, element diffusion, residual nuclear burning, and convective coupling at low luminosities (Fontaine et al. 2001). As is shown below, the final mass of the remnants, the role of overshooting during the thermally pulsing AGB, and the cooling properties of white dwarfs markedly differ from those corresponding to progenitor stars with the standard initial He abundance.
The paper is organized as follows. In Sect. 2 we briefly describe our numerical tools and the main ingredients of the evolutionary sequences, while in Sect. 3 we present in detail our main evolutionary results for both the white dwarfs and their progenitors. In this section we also explore the pulsational properties of the resulting white dwarfs during the ZZ Ceti stage. Finally, in Sect. 4 we summarize the main findings of the paper, and we elaborate on our conclusions.
Basic model properties for sequences with Y = 0.4 and Z = 0.001 and 0.0005.
2. Numerical setup and input physics
The evolutionary sequences presented here were calculated with the LPCODE stellar evolutionary code; see Althaus et al. (2003), Althaus et al. (2005, 2012, 2015), and Miller Bertolami (2016) for relevant information about the code. The LPCODE is a well-tested and calibrated code that has been amply used to study different aspects of the evolution of low-mass and white dwarf stars, including the formation and evolution of extremely low-mass white dwarfs; see Miller Bertolami et al. (2008), García-Berro et al. (2010), Althaus et al. (2010a), Renedo et al. (2010), Miller Bertolami et al. (2011), Wachlin et al. (2011), Córsico et al. (2012), Althaus et al. (2013), and references therein. Recently, it has also been used to generate a new grid of models for post-AGB stars (Miller Bertolami 2016). The LPCODE has been tested against other evolutionary codes during the main sequence, RGB, and white dwarf regime (Salaris et al. 2013; Miller Bertolami 2016) with satisfactory results.
Next we provide a description of the main input physics of the code relevant for the present work. Extra mixing due to diffusive convective overshooting was considered during the core H and He burning, but not during the thermally pulsing AGB phase. The nuclear network accounts for the following elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne, together with 34 thermonuclear reaction rates for the pp-chains, CNO bi-cycle, and He burning that are identical to those described in Althaus et al. (2005), with the exception of the reactions 12C+p → 13N + γ → 13C + e+ + νe and 13C(p, γ)14N, which are taken from Angulo et al. (1999). In addition, the reaction rate 14N(p, γ)15O was taken from Imbriani et al. (2005). Radiative and conductive opacities are computed using the OPAL tables (Iglesias & Rogers 1996) and adopting the treatment of Cassisi et al. (2007), respectively. The equation of state during the main-sequence evolution is that of OPAL for H- and He-rich compositions and a given metallicity. Updated low-temperature molecular opacities with varying carbon-oxygen ratios are used, which is relevant for a realistic treatment of progenitor evolution during the thermally pulsing AGB phase (Weiss & Ferguson 2009). For this purpose, we adopted the low-temperature opacities of Ferguson et al. (2005) and Weiss & Ferguson (2009). For the white dwarf phase, we consider the equation of state of Magni & Mazzitelli (1979) for the low-density regime, while for the high-density regime, we employ the equation of state of Segretain et al. (1994). As the white dwarf cools down we take into account the effects of element diffusion due to gravitational settling along with chemical and thermal diffusion of 1H, 3He, and 4He, 12C, 13C, 14N , and 16O; see Althaus et al. (2003) for details. During the white dwarf regime and for effective temperatures that are smaller than 10 000 K, outer boundary conditions are derived from non-gray model atmospheres (Rohrmann et al. 2012). Energy sources resulting from nuclear burning, the release of latent heat of crystallization and the release of the gravitational energy associated with the C/O phase separation induced by crystallization are also taken into account during this phase.
In the present work, we took special care in computing the evolution along the TP-AGB phase. This is relevant for a correct assessment of the initial-to-final mass relation and for a realistic inference of the role of residual nuclear burning in cool white dwarfs (Althaus et al. 2015). In particular, we have not forced our sequences to abandon early the TP-AGB phase. As mentioned, overshooting was not taken into account during the TP-AGB phase. This assumption leads to upper limits of the final mass of the progenitor stars. Indeed, the inclusion of overshooting during this phase results in third dredge-up episodes, which prevent the growth of the H-free core (Salaris et al. 2009). Unlike the situation for metal-rich progenitors, evidence for the occurrence of extra-mixing episodes during the TP-AGB phase of low-mass, low-metallicity stars is not conclusive (Althaus et al. 2015). To assess the impact of the occurrrence of extra mixing in the TP-AGB phase, particularly on the final mass of progenitors and the role of residual nuclear burning during the white dwarf regime, we compute additional He-rich sequences in which we considered an exponentially decaying diffusive overshooting with the overshooting parameter set to f = 0.0075. As shown in Miller Bertolami (2016), this amount of overshooting reproduces many observational properties of AGB and post-AGB stars, such as the C/O ratios of AGB and post-AGB stars in the Galactic disk, C/O abundances in PG 1159 stars, and the mass range of C-rich stars in clusters of the Magellanic Clouds.
In this work, mass loss during the RGB was taken from Schröder & Cuntz (2005). This selection is an acceptable choice, however, it should be stressed that the RGB mass-loss law is uncertain; in particular, the dependence of this mass-loss law on the initial helium abundance is still unknown. For the AGB and TP-AGB phases, we again use the mass loss rate of Schröder & Cuntz (2005) for pulsation periods shorter than 50 days. For longer periods, mass loss is taken as the maximum of the Schröder & Cuntz (2005) and Groenewegen et al. (2009) rates for oxygen-rich stars or the maximum of the Schröder & Cuntz (2005) and Groenewegen et al. (1998) rates for carbon-rich stars. In all of our calculations, mass loss was suppressed after the post-AGB remnants reach log Teff = 4. In line with the findings of Cassisi et al. (2014), who reported that no enhanced mass loss should be expected in second generation HB stars, we assume no mass loss during the core He-burning phase on the HB.
We computed the full evolution of He-rich sequences with initial masses ranging from 0.6 to 2.0 M⊙. The initial He abundance of each sequence is Y = 0.4. Two sets of model sequences have been computed, one for metallcity Z = 0.001 and the other for Z = 0.0005. It is important to mention that the value of the initial helium abundance adopted here constitutes an extreme choice. In fact, only ω Centauri and NGC 2808 show evidence of subpopulations with such high large helium abundances, while the subpopulations of most typical clusters are characterized by helium abundances of generally ≲0.3 (Bastian et al. 2015). A description of the computed evolutionary sequences is provided in Table 1, which lists the initial mass of our sequences and the final white dwarf mass (in solar masses), together with the age (in Gyr) at the end of the RGB and the number of thermal pulses. The adopted metallicities are representative of the low-metal content of the second generation, He-rich population found in some globular clusters. In particular, Tailo et al. (2016) find that the metallicity of the He-rich population in ω Centauri is Z = 0.0006–0.001 and Y ~ 0.38. For all our sequences, we computed evolution starting from the ZAMS and followed through the stages of stable H and He core burning, the stage of mass loss during the entire TP-AGB, the domain of the planetary nebulae at high effective temperature and, finally, the terminal white dwarf cooling track down to very low surface luminosities, (log (L/L⊙) = −5.0). For most of our sequences, evolution has gone through the He core flash on the tip of the RGB, and the following recurrent subflashes before the progenitors reach the stable core He-burning stage on the HB.
3. Evolutionary results
In this work we focus on those aspects of the evolution of stars with enhanced initial helium abundances that are relevant for the formation and evolution of white dwarf stars. Other issues, such as the impact of the helium enhancement of the progenitor stars on the morphology of HB stars, on the existence of multiple populations in globular clusters, or on the consequences of the helium enhancement for the evolution and nucleosynthesis of AGB models, can be found in D’Antona et al. (2002), Charbonnel et al. (2013), Milone (2015), Shingles et al. (2015), and references therein.
 |
Fig. 1 Theoretical initial-to-final mass relationship and evolutionary stages (shown employing different gray scales) obtained following the evolution of stars with an initial helium-enhanced composition Y = 0.4 and a metallicity Z = 0.001. The color scale on the right shows the age (in Gyr) at the tip of the RGB. |
3.1. The evolution of white dwarf progenitors
It is well known that stars with an enhanced helium abundance have much shorter main-sequence lifetimes for a given initial mass than stars with a normal helium abundance. This is the logical consequence of a smaller hydrogen mass burned on the main sequence. However this is not the only reason for this behavior. Specifically, in the hydrogen burning core the mean molecular weight is larger. All in all, stars with enhanced helium abundances are brighter and hotter for a given mass; see Salaris & Cassisi (2005) and Charbonnel et al. (2013). Indeed, as can be noted in Table 1, progenitors with initial stellar masses as low as M ≃ 0.60 M⊙ reach the tip of the RGB in less than 14 Gyr. In addition, because of the larger temperature characterizing the hydrogen-exhausted core during the RGB, the helium flash for these stars occurs for lower helium core masses than for stars with normal helium abundances.
These facts have consequences for the initial-to-final mass relationship, as well as for the global evolution of these stars. This is illustrated in Fig. 1, where the initial-to-final mass relation for our less massive, helium-enhanced evolutionary sequences is shown for the case Z = 0.001. In this figure we also indicate the evolution paths of these stars according to their initial mass. In particular, progenitors with an initial mass of less than M ≃ 0.65 M⊙ do not evolve through the helium core flash at the tip of the RGB. Instead, they evolve directly to the white dwarf stage. For these progenitors, helium-core white dwarfs are formed in less than 14 Gyr (see Table 1). Our sequences with initial stellar masses higher than M ≃ 0.65 M⊙ end their lives by forming white dwarfs with C/O cores. Specifically, helium-enhanced stars with initial stellar masses within the range 0.65 ≲ M⊙ ≲ 1.0 evolve through the helium core flash and then to the HB. Those progenitors with masses in the interval 0.65 ≲ M⊙ ≲ 0.70 avoid the AGB phase (AGB manque) and evolve directly to the cooling sequence as C/O white dwarfs (see Chantereau et al. (2015) for a similar result), while those progenitors with 0.70 ≲ M⊙ ≲ 0.75 reach the AGB phase but do not reach the thermally pulsing AGB phase (TP-AGB manque).
 |
Fig. 2 Hertzsprung-Russell diagram for our helium-enhanced evolutionary sequences for metallicity Z = 0.001 and initial helium mass fraction Y = 0.4. Evolutionary tracks for progenitors with initial stellar mass of 0.65 M⊙, 0.70 M⊙, 0.75 M⊙, and 0.80 M⊙ (panels a), b), c), and d), respectively) are depicted from the ZAMS to advanced stages of white dwarf evolution. The color scale on the right shows the fraction of the total luminosity from hydrogn burning. The upper value of the color scale has been set to 1.2, so higher values of LCNO + pp/L∗ are not shown. |
 |
Fig. 3 Same as Fig. 2 but for the evolutionary sequences of stars with masses 0.85 M⊙, 1.0 M⊙, 1.5 M⊙, and 2.0 M⊙. |
In our simulations, only those progenitors with initial stellar mass larger than ≈0.70 M⊙ are able to reach the AGB phase. This is in good agreement with the calculations of Charbonnel et al. (2013). This is clearly illustrated in Figs. 2 and 3, which show the evolution in the Hertzsprung-Russell diagram of some selected sequences with Z = 0.001, from the ZAMS to the white dwarf stage. The color scale in each figure shows the fraction of the total luminosity due to hydrogen burning. The sequence with initial mass M = 0.70 M⊙ (panel b in Fig. 2) evolves directly to the white dwarf regime without passing through the AGB phase (AGB manque). Indeed, this sequence, which experiences the core helium flash shortly after departing from the RGB phase, settles onto the hot HB (at Teff = 22 400 K) to burn helium in a stable way. Because of its very thin hydrogen envelope, this sequence does not go through the AGB phase after the end of core helium burning. On the other hand, the sequence with initial mass M = 0.75 M⊙ (panel c in Fig. 2) reaches the AGB but abandons it before reaching the TP-AGB phase (TP-AGB manque). However, both sequences experience several helium shell flashes before reaching the white dwarf regime.
Panel a in Fig. 2 shows the complete evolution of our progenitor star of mass M = 0.65 M⊙, which ends its life as a helium-core white dwarf of mass M = 0.45 M⊙. Before reaching the terminal cooling track, this sequence experiences a CNO shell flash, which reduces the effects of residual hydrogen burning on its evolution at late cooling times. This is in contrast with the expectation for very massive helium-core white dwarfs resulting from progenitors with standard initial helium abundances. In this case, CNO flashes are not expected to occur, as reported in Serenelli et al. (2002) and Althaus et al. (2013). The occurrence, or lack of occurence, of a CNO shell flash is critical for the cooling times of these stars. Finally, Figs. 2 and 3 show that, except for the more massive and helium-core white dwarf sequences, residual hydrogen burning constitutes a main energy source for all the resulting white dwarfs, even at advanced stages of evolution (see later in this section).
The impact of the initial helium content on the resulting final mass is shown in Fig. 4, which represents the theoretical initial-to-final mass relation resulting for our helium-enhanced evolutionary sequences for metallicity Z = 0.001 and Z = 0.0005. The final mass is the stellar mass with which the remnant enters the white dwarf phase. The figure also shows the mass of the hydrogen-free core (HFC) at the first thermal pulse for the case in which Y = 0.4 and Z = 0.001 are adopted. For the sake of comparison, we also include in the figure the initial-final-mass relation for sequences that do not consider a helium enhancement. In particular, we plot, with a green solid line, the resulting relationship for the case Y = 0.247, Z = 0.001 (Althaus et al. 2015). The growth of the HFC mass during the TP-AGB, i.e., beyond the first thermal pulse, is evident for initial masses higher than M ~ 1.0 M⊙. Because of the small amount of mass remaining above the HFC at the first thermal pulse, the final mass for the less massive sequences does not differ appreciably from the mass of the HFC at the first thermal pulse.
It is also worth noting in this figure that in the case of helium-enhanced sequences, the final mass of the remnants is markedly higher than the final mass expected from sequences with a standard initial abundance of helium. This can be understood by examining Fig. 5, which shows the temporal evolution of the mass of the HFC from the onset of core helium burning to the moment at which the first thermal pulse is reached for the 1.0 M⊙, Z = 0.001 sequences in which Y = 0.4 and Y = 0.247 are considered. The color scale on the right of the figure shows the core helium abundance. Even though the HFC mass before the onset of core helium burning is lower for the helium-enhanced sequence, it grows more rapidly during the helium burning phase than in the case in which a standard initial helium abundance is considered. This is because hydrogen burning by the CNO cycle is more efficient in the helium-enhanced sequence. Thus, after helium exhaustion in the core, the helium-enhanced sequence ends up with a larger HFC.
 |
Fig. 4 Theoretical initial-to-final mass relation for our helium-enhanced evolutionary sequences with metallicity Z = 0.001 and Z = 0.0005 (black and red solid lines, respectively). We also show the mass of the HFC at the first thermal pulse for the case Y = 0.4, Z = 0.001 (blue solid line). In addition, the initial-to-final mass relation when overshooting is considered during the TP-AGB phase, and that resulting from sequences with standard helium content (Y = 0.247 and Z = 0.001) are also shown (blue dotted and green solid lines, respectively). |
We now compare the predictions for the final mass of our sequences with those of Chantereau et al. (2015). In particular, we pay special attention to the 0.8 M⊙, Z = 0.0005 sequence studied in detail by these authors. As can be seen in Fig. 4 for our 0.8 M⊙, Z = 0.0005 progenitor we obtain a mass of ~ 0.56 M⊙, which is markedly smaller than that derived by Chantereau et al. (2015) for the same initial helium abundance, 0.659 M⊙. This discrepancy is mostly due to the different mass-loss rates used in both studies, particularly during the AGB and early TP-AGB phases. In fact, as mentioned in Sect. 2, for those phases we rely on the mass-loss formulation of Schröder & Cuntz (2005), which is the same formulation we use for the RGB phase. In contrast, Chantereau et al. (2015) employed the mass-loss rate of Vassiliadis & Wood (1993) after the end of core helium burning. This treatment predicts mass-loss rates that are substantially smaller than those of Schröder & Cuntz (2005) during these phases. This is particularly true for low-mass stars. This results in a larger number of thermal pulses and a higher final mass when compared with those obtained using our prescriptions. To check this, we recomputed our 0.85 M⊙, Z = 0.0005 sequence, but this time we used the mass-loss rate of Vassiliadis & Wood (1993) after the end of helium core burning. During the AGB and early TP-AGB, the mass-loss rates are between 2 and 3 orders of magnitude smaller than those given by Schröder & Cuntz (2005). As a result, our sequence experiences many more thermal pulses (20) and ends its evolution with a final mass of 0.675 M⊙, which is markedly higher than the final mass of 0.58 M⊙ we find when the prescription of Schröder & Cuntz (2005) is used. This explains the much higher final mass found in Chantereau et al. (2015), as compared with that obtained here. However, we mention that for the AGB phase, the prescription of Vassiliadis & Wood (1993) yields a mass-loss rate that is much lower than expected for the RGB phase. This contradicts the mass-loss estimates obtained for stars in ω Centauri (McDonald et al. 2009). For instance, at log (L/L⊙) = 3.0 on the AGB the prescription of Vassiliadis & Wood (1993) yields a mass-loss rate that is three orders of magnitude smaller than that of Schröder & Cuntz (2005) for the RGB at the same luminosity. Also, Rosenfield et al. (2014) have shown that the mass-loss rates of Schröder & Cuntz (2005) provide a consistent description of predust AGB winds.
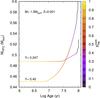 |
Fig. 5 Time evolution of the mass of the HFC from the onset of core helium burning until the occurrence of the first thermal pulse for the 1.0 M⊙, Z = 0.001 sequences with Y = 0.4 and Y = 0.247. The color scale on the right shows the core helium abundance (mass fraction). The HFC mass increases substantially during core helium burning for the helium-enhanced sequence. |
The theoretical initial-to-final mass relations shown in Fig. 4 correspond to evolutionary sequences for which overshooting was disregarded during the TP-AGB phase. For all of these sequences, we did not find third dredge-up episodes. However, at low metallicities overshooting also favors the occurrence of third dredge-up episodes and carbon enrichment of the envelope for very small stellar masses (Weiss & Ferguson 2009). Nevertheless, there is no conclusive evidence about the occurrence of third dredge-up episodes in metal-poor, low-mass progenitors (Althaus et al. 2015). To assess the impact of overshooting during the TP-AGB on the final mass of the remnant we recomputed some of our sequences for Y = 0.4, Z = 0.001 but allowed overshooting from the beginning of the thermally pulsing AGB phase. Results are depicted in Fig. 4 with a blue dotted line. Following Miller Bertolami (2016), we considered diffusive overshooting with the overshooting parameter set to f = 0.0075; see Renedo et al. (2010), Weiss & Ferguson (2009) for details. As shown in Miller Bertolami (2016) and mentioned in Sect. 2, the choice of f = 0.0075 reproduces several observational properties of AGB and post-AGB stars in our Galaxy and in the Magellanic Clouds. The occurrence of third dredge-up episodes in sequences with overshooting further reduce growth of the HFC, thus yielding lower final masses. Also, the increase in the C/O ratio resulting from a third dredge-up episode results in cooler stars. This, in turn, translates into significantly higher mass-loss rates. As a result, the remnant of the evolution departs from the AGB after a few more thermal pulses following the occurrence of third dredge-up. We find that only our 1.5 and 2.0 M⊙ sequences experience third dredge-up. In particular, for the 2.0 M⊙ sequence, C/O > 1 after the third thermal pulse and becomes C/O > 2.5 after the tenth thermal pulse. From Fig. 4 we conclude that the intial-to-final mass relation for helium-enhanced stars is not markedly modified by the occurrence of overshooting during the TP-AGB phase.
3.2. The evolution of white dwarfs
We now pay attention to the evolution of white dwarfs resulting from helium-enhanced progenitors. We begin examining Fig. 6, in which we plot the fraction of the total white dwarf luminosity due to hydrogen nuclear burning (CNO and pp burning) during the entire cooling phase for all our helium-enhanced evolutionary sequences of metallicity Z = 0.0005 and Z = 0.001 (upper and bottom panels, respectively) and initial helium mass fraction Y = 0.4. In this figure, the red lines show the predictions for those sequences that end as helium-core white dwarfs, whilst blue lines depict the results for those sequences that result in white dwarfs with C/O cores. In addition, in the bottom panel of this figure we include the prediction for a helium-core white dwarf sequence of mass 0.435 M⊙ resulting from the evolution of a progenitor with Z = 0.01 and standard initial helium abundance (Althaus et al. 2013). For the less massive C/O white dwarfs, residual hydrogen burning becomes a main energy source even at low luminosities. This is in line with the results of Miller Bertolami et al. (2013) and Althaus et al. (2015), who found that low-mass white dwarfs resulting from low-metallicity progenitors that have not experienced third dredge-up, are characterized by massive hydrogen envelopes. This, in turn, has one evident effect, namely that residual hydrogen burning becomes one of the main energy sources during the evolution of white dwarfs for substantial periods of time. The calculations performed here show that this is also true for white dwarfs resulting from helium-enhanced progenitors.
As shown in Althaus et al. (2015), see also Miller Bertolami (2016), overshooting during the TP-AGB phase leads to carbon enrichment of the envelope due to third dredge-up episodes for low-mass, low-metallicity progenitor stars and, consequently, reduces the final mass of the hydrogen envelope with which the corresponding white dwarfs enter into their cooling track. This, obviously, minimizes the role played by residual hydrogen burning. Hence, the conclusion reached by Althaus et al. (2015) and Miller Bertolami (2016) that residual hydrogen burning impacts the cooling of low-metallicity white dwarfs is not valid if some amount of overshooting is allowed during the TP-AGB phase of low-mass progenitors. This is in contrast with the situation we find for white dwarfs resulting from helium-enhanced progenitors. In fact, as mentioned previously, when overshooting is considered during the TP-AGB phase of helium-enhanced progenitors third dredge-up only occurs for our more massive sequences. For the less massive sequences, no carbon enrichement is predicted when overshooting is considered and, consequently, residual hydrogen burning plays a role in the evolution of the resulting white dwarfs. To summarize, the conclusion that stable hydrogen burning dominates a significant part of the evolution of low-mass white dwarfs resulting from low-metallicity, He-enhanced progenitors does not depend on the occurrence of overshooting during the TP-AGB evolution.
 |
Fig. 6 Fraction of the total white dwarf luminosity due to hydrogen nuclear burning (CNO and pp burning) for all our helium-enhanced sequences for metallicity Z = 0.0005 and Z = 0.001 (upper and bottom panel, respectively) and initial helium mass fraction Y = 0.4. Red (blue) lines show the predictions of our sequences that end as white dwarfs with helium (C/O) cores. The green line corresponds to a helium-core white dwarf sequence of 0.435 M⊙ resulting from a progenitor with Z = 0.01 and standard initial helium abundance, taken from Althaus et al. (2013). For less massive C/O white dwarfs, residual hydrogen burning becomes a relevant energy source even at low luminosities. |
Another interesting feature of the results shown in Fig. 6 is the small impact of residual hydrogen burning on the evolution of massive helium-core white dwarfs resulting from helium-enhanced progenitors. Again, this is because these white dwarfs experience a CNO shell flash during the cooling branch that reduces the mass of the residual hydrogen-rich envelope, thus minimizing the role of hydrogen burning at advanced stages of the evolution. This is in contrast with what occurs for helium-core white dwarfs resulting from progenitors with standard initial helium abundances (see Istrate et al. 2014; Althaus et al. 2013, for recent works) since for very massive helium-core white dwarfs CNO flashes do not occur, even when element diffusion is taken into account. To illustrate this, in Fig. 6 we indicate with a thick green line, the contribution of residual hydrogen burning for a helium-core white dwarf of mass 0.435 M⊙ resulting from a progenitor star with Z = 0.01 and a standard initial helium abundance (Althaus et al. 2013). For this star, no CNO flashes took place and, thus, in this case hydrogen burning contributes significantly to the luminosity of the white dwarf.
 |
Fig. 7 Cooling times for all our helium-enhanced sequences with Z = 0.001 and initial helium mass fractions Y = 0.4. Red and blue lines correspond to white dwarfs with helium and C/O cores, respectively. The solid green line corresponds to a helium-core white dwarf of mass 0.435 M⊙ resulting from a progenitor with Z = 0.01 and a standard initial helium abundance (Althaus et al. 2013), whilst the dashed green line corresponds to helium-core white dwarfs of mass 0.449 M⊙ resulting from a progenitor with Z = 0.001 and a standard initial helium abundance (Serenelli et al. 2002). |
 |
Fig. 8 Chemical abundance distribution of hydrogen, helium, carbon, and oxygen in terms of the outer mass fraction for selected white dwarf models at the ZZ Ceti stage (thick lines) resulting from helium-enhanced progenitors with Z = 0.001 and initial helium abundance Y = 0.4. The chemical profiles at the beginning of the cooling track are the thin lines. Panel a) corresponds to a helium-core white dwarf resulting from a progenitor of initially M = 0.65 M⊙, while panels b, c, and d) to C/O white dwarfs resulting from progenitors with M = 0.70 M⊙, M = 0.75 M⊙, and M = 1.0 M⊙, respectively. |
The resulting cooling times are shown in Fig. 7. This figure shows the cooling times of our sequences for helium-enhanced progenitors with Z = 0.001, Y = 0.4. The time origin is taken at the moment at which the remnants reach the point of maximum effective temperature at the beginning of the cooling branch. As in Fig. 6, we show the results for white dwarfs with C/O cores with blue lines and those for white dwarfs with helium cores with red lines. We find that residual nuclear burning yields substantial delays in the cooling time for the less massive C/O white dwarfs. At log (L/L⊙) ~ −3.0, residual hydrogen burning leads to an increase in the cooling times of low-mass white dwarfs that range between 20 and 40%. This conclusion is independent of the assumed initial helium abundance. In fact, Althaus et al. (2015) found a similar result for the case of white dwarfs resulting from progenitors with standard helium abundances. However, as mentioned earlier, in contrast with what is found for the case of standard sequences, the impact of residual hydrogen burning on the cooling times of low-mass white dwarfs resulting from helium-enhanced progenitors is not affected by the occurrence of overshooting on the TP-AGB phase of their progenitor stars.
The initial helium abundance also impacts the evolution of helium-core white dwarfs. To show this, in Fig. 7 we include the cooling curves for a helium-core white dwarf of mass 0.435 M⊙ resulting from a progenitor with Z = 0.01 and a standard initial helium abundance (Althaus et al. 2013), and for a helium-core white dwarf of mass 0.449 M⊙ resulting from a progenitor with Z = 0.001 and a standard initial helium abundance in solid and dashed green lines, respectively. (Serenelli et al. 2002). The helium-core white dwarfs resulting from helium-enhanced progenitors evolve much faster than their counterparts resulting from standard progenitors. As mentioned, this different behavior is due to the occurrence of a CNO shell flash in the helium-core white dwarf with helium-enhanced progenitors, which reduces the impact of further nuclear burning at advanced stages. In fact, at intermediate and low luminosities, the cooling times of massive helium-core white dwarfs with helium-enhanced progenitors are about a factor of 2 shorter, when compared with the helium-core white dwarfs formed from progenitors with standard initial helium abundances.
3.3. The pulsational properties
As already shown, the helium enhancement of progenitor stars has a significant impact on the formation and evolution of the resulting white dwarfs. In this sense, it is worthwhile to explore the pulsational properties of these white dwarfs as well. The pulsational properties of these stars are strongly dependent on the shape of the chemical profile left by the evolution of their progenitors. In this connection, in Fig. 8 we show, with thick lines, the inner abundance distribution of hydrogen, helium, carbon, and oxygen as a function of the outer mass fraction for selected white dwarf models resulting from helium-enhanced progenitors with Z = 0.001 and initial helium abundance Y = 0.4 at the ZZ Ceti stage. In addition, the thin lines show chemical profiles at the beginning of the cooling track. Panel a corresponds to a helium-core white dwarf that results from a progenitor of initial mass M = 0.65 M⊙, while panels b, c, and d correspond to C/O white dwarfs resulting from progenitors of masses M = 0.70 M⊙, M = 0.75 M⊙, and M = 1.0 M⊙, respectively. The carbon and oxygen profiles are the result of different processes acting during the evolution of the progenitor. In particular, we note the flat profile in the inner core left by convection during the core helium burning phase and signatures of the outward-moving helium burning shell, particularly for the more massive sequence illustrated, which reached the thermally pulsing AGB phase. In addition, chemical profiles at the beginning of the cooling track of the C/O sequences show the typical intershell rich in helium and carbon left by the pulse-driven convection zone during the thermally pulsing phase. This intershell is present in all our C/O white dwarf sequences. Although the M = 0.70 M⊙ and M = 0.75 M⊙ progenitors avoided the TP-AGB phase, they nonetheless experienced several thermal pulses at high effective temperatures before entering the white dwarf stage. The action of element diffusion is clearly also noticeable, and leads to the formation of a thick hydrogen envelope by the time evolution has reached the domain of the ZZ Ceti stars. But more importantly, it removes the double-layered structure at the intershell region for white dwarfs with masses higher than M ≃ 0.60 M⊙. For less massive white dwarfs, the intershell region is not removed by diffusion. In this regard, it is important to realize that the presence of a double-layered structure affects the theoretical g-mode period spectrum of ZZ Ceti stars; see Althaus et al. (2010a).
Once we studied the chemical stratification of these white dwarf models we continue our analysis computing the adiabatic pulsation periods of nonradial g (gravity) modes employing the LP-PUL pulsation code described in Córsico & Althaus (2006). In Fig. 9 we show the propagation diagrams (Unno et al. 1989) corresponding to the same stellar models depicted in Fig. 8. The propagation diagrams are the spatial run of the Brunt-Väisälä (buoyancy) frequency, N, and the Lamb (acoustic) frequency, Lℓ. The shape of the Brunt-Väisälä frequency largely determines the properties of the g-mode pulsation spectrum (Winget & Kepler 2008; Fontaine & Brassard 2008; Althaus et al. 2010b). The profile of N reflects all changes in the chemical composition of the white dwarf model in the form of local maxima of the buoyancy frequency (Unno et al. 1989). In the case of the helium-core white dwarf model, only one chemical interface exists, which is the helium-hydrogen transition region (see panel a of Fig. 8). This chemical interface induces a bump in N2 at −log (1−Mr/M⋆) ~ 3.5 (panel a of Fig. 9). This interface also affects the shape of the Lamb frequency. In the case of white dwarfs with carbon-oxygen cores, the internal chemical structure is substantially more complex than in the case of the helium-core white dwarf models (see panels b, c, and d in Fig. 8). This results in a much more complex form of the run N2, as can be seen in panels b, c, and d of Fig. 9. Indeed, in these cases, the Brunt-Väisälä frequency is characterized by additional maxima induced by the presence of the C/O-He and C/O chemical interfaces.
 |
Fig. 9 Propagation diagrams, the spatial run of the logarithm of the squared Brunt-Väisälä and Lamb frequencies (Unno et al. 1989), corresponding to the white dwarfs models shown in Fig. 8 for ℓ = 1. |
The number and shape of the chemical interfaces present in the interior of DA white dwarf models strongly affect the propagation properties of nonradial pulsation g modes, in particular through mode trapping and confinement (Brassard et al. 1992; Bradley 1996; Córsico et al. 2002). Mode trapping or confinement results in a strong departure from uniformity of the forward period separation, ΔΠk (≡ Πk + 1−Πk), when plotted in terms of the pulsation period Πk, where k is the radial order of the mode. Thus, the period difference between an observed mode and adjacent modes can be considered as an observational diagnostic of mode trapping. For a helium-core white dwarf, which is characterized by a single chemical interface such as that of the model of mass M = 0.45 M⊙ considered here, local minima in ΔΠk usually correspond to modes trapped in the hydrogen envelope; this is in contrast to local maxima in ΔΠk, which are associated with modes trapped in the inner core. The forward period spacing for ℓ = 1g modes in terms of the periods corresponding to the helium-core model of mass M = 0.45 M⊙ is depicted in panel a of Fig. 10. We also show the asymptotic period spacing, computed as in Tassoul et al. (1990), with a dotted blue line. Mode-trapping signatures are clearly noticeable, particularly for periods shorter than ~1500 s. Longer periods seem to fit the asymptotic predictions, although small departures from constant period spacing are still clearly seen. In the case of white dwarfs with carbon-oxygen cores, the presence of multiple chemical transition regions causes much more complex patterns of mode-trapping/confinement, as can be seen in panels b, c, and d of Fig. 10. In particular, strong departures from uniform period separation are evident for the models with M = 0.489 M⊙, M = 0.528 M⊙, and M = 0.615 M⊙. These features persist for the entire range of periods analyzed here. Also, we note some “beating” modulating the amplitudes of the departures of ΔΠk. This beating is due to the combined mode-trapping and confinement effects caused by the various steps in the C/O profile in the core; see Córsico & Althaus (2006) for the case of PG1159 star models. Clearly, the mode trapping and confinement features of models with C/O cores are by far more pronounced than for the case of the helium-core white dwarf.
 |
Fig. 10 Dipole (ℓ = 1) forward period spacing (ΔPik) as a function of the periods (Πk) corresponding to the models shown in Fig. 8. |
4. Summary and conclusions
In this work we computed the full evolution of helium-enhanced (Y = 0.4) sequences with initial masses ranging from 0.60 to 2.0 M⊙. Two sets of model sequences were computed; for the first sequence we adopted a metallicity Z = 0.001, whereas for the second Z = 0.0005 was employed. We emphasized those aspects of evolution of helium-enhanced star that are relevant for the formation and evolution of white dwarfs. For all our sequences, we computed the evolution starting from the ZAMS and followed through the stages of stable hydrogen and helium core burning, the stage of mass loss during the entire thermally pulsing AGB, the domain of the planetary nebulae at high effective temperature and, finally, the terminal white dwarf cooling track up to very low surface luminosities. To the best of our knowledge, the sequences presented here constitute the first set of consistent evolutionary tracks from the ZAMS to the white dwarf stage covering a wide range of masses. This set of sequences is appropriate for the study of the formation and evolution of white dwarfs resulting from stars with very high initial helium abundances, such as those found in ω Centauri and NGC 2808.
We explored different aspects of the evolution of the resulting white dwarfs and of their progenitors. In particular, we studied the initial-to-final mass relation, and we found that the final mass of white dwarfs resulting from helium-enhanced progenitors is markedly larger than the final mass expected from sequences with a standard helium initial abundance. Progenitors with initial mass smaller than M ≃ 0.65 M⊙ evolve directly into white dwarfs with helium cores in less than 14 Gyr, while those descending from more massive progenitors and with initial stellar mass smaller than M ≃ 0.75 M⊙, reach the white dwarf stage avoiding the TP-AGB phase, TP-AGB manque (or AGB manque if the stellar mass is less than M ≃ 0.70 M⊙). However, before reaching the terminal cooling track, these remnants experience several helium thermal pulses at high effective temperatures. The formation of helium-core white dwarfs in our simulations is not the result of binary evolution, but a consequence of the much shorter ages of the low-mass, helium-enhanced progenitors. This is in accordance with the results of Calamida et al. (2008), Cassisi et al. (2009), and Bellini et al. (2013a), who found evidence for the existence of an important percentage of helium-core white dwarfs in ω Centauri.
Our simulations show that the hydrogen-free core grows during the TP-AGB for initial masses higher than M ~ 1.0 M⊙. For lower stellar masses, the final mass of the remnants of helium-enhanced progenitors does not differ appreciably from the mass of the hydrogen-free core at the first thermal pulse. We also explored the impact of overshooting during the TP-AGB, and found that the occurrence of third dredge-up and the related carbon enrichment of the envelope is expected to occur for initial masses larger than ~1.5 M⊙. However, we found that the intial-to-final mass relation for helium-enhanced stars is not markedly altered by the occurrence of overshooting during the TP-AGB phase.
With regard to the evolution of the resulting white dwarfs, we find that for the less massive C/O white dwarfs, residual hydrogen burning becomes a main energy source even at low luminosities. This result agrees with the predictions of Althaus et al. (2015). These authors found that low-mass white dwarfs resulting from low-metallicity progenitors, which have not experienced third dredge-up, are characterized by residual hydrogen burning and, therefore, this energy source dominates the evolution for substantial periods of time. The resulting delays in the cooling times range from 20 to 40% at low luminosities. However, in contrast with the situation encountered for white dwarfs resulting from standard progenitors, we found that the role played by stable hydrogen burning in low-mass white dwarfs descending from helium-enhanced progenitors does not depend on the occurrence of overshooting during the TP-AGB evolution. In addition, according to our simulations, the very massive helium-core white dwarfs descending from helium-enhanced progenitors experience a CNO shell flash during the cooling branch, thus minimizing the impact of hydrogen burning at advanced stages of the evolution. As a consequence, at intermediate and low luminosities, cooling times of massive, helium-core white dwarfs formed from helium-enhanced progenitors are about a factor of 2 lower, as compared with helium-core white dwarfs resulting from progenitors with a standard initial helium abundance.
We also find that a double-layered structure in the outer chemical profile is formed in all the resulting C/O models. This double-layered chemical profile is the result of mixing in the pulse-driven convection zone that appears as a result of the helium thermal pulses. However, by the time the ZZ Ceti regime is reached, this structure is removed by element diffusion for masses higher than M ≃ 0.60 M⊙. This behavior impacts the pulsational properties of the models at the ZZ Ceti stage.
Finally, we explored the pulsational properties of our models. We found that in the case of white dwarfs with carbon-oxygen cores, the shape of the Brunt-Väisälä frequency is substantially more complex than in the case of white dwarfs with helium cores. This leads to a markedly different behavior of the mode-trapping and confinement properties and the forward period separation, ΔΠk (≡ Πk + 1−Πk). In spite of the similarity of the stellar masses analyzed here, the mode trapping and confinement features of models with C/O cores are substantially different from those models with helium cores. Then, if pulsations are detected in future photometric observations of white dwarfs, provided that enough consecutive pulsation periods of g modes were detected, this distinctive difference in the ΔΠk distribution could be employed as a seismic diagnostic tool to distinguish white dwarfs with helium cores from those with C/O cores. This constitutes a promising avenue to constrain the evolutionary history of cluster stars.
Acknowledgments
We thank our referee for his/her valuable comments. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnolǵica BID 1728/OC-AR, by the PIP 112-200801-00940 grant from CONICET, by MINECO grant AYA2014-59084-P, and by the AGAUR. This research has made use of NASA Astrophysics Data System.
References
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010a, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010b, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 537, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Anderson, J., Salaris, M., et al. 2013a, ApJ, 769, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Piotto, G., Milone, A. P., et al. 2013b, ApJ, 765, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Salaris, M., & Gilmozzi, R. 2013, A&A, 549, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, P. A. 1996, ApJ, 468, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., & Hansen, C. J. 1992, ApJS, 80, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Corsi, C. E., Bono, G., et al. 2008, ApJ, 673, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Caloi, V., & D’Antona, F. 2007, A&A, 463, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Anderson, J., et al. 2009, ApJ, 702, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Pietrinferni, A., Vink, J. S., & Monelli, M. 2014, A&A, 571, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chantereau, W., Charbonnel, C., & Decressin, T. 2015, A&A, 578, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., Chantereau, W., Decressin, T., Meynet, G., & Schaerer, D. 2013, A&A, 557, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Benvenuto, O. G., & Serenelli, A. M. 2002, A&A, 387, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., et al. 2012, MNRAS, 424, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Caloi, V. 2008, MNRAS, 390, 693 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & Weiss, A. 2004, ApJ, 603, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., & Oswalt, T. D. 2016, New Astron. Rev., 72, 1 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum, F. 1998, MNRAS, 293, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Istrate, A. G., Tauris, T. M., Langer, N., & Antoniadis, J. 2014, A&A, 571, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffery, E. J., von Hippel, T., DeGennaro, S., et al. 2011, ApJ, 730, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Joo, S.-J., & Lee, Y.-W. 2013, ApJ, 762, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- McDonald, I., van Loon, J. T., Decin, L., et al. 2009, MNRAS, 394, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Rohrmann, R. D., Granada, A., & Althaus, L. G. 2011, ApJ, 743, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & García-Berro, E. 2013, ApJ, 775, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P. 2015, MNRAS, 446, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Cassisi, S., et al. 2012, ApJ, 754, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., García-Berro, E., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 546, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenfield, P., Marigo, P., Girardi, L., et al. 2014, ApJ, 790, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar (Wiley-VCH), 400 [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A. M., Althaus, L. G., Rohrmann, R. D., & Benvenuto, O. G. 2002, MNRAS, 337, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Shingles, L. J., Doherty, C. L., Karakas, A. I., et al. 2015, MNRAS, 452, 2804 [NASA ADS] [CrossRef] [Google Scholar]
- Tailo, M., Di Criscienzo, M., D’Antona, F., Caloi, V., & Ventura, P. 2016, MNRAS, 457, 4525 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars, 2nd edn. (Tokyo: University of Tokyo Press) [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Theoretical initial-to-final mass relationship and evolutionary stages (shown employing different gray scales) obtained following the evolution of stars with an initial helium-enhanced composition Y = 0.4 and a metallicity Z = 0.001. The color scale on the right shows the age (in Gyr) at the tip of the RGB. |
| In the text | |
 |
Fig. 2 Hertzsprung-Russell diagram for our helium-enhanced evolutionary sequences for metallicity Z = 0.001 and initial helium mass fraction Y = 0.4. Evolutionary tracks for progenitors with initial stellar mass of 0.65 M⊙, 0.70 M⊙, 0.75 M⊙, and 0.80 M⊙ (panels a), b), c), and d), respectively) are depicted from the ZAMS to advanced stages of white dwarf evolution. The color scale on the right shows the fraction of the total luminosity from hydrogn burning. The upper value of the color scale has been set to 1.2, so higher values of LCNO + pp/L∗ are not shown. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but for the evolutionary sequences of stars with masses 0.85 M⊙, 1.0 M⊙, 1.5 M⊙, and 2.0 M⊙. |
| In the text | |
 |
Fig. 4 Theoretical initial-to-final mass relation for our helium-enhanced evolutionary sequences with metallicity Z = 0.001 and Z = 0.0005 (black and red solid lines, respectively). We also show the mass of the HFC at the first thermal pulse for the case Y = 0.4, Z = 0.001 (blue solid line). In addition, the initial-to-final mass relation when overshooting is considered during the TP-AGB phase, and that resulting from sequences with standard helium content (Y = 0.247 and Z = 0.001) are also shown (blue dotted and green solid lines, respectively). |
| In the text | |
 |
Fig. 5 Time evolution of the mass of the HFC from the onset of core helium burning until the occurrence of the first thermal pulse for the 1.0 M⊙, Z = 0.001 sequences with Y = 0.4 and Y = 0.247. The color scale on the right shows the core helium abundance (mass fraction). The HFC mass increases substantially during core helium burning for the helium-enhanced sequence. |
| In the text | |
 |
Fig. 6 Fraction of the total white dwarf luminosity due to hydrogen nuclear burning (CNO and pp burning) for all our helium-enhanced sequences for metallicity Z = 0.0005 and Z = 0.001 (upper and bottom panel, respectively) and initial helium mass fraction Y = 0.4. Red (blue) lines show the predictions of our sequences that end as white dwarfs with helium (C/O) cores. The green line corresponds to a helium-core white dwarf sequence of 0.435 M⊙ resulting from a progenitor with Z = 0.01 and standard initial helium abundance, taken from Althaus et al. (2013). For less massive C/O white dwarfs, residual hydrogen burning becomes a relevant energy source even at low luminosities. |
| In the text | |
 |
Fig. 7 Cooling times for all our helium-enhanced sequences with Z = 0.001 and initial helium mass fractions Y = 0.4. Red and blue lines correspond to white dwarfs with helium and C/O cores, respectively. The solid green line corresponds to a helium-core white dwarf of mass 0.435 M⊙ resulting from a progenitor with Z = 0.01 and a standard initial helium abundance (Althaus et al. 2013), whilst the dashed green line corresponds to helium-core white dwarfs of mass 0.449 M⊙ resulting from a progenitor with Z = 0.001 and a standard initial helium abundance (Serenelli et al. 2002). |
| In the text | |
 |
Fig. 8 Chemical abundance distribution of hydrogen, helium, carbon, and oxygen in terms of the outer mass fraction for selected white dwarf models at the ZZ Ceti stage (thick lines) resulting from helium-enhanced progenitors with Z = 0.001 and initial helium abundance Y = 0.4. The chemical profiles at the beginning of the cooling track are the thin lines. Panel a) corresponds to a helium-core white dwarf resulting from a progenitor of initially M = 0.65 M⊙, while panels b, c, and d) to C/O white dwarfs resulting from progenitors with M = 0.70 M⊙, M = 0.75 M⊙, and M = 1.0 M⊙, respectively. |
| In the text | |
 |
Fig. 9 Propagation diagrams, the spatial run of the logarithm of the squared Brunt-Väisälä and Lamb frequencies (Unno et al. 1989), corresponding to the white dwarfs models shown in Fig. 8 for ℓ = 1. |
| In the text | |
 |
Fig. 10 Dipole (ℓ = 1) forward period spacing (ΔPik) as a function of the periods (Πk) corresponding to the models shown in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


