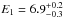| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628238 | |
| Published online | 01 December 2016 | |
The 2015 outburst of the accreting millisecond pulsar IGR J17511–3057 as seen by INTEGRAL, Swift, and XMM-Newton
1 INAF, Osservatorio Astronomico di Roma, via di Frascati 33, 00044 Monte Porzio Catone (Roma), Italy
e-mail: alessandro.papitto@oa-roma.inaf.it
2 Institut de Ciències de l’Espai (IEEC-CSIC), Campus UAB, Carrer de Can Magrans s/n, 08193 Barcelona, Spain
3 ISDC Data Centre for Astrophysics, Chemin d’Ecogia 16, 1290 Versoix, Switzerland
4 European Space Astronomy Centre (ESA/ESAC), Science Operations Department, 28691 Villanueva de la Cañada, Madrid, Spain
5 INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica – Palermo, via U. La Malfa 153, 90146 Palermo, Italy
6 Institució Catalana de Recerca i Estudis Avançats (ICREA), 08010 Barcelona, Spain
Received: 2 February 2016
Accepted: 1 September 2016
We report on INTEGRAL, Swift, and XMM-Newton observations of IGR J17511–3057 performed during the outburst that occurred between March 23 and April 25, 2015. The source reached a peak flux of 0.7(2) × 10-9 erg cm-2 s-1 and decayed to quiescence in approximately a month. The X-ray spectrum was dominated by a power law with photon index between 1.6 and 1.8, which we interpreted as thermal Comptonization in an electron cloud with temperature >20 keV. A broad (σ ≃ 1 keV) emission line was detected at an energy (E = 6.9+0.2-0.3 keV) compatible with the K-α transition of ionized Fe, suggesting an origin in the inner regions of the accretion disk. The outburst flux and spectral properties shown during this outburst were remarkably similar to those observed during the previous accretion event detected from the source in 2009. Coherent pulsations at the pulsar spin period were detected in the XMM-Newton and INTEGRAL data at a frequency compatible with the value observed in 2009. Assuming that the source spun up during the 2015 outburst at the same rate observed during the previous outburst, we derive a conservative upper limit on the spin-down rate during quiescence of 3.5 × 10-15 Hz s-1. Interpreting this value in terms of electromagnetic spin-down yields an upper limit of 3.6 × 1026 G cm3 to the pulsar magnetic dipole (assuming a magnetic inclination angle of 30°). We also report on the detection of five type-I X-ray bursts (three in the XMM-Newton data, two in the INTEGRAL data), none of which indicated photospheric radius expansion.
Key words: pulsars: general / stars: neutron / X-rays: binaries / X-rays: individuals: IGR J17511-3057
© ESO, 2016
1. Introduction
Accreting millisecond pulsars (AMSPs) are neutron stars (NS) that accrete matter transferred from a low-mass (M2 ≲ M⊙) companion star (Wijnands & van der Klis 1998); their magnetospheres are able to truncate the disk in-flow and channel the in-falling matter to the regions of the surface close to the magnetic poles, producing coherent pulsations in the X-ray light curve. The extremely quick rotation of AMSPs is attained during a previous Gyr-long phase of sustained mass accretion, and these sources are considered the most immediate progenitors of millisecond radio pulsars (Bisnovatyi-Kogan & Komberg 1974; Alpar et al. 1982; Radhakrishnan & Srinivasan 1982; Archibald et al. 2009; Papitto et al. 2013). So far, accretion driven coherent pulsations have been detected from 17 transient low-mass X-ray binaries (see e.g. Patruno & Watts 2012, for a review). Pulsations from 15 of these objects have been observed during relatively bright (LX ≈ few × 1036 erg s-1) X-ray outbursts lasting from a few weeks to a few months. In two cases, PSR J1023+0038 and XSS J12270-4859 (Archibald et al. 2015; Papitto et al. 2015), the coherent signal was detected when the source was at a much lower luminosity level (LX ≈ few × 1033 erg s-1); these two sources were also detected as radio pulsars during X-ray quiecence (Archibald et al. 2009; Roy et al. 2015), similar to the AMSP IGR J18245–2452 (Papitto et al. 2013).
Log of the Swift and XMM-Newton observations considered in this paper.
IGR J17511–3057 was discovered by INTEGRAL during an outburst in September 2009 (Baldovin et al. 2009; Bozzo et al. 2010). The detection of 4.1 ms coherent pulsations in the Rossi X-ray Timing Explorer light curve allowed the identification of the source as an AMSP in a binary system with a 3.47 h orbital period (Markwardt et al. 2009). The measured pulsar mass function indicated a main-sequence companion star with a mass between 0.15 and 0.44 M⊙ (Papitto et al. 2010). At discovery, 18 type-I X-ray bursts were observed from the pulsar (Altamirano et al. 2010; Bozzo et al. 2010; Papitto et al. 2010; Falanga et al. 2011). Evidence of photospheric radius expansion was not seen in any of these bursts, and an upper limit to the source distance (6.9 kpc) was provided by Altamirano et al. (2010).
A new outburst of IGR J17511–3057 was detected by INTEGRAL on March 23, 2015 (Bozzo et al. 2015a,b). Here, we report on a series of INTEGRAL and Swift observations performed throughout the event, and on a XMM-Newton Target of Opportunity observation performed three days after the onset of the outburst.
2. Observations
2.1. Swift
The Swift-XRT (Burrows et al. 2005) observed IGR J17511–3057 from March 23, 2015, at 14:08:39 (UTC) for a total of 19 ks. A log of all available observations for this outburst is given in Table 1. Swift-XRT data – which were collected in windowed-timing (WT) or in photon-counting (PC) mode, depending on the source count rate – were processed and analysed using the standard software (FTOOLS v6.17), calibration (CALDB 20150721), and methods. The WT data were never affected by pile-up; on the contrary, the PC data were corrected, when required, by adopting standard procedures (Vaughan et al. 2006). Therefore WT source events were generally extracted from circular regions of 20 pixels (1 pixel ≃ 2.36′′), while PC source events from annuli with outer radius of 20 pixels and inner radius ranging from 3 to 7 pixels, depending on the severity of pile-up. Background events were extracted from nearby source-free regions. Throughout the campaign, a spectrum was accumulated for each observation and each observing mode, with the exception of the last four observations (036−039) for which a single spectrum was extracted to increase statistics. The data were binned to ensure at least 20 counts per energy bin and were fit in the 0.3−10 keV energy range. The latest responses within CALDB were used. Spectral modelling was performed using xspec v.12.8.2.
2.2. XMM-Newton
XMM-Newton (Jansen et al. 2001) observed IGR J17511–3057 for 76 ks starting on March 26, 2015, at 22:16:52 (UTC). A log of the observations analysed is given in Table 1. The data were reduced using SAS v.14.0.0.
The EPIC-pn camera was operated in timing mode to achieve a time resolution of 29.5 μs, and was equipped with a medium optical blocking filter. We removed soft proton flaring episodes characterized by an EPIC-pn 10−12 keV count rate exceeding 0.8 c/s; this reduced the effective exposure to 55.6 ks. In timing mode, the spatial information along one of the optical axes is lost to allow a faster readout. The maximum number of counts was recorded in pixels characterized by RAWX coordinate 37 and 38. To extract the source emission we considered a 21 pixel wide region (1 pixel ≃ 4.1′′), spanning from RAWX = 27 to 47. Background was extracted far from the source, in a 3 pixel wide region centred on RAWX = 4. Spectra were accumulated using single and double event patterns, and re-binned with the tool specgroup to have at least 25 counts per channel, and not more than three bins per resolution element. For the spectral extraction we followed the recommendations of the latest calibration document on the spectral accuracy of EPIC-pn in fast modes (Smith et al. 20151) and applied the special gain, together with the rate dependent CTI corrections.
Three type-I X-ray bursts were detected during the XMM-Newton observation. To analyse the persistent emission we created good time intervals (GTIs) that eliminated a time interval starting 10 s before and ending 150 s after each of these bursts. The burst onset was identified as the first 1 s-long bin of the light curve that exceeded the average persistent count rate of 65.6 c/s by more than 5σ. Apart from the bursts, no evident variability trend was seen over timescales going from a few seconds to the length of the observation. At the average persistent count rate observed photon pile up is not expected to affect significantly the spectral response of the EPIC-pn in timing mode (Smith et al. 2015).
The Reflection Grating Spectrometer (RGS) was operated in standard spectroscopy mode. We extracted spectra from the first order of diffraction where a count rate of 5.0 and 5.9 c/s was observed by the RGS1 and RGS2 camera, respectively. We removed the same time intervals characterized by high flaring background and type-I X-ray bursts, as was done for the EPIC-pn.
The EPIC MOS1 and MOS2 camera operated in Large Window and Timing mode, respectively. We did not consider these data in the analysis presented here as ≃ 21% and ≃ 12% of the photons respectively detected by the two cameras suffered from pile-up distortion of the spectral response, as evaluated with the epatplot tool.
2.3. INTEGRAL
IGR J17511–3057 was observed within the field of view (FoV) of the instruments on board INTEGRAL from satellite revolution 1517 (starting on March 3, 2015) to 1533 (ending on April 25, 2015).
We analysed all the publicly available INTEGRAL data and the data for which we obtained data rights on the source during INTEGRAL AO12 using version 10.1 of the Off-line Scientific Analysis software (OSA) distributed by the INTEGRAL Science Data Center (ISDC; Courvoisier et al. 2003). The INTEGRAL data on the source were accumulated during observations of the Galactic Centre, which are executed following a rectangular pattern (5 × 5 pointings, or science windows, SCWs) around the Galactic Centre position with typical durations of 2−3 ks and a 2.17 degree step between successive pointings. Only SCWs in which the source was located within 4.5° of the centre of the JEM-X FoV (Lund et al. 2003) were included in the analysis of the data from this instrument. For IBIS/ISGRI, we included all SCWs where the source was located within 12° of aim point of the instrument in order to avoid calibration uncertainties (as suggested in the OSA manual). We first extracted both the IBIS/ISGRI (Ubertini et al. 2003; Lebrun et al. 2003) mosaics in the 20−80 keV and 80−100 keV energy band and noticed that there was no significant detection of the source in the hard band. IGR J17511–3057 was significantly detected in both the JEM-X mosaics extracted in the 3−10 keV and 10−20 keV energy bands. The ISGRI and JEM-X light curves of the source were extracted with a time resolution of 1 SCW in the 20−80 keV and 3−20 keV, respectively, and later rebinned, to improve the statistics, with a time resolution of 2 h (see panels c and d in Fig. 1).
 |
Fig. 1 0.5−10 keV unabsorbed flux (in units of 10-9 erg cm-2 s-1; panel a)) and photon index of the best-fitting power law (panel b)) measured by the Swift-XRT in WT (blue points) and PC mode (red points), and by XMM-Newton (green point). JEM-X (panel c)) and ISGRI (panel d)) light curves were binned with a time resolution of 2 h. |
We accumulated a single spectrum of the source for each of the two JEM-X units and for IBIS/ISGRI using the data in revolution 1522, between 2015 March 25 at 03:55:44 and March 26 at 23:14:27, leading to an effective on-source exposure time of 31.2 ks and 24.3 ks, respectively. This time interval was chosen because it is the closest to the XMM-Newton observation, having an overlap of 4.5 ks with it. In particular, for the extraction of this spectrum we selected only the SCWs where the source was detected at more than 5σ and within an off-axis angle of 4.5° in order to optimize the signal-to-noise ratio and have a fully simultaneous JEM-X+ISGRI spectrum. The spectra response matrices were generated using the standard energy binning of 16 channels for JEM-X and 13 channels for IBIS/ISGRI. The fit to these spectra was carried out simultaneously with the XMM-Newton spectrum and discussed in Sect. 2.2.
We also extracted the JEM-X1 and JEM-X2 light curves with a time resolution of 2 s to search for type-I X-ray bursts, and identified two, neither of which in the time window overlapping with the XMM-Newton exposure. The properties of these bursts are discussed in Sect. 3.3. On the other hand, we did not identify any bursts in the ISGRI light curve.
3. Results
3.1. Persistent emission
The Swift-XRT 0.3−10 keV spectra were modelled simultaneously with an absorbed power law, forcing the absorption column to take the same value in every observation. This resulted in an estimate of the absorption column density (described with the model phabs in xspec) of NH = 1.18(4) × 1022 cm-2. The chi squared of the fit was 1632 for 1411 degrees of freedom. If the data are drawn from the model distribution, the probability of obtaining a chi squared as high, or higher, is 3.5 × 10-5, which is smaller than the significance level of 2.7 × 10-3 we set to determine the goodness of the fit. However, we did not find any evident residuals that motivated the addition of more spectral components, and the chi squared of the individual spectra resulted in a null hypothesis probability always larger than the significance level adopted. Using the absorption column as a free parameter in different observations did not yield a statistically significant decrease in the chi squared of the fit. However, we did not find any evident unmodelled residuals that motivated the addition of more spectral components, and the chi squared of the individual spectra resulted in a null hypothesis probability always larger than the significance level adopted. Systematic errors we did not take into account possibly yielded the relatively large residuals of the simultaneous modelling of the Swift-XRT spectra with an absorbed power law. The 0.5−10 keV unabsorbed flux attained a maximum of 0.7(2) × 10-9 erg cm-2 s-1 on March 24, during observation 00031492021 (see Table 1). The flux decay started around March 29 and was characterized by a roughly linear decay, until the flux decreased abruptly on April 16 (i.e. 25 days after the first detection of the outburst) to a level ≃ 100 fainter than the outburst peak (F(0.5−10 keV) = 7.2(8) × 10-12 erg cm-2 s-1 measured by coadding the observations performed between April 16 and April 25). The photon index of the power law that fitted the Swift-XRT spectra lay in the range between 1.3 and 1.6, becoming much steeper (Γ = 2.1(2)) in the last group of observations performed when the source had already fainted significantly. The values of the unabsorbed 0.5−10 keV flux and power-law index are plotted in the upper panels (a and b) of Fig. 1 using blue and red points for observations performed in WT and PC modes, respectively.
 |
Fig. 2 Top panel: X-ray spectrum of IGR J17511–3057 observed by the EPIC-pn (blue points), RGS1 (red points), and RGS2 (green points) during the XMM-Newton observation. Spectra were rebinned for graphical purposes. Bottom and middle panels: residuals with respect to the model listed in the central column of Table 2 (see text for details), with and without the addition of an emission line centred at |
The spectra observed on March 26, 2015, by the EPIC-pn (1.4−11 keV)2 and the two RGS cameras (0.6−2.0 keV) on board XMM-Newton were modelled simultaneously by treating the normalization of the two RGS spectra with respect to the EPIC-pn as free parameters (see top panel of Fig. 2). We used a thermal Comptonization model (nthcomp, Zdziarski et al. 1996; Życki et al. 1999) modified by the interstellar absorption. No high-energy cut-off was detected in the XMM-Newton energy band, and we fixed the temperature of the Comptonizing electron cloud to kTe = 30 keV, in line with the results obtained modelling the INTEGRAL spectrum observed immediately before the XMM pointing (see below). The Comptonization component was described by an asymptotic photon index 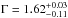 and a temperature of soft input photons of kTs< 0.98 keV, yielding a high value of the chi-squared fit of 1963.3 for 1286 degrees of freedom. To account for the residuals at soft (kT ≲ 1.5 keV) energies we added a single-temperature black-body component (bbodyrad in xspec) with
and a temperature of soft input photons of kTs< 0.98 keV, yielding a high value of the chi-squared fit of 1963.3 for 1286 degrees of freedom. To account for the residuals at soft (kT ≲ 1.5 keV) energies we added a single-temperature black-body component (bbodyrad in xspec) with 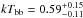 keV and a disk emission component (diskbb in xspec) with temperature of
keV and a disk emission component (diskbb in xspec) with temperature of 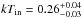 keV. The addition of these two components yielded a significant decrease in the χ2 by Δχ2 = −74.3 (giving χ2 = 1888.9 for 1284 d.o.f.) and − 124.6 (giving χ2 = 1764.29 for 1282 d.o.f.) for the addition of two degrees of freedom each, respectively. We evaluated with an F-test that such improvements of the model χ2 are equivalent to a probability of < 10-11 that they are due to chance. The normalizations of these two thermal components indicate apparent radii of Rin/ (cosi)1/2 = (34 ± 20) d6.9 km and
keV. The addition of these two components yielded a significant decrease in the χ2 by Δχ2 = −74.3 (giving χ2 = 1888.9 for 1284 d.o.f.) and − 124.6 (giving χ2 = 1764.29 for 1282 d.o.f.) for the addition of two degrees of freedom each, respectively. We evaluated with an F-test that such improvements of the model χ2 are equivalent to a probability of < 10-11 that they are due to chance. The normalizations of these two thermal components indicate apparent radii of Rin/ (cosi)1/2 = (34 ± 20) d6.9 km and 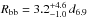 km for the disk and the black-body component, respectively. Here, d6.9 is the distance to the source in units of 6.9 kpc. Local residuals of the EPIC-pn data at energies of 1.8, 2.2, and 6.9 keV were modelled using three Gaussian emission features. The first two features are narrow, and their energies are compatible with calibration residuals of the Si K and Au M edges, known to frequently affect the EPIC-pn spectra in timing mode. The feature at higher energy had a centroid at
km for the disk and the black-body component, respectively. Here, d6.9 is the distance to the source in units of 6.9 kpc. Local residuals of the EPIC-pn data at energies of 1.8, 2.2, and 6.9 keV were modelled using three Gaussian emission features. The first two features are narrow, and their energies are compatible with calibration residuals of the Si K and Au M edges, known to frequently affect the EPIC-pn spectra in timing mode. The feature at higher energy had a centroid at 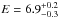 keV, compatible with the Kα transition of ionized Fe. With the inclusion of this feature the model χ2 decreased by Δχ2 = 130.8 for the addition of three free parameters (see Protassov et al. 2002; and Stewart 2009, for a discussion of the use of the chi-squared fit to measure the significance of spectral lines). The residuals obtained with and without the addition of the Fe emission line to the model are shown in the bottom and middle panel of Fig. 2, respectively. The line width (
keV, compatible with the Kα transition of ionized Fe. With the inclusion of this feature the model χ2 decreased by Δχ2 = 130.8 for the addition of three free parameters (see Protassov et al. 2002; and Stewart 2009, for a discussion of the use of the chi-squared fit to measure the significance of spectral lines). The residuals obtained with and without the addition of the Fe emission line to the model are shown in the bottom and middle panel of Fig. 2, respectively. The line width (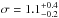 keV) and strength (equivalent width of ≃ 150 eV) suggested broadening in the inner parts of an accretion disk. An absorption edge at an energy compatible with the OVIII transition (0.871 keV) was also added to model residuals of the RGS spectra. With the addition of such emission features, the reduced χ2 of the fit attained a value of 1441.8 (for 1274 degrees of freedom). The probability that a value of the χ2 as high, or higher, is obtained if the data are drawn from the model distribution is 6.8 × 10-4. This probability is smaller than significance level we set (p = 2.7 × 10-3), but the absence of evident residuals and the 2% uncertainty quoted by Smith et al. (2015)3 for the relative effective area calibration of the EPIC-pn motivated us to accept this model without the addition of further components. Model parameters of the best fit are listed in the central column of Table 2.
keV) and strength (equivalent width of ≃ 150 eV) suggested broadening in the inner parts of an accretion disk. An absorption edge at an energy compatible with the OVIII transition (0.871 keV) was also added to model residuals of the RGS spectra. With the addition of such emission features, the reduced χ2 of the fit attained a value of 1441.8 (for 1274 degrees of freedom). The probability that a value of the χ2 as high, or higher, is obtained if the data are drawn from the model distribution is 6.8 × 10-4. This probability is smaller than significance level we set (p = 2.7 × 10-3), but the absence of evident residuals and the 2% uncertainty quoted by Smith et al. (2015)3 for the relative effective area calibration of the EPIC-pn motivated us to accept this model without the addition of further components. Model parameters of the best fit are listed in the central column of Table 2.
Spectral parameters of IGR J17511–3057.
The broadness of the Fe line motivated us to attempt modelling it using a diskline component (Fabian et al. 1989). However, the best fit was obtained only for extreme values of the parameters that control the line width (Rin< 8.5Rg, i> 67°), and did not yield a significant improvement of the description of the spectrum as the chi-squared of the fit decreased by Δχ2 = 3.7 with the addition of three free parameters.
We then fitted the XMM-Newton EPIC-pn and RGS spectra together with the INTEGRAL JEM-X (5−25 keV) and ISGRI (20−150 keV) spectra which were taken on March 26 (between 03:55:44 and 23:14:27). An AMSP-like IGR J17511–3057 does not usually show drastic spectral variability on timescales of a day or less (Ibragimov et al. 2011), and the analysis of Swift data presented earlier where no significant spectral changes were detected over the outburst supports the simultaneous modelling of the XMM-Newton and INTEGRAL data in spite of the limited overlap (≃ 4.5 ks) between these observations. The ISGRI spectrum allowed us to weakly constrain the electron temperature of the Comptonized component as 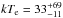 keV, while the rest of the spectral parameters are basically unchanged with respect to those determined by XMM-Newton spectra alone. The spectrum and residuals from the best fit are plotted in Fig. 3, while model parameters are listed in the rightmost column of Table 2.
keV, while the rest of the spectral parameters are basically unchanged with respect to those determined by XMM-Newton spectra alone. The spectrum and residuals from the best fit are plotted in Fig. 3, while model parameters are listed in the rightmost column of Table 2.
We also considered the addition to the model of a component describing the reflection of the Comptonizing photon spectrum off the accretion disk. We removed the Gaussian describing the Fe emission line, and added a reflionx (Ross & Fabian 2005) component to the model convolved with relativistic disk blurring (rdblur, Fabian et al. 1989). The parameters of the disk reflecting surface were held fixed to inner and outer radii of Rin = 10Rg and Rout = 1000Rg, respectively, and index of the power-law dependence of emissivity β = −2. The best fit was obtained for an ionization parameter 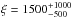 , and a flux of 0.10(5) × 10-10 erg cm-2 s-1 in the reflection component, equal to ≃ 10% of the irradiating flux and similar to the value observed by Papitto et al. (2011). The addition of reflection did not yield a significant decrease in the model chi-squared (χ2 = 1457.1 for 1291 degrees of freedom), though, and we could not conclude that a reflection component was significantly detected in the considered dataset, probably because of low counting statistics.
, and a flux of 0.10(5) × 10-10 erg cm-2 s-1 in the reflection component, equal to ≃ 10% of the irradiating flux and similar to the value observed by Papitto et al. (2011). The addition of reflection did not yield a significant decrease in the model chi-squared (χ2 = 1457.1 for 1291 degrees of freedom), though, and we could not conclude that a reflection component was significantly detected in the considered dataset, probably because of low counting statistics.
 |
Fig. 3 Top panel: X-ray spectrum of IGR J17511–3057 observed by the EPIC-pn (blue points), RGS1 (red points), RGS2 (green points), JEM-X (magenta points), and ISGRI (cyan points) during the 2015 outburst. RGS1 and RGS2 spectra were rebinned for graphical purposes. The best-fit model (black line), the Fe line (green line), the disk (red line), single-temperature black body (magenta line), and the Comptonized (blue line) spectra are also shown. Bottom panel: residuals with respect to the best-fit model. |
3.2. Timing analysis
To perform a timing analysis of the coherent signal shown by the source in the XMM-Newton EPIC-pn data, we first converted the times of arrival of the X-ray photons to the solar system barycentre using the source position determined by Nowak et al. (2009) using Chandra observations (see also Paizis et al. 2012). Coherent pulsations at 244.8 Hz were easily detected at an rms amplitude of ≃ 15 per cent in 50 s intervals. Starting from the orbital solution provided by Riggio et al. (2011b), we applied standard timing techniques (see e.g. Papitto et al. 2011) to study the evolution of the pulse phase computed over 500 s intervals. The values of the orbital parameters we obtained, namely the semi-major axis of the NS orbit asini/c, the orbital period Porb, the epoch of passage at the ascending node T∗ and eccentricity e, as well as the value of the spin frequency ν and spin frequency derivative 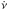 , are given in Table 3. The spin frequency derivative could not be constrained over the relatively short exposure of the XMM-Newton observation. As we show in Sect. 4, spin-up torques are expected to increase the pulsar frequency at a rate of a few × 10-13 Hz s-1, two orders of magnitude lower with respect to the upper limit we measured (
, are given in Table 3. The spin frequency derivative could not be constrained over the relatively short exposure of the XMM-Newton observation. As we show in Sect. 4, spin-up torques are expected to increase the pulsar frequency at a rate of a few × 10-13 Hz s-1, two orders of magnitude lower with respect to the upper limit we measured (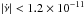 Hz s-1, at 3σ confidence level). Because of the relatively short exposure, the best-fit values of the spin frequency correlated to a high degree with the (unconstrained) spin frequency derivative. Similarly to what was done by Papitto et al. (2010) for the 2009 outburst of IGR J17511–3057, we quote in Table 3 the pulsar spin frequency obtained by fixing
Hz s-1, at 3σ confidence level). Because of the relatively short exposure, the best-fit values of the spin frequency correlated to a high degree with the (unconstrained) spin frequency derivative. Similarly to what was done by Papitto et al. (2010) for the 2009 outburst of IGR J17511–3057, we quote in Table 3 the pulsar spin frequency obtained by fixing 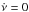 in the fit (i.e. the average spin frequency over the considered interval). A compatible value of the spin frequency is obtained if a value of the spin-up rate of the order of that expected from the observed X-ray luminosity (
in the fit (i.e. the average spin frequency over the considered interval). A compatible value of the spin frequency is obtained if a value of the spin-up rate of the order of that expected from the observed X-ray luminosity ( Hz s-1) is considered, justifying our choice.
Hz s-1) is considered, justifying our choice.
Spin and orbital parameters of IGR J17511–3057.
The error on the position of the source is an additional source of uncertainty on the value of the spin frequency (see e.g. Lyne & Graham-Smith 1990). To evaluate the frequency shift produced by a difference between the actual value of the ecliptic coordinates of the source and that used to report X-ray photons to the solar system barycentre, we used (see e.g. Eq. (4) in Papitto et al. 2011) ![\begin{equation} \label{eq:poserr} \delta\nu_{\rm pos}=\nu\,y\frac{2\pi}{P_{\oplus}}[\cos{M_i}\cos{\beta}\,\delta\lambda+\sin{M_i}\sin{\beta}\delta\beta], \end{equation}](/articles/aa/full_html/2016/12/aa28238-16/aa28238-16-eq145.png) (1)here, y is the Earth distance from the solar system barycentre in lt-s, λ and β are the ecliptic longitude and latitude, respectively, δλ and δβ are the respective uncertainties, Mi = [2π(Ti−Tγ) /P⊕] −λ, Ti is the start time of observations considered, Tγ is the nearest epoch of passage at the vernal point, and P⊕ is the Earth orbital period. The error of the position of the source (0.6′′ at 90% confidence level, Nowak et al. 2009; Paizis et al. 2012, which translates into σλ = 1.5 × 10-6 rad, σβ = 1.8 × 10-6 rad) yielded an uncertainty of
(1)here, y is the Earth distance from the solar system barycentre in lt-s, λ and β are the ecliptic longitude and latitude, respectively, δλ and δβ are the respective uncertainties, Mi = [2π(Ti−Tγ) /P⊕] −λ, Ti is the start time of observations considered, Tγ is the nearest epoch of passage at the vernal point, and P⊕ is the Earth orbital period. The error of the position of the source (0.6′′ at 90% confidence level, Nowak et al. 2009; Paizis et al. 2012, which translates into σλ = 1.5 × 10-6 rad, σβ = 1.8 × 10-6 rad) yielded an uncertainty of 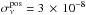 Hz on the value of the measured spin frequency. Adding in quadrature this uncertainty to the statistical error gave an error of σν = 4 × 10-8 Hz on the average spin frequency measured by XMM-Newton in 2015.
Hz on the value of the measured spin frequency. Adding in quadrature this uncertainty to the statistical error gave an error of σν = 4 × 10-8 Hz on the average spin frequency measured by XMM-Newton in 2015.
Folding the entire EPIC-pn observation around the best-fitting value of the spin frequency, we obtained the 0.3−10 keV pulse profile shown in Fig. 4. It was successfully modelled by four harmonic components, similar to the pulse profile observed in 2009 (Papitto et al. 2010).
We searched for coherent pulsations in the hard X-rays ISGRI band, considering the data observed by ISGRI from 2015 March 22 at 08:56:29 to April 9 at 05:52:01 UTC. We converted the arrival times of the events recorded by ISGRI at the solar system barycentre using the position derived by Chandra, and then to the line of nodes using the ephemeris listed in Table 3. We employed a customary software dedicated to phase-resolved spectroscopy of X-ray binaries with IBIS (Segreto & Ferrigno 2007) to extract the background subtracted pulse profile in the broad 20−100 keV energy band. We detected the signal at the pulsar spin frequency determined by XMM-Newton, but the low signal-to-noise ratio of the ISGRI data prevented us from obtaining an independent measurement. The pulse profile is shown in Fig. 5. Fitting the profile with a constant and a sinusoid, we determined that the ratio between the sine amplitude and the constant is 14 ± 3%, in agreement with the value found by Falanga et al. (2011) during the 2009 outburst of this source. Splitting the energy range into two bands, we obtained amplitudes of 22 ± 6% and 12 ± 3% for the energy ranges 20−30 keV and 30−100 keV, respectively, suggesting a decrease in the pulsed emission at higher energy.
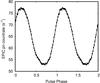 |
Fig. 4 0.3–10 keV pulse profile of IGR J17511–3057 as observed by the EPIC pn during the 2015 outburst. The best-fitting model (solid line) is composed of four harmonics with background subtracted rms amplitudes of 14.31(6)%, 1.53(6)%, 0.72(6)%, and 0.26(6)%. Two cycles are shown for clarity. |
 |
Fig. 5 Background subtracted pulse profile of IGR J17511–3057 in the 20−100 keV energy band extracted from 221 ks of dead-time corrected on-axis equivalent exposure time in the IBIS/ISGRI data (from 2015-03-22 08:56:29 to 04−09 05:52:01 UTC); the vertical axis displays equivalent count per second for on-axis pointing. |
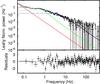 |
Fig. 6 Average Leahy normalized power spectrum of the EPIC-pn time series (top panel). A counting noise constant level of 1.9993(4) is subtracted to the power. The two flat-top noise components are plotted with a red and a blue solid line, and the discrete feature centred at ν3 = 0.5 ± 0.1 Hz as a green solid line (see text for details). The spike at the pulsar spin frequency was removed for display purposes. The bottom panel shows residuals in units of the standard deviation σ. |
In order to study the aperiodic time variability, we produced a power density spectrum of the 0.5−10 keV EPIC-pn time series with 59 μs time resolution (yielding a Nyquist frequency of 8468 Hz). We averaged the Leahy-normalized fast Fourier transforms performed over approximately 8 s intervals (for a total of 9457 spectra, each extending down to 0.1 Hz). The resulting average power density spectrum was rebinned as a geometrical series with a ratio of 1.02. The 0.1−500 Hz spectrum was modelled with the sum of two flat-top noise components modelled with Lorentizian functions centred at ν = 0 with widths W1 = (3 ± 1) × 10-2 Hz and W2 = 11.5 + /−1.3 Hz, and a discrete feature centred at ν3 = 0.5 ± 0.1 Hz with width W3 = 1.2 ± 0.2 Hz, giving a fit χ2 of 611.2 for 522 degrees of freedom. We searched for kHz quasi-periodic oscillations (QPOs), fitting a Lorentzian with quality factor fixed to a value of 4, but found no significant QPO with a 3σ upper limit of 1% on the rms amplitude, a value lower than that characterizing the high-frequency QPOs reported by Kalamkar et al. (2011). The average power spectrum and residuals with respect to the best-fit model are plotted in Fig. 6.
3.3. Type-I X-ray bursts
During the XMM-Newton observation, three type-I X-ray bursts with very similar properties were detected. The light curve of the first burst is displayed in panel a of Fig. 7. The start times of the three bursts were T1 = 57 108.01023(1) MJD, T2 = 57 108.34130(1) MJD, and T3 = 57108.67847(1) MJD. The burst rise times were ≈ 1 s, and were followed by exponential decays which started a few seconds after the maxima. The measured decay e-folding times were τ1 = 12.1(2) s, τ2 = 12.6(2) s, and τ3 = 12.4(2) s for the three bursts. The time elapsed between consecutive bursts was Δt1 = 28.6 ks and Δt2 = 29.1 ks.
 |
Fig. 7 0.3−10 keV light curve of the first type-I X-ray burst oserved by XMM-Newton during the 2015 observation (panel a)). The burst onset took place at MJD 57108.01023. The temperature and the apparent radius (evaluated considering a distance to the source of 6.9 kpc) are plotted in panels b) and c). Panel d) shows the rms amplitude of pulsations at the spin frequency of the pulsar (see Table 3). |
We extracted the EPIC-pn burst spectra removing the two brightest pixel columns to minimize the effect of pile up, and subtracted the spectrum of the persistent emission as the background. Close to the burst peak, spectra were extracted over 2 s intervals; at later times the exposure was increased to ensure that the counting statistics allowed a meaningful spectral modelling. Spectral channels were rebinned in the same way as the persistent spectrum. The spectra extracted over the different intervals were simultaneously fit by an absorbed black body with variable temperature and radius, resulting in a χ2 fit of 510.9 (for 556 degrees of freedom), 559.43 (522), and 589.16 (518) for the three bursts. The 0.5−10 keV burst flux attained a maximum value of (1.5 ± 0.1) × 10-8 erg cm-2 s-1. The temperature decreased steadily from ≃ 3 keV during the burst evolution (see panel b of Fig. 7), while the apparent radius of the emitting region peaked at ≃ 6 d6.9 km ten seconds after the burst onset, and then decayed smoothly (see panel c of Fig. 7).
Coherent oscillations at the pulsar spin frequency were detected at a somewhat lower rms amplitude (≃ 10 per cent) than that of persistent pulsations; see panel d of Fig. 7). Considering that the burst emission was up to 25 times brighter than the persistent flux, such a decrease of the pulse amplitude could not be ascribed to the increase of the unpulsed flux, but suggests instead that the oscillations detected during the burst were different than the coherent signal observed during quiescence. Pulsations were detected close to the burst peak and during the burst decay. The phase of burst oscillations measured over 5 s intervals is generally consistent within the uncertainties with the phase of the persistent profile, even if deviations of up to 0.2 in phase are observed close to the burst peaks.
Two bursts were detected by INTEGRAL, with trigger times of T4 = 57 116.43276(2) MJD and 57 120.11919(2) MJD. From the JEM-X light curves, we measured a peak count rate of 344.6+/−47.6 c/s (3−20 keV) and 177.5+/−38.8 c/s (3−20 keV), respectively, for the two bursts. Because JEM-X spectra cannot be extracted for time intervals shorter than 8 s, we estimated the peak flux by comparing the above count rates with that of the Crab in the same energy band as obtained from the INTEGRAL calibration observations performed in the satellite revolution 1520 (on 2015 March 19). We obtained a 3−20 keV X-ray flux of 1.3+/− 0.2 Crab and 0.7+/− 0.1 Crab, respectively. These translate into ~ 3.0 × 10-8 erg cm-2 s-1 and ~ 1.6 × 10-8 erg cm-2 s-1. The e-folding decay times of the two bursts measured from the JEM-X lightcurves were 7.3 ± 0.1 s and 6.0 ± 0.1 s.
4. Discussion
During the outburst detected in early 2015, IGR J17511–3057 attained a peak flux of ≃ 0.6−0.7 × 10-9 erg cm-2 s-1 (0.5−10 keV, unabsorbed, see Sect. 3.1). This value is compatible with the peak flux observed in the last outburst detected in 2009 (Bozzo et al. 2010). Assuming a bolometric correction factor of ~ 2 (estimated from the ratio between the flux estimated in the 0.5−100 keV and 0.5−10 keV energy band; see Table 2), the observed peak flux corresponds to a 0.5−100 keV luminosity of ≃ 8 × 1036d6.9 erg s-1. The outburst flux decayed over ≈ 25 d before the source was no longer detectable. The spectral shape observed by Swift-XRT was roughly constant, with a softening of the spectrum at the end of the outburst.
Similarly to the 2009 outburst (Papitto et al. 2010; Falanga et al. 2011; Ibragimov et al. 2011), and to other AMPSs (Patruno & Watts 2012), the X-ray spectrum of IGR J17511–3057 observed during the 2015 outburst was dominated by a hard component described by a power law with index Γ ≃ 1.6−1.8, and a cut-off at a temperature of ≳ 20 keV. The emission observed by XMM-Newton and INTEGRAL during the 2015 outburst was modelled as thermal Comptonization of soft photons with temperature kTs ≳ 1 keV, off a cloud of hot electrons (kTe ≳ 20 keV). Two thermal components were detected at soft X-rays, and interpreted as radiation coming from an accretion disk truncated a few tens of km from the NS surface and from the NS surface itself. Signatures of disk reflection such as a broadened (σ ≈ 1 keV) line centred at an energy compatible with ionized iron was also observed in the XMM-Newton spectrum.
X-ray pulsations at the spin period of IGR J17511–3057 were detected by the XMM-Newton EPIC-pn at an RMS amplitude of ≃ 15 per cent in the 0.5−10 keV band, and by INTEGRAL at an amplitude of 14 per cent in the 20−100 keV band. Up to four harmonics were needed to model the pulse profile observed in the soft X-ray band, similar to the case of the 2009 outburst (Papitto et al. 2010). We searched for kHz quasi-periodic oscillations like those reported by Kalamkar et al. (2011), but did not find any hint in the Fourier power spectrum.
The relatively short exposure (~70 ks) over which pulsations were detected prevented us from studying the frequency evolution driven by the accretion of matter. Only a loose upper limit on the spin frequency derivative of ~ 10-11 Hz s-1 could be obtained. On the other hand, the expected spin-up rate driven by accretion torques is 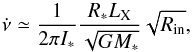 (2)where M∗, R∗, and I∗ are the NS mass, radius, and moment of inertia, respectively; Rin is the disk truncation radius; and LX is the accretion luminosity. The accretion luminosity derived from the flux observed in the 0.5−100 keV band is LX = 8.1 × 1036d6.9 erg s-1. Evaluating Eq. (2) for a disk truncated at the corotation radius (
(2)where M∗, R∗, and I∗ are the NS mass, radius, and moment of inertia, respectively; Rin is the disk truncation radius; and LX is the accretion luminosity. The accretion luminosity derived from the flux observed in the 0.5−100 keV band is LX = 8.1 × 1036d6.9 erg s-1. Evaluating Eq. (2) for a disk truncated at the corotation radius (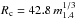 km for IGR J17511–3057), and taking M∗ = 1.4M⊙, R∗ = 10 km, and I = 1045 g cm2 yields
km for IGR J17511–3057), and taking M∗ = 1.4M⊙, R∗ = 10 km, and I = 1045 g cm2 yields 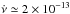 Hz s-1, two orders of magnitude lower than the upper limit we were able to set based on the XMM-Newton observation alone. A spin-up at an average rate of
Hz s-1, two orders of magnitude lower than the upper limit we were able to set based on the XMM-Newton observation alone. A spin-up at an average rate of 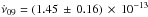 Hz s-1 was indeed reported by Riggio et al. (2011b) for the 2009 outburst, when the source emitted a luminosity similar to that observed during the 2015 outburst.
Hz s-1 was indeed reported by Riggio et al. (2011b) for the 2009 outburst, when the source emitted a luminosity similar to that observed during the 2015 outburst.
Assuming that the spin frequency observed by XMM-Newton during a ≈ 70 ks exposure is a good tracer of the actual spin frequency of the pulsar, we can derive constraints on the evolution of the spin frequency of the pulsar during the Δtq = 1991 d elapsed between the end of 2009 outburst (MJD 55 113; see Fig. 1 of Riggio et al. 2011b), and the beginning of the 2015 outburst (MJD 57 104; Bozzo et al. 2015a). In 2009, XMM-Newton measured an average spin frequency of ν09 = 244.83395121(4) Hz (Papitto et al. 2010), and the frequency decrease between this value and that measured in 2015 outburst is Δν = (ν15−ν09) = (−1.0 ± 0.5) × 10-7 Hz. To evaluate the effect on this value of the positional uncertainty we maximized the difference between the frequency shift evaluated using Eq. (1) for the 2009 and the 2015 outburst, respectively, obtaining 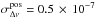 Hz. Adding in quadrature this term to the statistical uncertainty yields an estimate of the frequency change Δν = (−1.0 ± 0.7) × 10-7 Hz, compatible with zero within less than 2σ. A spin-down rate of a few × 10-15 Hz s-1 has been observed from all four of the AMSPs for which pulsations have been detected during consecutive outbursts so far (Hartman et al. 2008, 2009, 2011; Patruno et al. 2012; Patruno 2010; Papitto et al. 2011; Riggio et al. 2011a; Patruno et al. 2009). It is therefore useful to quote the measured 3σ upper limit on the spin frequency decrease of IGR J17511–3057 (| Δν | < 3 × 10-7 Hz), and the corresponding limit on the average rate of spin frequency variation (
Hz. Adding in quadrature this term to the statistical uncertainty yields an estimate of the frequency change Δν = (−1.0 ± 0.7) × 10-7 Hz, compatible with zero within less than 2σ. A spin-down rate of a few × 10-15 Hz s-1 has been observed from all four of the AMSPs for which pulsations have been detected during consecutive outbursts so far (Hartman et al. 2008, 2009, 2011; Patruno et al. 2012; Patruno 2010; Papitto et al. 2011; Riggio et al. 2011a; Patruno et al. 2009). It is therefore useful to quote the measured 3σ upper limit on the spin frequency decrease of IGR J17511–3057 (| Δν | < 3 × 10-7 Hz), and the corresponding limit on the average rate of spin frequency variation (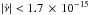 Hz s-1).
Hz s-1).
A more conservative upper limit of the magnitude of the spin frequency derivative of IGR J17511–3057 during quiescence was obtained taking into account that the pulsar spun up during the ≈18 d elapsed since the 2009 XMM-Newton observation and the end of that outburst (Riggio et al. 2011b), and assuming that it did the same during the nearly three days which occurred since the 2015 outburst beginning and the XMM-Newton observation. Considering the spin-up rate derived by Riggio et al. (2011b) (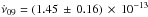 Hz s-1), we estimated a frequency increase of Δνaccr ≃ ( + 2.6 ± 0.3) × 10-7 Hz taking place at the end of the 2009 outburst and at the beginning of the 2015 outburst. Adding this value to the upper limit on the measured frequency change, we obtained an upper limit on the spin-down rate of the pulsar during quiescence of | Δν | < | Δνaccr−Δν | < 6 × 10-7 Hz. The corresponding limit on the spin-down rate is
Hz s-1), we estimated a frequency increase of Δνaccr ≃ ( + 2.6 ± 0.3) × 10-7 Hz taking place at the end of the 2009 outburst and at the beginning of the 2015 outburst. Adding this value to the upper limit on the measured frequency change, we obtained an upper limit on the spin-down rate of the pulsar during quiescence of | Δν | < | Δνaccr−Δν | < 6 × 10-7 Hz. The corresponding limit on the spin-down rate is 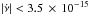 Hz s-1.
Hz s-1.
Assuming that the main torque operating on AMSPs during quiescence was due to electromagnetic spin-down, the upper limit on the spin-down rate can be translated into a constraint on the strength of the magnetic dipole moment. Considering the relation derived by Spitkovsky (2006) for the spin-down of a force-free rotating magnetosphere, it is possible to estimate the NS magnetic dipole moment, μ, needed to produce a certain spin-down as ![\begin{equation} \mu=\left[\frac{I_* c^3\dot{\nu}}{(1+\sin^2\alpha)(2\pi)^2\nu^3} \right]^{1/2}, \end{equation}](/articles/aa/full_html/2016/12/aa28238-16/aa28238-16-eq230.png) (3)here, α is the magnetic inclination angle. Setting α = 30°, and considering the conservative upper limit on the spin-down rate estimated earlier (
(3)here, α is the magnetic inclination angle. Setting α = 30°, and considering the conservative upper limit on the spin-down rate estimated earlier (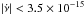 Hz s-1) yielded an upper limit of μ< 3.6 × 1026 G cm3.
Hz s-1) yielded an upper limit of μ< 3.6 × 1026 G cm3.
In principle, the torque acting on a pulsar that is propelling away the inflowing matter through centrifugal inhibition of accretion (the so-called propeller effect, Illarionov & Sunyaev 1975) is an alternative explanation of the spin-down of AMSP during quiescence. Assuming that an accretion disk surrounds the pulsar even during quiescence and is truncated at a radius Rin exceeding the co-rotation radius Rc, the propeller spin-down torque is ![\hbox{$N_{\rm sd}=\dot{M}_{\rm d}\sqrt{GMR_{\rm in}}[(R_{\rm in}/R_{\rm c})^{2/3}-1]$}](/articles/aa/full_html/2016/12/aa28238-16/aa28238-16-eq236.png) (see e.g. Eq. (17) of Papitto & Torres 2015, evaluated for completely anelastic propeller interaction). Assuming Rin = 80 km, a disk mass accretion rate of ≈ 1.5 × 10-11M⊙ yr-1 is required to explain a spin-down rate of ≃ 3 × 10-15 Hz s-1 in terms of the propeller effect. The propeller luminosity associated with such a value is Lprop ≃ 2.5 × 1034 erg s-1 (see Eq. (18) of Papitto & Torres 2015). No estimates of the high-energy emission during quiescence are available for IGR J17511–3057. However, such a value exceeds the X-ray emission observed from other AMSPs in quiescence by up to two orders of magnitude, and we deem it unlikely. A value of the X-ray luminosity in excess of ≈ 1033 erg s-1 would then be taken as an indication of the presence of strong outflows from the system, as was done by Papitto et al. (2014) and Papitto & Torres (2015) to interpret the emission of two transitional millisecond pulsars in the accretion disk state.
(see e.g. Eq. (17) of Papitto & Torres 2015, evaluated for completely anelastic propeller interaction). Assuming Rin = 80 km, a disk mass accretion rate of ≈ 1.5 × 10-11M⊙ yr-1 is required to explain a spin-down rate of ≃ 3 × 10-15 Hz s-1 in terms of the propeller effect. The propeller luminosity associated with such a value is Lprop ≃ 2.5 × 1034 erg s-1 (see Eq. (18) of Papitto & Torres 2015). No estimates of the high-energy emission during quiescence are available for IGR J17511–3057. However, such a value exceeds the X-ray emission observed from other AMSPs in quiescence by up to two orders of magnitude, and we deem it unlikely. A value of the X-ray luminosity in excess of ≈ 1033 erg s-1 would then be taken as an indication of the presence of strong outflows from the system, as was done by Papitto et al. (2014) and Papitto & Torres (2015) to interpret the emission of two transitional millisecond pulsars in the accretion disk state.
We detected three consecutive type-I X-ray bursts during the XMM-Newton observation performed in 2015. Two more were detected by INTEGRAL, but the much longer time elapsed between them (≈3.5 d) indicates that they were not consecutive. No evidence of burst radius expansion was detected in the three bursts. The peak flux observed during the bursts presented here (~ 1.5 × 10-8 erg cm-2 s-1 in the 0.5−10 keV band, ~ 3 × 10-8 erg cm-2 s-1 in the 3−20 keV) is not larger than the value reported by Altamirano et al. (2010) for the burst seen during the 2009 outburst (6.7 × 10-8 erg cm-2 s-1). As a consequence, the non-observation of photospheric radius expansion during the bursts analysed here could not yield a tighter constraint on the source distance than that reported by Altamirano et al. (2010, 6.9 kpc). During the 2009 event, eighteen bursts were detected, each characterized by an exponential decay timescale of ≃ 10 s (Altamirano et al. 2010; Bozzo et al. 2010; Papitto et al. 2010; Falanga et al. 2011). The dependence of the burst recurrence time trec on the persistent X-ray flux was studied by Falanga et al. (2011), who found a dependence 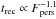 . Using the relation plotted in their Fig. 10, at a bolometric flux of ≃ 1.4 × 10-9 erg cm-2 s-1 (like the value deduced from the simultaneous XMM-Newton-INTEGRAL spectral modelling, see Table 2), a recurrence time of ≃ 9 h is expected. This is only slightly longer than the recurrence time observed by XMM-Newton in 2015 (≃ 8 h).
. Using the relation plotted in their Fig. 10, at a bolometric flux of ≃ 1.4 × 10-9 erg cm-2 s-1 (like the value deduced from the simultaneous XMM-Newton-INTEGRAL spectral modelling, see Table 2), a recurrence time of ≃ 9 h is expected. This is only slightly longer than the recurrence time observed by XMM-Newton in 2015 (≃ 8 h).
5. Conclusions
We have presented an analysis of XMM-Newton, INTEGRAL and Swift observations performed during the outburst detected from IGR J17511–3057 during early 2015, the second observed from the pulsar after the discovery outburst in 2009. The outburst profile, spectral and burst properties were remarkably similar to those observed during the last accretion event detected in 2009, suggesting that the properties of the accretion flow did not change much in the two episodes. The frequency of the coherent signal detected by XMM-Newton three days after the beginning of the outburst was compatible with the value measured by the same observatory during the 2009 outburst. Therefore, a detailed assessment of the spin evolution of the pulsar during the time elapsed between the two outbursts was not possible. However, taking into account the accretion driven spin-up observed during the 2009 outburst, and assumed for the 2015 outburst, we derived an upper limit of 3.5 × 10-15 Hz s-1 on the spin-down rate during quiescence. Electromagnetic spin-down of a NS with a magnetic field weaker than 3.5 × 108 G (at the equator of the NS and assuming a magnetic inclination of 30°) can account for this inferred spin-down. A magnetic field of the same order has also been inferred for other AMSPs. Observations of future outbursts will allow us to derive more stringent constraints on the long-term spin evolution of the pulsar, and will also enable us to derive a first estimate of the orbital period.
EPIC-pn data below 1.4 keV were discarded to avoid the spurious soft excess that sometimes appears in the EPIC-pn spectra obtained in fast modes, and of which we also found hints in this observation (see e.g. Hiemstra et al. 2011).
Acknowledgments
We thank N. Schartel, who accepted the XMM-Newton ToO observation in the Director Discretionary Time, and the XMM-Newton team who performed and supported this observation. This work is also based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), and with the participation of Russia and the USA. This work was partly done in the framework of the grant SGR2014-1073 and AYA2015-71042-P. A.P., E.B., D.F.T., and C.F. acknowledge the International Space Science Institute (ISSI-Bern) which funded and hosted the international team “The disk-magnetosphere interaction around transitional millisecond pulsars”. A.P. acknowledges support via an EU Marie Skłodowska-Curie fellowship under grant No. 660657-TMSP-H2020-MSCA-IF-2014, and partial support from “NewCompStar”, COST Action MP1304. P.R. acknowledges contract ASI-INAF I/004/11/0. J.J.E.K. acknowledges support from the ESA research fellowship programme.
References
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Altamirano, D., Watts, A., Linares, M., et al. 2010, MNRAS, 409, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Archibald, A. M., Bogdanov, S., Patruno, A., et al. 2015, ApJ, 807, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Baldovin, C., Kuulkers, E., Ferrigno, C., et al. 2009, ATel, 2196, 1 [NASA ADS] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Komberg, B. V. 1974, Sov. Astron., 18, 217 [NASA ADS] [Google Scholar]
- Bozzo, E., Ferrigno, C., Falanga, M., et al. 2010, A&A, 509, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bozzo, E., Kuulkers, E., Bazzano, A., et al. 2015a, ATel, 7275, 1 [NASA ADS] [Google Scholar]
- Bozzo, E., Papitto, A., Sanna, A., et al. 2015b, ATel, 7852, 1 [NASA ADS] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Falanga, M., Kuiper, L., Poutanen, J., et al. 2011, A&A, 529, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2008, ApJ, 675, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2009, ApJ, 702, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. M., Galloway, D. K., & Chakrabarty, D. 2011, ApJ, 726, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Hiemstra, B., Méndez, M., Done, C., et al. 2011, MNRAS, 411, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A., Kajava, J. J. E., & Poutanen, J. 2011, MNRAS, 415, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalamkar, M., Altamirano, D., & van der Klis, M. 2011, ApJ, 729, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyne, A. G., & Graham-Smith, F. 1990, Pulsar astronomy (Cambridge, England and New York: Cambridge University Press), Cambridge Astrophysics Series, 285 [Google Scholar]
- Markwardt, C. B., Altamirano, D., Swank, J. H., et al. 2009, ATel, 2197, 1 [NASA ADS] [Google Scholar]
- Nowak, M. A., Paizis, A., Wilms, J., et al. 2009, ATel, 2215, 1 [NASA ADS] [Google Scholar]
- Paizis, A., Nowak, M. A., Rodriguez, J., et al. 2012, ApJ, 755, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., & Torres, D. F. 2015, ApJ, 807, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Riggio, A., Di Salvo, T., et al. 2010, MNRAS, 407, 2575 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Riggio, A., Burderi, L., et al. 2011, A&A, 528, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., Ferrigno, C., Bozzo, E., et al. 2013, Nature, 501, 517 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Papitto, A., Torres, D. F., & Li, J. 2014, MNRAS, 438, 2105 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., de Martino, D., Belloni, T. M., et al. 2015, MNRAS, 449, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A. 2010, ApJ, 722, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Altamirano, D., Hessels, J. W. T., et al. 2009, ApJ, 690, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Bult, P., Gopakumar, A., et al. 2012, ApJ, 746, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., & Watts, A. L. 2012, ArXiv e-prints [arXiv:1206.2727] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., & Srinivasan, G. 1982, Current Science, 51, 1096 [Google Scholar]
- Riggio, A., Burderi, L., Di Salvo, T., et al. 2011a, A&A, 531, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riggio, A., Papitto, A., Burderi, L., et al. 2011b, A&A, 526, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Roy, J., Ray, P. S., Bhattacharyya, B., et al. 2015, ApJ, 800, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Segreto, A., & Ferrigno, C. 2007, in The Obscured Universe, Proc. VI INTEGRAL Workshop, July 2–8, 633 [Google Scholar]
- Spitkovsky, A. 2006, ApJ, 648, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, I. M. 2009, A&A, 495, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, S., Goad, M. R., Beardmore, A. P., et al. 2006, ApJ, 638, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 0.5−10 keV unabsorbed flux (in units of 10-9 erg cm-2 s-1; panel a)) and photon index of the best-fitting power law (panel b)) measured by the Swift-XRT in WT (blue points) and PC mode (red points), and by XMM-Newton (green point). JEM-X (panel c)) and ISGRI (panel d)) light curves were binned with a time resolution of 2 h. |
| In the text | |
 |
Fig. 2 Top panel: X-ray spectrum of IGR J17511–3057 observed by the EPIC-pn (blue points), RGS1 (red points), and RGS2 (green points) during the XMM-Newton observation. Spectra were rebinned for graphical purposes. Bottom and middle panels: residuals with respect to the model listed in the central column of Table 2 (see text for details), with and without the addition of an emission line centred at |
| In the text | |
 |
Fig. 3 Top panel: X-ray spectrum of IGR J17511–3057 observed by the EPIC-pn (blue points), RGS1 (red points), RGS2 (green points), JEM-X (magenta points), and ISGRI (cyan points) during the 2015 outburst. RGS1 and RGS2 spectra were rebinned for graphical purposes. The best-fit model (black line), the Fe line (green line), the disk (red line), single-temperature black body (magenta line), and the Comptonized (blue line) spectra are also shown. Bottom panel: residuals with respect to the best-fit model. |
| In the text | |
 |
Fig. 4 0.3–10 keV pulse profile of IGR J17511–3057 as observed by the EPIC pn during the 2015 outburst. The best-fitting model (solid line) is composed of four harmonics with background subtracted rms amplitudes of 14.31(6)%, 1.53(6)%, 0.72(6)%, and 0.26(6)%. Two cycles are shown for clarity. |
| In the text | |
 |
Fig. 5 Background subtracted pulse profile of IGR J17511–3057 in the 20−100 keV energy band extracted from 221 ks of dead-time corrected on-axis equivalent exposure time in the IBIS/ISGRI data (from 2015-03-22 08:56:29 to 04−09 05:52:01 UTC); the vertical axis displays equivalent count per second for on-axis pointing. |
| In the text | |
 |
Fig. 6 Average Leahy normalized power spectrum of the EPIC-pn time series (top panel). A counting noise constant level of 1.9993(4) is subtracted to the power. The two flat-top noise components are plotted with a red and a blue solid line, and the discrete feature centred at ν3 = 0.5 ± 0.1 Hz as a green solid line (see text for details). The spike at the pulsar spin frequency was removed for display purposes. The bottom panel shows residuals in units of the standard deviation σ. |
| In the text | |
 |
Fig. 7 0.3−10 keV light curve of the first type-I X-ray burst oserved by XMM-Newton during the 2015 observation (panel a)). The burst onset took place at MJD 57108.01023. The temperature and the apparent radius (evaluated considering a distance to the source of 6.9 kpc) are plotted in panels b) and c). Panel d) shows the rms amplitude of pulsations at the spin frequency of the pulsar (see Table 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.