| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628210 | |
| Published online | 23 November 2016 | |
Study of the reflection spectrum of the LMXB 4U 1702-429
1 Dipartimento di Fisica e Chimica, Università di Palermo, via Archirafi 36, 90123 Palermo, Italy
e-mail: rosario.iaria@unipa.it
2 Istituto Nazionale di Astrofisica, IASF Palermo, via U. La Malfa 153, 90146 Palermo, Italy
3 INAF-Istituto di Astrofisica Spaziale e Fisica Cosmica – Milano, via E. Bassini 15, 20133 Milano, Italy
4 Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu, KM 0.7, 09042 Monserrato, Italy
5 Institute of Space Sciences (ICE, CSIC-IEEC), Carrer de Can Magrans, S/N, 08193 Barcelona, Spain
6 INAF, Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone (Roma), Italy
Received: 28 January 2016
Accepted: 6 September 2016
Context. The source 4U 1702-429 (Ara X-1) is a low-mass X-ray binary system hosting a neutron star. Albeit the source is quite bright (~1037 erg s-1) its broadband spectrum has never been studied. Neither dips nor eclipses have been observed in the light curve suggesting that its inclination angle is smaller than 60°.
Aims. We analysed the broadband spectrum of 4U 1702-429 in the 0.3–60 keV energy range, using XMM-Newton and INTEGRAL data, to constrain its Compton reflection component if it is present.
Methods. After excluding the three time intervals in which three type-I X-ray bursts occurred, we fitted the joint XMM-Newton and INTEGRAL spectra obtained from simultaneous observations.
Results. A broad emission line at 6.7 keV and two absorption edges at 0.87 and 8.82 keV were detected. We found that a self-consistent reflection model fits the 0.3–60 keV spectrum well. The broadband continuum is composed of an emission component originating from the inner region of the accretion disc, a Comptonised direct emission coming from a corona with an electron temperature of 2.63 ± 0.06 keV and an optical depth τ = 13.6 ± 0.2, and, finally, a reflection component. The best-fit indicates that the broad emission line and the absorption edge at 8.82 keV, both associated with the presence of Fe xxv ions, are produced by reflection in the region above the disc with a ionisation parameter of Log(ξ) ≃ 2.7. We have inferred that the inner radius, where the broad emission line originates, is 64+52-15 km, and the inner radius of the accretion disc is 39+6-8 km. The emissivity of the reflection component and the inclination angle of the system are r-3.2+0.5-5.1and 44+33-6degrees, respectively. The absorption edge at 0.87 keV is associated to the presence of O viii ions and it is produced in a region above the disc with Log(ξ) ≃ 1.9.
Key words: accretion, accretion disks / stars: neutron / stars: individual: 4U 1702-429 / X-rays: binaries
© ESO, 2016
1. Introduction
Low-mass X-ray binaries (LMXBs) usually show discrete features such as emission lines and absorption edges. The most prominent feature is an emission line at 6.4–6.97 keV, usually interpreted as a fluorescence line from iron at different ionisation states. In fact, iron is a relatively abundant element with the highest fluorescence yield among the most abundant atomic species. These features are powerful tools to investigate the structure of the accretion flow close to the central source; in particular, important information can be obtained from the detailed spectroscopy of the line profile, since it is determined by the ionisation state, geometry, and velocity field of the reprocessing plasma (see Cackett et al. 2010, for a review).
These emission lines are usually broad with Gaussian σ from 0.3 up to more than 1 keV. This broadness is incompatible with a simple thermal broadening caused by the plasma temperature, because of the large mass of iron atoms. It has been interpreted as being caused by Compton broadening in a Comptonising medium of moderate temperatures and optical depth (see e.g. Ng et al. 2010) or Compton scattering caused by strong outflowing winds illuminated by the radiation from the innermost part of the system (Titarchuk et al. 2009). Similarities were found between the accretion flows and the overall spectral shapes in LMXBs hosting neutron stars (NSs) and black holes (BHs). In both systems, an accretion disc surrounds a Comptonising corona located around the compact objects. This has led to the conclusion that in both LMXB systems, these emission lines may be produced by reflection of the primary continuum over the inner accretion disc. In this scenario, the line profile is shaped by Doppler and relativistic effects caused by the fast (Keplerian) motion of the plasma in the inner regions of the accretion disc. As a consequence, the line shows a characteristic broad and asymmetric (red-skewed) profile, the detailed shape of which depends on the inclination of the system with respect to the line of sight, and on how deep the accretion disc extends into the NS gravitational potential (see Fabian et al. 1989; Matt et al. 1992).
If the origin of this line is from disc reprocessing, one would also expect the presence in the spectra of other discrete features (such as emission lines and absorption edges from the other abundant elements) and an excess of emission (Compton hump) caused by direct Compton scattering of the primary spectrum by the electrons in the disc. Indeed, broad emission lines from silicon, argon, and calcium have been detected together with iron features in the spectra of bright NS LMXBs (such as 4U 1705-44, e.g. Di Salvo et al. 2009; GX 349+2, Iaria et al. 2009; GX340+0, D’Aì et al. 2009; GX 3+1, Piraino et al. 2012; and Pintore et al. 2015), and in some cases, a broadened absorption edge at 8−8.5 keV was also required. The ionisation states of these elements were compatible with similar values of the ionisation parameter ξ, and the ratios of the widths of these features with respect to the corresponding energy were compatible with being constant for each source, implying that all these features were produced in the same disc region. The Compton hump at 20−40 keV has also been detected in the hard spectral state of these sources with high statistical significance (see e.g. Di Salvo et al. 2015; Miller et al. 2013; Degenaar et al. 2015; Piraino et al. 2016), in combination with the presence of the iron line, and both these features have been modelled with self-consistent reflection models. The reflection model is able to simultaneously fit all these features (broad emission lines and absorption edges as well as the Compton hump) and is therefore the most promising explanation for their origin (see e.g. Di Salvo et al. 2015; D’Aì et al. 2010; Reis et al. 2009; Cackett et al. 2010).
The X-ray source 4U 1702-429 (Ara X-1) is a NS LMXB showing type-I X-ray bursts. The source was detected as a burster with OSO 8 (Swank et al. 1976), whilst the persistent X-ray emission was detected by Lewin & Clark (1979). Oosterbroek et al. (1991) classified 4U 1702-429 as an atoll source using EXOSAT data. Using Chandra HRC-I data, Wachter et al. (2005) gave the accurate position of the X-ray source with an associated error of 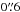 . Galloway et al. (2008), analysing the photospheric radius expansion during the observed type-I X-ray bursts, inferred a distance to the source of 4.19 ± 0.15 kpc and 5.46 ± 0.19 kpc for a pure hydrogen and pure helium companion star, respectively. Furthermore, these authors suggested that the companion star should have a mass fraction of hydrogen lower than 50%. Markwardt et al. (1999), using the data of the proportional counter array (PCA) onboard the Rossi-XTE (RXTE) satellite, detected burst oscillations at 330 Hz that could be associated with the spin frequency of the NS.
. Galloway et al. (2008), analysing the photospheric radius expansion during the observed type-I X-ray bursts, inferred a distance to the source of 4.19 ± 0.15 kpc and 5.46 ± 0.19 kpc for a pure hydrogen and pure helium companion star, respectively. Furthermore, these authors suggested that the companion star should have a mass fraction of hydrogen lower than 50%. Markwardt et al. (1999), using the data of the proportional counter array (PCA) onboard the Rossi-XTE (RXTE) satellite, detected burst oscillations at 330 Hz that could be associated with the spin frequency of the NS.
Up to now a few works reported the analysis of the persistent spectrum of 4U 1702-429. Christian & Swank (1997) analysed three observations taken by the Einstein satellite combining the data of the solid-state spectrometer (SSS; 0.5–4.5 keV) and of the monitor proportional counter (MPC; 1.2–20 keV). The authors fitted the spectrum of the source with an absorbed cut-off power-law obtaining an equivalent hydrogen column density NH of the interstellar medium between 1.1 × 1022 and 1.7 × 1022 cm-2. The photon-index spanned the range between 1.3 and 1.5, and the cut-off temperature between 8 and 16 keV. Markwardt et al. (1999) analysed three observations of 4U 1702-429 taken with RXTE/PCA. These authors fitted the persistent spectrum with a cut-off power-law inferring a cut-off-temperature between 3.5 and 4.6 keV.
 |
Fig. 1 Top-left panel: EPIC-pn light curve of 4U 1702-429 with a bin time of 1 s. Three type-I X-ray bursts occur during the observation: between 2860 and 2980 s, 20 780 and 20 900 s, and 36 150 and 36 300 s from the start time. Top-right panel: 0.3–10 keV EPIC-pn persistent light curve. The bin time is 100 s. Bottom-left panel: 0.3–2 keV EPIC-pn persistent light curve (upper panel), 2–10 keV EPIC-pn persistent light curve (middle panel) and the corresponding HR (lower panel). The bin time is 100 s. Bottom-right panel: HR vs. intensity (bin time of 400 s). |
In this work we show the spectral analysis of the persistent spectrum of 4U 1702-429 in the 0.3–60 keV energy range using both XMM-Newton and INTEGRAL observations.
2. Observations and data reduction
The XMM-Newton observatory (Jansen et al. 2001) includes three 1500 cm2 X-ray telescopes each with an European Photon Imaging Camera (EPIC, 0.1–15 keV) at the focus. Two of the EPIC imaging spectrometers use MOS charge-coupled devices CCDs (Turner et al. 2001) and one uses pn CCDs (Strüder et al. 2001). Reflection grating spectrometers (RGS, 0.35–2.5 keV, den Herder et al. 2001) are located behind two of the telescopes.
The region of sky containing 4U 1702-429 was observed by XMM-Newton between 2010 March 09 14:11:26 UT and March 10 00:22:08 UT (OBSid 0604030101) for a duration of 38 ks. During the observation, the MOS1 and MOS2 instruments were operating in Small window mode, while the EPIC-pn camera was operating in Timing mode with medium filter. To reduce the XMM-Newton data, we used the Science Analysis Software (SAS) v. 14.0.0 and the calibration files at the date of 2014 April 25. Initially we produced the EPIC-pn light curve in the 0.3–10 keV energy range. We extracted the 0.3–10 keV EPIC-pn events of the source selecting RAWX between 24 and 48 and setting PATTERN ≤ 4 (single and double pixel events) and FLAG = 0. The 0.3–10 keV background events were extracted by selecting RAWX between two and 12. Then, we used the epiclccorr to obtain the background-subtracted EPIC-pn light curve that is shown in Fig. 1 (top-left panel) with a bin time of 1 s. Three type-I X-ray bursts occurred during the observation, between 2860 and 2980 s, 20 780 and 20 900 s, and 36 150 and 36 300 s from the start time. The persistent emission has a count rate of 280 c s-1 whilst during the bursts the count rate increases to 2100 c s-1. Since the aim of this work is the spectral analysis of the persistent emission, we excluded the time intervals containing the bursts in all the analysed datasets. The light curve of the persistent emission is shown in Fig. 1 (top-right panel) and the bin time is 100 s. The light curve shows a count rate almost constant at 280 c s-1 up to 28 000 s from the start time, then the count rate suddenly decreases at 260 c s-1 and gradually increases again up to the end of the observation, coming back to 280 c s-1. Since the maximum count rate to avoid pile-up issues is 800 c s-1 for the EPIC-pn camera used in Timing mode, we are confident that the persistent EPIC-pn spectrum is not affected by pile-up. Using the SAS tool epatplot, we found that the pile-up fraction for single and double events is only 0.1% and 3.3%, respectively, in the 2.4–10 keV energy range.
We also extracted the 0.3–2 keV and 2–10 keV EPIC-pn light curves and produced the corresponding hardness ratio (HR, see bottom-left panel in Fig. 1). The HR value is quite constant at 2.85 from the beginning of the observation up to 28 ks; after this, its value ranges between 2.65 and 2.8, suggesting that the spectral shape is softer in the last 10 ks of the observation. Finally, we show the HR vs. the 0.3–10 keV EPIC-pn count rate in Fig. 1 (bottom-right panel); the HR increases when the count rate increases.
The MOS1 and MOS2 light curves were initially extracted using a circular region centred to the source position and with a radius of 45″. The count rate of the 0.2–10 keV MOS1 and MOS2 light curves is close to 50 c s-1. Since the maximum count rate to avoid pile-up issue is 4.5 c s-1 for MOS cameras used in Small window mode1, we expected the presence of heavy pile-up in this case. Using the SAS tool epatplot, we estimated a large pile-up fraction of 20% in the 0.2–10 keV energy range. To minimise the pile-up issues, we extracted the MOS1 and MOS2 source events from an annular region centred on the X-ray position of the source and with an inner and outer radius of 35″ and 45″, respectively. In this case the persistent count rate is 3.7 c s-1 and the pile-up fraction is less than 2% for MOS1 and MOS2 events in the 0.2–10 keV energy range. We show the 0.2–10 keV MOS1 light curve in Fig. 2 (left panel).
 |
Fig. 2 Left panel: 0.2–10 keV MOS1 light curve obtained extracting the events from an annular region with inner and outer radius of 35″ and 45″. The bin time is 10 s. Right panel: the first-order RGS1 and RGS2 light curves (bursts excluded) with a bin time of 100 s. |
Finally, we extracted the first order RGS1 and RGS2 light curves of the persistent emission. The count rate of the RGS1 and RGS2 light curves is 1.63 and 1.66 c s-1, respectively, during the persistent emission. We show the two light curves excluding the bursts in Fig. 2 (right panel).
To analyse the persistent spectrum of 4U 1702-429, we extracted the EPIC-pn spectrum from events with PATTERN ≤ 4 and FLAG = 0. Source and background spectra were extracted selecting the ranges RAWX = [24:48] and RAWX = [2:12], respectively. EPIC-pn spectra were rebinned in energy with an oversample of three using the SAS tool specgroup. MOS1 and MOS2 spectra were extracted from events with PATTERN ≤ 12 and FLAG = 0. The MOS1 and MOS2 background spectra were obtained using the same settings and the same annulus centred in a source-free region. Furthermore, using the SAS tool epatplot, we found that the fraction of pile-up is close to 3% in MOS1 and MOS2 spectra. After checking that the MOS1 and MOS2 spectra were similar and that systematic features were absent in the 0.3–10 keV energy range, we used the SAS tool epicspeccombine to obtain the merged spectrum (hereafter MOS12 spectrum). The MOS12 spectrum was grouped with a minimum of 25 counts per energy channel.
We extracted the first-order RGS spectra using the SAS tool rgsproc and excluding the time intervals in which the three bursts occur. After checking that the RGS1 and RGS2 spectra were similar and without systematic features in the 0.5–2 keV energy range, we used the SAS tool rgscombine to obtain the merged spectrum (hereafter RGS12 spectrum). The RGS12 spectrum was grouped with a minimum of 25 counts per energy channel. The effective times of the persistent spectra are 37 ks for the RGS12 spectrum and 36 ks for MOS12 and EPIC-pn spectra, respectively.
We searched for INTEGRAL observations performed on 2010 March, both with the JEM-X (Lund et al. 2003) and IBIS (Ubertini et al. 2003). We selected three JEM-X pointings, namely science windows (SCW), performed in March 10 and 11, and 58 IBIS SCWs performed in March between 5 and 15. The data-set selection criterion was based on the maximisation of the spectral response of the two telescopes, obtained with the source located within 4.5° and 3.5° from the centre of the IBIS and JEM-X FOVs, respectively. Thus, we analysed IBIS/ISGRI (Lebrun et al. 2003) and JEM-X2 (JEM-X1 was switched-off at that time) data with the INTEGRAL standard software OSA 10.1 (Courvoisier et al. 2003).
A JEM-X2 spectrum was extracted in 16 channels and an effective exposure time of 6 ks was derived. Because of the faintness of the source in hard X-rays, the IBIS/ISGRI spectrum was extracted by the mosaic of the pointing images. We obtained a total mosaic in three energy ranges, 20–26 keV, 26–37 keV, and 37–60 keV, and an IBIS/ISGRI spectrum (130 ks effective exposure) by using the mosaic_spec tool on this image. We note that, based on the latest calibration issues, the JEM-X2 spectrum was used from 5 keV up to 22 keV.
We fitted simultaneously the XMM-Newton (RGS12, MOS12, and EPIC-pn) and INTEGRAL (JEM-X2 and ISGRI) spectra using XSPEC v. 12.8.2. We selected the energy ranges 0.6–2.0 keV for RGS12, 0.3–10 keV for MOS12, 2.4–10 keV for EPIC-pn, 5–25 keV for JEM-X2, and 20–50 keV for ISGRI. We ignored the EPIC-pn energies channels lower than 2.4 keV since a soft excess is present that is not reconciled with the RGS12 and MOS12 spectra, suggesting that the EPIC-pn calibrations are still uncertain below this energy (internal XMM-Newton report CAL-TN- 2 00832; see also Piraino et al. 2012; Pintore et al. 2015).
 |
Fig. 3 Left panel: 0.3–60 keV residuals corresponding to the trial models (see Table 1) described in the text. Right panel: unfolded spectrum and residuals corresponding to the model CEE+Reflection. The red, black, green, blue, and light-blue data correspond to MOS12, RGS12, EPIC-pn, JEM-X2, and ISGRI spectra, respectively. The shown data are graphically rebinned. |
3. Spectral analysis
Initially, we fitted the data adopting the model composed of a multicoloured disc black-body (diskbb in XSPEC, see Mitsuda et al. 1984; Makishima et al. 1986) plus a thermal Comptonisation component (nthcomp in XSPEC, see Zdziarski et al. 1996; Życki et al. 1999). The parameter inp_type of the nthcomp component was fixed at zero, imposing that the seed-photons of the Comptonised component describe a black-body spectrum; in our scenario, the seed-photons originate from the NS surface and/or the boundary layer. We took into account photoelectric interstellar absorption using the multiplicative component phabs, assuming the cosmic abundances and the photoelectric cross sections shown by Wilms et al. (2000) and Verner et al. (1996), respectively. The fit to the data provided a χ2(d.o.f.) of 2845(2252). The best-fit values and the corresponding residuals are shown in the third column of Table 1 and in the left-top panel of Fig. 3. Due to the large residuals observed between 0.8 and 1 keV, we added to the model an absorption edge (edge in XSPEC) with the threshold energy and the depth left free to vary. We found that the threshold energy associated with the absorption edge is 0.89 ± 0.02 keV with the error at 3σ confidence level (c.l.); the obtained χ2(d.o.f.) is 2761(2250). The absorption edge can be only associated with the O viii (~0.871 keV) or Ca xv (~0.895 keV) ions (see Verner et al. 1996). Since Wilms et al. (2000) showed that the abundance of oxygen and calcium are 4.9 × 10-4 and 2.19 × 10-6, respectively, we conclude that the absorption edge close to 0.89 keV is associated with the presence of O viii ions. Fixing the threshold energy at 0.871 keV, we obtained a χ2(d.o.f.) of 2771(2251); the improvement from allowing the energy threshold to be free to vary compared to being fixed gives an F-test probability of only 4.3 × 10-4. The latter model (hereafter model2) is shown in the fourth column of Table 1. The addition of the edge component to the initial model gave a F-test probability of chance improvement of 1.3 × 10-14 and suggested that its addition is highly significant.
The residuals shown in the top-left panel of Fig. 3 suggest the presence of an absorption edge close to 9 keV. Adding this component to model2 (the model composed of the continuum plus the two absorption edges is hereafter named CEE), we obtained a threshold energy of 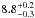 keV (3σ confidence level). This value is marginally compatible with the energy threshold of an absorption edge associated with Fe xxv ions. For this reason, we fitted the spectrum again fixing the threshold energy value at 8.829 keV, obtaining a χ2(d.o.f.) of 2729(2250) and a corresponding F-test probability of chance improvement of 4.6 × 10-9 with respect to model2; that is, we achieved a statistical improvement at more than 5σ c.l. The best-fit parameters and the corresponding residuals are shown in the fifth column of Table 1 and in Fig. 3 (the second panel from the top, left side), respectively. We show the corresponding residuals in Fig. 3 (the second panel from the top, left side). There is still a large excess in the residuals between 6 and 7 keV.
keV (3σ confidence level). This value is marginally compatible with the energy threshold of an absorption edge associated with Fe xxv ions. For this reason, we fitted the spectrum again fixing the threshold energy value at 8.829 keV, obtaining a χ2(d.o.f.) of 2729(2250) and a corresponding F-test probability of chance improvement of 4.6 × 10-9 with respect to model2; that is, we achieved a statistical improvement at more than 5σ c.l. The best-fit parameters and the corresponding residuals are shown in the fifth column of Table 1 and in Fig. 3 (the second panel from the top, left side), respectively. We show the corresponding residuals in Fig. 3 (the second panel from the top, left side). There is still a large excess in the residuals between 6 and 7 keV.
To fit the residuals between 6 and 7 keV, we added to the CEE model a Gaussian component. The addition of the Gaussian line to the model substantially changes the best-fit parameters of the continuum components. We found that the inner-disc temperature (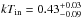 keV) is compatible with the temperature of the seed photons of the Comptonisation (
keV) is compatible with the temperature of the seed photons of the Comptonisation (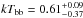 keV). Thus, we performed a new fit with the kTin and kTbb parameters being anchored and imposing the value of the parameter inp_type to 1, that is, assuming that the seed-photons of the Comptonising spectrum has a multicoloured disc black-body distribution. We obtained a χ2(d.o.f.) of 2571(2248) and a F-test probability of chance improvement of 5 × 10-30 with respect to the CEE model (see the best-fit values in the sixth column of Table 1 and residuals of the fit in Fig. 3). The Gaussian component has an energy of 6.75 ± 0.07 keV, a width of 0.46 ± 0.09 keV, and a normalisation of
keV). Thus, we performed a new fit with the kTin and kTbb parameters being anchored and imposing the value of the parameter inp_type to 1, that is, assuming that the seed-photons of the Comptonising spectrum has a multicoloured disc black-body distribution. We obtained a χ2(d.o.f.) of 2571(2248) and a F-test probability of chance improvement of 5 × 10-30 with respect to the CEE model (see the best-fit values in the sixth column of Table 1 and residuals of the fit in Fig. 3). The Gaussian component has an energy of 6.75 ± 0.07 keV, a width of 0.46 ± 0.09 keV, and a normalisation of 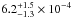 photons cm-2 s-1; the corresponding equivalent width is 35 ± 4 eV.
photons cm-2 s-1; the corresponding equivalent width is 35 ± 4 eV.
Best-fit values of the parameters.
Motivated by the broadening of the Gaussian component, we investigated the scenario in which the residuals between 6 and 7 keV are produced by an emission line smeared by relativistic effects. Thus, we fitted the spectrum using the diskline component (see Fabian et al. 1989, for an accurate description of the diskline component) instead of the Gaussian component. We fixed the outer radius of the diskline component at 1000 gravitational radii because of the fit was insensitive to its change. We started by leaving the inner-disc temperature and the seed-photons temperature free to vary during the fit. We obtained 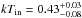 keV and
keV and 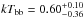 keV, respectively. Since kTin and kTbb were compatible within the uncertainties, we fitted the spectrum with the kTin and kTbb parameters being anchored and imposing the value of the parameter inp_type to 1. We found a χ2(d.o.f.) of 2551(2246) and the F-test probability of chance improvement was 6.1 × 10-32 with respect to the CEE model and 1.6 × 10-4 (significance of improvement of 3.1σ c.l.) with respect to the CEE+Gaussian model, respectively. We show the corresponding residuals in Fig. 3 (bottom panel, left side). The best-fit values are shown in the seventh column of Table 1. We found that the energy of the smeared emission line is
keV, respectively. Since kTin and kTbb were compatible within the uncertainties, we fitted the spectrum with the kTin and kTbb parameters being anchored and imposing the value of the parameter inp_type to 1. We found a χ2(d.o.f.) of 2551(2246) and the F-test probability of chance improvement was 6.1 × 10-32 with respect to the CEE model and 1.6 × 10-4 (significance of improvement of 3.1σ c.l.) with respect to the CEE+Gaussian model, respectively. We show the corresponding residuals in Fig. 3 (bottom panel, left side). The best-fit values are shown in the seventh column of Table 1. We found that the energy of the smeared emission line is 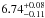 keV, the power-law dependence of emissivity (the parameter betor10 of the diskline component) is
keV, the power-law dependence of emissivity (the parameter betor10 of the diskline component) is 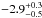 , the inner radius of the accretion disc at which the line originates is
, the inner radius of the accretion disc at which the line originates is 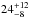 gravitational radii (Rg = GM/c2), the inclination angle of the binary system is
gravitational radii (Rg = GM/c2), the inclination angle of the binary system is 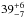 degrees and, finally, the equivalent width of the smeared emission line is 38 ± 7 eV.
degrees and, finally, the equivalent width of the smeared emission line is 38 ± 7 eV.
Finally, we adopted a self-consistent model (hereafter CEE+Reflection) to take into account the possible presence of a reflection component from the accretion disc. The adopted reflection model rfxconv in XSPEC combines the ionised disc table model (see Ross & Fabian 2007) with the Compton reflection code of Magdziarz & Zdziarski (1995). An accurate description of the rfxconv model was shown by Kolehmainen et al. (2011). To take into account possible smearing from relativistic effects, we convolved the rfxconv model with the rdblur model. The convolution model rdblur has the same parameters of the diskline above defined. We tied the seed-photon temperature of the Comptonised component to the inner-disc temperature, and the outer radius of rdblur was fixed at 1000 gravitational radii. Initially, we left free to vary the value of the abundance of iron, but the spectrum does not have enough statistics to constrain it. Then, we fitted the data keeping fixed the value of the parameter at 1, 1.5, 2, 2.5, and 3. We found a slight flattening of the residuals close to 7 keV for a value of 2 of the parameter, while there was not a substantial change in the residuals for the largest values of the abundance. We obtained a χ2(d.o.f.) of 2582(2246) and 2572(2246) for a value of 1 and 2 of the parameter, respectively. We show the best-fit values for an abundance of iron of 2 in Table 1. The spectrum and the corresponding residuals are shown in Fig. 3 (right side). We found that the best-fit parameters of rdblur are compatible with those obtained using diskline: the ionisation parameter, Log(ξ), of the reflecting medium is 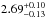 and the reflection fraction is
and the reflection fraction is 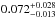 .
.
4. Discussion
We fitted the broadband spectrum of 4U 1702-429 using three different models: a) CEE+Gaussian; b) CEE+Diskline; and c) CEE+Reflection. Hereafter, the discussion will be focussed on the latter. In fact, comparing the fitting results reported in Table 1, we observe that a diskline component gives a slightly better fit of the iron line profile with respect to a Gaussian component.
The reflection fraction obtained from the fit, which is a measure of the solid angle subtended by the reflector as seen from the Comptonising corona in units of 2π, is small with respect to the values obtained for these sources (see e.g. Di Salvo et al. 2015; Pintore et al. 2015, where values of Ω/2π around 0.2−0.3 are found), but it is compatible with the values shown by Cackett et al. (2010) for Ser X-1 and 4U 1820-30; moreover, a similar value of the reflection fraction (Ω/2π = 0.094 ± 0.008) has been measured in the case of the accreting millisecond pulsar SAX J1748.9-2021 (see Pintore et al. 2016). Such a small reflection amplitude might indicate a small solid angle subtended by the reflector as seen from the corona, caused, for instance, by a quite compact corona with no superposition with the disc, or a patchy corona above the inner part of the disc, or by a (mildly) relativistic velocity of the corona away from the disc.
The self-consistent model should include also the absorption edges associated with transitions of ionised iron; however, we needed to add an absorption edge associated with highly ionised iron (transition of Fe xxv). This incongruity was discussed by Egron et al. (2013) studying the broadband spectrum of 4U 1705-44 in the soft state. In that case, the authors fitted the broadband spectrum of the source using the self-consistent models reflionx and xillver reproducing the spectrum; nevertheless, the authors needed to add an absorption edge at 8.7 ± 0.1 keV and 8.5 ± 0.1 keV (using the reflionx and xillver model, respectively) and suggested that the high energy resolution and the large statistics available with the XMM-Newton observatory require an improvement of the self-consistent model to well account for the threshold energy of the absorption edges associated with ionised iron.
Galloway et al. (2008), assuming a neutron star mass of 1.4 M⊙, estimated as a possible distance to the source 4.19 ± 0.15 and 5.46 ± 0.19 kpc for pure hydrogen and pure helium companion stars, respectively. Furthermore, the same authors suggested that the companion star should have a mass fraction of hydrogen, X, of less than 50% (i.e. X< 0.35) because the observed bursts have short rise times (<2 s) and low τ-values (τ = 7.8 ± 0.7 s). Using this argumentation, the lower limit of the distance is 4.70 ± 0.16 kpc for X = 0.35.
We estimate the distance to the source using the obtained value of the equivalent hydrogen column, NH of the interstellar matter. Güver & Özel (2009) show that NH is related to the visual extinction AV from the relation
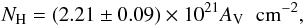 while AV is related to the infrared extinction in the Ks band through the relation
while AV is related to the infrared extinction in the Ks band through the relation
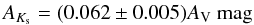 (see Nishiyama et al. 2008). Combining the last two relations we find NH = (3.6 ± 0.3) × 1022AKs. Using the value of NH obtained by our fit and combining these two relations, we find that AKs = 0.70 ± 0.06. We take into account the 3D extinction map of the radiation in the Ks band for our Galaxy (Marshall et al. 2006) to infer the distance to the source. We use the available radial profile of Aks closest to 4U 1702-429 obtained for l = 344° and b = −1.25° (the Galactic coordinates of 4U 1702-429 are l = 343.9° and b = −1.32°).
(see Nishiyama et al. 2008). Combining the last two relations we find NH = (3.6 ± 0.3) × 1022AKs. Using the value of NH obtained by our fit and combining these two relations, we find that AKs = 0.70 ± 0.06. We take into account the 3D extinction map of the radiation in the Ks band for our Galaxy (Marshall et al. 2006) to infer the distance to the source. We use the available radial profile of Aks closest to 4U 1702-429 obtained for l = 344° and b = −1.25° (the Galactic coordinates of 4U 1702-429 are l = 343.9° and b = −1.32°).
We show Aks versus the distance in Fig. 4.
 |
Fig. 4 Infrared extinction AKs versus the distance along the Galactic coordinates l = 344° and b = −1.25° (Marshall et al. 2006). The solid and dashed horizontal lines indicate the values of AKs and the corresponding errors that we infer from the equivalent hydrogen column density NH obtained from the fit. |
In the same figure, the horizontal solid line indicates the best-value of Aks obtained above and the horizontal dashed lines indicate the values of Aks taking into account the associated error at 90% of confidence level. The vertical lines indicate the corresponding range of the distance to the source. We find a distance to the source of 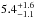 kpc that is compatible with the range 4.5–5.7 kpc suggested by Galloway et al. (2008) and indicates that our estimate of the equivalent hydrogen column density of the interstellar medium is correct. The value of NH ~ 1.7 × 1022 cm-2 shown by Christian & Swank (1997) implies a distance to the source smaller than 4.3 kpc, while a value of NH ~ 0.9 × 1022 cm-2 suggested by Oosterbroek et al. (1991) implies a distance smaller than 2.8 kpc. We adopt hereafter a distance to the source of 5.5 kpc.
kpc that is compatible with the range 4.5–5.7 kpc suggested by Galloway et al. (2008) and indicates that our estimate of the equivalent hydrogen column density of the interstellar medium is correct. The value of NH ~ 1.7 × 1022 cm-2 shown by Christian & Swank (1997) implies a distance to the source smaller than 4.3 kpc, while a value of NH ~ 0.9 × 1022 cm-2 suggested by Oosterbroek et al. (1991) implies a distance smaller than 2.8 kpc. We adopt hereafter a distance to the source of 5.5 kpc.
We extrapolate an unabsorbed flux of 4 × 10-9 erg s-1 cm-2 in the 0.1–100 keV energy band, corresponding to an unabsorbed luminosity of 1.5 × 1037 erg s-1. For comparison with Markwardt et al. (1999), we extrapolate the unabsorbed flux in the 1.6–30 keV (1.6 × 10-9 erg s-1 cm-2) which is in line with their findings. Finally, we extrapolate the unabsorbed flux of the Comptonisation spectrum, fbol, obtaining 3.4 × 10-9 erg s-1 cm-2 in the 0.1–100 keV energy band.
The Rin value shown in Table 1 represents the apparent inner radius of the accretion disc. We apply a correction factor to convert the apparent inner radius Rin into the realistic inner radius rin (see Kubota et al. 1998, for a detailed discussion). The relation between rin and Rin is rin = ακ2Rin, where κ ≃ 1.7 for a luminosity close to 10% of the Eddington luminosity (see Shimura & Takahara 1995) and α ≃ 0.41 for a zero-torque condition (Kubota et al. 1998). We obtain 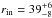 km using the inclination angle of 44° obtained from the best-fit and adopting a distance to the source of 5.5 kpc. Furthermore, the inner radius, Rrefl, where the reflection component originates, is
km using the inclination angle of 44° obtained from the best-fit and adopting a distance to the source of 5.5 kpc. Furthermore, the inner radius, Rrefl, where the reflection component originates, is 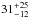 gravitation radii (see Table 1) that, assuming a NS mass of 1.4 M⊙, corresponds to a radius of
gravitation radii (see Table 1) that, assuming a NS mass of 1.4 M⊙, corresponds to a radius of 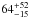 km.
km.
To estimate the optical depth τ of the Comptonising region, we adopted the relation
![$$ \Gamma_{\rm comp} = \left[\frac{9}{4}+ \frac{1}{\tau \left(1+\frac{\tau}{3}\right)\left(\frac{kT_{\rm e}}{m_{\rm e}c^2}\right)} \right]^{1/2}-\frac{1}{2} $$](/articles/aa/full_html/2016/12/aa28210-16/aa28210-16-eq180.png) (see Zdziarski et al. 1996), where me and c are the electron rest mass and the speed of light, respectively. Using the best-fit values of Γcomp and kTe we obtain τ = 13.6 ± 0.2. We estimate the emission radius of the seed photons, assuming a spherical emission and that most of the seed photons are scattered in the optically thick corona. Following in ’t Zand et al. (1999), the emission radius of the seed photons in units of km can be calculated as R0 = 3 × 104d [fbol/ (1 + y)] 1/2(kT0)-2, where d is the source distance in units of kpc, y, defined as y = 4kTeτ2/ (mec2), is the Compton parameter and kT0 is the seed photons temperature; in our case kT0 = kTin. We find that R0 = 38 ± 7 km, assuming a conservative error of 10% associated with fbol. We conclude that the values of Rin, R0, and Rrefl are consistent with each other.
(see Zdziarski et al. 1996), where me and c are the electron rest mass and the speed of light, respectively. Using the best-fit values of Γcomp and kTe we obtain τ = 13.6 ± 0.2. We estimate the emission radius of the seed photons, assuming a spherical emission and that most of the seed photons are scattered in the optically thick corona. Following in ’t Zand et al. (1999), the emission radius of the seed photons in units of km can be calculated as R0 = 3 × 104d [fbol/ (1 + y)] 1/2(kT0)-2, where d is the source distance in units of kpc, y, defined as y = 4kTeτ2/ (mec2), is the Compton parameter and kT0 is the seed photons temperature; in our case kT0 = kTin. We find that R0 = 38 ± 7 km, assuming a conservative error of 10% associated with fbol. We conclude that the values of Rin, R0, and Rrefl are consistent with each other.
Assuming that the Comptonising region has a spherical geometry surrounding the NS and that it has a roughly homogeneous density, we estimate the electron density ne from τ = neσTl, where σT and l are the Thomson cross-section and the geometrical size of the Comptonising plasma, respectively. Assuming that the region extends from the NS surface up to the observed inner accretion disc radius, we find that 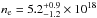 cm-3.
cm-3.
We also estimate the electron density ne of the reflecting skin above the accretion disc using the relation ξ = Lx/ (ner2), where Lx is the unabsorbed incident luminosity in the 0.1–100 keV energy range, ξ is the ionisation parameter (see Table 1), and r is the inner radius of the disc where the reflection component originates, Rrefl. Since we find that Lx ≃ 1 × 1037 erg s-1, we obtain ne ~ 5 × 1020 cm-3 adopting r = 64 km. The electron density associated with the reflecting skin is a factor of one hundred larger than that associated with the Comptonised corona surrounding the NS. Because the reflecting region above the disc has to be optically thin, using the relation neσTl< 1, we find that the upper limit to its geometrical depth is 0.03 km.
The height, H, of the accretion disc is 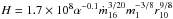 cm (see Eq. (5.46) in Frank et al. 2002), where ṁ16 is the mass accretion rate in units of 1016 g s-1, m1 is the NS mass in units of solar masses, and r10 is the radius of the accretion disc in units of 1010 cm. Adopting α = 0.1 and using ṁ16 ≃ 8 g s-1 (obtained from the unabsorbed flux showed above), we find that H ≃ 0.65 km for a radius of 64 km. This implies that the height of the accretion disc is a factor of 20 larger than the reflecting skin at a radius of 64 km.
cm (see Eq. (5.46) in Frank et al. 2002), where ṁ16 is the mass accretion rate in units of 1016 g s-1, m1 is the NS mass in units of solar masses, and r10 is the radius of the accretion disc in units of 1010 cm. Adopting α = 0.1 and using ṁ16 ≃ 8 g s-1 (obtained from the unabsorbed flux showed above), we find that H ≃ 0.65 km for a radius of 64 km. This implies that the height of the accretion disc is a factor of 20 larger than the reflecting skin at a radius of 64 km.
We detect two absorption edges associated with O viii and Fe xxv ions, respectively. We estimate that the corresponding photoionisation cross-section values are σO8 = 9.9 × 10-20 and σFe25 = 2.2 × 10-20 cm2 (see Verner et al. 1996). The observed optical depth τ associated with the absorption edge of the Fe xxv is τ = σFe25nFe25l, where nFe25 is the number density of Fe xxv ions and l is the geometrical size along the line of sight of the region where the absorption edge originates. The corresponding equivalent column of Fe xxv can be written as NFe25 = nFe25l and the optical depth can be re-written as
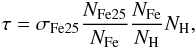 where fFe25 = NFe25/NFe is the fraction of Fe xxv ions with respect to whole population of iron-ions and NFe/NH is the abundance of iron with respect to hydrogen abundance. Adopting the cosmic abundances shown by Wilms et al. (2000)NFe/NH is 2.69 × 10-5. The parameter fFe25 is inferred using the results of Kallman & Bautista (2001) for an electron density equal or larger than 1017 cm-3 and an ionisation parameter of Log(ξ) = 2.69 as obtained from the fit. We find that fFe25 ≃ 0.50. Considering that the spectral fit indicates an iron abundance twice that of the cosmic one, we find that the corresponding equivalent hydrogen column associated with the Fe xxv ion is NH = (6 ± 2) × 1022 cm-2.
where fFe25 = NFe25/NFe is the fraction of Fe xxv ions with respect to whole population of iron-ions and NFe/NH is the abundance of iron with respect to hydrogen abundance. Adopting the cosmic abundances shown by Wilms et al. (2000)NFe/NH is 2.69 × 10-5. The parameter fFe25 is inferred using the results of Kallman & Bautista (2001) for an electron density equal or larger than 1017 cm-3 and an ionisation parameter of Log(ξ) = 2.69 as obtained from the fit. We find that fFe25 ≃ 0.50. Considering that the spectral fit indicates an iron abundance twice that of the cosmic one, we find that the corresponding equivalent hydrogen column associated with the Fe xxv ion is NH = (6 ± 2) × 1022 cm-2.
Assuming that the absorption edge associated with the O viii ion originates from a region in the accretion disc surface close to the region where the smeared relativistic line and the absorption edge of Fe xxv originate, we can roughly assume that the equivalent column of neutral hydrogen associated with the O viii ion is the same as that inferred for the Fe xxv ion. Using the relation
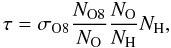 we estimate fO8 = NO8/NO knowing that NO/NH is 4.9 × 10-4 (see Wilms et al. 2000). We obtain fO8 ≃ 0.26 that, for an electron density equal or larger than 1017 cm-3, corresponds to an ionisation parameter of Log(ξ) ≃ 1.9 (see Kallman & Bautista 2001).
we estimate fO8 = NO8/NO knowing that NO/NH is 4.9 × 10-4 (see Wilms et al. 2000). We obtain fO8 ≃ 0.26 that, for an electron density equal or larger than 1017 cm-3, corresponds to an ionisation parameter of Log(ξ) ≃ 1.9 (see Kallman & Bautista 2001).
Even if the absorption edges associated with the O viii and Fe xxv ions originate in close regions above the accretion disc, we should observe only the smeared relativistic iron line associated with the Fe xxv ions because the fluorescence yield F depends on Z4/ (304 + Z4), where Z is the atomic number. F is 5 × 10-3 and 0.36 for oxygen and iron, respectively; weighting the fluorescence yield for the cosmic abundances and the fraction f of O viii and Fe xxv shown above, we obtain that F is 6.4 × 10-7 and 1 × 10-5 for oxygen and iron, respectively. This means that the strength of the smeared relativistic line associated with the O viii ion should be only 6.6% of that associated with the Fe xxv ion. The large interstellar photoelectric absorption does not allow us to significantly detect the presence of the smeared relativistic line associated with the O viii ion. To test this, we added an additional diskline model to the CEE+Diskline model, fixing the smearing parameters to that of the smeared relativistic iron line. This does not include the energy which has been fixed at 0.6536 keV, which is the expected energy for an emission line associated with O viii. We find an upper limit to the normalisation of 0.17 phot. cm-2 s-1 at 3σ c.l., and the fit is not improved by adding this further component.
5. Conclusions
In this work, we have shown the first broadband spectral analysis of the persistent spectrum of 4U 1702-429 in the 0.3–60 keV energy range. We detect the presence of a prominent feature close to 6.7 keV and two absorption edges at 0.87 and 8.83 keV, respectively. The emission line at 6.7 keV is associated with the fluorescence emission of Fe xxv ions and it can be modelled using a Gaussian component with σ = 0.46 keV and an equivalent width of 36 eV. Alternatively, it can be described by a relativistic smeared line caused by Compton reflection originating from the inner disc. We have fitted the spectrum with a self-consistent model composed of a multicoloured disc black-body component plus a Comptonisation component and a reflection component. We find that the inclination angle of the system is 44°, the inner radius of the accretion disc is 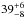 km, and its inner temperature is 0.34 keV. The inner radius of the reflecting region, where the Fe xxv smeared relativistic line and the Fe xxv absorption edge are produced, is
km, and its inner temperature is 0.34 keV. The inner radius of the reflecting region, where the Fe xxv smeared relativistic line and the Fe xxv absorption edge are produced, is 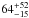 km, and the corresponding ionisation parameter is Log(ξ) = 2.69. The ionisation parameter of the reflecting region where the absorption edge associated with O viii ions originates is Log(ξ) ~ 1.9. The electron temperature of the Comptonised component is 2.6 keV and the corresponding optical depth is τ ~ 13.6.
km, and the corresponding ionisation parameter is Log(ξ) = 2.69. The ionisation parameter of the reflecting region where the absorption edge associated with O viii ions originates is Log(ξ) ~ 1.9. The electron temperature of the Comptonised component is 2.6 keV and the corresponding optical depth is τ ~ 13.6.
From the best-fit value of the equivalent hydrogen column density of the interstellar medium (NH ~ 2.5 × 1022 cm-2), we have estimated the infrared extinction AKs = 0.70 ± 0.06 mag and inferred a distance to the source of 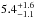 kpc. This value is compatible with a previous estimation obtained from the analysis of the photospheric radius expansion of the type-I X-ray bursts observed for 4U 1702-429.
kpc. This value is compatible with a previous estimation obtained from the analysis of the photospheric radius expansion of the type-I X-ray bursts observed for 4U 1702-429.
Acknowledgments
This research has made use of data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. The High-Energy Astrophysics Group of Palermo acknowledges support from the Fondo Finalizzato alla Ricerca (FFR) 2012/13, project No. 2012-ATE-0390. We also acknowledge a financial contribution from the agreement ASI-INAF I/037/12/0. M.D.S. thanks the Dipartimento di Fisica e Chimica, Università di Palermo, for its hospitality. A.R. and A.S. gratefully acknowledge the Sardinia Regional Government for its financial support (P.O.R. Sardegna F.S.E. Operational Programme of the Autonomous Region of Sardinia, European Social Fund 2007-2013 – Axis IV Human Resources, Objective l.3, Line of Activity l.3.1.). A.P. acknowledges grant SGR2014-1073 and partial support from “NewCompStar”, COST Action MP1304. A.P. acknowledges support via an EU Marie Skłodowska-Curie fellowship under grant No. 660657-TMSP-H2020-MSCA-IF-2014, as well as fruitful discussion with the international team on “The diskmagnetosphere interaction around transitional millisecond pulsars” at ISSI (International Space Science Institute), Bern.
References
- Cackett, E. M., Miller, J. M., Ballantyne, D. R., et al. 2010, ApJ, 720, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Christian, D. J., & Swank, J. H. 1997, ApJS, 109, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Aì, A., Iaria, R., Di Salvo, T., Matt, G., & Robba, N. R. 2009, ApJ, 693, L1 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., di Salvo, T., Ballantyne, D., et al. 2010, A&A, 516, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degenaar, N., Miller, J. M., Chakrabarty, D., et al. 2015, MNRAS, 451, L85 [NASA ADS] [CrossRef] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Salvo, T., D’Aí, A., Iaria, R., et al. 2009, MNRAS, 398, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Iaria, R., Matranga, M., et al. 2015, MNRAS, 449, 2794 [NASA ADS] [CrossRef] [Google Scholar]
- Egron, E., Di Salvo, T., Motta, S., et al. 2013, A&A, 550, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 2002, Accretion Power in Astrophysics (Cambridge University Press) [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., D’Aí, A., di Salvo, T., et al. 2009, A&A, 505, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Verbunt, F., Strohmayer, T. E., et al. 1999, A&A, 345, 100 [NASA ADS] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kolehmainen, M., Done, C., & Díaz Trigo, M. 2011, MNRAS, 416, 311 [NASA ADS] [Google Scholar]
- Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASJ, 50, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewin, W. H. G., & Clark, G. W. 1979, in Proc. Symp. on the Results and Future Prospects of X-ray Astronomy, 3 [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B., Strohmayer, T. E., & Swank, J. H. 1999, ApJ, 512, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G., Perola, G. C., Piro, L., & Stella, L. 1992, A&A, 263, 453 [NASA ADS] [Google Scholar]
- Miller, J. M., Parker, M. L., Fuerst, F., et al. 2013, ApJ, 779, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Ng, C., Díaz Trigo, M., Cadolle Bel, M., & Migliari, S. 2010, A&A, 522, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterbroek, T., Penninx, W., van der Klis, M., van Paradijs, J., & Lewin, W. H. G. 1991, A&A, 250, 389 [NASA ADS] [Google Scholar]
- Pintore, F., Di Salvo, T., Bozzo, E., et al. 2015, MNRAS, 450, 2016 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Sanna, A., Di Salvo, T., et al. 2016, MNRAS, 457, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Piraino, S., Santangelo, A., Kaaret, P., et al. 2012, A&A, 542, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piraino, S., Santangelo, A., Mück, B., et al. 2016, A&A, 591, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reis, R. C., Fabian, A. C., & Young, A. J. 2009, MNRAS, 399, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2007, MNRAS, 381, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Shimura, T., & Takahara, F. 1995, ApJ, 445, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swank, J. H., Becker, R. H., Pravdo, S. H., Saba, J. R., & Serlemitsos, P. J. 1976, IAU Circ., 3010, 1 [NASA ADS] [Google Scholar]
- Titarchuk, L., Laurent, P., & Shaposhnikov, N. 2009, ApJ, 700, 1831 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wachter, S., Wellhouse, J. W., Patel, S. K., et al. 2005, ApJ, 621, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top-left panel: EPIC-pn light curve of 4U 1702-429 with a bin time of 1 s. Three type-I X-ray bursts occur during the observation: between 2860 and 2980 s, 20 780 and 20 900 s, and 36 150 and 36 300 s from the start time. Top-right panel: 0.3–10 keV EPIC-pn persistent light curve. The bin time is 100 s. Bottom-left panel: 0.3–2 keV EPIC-pn persistent light curve (upper panel), 2–10 keV EPIC-pn persistent light curve (middle panel) and the corresponding HR (lower panel). The bin time is 100 s. Bottom-right panel: HR vs. intensity (bin time of 400 s). |
| In the text | |
 |
Fig. 2 Left panel: 0.2–10 keV MOS1 light curve obtained extracting the events from an annular region with inner and outer radius of 35″ and 45″. The bin time is 10 s. Right panel: the first-order RGS1 and RGS2 light curves (bursts excluded) with a bin time of 100 s. |
| In the text | |
 |
Fig. 3 Left panel: 0.3–60 keV residuals corresponding to the trial models (see Table 1) described in the text. Right panel: unfolded spectrum and residuals corresponding to the model CEE+Reflection. The red, black, green, blue, and light-blue data correspond to MOS12, RGS12, EPIC-pn, JEM-X2, and ISGRI spectra, respectively. The shown data are graphically rebinned. |
| In the text | |
 |
Fig. 4 Infrared extinction AKs versus the distance along the Galactic coordinates l = 344° and b = −1.25° (Marshall et al. 2006). The solid and dashed horizontal lines indicate the values of AKs and the corresponding errors that we infer from the equivalent hydrogen column density NH obtained from the fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


