| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629799 | |
| Published online | 28 October 2016 | |
Asteroseismic versus Gaia distances: A first comparison
1 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: joris@ster.kuleuven.ac.be
2 I-BioStat, Universiteit Hasselt, Martelarenlaan 42, 3500 Hasselt, Belgium
3 I-BioStat, KU Leuven, Kapucijnenvoer 35, 3000 Leuven, Belgium
4 Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
5 Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received: 28 September 2016
Accepted: 17 October 2016
Context. The Kepler space mission led to a large number of high-precision time series of solar-like oscillators. Using a Bayesian analysis that combines asteroseismic techniques and additional ground-based observations, the mass, radius, luminosity, and distance of these stars can be estimated with good precision. This has given a new impetus to the research field of galactic archeology.
Aims. The first data release of the Gaia space mission contains the Tycho-Gaia Astrometric Solution (TGAS) catalogue with parallax estimates for more than 2 million stars, including many of the Kepler targets. Our goal is to make a first proper comparison of asteroseismic and astrometric parallaxes of a selection of dwarfs, subgiants, and red giants observed by Kepler for which asteroseismic distances were published.
Methods. We compare asteroseismic and astrometric distances of solar-like pulsators using an appropriate statistical errors-in-variables model on a linear and on a logarithmic scale.
Results. For a sample of 22 dwarf and subgiant solar-like oscillators, the TGAS parallaxes considerably improved on the Hipparcos data, yet the excellent agreement between asteroseismic and astrometric distances still holds. For a sample of 938 Kepler pulsating red giants, the TGAS parallaxes are much more uncertain than the asteroseismic ones, making it worthwhile to validate the former with the latter. From errors-in-variables modelling we find a significant discrepancy between the TGAS parallaxes and the asteroseismic values.
Conclusions. For the sample of dwarfs and subgiants, the comparison between astrometric and asteroseismic parallaxes does not require a revision of the stellar models on the basis of TGAS. For the sample of red giants, we identify possible causes of the discrepancy, which we will likely be able to resolve with the more precise Gaia parallaxes in the upcoming releases.
Key words: asteroseismology / stars: fundamental parameters / stars: oscillations / astronomical databases: miscellaneous / parallaxes / Galaxy: structure
© ESO, 2016
1. Introduction
The seismic study of stars has undergone a revolution during the past decade, thanks to the space missions CoRoT (launched in 2006; Auvergne et al. 2009) and Kepler (launched in 2009; Borucki et al. 2010). Not only did these space data confirm the method of asteroseismology (for an extensive monograph; see Aerts et al. 2010), they also allowed powerful applications to thousands of stars across stellar evolution for a wide variety of stellar birth masses. Major breakthroughs of relevance to the current study of stellar distances were the discovery of acoustic non-radial pulsation modes in red giants (De Ridder et al. 2009) and the excitation of dipole mixed modes probing both the deep interior and the structure of the outer envelope of such stars (e.g. Beck et al. 2011). Thanks to their mixed gravity and acoustic character, mixed modes allow the core properties of a star to be tuned and therefore can be used to pinpoint the evolutionary status (Bedding et al. 2011).
Asteroseismology of red giants offers the unique opportunity of providing stellar ages for studies of the Milky Way, termed galactic archeology (e.g. Miglio et al. 2013). Indeed, the measurement of the frequency at maximum oscillation power and of the large frequency separation, along with a spectroscopic estimate of the effective temperature, can be transformed into high-precision estimates of the stellar mass and radius by assuming that the input physics of solar models is also applicable to solar-like stars. Under this reasonable assumption, stellar masses and radii can be derived with relative precisions of merely a few per cent, while further comparison with stellar models provides a seismic age estimate with a precision below 20% when systematic uncertainties due to modest variations in the input physics are taken into account (Chaplin et al. 2014; Metcalfe et al. 2014). Proper computation of the apparent CoRoT or Kepler magnitude according to the passbands of these satellites then allows the luminosity of the stars to be transformed into an “asteroseismic” distance (Silva Aguirre et al. 2012; Rodrigues et al. 2014; Anders et al. 2016).
So far, the asteroseismic distances of stars in the solar neighbourhood have been compared a posteriori with Hipparcos values for the distances whenever available, with good agreement (e.g. Silva Aguirre et al. 2012). With the Gaia mission in full swing, we foresee a quantum leap forward in this research, both in the number of targets and the precision in measuring the distance. After five years of nominal monitoring, the Gaia distance estimates are expected to be so precise that they can serve as input to improve the physics of stellar interiors, leading to model-independent radii and better ages than currently available as input for exoplanet studies and galactic archeology. Here we take a first step to compare asteroseismic distances with the astrometric values by considering the first Gaia data release (Gaia DR1; e.g. Gaia Collaboration et al. 2016a,b,c).
2. Nearby Kepler dwarfs and subgiants
In their original study to verify asteroseismically determined parameters with Hipparcos distances in a self-consistent way, Silva Aguirre et al. (2012) investigated 22 dwarfs and subgiants having Hipparcos parallaxes with a relative error better than 20%. These stars are close neighbours of the Sun, with distances ranging from 20 to 260 pc, and are not known to have companions. In their seismic modelling method, Silva Aguirre et al. (2012) included corrections for reddening in an iterative approach based on distance-dependent integrated maps of extinction. The seismic distance estimates are also mildly dependent on the adopted metallicity and this was taken into account in their estimates of the uncertainty for the seismic distance.
Figure 1 shows the uncertainties of the parallaxes obtained with TGAS versus those corresponding with Hipparcos.
 |
Fig. 1 Uncertainty of the TGAS and Hipparcos parallaxes of the sample of 22 nearby pulsators. The grey line is the bisector. |
The TGAS parallaxes considerably improve the Hipparcos values, making a new comparison between astrometric and asteroseismic parallaxes appropriate. In Fig. 2 we show the comparison between the two.
 |
Fig. 2 TGAS vs. seismic parallaxes of the sample of 22 nearby pulsators. The grey line is the bisector. The red line is the fit using the errors-in-variables model (4) with uncertainties in both measures taken into account. |
The overall correspondence between the two parallax determinations is excellent, showing the remarkable achievement of asteroseismology. The best fit, shown in red, is slightly offset with respect to the bisector, but as we show in the following, the offset is not nearly significant enough to justify a revision of the seismic models.
The statistical problem at hand is one where we wish to verify a linear relationship between the true parallaxes 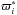 obtained from TGAS and the true parallaxes
obtained from TGAS and the true parallaxes 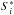 derived using seismology:
derived using seismology: 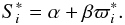 (1)Neither
(1)Neither 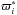 nor
nor 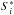 is observed. Instead, the corresponding observed quantities ϖi and Si can be modelled with
is observed. Instead, the corresponding observed quantities ϖi and Si can be modelled with  where ηi and εi are the measurement errors. Such a model is called an errors-in-variables model (also known as the measurement error model) and has been studied extensively in the statistics literature, see e.g. Fuller (1987). Here, we have the additional feature that the variances of both ηi and εi have been quantified. Because these measurement errors may vary considerably in magnitude between stars, it is beneficial to explicitly take this between-star heterogeneity into account.
where ηi and εi are the measurement errors. Such a model is called an errors-in-variables model (also known as the measurement error model) and has been studied extensively in the statistics literature, see e.g. Fuller (1987). Here, we have the additional feature that the variances of both ηi and εi have been quantified. Because these measurement errors may vary considerably in magnitude between stars, it is beneficial to explicitly take this between-star heterogeneity into account.
Equations (1)−(3) yield the following relationship in terms of observable quantities: 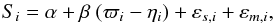 (4)here we decomposed the error of Si in a purely measurement error component, εs,i with star-specific known variance
(4)here we decomposed the error of Si in a purely measurement error component, εs,i with star-specific known variance 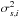 , and an error component capturing variability in the relationship between ϖi and Si, denoted by εm,i, for which we assume a constant but unknown variance σ2. Likewise, the star-specific variance of ηi is denoted by
, and an error component capturing variability in the relationship between ϖi and Si, denoted by εm,i, for which we assume a constant but unknown variance σ2. Likewise, the star-specific variance of ηi is denoted by 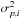 . If the relationship is indeed linear, then estimates of σ2 close to zero are expected. Furthermore, if the linear relationship coincides with the bisector, then α is expected to be close to zero and β close to one. From Eq. (4) it follows that
. If the relationship is indeed linear, then estimates of σ2 close to zero are expected. Furthermore, if the linear relationship coincides with the bisector, then α is expected to be close to zero and β close to one. From Eq. (4) it follows that 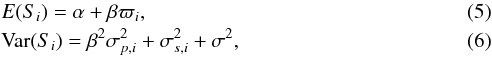 implying that the parameters can be estimated by maximising the likelihood, for example based on a normal distribution
implying that the parameters can be estimated by maximising the likelihood, for example based on a normal distribution 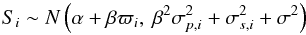 (7)or the moments derived therefrom. We note that by setting
(7)or the moments derived therefrom. We note that by setting 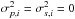 , an ordinary linear regression follows with homoskedastic measurement error (contrary to what is observed). Ordinary linear regression is expected to yield similar regression estimates as the errors-in-variables model when the uncertainty in the dependent variable is considerably larger than the uncertainty in the predictor; in the reverse case, a different regression is obtained, an effect termed regression attenuation in statistics.
, an ordinary linear regression follows with homoskedastic measurement error (contrary to what is observed). Ordinary linear regression is expected to yield similar regression estimates as the errors-in-variables model when the uncertainty in the dependent variable is considerably larger than the uncertainty in the predictor; in the reverse case, a different regression is obtained, an effect termed regression attenuation in statistics.
 |
Fig. 3 Uncertainties on TGAS (blue triangles) and seismic (red circles) parallaxes as a function of the seismic parallax of a sample of 938 red giants. |
We fitted model (7) using the SAS procedure NLMIXED (SAS Institute Inc. 2014) and list the results in Tables 1 and A.3 (including the measurement errors), and A.1 and A.2 (ignoring the measurement errors).
As expected from the plot, in both cases the value 0 (resp. 1) is in the 95% confidence interval of the intercept α (resp. the slope β), clearly indicating that the bisector cannot be rejected as a plausible model.
3. Kepler red giants
Relying on a Bayesian framework and a similar procedure for reddening corrections to those adopted by Silva Aguirre et al. (2012), Rodrigues et al. (2014) derived distances to 1989 red giants observed by Kepler and followed up spectroscopically with APOGEE (Pinsonneault et al. 2014). This resulted in seismic distances between 0.5 and 5 kpc, with relative uncertainties of less than 2%. For 938 of these giants we were able to find a reliable crossmatch in the Gaia DR1 TGAS catalogue. We discarded stars with negative TGAS parallaxes as we compare them later on with asteroseismic parallaxes that were imposed to be positive. The red giants are considerably more distant than the pulsating dwarfs, leading to much more uncertain TGAS parallaxes. Figure 3 shows that the uncertainties of the TGAS parallaxes are substantially larger than those obtained from the seismic distance. Hence the current TGAS parallaxes cannot be used to calibrate the seismic values, but a reverse validation is meaningful at this stage of the Gaia mission. We carried out such a validation using the same methodology as in the previous section. We prefer to analyse parallaxes rather than distances in order to avoid having to take the reciprocal of the more variable measurements. We note that, unlike for the dwarfs, we have no information on their possible binarity; the current TGAS parallaxes and their error estimates assume that they are single stars.
Figure 4 shows the astrometric and asteroseismic parallax of the sample of 938 red giants. Clearly the relation is far less stringent than for the dwarfs and subgiants in the previous section. This, together with the fact that the uncertainties of one measure are much larger than the other, prompted us to add two other models to our analysis. First, like for ordinary least-squares, the errors-in-variables model (4)–(7) is not symmetric, i.e. fitting the seismic parallax Si as a function of the TGAS parallax ϖi or the other way around can lead to different results. We therefore added the errors-in-variables model ϖi = κ + ρiSi.
Second, the models outlined above work under the assumption that the noise sources are additive. To assess the impact of this assumption, we add a model that assumes multiplicative noise, which can be conveniently set up on a logarithmic scale. The relation to be tested is 103/Di = ϖi, where Di = 1 /Si is the asteroseismic distance expressed in pc and ϖi the astrometric parallax expressed in mas. Using decadic logarithms, this leads to the following linear model of the logarithmic observables log Di and log ϖi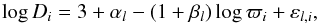 (8)where we assume the noise component εl,i to be normally distributed,
(8)where we assume the noise component εl,i to be normally distributed, 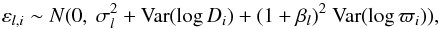 (9)with
(9)with 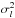 a constant but unknown variance that captures the variability in the relationship between log Di and log ϖi. The variance of the decadic logarithms of the observed quantities can be approximated as
a constant but unknown variance that captures the variability in the relationship between log Di and log ϖi. The variance of the decadic logarithms of the observed quantities can be approximated as 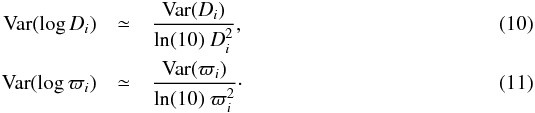 The parameters were again estimated using the SAS procedure NLMIXED.
The parameters were again estimated using the SAS procedure NLMIXED.
Figure 4 synthesises the analysis results for the fits including all 938 stars.
 |
Fig. 4 Seismic vs. TGAS parallaxes for the sample of 938 analysed red giant pulsators. The thick grey line is the bisector. Red lines: fits from an errors-in-variables model where the uncertainties on both parallaxes were taken into account; blue lines: fits obtained without taking any uncertainties into account. Solid lines are a fit using the linear model Si = α + βϖi. Dashed lines are a fit using the model ϖi = κ + ρSi. The curved dotted line is a fit using the model log Di = 3 + αl−(1 + βl)log ϖi. |
The corresponding parameter estimates and their uncertainties are listed in Tables 2, and A.5–A.8.
Not surprisingly, of all linear fits, the ordinary least-squares fit Si = α + βϖi (solid blue line) that does not incorporate any uncertainties deviates most from the bisector. When we do include the uncertainties of both measures, the resulting fit (solid red line) considerably improves, but with a slope of 0.75 it is still significantly tilted with respect to the bisector. This occurs in part because the fit tries to accommodate the fact that the asteroseismic analysis locates remote giants systematically nearer than TGAS. We note that the intercept of the solid red line (as listed in Table 2) is 0.29 ± 0.02 mas, which is similar to the value of 0.3 mas that Gaia Collaboration et al. (2016c) quote as the typical systematic error on the parallax, depending on position and colour. It is unclear whether this a coincidence or not.
Since the uncertainties on the TGAS parallaxes are so much larger than the seismic values, the fit of the inverse model ϖi = κ + ρSi treats the seismic parallaxes almost as fixed and known, similar to ordinary weighted least-squares. Also in this case, taking the uncertainties into account (dashed red line) tilts the fit closer to the bisector than ignoring them, although the difference is less pronounced than for the first model.
We also verified whether model (8) with multiplicative noise would be appropriate for this dataset. The resulting fit is shown as a red dotted line in Fig. 4, and the corresponding parameter estimates are listed in Table A.5.
The result of each of these models is that the 95% confidence interval for the slope never contains 1, and the corresponding interval for the intercept never contains 0. That is, the bisector is not a plausible model.
4. Conclusions
Astrometric parallaxes in the Gaia DR1 TGAS catalogue have been compared with published asteroseismic distances of pulsating dwarfs and giants using an errors-in-variables approach. Deviation from the bisector would imply that either the models of stellar interiors combined with reddening models at the basis of the asteroseismic distances need revision, or that there is an unknown systematic uncertainty on the current version of the astrometric parallaxes, or both.
Proper statististical analysis of the two parallax estimates is a priori more complicated than ordinary least-squares as we now have uncertainties on both estimates of one and the same quantity. We therefore set up an errors-in-variables model, on a linear scale and on a logarithmic scale, to do the fitting. For the 22 dwarfs and subgiants of Silva Aguirre et al. (2012), the results reveal excellent agreement between the two distances, re-confirming the asteroseismic achievement for these stars now that we have more precise parallaxes from TGAS.
For our sample of 938 giants taken from Rodrigues et al. (2014) and crossmatched with TGAS, the relative uncertainties on the astrometric parallaxes are much larger than on the seismic distances, turning the latter into a valuable instrument to validate the former. All the models we applied – an errors-in-variables model, ordinary least-squares, and a logarithmic model – lead to a significant difference between astrometric and asteroseismic parallaxes. There can be several underlying causes. The uncertainties of the TGAS parallaxes may be underestimated or could be subject to systematic errors. On the other hand, interstellar extinction corrections and/or too poorly known bulk metallicity may have introduced a systematic uncertainty for the asteroseismic parallax. Given that all stars in the Gaia DR1 TGAS catalogue were assumed to be single, binarity may also be part of the cause.
Expectations are that the accuracy of the Gaia astrometric distance measurements will surpass the seismic measurements by the end of the mission. Gaia Data Release 2 (end 2017) will contain the astrometry of a billion stars, while Gaia Data Release 3 (end 2018) will deliver the orbital astrometric solutions for binaries with periods longer than 2 months. This will allow us to improve our current research and transfer it into a quantitative calibration of asteroseismic distances for a variety of stellar populations.
Acknowledgments
J.D.R. and C.A. gratefully acknowledge the support from the Belgian Federal Science Policy Office (Belspo, Gaia-DPAC) and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 670519: MAMSIE). G.M. gratefully acknowledges support from IAP research Network P7/06 of the Belgian Government (Belgian Science Policy). This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France, and of the SAO/NASA Astrophysics Data System.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Heidelberg: Springer Berlin) [Google Scholar]
- Anders, F., Chiappini, C., Rodrigues, T. S., et al. 2016, A&A, in press DOI: 10.1051/0004-6361/201527204 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
- Fuller, W. 1987, Measurement Error Models (New York: John Wiley & Sons) [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, in press DOI: 10.1051/0004-6361/201629512 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, in press DOI: 10.1051/0004-6361/201629272 [Google Scholar]
- Gaia Collaboration (Lindegren, L., et al.) 2016c, A&A, in press DOI: 10.1051/0004-6361/201628714 [Google Scholar]
- Metcalfe, T. S., Creevey, O. L., Doğan, G., et al. 2014, ApJS, 214, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Chiappini, C., Morel, T., et al. 2013, MNRAS, 429, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, T. S., Girardi, L., Miglio, A., et al. 2014, MNRAS, 445, 2758 [NASA ADS] [CrossRef] [Google Scholar]
- SAS Institute Inc. 2014, SAS OnlineDoc 9.4 [Google Scholar]
- Silva Aguirre, V., Casagrande, L., Basu, S., et al. 2012, ApJ, 757, 99 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional parameter estimates
In this appendix, we provide the outcome of parameter estimates using the models discussed in the main text. Tables A.1−A.4 concern the sample of 22 nearby dwarfs and subgiants. Tables A.5−A.8 relate to the sample of 938 red giants. Tables A.2 and A.3 provide the estimates of the intercept and slope for the reverse model ϖi = κ + ρSi, which was introduced specifically for the giants, but which we also fitted for the dwarfs for the sake of completeness. The fits lead to exactly the same conclusion as the normal model (7). Also here the value zero is well within the 95% confidence interval of the intercept, and the value 1 is within the corresponding interval of the slope, indicating that the bisector is a plausible model for the relation between astrometric and asteroseismic parallaxes. Not taking the uncertainties into account leads to an estimate of σ2 (the error component capturing variability in the linear relationship), which is significantly different from zero, but this significance disappears when the uncertainties are taken into account showing that the linear model is adequate.
All Tables
All Figures
 |
Fig. 1 Uncertainty of the TGAS and Hipparcos parallaxes of the sample of 22 nearby pulsators. The grey line is the bisector. |
| In the text | |
 |
Fig. 2 TGAS vs. seismic parallaxes of the sample of 22 nearby pulsators. The grey line is the bisector. The red line is the fit using the errors-in-variables model (4) with uncertainties in both measures taken into account. |
| In the text | |
 |
Fig. 3 Uncertainties on TGAS (blue triangles) and seismic (red circles) parallaxes as a function of the seismic parallax of a sample of 938 red giants. |
| In the text | |
 |
Fig. 4 Seismic vs. TGAS parallaxes for the sample of 938 analysed red giant pulsators. The thick grey line is the bisector. Red lines: fits from an errors-in-variables model where the uncertainties on both parallaxes were taken into account; blue lines: fits obtained without taking any uncertainties into account. Solid lines are a fit using the linear model Si = α + βϖi. Dashed lines are a fit using the model ϖi = κ + ρSi. The curved dotted line is a fit using the model log Di = 3 + αl−(1 + βl)log ϖi. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


