| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 14 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201629206 | |
| Published online | 31 October 2016 | |
Role of dark matter haloes on the predictability of computed orbits
1 European Space Astronomy Centre, PO Box 78, 28691 Villanueva de la Canada, Madrid Spain
e-mail: Juan.Carlos.Vallejo@esa.int
2 Nonlinear Dynamics, Chaos and Complex Systems Group, Departamento de Física, Universidad Rey Juan Carlos, Tulipan s/n, 28933 Mostoles, Madrid, Spain
e-mail: miguel.sanjuan@urjc.es
Received: 29 June 2016
Accepted: 17 August 2016
Aims. The predictability of a system indicates how often a computed orbit is close to a real orbit of the system, independent of its stability or chaotic nature. We explore the effect of dark halo shapes on the predictability of computed orbits in a Milky Way mean field model. We also present the sources for the low predictability found in some orbits.
Methods. We derived a predictability index from the distributions of the finite-time Lyapunov exponents. We computed those distributions and analysed the evolution of their shapes when the finite-time interval sizes are varied. The predictability index can be computed using the interval lengths corresponding to the timescales when the flow dynamics leaves the local regime and enters the global regime.
Results. These analyses reveal that not all chaotic orbits have the same predictability and that the predictability of some orbits is more affected than others by the orientation and shape of the dark halo. We show that the lowest predictability may be linked to strong unstable dimension variability.
Key words: galaxies: halos / Galaxy: kinematics and dynamics / chaos
© ESO, 2016
1. Introduction
One prediction of the cold dark matter (CDM) models is that galaxy-scale dark matter haloes are described by a triaxial density ellipsoid. Cosmological simulations typically lead to triaxial haloes in galaxies that considerably deviate from a spherical shape, as discussed for example by Frenk et al. (1988), Dubinski & Carlberg (1991), Warren et al. (1992), Navarro et al. (1997), and Moore et al. (1999). For the shape of the Galactic halo, different claims have been voiced in the literature, for instance by Bowden et al. (2015), Smith et al. (2009) and Banerjee & Jog (2011). A triaxial shape was used in Law et al. (2009), where the observed constraints provided by the structure of the Sgr debris matched a fully triaxial model. The observational confirmation of these hypotheses in the Milky Way and individual galaxies can rely on the flaring of the HI layer, the analysis of the kinematics of the stars, gravitational lensing, and X-ray observations. But this is still an open question, and many observations are only sensitive to the integral of the density profile along the line of sight, without providing full three-dimensional information, and different modelling approaches are used by the different teams (Honma & Sofue 1997; El-Zant & Hassler 1998; Bowden et al. 2016).
Triaxial models must be handled with particular care. In a general triaxial potential, two effective integrals in addition to the energy may be present, and the fraction of irregular orbits may be small. Triaxial haloes may also create the necessary coupling between the degrees of freedom to destroy the integrals of motion for a large enough fraction of orbits, however; see El-Zant & Shlosman (2002) and references therein. Depending on the degree of triaxility, the phase space of a logarithmic potential can be occupied to a large extent by chaotic orbits. The number of chaotic orbits increases with the galaxy disc mass. Spherically symmetric haloes decrease this number. And triaxial haloes increase it, producing unstable orbits in the plane of the galactic disc (Papaphilippou & Laskar 1998; Caranicolas & Zotos 2010; Zotos & Caranicolas 2013; Zotos 2014).
The nonlinear coupling introduced by dark triaxial haloes increases the degree of chaoticity and may affect the goodness of the computed orbits. Many works have characterised the presence of chaos, or presence of strong sensitivity to initial conditions. These studies typically computed the standard asymptotic Lyapunov exponents. These are indicators on the globally averaged chaoticity of the system during an infinite integration time. Because sometimes convergence towards the asymptotic value is slow, many other numerical indexes and fast averaged indicators have been developed, aiming to distinguish between regular and chaotic orbits. We can cite, among others, the rotation index (Voglis et al. 1999), the smaller alignment index (Skokos 2001) and its generalisation, the generalised alignment k-index (Skokos et al. 2007), the mean exponential growth factor of nearby orbits (Cincotta & Simó 2000), the fast Lyapunov indicator (Froeschlé 2000), the relative Lyapunov indicator (Sandor et al. 2004), or the finite-time rotation number (Szezech et al. 2013).
Less attention has been paid to characterising the predictability of the computed orbits in the field of simulations of self-consistent models based on a single mean potential. All numerical calculations have inherent inaccuracies, and beyond certain timescales, even the best method will diverge from the true orbit. The concept of predictability allows characterising the reliability of a computer-generated orbit because it indicates how long a computed orbit is close to an actual orbit. This concept is related to but is independent of its stability or the chaotic nature of a given orbit. A system is said to be chaotic when it exhibits strong sensitivity to the initial conditions. This means that the exact solution and a numerical solution starting very close to it may diverge exponentially from each other. The predictability aims to characterise whether a numerically computed orbit may sometimes be sufficiently close to another true solution, even when it is chaotic. If so, then it may still be reflecting real properties of the model and lead to correct predictions. The real orbit is called a shadow, and a computed solution can be considered an experimental noisy observation of one exact trajectory. The distance to the shadow is then an observational error, and within this error, the observed dynamics can be considered reliable (Sauer et al. 1997).
The shadowing property characterises the validity of long computer simulations and how they may be globally sensitive to small errors. The shadows can exist, but it may happen that after a while, they may deviate strongly from the true orbit. Consequently, estimating this time interval, called shadowing time or predictability time, is a key issue in any simulation and provides an indication about its predictability. This time interval is directly linked to the hyperbolic or non-hyperbolic nature of the orbits. Hyperbolic systems are structurally stable in the sense that shadowing is present during long times and numerical trajectories stay close to the true ones. In the case of non-hyperbolicity, an orbit may be shadowed, but only for a very short time, and the computed orbit behaviour may be completely different from the true orbit after this period.
A gravitational N-body simulation is a common tool to study the evolution of galaxies and formation of their features. However, the available computational resources impose a limit on the number of particles that can be taken into account. This usually implies an artificial smoothing of the potential and a proper handling of the required scaling parameters. As an alternative, another approach that might be taken is the use of simulations based on a single mean field potential. As there are no collisions among particles, the dynamics of a galaxy can be considered to be formed by independent trajectories within the global potential where the motion of each star is only driven by a continuous smooth potential. A dynamical model typically mathematically describes the potential as a function of the distance from the centre of the galaxy. Some potentials are derived at specific snapshots of the N-body simulations and others are selected to physically represent desired characteristics of the galaxies.
Predictability times have been calculated and applied to the field of N-body simulations in Hayes (2003), where an iterative refinement method was applied to simulate noisy trajectories and to estimate the shadowing times. Our work focuses on analysing the predictability times in galactic systems using mean field potentials. These times can be estimated from the analysis of the distributions of finite-time Lyapunov exponents. By analysing the evolution of the shapes of the finite-time Lyapunov exponent distributions as the finite-time interval size increases, we can detect when the flow leaves the local regime and reaches the global regime (Vallejo et al. 2008). At this point, we can estimate the predictability index using the obtained distribution and identify the orbits with the shortest predictability times (Vallejo & Sanjuan 2015).
The main conclusions of our previous work are summarised here. First, every model has its own timescales and intrinsic dynamics. Regular and chaotic orbits may therefore have different timescales and predictability times depending on the selected model. Second, chaos does not always imply a low predictability. An orbit can be chaotic and still be predictable. Conversely, regular orbits can also have different predictability times, and for strongly stiff systems, the predictability could be lower than expected. Finally, the predictability times can sometimes be very short, indicating systems for which the computations can be physically meaningless in a very short time.
The main goal of this work is to analyse the role of the shapes and orientations of triaxial dark matter haloes on the predictability of the computed orbits. To do this, we selected a mean smooth fixed gravitational time-independent potential that models the Milky Way, focusing on the parameters controlling the shape and orientation of a triaxial dark halo. We aim to analyse the correlation between chaos and low predictability values, and how they depend on the dark halo parameter values. We also aim to detect the parameters leading to the lowest predictability values and to analyse the possible sources for these lowest values.
The structure of the paper is the following. Section 2 introduces the model. Section 3 shows the computational techniques and reviews basic concepts of finite-exponent distributions. We use these distributions in Sect. 4 to obtain the hyperbolicity indicators that characterize the system. Section 5 discusses the numerical results. Finally, some concluding remarks are made in Sect. 6.
2. Milky Way model
Very many realistic galactic models in the literature have captured and described several observed features such as bars, spirals, or rings; see, among others, Pfenniger (1984), Skokos et al. (2002), Wang et al. (2012) and Contopoulos & Harsoula (2013). We have selected the potential described in Law et al. (2009) and references therein. This is a smooth fixed gravitational time-independent potential that models the Milky Way and allow us to focus on the parameters controlling the shape and orientation of a triaxial dark halo. The dynamical system to solve is a particle (star) subject to a potential built upon three components: a Miyamoto-Nagai disc (Miyamoto & Nagai 1975), a Hernquist spheroid, and a logarithmic halo: 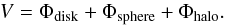 (1)The respective contribution of every component to the gravitational potential is given by
(1)The respective contribution of every component to the gravitational potential is given by
![\begin{eqnarray} && \Phi _{\rm disk} = - \alpha \frac{G M_{\rm disk}}{\sqrt{R^2 +(a+\sqrt{z^2+b^2})^2}}, \label{disk} \\[2mm] && \Phi _{\rm sphere} = - \alpha \frac{G M_{\rm sphere}}{ r + c }, \label{sphere} \\[2mm] && \Phi _{\rm halo} = v^2 _{\rm halo} \ln { (C_1 x^2 + C_2 y^2 + C_3 x y + (z/q_z)^2 + r^2 _{\rm halo})}, \label{halo} \end{eqnarray}](/articles/aa/full_html/2016/11/aa29206-16/aa29206-16-eq4.png) where the various constants C1, C2, and C3 are given by
where the various constants C1, C2, and C3 are given by
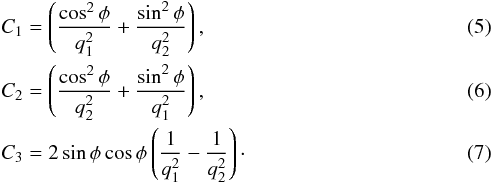 This model does not take the gravitational influence of a rotating galactic bar into account, but it is considered sufficient because it reproduces the flat rotation curve for a Milky Way type galaxy and can be easily shaped to the axial ratios of the ellipsoidal isopotential surfaces. By selecting different values of the model parameters, it allows focusing on their effect on the predictability of the model. These control parameters are the orientation of the major axis of the triaxial halo and the flattening.
This model does not take the gravitational influence of a rotating galactic bar into account, but it is considered sufficient because it reproduces the flat rotation curve for a Milky Way type galaxy and can be easily shaped to the axial ratios of the ellipsoidal isopotential surfaces. By selecting different values of the model parameters, it allows focusing on their effect on the predictability of the model. These control parameters are the orientation of the major axis of the triaxial halo and the flattening.
The flattening is introduced along the three axes by the parameters q1, q2, and qz. qz represents the flattening perpendicular to the Galactic plane, while q1 and q2 are free to rotate in the Galactic plane at an angle φ to a right-handed Galactocentric X, Y coordinate system. We note that there is no symmetry of the potential, and V(φ) ≠ V( − φ) because the sign dependency on C3, the coupling factor of the term xy. Regarding the orientation, when φ = 0, q1 is aligned with the Galactic X-axis and Eq. (4) reduces to 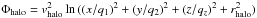 . The results with φ = 0 are then comparable with non-triaxial, purely logarithmic potentials. When φ = 90, q1 is aligned with the Galactic Y-axis and takes the role of q2. This means that without loss of generality, and following previous papers, we have fixed q1 = 1.4 and q2 = 1.0, leaving qz as the control parameter that drives the shape of the halo.
. The results with φ = 0 are then comparable with non-triaxial, purely logarithmic potentials. When φ = 90, q1 is aligned with the Galactic Y-axis and takes the role of q2. This means that without loss of generality, and following previous papers, we have fixed q1 = 1.4 and q2 = 1.0, leaving qz as the control parameter that drives the shape of the halo.
Remaining parameters are fixed as follows: the parameter α was allowed range from 0.25 up to 1.0, and following Law et al. (2009) and Johnston et al. (1995), α was fixed to 1.0. We also adopted Mdisk = 1.0 × 1011Msun, Msphere = 3.4 × 1010Msun, a = 6.5 kpc, b = 0.26 kpc, c = 0.7 kpc, and rhalo = 12 kpc. We also fixed vhalo = 128 km s-1 (leading to a Local Standard of Rest, LSR, of 220 km s-1). The time units are in Gyr with these values of the parameters.
3. Computational methods
The ordinary, or asymptotic, Lyapunov exponent describes the evolution in time of the distance between two nearly initial conditions by averaging the exponential rate of divergence of the trajectories. It can be defined as 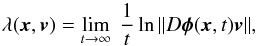 (8)provided this limit exists (Ott & Yorke 2008). Here, φ(x,t) denotes the solution of the flow equation, such that φ(x0,0) = x0, and D is the spatial derivative in the direction of an infinitesimal displacement v.
(8)provided this limit exists (Ott & Yorke 2008). Here, φ(x,t) denotes the solution of the flow equation, such that φ(x0,0) = x0, and D is the spatial derivative in the direction of an infinitesimal displacement v.
We computed the predictability index by calculating the distributions of finite-time Lyapunov exponents. The finite-time Lyapunov exponents definition is derived from the standard asymptotic Lyapunov exponent for finite averaging times as follows: 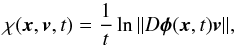 (9)with the implicit dependence on the point x and the deviation vector v. These finite-time Lyapunov exponents are sometimes named effective Lyapunov exponents when the intervals used to compute them are large enough, and the distributions can be analysed from the cumulant generating function (Grassberger et al. 1988).
(9)with the implicit dependence on the point x and the deviation vector v. These finite-time Lyapunov exponents are sometimes named effective Lyapunov exponents when the intervals used to compute them are large enough, and the distributions can be analysed from the cumulant generating function (Grassberger et al. 1988).
If we make a partition of the whole integration time along one orbit into a series of time intervals of size Δt, then it is possible to compute the finite-time Lyapunov exponent χ(Δt) for every interval and to plot its distribution. Obviously, λ = χ(Δt → ∞). By plotting the distribution of values obtained by starting from a given initial condition instead of building the distribution from an ensemble of initial conditions belonging to the same dynamical domain, we can study the shadowing property. These distributions depend on the choice of the finite-time interval length, the initial directions of perturbation vectors, and the total integration time used to compute the distribution.
The shadowing distance is the local phase space distance between the computed trajectory and a true orbit. This distance can be described as a diffusion equation of a particle, which may find different escape routes along its trajectory. The shadowing time τ measures how long the numerical trajectory remains valid by staying close to the true orbit. The longer shadowing times become improbable because of the diffusion processes. The model described in Sauer (2002) assumes an exponential distribution of log shadowing distances to follow a biased random walk with drift towards a reflecting barrier. The expected shadowing time has a power-law dependency on the size of the one-step error made in a computer simulation, linked to the computer precision δ.
A sign of poor shadowing is the fluctuating behaviour around zero of the closest-to-zero finite-time Lyapunov exponent. Plotting the finite-time distribution and assuming both the mean m and the standard deviation σ to be very small, the shadowing, or predictability, time τ is given by 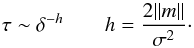 (10)The exponent h is labelled as hyperbolicity or predictability index. We used it as an indicator of the orbit predictability. The lowest predictability occurs when h is very small and there is no improvement in τ, even for high values of δ. Conversely, the larger the h index, the better the shadowing.
(10)The exponent h is labelled as hyperbolicity or predictability index. We used it as an indicator of the orbit predictability. The lowest predictability occurs when h is very small and there is no improvement in τ, even for high values of δ. Conversely, the larger the h index, the better the shadowing.
This scaling law is closely related to intermittency, and can be considered intermittency in miniature. The exponential distribution is the result of small excursions that periodically move the computed trajectory away from the true trajectory, and then return towards it. The assumption is that the motion follows a biased random walk, with a drift toward a reflecting barrier. The flow sometimes goes in one direction, far away from the true solution, and sometimes moves towards it. The reflecting barrier is caused by the single-step error δ, since new errors are created at each step, so that the computed trajectory can never be expected to be closer than δ to the true trajectory.
The computation of the predictability index depends on the identification of the closest-to-zero exponent and its fluctuations around zero. We note here that because of their conservative nature, two exponents are at least close to zero in N-dimensional Hamiltonians because the Lyapunov exponents follow the pairing property λi = − λN − i for (i = 1,2,...,N − 1). Moreover, when we consider quasi-periodic orbits or irregular but not chaotic orbits, additional exponents will be zero. We identified the closest-to-zero exponent by calculating the finite-time exponent distributions for all available exponents and selecting the exponent corresponding to the distribution whose mean is closest to zero.
This technique was detailed in Vallejo & Sanjuan (2015) and is summarised here. It relies on the fact that the finite-time Lyapunov exponents reflect the growth rate of the orthogonal semi-axes (equivalent to the initial deviation vectors) of one ellipse centred on the initial position, and these axes change their orientation and length as the orbit is integrated. The initial axes of the ellipse are a set of orthogonal vectors randomly oriented (with no initial preferred orientation). The evolution of the deviation vectors is a direct consequence of the flow timescales.
The key factor to building the finite-time distributions is finding the most adequate Δt, which needs to be large enough to ensure a satisfactory reduction of the fluctuations, but small enough to reveal slow trends. In principle, this finite-time interval is specific to every system and every individual orbit, and we need to calculate the distributions for a variety of finite intervals lengths. When the smallest intervals are used, the deviation vectors will trace the very local flow dynamics. The distributions show many peaks because the randomly oriented deviation vectors are unable to evolve during such very short intervals. For longer intervals, the local regime of the flow is replaced by the global dynamics regime, and the vectors are oriented depending on the global properties of the flow, including any transient behaviour. The resulting finite-time exponent distributions begin to resemble flat uniform distributions. The finite-time exponents cannot be regarded at these time-scales as similar to random variables leading to Gaussian distributions because the deviation vectors have been allowed to evolve from the initially randomly selected deviation directions, but they did not have enough time to tend to the finally fastest growing directions. These distributions are then characterised by high negative kurtosis. When the finite intervals are longer, the deviation vectors are oriented to the globally fastest growth direction, which may or may not be the final asymptotic behaviour. This asymptotic direction is only reached at very long (infinite) intervals, when the mean of the distributions begins to be centred on the final asymptotic value (Vallejo et al. 2008).
As a consequence, the key finite-time interval length when a change from the local to the global regime occurs is detected by computing the kurtosis of the distributions as the finite-time interval increases. When a behaviour change in the kurtosis value from negative to positive values is detected, the global regime is reached. To estimate the starting interval length, we used the Poincaré crossing time with the surface of section. This crossing time depends on the selection of the surface of section, unless the orbit is periodic. Indeed, it is not constant in the phase space once the surface has been selected. Therefore the Poincaré crossing time is typically computed with three surfaces of section in a problem with three degrees of freedom, and the lowest value is a reliable threshold from which to start exploring the finite time lengths, leaving them to grow until the distributions change in shape.
Massless particles subject to the selected gravitational potentials are integrated using a standard variational method to compute the finite-time Lyapunov exponents. We solved at the same time the flow equations and the fundamental equations or evolution of the distortion tensor, associated with the initial set of deviation vectors used for the exponents computation. Here we raise a final concern about the selection of the integrator. Standard integrators may be thought of as quantitatively accurate, but not qualitatively accurate, since small errors may not conserve the energy, in contrast to a symplectic scheme. However, selecting a given symplectic scheme is not straightforward. Energy conservation is not always the invariant that must be preserved (it may be the angular moment first integral), and integrable Hamiltonians approximated by symplectic schemes may manifest apparent chaos (Newman & Lee 2005). The only integrator that preserves all invariants has been proved to be the true solution itself (Stuchi 2002). As a consequence, we used as integrator the well-known and reliable Dop853 algorithm described in Hairer & Lega (1993). We checked that the Lyapunov exponents followed the pairing property and that the energy value was constant throughout the computation; it typically had a percentual error of 10-8 for the potential.
4. Numerical results
We applied the finite-time Lyapunov exponent technique to a set of representative orbits and identified those with the lowest predictability. We computed their respective predictability indexes as one control parameter of the model is varied. We checked the role that the orientation and flattening of the dark halo has on the predictability and timescales of every orbit.
Triaxial galaxies have four main orbit families: box orbits, and three tube orbits (short axis tubes, inner long-axis tubes, and outer long-axis tubes). The orbit structure and number of orbits belonging to each family is different in cusp, core, main body, and outer part (the halo), reaching from box obits in the central core to tube orbits outside the core region, and boxlets and stochastic orbits (but generally, a small fraction) at the largest radii, or halo region. It is noteworthy that different combinations of orbits with distinct shapes can produce the same triaxial density distributions, so that there is a high degree of non-uniqueness in the distribution functions consistent with a given mass model.
We started by selecting a representative set of initial conditions and analysed how their chaotic nature and predictability changed with the dark halo parameters. We selected the initial conditions listed in Table 1. We used stars with velocities within the halo kinematics range (Casertano et al. 1990; Chiba & Beers 2001). The initial velocity vector in all cases is contained in the z = 0 plane, meaning Vz = 0.0, and is normal to the x-axis, meaning Vx = 0.0. We selected in every initial condition the velocity modulus, | v | = Vy.
For labelling purposes, the set of initial conditions was divided into orbits with high initial z position, or out-of-disc H-orbits, and those with an lower initial z position, or close-to-disc L-orbits.
For comparison purposes, three of these orbits are the same as the initial conditions described in our previous work (Vallejo & Sanjuan 2015). Specifically, orbit HF1 corresponds to orbit M2 and orbit HF2 corresponds to orbit M3 (orbit LC1 was labelled M4, but referred to a different velocity).
4.1. Role of the dark halo orientation
This section presents the variation in chaos, predictability, and flow timescales with dark halo orientation φ. The triaxiality is fixed in this section to be qz = 1.25, following Law et al. (2009) and Vallejo & Sanjuan (2015).
4.1.1. Chaos
The possible chaotic nature of an orbit is reflected by a positive asymptotic Lyapunov exponent λ. An irregular motion is chaotic when it is bounded, the ω-limit set does not merely consist of connecting arcs, and there is at least one asymptotic positive λ (Alligood et al. 1996). Conversely, a regular orbit has vanishing Lyapunov exponents. The notion of a given orbit being weakly or strongly chaotic is here associated with the respective lower or higher value of λ.
Figure 1 shows the variation in highest asymptotic Lyapunov exponent, or Maximal Lyapunov exponent, with dark halo orientation φ for the selected orbits. The total integration time was T = 106 Gyr, long enough to reach convergence towards the final asymptotic state.
The orbits with lower velocities, light red lines (LC1, LF1, HC1, and HF1), seem to be the most strongly chaotic orbits (LC1 the most). All these low-velocity orbits have high values of the highest asymptotic Lyapunov exponents without any apparent dependency on the dark halo orientation.
The orbits with higher velocities, dark blue lines (LC2, LF2, HC2, and HF2), are mainly regular. Of these, the H-orbits, out of the disc, blue continuous lines (HC2 and HF2) seem to be more affected by the halo orientation, while the regular nature of the orbits close to the disc, blue dashed lines (LC2 and LF2), is not affected by the halo orientation.
 |
Fig. 1 Variation in the highest asymptotic Lyapunov exponent λ, or Maximal Lyapunov exponent, with dark halo orientation φ. The flattening is fixed to be qz = 1.25. The red curves, lowest velocities, show higher values of λ, meaning stronger chaos. The blue curves, highest velocities, are mainly regular. The L-orbits, closest to the disc (dashed blue), remain regular at any orientation, the H-orbits (continuous blue) convert into chaotic at orientations around 90 degrees. |
The following figures are intended to illustrate these changes from a descriptive point of view. Figure 2 shows the trajectories in the physical configuration space (x,y,z) integrated during T = 50 Gyr for the orbits of Table 1, with a dark halo orientation of φ = 0 and a flattening parameter qz = 1.25. This flattening was chosen for comparison with previous works. The figure also shows the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0, integrated during T = 5000 Gyr. Spherical-like and short-axis tube-like orbits in the physical space are visible, with regular behaviour at the highest velocities, LC2, LF2, HC2, and HF2. Figure 3 shows the same plots when the dark halo orientation changes to φ = 90. This figure illustrates the evolution of the shapes of the different types of orbits when the dark halo is varied. The orbits with lower velocities (LC1, LF1, HC1, and HF1) show stronger chaos. The H-orbits that previously were regular (HF2 and HC2) are now chaotic. Conversely, the L-orbits remain regular.
 |
Fig. 2 Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 0.0, the flattening is qz = 1.25. The asymptotic Lyapunov exponent λ characterises the chaos intensity. The predictability index h characterises the predictability. There are spherical-like and tube-like orbits in the physical space, with regular behaviours at the highest velocities (LF2, HF2, LC2, and HC2). |
 |
Fig. 3 Effect of the halo orientation. Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 90.0, the flattening is qz = 1.25. The orbits with lower velocities, LC1, LF1, HC1, and HF1, previously chaotic, remain chaotic. Regarding the higher velocities, H-orbits HF2 and HC2, which were previously regular, are now chaotic. L-orbits LC2 and LF2, previously regular, remain regular. The predictabilities remain the same for low velocities, but they change towards lower values for the highest velocities (except for LF2). |
4.1.2. Predictability
We aim to show the variation in predictability with orientation of the dark halo. The predictability of an orbit is related to, but independent of, its stability or its chaotic nature. We are interested here in analysing whether the predictability evolves in the same way the chaoticity does when the dark halo orientation φ is varied. Figure 4 shows this evolution. The values in the predictability index h were derived from finite-time exponents distributions generated by gathering the finite-time intervals Δt during a total time of T = 105 Gyr. Such a long integration leads to very good statistics, even when shorter integrations are enough because of the typically much shorter Poincaré crossing times, hence applicable timescales (detailed in next subsection).
The left panel shows the predictability index for the L-orbits. As before, orbits with higher velocities (LC2 and LF2) have higher values of the h index, meaning better predictabilities. This agrees with Fig. 1, which shows that they have the lowest asymptotic Lyapunov exponents. But this left panel also shows that the (good) predictability of these orbits depends more strongly on the orientation of the halo than the chaoticity dependency seen in Fig. 1. Moreover, orbits with the lowest h predictabilities, those with lower velocities (LC1 and LF1), depend less strongly for h on φ.
 |
Fig. 4 Dependency of the predictability index on the dark halo orientation φ. The flattening is fixed to qz = 1.25. A higher value means a better shadowing, thus a better predictability. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. The inset zooms on the orientation angles around 90 deg. In this interval we see that HC2 and HF2, the blue orbits with higher initial velocities, have very low predictabilities. Specifically, HC2 has a close-to-zero predictability at φ = 115. This orbit is plotted in Fig. 5. |
The predictability indexes h corresponding to the H-orbits are shown in the right panel of Fig. 4. Here, orbits with higher velocities (HC2 and HF2) show a strong dependency on φ. They are again the orbits with better (higher) h values, and for certain orientations, they also show very low values of h for other orientations. These are shown in the inset of Fig. 4 (right). This inset shows that the values of h can sometimes be extremely low. For instance, the orbit HC2 at around φ ~ 115.
This case of very low h is shown in Fig. 5. Here we show the trajectories in the physical configuration space (x,y,z) for the HC2 orbit and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0. Standard double-precision computations may set a value of δ = 10-16, that with an h value as low as 10-4 may lead to predictability times as short as τ ~ 1 Gyr. Some refined integration schemes may be implemented in cases like this.
Interestingly, the h index follows a very similar pattern for HC2 and HF2. This means that the dependency with φ does not depend on the initial distance to the centre. As for L-orbits, the H-orbits with the lowest velocities (HC1 and HF1) show on average the poorest predictabilities, without any strong dependency on φ.
Figure 1 showed that only HF2 and LC2 have a chaotic or regular nature depending on the halo orientation, which changes from regular to chaotic and back at around φ ~ 90. Figure 4 shows that both orbits have low predictabilities for the same range of φ ~ 90 values. Figure 4 also shows a dependency of the predictability h on φ out of the φ ~ 90 interval, however. The predictability h of these orbits also varies for a broader range of orientations, when h has higher values, even for the orientations leading to regular-like behaviours, with highest zero Lyapunov exponents.
 |
Fig. 5 One of the orbits with lowest predictabilities is HC2 when the halo has an orientation of φ = 115.0 and a flattening of qz = 1.25. This trajectory in the physical configuration space (x,y,z) is shown in the leftmost panel, and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0 is shown in the rightmost panel. This orbit has λ = 0.0 and h = 10-4, corresponding to a case of a regular orbit with a very low predictability, linked to a very stiff problem. |
 |
Fig. 6 Variation in φ of the critical Δt interval length when the behaviour of the distributions change. The flattening is fixed to qz = 1.25. This critical interval length reflects the timescales when the dynamical flow reaches the global regime. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. |
 |
Fig. 7 Variation in the Maximal Lyapunov exponent with the dark halo flattening qz. The halo orientation is fixed to φ = 90. The higher exponent values, corresponding to the most strongly chaotic orbits, are found with the lowest initial velocities (red curves). The inset shows the range of qz values where the HC2 and HF2 orbits are chaotic (otherwise they are regular). |
4.1.3. Timescales
The distribution shapes of the finite-time Lyapunov exponents change as the finite-time interval sizes increases. The critical size of the interval Δt used to calculate h corresponds to the size when the distribution changes from a negative kurtosis to a positive kurtosis. This coincides with the timescale when the flow leaves the local dynamics and enters the global dynamics, causing the variational ellipse axes to orient themselves towards the most growing direction.
The kurtosis can have many other zero crossings at very short intervals, when the distribution shapes vary strongly. Of these, the very first zero crossing in the kurtosis at an interval beyond the Poincaré section crossing time can be used as an indicator of the proper timescale.
The variation in this critical Δt with the orientation of the dark halo is presented in Fig. 6, the left panel corresponding to the L-orbits, and the right panel to the H-orbits. We show that the L-orbits with different velocities can have similar timescales. The L-orbits close to the axis (LC1 and LC2) seem to have the smallest Δt, with no apparent dependency on the orientation of the halo. Conversely, the higher values of Δt corresponds to the L-orbits far from the axis (LF1 and LF2), showing a stronger dependency on φ.
The right panel corresponds to the H-orbits. As before, the H-orbits with different velocities have similar same timescales. The longest Δt intervals correspond to HF2 and HC2 (higher velocities), but these timescales are not very different from the low-velocity stars. Regarding the initial distance to the centre, all timescales are similar as well. There is no dependency on the orientation φ in any case. This is interesting because such a dependency was observed for HF2 and HC2 when we plotted the predictability index.
When we compare the two panels, the L-orbits have shorter interval lengths than the H-orbits. These results can be compared with the h dependency seen in Fig. 4. The timescales of the H-orbits do not depend strongly on the halo orientation, but they showed stronger dependencies in the plots of their chaotic nature and their predictability.
The variability in h values can be directly correlated to the variability in Δt values, as is evident when we compare Figs. 4. The same variation in Δt may lead to different values of h in different orbits, however, as a consequence of Eq. (10) and the dependency on the specific characteristic of the orbit. We can therefore identify the orbits with the lowest predictabilities and the sources of these low values (see Sect. 5).
4.2. Role of the dark halo flattening
We analysed the dependency of the Maximal Lyapunov exponent (as chaos indicator) and the predictabilities indexes on the dark halo orientation. Because we found that the strongest influence of the orientation was found at around φ = 90, now we fixed the halo orientation to that value, and this section presents the variation in chaoticity and predictability when we varied the flattening, with qz ranging from 1 to 1.8, to the potential with a rotated halo (φ = 90).
4.2.1. Chaos
Figure 7 plots the dependency of the Maximal Lyapunov exponent as the qz parameter evolves. The most strongly chaotic orbits are those with the lower velocities, as in Fig. 1. A clear change from a regular to chaotic nature of the orbits for the orbits HC2 and HF2 (blue dark continuous line) is found, which are the two orbits with initial conditions out of the disc and with the highest velocity. From Figs. 1 and 7 we can conclude that these orbits are the most dependant on the halo parameters, both φ and qz.
Following Figs. 2 and 3, Fig. 8 illustrates the above by showing the trajectories in the physical configuration space (x,y,z) integrated during T = 50 Gyr, for the orbits of Table 1, with a dark halo orientation of φ = 90 and a flattening parameter qz = 1.4, increased with respect to previous cases. This figure also shows the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0, integrated during T = 5000 Gyr.
4.2.2. Predictability
The variation in predictability index h of the orbits with the flattening qz is shown in Fig. 9. The leftmost panel corresponds to the L-orbits. It shows no apparent dependency of the predictability h on qz. The predictability is higher, thus the shadowing is better, for the orbits with higher velocities (LC2 and LF2, in dark colour), in agreement with the previous section.
The rightmost panel shows the H-orbits, and we see a non-uniform curve, without a clear trend (increasing or decreasing) of h with qz. The two panels show a similar averaged range of predictability indexes of the L-orbits and the H-orbits. The inset in Fig. 9 zooms in the range of qz values where h is close to zero.
This figure also shows for the orbit HC2 a high peak of the h value around qz = 1.45. A large h means very good predictability for this orbit. This orbit also shows very low predictability values when the flattening qz is below 1.3 (as shown by the inset), however. This behaviour agrees with the dependency of the dark halo orientation φ seen in previous section. The orbit with the lowest predictability is found at qz = 1.32. Figure 10 presents this case, showing in the left panel the trajectories in the physical configuration space (x,y,z), and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0 in the right panel. We conclude that HC2 is very sensitive to the dark halo shape and orientation. The HF2 orbit, which also showed a dependency of h on the halo orientation, does not seem to have such a dependency on qz.
 |
Fig. 8 Effect of the halo flattening. Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 90.0, the flattening has been increased with respect to Fig. 3 to be qz = 1.4. The L-orbits, close to disc, with high velocities remain similar. The predictability of orbits with low velocities slightly decreases. The H-orbits with low velocities remain similar. The predictability of orbits with high velocities increases (and the chaos decreases). |
 |
Fig. 9 Variation in predictability index with the flattening of the halo, qz, with a dark halo orientation fixed to φ = 90. A higher value means a better shadowing, thus a better predictability. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. The inset zooms in some flattening values leading to very low predictabilities for the blue orbits with high initial velocities, coincident with the chaotic nature of the orbits with the flattening parameter values seen in Fig. 7. The orbit with the lowest predictability is HC2 when qz = 1.32. |
 |
Fig. 10 Another case of low predictability is shown in the orbit HC2 with a dark halo orientation of φ = 90.0 and a flattening of qz = 1.32. This orbit corresponds to the case with the lowest predictability seen in the inset of Fig. 9. This trajectory in the physical configuration space (x,y,z) is shown in the leftmost panel, and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0 is shown in the rightmost panel. This orbit has λ = 0.39 and h = 0.02. The orbit has moderate chaos and the predictability grows, but remains very low. |
4.2.3. Timescales
Figure 11 shows the variation in critical Δt, when the distributions change, with the flattening parameter qz. The leftmost panel corresponds to the L-orbits, and it shows that the intervals are longer for orbits far from the axis (LF1 and LF2) than for orbits close to the axis (LC1 and LC2). This agrees with the variation in Δt with the halo orientation shown in Fig. 6. The intervals Δt are roughly constant with the qz parameter, in contrast with the dependency of Δt on φ shown in Fig. 6. This uniformity correlates with the absence of a dependency of h on qz shown in Fig. 9.
The rightmost panel of Fig. 11 corresponds to the H-orbits. The critical timescales of these orbits are longer than for the previous L-orbits. We see a stronger fluctuating of Δt with qz, but without any clear trend.
 |
Fig. 11 Variation depending on qz of the critical Δt interval length when the behaviour of the distributions changes. The orientation is fixed to φ = 90. This critical interval length reflects the timescales when the dynamical flow reaches the global regime. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. |
5. Analysis of the results
In the previous sections we have shown the dependency of the predictability index h on the dark halo orientation φ and the flattening qz. When the h values are very low, following Eq. (10), the predictability times τ can be very short. The lowest values of h are found in the right panels of Figs. 4 and 9, orbits out of the disc and with the highest velocities, HF2 and HC2. This section analyses the possible sources for the low predictability values found on these orbits.
The lowest predictability indexes h are associated with the non-hyperbolic nature of the dynamical flow. A dynamical system is hyperbolic when the phase space can be spanned locally by a fixed number of independent stable and unstable directions, which are consistent under the operation of the dynamics, and when the angle between the stable and unstable manifolds is different from zero (Viana & Grebogi 2000; Kantz et al. 2002). In hyperbolic regions, the shadowing theory guarantees the existence of a nearby true trajectory. The exponents oscillate around zero because the shadowing distance changes from exponential increases to exponential decreases, mimicking a random walk. In a non-hyperbolic region, a normally expanding direction converts itself into a contracting direction, causing an excursion away from the reflecting barrier. The finite exponent values strongly deviate from zero, and a breakdown in the shadowing occurs.
Non-hyperbolic behaviour can arise from tangencies, homoclinic tangencies, between stable and unstable manifolds, from unstable dimension variability or from both. For tangencies, there is a higher, but still moderate obstacle to shadowing. But in the so-called pseudo-deterministic systems, the shadowing is only valid during trajectories of short lengths because of the unstable dimension variability (UDV).
The UDV is reflected and quantified by the fluctuations around zero of the finite-time exponent closest to zero (Davidchack & Lai 2000; Viana et al. 2005). These fluctuations around the zero value of the finite-time exponents are then a good indicator of the non-hyperbolic nature of the orbit.
A typical source of UDV is the hyper-chaos phenomenon, defined as the presence of more than one positive asymptotic Lyapunov exponent. There is hyper-chaos in this system because every time there is one positive Lyapunov exponent, the second one is also positive (and the third one is zero, as expected).
We must emphasize that there are situations where the positive tails appear in the distributions not due to UDV, but rather to other mechanisms, such as the quasi-tangencies between the stable and unstable manifolds near a homoclinic crisis point. Regardless of the above, oscillations still reflect both expanding and contracting directions, and it remains a useful index to compute.
The strength of the fluctuations can be derived by computing the probability of the positivity P+ of the distributions. This index can be calculated as follows. The distribution of finite-time Lyapunov exponents can be normalised by dividing it by the total number of intervals, thus obtaining a probability density function P(χ) that gives the probability of obtaining a given value χ between [χ,χ + dχ]. Hence, the probability P+ for obtaining a positive χ(Δt) can be defined as 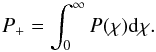 (11)This value provides the probability of obtaining an expanding value of the finite-time exponent once the distribution is fixed. There is an equivalent definition of P− for the contracting exponent values, and the sum of both is unity. The distance d0.5 is defined by the distance of P+ from the 0.5 value. It therefore indicates how strong the oscillations are around zero. The closer d0.5 is to 0, the stronger UDV may be present (Vallejo & Sanjuan 2013).
(11)This value provides the probability of obtaining an expanding value of the finite-time exponent once the distribution is fixed. There is an equivalent definition of P− for the contracting exponent values, and the sum of both is unity. The distance d0.5 is defined by the distance of P+ from the 0.5 value. It therefore indicates how strong the oscillations are around zero. The closer d0.5 is to 0, the stronger UDV may be present (Vallejo & Sanjuan 2013).
 |
Fig. 12 One of the sources of low predictability are oscillations around zero of the closest-to-zero finite-time Lyapunov exponent. The existence of both expanding and contracting directions is stronger when d0.5 ≈ 0.0. Left: variation in d0.5 for the L-orbits, close to disc orbits. Right: variation in d0.5 for the H-orbits, orbits with higher z. The flattening is fixed to be qz = 1.25 in both panels. The H-orbits show the lowest values, with the orbits of higher initial velocities having the closest-to-zero values. These strong oscillations around zero are the source for the very low predictabilities shown in Fig. 4. |
 |
Fig. 13 Variation in distance d0.5 with the dark halo flattening, qz. The orientation is fixed to φ = 90. Left: variation in the L-orbits, close to disc orbits. Right: variation in the H-orbits, orbits with higher z. The L-orbits show the higher values. The H-orbits show the lowest values, but they are never low enough to produce low predictabilities. |
5.1. Dark halo orientation
This subsection analyses the variation in distance d0.5 with the dark halo orientation φ. Figure 12 (left panel) plots this variation for the L-orbits. There is no strong dependency of this distance on the dark halo orientation φ, but for LF2, which was also the orbit with the strongest variation in predictability h on φ (seen in Fig. 4). The orbit LF2 also shows the strongest oscillations around zero, reflected in the shortest distance d0.5 ≈ 0.10 with φ ≈ 40. At this orientation, the predictability of LF2 was low, but not much lower than the h values of the remaining L-orbits. We conclude that a weak UDV does not modify the predictability of the orbit very much.
We show in Fig. 12 that the distances are sometimes far from 0.5, meaning a P+ ~ 1. This can occur when the changes from the local to global behaviour occur when the critical finite-intervals are not long enough to reach the asymptotic regime and the mean of the closest-to-zero exponent may not be so close to zero.
Regarding the H-orbits, the strongest dependency of the distance is found in HF2 and HC2 orbits, as expected from Fig. 4 (right). We observe in these cases that the distance can reach the zero value around φ ≈ 90. This means a very strong UDV, a good source for the very low predictability of these orbits.
Some points for HF2 and HC2 are also around φ ≈ 10 with short d0.5 distances, that is, with strong UDV oscillations. The associated h values are not so low in these cases, however. As for the L-orbits, we may conclude that only when the distance d0.5 is really close to zero, is the UDV strong enough to lower the orbit predictability. This agrees with the comparison of Figs. 4 and 12, and there can be orbits with high h predictabilities even for relatively short distances d0.5.
5.2. Flattening
We now analyse the variation in distance d0.5 with the dark halo flattening qz, with the dark halo orientation fixed to φ = 90. The left panel of Fig. 13 plots this variation for the L-orbits. There is no strong variation of this distance with qz. The orbits LC1 and LC2, those close to the centre, show some fluctuating behaviour, but the values of d0.5 are never close to zero enough to have very low predictabilities.
Regarding the H-orbits, the right panel of Fig. 13 shows the variation of the distance d0.5 with qz for these orbits. There is a wider spread of values of d0.5 as qz varies. Following previous discussions, only the closest-to-zero values will lead to very low predictabilities. The lowest values of d0.5 are seen for HC2 around qz ≈ 1.32. This seems to agree with the low h values seen in Fig. 9.
6. Conclusions
We examined the effect of the dark halo shapes and orientation on the predictability of the computed orbits in a Galactic mean field potential, even when the technique and results can be used in any generic potential.
Simple galactic models are integrable systems, but when perturbations are added, they loose integrability. Irregular orbits are characterized by exponential sensitivity to perturbations, and the predictions in non-integrable potentials can be rapidly inaccurate, as perturbations such as granularity or neighbour galaxies are present and are amplified because of the strong dependency on initial conditions. This can occur with rotation, bars, asymmetries or bulges with density peaks, for instance. In our case, the triggering factor was the triaxility in the dark halo, but the results can be considered of general interest for other models.
The predictability of a system is understood here as a measure of its shadowing properties, reflecting the time during the computed orbit that is followed by a real, physically meaningful orbit. We note that this time length is different from another widely used index, the reliability time, which is the inverse of the asymptotic Lyapunov exponent, which considers the possible chaotic or regular nature of one orbit.
We computed both the asymptotic Lyapunov exponents λ and the predictability index h for a representative sample of orbits. We used a technique that is based on computing the distribution of finite-time Lyapunov exponents to identify the orbits with the lowest predictabilities.
We can conclude that both terms are closely related, but they do not always follow the same trend. We showed that not all chaotic orbits have the same values of the predictability index, and that some chaotic orbits show good predictability behaviour, while others show a very poor behaviour. We also showed that not all regular orbits have the same predictabilities. Orbits at certain ranges of the control parameters can be found where all Lyapunov exponents are zero but low predictability values are present. Conversely, we showed that there are orbits that are more strongly chaotic (with no dependency on the halo orientation), but can be predictable and show a good shadowing behaviour.
When the dark halo orientation φ is varied and the flattening remains fixed, the variation in λ with φ from zero to positive is only seen in the orbits with highest velocities and initial z out of the disc. These are orbits that are regular but with φ around 90. Finding regular orbits out of the disc that depend the most on φ may be considered obvious. The evolution of the changes in their predictabilities is less straightforward, however.
We therefore also analysed the variation in predictability index h with the dark halo orientation. The predictability of the most chaotic orbits, usually those with slower velocities, does not show a strong dependency on the dark halo orientation. The variation of the predictability with φ for all orbits is wider than the variation in chaoticity, however, confirming that chaoticity is different from predictability.
We also showed that the orbits with higher predictability values, usually those with higher velocities, depend most strongly on φ. For these high-velocity orbits, those out of the disc have the lowest values of h, for instance, HC2 and HF2.
A similar analysis was carried out by adding a variation in flattening of the halo qz to the fixed rotation φ = 90. The orbits with initial z out of the disc and highest velocities are the orbits whose chaos depends most upon the halo flattening. However, in contrast to the previous case, the flattening seems to produce a weaker effect on the predictability than the orientation, except for the HC2 orbit (which again shows the lowest value).
The effect of the dark halo orientation φ on the predictability is stronger than the effect of the flattening qz. Interestingly, orbits HC2 and HF2 have the shortest predictability times for certain halo parameters. Even when they have high values of the Maximal Lyapunov exponent, however, they are not the orbits with the highest values. Again, predictability is different from chaoticity, and some strongly chaotic orbits can be more predictable than others with weaker chaos.
We also showed the evolution of the timescales where the flow leaves the local dynamics with the dark halo parameters. The longest timescales can be seen with the orbits with initial z out of the disc. Finally, we analysed the presence of UDV as source for low predictability. We showed that the lowest predictability indexes are linked to the strongest oscillations around zero of the finite-time exponents.
A low predictability does not mean that a model is incorrect, but it means that for a given range of parameters, the model may lead to very short predictability times. As a general conclusion, we showed that certain areas in the parametric space must be taken with care. When fitting observed quantities with certain model parameters, we may be fitting in areas where the validity of the model predictions may be very short and refined numerical schemes may be needed. The predictability index is linked to the hyperbolic or non-hyperbolic nature of the orbit. This is related, in turn, to its energy and stiffness. Different energy values lead to different dynamical times and consequently to different timescales. The existence of two or more timescales in different directions, one quickly growing, one slowly growing, can lead to stiffness. The finite-time exponents reflect these expanding or contracting behaviours, and the predictability indexes depend on the timescales when these behaviours change.
We showed very low predictabilities, sometimes as low as h ~ 10-4. Following Eq. (10), we can take a typical value for the round-off error δ ~ 10-16 and these low values of h lead to predictability times as short as 1 Gyr. A given numerical scheme with certain precision can be enough when the shadowing times are long and high-precision time-consuming schemes are not necessary. However, for low-predictability orbits, more powerful schemes may be necessary, but we note that in the extreme cases with very short predictability times, strong increases in precision do not mean strong increases in shadowing times. The cost of implementing more complex and time-consuming schemes and the relatively small gain in shadowing time need to be considered in these extreme cases.
Our technique uses interval lengths shorter than the Hubble time tH in the computations. This allowed us to apply it to transient behaviours and unbounded orbits, or potential scattering problems, because it does not use long integration times in principle. One limitation is found when using very short integration times. In this case, the number of finite-time intervals needed to obtain good statistics may be not large enough. For the analysed cases, we used total integration times of up T ≈ 105, but shorter integration times can still be used for the typical Δt interval lengths we have obtained.
The physical meaning of using total integration times some orders of magnitude larger than tH may be debated. Simple simulations that consider static potentials should be constrained to times of about 5 Gyr (Martinez-Valpuesta & Shlosman 2004), because longer integrations lasting several times the age of the Universe should take into consideration that the galaxies may have evolved and disappeared. The rationale is that our long integrations can be read as the sum of individual integrations, each one sized shorter than tH. Considering that the initial conditions are reset after every finite interval, the galaxy model can be considered valid.
This paper aimed to work on a reduced set of representative initial conditions, and to check how their chaotic nature and predictability can change with the dark halo parameters. When this initial representative analysis has been done, calculating the predictability indexes using a complete exploration of different initial conditions on a given potential, including a detailed model of a galactic bar, and the analysis of the variation in percentages of high- and low-predictability orbits, is an interesting research topic to extend our results.
Acknowledgments
This work was supported by the Spanish Ministry of Economy and Competitiveness under project number FIS2013-40653-P.
References
- Alligood, K., Sauer, T. D., & Yorke, J. A. 1996, Chaos. An Introduction to Dynamical Systems (New-York: Springer Verlag) [Google Scholar]
- Banerjee, A., & Jog, C. J. 2011, ApJ, 732, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Bowden, A., Belokurov, V., & Evans, N. W. 2015, MNRAS, 449, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Bowden, A., Evans, N. W., & Williams, A. A. 2016, MNRAS, 460, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Caranicolas, N. D., & Zotos, E. E. 2010, Astron. Nachr., 331, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Casertano, S., Ratnatunga, K. U., & Bahcalli, J. N. 1990, ApJ, 357, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Chiba, M., & Beers, T. C. 2001, ApJ, 549, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Cincotta, P. M., & Simó, C. 2000, A&A, 147, 205 [NASA ADS] [Google Scholar]
- Contopoulos, G., & Harsoula, M. 2013, MNRAS, 436, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Davidchack, R. L., & Lai, Y. C. 2000, Phys. Lett. A, 270, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496 [Google Scholar]
- Frenk, C. S., White, S. D. M., Davis, M., & Efstathiou, G. 1988, ApJ, 327, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Froeschlé, C., & Lega, E. 2000, Celest. Mech. Dyn. Astron., 78, 167 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hairer, E., Norsett, S. P., & Wanner, G. 1993, Springer Series in Computational Mathematics, Solving Ordinary Differential Equations, Vol. I (Berlin: Springer-Verlag) [Google Scholar]
- Grassberger, P., Badii, R., & Politi, A. 1988, J. Stat. Phys., 51, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, W. B. 2003, ApJ, 587, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Honma, M., & Sofue, Y. 1997, PASJ, 49, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Spergel, D. N., & Hernquist, L. 1995, ApJ, 451, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Kantz, H., Grebogi, C., Prasad, A., Lai, Y. C., & Sinde, E. 2002, Phys. Rev. E, 65, 026209 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Majewski, S. R., & Johnston, K. V. 2009, ApJ, 703, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Shlosman, I. 2004, ApJ, 613, L613 [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASP, 27, 533 [Google Scholar]
- Moore, B., Quinn, T., Governato, F., Stadel, J., & Lake, G. 1999, MNRAS, 310, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, W. I., & Lee, A. Y. 2005, BAAS, 37, 531 [NASA ADS] [Google Scholar]
- Ott, W., & Yorke, J. A. 2008, Phys. Rev. E, 78, 056203 [NASA ADS] [CrossRef] [Google Scholar]
- Papaphilippou, Y., & Laskar, J. 1998, A&A, 329, 451 [NASA ADS] [Google Scholar]
- Pfenniger, D. 1984, A&A, 134, 373 [NASA ADS] [Google Scholar]
- Sandor, Z., Erdi, B., Szell, A., & Funk, B. 2004, Celest. Mech. Dyn. Astron., 90, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Sauer, T. 2002, Phys. Rev. E., 65, 036220 [NASA ADS] [CrossRef] [Google Scholar]
- Sauer, T., Grebogi, C., & Yorke, J. A. 1997, Phys. Lett. A, 79, 59 [Google Scholar]
- Skokos, Ch. 2001, J. Phys. A, 34, 10029 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Skokos, Ch., Patsis, P. A., & Athanassoula, E. 2002, MNRAS, 333, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Skokos, Ch., Bountis, T. C., & Antonopoulos, Ch. 2007, Phys. D, 231, 30 [CrossRef] [Google Scholar]
- Smith, M. C., Evans, N. W., & An, J. H. 2009, ApJ, 698, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchi, T. J. 2002, Braz. J. Phys., 32, 4 [CrossRef] [Google Scholar]
- Szezech, Jr, J. D., Schelin, A. B., Caldas, I. L., et al. 2013, Phys. Lett. A, 377, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Vallejo, J. C., & Sanjuan, M. A. F. 2013, New J. Phys., 15, 113064 [NASA ADS] [CrossRef] [Google Scholar]
- Vallejo, J. C., & Sanjuan, M. A. F. 2015, MNRAS, 447, 3797 [NASA ADS] [CrossRef] [Google Scholar]
- Vallejo, J. C., Viana, R., & Sanjuan, M. A. F. 2008, Phys. Rev. E, 78, 066204 [NASA ADS] [CrossRef] [Google Scholar]
- Viana, R. L., & Grebogi, C. 2000, Phys. Rev. E, 62, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Viana, R. L., Barbosa, J. R., Grebogi, C., & Batista, C. M. 2005, Braz. J. Phys., 35, 1 [CrossRef] [Google Scholar]
- Voglis, N., Contopoulos, G., & Efthymiopoulos, C. 1999, Celest. Mech. Dyn. Astron., 73, 211 [Google Scholar]
- Wang, Y., Zhao, H., Mao, S., & Rich, R. M. 2012, MNRAS, 427, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, M. S., Quinn, P. J., Salmon, J. K., & Zurek, W. H. 1992, ApJ, 399, 405 [NASA ADS] [CrossRef] [Google Scholar]
- El-Zant, A. A., & Hassler, B. 1998, New Astron., 3, 493 [NASA ADS] [CrossRef] [Google Scholar]
- El-Zant, A. A., & Shlosman, I. 2002, ApJ, 577, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Zotos, E. E. 2014, A&A, 563, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zotos, E. E., & Caranicolas, N. D. 2013, A&A, 560, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Variation in the highest asymptotic Lyapunov exponent λ, or Maximal Lyapunov exponent, with dark halo orientation φ. The flattening is fixed to be qz = 1.25. The red curves, lowest velocities, show higher values of λ, meaning stronger chaos. The blue curves, highest velocities, are mainly regular. The L-orbits, closest to the disc (dashed blue), remain regular at any orientation, the H-orbits (continuous blue) convert into chaotic at orientations around 90 degrees. |
| In the text | |
 |
Fig. 2 Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 0.0, the flattening is qz = 1.25. The asymptotic Lyapunov exponent λ characterises the chaos intensity. The predictability index h characterises the predictability. There are spherical-like and tube-like orbits in the physical space, with regular behaviours at the highest velocities (LF2, HF2, LC2, and HC2). |
| In the text | |
 |
Fig. 3 Effect of the halo orientation. Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 90.0, the flattening is qz = 1.25. The orbits with lower velocities, LC1, LF1, HC1, and HF1, previously chaotic, remain chaotic. Regarding the higher velocities, H-orbits HF2 and HC2, which were previously regular, are now chaotic. L-orbits LC2 and LF2, previously regular, remain regular. The predictabilities remain the same for low velocities, but they change towards lower values for the highest velocities (except for LF2). |
| In the text | |
 |
Fig. 4 Dependency of the predictability index on the dark halo orientation φ. The flattening is fixed to qz = 1.25. A higher value means a better shadowing, thus a better predictability. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. The inset zooms on the orientation angles around 90 deg. In this interval we see that HC2 and HF2, the blue orbits with higher initial velocities, have very low predictabilities. Specifically, HC2 has a close-to-zero predictability at φ = 115. This orbit is plotted in Fig. 5. |
| In the text | |
 |
Fig. 5 One of the orbits with lowest predictabilities is HC2 when the halo has an orientation of φ = 115.0 and a flattening of qz = 1.25. This trajectory in the physical configuration space (x,y,z) is shown in the leftmost panel, and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0 is shown in the rightmost panel. This orbit has λ = 0.0 and h = 10-4, corresponding to a case of a regular orbit with a very low predictability, linked to a very stiff problem. |
| In the text | |
 |
Fig. 6 Variation in φ of the critical Δt interval length when the behaviour of the distributions change. The flattening is fixed to qz = 1.25. This critical interval length reflects the timescales when the dynamical flow reaches the global regime. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. |
| In the text | |
 |
Fig. 7 Variation in the Maximal Lyapunov exponent with the dark halo flattening qz. The halo orientation is fixed to φ = 90. The higher exponent values, corresponding to the most strongly chaotic orbits, are found with the lowest initial velocities (red curves). The inset shows the range of qz values where the HC2 and HF2 orbits are chaotic (otherwise they are regular). |
| In the text | |
 |
Fig. 8 Effect of the halo flattening. Physical trajectories and the corresponding Poincaré sections y − vy with plane x = 0 and vx> 0 for the orbits listed in Table 1. The orientation is φ = 90.0, the flattening has been increased with respect to Fig. 3 to be qz = 1.4. The L-orbits, close to disc, with high velocities remain similar. The predictability of orbits with low velocities slightly decreases. The H-orbits with low velocities remain similar. The predictability of orbits with high velocities increases (and the chaos decreases). |
| In the text | |
 |
Fig. 9 Variation in predictability index with the flattening of the halo, qz, with a dark halo orientation fixed to φ = 90. A higher value means a better shadowing, thus a better predictability. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. The inset zooms in some flattening values leading to very low predictabilities for the blue orbits with high initial velocities, coincident with the chaotic nature of the orbits with the flattening parameter values seen in Fig. 7. The orbit with the lowest predictability is HC2 when qz = 1.32. |
| In the text | |
 |
Fig. 10 Another case of low predictability is shown in the orbit HC2 with a dark halo orientation of φ = 90.0 and a flattening of qz = 1.32. This orbit corresponds to the case with the lowest predictability seen in the inset of Fig. 9. This trajectory in the physical configuration space (x,y,z) is shown in the leftmost panel, and the corresponding Poincaré section y − vy with plane x = 0 and vx> 0 is shown in the rightmost panel. This orbit has λ = 0.39 and h = 0.02. The orbit has moderate chaos and the predictability grows, but remains very low. |
| In the text | |
 |
Fig. 11 Variation depending on qz of the critical Δt interval length when the behaviour of the distributions changes. The orientation is fixed to φ = 90. This critical interval length reflects the timescales when the dynamical flow reaches the global regime. Left: L-orbits, close to the disc orbits. Right: H-orbits, initial conditions with higher z. |
| In the text | |
 |
Fig. 12 One of the sources of low predictability are oscillations around zero of the closest-to-zero finite-time Lyapunov exponent. The existence of both expanding and contracting directions is stronger when d0.5 ≈ 0.0. Left: variation in d0.5 for the L-orbits, close to disc orbits. Right: variation in d0.5 for the H-orbits, orbits with higher z. The flattening is fixed to be qz = 1.25 in both panels. The H-orbits show the lowest values, with the orbits of higher initial velocities having the closest-to-zero values. These strong oscillations around zero are the source for the very low predictabilities shown in Fig. 4. |
| In the text | |
 |
Fig. 13 Variation in distance d0.5 with the dark halo flattening, qz. The orientation is fixed to φ = 90. Left: variation in the L-orbits, close to disc orbits. Right: variation in the H-orbits, orbits with higher z. The L-orbits show the higher values. The H-orbits show the lowest values, but they are never low enough to produce low predictabilities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


