EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 595 (November 2016) A&A, 595 (2016) A52 Full HTML
Free Access
Issue
A&A
Volume 595, November 2016
Article Number A52
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201628585
Published online 28 October 2016

© ESO, 2016

1. Introduction

IGR J17451−3022 is a transient eclipsing and dipping low-mass X-ray binary (LMXB) discovered by INTEGRAL on 2014 August 22 in the direction of the Galactic Centre (Chenevez et al. 2014). An XMM-Newton observation carried out during this event allowed us (Bozzo et al. 2016) to accurately measure the eclipse duration (te ≃ 822 ± 2 s) and refine the estimate of the source orbital period at 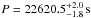. The eclipses observed from IGR J17451−3022 are virtually rectangular, displaying sharp ingresses and egresses due to the obscuration of the X-ray source by the donor star. The lack of multi-wavelength follow-up observations during the outburst of IGR J17451−3022 did not allow a direct investigation of the nature of its donor star. The non-detection of either X-ray pulsations or type-I X-ray bursts left also the nature of the compact object in this system poorly constrained, though the properties of the source X-ray spectrum provided an indication in favour of a neutron star (NS). If the accretor is an NS, its mass is probably in the range of 1.26 M⊙ < M1 ≲ 2.0 M⊙, where the lower bound corresponds to the Chandrasekhar limit for a white dwarf minus the collapse binding energy and the upper bound is related to the current highest reliable measurements (Demorest et al. 2010; Antoniadis et al. 2013). Masses as high as ~ 2.4 M⊙ cannot, however, be excluded, as this is the maximum theoretical mass that an NS can achieve (Lattimer & Prakash 2010).

In this work, we extend our previous investigations of IGR J17451−3022 by providing constraints on the nature of its donor under the assumption of either an NS or a black-hole (BH) accretor. Our constraints in Sect. 2 are derived from the orbital period and eclipse duration of IGR J17451−3022, extending previous studies on similar constraints provided, for example, for SWIFT J1749.4–2807 by Markwardt & Strohmayer (2010) and Altamirano et al. (2011). In Sect. 3, we perform evolutionary calculations in order to constrain the nature of the donor in this system.

2. Constraints on the binary parameters

As IGR J17451−3022 is an accreting LMXB, the donor star with a mass of M2 should fill its Roche lobe. We can estimate its volume-averaged Roche-lobe radius, R2, using an equation valid in the case M2/M12 ≲ 0.6, where M12 = M1 + M2 and M1 is the mass of the compact object. Following Paczyński (1967), we have, 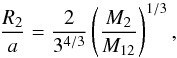(1)where a is the semimajor axis of the binary given by the Kepler law, 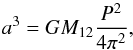(2)and G is the gravitational constant. The above equations can be combined to obtain a relation between the Roche-lobe radius and the mass of the donor, 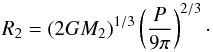(3)We use hereafter Eqs. (1) and (3) instead of the somewhat more accurate, but more complex, approximation by Eggleton (1983). For the range of M2/ (M12) ≲ 0.4 that we find possible for IGR J17451−3022 (Sect. 3), the maximum fractional error of either Eq. (1) or (3) is ≲ 1%, and quickly decreases for the decreasing mass ratio. From Eq. (3), it can be noticed that the average donor-star density depends only on P (Faulkner et al. 1972). The R2(M2) relationship is plotted in Fig. 1a. Hereafter, we use the best-fit values of P and te.

thumbnail Fig. 1

a) Size of Roche-lobe radius of the donor as a function of its mass, M2, for the orbital period of P = 22620.5 s. As IGR J17451−3022 is an accreting LMXB, R2 is the actual radius of the donor. b) Relation between the system inclination and the donor mass obtained by using the measured orbital period and eclipse duration. The black solid (red dashed) curve represents the obtained relation in case of an NS accretor with M1 = 1.26 M⊙ (M1 = 2 M⊙). We also show the relation for a BH accretor of M1 = 10 M⊙ (blue dotted curve).

By using the measured orbital period and the eclipse duration of IGR J17451−3022, we can also relate the system inclination angle, i, to M2/M12. At i = 90°, the X-ray source is eclipsed by the equator of the donor star, with the radius R2. At progressively lower inclinations, a correspondingly smaller circle above the equator is eclipsing the compact object. Assuming a circular orbit (Chakrabarty et al. 1993) and neglecting the flattening of the Roche lobe (Chanan et al. 1976), we have the standard relation, 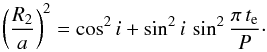(4)The above equation can be readily solved for the inclination, (5)which yields i between 90° and 0° in the allowed range of R2/a. From Eq. (5), we can obtain a relation between the inclination and the mass ratio by using the dependence of R2(M2) /a(M12) provided by Eq. (1). We show the results in Fig. 1b for M1 = 1.26 M⊙ and 2 M⊙. As a BH accretor in IGR J17451−3022 cannot be completely ruled out (see Sect. 1), we also show the relation i(M2) for M1 = 10 M⊙. We can also determine the minimum allowed donor-to-accretor mass ratio by solving Eqs. (1) and (4) at i = 90°, which results in 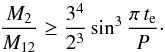(6)This yields M2/M1 ≥ 0.0152.

3. The nature of the donor

We can now use the constraints obtained in Sect. 2 to investigate different possibilities for the nature of the donor in IGR J17451−3022. The most straightforward case is that this star belongs to the main sequence (MS), as it is the case for many other known LMXBs (see, e.g., Liu et al. 2007, and references therein). In Fig. 2, we compare the previously obtained Roche-lobe radius as a function of the donor mass with the mass-radius relations for MS stars. Given the very small fractional error on P (Bozzo et al. 2016), the former relationship has virtually no observational error.

We made this comparison using theoretical evolutionary models. We use the Warsaw stellar-evolution code (described in Ziółkowski 2005) calibrated to reproduce the Sun at the solar age. This calibration resulted in a chemical composition of the H mass fraction of X = 0.74, a metallicity of Z = 0.014, and a mixing length parameter of α = 1.55. In Fig. 2, we show in the green curve the resulting models for the zero-age MS (ZAMS) and, in the cyan curve, models for stars nearing the end of their MS evolution, at the termination-age MS (TAMS). We find that MS (i.e., central H burning) models with masses in the range ≃ (0.52−0.84) M⊙ could fit the Roche lobe of the mass donor in IGR J17451−3022. The lowest and highest mass corresponds to the TAMS and ZAMS, respectively. Models with intermediate masses correspond to intermediate phases of the MS evolution. The corresponding range of the radius is R2 ≃ (0.64−0.75) R⊙. In addition, the blue points in Fig. 2 show a selection of the observationally determined masses and radii of low-mass MS stars from Cox (2000), Ségransan et al. (2003, and references therein), and Pont et al. (2005). We see they agree with our theoretical MS bounds. The inclination corresponding to the obtained allowed mass range is i ≃ (76−71)° if the donor is an NS, cf. Fig. 1b. At M1 = 10 M⊙, i ≃ (83−81)°.

thumbnail Fig. 2

Roche-lobe radius of donor star in IGR J17451−3022 as a function of its mass, M2 (black solid line), compared to a selection of the measured masses and radii of stars on the MS (blue points). The dashed red line shows the relation of R2 = R⊙(M2/M⊙)0.9 for M2 ≥ 0.1 M⊙, which approximates the middle of the MS, and R2 = 0.1 R⊙ for M2< 0.1 M⊙, which approximately describes the case of old brown dwarfs. The green and cyan curves show the models of stars on the ZAMS and TAMS, respectively. The intersections of these curves with the Roche-lobe radius show that MS stars in the mass range of ≃ (0.52−0.84) M⊙ are acceptable models of the donor star.

We then examine alternatives and first investigate whether the donor in IGR J17451−3022 could be a standard red giant. This could, in principle, be the case if the star had an initial mass ≳ 0.9 M⊙; otherwise the evolution within the MS would last longer than the lifetime of the Galaxy (see, e.g., Girardi et al. 2000). A low-mass donor may be created if a star with a large enough initial mass evolves off the MS, forms a He core, and then loses mass from its H envelope by accretion onto the compact object (see, e.g., Webbink et al. 1983). Such a process leads to the formation of so-called partially stripped giants. Donors of this type are present in a number of well-known accreting LMXBs (e.g., GRO 1744−28, GRS 1915+105, and V404 Cyg).

The radius of a giant with a total mass ≳ 0.3 M⊙ depends primarily on the mass of the core, Mc (Paczyński 1970; see also Fig. 1 in Rappaport et al. 1995), until its H-rich envelope disappears almost completely. We illustrate this by the three dashed curves in Fig. 3, for the donor masses of 0.3, 0.5, and 0.9 M⊙, obtained using the Warsaw stellar evolutionary code. As we noted above, the initial mass of the donor has to be M2 ≳ 0.9 M⊙. The mass of its core is constrained by the Schönberg-Chandrasekhar limit (Schönberg & Chandrasekhar 1942) to be Mc ≳ (0.1−0.15)M2. Unless the star loses a large fraction of its mass before forming an He core, the minimum mass of the core is thus ≳ 0.1 M⊙. During the subsequent evolutionary stages, the core continuously gains mass and the stellar radius grows and remains ≳ 1 R⊙, as can be seen from the dashed curves in Fig. 3. Those minimum radii are significantly above the possible Roche-lobe radius in IGR J17451−3022. The radius of the giant only shrinks when the star loses almost all the mass in its envelope (due to the H-burning shell approaching the surface, see Fig. 3). This quickly stops the accretion, given that accretion from the less massive star onto the more massive one leads to a widening of the orbit. The core becomes eventually a low-mass He white dwarf.

The above considerations are also in agreement with the observational evidence that accreting LMXBs with giant donors have large periods (12 d for GRO 1744−28, 34 d for GRS 1915+105, and 6.5 d for V404 Cyg), implying also relatively large Roche-lobe radii (see Eq. (3)). As the orbital period of IGR J17451−3022 is only 6.3 h, we conclude that a standard giant donor star cannot be hosted in this system.

thumbnail Fig. 3

Evolution of partially stripped giants in the Mc−R2 diagram. The total star masses are 0.15, 0.16, 0.175, 0.2, 0.3, 0.5, and 0.9 M⊙ for the solid black, blue, green, and red curves, and dashed cyan, magenta, and black curves, respectively. The evolution proceeds (from left to right) at the constant total mass, during which the H-burning shell is moving outwards. This increases the mass of the He core and decreases the mass of the H-rich envelope. The black and red dotted lines show the radius of the Roche-lobe around the donor (and so, to a good approximation, also the radius of this star) for M2 = 0.15 M⊙ and M2 = 0.2 M⊙, respectively. Possible solutions for the donor in IGR J17451−3022 are given by the intersections between the dotted and the solid lines on the left-hand side of the plot.

Still, we cannot exclude the possibility that a giant has undergone a substantial mass loss before the formation of its He core. An argument in support of this is given by the existence of some LMXBs with very low-mass white-dwarf donors (which were giant cores in the past), for example 4U 1820–303 with M2 ≃ (0.06−0.08) M⊙ (Rappaport et al. 1987). In order to test this scenario, we have performed evolutionary calculations by exploiting again the Warsaw stellar evolutionary code, shown in Fig. 3. To reproduce a system close to IGR J17451−3022, we followed the evolution of a 1 M⊙ star, which was maintained at a constant mass until hydrogen was nearly exhausted in its centre. At this stage, the He core was not yet formed. Then, the mass removal from the surface started and continued until the donor star reached seven different values of the mass, 0.15, 0.16, 0.175, 0.2, 0.3, 0.5, and 0.9 M⊙. The He core still did not form by that time. We applied two different (arbitrary) rates of the mass removal, 1.3 × 10-9, 1.3 × 10-8 M⊙/yr. We found that the structure of the remnants was identical in both cases. Our motivation was to obtain thermal-equilibrium remnants of a given mass. Since the structure of such remnants does not depend on their evolutionary history, the prescription for mass removal from the surface was unimportant. The further evolution of the remnants was followed at a constant total mass. The H-burning shell moves outwards, increasing the mass of the He core and decreasing that of the H-rich envelope. The radii of the partially stripped giants also increase with Mc, but when the mass of their envelopes gets sufficiently low, they shrink, as shown in Fig. 3.

We found that the giant radius in the considered cases can be equal to the Roche-lobe radius only for M2 ≤ 0.2 M⊙. Figure 3 thus shows the Roche-lobe radii for M2 = 0.15 and 0.2 M⊙. The possible solutions for the case of IGR J17451−3022 are represented by the intersections between the evolutionary tracks and the Roche-lobe values on the left side of the plot. Solutions on the right side of the plot are not viable due to the fact that in this evolutionary stage the donor star radius shrinks rapidly within the Roche-lobe, and the mass transfer toward the compact object cannot be sustained. The partially-stripped-giant solutions presented here show that it is possible to form a very low-mass He core in the donors of short orbital period LMXBs, but only if the donor loses a substantial fraction of its mass before forming the core. Thus, if the donor in IGR J17451−3022 is a giant, we find the possible range of its mass to be M2 ≃ (0.16−0.20) M⊙. In this case, R2 ≃ (0.43−0.47) R⊙ and, for an NS accretor, i ≃ (79−81)°. In the case of the BH accretor, i ≃ 84−85° and 88−89° for M1 = 5 M⊙ and ≃ 10 M⊙, respectively. We have, however, neglected irradiation of the donor by the X-ray source, which may somewhat modify the above parameters.

We note that IGR J17451−3022 shows both dips and nearly total eclipses (Bozzo et al. 2016). This is the case corresponding to an intermediate range of high inclinations, with values of i lower than those of dip-only sources and higher than those for almost edge-on systems, where the disc obscures the central X-ray source (Frank et al. 1987). Frank et al. (1987), based on considerations of the geometry of an accreting binary with an accretion disc corona, estimated the expected inclination range of binaries showing both dips and total eclipses as ~(75−80)°. Unfortunately, even accepting this range at face value does not allow us to discriminate between the above solutions with either an MS star or a very low-mass giant, except that we can exclude the case of a very low-mass giant accreting onto a BH (which has i close to 90°).

Partially stripped giants have no memory of their past evolution, and their structure is primarily determined by Mc and the total mass. In the standard case, with the total giant mass ≳ 0.3 M⊙, the stellar radius depends mostly on Mc, with only a minor effect of the total mass (Paczyński 1970; Rappaport et al. 1995), as we have already noted. However, we find here a new and interesting effect that the giant radii become strongly dependent on their total masses when they are low. This is illustrated in Fig. 3, which shows that the dependence of the radii on the total mass becomes progressively stronger as the mass decreases. It is relatively weak between the masses of 0.9 and 0.3 M⊙, but becomes highly significant for lower masses. This also shows that the approximate analytical formulae for R2(Mc) of Webbink et al. (1983) and King (1993) are no longer applicable in this regime.

We also note that our new evolutionary solutions for very low-mass giants could be applicable in the case of the LMXB X2127+119 in the globular cluster M15. In that object, with the orbital period of P = 17.1 h, van Zyl et al. (2004a,b) found evidence for the presence of a very low-mass donor with M2 ~ (0.1−0.15) M⊙. In this range, we still find no possible solutions, but at a slightly larger value of M2 = 0.175 M⊙, the Roche-lobe radius of the donor would be ≃ 0.87 R⊙, and our solution for this mass in Fig. 3 (the green curve) could be applicable for that source.

Our results are compatible with those of Lin et al. (2011), who have performed extensive evolutionary calculations following evolution for binaries with a 1.4 M⊙ neutron star down to the donor masses of 0.01 M⊙. Their Fig. 1 shows results fully consistent with ours. For P ≃ 6.3 h of IGR J17451−3022, they obtain the allowed range of the donor mass of 0.15−0.8 M⊙ and 1.5−2.5 M⊙. The former range corresponds to that obtained by us, while the latter appears to correspond to very fast outflows with very short duration. In their Fig. 2, two evolution tracks going through the period of IGR J17451−3022 are marked CV (cataclysmic variables) and UC (ultracompact). On the CV track, the donor star is only moderately evolved when the mass transfer starts, and it remains H-rich while losing mass by accretion. The position of IGR J17451−3022 on this track corresponds to our solution with an MS donor. On the UC track, the mass transfer starts when the donor star is evolved, typically with H just having been depleted at the stellar centre and before the formation of an He core. The position of IGR J17451−3022 on the UC track roughly corresponds to our solution with a partially-stripped-giant donor. However, without access to the details of their calculations, we cannot directly use those results.

Finally, we show that either brown or white dwarf donors in IGR J17451−3022 can be firmly ruled out. Old brown dwarfs are self-sustained by both the classical ionic-Coulomb pressure, dominating at their low-mass range of M ≳ 0.012 M⊙, and by partial electron degeneracy, dominating at the high-mass range of M ≲ 0.075 M⊙. Their radii are close to 0.1 R⊙ in the entire mass range (Chabrier et al. 2009), which is far below any reasonable assumption for the size of the Roche-lobe in IGR J17451−3022. We note that there has been a measurement of substantially higher radii in the double brown-dwarf binary 2MASS J05352184–0546085, namely R/R⊙ = 0.669 ± 0.034 at M/M⊙ = 0.054 ± 0.005 and R/R⊙ = 0.511 ± 0.026 at M/M⊙ = 0.034 ± 0.003 (Stassun et al. 2006). However, this is a recently formed system, with an age of ~ 106 y, orders of magnitude smaller than the typical age of LMXBs (~ 108−109 y).

Concerning low-mass white dwarfs, their radii in the fully degenerate limit are given by R/R⊙ ≃ 0.0128(M/M⊙)− 1/3(1 + X)5/3 (Chandrasekhar 1939; Deloye & Bildsten 2003). A He or C/O white dwarf (with X ≃ 0) has thus an even smaller radius than that of a degenerate brown dwarf with a comparable mass (by a factor of ~ (1 + 0.7)− 5/3 ≃ 0.4), and can also be ruled out as the donor. An increase in the radius of an old white dwarf due to departures from degeneracy and a non-negligible H content can be only moderate, and would still result in a much smaller radius than the size of the Roche lobe in IGR J17451−3022. On the other hand, young low-mass white dwarfs (i.e., shortly after their formation from cores of stripped giants) can be thermally bloated to significantly larger radii (Maxted et al. 2011, 2013; Rappaport et al. 2015). However, the evolution of such objects is characterised by a fast shrinking radius (due to the white dwarf cooling), and thus they are unable to sustain a stable Roche-lobe overflow phase, as observed in IGR J17451−3022.

4. Conclusions

We have constrained the binary parameters of IGR J17451−3022 using the recent measurements of the period and the eclipse duration of that system by Bozzo et al. (2016). We have determined that the donor is most likely an MS star with a mass within ~(0.5−0.8) M⊙ and a radius of ~ 0.7 R⊙. As found by Bozzo et al. (2016), the properties of the source X-ray spectra suggest the presence of an NS accretor, even though a BH could not be firmly ruled out. In the NS case, we find the system inclination is 71° ≲ i ≲ 76°.

We have also studied an alternative possibility that the donor is a very low-mass and small-radius partially stripped giant. This solution requires that an initially heavy progenitor of the donor (with M2 ≳ 1 M⊙) lost a substantial amount of mass prior to the formation of its He core. From evolutionary calculations, we have found M2 ~ (0.15−0.2) M⊙, R2 ~ 0.4 R⊙, i ~ 80°. A similar solution could apply to X2127+119, where van Zyl et al. (2004a,b) required the donor to have a very low mass. We have ruled out the cases of the donor in IGR J17451−3022 being either a standard (i.e., without major mass loss before the core formation) giant, or a brown or white dwarf.

We have also obtained two general results. First, we have found that the radius of a giant depends sensitively on the giant mass at the masses ≲ 0.3 M⊙. This is unlike the standard, higher-mass case, where the radius depends mostly on the core mass, with only a secondary dependence on other parameters. We have also obtained an analytical solution, Eq. (5), of the standard eclipse equation, providing an explicit formula for the inclination as a function of the donor radius, the period, and the eclipse duration.

Acknowledgments

We thank Tomek Bulik, Phil Charles, Joanna Mikołajewska, and Ashley Ruiter for valuable discussions, and the referee for valuable suggestions. This research has been supported in part by the Polish National Science Centre grants 2012/04/M/ST9/00780, 2013/10/M/ST9/00729 and 2015/18/A/ST9/00746.

References

  1. Altamirano, D., Cavecchi, Y., Patruno, A., et al. 2011, ApJ, 727, L18 [NASA ADS] [CrossRef] [Google Scholar]
  2. Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
  3. Bozzo, E., Pjanka, P., Romano, P., et al. 2016, A&A, 589, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Chabrier, G., Baraffe, I., Leconte, J., Gallardo, J., & Barman, T. 2009, AIP Conf. Proc., 1094, 102 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chakrabarty, D., Grunsfeld, J. M., Prince, T. A., et al. 1993, ApJ, 403, L33 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chanan, G. A., Middleditch, J., & Nelson, J. E. 1976, ApJ, 208, 512 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chandrasekhar, S. 1939, An Introduction to the Study of Stellar Structure (Univ. of Chicago Press) [Google Scholar]
  8. Chenevez, J., Vandbaek Kroer, L., Budtz-Jørgensen, C., et al. 2014, ATel, 6451 [Google Scholar]
  9. Cox, A. N. 2000, Allen’s Astrophysical Quantities (Springer) [Google Scholar]
  10. Deloye, C., & Bildsten, L. 2003, ApJ, 598, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  11. Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
  13. Faulkner, J., Flannery, B. P., & Warner, B. 1972, ApJ, 175, L79 [Google Scholar]
  14. Frank, J., King, A. R., & Lasota, J.-P. 1987, A&A, 178, 137 [NASA ADS] [Google Scholar]
  15. Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. King, A. R. 1993, MNRAS, 260, L5 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lattimer, J. M., & Prakash, M. 2010, in From Nuclei to Stars (Singapore: World Scientific), ed. S. Lee, 275 [Google Scholar]
  18. Lin, J., Rappaport, S., Podsiadlowski, P., et al. 2011, ApJ, 732, 70 [NASA ADS] [CrossRef] [Google Scholar]
  19. Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2007, A&A, 469, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Markwardt, C. B., & Strohmayer, T. E. 2010, ApJ, 717, L149 [NASA ADS] [CrossRef] [Google Scholar]
  21. Maxted, P. F. L., Anderson, D. R., Burleigh, M. R., et al. 2011, MNRAS, 418, 1156 [NASA ADS] [CrossRef] [Google Scholar]
  22. Maxted, P. F. L., Serenelli, A. M., Miglio, A., et al. 2013, Nature, 498, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Paczyński, B. 1967, Acta Astron., 17, 287 [NASA ADS] [Google Scholar]
  24. Paczyński, B. 1970, Acta Astron., 20, 47 [NASA ADS] [Google Scholar]
  25. Pont, F., Melo, C. H. F., Bouchy, F., et al. 2005, A&A, 433, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Rappaport, S., Nelson, L. A., Ma, C. P., & Joss, P. C. 1987, ApJ, 322, 842 [NASA ADS] [CrossRef] [Google Scholar]
  27. Rappaport, S., Podsiadlowski, P., Joss, P. C., Di Stefano, R., & Han, Z. 1995, MNRAS, 273, 731 [NASA ADS] [CrossRef] [Google Scholar]
  28. Rappaport, S., Nelson, L., Levine, A., et al. 2015, ApJ, 803, 82 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schönberg, M., & Chandrasekhar, S. 1942, ApJ, 96, 161 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ségransan, D., Kervella, P., Forveille, T., & Queloz, D. 2003, A&A, 397, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Stassun, K. G., Mathieu, R. D., & Valenti, J. A. 2006, Nature, 440, 311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. van Zyl, L., Charles, P. A., Arribas, S., et al. 2004a, MNRAS, 350, 649 [NASA ADS] [CrossRef] [Google Scholar]
  33. van Zyl, L., Ioannou, Z., Charles, P. A., & Naylor, T. 2004b, A&A, 428, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Webbink, R. F., Rappaport, S., & Savonije, G. J. 1983, ApJ, 270, 678 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ziółkowski, J. 2005, MNRAS, 358, 851 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

a) Size of Roche-lobe radius of the donor as a function of its mass, M2, for the orbital period of P = 22620.5 s. As IGR J17451−3022 is an accreting LMXB, R2 is the actual radius of the donor. b) Relation between the system inclination and the donor mass obtained by using the measured orbital period and eclipse duration. The black solid (red dashed) curve represents the obtained relation in case of an NS accretor with M1 = 1.26 M⊙ (M1 = 2 M⊙). We also show the relation for a BH accretor of M1 = 10 M⊙ (blue dotted curve).

In the text
thumbnail Fig. 2

Roche-lobe radius of donor star in IGR J17451−3022 as a function of its mass, M2 (black solid line), compared to a selection of the measured masses and radii of stars on the MS (blue points). The dashed red line shows the relation of R2 = R⊙(M2/M⊙)0.9 for M2 ≥ 0.1 M⊙, which approximates the middle of the MS, and R2 = 0.1 R⊙ for M2< 0.1 M⊙, which approximately describes the case of old brown dwarfs. The green and cyan curves show the models of stars on the ZAMS and TAMS, respectively. The intersections of these curves with the Roche-lobe radius show that MS stars in the mass range of ≃ (0.52−0.84) M⊙ are acceptable models of the donor star.

In the text
thumbnail Fig. 3

Evolution of partially stripped giants in the Mc−R2 diagram. The total star masses are 0.15, 0.16, 0.175, 0.2, 0.3, 0.5, and 0.9 M⊙ for the solid black, blue, green, and red curves, and dashed cyan, magenta, and black curves, respectively. The evolution proceeds (from left to right) at the constant total mass, during which the H-burning shell is moving outwards. This increases the mass of the He core and decreases the mass of the H-rich envelope. The black and red dotted lines show the radius of the Roche-lobe around the donor (and so, to a good approximation, also the radius of this star) for M2 = 0.15 M⊙ and M2 = 0.2 M⊙, respectively. Possible solutions for the donor in IGR J17451−3022 are given by the intersections between the dotted and the solid lines on the left-hand side of the plot.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.