| Issue |
A&A
Volume 697, May 2025
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202553937 | |
| Published online | 08 May 2025 | |
Resolution of a paradox: SDSS J1257+5428 can be explained as a descendant of a cataclysmic variable with an evolved donor
1
Departamento de Física, Universidad Técnica Federico Santa María, Av. España 1680, Valparaíso, Chile
2
São Paulo State University (UNESP), School of Engineering and Sciences, Guaratinguetá, Brazil
3
Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
⋆ Corresponding author: diogobellonizorzi@gmail.com
Received:
28
January
2025
Accepted:
18
March
2025
Context. The binary system SDSS J1257+5428 consists of an extremely low-mass white dwarf (WD) with a mass ranging from ∼0.1 to ∼0.24 M⊙, along with a more massive WD companion of approximately 1 M⊙ that is significantly hotter. Recently, a tertiary WD orbiting this binary was discovered, setting a lower limit for the total age (∼4 Gyr) of the triple and providing further constraints on SDSS J1257+5428 that could be used to constrain its formation pathways. Up to now, the existence of this system has been described as paradoxical since tested models for its formation cannot account for its properties.
Aims. Here we investigate under which conditions SDSS J1257+5428 could be understood as a descendant of a cataclysmic variable with an evolved donor star, which is a scenario that has never been explored in detail.
Methods. We used the rapid BSE code for pre-common-envelope (CE) evolution and the detailed MESA code for post-CE evolution to carry out binary evolution simulations and searched for potential formation pathways for SDSS J1257+5428 that lead to its observed characteristics. For the post-CE evolution, we adopted a boosted version of the CARB model, which has been successfully used to explain the properties of close binary stars hosting evolved solar-type stars.
Results. We find that SDSS J1257+5428 can be explained as a post-cataclysmic-variable system if (i) the progenitor of the extremely low-mass WD was initially a solar-type star that evolved into a subgiant before the onset of mass transfer and underwent hydrogen shell flashes after the mass transfer stopped, (ii) the massive WD was highly or entirely rejuvenated during the cataclysmic variable evolution, and (iii) magnetic braking was strong enough to make the evolution convergent. In this case, the torques due to magnetic braking need to be stronger than those provided by the CARB model by a factor of ∼100.
Conclusions. We conclude that SDSS J1257+5428 can be reasonably well explained as having originated from a cataclysmic variable that hosted an evolved donor star and should no longer be regarded as paradoxical. If our formation channel is correct, our findings provide further support that stronger magnetic braking acts on progenitors of (i) close detached WD binaries, (ii) close detached millisecond pulsar with extremely low-mass WDs, (iii) AM CVn binaries, and (iv) ultra-compact X-ray binaries, in comparison to the magnetic braking strength required to explain binaries hosting main-sequence stars and single main-sequence stars.
Key words: methods: numerical / binaries: close / stars: evolution / stars: individual: SDSS J1257+5428 / white dwarfs
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Binary stars that undergo episodes of mass transfer leading to pairs of white dwarfs (WDs) with small separations are likely the most abundant population among Type Ia supernova progenitors (see Liu et al. 2023, for a recent review). In addition, they are expected to be the main source of detectable low-frequency gravitational waves (e.g., Korol et al. 2020; Amaro-Seoane et al. 2023; Li & Chen 2024). Despite their importance, we still struggle to understand the mechanisms leading to their formation (see Belloni & Schreiber 2023a, for a recent review).
Among double WD binaries, SDSS J125733.63+542850.5 (hereafter SDSS J1257+5428) deserves special attention since its formation pathway has been a mystery for years. It was discovered by Badenes et al. (2009) as a circular, 4.56-hour period, single-lined, spectroscopic binary from SWARMS (Sloan White dwArf Radial velocity data Mining Survey). From the spectroscopic and photometric data, these authors estimated a mass of 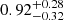 M⊙ for one of the components and concluded that the unseen companion must be more massive than
M⊙ for one of the components and concluded that the unseen companion must be more massive than 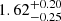 M⊙, suggesting that it is most likely a neutron star. As shown later by Kulkarni & van Kerkwijk (2010) and Marsh et al. (2011), follow-up B- and R-band spectroscopy confirmed that the system is instead composed of two WDs, a cool extremely low-mass WD and a hotter massive WD.
M⊙, suggesting that it is most likely a neutron star. As shown later by Kulkarni & van Kerkwijk (2010) and Marsh et al. (2011), follow-up B- and R-band spectroscopy confirmed that the system is instead composed of two WDs, a cool extremely low-mass WD and a hotter massive WD.
Subsequently, Bours et al. (2015) gathered ultraviolet data with the Hubble Space Telescope and refined the parameters of both WDs. They found that the cold component has a mass of ∼0.1 − 0.24 M⊙ and an effective temperature of ∼6400 K, while its hot companion has a mass of 1.06 ± 0.05 M⊙ and an effective temperature of ∼13 030 K. If the properties of the first WD formed are unaffected by the formation process of the second WD (something that cannot be confirmed by observations), then these masses and effective temperatures imply that the extremely low-mass WD is significantly older than the massive WD. Because of these apparently contradicting properties, the existence of SDSS J1257+5428 has been treated as a paradox for binary star evolution.
Most recently, Aros-Bunster et al. (2025) inspected the Gaia Data Release 3 archive and discovered that the object 1570271757456852096 is a common proper motion WD companion, making SDSS J1257+5428 the third known triple WD system. By using Keck Low Resolution Imaging Spectrometer spectroscopy, Gaia and Sloan Digital Sky Survey (SDSS) photometry, and WD atmosphere models, these authors estimated a cooling age of ≳4 Gyr for the tertiary, irrespective of the cooling model and its atmospheric composition. This then imposes strong constraints on the total age of the triple, regardless of whether the tertiary originated from single star evolution or from binary star evolution through a merger.
The age of the tertiary would not be a real constraint if it were not bound to the binary initially, that is, if the triple were formed dynamically through a three- or four-body interaction. As shown by Heggie & Hut (2003), the probability of triple formation through tidal capture in binary–single interactions is negligible. On the other hand, the probability of hierarchical triples forming through binary–binary interactions might be significant, according to numerical scattering experiments (e.g., Mikkola 1984; Leigh et al. 2016; Ryu et al. 2017; Barrera Retamal et al. 2024). Despite that, dynamical formation in the case of SDSS J1257+5428 seems very unlikely. The system is at a distance of 120 pc and belongs to the Galactic disk, where four-body interactions are not expected to happen as the disk is not dense enough for stellar encounters to play an important role (e.g., Binney & Tremaine 2008).
The present-day small orbital separations of close double WD binaries imply that these systems are currently much smaller in comparison to when they host a red giant (the progenitor of at least one of the WDs). Therefore, the orbit of these binaries must have been significantly reduced during their formation, most likely through common-envelope (CE) evolution triggered by dynamically unstable mass transfer. Although one of the required episodes of mass transfer was likely CE evolution, the other required episode could in principle be either CE evolution or dynamically stable mass transfer. Regarding the possible formation channels for SDSS J1257+5428, there are in principle three possibilities, all involving two episodes of mass transfer, each forming one WD: (i) two episodes of CE evolution to form the hot and cold components, (ii) dynamically stable mass transfer (to form the cold component) followed by CE evolution (to form the hot component), and (iii) CE evolution (to form the hot component) followed by dynamically stable mass transfer (to form the cold component).
The first scenario can be ruled out because the massive and hot WD would form first as it originates from an initially more massive star, which would mean that it should be cooler than observed. The mass of the progenitor of the massive WD (∼1 M⊙) was initially ∼5 M⊙ (e.g., Cummings et al. 2018), and it quickly evolved into a WD (∼100 Myr). The extremely low-mass WD companion must have originated from a star with an initial mass of ≲2 M⊙ as otherwise the helium core after the hydrogen-burning phase (lasting ≳1 Gyr) would be more massive than estimated from observations. This implies that the age of the massive WD must have been ≳1 Gyr when the extremely low-mass proto-WD was formed. At the present day, the extremely low-mass WD has an age of ≳1.0 Gyr, which would imply an age of ≳2 Gyr and a temperature of ≲10 000 K (Bédard et al. 2020) for the massive WD. This is much lower than observed (∼13 000 K). Another piece of evidence against this scenario comes from the total age of the triple. As it is ≳4 Gyr, the present-day temperature of the massive WD should be ≲8500 K (Bédard et al. 2020), which is much lower than observed.
The second scenario was recently investigated by Aros-Bunster et al. (2025). In this case, the cold, lower-mass WD is assumed to form first, as in principle this is consistent with the constraints from observations, which suggests that the cold, lower-mass WD is older than the hot component. However, the first episode of mass transfer would lead to a binary with a much shorter orbital period than what is required to accommodate the progenitor of a WD with a mass of ∼1 M⊙. Even if this difficulty could somehow be overcome, Aros-Bunster et al. (2025) show that the age difference between the cold and hot components would only correspond to ∼100 Myr, which is much shorter than estimated from observations.
Therefore, the only alternative left is the third scenario, that is, the hot WD formed first through CE evolution, and the cold component formed afterward, due to dynamically stable mass transfer (i.e., cataclysmic variable evolution). Although at first glance it may seem that this scenario should not even be considered because the hot WD would be colder if formed first, this is not necessarily true if the properties of the hot WD change during the formation of the cold WD. In this work we ran binary evolution models to investigate whether and under which conditions this third scenario, the only remaining option, could lead to the resolution of the paradox. We find that this scenario is indeed possible provided the donor star is a subgiant that later underwent hydrogen shell flashes as a proto-WD, the hot component is highly or entirely rejuvenated during cataclysmic variable evolution, and the magnetic braking is sufficiently strong to make the cataclysmic variable evolution convergent.
2. A testable formation channel for SDSS J1257+5428
In the scenario we investigate here, the WD that becomes the massive, hot WD was formed first via CE evolution, followed by the formation of the WD that becomes the extremely low-mass, cold WD via dynamically stable mass transfer. In what follows, we provide an overview of the general concepts on which this formation channel is based.
After the more massive star of the initial main-sequence binary system evolves off the main sequence, it becomes an asymptotic giant branch (AGB) star and eventually fills its Roche lobe. Provided this Roche-lobe-filling red giant cannot maintain hydrostatic equilibrium, the system enters a phase of dynamically unstable mass transfer. In such a case, the mass-loss timescale becomes extremely short, preventing the donor star from remaining within its Roche lobe, which results in the formation of a CE surrounding the dense giant core and the main-sequence star. This triggers a rapid orbital decay and ultimately leads to an episode of CE evolution and the formation of the WD that later becomes the hot WD in SDSS J1257+5428. If the orbital period of the resulting post-CE binary is sufficiently long (more than a few days), the companion of the WD will have enough time to evolve off the main sequence and become a subgiant, before filling its Roche lobe.
After CE evolution, the subsequent evolution of the binary, however, is not only driven by nuclear evolution but also by orbital angular momentum loss due to magnetic wind braking. The strength of magnetic braking and its dependence on stellar mass, stellar structure, and evolutionary stage are highly uncertain. However, there is growing evidence that for binary stars containing main-sequence star companions, magnetic braking is efficient for stars with a radiative core and a convective envelope but inefficient for fully convective stars and stars with a convective core (Schreiber et al. 2010; Knigge et al. 2011; Zorotovic & Schreiber 2017; Belloni & Schreiber 2023a; Belloni et al. 2024b; Schreiber et al. 2024).
While magnetic braking is even less constrained for slightly evolved stars, based on the above, it is likely that if the companion star has a radiative core, the evolution of the binary consisting of the WD and its evolved companion is driven by a combination of orbital angular momentum loss due to magnetic braking and mass loss through winds. On the other hand, for stars having convective cores, magnetic braking is likely inefficient and the evolution is driven by the mass loss through winds only. If the companion of the WD was a main-sequence star with a mass of ≳1.2 M⊙, then its core became radiative only after it became a subgiant and only at this point magnetic braking became the driver of the binary evolution. Alternatively, if its mass was smaller than that, then magnetic braking is always acting since the core of the star is radiative.
Regardless of when magnetic braking kicked in, the donor star has to be a subgiant at the onset of mass transfer and the evolution has to be driven by strong orbital angular momentum loss due to magnetic braking. Only if at the onset of mass transfer magnetic braking dominates over the nuclear evolution of the donor star, the system evolves toward shorter orbital periods, which is required to explain the properties of SDSS J1257+5428. As soon as the donor star fills its Roche lobe, dynamically stable mass transfer (i.e., cataclysmic variable evolution) starts. Assuming that magnetic braking dominates, the orbital period and the donor mass decrease as a consequence of the orbital angular momentum loss. When the mass transfer rate is sufficiently high, hydrogen can be stably burnt on the WD surface, which leads to an increase in its mass and an overall rejuvenation. As soon as the mass of the donor envelope becomes negligible, the mass transfer rate (due to magnetic braking and mass loss) drops and the binary detaches. At this point, mass transfer ends and the remaining binary consists of a massive WD paired with an extremely low-mass proto-WD (see Belloni & Schreiber 2023b, for more details).
We would like to draw the readers attention to the important differences between the detachment phase in standard cataclysmic variable evolution and the detachment phase leading to the formation of double WD binaries. In the former, the donor star is an unevolved main-sequence star that transitions to a fully convective main-sequence star when its mass drops to ∼0.2 M⊙ (McAllister et al. 2019). Although magnetic braking is not fully disrupted (e.g., El-Badry et al. 2022; Belloni et al. 2024b), angular momentum loss through magnetic braking becomes less efficient, allowing the donor to detach from its Roche lobe. On the other hand, when the donor star is a subgiant, its core is radiative and remains as such during the entire cataclysmic variable evolution. When the mass of the envelope of the donor star becomes sufficiently low, hydrogen shell burning can no longer prevent the contraction of the donor star. This contraction causes the donor star to detach from its Roche lobe and to evolve into an extremely low-mass proto-WD.
In the emerging double degenerate binary, the age of the massive WD is reset during cataclysmic variable evolution. The companion, an extremely low-mass proto-WD, is sufficiently massive to evolve through hydrogen shell flashes. Subsequently, the extremely low-mass WD enters its cooling sequence and from this point on the binary evolution is driven solely by the emission of gravitational waves, which causes the orbital period to decrease smoothly. The resulting system stellar and binary parameters may then be comparable to those of SDSS J1257+5428. Throughout the remainder of this paper, we test under which conditions this is the case. A schematic of our proposed scenario is provided in Fig. 1.
 |
Fig. 1. Proposed formation pathway for SDSS J1257+5428. After the more massive star in the zero-age main-sequence binary becomes an AGB star and fills its Roche lobe, the binary evolves through a CE phase. The resulting post-CE binary consists of the newly formed WD and a main-sequence companion star. The orbital period of the post-CE binary is such that the WD has time to cool and the main-sequence star has time to evolve and become a subgiant before filling its Roche lobe. During cataclysmic variable evolution, the WD is heated due to accretion and rejuvenated. Following cataclysmic variable evolution, the donor becomes an extremely low-mass proto-WD and after undergoing hydrogen flashes finally becomes an extremely low-mass WD. The binary eventually looks like SDSS J1257+5428. |
3. Binary evolution models
We tested the hypothesis that SDSS J1257+5428 is a descendant of a cataclysmic variable with an evolved donor adopting a two-code scheme. For pre-CE and CE evolution we used the BSE code (Hurley et al. 2000, 2002), which is a rapid population synthesis code that allows us to quickly explore a broad region of the parameter space (e.g., Belloni et al. 2024d). For post-CE evolution, we used the MESA code because it solves the fully coupled structure and composition equations simultaneously and is capable of calculating fully self-consistent evolutionary tracks through stable mass transfer. The results of these evolutionary tracks can be compared with the characteristics of SDSS J1257+5428. In what follows, we describe in detail our assumptions for pre-CE, CE and post-CE evolution.
3.1. Pre-common-envelope evolution modeling
Unless clearly stated otherwise, we used the standard BSE values for all stellar and binary evolution parameters (e.g., Hurley et al. 2002). Our approach follows closely that of Belloni et al. (2024d).
We assumed solar metallicity (i.e., Z = 0.02) and set the Reimers (1975) wind efficiency to 0.5 for the first giant branch evolution. During the evolution on the AGB, we adopted the prescription proposed by Vassiliadis & Wood (1993). Regarding wind accretion, we adopted the Bondi–Hoyle–Lyttleton prescription (Hoyle & Lyttleton 1939; Bondi & Hoyle 1944).
For CE evolution, we adopted the energy formalism, that is, the binding energy of the envelope of the red giant donor (Ebind) at the onset of the CE evolution is assumed to be equal to the change in orbital energy during the spiral-in phase (ΔEorb) scaled with a parameter αCE, corresponding to the fraction of the change in orbital energy that is used to unbind the envelope:
where Ma is the accretor mass, Md, c is the core mass of the donor, ai is the semimajor axis at the onset of the CE evolution, and af is the semimajor axis after CE ejection.
The binding energy is approximated by
where Md is the donor mass, Rd is the donor radius, and λ is the envelope-structure parameter (Dewi & Tauris 2000; Xu & Li 2010; Loveridge et al. 2011; Klencki et al. 2021; Marchant et al. 2021).
We set the CE efficiency to α = 0.3, which is consistent with the increasing evidence that short-period post-CE binary progenitors experience strong orbital shrinkage during CE evolution (e.g., Zorotovic et al. 2010; Toonen & Nelemans 2013; Camacho et al. 2014; Cojocaru et al. 2017; Belloni et al. 2019; Hernandez et al. 2022; Zorotovic & Schreiber 2022; Scherbak & Fuller 2023; Chen et al. 2024). The envelope-structure parameter λ was calculated according to a fitting scheme similar to that provided by Claeys et al. (2014, their Appendix A), which is based on the detailed numerical stellar evolution calculations by Dewi & Tauris (2000) and takes into account the structure and the evolutionary stage of the red giant donor and the envelope thermal energy as constrained by the virial theorem (i.e., increasing λ by a factor of 2).
3.2. Post-common-envelope evolution modeling
We used the version r15140 of the MESA code (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023) to calculate binary evolution after CE evolution. For reference, our approach follows closely that by Belloni & Schreiber (2023b)1, Belloni et al. (2024a)2, and Belloni et al. (2024c)3.
3.2.1. Stellar evolution
The MESA equation of state is a blend of the OPAL (Rogers & Nayfonov 2002), SCVH (Saumon et al. 1995), FreeEOS (Irwin 2004), HELM (Timmes & Swesty 2000), PC (Potekhin & Chabrier 2010) and Skye (Jermyn et al. 2021) equations of state. Nuclear reaction rates are a combination of rates from NACRE (Angulo et al. 1999), JINA REACLIB (Cyburt et al. 2010), plus additional tabulated weak reaction rates (Fuller et al. 1985; Oda et al. 1994; Langanke & Martínez-Pinedo 2000). Screening is included via the prescription of Chugunov et al. (2007) and thermal neutrino loss rates are from Itoh et al. (1996). Electron conduction opacities are from Cassisi et al. (2007) and radiative opacities are primarily from OPAL (Iglesias & Rogers 1993, 1996), with high-temperature Compton-scattering dominated regime calculated using the equations of Buchler & Yueh (1976).
We adopted a metallicity of Z = 0.02 and the grey Eddington T(tau) relation to calculate the outer boundary conditions of the atmosphere, using a uniform opacity that is iterated to be consistent with the final surface temperature and pressure at the base of the atmosphere. Radiative opacities are taken from Ferguson et al. (2005) for 2.7 ≤ log T ≤ 4.5 and OPAL (Iglesias & Rogers 1993, 1996) for 3.75 ≤ log T ≤ 8.7. For the evolutionary phases with convective core, that is, core hydrogen and helium burning, we took into account exponential diffusive overshooting, assuming a smooth transition in the range 1.2 − 2.0 M⊙ (e.g., Anders & Pedersen 2023). We assumed that the extent of the overshoot region corresponds to a fraction of Hp (e.g., Schaller et al. 1992; Freytag et al. 1996; Herwig 2000), with Hp being the pressure scale height at the convective boundary. We further used the nuclear network cno_extras.net, which accounts for the nuclear reactions of the carbon–nitrogen–oxygen cycle for hydrogen burning.
We allowed the star to lose mass through winds, adopting the Reimers (1975) prescription and setting the wind efficiency to 0.5. We treated convective regions using the scheme by Henyey et al. (1965) for the mixing-length theory, assuming that the mixing length is a factor of Hp (e.g., Joyce & Tayar 2023). In addition, the boundaries of convective regions are determined using the Schwarzschild criterion. We also included element diffusion due to gravitational settling and chemical and thermal diffusion (Paxton et al. 2015) for 1H, 3He, 4He, 12C, 13C, 14N, 16O, 20N, 24Mg, and 40Ca.
Regarding the WD accretor, we approximated it with a point mass. In addition, we assumed that it was entirely rejuvenated during cataclysmic variable evolution, that is, its age was reset to zero at the onset of the detachment (i.e., when the donor becomes a proto-WD), which is consistent with simple prescriptions for the cooling and heating of accreting WDs (Schreiber et al. 2023). The effective temperature and gravity of the cooling massive WD in the detached double degenerate binary were determined via interpolating the WD evolutionary models with thick atmospheres (surface hydrogen abundance of 10−4) computed by Bédard et al. (2020).
3.2.2. Binary evolution
The Roche-lobe radius of each star was computed using the fit of Eggleton (1983). The mass transfer rates due to Roche-lobe overflow are determined following the prescription of Ritter (1988), in which the atmosphere of the star is filling the Roche lobe. In this so-called atmospheric Roche-lobe overflow model, mass transfer occurs even when the star radius is smaller than the Roche-lobe radius.
Mass transfer due to Roche-lobe overflow is likely non-conservative. We allowed mass and angular momentum losses following the formalism of Soberman et al. (1997). The mass lost from the vicinity of the donor star as a fast wind (i.e., Jeans mode) corresponds to a fraction α of the transferred mass and is modeled as a spherically symmetric outflow from the donor star in the form of a fast wind. The mass lost from the vicinity of the WD accretor as a fast wind (i.e., isotropic re-emission) corresponds to a fraction β of the accreted mass. Finally, the mass lost from a circumbinary disk corresponds to a fraction δ of the transferred mass and is modeled as a time-dependent coplanar toroid (see below). Thus, the accretion efficiency during mass transfer is then given by
As we just mentioned, we assumed that the WD accretor can only accrete a part of the mass transferred from its companion. Depending on the accretion rate onto the WD, hydrogen shell burning can be stable resulting in an increase in its mass. This has been modeled by implementing the critical accretion rate calculated by Wolf et al. (2013), above which stable hydrogen shell burning occurs. For accretion rates lower than this critical value, the WD undergoes nova eruptions, such that almost all of the accreted mass is expelled from the binary. Since it is unlikely that exactly the entire accreted mass is ejected (e.g., José et al. 2020), we assumed that β = 85%. We further assumed that there is a maximum possible accretion rate (Wolf et al. 2013) such that WDs accreting at higher rates will burn stably at this maximum rate and the remaining non-accreted matter will be piled up forming a red-giant-like envelope, which is assumed to be lost from the binary in the form of stellar-like fast winds.
For the orbital angular momentum loss, we took into account not only those related to the mass loss from the system but also due to gravitational radiation and magnetic braking as
where
where G is the gravitational constant, MWD is the WD mass, M2 is the donor mass, and a is the orbital separation.
The fraction of accreted mass leaving the WD is assumed to carry away the specific angular momentum of the WD and the mass lost from the donor star carries the specific angular momentum of the donor star. In particular, the orbital angular momentum loss due to mass loss is given by
where q = M2/MWD is the ratio between donor star mass and the mass of the WD accretor.
For the orbital angular momentum loss due to a circumbinary disk, following Spruit & Taam (2001), we assumed that a fraction of the mass transfer rate feeds a circumbinary disk (i.e., is lost through the outer Lagrange point) and the circumbinary disk is modeled as a time-dependent toroid with inner radius ri corresponding to 1.7 times the binary separation, that is,
where
δ = 0.1%, tvi = 100 yr is the disk viscous timescale, and t* is the time in yr since the onset of mass transfer. The binary then has initially an empty circumbinary disk, which is fed with a rate corresponding to a fraction δ of the mass transfer rate. This progressive buildup of the disk mass implies a growing torque during the cataclysmic variable evolution.
The orbital decay due to the emission of gravitational waves is given by
For magnetic braking, we adopted a boosted version of the CARB prescription (Van & Ivanova 2019) given by
where Ṁwind, R2, Ω2, and τconv are the wind mass-loss rate, radius, spin and convective turnover timescale of the companion of the WD, respectively. We introduced the boosting parameter η ≥ 1 so that magnetic braking is allowed to be stronger than predicted by the standard CARB model. The convective turnover timescale was calculated by integrating the inverse of the velocity of convective cells, as given by the mixing-length theory, over the radial extent of the convective envelope following Van & Ivanova (2019). The spin of the Sun and its convective turnover timescale are 3 × 10−6 s−1 and 2.8 × 106 s, respectively, and K2 = 0.07. Finally, vesc is the escape velocity.
We enabled magnetic braking only during the evolutionary phases in which both the convective envelope and the radiative core are non-negligible. During cataclysmic variable evolution, when the mass fraction of the convective envelope becomes less than 2%, the strength of magnetic braking is reduced by a factor of e1 − 0.02/qconv (Podsiadlowski et al. 2002), where qconv is the mass fraction of the convective envelope. By doing that, we assumed that donors with very little mass in their convective envelopes do not generate strong magnetic fields and, as a result, experience minimal magnetic braking.
4. Searching for a reasonable binary model for SDSS J1257+5428
Based on the assumptions described in Sect. 3, our search for an evolutionary pathway leading to a system as similar as possible to SDSS J1257+5428 was performed in two steps. First, we searched for the best-fitting post-CE model with the MESA code by varying several stellar/binary evolution parameters as well as the initial post-CE binary parameters. Second, once the best-fitting post-CE model was found, we searched with the BSE code for the zero-age binary that evolves to an initial post-CE binary with the same properties we found in the previous steps. We describe below in more detail our fitting scheme.
In our search for the best-fitting post-CE model, we ran different grids of models. Upon finding the model within the grid that was nearest to the observed one, we refined the grid around this model to ultimately achieve an optimal fitting. The observed parameters we used to constrain the models are the (i) the mass, effective temperature and logg of the extremely low-mass WD (i.e., ≲0.24 M⊙, ∼6300 − 6600 K, ∼6 − 7, respectively); (ii) the mass, effective temperature and log g of the massive WD (i.e., 1.06 ± 0.05 M⊙, ∼12 600 − 13 200 K, ∼8.5 − 8.8, respectively); (iii) the orbital period (i.e., 4.56 hr); (iv) the age of the massive WD (i.e., ≳4 Gyr), and (v) the ratio between the radii of the extremely low-mass WD and the massive WD (i.e., ∼3.8 − 4.4).
In our fitting scheme, we varied the initial post-CE WD mass (from 0.65 to 1.05 M⊙, in steps of 0.05 M⊙), the initial post-CE main-sequence mass (from 1.05 to 1.30 M⊙, in steps of 0.05 M⊙), and the orbital period (from 1 to 10 d, in steps of 0.5 d). While both the fraction of mass lost from the WD and from the circumbinary disk were fixed, as described in Sect. 3.2.2, we varied the fraction of mass lost from the vicinity of the donor star α (from 0 to 0.15, in steps of 0.05). We further varied the magnetic braking boosting factor (η = 1, 10, 100), the mixing length (1.5 Hp, 1.0 Hp, 2.5 Hp), and the extent of the overshooting (from 0.015 Hp to 0.060 Hp, in steps of 0.015 Hp), where Hp is the pressure scale height at the convective boundary. In each model, we adopted solar metallicity (i.e., Z = 0.02) and assumed that the orbit was circular.
After finding the best-fitting post-CE model, we were able to search for the best-fitting pre-CE model, by using as constraints its initial parameters (i.e., the initial post-CE WD mass, donor star mass, and orbital period). For simplicity, we assumed that the zero-age main-sequence binary orbits were circular.
We ran a large grid of binary models varying the zero-age mass of the hot WD progenitor from 2 to 5 M⊙, in steps of 0.01 M⊙ and the zero-age orbital period from 103 to 104 d, in steps of 5 d. And, finally, the zero-age mass of the companion was chosen to be slightly smaller than the observed value as it increases during binary evolution due to wind accretion. After identifying within the grid the model in which the properties of the binary just after CE evolution were closest to the initial best-fitting post-CE model, we refined the grid around this model to obtain the best-fitting pre-CE model.
5. Formation pathway for SDSS J1257+5428
With the fitting scheme described in Sect. 4, we found that a binary with zero-age main-sequence masses of ∼3.9 and ∼1.2 M⊙ and orbital period of ∼3800 d, evolves to the required initial post-CE binary to explain SDSS J1257+5428, which corresponds to a WD mass of ∼0.85 M⊙, a main-sequence mass of ∼1.25 M⊙, and an orbital period of ∼7 d. In what follows we discuss in more detail how a zero-age main-sequence binary with these properties evolves to a binary having the properties of SDSS J1257+5428.
The best-fitting parameters for the post-CE evolution with MESA are summarized in Table 1, the sequence of events is given in Table 2, and the properties we predict in our modeling with MESA are compared with the observed ones in Table 3. The post-CE evolution of the main properties of the binary and both components are shown in Figs. 2, 3, 4, and 5, where we depict the evolution with orbital period and time of the donor mass, donor effective temperature, donor radius, donor log g, donor envelope mass, WD mass, mass transfer rate, accretion rate, and orbital angular momentum loss. We show in Fig. 6 the radii and log g of both components as a function of their effective temperatures.
Best-fitting MESA parameters for post-CE evolution.
Evolution of a zero-age main-sequence binary toward SDSS J1257+5428.
Predicted and observed (Bours et al. 2015; Aros-Bunster et al. 2025) parameters of SDSS J1257+5428.
 |
Fig. 2. Donor mass (top panels) and donor effective temperature (bottom panels) evolution with orbital period (left panels) and time (right panels). The magenta solar symbols mark the moment the orbital period is the same as observed, the green stars the onset of mass transfer, and the blue crosses the end of the cataclysmic variable phase. More details are provided in Sect. 5. |
 |
Fig. 3. Donor radius (top panels) and donor log g (bottom panels) evolution with orbital period (left panels) and time (right panels). The symbols have the same meaning as in Fig. 2. |
 |
Fig. 4. Donor envelope mass (top panels) and WD mass (bottom panels) evolution with orbital period (left panels) and time (right panels). The vertical blue lines mark the time and orbital period at which the binary detaches, the vertical magenta lines correspond to the observed orbital period, and the vertical green lines mark the onset of mass transfer. The symbols have the same meaning as in Fig. 2. |
 |
Fig. 5. Mass transfer rate, accretion rate, and donor wind mass loss rate (top panels) and orbital angular momentum loss rate (bottom panels) evolution with orbital period (left panels) and time (right panels). The vertical lines have the same meaning as in Fig. 4. |
 |
Fig. 6. Evolution of the massive WD (right panels) and the progenitor of the extremely low-mass WD (left panels) in the planes radius versus effective temperature (top panels) and log g versus effective temperature (bottom panels). The symbols have the same meaning as in Fig. 2. |
Initially, the more massive star (≈3.92 M⊙) evolves off the main sequence and becomes a subgiant (at ≈188.58 Myr), and subsequently a red giant star (at ≈189.50 Myr), a central helium burning star (at ≈190.24 Myr), an early AGB star (at ≈225.06 Myr), and a thermally pulsing AGB star at ≈226.65 Myr. Before filling its Roche lobe, the mass loss from the thermally pulsing AGB star reaches sufficiently high rates (up to ∼4 × 10−5 M⊙ yr−1). This makes wind accretion efficient enough so that the mass of the main-sequence star increases from ≈1.2 to ≈1.25 M⊙. The thermally pulsing AGB star fills its Roche lobe triggering CE evolution quickly afterward (at ≈227.15 Myr) when it has a mass of ≈2.82 M⊙ and its hydrogen-free core has a mass of ≈0.85 M⊙. After CE evolution, the binary hosts a WD and a main-sequence star with masses of ≈0.85 and ≈1.25 M⊙, respectively, and the orbital period is ≈7.07 d.
Just after the CE evolution, the companion of the WD is still a main-sequence star and has a convective core and radiative envelope, which means magnetic braking has not kicked in yet. The binary then evolves toward longer periods due to the mass loss from the main-sequence star through stellar winds. As soon as the central hydrogen abundance is substantially low (∼3%) so that the central hydrogen burning rate is not enough to prevent the collapse of the star (at ≈4920.40 Myr), the overall contraction phase starts. During this phase, the central hydrogen abundance drops to zero, the inert helium core becomes radiative, and a non-negligible portion of the envelope becomes convective.
When the temperature at the base of the hydrogen shell surrounding the inert helium core is sufficiently high, hydrogen shell burning starts and the overall contraction phase ends. The star then becomes a subgiant (at ≈5002.33 Myr) and its core is entirely radiative. Thus, the conditions for magnetic braking to act are satisfied (i.e., the core is radiative and a non-negligible portion of the envelope is convective) and from this point on it is allowed to extract orbital angular momentum. The binary then evolves toward shorter periods. Toward the onset of mass transfer, the rate at which orbital angular momentum is lost due to magnetic braking increases from ∼1035 to ∼1039 dyn cm.
The subgiant fills its Roche lobe when the orbital period is ≈1.16 d (at ≈5017.57 Myr). Just after the onset of mass transfer, the mass loss from the binary drives the evolution but quickly afterward magnetic braking becomes the main driver throughout cataclysmic variable evolution. During cataclysmic variable evolution, the orbital period and the donor mass quickly decrease as a result of the high mass transfer rates (∼10−6 − 10−5 M⊙ yr−1) due to the strong magnetic braking torques (∼1038 − 1039 dyn cm). As a consequence, the radius of the donor decreases, while its log g increases. Meanwhile, the donor effective temperature is roughly constant (∼5000 − 5500 K). As the mass accretion rate is sufficiently high so that stable hydrogen burning occurs, the WD mass increases to ≈1.03 M⊙ and its age is reset (i.e., the WD rejuvenates).
Toward the end of the cataclysmic variable evolution (at ≈5018.46 Myr), when the donor mass is ≈0.24 M⊙ and the orbital period is ≈3.87 hr, the mass fraction of the convective envelope becomes sufficiently small (≈2%). From this point on, the envelope of the donor is virtually entirely radiative and magnetic braking gets significantly reduced. As the orbital angular momentum loss rates due to mass loss (∼1036 dyn cm) and gravitational radiation (∼1034 dyn cm) are much weaker than magnetic braking before disruption (∼1037 dyn cm), they are not sufficiently strong to make the evolution convergent. The orbital period then starts to increase as a response to the nuclear evolution of the donor. The effective temperature and the radius of the donor increase, while its log g decreases in response.
At ≈5066.77 Myr, the binary detaches with an orbital period of ≈4.72 hr. The donor becomes an extremely low-mass proto-WD having a mass of ≈0.19 M⊙, an envelope mass of ≈0.035 M⊙, and an effective temperature of ≈11 258 K. From this point on, the newly formed proto-WD undergoes a few hydrogen flashes for ∼300 Myr. After this phase (at ≈5335.63 Myr), the proto-WD finally enters its cooling sequence (i.e., becomes an extremely low-mass WD). At the present day (i.e., at ≈6017.63 Myr), the orbital period and the properties of both extremely low-mass WD and massive WD are consistent with the observed.
6. Discussion
6.1. Impact of assumptions and model parameters
We found in the previous sections a reasonable model for SDSS J1257+5428. In our fitting scheme, several parameters were assumed while others were fitted. We discuss below the influence of these assumptions and fitted parameters.
6.1.1. White dwarf rejuvenation
The most important assumption we made is that the massive WD highly/completely rejuvenates during cataclysmic variable evolution, which means its age is reset to zero at the detachment. The properties of an accreting WD are likely to change due to the heating provided by the compression of the incoming matter. In particular, the release of gravitational energy (i.e., conversion into thermal energy) during the compression of the accreted material is expected to heat its interior (e.g., Sion 1995; Epelstain et al. 2007; Townsley & Bildsten 2004; Townsley & Gänsicke 2009). This energy is subsequently transported outward to the surface and inward to the core. This would then cause an overall rejuvenation of the WD.
According to the evolutionary models calculated by Bédard et al. (2020), the core and effective temperature of the 0.85-M⊙ WD at the onset of cataclysmic variable evolution are ∼3 × 106 and ∼6 × 103 K, respectively. At this moment, the 0.85-M⊙ WD is ∼4.79 Gyr old and is highly crystallized (∼78%). During cataclysmic variable evolution, the effective temperature of the WD increases to ≳105 K, according to Townsley & Gänsicke (2009, their Eq. (2)), due to the high mass transfer rates (∼10−7 − 10−6 M⊙ yr−1) onto the WD. This heating would then travel inward and should be enough to heat the core, causing an overall rejuvenation of the WD.
We should stress that this effective temperature we estimated is most likely wrong because Townsley & Gänsicke (2009) derived a relation between effective temperature due to compressional heating and the mass transfer rate for accreting WDs undergoing unstable hydrogen burning, which is not the case in our model during most of the evolution. To the best of our knowledge, unfortunately, there is no dedicated modeling (or even theory) available for WDs accreting at such high mass transfer rates and undergoing stable hydrogen burning. That being said, although our assumption for rejuvenation seems reasonable, it is still unclear how the deepness and the timescale for the heat traveling inward depend on the model parameters. Therefore, it remains to be verified under which conditions this idea could work.
6.1.2. Orbital angular momentum loss
The most important fitted parameter in our fitting scheme is the boosting factor of the CARB model, required to explain the properties of both WDs and the orbital period. To reproduce the age, log g, and effective temperature of the rejuvenated massive WD, the extremely low-mass proto-WD evolution needs to be shorter than a few hundred megayears. The evolution of an extremely low-mass proto-WD can be speeded up if it develops weak flashes as a result of thermal instabilities. These flashes cause the hydrogen envelopes to be thinner, which prevents stable nuclear burning from being a sizeable energy source at advanced stages of evolution (e.g., Althaus et al. 2001; Panei et al. 2007). Because of that, the cooling age of the extremely low-mass proto-WD becomes much shorter, with lifetimes of only a few hundred megayears. Thus, a required condition to explain SDSS J1257+5428 in the scenario we propose is that the extremely low-mass proto-WD undergoes hydrogen shell flashes.
In our best-fitting model, the CARB magnetic braking is enhanced by a factor of ∼100. This boosting is required to make the cataclysmic variable evolution strongly convergent during the formation of the an extremely low-mass proto-WD that undergoes hydrogen shell flashes, as otherwise the observed orbital period cannot be reproduced for this type of proto-WD. In the case the standard CARB model is assumed, or the boosting factor is smaller than ∼100, the resulting orbital period of the double WD binary is always longer than observed. This remains true regardless of the assumed strength of other sources of orbital angular momentum loss.
In our fitting scheme, we allowed other sources of orbital angular momentum loss, namely mass loss from the vicinities of the WD and the donor and mass loss through the outer Lagrange point (circumbinary disk). We found that the mass of the massive WD could only be reproduced if a non-negligible fraction (∼15%) of the mass that would be transferred from the donor to the WD leaves the binary and if the WD retains at least a non-negligible portion of the accreted mass (∼15%) regardless of the mass transfer rate. However, it is very likely that the mass of the massive WD can be fitted by different combinations of these mass loss efficiencies.
Most importantly, these orbital angular momentum losses originating from the mass transfer process itself, that is, the so-called consequential angular momentum loss, cannot contribute to reducing the strength of magnetic braking since the mechanisms responsible for consequential angular momentum losses cannot be the main driver of the evolution. This happens because there is a maximum rate at which angular momentum is extracted from the orbit during dynamically stable mass transfer. In the case more orbital angular momentum is lost than this maximum rate, a runway process will be triggered making mass transfer dynamically unstable and subsequently leading to a merger. For instance, in all our attempts to make the orbital angular momentum loss due to a circumbinary disk as strong as required to explain the observed orbital period, mass transfer became dynamically unstable. This happened because consequential angular momentum loss leads to positive feedback, that is, the larger the disk mass, the stronger the torque (i.e., the higher the orbital angular momentum loss rate) and in turn the higher the mass transfer rate. At a certain critical mass transfer rate, a runaway process is triggered for higher mass transfer rates. In the particular case of SDSS J1257+5428, the required mass transfer rates to explain their properties are higher than such a critical rate. Therefore, consequential orbital angular momentum loss has in general a minor impact on the evolution, except at the very beginning and the very end.
We would like to stress that we incorporated element diffusion due to gravitational settling and chemical and thermal diffusion into the calculations. As shown by Istrate et al. (2016), there is a minimum proto-WD mass above which hydrogen shell flashes occur. Such a minimum mass is ∼0.21 M⊙ for models without diffusion enabled but it drops to ∼0.17 M⊙ when diffusion is included. This happens because there is a tail in the hydrogen distribution that chemically diffuses inward where the temperature is high enough to burn it, triggering a thermal runaway for lower masses (Althaus et al. 2001). As the helium core mass correlates with the degree of nuclear evolution of a subgiant star, cataclysmic variable evolution without element diffusion would need to take place with a more nuclear evolved donor. In this case, the magnetic braking would need to be even stronger than we found while adopting element diffusion to make the evolution convergent.
6.1.3. Mixing and overshooting
Other less important parameters for the success of our modeling include the mixing length and the extent of the core overshooting. For a fixed initial donor mass, the change of its radius and the growth of its helium core mass during main-sequence and subgiant phases are affected by the mixing length and the extent of the core overshooting, respectively. In particular, the larger the mixing length, the smaller the radius, and the larger the extent of the core overshooting, the higher the helium core mass. We found that the characteristic of SDSS J1257+5428 can be explained if the mixing length is ∼2.5 Hp and the extent of the core overshooting is ∼0.06 Hp, which cause the onset of mass transfer to take place at a sufficiently short orbital period and the mass of the helium core of the donor to be sufficiently high.
The mixing length we obtained is larger than typically adopted values of this parameter (∼2; e.g., Claret & Torres 2019; Viani & Basu 2020; Joyce & Tayar 2023). However, it is very unlikely that the mixing length should be unique for all stars, irrespective of their masses, evolutionary phases, and metallicity (e.g., Creevey et al. 2017; Joyce & Tayar 2023). In addition, as shown by (e.g., Valle et al. 2019), the standard mixing-length calibrations can result in values with a large spread, being on average ∼2.20 ± 0.52. That being said, we believe our best-fitting mixing length is reasonable. The extent of the core overshooting is a bit more complicated to compare to observationally derived values because the employed method may not be reliable (e.g., eclipsing binaries Constantino & Baraffe 2018) and there are several treatments available for core overshooting (e.g., Anders & Pedersen 2023). Bearing that in mind, our extent is higher (by a factor of at least ∼2) than asteroseismically derived extents of pulsating main-sequence stars (Anders & Pedersen 2023, their Fig. 12e). Despite that, considering the underlying uncertainties in constraining the amount of overshoot, we believe our higher-than-average extent does not invalidate the scenario we propose.
6.1.4. Total age
To reproduce the total age of the triple (i.e., ≳4 Gyr), the zero-age mass of the progenitor of the extremely low-mass WD has to be ≲1.3 M⊙ (for a metallicity of Z = 0.02), which implies a pre-CV evolution time of ≳3 Gyr. cataclysmic variable evolution is very quick due to the strong orbital angular momentum loss making the onset of the detachment (i.e., the moment at which the extremely low-mass proto-WD is formed) at ≳3 Gyr. The massive WD and its companion then evolve for ∼1 Gyr to the present day.
Thus, for higher zero-age masses of the progenitor of the extremely low-mass WD, the present-day total age of SDSS J1257+5428 would be smaller than ∼4 Gyr. We found that an initial post-CE mass of ∼1.25 M⊙ for the progenitor of the extremely low-mass WD leads to a total age of ∼6 Gyr, consistent with observations. To achieve older (younger) total ages, we would simply need to assume a lower (higher) initial post-CE mass.
6.1.5. Additional considerations
We would like to draw the readers attention to the fact that the combination of model parameters we found in our fitting scheme is most likely not the only one that can explain SDSS J1257+5428. It is actually very likely that the properties of SDSS J1257+5428 can be reproduced by different combinations of mass loss efficiency, mass accretion efficiency, wind mass loss rates, wind mass accretion rates, extent of core overshooting, mixing length, zero-age properties and initial post-CE properties.
However, as we mentioned earlier, the zero-age (or initial post-CE) mass of the progenitor of the extremely low-mass WD is relatively well constrained by the total age of the triple. The orbital angular momentum loss rates are also relatively well constrained by the present-day properties of both WDs and the present-day orbital period. In addition, to reproduce the present-day mass of the massive WD, the initial post-CE WD mass needs to be significantly smaller than that since during cataclysmic variable evolution its mass increases due to the required high mass transfer rates. Furthermore, the zero-age mass of the progenitor of the extremely low-mass WD needs to be smaller than the required initial post-CE mass as its mass is likely increased due to wind mass accretion prior to the CE evolution. That being said, we should also stress that despite the fact the model parameters can change, the overall formation pathway we propose here is thus far the most likely, as we discuss in Sect. 6.3.
6.2. Strength of magnetic braking in different populations
We adopted the CARB model in this paper and found that magnetic braking needs to be very strong (∼1038 − 1039 dyn cm) to explain SDSS J1257+5428. These rates are much higher than those expected to explain single stars and other types of binaries. We discuss below how this compares to the strength and the form of magnetic braking typically used to explain different populations.
Regarding detached binaries with low-mass main-sequence stars, El-Badry et al. (2022) showed that the characteristics of detached binary main-sequence stars are better explained by a magnetic braking recipe that takes into account the saturation of the magnetic field. These authors found that torques resulting in orbital angular momentum loss rates on the order of ∼1032 − 1034 dyn cm are enough to reproduce their orbital period distributions. Afterward, Belloni et al. (2024b) showed that a saturated, boosted and disrupted magnetic braking could explain not only binary main-sequence stars but also the distribution of the fraction of detached post-CE binaries with WDs paired with M dwarfs across the M dwarf mass. For that, the boosting factor should be such that the angular momentum loss rates are at least ∼1035 − 1036 dyn cm for M dwarfs with radiative core and the disruption factor such that the rates are ∼1032 − 1033 dyn cm for fully convective M dwarfs. More recently, Blomberg et al. (2024) showed that detached post-CE binaries with hot subdwarfs orbiting M dwarf are also better reproduced by a saturated, boosted and disrupted magnetic braking.
The saturated, boosted and disrupted magnetic braking prescription was also applied to standard cataclysmic variables (i.e., those with unevolved donors) by Barraza-Jorquera et al. (2025). These authors showed that similar orbital angular momentum loss rates (i.e., ∼1035 − 1036 dyn cm) can explain the orbital period gap (Schreiber et al. 2024). These rates are consistent with those in previous calculations with the so-called RVJ (Rappaport et al. 1983) prescription, such as those carried out by Knigge et al. (2011).
Populations of compact objects accreting from nuclear evolved donors are in general better explained by stronger magnetic braking. For instance, Van & Ivanova (2019), who invented the CARB model, showed that stronger magnetic braking is required to explain persistent low-mass X-ray binaries. The same prescription was adopted by Belloni & Schreiber (2023b), who showed that the characteristic of cataclysmic variables can be reasonably well explained. A stronger magnetic braking is also required to solve the fine-tuning problem related to the formation of close detached binaries hosting millisecond pulsars with extremely low-mass WDs companions (Istrate et al. 2014; Chen et al. 2021; Soethe & Kepler 2021), which are descendants of low-mass X-ray binaries. Not surprisingly, a stronger magnetic braking can also solve the fine-tuning problem associated with the formation of AM CVn binaries from cataclysmic variables (Belloni & Schreiber 2023b).
We here found that the torques predicted by the CARB model are not strong enough to explain SDSS J1257+5428. For a successful fit, we needed to assume a boosted version of the CARB recipe. A useful extension of this work would be to fit the systems discovered by El-Badry et al. (2021) in a similar detailed fashion we did for SDSS J1257+5428 as this could shed more light on the required strength of magnetic braking to fit the population of cataclysmic variables with nuclear evolved donor. Another interesting follow-up exercise would be to verify under which conditions the saturated, boosted and disrupted magnetic braking recipe would lead to similarly satisfactory evolution to explain the characteristics of SDSS J1257+5428 and cataclysmic variables with nuclear evolved donors. It would also be interesting to apply the saturated, boosted and disrupted magnetic braking to low-mass X-ray binaries and progenitors of AM CVn binaries.
6.3. On the existence of alternative formation pathways
We argue in Sect. 1 that the main formation channels tested for SDSS J1257+5428 does not work. A formation pathway involving two episodes of CE evolution, having the massive WD formed first followed by the formation of the extremely low-mass WD, does not work because the more massive WD would be much colder than its extremely low-mass WD companion. In addition, it is very unlikely that the binary would survive the second episode of CE evolution since the progenitor of the extremely low-mass WD would be at best a red giant star descending from a solar-type star, which has a strongly bound envelope that cannot be easily ejected. A formation channel in which the extremely low-mass WD is formed first through dynamically stable mass transfer, followed by the formation of the massive WD via CE evolution, also does not work because the massive WD would be formed quickly after the extremely low-mass WD leading to an extremely low-mass WD that is much hotter than observed (Aros-Bunster et al. 2025).
As an alternative to these standard formation channels, Jiang et al. (2018) proposed a “strange” scenario for SDSS J1257+5428 in which the estimated different cooling ages of both WDs originate from the heating process during the formation of a strange dwarf. These authors assumed that if the central density of a WD exceeds a critical density, a strange quark core would emerge in the central parts and the WD would evolve into a strange dwarf. In this case, during this transformation, the mass of the massive WD in SDSS J1257+5428 would decrease and the transport of energy would heat the WD, resulting in a hotter WD. However, in the calculations by Jiang et al. (2018), the effective temperature of the extremely low-mass WD can only be reproduced for a metallicity of Z ≲ 10−4, which is inconsistent with the distance of SDSS J1257+5428 (i.e., ∼120 pc, Bailer-Jones et al. 2021) and its location (Milky Way disk). We therefore believe that this scenario seems to be very unlikely.
7. Conclusions
We ran binary evolution models using the MESA code in a bid to model SDSS J1257+5428 assuming the cataclysmic variable channel. We adopted a boosted version of the CARB model for magnetic braking, which provides sufficiently high orbital angular momentum loss rates that cataclysmic variable evolution with more nuclear evolved donors is convergent, leading to double WDs in tighter orbits. We find that SDSS J1257+5428 can be understood as being a descendant of a cataclysmic variable with an evolved donor, resolving the paradox. In this scenario, the progenitor of the extremely low-mass WD would have initially been a solar-type star that evolved into a subgiant before mass transfer began. During cataclysmic variable evolution, the more massive WD would have undergone significant rejuvenation and the magnetic braking torques would need to be around 100 times stronger than those predicted by the CARB model. Our results further support the idea that cataclysmic variables most likely play an important role in the formation of AM CVn binaries and close double WDs in general.
Acknowledgments
We would like to thank an anonymous referee for constructive comments and suggestions that helped to improve this manuscript. DB acknowledges partial support from FONDECYT (grant number 3220167) and partial support from the São Paulo Research Foundation (FAPESP), Brazil, Process Numbers #2024/03736-2 and #2025/00817-4. MRS acknowledge financial support from FONDECYT (grant number 1221059).
References
- Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001, MNRAS, 323, 471 [Google Scholar]
- Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Living Reviews in Relativity, 26, 2 [Google Scholar]
- Anders, E. H., & Pedersen, M. G. 2023, Galaxies, 11, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nuclear Physics A, 656, 3 [CrossRef] [Google Scholar]
- Aros-Bunster, C., Schreiber, M. R., Toloza, O., et al. 2025, A&A, 693, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badenes, C., Mullally, F., Thompson, S. E., & Lupton, R. H. 2009, ApJ, 707, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Barraza-Jorquera, J. A., Schreiber, M. R., & Belloni, D. 2025, A&A, 696, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrera Retamal, C. M., Leigh, N. W. C., & Stone, N. C. 2024, MNRAS, 528, 198 [Google Scholar]
- Bédard, A., Bergeron, P., Brassard, P., & Fontaine, G. 2020, ApJ, 901, 93 [Google Scholar]
- Belloni, D., & Schreiber, M. R. 2023a, Handbook of X-ray and Gamma-ray Astrophysics, 129 [Google Scholar]
- Belloni, D., & Schreiber, M. R. 2023b, A&A, 678, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, D., Giersz, M., Rivera Sandoval, L. E., Askar, A., & Ciecielag, P. 2019, MNRAS, 483, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, D., Mikołajewska, J., & Schreiber, M. R. 2024a, A&A, 686, A226 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, D., Schreiber, M. R., Moe, M., El-Badry, K., & Shen, K. J. 2024b, A&A, 682, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, D., Schreiber, M. R., & Zorotovic, M. 2024c, A&A, 687, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, D., Zorotovic, M., Schreiber, M. R., et al. 2024d, A&A, 686, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton: Princeton University Press) [Google Scholar]
- Blomberg, L., El-Badry, K., Breivik, K., et al. 2024, PASP, 136, 124201 [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [Google Scholar]
- Bours, M. C. P., Marsh, T. R., Gänsicke, B. T., et al. 2015, MNRAS, 450, 3966 [NASA ADS] [CrossRef] [Google Scholar]
- Buchler, J. R., & Yueh, W. R. 1976, ApJ, 210, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, J., Torres, S., García-Berro, E., et al. 2014, A&A, 566, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-L., Tauris, T. M., Han, Z., & Chen, X. 2021, MNRAS, 503, 3540 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Z., Chen, Y., Chen, C., Ge, H., & Ma, B. 2024, A&A, 687, A256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chugunov, A. I., Dewitt, H. E., & Yakovlev, D. G. 2007, Phys. Rev. D, 76, 025028 [NASA ADS] [CrossRef] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Cojocaru, R., Rebassa-Mansergas, A., Torres, S., & García-Berro, E. 2017, MNRAS, 470, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Constantino, T., & Baraffe, I. 2018, A&A, 618, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Creevey, O. L., Metcalfe, T. S., Schultheis, M., et al. 2017, A&A, 601, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cummings, J. D., Kalirai, J. S., Tremblay, P. E., Ramirez-Ruiz, E., & Choi, J. 2018, ApJ, 866, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- El-Badry, K., Rix, H.-W., Quataert, E., Kupfer, T., & Shen, K. J. 2021, MNRAS, 508, 4106 [CrossRef] [Google Scholar]
- El-Badry, K., Conroy, C., Fuller, J., et al. 2022, MNRAS, 517, 4916 [NASA ADS] [CrossRef] [Google Scholar]
- Epelstain, N., Yaron, O., Kovetz, A., & Prialnik, D. 2007, MNRAS, 374, 1449 [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Fuller, G. M., Fowler, W. A., & Newman, M. J. 1985, ApJ, 293, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D., & Hut, P. 2003, The Gravitational Million-body Problem: a Multidisciplinary Approach to Star Cluster Dynamics (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [Google Scholar]
- Hernandez, M. S., Schreiber, M. R., Parsons, S. G., et al. 2022, MNRAS, 512, 1843 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, Proceedings of the Cambridge Philosophical Society, 35, 405 [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, A. W. 2004, The FreeEOS Code for Calculating the Equation of State for Stellar Interiors, http://freeeos.sourceforge.net/ [Google Scholar]
- Istrate, A. G., Tauris, T. M., & Langer, N. 2014, A&A, 571, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Istrate, A. G., Marchant, P., Tauris, T. M., et al. 2016, A&A, 595, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Jermyn, A. S., Schwab, J., Bauer, E., Timmes, F. X., & Potekhin, A. Y. 2021, ApJ, 913, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Chen, W.-C., & Li, X.-D. 2018, MNRAS, 476, 109 [Google Scholar]
- José, J., Shore, S. N., & Casanova, J. 2020, A&A, 634, A5 [EDP Sciences] [Google Scholar]
- Joyce, M., & Tayar, J. 2023, Galaxies, 11, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [Google Scholar]
- Korol, V., Toonen, S., Klein, A., et al. 2020, A&A, 638, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulkarni, S. R., & van Kerkwijk, M. H. 2010, ApJ, 719, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Langanke, K., & Martínez-Pinedo, G. 2000, Nuclear Physics A, 673, 481 [Google Scholar]
- Leigh, N. W. C., Stone, N. C., Geller, A. M., et al. 2016, MNRAS, 463, 3311 [Google Scholar]
- Li, Z., & Chen, X. 2024, Results in Physics, 59, 107568P [Google Scholar]
- Liu, Z.-W., Röpke, F. K., & Han, Z. 2023, Research in Astronomy and Astrophysics, 23, 082001 [Google Scholar]
- Loveridge, A. J., van der Sluys, M. V., & Kalogera, V. 2011, ApJ, 743, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, T. R., Gänsicke, B. T., Steeghs, D., et al. 2011, ApJ, 736, 95 [NASA ADS] [CrossRef] [Google Scholar]
- McAllister, M., Littlefair, S. P., Parsons, S. G., et al. 2019, MNRAS, 486, 5535 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S. 1984, MNRAS, 207, 115 [Google Scholar]
- Oda, T., Hino, M., Muto, K., Takahara, M., & Sato, K. 1994, Atomic Data and Nuclear Data Tables, 56, 231 [CrossRef] [Google Scholar]
- Panei, J. A., Althaus, L. G., Chen, X., & Han, Z. 2007, MNRAS, 382, 779 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2010, Contributions to Plasma Physics, 50, 82 [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [Google Scholar]
- Reimers, D. 1975, Memoires of the Societe Royale des Sciences de Liege, 8, 369 [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Ryu, T., Leigh, N. W. C., & Perna, R. 2017, MNRAS, 467, 4447 [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Scherbak, P., & Fuller, J. 2023, MNRAS, 518, 3966 [Google Scholar]
- Schreiber, M. R., Gänsicke, B. T., Rebassa-Mansergas, A., et al. 2010, A&A, 513, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., Belloni, D., & van Roestel, J. 2023, A&A, 679, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., Belloni, D., & Schwope, A. D. 2024, A&A, 682, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sion, E. M. 1995, ApJ, 438, 876 [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Soethe, L. T. T., & Kepler, S. O. 2021, MNRAS, 506, 3266 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 2001, ApJ, 548, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, D. M., & Gänsicke, B. T. 2009, ApJ, 693, 1007 [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2019, A&A, 623, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van, K. X., & Ivanova, N. 2019, ApJ, 886, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [Google Scholar]
- Viani, L. S., & Basu, S. 2020, ApJ, 904, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, W. M., Bildsten, L., Brooks, J., & Paxton, B. 2013, ApJ, 777, 136 [Google Scholar]
- Xu, X.-J., & Li, X.-D. 2010, ApJ, 716, 114 [Google Scholar]
- Zorotovic, M., & Schreiber, M. 2022, MNRAS, 513, 3587 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., & Schreiber, M. R. 2017, MNRAS, 466, L63 [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Predicted and observed (Bours et al. 2015; Aros-Bunster et al. 2025) parameters of SDSS J1257+5428.
All Figures
 |
Fig. 1. Proposed formation pathway for SDSS J1257+5428. After the more massive star in the zero-age main-sequence binary becomes an AGB star and fills its Roche lobe, the binary evolves through a CE phase. The resulting post-CE binary consists of the newly formed WD and a main-sequence companion star. The orbital period of the post-CE binary is such that the WD has time to cool and the main-sequence star has time to evolve and become a subgiant before filling its Roche lobe. During cataclysmic variable evolution, the WD is heated due to accretion and rejuvenated. Following cataclysmic variable evolution, the donor becomes an extremely low-mass proto-WD and after undergoing hydrogen flashes finally becomes an extremely low-mass WD. The binary eventually looks like SDSS J1257+5428. |
| In the text | |
 |
Fig. 2. Donor mass (top panels) and donor effective temperature (bottom panels) evolution with orbital period (left panels) and time (right panels). The magenta solar symbols mark the moment the orbital period is the same as observed, the green stars the onset of mass transfer, and the blue crosses the end of the cataclysmic variable phase. More details are provided in Sect. 5. |
| In the text | |
 |
Fig. 3. Donor radius (top panels) and donor log g (bottom panels) evolution with orbital period (left panels) and time (right panels). The symbols have the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 4. Donor envelope mass (top panels) and WD mass (bottom panels) evolution with orbital period (left panels) and time (right panels). The vertical blue lines mark the time and orbital period at which the binary detaches, the vertical magenta lines correspond to the observed orbital period, and the vertical green lines mark the onset of mass transfer. The symbols have the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 5. Mass transfer rate, accretion rate, and donor wind mass loss rate (top panels) and orbital angular momentum loss rate (bottom panels) evolution with orbital period (left panels) and time (right panels). The vertical lines have the same meaning as in Fig. 4. |
| In the text | |
 |
Fig. 6. Evolution of the massive WD (right panels) and the progenitor of the extremely low-mass WD (left panels) in the planes radius versus effective temperature (top panels) and log g versus effective temperature (bottom panels). The symbols have the same meaning as in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



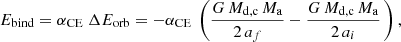
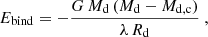
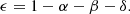
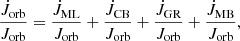
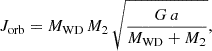
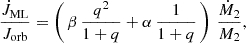
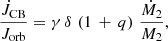
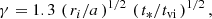
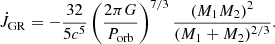
![$$ \begin{aligned} \dot{J}_{\rm MB}&= - \, \eta \times \ \left( 2\times 10^{-6} \right) \left( \frac{-\dot{M}_{\rm wind}}{\mathrm{g~s^{-1}}} \right)^{-1/3} \left( \frac{R_2}{\mathrm{cm}} \right)^{14/3} \left( \frac{\Omega _2}{\Omega _\odot } \right)^{11/3} \nonumber \\&\times \left( \frac{\tau _{\rm conv} }{\tau _{\odot , \mathrm {conv}}} \right)^{8/3} \left[ \left( \frac{v_{\rm esc}}{\mathrm{cm\,s^{-1}}} \right)^2\,+\,\frac{2}{K_2^2}\, \left( \frac{\Omega _2}{\mathrm{s^{-1}}} \right)^2 \left( \frac{R_2}{\mathrm{cm}} \right)^2 \right]^{-2/3} , \end{aligned} $$](/articles/aa/full_html/2025/05/aa53937-25/aa53937-25-eq12.gif)