| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201528066 | |
| Published online | 28 October 2016 | |
Dark influences
III. Structural characterization of minor mergers of dwarf galaxies with dark satellites
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: tjitske@astro.rug.nl
2 Department of Physics and Astronomy, University of California, Riverside, CA 92521, USA
Received: 31 December 2015
Accepted: 4 August 2016
Context. In the current concordance cosmology small halos are expected to be completely dark and can significantly perturb low-mass galaxies during minor merger interactions. These interactions may well contribute to the diversity of the dwarf galaxy population. Dwarf galaxies in the field are often observed to have peculiarities in their structure, morphology, and kinematics, as well as strong bursts of star formation without apparent cause.
Aims. We aim to characterise the signatures of minor mergers of dwarf galaxies with dark satellites to aid their observational identification.
Methods. We explored and quantified a variety of structural, morphological, and kinematic indicators of merging dwarf galaxies and their remnants using a suite of hydrodynamical simulations.
Results. The most sensitive indicators of mergers with dark satellites are large asymmetries in the gaseous and stellar distributions, enhanced central surface brightness and starbursts, and velocity offsets and misalignments between the gas and stellar components. In general, merging systems span a wide range of values of the most commonly used indicators, while isolated objects tend to have more confined values. Interestingly, we find in our simulations that a significantly off-centred burst of star formation can pinpoint the location of the dark satellite. Observational systems with such characteristics are perhaps the most promising for unveiling the presence of the hitherto missing satellites.
Key words: galaxies: dwarf / galaxies: evolution / galaxies: interactions / galaxies: irregular / galaxies: starburst / dark matter
© ESO, 2016
1. Introduction
In a Lambda cold dark matter (ΛCDM) universe the halo mass function is scale-free: independently of their mass, halos have their own system of substructures (van den Bosch et al. 2005; van den Bosch & Jiang 2014). Below a halo mass of ~ 109.5 M⊙ however star formation is expected to be largely inhibited due to reionization, photo-ionization of the gas, and possibly feedback (Gnedin 2000; Hoeft et al. 2006; Kaufmann et al. 2007; Okamoto et al. 2008; Gnedin et al. 2009; Li et al. 2010; Sawala et al. 2013). The galaxy mass function is thus not scale-free, while the stellar mass-halo mass function is predicted to steepen toward lower halo masses (Behroozi et al. 2013; Moster et al. 2013; Garrison-Kimmel et al. 2014; Sawala et al. 2015; Kormendy & Freeman 2016). Therefore, dwarf galaxy halos have significantly lower baryon fractions and their satellites are expected to be predominantly completely star-free, or dark (Helmi et al. 2012).
Although the Hubble sequence (Hubble 1926) generally describes well the properties of large galaxies, on the scale of dwarfs no clear classification scheme exists. The simplest separation is given by the fact that star-forming dwarfs often show irregular morphologies, while those quiescent have generally a spheroidal appearence. It is still not well understood how these classes of objects are related (see e.g. Mateo 1998; Tolstoy et al. 2009). Furthermore, blue compact dwarfs (BCDs), and more generally starbursting dwarf galaxies, have central regions that are very blue reflecting a centrally concentrated young stellar population so bright that an underlying, older population is not readily apparent (e.g., Gil de Paz et al. 2003; Paudel et al. 2015). Just like dwarf irregulars, BCDs can furthermore depict irregular morphologies and kinematics, with star-formation regions far from the centre (Taylor et al. 1995; Ekta & Chengalur 2010; López-Sánchez 2010; Holwerda et al. 2013; Lelli et al. 2014; Knapen & Cisternas 2015). Off-centre bursts of star formation have also been observed in a number of extremely metal-poor galaxies as well as large differences in the average line-of-sight velocities between the HI gas and the stellar component (Filho et al. 2013, 2015). As galaxy mass reduces, it appears that a higher fraction of the systems are peculiar.
Structural and numerical parameters for the host dwarf galaxies.
We have recently postulated that this may be partly explained by dwarf galaxies experiencing minor mergers with dark companions (Helmi et al. 2012). In Starkenburg & Helmi (2015) and Starkenburg et al. (2016), we show that such minor mergers can significantly alter the morphological properties of dwarf galaxies. The disturbances induced by dark objects are much more dramatic on this scale because of the lower galaxy formation efficiency (i.e. lower baryon fractions) in dwarfs compared to giant galaxies. One of the most direct imprints in gas-rich dwarfs is a vast increase in star formation: both in short bursts (during close passages of the satellite) as well as sustained high star formation rates lasting several Gyrs. In Starkenburg et al. (2016) we show that the general properties of our simulated dwarf systems compare very well to a large sample of dwarf irregular galaxies and blue compact dwarfs from the literature.
In this paper we provide a quantitative characterization of the morphological and kinematic properties of the dwarf systems during the minor merger events and thereby facilitate a more detailed comparison to observations. For the analysis we used morphological descriptions that have been applied to characterise where galaxies lie along the Hubble sequence, to disentangle interacting from isolated systems, and to describe the stellar distributions in major mergers of ~ L⋆ or larger spiral galaxies, such as the CAS (concentration, asymmetry and smoothness) and GM (Gini coefficient and M20) indicators (see e.g. Conselice et al. 2000; Conselice 2003; Abraham et al. 2003; Lotz et al. 2004, and references therein). These have also been applied to describe the stellar components of isolated irregular dwarf galaxy samples (Conselice 2003; Lotz et al. 2004), to characterise the gas distribution in starbursting dwarf galaxies (Lelli et al. 2014) and in simulations of major mergers (Holwerda et al. 2011a), as well as a variety of observational samples (Holwerda et al. 2011b,c,d,e, 2012, 2013, 2014).
This paper is organised as follows. The hydrodynamical simulations are described concisely in Sect. 2, while in Sect. 3 we focus on one specific simulated system and highlight key tidal features as the merger takes place. In Sect. 4 we introduce the morphological and kinematic indicators used and compare the results to some observational samples. We present a brief comparison to two dwarf galaxies with peculiar properties, namely IC10 and NGC 6822 in Sect. 5. The summary and conclusions are given in Sect. 6.
2. Method
We analyse the structural properties of dwarf galaxies during minor mergers with dark satellites for a suite of hydrodynamical simulations recently presented in Starkenburg et al. (2016). The simulations span a range of initial conditions for the dwarf galaxy, its satellite and a variety of orbital configurations for the interaction. They were performed using the OWLS (Schaye et al. 2010) version of Gadget-3 (based on Springel et al. 2001; Springel 2005) with implementations for star formation and feedback as described in Schaye & Dalla Vecchia (2008), Dalla Vecchia & Schaye (2008).
Parameters for the orbits.
 |
Fig. 1 Evolution of the model-A dwarf galaxy with Rg = 4Rd, merging with a 20% mass ratio dark satellite with c = 25 on a co-planar relatively radial orbit (the intermediate orbit in Table 2). All figures show an inclined view of the disk, 60 deg from face-on. The top row shows the gas in the disk above a certain column density (contours at 0.4, 1, 4, and 10 × 1020 N cm-2) with the star-forming gas highlighted in green (see colourbar for SFR values). The central row panels show the old stars in red, and those newly formed in blue, along with two surface brightness contours of 25 mag/arcsec2 and 28 mag/arcsec2, obtained assuming an M/L = 0.5 for all stellar particles. The bottom panels show the gas contours with the gas velocity maps. In all panels the satellite is shown in grey (5% of the particles are plotted), with the purple cross denoting its centre of mass. The insets indicate the values of asymmetry, concentration and difference in average velocity between stars and gas computed as described in Sect. 4. |
The host dwarf galaxy consists of a dark matter halo, a stellar disk and a (generally more radially extended) gaseous disk. Both the stellar and gaseous disks follow an exponential surface density profile with radius, while the vertical distribution of the gas is determined by requiring hydrostatic equilibrium, and assuming an effective equation of state of the multiphase interstellar medium (ISM) model by Schaye & Dalla Vecchia (2008), Dalla Vecchia & Schaye (2008). Star formation occurs following the Kennicutt-Schmidt relation when the density of the gas is above a threshold of 0.1 cm-3, while at lower densities the gas follows an isothermal equation of state (see Schaye & Dalla Vecchia 2008, for more details). Feedback and stellar winds are included such that the systems, when evolved in isolation, are self-regulating over the timescale of the simulations. Our ISM model results in a more regular and spatially extended star-formation activity than when using higher density thresholds for star formation and models that resolve the multi-phase structure of the gas (e.g. Governato et al. 2010; Hopkins et al. 2011; Hu et al. 2016). However, although we expect the results to change quantitatively when using a different ISM model, the main trends identified in our merger simulations should remain. Indeed, the more modulated star formation history naturally associated to our model suggests that the results presented here represent safe lower-limits to the star formation events expected in more bursty prescriptions.
 |
Fig. 2 Evolution of the inner parts of the dwarf galaxy shown in Fig. 1 around the time the satellite merges with the host. The threshold is 0.4 × 1020 N cm-2 and the contours indicate 1, 4, and 10 × 1020 N cm-2; see colourbar for the relative values. |
The satellite is a dark subhalo (no baryons) that follows an NFW-profile with two different concentrations (c ~ 15−18, based on the Mvir−c relation Muñoz-Cuartas et al. 2011; c = 25). In most of the simulations, it has an initial mass of 20% of that of the dwarf galaxy’s halo, but we also consider 5% and 10% mass ratios. Table 1 gives the virial radius of the dwarf galaxies and the mass of the satellites with respect to the virial mass of the dwarf galaxies. The satellite is typically placed on a fairly radial orbit (Table 2 gives the general orbit parameters) with different inclinations and is launched close to its apocentre (with vr/vvirmain ~ 0) at 0.67rvir of the host.
For the numerical parameters, we use 1 × 106 particles for the dwarf’s dark matter halo, a softening length ϵhalo = 0.025 kpc, 2 × 105 particles in baryonic mass, divided among the stellar and gas disks according to the gas fraction fg = Mgas/ (Mgas + M⋆), with softening length ϵbar = 0.008 kpc. The satellite is modelled with 1 × 105 particles that have a softening length ϵsat = 0.016 kpc.
Table 1 contains the parameters for the dwarf galaxy and the ratio of the initial virial mass of the satellite to the dwarf galaxy virial mass. The particle mass for the dark satellite is in between the particle masses of the main dark matter halo and the baryons to avoid numerical effects in interactions with both the halo and the disk.
We will focus mostly on one of the simulated dwarfs, which we refer to as model-A (Starkenburg et al. 2016) for which we explore ranges in the extend of the gas disk with respect to the stellar disk, the satellite mass, and the satellite orbit. We will also report results for smaller mass systems with a range of disk thickness and halo concentrations, models B, C, and D in Table 1 (see Starkenburg et al. 2016, for more detailed information).
3. Tidal effects
As an example, we present in Fig. 1 the evolution of the model-A dwarf as it experiences a 20% minor merger. In this example the dwarf has initially a very extended gas disk, with scale length Rg = 4Rd. This set-up is motivated by observations showing that gas may spread out much farther than the stars (see e.g. Begum et al. 2008; Filho et al. 2015, and references therein).
The satellite in Fig. 1 has a high concentration (c = 25) and is launched from apocentre at a distance of ~ 51 kpc on a fairly radial orbit with tangential velocity vt = 0.5vvir. During close passages to the disk the satellite (marked with a cross) induces large tidal tails in both the gas and stars, as shown in the second column of this figure.
During the second pericentric passage (third column of Fig. 1), the satellite meets up with a gaseous tidal tail and causes a local overdensity where star formation takes place (as can be seen from e.g. the newly born stars plotted in blue in the middle panel). The star formation rate density in this tidal structure is higher than in the centre so that the brightest star-forming core at this point in time is actually located more than 7 kpc from the centre. Intriguingly, such features are also found in extremely metal-poor galaxies (XMP; galaxies with oxygen abundances smaller than a tenth of the solar value; Filho et al. 2013).
 |
Fig. 3 Blue curve: evolution of the star formation rate of the dwarf galaxy shown in Figs. 1 and 2. The black curve is for the same model-A dwarf run in isolation. The star formation rate in the tidal tail within 1 kpc of the position of the satellite is shown with the red dashed curve, and constitutes a significant fraction of the total SFR in the system around the time of the merger. The satellite is completely disrupted after 2.5 Gyr, but its effects on the SFR are longlasting. The pericentre passages of the satellite are indicated by the black arrows. |
Figure 2 zooms into the gas column densities in the inner parts of the dwarf galaxy around this time. Note again the high gas densities in the tidal tails and how they correlate with the position of the satellite. Also, and as expected, the young star particles trace the motion of the satellite through the disturbed dwarf galaxy (see the blue points in the middle row of Fig. 1). Since these dominate the light, the associated local star-forming regions may well be the analogues of what is seen in XMP galaxies (Filho et al. 2013, 2015).
Figure 3 shows the star formation rate (SFR) during the encounter. The blue curve shows that the total SFR has pronounced peaks during the pericentric passages of the satellite. Interestingly, during the later passages, a significant fraction (4 × 10-3 M⊙ yr-1) of the total star formation takes place in the tidal tail at the location of the satellite (red curve). Subsequently the total SFR increases, due to the gas that is channeled to the centre, and reaches a plateau around a value that is more than a factor 10 higher than for the equivalent dwarf in isolation.
In summary, besides the characteristic starburst, signatures of the merger can be found in the morphology of the old stellar disk, the distribution and morphology of the young stellar population that is formed during the encounter, and in the morphology and kinematics of the gas. The gaseous and stellar disks show distinguishable effects both in the outskirts and in the inner parts. Interestingly, in the simulated system shown here star-forming regions outside the centre pinpoint the location of the merging dark satellite.
4. Quantitative measures of structural properties
Although clear effects can be seen in the simulated dwarf galaxy which are due to the minor merger, it is important to quantify these in order to make comparisons to observations. A variety of quantitative structural descriptions of the morphology and kinematics of galaxies have been put forward in the literature. Morphologically the structure is often characterised by the CAS (concentration, asymmetry, and smoothness; Conselice 2003) and GM (Gini and M20; Lotz et al. 2004) indicators. Additionally for dwarf irregulars and BCDs, the difference in central surface brightness obtained by fitting the inner and outer regions is also used (Hunter & Elmegreen 2006; Papaderos et al. 2008). For XMP galaxies, the often used indicators include differences in the average velocity, and in the position angles of the HI gas and stellar components (Filho et al. 2015, 2013). We apply the morphological indicators to our simulations and present the results in Sect. 4.1, while we focus on the results of the kinematic indicators of the stellar and gas disks in Sect. 4.2.
4.1. Morphological parameters
We estimate the morphological CAS and GM parameters, including modifications by Lelli et al. (2014), Holwerda et al. (2011d), on a grid with initial size of 20 by 20 kpc which is cropped to the regions above a fixed threshold, and a default bin size of 0.2 kpc. The thresholds adopted are close to those reported for observational studies in the literature, NHI> 4 × 1019 cm2 for the surface density of neutral gas and μV< 28 mag/arcsec2 for the V-band magnitude, respectively. This means that in practice each bin holds at least 12 gas particles. For the stars, assuming an average M/L = 0.5, appropriate for the V-band, each bin holds at least 4 stellar particles. The calculations are done on the stellar densities though (in M⊙/ kpc2).
For many of the indicators it is necessary to define the centre of the system. This is done by fitting a 2-dimensional Gaussian to the projected density (although our results are robust to the centering method used), with the threshold values described above. We have tested the effect of different thresholds (NHI> 1019 cm2, NHI> 1020 cm2, μV< 26 mag/arcsec2, and μV< 30 mag/arcsec2), and assumptions regarding the mass-to-light ratios for the newly formed and original stellar populations, and found that when a sufficient area of the system is visible (as smaller systems can mostly disappear below the thresholds) the numerical values for the morphological parameters can change but the trends stay intact.
4.1.1. Definitions
We now describe in detail the different morphological indicators we use in our analysis.
-
Concentration. This describes thedistribution of light over the image:
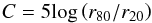 (1)where r80 and r20 are the radii which contain 80% and 20% of the total light (Conselice 2003), where for a purely exponential profile C = 2.7, and for a de Vaucouleurs profile C = 5.2. We note that since the projected surface brightness and gas column densities are computed on a grid, we determine a slightly coarse value of C.
(1)where r80 and r20 are the radii which contain 80% and 20% of the total light (Conselice 2003), where for a purely exponential profile C = 2.7, and for a de Vaucouleurs profile C = 5.2. We note that since the projected surface brightness and gas column densities are computed on a grid, we determine a slightly coarse value of C. -
Asymmetry. This describes the relative difference in intensity when the image is rotated 180 deg:
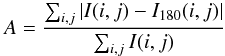 (2)where I(i,j) is the intensity of the pixel (i,j) (Conselice 2003). With this definition, 0 <A< 2.
(2)where I(i,j) is the intensity of the pixel (i,j) (Conselice 2003). With this definition, 0 <A< 2. -
Outer Asymmetry. To give more weight to the outer parts, Lelli et al. (2014) have defined an outer asymmetry parameter as:
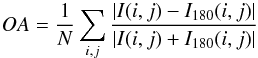 (3)(Lelli et al. 2014), where we define N as the number of the pixels with | I(i,j) + I180(i,j) | > 0. However, this outer asymmetry (OA) indicator is more susceptible to noise. Both for the A and OA parameters the detectability of asymmetries in the outskirts depend greatly on the surface brightness or column density thresholds, especially for low mass and low surface brightness galaxies.
(3)(Lelli et al. 2014), where we define N as the number of the pixels with | I(i,j) + I180(i,j) | > 0. However, this outer asymmetry (OA) indicator is more susceptible to noise. Both for the A and OA parameters the detectability of asymmetries in the outskirts depend greatly on the surface brightness or column density thresholds, especially for low mass and low surface brightness galaxies. -
M20. This parameter is a relative second order moment of the 20% brightest pixels and was originally introduced as an alternative to the concentration parameter:
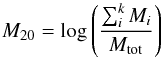 (4)where
(4)where 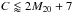 and Mi = Ii [(xi−xc)2 + (yi−yc)2] (Lotz et al. 2004). Its advantage compared to the concentration is that there is no assumption of circular symmetry and that it is more sensitive to phenomena like multiple nuclei that are thought to be common in merging, or post-merging, systems.
and Mi = Ii [(xi−xc)2 + (yi−yc)2] (Lotz et al. 2004). Its advantage compared to the concentration is that there is no assumption of circular symmetry and that it is more sensitive to phenomena like multiple nuclei that are thought to be common in merging, or post-merging, systems. -
Gini coefficient. This statistic originally used in economics to describe the distribution of wealth within a society, was adapted to galaxy morphology by Abraham et al. (2003). It correlates with concentration but does not assume circular symmetry. We use the Gini coefficient based on the second intensity moment weighted by position:
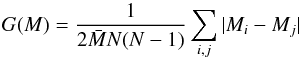 (5)where again Mi = Ii [(xi−xc)2 + (yi−yc)2], and
(5)where again Mi = Ii [(xi−xc)2 + (yi−yc)2], and 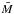 denotes the mean of Mi over all N pixels (Lotz et al. 2004; Holwerda et al. 2011d). G(M) is larger when the brightest pixels are farther from the centre. We only consider the pixels above the threshold in this calculation, which tends to lower the values of G(M) compared to including the background pixels.
denotes the mean of Mi over all N pixels (Lotz et al. 2004; Holwerda et al. 2011d). G(M) is larger when the brightest pixels are farther from the centre. We only consider the pixels above the threshold in this calculation, which tends to lower the values of G(M) compared to including the background pixels. -
Excess central surface brightness: | μ0,HSB−μ0,LSB |. We compute this by taking the difference in the central bin’s surface brightness obtained from exponential fits to the inner and outer parts of the system.
4.1.2. Results
 |
Fig. 4 Distribution of the asymmetry A (red), concentration C (blue), and M20 (green) values for the gaseous disk for 5 random inclinations in time intervals of 0.1 Gyr for the model-A dwarf during the minor merger shown in Fig. 1. These quantities have been normalised to their median (over all inclinations) initial value. The pericentre passages of the satellite are indicated by the black arrows. |
Figure 4 shows the evolution of three morphological indicators: asymmetry, concentration and M20, for the gas distributions in the system shown in Fig. 1, for five different random inclinations. This figure evidences that the indicators have a strong time dependence as the merger occurs, and that each evolves quite differently with time. For example, the asymmetry (in red) increases with time reaching a peak value when the satellite fully merges (with less than 100 particles, 0.1% of the initial satellite mass, of the satellite still gravitationally self-bound), as a consequence of the extended tidal tails clearly seen in Fig. 1, and decreases strongly afterwards. The concentration (in blue) also increases significantly around the time of the merger but it remains high afterwards, as a result of the strong central influx of gas. On the other hand, the M20 (in green) depicts an oscillatory behaviour with peaks that roughtly coincide with each pericentre passage of the satellite. Because M20 is negative, and in this figure it has been normalised to the initial value, these peaks actually imply that the 20% brightest pixels are more centrally concentrated, with the dips indicating high gas densities at larger radii, suggesting that star formation occurs at larger distances. The plateau value at late times reflects the strong centrally concentrated sustained enhancement in gas density. The parameters describing the stellar distribution follow similar trends.
Figure 5 shows the distribution of photometric indicators for all the merger simulations we have carried out with the model-A dwarf. These simulations include a range of different orbits (orbital inclinations and eccentricities), concentrations and masses for the satellite, and varying extents of the gaseous disk. For each simulation the parameters are calculated initially (i.e. in isolation) and at 1, 2, 3, and 4 Gyr and at five random inclination angles for each point in time.
This figure shows that isolated systems (blue for gas, and green for stars) tend to occupy small regions of parameter space, whereas for mergers (red for gas and black for stars) a broad range of parameter values appears to be plausible. At face value, there is no parameter (combination) for which mergers and isolated systems can be fully separated. This might not be unexpected given the time variability of the parameters. Furthermore, cases in which the effects of the merger on the gas and stellar disks are small (e.g. if the satellite sinks in very slowly or has too low mass, or for specific viewing angles), will be hard to disentangle from systems in isolation.
Most isolated systems have low values for concentration, asymmetry, outer asymmetry, and G(M). On the other hand, for the mergers, the asymmetry parameters for both the gas and the stars spread over a much larger range. Also the outliers in M20 correspond to merging systems. The difference in central surface brightness can reach up to to 3 mag/arcsec2 for merging systems, but is smaller than 1 mag/arcsec2 for all isolated cases.
It is therefore easier to demark regions populated by isolated systems in the parameter subspaces plotted in Fig. 5. For example A< 0.38 for the gas, A< 0.3 for the stars, OA< 0.4 for gas and stars, G(M) < 0.4 for the gas, and a relation 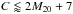 for the gas and
for the gas and 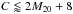 for the stars. These regions are indicated by grey lines in the figure. Interestingly we find G(M) > 0.4 for the HI component of merging systems, while G(M) > 0.6 has been put forward by Holwerda et al. (2011d), and A> 0.4 has been used for the stellar component in major mergers (Conselice 2003).
for the stars. These regions are indicated by grey lines in the figure. Interestingly we find G(M) > 0.4 for the HI component of merging systems, while G(M) > 0.6 has been put forward by Holwerda et al. (2011d), and A> 0.4 has been used for the stellar component in major mergers (Conselice 2003).
In Fig. 5 we have focused on the model-A dwarf, a relatively massive system with M⋆ = 1.4 × 108 M⊙, and demonstrated that it may be possible to disentangle partly mergers from isolated systems. However, for lower mass dwarfs, with initial M⋆ = 4.4−27 × 106 M⊙, the morphological parameters of either isolated and merging systems strongly overlap. Although a 20% merger can cause irregular features in the gas and stellar distributions (ideally resulting in higher asymmetry and outer asymmetry values), often these features are not strong enough (given reasonable thresholds) to be clearly identified by the CAS or GM indicators as being different from irregular gas densities and patchy star formation that may happen in isolation as well. Therefore, such morphological indicators are not useful to identify merger candidates in the case of low mass dwarfs.
 |
Fig. 5 Concentration C, asymmetry A, outer asymmetry OA, M20, Gini(M), and excess central surface brightness | μ0,HSB−μ0,LSB |, for the gas in merger simulations (red) and in isolation (blue), and for the stars in merger simulations (black) and in isolation (green). The simulations shown correspond to the model-A dwarf, and encompass 14 different runs with varying satellite masses, halo concentrations, orbits, and radial extend of the gas disks with respect of the stellar disks (with Rg = Rd, 2Rd, or 4Rd) as described in Sect. 2. For more details on the simulations, see Starkenburg et al. (2016). The dotted, dashed and solid lines indicate regions where the isolated and merger systems are well separated for the stars, for the gas or for both, respectively. |
4.1.3. Comparison to observations
Lotz et al. (2004) have estimated the asymmetry, concentration, and M20 parameters for 22 systems from a sample of isolated dwarf irregular galaxies observed in the B-band by van Zee (2000, 2001). Many of these systems are brighter than those in our simulations and seem to be more clumpy. Although the range of concentrations is similar (2.39 <C< 4.17), the values for M20 are higher (− 1.79 <M20< −0.70) than we find for the stellar components even in isolation. This implies a smoother distribution in the simulations, and this could be the result of an initial smooth set up as well as to the absence of H2 or metal-line cooling in the simulations which could induce a patchier star formation. On the other hand, the asymmetry values of these observed late-type dwarf galaxies are in the range of 0.01 <A< 0.45 (Conselice 2003). We note that the observed sample is not selected as likely merger remnants but because they are faint, gas-rich, and isolated. The asymmetry values are consistent with what we find for the stellar components of isolated systems.
 |
Fig. 6 Average velocity differences between the gas and the stellar disk normalised to the average observed rotational velocity of the gas, difference in position angle between the projected distributions of the gaseous and stellar disks, and between the projected stellar disk and the kinematic axis of the gas, for merger simulations (black) and for systems in isolation (red). The different rows correspond to different ranges of viewing angles. In this figure we have included the model-A dwarf with M⋆ = 1.4 × 108 M⊙ (solid circles), as well as values for systems with M⋆ = 4.4 × 106 M⊙ (dashes) and with M⋆ = 1.1−2.7 × 107 M⊙ (diamonds). |
Lelli et al. (2014) have described the gas outer asymmetry for 18 starburst dwarf galaxies and for a control sample of 17 dwarf irregular galaxies from the VLA-ANGST survey (Ott et al. 2012). The outer asymmetry values of the observed starburst systems are in the range OA = 0.42−0.77, with a median value of ~ 0.6, that is similar to the values we find in our merger simulations. On the other hand, all the simulated dwarf galaxies in isolation have outer asymmetries lower than 0.4, and hence are more comparable to those in the dwarf irregular sample, which typically have OA ~ 0.3−0.5.
From these comparisons, we may conclude that both the stellar and gas components of dwarf irregular galaxies have similar parameter distributions to the simulated dwarfs in isolation. Furthermore, the outer asymmetries seen in the gas in observations of starburst dwarf galaxies agree with those of interacting simulated dwarfs.
4.2. Kinematic parameters
Besides morphology, kinematics can also encode information about past merger events. For example, in our merger simulations the 3D direction of the total angular momentum vectors of the gas and of the stars can differ significantly, and up to 60 deg, while for the isolated simulated dwarfs the difference is < 5 deg. However, angular momenta cannot be directly measured from observations and so we discuss below some of the kinematic indicators that may be used instead.
-
Difference in average velocity between gas and stars. This hasbeen found to be quite large for a number of extremely metal-poor(XMP) galaxies (Filho et al. 2013).In our simulations the average line-of-sight velocities are mass-weighted and computed for all particles within a bin with surfacebrightness or column density above the thresholds. We comparethis difference to the “maximum” rotational velocity defined as
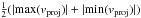 , where these stem from the projected gas velocities within the observed region.
, where these stem from the projected gas velocities within the observed region. -
Misalignment between stars and gas. A relatively straightforward measurement consists in comparing the orientation of the major axis of the surface brightness to that of the projected gas distribution. These are computed by fitting a 2D-Gaussian to these projected distributions. Since measuring velocity fields for stars is challenging, in general it will not be possible to estimate the misalignment between the kinematic axes of stars and of gas. Therefore instead, we compare the orientation of the photometric major axis of the stars to the gas kinematic major axis which can easily determined observationally from HI velocity maps. The gas kinematic major axis is determined in our simulations using the line connecting the maximum and minimum velocities observed. To obtain an estimate of the uncertainty in the orientation we compute the kinematic axis 50 times, each time using two randomly chosen values amongst those ranked in the top 10% as maximum and minimum. From this random sampling we estimate an uncertainty of 9.8 deg, for the merging systems (lower for isolated systems). However, this estimate depends strongly on the amplitude of the velocity field, for example for systems close to face on, the uncertainty can be as large as ~ 54 deg.
Figure 6 presents the results for all our simulated systems. We have separated the analysis according to the projected inclination because this has a significant impact on the ability to separate isolated from merging systems.
For low mass systems (indicated by the dashes), we find the largest average velocity differences between stars and gas in mergers, while for all isolated systems, independently of their mass, Δ = | vgas−vstars | ≲ 0.1vrot, and this appears to be relatively robust to inclination effects. Inspection of the simulations shows that the largest amplitude is reached around the time the satellite reaches the disk, that is around the first pericentre passages.
The velocity differences in our simulations are typically smaller (a few km s-1) than those observed for XMP dwarfs by Filho et al. (2013; these authors disregard offsets smaller than 10 km s-1 because of uncertainties and their expectation that HI velocity dispersions are ~ 10 km s-1 for dwarf galaxies). However, their normalised velocity differences (the difference between the average HI line-of-sight velocity and the average velocity of the stars divided by the full width at half max of the HI line, w50), are 0 ≲ ΔHI/w50 ≲ 1, and hence consistent with those in our simulations.
Comparison of the different rows in Fig. 6 directly shows that the effects of inclination are important. Especially for nearly face-on systems, the separation between mergers and isolated dwarfs is not straightforward. This is entirely due to the large uncertainties in the determination of the orientation of the photometric and kinematic axes. For example, isolated systems have close to circular spatial distributions, so that major and minor axes directions are hard to define. Furthermore, the line-of-sight velocities are typically small in this case and so also the rotation axis is not well constrained. This leads to more scatter in these distributions.
For other inclinations, the isolated systems tend to be clustered around small average velocity differences, and small misalignments. In other words, mergers are clearly more likely to have misaligned stellar photometric and gas photometric or kinematic major axes. The lack of correlation seen in the bottom left panel of Fig. 6 is a result of the misalignment between the photometric and kinematic axes for the gas in the case of mergers.
Figure 7 provides a visual impression of a projection where the gas kinematic and the stellar distribution major axes are misaligned for the system from Fig. 1 at 2 Gyr seen for an inclination of 72.6 deg. The gas column density distribution and stellar surface brightness distribution have roughly the same orientation (the misalignment angle is ~ 2 deg), but for both the orientation in the inner regions is different from that in the outer parts. The gas kinematic axis however has a significantly different major axis orientation, offset by ~ 28 deg.
 |
Fig. 7 Gas line-of-sight velocity field with the stellar surface brightness overplotted as contours for the model-A dwarf system during the minor merger shown in Fig. 1 at t = 2 Gyr, but now for an inclination angle of i = 72.6 deg from face-on. The kinematic axis for the gas (solid line) and the major axis of the surface brightness distribution (dotted line) are misaligned. The fitted profiles to the stellar and gas (dashed line) distributions have similar orientations, and this is because they are dominated by the behaviour in the central regions. |
5. Some intriguing cases
So far we have focused on general trends followed by our morphological and kinematic indicators, and especially on the differences between isolated and merger systems to facilitate the observational identification of dwarf galaxies undergoing a merger when the secondary is not visible, in our case being a dark satellite. We now make a rough comparison to a few intriguing cases from the literature.
The system depicted in Fig. 1 shows a distribution of gas and stars that shares characteristics with the irregular dwarf galaxy IC10: a disturbed gas and stellar distribution with multiple star-forming cores and an extended HI distribution with plums and spurs with velocities that differ from that of the main gas disk (see for example Ashley et al. 2014). On the other hand, the HII regions have a low metallicity (Garnett 1990) which has been suggested as being due to the influx of fresh pristine gas from the environment (Sánchez Almeida et al. 2014). However, another interpretation is possible since as we have seen the merger leads to an extended starburst that is fueled from gas that was originally present in the outskirts of the main system, and which presumably also had a lower metallicity (see also Starkenburg et al. 2016).
Another intriguing system, though for different reasons, is the dwarf irregular galaxy NGC 6822. In addition to a disturbed gas and stellar distribution and a high rate of recent star formation, this system has a star formation core located very far from the centre. This outer star-forming region was proposed to indicate the location of a companion system, also due to a significant velocity offset (de Blok & Walter 2000), but this has been discarded because no older stellar population has been found at that location (Cannon et al. 2012). An interaction with a dark substructure will however display exactly this signature: a star formation region at a large distance without an underlying older population and a metallicity similar to the main system.
6. Conclusions
We have investigated the distribution of quantitative morphological and kinematic parameters (often used to characterise interacting, starburst, or peculiar systems), measured during a minor merger between a dwarf galaxy and a dark satellite. For our system with M⋆> 108 M⊙ the very disturbed morphologies for the gas and stellar distributions induced by the merger are reflected most notably in asymmetry parameters during the merger itself. A post-merger system however stands out the most in its high values for concentration related parameters, such as C, M20 and the Gini coefficient. This is the result of an increase in central stellar and gas density due to gas being driven toward the centre by tidal torques and causing a nuclear starburst episode, which can last several Gyrs.
Kinematic based parameters can be used to identify merger systems, for example via the large differences between average projected gas and stellar velocities. This works particularly well for smaller mass systems (M⋆< 2 × 107 M⊙), for which the morphological indicators fail. Misalignments between the gas kinematic major axis and the stellar surface brightness major axis are also useful, but can only be applied for systems that are far from face-on.
Although we still have to determine the smoking-gun that will allow to determine that an interaction between a dwarf galaxy and a dark satellite has taken place, in our simulations star-forming cores located far from the centre actually seem to pinpoint the location of the satellite. This could be the way to shed light on a missing satellite.
Acknowledgments
We are grateful to Claudio Dalla Vecchia, Joop Schaye, Carlos Vera-Ciro, Alvaro Villalobos and Volker Springel for providing code. A.H. acknowledges financial support from the European Research Council under ERC-StG grant GALACTICA-240271 and The Netherlands Research Organisation NWO for a Vici grant.
References
- Abraham, R. G., van den Bergh, S., & Nair, P. 2003, ApJ, 588, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Ashley, T., Elmegreen, B. G., Johnson, M., et al. 2014, AJ, 148, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Begum, A., Chengalur, J. N., Karachentsev, I. D., Sharina, M. E., & Kaisin, S. S. 2008, MNRAS, 386, 1667 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., O’Leary, E. M., Weisz, D. R., et al. 2012, ApJ, 747, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bershady, M. A., & Jangren, A. 2000, ApJ, 529, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla Vecchia, C., & Schaye, J. 2008, MNRAS, 387, 1431 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Walter, F. 2000, ApJ, 537, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Ekta, B., & Chengalur, J. N. 2010, MNRAS, 403, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Filho, M. E., Winkel, B., Sánchez Almeida, J., et al. 2013, A&A, 558, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filho, M. E., Sánchez Almeida, J., Muñoz-Tuñón, C., et al. 2015, ApJ, 802, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 1990, ApJ, 363, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Garrison-Kimmel, S., Boylan-Kolchin, M., Bullock, J. S., & Lee, K. 2014, MNRAS, 438, 2578 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y. 2000, ApJ, 542, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., Tassis, K., & Kravtsov, A. V. 2009, ApJ, 697, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Helmi, A., Sales, L. V., Starkenburg, E., et al. 2012, ApJ, 758, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., Yepes, G., Gottlöber, S., & Springel, V. 2006, MNRAS, 371, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., Cox, T. J., et al. 2011a, MNRAS, 416, 2426 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., et al. 2011b, MNRAS, 416, 2437 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., et al. 2011c, MNRAS, 416, 2401 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., et al. 2011d, MNRAS, 416, 2415 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., & van Driel, W. 2011e, MNRAS, 416, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., & Heiner, J. S. 2012, MNRAS, 427, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., & Blyth, S.-L. 2013, MNRAS, 435, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Muñoz-Mateos, J.-C., Comerón, S., et al. 2014, ApJ, 781, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2011, MNRAS, 417, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, C.-Y., Naab, T., Walch, S., Glover, S. C. O., & Clark, P. C. 2016, MNRAS, 458, 3528 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1926, ApJ, 64, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., & Elmegreen, B. G. 2006, ApJS, 162, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, T., Wheeler, C., & Bullock, J. S. 2007, MNRAS, 382, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. H., & Cisternas, M. 2015, ApJ, 807, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Freeman, K. C. 2016, ApJ, 817, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014, MNRAS, 445, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y.-S., De Lucia, G., & Helmi, A. 2010, MNRAS, 401, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R. 2010, A&A, 521, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M. L. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Cuartas, J. C., Macciò, A. V., Gottlöber, S., & Dutton, A. A. 2011, MNRAS, 411, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T., Gao, L., & Theuns, T. 2008, MNRAS, 390, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, J., Stilp, A. M., Warren, S. R., et al. 2012, AJ, 144, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P., Guseva, N. G., Izotov, Y. I., & Fricke, K. J. 2008, A&A, 491, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paudel, S., Duc, P. A., & Ree, C. H. 2015, AJ, 149, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Elmegreen, B. G., Muñoz-Tuñón, C., & Elmegreen, D. M. 2014, A&ARv, 22, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Sawala, T., Frenk, C. S., Crain, R. A., et al. 2013, MNRAS, 431, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Sawala, T., Frenk, C. S., Fattahi, A., et al. 2015, MNRAS, 448, 2941 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., & Dalla Vecchia, C. 2008, MNRAS, 383, 1210 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaye, J., Dalla Vecchia, C., Booth, C. M., et al. 2010, MNRAS, 402, 1536 [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Starkenburg, T. K., & Helmi, A. 2015, A&A, 575, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starkenburg, T. K., Helmi, A., & Sales, L. V. 2016, A&A, 587, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, C. L., Brinks, E., Grashuis, R. M., & Skillman, E. D. 1995, ApJS, 99, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., & Jiang, F. 2014, MNRAS, submitted [arXiv:1403.6835] [Google Scholar]
- van den Bosch, F. C., Tormen, G., & Giocoli, C. 2005, MNRAS, 359, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L. 2000, AJ, 119, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L. 2001, AJ, 121, 2003 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the model-A dwarf galaxy with Rg = 4Rd, merging with a 20% mass ratio dark satellite with c = 25 on a co-planar relatively radial orbit (the intermediate orbit in Table 2). All figures show an inclined view of the disk, 60 deg from face-on. The top row shows the gas in the disk above a certain column density (contours at 0.4, 1, 4, and 10 × 1020 N cm-2) with the star-forming gas highlighted in green (see colourbar for SFR values). The central row panels show the old stars in red, and those newly formed in blue, along with two surface brightness contours of 25 mag/arcsec2 and 28 mag/arcsec2, obtained assuming an M/L = 0.5 for all stellar particles. The bottom panels show the gas contours with the gas velocity maps. In all panels the satellite is shown in grey (5% of the particles are plotted), with the purple cross denoting its centre of mass. The insets indicate the values of asymmetry, concentration and difference in average velocity between stars and gas computed as described in Sect. 4. |
| In the text | |
 |
Fig. 2 Evolution of the inner parts of the dwarf galaxy shown in Fig. 1 around the time the satellite merges with the host. The threshold is 0.4 × 1020 N cm-2 and the contours indicate 1, 4, and 10 × 1020 N cm-2; see colourbar for the relative values. |
| In the text | |
 |
Fig. 3 Blue curve: evolution of the star formation rate of the dwarf galaxy shown in Figs. 1 and 2. The black curve is for the same model-A dwarf run in isolation. The star formation rate in the tidal tail within 1 kpc of the position of the satellite is shown with the red dashed curve, and constitutes a significant fraction of the total SFR in the system around the time of the merger. The satellite is completely disrupted after 2.5 Gyr, but its effects on the SFR are longlasting. The pericentre passages of the satellite are indicated by the black arrows. |
| In the text | |
 |
Fig. 4 Distribution of the asymmetry A (red), concentration C (blue), and M20 (green) values for the gaseous disk for 5 random inclinations in time intervals of 0.1 Gyr for the model-A dwarf during the minor merger shown in Fig. 1. These quantities have been normalised to their median (over all inclinations) initial value. The pericentre passages of the satellite are indicated by the black arrows. |
| In the text | |
 |
Fig. 5 Concentration C, asymmetry A, outer asymmetry OA, M20, Gini(M), and excess central surface brightness | μ0,HSB−μ0,LSB |, for the gas in merger simulations (red) and in isolation (blue), and for the stars in merger simulations (black) and in isolation (green). The simulations shown correspond to the model-A dwarf, and encompass 14 different runs with varying satellite masses, halo concentrations, orbits, and radial extend of the gas disks with respect of the stellar disks (with Rg = Rd, 2Rd, or 4Rd) as described in Sect. 2. For more details on the simulations, see Starkenburg et al. (2016). The dotted, dashed and solid lines indicate regions where the isolated and merger systems are well separated for the stars, for the gas or for both, respectively. |
| In the text | |
 |
Fig. 6 Average velocity differences between the gas and the stellar disk normalised to the average observed rotational velocity of the gas, difference in position angle between the projected distributions of the gaseous and stellar disks, and between the projected stellar disk and the kinematic axis of the gas, for merger simulations (black) and for systems in isolation (red). The different rows correspond to different ranges of viewing angles. In this figure we have included the model-A dwarf with M⋆ = 1.4 × 108 M⊙ (solid circles), as well as values for systems with M⋆ = 4.4 × 106 M⊙ (dashes) and with M⋆ = 1.1−2.7 × 107 M⊙ (diamonds). |
| In the text | |
 |
Fig. 7 Gas line-of-sight velocity field with the stellar surface brightness overplotted as contours for the model-A dwarf system during the minor merger shown in Fig. 1 at t = 2 Gyr, but now for an inclination angle of i = 72.6 deg from face-on. The kinematic axis for the gas (solid line) and the major axis of the surface brightness distribution (dotted line) are misaligned. The fitted profiles to the stellar and gas (dashed line) distributions have similar orientations, and this is because they are dominated by the behaviour in the central regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


