| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527956 | |
| Published online | 08 November 2016 | |
Multiwavelength campaign on Mrk 509
XV. Global modeling of the broad emission lines in the optical, UV, and X-ray bands
1 SRON, Netherlands Institute for Space Research, Sorbonnelaan, 2, 3584 CA Utrecht, The Netherlands
e-mail: e.costantini@sron.nl
2 Anton Pannekoek Institute, University of Amsterdam, Postbus 94249, 1090 GE Amsterdam, The Netherlands
3 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
4 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
5 Dipartimento di Matematica e Fisica, Universitá degli Studi Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
6 Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey, RH5 6NT, UK
7 INAF-IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
8 Max-Planck Institüt für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching bei München, Germany
9 XMM-Newton Science Operations Centre, ESAC, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
10 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
11 CNRS, IPAG, 38000 Grenoble, France
12 ISDC Data Centre for Astrophysics, Astronomical Observatory of the University of Geneva, 16 Ch. d’Écogia, 1290 Versoix, Switzerland
13 Instituto de Astronomía, Universidad Católica del Norte, 0610 Avenida Angamos, Antofagasta, Chile
14 Department of Physics, Virginia Tech, Blacksburg, VA 24061, USA
Received: 14 December 2015
Accepted: 17 June 2016
Aims. We model the broad emission lines present in the optical, UV, and X-ray spectra of Mrk 509, a bright type 1 Seyfert galaxy. The broad lines were simultaneously observed during a large multiwavelength campaign, using the XMM-Newton-OM for the optical lines, HST-COS for the UV lines, and XMM-Newton-RGS and Epic for the X-ray lines. We also used FUSE archival data for the broad lines observed in the far-ultraviolet. The goal is to find a physical connection among the lines measured at different wavelengths and to determine the size and the distance from the central source of the emitting gas components.
Methods. We used the Locally Optimally emission Cloud (LOC) model which interprets the emissivity of the broad line region (BLR) as regulated by power law distributions of both gas density and distances from the central source.
Results. We find that one LOC component cannot model all the lines simultaneously. In particular, we find that the X-ray and UV lines may likely originate in the more internal part of the AGN at radii in the range ~5 × 1014−3 × 1017 cm, while the optical lines and part of the UV lines may likely originate farther out at radii ~3 × 1017−3 × 1018 cm. These two gas components are parametrized by a radial distribution of the luminosities with a slope γ of ~1.15 and ~1.10, respectively, both of them covering at least 60% of the source. This simple parametrization points to a structured broad line region where the higher ionized emission comes from closer in, while the emission of the low-ionization lines is more concentrated in the outskirts of the broad line region.
Key words: galaxies: individual: Mrk 509 / galaxies: Seyfert / quasars: emission lines / X-rays: galaxies
© ESO, 2016
1. Introduction
The optical-UV spectra of Seyfert 1 galaxies and quasars are characterized by strong and broad emission lines, which are believed to be produced by gas photoionized by the central source. The broad line region (BLR) gas was initially thought to be in the form of a set of clouds (e.g., Krolik et al. 1981). However, the confinement of these clouds was problematic (Mathews & Ferland 1987); in addition, an accurate analysis of the smoothness of the broad line wings revealed that in fact the gas could not be in the form of discrete clouds, but rather a continuous distribution of gas (Arav et al. 1998). Another hypothesis is that the gas is ejected from the accretion disk outskirts in the form of a wind (e.g., Murray & Chiang 1995; Bottorff et al. 1997; Elvis 2000; Czerny & Hryniewicz 2011). Finally, the gas reservoir could be provided by disrupted stars in the vicinity of the black hole (Baldwin et al. 2003).
Extensive observation of this phenomenon, through the reverberation mapping technique, has led to the conclusion that the BLR is extended over a large area and that the radius of the BLR scales with the square root of the ionizing luminosity (Peterson 1993). The BLR does not have a homogeneous, isotropic distribution (e.g., Decarli et al. 2008). Several studies have pointed out that higher ionized lines (represented by C iv) are incompatible with an origin in the same region where the bulk of Hβ is produced (Sulentic et al. 2000). Different approaches to this problem have lead to divergent results. A flat disk structure would preferentially emit C iv, while Hβ would be produced in a vertically extended region farther from the central source (Sulentic et al. 2000; Decarli et al. 2008; Goad et al. 2012). Other interpretations propose a different scenario where the gas emitting Hβ has a flat geometry near the accretion disk, while C iv would be emitted in an extended region (Kollatschny & Zetzl 2013, and references therein). By virtue of the tight correlation found between the BLR size and the AGN luminosity (Bentz et al. 2013), the BLR gas could also arise from the accretion disk itself and generate a failed wind. The confinement of such cloud motion, involving the outflow and the inflow of gas, would be set by the dust sublimation radius (Czerny & Hryniewicz 2011; Galianni & Horne 2013). Studies of gas dynamics within the BLR indeed point to a complex motion of the gas (Pancoast et al. 2012) where the matter may sometimes infall towards the black hole (Pancoast et al. 2014; Gaskell & Goosmann 2013). Observationally, the broad lines centroids often show shifts (up to hundreds of km s-1) with respect to the systemic velocity of the AGN. Higher ionization lines (like C ivλ1548) show in general more pronounced blueshifts with respect to lower ionization lines (Peterson 1997). This also points to a stratified medium where the illumination of the cloud is related to the ionization of the clouds (Peterson et al. 2004). A way to model the BLR emission without a priori assumptions on its origin is the Locally Optimally emitting Cloud model (LOC; Baldwin et al. 1995), which describes the total emission of a line as a function of the density and the distance of the gas from the central source (see Korista et al. 1997, for a review). This model has been successfully applied to the broad lines detected in the UV of NGC 5548, for example (e.g., Korista & Goad 2000).
Emission from the BLR can in principle extend from the optical-UV up to the X-ray band. With the advent of XMM-Newton and Chandra, relatively weak but significant broad emission lines have been detected in the soft X-ray band. Often these lines display a symmetric profile, suggesting an origin far from the accretion disk where relativistic effects would instead distort the line profile (e.g., Steenbrugge et al. 2009; Fabian et al. 2009). The most prominent X-ray lines with a non-relativistic profile are found at the energy of the O vii triplet and the O viii Lyα (e.g., Boller et al. 2007; Steenbrugge et al. 2009; Longinotti et al. 2010; Ponti et al. 2010; Costantini et al. 2007,hereafter C07).
An extension of the LOC model that adds the X-ray band in the modeling has been applied to Mrk 279 (C07). In this case, the luminosities of the soft X-ray emission lines (C vi, N vii, O vii, O viii, and Ne ix) were clearly predicted by the LOC model, suggesting that the bulk of the X-ray lines could possibly arise up to three times closer to the black hole than the UV lines.
A contribution of the BLR to the Fe Kα line at 6.4 keV has often been debated. A comparison between the full width half maximum (FWHM) of the Hβ line at 4861 Å and the FWHM of the narrow component of the Fe Kα line as measured by Chandra-HETG did not reveal any correlation, as would have been expected if the lines originated from the same gas (Nandra 2006). However, on a specific source, namely the liner NGC 7213 where no hard X-ray reflection was observed, the Fe Kα line and the Hβ line are consistent with having the same FWHM (Bianchi et al. 2008). On the other hand, as seen above, X-ray lines may originate in different regions of the BLR. Therefore a direct comparison between the FWHM of Fe Kα and Hβ do not prove or disprove that Fe Kα is also produced in the BLR. A further extension of the LOC model to the 6.4 keV region showed, in the case of Mrk 279, that the BLR emission contributed to 17% of the total Fe Kα emission at most, suggesting instead that reflection either from the disk or from the torus had to be the dominant emitter of that line (Costantini et al. 2010).
Mrk 509 was the subject of a large multiwavelength campaign carried out in 2009 (Kaastra et al. 2011). The source was an ideal laboratory for the study of the ionized gas outflowing from the source (Detmers et al. 2011; Ebrero et al. 2011; Kaastra et al. 2012; Kriss et al. 2011; Steenbrugge et al. 2011; Arav et al. 2012). The broad-band continuum was investigated in Mehdipour et al. (2011), Petrucci et al. (2013) and Boissay et al. (2014). The Fe Kα long-term variability was investigated in Ponti et al. (2013). In this paper of the series we investigate the BLR emission through the emission lines simultaneously detected by different instruments from the optical to the X-ray.
The paper is organized as follows. In Sect. 2 the data are described. In Sect. 3 we describe the application of the LOC model to the data. The discussion is in Sect. 4, followed by the conclusions in Sect. 5.
We adopt a redshift of 0.034397 (Huchra et al. 1993). The cosmological parameters used are H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. The errors are calculated at 1σ significance, obtained using the χ2 statistical method.
Main parameters of the broad line components used in this analysis.
2. Data
Here we make use of the analyses already presented in the other papers in this series on Mrk 509. In particular the XMM-Newton-OM optical lines are taken from Mehdipour et al. (2011), the COS and FUSE broad emission line fluxes are taken from Kriss et al. (2011, hereafter K11). The X-ray broad line data are from Detmers et al. (2011), Ebrero et al. (2011, using RGS and LETGS ), and Ponti et al. (2013, using PN).
The lines that we use in our modeling are listed in Table 1.
2.1. X-ray broad lines
The XMM-Newton-RGS spectrum shows evidence of broad emission at energies consistent with the transitions of the main He-like (O vii and Ne ix triplets) and H-like (C vi, N vii, O viii) lines (see Table 2 and Fig. 3 in Detmers et al. 2011). The FWHM of non-blended lines was about 4000 km s-1. For the triplets, neither the FWHM nor the individual-line fluxes could be disentangled. In particular, only for the resonance lines has a significant detection been found. We therefore took the FWHM of the resonance line as a reference value and derived the upper limits of the intercombination and forbidden lines for both the O vii and Ne ix triplets. In Table 1 we list the intrinsic line luminosities.
The luminosity of the Fe Kα line (Table 1) was measured by the EPIC-PN instrument. The line is formed by a constant, narrow component plus a broad, smoothly variable component (Ponti et al. 2013). We do not consider here the narrow component whose FWHM has not been resolved by XMM-Newton. This component is not variable on long time scales and may be caused by reflection from regions distant from the black hole, like the molecular torus. The broad and variable component of the Fe Kα line has a FWHM of about 15 000−30 000 km s-1, which probably partly arises from the BLR (Ponti et al. 2013). The EPIC-PN spectrum of Mrk 509 also shows hints of highly ionized lines from Fe xxv and Fe xxvi. These are too ionized to be produced in the BLR (e.g., Costantini et al. 2010), but they are likely to come from a hot inner part of the molecular torus (Costantini et al. 2010; Ponti et al. 2013). Thus, we do not include these lines in this analysis.
2.2. UV broad lines
In the HST-COS modeling of the emission lines, more than one Gaussian component is necessary to fit the data (see Tables 3−6 and Fig. 4 in K11). The most prominent lines (i.e., Lyα and C iv) show as many as four distinct components. A first narrow component has a FWHM of about 300 km s-1, then an intermediate component with FHWM of about 1000−3000 km s-1 and a broad component with 4000−5000 km s-1 are also present in the fit. Finally, a very broad component with FWHM of about 9000−10 000 km s-1 is present for the most prominent lines (Table 1). In this study we ignore the narrow component (FWHM ~ 300 km s-1), which is unlikely to be produced in the BLR but should instead come from the narrow line region (NLR). Owing to the complex and extended morphology of the narrow-line emitting gas, the distance of the NLR in this source is uncertain (Phillips et al. 1983; Fischer et al. 2015). From the width of the narrow lines, the nominal virial distance ranges between 6 and 13 pc, depending on the black hole mass estimate (see Sect. 4.3). We note that with respect to Table 3 in K11, we summed the doublet luminosities as in many cases they are partially blended with each other. We corrected the line fluxes for the Galactic extinction (E(B−V) = 0.057) following the extinction law in Cardelli et al. (1989). The errors listed in Table 1 are discussed below (Sect. 2.4).
We also used the archival FUSE data, which offer the flux measurements of shorter wavelength lines. The drawback of this approach is that the FUSE observations were taken about ten years before our campaign (in 1999–2000). In this time interval the source’s flux and emission profiles might have changed significantly. In this analysis we chose the 1999 observation (Kriss et al. 2000), as on that occasion the flux was comparable to the HST-COS data in the overlapping band and the FWHM most resemble the present data. In Table 1 we present the FUSE line luminosities used in this paper. Also in this case we summed doublets and the blended lines.
2.3. Optical broad lines
The optical monitor (OM) data were collected at the same time as the X-ray data presented in this paper. The data reduction and analysis has been presented by Mehdipour et al. (2011) and includes correction for Galactic absorption and subtraction of the stellar contribution from the host galaxy from both the continuum and the emission lines. The optical grism data, covering the 3000–6000 Å wavelength range, displayed clear emission lines of the Balmer series (see Table 3 and Fig. 4 in Mehdipour et al. 2011). For the Hα line two line components could be disentangled into a narrow and unresolved component with a flux of ~3.3 × 10-13 erg cm-2 s-1, and a broader component with a FWHM of ~4300 km s-1. For the other lines in the series, the narrow component could not be disentangled. In order to obtain an estimate of the flux of the broad component alone, we simply scaled the flux of the Hα-narrow component for the line ratio of the other lines in the Balmer series (e.g., Rafanelli & Schulz 1991). We then subtracted the estimated narrow-line flux from the total flux measured by OM, resulting in a relatively small correction with respect to the total line flux. The intrinsic luminosities of the broad lines are listed in Table 1.
2.4. Notes on the uncertainties
The uncertainties associated with the measurements are quite heterogeneous, reflecting the performance of the different instruments. In the UV data, the statistical errors on the fluxes are extremely small (2–4%, K11). However, the line luminosities are affected by additional systematic uncertainties owing to the derivation of specific line components, namely those coming from the BLR, among a blend of different emission lines with different broadening, fluxes, and velocity shifts. For instance, the C iv line doublet at 1548 Å is the sum of as many as seven components that suffer significant blending (K11). As seen in Sect. 2.2, only for the strongest lines could three broad line widths be disentangled. However, for the lower flux lines this decomposition could not be done, leaving room for additional uncertainties on the line flux of the broad components. Therefore, we assigned more realistic error bars to the UV data. We associated an error of 20% to the fluxes, which is roughly based on the ratio between the narrow and the broad components of the C iv doublet. We also left out Si ii (λλ1260,1526 Å) and N iv] from the final modeling as in the original COS data (see K11) these lines are easily confused with the continuum and are therefore affected by a much larger uncertainty that is more difficult to quantify than the one provided by the statistical error.
The line fluxes and widths observed by FUSE in 1999 may also be different from 2009. In K11, they estimated that the continuum flux was 34–55% lower and the emission lines could have been affected. In order to take into account the possible line variability, to the FUSE detections we assigned an error of 40% on the flux. We also left out the N iii from the fit. Because N iii is a weak and shallow line, only a very broad component is reported, which may be contaminated by the continuum emission (Kriss et al. 2000).
For the O vii triplet, in the RGS band, we summed up the values of the line fluxes, but formally retaining the percentage error on the best-measured line, as upper limits were also present (Detmers et al. 2011). We considered C vi and N vii as upper limits because the detection was not more significant than 2.5σ in the RGS analysis. However, we used these two points as additional constraints to the fit, using them as an upper limit value on the model.
For the iron broad component detected at 6.4 keV in the EPIC-PN spectrum, which we consider in this work, we also summed the Fe Kα line with the Fe Kβ line (about 10% of the flux of the Fe Kα) as we do in the model.
3. Data modeling
3.1. The LOC model
In analogy with previous works (Costantini et al. 2007, 2010), we interpret the broad emission features using a global model. In the LOC model, the emerging emission spectrum is not dominated by the details of the clouds (or more generally gas layers), but rather by their global distribution in hydrogen number density, n, and radial distance from the source, r (Baldwin et al. 1995). The gas distribution is indeed described by the integrated luminosity of every emission line, weighted by a power law distribution for n and r: 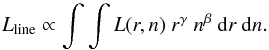 (1)The power law index of n has been reported to be typically consistent with unity in the LOC analysis of quasars (Baldwin 1997). A steeper (flatter) index for the density distribution would enhance regions of the BLR where the density is too low (high) to efficiently produce lines (Korista & Goad 2000). Here we assume the index β to be unity. Following C07, the density ranges between 108−12.5 cm-3. This is the range where the line emission is effective (Korista et al. 1997). The radius ranges between 1014.75−18.5 cm to include the possible X-ray emission from the lines in addition to the UV and optical emission (C07). The gas hydrogen column density was fixed to 1023 cm-2 where most of the emission should occur (Korista et al. 1997; Korista & Goad 2000). Furthermore, the emission spectrum is not significantly sensitive to the column density in the range 1022−24 cm-2 (Korista & Goad 2000). The grid of parameters has been constructed using Cloudy (ver. 10.00), last described in Ferland et al. (2013). For each point of the grid, L(r,n) is calculated and then integrated according to Eq. (1).
(1)The power law index of n has been reported to be typically consistent with unity in the LOC analysis of quasars (Baldwin 1997). A steeper (flatter) index for the density distribution would enhance regions of the BLR where the density is too low (high) to efficiently produce lines (Korista & Goad 2000). Here we assume the index β to be unity. Following C07, the density ranges between 108−12.5 cm-3. This is the range where the line emission is effective (Korista et al. 1997). The radius ranges between 1014.75−18.5 cm to include the possible X-ray emission from the lines in addition to the UV and optical emission (C07). The gas hydrogen column density was fixed to 1023 cm-2 where most of the emission should occur (Korista et al. 1997; Korista & Goad 2000). Furthermore, the emission spectrum is not significantly sensitive to the column density in the range 1022−24 cm-2 (Korista & Goad 2000). The grid of parameters has been constructed using Cloudy (ver. 10.00), last described in Ferland et al. (2013). For each point of the grid, L(r,n) is calculated and then integrated according to Eq. (1).
The emitted spectrum is dependent on the spectral energy distribution (SED) of the source. In this case we benefited from the simultaneous instrument coverage from optical (with OM) to UV (with HST-COS) and X-rays (EPIC-PN and INTEGRAL). As a baseline we took the SED averaged over the 40-day XMM-Newton monitoring campaign (labeled standard SED in Fig. 3 in Kaastra et al. 2011), taking care that the SED is truncated at infrared frequencies (no-IR case in that figure). Although the accretion disk must have some longer wavelength emission, most of the infrared part (especially the far-IR bump) is likely to emerge from outer parts of the system, like the molecular torus. An overestimate of the infra-red radiation would mean adding free-free heating to the process. This effect becomes important at longer wavelengths as it is proportional to n2/ν2, where ν is the photon frequency. Free-free heating significantly alters the line ratios, for example of Lyα to C iv or O vi (Ferland et al. 2002). To avoid this effect, we truncated the SED at about 4 μm. During the XMM-Newton campaign the light curve of both the hard (2–10 keV) and the soft (0.5–2 keV) X-ray flux increased gradually to a factor of 1.3 and decreased by about the same factor in about one month (Kaastra et al. 2011). The OM photometric points followed the same trend (see, e.g., Fig. 1 in Mehdipour et al. 2011). Variations of the continuum fitting parameters were not dramatic (Mehdipour et al. 2011; Petrucci et al. 2013). Therefore at first order, the SED did not change significantly in shape while at the same time the normalization did vary.
3.2. LOC fitting
The best-fit distribution of the gas in the black hole system is dependent on many parameters using the LOC model. The radial distribution and the covering factor of the gas, which are the free parameters in the fit, in turn depend on pre-determined parameters, namely the SED, the metallicity (which we assume to be solar for the moment; see Sect. 4.1), and the inner and outer radii of the gas. Moreover, broad lines measured in an energy range covering more than three decades in energy are likely to arise from gas distributed over a large region with inhomogeneous characteristics.
 |
Fig. 1 LOC fitting considering the sum of the broad and very broad line components consistently provides a better description of the data for any other choice of parameters. From top to bottom: combination of intermediate+broad, broad+very broad, intermediate+broad+very broad, and broad lines alone. In this example, we only show the fit to the UV data. |
 |
Fig. 2 LOC fits over individual bands: X-rays (dashed line), UV (solid line), and optical band (dash-dotted line). |
In fitting our model, we considered four different combinations of UV line-widths: intermediate+broad, broad+very broad, intermediate+broad+very broad, and broad lines alone (Table 1). We also selected six bands over which to perform the χ2 test on the line flux modeling: optical, X-ray, UV, optical+UV, X-ray+UV, and X-ray+UV+optical. The individual bands are defined by the instruments used (Table 1). We used an array of six possible inner radii ranging from log r = 14.75 to 17.7 cm (the actual outer radius being log r = 18.5 cm) to construct the model. Considering all the combinations of parameters, we obtain 144 different fitting runs. Whenever a limited number of lines are fitted (e.g., the UV band lines alone), the model is extrapolated to the adjacent bands to inspect the contribution of the best-fit model to the other lines. Not all the runs are sensitive to all the parameters, of course. For instance, a run that fits only the X-ray band will be insensitive to any UV line widths. Free parameters of the fit are the covering factor CV of the gas and the slope γ of the radial distribution. The covering factor (Ω/4π, where Ω is the opening angle) measured by the LOC is the fraction of the gas as seen by the source. The value of CV is constrained to lie in the range 0.05−0.6 based on the range of past estimates for the BLR obtained with different techniques (see Sect. 4.3). In the following we describe the dependence of the fit on the different parameters based on the goodness of fit.
In Fig. 1 we show the comparison among best fits with different line widths for the UV lines. Considering the same band (the UV-only here), the inclusion of the intermediate component (Sect. 2.2) systematically slightly worsens the fit. For simplicity, in the following we describe the sum of the broad and very broad components (broad+very broad), as they provide a slightly better fit, although the other combinations were also always checked in parallel.
We show the fits in the different wavelength bands in Fig. 2. In Table 2 the best-fit parameters are shown for each combination of bands using the full range of radii. We note that the UV data certainly dominate the fit by virtue of the larger number of data points with a relatively smaller error bar. The global fit, however, does not completely explain the high- and low-energy ends of the data. A fit based on the X-ray data underpredicts the UV and optical data, perhaps suggesting the presence of an additional component. On the other hand, the fit based on the optical band, nicely describes both the optical and the C iv UV lines, albeit with a large overestimate of the rest of the UV and X-ray lines.
The LOC fitting also depends on the inner radius over which the radial gas distribution is calculated. We fitted the data for a choice of six inner radii, separated by roughly half a decade. In Fig. 3 a fit considering all the data is plotted for a selection of inner radii. We see that while the UV band is only marginally affected by the choice of inner radius, this parameter can make a difference for the optical and X-ray bands.
The application of a single component of the LOC model with some tunable parameters does not totally explain the data. In the following we explore other effects that may play a role in the line emission.
 |
Fig. 3 LOC fits over the whole spectral band (X-ray+UV+optical) with three representative inner radii. The X-ray band is best fitted for smaller inner radii, while the optical band is better described if larger radii are used. |
Results of the LOC fitting considering different spectral bands.
3.3. Extinction in the BLR
As seen above, the application of the LOC model to Mrk 509 points out that the optical lines are systematically underestimated. A possible solution is to include extinction in the BLR itself. The UV/optical continuum Mrk 509 is not signi- ficantly reddened (Osterbrock 1977). However, the dust may be associated only with the line emission region in such a way that the continuum we measure would be unaffected (Osterbrock & Ferland 2006). In principle, the He ii(1640 Å)/ He ii(4686 Å) ratio would be an indicator of reddening intrinsic to the BLR (e.g., Osterbrock & Ferland 2006). In practice, both lines are severely blended with neighboring lines and with the wing of higher flux lines, namely C iv for He ii(1640 Å) and Hβ for He ii(4686 Å) (Bottorff et al. 2002). In our case, the observed line ratio is very low (~1.7) when compared to the theoretical value derived from the LOC model (6–8; Bottorff et al. 2002). This line ratio would imply an extinction E(B−V) = 0.18 (Eq. (4) in Annibali et al. 2010), when a Small Magellanic Cloud (SMC) extinction curve, possibly more appropriate for AGN, is used (Hopkins et al. 2004; Willott 2005). Knowing the uncertainties (i.e., line blending) associated with our He ii measurements, we took this value as the upper limit of a series of E(B−V) values to be applied to our lines. Namely, we tested E(B−V) = (0.18,0.15,0.10,0.075,0.05,0.025). We then corrected the observed optical and UV fluxes accordingly (Annibali et al. 2010). For the lines observed by FUSE (Table 1), we extrapolated the known SMC extinction curve with a λ4 function to reach those wavelengths. The extinction in the X-rays was simply estimated using the E(B−V)−NH relation provided in Predehl & Schmitt (1995), considering a SMC-like selective to total extinction ratio RV of 2.93 (Pei 1992).
When only the UV lines are modeled, the χ2 method chooses lower values of the BLR extinction, with a final 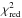 of 6.1 (d.o.f. = 8) for E(B−V) = 0.025. The effect of the BLR extinction is relatively modest in the X-ray band and mainly affects the O vii lines. However, any value of the BLR extinction largely overcorrects the Balmer series lines. Therefore, when the optical lines are included in the model, the resulting fit becomes even worse (
of 6.1 (d.o.f. = 8) for E(B−V) = 0.025. The effect of the BLR extinction is relatively modest in the X-ray band and mainly affects the O vii lines. However, any value of the BLR extinction largely overcorrects the Balmer series lines. Therefore, when the optical lines are included in the model, the resulting fit becomes even worse (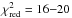 , for 18 d.o.f.).
, for 18 d.o.f.).
3.4. Two-component LOC model
Just one LOC component does not provide a fully satisfactory fit. This is not surprising, given the wide range of ionization potentials of the lines and so we attempt here to test a two-component model. As before, for each of the two components we fit all the combinations of line widths (as in Fig. 1). We first considered the whole range of radii (Model 1 in Table 3). Then we made the inner radius (as defined in Sect. 3.2) of both components vary (Model 2 in Table 3). Finally, we took into account the different emissivity depending on the size of the region by also varying the outer radius. To do this, we divided the radial range into four regions (starting at log r = 14.75,15.53,16.56,17.47) in order to have roughly an order of magnitude difference between two adjacent radii. Then, for each component we considered all the combinations of the adjacent regions (or single regions). Therefore, we have a total of ten options for the size of each component of the gas (Model 3 in Table 3). We note that for each run the inner and outer radii were fixed parameters. We fitted the whole band (X-ray, UV, optical: XUVO) for the two LOC components. The fit is driven by the UV band where the uncertainties on the data are the smallest. We note that the slope of the power law is dependent on the covering factor, as flatter slopes (γ< 1.1) systematically correspond to very small covering factors (CV< 0.05). Conversely, the upper limit we set for the covering factor (CV = 0.6) corresponds to steeper radial slopes (see also Korista & Goad 2000). The covering factor has the effect of regulating the predicted line luminosities. A steeper radial distribution would enhance the lines at smaller radii where the gas illumination is stronger. Therefore, a larger CV would be required to reduce the line luminosities. On the contrary, a flatter slope would lower the contribution of the highly illuminated region, while the outer radii are enhanced. However, the radiation field weakens with the distance, therefore a smaller CV is necessary to adapt the predicted fluxes to the real data. In the last line of Table 3 we report the reduced χ2. The reduced χ2 never falls below ~2, even for the better-fitting models. This is especially due to the outlying data points, namely Si iv, C iv, and He ii. The exclusion of Fe Kα did not resolve the problem as this line has a larger uncertainty with respect to the UV lines (see Fig. 4, Model 3). As expected, the more sensitive lines were the optical and the X-ray lines. A highly ionized component, extending down to log r< 14.7 cm is necessary in order to reproduce the O viii and Ne ix lines in the X-ray. All the optical lines and part of the C iv line are best fitted by adding a component with a larger inner radius.
Best-fit parameters for a two-component model and different emitting regions.
 |
Fig. 4 Upper panel: LOC fit with two components, acting in different regions near the AGN (Model 3 in Table 3). X-ray data are best fitted by a component near the black hole, while the optical data are better fitted by a component farther away. Lower panel: residuals to the fit. |
4. Discussion
4.1. Abundances and the influence of the SED
Abundances in the BLR should be either solar or super-solar. The metal enrichment should come from episodic starburst activity (Romano et al. 2002). The N v line is often taken as an abundance indicator in AGN since it is a product of the CNO cycle in massive stars. Using the broad component ratios in our data for N v/C iv and N v/He ii, the diagnostic plots of Hamann et al. (2002) suggest abundances in Mrk 509 of 1 <Z< 3 (see Steenbrugge et al. 2011, for the limitations in determining abundances in the BLR). In this analysis we considered a SED with solar abundances, as defined in Cloudy. We therefore also tested the fits presented above using a metallicity 3 times solar. The fits obtained are systematically worse (Δχ2 = 2−7 for the same number of degrees of freedom). This suggests that the abundances are close to solar.
The present HST-COS data were taken 20 days after the last XMM-Newton pointing (Kaastra et al. 2011) as the closing measurements of the campaign, which lasted in total about 100 days. Spectral coverage simultaneous to HST-COS was provided instead by both Chandra-LETGS (Ebrero et al. 2011) and Swift-XRT (Mehdipour et al. 2011). We used the average SED recorded by the XMM-Newton instruments 20–60 days before the HST-COS observation. The choice of SED is very important in the BLR modeling, as different lines respond to the continuum variations on different time scales (Korista & Goad 2000; Peterson et al. 2004). Reverberation mapping studies of Mrk 509 report that the delay of the Hβ with respect to the continuum is very long (about 80 days for Hβ, Carone et al. 1996; Peterson et al. 2004). However, higher ionization lines respond more quickly to the continuum variations. Taking as a reference the average Hβ/C iv delay ratio for NGC 5548 (Peterson et al. 2004), for which – contrary to Mrk 509 – a large set of line measurements is available, we obtain that the C iv line in Mrk 509 should respond in approximately 40 days. A similar (but shorter) time delay should apply to the Lyα line (Korista & Goad 2000). This delay falls in the time interval covered by the XMM-Newton data. Therefore, our choice of SED should be appropriate for the modeling of at least the main UV lines. Variability of the X-ray broad lines has been reported on time scales of years (Costantini et al. 2010); however, no short-term studies are available. We expect that the X-ray broad lines should respond promptly to the continuum variations, as they may be located up to three times closer to the black hole with respect to the UV lines (C07). During the XMM-Newton campaign the flux changed by 30% at most, with a minimal change in spectral shape (Sect. 3.1). The used SED should therefore represent what the BLR gas sees for the X-ray band. However, for the optical lines the used SED might be too luminous as we observed an increase in luminosity of about 30% during the XMM-Newton campaign and, as seen above, the time-delay of the optical lines may be large.
4.2. UV-optical emitting region
The LOC model has been extensively used to model the UV and optical lines of AGN (e.g., Korista et al. 1997). In this study we find that a single radial distribution of the gas over the whole range of radii and applied to the UV band would have a slope γ ~ 1, as prescribed by the standard LOC model (Table 2). The covering factor is unconstrained as it hits the lower limit that we imposed on this parameter. As in the case of Mrk 279 (C07), the C iv line is a systematic outlier. This line may obey mechanisms other than pure gravitation (e.g., inflows or outflows) or may arise in a geometrically different region than the optical lines (e.g., Goad et al. 2012,and references therein). Finally, Lyα and C vi are found in some sources to respond on a slightly different time scale to the continuum variation. In the case of NGC 5548, this difference in response is on the order of 20 days (Korista & Goad 2000,Sect. 4.1). This may account for some of the mismatch between the two lines in our fit. As tested above (Sect. 3.3), the extinction in the BLR of Mrk 509 must be negligible; therefore, the discrepancy with the model cannot be ascribed to dust in the emitting region. The ionization of the BLR follows the rules of photoionization. In particular for a given UV-emitting ion (e.g., C iv, Lyα, O vi, as detailed in Korista et al. 1997), the ionization parameter remains constant throughout the region (dashed lines in Fig. 5). We note that for lower ionization lines (i.e., the Balmer lines, Fig. 5, right panel), density effects come into play in addition to pure recombination (Kwan & Krolik 1979; Osterbrock & Ferland 2006) and the ionization parameter does not follow the emission contour (Korista et al. 1997). This model does not require a universal ionization parameter because of the assumption of the stratified nature of the gas. A pressure confined gas model, which may also allow for a range of ionization parameters in a stratified medium, would also predict – given a bolometric luminosity – a gas hydrogen density as a function of radius (Eq. (21) in Baskin et al. 2014). This prediction is drawn in Fig. 5 (magenta solid line), using Lbol ~ 3L1350 Å (Kaspi et al. 2005), where L1350 Å has been extrapolated from the average SED of Mrk 509 (Kaastra et al. 2011). This density prediction is not too far off; however, it overestimates the optimal emitting region density of the higher ionization ions (see an example in the left panel of Fig. 5), while it would match the Balmer lines emitting region (right panel).
 |
Fig. 5 Contour profiles of O vi and Hα as a function of density and distance, here using a radial slope γ of 0.10. The dashed lines indicates constant ionization parameters as detailed in the legend. The solid magenta line follows the density prediction of the pressure confined emission model of Baskin et al. (2014). |
4.3. Size and gas distribution of the BLR
Several arguments point to a natural outer boundary for the BLR, which should be intuitively given by the dust sublimation radius (Suganuma et al. 2006; Landt et al. 2014). For Mrk 509, this radius corresponds to 3.6 × 1018 cm (Mor & Netzer 2012).
The maximum radius of our LOC model is 3 × 1018 cm. An expansion of the BLR outer radius to 7.6 × 1018 cm does not improve the fit. This is a natural consequence of the LOC model construction. For radial distributions with slopes γ ≳ 1 the line emissivity of some major lines (O vi, C iv) already drops at 1018 cm (C07, Baskin et al. 2014). Therefore, our fit is consistent with a confined BLR region, possibly within the sublimation radius.
The radius of the BLR has been found to scale with the UV luminosity. If we take the C iv line as a reference, 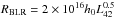 (C iv), where h0 is the Hubble constant in units of 100 km s-1 and L42 is the C iv luminosity in units of 1042 erg s-1 (Peterson 1997). For Mrk 509, the radius of the BLR based on this equation is ~2.6 × 1017 cm. Using instead the known relation between the size of the Hβ emitting region and the luminosity at 5100 Å, for Mrk 509 we obtain RHβ ~ 1.2 × 1017 cm (Bentz et al. 2013).
(C iv), where h0 is the Hubble constant in units of 100 km s-1 and L42 is the C iv luminosity in units of 1042 erg s-1 (Peterson 1997). For Mrk 509, the radius of the BLR based on this equation is ~2.6 × 1017 cm. Using instead the known relation between the size of the Hβ emitting region and the luminosity at 5100 Å, for Mrk 509 we obtain RHβ ~ 1.2 × 1017 cm (Bentz et al. 2013).
In our fit the location of the UV emitting lines is consistent with these estimates, as a large fraction of the UV line luminosity could come from radii ≥1017 cm (Models 2, 3 in Table 3, Fig. 4), although UV lines are efficiently emitted in a large range of radii (Fig. 3 and C07). Assuming Keplerian motion, the FWHM of our lines imply that the very broad lines (FWHM ~ 9000−10 000 km s-1) are located at approximatively 2.5−5 × 1016 cm, depending on the mass of the black hole: 1.43 × 108 M⊙ (Peterson et al. 2004) or 3 × 108 M⊙ (Mehdipour et al. 2011). For the broad lines (FWHM ~ 4000−5000 km s-1) the distance would then be 1.3−2.5 × 1017 cm, consistent with our results for the UV-optical component. Finally, for the intermediate lines (FWHM ~ 1000−3000 km s-1) the calculated distance is 2−4 × 1018 cm. The location of the line emitting gas is stratified; therefore, these single-radius estimates are only taken as a reference. The very broad and broad lines are well within the estimated radius for the BLR. The so-called intermediate-line region could possibly bridge the BLR and the NLR (Baldwin 1997).
In interpreting the BLR emission, we tested a two-component model characterized not only by different radial distributions and covering factors, but also by different physical sizes and inner/outer radii of the emitting plasmas.
Our fits are not completely satisfying because important outliers, like C iv, are present. However, the best fit points to the interesting possibility that the optical region and part of the UV region originate at larger radii (starting at 3 × 1017 cm), while the X-ray region and some fraction of the UV-emission regions would have an inner radius smaller than 6 × 1014 cm (as also found in C07) and a larger extension up to about the beginning of the optical BLR (Sect. 3.4). This would point to a scenario in which the optical lines, including the Hβ, would come from the outer region of the BLR. Such a span in distance between the optical and the X-ray lines would also imply for the latter a faster response-time to any continuum variation. Such an effect has not been systematically studied, although a strong flux variation of the O vii broad line has been observed before (Costantini et al. 2010). The inability to find a good fit with the present model, which assumes a simple plane parallel geometry, could suggest a more complex geometry. For instance, an inflated geometry (“bowl geometry”; Goad et al. 2012) for the outer region, possibly confined by a dusty torus has recently been suggested using different approaches (Goad et al. 2012; Pancoast et al. 2012; Gaskell & Goosmann 2013).
The covering factor was set in our fits to be in the range 0.05−0.6. The lower limit has been chosen following early studies on the relation between the equivalent width of the Lyα and the covering factor (0.05–0.1, e.g., Carswell & Ferland 1988). However, subsequent studies – using the LOC model technique among others – have pointed out that the covering factor can be larger: from 0.30 (e.g., Maiolino et al. 2001, and references therein) up to 0.5−0.6 (Korista & Goad 2000). The covering factor here is the fraction of the gas as seen by the source. This is equal to the observer’s line of sight covering factor only if a spherical distribution of the gas is assumed. A more flattened geometry would then reconcile a large covering factor with the fact that absorption lines from the broad line region are in general not observed in the optical-UV band. In our fits the covering factor is unconstrained. However, large covering factors were preferentially found when a two-component model was applied, especially when the inner and outer radius were allowed to vary for both components. The measured high covering fraction, necessary to explain the line luminosities of the two components, would then point to a gas with non-spherical geometry. As these two components are along our line of sight, one may be below the other, therefore the sum of the two CV is likely above one as long as the individual covering factors do not entirely cover the source (i.e., CV< 1).
Despite the extensive exploration of the impact of different parameters on the modeling, our analysis also underlines that a simple parametrization may be inadequate to explain the complexity of the BLR. Reasons for not reaching a better fit include minor effects, such as possible different responses of Lyα and C iv to continuum variations, non-simultaneity of the FUSE data, and inhomogeneous information on the broad-band line profiles. The CV may not be a simple step function, but the clouds and gas layers may experience a differential covering factor for instance as a function of the distance or line ionization. A major effect would be the complex dynamics and geometry of the BLR, which needs more sophisticated models to be explained.
4.4. The iron line at 6.4 keV
In this paper we include the 6.4 keV Fe Kα line, observed simultaneously with the other soft X-ray, UV, and optical lines. The narrow and non-variable component, probably produced in distant regions, was not considered in the fit. We find that the derived emission of the BLR contribution to the broad Fe Kα line component is around 30%, if we use a two-component model. The emission would happen at a range of distances from the source, although at small radii (log r ≳ 14.75 cm) the emission is enhanced (Fig. 3). We note that fortuitously, a single-component fit, based on the optical lines, would provide a perfect fit to the Fe Kα line (Fig. 2). However, such a gas would produce both UV and soft X-ray line fluxes at least a factor of 6 larger than observed. A modest contribution (~17%) of the BLR to the iron line has been also reported in Mrk 279, using non simultaneous UV and X-ray data (Costantini et al. 2010).
5. Conclusions
In this paper we attempted to find a global explanation of the structure of the gas emitting broad lines in Mrk 509, from the optical to the X-ray band using a simple parametrization of the BLR. This study was possible thanks to the simultaneous and long observations of XMM-Newton and HST-COS.
We find that lines broader than FWHM> 4000 km s-1 contribute to the bulk of the BLR emission. A two-component LOC model provides a statistically better, but not conclusive, description of the data. The two components are characterized by similar radial emissivity distribution (γ ~ 1.10−1.15), but different size and distance from the central source. The X-rays and part of the UV radiation come from an inner and extended region (r ~ 5 × 1014−3 × 1017 cm), while the optical and part of the UV gas would be located at the outskirts of the BLR (r ~ 3 × 1017−3 × 1018 cm). This picture appears to be in agreement with recent results on the geometry of the BLR, where the Hβ line is located away from the ionizing source. However, more sophisticated parametrizations are needed in order to have a definitive answer.
The Fe Kα broader line cannot completely be accounted for by emission from the BLR gas. The contribution of the BLR is around 30% for this line.
Acknowledgments
The Netherlands Institute for Space Research is supported financially by NWO, the Netherlands Organization for Scientific Research. XMM-Newton is an ESA science missions with instruments and contributions directly funded by ESA Members States and the USA (NASA). We thank the referee, E. Behar, for his useful comments. We also thank L. di Gesu for commenting on the manuscript and G. Ferland and F. Annibali for the discussion on extinction in the BLR and host galaxy. G.P. acknowledges support of the Bundsministerium für Wirtschaft und Technologie/Deutsches Zentrum für Luft-und Raumfahrt (BMWI/DLR, FKZ 50 OR 1408). P.-O.P. and S.B. acknowledge financial support from the CNES and Franco-Italian CNRS/INAF PICS. G.K. was supported by NASA through grants for HST program number 12022 from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555.
References
- Annibali, F., Bressan, A., Rampazzo, R., et al. 2010, A&A, 519, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arav, N., Barlow, T. A., Laor, A., et al. 1998, MNRAS, 297, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Arav, N., Edmonds, D., Borguet, B., et al. 2012, A&A, 544, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A. 1997, IAU Colloq. 159: Emission Lines in Active Galaxies: New Methods and Techniques, 113, 80 [NASA ADS] [Google Scholar]
- Baldwin, J., Ferland, G., Korista, K., & Verner, D. 1995, ApJ, 455, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Korista, K. T., et al. 2003, ApJ, 582, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Baskin, A., Laor, A., & Stern, J. 2014, MNRAS, 438, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., La Franca, F., Matt, G., et al. 2008, MNRAS, 389, L52 [NASA ADS] [Google Scholar]
- Boissay, R., Paltani, S., Ponti, G., et al. 2014, A&A, 567, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Balestra, I., & Kollatschny, W. 2007, A&A, 465, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottorff, M., Korista, K. T., Shlosman, I., & Blandford, R. D. 1997, ApJ, 479, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Bottorff, M. C., Baldwin, J. A., Ferland, G. J., Ferguson, J. W., & Korista, K. T. 2002, ApJ, 581, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, T. E., Peterson, B. M., Bechtold, J., et al. 1996, ApJ, 471, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Carswell, R. F., & Ferland, G. J. 1988, MNRAS, 235, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Costantini, E., Kaastra, J. S., Arav, N., et al. 2007, A&A, 461, 121 (C07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costantini, E., Kaastra, J. S., Korista, K., et al. 2010, A&A, 512, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2011, A&A, 525, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decarli, R., Labita, M., Treves, A., & Falomo, R. 2008, MNRAS, 387, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Detmers, R. G., Kaastra, J. S., Steenbrugge, K. C., et al. 2011, A&A, 534, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebrero, J., Kriss, G. A., Kaastra, J. S., et al. 2011, A&A, 534, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Zoghbi, A., Ross, R. R., et al. 2009, Nature, 459, 540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ferland, G. J., Martin, P. G., van Hoof, P. A. M., & Weingartner, J. C. 2002, X-ray Spectroscopy of AGN with Chandra and XMM-Newton, 103 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., et al. 2015, ApJ, 799, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Galianni, P., & Horne, K. 2013, MNRAS, 435, 3122 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., & Goosmann, R. W. 2013, ApJ, 769, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Goad, M. R., Korista, K. T., & Ruff, A. J. 2012, MNRAS, 426, 3086 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., Korista, K. T., Ferland, G. J., Warner, C., & Baldwin, J. 2002, ApJ, 564, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Strauss, M. A., Hall, P. B., et al. 2004, AJ, 128, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Geller, M. J., Clemens, C. M., et al. 1993, VizieR Online Data Catalog: VII/164 [Google Scholar]
- Kaastra, J. S., Petrucci, P.-O., Cappi, M., et al. 2011, A&A, 534, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Detmers, R. G., Mehdipour, M., et al. 2012, A&A, 539, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2013, A&A, 558, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korista, K. T., & Goad, M. R. 2000, ApJ, 536, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Korista, K., Baldwin, J., Ferland, G., & Verner, D. 1997, ApJS, 108, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. A., Green, R. F., Brotherton, M., et al. 2000, ApJ, 538, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. A., Arav, N., Kaastra, J. S., et al. 2011, A&A, 534, A41 (K11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krolik, J. H., McKee, C. F., & Tarter, C. B. 1981, ApJ, 249, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Kwan, J., & Krolik, J. H. 1979, ApJ, 233, L91 [Google Scholar]
- Landt, H., Ward, M. J., Elvis, M., & Karovska, M. 2014, MNRAS, 439, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Longinotti, A. L., Costantini, E., Petrucci, P. O., et al. 2010, A&A, 510, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Salvati, M., Marconi, A., & Antonucci, R. R. J. 2001, A&A, 375, 25 [Google Scholar]
- Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mor, R., & Netzer, H. 2012, MNRAS, 420, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Chiang, J. 1995, ApJ, 454, L105 [NASA ADS] [Google Scholar]
- Nandra, K. 2006, MNRAS, 368, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1977, ApJ, 215, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Sausalito: University Science Books) [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2012, ApJ, 754, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2014, MNRAS, 445, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1997, An introduction to active galactic nuclei (Cambridge, New York: Cambridge University Press), 238 [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, M. M., Baldwin, J. A., Atwood, B., & Carswell, R. F. 1983, ApJ, 274, 558 [Google Scholar]
- Ponti, G., Gallo, L. C., Miuiutti, G., et al. 2010, MNRAS, 406, 2591 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Cappi, M., Costantini, E., et al. 2013, A&A, 549, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Rafanelli, P., & Schulz, H. 1991, Astron. Nachr., 312, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Silva, L., Matteucci, F., & Danese, L. 2002, MNRAS, 334, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbrugge, K. C., Fenovčík, M., Kaastra, J. S., et al. 2009, A&A, 496, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbrugge, K. C., Kaastra, J. S., Detmers, R. G., et al. 2011, A&A, 534, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suganuma, M., Yoshii, Y., Kobayashi, Y., et al. 2006, ApJ, 639, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000, ARA&A, 38, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J. 2005, ApJ, 627, L101 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 LOC fitting considering the sum of the broad and very broad line components consistently provides a better description of the data for any other choice of parameters. From top to bottom: combination of intermediate+broad, broad+very broad, intermediate+broad+very broad, and broad lines alone. In this example, we only show the fit to the UV data. |
| In the text | |
 |
Fig. 2 LOC fits over individual bands: X-rays (dashed line), UV (solid line), and optical band (dash-dotted line). |
| In the text | |
 |
Fig. 3 LOC fits over the whole spectral band (X-ray+UV+optical) with three representative inner radii. The X-ray band is best fitted for smaller inner radii, while the optical band is better described if larger radii are used. |
| In the text | |
 |
Fig. 4 Upper panel: LOC fit with two components, acting in different regions near the AGN (Model 3 in Table 3). X-ray data are best fitted by a component near the black hole, while the optical data are better fitted by a component farther away. Lower panel: residuals to the fit. |
| In the text | |
 |
Fig. 5 Contour profiles of O vi and Hα as a function of density and distance, here using a radial slope γ of 0.10. The dashed lines indicates constant ionization parameters as detailed in the legend. The solid magenta line follows the density prediction of the pressure confined emission model of Baskin et al. (2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


