| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629233 | |
| Published online | 20 October 2016 | |
The age-mass-metallicity-activity relation for solar-type stars: comparisons with asteroseismology and the NGC 188 open cluster
1 Universidade Federal do Rio de Janeiro, Observatório do Valongo, Ladeira do Pedro Antonio 43, CEP: 20080-090, Rio de Janeiro, RJ, Brazil
e-mail: diego@astro.ufrj.br; gustavo@astro.ufrj.br
2 Astrophysics Research Institute, Liverpool John Moores University, Liverpool, L3 5RF, UK
e-mail: R.P.Schiavon@ljmu.ac.uk
Received: 3 July 2016
Accepted: 21 September 2016
Context. The Mount Wilson Ca ii index log is the accepted standard metric of calibration for the chromospheric activity versus age relation for FGK stars. Recent results claim its inability to discern activity levels, and thus ages, for stars older than ~2 Gyr, which would severely hamper its application to date disk stars older than the Sun.
is the accepted standard metric of calibration for the chromospheric activity versus age relation for FGK stars. Recent results claim its inability to discern activity levels, and thus ages, for stars older than ~2 Gyr, which would severely hamper its application to date disk stars older than the Sun.
Aims. We present a new activity-age calibration of the Mt. Wilson index that explicitly takes mass and [Fe/H] biases into account; these biases are implicit in samples of stars selected to have precise ages, which have so far not been appreciated.
Methods. We show that these selection biases tend to blur the activity-age relation for large age ranges. We calibrate the Mt. Wilson index for a sample of field FGK stars with precise ages, covering a wide range of mass and [Fe/H] , augmented with data from the Pleiades, Hyades, M 67 clusters, and the Ursa Major moving group.
Results. We further test the calibration with extensive new Gemini/GMOS log ()R'HK) data of the old, solar [Fe/H] clusters, M 67 and NGC 188. The observed NGC 188 activity level is clearly lower than M 67. We correctly recover the isochronal age of both clusters and establish the viability of deriving usable chromospheric ages for solar-type stars up to at least ~6 Gyr, where average errors are ~0.14 dex provided that we explicitly account for the mass and [Fe/H] dimensions. We test our calibration against asteroseismological ages, finding excellent correlation (ρ = + 0.89). We show that our calibration improves the chromospheric age determination for a wide range of ages, masses, and metallicities in comparison to previous age-activity relations.
Key words: stars: late-type / stars: activity / stars: chromospheres / open clusters and associations: individual: M 67 / open clusters and associations: individual: NGC 188
© ESO, 2016
1. Introduction
Stellar ages are fundamental parameters in our understanding of the chemo-dynamical evolution of the Galaxy and other stellar systems as well as exoplanetary systems. Ages, which are very difficult to gauge, are usually only estimated through methods optimized to restricted classes of stars since these are indirect parameters inferred from the time evolution of a range of observational quantities that do not uniquely characterize this range. Strong spectral lines are useful indicators of stellar chromospheric activity (CA) that is physically linked to the efficiency of angular momentum evolution. The stellar rotation and CA in single main-sequence stars decay monotonically with time, under the action of the torque produced by the magnetized stellar wind, as it is a potential indicator of age (Soderblom et al. 1991). The Mount Wilson (MW) project (Baliunas et al. 1995) has been monitoring the widely used S index, which is the ratio of the flux in the line cores of the Ca ii H & K lines and two nearby continuum regions; this S index can be converted into the log index, which is defined as the absolute line excess flux (line flux − photospheric flux) normalized to the bolometic flux (Linsky et al. 1979; Noyes et al. 1984). The log
index, which is defined as the absolute line excess flux (line flux − photospheric flux) normalized to the bolometic flux (Linsky et al. 1979; Noyes et al. 1984). The log is the standard metric in the literature to retrieve stellar ages through CA-age relations (hereafter CAR, e.g., Mamajek & Hillenbrand 2008, hereafter MH08).
is the standard metric in the literature to retrieve stellar ages through CA-age relations (hereafter CAR, e.g., Mamajek & Hillenbrand 2008, hereafter MH08).
Recent claims that the evolution of CA fluxes cannot be traced beyond ~2 Gyr (Pace 2013) imply that the derivation of CA ages is severely hampered for most of the age dispersion of the Galactic disk, thereby negating its usefulness as a tool to investigate Galactic evolution. Here we analyze the presence, in the CA-age relation, of mass and metallicity ([ Fe / H ]) biases that are implicit in conventional methods of selecting solar-type stars with precise isochronal ages. We show that these biases have masked structural complexity in the CAR and present a new calibration explicitly relating age, activity, mass, and [ Fe / H ]. We test this calibration against asteroseismological ages and new Gemini data on the log indexes of the M 67 and NGC 188 clusters (ages 4.0 and 6.0 Gyr, respectively). As an extension of MH08 CAR, we provide the activity distribution expected for 6 Gyr solar metallicity stars anchored on 49 NGC 188 members (16× the M08 sample for NGC 188), constraining the activity average and dispersion beyond the solar age.
indexes of the M 67 and NGC 188 clusters (ages 4.0 and 6.0 Gyr, respectively). As an extension of MH08 CAR, we provide the activity distribution expected for 6 Gyr solar metallicity stars anchored on 49 NGC 188 members (16× the M08 sample for NGC 188), constraining the activity average and dispersion beyond the solar age.
2. Biases in the age-chromospheric activity relation
The authors of MH08 pointed out a slight positive trend of CA with color index (B − V) in the sense that hotter (more massive) stars appear less active than cooler ones; yet it was not clear that this trend extended beyond the Hyades age. Also, it was proposed that the M 67 cluster presented the opposite trend of that observed in younger clusters, suggesting that evolutionary effects on color indices might affect the gauging of CA levels. Indeed, as solar-type stars age away from the Zero Age Main Sequence (ZAMS), Teff swings in the Hertzsprung-Russell (HR) diagram are bound to introduce biases into the flux calibration of the CAR. The inclusion by MH08 of an explicit color correction in their CAR hints at the presence of such degeneracy, possibly making standard age-activity calibrations not uniquely adequate for different levels CA.
However, even though mass and/or color terms may be explicitly incorporated into the CAR, a deeper reason for these corrections lies in their effects in the convective efficiency, which establishes the theoretical connection between chromospheric and rotational evolution and is usually represented by the Rossby number (Barnes & Kim 2010). Noyes et al. (1984) found a strong correlation between the Rossby number (defined as the ratio of the rotational period and the convective overturn time τC) and log in FGK stars. Empirically, metallicity is expected to affect τC, since stars that are more metal rich have deeper convection zones and thus longer τC, other parameters being equal. This structural connection was already hinted at by Lyra & Porto de Mello (2005) in their analysis of Hα fluxes and ages. However, such structural effects cannot be separated for the case of the Ca ii lines from the intrinsic observed profile which, unlike Hα (Fuhrmann et al. 1993), responds directly to metallicity. Thus metal-poor stars have shallower Ca ii profiles that mimic high levels of chromospheric fill-in, and thus appear more active and younger than metal-rich stars at a given Teff, or mass (Rocha-Pinto & Maciel 1998).
in FGK stars. Empirically, metallicity is expected to affect τC, since stars that are more metal rich have deeper convection zones and thus longer τC, other parameters being equal. This structural connection was already hinted at by Lyra & Porto de Mello (2005) in their analysis of Hα fluxes and ages. However, such structural effects cannot be separated for the case of the Ca ii lines from the intrinsic observed profile which, unlike Hα (Fuhrmann et al. 1993), responds directly to metallicity. Thus metal-poor stars have shallower Ca ii profiles that mimic high levels of chromospheric fill-in, and thus appear more active and younger than metal-rich stars at a given Teff, or mass (Rocha-Pinto & Maciel 1998).
The selection of stars with precise ages automatically packs these biases into stellar samples. Pace (2013, hereafter P13) selected stars with small age uncertainties (<2 Gyr or σage/age <30%), from the Geneva-Copenhagen survey (GCS) of photometric atmospheric parameters (Casagrande et al. 2011), in addition to data from clusters spanning from 0.5 to 6 Gyr. Pace crossed this sample with log indices and reported the absence of CA evolution beyond ~2 Gyr. The difficulty in building a sample of stars with precise ages is not only dependent on the quality of the atmospheric parameters. Demanding precise ages implies that most stars in such a sample are more massive than the Sun because of the need for a sizable detachment from the ZAMS to enable a reliable age determination. Besides, such a sample necessarily has a large metallicity range: young stars are preferably more metal rich because of the age-metallicity relation, and possess deeper H & K profiles, thereby mimicking a more subdued CA. Also, in order for young stars to make their way into a sample of objects with precise ages they tend to be farther from the ZAMS and thus more massive. A higher mass decreases their convective efficiency (other parameters being equal) and they appear less active. These two effects combine to lower their CA level as deduced from log
indices and reported the absence of CA evolution beyond ~2 Gyr. The difficulty in building a sample of stars with precise ages is not only dependent on the quality of the atmospheric parameters. Demanding precise ages implies that most stars in such a sample are more massive than the Sun because of the need for a sizable detachment from the ZAMS to enable a reliable age determination. Besides, such a sample necessarily has a large metallicity range: young stars are preferably more metal rich because of the age-metallicity relation, and possess deeper H & K profiles, thereby mimicking a more subdued CA. Also, in order for young stars to make their way into a sample of objects with precise ages they tend to be farther from the ZAMS and thus more massive. A higher mass decreases their convective efficiency (other parameters being equal) and they appear less active. These two effects combine to lower their CA level as deduced from log . Conversely, older stars are mostly less massive as a result of age selection effects and appear more active owing to a heightened convective efficiency. They also tend to be more metal poor, and their shallower H & K profiles mimic a higher level of CA. The net result is to strongly blur the range of log
. Conversely, older stars are mostly less massive as a result of age selection effects and appear more active owing to a heightened convective efficiency. They also tend to be more metal poor, and their shallower H & K profiles mimic a higher level of CA. The net result is to strongly blur the range of log between young and old stars, thus masking the intrinsic structure in the age-CA plane.
between young and old stars, thus masking the intrinsic structure in the age-CA plane.
3. The age-mass-metallicity-activity relation
We present a new version of the CAR by explicitly considering its mass and metallicity dimensions. Our sample is composed of field stars selected from Adibekyan et al. (2012); in addition to field stars, we further selected objects from the Pleiades (0.1 Gyr) and Hyades (0.6 Gyr) clusters and the Ursa Major (0.3 Gyr) moving group from Lorenzo-Oliveira et al. (2016). Field stars were required to have age errors ≤ 25%. From Giampapa et al. (2006, hereafter G06) we took data for the 4.0 Gyr (see Sect. 3) M 67 cluster. The sample totals 222 stars spanning the 0.75 <M/M⊙< 1.40 and −0.75 <[Fe/H]<+0.45 ranges. The log values come from a variety of sources, where the main sources are Arriagada (2011), Duncan et al. (1991), Gray et al. (2003), Gray et al. (2006), Henry et al. (1996), Isaacson & Fischer (2010), Jenkins et al. (2011), Schröder et al. (2009), and Wright et al. (2004). Ages and masses were inferred from the Yale isochrones (Kim et al. 2002).
values come from a variety of sources, where the main sources are Arriagada (2011), Duncan et al. (1991), Gray et al. (2003), Gray et al. (2006), Henry et al. (1996), Isaacson & Fischer (2010), Jenkins et al. (2011), Schröder et al. (2009), and Wright et al. (2004). Ages and masses were inferred from the Yale isochrones (Kim et al. 2002).
 |
Fig. 1 Upper panels: comparison of asteroseismological with chromospheric ages from our calibration (black circles) and MH08 (red squares) for a sample of stars spanning a wide interval in age, mass, and metallicity. The dashed line is the 1:1 relation. Lower panels: difference between the age estimates Δlog (t) (log (tastero) − log (tchrom)) as a function of [Fe/H] . The dashed lines stand for ±1σ chromospheric age uncertainty. |
The age-mass-metallicity-activity relation (hereafter AMMAR) was derived from an iterated, re-weighted least-squares regression, yielding ![\begin{eqnarray} \label{eq:mod_crom_comp} \log(t)\!& =&\! \beta_0 + \beta_1\log(R^\prime_{\rm HK}) + \beta_2{\rm [Fe/H]}\notag\\ && +~~ \beta_3\log(M/M_\odot) + \beta_4\log(R^\prime_{\rm HK})^2, \end{eqnarray}](/articles/aa/full_html/2016/10/aa29233-16/aa29233-16-eq22.png) (1)where β0 = −56.01 ± 4.74; β1 = −25.81 ± 1.97; β2 = −0.44 ± 0.06; β3 = −1.26 ± 0.25; and β4 = −2.53 ± 0.21. The standard deviation of the relation is ~0.14 dex in log(age in years). Activity is the most significant variable in the regression (>12σ) but mass and metallicity terms also show a strong statistical significance with 5σ and 8σ, respectively − a crucial feature for the retrieval of reliable ages for old and/or evolved stars. As stars evolve to lower levels of
(1)where β0 = −56.01 ± 4.74; β1 = −25.81 ± 1.97; β2 = −0.44 ± 0.06; β3 = −1.26 ± 0.25; and β4 = −2.53 ± 0.21. The standard deviation of the relation is ~0.14 dex in log(age in years). Activity is the most significant variable in the regression (>12σ) but mass and metallicity terms also show a strong statistical significance with 5σ and 8σ, respectively − a crucial feature for the retrieval of reliable ages for old and/or evolved stars. As stars evolve to lower levels of  , these terms increase in their importance to explain the variance of the age variable. We have compared our chromospheric ages (Eq. (1)) and those derived from the age-color-activity relation (hereafter ACAR) from MH08 to asteroseismological ages in a sample of 26 stars spanning 0.80 <M/M⊙< 1.57 and −0.80 <[Fe/H]<+0.46 with ages from 0.4 to over 10.0 Gyr, including the Sun (Vauclair et al. 2008; Tang & Gai 2011; Mosser et al. 2008; Yıldız et al. 2003, and others). The ACAR from MH08 combines the CA-Rossby number and girochronology relations that are anchored on τC (Noyes et al. 1984) and (B − V) color index (van Leeuwen 2007). In the upper diagrams of Fig. 1 we plot the results of 104 Monte Carlo simulations of ages derived from Eq. (1) (black circles) and MH08 ACAR (red squares) by spanning 4σ intervals around each star’s mass/color, metallicity, and log
, these terms increase in their importance to explain the variance of the age variable. We have compared our chromospheric ages (Eq. (1)) and those derived from the age-color-activity relation (hereafter ACAR) from MH08 to asteroseismological ages in a sample of 26 stars spanning 0.80 <M/M⊙< 1.57 and −0.80 <[Fe/H]<+0.46 with ages from 0.4 to over 10.0 Gyr, including the Sun (Vauclair et al. 2008; Tang & Gai 2011; Mosser et al. 2008; Yıldız et al. 2003, and others). The ACAR from MH08 combines the CA-Rossby number and girochronology relations that are anchored on τC (Noyes et al. 1984) and (B − V) color index (van Leeuwen 2007). In the upper diagrams of Fig. 1 we plot the results of 104 Monte Carlo simulations of ages derived from Eq. (1) (black circles) and MH08 ACAR (red squares) by spanning 4σ intervals around each star’s mass/color, metallicity, and log values. The differences between asteroseismological and chromospheric ages, as a function of [Fe/H] , are shown in the lower panels. The agreement of the AMMAR with the asteroseismological ages is excellent: the standard deviation is σ ≈ 0.14 dex and the linear correlation coefficient is ρ ≈ 0.89 (p-value = 10-7%). The MH08 ACAR shows higher scatter, weaker correlation (σ = 0.3 dex, ρ = + 0.5), and strong residual [Fe/H] trend in the sense that higher metallicity stars tend to have higher chromospheric ages in comparison to asteroseismology. In addition, we tested the MH08 CA-age relation against the asteroseismological ages and, in comparison to ACAR, we found a similar correlation and residual [Fe/H] trend. Using the solar log
values. The differences between asteroseismological and chromospheric ages, as a function of [Fe/H] , are shown in the lower panels. The agreement of the AMMAR with the asteroseismological ages is excellent: the standard deviation is σ ≈ 0.14 dex and the linear correlation coefficient is ρ ≈ 0.89 (p-value = 10-7%). The MH08 ACAR shows higher scatter, weaker correlation (σ = 0.3 dex, ρ = + 0.5), and strong residual [Fe/H] trend in the sense that higher metallicity stars tend to have higher chromospheric ages in comparison to asteroseismology. In addition, we tested the MH08 CA-age relation against the asteroseismological ages and, in comparison to ACAR, we found a similar correlation and residual [Fe/H] trend. Using the solar log = −4.906 (MH08), Eq. (1) yields 5.2 Gyr in good agreement with its canonical age, within 15%. These results reinforce the need for considering a new approach to obtain consistent chromospheric ages for a wide range of masses, metallicities and activity levels.
= −4.906 (MH08), Eq. (1) yields 5.2 Gyr in good agreement with its canonical age, within 15%. These results reinforce the need for considering a new approach to obtain consistent chromospheric ages for a wide range of masses, metallicities and activity levels.
A suitable test for the AMMAR is to try to reproduce the lack of an activity evolution scenario observed by P13. In this respect, we selected stars from the GCS, using their Padova mass and age estimates (16%, 50%, and 84% confidence intervals) and metallicity data, following the same sample selection procedure as in P13. We kept only dwarfs and separated them in bins of 1 Gyr. We computed their mass, age, and metallicity distributions plus the dispersions in each age bin and calculated the related log distribution inverting Eq. (1), from which we obtained mean log
distribution inverting Eq. (1), from which we obtained mean log and dispersions. In Fig. 2 we plot our results for the
and dispersions. In Fig. 2 we plot our results for the  -age plane and explicit ignore the metallicity and mass dimensions. We found a constant metallicity dispersion (≈0.2 dex) along the age domain, which can be understood as an additional source of scatter in the age-AC diagram. In addition, the mean stellar mass representative of each age bin strongly varies with age. The sample is increasingly biased toward higher mass stars as we consider the younger stars. This feature qualitatively explains the reduced activity levels observed in each age domain in light of AMMAR. For instance, around 1 Gyr, the typical mass is ≈1.3 M/M⊙ and, after 7 Gyr, it becomes possible to select 1 M/M⊙ stars. Another consequence of the selection effects is that the mean activity values overlap strongly among the age intervals and maintain large dispersions throughout the age range of the sample. Young stars show a particularly high log
-age plane and explicit ignore the metallicity and mass dimensions. We found a constant metallicity dispersion (≈0.2 dex) along the age domain, which can be understood as an additional source of scatter in the age-AC diagram. In addition, the mean stellar mass representative of each age bin strongly varies with age. The sample is increasingly biased toward higher mass stars as we consider the younger stars. This feature qualitatively explains the reduced activity levels observed in each age domain in light of AMMAR. For instance, around 1 Gyr, the typical mass is ≈1.3 M/M⊙ and, after 7 Gyr, it becomes possible to select 1 M/M⊙ stars. Another consequence of the selection effects is that the mean activity values overlap strongly among the age intervals and maintain large dispersions throughout the age range of the sample. Young stars show a particularly high log dispersion and older stars tend to pile up in essentially the same log
dispersion and older stars tend to pile up in essentially the same log level with a slightly lower dispersion. In comparison, we also show the activity distribution of P13 in Fig. 2. The shaded area is the 68% confidence interval and the dashed curve stands for the most probable activity value for a given age step. The features of our calculations are in good agreement with P13 results, and under these conditions no CAR can be gleaned from the data.
level with a slightly lower dispersion. In comparison, we also show the activity distribution of P13 in Fig. 2. The shaded area is the 68% confidence interval and the dashed curve stands for the most probable activity value for a given age step. The features of our calculations are in good agreement with P13 results, and under these conditions no CAR can be gleaned from the data.
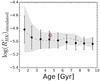 |
Fig. 2 Mean log |
4. Chromospheric activity in old clusters: NGC 188
Clusters are often employed as testbeds of CAR relations as they offer a coeval stellar population with similar metallicity, allowing the direct gauging of age (MH08) and metallicity (Rocha-Pinto & Maciel 1998) effects. Within a given cluster population, stellar mass effects can also be quantified. The main pitfall of introducing cluster stars into the CAR is the very narrow metallicity interval of accessible clusters, negating the metallicity dimension of the relation in large age intervals. Systematic observations aimed at deriving the CA level of open clusters are very scarce in the literature and no study has ever tackled clusters with both non-solar metallicity and age beyond solar; the oldest cluster with a dedicated CA analysis is the 4 Gyr old, solar metallicity cluster M 67 (G06).
NGC 188 is a solar-metallicity, 6 Gyr old cluster that offers a prime opportunity to test the feasibility of extracting CA ages, by means of the AMMAR, for stars substantially older than the Sun. We acquired Gemini-N/GMOS spectra at R = 2500 resolution of the M 67 and NGC 188 clusters in a series of 2014−2015 observing runs. We employed the B1200 grating and 0.75′′ slit width in a total of 9.7 observed hours: the mean S/N in the continuum was in excess of 60 for all targets. Membership and color data come from Yadav et al. (2008), Geller et al. (2008), and Geller et al. (2015). We derived Teff from the relations of Casagrande et al. (2011) (typical errors are ≤150 K for all stars, including color, Teff calibration, and metallicity errors), and computed luminosities (bolometric corrections from Flower 1996). Distance moduli and color excess come from Yadav et al. (2008) and Meibom et al. (2009). Isochronal ages derived (Kim et al. 2002,the same used to derive Eq. (1)) for the cluster HR diagrams are 4.0 ± 0.5 and 6.0 ± 0.5 Gyr for M 67 and NGC 188, respectively. These age estimates are in agreement with Yadav et al. (2008; M 67, 4.15 ± 0.65 Gyr) and Meibom et al. (2009; NGC 188, 6.2 ± 0.2 Gyr).
 |
Fig. 3 Left: observed distribution of log |
We applied blanketing corrections (Hall & Lockwood 1995) to the spectra and converted the instrumental HK indexes to the system of G06 by means of 12 common stars. The HK index conversion error is 15 mÅ (≤10%), which is compatible with the variability expected for M 67 (G06). The HK indexes were converted into log using 76 M 67 stars observed by G06 and MH08. The HK-
using 76 M 67 stars observed by G06 and MH08. The HK- transformation was performed as a function of (B − V) and the error was 0.01 dex. Then, our M 67 Gemini sample was augmented by G06 members. The distribution of the log
transformation was performed as a function of (B − V) and the error was 0.01 dex. Then, our M 67 Gemini sample was augmented by G06 members. The distribution of the log for the two clusters is shown in Fig. 3 (left panel); uncertainties are estimated considering errors in photon counting, normalization, line blanketing, colors, and transformation equations, amounting to ≤0.10 dex for all stars. The (B − V) distribution in the two clusters is very similar, and we are thus comparing stars with similar Teff, minimizing any color effect that is prone to distorting the log
for the two clusters is shown in Fig. 3 (left panel); uncertainties are estimated considering errors in photon counting, normalization, line blanketing, colors, and transformation equations, amounting to ≤0.10 dex for all stars. The (B − V) distribution in the two clusters is very similar, and we are thus comparing stars with similar Teff, minimizing any color effect that is prone to distorting the log distributions.
distributions.
The median log and dispersions for M 67 and NGC 188 are −4.83 ± 0.08 and −5.03 ± 0.10, respectively. Our mean figure for the log
and dispersions for M 67 and NGC 188 are −4.83 ± 0.08 and −5.03 ± 0.10, respectively. Our mean figure for the log of NGC 188 agrees well with log
of NGC 188 agrees well with log = −5.08 from Soderblom et al. (1991) and differs from the log
= −5.08 from Soderblom et al. (1991) and differs from the log = −4.70 used by P13 (see his Fig. 2) based on only three stars that are slightly hotter than the 49 stars of our sample. We confirm, using the largest sample of NGC 188 stars ever, a significantly lower level of CA with respect to M 67. The probability (Anderson-Darling test) that the two distributions of Fig. 3 (left panel) are statistically indistinguishable is 0.03%. In Fig. 3 (right panel) we plot the log
= −4.70 used by P13 (see his Fig. 2) based on only three stars that are slightly hotter than the 49 stars of our sample. We confirm, using the largest sample of NGC 188 stars ever, a significantly lower level of CA with respect to M 67. The probability (Anderson-Darling test) that the two distributions of Fig. 3 (left panel) are statistically indistinguishable is 0.03%. In Fig. 3 (right panel) we plot the log values of the Sun, M 67 and NGC 188 over an extrapolation of Eq. (1) to log
values of the Sun, M 67 and NGC 188 over an extrapolation of Eq. (1) to log <−5.1 (for solar metallicity) for two distinct masses around the solar value. We emphasize that the NGC 188 data were not used to derive Eq. (1), so it is an interesting oportunity to check the consistency of our approach for stars older than the Sun. The chromospheric ages from Eq. (1) for M 67 and NGC 188 are 4.1 ± 1.2 and 5.4 ± 0.8 Gyr, respectively, in good agreement with the canonical isochronal ages. The ACAR from MH08 gives slightly lower age estimates of 3.0 ± 1.2 Gyr (M 67) and 4.6 ± 1.9 Gyr (NGC 188) in agreement with our results within the uncertainties. The reason for these lower age estimates using ACAR is possibly due to the lack of old and inactive calibrating stars in rotation-activity and girochronology relations of MH08. In comparison to ACAR, M 67 and NGC 188 chromospheric ages derived through MH08 age-activity relation are in better agreement with the canonical isochronal ages of 3.6 ± 1.3 and 7.1 ± 1.8 Gyr, respectively. However, it should be stressed that, unlike the ACAR, the CA-age relation from MH08 were calibrated using 76 M 67 members from G06 and 3 NGC 188 members from Soderblom et al. (1991). Therefore, our approach can be considered as an extension of MH08 calibration for stars with different masses and metallicities. Our results are also in line with those of Barnes et al. (2016), who find a well-defined progression in the stellar rotational periods of the clusters NGC 6811, NGC 6819 (Meibom et al. 2011, 2015), and M 67, up to the rotational period of the Sun, thereby supporting age determinations linked to CA for stars at least as old as the Sun. Their gyrochoronological age for M 67 is 4.2 ± 0.7 Gyr, which is in excellent agreement with our chromospheric value.
<−5.1 (for solar metallicity) for two distinct masses around the solar value. We emphasize that the NGC 188 data were not used to derive Eq. (1), so it is an interesting oportunity to check the consistency of our approach for stars older than the Sun. The chromospheric ages from Eq. (1) for M 67 and NGC 188 are 4.1 ± 1.2 and 5.4 ± 0.8 Gyr, respectively, in good agreement with the canonical isochronal ages. The ACAR from MH08 gives slightly lower age estimates of 3.0 ± 1.2 Gyr (M 67) and 4.6 ± 1.9 Gyr (NGC 188) in agreement with our results within the uncertainties. The reason for these lower age estimates using ACAR is possibly due to the lack of old and inactive calibrating stars in rotation-activity and girochronology relations of MH08. In comparison to ACAR, M 67 and NGC 188 chromospheric ages derived through MH08 age-activity relation are in better agreement with the canonical isochronal ages of 3.6 ± 1.3 and 7.1 ± 1.8 Gyr, respectively. However, it should be stressed that, unlike the ACAR, the CA-age relation from MH08 were calibrated using 76 M 67 members from G06 and 3 NGC 188 members from Soderblom et al. (1991). Therefore, our approach can be considered as an extension of MH08 calibration for stars with different masses and metallicities. Our results are also in line with those of Barnes et al. (2016), who find a well-defined progression in the stellar rotational periods of the clusters NGC 6811, NGC 6819 (Meibom et al. 2011, 2015), and M 67, up to the rotational period of the Sun, thereby supporting age determinations linked to CA for stars at least as old as the Sun. Their gyrochoronological age for M 67 is 4.2 ± 0.7 Gyr, which is in excellent agreement with our chromospheric value.
We stress that our results do not invalidate the analysis of P13: observational biases, the multiparametric nature of the problem, and perhaps the age-metallicity relation conspire to produce a complex behavior of the age-activity relation. Even though our age-mass-metallicity-activity relation is in line with independent observational constraints. This should not be taken as final proof that the evolution of CA can be traced for old stars. Further inquiry into the suitability of the log index in wider, well-populated domains of mass, metallicity, age, and evolutionary states are clearly necessary.
index in wider, well-populated domains of mass, metallicity, age, and evolutionary states are clearly necessary.
5. Summary and conclusions
We show that mass and metallicity biases are inevitably present in samples of stars selected to have small errors in age, severely distorting the intrinsic distribution of the CA versus age plane. The result is a dilution of the decay of CA with time, apparently hampering the derivation of ages through CA beyond ~2 Gyr. These biases can be corrected by means of an age-mass-metallicity-CA relation, whichsuccessfully reproduces stellar asteroseismological ages up to 10 Gyr. We further test this calibration by measuring the log index of the 6.0 Gyr-old NGC 188 cluster from new and extensive Gemini/GMOS data. The CA level of NGC 188 is clearly lower than in the well-studied, 4.0 Gyr-old cluster M 67. Our calibration successfully recovers correct ages for both clusters: chromospheric ages can be derived within ~0.15 dex. We show that a more complete approach of the CA-age relation, including more variables, appears promising and may imply the ability of the age-mass-metallicity-activity relation to recover reliable stellar ages well beyond the solar age. Present calibrating samples, however, are far from representative of the whole relevant domain of mass, age, metallicity, and stellar activity. Particularly, further data on open clusters with a wide range of age and metallicity are essential to test this approach and possibly push the feasibility of chromospheric age determinations to the full range of age and metallicity of the Galactic disk.
index of the 6.0 Gyr-old NGC 188 cluster from new and extensive Gemini/GMOS data. The CA level of NGC 188 is clearly lower than in the well-studied, 4.0 Gyr-old cluster M 67. Our calibration successfully recovers correct ages for both clusters: chromospheric ages can be derived within ~0.15 dex. We show that a more complete approach of the CA-age relation, including more variables, appears promising and may imply the ability of the age-mass-metallicity-activity relation to recover reliable stellar ages well beyond the solar age. Present calibrating samples, however, are far from representative of the whole relevant domain of mass, age, metallicity, and stellar activity. Particularly, further data on open clusters with a wide range of age and metallicity are essential to test this approach and possibly push the feasibility of chromospheric age determinations to the full range of age and metallicity of the Galactic disk.
Acknowledgments
We would like to acknowledge the anonymous referee, whose comments have unquestionably led to an improved paper. D.L.O. and G.F.P.M. acknowledge grants and scholarships from CNPq and CAPES. We thank the support of Gemini Observatory, operated by the Association of Universities for Research in Astronomy, Inc., on behalf of the international partnership of Argentina, Brazil, Canada, Chile, and the USA.
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arriagada, P. 2011, ApJ, 734, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A., & Kim, Y. C. 2010, ApJ, 721, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A., Weingrill, J., Fritzewski, D., et al. 2016, ApJ, 823, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schnrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Geller, A. M., Mathieu, R. D., Harris, H. C., et al. 2008, AJ, 135, 2264 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, A. M., Latham, D. W., & Mathieu, R. D. 2015, AJ, 150, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Giampapa, M. S., Hall, J. C., Radick, R. R., et al. 2006, ApJ, 651, 444 [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2003, AJ, 126, 2048 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., & Lockwood, G. W. 1995, ApJ, 438, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Soderblom, D. R., Donahue, R. A., et al. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. S., Murgas, F., Rojo, P., et al. 2011, A&A, 531, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, Y. C., Demarque, P., & Yi, S. K. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., McClintock, W., Robertson, R. M., et al. 1979, ApJS, 41, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenzo-Oliveira, D., Porto de Mello, G. F., Dutra-Ferreira, L., & Ribas, I. 2016, A&A, accepted [Google Scholar]
- Lyra, W., & Porto de Mello, G. F. 2005, A&A, 431, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Grundahl, F., & Clausen, J. V. 2009, ApJ, 137, 5086 [Google Scholar]
- Meibom, S., Barnes, S. A., & Latham 2011, ApJ, 733, 9 [Google Scholar]
- Meibom, S., Barnes, S. A., & Platais 2015, Nature, 517, 589 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mosser, B., Deheuvels, S., Michel, E., et al. 2008, ApJ, 488, 635 [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., et al. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, G. 2013, A&A, 551, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rocha-Pinto, H. J., & Maciel, W. 1998, MNRAS, 298, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Duncan, D. K., & Johnson, D. R. H. 1991, ApJ, 375, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, C., Reiners, A., & Schmitt, J. H. M. M. 2009, A&A, 493, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, Y. K., & Gai, N. 2011, A&A, 526, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2011, A&A, 474, 653 [Google Scholar]
- Vauclair, S., Laymand, M., Bouchy, F., et al. 2008, A&A, 482, 5 [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., et al. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K. S., Bedin, L. R., Piotto, G., et al. 2008, A&A, 484, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yıldız, M. 2008, MNRAS, 388, 1143 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Upper panels: comparison of asteroseismological with chromospheric ages from our calibration (black circles) and MH08 (red squares) for a sample of stars spanning a wide interval in age, mass, and metallicity. The dashed line is the 1:1 relation. Lower panels: difference between the age estimates Δlog (t) (log (tastero) − log (tchrom)) as a function of [Fe/H] . The dashed lines stand for ±1σ chromospheric age uncertainty. |
| In the text | |
 |
Fig. 2 Mean log |
| In the text | |
 |
Fig. 3 Left: observed distribution of log |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


