| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201528019 | |
| Published online | 13 October 2016 | |
Self-similarity in the chemical evolution of galaxies and the delay-time distribution of SNe Ia
1 Leibniz-Institut für Astrophysik
Potsdam (AIP), An der Sternwarte
16, 14482
Potsdam,
Germany
e-mail: jwalcher@aip.de
2 Max-Planck Institut für
Extraterrestrische Physik, Giessenbachstraße 1, 85748
Garching,
Germany
3 Max-Planck Institut für Astrophysik,
Karl-Schwarzschild-Str.
1, 85748
Garching,
Germany
4 Max-Plank Institut für Astronomie,
Königstuhl 17,
69917
Heidelberg,
Germany
5 Instituto de Radiastronomia and
Astrofisica (IRyA), Morelia, 58089
Michoacan,
Mexico
6 Sorbonne Universités, UPMC-CNRS, UMR
7095, Institut d’Astrophysique de Paris, 75014
Paris,
France
7 Instituto de Astronomia, Geofisica e Ciencias Atmosféricas,
Universidade de São Paulo, Rua do Matao 1226, 05508-090 − São Paulo, Brasil
8 INAF−Osservatorio
Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125
Firenze,
Italy
Received:
21
December
2015
Accepted:
19
July
2016
Recent improvements in the age dating of stellar populations and single stars allow us to study the ages and abundance of stars and galaxies with unprecedented accuracy. We here compare the relation between age and α-element abundances for stars in the solar neighborhood to that of local, early-type galaxies. We find these two relations to be very similar. Both fall into two regimes with a shallow slope for ages younger than ~9 Gyr and a steeper slope for ages older than that value. This quantitative similarity seems surprising because of the different types of galaxies and scales involved. For the sample of early-type galaxies we also show that the data are inconsistent with literature delay-time distributions of either single- or double-Gaussian shape. The data are consistent with a power-law delay-time distribution. We thus confirm that the delay-time distribution inferred for the Milky Way from chemical evolution arguments must also apply to massive early-type galaxies. We also offer a tentative explanation for the seeming universality of the age-[α/Fe] relation: it is the manifestation of averaging different stellar populations with varying chemical evolution histories.
Key words: stars: abundances / galaxies: abundances / galaxies: elliptical and lenticular, cD / supernovae: general / Galaxy: evolution
© ESO, 2016
1. Introduction
It has long been recognized (Tinsley 1979; Matteucci & Greggio 1986) that the element abundance ratio [α/Fe] is a powerful estimator of the duration of star formation events in galaxies. The reasons are different explosion timescales and yields of different types of supernovae. A direct consequence of this insight is that we expect a correlation between the ages of stars in galaxies and their [α/Fe] ratios. A recent example is Fig. 1 in Chiappini et al. (2015), which shows the generic prediction for single stars in the Milky Way. It is unclear, however, how this relation would translate into galaxy-wide average properties. Generally, we expect that galaxies that have stopped forming stars at an earlier time in the history of the Universe (equivalent to a shorter star formation timescale) would show less light from Fe-enriched stars in their spectra and consequently a higher overall [α/Fe] enrichment. There does not seem to be a good reason why the relations between age and [α/Fe] should be quantitatively the same for entire galaxies and single stars, with the hope that possible differences might be used to study the different star formation histories. However, the exploration of this expected correlation has been hampered by uncertainties in stellar and galaxy ages, related to model uncertainties and intrinsic degeneracies, such as the age-metallicity degeneracy.
We have recently been able to take a significant step forward by showing this correlation for early-type galaxies (ETGs; Walcher et al. 2015, hereafter W15). Jørgensen (1999) previously found no correlation between [α/Fe] and age. This correlation was tentatively first reported by Gallazzi et al. (2006). A correlation of age and [α/Fe] was unambiguously shown by Graves et al. (2010) from stacked spectra (their Fig. 4), but the very nature of stacked spectra prevented studying the scatter in the relation. The relation was shown on a per-galaxy basis by Kuntschner et al. (2010, their Fig. 6), but in this case the small sample size and continued large uncertainties on age made an interpretation difficult. Other recent work, such as Thomas et al. (2010) and Johansson et al. (2012), showed and discussed the parameters age, [Fe/H] and [α/Fe], but did not directly address the age-[α/Fe] relation explored here. The W15 results nevertheless qualitatively agree with these earlier papers and reinforce and expand on them. We emphasize that for this same correlation, it is important to heed the warnings of Thomas et al. (2005), who discussed the importance of degeneracies when using age as a parameter. We quantitatively showed in W15 that the age-metallicity degeneracy does not give rise to the observed correlation.
An interesting parallel development has been the verification of the expected similar correlation in the stars of the Milky Way. The unique age-metallicity relation in the Galactic disk has been first suggested by Twarog (1980) using multiband photometry data. However, Edvardsson et al. (1993) and later studies (Feltzing et al. 2001; Nordström et al. 2004; Holmberg et al. 2007, 2009; Casagrande et al. 2011) have found that there is no one-to-one relationship between ages and metallicities of stars and a large scatter at any age that may have an astrophysical cause. Finally, the most recent work by Bergemann et al. (2014, hereafter B14), using the high-resolution spectra from the Gaia-ESO stellar survey, has conclusively established the weak age-metallicity relation in the solar vicinity of the Galactic disk. This is the first study to carefully analyze the survey target selection effects and their effect on the age-metallicity diagram. For stars with ages below 8 Gyr and for the solar vicinity, the observed age-metallicity relation was found to be nearly flat, and the majority of older stars are metal-poor and enhanced in α elements. Similar conclusions were reached by Haywood et al. (2013, hereafter H13) and Bensby et al. (2014). As discussed in Bensby et al. (2014), the H13 analysis lead to a very tight [α/Fe]-age relation as a result of the problems in the spectroscopic analysis and sample selection biases. Generally, B14 established that [α/Fe] is a good proxy for the age of a star, even though they reported a significant dispersion of [Mg/Fe], especially at ages above 9 Gyr.
This paper attempts to establish two new statements. First, the correlation between age and [α/Fe] as expected from chemical evolution is seen in ETGs and is quantitatively similar to the correlation for stars in the solar neighborhood. This is true despite the very different star formation histories of these two different types of stellar systems. Second, this universality allows us to explore the dependence on the yields and delay-time distributions (DTDs) of supernovae (SNe) Ia and II. When fixing the yields, the age-[α/Fe] relation of ETGs thus provides additional interesting constraints on the DTD of SNe Ia.
2. Data and models
We are interested in comparing the relation between age and [α/Fe]for galaxies and stars and for data and models. We here describe the data and models we used for the present contribution.
2.1. Data for ETGs
For observational data of galaxies we turn to our publication of W15. There we analyzed a spectroscopic sample of 2286 ETGs selected from the SDSS survey, data release 7 (Abazajian et al. 2009). The galaxies were selected according to the following criteria: they showed no emission lines (and therefore no visible star formation), were photometrically concentrated, and had spectra with a sufficiently high signal-to-noise ratio (S/N> 40) to allow a careful analysis of the stellar population content. To analyze the spectra we used the pixel-fitting code paradise. This algorithm fits a linear combination of simple stellar populations to the galaxy data, at the same time as deriving the best-fit kinematic parameter velocity and velocity dispersion. The stellar population models used were the differential stellar population models of Walcher et al. (2009). In particular, we derived the physical parameters age, [Fe/H], and [α/Fe]. In the present contribution we only used those physical properties as derived in a luminosity-weighted sense, meaning that every stellar population contributes to the total signal according to its luminosity contribution to the overall spectrum. In W15 we also addressed the ability to separate the properties of the old- and intermediate-age stars on a per-galaxy basis. Typical error bars (precision) on age are 0.2 Gyr and 0.01 dex on [Fe/H] and [α/Fe]. These age precisions are obtained for stellar populations, that is, they are averages of many stars. The techniques used to derive these ages are very different from the techniques used for single stars. The definition of the α-element abundances groups together the elements O, Ne, Mg, Si, S, Ca, and Ti (Coelho et al. 2007), but the dominant signal in the wavelength range we used to determine the abundance comes from Mg. The models are normalized to the solar abundances from Grevesse & Sauval (1998). The galaxies cover a mass range from 1010.2 to 1011.5M⊙.
2.2. Data for Milky Way stars
For data on stars we turn to the publications of B14 and H13. First, we used the data from the Gaia-ESO spectroscopic survey, presented in B14. The Gaia-ESO survey (Gilmore et al. 2012; Randich et al. 2013) is a large high-resolution spectroscopic survey of FGK stars in the Milky Way disk to date. The B14 dataset consists of 144 stars with ages from 0.5 to 13.5 Gyr, which were determined consistently using advanced stellar evolution models (Serenelli et al. 2013), which we verified on the accurate seismic estimates for the reference benchmark stars (Jofré et al. 2014; Heiter et al. 2015). The chemical abundances of 15 elements were determined using the high-resolution (R ~ 47 000) Gaia-ESO UVES spectra using the MARCS model atmospheres and experimental atomic line lists. The mean uncertainties are 1.5 Gyr in age, and 0.06 dex in metallicity and chemical abundances of α-elements. The stars in the sample are all within 6 kpc to 9.5 kpc from the Galactic center and are located close to the plane, | Zl< 1.5 kpc.
Second, we used the data from H13. These authors published ages for single stars with known [Fe/H], and [α/Fe] in the solar neighborhood. Their sample is based on the HARPS GTO observations of 1111 stars as published in Adibekyan et al. (2012). The original sample had to be severely pruned to 363 stars with clearly defined ages. This down-selection was based on an absolute magnitude cut at MV< 4.75 and on a somewhat less reproducible selection of stars with “a well defined probability function” (H13). H13 noted that their absolute age scale might be incorrect by 1 to 1.5 Gyr, while relative ages would have uncertainties of 1 Gyr. The definition of [α/Fe] reported in H13 includes the mean of Mg, Si, and Ti abundances. In the analysis of W15 the Mgb feature dominated, therefore these two observational definitions are very comparable despite the different definition of the α group.
The stellar data for H13 were adopted from Figs. 6 and 17 using the PlotDigitizer application. We were able to read off 112 points in Fig. 6 (age vs. [α/Fe]) and 300 points in Fig. 9 (age vs. [Fe/H]). The larger number of points in the age vs. [Fe/H] plane is caused by the larger scatter, which enables distinguishing more data points in the figure. We are not interested in the properties of single stars but in the slopes and zero points of the correlations, therefore we expect little if any bias from this sample incompleteness. In particular, for the age vs. [α/Fe] relation, most of the invisible (crowded) points seem to be concentrated at low ages and low [α/Fe], which agrees with the general trend. Including the whole sample would therefore presumably mainly decrease the scatter around this mean relation, but would not change the parameters of the relation.
Since we began writing this paper, more samples have appeared that extended the very local samples used here with CoRoT and Kepler data with spectroscopic follow-up (Chiappini et al. 2015; Anders et al. 2016; Martig et al. 2015). Adding these stars would not change the conclusions of this paper in any way.
2.3. Semi-analytic models of ETG formation
The galaxy models are based on the semi-analytic models described in Yates et al. (2013, hereafter Y13), which are themselves an update of the Munich semi-analytic model, L-GALAXIES (Springel et al. 2001; Guo et al. 2011). The model is built on merger trees from the Millennium (Springel et al. 2005) and Millennium-II (Boylan-Kolchin et al. 2009) N-body simulations of dark matter (DM) structure formation and uses an analytic treatment to track the transfer of mass between different baryonic components of a galaxy, such as bulge and disk stars, and hot and cold gas. Prescriptions for supernova and AGN feedback are included. The most important ingredients for the present contribution are those that directly influence the chemical evolution, that is, SN yields, initial mass function (IMF), stellar lifetimes etc. All of these are described in detail in Y13.
The only parameter that we treat as a variable in the present contribution is the DTD of SNeIa. The DTD describes the probability for a SN Ia to explode as a function of the time elapsed since a star formation event. The overall explosion rate of SNe Ia in a galaxy will depend on the DTD and the star formation history. Y13 considered three DTDs: power-law, bimodal, and Gaussian. The bimodal DTD could be reasonably close to a power-law DTD for a specific choice of parameters (normalization, slope, characteristic time, etc.). Here we chose parameters that have been proposed in the literature based on observations of the SNIa rate, but that still keep the DTDs sufficiently unique that our data and model matching allow us to distinguish between them. Formal parameter minimization of different DTDs and further dependencies (such as a metallicity dependance of the DTD) will be explored in future work.
The Y13 model provides the same parameters as for the W15 ETGs: age, [Fe/H], and [α/Fe]. Just as for the ETG data from W15, the ages are calculated as r band luminosity-weighted ages. The [α/Fe] value used in Y13 is the value of [O/Fe] and is normalized to the Anders & Grevesse (1989) meteoric abundances (i.e., [O/H] = 8.93 and [Fe/H] = 7.51). Normalizing to the Grevesse & Sauval (1998) abundances would shift the overall normalization down by 0.1 dex in [α/Fe]. We have also tested the effect of taking the average of the enhancements of O, Si, S, and Ca (i.e., excluding Mg) as our value for [α/Fe]. All results of this paper are independent of whether we use [O/Fe] or this restricted definition of [α/Fe] for the model galaxies. We decided to avoid [Mg/Fe] because there are some known peculiarities with the yields of this element in the yield set used (Portinari et al. 1998). In particular, uncertainties concern the greater Mg production in low-metallicity stars as compared to high-metallicity stars, which is due to complex assumptions about pre-SN stellar winds.
It is also important to note exactly which sample we are using. To the basic set of model ellipticals from Sect. 6.3 of Y13 we imposed an overall lower mass limit of log (M ∗ ) = 10.0 to roughly match that of the W15 sample. Here, we did not impose the additional cut based on the 1σ scatter of the Johansson et al. (2012) mass-age relation (see Sect. 6.3.1 of Y13). This additional cut would have removed those low-mass model galaxies that we know are too old and red as a result of efficient stripping and SN feedback in the model, which causes these objects to have run out of star-forming gas very early. Low-mass galaxies are, however, not considered in the present contribution.
2.4. Simulations of disk assembly
For a chemical evolution model of the solar neighborhood stars that closely matches the B14 sample, we considered Minchev et al. (2013, hereafter M13). The Y13 model also predicts abundance trends for disk galaxies and could have been used in the same way. However, the M13 model has been constructed specifically for the Milky Way and thus is most directly comparable to the B14 data. Moreover, using two entirely different chemical evolution models reinforces our statement that the age-[α/Fe] relation is universal.
The M13 model is based on a simulation in the cosmological context by Martig et al. (2012), and we refer to that paper for all details on the method. The main point for our discussion is that M13 chose the one galaxy out of all Martig et al. (2012) galaxies that most resembles the Milky Way. The chemical evolution model is tied to the dynamic evolution by having both disks grow inside out, by a similar gas-to-stellar mass ratio, and by resampling the star formation rate in the simulation to match that of the semi-analytical chemical model. This method allows circumventing problems with fully self-consistent chemo-dynamical simulations, which are due to uncertainties in subgrid physics – even in high-resolution cosmological simulations, one particle represents 104−105M⊙. M13 listed the [Mg/Fe] abundances of the stars out of a total of ~30 elements. The M13 model uses Mg as its proxy of the α-element group, which is compatible with the W15 and B14 analyses.
The H13 data are limited to the Hipparcos volume, while the B14 data cover a somewhat more extended solar vicinity. To reproduce the limited volume in the data, we considered a ring at radius r = 8 kpc, of radial width Δr = 0.1 kpc, and of vertical height Δ | z | = 0.05 kpc. We convolved the model with ad hoc but realistic error bars, namely Δage = 1 Gyr and Δ[α/Fe] = 0.11. Out of the total sample of available stars in the model (~105), we randomly selected 400 stars, which is approximately the size of the B14 and H13 samples combined.
An important feature of the model is that its oldest stars are 11.2 Gyr old (12.2 Gyr including fiducial errorbars). The oldest stars in the observations can be as old as 15 Gyr. Clearly, there is a difference in age scale, which may be imputed both to the observations and the simulations, for different reasons. Observationally, age scales may be uncertain for several reasons, as discussed in B14. In the simulations, on the other hand, the main effect is that the model is a pure thin disk model, that is, a chemodynamical simulation that was run for 11.2 Gyr. In the two-infall model from Chiappini et al. (1997), the thick disk does pre-enrich the thin disk. Nevertheless, thin-disk stars are chemically nearly independent of the thick-disk stars, the chemical clock is essentially reset at the beginning of the second infall. The use of M13 simulation is justified because the thick-disk population shown in Fig. 1 of Chiappini et al. (2015) is absent from the observational samples used here, see Sect. 2.2. The net effect is that in simulations chemical evolution starts at 11.2 Gyr instead of ~13. For our application this has the effect that we need to slightly stretch the age axis for the simulations to match the chemical evolution patterns of the observed Milky Way. The stretch factor therefore should be ~1.2. This stretch factor is further discussed in Sect. 3.1.
3. Results
3.1. Age-[α/Fe] relation
In this section we plot and compare the relations between age and [α/Fe] and [Fe/H]. As discussed above, the different datasets have to be set to the same scale before they can be directly compared. We applied the following scaling factors: (1) None to the W15 data. (2) A downward shift to the [α/Fe] value of Y13 of 0.1 dex, which is justified by the different solar abundances used as reference. No shift was applied to [Fe/H], as the nominal shift of 0.01 dex is not significant for the present work. (3) None to the B14/H13 data. (4) As justified in Sect. 2.4, a correction factor of order 1.2 is expected to be needed due to differences in timescale between the M13 model and the Milky Way data. In practice the factor 1.17 works well for the self similarity arguments exposed here. This ad hoc stretch factor makes it impossible for the moment to use the M13 models to infer information on the SNe Ia DTD.
We plot the relation between age and [α/Fe] in Fig. 1. Qualitative agreement was expected from the literature on chemical evolution cited in Sect. 1. Surprisingly, the relations are also quantitatively similar, all showing a clear change of slope at ages between 9 and 10 Gyr in both datasets and both model sets. On the other hand, the age-[Fe/H] relations in Fig. 2, while showing the overall same trend of [Fe/H] decreasing with lookback time, are quantitatively very different in the sense that [Fe/H] for old stars is much lower in the solar neighborhood. The galaxy data do not seem to require a two-slope regime, whereas the stellar data do. We discuss possible reasons for this in Sect. 4.1.
 |
Fig. 1 Comparison of the correlations between age and [α/Fe] for two very different types of astrophysical objects. Upper left panel: the luminosity-weighted average properties of early-type galaxies from W15. The solid line is a formal fit to the two regimes, separated at 9 Gyr. Upper right panel: stars in the local neighborhood from B14 (solid squares) and H13 (stars). The dashed line is a formal fit to the B14 data for the two regimes, separated at 9 Gyr. The solid line repeats the fit for galaxies from the left panel. Lower left panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13. The solid line repeats the fit for the W15 data for comparison. No observational errors have been added to the model galaxy properties, which largely explains the difference in scatter. Lower right panel: single-star properties for a simulated solar neighborhood from M13. The dashed line repeats the fit to the B14 data for comparison. Here, observational errors have been added for better comparison of scatter. |
 |
Fig. 2 Comparison of the correlations between age and [Fe/H] for two very different types of astrophysical objects. The panels and lines are the same as in Fig. 1. |
We have verified that for all relations we studied here the Spearman-Rank test indicates that the probability of absence of any correlation is zero. We quantified the correlations by means of formal fits to each set of two-parameter combinations using the LINFIT module in IDL. We fit the two regimes separately and report the results in Table 1. For the age-[α/Fe] relation all slopes are consistent at the 2σ level (error bars reported in the table are 1σ error bars). Likewise, all intercepts are the same within 2σ, with the exception of the [Fe/H] intercepts in the young regime. These last intercepts will depend more strongly on sample selection than any other, so that we neglected this difference for the present contribution.
Coefficients of linear fits to the datasets.
3.2. Delay-time distribution of SNeIa
We repeat the relation between age and [α/Fe] in Fig. 3, this time comparing it to the results from the Y13 model for different SNe Ia DTD. It seems fair to say that there is considerable debate in the literature on SNe Ia DTDs determined from direct observations of SNe and their host galaxies. Different authors claimed different results with high certainty. In the hope of being representative, we chose three DTDs, without any prejudice against other work. In all cases the delay time is denoted by τ and all DTDs are normalized to 1, such that 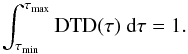 (1)Mannucci et al. (2006) found strong evidence for two different types of SNe Ia progenitors and proposed a bimodal DTD:
(1)Mannucci et al. (2006) found strong evidence for two different types of SNe Ia progenitors and proposed a bimodal DTD: 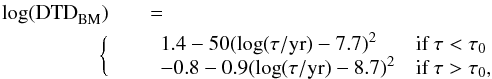 (2)where τ0 = 0.0851 Gyr separates the times where one or the other progenitor dominates the SN Ia rate.
(2)where τ0 = 0.0851 Gyr separates the times where one or the other progenitor dominates the SN Ia rate.
Strolger et al. (2004), on the other hand, rejected the double-progenitor scenario “at the 99% confidence level” and were able to describe their data by a narrow Gaussian DTD: 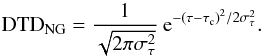 (3)Here τc = 1 Gyr is the average delay time and στ = 0.2τc Gyr is the width of the distribution.
(3)Here τc = 1 Gyr is the average delay time and στ = 0.2τc Gyr is the width of the distribution.
Finally, Maoz et al. (2012) argued that the most recent data favor a power-law DTD, which is described by 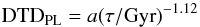 (4)with normalization constant a = 0.15242 Gyr-1. Similar DTDs have also been advocated by numerous other authors, for instance, Totani et al. (2008), Graur et al. (2011), and Graur et al. (2014).
(4)with normalization constant a = 0.15242 Gyr-1. Similar DTDs have also been advocated by numerous other authors, for instance, Totani et al. (2008), Graur et al. (2011), and Graur et al. (2014).
Figure 3 shows that the old-part slope of the age-[α/Fe] relation is sensitive to the SNIa DTD. The power-law DTD is clearly the best approximation of the data, while the two other DTDs fail at old ages. This result had been anticipated by earlier work. Matteucci & Recchi (2001) have shown that a significant fraction of SNe Ia need to explode significantly before the 1 Gyr timescale often quoted for SNe Ia. For an instantaneous burst as assumed in the DTD, they quoted a typical timescale of very roughly 50 Myr, which is what we find here. The fraction of SNe Ia to explode within 100 Myr after the burst of star formation has been further constrained by Matteucci et al. (2009) to be between 13% and lower than 30%. It was estimated by Y13 to be ~23% for the power-law DTD used here as well.
We emphasize that the DTDs have been chosen directly from the literature from lookback studies of SNe Ia explosion rates. These literature DTDs are naturally distinct, and we made no attempt on purpose to vary their functional parameters. For example, we could probably tweak the parameters of the bi-modal distribution to yield similar results to the power-law DTD within our systematic measurement uncertainties. This would imply that the two DTDs are essentially the same as well, however. We also note that the downward renormalization of the Y13 data effected in Sect. 3.1 is applied here as well, but does not affect our conclusions in any way. The shape of the age-[α/Fe] correlation allows us to diagnose the DTD, not the normalization of the [α/Fe] values.
4. Discussion
4.1. Self-similarity, or the independence of star formation history
The quantitative similarity of the relation age-[α/Fe] presented in Fig. 1 for Milky Way stars and ETGs is not only not evident, it is even decidedly surprising. Objects reported in W15 and Y13 correspond to luminosity-weighted average properties of massive galaxies, that is, to ensembles of more than 1010 stars, in galaxies that stopped forming the majority of their stars a long time ago. On the other hand, objects in B14 and M13 are single stars in the solar neighborhood, or in other words, the thin disk of a nearly bulgeless disk galaxy that is still forming a few solar masses of stars every year (a much higher specific star formation rate than seen in present-day early-type galaxies). The apparent conundrum could be interpreted as follows: the B14 age-[α/Fe] relation for Milky Way stars could be tracing, down to z = 0, a generic lookback time vs. [α/Fe] relation. If so, ETGs are simply galaxies that stopped forming stars somewhere earlier on that curve. An ETG sample with a range of ages would, therefore, populate an age-[α/Fe] relation very similar to that of MW stars. Thus the most naive interpretation of the data would be that there is a common underlying age-[α/Fe] relation that does not depend sensitively on the SFH of the galactic system.
Such an interpretation is clearly oversimplified, however. The thin-disk curves in Fig. 7 of Minchev et al. (2013; see also Fig. 1 of Chiappini et al. 2015) show that within the Milky Way the relation between age and [α/Fe] is expected to depend on the radius of formation of the stars. The magenta line in that figure is very similar to our result here but is the average result of chemo-dynamical evolution. In other words, the stellar line by itself mixes stars from different radii. The very recent results of Anders et al. (2016, their Fig. 13) would also seem to show significant scatter at the location of the knee of the [Fe/H] vs. [α/Fe] plot, which might be tied to a variation in the age vs. [α/Fe] relation. We point out that in addition to expected intrinsic variations in the age − [α/Fe] relation in stellar systems, even for the Milky Ways stars, not all stars in this plot belong together in a causal sense. The thick-disk and thin-disk stars are distinct in their formation history, although formation times may overlap. This mirrors the statement made in W15 that the intermediate-age stellar populations in ETGs are not causally connected to the old stellar populations.
 |
Fig. 3 Comparison of the correlations between age and [α/Fe] for three different prescriptions for the DTD of SNeIa in the Y13 model. Upper left panel: the luminosity-weighted average properties of early-type galaxies from W15. The solid line is a formal fit to the two regimes, separated at 9 Gyr and repeated in all the other panels. Upper right panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13, using a Gaussian DTD. Lower left panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13 using a power law DTD. Lower right panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13 using a bimodal DTD. |
The chemical evolution models additionally allow exploring the plausibility of the two-slope parametrization we have presented here for the observational data. The two-infall model of Chiappini et al. (1997) essentially produces two different types of chemical evolutionary systems: (1) The thick disk, with high star formation efficiency and a short accretion timescale. (2) The thin disk, with lower star formation efficiency and an overall longer accretion timescale. The thin disk additionally has a varying accretion timescale with radius, which is longer for larger radii in the Milky Way. Figure 2 of Minchev et al. (2013) shows the dependence of star formation history on radius within the Milky Way. Clearly, the center of the Milky Way experiences a star formation history that peaks at very early times, entirely opposite to the outermost radii, which have a very gentle increase of star formation rate over cosmic time. Figure 7 of Minchev et al. (2013) shows, however, that for the first three Gyr, the age-[α/Fe] relation has a steep slope that varies only very slightly with radius, hence star formation history. The main effect of the varying star formation histories is in the slope of the age-[α/Fe] relation at lookback times shorter than 9 Gyr. To translate these insights for the ETGs, we additionally need to take into account that the number of stars on each of these tracks will vary widely: the longer the timescale of star formation (which corresponds to a larger radius in the Milky Way), the larger the fraction of stars on the tracks with an age younger than 9 Gyr. The converse is also true: a system with a very intense star formation burst at very early cosmic times will produce very few stars with very low [α/Fe] values and ages younger than 9 Gyr. Thus the net effect of averaging stellar populations from chemical evolutionary systems with varying star formation histories may be to drive toward a relation that is similar to the one shown here, or indeed to the average relation in the vicinity of the Sun, as exemplified by the magenta line in Fig. 7 of Minchev et al. (2013). An example of how this averaging effect works at different radii in the disk of the Milky Way is shown in Fig. 5 of Minchev et al. (2014).
Thus, the apparent universality of the age-[α/Fe] relation and its independence on the specific stellar assembly history for the two types of systems that we were able to test here might be more than just a coincidence. It would rather be the expected average for complex stellar systems. It will be worthwhile and interesting to further study observationally whether this common relation exists for more stellar systems and to identify where and how different systems finally diverge, given small enough error bars and as expected from chemical evolution models. Lehnert et al. (2014) argued that “the low scatter in the [α/Fe] as a function of age and the rapid decrease in [α/Fe] with time suggests that mixing of metals was very efficient”. It seems in light of the ETG data presented here that efficient mixing is not necessarily needed if the age-[α/Fe] relation is universal enough to apply to any star-forming system with a mixture of stellar populations. It follows, however, that a lower mass limit to the validity of this relation must be expected, below which mixing arguments would have to be invoked to keep the relation universal.
The apparent universality of the age-[α/Fe] relation is not mirrored by the age-[Fe/H] relation, which shows strong differences between the Milky Way stars and massive ETGs. Data reported in W15 show universally high [Fe/H] values, while the B14 data show [Fe/H] values that are lower by 1 dex for old stars. While the M13 model successfully reproduces the B14 data in this figure, the Y13 model shows an offset in [Fe/H] as compared to W15. A detailed discussion of this offset is beyond the scope of this paper. A tentative solution to be explored elsewhere is that the negative offset and shallower slope of the relation is a mass effect. The typical ~6 Gyr old ETG in the Y13 model is less massive than that in the W15 sample, even though the Y13 sub-sample used here is mass selected. This sample selection effect might be partially caused by the selection on S/N for the observational data points, as discussed in W15. However, the overall trend is the same as shown in the W15 data: an anticorrelation between age and [Fe/H].
Beyond the mean relations, the scatter of the age-[α/Fe] and age-[Fe/H] relations may contain physical insight if the error bars can be driven further down. Discussing the case of the ETGs, the oldest ellipticals with ages >11 Gyr and log (M ∗ ) > 11.5M⊙ at z = 0, did not have time to enrich heavily in iron, therefore they should show very small scatter in [α/Fe]. Some slightly younger massive ellipticals would have had slightly longer star formation timescales, hence lowering the [α/Fe] and increasing their [Fe/H]. Other slightly younger massive ellipticals would have started forming their stars later in the history of the Universe, leading them to show overall higher [α/Fe] and lower [Fe/H] at the same age. The scatter in [α/Fe] and [Fe/H] may thus be a good diagnostic of the time of onset of star formation, a quantity that has eluded observational constraints from galactic archeology for any galaxy we cannot resolve in single stars.
4.2. Constraints on the delay-time distribution of SNeIa
In Sect. 4.1 we have stated that the shape of the age-[α/Fe] relation is relatively independent of the specific star formation history within the two stellar systems probed here. As shown in Fig. 3, the power-law SNe Ia DTD reproduces the W15 results best. A very similar DTD was inferred from earlier constraints on chemical evolution models using Milky Way data in Matteucci & Recchi (2001), with a similar peak in SNe Ia rate at 40−50 Myr after the burst. This DTD was also preferred in Y13 for the M*-[O/Fe] relation and for the oxygen enhancement in MW disk stars. While the use of the power-law DTD is consistent with the literature for direct supernova observations (Maoz & Mannucci 2012), as shown by Bonaparte et al. (2013), the tighter constraint on the DTD apparently comes from chemical evolution arguments as used here for ETGs and earlier in Matteucci et al. (2006) and Matteucci et al. (2009) for the Milky Way.
When we examine the different DTDs, we find that the slope of the relation below 9 Gyr is roughly the same for all DTDs. While the normalization changes slightly, for reasons discussed above, we do not consider the normalization a robust discriminant. However, the steepness of the slope for the >9 Gyr population is sensitive to the DTD. We emphasize that this is also the part of the age-[α/Fe] relation, which tends to look more universal. A DTD that produces fewer prompt SNe-Ia exhibits a steeper slope because of the higher starting [α/Fe] values. This can be understood through the luminosity-weighted average nature of the plotted quantities. For more prompt SNeIa, the [α/Fe] of the old stars will still be a mix of high and low [α/Fe] stars. Thus, even for the oldest galaxies the [α/Fe] will be low. If there are fewer prompt SNe Ia, the oldest galaxies will be dominated by high [α/Fe] stars. On the other hand, for all DTDs, 3 Gyr after the onset of star formation (i.e., around 9 to 10 Gyr lookback time), the [α/Fe] ratio will have reached the same low value of about 0.05.
This point is complimentary to the dependence of the slope of the M ∗-[O/Fe] relation on the DTD that has been discussed in Y13. Older model galaxies have shorter star formation timescales, and the [O/Fe] at z = 0 of the oldest galaxies will be higher (i.e., closer to the ratio produced by low-metallicity SNe II) for DTDs with smaller prompt components.
Finally, we note as a caveat that we have neglected IMF variations for the arguments presented here. As very recently pointed out again in Martín-Navarro (2016), a change of IMF does have an effect on [α/Fe] evolution and therefore might affect the inferences concerning the DTD. On the other hand, changes in the IMF result mostly in changes of the [α/Fe] plateau value and not in the actual evolution of [α/Fe] with age (Romano et al. 2005). In addition, O is more affected than Mg because O yields change more significantly with stellar mass than those of Mg.
4.3. Other combinations of DTD and SFH that fit the data
Snaith et al. (2014) showed that the stellar data of H13 can be fit with a significantly different DTD. Their DTD was based on a physical model with a single degenerate progenitor (Kawata & Gibson 2003). It was bimodal, with one component due to main-sequence mass donors and a more delayed component due to red giant mass donors. However, none of those was a prompt component in the classical sense because no SN Ia explodes before 0.7 Gyr after star formation. In both the bimodal and the power law DTD we used, the first SNe Ia explode after 0.035 Gyr and about half of all SNe Ia explode before 0.4 Gyr. Our chosen shortest delay time reflects the lifetime of an 8 M⊙ star, the most massive secondary companion normally assumed in SNIa progenitor models Matteucci & Greggio (1986), Greggio (2005), Matteucci et al. (2006, 2009). It also allows us to meet observational constraints on the SNIa rate (Brandt et al. 2010; Maoz & Badenes 2010).
The difference in DTD choice between Snaith et al. (2014) and this work (and e.g. Matteucci & Recchi 2001) has a consequence on the old-part slope of the age-[α/Fe] relation. In their case, the starting value of [α/Fe] (~13 Gyr ago) is always the same, but the end value of [α/Fe] (at ~9 Gyr) depends on the star formation history. In our case, the end value is always the same, but the starting value depends on the DTD (i.e., number of prompt SNeIa with delay times between 35 and 100 Myr). Therefore, we can both obtain very similar old-part slopes, but for very different reasons. Distinguishing between the Snaith et al. (2014) results and ours thus hinges on the SN Ia rates at delay times between 35 and 100 Myr.
5. Conclusions
We have compared the age-[α/Fe] relation between ETGs and the solar neighborhood for data and models. We found that the relation is quantitatively the same and that both Milky Way and early-type galaxy data require a DTD with a small prompt component (<30% of SNe-Ia exploding within 100 Myr). For example, a power-law DTD, such as those commonly derived from observations of the SN-Ia rate, matches this requirement. We also suggested that the observed scatter in the age-[α/Fe] relation for ETGs might be driven by differences in the onset of star formation in those systems. For the existing range of galactic systems and therefore star formation histories we studied, the age-[α/Fe] relation is self-similar on widely different scales. A tentative explanation for this seeming universality of the age-[α/Fe] relation is that is results from averaging of different stellar populations with varying chemical evolution histories. It thus does not seem to be a useful tool for understanding the star formation histories of galaxies, in contrast to the more widely used [Fe/H]-[α/Fe] relations.
Acknowledgments
We acknowledge the report from the anonymous referee that helped to significantly sharpen the arguments presented in this paper. C.J.W. and P.C. acknowledge support through the Marie Curie Career Integration Grant 303912. R.M.Y. acknowledges support through the Sofia Kovalevskaja Award to P. Schady from the Alexander von Humboldt Foundation of Germany. S.C. acknowledges support from the European Research Council via an Advanced Grant under grant agreement No. 321323-NEOGAL. G.B. acknowledges support for this work from the National Autonomous University of México (UNAM), through grant PAPIIT IG100115. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anders, F., Chiappini, C., Rodrigues, T. S., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527204 [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonaparte, I., Matteucci, F., Recchi, S., et al. 2013, MNRAS, 435, 2460 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Springel, V., White, S. D. M., Jenkins, A., & Lemson, G. 2009, MNRAS, 398, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Tojeiro, R., Aubourg, É., et al. 2010, AJ, 140, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Anders, F., Rodrigues, T. S., et al. 2015, A&A, 576, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Bruzual, G., Charlot, S., et al. 2007, MNRAS, 382, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Feltzing, S., Holmberg, J., & Hurley, J. R. 2001, A&A, 377, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., & White, S. D. M. 2006, MNRAS, 370, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Graur, O., Poznanski, D., Maoz, D., et al. 2011, MNRAS, 417, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Rodney, S. A., Maoz, D., et al. 2014, ApJ, 783, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, G. J., Faber, S. M., & Schiavon, R. P. 2010, ApJ, 721, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansson, J., Thomas, D., & Maraston, C. 2012, MNRAS, 421, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I. 1999, MNRAS, 306, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Kawata, D., & Gibson, B. K. 2003, MNRAS, 346, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntschner, H., Emsellem, E., Bacon, R., et al. 2010, MNRAS, 408, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Di Matteo, P., Haywood, M., & Snaith, O. N. 2014, ApJ, 789, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Badenes, C. 2010, MNRAS, 407, 1314 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2012, PASA, 29, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Brandt, T. D. 2012, MNRAS, 426, 3282 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Bournaud, F., Croton, D. J., Dekel, A., & Teyssier, R. 2012, ApJ, 756, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Rix, H.-W., Silva Aguirre, V., et al. 2015, MNRAS, 451, 2230 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I. 2016, MNRAS, 456, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- Matteucci, F., & Recchi, S. 2001, ApJ, 558, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., Panagia, N., Pipino, A., et al. 2006, MNRAS, 372, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., Spitoni, E., Recchi, S., & Valiante, R. 2009, A&A, 501, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portinari, L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505 [NASA ADS] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Romano, D., Chiappini, C., Matteucci, F., & Tosi, M. 2005, A&A, 430, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A. M., Bergemann, M., Ruchti, G., & Casagrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strolger, L.-G., Riess, A. G., Dahlen, T., et al. 2004, ApJ, 613, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Tinsley, B. M. 1979, ApJ, 229, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Coelho, P., Gallazzi, A., & Charlot, S. 2009, MNRAS, L275 [Google Scholar]
- Walcher, C. J., Coelho, P. R. T., Gallazzi, A., et al. 2015, A&A, 582, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yates, R. M., Henriques, B., Thomas, P. A., et al. 2013, MNRAS, 435, 3500 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison of the correlations between age and [α/Fe] for two very different types of astrophysical objects. Upper left panel: the luminosity-weighted average properties of early-type galaxies from W15. The solid line is a formal fit to the two regimes, separated at 9 Gyr. Upper right panel: stars in the local neighborhood from B14 (solid squares) and H13 (stars). The dashed line is a formal fit to the B14 data for the two regimes, separated at 9 Gyr. The solid line repeats the fit for galaxies from the left panel. Lower left panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13. The solid line repeats the fit for the W15 data for comparison. No observational errors have been added to the model galaxy properties, which largely explains the difference in scatter. Lower right panel: single-star properties for a simulated solar neighborhood from M13. The dashed line repeats the fit to the B14 data for comparison. Here, observational errors have been added for better comparison of scatter. |
| In the text | |
 |
Fig. 2 Comparison of the correlations between age and [Fe/H] for two very different types of astrophysical objects. The panels and lines are the same as in Fig. 1. |
| In the text | |
 |
Fig. 3 Comparison of the correlations between age and [α/Fe] for three different prescriptions for the DTD of SNeIa in the Y13 model. Upper left panel: the luminosity-weighted average properties of early-type galaxies from W15. The solid line is a formal fit to the two regimes, separated at 9 Gyr and repeated in all the other panels. Upper right panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13, using a Gaussian DTD. Lower left panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13 using a power law DTD. Lower right panel: the luminosity-weighted average properties of early-type galaxies in the semi-analytic model of Y13 using a bimodal DTD. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


