| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 20 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201528010 | |
| Published online | 20 October 2016 | |
The Gaia-ESO Survey: Hydrogen lines in red giants directly trace stellar mass
1 Max-Planck Institute for Astronomy, 69117 Heidelberg, Germany
e-mail: bergemann@mpia-hd.mpg.de
2 Instituto de Ciencias del Espacio (ICE-CSIC/IEEC), Campus UAB, Carrer Can Magrans S/N, 08193 Bellaterra, Spain
3 Rudolf-Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, OX1 3NP, Oxford, UK
4 Lund Observatory, Box 43, 221 00 Lund, Sweden
5 Department of Physics and Astronomy, Division of Astronomy and Space Physics, Angstrom laboratory, Uppsala University, Box 516, 75120 Uppsala, Sweden
6 Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077 Gttingen, Germany
7 Institute of Astronomy, University of Cambridge, Madingley Road, CB3 0HA, Cambridge, UK
8 INAF−Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
9 Research School of Astronomy & Astrophysics, Mount Stromlo Observatory, The Australian National University, ACT 2611, Australia
10 INAF−Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
11 Laboratoire Lagrange, Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, BP 4229, 06304 Nice Cedex 4, France
12 Department for Astrophysics, Nicolaus Copernicus Astronomical Center, ul. Rabianska 8, 87-100 Torun, Poland
13 Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munckegade 120, 8000 Aarhus, Denmark
14 Institute of Theoretical Physics and Astronomy, Vilnius University, Goštauto 12, 01108 Vilnius, Lithuania
15 ASI Science Data Center, via del Politecnico SNC, 00133 Roma, Italy
16 Instituto de Fisica y Astronomia, Fac. de Ciencias, U de Valparaiso, 1111 Gran Bretana, Playa Ancha, Chile
17 INAF−Osservatorio Astronomico di Palermo, Piazza del Parlamento, 1, 90134 Palermo, Italy
18 Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya st. 48, 119017 Moscow, Russia
Received: 18 December 2015
Accepted: 16 June 2016
Red giant stars are perhaps the most important type of stars for Galactic and extra-galactic archaeology: they are luminous, occur in all stellar populations, and their surface temperatures allow precise abundance determinations for many different chemical elements. Yet, the full star formation and enrichment history of a galaxy can be traced directly only if two key observables can be determined for large stellar samples: age and chemical composition. While spectroscopy is a powerful method to analyse the detailed abundances of stars, stellar ages are the missing link in the chain, since they are not a direct observable. However, spectroscopy should be able to estimate stellar masses, which for red giants directly infer ages provided their chemical composition is known. Here we establish a new empirical relation between the shape of the hydrogen line in the observed spectra of red giants and stellar mass determined from asteroseismology. The relation allows determining stellar masses and ages with an accuracy of 10−15%. The method can be used with confidence for stars in the following range of stellar parameters: 4000 < Teff < 5000 K, 0.5 < log g< 3.5, −2.0 < [Fe/H] < 0.3, and luminosities log L/LSun < 2.5. Our analysis provides observational evidence that the Hα spectral characteristics of red giant stars are tightly correlated with their mass and therefore their age. We also show that the method samples well all stellar populations with ages above 1 Gyr. Targeting bright giants, the method allows obtaining simultaneous age and chemical abundance information far deeper than would be possible with asteroseismology, extending the possible survey volume to remote regions of the Milky Way and even to neighbouring galaxies such as Andromeda or the Magellanic Clouds even with current instrumentation, such as the VLT and Keck facilities.
Key words: techniques: spectroscopic / stars: fundamental parameters / stars: late-type / Galaxy: stellar content
© ESO, 2016
1. Introduction
One of the key problems in stellar and galactic astrophysics is determining the age of a star. The star formation history of a population or galaxy can be best traced when we know how to connect the chemo-dynamical data of stars to their formation time.
Age determinations for the Galactic field stars have traditionally been limited to stars on the upper main sequence and on the subgiant branch. The most convenient and widely used approach relies on fitting stellar isochrones to the classical observables (e.g. Teff, log g, and [Fe/H]) (Pont & Eyer 2004; Jørgensen & Lindegren 2005). To a lesser extent, empirically calibrated methods are used (Soderblom 2010, 2015). They rely on various observational findings, such as emission lines that are related to the chromospheric activity, the depletion of Li with stellar age as the convection zone of a star thickens, and surface rotation, which slows down with increasing age. For the cool main-sequence stars, more elegant and accurate adaptations of the rotation method have been proposed (García et al. 2014; Meibom et al. 2015), but they also rely on ultra-precise light-curves.
For red giant stars, which are the stars of most prominent interest in the context of Galactic and extra-galactic archaeology, classical isochrone methods are not useful: even when the metal content is known, isochrones of different ages are very close and would require Teff and log g determinations with better than 0.5% accuracy, including the systematic uncertainty of the theoretical Teff scale. Only if luminosities of the stars are accurately known, for instance, because distances are available and reddening is not a problem, can evolutionary models be used to determine stellar mass (Ghezzi & Johnson 2015). However, these determinations also suffer from systematic errors in input stellar parameters and uncertainties of the stellar models. The process of ageing may be related to in situ stellar nucleosynthesis, for example the ratio of carbon over nitrogen abundance increases as the star experiences multiple dredge-up episodes and the products of stellar nucleosynthesis are mixed to the surface (Masseron & Gilmore 2015; Martig et al. 2016; Ness et al. 2016).
Recently, asteroseismology has emerged as a promising tool to determine masses of stars that display solar-like oscillations, that is stochastic oscillations excited by turbulent motions in the stellar convective envelope. Asteroseismic observations provide the surface gravity and mean density of a star, and, in combination with Teff and [Fe/H], yield precise masses for stars of all types (Chaplin et al. 2014; Pinsonneault et al. 2014), from the main sequence through the hydrogen-shell burning (red giant, hereafter RGB) to the core-helium burning (red clump, hereafter RC) phase. Asteroseismology is a very promising method, but it has two caveats. First, the accuracy of masses and ages derived depends on asteroseismic scaling relations. These relations may suffer from systematic biases of a few percent. A systematic error in νmax propagates to the 3rd power in mass and the error in Δν to the fourth power (Belkacem et al. 2011; Miglio et al. 2012; Coelho et al. 2015; White et al. 2015). Second, the method is mainly useful for sub-Galactic studies in the limited volume of the Milky Way, since the photometric data quality quickly deteriorates with magnitude and hence distance. Thus the technique cannot provide any mass or age estimates for larger distances, in- and outside the Galaxy.
The determination of the mass and composition of an evolved red giant star is, unlike for a main sequence star, an excellent proxy for its age. The time a star lives as a red giant is a small fraction of its total main sequence lifetime. The latter is determined through stellar evolutionary models by the initial mass and composition of the star. Then, the age of a red giant star is to a very good approximation only a function of those two quantities. If masses, or proxies for masses, can be estimated from observations, age-dating of giants is more straightforward than for main-sequence stars (Soderblom 2010).
Here we report on a newly observed relationship between the shape of the optical hydrogen line (Hα) and the mass of red giant stars. More massive stars appear to have fainter, that is weaker, Hα lines. We make use of high-resolution spectra with high signal-to-noise ratios (S/Ns) from different observational programs, including the Gaia-ESO large spectroscopic survey (Gilmore et al. 2012; Randich et al. 2013) and asteroseismic data from the CoRoT and Kepler space missions. Our approach is purely empirical. We cannot yet identify the physical mechanism underlying the relation, because there are no red giant model atmospheres built from first principles that could be used to reproduce the observed Hα line, to guide our understanding of the relationship with the stellar mass. The relationship, which we established on Galactic field stars, also gives accurate results for the stars in open and globular clusters, enabling direct spectroscopic stellar mass measurements without isochrone fitting.
The paper is structured as follows. Our observations and the data analysis are presented in Sect. 2, along with a brief summary of the current modelling of Balmer lines in the spectra of cool stars. The new method to derive masses and their implied ages is described in Sect. 3.2. In Sect. 5 we outline some applications of the method in the context of Galactic and extra-galactic astrophysics.
2. Observations and analysis
2.1. Spectroscopic observations
Our main dataset contains the high-resolution stellar spectra from the Gaia-ESO second and third data releases (iDR2, iDR3). The high-resolution Gaia-ESO spectra are obtained with UVES spectrograph at the VLT, R ~ 47 000. The data are publicly available through the ESO archive. The majority of the spectra have S/Ns between 50 and 220. In the top tier we have the stars with high-quality asteroseismic data from CoRoT, but we also include red giants observed in open and globular clusters (Table 1). The stars in clusters do not belong to our core dataset, however, since their masses and ages are determined by another method, the cluster colour-magnitude diagram fitting. We assumed the same mass for all stars in a cluster. The stars are nearly coeval (to about 10%), thus their initial masses differ by no more than 3%. As most of the stars are not so high on the RGB to be significantly affected by mass loss, we may assume that their present-day mass is a good proxy for their initial mass.The data reduction of the UVES spectra has been described in detail by Sacco et al. (2014). The radial velocity correction was performed by masking the Balmer lines and regions affected by telluric contamination. The spectra were normalised by dividing them with a function that describes the stellar continuum emission convolved with the FLAMES-UVES instrumental response as described in Sacco et al. (2014). In total, the Gaia-ESO sub-sample contains 21 CoRoT stars in the Galactic field and 73 stars in 7 star clusters. The observational details are listed in Tables A.1 and A.3.
In addition, we included 47 stars from Thygesen et al. (2012) that were observed by Kepler and included in the first APOKASC Catalog (Pinsonneault et al. 2014). The evolutionary status is known for some of them. The stellar spectra were taken on different facilities with resolving powers ranging from 67 000 (NOT) to 80 000 (NARVAL). The spectra are available from Thygesen et al. (2012). The S/Ns are between 80 − 100 to 200. Our sample also includes two very metal-poor stars, KIC 4671239 (Hennes, Casagrande et al. 2014a) and KIC 7693833 (Rogue, Thygesen et al. 2012). These objects are the targets of Silva Aguirre et al. (in prep.). The spectrum of KIC 4671239 is now publicly available from the NOT database, and KIC 7693833 was observed by Thygesen et al. (2012). The data reduction of these spectra is described in Thygesen et al. (2012).
The full sample contains 69 Galactic field stars with asteroseismic masses and 73 stars in the clusters. Figure 1 shows the location of the stars on the Hertzsprung-Russell diagram. These are red giants or red clump stars with Teff in the range 4000 − 5000 K, and log g from 0.5 to 3.6. The stars span a wide range of metallicity from − 2.64 to 0.5.
For consistency, we renormalised all available spectra using the same procedure as in Schönrich & Bergemann (2014), which fits selected continuum windows with a low-order polynomial.
 |
Fig. 1 Hertzsprung-Russell diagram for the observed stellar sample: black filled points show the stars with asteroseismic masses, triangles depict the stars in stellar clusters. The stars in the globular clusters NGC 2808 and NGC 4372 are shown with green triangles and brown squares, respectively. The Garstec evolutionary tracks (Serenelli et al. 2013) for different masses and metallicities are also shown. |
Stellar parameters for star clusters.
2.2. Model atmospheres and spectroscopic analysis
For the Gaia-ESO dataset, we used the recommended Teff and [Fe/H] available from the iDR3 stellar parameter analysis run (Table A.2). The parameter values were determined as described in Smiljanic et al. (2014) and in Bergemann et al. (2014), using several different methods of spectroscopic analysis. The radiation transport was solved in local thermodynamic equilibrium (LTE) with MARCS model atmospheres (Gustafsson et al. 2008). The typical uncertainty in the parameter values is 100 K in Teff and 0.1 dex in [Fe/H]. For one of the NGC 4372 stars, 12253419-7235252, we adopted the following uncertainties: δ Teff = 100 K, δlog g = 0.5 dex, δ [Fe/H] = 0.2 dex, because no data are available in the survey database. The uncertainties are conservative and reflect the deviation of individual spectroscopic estimates. These uncertainties have a very small effect on the mass estimates: the 100 K error in Teff propagates as a 5% error in mass, and the error of 0.1 dex in [Fe/H] propagates as a 1.5% error in mass. The comparison with the independent photometric estimates gives us confidence in the accuracy of stellar parameters. The spectroscopic Teff estimates agree to better than 70 K with the temperatures determined using the method of infra-red fluxes by Casagrande et al. (2014b).
For the Thygesen et al. (2012) stellar sample, we used the values of Teff and [Fe/H] that were determined by Bruntt et al. (2012). The stellar parameters are provided in Table A.5. One of the very metal-poor (VMP) stars, Rogue, has metallicity [Fe/H] = − 2.23 and was analysed by Thygesen et al. (2012). For the other, Hennes, we used the mean of two values, kindly provided to us by A. Korn and G. Ruchti, [Fe/H] = − 2.64 ± 0.22.
2.3. Asteroseismic data and analysis
Stellar masses were determined using the global seismic quantities that are available from the CoRoT and Kepler space mission observations. For the Gaia-ESO stellar sample, the asteroseismic data were taken from Mosser et al. (2010). The large frequency separation, Δν, is approximately the average frequency separation of radial oscillation modes of consecutive order. The second seismic quantity is νmax, the frequency at which the oscillation power spectrum exhibits its maximum power. Δν and νmax scale with global stellar parameters as 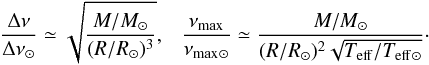 (1)For each star, Δν and νmax together with Teff and [Fe/H] values (Sect. 2.2) were used as inputs to the BeSPP code (Serenelli et al. 2013), which is a Bayesian grid-based modelling algorithm for determining fundamental stellar properties (mass, age, evolutionary stage). BeSPP uses a large grid of Garstec stellar evolutionary tracks (6 × 107 stellar models, 0.6 ≤ M/M⊙ ≤ 3.0), from the pre-main sequence to the beginning of the thermal pulses on the asymptotic giant branch (Weiss & Schlattl 2008). The posterior probability of each model is constructed as the product of the likelihood of the observables given the model and a set of prior probabilities related to the initial mass function, star formation rate, and age-metallicity relation (see Serenelli et al. 2013 for details). The evolutionary state of stars, when known as is the case for some stars in Thygesen’s sample, is also added as a binary prior. The full probability distribution function is then marginalised to obtain the posterior probability distributions for stellar mass and age. For the VMP stars, Rogue and Hennes, we computed the asteroseismic masses using the scaling relations with a reference value for Δν computed from the function by Guggenberger et al. (2016). We used their results because the validity of standard solar references in the scaling relations at low metallicity is currently under debate (Epstein et al. 2014). Our mass estimate for Hennes agrees within the uncertainties with the value by Casagrande et al. (2016), who estimate its mass to be 1.07 MSun. Both stars will be the subject of a detailed asteroseismic investigation (Silva Aguirre et al., in prep.).
(1)For each star, Δν and νmax together with Teff and [Fe/H] values (Sect. 2.2) were used as inputs to the BeSPP code (Serenelli et al. 2013), which is a Bayesian grid-based modelling algorithm for determining fundamental stellar properties (mass, age, evolutionary stage). BeSPP uses a large grid of Garstec stellar evolutionary tracks (6 × 107 stellar models, 0.6 ≤ M/M⊙ ≤ 3.0), from the pre-main sequence to the beginning of the thermal pulses on the asymptotic giant branch (Weiss & Schlattl 2008). The posterior probability of each model is constructed as the product of the likelihood of the observables given the model and a set of prior probabilities related to the initial mass function, star formation rate, and age-metallicity relation (see Serenelli et al. 2013 for details). The evolutionary state of stars, when known as is the case for some stars in Thygesen’s sample, is also added as a binary prior. The full probability distribution function is then marginalised to obtain the posterior probability distributions for stellar mass and age. For the VMP stars, Rogue and Hennes, we computed the asteroseismic masses using the scaling relations with a reference value for Δν computed from the function by Guggenberger et al. (2016). We used their results because the validity of standard solar references in the scaling relations at low metallicity is currently under debate (Epstein et al. 2014). Our mass estimate for Hennes agrees within the uncertainties with the value by Casagrande et al. (2016), who estimate its mass to be 1.07 MSun. Both stars will be the subject of a detailed asteroseismic investigation (Silva Aguirre et al., in prep.).
2.4. Current modelling of Hα spectra of cool stars
It is well-known that strong spectral lines, including the Hα, Mg II UV doublet, and Ca II near-IR triplet, cannot be fit in the spectra of cool stars with the classical models of stellar photospheres, that is, with models based on the standard assumptions of 1D hydrostatic equilibrium and LTE (Rutten 2008; Rutten & Uitenbroek 2012, and references therein).
To illustrate the problem, we show the observed and synthetic line profiles for the two reference stars, the Sun (KPNO FTS atlas), and HD 122563 (the UVES POP spectrum Bagnulo et al. 2003) in Fig. 2. The model spectra were computed in LTE using the broadening theory of Barklem et al. (2000) using the time- and spatially averaged 3D hydrodynamical models from the Stagger grid (Collet et al. 2011; Bergemann et al. 2012; Magic et al. 2013a,b) and the MARCS models (Gustafsson et al. 2008). In both cases, the models fail to describe the observed line shape: the observed profile is stronger than the best-fit model. The plot also shows non-LTE (NLTE) line profiles computed using the H model atom from Mashonkina et al. (2008). While NLTE radiation transport does improve the fit in the Hα core, the model line is still too narrow compared to the observed data.
Remarkably, every RGB and RC star in the sample suffers from a similar systematic offset. Figure 3 compares the observed equivalent widths (EWs) of the Hα line for our stellar sample with asteroseismic masses (Sect. 2.1) with the best-fit 1D and average 3D model atmospheres. Comparison with the observed EWs shows a much greater than expected spread of the line strengths: the differences amount to almost ~700 mÅ for the coolest stars, which is an error greater than 50%. The error shows a striking correlation with the surface stellar parameters, the effective temperature, and the surface gravity. Taking the mean 3D structures into account (Fig. 3, bottom panel) does not improve the agreement with the Hα observations, which suggests that some other physical process is needed to explain the data.
 |
Fig. 2 Model line profiles (colour lines) computed with different physics (1D LTE, mean 3D LTE, 1D NLTE) in comparison with the observed spectrum of the Sun (dots, top) and the metal-poor red giant HD 122563 (dots, bottom). The models lie far away from the data, thus we resort to an empirical method (Sect. 2.5). |
While the systematic discrepancy has been known for decades, the methodological strategies to improve the models have been quite fragmented so far. Dupree et al. (1984) were among the first to suggest that adding chromospheres and mass flows to the 1D static model photospheres in the framework of “extended atmosphere models” may work for cool stars. Such semi-empirical models assume that the chromospheres are excited by magnetic and mechanical disturbances propagating as electromagnetic-hydrodynamical waves (Alfvén 1942; Babcock 1961; Hartmann & MacGregor 1980). The deposition of energy and momentum due to shock waves defines chromospheric energy balance, thus, at the very least, incident wave energy flux and the magnetic field are needed to compute the model. The ability of such models to fit the observed stellar spectra, however, critically depends on the availability of additional information. The observed Hα line profiles in the stellar spectra were used to iteratively constrain the free parameters, including the temperature (hereafter, T)-depth slope, the location of the T minimum, and the velocity field (Meszaros et al. 2009; Dupree et al. 2016). All these parameters cannot yet be calculated from first principles: in particular, the choice of the profile of turbulent velocity with depth is essential to fit the Hα width (Dupree et al. 2016). Moreover, one essential ingredient in the chromospheric models is NLTE radiation transport, since under the LTE assumption the line source function couples to the outwardly increasing temperature and causes an unphysical emission in the line cores (Przybilla & Butler 2004).
 |
Fig. 3 Comparison of the observed and synthetic equivalent widths of the Hα line for the reference asteroseismic stellar sample. See Sect. 2.4 for more detail. |
Rutten & Uitenbroek (2012) explored the formation of the solar Hα line using the 1D solar plane-parallel Kurucz model atmosphere and the semi-empirical solar chromospheric model by Fontenla et al. (2009). Their results (see their Fig. 8) suggest that NLTE radiation transport and chromospheric back-radiation are two necessary, albeit not sufficient, ingredients to describe the Hα profile. While the Kurucz (Kurucz 1979) model predicts too narrow Hα line cores, in the model with an overlying (but empirically constrained1) chromosphere the Hα core forms much higher in the atmosphere and is more opaque. On the other hand, their best model also produces too little opacity in the Hα core to fit the observed solar spectrum, similar to what is shown in Fig. 2 (top panel), although the NLTE line centre intensity (at 6562.8 Å) is closer to the observational data. A similar approach has been explored by Przybilla & Butler (2004), who showed that the irradiation of the inner photospheric layers by the chromosphere does little for the Hα profile in the solar spectrum (their Fig. 2, top panel). Remarkably, four different solar model atmospheres, with and without chromospheres, produce essentially identical NLTE Hα profiles, challenging the argument that chromospheres are essential in describing the Hα line shapes. Thus, apart from the conceptual difficulty with computing chromospheres from first principles, the effect of chromospheres on the stellar Hα lines is still unclear. Disconcerting as it may be, as such, the 1D static or dynamical models with parametrised chromospheres do not yet offer a suitable framework for the quantitative analysis of Hα profiles in stellar spectra.
More advanced 3D radiation magneto-hydrodynamic (MHD) simulations of chromospheres have been developed only recently (Carlsson & Stein 2002; Hansteen 2004; Leenaarts 2010; Gudiksen et al. 2011; Hansteen et al. 2015). The models are clearly more physically realistic than the 1D or 2D implementations, but at present their applicability to other stars than the Sun remains questionable, since the simulations are also parametrised and require making use of spatially resolved stellar observations, such as those provided by the MDI instrument for the Sun (Leenaarts et al. 2012). In the MHD simulations of the solar chromosphere, the velocity fields that generate acoustic waves at the bottom of the MHD solar simulation are set to reproduce the velocity profiles deduced from the Ni line-core imaging, the type of observations that is currently unavailable for any other star. There are also still some open questions that pose a challenge to the simulations (Leenaarts 2010). First, the MHD models combined with the Hinode/SOT Ca II observations of the Sun predict that the power in acoustic waves is far too small to explain the chromospheric radiative energy losses (Carlsson et al. 2007). In this discussion, the relevant waves are those with frequencies above 20 mHz and 50 mHz, above this limit, most of the acoustic energy produced in the convective zone is strongly damped in the photosphere (Carlsson & Stein 2002). Second, fitting the Hα core with the MHD simulations has traditionally been problematic because of the missing Hα opacity in the chromosphere. Leenaarts et al. (2012, 2015) showed that including non-equilibrium ionisation of hydrogen in the calculations of the equation-of-state in the 3D MHD models could help to resolve the long-standing disagreement with the Hα line-core imaging observations of the Sun. The simulations show that the opacity in the outer Hα core is correlated with the gas temperature, while the opacity in the inner core is mostly sensitive to the gas density. However, it yet remains to be investigated whether the MHD models with prescribed radiative cooling rates (from the 1D chromospheric simulations that are only computationally tractable at present) describe the observed solar Hα line profile shape, not only the monochromatic brightness contrast across small areas on the solar surface. Finally, the 3D MHD chromospheric simulations for stars other than the Sun are currently not available, therefore neither quantitative nor qualitative statements about the behaviour of Hα lines in other stars, especially those with very different interior properties, such as RGB or RC, can be made.
2.5. Empirical fits to the Hα profile
As discussed in the previous section, it is currently not possible to construct a grid of stellar atmosphere models that include all the sophisticated physical processes needed to describe the hydrogen line profiles in the observed spectra of RGB and RC stars. On the other hand, the obvious systematic misfit in the Hα line (Figs. 2 and 3) is puzzling, and it has prompted us to take a different, empirically motivated, approach to the problem. We ask whether there is a mathematical function that fits the Hα line profiles in the spectra of all our sample stars.
Since the red wing of the Hα line is blended by a metallic feature (the line of neutral cobalt), we focused on the unblended left side of the core of the line, as shown by bold blue lines in Fig. 5. The line mask is the same for all stars, it covers the wavelength range 6562.0 − 6562.8 Å. By selecting this mask, we ensure that the Co I blend has no effect on the fit. The left limit at 6562.0 Å is set to minimise the contribution of the Si I and Fe I blends. None of the stars in the sample show evidence of emission in the wings or significant core shifts that could introduce spurious artefacts in the fit. Such features are usually seen in the spectra of metal-poor, [Fe/H] < − 1, red giants brighter than log L/L⊙ ~ 2.5 (Cacciari et al. 2004; Meszaros et al. 2009), while all but two of our reference stars with asteroseismic masses are fainter than this luminosity threshold (Fig. 1). We also do not see signatures of emission or line core shift in the most metal-poor stars in our sample, for instance KIC 7693833 and KIC 8017159 (Fig. 5).
We explored different functions and found that the observed blue wing of the Hα line is well described by a cubic exponential function: 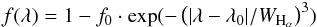 (2)where λ0 is the central wavelength of the line, 6562.819 Å (Baker 2008) and is fixed, f0 the minimum flux in the line core, and WHα a free parameter that correlates with the width of the spectral line and, as we show below, with the mass of a star. It is important to stress that this is a purely mathematical function that has no input from the stellar atmosphere models or instrumental effects, such as the spectrograph line spread function. For our spectra, the resolving power is so high that the latter effects do not matter. However, for low-resolution spectra, values of WHα derived from different observational set-ups cannot be compared directly. The free parameters to be fit to an observed profile are the line depth parameter, f0, and the line width parameter, WHα; their measured values for the full stellar sample are given in Tables A.2, A.4, A.5. The uncertainty of the fitting was determined by shifting the continuum by ±2σ from the best-fit solution and repeating the function fit. The difference with the best-fit normalisation then gives the uncertainty in the WHα estimate, which for all stars in the sample is below 0.01 Å. It is thus reasonable to adopt the same error of WHα for all stars.
(2)where λ0 is the central wavelength of the line, 6562.819 Å (Baker 2008) and is fixed, f0 the minimum flux in the line core, and WHα a free parameter that correlates with the width of the spectral line and, as we show below, with the mass of a star. It is important to stress that this is a purely mathematical function that has no input from the stellar atmosphere models or instrumental effects, such as the spectrograph line spread function. For our spectra, the resolving power is so high that the latter effects do not matter. However, for low-resolution spectra, values of WHα derived from different observational set-ups cannot be compared directly. The free parameters to be fit to an observed profile are the line depth parameter, f0, and the line width parameter, WHα; their measured values for the full stellar sample are given in Tables A.2, A.4, A.5. The uncertainty of the fitting was determined by shifting the continuum by ±2σ from the best-fit solution and repeating the function fit. The difference with the best-fit normalisation then gives the uncertainty in the WHα estimate, which for all stars in the sample is below 0.01 Å. It is thus reasonable to adopt the same error of WHα for all stars.
Figure 5 compares the function fit from Eq. (2) with the observed Hα line profiles in several program stars. The theoretical line profiles computed in 1D LTE and NLTE are also shown.
Line bisectors, included in the plot insets, help to understand how the observed Hα shape changes as a function of stellar parameters. The bisectors were computed by dividing the spectral line into 15 segments. Then the bisector velocity vbis was estimated at full width at half-maximum of the line profile, as the wavelength shift relative to the central Hα wavelength. The Co I blend at 6563.42 Å, which is very strong in solar metallicity giants ([Fe/H] > − 1), causes an inverse c-shaped bisector profile (Fig. 5, bottom panels), with vbis up to 2 km s-1. In the low-metallicity spectra, [Fe/H] < − 2, the behaviour is inverted and the bisector profile has a c-shape. The bisector velocity measurements for the full asteroseismic sample are shown in Fig. 4. The line blending explains why the bisector velocity vbis shows a strong correlation with [Fe/H]. We stress, however, that we fitted only the blue part of the Hα core, so that the Co blend in the red wing has no effect on the WHα measurements.
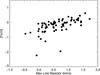 |
Fig. 4 Bisector velocity at the FWHM of the Hα profile (km s-1) as a function of metallicity [Fe/H] for the observed stellar sample. |
 |
Fig. 5 Observed Hα profile (black dots) in the selected program stars and the best-fit empirical model from Eq. (2) (bold blue line, 6562.0 to 6562.8 Å). The red and black lines correspond to the best-fit theoretical models computed in 1D LTE and 1D NLTE, respectively. The part of the Hα line used in the fit is the same for all stars in the sample. The thin blue line is only shown to help guide the eye; the red wing of Hα was not used in the fit. Line bisectors are indicated in the inset. The spectra are arranged in order of increasing metallicity. |
It should be noted that the Hα line develops strong wings in stars hotter than about 4900 − 5000 K, depending on metallicity; this is the temperature limit where interactions with ions, electrons, and hydrogen atoms become important, which leads to the specific profile shape with self-broadening, van der Waals, and Stark damping wings. Thus, the simple shape, as described by the cubic exponential function, may not apply, and caution is advised when fitting Eq. (2) to the spectra of lower RGB or subgiant branch stars.
 |
Fig. 6 Hα width parameter measurements in the observed stellar sample versus stellar effective temperature, surface gravity, and metallicity. The stars with asteroseismic data are shown with filled circles and the stars in the clusters with filled triangles. |
3. Results
3.1. Hα and stellar parameters
We have explored the correlation of the measured Hα line properties with different stellar parameters. The results for our reference asteroseismic sample and for the stars in the clusters are shown in Fig. 6. In the [Fe/H] − WHα plot, only the mean values of the measured cluster metallicity and WHα are shown because the observed scatter in [Fe/H] (as seen in Table 6) could be caused by the measurement uncertainties. Some clusters show variations in metallicity (D’Antona et al. 2016, and references therein), but this variation is small enough to not affect our conclusions. The standard error of our metallicity measurements is ~0.1 dex, comparable to the intra-cluster metallicity variations. The error bars show 1σ standard deviation of the individual WHα measurements within each cluster.
The plots show that there is no clear dependence on Teff, but there are correlations between WHα and log g, as well as between WHα and metallicity. The more metal-rich stars appear to have narrower Hα lines (smaller WHα), as opposed to the more metal-poor stars, which show broader Hα profiles and, thus, lie at high values for WHα. This correlation with metallicity is interesting because it already looks quite similar to a classic age-metallicity relation (Fig. A.1). In addition, given the WHα-metallicity correlation, it is also not surprising to find the correlation of WHα with asteroseismic log g. Surface gravity depends on the stellar mass and radius, thus this correlation may indicate that there is a more fundamental underlying relationship, such as that with stellar mass.
The stars in NGC 2808 ([Fe/H] = − 1.11) show the largest intra-cluster spread of the WHα estimates that is reflected in the large uncertainty of its mean value. The most metal-poor cluster NGC 4372 ([Fe/H] = − 2.20) also stands out in the WHα − [Fe/H] plot. The only noteworthy difference of the NGC 2808 and NGC 4372 stars with respect to the other clusters is their comparatively high luminosity (Fig. 1): most of the observed stars in these two clusters have log L/L⊙ ≥ 2.5, which is where the effect of asymmetries and periodic variations in the Hα profile might be expected to become important (Cacciari et al. 2004; Meszaros et al. 2009). However, visual inspection of the observed data did not reveal any obvious problems with the spectra. Neither do we have repeated observations of these stars to check the effect of variability. We therefore currently we do not have a suitable explanation for the behaviour of WHα in the most luminous stars in the globular clusters and set it aside as a problem to be addressed in future work.
3.2. Mass effects in the Balmer line
While the WHα vs. [Fe/H] and log g plots have suggested that WHα is related to the mass and hence age of stars, we can directly probe this by plotting the dependence between WHα and the independently determined asteroseismic mass (Fig. 7). This correlation is well defined and it appears that all stars, also those in star clusters, follow the same WHα-mass trend within the errors. Hα lines tend to be narrower in the spectra of more massive stars, but broader in the spectra of less massive stars. All we now need for a mass estimate from spectroscopy is to fit a relationship between WHα and the independent mass determinations. For the sake of simplicity, we fitted a linear relation between Hα and the logarithmic mass of stars in our sample, that is, log M = a·WHα + b. First, we applied bootstrapping to our dataset, using sampling with replacement. The sampling process was repeated n2 (about 2900) times. Then we performed a χ2 fit to the bootstrapped data to avoid that a few stars with small mass uncertainties dominate the results. In addition, we found an almost perfect linear relation between a and b. Thus, b can in turn be expressed as a linear function of the slope a, with the advantage that the uncertainty of the fit can be expressed in terms of the uncertainty in a, determined from the bootstrapping. The final result is 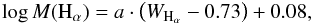 (3)where a = − 2.73 ± 0.72. This is shown in Fig. 7 as the black solid line. Dashed black lines show the 1σ uncertainty of the fit, as obtained from the bootstrap analysis described above. The shaded area is the average root-mean-square difference between the data and the fit.
(3)where a = − 2.73 ± 0.72. This is shown in Fig. 7 as the black solid line. Dashed black lines show the 1σ uncertainty of the fit, as obtained from the bootstrap analysis described above. The shaded area is the average root-mean-square difference between the data and the fit.
 |
Fig. 7 Observed relation between the Hα spectral line widths versus asteroseismic masses of stars. Star clusters from the Gaia-ESO survey are shown with green squares. The very metal-poor stars in the sample, [Fe/H] < − 2, are shown with red symbols. Dashed black lines show the 1σ uncertainty of the fit. The shaded area is the average rms between the data and the fit. See Sect. 3. |
Figure 8a compares our empirical masses determined from Eq. (3) with the reference asteroseismic masses for the program stars. Panel b shows the results from the classical stellar isochrone approach that makes use of the stellar parameters from spectroscopy (Teff, log g, [Fe/H]) and isochrones (Serenelli et al. 2013). The masses determined empirically from the Hα measurements are more precise than the classical stellar evolution approach. The plot reveals, however, that we slightly over-estimate masses at the low-mass end and under-estimate masses for more massive stars. At present, the origin of this systematics is unclear. It might be the asteroseismic estimates or some second parameter problem in Hα. More data are needed to explore these differences. Taking the uncertainty in the a coefficient into account and from cross-validating with the reference asteroseismic masses, we conclude that the accuracy of our mass estimates is about 0.15 M⊙.
3.3. Stellar ages
 |
Fig. 8 Comparison of masses (top panel) and ages (bottom panel) determined using the WHα coefficient directly (a), c)) and the classical method of stellar isochrones (b), d)). |
In view of the relationship discussed above, another interesting point is whether the Hα line profiles show any evidence of ageing, or in other words, of a star getting older. This is unlikely, even though there is observational evidence that chromospheric activity decreases with stellar age (Steiman-Cameron et al. 1985). If true, we might see some effects in the observed stellar spectra, since the degree of line core filling by the chromospheric temperature inversion would change in lockstep with age. Younger and more active stars would show brighter line cores.
However, we can use a different approach. The initial mass and chemical composition are the two fundamental quantities needed to determine the age of red giant stars. One complication is a substantial mass loss: from observations only the present-day mass can be determined, while age estimates require knowledge of the initial mass of a star. Mass loss may affect the absolute ages of very evolved (log g ≲ 1.5) low-mass RGB and RC stars. This difficulty, however, is universally present in any method for determining the age of red giant stars based on their mass, including asteroseismology, and addressing it is beyond the scope of the paper. In this work, we wish to understand whether stellar ages derived from the Hα width coefficient directly are consistent with the ages determined from asteroseismology, which is the best currently available method.
We used the masses determined from the Hα line width parameter (Eqs. (2)) and (3) in BeSPP, the Bayesian grid-based modelling code (see Sect. 2.3). The resulting ages are shown in Fig. 8 (panel c) for those stars, for which we have confidence in the reliability of the Hα mass estimates (i.e. those with Teff< 4900 K, Sect. 2.5). The age uncertainties were computed as ± 34% around the median value. This choice is supported by running the code on the ideal set of data and quantifying the offsets assuming different types of location parameter and its dispersion. The Hα ages are more consistent with the asteroseismic data than the ages derived using the classical method (panel d), that is, BeSPP with masses computed from the spectroscopic estimates of Teff, log g, and [Fe/H]. The very large errors of the ages determined with the classical method reflect the uncertainty of the input spectroscopic gravities, which are of the order ~0.2 dex.
Figure 8 highlights the main problem of the classical mass and age determination on the RGB. In the standard isochrone fitting method (panels b and d of Fig. 8), the likelihood on the RGB is nearly flat because all isochrones line up together. To distinguish stars with an age difference of even 10 Gyr, extreme and so far unachievable precision in Teff and log g (10 K and 0.02 dex) is needed. In the Bayesian framework, the ages determined using uninformative data are completely dominated by the priors, especially the initial mass function (Serenelli et al. 2013, Fig. 4). For a simple stellar population, this approach may work and produce an age distribution that does not look too odd, but this is just by chance. Moreover, this is barely applicable to any real astrophysical system, such as the Galactic disk, which is a conglomerate of stars formed in different environments in situ or even outside the Milky Way.
4. Testing for biases
The observed correlation between the measured parameter WHα and the stellar metallicities in Fig. 6 raises the question whether our fitting relation might be merely an omitted variable bias of some age-metallicity relation, or if our mass estimates are affected by a metallicity bias, for example through the dependence of the Hα line profile shape on the chemical composition of the stellar atmosphere, that is, on metallicity. Similarly, we need to check for dependencies on log g and Teff.
 |
Fig. 9 Difference between the Hα masses and asteroseismic masses as a function of Teff, [Fe/H], and log g. |
We can test this quite easily: since our sample is well populated (independently) in all dimensions (asteroseismic mass, Teff, [Fe/H], log g), additional dependencies would be detected in a regression analysis against the other variables and thus would indicate if the equation is subject to omitted variable bias. Our relation between mass and WHα was derived from the comparison with asteroseismic masses without respect to the other parameters, therefore we can simply test for a correlation between the residuals of the mass determination and log g, for example. If log g had an effect on our WHα estimates, it would be detected in the regression analysis and be apparent in the plot of residuals (Fig. 9). However, visual inspections as well as the sample statistics affirm that the mass residuals between our spectroscopic method and asteroseismology show no correlation with the other stellar parameters (Fig. 9). To test this statistically, we performed a linear regression with the equation 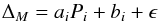 (4)where ΔM = MHα − Mseismic is the difference or residual between our masses and the asteroseismic masses, Pi is the parameter in question ([Fe/H], log g, Teff), ai is the slope (which should be ~0 in the ideal case) and bi is the offset. The results are reported in Table 2, where we show on the left the fit parameters in a weighted regression using the errors from asteroseismic and spectroscopic mass determinations and on the right the fit parameters from a simple linear regression. The table shows that the only trend that reaches the 2σ significance limit is the trend with metallicity. However, this trend was halved when we performed a simple linear regression instead of weighted least squares. It is mostly caused by mild outliers on the very metal-poor end and the most metal-rich star in the sample: any trend fully vanishes when we exclude the stars with [Fe/H] < −2.0 and [Fe/H] > 0.3. While this might well be a fortuitous, it might point to (partly known) problems with asteroseismic scaling relations. On the other hand, this test indicates that our method can be used with good confidence in the metallicity range −2.0 < [Fe/H] < 0.3.
(4)where ΔM = MHα − Mseismic is the difference or residual between our masses and the asteroseismic masses, Pi is the parameter in question ([Fe/H], log g, Teff), ai is the slope (which should be ~0 in the ideal case) and bi is the offset. The results are reported in Table 2, where we show on the left the fit parameters in a weighted regression using the errors from asteroseismic and spectroscopic mass determinations and on the right the fit parameters from a simple linear regression. The table shows that the only trend that reaches the 2σ significance limit is the trend with metallicity. However, this trend was halved when we performed a simple linear regression instead of weighted least squares. It is mostly caused by mild outliers on the very metal-poor end and the most metal-rich star in the sample: any trend fully vanishes when we exclude the stars with [Fe/H] < −2.0 and [Fe/H] > 0.3. While this might well be a fortuitous, it might point to (partly known) problems with asteroseismic scaling relations. On the other hand, this test indicates that our method can be used with good confidence in the metallicity range −2.0 < [Fe/H] < 0.3.
Left: fit parameters in a weighted regression using the errors from asteroseismic and spectroscopic mass determinations. Right: fit parameters from a simple linear regression.
5. Discussion
The applicability of our method is an important question. Currently, the best methods for measuring the mass and age of stars use either asteroseismology or fits of turn-off or sub-giant stars to evolutionary tracks. Asteroseismology requires bright apparent magnitudes, while turn-off stars and subgiants are too faint for observations at large distances.
Under conservative assumptions, we have shown that our method works for stars with 0.5 < log g< 3.5, 4000 <Teff< 5000 K, − 2 < [Fe/H] < 0.3, and log L/L⊙ ≲ 2.5. These stars, which comprise the RGB, HB, and AGB branches in the H-R diagram, are intrinsically bright, especially when compared to their dwarf and TO counterparts. Thus, our method may prove to be a valuable tool to measure masses and ages for spectroscopically feasible stars beyond the solar neighbourhood, extending to even dwarf galaxies and the Andromeda galaxy.
To examine the effect of spectral resolution of the observed data, the WHα measurements for the Gaia-ESO stellar sample are shown in Fig. 11. The original UVES spectra were degraded from R = 47 000 to several values of resolving power, representative of other instrument facilities (Fig. 10), such as the medium-resolution Giraffe spectrograph at the VLT (R = 16 000) and the high-resolution mode of the WEAVE and 4MOST facilities (R = 20 000). No changes were made to the fitting procedure or the Hα linemask. Interestingly, degrading the data to about half (R = 20 000) or one third (R = 16 000) of the original resolution does not have a significant effect on the Hα measurements. The offset from the high-resolution data is of the order 0.02 and 0.03 Å, respectively, which can be taken into account by shifting the zero-point of the WHα-mass relationship (Eq. (3)). For resolving powers R = 10 000 and lower, the differences between the original resolution and degraded measurements are large enough to introduce systematic errors in the mass estimates. However, the relationship is still there, thus it may be possible to calibrate Eq. (3) on low-resolution spectra.
 |
Fig. 10 Effect of spectral resolution on the Hα line profile. The observed UVES spectrum of the star 19251846 + 0016550 was taken from the Gaia-ESO archive. |
 |
Fig. 11 Comparison of the Hα width parameter measurements for different values of spectral resolving power. |
In terms of galaxy formation, an interesting question is which fraction of observable stars in a typical L∗ type galaxy might be studied with this technique. Figure 12 shows the number of stars in our Teff-log g parameter space per 1000 L⊙ in the Johnson-Cousins V band as a function of age (x-axis) and metallicity (colour coding). The plot was created using the population synthesis code underlying Schönrich & Bergemann (2014), and it represents a typical Galactic disk, calculated with the updated version (Schönrich & McMillan 2016) of the Schönrich & Binney (2009) model. The plot shows that all stellar populations with ages above 1 Gyr are well sampled at any metallicity, from the metal-rich [Fe/H] = + 0.5 to the most metal-poor [Fe/H] = − 2.5. The selection is up to an order of magnitude more efficient for metal-rich populations because the cooler effective temperatures move larger parts of the giant branches into our Teff−log g parameter region. The gradient mostly reflects the radial metallicity gradient, with more stars being selected in the more metal-rich inner disk regions. This bias must be taken into account when comparing to galaxy models or when an unbiased dataset is constructed. Nevertheless, the selection probability is sufficiently high for all ages and metallicities, allowing us to sample any population with age τ> 1 Gyr in units of ≥105 solar masses.
To test for omitted variable biases in our empirical formula, we tested the residuals between masses derived from our method and the asteroseismic values for trends with the stellar parameters Teff, log g, [Fe/H]. This test confirmed that no significant trends were found. This means that our method does not have any significant bias with any stellar parameter, arguing against omitted variable biases and supporting the validity of the empirical formula. To conclude, we have shown that our method samples all stellar populations with ages above 1 Gyr well and still delivers sufficient sample sizes for moderate-mass dwarf galaxies. When bright giants are targeted, the method allows obtaining simultaneous age and chemical abundance information (by applying the usual spectroscopic method of model atmospheres to the observed stellar spectrum) far deeper than would be possible with asteroseismology of red giants, which extends the possible survey volume to remote regions of the Milky Way and even to neighbouring galaxies such as Andromeda or the Magellanic Clouds with current instrumentation on telescopes, such as the VLT, Keck, or LBT. For example, with UVES/VLT or with the HIRES instrument at Keck (Vogt et al. 1994), optical high- or medium-resolution spectra can be acquired for stars with V magnitude ~19; in contrast, the majority of red giants with asteroseismic ages from CoRoT or Kepler missions are brighter than 14 mag (Mosser et al. 2010; Batalha et al. 2010; Hekker et al. 2011; Huber et al. 2014). In the future, our method opens a novel possibility of directly and consistently measuring ages and chemical abundances of individual stars in more distant galaxies in the Local Group, for instance, with 4MOST, WEAVE, and E-ELT (Zerbi et al. 2014), which will reach stars with V ~ 21.
 |
Fig. 12 Number of red giant stars per 1000 L⊙ in the Johnson-Cousins V band, depending on age and metallicity (colour coding). |
6. Summary and conclusions
We have analysed hydrogen (Hα) line profiles of 69 red giant stars with high-resolution optical spectra obtained with different instruments. A part of the stellar spectra was acquired within the Gaia-ESO spectroscopic survey (Gilmore et al. 2012; Randich et al. 2013). For all these stars, asteroseismic data from CoRoT and Kepler observations are available, allowing us to compute their mass and age. We also included 73 stars in 7 open and globular clusters; their masses were derived from the colour-magnitude diagram fitting. The sample covers a wide range in metallicity, from metal-rich, [Fe/H] = + 0.5 to very metal-poor, [Fe/H] < −2.5, stars.
We found that the observed Hα profile presents a systematic dependence on fundamental stellar parameters. The profile of the unblended blue wing can be represented by a simple cubic-exponential function, which provides an excellent fit to the observed line profiles. The only parameters in the fit are the steepness, or width, of the Hα line and the minimum flux in the line core (Eq. (2)). Both values appear to correlate with surface gravity and metallicity, which suggests a more fundamental underlying relationship with the mass of a star. The correlation between the steepness of Hα and stellar mass is clearly defined and can be described by a simple linear model (Eq. (3)). This allows determining masses with an accuracy of 10−15% independent of stellar atmosphere and interior modelling. Although masses can be determined quite precisely with our method, it should be kept in mind that the estimates are slightly offset from the asteroseismic scale, such that at the low-mass end stellar masses are on average too high by ~0.1 M⊙ and slightly lower at the high-mass end. This discrepancy could be caused by the asteroseismic mass estimates or by the second-parameter problem of the Hα line. Still, the empirical masses can be used to determine ages of stars. The uncertainties of ages derived from the Hα line profile measurements are 20 − 30%, which is better than the classical stellar isochrone methods.
We cannot yet identify the physical mechanism underlying the relationship because no stellar model atmospheres built from first principles are available that could be used to reproduce the observed Hα lines in red giants and explore their sensitivity to stellar mass. The standard 1D LTE models predict Hα profiles that are too weak compared to the observations. The more advanced 1D NLTE models with dynamics and winds are parametrised and do not explain the formation of the Hα lines because they are designed to match the observed Hα profile shapes. Three-dimensional MHD chromospheric models have been computed for the Sun, but are not yet available for quantitative spectroscopy of stars with very different properties, such as the RGB and RC stars. Models like this for a few red giants would be essential for understanding the slope of the Hα-mass relation. Most likely, this would require global convection modelling and the inclusion of chromosphere. One other possibility is that stellar model atmospheres lack information about the stellar interior structure, which nevertheless has an effect on the stellar atmosphere properties, as recent work suggests (Pinsonneault et al. 2014; Christensen-Dalsgaard et al. 2014). One interesting problem for the follow-up work would be to test the effect of variability in the Hα line on the WHα mass diagnostic. There is observational evidence (e.g. Cacciari et al. 2004; Meszaros et al. 2009, and references therein) that metal-poor stars ([Fe/H] ≲ − 1.0) more luminous than log (L/L⊙) ~ 2.5 show time-dependent emission in the Hα wings and asymmetries in the line core. There is currently no evidence for such processes in more metal-rich stars. Most red giants in our asteroseismic sample are fainter than this luminosity threshold and do not show emission or core shifts in the Hα line. With a large sample of stars for which spectra taken at different epochs are available it would be possible to test the effect of variability and possibly extend the method to very luminous red giants.
Our empirical results have interesting implications for spectroscopic observations of distant evolved stars: extremely metal-poor first stars, and stars in the dark part of the Galaxy, that is, in the halo, in distant star clusters, in the Magellanic Clouds and in other galaxies of the Local Group, which will be routinely observable with new facilities such as 4MOST and E-ELT. The instruments will reach targets as faint as V ~ 21 mag, which is five times fainter than what is currently possible with asteroseismic methods, for example, using Kepler or CoRoT mission data, and even with future missions like TESS. The observed optical spectra, in particular the conspicuous Hα line, may directly provide mass and age determinations for these stars, eliminating the need for model-dependent fitting methods based on stellar evolution and population synthesis models. We also showed that our method, based on the spectral line Hα, samples all stellar populations with ages above 1 Gyr well and still delivers sufficient sample sizes for moderate-mass dwarf galaxies. This shows that the applications of our method are numerous and extend our ability of measurig the mass and age of stars to a much larger volume.
Acknowledgments
We thank Luca Casagrande for the IRFM temperatures of the program stars and Achim Weiss for the data of the very metal-poor stars. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the Gaia-ESO Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541, and grants 2014SGR-1458 (Generalitat de Catalunya), ESP2014-56003-R and ESP2015-66134-R. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme. The research leading to the presented results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no 338251 (StellarAges).
References
- Alfvén, H. 1942, Nature, 150, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Baker J. 2008, Natl. Inst. Stand. Technol. Technical Note 1612, 8 [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&A, 355, L5 [NASA ADS] [Google Scholar]
- Batalha, N. M., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Cacciari, C., Bragaglia, A., Rossetti, E., et al. 2004, A&A, 413, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., & Stein, R. F. 2002, ApJ, 572, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., de Pontieu, B., et al. 2007, PASJ, 59, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Silva Aguirre, V., Stello, D., et al. 2014a, ApJ, 787, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014b, MNRAS, 439, 2060 [Google Scholar]
- Casagrande, L., Silva Aguirre, V., Schlesinger, K. J., et al. 2016, MNRAS, 455, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Silva Aguirre, V., Elsworth, Y., & Hekker, S. 2014, MNRAS, 445, 3685 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, H. R., Chaplin, W. J., Basu, S., et al. 2015, MNRAS, 451, 3011 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Hayek, W., Asplund, M., et al. 2011, A&A, 528, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Antona, F., Vesperini, E., D’Ercole, A., et al. 2016, MNRAS, 458, 2122 [NASA ADS] [CrossRef] [Google Scholar]
- De Angeli, F., Piotto, G., Cassisi, S., et al. 2005, AJ, 130, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Hartmann, L., & Avrett, E. H. 1984, ApJ, 281, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Avrett, E. H., & Kurucz, R. L. 2016, ApJ, 821, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, C. R., Elsworth, Y. P., Johnson, J. A., et al. 2014, ApJ, 785, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Curdt, W., Haberreiter, M., Harder, J., & Tian, H. 2009, ApJ, 707, 482 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Ceillier, T., Salabert, D., et al. 2014, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghezzi, L., & Johnson, J. A. 2015, ApJ, 812, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guggenberger, E., Hekker, S., Basu, S., & Bellinger, E. 2016, MNRAS, 460, 4277 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansteen, V. H. 2004, Multi-Wavelength Investigations of Solar Activity, 223, 385 [NASA ADS] [Google Scholar]
- Hansteen, V., Guerreiro, N., De Pontieu, B., & Carlsson, M. 2015, ApJ, 811, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., & MacGregor, K. B. 1980, ApJ, 242, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., Gilliland, R. L., Elsworth, Y., et al. 2011, MNRAS, 414, 2594 [Google Scholar]
- Huber, D., Silva Aguirre, V., Matthews, J. M., et al. 2014, ApJS, 211, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J. 2010, Mem. Soc. Astron. Nachr., 81, 576 [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2015, ApJ, 802, 136 [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martig, M., Fouesneau, M., Rix, H.-W., et al. 2016, MNRAS, 456, 3655 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., & Gilmore, G. 2015, MNRAS, 453, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Barnes, S. A., Platais, I., et al. 2015, Nature, 517, 589 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meszaros, S., Avrett, E., & Dupree, A. K. 2009, AJ, 138, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ness, M., Hogg, D. W., Rix, H.-W., et al. 2016, ApJ, 823, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., & Eyer, L. 2004, MNRAS, 351, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., & Butler, K. 2004, ApJ, 610, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Rutten, R. J. 2008, First Results From Hinode, ASP Conf. Ser., 397, 54 [NASA ADS] [Google Scholar]
- Rutten, R. J., & Uitenbroek, H. 2012, A&A, 540, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Weiss, A., & Percival, S. M. 2004, A&A, 414, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., & Bergemann, M. 2014, MNRAS, 443, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & McMillan, P. 2016, MNRAS, submitted [arXiv:1605.02338] [Google Scholar]
- Serenelli, A. M., Bergemann, M., Ruchti, G., & Casagrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soderblom, D. R. 2010, ARA&A, 48, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R. 2015, Nature, 517, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Steiman-Cameron, T. Y., Johnson, H. R., & Honeycutt, R. K. 1985, ApJ, 291, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Thygesen, A. O., Frandsen, S., Bruntt, H., et al. 2012a, A&A, 543, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thygesen, A. O., Frandsen, S., Bruntt, H., et al. 2012b, VizieR Online Data Catalog: J/A+A/543/A160 [Google Scholar]
- VandenBerg, D. A., Brogaard, K., Leaman, R., & Casagrande, L. 2013, ApJ, 775, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, Proc. SPIE, 2198, 362 [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Silva Aguirre, V., Boyajian, T., et al. 2015, EPJ Web Conf., 101, 06068 [CrossRef] [EDP Sciences] [Google Scholar]
- Zerbi, F. M., Bouchy, F., Fynbo, J., et al. 2014, Proc. SPIE, 9147, 914723 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional material
 |
Fig. A.1 Age-metallicity relation (AMR) for our observed stellar sample in the Milky Way disk, computed using the asteroseismic masses and spectroscopic metallicities. The AMR for different Galactocentric radii (R in kpc) from a chemical evolution model of the Galactic disk (Schönrich & Binney 2009) is represented by the colour map. |
Observational data for the Gaia-ESO stars.
Stellar parameters and Hα measurements for the Gaia-ESO field stars.
Observational data for the Gaia-ESO stars in clusters.
Stellar parameters and Hα measurements for the Gaia-ESO cluster stars.
Stellar parameters and Hα measurements for the Kepler stars from Thygesen et al. (2012).
All Tables
Left: fit parameters in a weighted regression using the errors from asteroseismic and spectroscopic mass determinations. Right: fit parameters from a simple linear regression.
Stellar parameters and Hα measurements for the Kepler stars from Thygesen et al. (2012).
All Figures
 |
Fig. 1 Hertzsprung-Russell diagram for the observed stellar sample: black filled points show the stars with asteroseismic masses, triangles depict the stars in stellar clusters. The stars in the globular clusters NGC 2808 and NGC 4372 are shown with green triangles and brown squares, respectively. The Garstec evolutionary tracks (Serenelli et al. 2013) for different masses and metallicities are also shown. |
| In the text | |
 |
Fig. 2 Model line profiles (colour lines) computed with different physics (1D LTE, mean 3D LTE, 1D NLTE) in comparison with the observed spectrum of the Sun (dots, top) and the metal-poor red giant HD 122563 (dots, bottom). The models lie far away from the data, thus we resort to an empirical method (Sect. 2.5). |
| In the text | |
 |
Fig. 3 Comparison of the observed and synthetic equivalent widths of the Hα line for the reference asteroseismic stellar sample. See Sect. 2.4 for more detail. |
| In the text | |
 |
Fig. 4 Bisector velocity at the FWHM of the Hα profile (km s-1) as a function of metallicity [Fe/H] for the observed stellar sample. |
| In the text | |
 |
Fig. 5 Observed Hα profile (black dots) in the selected program stars and the best-fit empirical model from Eq. (2) (bold blue line, 6562.0 to 6562.8 Å). The red and black lines correspond to the best-fit theoretical models computed in 1D LTE and 1D NLTE, respectively. The part of the Hα line used in the fit is the same for all stars in the sample. The thin blue line is only shown to help guide the eye; the red wing of Hα was not used in the fit. Line bisectors are indicated in the inset. The spectra are arranged in order of increasing metallicity. |
| In the text | |
 |
Fig. 6 Hα width parameter measurements in the observed stellar sample versus stellar effective temperature, surface gravity, and metallicity. The stars with asteroseismic data are shown with filled circles and the stars in the clusters with filled triangles. |
| In the text | |
 |
Fig. 7 Observed relation between the Hα spectral line widths versus asteroseismic masses of stars. Star clusters from the Gaia-ESO survey are shown with green squares. The very metal-poor stars in the sample, [Fe/H] < − 2, are shown with red symbols. Dashed black lines show the 1σ uncertainty of the fit. The shaded area is the average rms between the data and the fit. See Sect. 3. |
| In the text | |
 |
Fig. 8 Comparison of masses (top panel) and ages (bottom panel) determined using the WHα coefficient directly (a), c)) and the classical method of stellar isochrones (b), d)). |
| In the text | |
 |
Fig. 9 Difference between the Hα masses and asteroseismic masses as a function of Teff, [Fe/H], and log g. |
| In the text | |
 |
Fig. 10 Effect of spectral resolution on the Hα line profile. The observed UVES spectrum of the star 19251846 + 0016550 was taken from the Gaia-ESO archive. |
| In the text | |
 |
Fig. 11 Comparison of the Hα width parameter measurements for different values of spectral resolving power. |
| In the text | |
 |
Fig. 12 Number of red giant stars per 1000 L⊙ in the Johnson-Cousins V band, depending on age and metallicity (colour coding). |
| In the text | |
 |
Fig. A.1 Age-metallicity relation (AMR) for our observed stellar sample in the Milky Way disk, computed using the asteroseismic masses and spectroscopic metallicities. The AMR for different Galactocentric radii (R in kpc) from a chemical evolution model of the Galactic disk (Schönrich & Binney 2009) is represented by the colour map. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


