| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628908 | |
| Published online | 26 September 2016 | |
The slow spin of the young substellar companion GQ Lupi b and its orbital configuration
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: schwarz@strw.leidenuniv.nl
2 SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
3 Center for Astrophysics and Space Astronomy, University of Colorado at Boulder, CO 80309 Boulder, USA
4 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, MA 02138 Cambridge, USA
Received: 12 May 2016
Accepted: 30 June 2016
The spin of a planet or brown dwarf is related to the accretion process, and therefore studying spin can help promote our understanding of the formation of such objects. We present the projected rotational velocity of the young substellar companion GQ Lupi b, along with its barycentric radial velocity. The directly imaged exoplanet or brown dwarf companion joins a small but growing ensemble of wide-orbit, substellar companions with a spin measurement. The GQ Lupi system was observed at high spectral resolution (R ~ 100 000), and in the analysis we made use of both spectral and spatial filtering to separate the signal of the companion from that of the host star. We detect both CO (S/N = 11.6) and H2O (S/N = 7.7) in the atmosphere of GQ Lupi b by cross-correlating with model spectra, and we find it to be a slow rotator with a projected rotational velocity of 5.3+0.9-1.0 km s-1. The slow rotation is most likely due to its young age of <5 Myr, as it is still in the process of accreting material and angular momentum. We measure the barycentric radial velocity of GQ Lupi b to be 2.0 ± 0.4 km s-1, and discuss the allowed orbital configurations and their implications for formation scenarios for GQ Lupi b.
Key words: planets and satellites: individual: GQ Lupi b / techniques: imaging spectroscopy / infrared: planetary systems / planets and satellites: atmospheres / brown dwarfs
© ESO, 2016
1. Introduction
Measurements of the spin and the orbit of giant extrasolar planets and brown dwarf companions may hold important clues to their origin and evolution. Generally, two formation processes are considered for giant planets: (i) core accretion and (ii) disk fragmentation. Jupiter and Saturn are commonly accepted to have formed through core accretion. In this class of formation models, gas accretes onto solid planetary embryos of several to ten Earth masses that may have formed beyond the iceline by runaway accretion from kilometer-sized planetesimals (Pollack et al. 1996; Laughlin et al. 2004; Hubickyj et al. 2005). The discovery of extrasolar giant planets led to the reinvigoration of the disk fragmentation hypothesis, which states that giant (exo)planets may form as a disk gravitational instability that collapses on itself in the outer protoplanetary disk (Boss 1997, 2000). Disk fragmentation is also considered a potential formation scenario for the more massive brown dwarf companions (Chabrier et al. 2014), or alternatively brown dwarf companions can be the result of prestellar core fragmentation during the earliest stages of the cloud collapse (Jumper & Fisher 2013).
Spin is predominantly a result of accretion of angular momentum during the formation, and if core accretion and gravitational instability result in differences in spin angular momentum, it is possible this will show up in studies of spin of substellar companions as function of mass. In the solar system, the spin angular momenta of those planets not influenced by tidal effects or tidal energy dissipation by a massive satellite follow a clear relationship, spinning faster with increasing mass (Hughes 2003). In particular, gas giants far away from their central star are likely to have primordial spin angular momentum, making the directly imaged substellar companions ideal candidates for exploring the connection between formation and spin.
The rotational velocity of an exoplanet was measured for the first time by Snellen et al. (2014), who observed the directly imaged planet β Pictoris b with high-dispersion spectroscopy and measured this planet to have a projected rotational velocity of vsin (i) =25 km s-1. Another young directly imaged planet, 2M1207 b, became the first exoplanet to directly have its rotational period measured (Prot =10.7 h), when Zhou et al. (2016) detected rotational modulations with Hubble Space Telescope (HST) photometric monitoring of the object. Both results are in accordance with an extrapolation of the spin-mass trend observed in the solar system planets (see Fig. 8).
Apart from being related to the accretion process, the spin of an exoplanet is also a fundamental observable that, in particular, affects its atmospheric dynamics and climate as well as, for example, its magnetic fields. On Earth, the Coriolis effect generates large-scale ocean currents that in turn promote cyclones. For fast rotators, including many brown dwarfs, the wind flows are rotation dominated (Showman & Kaspi 2013). On the other hand, exoplanets orbiting close to their parent star are expected to be tidally locked. Brogi et al. (2016) and Louden & Wheatley (2015) both recently made use of high-dispersion spectroscopy to detect a Doppler signature in the transmission spectrum of the hot Jupiter HD 189733 b, which is consistent with synchronous rotation. Synchronous rotation is the cause of large temperature differences between the day- and nightside, which in turn can cause fast winds flowing from the hot dayside to the cold nightside.
Another approach to understanding the formation and dynamical evolution of exoplanets is to study their orbits. In the case of directly imaged substellar companions, it is often difficult to constrain the orbits because of the long timescales involved (e.g. Pearce et al. 2015; Ginski et al. 2014a). However, using a high-dispersion slit spectrograph in combination with adaptive optics, it is possible to extract spatially resolved high-dispersion spectra for the companion (Snellen et al. 2014), and thereby measure even very small Doppler shifts due to the orbital motion of the companion. Thus, even just one radial velocity measurement can in some cases prove to be a powerful orbital constraint (Nielsen et al. 2014; Lecavelier des Etangs & Vidal-Madjar 2016).
In this paper we present both the spin measurement and the barycentric radial velocity (RV) of the widely separated, substellar companion GQ Lupi b as obtained from high-dispersion spectroscopy. We introduce the GQ Lupi system in Sect. 2, and give the details of the observations in Sect. 3. The data analysis is detailed in Sect. 4 with special emphasis on how the spatially resolved spectrum of the companion is extracted and cleaned from telluric and stellar spectral lines. In Sect. 5 we explain the cross-correlation analysis that is employed to measure the rotational broadening and doppler shifts of the molecular lines in the companion spectrum, and the results from the companion are presented in Sect. 6, along with the host star spin and systemic velocity. We discuss the implications of the spin measurement in Sect. 7.1 and the constraints on orbital elements in Sect. 7.2.
2. The GQ Lupi system
GQ Lupi A is a classical T Tauri star with spectral type K7 V (Kharchenko & Roeser 2009) that is located in the star-forming cloud Lupus I (Tachihara et al. 1996) at an approximate distance of 50140 pc (e.g. Neuhäuser & Brandner 1998). The system is less than five million years old (Neuhäuser et al. 2005; Seperuelo Duarte et al. 2008; Weise et al. 2010), and there is strong observational evidence for a circumstellar warm dust disk (Hughes et al. 1994; Kessler-Silacci et al. 2006; Morales et al. 2012; Donati et al. 2012), extending to between 25 and 75 au from the star (Dai et al. 2010). The inclination of the spin axis of GQ Lupi A is estimated to be 30° (Donati et al. 2012), which is roughly consistent with the inclination of the warm inner parts of the circumstellar disk determined by Hügelmeyer et al. (2009) to be ~22°. Additional stellar parameters are given in Table 1.
The star has a directly imaged substellar companion, GQ Lupi b, with a highly uncertain and model dependent mass most likely in the range 10 MJ to36 MJ, (Marois et al. 2007; Seifahrt et al. 2007), placing it somewhere on the border between a giant planet and a brown dwarf, although this boundary is becoming increasingly blurred (Chabrier et al. 2014; Hatzes & Rauer 2015). The exoplanet candidate was first discovered with HST by Neuhäuser et al. (2005), and it was recently imaged as part of the SEEDS survey (Uyama et al. 2016). It is located at a projected separation of 0.7′′ west (100 au at 140 pc) and an astrometric analysis by Ginski et al. (2014b) points to a best-fit semimajor axes of a =76 au to129 au (at 140 pc) and high eccentricity in the range 0.21 to0.69. The GQ Lupi system has a favourable companion to star contrast ratio, with the host star (Kharchenko & Roeser 2009) and companion (Ginski et al. 2014b) having K-band magnitudes of 7.1 and 13.3, respectively. Selected parameters for GQ Lupi b are given in Table 2.
Parameters for GQ Lupi A from Donati et al. (2012).
3. Observations
We observed the GQ Lupi system for one hour (including acquisition) on 29 May 2014 with the Cryogenic High-Resolution Infrared Echelle Spectrograph (CRIRES; Kaeufl et al. 2004), located at the Nasmyth A focus of the Antu telescope of the Very Large Telescope array (VLT) at Cerro Paranal in Chile. The long slit spectrograph has a slit length of 40′′, and we chose a slit width of 0.2′′ to achieve the maximal spectral resolving power R ~ 100 000. The slit was positioned in a near east to west orientation to both encompass the host star and the substellar companion located at position angle PA = −83.6° (Zhou et al. 2014), allowing a combination of high-dispersion spectroscopy with high-contrast imaging (Snellen et al. 2015).
We took 18 exposures of 120 s in a classical ABBA pattern, where the telescope was nodded sequentially 10′′ in the slit direction between postions A and B, then B and A to allow accurate background subtraction. At each position an additional small random jitter offset was introduced to minimise issues from flatfielding and hot pixels.
The four CRIRES detectors are of type Aladdin III InSb, and each has a size of 1024 × 512 pixels with a gap of approximately 280 pixels in between. Unfortunately, the two outer detectors have severe odd-even column non-linearity effects1, which were not possible to accurately calibrate in these data. These are therefore left out of the analysis. The observations were performed with the standard wavelength settings for order 24 (λcen = 2.3252 μm), using the two central detectors to target the ro-vibrational (2, 0) R branch of carbon monoxide. The wavelength range 2.302 μm−2.331 μm of the two central detectors covers more than 30 strong CO lines.
We used the Multi Application Curvature Adaptive Optics system (MACAO; Arsenault et al. 2003) in 1.0′′ to 1.1′′ seeing conditions. To further maximise the performance of MACAO, the target system was observed at low airmasses between 1.056 and 1.121. This resulted in the starlight being suppressed by a factor ~45 at the companion position. With a K-band contrast ratio of 3.3 × 10-3, the companion contributes with (Fb/FA) ∗ 45 ∗ 100 =15 ± 3% of the total flux at the companion position. The remaining 85% flux is from the host star.
 |
Fig. 1 One of the combined image frames from detector 2. This is an intermediate data product from the CRIRES pipeline, and it is the combination of an AB nodding pair of exposures. The central rows that are used in the further data analysis are indicated on the right axis. The stellar spectral trail is clearly visible as the central white band, and the location of the hidden spectral trail from GQ Lupi b is indicated with a dashed line. The two diagonal stripes towards the right end are detector defects. |
4. Data analysis
4.1. Basic data reduction
The data was processed with the CRIRES pipeline version 2.3.2 and the corresponding version 3.10.2 of ESOREX. The pipeline performed the basic image processing, i.e. the images were dark subtracted, flatfielded, and were corrected for known bad pixels and non-linearity effects. Furthermore, the pipeline combined the images in AB nodding pairs performing a background subtraction, and extracted a one-dimensional (1D) spectrum from each of these combined images with the optimal extraction technique (Horne 1986).
We made use of the intermediate data products, i.e. the combined images, and the optimally extracted 1D spectra of the host star as follows. From the 18 exposures, 9 combined image frames were produced for each detector. An example of such a frame for detector 2 is shown in Fig. 1. We cut away everything but the central 51 rows that contain the stellar spectral trail, the hidden companion spectral trail (8 pixels above the centre), and enough extra rows to properly determine the stellar point spread function along the slit. The bad pixel correction in the CRIRES pipeline is insufficient. Therefore the remaining bad pixels (including cosmic rays) were visually identified with the programme DS9, and they were corrected with cubic spline interpolation using the four nearest neighbours in the row on both sides. The 9 optimally extracted 1D spectra of the host star were corrected for bad pixels in the same manner and then median normalised. Subsequently they were averaged over time to a single reference spectrum, representing the average spectrum of the host star, GQ Lupi A, plus telluric absorption in the Earth’s atmosphere.
The wavelength calibration was performed using line matching between deep and isolated telluric lines in the reference spectrum and a synthetic transmission spectrum from ESO SkyCalc2. We used 15 to 20 lines per detector and fitted a second-order polynomial to the pairs of pixel and wavelength centroids, where the centroids were determined from Gaussian fits. The highest residuals to the second-order polynomial fits were at a level of 20% of a pixel.
 |
Fig. 2 Illustration of the data analysis steps from a short wavelength range from detector 2. The y-axis depicts the slit position relative to the star, with the slit position of the companion indicated by a “b” on the right-hand axes. The greyscales were adjusted individually for each array with an IRAF-like z-scale algorithm. Top to bottom: A) the AB-combined image corrected for bad pixels; B) the spatial profiles of the star; C) the image after each row has been normalised with the rows of the spatial profile array; D) the spatial spectra (i.e. rectified for the trace); and E) the residual spatial spectra after removing stellar and telluric lines. |
4.2. Extraction of spectra for each slit position
From the clean combined image frames (Fig. 2A), we optimally extracted a spectrum for each slit position. Figure 2 illustrates the procedure, which was performed individually for each frame and each detector. Looking at the star trail in Fig. 1, it can be seen that the y-position of the intensity peak shifts with wavelength, and it is an important step in the data analysis to correct for this tilt of the trail of the star. In detector 2, the pixel with the maximum intensity shifts by 4 pixels from one end of the detector to the other, and in detector 3 the shift is 2 pixels. The tilted trail introduces a curvature in the continuum for a given row, and therefore we normalised each row with a polynomial fit of the curvature, where the degree of the polynomial depended on the distance from the stellar spectral trail. The fitted curves also provide the spatial profiles of the star as a function of wavelength (Fig. 2B). We used the spatial profiles to optimally extract a spectrum for each of the 31 most central rows from the normalised arrays (Fig. 2C). We refer to these collectively as the spatial spectra (Fig. 2D). The nine AB frames of spatial spectra were combined to a single frame to increase the signal-to-noise ratio of a given spectrum. Each pixel was normalised by the median of the pixel value through the nine frames and then combined as a weighted average. The weights were determined according to the varying width of the spatial profile (Fig. 2B), which is a seeing proxy. Pixels that deviated >4σ for the given pixel position were excluded.
4.3. Removal of telluric and stellar spectrum
The spatial spectra are dominated by the telluric absorption and the stellar spectrum, which has prominent CO lines. In contrast, the additional component to the spectra from the companion is strongly localised on the detector at the slit position of the companion. The stellar and telluric components are quasi identical at all slit positions, although the spectral resolution changes slightly with slit position. This is due to variations in the spatial profile of the star along the slit. Furthermore a small offset of the position of the star with respect to the centre of the slit can result in a small wavelength offset, and in addition there is a scaling factor. In order to remove both the telluric and stellar components, we made use of the reference spectrum we constructed in Sect. 4.1. The reference spectrum was adjusted to each slit position to correct for the above-mentioned effects by convolving with an appropriate broadening function, which was determined with the singular value decomposition technique (Rucinski 1999). The telluric and stellar spectrum was then removed from the spatial spectra by dividing with the adjusted reference spectrum (Fig. 2E).
4.3.1. Companion position
The presence of CO lines in the spectrum of the host star is a complicating factor because they potentially overlap with the CO lines of the companion. If the orbital motion of the companion has a significant radial component, the lines are red- or blueshifted relative to the lines of the star, but because of the wide separation between host and companion in the GQ Lupi system, the upper limit on the absolute value of this shift is 2.5 to 3.5 km s-1, depending on the exact semimajor axis and mass of GQ Lupi A. Furthermore, both the molecular lines of the companion and of the host star are rotationally broadened. Guenther et al. (2005) measured the projected rotational velocity of GQ Lupi A to be 6.8 ± 0.4 km s-1, and more recently Donati et al. (2012) found a similar value of 5 ± 1 km s-1. The concern is that the shape and strength of the companion lines may be affected by the process of removing the stellar lines, thereby compromising the vsin (i) and/or Doppler shift measurements.
The severity of this issue is greatly reduced by the angular separation between the host and the companion of 0.7′′. As stated in Sect. 3, we achieved a suppression of the starlight at the position of the companion to a few percent, which means that 15% of the total flux at this slit position originates from the companion and 85% originates from the host star. We therefore scaled the stellar lines in the reference spectrum down by 15% before proceeding as described in Sect. 4.3 with removing the stellar and telluric spectrum from the spatial spectrum of the companion position.
We isolated the stellar lines from the telluric parts of the reference spectrum to rescale the stellar reference spectrum. This was carried out as an iterative process, where a telluric model spectrum and a stellar model spectrum were fitted and removed separately from the reference spectrum. The steps were as follows:
-
We used the same telluric model spectrum from ESO SkyCalc,which was used to perform the wavelength calibration. Theairmass and the precipitable water vapor (PWV) was setmanually at airmass 1.1 and PWV 1.5 to best fit the observedreference spectrum. The stellar model is a PHOENIX spectrumfrom Husser et al. (2013) withTeff =4300 K and log g = 3.5. The telluric model was smoothed, and both the telluric and the stellar model were resampled to the observed wavelength solution.
-
We convolved the telluric model with a broadening kernel to adjust the resolution to that of the reference spectrum. As in Sect. 4.3 the singular value decomposition (SVD) technique (Rucinski 1999) was employed to determine the appropriate kernel, but here it was performed in log space to avoid the deepest telluric lines from dominating. The telluric spectrum was then removed from the reference spectrum by dividing by the telluric fit.
-
The stellar template was fitted to the telluric-removed reference spectrum by convolving with an SVD broadening kernel in log space. Following this, the stellar lines were removed from the original reference spectrum by dividing by the stellar fit.
-
The telluric SVD fit and removal was redone, adjusting the telluric model to the stellar-removed reference spectrum before dividing the original reference spectrum by the fit, thus producing an improved telluric-removed reference spectrum.
-
The continuum of the new telluric-removed reference spectrum was fitted with a second order polynomial and removed. Subsequently the stellar SVD fit was redone, fitting the stellar model to the flat telluric-removed reference spectrum. This stellar fit was then scaled to 15% of the line strength, and the original reference spectrum was divided by this scaled down stellar model, resulting in a reference spectrum with the strength of the stellar lines reduced by 15%.
5. Measuring the signal from the companion
After removing the telluric and stellar spectrum, the residual spatial spectra consist of residual noise, with the exception at the slit position of the companion, which also has a contribution from the companion spectrum. Figure 2E shows a short wavelength range of the residual spatial spectra. At the high spectral resolution of the CRIRES data, the molecular bands are resolved into individual lines, and the signal from all of the lines from a given molecule within the wavelength range can be combined through cross-correlation with a model spectrum. Molecules are identified in the spectrum of the companion as a peak in the cross-correlation function (CCF). The CCF profile is sensitive to both the shape and the Doppler shift of the companion spectral lines. Lines that are broadened by rotation result in broadened CCF profiles, and lines that are shifted also shift the peak of the CCF. In this section we describe the model spectra and the cross-correlation analysis, as well as the procedure for measuring the rotation and radial velocity of the companion from the cross-correlation function.
5.1. The model spectra
The GQ Lupi system is thought to be very young (<5 Myr), and as a result GQ Lupi b is very hot with an effective temperature (Teff) of approximately 2650 K (Seifahrt et al. 2007). At such high temperatures the most abundant trace gas molecules in the K-band are expected to be CO and H2O. We cross-correlated with models with CO or H2O as a single trace gas and with a suit of models containing both CO and H2O. The models were calculated line by line, assuming H2-H2 collision-induced absorption (Borysow et al. 2001; Borysow 2002). The CO and H2O data were taken from HITEMP 2010 (Rothman et al. 2010) and a Voigt line profile was employed.
 |
Fig. 3 Models with a T/p profile and abundance that give rise to the strongest cross-correlation signals from the companion. The top panel shows the model with CO as a single trace gas, the middle panel the model with only H2O, and the bottom panel model contains both CO and H2O. The temperature is set to decrease from 2150 K at 1 bar to 1100 K at 0.03 bar and is isothermal outside this pressure range. The volume mixing ratios for CO and/or H2O in these three models are 10-4. |
The models were constructed from a narrow grid of parameterised temperature-pressure profiles (T/p profiles). All the models are isothermal with a temperature of T0 = [1650 K, 1900 K, 2150 K] at pressures higher than p0 = 1 bar. The temperature decreases with a constant lapse rate (i.e. the rate of temperature change with log pressure) until it reaches T1 = [750 K, 1100 K, 1450 K, 1800 K] at pressure p1 = [10-1.5 bar, 10-2.5 bar, 10-3.5 bar, 10-4.5 bar]. The models are isothermal again at higher altitudes or equivalently lower pressures. Both CO and H2O were tested with four different volume mixing ratios, VMR = [10-5.5, 10-5.0, 10-4.5, 10-4.0]. Figure 3 illustrates the CO-only, H2O-only and CO+H2O models with the best T/p profile and volume mixing ratios from the grid.
5.2. Cross-correlation analysis
The model spectrum was first convolved to the CRIRES spectral resolution using a Gaussian filter, then Doppler shifted over the range -250 to 250 km s-1 in steps of 1.5 km s-1, and for each velocity step cross-correlated with the residual spatial spectra. We assumed R = 100 000 for the instrumental profile, but we measured the actual resolving power to be in the range 80 000 to90 000. This causes a small overestimation of vsin (i) of the order of 60 ms-1, which is included in the lower uncertainty bound of the final result. The cross-correlation was performed for every slit position as a means to investigate the strength of spurious signals and issues with, for example stellar residual signals. Each detector was treated separately and only combined as an average after the cross-correlation analysis. This results in two-dimensional arrays with the cross-correlation coefficient as a function of slit position and applied Doppler shift.
 |
Fig. 4 The residual spectrum after removing telluric and stellar lines at the companion position. Overplotted in red is the CO model from the top panel of Fig. 3, convolved to the CRIRES resolution, rotationally broadened, and Doppler shifted to match the measured vsini (5.3 km s-1) and radial velocity (2 km s-1) of GQ Lupi b. For illustration purposes, the model was also fitted to the residual companion spectrum with a vertical offset and a scaling factor. The companion spectrum is dominated by noise, but the individual CO lines are discernible. |
5.3. Measuring the companion v sin (i) and RV
The cross-correlation function (CCF) from the residual spectrum at the companion position using any of the models contains the rotational broadening and radial velocity of the companion. We selected the model with the strongest cross-correlation signal for the purpose of measuring vsin (i) and RV. The CCFs from the two detectors were averaged to further maximise the signal-to-noise (S/N). We refer to the average CCF from the companion position and the best model as the measured companion CCF.
We determined the best-fit vsin (i) and RV of the measured companion CCF through 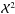 minimisation with a suite of model CCFs, along with confidence intervals from rescaling the errors so
minimisation with a suite of model CCFs, along with confidence intervals from rescaling the errors so 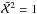 . The model CCFs were constructed by cross-correlating the non-broadened best model with broadened and shifted versions of the model itself. Both the broadened and non-broadened models were convolved to the CRIRES spectral resolution prior to the cross-correlation. We tested projected rotational velocities in the range 0 to 10 km s-1 and Doppler shifts in the range -5 to 5 km s-1. For both parameters the step size was 0.1 km s-1. Each of these model CCFs were then offset (y-direction) and scaled with a least-squares fit to best match the measured companion CCF, after which the
. The model CCFs were constructed by cross-correlating the non-broadened best model with broadened and shifted versions of the model itself. Both the broadened and non-broadened models were convolved to the CRIRES spectral resolution prior to the cross-correlation. We tested projected rotational velocities in the range 0 to 10 km s-1 and Doppler shifts in the range -5 to 5 km s-1. For both parameters the step size was 0.1 km s-1. Each of these model CCFs were then offset (y-direction) and scaled with a least-squares fit to best match the measured companion CCF, after which the 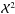 minimisation routine was performed. The measured radial velocity was corrected to the barycentric radial velocity using the systemic velocity (vsys) determined from the host star spectrum as described in Sect. 5.4, and the heliocentric correction term for the time of observation. The results are presented in Sect. 6.2 and discussed in Sects. 7.1 and 7.2.
minimisation routine was performed. The measured radial velocity was corrected to the barycentric radial velocity using the systemic velocity (vsys) determined from the host star spectrum as described in Sect. 5.4, and the heliocentric correction term for the time of observation. The results are presented in Sect. 6.2 and discussed in Sects. 7.1 and 7.2.
5.4. Measuring the systemic velocity and the host star v sin(i)
We took the same approach to measuring vsin (i) and RV of the host star as we did for the companion. In this case, the measured host star CCF was the cross-correlation function of the flat telluric-removed reference spectrum from the final step of Sect. 4.3.1 and a synthetic PHOENIX spectrum from Husser et al. (2013) with Teff =4300 K and log g = 3.5. A suite of model CCFs were constructed from the PHOENIX model with a range of vsin (i) and RV values, and we performed the 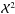 analysis for the host star, comparing the measured and modelled CCFs. The measured radial velocity was corrected to the barycentric radial velocity (i.e. the systemic velocity) using the heliocentric correction term for the time of observation. We carried out this analysis for PHOENIX models with Teff ±100 K and log g ± 0.5 to test the sensitivity to the stellar parameters, and found that this temperature difference can affect the radial velocity with up to 100 ms-1 and the vsin (i) with up to 200 ms-1. The radial velocity is not sensitive to the choice of log g, but the vsin (i) can be affected by up to 200 ms-1. The results are presented and discussed in Sects. 6.3 and 7.3, respectively.
analysis for the host star, comparing the measured and modelled CCFs. The measured radial velocity was corrected to the barycentric radial velocity (i.e. the systemic velocity) using the heliocentric correction term for the time of observation. We carried out this analysis for PHOENIX models with Teff ±100 K and log g ± 0.5 to test the sensitivity to the stellar parameters, and found that this temperature difference can affect the radial velocity with up to 100 ms-1 and the vsin (i) with up to 200 ms-1. The radial velocity is not sensitive to the choice of log g, but the vsin (i) can be affected by up to 200 ms-1. The results are presented and discussed in Sects. 6.3 and 7.3, respectively.
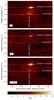 |
Fig. 5 Strength of the cross-correlation as function of slit position and radial velocity for the three best-fit models (see Fig. 3). We detect both CO and H2O using single-trace gas models with a S/N of 11.6 for CO and 7.7 for H2O, and the signal from the double-trace gas model is marginally stronger with a S/N of 12.3. These cross-correlation arrays are the averages from the two central CRIRES detectors. |
6. Results
Although the residual spectrum at the companion position is noisy, the absorption lines from CO in the companion atmosphere are in some cases visible (Fig. 4). To help guide the eye, we overplotted the best CO model shifted to the best-fit radial velocity. Although we can visually detect the individual CO lines, the companion spectrum is too noisy to allow the rotational broadening or the Doppler shift to be measured directly from the CO lines, and we therefore need to make use of the CCF.
6.1. Detection of CO and H2O
We clearly detect the substellar companion at the expected distance from the host star (0.7′′) in the CCF arrays (see Fig. 5). We detect CO with a S/N of 11.6 and H2O with a S/N of 7.7. The best model containing both CO and H2O is detected with a S/N of 12.3. These are average values from the two central CRIRES detectors, but both CO and H2O are detected separately in each detector. The S/N values were obtained by dividing the cross-correlation coefficients with the standard deviation of the array, excluding points in parameter space that are close to the companion signal. Figure 5 shows the S/N cross-correlation arrays for the best CO-only, H2O-only and CO+H2O models from the tested T/p and VMR grid. These arrays are displayed here from -50 to 50 km s-1, but the S/N-values are based on the standard deviation of the full radial velocity range from -250 to 250 km s-1. These best models are illustrated in Fig. 3 and share the same T/p profile with the temperature decreasing from 2150 K at 1 bar to 1100 K at 0.03 bar. The steep decrease in temperature relatively deep in the atmosphere gives rise to strong absorption lines. The VMR for both CO and H2O in these models are in all cases 10-4. All the models in the grid described in Sect. 5.1 give rise to significant molecular detections, and for a given VMR the significance of a detection from the different T/p profiles agree to within 1σ.
The CO signal and the CO+H2O signal are detected with a stronger significance in detector 3 compared to detector 2. This is in line with expectations because the third detector has a higher number of CO lines. In detector 3 there are stellar CO residuals in the row just above the star position, although at a lower level than the companion signal. The residuals are strong enough to also show up in the average cross-correlation arrays in Fig. 5. It is unclear why the procedure for removing the stellar light has partly failed at this one slit position, and also why the issue only involves one of the detectors. The companion is a further 7 pixels away where the light from the star is decreased to only ~2% of its peak intensity, so we expect this issue to have negligible effect on the vsin (i) and RV measurements.
6.2. Companion v sin (i) and RV
It is already clear from the Fig. 5 cross-correlation arrays that the companion signal is quite narrow, and that it is redshifted relative to the stellar radial velocity by only a small amount. The measured companion CCF is shown in Fig. 6 together with the best-fit model CCF, and the CCF for the same model, but without rotational broadening. We find from the 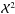 minimisation routine that the projected rotational velocity of GQ Lupi b is
minimisation routine that the projected rotational velocity of GQ Lupi b is 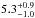 km s-1 and its barycentric radial velocity is 2.0 ± 0.4km s-1.
km s-1 and its barycentric radial velocity is 2.0 ± 0.4km s-1.
 |
Fig. 6 The measured companion cross-correlation function (CCF) is best fit by a CO + H2O model CCF, which is redshifted 2.0 km s-1 and rotationally broadened by 5.3 km s-1. For comparison we also show the model CCF without rotational broadening for which the width is dominated by the spectral resolution of the CRIRES instrument. |
6.3. Host star v sin (i) and vsys
As a by-product of the analysis carried out in this work, we have estimates of the systemic velocity and the projected rotational velocity of GQ Lupi A. The systemic velocity is of direct importance as it is required to translate the measured companion RV to the barycentric frame. We find vsys = −2.8 ± 0.2km s-1. For the host star, we measured a rotational broadening corresponding to vsin (i) = 6.8 ± 0.5km s-1. However, we have not taken additional broadening terms (e.g. macro-turbulence) into account when determining vsin (i) of GQ Lupi A.
6.4. Orbital constraints for GQ Lupi b
The radial velocity measurement of 2.0 ± 0.4km s-1 can be used to constrain the orbit of GQ Lupi b. We approached this by applying the radial velocity as a constraint to the best-fitting orbital solutions from Ginski et al. (2014b). They applied astrometry to 15 astrometric epochs from VLT and HST spanning a time frame of 18 years to determine the angular separation and relative position angle. They applied least-squares Monte Carlo (LSMC) statistics to constrain the orbit. The details of the LSMC approach, along with a comparison to the more widely used Markov chain Monte Carlo (MCMC) approach, are described in Ginski et al. (2013). The mass of the host star was assumed to be 0.7 M⊙, and the distance to the system 140 pc. The left-hand panels of Fig. 7 are a reproduction of Ginski et al. (2014b) Fig. 5a and b. The orbital solutions in this figure represent the 1% best-fitting solutions out of 5 000 000 LSMC runs. Dismissing the solutions from this best-fitting subset that are inconsistent with the new radial velocity measurement produces the right-hand panels of Fig. 7.
The new radial velocity constraint dramatically reduces the number of possible solutions, and certain families of orbital solutions are excluded. In particular, the observations no longer support long-period orbits (a>185 au) with eccentricities below 0.8, or circular orbits.
The remaining allowed solutions fall into three different families:
-
1.
Orbits with a semimajor axis ~100 au, inclination ~57°, and eccentricity ~0.15.
-
2.
Orbits with a semimajor axis <185 au, a range of eccentricities 0.2 < e < 0.75, and inclinations 28°<i < 63°.
-
3.
Highly eccentric, long-period orbits with a semimajor axis >300 au, eccentricities >0.8, and high inclinations 52°<i<63°.
 |
Fig. 7 Orbital parameters as function of eccentricity for the substellar companion GQ Lupi b around its host star with the colour scale indicating the logarithmic density of solutions. The panels in the left column are reproduced from Ginski et al. (2014b) and they show the 1% best-fitting solutions out of 5 000 000 runs of their LSMC fit. The right-hand panels show the orbital solutions, which are consistent with the radial velocity measurement from this work. |
7. Discussion
7.1. The slow spin of GQ Lupi b
The CO and H2O lines in the spectrum of GQ Lupi b are narrow, with only a moderate rotational broadening corresponding to a projected rotational velocity of 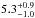 km s-1. This strongly suggests that GQ Lupi b is a slow rotator when compared to the giant planets in the solar system or the recent spin measurements of β Pictoris b and 2M1207 b (see Table 2 and Fig. 8).
km s-1. This strongly suggests that GQ Lupi b is a slow rotator when compared to the giant planets in the solar system or the recent spin measurements of β Pictoris b and 2M1207 b (see Table 2 and Fig. 8).
The vsin (i) measured for GQ Lupi b could have been influenced by the removal of the stellar lines, for example, by removing too much of the CO, which actually originates from the companion and not from the star. This removal could have over-subtracted the short-wavelength wing of the companion signal, thereby making it more narrow. We compared the widths of the CO+H2O signal for the analyses with and without rescaling the stellar CO and found 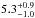 km s-1 and 4.8 ± 1.0km s-1, respectively. This suggests that the influence in any case is only minor and cannot have resulted in the vsin (i) of the companion to be artificially small. The measured companion CCFs for the two cases are plotted together in Fig. 9.
km s-1 and 4.8 ± 1.0km s-1, respectively. This suggests that the influence in any case is only minor and cannot have resulted in the vsin (i) of the companion to be artificially small. The measured companion CCFs for the two cases are plotted together in Fig. 9.
Micro- and macro-turbulence act as additional broadening of line profiles and can therefore cause an overestimation of the projected rotational velocity. Wende et al. (2009) investigated the effective temperature and log g dependence of the velocity field for M stars extending to temperatures as low as 2500 K, thereby just covering the estimated temperature of GQ Lupi b. Micro- and macro-turbulent velocities decrease with lower effective temperatures and, in particular, micro-turbulence increases towards lower surface gravities. Assuming a surface gravity for GQ Lupi b in the range log g =3.0 to4.2, a realistic upper limit for the sum of the squares of the turbulent velocities is 1.5 km s-1, corresponding to an overestimate of vsin (i) by 0.22 km s-1. We included this in the lower bound of the uncertainty estimate of the vsin (i) measurement.
If the orientation of the spin axis is edge-on, the measured spin velocity corresponds to a rotational period of 82 h, assuming a companion radius of 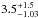 RJ (Seifahrt et al. 2007). Since the spin axis orientation is unknown, it could possibly be nearly pole on. Therefore the equatorial rotation velocity (veq) could be much higher than vsin (i). However, the inclination of the axis of rotation would have to be less than 15° to make the spin of GQ Lupi b comparable to β Pic b or the solar system giant planets. Assuming a random orientation, this has only a probability of 3.4%. If we make the assumption that orbital and spin axes are aligned, then based on Fig. 7 we can rule out inclinations below 28°, corresponding to veq faster than 11.3 km s-1. This is still well below the vsin (i) of 25 km s-1, which Snellen et al. (2014) measured for β Pic b. Therefore, it is unlikely that GQ Lupi b is a fast rotator.
RJ (Seifahrt et al. 2007). Since the spin axis orientation is unknown, it could possibly be nearly pole on. Therefore the equatorial rotation velocity (veq) could be much higher than vsin (i). However, the inclination of the axis of rotation would have to be less than 15° to make the spin of GQ Lupi b comparable to β Pic b or the solar system giant planets. Assuming a random orientation, this has only a probability of 3.4%. If we make the assumption that orbital and spin axes are aligned, then based on Fig. 7 we can rule out inclinations below 28°, corresponding to veq faster than 11.3 km s-1. This is still well below the vsin (i) of 25 km s-1, which Snellen et al. (2014) measured for β Pic b. Therefore, it is unlikely that GQ Lupi b is a fast rotator.
The slow rotation of GQ Lupi b may be caused by a different formation path from β Pic b, 2M1207 b, and the giant planets in the solar system. GQ Lupi b at ~100 au is significantly further away from its host star than the other mentioned planets. In addition it is likely more massive with a mass range 10 MJ to36 MJ extending well into the brown dwarf regime. It could therefore have formed through either disk gravitational instability or even fragmentation of the collapsing proto-stellar core, rather than through core accretion, which is a possible common formation path for the (exo)planets showing the spin-mass trend that we see in Fig. 8. Allers et al. (2016) have recently measured the projected rotational velocity of PSO J318.5338-22.8603, which is a free-floating planetary mass member of the β Pictoris moving group with an estimated age of 23 ± 3 Myr. Their measured 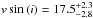 km s-1 is also consistent with the solar system spin-mass trend. Such an object is most likely the result of gravitational instability (Chabrier et al. 2014; Stamatellos 2014), possibly followed by photo-erosion, but it could also have been dynamically kicked out of an orbit around a star, and core accretion can therefore not be ruled out. Low resolution spectra of GQ Lupi b are consistent with a spectral type of late M to early L (Neuhäuser et al. 2005), and comparable brown dwarf binaries and field brown dwarfs from the literature show a wide variety of rotational velocities and no simple correlation with mass (Konopacky et al. 2012; Zapatero Osorio et al. 2006; Metchev et al. 2015; Scholz et al. 2015). Most brown dwarfs are rapid rotators (vsin (i) >10 km s-1), and their minimum rotation rates are a function of their spectral types with the higher mass objects rotating more slowly than their lower mass counterparts, in contrast with the planetary trend. This is because magnetic breaking plays an increasing role in the more massive brown dwarfs. However, it is much too early to make any claims about relations between spin, mass, and orbital distance based on the limited observations; this is the case in particular because there is another very probable explanation for the slow spin of GQ Lupi b.
km s-1 is also consistent with the solar system spin-mass trend. Such an object is most likely the result of gravitational instability (Chabrier et al. 2014; Stamatellos 2014), possibly followed by photo-erosion, but it could also have been dynamically kicked out of an orbit around a star, and core accretion can therefore not be ruled out. Low resolution spectra of GQ Lupi b are consistent with a spectral type of late M to early L (Neuhäuser et al. 2005), and comparable brown dwarf binaries and field brown dwarfs from the literature show a wide variety of rotational velocities and no simple correlation with mass (Konopacky et al. 2012; Zapatero Osorio et al. 2006; Metchev et al. 2015; Scholz et al. 2015). Most brown dwarfs are rapid rotators (vsin (i) >10 km s-1), and their minimum rotation rates are a function of their spectral types with the higher mass objects rotating more slowly than their lower mass counterparts, in contrast with the planetary trend. This is because magnetic breaking plays an increasing role in the more massive brown dwarfs. However, it is much too early to make any claims about relations between spin, mass, and orbital distance based on the limited observations; this is the case in particular because there is another very probable explanation for the slow spin of GQ Lupi b.
Comparison of key parameters of the three substellar companions with spin measurements.
 |
Fig. 8 Spin as function of mass for extrasolar substellar companions and solar system planets, together with the free-floating planetary mass object PSO J318.5-22 and field brown dwarfs. The solar system planets and 2M1207 b have equatorial rotation velocities and β Pictoris b and GQ Lupi b have projected rotation velocities, as does PSO J318.5-22. Mercury and Venus are not included in the plot because their proximity to the Sun has caused their spin to be dominated by tidal interactions with the Sun. For comparison, field brown dwarfs with estimated masses and either a rotational period measurement or vsin (i) measurement are shown as empty circles, with the typical uncertainty in mass indicated for a single object. Their masses and radii are from Filippazzo et al. (2015), rotational periods are from Metchev et al. (2015), and vsin (i)’s are from either Zapatero Osorio et al. (2006) or Blake et al. (2010). The field brown dwarfs are much older than the substellar companions and PSO J318.5-22 with highly uncertain ages in the range 500 Myr to 10 Gyr. |
We believe that the slow spin of GQ Lupi b is linked to its young age. All current estimates set the age of the GQ Lupi system to <5 Myr, and Neuhäuser et al. (2005) estimated the age to be only 1 ± 1 Myr. In fact, observational evidence exists of GQ Lupi b actively accreting, through the detection of Paβ emission (Seifahrt et al. 2007) and the detection of Hα in emission together with excess optical continuum emission (Zhou et al. 2014). This means that a significant amount of angular momentum could still be accreted in the future. Furthermore, its radius is now estimated at 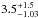 RJ (Seifahrt et al. 2007), meaning that even without extra accretion it is still expected to contract significantly to ~1RJ radius and spin up to 10−25 km s-1. This would bring it much nearer the mass-spin relation of the other giant planets. In this context, it is interesting that 2M1207 b, with an age in between that of GQ Lupi b and β Pic b, is also seen to have an intermediate spin.
RJ (Seifahrt et al. 2007), meaning that even without extra accretion it is still expected to contract significantly to ~1RJ radius and spin up to 10−25 km s-1. This would bring it much nearer the mass-spin relation of the other giant planets. In this context, it is interesting that 2M1207 b, with an age in between that of GQ Lupi b and β Pic b, is also seen to have an intermediate spin.
The spin angular momenta of brown dwarfs and low-mass stars also evolve over time (Bouvier et al. 2014; Irwin et al. 2011; Newton et al. 2016; Scholz et al. 2015). Analogously to the spin evolution of giant planets, gravitational contraction causes the brown dwarfs to spin up, but after 10 Myr to100 Myr magnetic breaking starts dominating the spin evolution. The angular momentum loss mechanisms are more inefficient for smaller and cooler objects (Reiners & Basri 2008). This stands in contrast to planets, which are expected to retain their spin angular momenta, unless they are gravitationally disturbed by a third object.
Measurements of spin as a function of mass, orbital distance, and crucially, age, for numerous substellar companions and free-floating low-mass objects, are necessary to determine the effects of formation pathways on spin-mass relationships. Yet at this early stage, every spin measurement of a substellar companion is likely to lead to new insights.
7.2. The orbital orientation of GQ Lupi b
We used the radial velocity measurement for GQ Lupi b of 2.0 ± 0.4km s-1 in conjunction with previous astrometry from Ginski et al. (2014b) to constrain its orbital elements. This allows us to rule out both circular orbits and long-period orbits (a > 185 au) with eccentricities below 0.8. If we allow for a larger uncertainty in the astrometry, then circular orbits with inclinations 60°<i< 78° are still possible. The orbital solutions that are consistent with the RV measurement show a degeneracy between eccentricity and inclination. Orbits with a relatively low eccentricity (0.1 < e < 0.4) have high inclinations 48° < i < 63°, which are distinctly different from that of the circumstellar disk (~22°). In the case of the more eccentric solutions 0.4 < e < 0.75, the inclinations are less well constrained, yet there is a tendency towards allowing for smaller inclinations towards higher eccentricities. This includes orbits with 0.65 < e < 0.7 that are nearly aligned with the circumstellar disk. Finally we have a subset of orbital solutions with extremely wide orbits (a > 300 au) and high eccentricities e > 0.8. This last subset seems less likely because it would imply that we observe the companion at a special moment near periastron. All solutions shown in the right column of Fig. 7 fit both our new radial velocity measurement and the available astrometric data well and the density of solutions does not correspond directly to the likelihood of solutions.
As in the case of the measured vsin (i), the RV measurement of the companion could also have been influenced by the contribution of the stellar lines. If we over-subtracted the short-wavelength wing of the companion CO lines when we removed the stellar spectrum, this could introduce an artificial redshift. Comparison of the RV measurement with and without the scaling of the stellar contribution (Fig. 9) indicates that this effect is confined to 0.2 km s-1. Assuming that we have performed the stellar removal to a precision of ~10%, this should not add to the uncertainty in RV to a level of more than 0.1 km s-1.
Our RV measurement improves the orbital constraints significantly. A large family of possible orbital solutions found by Ginski et al. (2014b), in particular with intermediate eccentricities and large semimajor axes, are now no longer in line with the observations. Further constraints from either astrometry or high-dispersion spectroscopy will take at least another decade such that GQ Lupi b has moved significantly enough in its orbit and/or changed its radial velocity.
The orbital solutions that are misaligned with the circumstellar disk are particularly intriguing. A companion in such an orbit must either have been scattered to that position, or it must have formed in situ, yet outside of the protoplanetary disk. The latter would indicate a formation scenario that is analogous to that of a binary star system with the collapsing proto-stellar core fragmenting into smaller objects.
The orbit of GQ Lupi b is wide enough that disk instability is a possible formation mechanism. Fragmentation of the disk is allowed from approximately 50 au to300 au (Vorobyov & Basu 2012), and although only a small number of fragments are expected to survive to become orbiting planets or brown dwarfs, this is in line with the small number of observed systems that fit the description. HR 8799 and HIP 78530 are other examples. However, if GQ Lupi b formed in situ through disk instability, one would expect low eccentricity orbits within or near the plane of the circumstellar disk. This type of orbit is not supported by the previous astrometric analysis by Ginski et al. (2014b) and our RV measurement strengthens this conclusion. Instead GQ Lupi b may have a high eccentricity orbit, which could be an indication that the companion has been scattered to its current position.
7.3. The systemic velocity and v sin (i) of GQ Lupi A
We measured the systemic velocity from the observed spectrum of the star and find it to be vsys = −2.8 ± 0.2km s-1. The major contributor to the uncertainty is the accuracy of the wavelength solution. Donati et al. (2012) measured the radial velocity in July 2009 to be −3.2 ± 0.1km s-1 and again in June 2011 to be −2.8 ± 0.1km s-1. They argue that the 0.4 km s-1 change is real and explain it as either long-term changes of the surface granulation pattern or as the result of a third body, a brown dwarf of a few tens of Jupiter masses orbiting the central star at a few au.
We measured the vsin (i) of GQ Lupi A to be 6.8 ± 0.5km s-1, although without including additional potential broadening mechanisms, which in the case of stars with relatively low projected rotational velocities may contribute significantly to the broadening. The 6.8 km s-1 is therefore likely to be an overestimate. Our result is in agreement with a previous estimate by Guenther et al. (2005) of 6.8 ± 0.4km s-1. Donati et al. (2012) estimated vsin (i) to be 5 ± 1 km s-1 and highlighted that, unlike Guenther et al. (2005), they included magnetic broadening. Also micro-turbulence (Donati et al. 2012) and macro-turbulence from subsurface convective zones (Grassitelli et al. 2015) may contribute to the broadening of stellar spectral lines. The rotation period of GQ Lupi A of 8.4 days (Broeg et al. 2007; Donati et al. 2012) is typical of classical T Tauri stars, and is often attributed to a disk-locking mechanism (Choi & Herbst 1996; Landin et al. 2016).
 |
Fig. 9 Measured cross-correlation function between the companion spectrum and the CO + H2O model with and without the rescaling of the stellar lines described in Sect. 4.3.1. The difference between the two stems from when the reference spectrum containing the stellar and telluric lines was removed from the companion spectrum. The solid line is the resulting CCF from the approach we have taken in this paper, where we have scaled the stellar lines in the reference spectrum down by 15% to match the companion to star flux ratio at the companion position. The dashed line is the CCF for the case where the reference spectrum is removed from the companion spectrum without rescaling the stellar lines. The bottom panel shows the difference between the two. |
8. Summary and conclusions
The young GQ Lupi system has a central classical T Tauri star surrounded by a warm dust disk, and is orbited by a substellar companion GQ Lupi b at ~100 au, which is either a gas giant or a brown dwarf. We observed the parent star and the companion simultanously in the K-band by careful positioning of the slit of the high-dispersion spectrograph CRIRES, in combination with adaptive optics. We made use of both the spatial and spectral information to separate the spectrum of the companion from that of the host star. We detect both water and CO in the companion spectrum. The molecular lines are rotationally broadened and Doppler shifted due to the orbital motion of the companion. We measured the projected rotational velocity to be 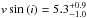 km s-1 and the barycentric radial velocity to be RV =2.0 ± 0.4 km s-1.
km s-1 and the barycentric radial velocity to be RV =2.0 ± 0.4 km s-1.
GQ Lupi b is a slow rotator compared to the giant planets in the solar system, and to the recent spin measurements of the exoplanets β Pic b (vsin (i) =25 km s-1; Snellen et al. 2014) and 2M1207 b (vsin (i) =17 km s-1, Zhou et al. 2016). This is in spite of GQ Lupi b being likely more massive than either of these, and thus this new spin measurement does not agree with the spin-mass trend of the others. However, we argue that the slow spin is a manifestation of the young age of GQ Lupi, and that the discrepancy cannot be used to argue for fundamental differences in formation path at this time.
We used the barycentric radial velocity measurement to place new constraints on orbital elements such as the semimajor axis, eccentricity, and orbital inclination with respect to the observer. This shows the strength of high-dispersion spectroscopy because it is possible to measure even small radial velocities.
The spin and RV measurements of GQ Lupi b demonstrate the potential of the combination of spatial and spectral filtering through the use of high-dispersion spectrographs together with adaptive optics.
Acknowledgments
This work is part of the research programmes PEPSci and VICI 639.043.107, which are financed by The Netherlands Organisation for Scientific Research (NWO). Support for this work was provided by NASA through Hubble Fellowship grant HST-HF2-51336 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. Furthermore, this work was performed in part under contract with the Jet Propulsion Laboratory (JPL) funded by NASA through the Sagan Fellowship Program executed by the NASA Exoplanet Science Institute.
References
- Allers, K. N., Gallimore, J. F., Liu, M. C., & Dupuy, T. J. 2016, ApJ, 819, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Arsenault, R., Alonso, J., Bonnet, H., et al. 2003, in Adaptive Optical System Technologies II, eds. P. L. Wizinowich, & D. Bonaccini, SPIE Conf. Ser., 4839, 174 [Google Scholar]
- Binks, A. S., & Jeffries, R. D. 2014, MNRAS, 438, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C. H., Charbonneau, D., & White, R. J. 2010, ApJ, 723, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., Jørgensen, U. G., & Fu, Y. 2001, J. Quant. Spec. Radiat. Transf., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 1997, Science, 276, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2000, ApJ, 536, L101 [CrossRef] [Google Scholar]
- Bouvier, J., Matt, S. P., Mohanty, S., et al. 2014, Protostars and Planets VI, 433 [Google Scholar]
- Broeg, C., Schmidt, T. O. B., Guenther, E., et al. 2007, A&A, 468, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogi, M., de Kok, R. J., Albrecht, S., et al. 2016, ApJ, 817, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, Protostars and Planets VI, 619 [Google Scholar]
- Choi, P. I., & Herbst, W. 1996, AJ, 111, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Burrows, A., Madhusudhan, N., et al. 2013, ApJ, 776, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Y., Wilner, D. J., Andrews, S. M., & Ohashi, N. 2010, AJ, 139, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Gregory, S. G., Alencar, S. H. P., et al. 2012, MNRAS, 425, 2948 [Google Scholar]
- Filippazzo, J. C., Rice, E. L., Faherty, J., et al. 2015, ApJ, 810, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Ginski, C., Neuhäuser, R., Mugrauer, M., Schmidt, T. O. B., & Adam, C. 2013, MNRAS, 434, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Ginski, C., Mugrauer, M., Neuhäuser, R., & Schmidt, T. O. B. 2014a, MNRAS, 438, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Ginski, C., Schmidt, T. O. B., Mugrauer, M., et al. 2014b, MNRAS, 444, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Grassitelli, L., Fossati, L., Langer, N., et al. 2015, A&A, 584, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guenther, E. W., Neuhäuser, R., Wuchterl, G., et al. 2005, Astron. Nachr., 326, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., & Rauer, H. 2015, ApJ, 810, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Hügelmeyer, S. D., Dreizler, S., Hauschildt, P. H., et al. 2009, A&A, 498, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, D. W. 2003, Planet. Space Sci., 51, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J., Hartigan, P., Krautter, J., & Kelemen, J. 1994, AJ, 108, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Jumper, P. H., & Fisher, R. T. 2013, ApJ, 769, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, SPIE Conf. Ser., 5492, 1218 [Google Scholar]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., & Roeser, S. 2009, VizieR Online Data Catalog: I/280 [Google Scholar]
- Konopacky, Q. M., Ghez, A. M., Fabrycky, D. C., et al. 2012, ApJ, 750, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Landin, N. R., Mendes, L. T. S., Vaz, L. P. R., & Alencar, S. H. P. 2016, A&A, 586, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., & Vidal-Madjar, A. 2016, A&A, 588, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Louden, T., & Wheatley, P. J. 2015, ApJ, 814, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., & Barman, T. 2007, ApJ, 654, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Metchev, S. A., Heinze, A., Apai, D., et al. 2015, ApJ, 799, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, F. Y., Padgett, D. L., Bryden, G., Werner, M. W., & Furlan, E. 2012, ApJ, 757, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., & Brandner, W. 1998, A&A, 330, L29 [NASA ADS] [Google Scholar]
- Neuhäuser, R., Guenther, E. W., Wuchterl, G., et al. 2005, A&A, 435, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E. R., Irwin, J., Charbonneau, D., et al. 2016, ApJ, 821, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., Liu, M. C., Wahhaj, Z., et al. 2014, ApJ, 794, 158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearce, T. D., Wyatt, M. C., & Kennedy, G. M. 2015, MNRAS, 448, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2008, ApJ, 684, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2139 [Google Scholar]
- Rucinski, S. 1999, in ASP Conf. Ser., 185, IAU Colloq. 170: Precise Stellar Radial Velocities, eds. J. B. Hearnshaw & C. D. Scarfe, ASP Conf. Ser., 185, 82 [Google Scholar]
- Scholz, A., Kostov, V., Jayawardhana, R., & Mužić, K. 2015, ApJ, 809, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seperuelo Duarte, E., Alencar, S. H. P., Batalha, C., & Lopes, D. 2008, A&A, 489, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., & Kaspi, Y. 2013, ApJ, 776, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Brandl, B. R., de Kok, R. J., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I., de Kok, R., Birkby, J. L., et al. 2015, A&A, 576, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, I., Schneider, G., Zuckerman, B., et al. 2006, ApJ, 652, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D. 2014, Astrophys. Space Sci. Proc., 36, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tachihara, K., Dobashi, K., Mizuno, A., Ogawa, H., & Fukui, Y. 1996, PASJ, 48, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Uyama, T., Hashimoto, J., Kuzuhara, M., et al. 2016, AAS journals, submitted [arXiv:1604.04697] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2012, in Advances in Computational Astrophysics: Methods, Tools, and Outcome, eds. R. Capuzzo-Dolcetta, M. Limongi, & A. Tornambè, ASP Conf. Ser., 453, 407 [Google Scholar]
- Weise, P., Launhardt, R., Setiawan, J., & Henning, T. 2010, A&A, 517, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H.-G. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zapatero Osorio, M. R., Martín, E. L., Bouy, H., et al. 2006, ApJ, 647, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y., Herczeg, G. J., Kraus, A. L., Metchev, S., & Cruz, K. L. 2014, ApJ, 783, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y., Apai, D., Schneider, G. H., Marley, M. S., & Showman, A. P. 2016, ApJ, 818, 176 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of key parameters of the three substellar companions with spin measurements.
All Figures
 |
Fig. 1 One of the combined image frames from detector 2. This is an intermediate data product from the CRIRES pipeline, and it is the combination of an AB nodding pair of exposures. The central rows that are used in the further data analysis are indicated on the right axis. The stellar spectral trail is clearly visible as the central white band, and the location of the hidden spectral trail from GQ Lupi b is indicated with a dashed line. The two diagonal stripes towards the right end are detector defects. |
| In the text | |
 |
Fig. 2 Illustration of the data analysis steps from a short wavelength range from detector 2. The y-axis depicts the slit position relative to the star, with the slit position of the companion indicated by a “b” on the right-hand axes. The greyscales were adjusted individually for each array with an IRAF-like z-scale algorithm. Top to bottom: A) the AB-combined image corrected for bad pixels; B) the spatial profiles of the star; C) the image after each row has been normalised with the rows of the spatial profile array; D) the spatial spectra (i.e. rectified for the trace); and E) the residual spatial spectra after removing stellar and telluric lines. |
| In the text | |
 |
Fig. 3 Models with a T/p profile and abundance that give rise to the strongest cross-correlation signals from the companion. The top panel shows the model with CO as a single trace gas, the middle panel the model with only H2O, and the bottom panel model contains both CO and H2O. The temperature is set to decrease from 2150 K at 1 bar to 1100 K at 0.03 bar and is isothermal outside this pressure range. The volume mixing ratios for CO and/or H2O in these three models are 10-4. |
| In the text | |
 |
Fig. 4 The residual spectrum after removing telluric and stellar lines at the companion position. Overplotted in red is the CO model from the top panel of Fig. 3, convolved to the CRIRES resolution, rotationally broadened, and Doppler shifted to match the measured vsini (5.3 km s-1) and radial velocity (2 km s-1) of GQ Lupi b. For illustration purposes, the model was also fitted to the residual companion spectrum with a vertical offset and a scaling factor. The companion spectrum is dominated by noise, but the individual CO lines are discernible. |
| In the text | |
 |
Fig. 5 Strength of the cross-correlation as function of slit position and radial velocity for the three best-fit models (see Fig. 3). We detect both CO and H2O using single-trace gas models with a S/N of 11.6 for CO and 7.7 for H2O, and the signal from the double-trace gas model is marginally stronger with a S/N of 12.3. These cross-correlation arrays are the averages from the two central CRIRES detectors. |
| In the text | |
 |
Fig. 6 The measured companion cross-correlation function (CCF) is best fit by a CO + H2O model CCF, which is redshifted 2.0 km s-1 and rotationally broadened by 5.3 km s-1. For comparison we also show the model CCF without rotational broadening for which the width is dominated by the spectral resolution of the CRIRES instrument. |
| In the text | |
 |
Fig. 7 Orbital parameters as function of eccentricity for the substellar companion GQ Lupi b around its host star with the colour scale indicating the logarithmic density of solutions. The panels in the left column are reproduced from Ginski et al. (2014b) and they show the 1% best-fitting solutions out of 5 000 000 runs of their LSMC fit. The right-hand panels show the orbital solutions, which are consistent with the radial velocity measurement from this work. |
| In the text | |
 |
Fig. 8 Spin as function of mass for extrasolar substellar companions and solar system planets, together with the free-floating planetary mass object PSO J318.5-22 and field brown dwarfs. The solar system planets and 2M1207 b have equatorial rotation velocities and β Pictoris b and GQ Lupi b have projected rotation velocities, as does PSO J318.5-22. Mercury and Venus are not included in the plot because their proximity to the Sun has caused their spin to be dominated by tidal interactions with the Sun. For comparison, field brown dwarfs with estimated masses and either a rotational period measurement or vsin (i) measurement are shown as empty circles, with the typical uncertainty in mass indicated for a single object. Their masses and radii are from Filippazzo et al. (2015), rotational periods are from Metchev et al. (2015), and vsin (i)’s are from either Zapatero Osorio et al. (2006) or Blake et al. (2010). The field brown dwarfs are much older than the substellar companions and PSO J318.5-22 with highly uncertain ages in the range 500 Myr to 10 Gyr. |
| In the text | |
 |
Fig. 9 Measured cross-correlation function between the companion spectrum and the CO + H2O model with and without the rescaling of the stellar lines described in Sect. 4.3.1. The difference between the two stems from when the reference spectrum containing the stellar and telluric lines was removed from the companion spectrum. The solid line is the resulting CCF from the approach we have taken in this paper, where we have scaled the stellar lines in the reference spectrum down by 15% to match the companion to star flux ratio at the companion position. The dashed line is the CCF for the case where the reference spectrum is removed from the companion spectrum without rescaling the stellar lines. The bottom panel shows the difference between the two. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


