| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628690 | |
| Published online | 04 October 2016 | |
HADES RV program with HARPS-N at the TNG GJ 3998: An early M-dwarf hosting a system of super-Earths⋆,⋆⋆
1 INAF–Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
e-mail: affer@astropa.inaf.it
2 INAF–Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy
3 Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB, Carrer de Can Magrans s/n, 08193 Cerdanyola del Vallés, Spain
4 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
5 Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
6 Consejo Superior de Investigaciones Científicas, 28006 Madrid, Spain
7 INAF–Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
8 INAF–Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
9 Dipartimento di Fisica e Astronomia G. Galilei, Universitá di Padova, Vicolo dell’Osservatorio 2, 35122 Padova, Italy
10 INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
11 INAF–Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
12 Osservatorio Astronomico della Regione Autonoma Valle d’Aosta, Fraz. Lignan 39, 11020 Nus (Aosta), Italy
13 INAF – Fundación Galileo Galilei, Rambla José Ana Fernandez Pérez 7, 38712 Breña Baja, TF, Spain
Received: 11 April 2016
Accepted: 8 July 2016
Context. Many efforts are currently made to detect Earth-like planets around low-mass stars in almost every extra-solar planet search. M dwarfs are considered ideal targets for Doppler radial velocity searches because their low masses and luminosities make low-mass planets orbiting in these stars’ habitable zones more easily detectable than those around higher mass stars. Nonetheless, the frequency statistics of low-mass planets hosted by low-mass stars remains poorly constrained.
Aims. Our M-dwarf radial velocity monitoring with HARPS-N within the collaboration between the Global architectures of Planetary Systems (GAPS) project, the Institut de Ciències de l’Espai/CSIC-IEEC (ICE) and the Instituto de Astrofísica de Canarias (IAC) can provide a major contribution to the widening of the current statistics through the in-depth analysis of accurate radial velocity observations in a narrow range of spectral sub-types (79 stars, between dM0 to dM3). Spectral accuracy will enable us to reach the precision needed to detect small planets with a few Earth masses. Our survey will contribute to the surveys devoted to the search for planets around M-dwarfs, mainly focused on the M-dwarf population of the northern emisphere, for which we will provide an estimate of the planet occurrence.
Methods. We present here a long-duration radial velocity monitoring of the M1 dwarf star GJ 3998 with HARPS-N to identify periodic signals in the data. Almost simultaneous photometric observations were carried out within the APACHE and EXORAP programs to characterize the stellar activity and to distinguish those due to activity and to the presence of planetary companions from the periodic signals. We ran a Markov chain Monte Carlo simulation and used a Bayesian model selection to determine the number of planets in this system, to estimate their orbital parameters and minimum mass, and to properly treat the activity noise.
Results. The radial velocities have a dispersion in excess of their internal errors due to at least four superimposed signals with periods of 30.7, 13.7, 42.5, and 2.65 days. Our data are well described by a two-planet Keplerian (13.7 d and 2.65 d) and a fit with two sinusoidal functions (stellar activity, 30.7 d and 42.5 d). The analysis of spectral indexes based on Ca II H & K and Hα lines demonstrates that the periods of 30.7 and 42.5 days are due to chromospheric inhomogeneities modulated by stellar rotation and differential rotation. This result is supported by photometry and is consistent with the results on differential rotation of M stars obtained with Kepler. The shorter periods of 13.74 ± 0.02 d and 2.6498 ± 0.0008 d are well explained with the presence of two planets, with masses of at least 6.26-0.76+0.79 M⊕ and 2.47 ± 0.27 M⊕ and distances of 0.089 AU and 0.029 AU from the host, respectively.
Key words: techniques: radial velocities / techniques: photometric / methods: data analysis / stars: individual: GJ3998 / instrumentation: spectrographs / planets and satellites: detection
Based on: observations made with the Italian Telescopio Nazionale Galileo (TNG), operated on the island of La Palma by the INAF – Fundación Galileo Galilei at the Roche de Los Muchachos Observatory of the Instituto de Astrofísica de Canarias (IAC); photometric observations made with the APACHE array located at the Astronomical Observatory of the Aosta Valley; photometric observations made with the robotic telescope APT2 (within the EXORAP program) located at Serra La Nave on Mt. Etna.
© ESO, 2016
1. Introduction
In the two decades since the discovery of the first giant planetary mass companion to a main-sequence star (Mayor & Queloz 1995) the search for and characterization of extrasolar planets has quickly developed to become a major field of modern-day astronomy. Thanks to concerted efforts with a variety of observational techniques (both from the ground and in space), thousands of confirmed and candidate planetary systems are known to date (e.g., Schneider et al. 20111), encompassing orders of magnitude in mass and orbital separation. The frontier today is being pushed ever closer to identifying potentially habitable low-mass planets with a well-determined rocky composition similar to that of Earth. Planetary systems harboring objects with these characteristics are likely to be discovered first around primaries with later spectral types than that of the Sun.
Stars in the lower main sequence (M dwarfs) constitute the vast majority (> 70−75%) of all stars, both in the solar neighborhood and in the Milky Way as a whole (Henry et al. 2006; Winters et al. 2015). They are particularly promising targets for exoplanet search programs for a number or reasons. In particular, the favorable mass and radius ratios lead to readily detectable radial-velocity (RV) and transit signals produced by terrestrial-type planets. Furthermore, the low luminosities of M dwarfs imply that the boundaries of their habitable zones (HZ) are located at short separations (typically between 0.02 AU and 0.2 AU, see, e.g., Mandell et al. 2007), making rocky planets orbiting within them more easily to detect with present-day observing facilities than those around more massive stars (e.g., Charbonneau & Deming 2007). Finally, the favorable planet-star contrast ratios for small stars creates the best opportunities in the near future for detailed characterization studies of small planets and their atmospheres (e.g., Seager & Deming 2010).
While the first planets discovered around M dwarfs were Jovian-type companions (Delfosse et al. 1998; Marcy et al. 1998, 2001), it is now rather well observationally established that their frequency is lower than that of giant planets around solar-type hosts (e.g., Sozzetti et al. 2014, and references therein), a result understood within the context of the core-accretion formation model (e.g., Laughlin et al. 2004). The most recent evidence gathered by RV surveys and ground-based as well as space-borne transit search programs points instead toward the ubiquitousness of low-mass companions with small radii around M dwarfs. The outstanding photometric dataset of transit candidates around early-M dwarfs from the Kepler mission has allowed Gaidos et al. (2016) and Dressing & Charbonneau (2015) to derive cumulative occurrence rates of 2.3 ± 0.3 and 2.5 ± 0.2 planets with 1−4 R⊕ for orbital periods P shorter than 180 days and 200 days, respectively. Approximately one in two stars of early-M type appears to host either an Earth-sized (1−1.5 R⊕) or a super-Earth (1.5−2.0 R⊕) planet (Dressing & Charbonneau 2015) with an orbital period < 50 days. Based on different recipes for the definition of the HZ boundaries and planetary atmospheric properties, Kopparapu (2013) and Dressing & Charbonneau (2015) obtained frequency estimates of potentially habitable terrestrial planets (1−2 R⊕) around the Kepler sample of early-M dwarfs of 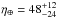 % and
% and 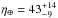 %, respectively. The inference from RV surveys of early- and mid-M dwarfs instead indicates
%, respectively. The inference from RV surveys of early- and mid-M dwarfs instead indicates 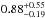 super-Earth planets per star with P< 100 d and msini = 1−10 M⊕, and a frequency of such planets orbiting within the host’s HZ
super-Earth planets per star with P< 100 d and msini = 1−10 M⊕, and a frequency of such planets orbiting within the host’s HZ 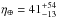 % (Bonfils et al. 2013). The η⊕ estimates from Doppler and transit surveys thus seem to agree broadly. However, a) the uncertainties associated with these occurrence rate estimates are still rather large; and b) the known compositional degeneracies in the mass-radius parameter space for super-Earths (e.g., Rogers & Seager 2010) make the mapping between the η⊕ estimates based on (minimum) mass and radius difficult. Any additional constraints coming from ongoing and upcoming planet detection experiments targeting M dwarfs are therefore particularly valuable.
% (Bonfils et al. 2013). The η⊕ estimates from Doppler and transit surveys thus seem to agree broadly. However, a) the uncertainties associated with these occurrence rate estimates are still rather large; and b) the known compositional degeneracies in the mass-radius parameter space for super-Earths (e.g., Rogers & Seager 2010) make the mapping between the η⊕ estimates based on (minimum) mass and radius difficult. Any additional constraints coming from ongoing and upcoming planet detection experiments targeting M dwarfs are therefore particularly valuable.
We present here high-precision, high-resolution spectroscopic measurements of the bright (V = 10.83 mag) M1 dwarf GJ 3998 gathered with the HARPS-N spectrograph (Cosentino et al. 2012) on the Telescopio Nazionale Galileo (TNG) as part of an RV survey for low-mass planets around a sample of northern-hemisphere early-M dwarfs. The HArps-n red Dwarf Exoplanet Survey (HADES) observing program is the result of a collaborative effort between the Italian Global Architecture of Planetary Systems (GAPS, Covino et al. 2013; Desidera et al. 2013; Poretti et al. 2016) Consortium, the Institut de Ciències de l’Espai de Catalunya (ICE), and the Instituto de Astrofísica de Canarias (IAC). Analysis of the Doppler time-series, spanning ~ 2.4 yr, reveals a system of two super-Earths orbiting at 0.029 AU and 0.089 AU from the central star. After a short presentation of the HADES RV program, we describe in Sect. 2 the observations and reduction process and in Sect. 3 summarize the atmospheric, physical, and kinematic properties of GJ 3998. In Sect. 4 we describe the RV analysis and discuss the effect of stellar activity. Section 5 presents the analysis and results of a multi-site photometric monitoring campaign. In Sect. 6 we describe the Bayesian analysis and the model selection and derive the system parameters. We summarize our findings and conclude in Sect. 7.
 |
Fig. 1 Radial velocity (top) and activity indexes Hα (middle) and S index (bottom) time series for GJ 3998 measured with the TERRA pipeline. |
2. HADES RV program
The HADES RV program has completed the sixth observation semester. The complete original sample is composed of 106 stars, ranging from dM0 to dM3 spectral type, selected from the catalogs of Lépine & Gaidos (2013) and of the Palomar/Michigan State University (PMSU, Reid et al. 1995), with the additional criterion that the stars needed to be part of the APACHE catalog (Sozzetti et al. 2013), with a visible magnitude lower than 12 and with a high number of Gaia mission scans. The M stars are also photometrically monitored by the EXORAP program at Serra La Nave. These selection criteria are meant to ensure a good characterization of the systems. Twenty-seven stars were rejected from the complete sample during the first observation semester (binary systems, fast rotators, peculiar stars, stars with high activity or of earlier type and/or those with incorrect spectral type). Some of the targets (≈15% of the cleaned sample) already have more than 80 RV points with an excellent precision (1−1.8 m s-1 at V≈ 10−11). The star GJ 3998 emerged as best suited among several possible candidates, since it shows clear periodic signals that are consistent with the presence of planets.
The statistical analysis of the capability of our survey is the purpose of the second paper of the HADES series (Perger et al. 2016). It is focused on simulating the planet detection rates on low-mass stars and predicting the number of planets that may be detected, using the most recent planet occurrence statistics applied to our stellar sample and the actual observation times of our survey. The simulations performed by Perger et al. show as first statistical results that 1) the observations of the HADES program analyzed to date might enable the detection of 2.3±1.6 planets (3.6% detection rate), in agreement with our findings; 2) with 120 obs/star we are able to detect about 10% of the distributed planets; 3) the best average number of observations per target for a time-limited survey is about 35 for a sample of early-M dwarfs and exposure times of 900 s (for further information see Perger et al. 2016, and references therein).
The star GJ 3998 has been monitored from BJD = 2 456 439.6 (26 May 2013) to BJD = 2 457 307.8 (12 October 2015). We obtained a total of 136 data points spanning 869 days (Fig. 1). The spectra were obtained at high resolution (R~ 115 000) with the optical echelle spectrograph HARPS-N with exposure times of 15 min and an average signal-to-noise ratio (S/N) of 45 at 5500 Å. Of the 136 epochs, 76 were obtained within the GAPS time and 60 within the Spanish time. Observations were gathered without the simultaneous Th-Ar calibration, which is commonly used to correct for instrumental drifts during the night. This choice avoided the contamination of the Ca II H & K lines, which are particularly important for the stellar activity analysis of M dwarfs (Giampapa et al. 1989; Forveille et al. 2009; Lovis et al. 2011). The M-type stars were observed by the Italian team in conjunction with other GAPS targets, which used the Th-Ar simultaneous calibration, therefore we estimated the drift data between the two fibers (star and reference calibration) for each night from these observations and evaluated the interpolated drift for GJ 3998.
Data reduction and spectral extraction were performed using the Data Reduction Software (DRS v3.7, Lovis & Pepe 2007). RVs were measured by means of a weighted cross-correlation function (CCF) with the M2 binary mask provided with the DRS (Baranne et al. 1996; Pepe et al. 2002). This approach is not best suited for M-dwarf stars, however, since their spectra suffer from heavy blends that can lead to a mismatch of several features of the binary mask. As a result, the CCF shows sidelobes that affect the RV precision and the asymmetry indexes of the CCF. A better alternative is to measure the RVs by matching the spectra with a high S/N template obtained by coadding the spectra of the target, as implemented in the TERRA pipeline (Anglada-Escudé & Butler 2012), which possibly provides a better RV accuracy when applied to M dwarfs.
We list the data in Table A.1 including the observational dates (barycentric Julian date or BJD), the S/Ns, the RVs from the DRS and TERRA pipelines, and the Hα and S indexes. We have an average S/N of 43, ranging from 18 to 65 and a mean RV of −44.81 km s-1. The TERRA RVs show a root mean squares (rms) dispersion of 4.24 m s-1 and a mean error of 1.12 m s-1, whereas the DRS shows a dispersion of 4.89 m s-1 and an error of 1.82 m s-1. The standard deviation of the interpolated drift for GJ 3998 is 0.7 m s-1, which is smaller than the typical DRS RV error of 1.8 m s-1 and TERRA RV error of 1.1 m s-1. The analysis described in the next sections has been performed on either the DRS and TERRA RVs and led to the same global results, with the latter providing better precision. In the following, only the results obtained with the TERRA RVs are listed.
3. Stellar properties of GJ 3998
The star GJ 3998 is a high proper motion early-M dwarf (spectral type M1) at a distance of 17.8 pc from the Sun (π = 56.20 ± 2.26 mas). Accurate stellar parameters were determined using the empirical relations by Maldonado et al. (2015)2 on the same spectra as in the present work to derive RVs. This technique relies on the ratios of pseudo-equivalent widths of spectral features as a temperature diagnostic, while combinations and ratios of features were used to derive calibrations for the stellar metallicity. The derived temperature and metallicity are used in association to photometric estimates of mass, radius, and surface gravity to calibrate empirical relationships for these parameters. The study of Maldonado et al. reported typical uncertainties of about 13.1% for the stellar mass, 11.8% for the radius, 25% for luminosities, and 0.05 dex for log g. We note that these uncertainties were computed by taking into account the σ of the corresponding calibration and the propagation of the errors in Teff and [Fe/H].
The temperature of GJ 3998 is Teff = 3722 ± 68 K, and its surface gravity is log g = 4.77 ± 0.04.
Stellar parameters for the star GJ 3998 from the analysis of the HARPS-N spectra using the technique reported by Maldonado et al. (2015) (upper part). Lower part: coordinates, V and K magnitudes, parallax, proper motions and space velocities.
Stars that are present near the Sun may come from a wide range of Galactic locations. Therefore, stellar space velocity, as a clue to the origin of a star in the Galaxy, is very important. The accurate distance and proper motion available in the Hipparcos Catalog (ESA 1997), combined with the stellar radial velocity, enable us to derive reliable space velocities for GJ 3998. The calculation of the space velocity with respect to the Sun is based on the procedure presented by Johnson & Soderblom (1987), corrected for the effect of differential Galactic rotation (Scheffler & Elsasser 1988) by adopting a solar Galactocentric distance of 8.5 kpc and a circular velocity of 220 km s-1. The correction of space velocity to the Local Standard of Rest is based on a solar motion, (U, V, W)⊙ = (10.0, 5.2, 7.2) km s-1, as derived from Hipparcos data by Dehnen & Binney (1998). In the present work, U is defined to be positive in the direction of the Galactic center. The peculiar space velocity S, given by S = (U2 + V2 + W2)1/2, is quoted with all kinematic data and stellar properties in Table 1. GJ 3998 shows kinematic properties typical of the thin-disk population. We have calculated the probabilities that the star belongs to a specific population, thick disk (TD), thin disk (D), or stellar halo (H), following the method used by Bensby et al. (2004). On account of these probabilities, GJ 3998 could belong to the thin disk because its ratio of the respective probabilities for the thick and thin disks is TD/D ≲ 0.5 (Bensby et al. 2004).
 |
Fig. 2 Periodogram power of the inspected periods as a function of the number of observations. The most significant periods (dark red) at 30.7 d and 13.7 d are clearly visible with a high power for Nobs> 60, as well as the period at 2.65 d with a moderate Scargle power, which increases for Nobs> 80, and the period at 42.5 d, whose power increases for Nobs> 110 (2D plot adapted from A. Mortier, priv. comm.). |
 |
Fig. 3 GLS periodograms of the radial velocities of GJ 3998, of the original data (upper panel), and after removing (from top to bottom) the 30.7 d (marked with the red dot), the 42.5 d (magenta dot), the 13.7 d (blue dot), and finally the 2.65 d (cyan dot) signals. The dashed lines indicate the 0.1%, 1%, and 10% level of false-alarm probability. |
4. Data analysis
The raw rms dispersion of the RVs is 4.24 m s-1, which is much higher than the average (Doppler + jitter) uncertainty ⟨σi⟩≈ 1.4−2.6 m s-1, depending on the assumed jitter (σjitter = 0.8 m s-1, from our first estimate from a Gaussian process, and σjitter = 2.4 m s-1, following the derivation from Perger et al. (2016). An F-test with F = 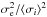 (Zechmeister & Kürster 2009) returned a negligible probability (< 10-8) that the photon noise combined with stellar jitter explains the measured dispersion.
(Zechmeister & Kürster 2009) returned a negligible probability (< 10-8) that the photon noise combined with stellar jitter explains the measured dispersion.
The first step of the RV data analysis consists of identifying significant periodic signals in the data. Pre-whitening is a commonly used tool for finding multi-periodic signals in time series data. With this method we sequentially determined the dominant Fourier components in a time series and removed them. The pre-whitening procedure was applied to the full RV data using the generalized Lomb-Scargle (GLS) periodogram algorithm (Zechmeister & Kürster 2009) and the program Period04 (Lenz & Breger 2004) for an independent test. The two methods yielded the same results in terms of extracted frequencies from our RV time series. Owing to the limited range in frequency covered by the signals, we repeated the analysis by using the iterative sine-wave fitting least-squares method (Vaníček 1971). This approach is used in the asteroseismic analysis of multiperiodic pulsating stars to minimize the subtle effects of pre-whitening, such as power exchange between a signal frequency and an alias of another signal frequency. After each detection, only the frequency values were introduced as known constituents in the new search. In this way, their amplitudes and phases were recalculated for each new trial frequency, always subtracting the exact amount of signal for any known constituent. This new analysis again confirmed the previously determined frequencies.
We calculated the false-alarm probabilities (FAP) of detection using 10 000 bootstrap randomization (Endl et al. 2001) of the original RV time series. When a significant peak was located at a given period, the corresponding sinusoidal function was adjusted and removed. The process was repeated several times until no significant peak remained.
To visualize (Fig. 2) the cumulative contribution of data points to the significance of the detected frequencies, we calculated the GLS periodograms increasing the number of observations, from 20 to 136, adding one observation at a time (following the exact order of data acquisition). We computed the power corresponding to each of the 5000 periods in the range 1.2 d to 500 d for each of the 117 periodograms. Each horizontal slice in Fig. 2 shows powers (indicated by the color scale) versus periods for the periodogram corresponding to the observations number, indicated on the vertical axis. Figure 2 is a 2D representation adapted from A. Mortier (priv. comm.).
Following this procedure, we identified three frequencies with an FAP lower than 0.1%, at 0.0326 d-1 (P = 30.7 d), 0.0729 d-1 (P = 13.7 d), and 0.0235 d-1 (P = 42.5 d), in order of decreasing power. After removing the sinusoid corresponding to the period of 30.7 d, with a semi-amplitude of 3.4 m s-1, two highly significant peaks are visible in the periodogram, at 42.5 d and 13.7 d, with semi-amplitudes of 2.5 and 2.1 m s-1 (Fig. 3). One additional peak remains at 0.3773 d-1 (P = 2.65 d) with a significant FAP lower than 0.1% and a semi-amplitude of 1.7 m s-1. A low-frequency signal with an FAP of about 1% remains after subtracting the four significant periods. This unresolved peak is probably the signature of a long-term variation of the activity, which has a timescale of about 600 d or more. This low-frequency peak was found in both the activity indicators (S index and Hα, Sect. 4.1). Moreover, it almost disappears when a linear term is introduced in the frequency analysis of the RV time series.
A careful analysis of the spectral window, following the methods of Dawson & Fabrycky (2010), ruled out that the peaks in the periodograms are artifacts due to the combination of the long-term activity with the spectral window (or to the time sampling alone).
4.1. Periodic signals: planet vs. activity-related origin
The purely frequentistic approach highlighted the presence of four significant frequencies in the RV time series. However, when dealing with M-type stars we have to face one of the major drawbacks of this kind of stars: many M stars show some level of activity, even if moderate, and display inhomogeneities on their surface that rotate with the star. These inhomogeneities cause RV shifts due to the distortion of the spectral line shape, and these shifts can mimic, confuse or even hide the planetary signal.
To investigate RV variability against stellar activity, we made use of spectral indexes based on Ca II H & K (S index) and Hα lines, and we took advantage of the photometric observations of the star within the APACHE and EXORAP photometric programs to check whether plages or spots might produce the observed Doppler changes (Sect. 5).
Ca II H & K (top) and Hα (bottom) windows.
 |
Fig. 4 From top to bottom: GLS periodograms of RVs, S index, and Hα, zoomed around the frequencies of interest. The dotted blue and cyan lines indicate the frequencies corresponding to orbital periods of the candidate planets at 13.7 d and 2.65 d, respectively, while the dotted red and magenta lines show the frequencies corresponding to the activity periods at 30.7 d and 42.5 d, respectively. These frequencies and periods are marked with dots in the same color code in the upper RV panel. |
Stellar activity is commonly characterized by the strength of the central cores of the Ca II H & K lines with respect to a reference flux measured at each side of the lines. Activity S indexes are measured by summing the fluxes in the central cores of the Ca II H & K lines and rationing this sum to the sum of fluxes in two 20 Å windows on either side of the lines. We defined the windows following Henry et al. (1996) (Suárez Mascareño et al. 2015), and the results are summarized in Table 2. Fluxes were measured using the IRAF3 task sbands. Before measuring the fluxes, each individual spectrum was corrected for its corresponding RV by using the IRAF task dopcor. Uncertainties in the S indexes were obtained by shifting the center of the red and blue wings by ±0.2 Å. Typical uncertainties vary between 1 × 10-3 and 5 × 10-4 (Maldonado et al. 2016).
We measured the Hα emission by summing the fluxes in the central core of the line at 6562.808 Å with a width of 1.6 Å and rationing this sum to the sum of fluxes in two windows on either side of the line (see Table 2). The Hα line at λ = 6562.808 Å is sensitive to the mean chromospheric activity (Kürster et al. 2003; Bonfils et al. 2007; Robertson et al. 2013), such as Ca II H & K lines. The RV and activity indexes Hα and S index measurements of the star GJ 3998 are displayed in Fig. 1 as a function of time.
 |
Fig. 5 GLS periodograms around the frequency ranges of interest for two subsets of the original RV data. The first season has 61 data points and its periodogram is black (FAP: 0.1%, 1%, 10% horizontal black dotted lines), the second season has 75 data points and is plotted in red (FAP: 0.1%, 1%, 10% horizontal red dashed lines). The two upper panels refer to the frequencies related to activity (upper left: f = 0.0235 d-1 – P = 42.5 d; upper right: f = 0.0326 d-1 – P = 30.7 d). The two lower panels refer to the frequencies related to the candidate planets (lower left: f = 0.0729 d-1 – P = 13.7 d; lower right: f = 0.3773 d-1 – P = 2.65 d). The relevant frequencies derived from all the methods used on the full dataset are indicated with vertical lines green from RV analysis, blue from activity indexes, and orange from photometry (see Sect. 5). |
The analysis of the activity indicators was performed with the GLS algorithm and periodic variations around 30.7 d and 42.5 d were observed in the S index and Hα, whereas no signal appeared around 13.7 and 2.65 days, as illustrated in Fig. 4, which shows the GLS periodograms of these parameters zoomed around the frequencies of interest.
The results of the activity analysis support the non-planetary origin of the 30.7 d and 42.5 d signals and give us an indication of the stellar rotation period and of a differential rotation, consistently with the results of a recent analysis that was based on a wide dataset, including M stars, of Kepler time series, as discussed in Sect. 7. This rotation period is consistent with the predicted Prot ≈34.7 ± 6.9 d from the formula in Suárez Mascareño et al. (2015) according to the log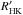 ≈−5.01.
≈−5.01.
To avoid any misinterpretation of the stellar activity as a planetary signal, we analyzed two subsets of the data (before and after BJD-2 457 000.0 d) to check the persistence of the planetary signals over time and to mitigate the possible effects of discontinuities in the data sampling. In Fig. 5 we show the GLS periodograms zoomed around the frequency ranges of interest. The black line shows the first subset (61 RV points) and the red-line the second subset (75 RV points). In the plot we indicate the frequencies obtained from the RV (green) and activity indexes (blue) analysis and from the photometry (orange) (see Sect. 5). The periods related to activity effects (related to magnetic phenomena such as spots and faculae, which rotate on the stellar surface, and to differential rotation) span a range from 28 to 41 d in the two seasons (f = 0.036 d-1 to f = 0.024 d-1), while the two features at P1 = 2.65 d (f = 0.3773 d-1) and P2 = 13.7 d (f = 0.0729 d-1) are observed in both seasons. This constitutes further evidence that these two signals are present in the RVs at any time, leading us conclude that both signals have a planetary origin.
Another argument in favor of the planetary interpretation of the 2.65 d and 13.7 d signals is provided in Fig. 6 by the low Spearman rank correlation coefficients between the S index (ρ = 0.17) and Hα (ρ = 0.18) and the RV residuals after removing the activity contributions (30.7 d and 42.5 d). Such a correlation would be expected if the radial velocity variation were still induced by activity features on the star surface.
The activity index analysis was performed with the values calculated by the TERRA pipeline and those calculated independently, using the method described above. We obtained the same results.
5. Photometry
The targets of the HADES program are photometrically monitored by two independent programs: APACHE and EXORAP4.
These two programs regularly follow up the sample of M stars to provide an estimate of the stellar rotation periods by detecting periodic modulation in the differential light curves.
5.1. EXORAP photometry: dataset
The star GJ 3998 was monitored at INAF-Catania Astrophysical Observatory with an 80 cm f/8 Ritchey-Chretien robotic telescope (APT2) located at Serra la Nave (+14.973°E, +37.692°N, 1725 m a.s.l.) on Mt. Etna. The APT2 camera is an ASPEN CG230 equipped with a 2k×2k e2v CCD 230-42 detector operated with a binning factor of 2 (pixel scale 0.94′′) and a set of standard Johnson-Cousins UBVRI filters. The data were reduced by overscan, bias, dark subtraction, and flat fielding with the IRAF procedures and were visually inspected to check the quality. We collected BVRI photometry of GJ 3998 in 75 nights between 5 May 2014 and 17 September 2015. The log of the two observing seasons is given in Table 3. We used aperture photometry as implemented in the IDL routine aper.pro, trying a range of apertures to minimize the rms of the ensemble stars.
To measure the differential photometry, we started with an ensemble of about six stars, the nearest and brightest to GJ 3998, and checked the variability of each by building their differential light curves using the remaining ensemble stars as reference. With this method we selected the least variable stars of the sample, typically four. The rms of the ensemble stars is ≲ 9 mmag in all bands.
 |
Fig. 6 Radial velocity after subtracting the contributions of the activity signals at 30.7 d and 42.5 d, displayed as a function of the S index (top) and Hα (bottom). The extremely low correlation values support the interpretation that the 2.65 d and 13.7 d signals are of planetary origin. |
5.1.1. EXORAP photometry: Searching for periodic variability
The differential photometry of the target was analyzed using the GLS algorithm. We analyzed the full dataset and each season separately (Table 3). No data were rejected after evaluation for outliers (clip at 5σ). For each band, we analyzed the periodograms, assigning them an FAP using the bootstrap method with 10 000 iterations. The periodograms of the R and I magnitudes do not show any peak above the 10% significance level. The periodogram of the B measurements is affected by a long-term trend: the combination with the spectral window aliasing makes the determination of the periodicities, if any, very difficult. The results obtained from the V measurements are more reliable. We find a good confirmation of the 30.7 d period (P = 30.75 ± 0.12 d, the precision is the formal error from the least-squares fitting), although it is flanked by the aliases at ±1 cycle/year and at ±1 cycle/synodic month. To check for possible systematic effects, we repeated the search for periodicity on all the measured stars in the field of view of GJ 3998 (about 70 targets), but none of them shows significant variability with the same periodicity as our target star.
The photometric period is consistent with the one found by analyzing the variability of features sensitive to stellar activity in the HARPS-N data (Sect. 4.1). The V light-curve folded with the observed periodicity is shown in Fig. 7 (the B light-curve folded with the same periodicity is also shown). It shows a full amplitude of 0.012 mag. We note that the observed variability amplitude in the V band is typical for an M2 dwarf as shown by Rockenfeller et al. (2006), who also reported variability amplitudes in the R and I bands that are about half that of the V band. With a precision of a few millimag, a signal with only a five-millimag full-amplitude remains elusive to us, hence the lack of period detection in the R and I data.
 |
Fig. 7 Phase-folded V and B curves at the period P = 30.75 ± 0.12 d, the precision reported is the formal error from the least-squares fitting. |
5.2. APACHE photometry: dataset
APACHE is a photometric survey devised to detect transiting planets around hundreds of early-to-mid-M dwarfs (Sozzetti et al. 2013). GJ 3998 was monitored for 41 nights between 30 June 2014 and 13 August 2015 with one of the five 40 cm telescopes composing the APACHE array, located at the Astronomical Observatory of the Autonomous Region of the Aosta Valley (OAVdA, +45.7895 N, +7.478 E, 1650 m.a.s.l.). Each telescope is a Carbon Truss f/8.4 Ritchey-Chretien equipped with a GM2000 10-MICRON mount and an FLI Proline PL1001E-2 CCD camera, with a pixel scale of 1.5′′/pixel and a field of view of 26′× 26′. The observations were carried out using a Johnson-Cousins V filter following the standard strategy used by APACHE, consisting of three consecutive exposures repeated at intervals of ~20−25 min while the target is ~35° above the horizon. The images were reduced with the standard pipeline TEEPEE written in IDL5 by the APACHE team (see Giacobbe et al. 2012). TEEPEE is devised to perform ensemble differential aperture photometry by testing up to 12 different apertures and choosing the best set of comparison stars that give the smallest rms for the differential light curve of the target.
 |
Fig. 8 Differential light curve of GJ 3998 observed by APACHE, folded at the best period P = 31.5 days found through a frequency analysis of the time series. The red dot in the lower left corner shows the average uncertainty of the data. |
5.2.1. APACHE photometry: Analysis of the light curves
The APACHE data were obtained by using an aperture of 4.5 pixels and a set of four comparison stars (UCAC4 506-065211, UCAC4 506-065134, UCAC4 505-066479, and UCAC4 506-065155). The stellar brightness decreases almost linearly during the second season (Spearman rank correlation coefficient ρ = −0.66, computed with the r_correlate IDL function), and the ~6 mmag rms of the data, which is comparable to the typical photometric precision of the measurements, is not indicative of high photospheric variability. The brightness decrease is not confirmed by the EXORAP V photometry, and hence its origin remains unclear. We searched the light curve for sinusoidal-like modulation by using the complete dataset consisting of 455 points, each being the average of three consecutive measurements with an uncertainty equal to their rms. We used the GLS and Period04 algorithms to calculate the frequency periodograms. Gaps in the data and in the folded light curves make the accurate identification of the true period around 30−35 d slightly uncertain. The analysis performed with Period04 returned a maximum frequency corresponding to a period of about 31.5 d, in good agreement with the results of the EXORAP photometry, while the GLS analysis returned the one-cycle/year alias at 34.5 d. The best-fit semi-amplitude of the sinusoid is ~5 mmag. Figure 8 shows the light curve folded at the best period found. To estimate the significance of the detection, we performed a bootstrap analysis (with replacement) by using 10 000 fake datasets derived from the original photometric data, and found an FAP ≤ 1.0%. While indicating a rather significant detection, this result should be taken with caution because the signal semi-amplitude is close to the typical precision of the data. However, it is noteworthy that the best photometric frequency we find is close to that found in the RVs and spectroscopic activity index time series, which we explained as related to the stellar rotation frequency. In light of this, we conclude that the APACHE photometry further supports the interpretation based on spectroscopic evidence. We searched the light curve also for possible transit-like signals of the candidate planets, but none was detected. However, this search is not conclusive since the number of observations and the photometric precision are too low to rule out signals in this period domain.
5.3. FastCam lucky imaging observations
On 1 October 2014 at 22:04 UT, we collected 50 000 individual frames of GJ3998 in the I band using the lucky imaging FastCam instrument (Oscoz et al. 2008) at the 1.5 m Carlos Sánchez Telescope (TCS) at the Observatorio del Teide, Tenerife, with 30 ms exposure time for each frame. FastCam is an optical imager with a low-noise EMCCD camera that allows obtaining speckle-featuring of unsaturated images at a fast frame rate, see Labadie et al. (2011).
To construct an image with high resolution and long exposure that is diffraction limited, the individual frames were bias subtracted, aligned, and co-added using our own lucky imaging (LI) algorithm, see Law et al. (2006). Figure 9 presents the high-resolution image constructed by co-adding 20% of the best frames, resulting in a total integration time of 300 s. The combined image achieved ΔmI = 2.5−3.0 at 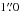 . We did not find a bright contaminant star in the diffraction limited image.
. We did not find a bright contaminant star in the diffraction limited image.
 |
Fig. 9 Diffraction-limited image of GJ3998 after lucky imaging processing with a 20% selection of the best individual TCS/FastCam frames. |
6. MCMC analysis of the RV time series
To derive the system parameters with the associated uncertainties and also to double-check the purely frequentist approach, we performed a Bayesian analysis of the RV data by using the publicly available emcee tool (Foreman-Mackey et al. 2013), a Python implementation of the affine invariant Markov chain Monte Carlo (MCMC) ensemble sampler. Under the hypothesis that up to four significant signals exist in the data (i.e., two of planetary origin and two ascribable to the stellar activity), as inferred from the analysis described in Sect. 4.1, we tested several different models by changing the number of planets, assuming circular or eccentric orbits for the outer planet, and examining different ways to model the stellar activity noise. In all the cases we included an additional jitter term summed in quadrature with the RV uncertainties. We used uniform priors for all the fitted parameters by keeping their range of variability unchanged when passing from one model to the other. The best-fit values are calculated as medians of the marginal posterior distributions, and the uncertainties represent their 16% and 84% quantiles. In modeling the RVs we ignored the mutual gravitational perturbations between the two planets.
6.1. Modeling the stellar activity noise
The comparative analysis of the periodograms for the S activity index and RVs, also supported by photometry, showed a clear nearly periodic noise term of stellar origin, whose recurrence is likely ascribable to the stellar rotation. We took this evidence into account in our RV analysis by treating the short-term activity (i.e., related to the stellar rotation) in two different ways.
As a first trial, we considered a strictly periodic term by fitting a sinusoid with a period constrained to between 25 and 45 days. Additionally, we used PyORBIT (Malavolta et al. 2016) to test several combinations of sinusoids at the stellar rotational period and its harmonics and independent amplitudes and phases for each observing season, without observing a significant improvement with respect to a single-sinusoid approach.
As a second, more sophisticated trial we treated the stellar activity term as correlated quasi-periodic noise by using the approach based on Gaussian processes (GPs; see, e.g., Rasmussen & Williams 2006 and Roberts et al. 2013). In this case the stellar noise is conveniently described by means of a covariance function, opportunely selected, whose functional form and parameters have some correspondence to the physical phenomena to be modeled. The GP framework can thus be used to characterize the activity signal without requiring a detailed knowledge, for instance, of the distribution of the active regions on the stellar surface, their lifetime, or their temperature contrast, which is almost always inaccessible.
To model the short-term activity in the GP framework, we used the publicly available GEORGE Python library for GP regression (Ambikasaran et al. 2014) and adopted the quasi-periodic kernel described by the covariance matrix, ![\begin{eqnarray} k(t, t^{\prime}) \!\!&=&\!\! h^2\cdot\exp\left[-\frac{(t-t^{\prime})^2}{2\lambda^2} - \frac{\sin^{2}(\pi(t-t^{\prime})/\theta)}{2w^2}\right] \nonumber \\ &&+\, (\sigma^{2}_{\rm RV}(t)\,+\,\sigma_{j}^{2})\cdot\delta_{t, t^{\prime}}, \label{eq:eqgpkernel} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28690-16/aa28690-16-eq108.png) (1)where t and t′ indicate two different epochs. This kernel has been used with profit in several recent works on exoplanets to mitigate the effect of the stellar noise on the RV data (see, e.g., Haywood et al. 2014; Grunblatt et al. 2015; Faria et al. 2016; Mortier et al. 2016) because its functional form encompasses some properties of stellar activity that we can reasonably conceive. Because it is composed of a periodic term coupled to an exponential decay term, this kernel describes a recurrent signal linked to the stellar rotation and takes a finite lifetime of the active regions and evolution of their sizes into account. The parameters of the covariance function (also called hyper parameters) can be interpreted as follows:
(1)where t and t′ indicate two different epochs. This kernel has been used with profit in several recent works on exoplanets to mitigate the effect of the stellar noise on the RV data (see, e.g., Haywood et al. 2014; Grunblatt et al. 2015; Faria et al. 2016; Mortier et al. 2016) because its functional form encompasses some properties of stellar activity that we can reasonably conceive. Because it is composed of a periodic term coupled to an exponential decay term, this kernel describes a recurrent signal linked to the stellar rotation and takes a finite lifetime of the active regions and evolution of their sizes into account. The parameters of the covariance function (also called hyper parameters) can be interpreted as follows:
-
h represents the amplitude of the correlations;
-
θ is usually related to the rotation period of the star (or one of its harmonics);
-
w is the length scale of the periodic component and can be linked to the size evolution of the active regions;
-
λ is the correlation decay timescale, and it can be related to the lifetime of the active regions.
Equation (1) also includes a term with the uncorrelated noise, added quadratically to the diagonal of the covariance matrix. Here, σRV(t) is the RV uncertainty at time t, σj is the additional noise we fit in our models to take into account instrumental effects and other ≲ 1 m s-1 noise sources not included in the internal errors and in our stellar activity framework, and δt,t′ is the Dirac delta function.
Although the time series of activity index suggests the existence of a long-term trend (i.e., hundreds of days), with properties that are far to be constrained by our data (see Sect. 4), the similar trend shown by the RV time series is very weak. For this reason we decided to exclude a long-term trend from our general RV model.
In the GP framework, the log-likelihood function to be maximized by the MCMC procedure is 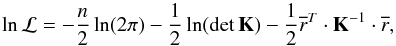 (2)where n is the number of the data points, K is the covariance matrix built from the covariance function in Eq. (1), and
(2)where n is the number of the data points, K is the covariance matrix built from the covariance function in Eq. (1), and 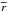 represent the RV residuals, obtained by subtracting the offset and the Keplerian(s) signal(s) (i.e., the “deterministic” component) from the original RV dataset.
represent the RV residuals, obtained by subtracting the offset and the Keplerian(s) signal(s) (i.e., the “deterministic” component) from the original RV dataset.
A general form for the different models that we tested in this work is given by the equation ![\begin{eqnarray} \Delta RV(t)\!\! &=& \!\! \gamma + \sum_{j\,=\,1}^{n_{\rm planet}} \Delta RV_{{\rm Kep},j}(t) +\, \Delta RV(t)_{\rm(activity,\, short-term)} \nonumber \\ &=&\!\! \gamma + \sum_{j\,=\,1}^{n_{\rm planet}} K_{j}\left[\cos(\nu_{j}(t, e_{j}, T_{0j}, \textit{P}_{j}) + \omega_{j}) + e_{j}\cos(\omega_{j})\right] \nonumber \\ && +\, GP\ \left( {\rm or}\, A\cdot\sin\left[\frac{2\pi\,t}{P_{\rm rot,*}} + \phi \right]\right), \label{eq:eqrvmodel} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28690-16/aa28690-16-eq121.png) (3)where nplanet = 1,2, γ is the RV offset, Prot, ∗ is the stellar rotation period. Instead of fitting the eccentricity ej and the argument of periapsis ωj separately, we introduced the parameters
(3)where nplanet = 1,2, γ is the RV offset, Prot, ∗ is the stellar rotation period. Instead of fitting the eccentricity ej and the argument of periapsis ωj separately, we introduced the parameters 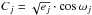 and
and 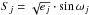 to reduce the covariance between ej and ωj (Ford 2006).
to reduce the covariance between ej and ωj (Ford 2006).
The choice in our analysis of the covariance function in Eq. (1) appears appropriate by considering the results obtained from a GP analysis of the S index time series. Here the “deterministic” component is the mean of the S index. The best-fit values of the hyper parameters are shown in Table 4. For θ we find a value that agrees well with the stellar rotation period previously estimated, and the value for λ appears physically plausible for a main-sequence star because it indicates an evolutionary timescale of about one month for the active regions, which is comparable to the stellar rotation period. Thus, the quasi-periodic kernel in Eq. (1) reliably describes the short-term stellar activity pattern imprinted on the S index.
We used 80 random walkers for the MCMC analysis of the RVs for each model to explore the parameter space, with the GP hyperparameters w, λ, and θ randomly initialized from normal distributed values around the best estimates summarized in Table 4, using their uncertainties as σ of the distributions. The same was done for the guess values of the planetary parameters K and P, for which we used the estimates found through the preliminary periodogram analysis, while T0,conj was initialized to an intermediate value in the prior range we defined. We applied an initial burn-in by removing the first 3000 steps from each chain. After the selection of the best model, based upon the estimates of the Bayesian evidence (see below), we performed an additional burn-in to derive the parameter estimates by removing from the full list of the posterior samples those having a lnℒ lower than the median of the whole lnℒ dataset. Typically, the convergence of the MCMC chains was reached after ~35 000 steps of the random walkers, with parameter correlation lengths ~1000−2000.
6.2. Model selection and planetary parameters
Following the principles of Bayesian inference, for each of the tested models we calculated the logarithm of the Bayesian evidence 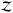 to perform a model comparison and selection. To this purpose, we used two different estimators proposed in literature because the estimate of
to perform a model comparison and selection. To this purpose, we used two different estimators proposed in literature because the estimate of 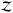 is notoriously a challenging numerical task (Chib & Jeliazkov 2001, hereafter C&J estimator; and Perrakis & Tsionas 2014, hereafter Perr estimator). To interpret the model probabilities, we followed a frequently used conventional empirical scale (a slightly modified version of the so-called Jeffreys’ scale), which states that the model with the highest
is notoriously a challenging numerical task (Chib & Jeliazkov 2001, hereafter C&J estimator; and Perrakis & Tsionas 2014, hereafter Perr estimator). To interpret the model probabilities, we followed a frequently used conventional empirical scale (a slightly modified version of the so-called Jeffreys’ scale), which states that the model with the highest 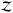 is strongly favored over the other when
is strongly favored over the other when 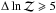 , while
, while 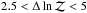 denotes moderate evidence,
denotes moderate evidence, 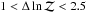 weak evidence, and
weak evidence, and 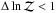 corresponds to inconclusive evidence.
corresponds to inconclusive evidence.
Summary of the Bayesian statistical evidence 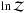 for the two-planet models.
for the two-planet models.
We report in Table 5 only the Bayesian evidences 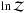 for the models involving two Keplerian signals, which are the object of our discussion. As expected from our previous analyses, models involving only one planet appear much less probable than those with two planets, independently of the framework used to account for the stellar activity. For instance, for circular orbits and considering only the C&J estimator,
for the models involving two Keplerian signals, which are the object of our discussion. As expected from our previous analyses, models involving only one planet appear much less probable than those with two planets, independently of the framework used to account for the stellar activity. For instance, for circular orbits and considering only the C&J estimator, 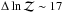 between the two-planet model and that with only the outer companion,
between the two-planet model and that with only the outer companion, 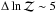 when the model with only the inner planet is considered. We note that the significant difference between the evidence
when the model with only the inner planet is considered. We note that the significant difference between the evidence 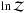 of the one-planet models is reflected in what is observed in the model residuals. When we analyzed the residuals of the 13.7-day planet model with GLS, the highest peak in the periodogram appears at the orbital period of the inner planet, and the estimate of signal semi-amplitude is ~ 1.6 m s-1, very close to our adopted value for the Keplerian semi-amplitude, meaning that the model can be improved by including an additional signal. In contrast, the residuals of the 2.6-day planet model still contain a signal at the orbital period of the outer planet, but this is not the most significant and has a semi-amplitude of just ~ 0.3 m s-1, indicating that the GP model has significantly absorbed it, but without removing it. Analyzing the results of the MCMC for the 2.6-day planet model, we note that the hyperparameter theta is 29+/−0.5 days, which is very close to twice the orbital period of the outer planet. It is therefore likely that the rotational term of the GP is mostly responsible for suppressing the 13.7-day signal.
of the one-planet models is reflected in what is observed in the model residuals. When we analyzed the residuals of the 13.7-day planet model with GLS, the highest peak in the periodogram appears at the orbital period of the inner planet, and the estimate of signal semi-amplitude is ~ 1.6 m s-1, very close to our adopted value for the Keplerian semi-amplitude, meaning that the model can be improved by including an additional signal. In contrast, the residuals of the 2.6-day planet model still contain a signal at the orbital period of the outer planet, but this is not the most significant and has a semi-amplitude of just ~ 0.3 m s-1, indicating that the GP model has significantly absorbed it, but without removing it. Analyzing the results of the MCMC for the 2.6-day planet model, we note that the hyperparameter theta is 29+/−0.5 days, which is very close to twice the orbital period of the outer planet. It is therefore likely that the rotational term of the GP is mostly responsible for suppressing the 13.7-day signal.
In Table 6 we summarize the results for the final model we selected. The short-term stellar activity is modeled better in the GP framework with respect to a sinusoid. For instance, for two-planet circular models the C&J estimator results in 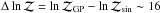 . The reason probably lies in the lifetime of the active regions λ, which is too short to be properly modeled by a strictly periodic function.
. The reason probably lies in the lifetime of the active regions λ, which is too short to be properly modeled by a strictly periodic function.
We adopt here the model that treats eccentricity of the outer planet as a free parameter (model 3 in Table 5). According to the statistical evidence, it is as likely as the simpler model with circular orbits (model 2), but we selected it for convenience even though it involves more free parameters. By adopting model 3 we provide an upper limit on the outer planet eccentricity that can be useful for statistical studies, even though our estimate of e is indicative of a circular orbit. For completeness, we also tested the model that treats the eccentricities of both planets as free parameters (model 4 in Table 5). Based on a simple tidal dissipation model, we expect that the orbital eccentricity of the inner planet is negligible. When the modified tidal quality factor of the inner planet, which probably is a super-Earth planet, is Q′ ~ 1400, that is, when it is similar to that of Earth in the case of the semidiurnal tide raised by the Moon (Lainey 2016), and when the outer planet does not significantly excite the eccentricity of its orbit, the tidal dissipation inside the inner planet can circularize its orbit with an e-folding timescale of only ~ 65 Myr. This is much shorter than the probable age of the system, as we can reasonably deduce from the quite long stellar rotation period. Our analysis results in  for the eccentricity of planet b and
for the eccentricity of planet b and 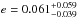 for that of planet c (16% and 84% quantiles), with a Bayesian evidence that is slightly poorer or slightly better than model 3, depending on the estimator (Table 5). This means that there is at most only weak statistical evidence to prefer model 4 over model 3, while the latter has fewer free parameters and therefore was adopted also because it is simpler. In Figs. 10 and 11 we show the RV data folded at the best-fit orbital period of the inner and outer planets, respectively, and the best-fit orbital solution. In each plot the signal of the other planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. In Fig. 12 we show the marginal posterior distributions for the parameters of the selected model. The RV residuals are shown in Fig. 13. No residual long-term trend is visible in the data, supporting our a priori decision of excluding an additional term to model a possible stellar activity cycle. The residual analysis with the GLS algorithm does not show any significant periodicity left in the data, meaning that the GP has absorbed the signal at ~ 42 days. This could be related to the best-fit value assumed by the λ timescale. The upper uncertainty on λ is quite high (~ 11 days), which is related to a secondary peak that is visible in the marginal posterior distribution for λ slightly higher than 40 days.
for that of planet c (16% and 84% quantiles), with a Bayesian evidence that is slightly poorer or slightly better than model 3, depending on the estimator (Table 5). This means that there is at most only weak statistical evidence to prefer model 4 over model 3, while the latter has fewer free parameters and therefore was adopted also because it is simpler. In Figs. 10 and 11 we show the RV data folded at the best-fit orbital period of the inner and outer planets, respectively, and the best-fit orbital solution. In each plot the signal of the other planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. In Fig. 12 we show the marginal posterior distributions for the parameters of the selected model. The RV residuals are shown in Fig. 13. No residual long-term trend is visible in the data, supporting our a priori decision of excluding an additional term to model a possible stellar activity cycle. The residual analysis with the GLS algorithm does not show any significant periodicity left in the data, meaning that the GP has absorbed the signal at ~ 42 days. This could be related to the best-fit value assumed by the λ timescale. The upper uncertainty on λ is quite high (~ 11 days), which is related to a secondary peak that is visible in the marginal posterior distribution for λ slightly higher than 40 days.
The best-fit values of the covariance function hyper parameters in Table 6 show that the distributions of λ and θ, which were constrained within a range that includes the two activity periods found through the periodogram analysis, appear quite similar to those for the S index. Because of how they are interpreted from a physical point of view, we can expect them to remain almost unchanged when passing from the S index to the RVs if the structure of the correlated (stellar) noise is similar in both data sets. Moreover, for the S index and RVs θ finely settles on a value that is compatible with the estimates of the stellar rotation period that have been derived previously. This is convincing evidence that the use of a GP efficiently mitigates the short-term activity noise present in the RV data, resulting in reliable estimates for the orbital and physical parameters of the planets.
 |
Fig. 10 RV data folded at the best-fit orbital period of the inner planet. The signal of the outer planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. Blue dots show the mean values in bins of amplitude 0.05. The red solid line indicates the best-fit orbital solution. |
 |
Fig. 11 RV data folded at the best-fit orbital period of the outer planet. The signal of the inner planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. Blue dots show the mean values in bins of amplitude 0.05. The red solid line indicates the best-fit orbital solution. |
7. Discussion and conclusions
We have presented the first results from the HADES program conducted with HARPS-N at the TNG. We found a planetary system with two super-Earths hosted by the M1 dwarf GJ 3998 by analyzing the high-precision high-resolution RV measurements in conjunction with almost-simultaneous photometric observations. We based our analysis on RV measurements obtained with the TERRA pipeline, which enabled us to circumvent a potential mismatch of the spectral lines that may happen using a CCF technique for M stars. The homogeneous analysis of the RV observations was carried out both with a frequentistic approach and by comparing models with a varying number of Keplerian signals and different models of the stellar activity noise. The analysis of the RV time series unveiled at least four significant periodic signals, two of which are linked to the activity of the host star and two to orbital periods:
-
P= 30.7 d, which gives us an estimate of the stellar rotational period;
-
P= 42.5 d, which might be indicative of a modulation in stellar variability due to differential rotation;
-
P= 2.6 d, the orbital period of GJ 3998b;
-
P= 13.7 d, the orbital period of GJ 3998c.
The conclusions on activity-related periods were confirmed by analyses of the activity indicators and of the photometric light curves of two independent sets of observations. The time series of S index and Hα show periodic variations around the 30.7 d and 42.5 d signals. The photometric results from the two programs confirm the variations in the period range 30–32 d, highlighting the strong connection of the long RV periods to chromospheric activity and to its rotational modulation. Owing to its smaller amplitude and weaker effect than the period of 30.7 d, the periodicity at 42.5 d could not be detected in the photometric time series, which also has a poorer time coverage than that of the spectroscopic series. For the same reason, the search for any reliable correlation such as BV photometry vs. Hα or S indexes is unfortunately inconclusive.
Our results show that the detection of small planets in these data could be hampered by activity-induced signals. As a target of the HADES program, GJ 3998 is included in several statistical studies with the aim to deeply scrutinize the activity properties and rotations of M dwarfs (Perger et al. 2016; Maldonado et al. 2016; Suárez Mascareño et al.; Scandariato et al., in prep.). In particular, the accurate analysis of activity indicators performed by Suárez Mascareño et al. (in prep.), which also includes six HARPS (ESO) observations of GJ 3998 acquired more than five years before the start of the HADES program, provides an estimate of 30.8 ± 2.5 d for the rotational period and the hint of an activity cycle 500−600 d long.
In general, differential rotation is not yet fully understood, see the discussion in Küker & Rüdiger (2011), for example, therefore empirical data are preferable. Reiners & Schmitt (2003) analyzed solar-type stars by analyzing the line shapes in the Fourier domain. They considered a calibration of the ratio between the positions of the two first zeros of the power spectrum of the line profile as a function of the ratio α between equatorial and polar rotation rate. They obtained an anticorrelation between differential rotation and equatorial velocity: differential rotation is mostly evident in slow rotators. Since GJ3998 is a slow rotator, this might be the case here. However, Reiners & Schmitt only considered solar-type stars and did not show that we might see such trends in time series of M dwarfs.
The most relevant data for us are therefore those provided by the analysis of the exquisitely sensitive time series obtained with Kepler. Using Kepler data, Reinhold & Gizon (2015) analyzed an extremely wide dataset of stars ranging from solar-type stars to M dwarfs and confirmed the relation found by Reiners & Schmitt between differential rotation and period. We may directly compare our result for GJ 3998 with Fig. 9 of Reinhold & Gizon, where they plotted the minimum rotation period (in our case 30.7 d), with the parameter α = (Pmax−Pmin)/Pmax. For GJ 3998, α = (42.5−30.7)/42.5 = 0.277. The point for GJ 3998 falls exactly in the middle of the points for the M stars. We conclude that the assumption that the two periods related to activity for GJ 3998 are due to rotation is fully consistent with what we know about differential rotation.
 |
Fig. 12 Marginal posterior distributions for the parameters of our model, which include two Keplerians and a GP-based fit for the short-term stellar noise. Vertical dashed lines indicate the median values and the 16% and 84% quantiles of the distributions. |
 |
Fig. 13 Residuals of the global fit (activity+Keplerians) we used to model the RV data set. |
We ran an MCMC simulation and used a Bayesian model selection to determine the number of planets in the system and estimate their orbital parameters and minimum masses. We tested several different models in which we varied the number of planets, the eccentricity, and the treatment of stellar activity noise. We selected a model involving two Keplerian signals, of which the inner planet had a circular orbit and where the eccentricity of the outer planet was treated as a free parameter. The short-term stellar activity was modeled with the Gaussian processes approach, and the long-term activity noise was not included.
 |
Fig. 14 Minimum mass vs. orbital period diagram for known Neptune-type and super-Earth planets around M dwarfs (http://www.exoplanet.eu – black dots, 2016 June 17), the green stars indicate GJ 3998b and GJ 3998c. Filled dots indicate planets with known radii. |
The two planets appeared to have minimum masses compatible with those of super-Earths, the inner planet had a minimum mass of 2.47 ± 0.27 M⊕ at a distance of 0.029 AU from the host star, the outer has a minimum mass of 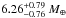 and a semi-major axis of 0.089 AU.
and a semi-major axis of 0.089 AU.
A very rough estimate of the equilibrium temperatures of the planets, from the Stefan–Boltzmann law assuming uniform equilibrium temperature throughout the entire planet and zero albedo, gives Teq = 740 K for the inner and Teq = 420 K for the outer planet.
These close distances strongly call for a search of potential transits in the next months, in particular for the inner planet, through a proposal for observing time on the Spitzer Space Telescope. This planet has an interestingly high geometric transit probability of ≈8%. With a minimum mass of 2.47 ± 0.27 M⊕, the radius of GJ 3998b most likely lies somewhere between ≈1 M⊕ (metal-rich composition) and ≈1.65 M⊕ (ice-rich composition) (Seager et al. 2007). Given its host star’s radius of ≈0.5 R⊙, this range of planetary sizes corresponds to plausible transit dephts of between 325 to 935 ppm. We therefore propose to use 20 h of Spitzer time to monitor a 2σ transit window of the innermost planet in the GJ 3998 system (P.I. M. Gillon). A potential transit might provide a constraining point in the mass-radius diagram of known planets and also enable determining the mean density and better characterizing the system architecture with future follow-up observations. In particular, there is currently no object with an accurately measured mass (≤20%) in the range 2−3 M⊕. This mass gap is even larger if we consider only M dwarf planets, as is evident in Fig. 14, which shows the minimum mass vs. orbital period diagram for known Neptune-type and super-Earth planets around main-sequence M stars, along with the location of GJ 3998 planets. The possibility of a transit, given the small distance from the host and the brightness of GJ 3998 (V = 10.83), would make this star a natural target for follow-up observations with the ESA CHEOPS space telescope and also one of the most interesting M-dwarf targets for a detailed atmospheric characterization.
Acknowledgments
We thanks Guillem Anglada-Escudé for distributing the latest version of the TERRA pipeline. We are also grateful to Michael Gillon for helpful information on the search for transit of the inner planet with the Spitzer Space Telescope. GAPS acknowledges support from INAF trough the "Progetti Premiali” funding scheme of the Italian Ministry of Education, University, and Research. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under Grant Agreement No. 313014 (ETAEARTH). L.A. acknowledges support from the Ariel ASI-INAF agreement No. 2015-038-R.0. M.P., I.R., J.C.M., A.R., E.H., and M.L. acknowledge support from the Spanish Ministry of Economy and Competitiveness (MINECO) and the Fondo Europeo de Desarrollo Regional (FEDER) through grants ESP2013-48391-C4-1-R and ESP2014-57495-C2-2-R. J.I.G.H. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2013 Ramón y Cajal program MINECO RYC-2013-14875, and A.S.M., J.I.G.H., and R.R.L. also acknowledge financial support from the Spanish ministry project MINECO AYA2014-56359-P. This article is based on observations made with the Carlos Sánchez Telescope operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. We wish to thank the anonymous referee for thoughtful comments and suggestions that helped improve the manuscript.
References
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2014, ArXiv e-prints [arXiv:1403.6015] [Google Scholar]
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 421, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., & Deming, D. 2007, ArXiv e-prints [arXiv:0706.1047] [Google Scholar]
- Chib, S., & Jeliazkov, I. 2001, J. Am. Stat. Association, 96, 270 [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84461 [CrossRef] [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
- Desidera, S., Sozzetti, A., Bonomo, A. S., et al. 2013, A&A, 554, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., Kürster, M., Els, S., Hatzes, A. P., & Cochran, W. D. 2001, A&A, 374, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA 1997, VizieR Online Data Catalog, I/239 [Google Scholar]
- Faria, J. P., Haywood, R. D., Brewer, B. J., et al. 2016, A&A, 588, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaidos, E., Mann, A. W., Kraus, A. L., & Ireland, M. 2016, MNRAS, 457, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Giacobbe, P., Damasso, M., Sozzetti, A., et al. 2012, MNRAS, 424, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Giampapa, M. S., Cram, L. E., & Wild, W. J. 1989, ApJ, 345, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Grunblatt, S. K., Howard, A. W., & Haywood, R. D. 2015, ApJ, 828, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., Balkowski, C., Cayatte, V., Edmunds, M. G., & Pagel, B. E. J. 1996, MNRAS, 283, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Kopparapu, R. K. 2013, ApJ, 767, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Küker, M., & Rüdiger, G. 2011, Astron. Nachr., 332, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labadie, L., Rebolo, R., Villó, I., et al. 2011, A&A, 526, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V. 2016, Celest. Mech. Dyn. Astron., 126, 145 [Google Scholar]
- Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Law, N. M., Mackay, C. D., & Baldwin, J. E. 2006, A&A, 446, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2004, in The A-Star Puzzle, eds. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 786 [Google Scholar]
- Lépine, S., & Gaidos, E. 2013, Astron. Nachr., 334, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malavolta, L., Nascimbeni, V., Piotto, G., et al. 2016, A&A, 588, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Affer, L., Micela, G., et al. 2015, A&A, 577, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Scandariato, G., & Stelzer, B. 2016, A&A, submitted [Google Scholar]
- Mandell, A. M., Raymond, S. N., & Sigurdsson, S. 2007, ApJ, 660, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Faria, J. P., Santos, N. C., et al. 2016, A&A, 585, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oscoz, A., Rebolo, R., López, R., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701447 [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., Garcia-Piquer, A., & Ribas, I. 2016, A&A, submitted [Google Scholar]
- Perrakis, K., Ntzoufras, I., & Tsionas, E. G. 2014, Computational Statistics & Data Analysis, 77, 54 [Google Scholar]
- Poretti, E., Boccato, C., Claudi, R., et al. 2016, Mem. Soc. Astron. Italiana, 87, 141 [Google Scholar]
- Rasmussen, C. E., & Williams, C. 2006, Gaussian Processes for Machine Learning (The MIT press) [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Schmitt, J. H. M. M. 2003, A&A, 398, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reinhold, T., & Gizon, L. 2015, A&A, 583, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, S., Osborne, M., Ebden, M., et al. 2013, Phil. Trans. Roy. Soc. London A, 371, 20110550 [Google Scholar]
- Robertson, P., Endl, M., Cochran, W. D., & Dodson-Robinson, S. E. 2013, ApJ, 764, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Rockenfeller, B., Bailer-Jones, C. A. L., & Mundt, R. 2006, A&A, 448, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, L. A., & Seager, S. 2010, ApJ, 712, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Scheffler, H., & Elsasser, H. 1988, Science, 240, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Deming, D. 2010, ARA&A, 48, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumder, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Bernagozzi, A., Bertolini, E., et al. 2013, EPJ Web Conf., 47, 03006 [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Giacobbe, P., Lattanzi, M. G., et al. 2014, MNRAS, 437, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaníček, P. 1971, Ap&SS, 12, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Winters, J. G., Henry, T. J., Lurie, J. C., et al. 2015, AJ, 149, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Observing log for the GJ 3998 spectra and results
In this section we report the observing log for the GJ 3998 spectra and the RVs, S, and Hα indexes we obtained with the present study. We list the observation dates (barycentric Julian date or BJD), the signal-to-noise ratios (S/Ns), the radial velocities (RVs) from the DRS and TERRA pipelines and the Hα
and S indexes, calculated by the TERRA pipeline and in the present study. The RV errors reported are the formal ones and do not include the jitter term. The S index and Hα errors are calculated as described in the text and do not take into account the photon noise (Sect. 4.1). The S index and Hα errors derived from the TERRA pipeline are due to photon noise through error propagation.
All Tables
Stellar parameters for the star GJ 3998 from the analysis of the HARPS-N spectra using the technique reported by Maldonado et al. (2015) (upper part). Lower part: coordinates, V and K magnitudes, parallax, proper motions and space velocities.
All Figures
 |
Fig. 1 Radial velocity (top) and activity indexes Hα (middle) and S index (bottom) time series for GJ 3998 measured with the TERRA pipeline. |
| In the text | |
 |
Fig. 2 Periodogram power of the inspected periods as a function of the number of observations. The most significant periods (dark red) at 30.7 d and 13.7 d are clearly visible with a high power for Nobs> 60, as well as the period at 2.65 d with a moderate Scargle power, which increases for Nobs> 80, and the period at 42.5 d, whose power increases for Nobs> 110 (2D plot adapted from A. Mortier, priv. comm.). |
| In the text | |
 |
Fig. 3 GLS periodograms of the radial velocities of GJ 3998, of the original data (upper panel), and after removing (from top to bottom) the 30.7 d (marked with the red dot), the 42.5 d (magenta dot), the 13.7 d (blue dot), and finally the 2.65 d (cyan dot) signals. The dashed lines indicate the 0.1%, 1%, and 10% level of false-alarm probability. |
| In the text | |
 |
Fig. 4 From top to bottom: GLS periodograms of RVs, S index, and Hα, zoomed around the frequencies of interest. The dotted blue and cyan lines indicate the frequencies corresponding to orbital periods of the candidate planets at 13.7 d and 2.65 d, respectively, while the dotted red and magenta lines show the frequencies corresponding to the activity periods at 30.7 d and 42.5 d, respectively. These frequencies and periods are marked with dots in the same color code in the upper RV panel. |
| In the text | |
 |
Fig. 5 GLS periodograms around the frequency ranges of interest for two subsets of the original RV data. The first season has 61 data points and its periodogram is black (FAP: 0.1%, 1%, 10% horizontal black dotted lines), the second season has 75 data points and is plotted in red (FAP: 0.1%, 1%, 10% horizontal red dashed lines). The two upper panels refer to the frequencies related to activity (upper left: f = 0.0235 d-1 – P = 42.5 d; upper right: f = 0.0326 d-1 – P = 30.7 d). The two lower panels refer to the frequencies related to the candidate planets (lower left: f = 0.0729 d-1 – P = 13.7 d; lower right: f = 0.3773 d-1 – P = 2.65 d). The relevant frequencies derived from all the methods used on the full dataset are indicated with vertical lines green from RV analysis, blue from activity indexes, and orange from photometry (see Sect. 5). |
| In the text | |
 |
Fig. 6 Radial velocity after subtracting the contributions of the activity signals at 30.7 d and 42.5 d, displayed as a function of the S index (top) and Hα (bottom). The extremely low correlation values support the interpretation that the 2.65 d and 13.7 d signals are of planetary origin. |
| In the text | |
 |
Fig. 7 Phase-folded V and B curves at the period P = 30.75 ± 0.12 d, the precision reported is the formal error from the least-squares fitting. |
| In the text | |
 |
Fig. 8 Differential light curve of GJ 3998 observed by APACHE, folded at the best period P = 31.5 days found through a frequency analysis of the time series. The red dot in the lower left corner shows the average uncertainty of the data. |
| In the text | |
 |
Fig. 9 Diffraction-limited image of GJ3998 after lucky imaging processing with a 20% selection of the best individual TCS/FastCam frames. |
| In the text | |
 |
Fig. 10 RV data folded at the best-fit orbital period of the inner planet. The signal of the outer planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. Blue dots show the mean values in bins of amplitude 0.05. The red solid line indicates the best-fit orbital solution. |
| In the text | |
 |
Fig. 11 RV data folded at the best-fit orbital period of the outer planet. The signal of the inner planet, the RV offset, and the best-fit GP solution for the stellar activity noise have been subtracted. Blue dots show the mean values in bins of amplitude 0.05. The red solid line indicates the best-fit orbital solution. |
| In the text | |
 |
Fig. 12 Marginal posterior distributions for the parameters of our model, which include two Keplerians and a GP-based fit for the short-term stellar noise. Vertical dashed lines indicate the median values and the 16% and 84% quantiles of the distributions. |
| In the text | |
 |
Fig. 13 Residuals of the global fit (activity+Keplerians) we used to model the RV data set. |
| In the text | |
 |
Fig. 14 Minimum mass vs. orbital period diagram for known Neptune-type and super-Earth planets around M dwarfs (http://www.exoplanet.eu – black dots, 2016 June 17), the green stars indicate GJ 3998b and GJ 3998c. Filled dots indicate planets with known radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


