| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628382 | |
| Published online | 15 August 2016 | |
Spot modelling of periodic weak-line T Tauri stars observed by CoRoT in NGC 2264
1 INAF–Osservatorio Astrofisico di Catania, via S. Sofia, 78-95123 Catania, Italy
e-mail: nuccio.lanza@oact.inaf.it
2 INAF–Osservatorio Astronomico di Palermo “G. S. Vaiana”, Piazza del Parlamento, 1 – 90134 Palermo, Italy
Received: 25 February 2016
Accepted: 17 June 2016
Context. The space telescope CoRoT has provided light curves of T Tauri stars belonging to the star-forming region of NGC 2264 with unprecedented continuity and precision in the framework of a coordinated multi-wavelength observational project.
Aims. We perform spot modelling of the optical light curves of five weak-line T Tauri stars whose variability is dominated by starspots.
Methods. We apply two-spot and evolving single-spot models in the framework of a Bayesian Markov chain Monte Carlo approach to derive the a posteriori distributions of the starspot parameters and the inclination of the star rotation axis. We focus on the rotation periods of the spots that can provide evidence for differential rotation in those stars.
Results. We find meaningful results in the case of three stars with an inclination higher than 50° and a slow variation of the light curve amplitude. The relative difference of the spot rotation periods ranges from 0.02 to 0.05 that is 3−10 times larger than the amplitude of the differential rotation found in similar stars with Doppler imaging techniques.
Conclusions. We conclude that the intrinsic starspot evolution, although very slow, has a significant impact on the determination of the differential rotation by means of our spot modelling approach. We estimate typical timescales for the evolution of the starspot pattern between ~20 and ~50 rotation periods in our stars.
Key words: stars: variables: T Tauri, Herbig Ae/Be / starspots / stars: activity / stars: rotation / techniques: photometric
© ESO, 2016
1. Introduction
Weak-line T Tauri stars (WTTs), so called because of their lack of spectroscopic accrection signatures, are pre-main-sequence stars that generally display quasi-stable sinusoidal light curves attributed to cool magnetic starspots on their surface (e.g., Grankin et al. 2008). The space telescope CoRoT (Convection, Rotation, and Transits; Auvergne et al. 2009) observed a sample of such stars in the star-forming open cluster NGC 2264 in 2008 and 2011. Thanks to its relative proximity (~760 pc), well-defined stellar population, and low foreground extinction, NGC 2264 is a primary target for star formation and pre-main-sequence star studies (Dahm 2008).
The CoRoT 2011 observing run was part of a campaign coordinated with several other telescopes operating in different spectral domains, including Spitzer in the infrared and Chandra in the X-rays, and optical spectroscopy with Flames and UVES at the VLT. It was named as the Coordinated Synoptic Investigation (CSI) of NGC 2264 and its main purpose was to investigate the variability of young stars with an unprecedented time continuity and spectral range coverage (see Cody et al. 2014; Stauffer et al. 2014; Venuti et al. 2014, 2015; McGinnis et al. 2015, for details).In the case of WTTs, the simultaneous observation in several spectral domains allows us to investigate the correlations between photospheric spots and the higher atmospheric levels in active regions both during quiescent phases and flares. This provides clues on the heating mechanisms at work in the outer atmospheres of very active, young stars and on the energy release during flares.
In the present work, we model the CoRoT optical light curves of five WTTs by means of a simple spot modelling technique to extract information on spot rotation periods and their evolutionary timescales. This is particularly interesting for understanding rotation and magnetic activity in pre-main-sequence stars of solar mass. With an estimated age of its stars ranging in the 1−5 Myr interval, NGC 2264 is an ideal laboratory to address this field of study. The light curves of several WTTs were obtained by CoRoT with high precision along ~40 days of uninterrupted observations. Therefore, our exploratory investigation benefits from data of unprecedented quality that allow us to fully exploit the potential of spot modelling and to compare our differential rotation measurements with those obtained by means of Doppler imaging tomography on similar stars to derive information on spot evolution in WTTs.
2. Observations
CoRoT has a 27 cm aperture telescope and observed NGC 2264 continuously from 1 December 2011 to 3 January 2012. Targets have been observed with the CCD dedicated to searching planetary transits. CoRoT performs aperture photometry with a pre-selected mask for each target and also provides the light curves in three non-standardized passbands for targets brighter than R ~ 14 by means of a prism that disperses the star’s spectrum across the mask whose pixels are read in three groups along the wavelength range according to the fraction of collected photoelectrons (Auvergne et al. 2009). In our investigation, we always considered the total flux integrated over the whole mask of each star, i.e., by summing up the three passband fluxes in the case of targets with R ≲ 14. These white-light curves cover the wavelength range 300−1100 nm. They have a higher signal-to-noise ratio and are more stable than the light curves in the individual passbands. The exposure time was usually 512 s, except for a subset of selected targets that had 32 s.
We visually inspected the light curves of several WTT stars to find a subsample with the most stable modulation along the ~40 days of CoRoT observations and the lowest fluctuations, indicative of low accretion and quasi-stable spots in those targets. We are confident that these selection criteria give us stars whose variability is dominated by the rotational modulation produced by cool photospheric starspots. Our sample consists of five stars listed in Table 1 where we give, from left to right, the CoRoT ID number of the star, its Mon ID number according to Cody et al. (2014) to allow identification in the papers of the CSI NGC 2264 series, the spectral type, the reference for the spectral type, the R magnitude, its reference, the Ic magnitude, its reference, the equivalent width (EW) of the Hα line, its reference, the exposure time τe of CoRoT photometry, and the relative mean standard error per data point ϵ after averaging the flux along two consecutive CoRoT orbits (see below). Most of our targets display an Hα in absorption, i.e., a positive EW except during flares, in agreement with their WTT classification. The light curves of our stars are plotted in Fig. 1.
The low Earth orbit of CoRoT introduces perturbations associated with the crossings of the South Atlantic Anomaly of the Earth’s magnetic field and with the ingress in and egress from the Earth shadow that affect the detector temperature. Most of these effects have been corrected or flagged by the reduction pipeline. In our investigation, we use the so-called N2-level light curves that are freely available from the CoRoT Archive1 together with a detailed documentation. We discarded all the flagged flux measurements that amount to ≈7−15 percent of the points along one satellite orbit and averaged the flux along two consecutive orbits of 6184 s each to eliminate possible residual variations produced by changes in the telescope environment. Since we are interested in starspot rotation and evolution whose timescales are of the order of several days, our final cadence of one point per ~12 368 s does not introduce any limitation in our investigation and grants us an almost perfect continuity of our time series.
Properties of WTTs observed by CoRoT and modelled in this investigation.
 |
Fig. 1 Light curves of our five target stars displaying the flux normalized to the respective maximum value vs. the time as labelled. Errorbars are within the size of the symbols and indicate the standard error of each point that is an average of individual CoRoT measurements along two consecutive satellite orbits (open black circles). Filled orange circles indicate the segment of the light curve fitted to find the spot rotation periods (see Sect. 3). |
3. Model
A requisite for measuring stellar rotation by using starspots is the stability of spots themselves, i.e, their evolution timescale must be longer than the rotation period. If we want to measure a differential rotation of amplitude ΔΩ, where Ω is the rotation angular velocity, the starspot evolution timescale should not be shorter than ~1 / (ΔΩ). A simple measurement of the evolution timescale of the whole spot pattern can be obtained by computing the autocorrelation of the photometric time series as discussed by, e.g., Lanza et al. (2014). For stable spots, the autocorrelation function displays a periodic pattern with maxima and minima separated by a time lag τ equal to the mean rotation period Prot, while, in the case of starspots with a decaying area, the amplitude of the autocorrelation modulation decreases steadily and the rate of decrease can be used to estimate the evolution timescale. When the maximum of the autocorrelation at τ = Prot is lower than 0.5–0.6 times the maximum at τ = 0, the evolution of the spot pattern is generally too fast to obtain a measure of differential rotation using spot modelling in the case of solar-like stars (cf. Lanza et al. 2014).
A fundamental limitation is that spot modelling is an ill-posed problem because we try to reconstruct a two-dimensional map of the stellar surface starting from a photometric time series, i.e., a one-dimensional dataset. To alleviate this problem, a priori information can be included in the process of light curve modelling to make the solution unique and stable, for example in the case of the maximum entropy spot modelling (Lanza et al. 1998, 2006, 2007). In the case of CoRoT light curves, several approaches have been proposed taking advantage of the high precision and almost uniform sampling of the time series (e.g. Lanza et al. 2009; Fröhlich et al. 2009; Mosser et al. 2009; Huber et al. 2010).
In the present case, we apply a Markov chain Monte Carlo (MCMC) approach to statistically sample the a posteriori parameter space and the correlation among different parameters in a spot model. Such a technique has been proposed by Croll (2006) and Fröhlich (2007) and has been applied, among other approaches, to Kepler time series (Fröhlich et al. 2012). In principle, it allows a complete sampling of the different possible starspot configurations that fit a given light curve. In practice, the long computation time limits its applicability to rather simple models consisting of a few discrete starspots. This is a consequence of the strong correlations among the model parameters that become more and more important as the number of model starspots is increased (cf. Fröhlich et al. 2012, and references therein). Specifically, if more than 2−3 spots are assumed, the sampling of the a posteriori parameter space becomes very slow because the Markov chains cannot move freely across the space, but are constrained to follow paths determined by local parameter correlations(see Lanza et al. 2014, for more details). Nevertheless, a full MCMC approach is generally feasible when we consider two discrete starspots and an adjustable mean flux level to account for the variations in a background of small spots uniformly distributed in longitude, as was demonstrated by Lanza et al. (2014). We refer to that paper for a detailed description of our approach, while we provide here only a general introduction.
We consider an unperturbed distribution of the stellar photospheric brightness I as given by a quadratic limb-darkening law,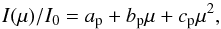 (1)where I0 is the brightness at the centre of the disc; ap, bp, and cp the limb-darkening coefficients; and μ ≡ cosψ, with ψ the angle between the normal to a point on the photosphere and the line of sight. For the CoRoT white passband, we adopt limb-darkening coefficients by Claret & Bloemen (2011, see Sect. 4.
(1)where I0 is the brightness at the centre of the disc; ap, bp, and cp the limb-darkening coefficients; and μ ≡ cosψ, with ψ the angle between the normal to a point on the photosphere and the line of sight. For the CoRoT white passband, we adopt limb-darkening coefficients by Claret & Bloemen (2011, see Sect. 4.
We fit a light curve by considering a variable inclination i of the stellar spin axis to the line of sight and assuming that the light variation is produced by two spots of area Ak located at colatitude θk and longitude λk, and rotating with rotation period Pk (k = 1,2), in addition to a longitude-independent flux term F0 that can be adjusted to take into account a uniformly distributed background of small spots. We do not consider any spot evolution along a given fitted interval of the light curve. The spots are assumed to be point-like; that is, we do not consider partial visibility of their area when they rise or set at the stellar limb. This simple model has a total of ten free parameters per light curve and their a posteriori distributions can be sampled in a reasonable time, in spite of their correlations. We need to reduce the number of free parameters only when there are strong correlations, usually by fixing the inclination i and/or F0 (see Lanza et al. 2014, for details).
The best fit to an entire light curve of ~40 days has an unacceptably large χ2 because of our assumption of non-evolving spots. Therefore, we cut the entire light curve into smaller and smaller equal segments until we find acceptable best fits. For a given segment, we compare the model allowing for different spot rotation periods, i.e., P1 ≠ P2 (DR model), with that assuming rigid rotation, i.e., P1 = P2 (RR model), by means of the Bayesian information criterion (BIC) as in Lanza et al. (2014). Specifically, we define the variation of the BIC statistics as 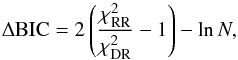 (2)where
(2)where 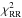 is the chi square obtained with the RR model,
is the chi square obtained with the RR model, 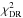 the one obtained with the DR model, and N the number of data points in the fitted segment; the −lnN term accounts for the additional free parameter in the case of the DR model with respect to the RR model. The best fits of the segments are computed by means of the IDL procedure MPFIT.PRO2, that implements a Levenberg-Marquardt minimization of the chi square with the imposed constraint of positive starspot areas, and the procedure AMOEBA.PRO that implements a Nelder-Mead minimization; the lowest χ2 between the two minimizations gives our best fit solution. To allow an efficient exploration of the different light curve segments and a comparison of their best fits, the inclination has generally been fixed at i = 60°3. The minima found by these optimization methods may depend on their starting points in the parameter space. The initial spot colatitudes are initially fixed at the value of the inclination, their rotation periods are fixed at the estimate given by the autocorrelation function, their areas are constrained by the depth of the light curve minimum in the segment to be fitted, and their initial longitudes – the most sensitive parameters in our model – are chosen to reproduce the phase of the observed light minimum of the fitted segment. Then the initial longitudes are varied in steps of 90° and the minimum of the χ2 recomputed to find the initial conditions that give the lowest minimum for each of the two optimization methods.
the one obtained with the DR model, and N the number of data points in the fitted segment; the −lnN term accounts for the additional free parameter in the case of the DR model with respect to the RR model. The best fits of the segments are computed by means of the IDL procedure MPFIT.PRO2, that implements a Levenberg-Marquardt minimization of the chi square with the imposed constraint of positive starspot areas, and the procedure AMOEBA.PRO that implements a Nelder-Mead minimization; the lowest χ2 between the two minimizations gives our best fit solution. To allow an efficient exploration of the different light curve segments and a comparison of their best fits, the inclination has generally been fixed at i = 60°3. The minima found by these optimization methods may depend on their starting points in the parameter space. The initial spot colatitudes are initially fixed at the value of the inclination, their rotation periods are fixed at the estimate given by the autocorrelation function, their areas are constrained by the depth of the light curve minimum in the segment to be fitted, and their initial longitudes – the most sensitive parameters in our model – are chosen to reproduce the phase of the observed light minimum of the fitted segment. Then the initial longitudes are varied in steps of 90° and the minimum of the χ2 recomputed to find the initial conditions that give the lowest minimum for each of the two optimization methods.
The DR model is considered to be statistically better than the RR model when ΔBIC ≥ 2. In this way, we select segments showing evidence of differential rotation and choose the best one by considering the largest ΔBIC value associated with adequate best fits; that is, we discard segments where the Levenberg-Marquardt or Nelder-Mead algorithms do not properly converge. For this segment only, we perform a full MCMC Bayesian analysis as described in Lanza et al. (2014).
We apply the Metropolis-Hasting algorithm to define a chain of randomly distributed points in the parameter space that sample the a posteriori distributions of the model parameters (Press et al. 2002). If the value of the chi square corresponding to the kth point of the chain is 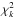 , we accept a new point as the (k + 1)th of the chain if
, we accept a new point as the (k + 1)th of the chain if 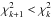 , otherwise we accept it with a probability proportional to
, otherwise we accept it with a probability proportional to ![\hbox{$\exp [-(\chi^{2}_{k+1} - \chi^{2}_{k})/\chi^{2}_{\rm min}]$}](/articles/aa/full_html/2016/08/aa28382-16/aa28382-16-eq63.png) , where
, where 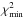 is the minimum of the chi square along the chain. To better sample the region with the highest likelihood, we start from the minimum of the chi square and consider only points that correspond to a chi square value up to 1 percent above the minimum. If a lower minimum is found by the Metropolis-Hasting algorithm, it is adopted as a new starting point for the Monte Carlo Markov chain. The amplitude of each random step of the Metropolis-Hasting algorithm is tuned to have an average acceptance rate between 20 and 35 percent. The sampling of the a posteriori parameter space is adequate only if the distributions of the model parameters have converged. A necessary condition for this has been expressed by Gelman & Rubin through their
is the minimum of the chi square along the chain. To better sample the region with the highest likelihood, we start from the minimum of the chi square and consider only points that correspond to a chi square value up to 1 percent above the minimum. If a lower minimum is found by the Metropolis-Hasting algorithm, it is adopted as a new starting point for the Monte Carlo Markov chain. The amplitude of each random step of the Metropolis-Hasting algorithm is tuned to have an average acceptance rate between 20 and 35 percent. The sampling of the a posteriori parameter space is adequate only if the distributions of the model parameters have converged. A necessary condition for this has been expressed by Gelman & Rubin through their 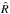 statistics, which should be smaller than 1.1−1.2 for all the parameters (cf. Croll 2006). To compute
statistics, which should be smaller than 1.1−1.2 for all the parameters (cf. Croll 2006). To compute 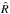 , we follow the scheme specified by Lanza et al. (2014) by splitting our long MCMCs, which consist of several million points, into four subchains that can be regarded as statistically independent and therefore can be statistically compared with each other.
, we follow the scheme specified by Lanza et al. (2014) by splitting our long MCMCs, which consist of several million points, into four subchains that can be regarded as statistically independent and therefore can be statistically compared with each other.
In Lanza et al. (2014) we performed a detailed comparison of our approach with that proposed by Croll (2006) in the case of ϵ Eridani and found perfectly compatible results in spite of our assumption of point-like spots and a chi square limit at 1 percent above the minimum, while Croll considered extended polar-cap spots and a somewhat larger chi square limit of ~4 percent.
The correlations between model parameters in MCMC chains is a critical issue that has been discussed by, e.g., Croll (2006), Fröhlich et al. (2012), and Lanza et al. (2014). Methods applied to other problems generally do not perform well in the case of spot modelling (Lanza et al. 2014). In the present case, we treat correlations by fixing some of the correlated parameters to their best fit values as obtained from the Metropolis-Hasting optimization according to Lanza et al. (2014). Future developments may consider techniques such as principal component analysis. They have been applied to light curve inversion and Doppler imaging problems considering a continuous brightness distribution (Berdyugina 1998; Savanov & Strassmeier 2005, 2008). However, their implementation is not straightforward when the dependence of the model on some of its parameters is non-linear, as in the case of few-spot models, or when the noise level of the data is not precisely known, as in the present case, because our models cannot fit light variations on timescales shorter than 0.2−0.3 of the rotation period owing to their limited number of degrees of freedom (see Sect. 5).
The adoption of a two-spot model is motivated by our search for stellar differential rotation. Nevertheless, given the nearly sinusoidal shape of the rotational modulation of our light curves with an almost constant phase of their minima and a slow variation of their amplitudes (cf. Fig. 1), it is useful to consider an alternative model with a single spot whose area is evolving with time according to a quadratic law, i.e., A1(t) = A10 + A11(t−t0) + A12(t−t0)2, where t is the time, t0 the initial time of each of the individual intervals to be fitted, A10 the area at time t0, and A11 and A12 coefficients found by fitting the light modulation. We add a time variable longitude-independent flux term, i.e., F0(t) = F00 + F01(t−t0) + F02(t−t0)2, with a similar meaning of the symbols, to take into account a simultaneous variation of the uniformly distributed background of small spots. This model is compared with the two-spot model introduced above to assess the actual improvement obtained by using two spots instead of a single evolving spot when fitting our light curve segments. Both models have ten free parameters, thus allowing us a simpler statistical comparison of their relative performance.
4. Stellar parameters
The limb-darkening coefficients adopted for our stars are indicated in Table 2, together with the effective temperature Teff and the gravity log g assumed to compute them after Claret & Bloemen (2011). The effective temperature Teff comes from the spectral type (cf. Table 1) and the Kenyon & Hartmann (1995, hereafter KH95) temperature scale. To evaluate the surface gravity g we need the mass and the radius of the star. The mass is computed from Teff, the bolometric luminosity Lbol, and Siess et al. (2000) pre-main-sequence evolutionary models. The radius is estimated from Teff and Lbol. The latter is estimated from the Ic magnitude, the bolometric correction on Ic (BCI), the absorption on Ic (AI), and the adopted distance to NGC 2264 (760 pc, Sung et al. 1997). The bolometric correction BCI is estimated from the spectral type and the KH95 tabulation; AI comes from the intrinsic R−I, a function of the spectral type (again from KH95), the observed R−I, and the Mathis (1990) extinction law.The metallicity of NGC 2264 is assumed to be [Fe / H] = −0.15 (King et al. 2000; Heiter et al. 2014). The spot contrast is fixed at the solar value (cs = 0.677) because we have no information on spot temperature.
To apply our MCMC Bayesian approach to the light curve segments, we assume uniform a priori distributions of the model parameters within the ranges specified in Table 3. The initial and final times t1 and t2 of each modelled light curve segment are measured from the beginning of its light curve. The area of the spots Ak is expressed as a fraction of the stellar disc, i.e., 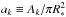 , R∗ being the radius of the star, while the ranges of the spot longitudes are given as the maximum deviations from their initial values Δλk, with k = 1,2. The parameter values of the starting point of the MCMC are those corresponding to the minimum of the chi square for each light curve segment(see Appendix A).
, R∗ being the radius of the star, while the ranges of the spot longitudes are given as the maximum deviations from their initial values Δλk, with k = 1,2. The parameter values of the starting point of the MCMC are those corresponding to the minimum of the chi square for each light curve segment(see Appendix A).
Stellar parameters and quadratic limb-darkening parameters.
Initial and final times of the segments considered for the MCMC analysis, together with the uniform prior intervals of the two-spot model parameters for each star.
5. Results
The autocorrelation functions of our five photometric time series are plotted in Fig. 2. The ratio of the second maximum to the first maximum is greater than 0.6 in all the cases, indicating that the light curves of these WTTs are stable enough to allow us to search for differential rotation. The dotted lines indicate the ±σ range, where σ is the standard deviation of the autocorrelation function in the case of a random variable with some degree of autocorrelation according to the so-called large-lag approximation (see Sect. 3.1 in Lanza et al. 2014, for detail).
By applying our approach, we selected segments with the best evidence of DR for all our targets. The minimum value of ΔBIC for them was 2.2, providing preliminary evidence for DR in all our cases. These segments were also fitted with the evolving single-spot plus background model; the ratio 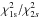 of the χ2 values obtained with that model and the two-spot model is reported in Table 4 together with the relative ΔBIC and its significance as obtained by the F-statistics, given that both models have the same number of free parameters. The significance is the probability of obtaining a
of the χ2 values obtained with that model and the two-spot model is reported in Table 4 together with the relative ΔBIC and its significance as obtained by the F-statistics, given that both models have the same number of free parameters. The significance is the probability of obtaining a 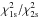 equal to or smaller than the listed value in the case of a random variable. Therefore, values close to unity are an indication that the two-spot model provides a statistically better fit than the evolving single-spot model. This is always the case, except for 223988865 for which we have comparable χ2 values with both models. Nevertheless, we also consider the two-spot model for that star.
equal to or smaller than the listed value in the case of a random variable. Therefore, values close to unity are an indication that the two-spot model provides a statistically better fit than the evolving single-spot model. This is always the case, except for 223988865 for which we have comparable χ2 values with both models. Nevertheless, we also consider the two-spot model for that star.
Statistical comparison between the best fits obtained with the two-spot and the evolving single-spot models with the Levenberg-Marquardt and Nelder-Mead optimizations for the light curve segments selected to search for differential rotation.
The segments selected with the above procedure were successively fitted with the MCMC algorithm to derive the a posteriori distributions of the spot model parameters and confirm the preliminary results based on the best fits computed with the Levenberg-Marquardtand Nelder-Mead algorithms (see Appendix A for a comparison of the respective results). For CoRoT 223982407 and 223988965, it was not possible to achieve convergence of the MCMC for the two-spot model even after refining the starting point of the chain with the Metropolis-Hasting algorithm and running chains of several hundred million points. Only after fixing the inclination of the stellar spin axis i and the uniform flux term F0, were we able to obtain convergence as measured by an 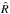 statistics smaller than 1.1 (cf. Table 6) along chains of 150 and 80 million points for these two stars, respectively.
statistics smaller than 1.1 (cf. Table 6) along chains of 150 and 80 million points for these two stars, respectively.
The best fits of the light curves corresponding to the minimum chi squares as obtained with the Metropolis-Hasting algorithm are plotted in Figs. 3 and 4 for the two-spot model and the evolving single-spot model plus background, respectively. The best fits obtained with the two-spot model are statistically better than those obtained with the evolving single-spot model plus background as indicated by the significantly lower values of the χ2 in Table 5 (we list in Appendix B all the best fit parameters with their uncertainties). The difference is clearly visible in the case of CoRoT 223982407 and, to a lesser extent, for the other stars. The single-spot model can reasonably fit the minima of the light curves, but the shape of the overall light variation is better reproduced with two spots whose longitudes can change from one rotation to the other. This confirms the results obtained with the Levenberg-Marquardt and Nelder-Mead optimizations. The values of 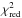 are significantly larger than the unity indicating that the variability of the light curves on timescales shorter than the mean rotation period is significantly larger than the standard errors of the individual data points as reported in Table 1. This can be ascribed to several small spots that are not included in our model or to flaring activity of the targets, e.g., in the case of 223988965 (cf. Fig. 3). A similar situation has been discussed by Lanza et al. (2014) in the case of Kepler-30.To quantify the short-term variability, we smoothed the observed light curves with a sliding box-car filter and computed the standard deviation of the residuals. For timescales from 0.1 to 0.15 of the mean rotation periods, which is much shorter than the phase range that can be accurately fitted with a two-spot model, we find a standard deviation in relative flux units of ~10-3 for CoRoT 223959652, 223988965, and 616919771; of 2.6 × 10-3 for CoRoT 616849446; and of 4.3 × 10-3 for CoRoT 223982407. Given that the reduced χ2 listed in Table 5 have been calculated considering the standard errors in Table 1, their values would become closer to unity, if we consider the standard deviations on the above time intervals.
are significantly larger than the unity indicating that the variability of the light curves on timescales shorter than the mean rotation period is significantly larger than the standard errors of the individual data points as reported in Table 1. This can be ascribed to several small spots that are not included in our model or to flaring activity of the targets, e.g., in the case of 223988965 (cf. Fig. 3). A similar situation has been discussed by Lanza et al. (2014) in the case of Kepler-30.To quantify the short-term variability, we smoothed the observed light curves with a sliding box-car filter and computed the standard deviation of the residuals. For timescales from 0.1 to 0.15 of the mean rotation periods, which is much shorter than the phase range that can be accurately fitted with a two-spot model, we find a standard deviation in relative flux units of ~10-3 for CoRoT 223959652, 223988965, and 616919771; of 2.6 × 10-3 for CoRoT 616849446; and of 4.3 × 10-3 for CoRoT 223982407. Given that the reduced χ2 listed in Table 5 have been calculated considering the standard errors in Table 1, their values would become closer to unity, if we consider the standard deviations on the above time intervals.
Reduced χ2 values obtained with the two-spot and the evolving single-spot models for our stars, respectively.
Gelman & Rubin 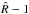 statistics measuring the convergence and mixing of the chains of the different parameters of our two-spot models.
statistics measuring the convergence and mixing of the chains of the different parameters of our two-spot models.
The mean values and the standard deviations of the spot rotation periods as derived with our MCMC approach for our five targets are listed in Table 7 together with the mean stellar inclination and relative differential rotation ΔP/P, where ΔP = | P1−P2 | and P = (P1 + P2) / 2, respectively. The relative differential rotation for CoRoT 223988965 and 616919771 is remarkably larger than for the other three targets, while their inclination is so low that the reliability of their spot rotation periods is questionable because the spot longitudes are ill-constrained in this case (see Sect. 6). Furthermore, in the case of CoRoT 223988965, the short-term variability of the light curve makes the fit not as good as in the other cases, while for CoRoT 616919771 the fitted segment covers one rotation period only. This reduces the relative longitudinal shift of the spots upon which our method is based and, when combined with a low inclination, makes our DR measurement uncertain. For these reasons, we do not consider the DR values obtained for those two stars significant. For CoRoT 616919771, we also considered a longer segment of 19.2525 days, but the best fit is not sufficiently good. Its minimum chi square is larger than that of the previously considered shorter segment by a factor of ~4.5, likely as a consequence of the intrinsic starspot evolution over a longer time interval. The decay of the autocorrelation function is faster for this star than for the other four targets, thus supporting the conclusion that an intrinsic spot evolution together with a low inclination mask any DR signal in its light curve (cf. Fig. 2, bottom panel).
In conclusion, we focus on the first three targets whose a posteriori rotation period distributions are plotted in Figs. 5–7. They have been obtained from MCMCs consisting of 60, 50, and 150 million points, and with an average acceptance fraction of 24.7, 26.7, and 23.7 percent, respectively. The distributions of P1 and P2 do not overlap, implying that the difference between the two rotation periods is statistically meaningful for all three stars. The correlation of P1 and P2 with the other model parameters is plotted in Fig. 8 for CoRoT 616849446, considering 15 000 representative points extracted from the middle of the MCMC; similar plots of the joint parameter distributions are also obtained for the other two stars. The rotation periods P1 and P2 appear to be strongly correlated with the initial spot longitudes λ1 and λ2, respectively, but the amplitude of the associated variation is not large enough to hamper the significance of the difference between the two periods. Other remarkable correlations are those between the inclination i and the colatitudes of the spots θ1,2 and between the colatitudes and their areas A1,2; they have been discussed in detail by Lanza et al. (2014).
Finally, we calculated best fits for the entire time series with the Levenberg-Marquardt algorithm by fixing the inclination i and the rotation periods P1 and P2 to their mean values as obtained from their a posteriori distributions. In Figs. 9and 10 we plot both best fits computed for the whole time interval (red solid lines) and for individual segments having the same length of the segment adopted for the MCMC analysis (green solid lines), respectively. When we fit the entire time series, the areas of the spots and their coordinates are held fixed for the whole interval, which results in a poor fit; see, for example, the top panel of Fig. 9 where the two spots are located on opposite hemispheres during the first part of the time series, but fall on the same hemisphere in the second part because they rotate with P1 ≠ P2, so their longitude separation changes vs. the time. The reproduction of the amplitude variations and times of light minima along this light curve are much better if, in addition to the relative shift of the spots produced by P1 ≠ P2, we allow for a variation of the spot areas and coordinates from one segment of the time series to the next (Fig. 10, solid green line). The same conclusion is found for the other two light curves, although the difference between the two best fits is less pronounced. Specifically, the variation of the total area of the spots Atot = A1 + A2 depends on the spot colatitudes and the variation of the amplitude of the light curve from one interval to the next. In particular, when spot colatitudes are fixed, Atot increases with increasing amplitude, e.g., in the case of CoRoT 223959652, otherwise, it stays approximately constant, e.g., in the case of the other two stars.
We conclude that some spot evolution is required to fit our time series because models that allow the spot parameters, in particular their areas, to change from one segment to the next provide significantly better fits of the light modulation.
In the light of the above results, it is interesting to consider the best fits obtained with the Levenberg-Marquardt and the Nelder-Mead algorithms for the entire light curves also with the evolving single-spot model plus background. Although we found that the model with two spots was better in the case of the intervals selected to search for differential rotation, in approximately fifty percent of the cases the evolving single-spot model gave a best fit of comparable quality. For each given interval, determining which model was better depended on the length of the interval and the details of the light modulation of the star. In Fig. 11, we consider the example of CoRoT 223959652 whose light curve is fitted in six individual intervals. The varying light amplitude is reproduced well by the evolving single-spot model along most of the modulation, except in the interval considered in our search for the differential rotation where the amplitude of the residuals with the two-spot model is smaller. The characteristic timescale for the evolution of the spot area [(1 /A1(t))(dA1/ dt)] -1 as derived from the model free parameters is of the order of 20 days, i.e., comparable with that shown by the variation of the light curve amplitude. However, in the case of other light curves, the timescales can be significantly shorter as the model tries to reproduce the small asymmetries of the light modulations by a faster evolution of the spot and the background.
 |
Fig. 2 Autocorrelation functions of our target light curves as labelled. The dotted lines indicate the ±σ interval (see text). |
 |
Fig. 3 Best fits of the considered segments of our light curves (open diamonds) obtained with the two-spot model (solid green line) and the Metropolis-Hasting algorithm as labelled. The increase in flux around 3.2 days in the light curve of CoRoT 223988965 is associated with an X-ray flare. |
 |
Fig. 4 Best fits of the considered segments of our light curves (open diamonds) obtained with the evolving single-spot model (solid green line) and the Metropolis-Hasting algorithm as labelled. The increase in flux around 3.2 days in the light curve of CoRoT 223988965 is associated with an X-ray flare. |
 |
Fig. 5 A posteriori marginal distributions of the rotation periods of the two spots as derived from the MCMC analysis for CoRoT 223959652. The solid line refers to the distribution of the rotation period of the first spot, the dashed line to that of the second. |
 |
Fig. 8 A posteriori joint distributions of pairs of model parameters in the two-spot model of CoroT 616849446 as derived from our MCMC analysis. Density isocontours as obtained with the CONTOUR procedure of IDL are superposed (red solid lines). |
 |
Fig. 9 Entire light curve best fits with the inclination and the rotation periods of the two spots held fixed at their mean values as derived from the a posteriori distributions computed with the MCMC. The black open circles indicate the observations, the red solid lines the best fits to the entire light curves (see text). |
 |
Fig. 10 As in Fig. 9, but plotting the best fits for the individual light curve segments (green lines) instead of the entire light curves (see text). |
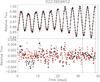 |
Fig. 11 Upper panel: entire light curve of CoRoT 223959652 (open diamonds) together with the best fits obtained by fitting individual intervals of the same length as that used to search for differential rotation (indicated by the dashed vertical lines) with the two-spot model (black solid line) and the evolving single-spot model (red solid line). Lower panel: residuals of the two best fit models; those of the two-spot model are plotted as black diamonds, while those of the evolving single-spot model as red triangles. |
6. Discussion and conclusions
We have compared best fits obtained with a two-spot model and an evolving single-spot plus background model in the case of TTSs whose light curves appear to be dominated by photospheric brightness inhomogeneities that vary slowly from one rotation to the next. We found time intervals during which the two-spot model with P1 ≠ P2 is statistically better than two rigidly rotating spots or the evolving single-spot model and focussed on those intervals to estimate the amplitude of stellar differential rotation. The Nelder-Mead algorithm improved the best fits obtained with the Levenberg-Marquardt method in a fraction of cases ranging from 3 to 10 percent (depending on the specific light curve) when we adopted a significance threshold of 95 percent, but it never changed the value of the ΔBIC to such an extent that the selection of the intervals with evidence of differential rotation was affected.
The final estimate of the differential rotation was obtained for those intervals by means of an MCMC approach that included a Metropolis-Hasting optimization of the best fit parameters. Therefore, we were able to further improve our solutions and reduce the χ2 in comparison to those found with the two deterministic methods considered in the previous stage of interval selection (cf. Appendix A for more details).
The MCMC approach was performed by considering the rotation periods of the spots as independent of their latitudes. As a matter of fact, we could have adopted a parametric law of the form P(θ) = Peq/ (1−kcos2θ), where P(θ) is the rotation period of a spot at colatitude θ, Peq the rotation period at the equator of the star, and k measures the amplitude of the differential rotation. We did experiments with this law and found that it makes the convergence of the MCMC chains worse, leading to non-convergent series after 150 × 106 and 300 × 106 steps for CoRoT 223959652 and 616849446, respectively. For CoRoT 223982407 we got a worse convergence after 150 × 106 steps with a maximum value of the Gelman-Rubin parameter 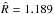 . The equatorial period Peq was found to be 2.731 ± 0.012 days, while the parameter k = −0.0950 ± 0.0095 indicated an amplitude of the differential rotation ~4.5 times larger than that estimated from the relative difference of the two periods when they were not tied to the spot colatitudes. This result is in line with that of Croll (2006) who adopted a similar model with the above parameterized differential rotation law in the case of ϵ Eri. The 68 percent mean likelihood credible interval in that case was 0.02 ≲ k ≲ 0.2 (cf. his Fig. 2, lower right panel), while the rotation periods of the individual spots were much better defined (cf. his Fig. 3). We conclude that the use of a parametric differential rotation law, although physically motivated, amplifies the dependences among model parameters, in particular between spot periods and colatitudes, thus making the convergence generally worse. Therefore, adopting spot periods as independent parameters is better also in view of the very limited information on spot latitude that can be extracted from wide-band light curves.
. The equatorial period Peq was found to be 2.731 ± 0.012 days, while the parameter k = −0.0950 ± 0.0095 indicated an amplitude of the differential rotation ~4.5 times larger than that estimated from the relative difference of the two periods when they were not tied to the spot colatitudes. This result is in line with that of Croll (2006) who adopted a similar model with the above parameterized differential rotation law in the case of ϵ Eri. The 68 percent mean likelihood credible interval in that case was 0.02 ≲ k ≲ 0.2 (cf. his Fig. 2, lower right panel), while the rotation periods of the individual spots were much better defined (cf. his Fig. 3). We conclude that the use of a parametric differential rotation law, although physically motivated, amplifies the dependences among model parameters, in particular between spot periods and colatitudes, thus making the convergence generally worse. Therefore, adopting spot periods as independent parameters is better also in view of the very limited information on spot latitude that can be extracted from wide-band light curves.
To further understand the results obtained with the MCMC method in the case of CoRoT 223988965 and 616919771, we consider the critical role played by the inclination of the stellar spin axis i in determining the accuracy of the spot longitudes as illustrated by Fig. 12. When i is low, a high-latitude spot is always in view and its light modulation has a shallow minimum that makes its longitude uncertain (top panel). On the other hand, when i is high, the spot is visible only for part of a rotation and the minimum of its light modulation is narrower and deeper making the determination of its longitude more accurate because the time of its transit across the central meridian of the stellar disc is better defined (lower panel). Since an accurate determination of the spot longitudes is at the base of the measurement of their rotation periods, the values of P1 and P2 are significantly more accurate in the case of the first three targets for which i ≥ 50°, while they are ill defined in the case of the other two targets for which i ≤ 15°. Therefore, we do not trust their spot rotation periods.
Differential rotation was measured through Doppler imaging techniques in four WTTs, i.e., V410 Tau (Skelly et al. 2010), LkCa 4 (Donati et al. 2014), V819 Tau, and V830 Tau (Donati et al. 2015) finding values in agreement with those derived from the long-term variations of their photometric periods (e.g., Grankin et al. 2008) and ranging from nearly solid-body rotation up to ΔΩ / Ω = 0.0055 ± 0.002, which is a factor of 3−10 times smaller than the present estimates for our three targets.
To explain this discrepancy, we suggest that an intrinsic starspot evolution is affecting our measurements. An illustrative case is displayed in Fig. 13, where we show how our simple two-spot model (M1 and M2) fits a more complex real spot configuration consisting of three spots (Sj, with j = 1,2,3). We consider the case where spot S1 stays fixed during the fitted time span, while the two close spots S2 & S3 evolve is such a way that the area of spot S2 decreases while that of spot S3 increases, and their total area AS2 + AS3 remains approximately constant. Our two-spot model can provide a very good fit of the light curve corresponding to this case, provided that the longitude of the model spot M2 is steadily increased during the time span of the observations to reproduce the change in the active region S2 & S3 whose photocentre is progressively shifted towards S3 by the intrinsic spot evolution. In other words, an intrinsic spot evolution can be fitted by a relative drift of the two model spots M1 and M2 yielding a difference in their rotation periods. Indeed, we have found evidence for intrinsic spot evolution, for example by comparing the different models in Figs. 9 and 10.
From a general point of view, our spot rotation periods can be combined to yield a spot evolutionary time tspot defined as 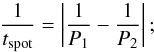 (3)tspotcan be regarded as a combination of the timescales of intrinsic spot evolution and of longitudinal shear associated with differential rotation. If there were no spot evolution, tspot would provide a measurement of the characteristic shear timescale associated with differential rotation, more precisely tspot ~ 1 / ΔΩ, where ΔΩ is the difference in the angular velocity of the two starspots. For our three targets, tspot ranges between ~20 and ~50 mean rotation periods. In the case of WTTs, the very small amplitude of the differential rotation makes the contribution of the intrinsic spot evolution to tspot significant in spite of their remarkably stable light curves, as indicated by the slow decay of their autocorrelation functions (cf. Fig. 2). We note that our evolving single-spot model gives a timescale of spot evolution between 1.8 and 6.6 rotation periods for the three stars with a meaningful period difference. Such short timescales are a consequence of using only one spot to fit light modulations that are not perfectly symmetric about their minima. In other words, to improve the best fit, the model adopts a fast evolution of the single spot to reproduce light minima which are not perfectly symmetric and which would be better fitted with two (or more) spots. On the other hand, introducing spot evolution directly into our two-spot model would imply an increase in the number of free parameters and in their correlations putting at risk the MCMC convergence and the possibility of finding a meaningful Bayesian model fitting our light curves.
(3)tspotcan be regarded as a combination of the timescales of intrinsic spot evolution and of longitudinal shear associated with differential rotation. If there were no spot evolution, tspot would provide a measurement of the characteristic shear timescale associated with differential rotation, more precisely tspot ~ 1 / ΔΩ, where ΔΩ is the difference in the angular velocity of the two starspots. For our three targets, tspot ranges between ~20 and ~50 mean rotation periods. In the case of WTTs, the very small amplitude of the differential rotation makes the contribution of the intrinsic spot evolution to tspot significant in spite of their remarkably stable light curves, as indicated by the slow decay of their autocorrelation functions (cf. Fig. 2). We note that our evolving single-spot model gives a timescale of spot evolution between 1.8 and 6.6 rotation periods for the three stars with a meaningful period difference. Such short timescales are a consequence of using only one spot to fit light modulations that are not perfectly symmetric about their minima. In other words, to improve the best fit, the model adopts a fast evolution of the single spot to reproduce light minima which are not perfectly symmetric and which would be better fitted with two (or more) spots. On the other hand, introducing spot evolution directly into our two-spot model would imply an increase in the number of free parameters and in their correlations putting at risk the MCMC convergence and the possibility of finding a meaningful Bayesian model fitting our light curves.
We conclude that our estimate of tspot primarily provides a measurement of the intrinsic evolutionary timescale of the spot pattern with the contribution of the differential rotation being secondary, given that the associated shear timescale 1 / ΔΩ is about 3−10 times longer according to the Doppler imaging measurements on similar stars. The evolution timescales of sunspots and starspots in different active stars have recently been discussed by Bradshaw & Hartigan (2014) who find that the mean spot lifetime is remarkably shorter in main-sequence stars than in the three TTVs analysed in this work (see also Hussain 2002).
 |
Fig. 12 Effect of the stellar spin axis inclination on the shape of the light modulation produced by a single spot. The case of a high-latitude spot in a low-inclination star is shown in the top panel and that of a high-inclination star in the bottom panel. The spot is plotted in red over the disc of the star, while the dotted circle indicates the equatorial plane of the star. |
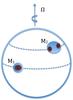 |
Fig. 13 Representation of a more complex starspot configuration (S1, S2, and S3) by means of only two spots M1 and M2 (see text). |
This allows the code to adjust the interval of visibility of a spot by varying its latitude, which is not possible when the inclination is 90° because the interval of visibility is half a rotation, independently of the latitude. In this way, the quality of the best fits with the DR and RR models is improved with respect to the i = 90° case.
Acknowledgments
The authors are grateful to an anonymous referee for a careful reading of the manuscript and several stimulating comments that helped to improve this work. A.F.L. and S.M. are grateful to Drs. J. Bouvier, A. Frasca, A. Klutsch, A. C. Lanzafame, and E. Moraux for interesting discussions. The authors acknowledge support through the PRIN-INAF 2012 funding scheme of the National Institute for Astrophysics (INAF) of the Italian Ministry of Education, University and Research. This work is based on data obtained by the CoRoT Space Experiment and made available through the CoRoT Archive at the IAS Operation Center whose availability is gratefully acknowledged. CoRoT is a space mission of the French Space Agency CNES in association with French CNRS Laboratories and participation of Austria, Belgium, Brazil, Germany, Spain, and the European Space Agency.
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V. 1998, A&A, 338, 97 [NASA ADS] [Google Scholar]
- Bradshaw, S. J., & Hartigan, P. 2014, ApJ, 795, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cody, A. M., Stauffer, J., Baglin, A., et al. 2014, AJ, 147, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B. 2006, PASP, 118, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E. 2008, Handbook of Star Forming Regions, Volume I, 4, 966 [Google Scholar]
- Dahm, S. E., & Simon, T. 2005, AJ, 129, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Hébrard, E., Hussain, G., et al. 2014, MNRAS, 444, 3220 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Hébrard, E., Hussain, G. A. J., et al. 2015, MNRAS, 453, 3706 [NASA ADS] [Google Scholar]
- Fröhlich, H.-E. 2007, Astron Nachr., 328, 1037 [Google Scholar]
- Fröhlich, H.-E., Küker, M., Hatzes, A. P., & Strassmeier, K. G. 2009, A&A, 506, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, H.-E., Frasca, A., Catanzaro, G., et al. 2012, A&A, 543, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grankin, K. N., Bouvier, J., Herbst, W., & Melnikov, S. Y. 2008, A&A, 479, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Soubiran, C., Netopil, M., & Paunzen, E. 2014, A&A, 561, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2010, A&A, 514, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hussain, G. A. J. 2002, Astron. Nachr., 323, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. R., Soderblom, D. R., Fischer, D., & Jones, B. F. 2000, ApJ, 533, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Lamm, M. H., Bailer-Jones, C. A. L., Mundt, R., Herbst, W., & Scholz, A. 2004, A&A, 417, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Catalano, S., Cutispoto, G., Pagano, I., & Rodono, M. 1998, A&A, 332, 541 [NASA ADS] [Google Scholar]
- Lanza, A. F., Piluso, N., Rodonò, M., Messina, S., & Cutispoto, G. 2006, A&A, 455, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Bonomo, A. S., & Rodonò, M. 2007, A&A, 464, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Das Chagas, M. L., & De Medeiros, J. R. 2014, A&A, 564, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makidon, R. B., Rebull, L. M., Strom, S. E., Adams, M. T., & Patten, B. M. 2004, AJ, 127, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- McGinnis, P. T., Alencar, S. H. P., Guimarães, M. M., et al. 2015, A&A, 577, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Baudin, F., Lanza, A. F., et al. 2009, A&A, 506, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++: the Art of Scientific Computing [Google Scholar]
- Rebull, L. M., Makidon, R. B., Strom, S. E., et al. 2002, AJ, 123, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Savanov, I. S., & Strassmeier, K. G. 2005, A&A, 444, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savanov, I. S., & Strassmeier, K. G. 2008, Astron. Nachr., 329, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Skelly, M. B., Donati, J.-F., Bouvier, J., et al. 2010, MNRAS, 403, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Stauffer, J., Cody, A. M., Baglin, A., et al. 2014, AJ, 147, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Sung, H., Bessell, M. S., & Lee, S.-W. 1997, AJ, 114, 2644 [NASA ADS] [CrossRef] [Google Scholar]
- Sung, H., Bessell, M. S., Chun, M.-Y., Karimov, R., & Ibrahimov, M. 2008, AJ, 135, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, J., Irwin, J., et al. 2015, A&A, 581, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Levenberg-Marquardt and Nelder-Mead vs. Metropolis-Hasting optimization
Comparison of the χ2 minima obtained with the Levenberg-Marquardt and Nelder-Mead methods with those obtained with the Metropolis-Hasting method.
The χ2 minima of our two-spot models found by means of the Metropolis-Hasting algorithm by running chains starting from the provisional minima found by the Levenberg-Marquardt or Nelder-Mead methods are always better than those provided by these deterministic methods. We run the Metropolis-Hasting optimization several times considering individual chains of 10−15 million points that restart from the minimum found by the previous chain until it is not possible to optimize the χ2 further. We set a criterion of acceptance for successive steps that discards all points where the χ2 increases by more than 1 percent with respect to the assumed minimum in the chain. Intuitively, it seems that this limits remarkably the ability of the algorithm to explore regions of the parameter space far away from its starting point, but we find that this is not the case because most of the time the chains move along the paths determined by the parameter correlations that connect distant points in the parameter space, while the adopted criterion reduces the time wasted in exploring vast domains where the χ2 is unacceptably large and the fit relatively poor (cf. Croll 2006; Lanza et al. 2014). The random parameter variations from one step to the next allow Metropolis-Hasting to explore extensive domains in the parameter space when tens of millions of steps are considered, as in the present case, thus finding the best minimum even if it is very far from the starting point.
To quantitatively illustrate the improvement provided by the Metropolis-Hasting method over the two other deterministic optimizations, we compare the reduced χ2 values and the parameters at the respective minimum points for our target stars in Table A.1. The minima found with the deterministic search methods are indicated with LN, while those
obtained with the Metropolis-Hasting method are indicated with MH in the second column. The other columns list the reduced χ2 and the other model parameters as in previous similar tables. We note that the inclination was fixed to 600 in the case of the LN optimization, while it was varied in the search with MH. The performance of the MH algorithm is always better than that of the two deterministic search methods with a significant variation of the parameters of the minima found with MH with respect to those found with LN. Only the longitudes of the spots and their rotation periods are similar, as expected for intervals that were selected to search for differential rotation.
Appendix B: Best fit parameters and their uncertainty ranges
We list in Tables B.1–B.3 the parameters corresponding to the two-spot model best fits of the individual light curve segments adopted to search for differential rotation for each of our targets. The uncertainty ranges of the parameters are computed from their marginalized a posteriori distributions as obtained with our MCMC approach and correspond to a probability of 68.2 percent. We note that the uncertainties of the rotation periods in Table 7 are the standard deviations of the distributions. They are always close to half the ranges listed here because the distributions of P1 and P2 are close to normal. However, this is not the case for all the other distributions; therefore, we adopted the above prescription to compute the uncertainty ranges. For each of the model parameters, we add further subscripts 1 and 2 to indicate the lower and upper limits of its uncertainty range. For example, a11 and a12 indicate the uncertainty range of the parameter a1 whose best fit value is listed for convenience between the two extrema.
Parameters of the best fits of the light curve segments obtained with the Metropolis-Hasting method and their uncertainty ranges (see text).
All Tables
Initial and final times of the segments considered for the MCMC analysis, together with the uniform prior intervals of the two-spot model parameters for each star.
Statistical comparison between the best fits obtained with the two-spot and the evolving single-spot models with the Levenberg-Marquardt and Nelder-Mead optimizations for the light curve segments selected to search for differential rotation.
Reduced χ2 values obtained with the two-spot and the evolving single-spot models for our stars, respectively.
Gelman & Rubin 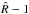 statistics measuring the convergence and mixing of the chains of the different parameters of our two-spot models.
statistics measuring the convergence and mixing of the chains of the different parameters of our two-spot models.
Comparison of the χ2 minima obtained with the Levenberg-Marquardt and Nelder-Mead methods with those obtained with the Metropolis-Hasting method.
Parameters of the best fits of the light curve segments obtained with the Metropolis-Hasting method and their uncertainty ranges (see text).
All Figures
 |
Fig. 1 Light curves of our five target stars displaying the flux normalized to the respective maximum value vs. the time as labelled. Errorbars are within the size of the symbols and indicate the standard error of each point that is an average of individual CoRoT measurements along two consecutive satellite orbits (open black circles). Filled orange circles indicate the segment of the light curve fitted to find the spot rotation periods (see Sect. 3). |
| In the text | |
 |
Fig. 2 Autocorrelation functions of our target light curves as labelled. The dotted lines indicate the ±σ interval (see text). |
| In the text | |
 |
Fig. 3 Best fits of the considered segments of our light curves (open diamonds) obtained with the two-spot model (solid green line) and the Metropolis-Hasting algorithm as labelled. The increase in flux around 3.2 days in the light curve of CoRoT 223988965 is associated with an X-ray flare. |
| In the text | |
 |
Fig. 4 Best fits of the considered segments of our light curves (open diamonds) obtained with the evolving single-spot model (solid green line) and the Metropolis-Hasting algorithm as labelled. The increase in flux around 3.2 days in the light curve of CoRoT 223988965 is associated with an X-ray flare. |
| In the text | |
 |
Fig. 5 A posteriori marginal distributions of the rotation periods of the two spots as derived from the MCMC analysis for CoRoT 223959652. The solid line refers to the distribution of the rotation period of the first spot, the dashed line to that of the second. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for CoRoT 616849446. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 for CoRoT 223982407. |
| In the text | |
 |
Fig. 8 A posteriori joint distributions of pairs of model parameters in the two-spot model of CoroT 616849446 as derived from our MCMC analysis. Density isocontours as obtained with the CONTOUR procedure of IDL are superposed (red solid lines). |
| In the text | |
 |
Fig. 9 Entire light curve best fits with the inclination and the rotation periods of the two spots held fixed at their mean values as derived from the a posteriori distributions computed with the MCMC. The black open circles indicate the observations, the red solid lines the best fits to the entire light curves (see text). |
| In the text | |
 |
Fig. 10 As in Fig. 9, but plotting the best fits for the individual light curve segments (green lines) instead of the entire light curves (see text). |
| In the text | |
 |
Fig. 11 Upper panel: entire light curve of CoRoT 223959652 (open diamonds) together with the best fits obtained by fitting individual intervals of the same length as that used to search for differential rotation (indicated by the dashed vertical lines) with the two-spot model (black solid line) and the evolving single-spot model (red solid line). Lower panel: residuals of the two best fit models; those of the two-spot model are plotted as black diamonds, while those of the evolving single-spot model as red triangles. |
| In the text | |
 |
Fig. 12 Effect of the stellar spin axis inclination on the shape of the light modulation produced by a single spot. The case of a high-latitude spot in a low-inclination star is shown in the top panel and that of a high-inclination star in the bottom panel. The spot is plotted in red over the disc of the star, while the dotted circle indicates the equatorial plane of the star. |
| In the text | |
 |
Fig. 13 Representation of a more complex starspot configuration (S1, S2, and S3) by means of only two spots M1 and M2 (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


